§ 7. Сила трения — ЗФТШ, МФТИ
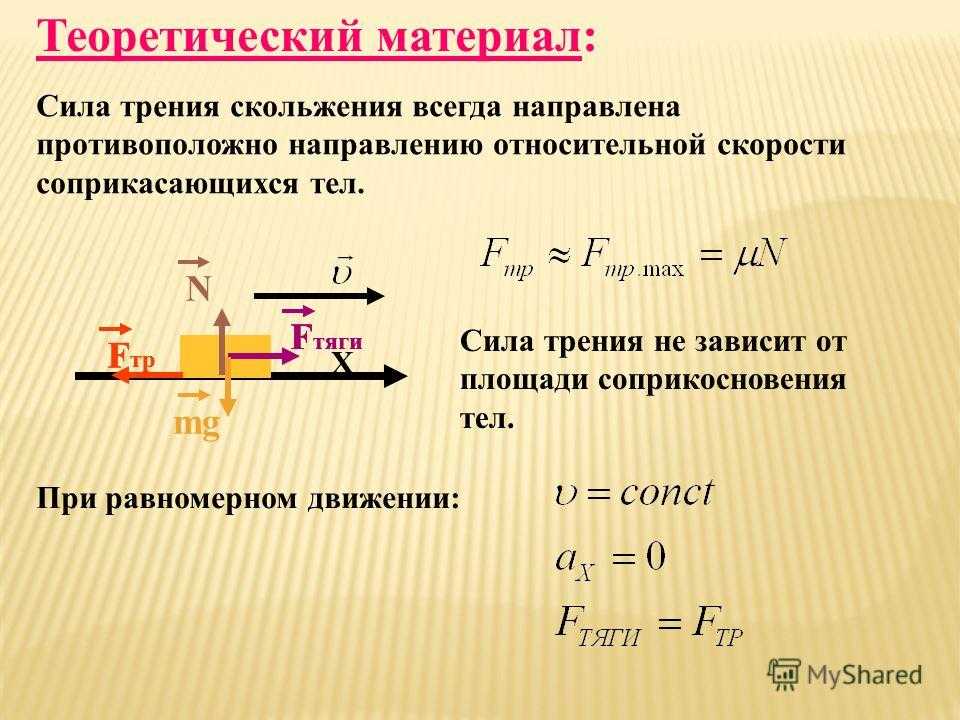
Сила сопротивления, действующая на тело, направлена противоположно относительному перемещению данного тела.
Сила трения возникает по двум причинам:
1) первая и основная причина заключается в том, что в местах соприкосновения молекулы веществ притягиваются друг к другу, и для преодоления их притяжения требуется совершить работу. Соприкасающиеся поверхности касаются друг друга лишь в очень небольших по площади местах. Их суммарная площадь составляет `0,01-:0,001` от общей (кажущейся) площади соприкосновения. При скольжении площадь реального соприкосновения не остается неизменной. Сила трения (скольжения) будет изменяться в процессе движения. Если тело, которое скользит, прижать сильнее к телу, по которому происходит скольжение, то вследствие деформации тел площадь пятен соприкосновения (и сила трения) увеличится пропорционально прижимающей силе.
2) вторая причина возникновения силы трения – это наличие шероховатостей (неровностей) поверхностей, и деформация их при движении одного тела по поверхности другого.
При относительном скольжении обе причины имеют место, потому характер взаимодействия имеет вид простого соотношения:
Величина коэффициента трения различна для разных комбинаций трущихся веществ даже при одинаковой их обработке (силы притяжения и упругие свойства зависят от рода вещества).
Если между трущимися поверхностями будет находится смазка, то сила притяжения изменится заметным образом (будут притягиваться другие молекулы, и сила трения скольжения частично заменится силой вязкого трения, которую мы рассмотрим ниже).
Если на тело, лежащее на горизонтальной поверхности, действует горизонтальная сила `vecF`, то движение будет вызвано этой силой только в том случае, когда она станет больше некоторого значения `(muN)`. До начала движения внешняя сила скомпенсирована силой трения покоя.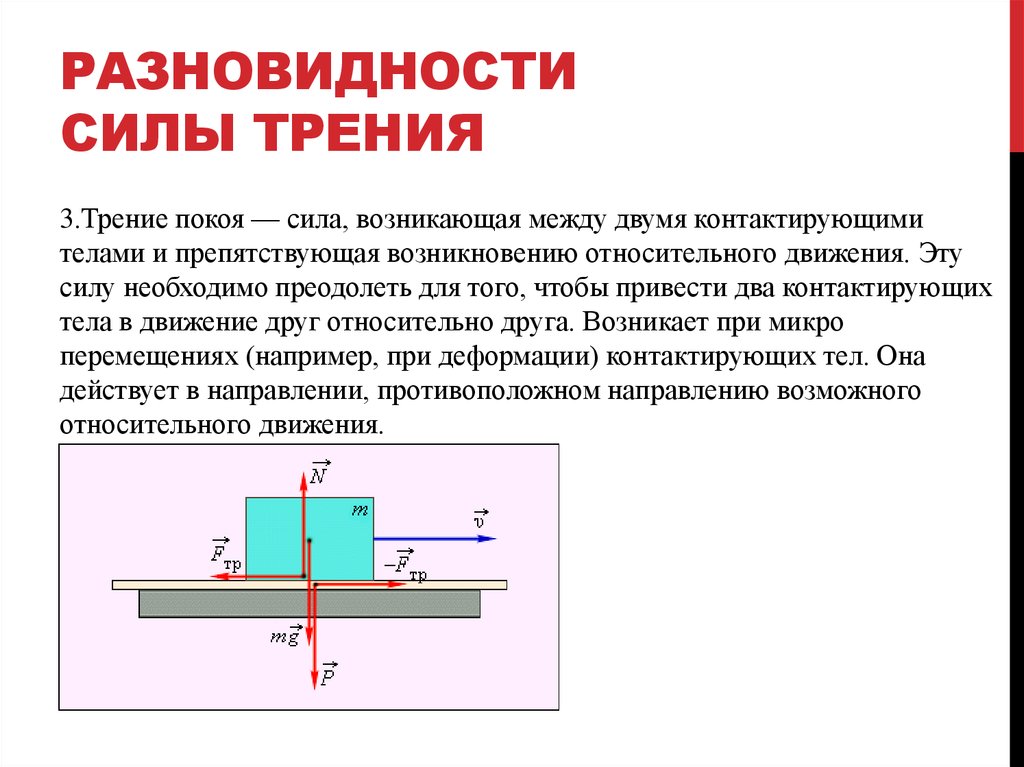 Сила трения покоя всегда равна внешней силе, параллельной поверхности, и возникает по причине притяжения между молекулами в областях пятен соприкосновения, и деформации шероховатостей.
Сила трения покоя всегда равна внешней силе, параллельной поверхности, и возникает по причине притяжения между молекулами в областях пятен соприкосновения, и деформации шероховатостей.
Сила трения покоя различна в разных участках поверхности, по которой будет происходить движение. Если тело долго лежит на поверхности, то вследствие вибраций (они всегда присутствуют на поверхности Земли) площадь пятен соприкосновения незначительно увеличится. Поэтому для начала движения придётся преодолеть немного большую силу трения, чем сила трения скольжения. Данное явление называется явлением застоя. С этим явлением мы сталкиваемся, например, передвигая мебель в комнате. (На рисунке 13 превосходство трения покоя над трением скольжения сильно преувеличено).
Силой трения покоя мы пользуемся для перемещения на лыжах или просто при ходьбе.
Рассмотренные виды силы трения относятся к сухому трению или внешнему. Но есть еще один вид силы трения – вязкое трение.
Но есть еще один вид силы трения – вязкое трение.
При движении тела в жидкости или газе происходят достаточно сложные процессы обмена молекулами между слоями обтекающей жидкости или газа. Эти процессы называют процессами переноса.
При небольших скоростях движения тела относительно газа или жидкости сила сопротивления будет определяться выражением:
Вывод о величине скорости (большая она или маленькая) можно сделать, определив безразмерный коэффициент, называемый
Если `Re<1700`, то движение газа (жидкости) вокруг тела ламинарное (слоистое), и скорости можно считать малыми.
Если `Re>1700`, то движение газа (жидкости) вокруг тела турбулентное (с завихрениями), и скорости можно считать большими.
В последнем случае на образование вихрей тратится большая часть кинетической энергии тела, а значит, сила трения становится большей, а зависимость перестаёт быть линейной.
Часто последнюю формулу можно видеть в виде:
Число Рейнольдса, выбранное равным `1700`, в действительности определяется конкретной задачей (условиями) и может принимать другие значения того же порядка.
Из-за такой сложной зависимости силы сопротивления от размеров, формы тела и его скорости рассчитать с необходимой точностью силу сопротивления невозможно.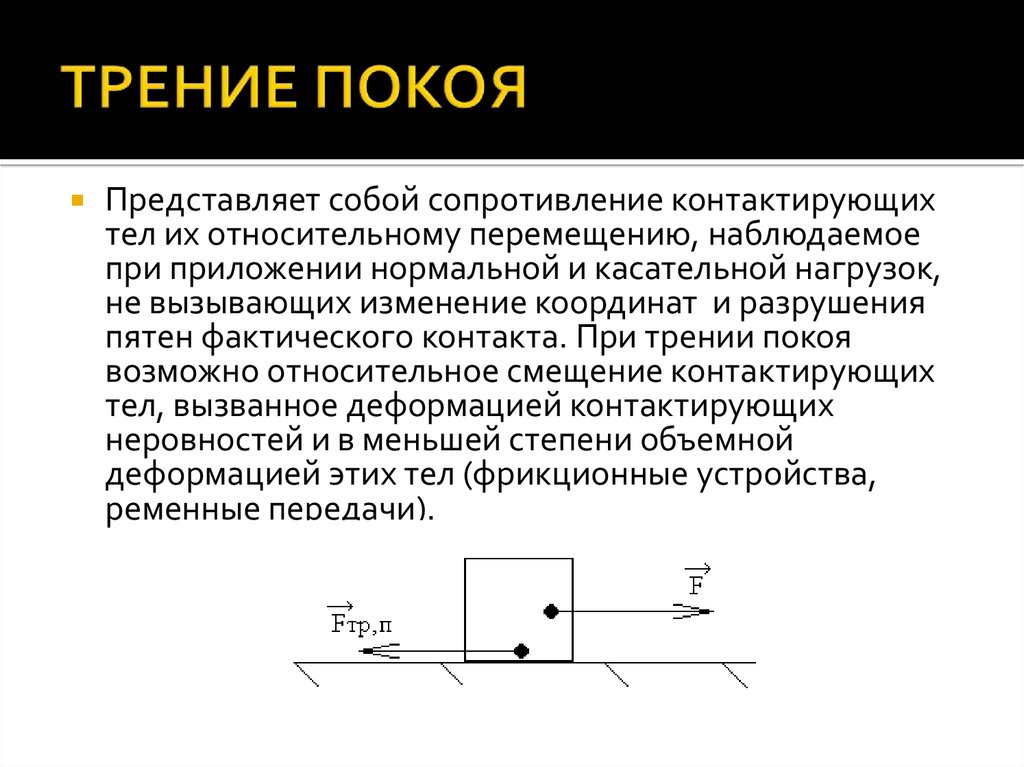 Потому приходится создавать макеты летательных аппаратов и измерять силу сопротивления опытным путём, продувая воздух в аэродинамических трубах.
Потому приходится создавать макеты летательных аппаратов и измерять силу сопротивления опытным путём, продувая воздух в аэродинамических трубах.
Сила трения – формула, определение и особенности
4.7
Средняя оценка: 4.7
Всего получено оценок: 176.
4.7
Средняя оценка: 4.7
Всего получено оценок: 176.
В задачах классической механики рассматриваются три основных вида сил, один из которых – силы трения. Они могут нести вред человеку, но и польза от них есть. Чтобы использовать их с толком, либо уменьшать ущерб, наносимый ими, необходимо понимать их природу и уметь находить.
Возникновение трения
Силы трения, причина которых кроется в том, что любая поверхность на микроуровне неровна, действуют на движущиеся и покоящиеся тела. Они могу возникать между твердыми телами, между твердыми и газообразными или жидкими.
Направление сил трения противоположно движению тела (силам, которые движут тело) и лежит в плоскости соприкосновения с поверхностью.
По тому, какая поверхность (со смазкой или без), силы трения делят на сухие и не сухие виды. К первым относят трение покоя (сцепления), скольжения и качения. К не сухим – жидкостное (вязкое).
С помощью подручных средств легко провести опыт. Возьмем любой предмет (например, книгу), положим его на стол и потянем. Если тянуть слабо, книга не сдвинется, ибо на нее действует сила трения покоя. Когда прикладываемся сила станет больше, сцепление также увеличится. Но у него есть максимальное (предельное) значение, и если тянущая сила превысит это значение, тело начнет движение, а покой сменится скольжением.
Если выстраивать строгую теорию трения скольжения, то придется учитывать ее зависимость от скорости. Но большая часть относительно простых задач решаются в приближении, когда силу трения скольжения считают равной максимальной силе сцепления.
На практике трение часто наносит ущерб. Например, оно вызывают истирание деталей. Эту проблему решают либо добавлением смазки, либо подшипниками. Во втором случае скольжение заменяется качением.
Эту проблему решают либо добавлением смазки, либо подшипниками. Во втором случае скольжение заменяется качением.
При движении в газообразной или жидкой среде возникает вязкое (жидкостное) трение, которое также называются сопротивлением среды. Оно слабее сухого трения, а главная его особенность в том, что оно зависит от скорости. В случае равенства последней нулю, сопротивление также обратится в нуль.
Расчетные формулы
Из экспериментов известно, что сила сцепления $\vec F_{тр} = – \vec F$, где F – внешняя сила. Максимальное сцепление пропорционально силе нормальной реакции опоры, умноженной на безразмерный коэффициент $\mu$, который определяется характером поверхности трения.
$$F_{тр}= \mu N$$ – (1) формула силы трения покоя
В случае, если тело находится на наклонной поверхности, проекция силы нормальной реакции опоры на ось Оу равна: $N = mgsin \varphi$. И тогда модуль сцепления равен: $F_{тр}= \mu mgsin \varphi$ – (2).
где $k_2$ – коэффициент жидкостного трения при больших скоростях.
Задачи
- Кирпич скатывается по деревянной поверхности, которая наклонена к горизонтали под углом 45 градусов. Масса кирпича – 200 грамм, коэффициент трения – 0,5. С каким ускорением он движется?
Решение первой задачи
Схема решения этой задачи та же, по которой решаются большинство задач на основное уравнение динамики.
Ось Оy проведем через вектор силы нормальной реакции опоры, Ось Ох – через вектор ускорения кирпича. Запишем второй закон Ньютона в векторной форме:
$$m \vec a = \vec F_{тр} + m \vec g + \vec N$$
И в проекциях на оси:
Ox: $ma = mgcos \varphi – \mu N$
Oy: $N=mgsin \varphi$
Учитывая уравнение на оси Оу запишем:
$$ma = mgcos \varphi – \mu mgcos \varphi = mg(cos \varphi – \mu sin \varphi)$$
$$a = g(cos \varphi – \mu sin \varphi) = 3,5 м/c$$
- Человек массой 100 кг совершил прыжок с парашютом.
 2$$
2$$Тогда:
$$v_1 = \sqrt{mg \over k_1} = 14,14 м/с$$
$$v_2 = \sqrt{mg \over k_2} = 1,38 м/c$$
Что мы узнали?
В ходе урока выяснили, как возникают силы трения, установили закон действия этих сил. После чего разделили силы трения на два вида – силы сухого трения и силы жидкостного трения, а также рассмотрели формулы, по которым производится их расчет. В закрепление урока разобрали две несложные задачи.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 176.
А какая ваша оценка?
Силы трения | Физика
Из предыдущих параграфов вы знаете, что на любое тело со стороны Земли действует сила тяжести Fт, направленная вертикально вниз. Поэтому на брусок, лежащий неподвижно на горизонтальной крышке стола, будет действовать сила реакции стола N = -Fт, направленная вертикально вверх.
 Модуль этой силы равен m · g.
Модуль этой силы равен m · g.А как заставить этот брусок двигаться вдоль крышки стола? Для этого потребуется приложить к бруску определенное усилие. Чтобы измерить величину этого усилия, воспользуемся динамометром. Расположим динамометр параллельно крышке стола так, чтобы ось его пружины была направлена горизонтально, как показано на рис. 114. Немного растянув пружину, мы обнаружим, что брусок, несмотря на действие силы, остается в покое. Следовательно, появилась сила, которая компенсирует направленную горизонтально силу упругости пружины. Эта сила действует на брусок со стороны крышки стола в горизонтальном направлении. Ее называют силой сухого трения покоя Fтр. Подчеркнем еще раз, что эта сила компенсирует силу F упругости пружины, пытающуюся сдвинуть брусок вдоль стола.
Продолжая растягивать пружину динамометра, мы обнаружим, что брусок начнет скользить по крышке только тогда, когда модуль силы упругости пружины, увеличиваясь, превысит некоторое значение Fmax.
 Опыт показывает, что для поддержания неизменной скорости скольжения бруска по горизонтальной крышке стола необходимо продолжать действовать на брусок в направлении его движения определенной силой. Следовательно, и в этом случае на брусок со стороны стола в горизонтальном направлении действует сила, компенсирующая силу упругости. Эту силу называют силой сухого трения скольжения. Так как сумма силы сухого трения скольжения и силы упругости пружины равна нулю, брусок движется по поверхности стола равномерно. О том, как зависит сила сухого трения скольжения от скорости движения тела по опоре, мы поговорим в старших классах. Пока же будем считать, что
Опыт показывает, что для поддержания неизменной скорости скольжения бруска по горизонтальной крышке стола необходимо продолжать действовать на брусок в направлении его движения определенной силой. Следовательно, и в этом случае на брусок со стороны стола в горизонтальном направлении действует сила, компенсирующая силу упругости. Эту силу называют силой сухого трения скольжения. Так как сумма силы сухого трения скольжения и силы упругости пружины равна нулю, брусок движется по поверхности стола равномерно. О том, как зависит сила сухого трения скольжения от скорости движения тела по опоре, мы поговорим в старших классах. Пока же будем считать, чтомодуль силы сухого трения скольжения равен максимальному модулю Fmax силы сухого трения покоя.
Чтобы выяснить, от чего зависит значение Fmax, поставим на наш брусок гирю, масса которой равна массе бруска (рис. 115). Теперь на брусок, кроме силы тяжести m · g, действует вес гири P, равный m · g. Эти силы направлены вертикально вниз.
 Поэтому модуль силы реакции стола N2 должен возрасти в два раза по сравнению с предыдущим случаем и стать равным 2m · g (сравните рис. 114 и 115).
Поэтому модуль силы реакции стола N2 должен возрасти в два раза по сравнению с предыдущим случаем и стать равным 2m · g (сравните рис. 114 и 115).Измерим максимальное значение силы сухого трения покоя Fmax2. Оказывается, что это значение также увеличится в два раза: Fmax2 = 2Fmax. Заменим гирю новой, имеющей массу в два раза больше. Ясно, что теперь модуль силы реакции опоры N3 будет равен Зm · g. Опыт показывает, что в этом случае Fmax3 = ЗFmax. Продолжая увеличивать массу гири, можно прийти к следующему выводу: при увеличении модуля силы реакции опоры в n раз максимальное значение Fmax силы сухого трения покоя также увеличивается в n раз. Таким образом, модуль максимальной силы сухого трения покоя Fmax прямо пропорционален модулю силы реакции опоры N.
Отношение максимального модуля силы сухого трения покоя к модулю силы реакции опоры называют коэффициентом трения.
Коэффициент трения обозначают греческой буквой μ (читается «мю»).
 Тогда μ = Fmax / N.
Тогда μ = Fmax / N.Эта закономерность была установлена французскими учеными Г. Амонтоном (1663-1705) и Ш. Кулоном (1736-1806). Поэтому соотношение Fmax = μ · N часто называют законом Амонтона-Кулона.
Коэффициент трения зависит от материалов соприкасающихся тел. Опыт показывает, что этот коэффициент зависит и от качества обработки соприкасающихся поверхностей. Примерные значения коэффициентов трения для различных материалов приведены в таблице 3.
При решении некоторых задач силами сухого трения можно пренебречь (например, при скольжении конькобежца по льду). В этих случаях говорят, что по крайней мере одна из соприкасающихся поверхностей является гладкой. В дальнейшем мы будем пользоваться этим термином.
Рассмотрим еще один вид силы трения. Если тело не скользит по поверхности другого тела, а подобно шарику или цилиндру катится, то препятствующую его движению силу трения называют силой трения качения. Опыт показывает, что силы трения качения значительно меньше сил сухого трения скольжения.
 Этот факт был обнаружен еще нашими предками. Для перемещения тяжелых грузов они подкладывали под них катки (рис. 116). По этой же причине на транспорте используют колеса. Опыт показывает, что силы трения качения уменьшается с увеличением твердости катящегося тела и поверхности, по которой оно катится. Поэтому в подшипниках (рис. 117) используют шарики (1) или ролики (2), изготовленные из твердых сплавов. Подшипники получили широкое распространение в технике. Они позволяют заменить скольжение на качение и тем самым уменьшить силы трения.
Этот факт был обнаружен еще нашими предками. Для перемещения тяжелых грузов они подкладывали под них катки (рис. 116). По этой же причине на транспорте используют колеса. Опыт показывает, что силы трения качения уменьшается с увеличением твердости катящегося тела и поверхности, по которой оно катится. Поэтому в подшипниках (рис. 117) используют шарики (1) или ролики (2), изготовленные из твердых сплавов. Подшипники получили широкое распространение в технике. Они позволяют заменить скольжение на качение и тем самым уменьшить силы трения.Во многих случаях трение играет в технике отрицательную роль. Из-за трения изнашиваются и разрушаются движущиеся части машин, уменьшается их эффективность. Часто для уменьшения сил трения между поверхностями трущихся твердых тел вводят жидкую смазку. При наличии такой смазки силы трения называют силами вязкого трения. Особенность этих сил состоит в том, что при отсутствии движения тел относительно находящейся между ними жидкости силы вязкого трения оказываются равными нулю.
 Однако при возникновении такого движения силы вязкого трения увеличиваются по мере роста скорости. Этим объясняется, почему находящуюся на плаву многотонную баржу может стронуть с места один человек. Эту баржу может заставить двигаться и легкий ветерок.
Однако при возникновении такого движения силы вязкого трения увеличиваются по мере роста скорости. Этим объясняется, почему находящуюся на плаву многотонную баржу может стронуть с места один человек. Эту баржу может заставить двигаться и легкий ветерок.Вместе с тем силы трения могут играть и положительную роль. Благодаря трению мы имеем возможность передвигаться по земле. Ведь без трения подошвы обуви и ведущие колеса автомобилей проскальзывали бы, не давая возможности тронуться с места. Двигаясь по гладкой поверхности, мы не смогли бы затормозить. Поэтому для увеличения силы трения скользкие дороги (в гололед) посыпают песком или каменной крошкой. В этом случае увеличивается коэффициент трения. Для увеличения силы трения также можно увеличить и силу реакции опоры N. С этой целью, например, искусственно увеличивают массу тягачей, загружая их балластом.
Итоги
При движении или попытке вызвать движение твердого тела по поверхности другого твердого тела между ними возникают силы сухого трения.

До возникновения относительного движения соприкасающихся тел силу трения между ними называют силой сухого трения покоя. Если же тела движутся друг относительно друга, то силу трения называют силой сухого трения скольжения.
Сила сухого трения покоя действует на данное тело противоположно направлению, в котором бы двигалось тело при отсутствии трения.
Сила сухого трения скольжения и сила вязкого трения направлены противоположно скорости движения данного тела по опоре.
Отношение максимального модуля силы сухого трения покоя к модулю силы реакции опоры называют коэффициентом трения.
μ = Fmax / N
Модуль силы сухого трения покоя не превышает произведения коэффициента трения μ на модуль силы реакции опоры N.
Модуль силы сухого трения скольжения обычно считают равным модулю максимальной силы сухого трения покоя.
Вопросы
- Какие виды сил трения вы знаете? Куда направлены эти силы и когда они возникают?
- Какие законы физики используются при проведении измерения силы сухого трения скольжения с помощью динамометра?
- Какие силы со стороны горизонтальной дороги действуют на человека, начинающего бег? Почему бегуны используют обувь с шипами?
- Приведите примеры, показывающие, что трение может быть: а) полезным; б) вредным.
 Какие способы уменьшения (увеличения) сил трения вы знаете?
Какие способы уменьшения (увеличения) сил трения вы знаете?
Упражнения
- С какой по модулю силой мальчик должен толкать ящик массой m, чтобы двигать его равномерно по горизонтальному полу? Коэффициент трения ящика о пол равен μ.
- С какой минимальной силой надо тянуть по льду стоящего на коньках ученика 7 класса массой 60 кг, чтобы сдвинуть его с места? Указание: для выполнения этого и последующих упражнений используйте данные, приведенные в таблице 3. Модуль ускорения свободного падения считайте равным g = 10 м/с2.
- Проведите эксперимент. Найдите на улице горизонтальную ледяную поверхность. Сравните силы, которые потребуются для того, чтобы, медленно увеличивая силу натяжения веревки санок, сдвинуть с места стоящие на этой поверхности: а) пустые санки; б) санки с одним семиклассником; в) санки с двумя такими же семиклассниками. Опишите результаты эксперимента и сформулируйте вывод.
- Ящик стоит на горизонтальном деревянном полу.
 Для того чтобы сдвинуть его с места, потребовалось приложить к нему в горизонтальном направлении силу, модуль которой равен 200 Н. Определите массу ящика, если коэффициент трения ящика о пол равен 0,5.
Для того чтобы сдвинуть его с места, потребовалось приложить к нему в горизонтальном направлении силу, модуль которой равен 200 Н. Определите массу ящика, если коэффициент трения ящика о пол равен 0,5. - Найдите максимальное значение модуля силы трения, действующей на кирпич массой m = 2 кг в тот момент, когда его кладут на движущуюся ленту транспортера.
- Какие силы действуют на автомобиль, начинающий движение? Все колеса автомобиля ведущие. Определите модуль максимального ускорения a, который может иметь этот автомобиль на горизонтальной бетонной дороге.
- Во сколько раз отличаются минимальные длины тормозного пути автомобиля при торможении на сухом асфальте и гладком льду? Считайте, что дорога в обоих случаях горизонтальная, а скорость автомобиля перед началом торможения в обоих случаях одинаковая.
«Сила трения»
Цель урока: познакомить обучающихся с силой трения.
Задачи:
Образовательная: ввести понятие силы трения
Развивающая: продолжить развивать у учащихся умение сравнивать, рассуждать, логически мыслить, выбирать главное
Воспитательная: воспитание у обучающихся доброжелательности друг к другу, уважения к мнению других, умения слушать.

Оборудование у учителя: штатив, линейка, машинка, кусок материи и меха, динамометр, деревянный брусок, набор грузов, проектор для показа презентации.
Оборудование у учащихся: динамометр, деревянный брусок, два груза, два карандаша (палочки), 5-6 картинок с различными видами трения, лист с практическими работами.
Ход урока
Вступительная беседа:
На протяжении нескольких последних уроков мы с вами изучали физическую величину, которую называют силой.
Вопросы учащимся:
1) Что такое сила? Что вы о ней знаете?
2) Какие виды сил вы уже изучили?
Сегодня на уроке мы познакомимся с ещё одной силой, и сейчас я вас приглашаю вместе с Вини пухом и Пятачком совершить небольшое путешествие.
Путешествие Пятачка и Вини-пуха.

Однажды Вини-пух и Пятачок отправились в гости к сове. Путь был длинным, с преградами, но они шли, разговаривая, и даже не замечая усталости.
Вдруг Вини-пух спросил: “А почему мы движемся вперёд?”
– Ноги сами переступают так, – ответил Пятачок.
– Верно. А почему вперёд, а не назад?
– Не знаю, может так быстрее?
Казалось глупые вопросы, глупые ответы, но им было весело шагать по ровной асфальтовой дорожке. Ничего не мешало, идти было легко, хотя и сыро. Вдруг Вини-пух потерял равновесие, его ноги заскользили, он громко закричал: “Спасите, помогите”. Оказывается, асфальт закончился, и под ногами была мокрая глина. Вдруг поднялся сильный ветер, залетали снежинки, стало очень холодно, земля покрылась снегом, стало скользко, так как на лужах образовался лёд, идти стало ещё сложнее. Чтобы не упасть, путешественники держались друг за друга и шли мелкими смешными шажками.
 Им осталось пройти совсем немного. Домик
совы был уже виден.
Им осталось пройти совсем немного. Домик
совы был уже виден.Ясно, что для нормальной ходьбы надо, прежде всего, чтобы ноги твёрдо опирались о дорогу и не скользили. Но почему они вдруг начинают скользить? Чем мокрая глина уступает асфальту, а лёд – и того хуже? Чтобы разобраться в этих не таких уж простых вопросах, давайте посмотрим несколько опытов.
Примечание: на доску предварительно выписать вопросы, поставленные в начале урока
Почему мы движемся? Почему по асфальту идти легко? Чем лёд и глина уступают асфальту?
Опыт 1: по наклонной плоскости съезжает машинка и доезжает до края стола
Опыт 2: на стол расстелить кусок материи, теперь машинка останавливается, не доезжая до края стола.
Опыт 3: на стол расстилает мех или поролон, машинка, заехав на них, сразу же останавливается.
Вопросы:
Что является причиной изменения скорости тела (машинки)?
Какая сила заставила остановиться машинку во всех трёх случаях и почему машинка проехала разные расстояния?
Далее объявляется тема урока “Сила трения” (учащиеся записывают в тетрадь тему урока) – слайд 1
Объяснение нового материала
Вопроc: От какого слова произошло слово “трение”?
Трение возникает при соприкосновении одного тела с другим и препятствующее их относительному движению (слово “трение” произошло от слова тереться).

Определение: сила трения – это сила, которая возникает при движении одного тела по поверхности другого тела и направленная против их относительного движения (записывают в тетрадь). Слайд 2.
Чтобы выяснить причины трения, учащиеся вспоминают опыты, показанные в начале урока.
Вопрос: Почему машинка при движении по меху сразу остановилась? (мех ворсистый, ворс зацепляется за колёса машинки и останавливает её).
Даже стол на первый взгляд ровный и гладкий имеет много неровностей (открывают учебник стр. 71, рис 79а).
1 причина трения: шероховатость соприкасающихся тел.
Вопрос: Как изменится сила трения, если неровности уменьшить, например тело отшлифовать очень хорошо и отполировать?
Практика показывает, что по мере уменьшения неровностей сила трения будет сначала уменьшаться, но когда поверхности будут очень хорошо отполированы, то сила трения снова увеличивается.
 Почему? (вспомните строение
вещества)
Почему? (вспомните строение
вещества)2 причина трения: взаимное притяжение молекул соприкасающихся тел. Слайд 3
Рассмотрим виды трения. Слайд 4.
Если тело скользит по поверхности другого тела, то возникает трение скольжения (примеры).
Если тело катится по поверхности другого тела, то возникает трение качения (примеры).
Если тело лежит на поверхности другого тела, то возникает трение покоя (примеры).
(записывают виды трения в тетрадь, оформляют в виде блок-схемы). Слайд 5
Виды трения: 1 трение скольжения
2 трение качения
3 трение покоя
Вопрос: на картинке найдите различные виды трения и укажите, между какими телами они возникают. Слайд 6
А теперь выясним, как измерить силу трения?
Вопрос: С помощью какого прибора измеряют силы? (с помощью динамометра).

Любой измерительный прибор имеет шкалу, поэтому давайте вспомним, как находится цена деления прибора (находят цену деления динамометра).
Чтобы измерить силу трения скольжения деревянного бруска по столу, надо прикрепить к нему динамометр, затем равномерно двигать брусок по столу, держа динамометр горизонтально.
Вопрос: Какую силу покажет динамометр? (силу упругости, так как пружина деформируется).
Но так как брусок движется равномерно, то на него действуют сразу две силы, направленные горизонтально, одна – это сила упругости пружины (она же является силой тяги), направленная в сторону движения, а другая – сила трения, направленная против движения. Так как брусок движется равномерно, то это значит, что равнодействующая этих двух сил равна нулю, а значит, эти силы равны по модулю и противоположны по направлению. Динамометр показывает силу упругости, равную по модулю силе трения (учащиеся измеряют силу трения скольжения).

Практическая часть
(на столах у учащихся лежит лист с ходом работы и таблицами для заполнения).Практическая работа № 1.
Цель выяснить, как зависит сила трения от силы, прижимающей тело к поверхности.
Оборудование: деревянный брусок, динамометр, два груза
Ход работы
- Прикрепить к бруску динамометр и равномерно тянуть его по поверхности стола (показания динамометра записать в таблицу – в графу “сила трения”)
- Измерить вес бруска с помощью динамометра (записать в таблицу)
- Положить на брусок груз и снова измерить силу трения (показания записать в таблицу – опыт № 2)
- Положить на брусок два груза и снова измерить
силу трения (записать в таблицу – опыт № 3)
Определить и записать в таблицу вес бруска и
грузов.

Примечание: в целях экономии времени вес груза можно считать 1Н, а бруска – 0,8 Н (можно проверить с помощью динамометра)
№ опыта Вес тела, Н Сила трения, Н 1 (брусок без груза) 0,8 2 (брусок с грузом) 1,8 3 (брусок с двумя грузами) 2,8 Вывод: чем больше сила, прижимающая тело к поверхности, тем больше сила трения. Слайд 7
Практическая работа № 2
Цель: сравнить силу трения скольжения, качения и покоя при одинаковых нагрузках (опыт лучше делать с одним грузом)
Оборудование: брусок, динамометр, груз, два карандаша (не гранёных)
Ход работы
- Положить на брусок груз, прикрепить к бруску
динамометр и равномерно начать тянуть его.
 Заметить показания динамометра в тот момент,
когда брусок сдвинется с места – это и будет сила
трения покоя (показания записать в таблицу)
Заметить показания динамометра в тот момент,
когда брусок сдвинется с места – это и будет сила
трения покоя (показания записать в таблицу) - Брусок с грузом с помощью динамометра равномерно перемещать по поверхности стола и измерить силу трения скольжения (записать в таблицу)
- Положить под брусок два карандаша и измерить силу трения качения (записать в таблицу)
- познакомить с таблицей, которую учащимся надо будет заполнить на следующем уроке, чтобы они знали, на что надо обратить внимание при подготовке домашнего задания.
- 1 Учебники
- 2 Механика
- 2.
 1 Кинематика
1 Кинематика - 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 2.
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.
 3 Магнетизм
3 Магнетизм - 4.4 Электромагнитные колебания и волны
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика.
 Квантовая теория
Квантовая теория - 6.2 Ядерная физика
- 6.1 Атомная физика.
- 7 Общие темы
- 8 Новые страницы
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
- Неоднородность поверхностей тел.
- Электромагнитная составляющая предметов. Такие силы присутствуют между предметами.
- Обсудите общие характеристики трения.
- Опишите различные виды трения.
- Рассчитайте величину статического и кинетического трения.
- Трение представляет собой контактную силу между системами, которая противодействует движению или попытке движения между ними. Простое трение пропорционально нормальной силе N сближение систем. (Нормальная сила всегда перпендикулярна поверхности контакта между системами.) Трение зависит от обоих задействованных материалов. Величина трения покоя f s между системами, неподвижными относительно друг друга, определяется выражением
[латекс]\boldsymbol{f_{\textbf{s}}\leq\mu\textbf{N},}[/латекс]
, где μ s — коэффициент статического трения, зависящий от обоих материалов.

- Кинетическая сила трения f k между системами, движущимися относительно друг друга, определяется выражением
[латекс]\boldsymbol{f_{\textbf{k}}=\mu_{\textbf{k}}\textbf{N},}[/latex]
, где μ k — коэффициент кинетического трения, который также зависит от обоих материалов.
- трение
- сила, препятствующая относительному движению или попыткам движения между контактирующими системами
- кинетическое трение
- сила, противодействующая движению двух систем, находящихся в контакте и движущихся относительно друг друга
- статическое трение
- сила, противодействующая движению двух систем, находящихся в контакте и не движущихся относительно друг друга
- величина статического трения
- f с ≤ μ с N , где μ s — коэффициент трения покоя и Н — величина нормальной силы
- величина кинетического трения
- f k = μ k N , где μ k кинетический коэффициент трения
- Сила трения в значительной степени зависит от текстуры поверхности и величины силы, которая приводит их в движение вместе.
- На силу трения влияют положение и угол объекта.
- Если мы поместим предмет плашмя на другой предмет, то сила трения будет равна массе предмета.

- Если мы прижимаем предмет к поверхности другого предмета, то увеличивается величина силы трения, которая становится больше, чем вес предмета.
- Статическое трение
- Сухое трение
- Трение качения
- Кинетическое трение
- Сухое трение
- Жидкостное трение
- Баскетбольный мяч, катящийся по корту, через некоторое время останавливается.
- Шина или колеса скейтборда, катящиеся по дороге, также являются примерами трения качения.
- На движение транспортных средств влияют такие факторы, как размер, форма и вес. Предположим, что тяжело нагруженный двадцатиколесный грузовик будет иметь большее трение качения, чем автомобиль TATA Nano.

- Использование малярных валиков при покраске стен.
- Смазка дверных петель обеспечивает плавное функционирование двери и предотвращает скрип при открывании и закрывании.
- Когда мяч падает в ведро с водой, вода выплескивается из ведра из-за плавучести жидкости.
- По замерзшему озеру тянется огромная ледяная глыба массой 300 кг. Между двумя ледяными поверхностями существует небольшая сила трения, равная µk = 0,05. Вычислите силу трения, действующую на ледяную глыбу.
- Мужчина толкает лодку на берег, чтобы набрать воды. Коэффициент трения между грязью и лодкой равен μ = 0,400. Вычислите величину силы трения, действующей на лодку, если масса лодки равна 40 кг.
Холмберг К. и Эрдемир А.
 Влияние трибологии на глобальное потребление энергии, затраты и выбросы. Трение 5 , 263–284 (2017).
Влияние трибологии на глобальное потребление энергии, затраты и выбросы. Трение 5 , 263–284 (2017).КАС Статья Google ученый
Хатчингс, И. М. Леонардо да Винчи, исследования трения. Wear 360–361 , 51–66 (2016).
Артикул Google ученый
Браун, О. М., Стенвик, Б., Вархадпанде, А. и Перссон, Б. Н. Дж. О зависимости трения от нагрузки: теория и эксперимент. EPL 113 , 56002 (2016).
ОБЪЯВЛЕНИЕ Статья Google ученый
Лин, Б., Вей, Дж., Суй, Т. и Ван, Х. Влияние обработки поверхности на трибологические характеристики C/SiC при сухом трении. науч. 10 , 5990 (2020).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
«>Дитрих, Дж. Х. и Килгор, Б. Д. Непосредственное наблюдение фрикционных контактов: новое понимание свойств, зависящих от состояния. Чистый Appl. Геофиз. 143 , 283–302 (1994).
ОБЪЯВЛЕНИЕ Статья Google ученый
Боуден Ф. П. и Табор Д. Площадь контакта между стационарными и движущимися поверхностями. Проц. Р. Соц. Математика. физ. англ. науч. 169 , 391–413 (1939).
ОБЪЯВЛЕНИЕ Google ученый
Арчард Дж. Ф. Упругая деформация и закон трения.
 Проц. Р. Соц. Математика. физ. англ. науч. 243 , 190–205 (1957).
Проц. Р. Соц. Математика. физ. англ. науч. 243 , 190–205 (1957).ОБЪЯВЛЕНИЕ Google ученый
Гринвуд, Дж. А. и Уильямсон, Дж. Б. П. Контакт номинально плоских поверхностей. Проц. Р. Соц. Математика. физ. англ. науч. 295 , 300–319 (1966).
ОБЪЯВЛЕНИЕ КАС Google ученый
Буш А. В., Гибсон Р. Д. и Томас Т. Р. Упругий контакт шероховатой поверхности. Wear 35 , 87–111 (1975).
Артикул Google ученый
Маджумдар А. и Бхушан Б. Фрактальная модель упругопластического контакта между шероховатыми поверхностями. Дж. Трибол. Транс. ASME 113 , 1–11 (1991).
Артикул Google ученый
Чаварелла, М.
 , Демелио, Г., Барбер, Дж. Р. и Джанг, Ю. Х. Линейный упругий контакт профиля Вейерштрасса. Проц. R Соц. Математика. физ. англ. науч. 456 , 387–405 (2000).
, Демелио, Г., Барбер, Дж. Р. и Джанг, Ю. Х. Линейный упругий контакт профиля Вейерштрасса. Проц. R Соц. Математика. физ. англ. науч. 456 , 387–405 (2000).ОБЪЯВЛЕНИЕ MathSciNet Статья Google ученый
Джексон, Р. Л. и Стриатор, Дж. Л. Многомасштабная модель контакта между шероховатыми поверхностями. Wear 261 , 1337–1347 (2006 г.).
КАС Статья Google ученый
Перссон, Б. Н. Дж. Теория трения резины и контактная механика. J. Chem. физ. 115 , 3840–3861 (2001).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Перссон, Б. Н. Дж. Упругопластический контакт между случайно шероховатыми поверхностями. Физ. Преподобный Летт. 87 , 116101 (2001).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
«>Хюн, С., Пей, Л., Молинари, Дж. Ф. и Роббинс, М. О. Конечно-элементный анализ контакта между упругими самоаффинными поверхностями. Физ. Ред. E 70 , 026117 (2004 г.).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Пей, Л., Хюн, С., Молинари, Дж. Ф. и Роббинс, М. О. Конечно-элементное моделирование упругопластического контакта между шероховатыми поверхностями. Дж. Мех. физ. Твердые вещества 53 , 2385–2409 (2005).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Сонг, Х.
 , Ван дер Гиссен, Э. и Лю, X. Анализ пластичности градиента деформации упругопластического контакта между шероховатыми поверхностями. Дж. Мех. физ. Solids 96 , 18–28 (2016).
, Ван дер Гиссен, Э. и Лю, X. Анализ пластичности градиента деформации упругопластического контакта между шероховатыми поверхностями. Дж. Мех. физ. Solids 96 , 18–28 (2016).ОБЪЯВЛЕНИЕ MathSciNet Статья Google ученый
Луан, Б. К. и Роббинс, М. О. Гибридное атомистическое/континуальное исследование контакта и трения между грубыми твердыми телами. Трибол. лат. 36 , 1–16 (2009).
КАС Статья Google ученый
Solhjoo, S. & Vakis, A.I. Механика сплошной среды в атомном масштабе: понимание неадгезивных контактов с использованием моделирования молекулярной динамики. Дж. Заявл. физ. 120 , 215102 (2016).
ОБЪЯВЛЕНИЕ Статья Google ученый
Ву, К.Л. и Томас, Т.Р. Контакт шероховатых поверхностей: обзор экспериментальной работы.
 Wear 58 , 331–340 (1980).
Wear 58 , 331–340 (1980).КАС Статья Google ученый
Сридхар, М. Р. и Йованович, М. М. Обзор моделей упругой и пластической контактной проводимости: сравнение с экспериментом. Дж. Термофиз. Теплопередача. 8 , 633–640 (1994).
КАС Статья Google ученый
Бхушан, Б. Реальная площадь контакта в полимерных магнитных средах-II: экспериментальные данные и анализ. АСЛЕ Транс. 28 , 181–197 (1985).
Артикул Google ученый
Дуайер-Джойс, Р. С., Дринкуотер, Б. В. и Куинн, А. М. Использование ультразвука при исследовании границ раздела шероховатых поверхностей. Дж. Трибол. Транс. ASME 123 , 8–16 (2001).
Артикул Google ученый
«>Овчаренко А., Гальперин Г., Эцион И. и Варенберг М. Новый испытательный стенд для оптических измерений на месте и в реальном времени эволюции контактной площадки во время предварительного скольжения сферического контакта. Трибол. лат. 23 , 55–63 (2006).
Артикул Google ученый
Крик, Б. А., Вейл, Дж. Р., Перссон, Б. Н. Дж. и Сойер, В. Г. Оптический микротрибометр in situ для анализа реальной площади контакта в экспериментах по механике контакта, адгезии и скольжению. Трибол. лат. 45 , 185–194 (2012).
Артикул Google ученый
«>Weber, B. и др. Молекулярные зонды выявляют отклонения от закона Амонтона в фрикционных контактах с множеством шероховатостей. Нац. коммун. 9 , 808 (2019).
Google ученый
Рубинштейн С.М., Коэн Г. и Файнберг Дж. Фронты отрыва и возникновение динамического трения. Природа 430 , 1005–1009 (2004).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Bennett, A.I. et al. Контактные измерения случайно шероховатых поверхностей. Трибол. лат. 65 , 134 (2017).

Артикул Google ученый
Li, L.T., Liang, X.M., Xing, Y.Z., Yan, D. & Wang, G.F. Измерение реальной площади контакта с шероховатыми металлическими поверхностями и различие вклада упругости и пластичности. Дж. Трибол. Транс. ASME 143 , 071501 (2021).
Артикул Google ученый
Сонг, Б. Дж., Ян, С. З. и Сян, В. В. К. Метод измерения для определения реальной площади контакта шероховатых поверхностей прозрачных твердых тел с использованием усовершенствованного метода Оцу. Подбородок. физ. В 24 , 014601 (2015).
ОБЪЯВЛЕНИЕ Статья Google ученый
Эцион, И. Пересмотр концепции Каттанео-Миндлина межфазного проскальзывания в податливых телах с тангенциальной нагрузкой. Дж. Трибол. Транс. ASME 132 , 020801 (2010).

Артикул Google ученый
Сахли Р. и др. Эволюция реальной площади контакта при сдвиге и величина статического трения мягких материалов. Проц. Натл. акад. науч. США 115 , 471–476 (2018).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Чжан Ю. и Чжао Ю. П. Адгезивный контакт нанопроволоки в испытании на трехточечный изгиб. J. Прилипатели. науч. Технол. 25 , 1107–1129 (2011).
КАС Статья Google ученый
Карбоне Г., Скараджи М. и Тартальино У. Адгезионный контакт шероховатых поверхностей: сравнение численных расчетов и аналитических теорий. евро. физ. J. E 30 , 65 (2009).
КАС Статья Google ученый
Кафедра инженерной механики, SVL и MMML, Сианьский университет Цзяотун, Сиань, 710049, Китай
Ван
- X. M. Liang
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- YZ Xing
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- L. T. Li
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- WK Yuan
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- G. F. Wang
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Существует два типа трения: статическое трение и кинетическое трение. Они не действуют одновременно, а существуют только независимо друг от друга.
- Статическое трение — это сила трения, действующая, когда объект находится в состоянии покоя.
- Кинетическое трение — это сила трения, действующая, когда объект находится в движении.
- Коэффициент трения зависит только от характера поверхности.
- На наклонной плоскости коэффициент можно определить исключительно по углу наклона.
- Типичные значения коэффициента трения не превышают 1 и никогда не могут быть отрицательными.

| Вид трения | Сила, Н | |
| 1 2 3 |
Трение покоя Трение скольжения Трение качения |
Вывод: сила трения покоя всегда больше силы трения скольжения, а сила трения скольжения больше силы трения качения – слайд 8
Вопрос: Почему тяжёлый шкаф трудно сдвинуть с места, но легче его тащить, а ещё легче катить, используя катки?
В древности люди для перетаскивания тяжёлых
грузов сначала использовали катки, а позднее
стали использовать колёса.
Вернуться к вопросам, поставленным в начале урока. Слайд 9,10
Когда трение полезно, его стараются увеличить (сделать поверхность более шероховатой), а когда вредно – то уменьшить (ввести смазку). Подробнее об этом мы поговорит на следующем уроке.
Домашнее задание: параграф 30,31, подумайте, как используют трение животные и растения, а также примеры полезного и вредного трения.
Закрепление изученного материала
каждой паре выдаётся по несколько картинок и
чистый лист бумаги (найти как можно больше
различных видов трения и записать на листке,
указав между какими телами они возникают).
Название силы |
Сила трения |
| Определение | |
| Обозначение | |
| Причины трения | |
| Виды трения | |
| Куда направлена (рис) | |
| Как уменьшить силу трения ? | |
| Как увеличить силу трения? |
Приложение
PhysBook:Электронный учебник физики — PhysBook
Содержание
Здесь размещена информация по школьной физике:
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Какие бывают силы трения?
Добавлено: 30 января 2022 в 10:35
Содержание
Физика присутствует в нашей жизни постоянно. Весь мир живет по ее законам. Любое природное явление, взаимодействие с предметами, приготовление пищи, занятие спортом — везде можно найти физические процессы. Зная основы данного предмета, проще справляться с бытовыми трудностями. Порой, физика может спасти жизнь человека. Например, знания понятия распределения веса тела на поверхности, человек на тонкий лед не встанет, а ляжет.
Зная основы данного предмета, проще справляться с бытовыми трудностями. Порой, физика может спасти жизнь человека. Например, знания понятия распределения веса тела на поверхности, человек на тонкий лед не встанет, а ляжет.
Можно привести множество примеров, где можно встретить физические явление. Наиболее интересны законы сил трения. Она возникает везде, где соприкасаются два или более предмета. Данная сила препятствует или затрудняет передвижение предметов.
Чтобы понять достаточно сложную тему, необходимо заинтересоваться ей, проявить любопытство или же нанять репетитора по физике в Москве. Также, важно понимать, что знания причины силы трения просто необходимы, обязательны. Без них невозможно понять, как устроен этот прекрасный мир.
Как появляется сила трения и что это такое
Какие бывают силы трения?
Сначала выясним, что это за сила.
Трение — это взаимодействие между поверхностями тел, которые касаются друг с другом.
Сила трения — это размер данного взаимодействия. Эта величина может быть различна как по модулю, так и направлению.
В физике присутствует несколько разновидностей сил. Трение, как и любая другая определяется Ньютонами (Н). Записывается сила буквой «ЭФ» Fтр.
Сопротивление движению возникает из-за того, что частицы, из которых состоят тела, которые соприкасаются друг с другом, имеют рельефную (на молекулярном уровне) поверхность. И при близком контактировании этих молекул, они сцепляются между собой.
Силу трения имеют обе плоскости. И они направлены в разные стороны, по отношению друг к другу. Поэтому тела не могут свободно перемещаться относительно друг друга.
Размер силы определяет структура поверхности и то, на сколько сильно они приближены друг к другу. Но даже если два тела имею гладкую поверхность и расположены горизонтально, и одно тело толкнуть (приложить силу), чтобы оно стало скользить по другому. В конечном итоге тело остановится. Это происходит потому, что идеально (абсолютно) гладких тел не бывает. В физике используется понятие абсолютно гладкое тело в тех случаях, когда необходимо решить задачу без учета трения.
Это происходит потому, что идеально (абсолютно) гладких тел не бывает. В физике используется понятие абсолютно гладкое тело в тех случаях, когда необходимо решить задачу без учета трения.
Для чего существует трение
Трение необходимо, чтобы тела могли быть в обездвиженном состоянии. Человек может стоять не падая благодаря силы трения. Иначе он бы просто поскользнулся. По аналогичным причинам, книги лежат на столе и не падают.
Машина может вовремя затормозить благодаря трению. В данном примере видно, как поверхность влияет на силу. Если гололед, то есть дорога будет гладкой, автомобилю сложнее затормозить. Это происходит, так как сцепление молекул льда и колес авто будет меньше, то есть, сила трения меньше и транспорт едет дальше.
Какие существуют разновидности сил тренияКакие бывают силы трения?
В физике отмечено сухое и вязкое трение.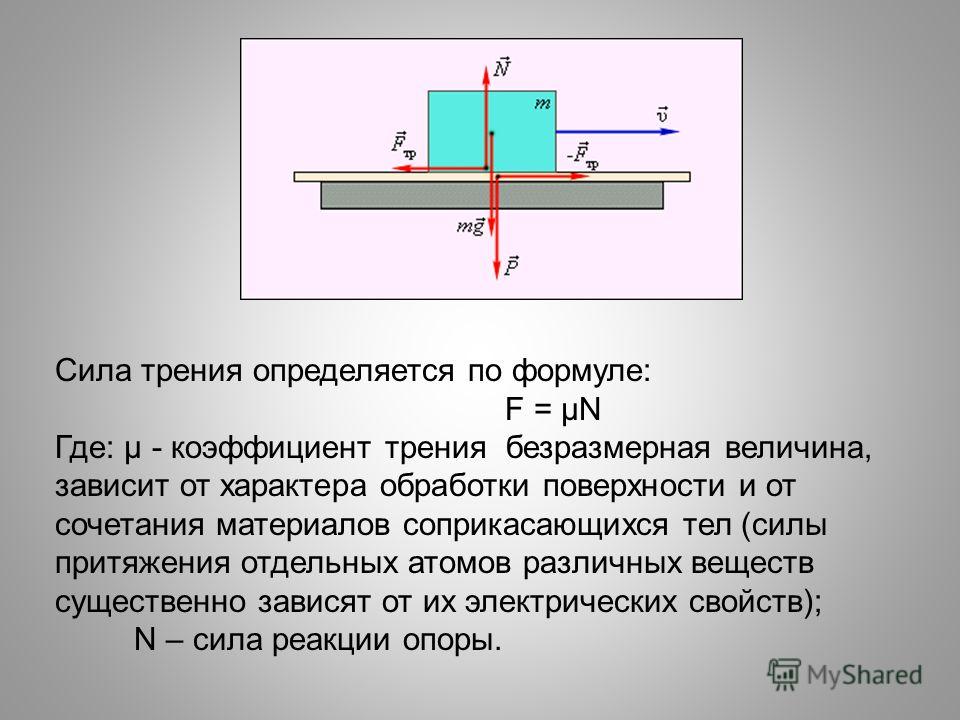 Выделяют три типа тел: твердое, жидкости, газы. Сухое трение встречаются между предметами твердыми.
Выделяют три типа тел: твердое, жидкости, газы. Сухое трение встречаются между предметами твердыми.
Сухое трение бывает:
— покой;
— скольжение;
— качели.
Покой
Данная сила образуется между телами, которые не передвигаются. Тумбочка стоит на полу. Пока тумбочку не трогаем, и нет сопротивления с ее стороны. Как только, ее начинают двигать, возникает эффект трения.
Она образуется из-за того, что молекулы сцепляются, препятствуют движению.
Трение покоя всегда стремится обратно усилию, которое к ней приложено. Если усилие незначительно, тумбочка будет оставаться на месте. Сила трения будет равна по модулю, но ее вектор смотрит обратно силы тяги (в данном случае тяга — это усилие).
Здесь будет верным равенство: Fтяги = F тр.покоя
Сила трения скольжения
Тумбочка сдвинется только в том случае, когда сама тяга будет больше трения. В этом случае, когда холодильник начал движение, начинает действовать данная сила.
В этом случае, когда холодильник начал движение, начинает действовать данная сила.
Когда наблюдается скольжение, можно отметить: Fтяги > F тр.покоя
Сила трения покоя предмета, на которое нет постороннего действия будет ноль. При прикладывании к предмету Тяги, единица покоя будет расти до какого-то максимума (он наступит при перемещении предмета). Дальше можно наблюдать силу скольжения. Предельный размер силы трения покоя зависит от характера поверхностей предметов.
Вектор трения направлен в другую сторону от тяги. Но по модулю при равномерном скольжении: Fтр. = Fтяги.
Какие бывают силы трения?
Расчет трения
Силу трения можно вычислить по формуле: F тр. = μ * N (Н)
μ (мю) — коэффициент силы трения. Он различен для разных поверхностей, находится в пределах до 1. Вычислен экспериментально. При решении задач, значение μ можно найти в специальной таблице.
N — сила реакции опоры. Она равна по числу и устремлена в другую сторону от силы тяжести.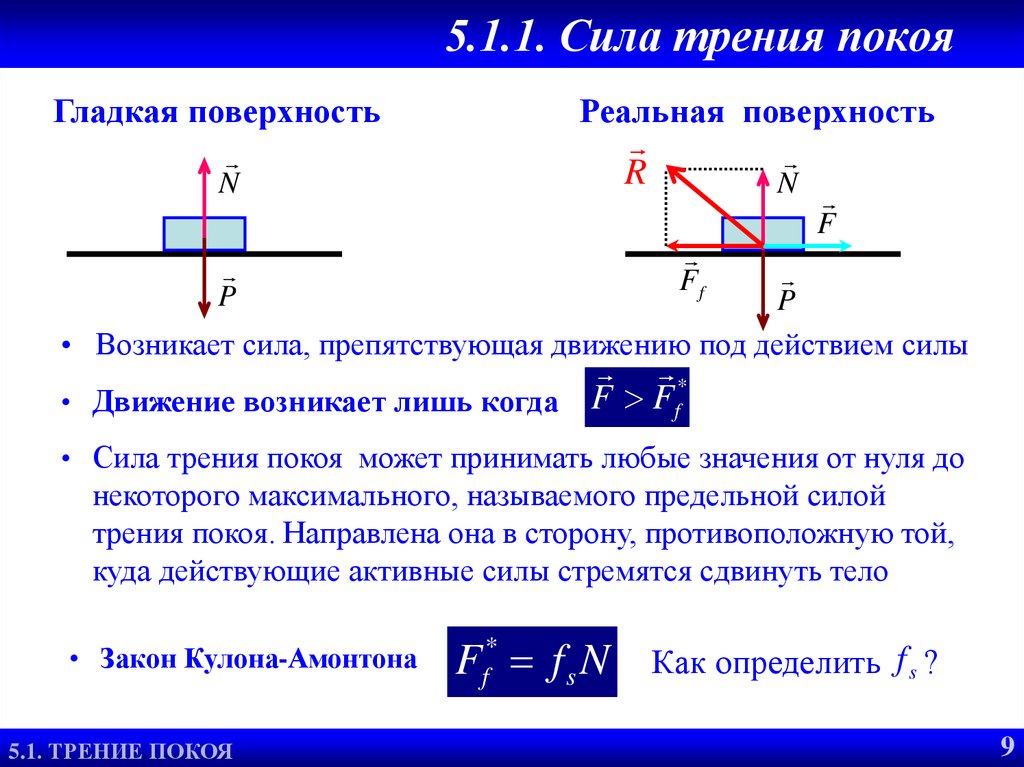
Сила трения качения
Она возникает при перекатывании одного тела относительно другого. На любой, перемещающийся предмет на колесиках, будет действовать сила трения качения.
Занимайтесь на курсах ЕГЭ и ОГЭ в паре TwoStu и получите максимум баллов на экзамене:
Владислав Барышников
Эксперт по подготовке к ЕГЭ, ОГЭ и ВПР
Задать вопрос
Закончил Московский физико-технический институт (Физтех) по специальности прикладная физика и математика. Магистр физико-математических наук. Преподавательский стаж более 13 лет. Соучредитель курсов ЕГЭ и ОГЭ в паре TwoStu.
Читайте также:
Сил
Сил Сопротивление трения относительному движению двух твердых тел обычно пропорционально силе, сжимающей поверхности вместе, а также шероховатости поверхностей. Поскольку это сила, перпендикулярная или «нормальная» к поверхностям, которая влияет на сопротивление трения, эта сила обычно называется «нормальной силой» и обозначается буквой N.
Также предполагается, что сила трения пропорциональна коэффициенту трения. Однако количество силы, необходимой для перемещения объекта из состояния покоя, обычно больше, чем сила, необходимая для поддержания его движения с постоянной скоростью после того, как он был запущен. Поэтому для данной пары поверхностей иногда указывают два коэффициента трения — коэффициент статического трения и коэффициент кинетического трения. Приведенное выше выражение силы можно назвать стандартной моделью поверхностного трения, и оно зависит от нескольких предположений о трении. Хотя это общее описание трения (которое я буду называть стандартной моделью) имеет практическое значение, оно ни в коем случае не является точным описанием трения. | Индекс Концепции трения График стандартной модели Ссылка | |||
| Назад |
В общем случае коэффициенты трения для статического и кинетического трения различны. Как и все простые утверждения о трении, эта картина трения слишком упрощена. Утверждение, что более шероховатые поверхности испытывают большее трение, звучит достаточно безопасно — два куска грубой наждачной бумаги, очевидно, будут труднее двигаться друг относительно друга, чем два куска мелкой наждачной бумаги. Но если два куска плоского металла делать все более гладкими, вы достигнете точки, в которой сопротивление относительному движению возрастет. Если вы сделаете их очень плоскими и гладкими и удалите все поверхностные загрязнения в вакууме, гладкие плоские поверхности фактически прилипнут друг к другу, образуя то, что называется «холодным сварным швом». При достижении определенной степени механической гладкости сопротивление трению оказывается зависящим от характера молекулярных сил в области контакта, так что вещества с сопоставимой «гладкостью» могут иметь существенно разные коэффициенты трения. Легко наблюдаемый контрпример к идее о том, что более шероховатые поверхности вызывают большее трение, — это матовое стекло по сравнению с гладким стеклом. | Индекс Концепции трения Коэффициенты трения График силы трения Ссылка | ||
| Назад |
Трение обычно характеризуется коэффициентом трения, который представляет собой отношение силы сопротивления трения к нормальной силе, прижимающей поверхности друг к другу. В этом случае нормальной силой является вес блока. Обычно существует значительная разница между коэффициентами статического трения и кинетического трения. Заметим, что коэффициент трения покоя не характеризует трение покоя вообще, а представляет собой условия на пороге движения только .
| Индекс Концепции трения Связь с шероховатостью поверхности График силы трения | ||
| Назад |
Силы сопротивления трения обычно пропорциональны силе, которая прижимает поверхности друг к другу. Эта сила, которая будет влиять на сопротивление трения, представляет собой компонент приложенной силы, который действует перпендикулярно или «нормально» к поверхностям, которые находятся в контакте, и обычно называется нормальной силой. Во многих распространенных ситуациях нормальная сила — это просто вес объекта, находящегося на некоторой поверхности, но если объект находится под наклоном или имеет компоненты приложенной силы, перпендикулярные поверхности, то он не равен весу. Вышеуказанные случаи являются часто встречающимися ситуациями для объектов в состоянии покоя или прямолинейного движения. Для криволинейного движения есть случаи, такие как автомобиль на кривой с наклоном, где нормальная сила определяется динамикой ситуации. В этом случае нормальная сила зависит от скорости автомобиля, а также от угла крена. | Индекс Концепции трения | ||
| Вернуться назад |
6.6 Трение – биомеханика движений человека
Резюме
Трение — это сила, постоянно присутствующая вокруг нас, которая противодействует относительному движению между контактирующими системами, но также позволяет нам двигаться (что вы обнаружили, если когда-либо пытались ходить по льду). Хотя трение является обычной силой, поведение трения на самом деле очень сложное и до сих пор полностью не изучено. Мы должны в значительной степени полагаться на наблюдения для любого понимания, которое мы можем получить. Однако мы все еще можем иметь дело с его более элементарными общими характеристиками и понять обстоятельства, в которых он ведет себя.
Хотя трение является обычной силой, поведение трения на самом деле очень сложное и до сих пор полностью не изучено. Мы должны в значительной степени полагаться на наблюдения для любого понимания, которое мы можем получить. Однако мы все еще можем иметь дело с его более элементарными общими характеристиками и понять обстоятельства, в которых он ведет себя.
ТРЕНИЕ
Трение – это сила, противодействующая относительному движению между контактирующими системами.
Одной из самых простых характеристик трения является то, что оно параллельно поверхности контакта между системами и всегда в направлении, противодействующем движению или попытке движения систем друг относительно друга. Если две системы находятся в контакте и движутся друг относительно друга, то трение между ними называется кинетическим трением . Например, трение замедляет скольжение хоккейной шайбы по льду. Но когда объекты неподвижны, между ними может действовать статическое трение ; статическое трение обычно больше, чем кинетическое трение между объектами.
КИНЕТИЧЕСКОЕ ТРЕНИЕ
Если две системы находятся в контакте и движутся относительно друг друга, то трение между ними называется кинетическим трением.
Представьте, например, что вы пытаетесь сдвинуть тяжелый ящик по бетонному полу — вы можете давить на ящик все сильнее и сильнее и не двигать его вообще. Это означает, что статическое трение реагирует на то, что вы делаете — оно увеличивается, чтобы быть равным вашему толчку и в противоположном направлении. Но если вы, наконец, нажмете достаточно сильно, ящик, кажется, внезапно соскользнет и начнет двигаться. Находясь в движении, его легче поддерживать в движении, чем было запустить, что указывает на то, что кинетическая сила трения меньше, чем статическая сила трения. Если вы добавляете массу к ящику, скажем, кладете на него коробку, вам нужно давить еще сильнее, чтобы он начал двигаться, а также чтобы он продолжал двигаться. Кроме того, если вы смазаете бетон маслом, вам будет легче запустить ящик и поддерживать его в рабочем состоянии (как и следовало ожидать).
Рисунок 1 представляет собой грубое графическое представление того, как возникает трение на границе раздела двух объектов. При ближайшем рассмотрении этих поверхностей видно, что они шероховатые. Поэтому, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет прыгать вместе с ударами только кончиками поверхности, отламывать точки или делать и то, и другое. Значительной силе можно сопротивляться трением без видимого движения. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик кладут еще одну коробку), тем больше усилий требуется для их перемещения. Часть трения обусловлена силами сцепления между поверхностными молекулами двух объектов, которые объясняют зависимость трения от природы веществ. Адгезия зависит от контактирующих веществ и представляет собой сложный аспект физики поверхности. Когда объект движется, становится меньше точек соприкосновения (меньше прилипающих молекул), поэтому для удержания объекта в движении требуется меньшее усилие. При малых, но отличных от нуля скоростях трение почти не зависит от скорости.
При малых, но отличных от нуля скоростях трение почти не зависит от скорости.
Величина силы трения имеет две формы: одна для статических ситуаций (статическое трение), другая для движения (кинетическое трение).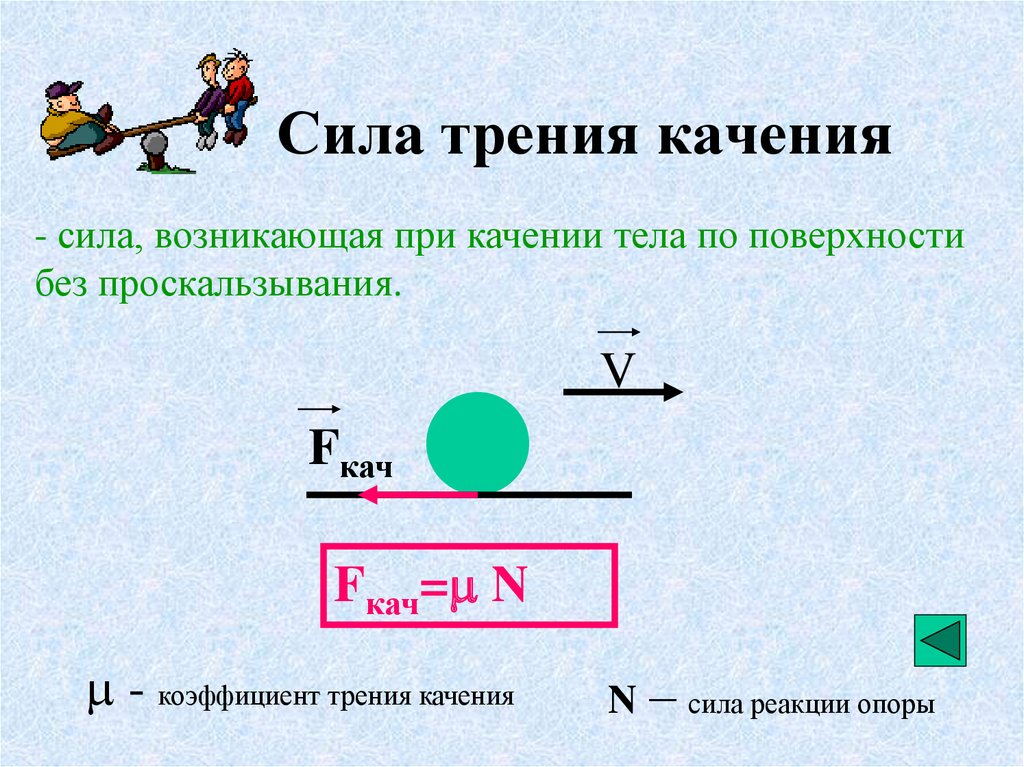
Когда между объектами нет движения, величина трения покоя f s равна
[латекс] \boldsymbol {f _ {\ textbf {s}} \ leq \ mu _ {\ textbf {s}} \: N,} [/ латекс]
, где μ s — коэффициент трения покоя, а Н — величина нормальной силы (силы, перпендикулярной поверхности).
ВЕЛИЧИНА СТАТИЧЕСКОГО ТРЕНИЯ
Величина статического трения f s равно
[латекс]\boldsymbol{f _{\textbf{s}}\leq{s}\textbf: N,}[/latex]
, где μ s — коэффициент трения покоя, а N — величина нормальной силы.
Символ ≤ означает меньше или равно , что означает, что статическое трение может иметь минимальное и максимальное значение μ с N . Статическое трение — это реактивная сила, которая увеличивается, чтобы быть равной и противоположной любой приложенной силе, вплоть до своего максимального предела. Как только приложенная сила превысит f s(max) , объект начнет двигаться. Таким образом,
Как только приложенная сила превысит f s(max) , объект начнет двигаться. Таким образом,
[латекс]\boldsymbol{f _{\textbf{s(max)}}=\mu _{\textbf{s}}N}.[/latex]
Когда объект движется, величина кинетического трения f k определяется как
[латекс]\boldsymbol{f_{\textbf{k}}=\mu_{\textbf{k}}N},[/latex]
, где μ k — коэффициент кинетического трения. Система, в которой f k = μ k N описывается как система, в которой трение ведет себя просто .
ВЕЛИЧИНА КИНЕТИЧЕСКОГО ТРЕНИЯ
Величина кинетического трения f k определяется выражением
[латекс]\boldsymbol{f_{\textbf{k}}=\mu_{\textbf{k}}N},[/latex ]
где μ k — коэффициент кинетического трения.
Как видно из таблицы 1, коэффициенты кинетического трения меньше, чем их статические аналоги. То, что значения μ в таблице 1 указаны только с одной или, самое большее, с двумя цифрами, является указанием на приблизительное описание трения, данное двумя приведенными выше уравнениями.
| [латекс]\textbf{Система}[/латекс] | [латекс]\textbf{Статическое трение}\boldsymbol{\mu _{\textbf{s}}}[/латекс] | [латекс]\textbf{Кинетическое трение}\boldsymbol{\mu _{\textbf{k}}}[/латекс] |
|---|---|---|
| Резина на сухом бетоне | 1,0 | 0,7 |
| Резина на мокром бетоне | 0,7 | 0,5 |
| Дерево на дереве | 0,5 | 0,3 |
| Вощеная древесина на мокром снегу | 0,14 | 0,1 |
| Металл на дереве | 0,5 | 0,3 |
| Сталь по стали (сухая) | 0,6 | 0,3 |
| Сталь по стали (промасленный) | 0,05 | 0,03 |
| Тефлон на стали | 0,04 | 0,04 |
| Кость, смазанная синовиальной жидкостью | 0,016 | 0,015 |
| Обувь на дереве | 0,9 | 0,7 |
| Обувь для льда | 0,1 | 0,05 |
| Лед на льду | 0,1 | 0,03 |
| Сталь на льду | 0,4 | 0,02 |
Таблица 1. Коэффициенты статического и кинетического трения. Коэффициенты статического и кинетического трения. | ||
Приведенные ранее уравнения включают зависимость трения от материалов и нормальную силу. Направление трения всегда противоположно движению, параллельно поверхности между объектами и перпендикулярно нормальной силе. Например, если ящик, который вы пытаетесь толкнуть (с усилием, параллельным полу), имеет массу 100 кг, то нормальная сила будет равна его весу, Вт = мг = (100 кг)(9,80 м/с 2 ) = 980 Н , перпендикулярно полу. Если коэффициент статического трения равен 0,45, вам придется приложить силу, параллельную полу, большую, чем f с(макс.) = мкН = (0,45)(980 Н) = 440 Н для перемещения ящик. Когда есть движение, трение меньше, а коэффициент кинетического трения может быть равен 0,30, так что сила всего 290 Н ( f k = μ k Н = (0,30)(980 Н) = 290 Н ) будет поддерживать его движение с постоянной скоростью. Если пол смазан, оба коэффициента значительно меньше, чем без смазки. Коэффициент трения – это безразмерная величина, величина которой обычно находится в диапазоне от 0 до 1,0. Коэффициент трения зависит от двух соприкасающихся поверхностей.
Если пол смазан, оба коэффициента значительно меньше, чем без смазки. Коэффициент трения – это безразмерная величина, величина которой обычно находится в диапазоне от 0 до 1,0. Коэффициент трения зависит от двух соприкасающихся поверхностей.
Многие люди испытывали скользкость при ходьбе по льду. Однако многие части тела, особенно суставы, имеют гораздо меньший коэффициент трения — часто в три-четыре раза меньше, чем лед. Сустав образован концами двух костей, которые соединены толстыми тканями. Коленный сустав образован костью голени (голенью) и бедренной костью (бедренной костью). Тазобедренный сустав представляет собой шаровидный (на конце бедренной кости) и впадинный (часть таза) сустав. Концы костей в суставе покрыты хрящом, что обеспечивает гладкую, почти стекловидную поверхность. Суставы также вырабатывают жидкость (синовиальную жидкость), которая уменьшает трение и износ. Поврежденный или пораженный артритом сустав можно заменить искусственным суставом (рис. 2). Эти заменители могут быть изготовлены из металлов (нержавеющая сталь или титан) или пластмассы (полиэтилен), также с очень низкими коэффициентами трения.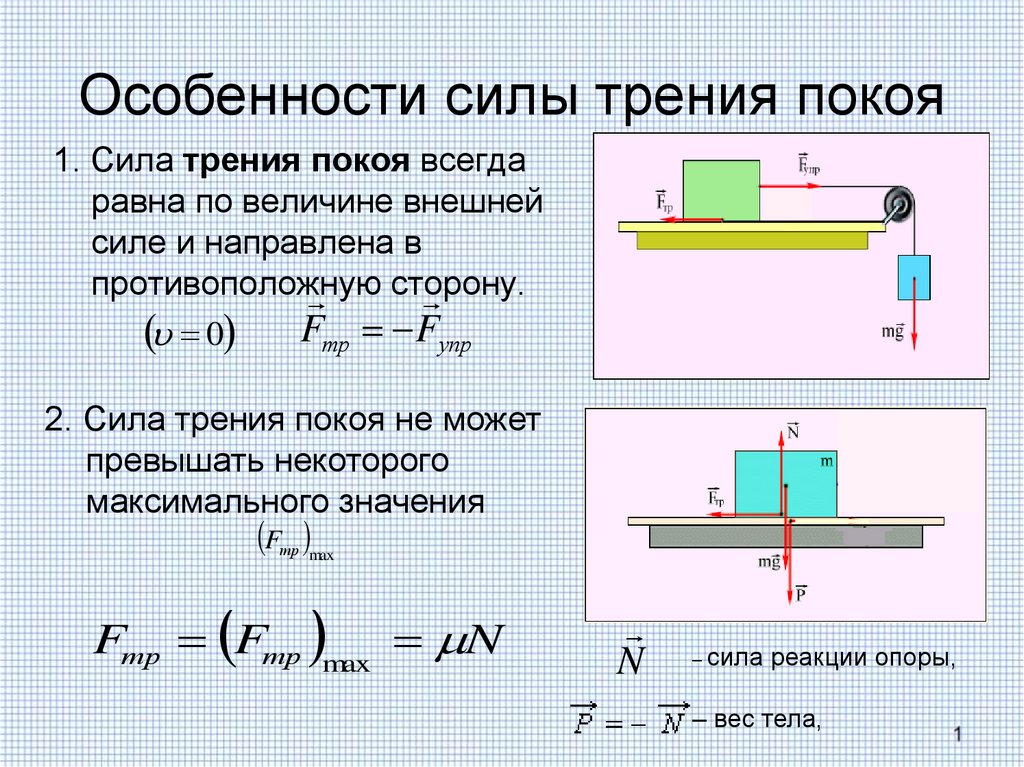
Другие природные смазки включают слюну, вырабатываемую во рту, чтобы помочь в процессе глотания, и скользкую слизь, находящуюся между органами в теле, позволяющую им свободно перемещаться друг мимо друга во время сердцебиения, во время дыхания, и когда человек двигается. Искусственные смазки также распространены в больницах и поликлиниках. Например, при ультразвуковой визуализации гель, соединяющий датчик с кожей, также служит для смазывания поверхности между датчиком и кожей, тем самым снижая коэффициент трения между двумя поверхностями. Это позволяет датчику свободно перемещаться по коже.
Пример 1. Упражнение на лыжах
Лыжник массой 62 кг скользит по заснеженному склону. Найдите коэффициент кинетического трения для лыжника, если известно, что трение равно 45,0 Н.
Стратегия
Величина кинетического трения равна 45,0 Н. Кинетическое трение связано с нормальной силой Н как f k = μ k N ; таким образом, коэффициент кинетического трения можно найти, если мы сможем найти нормальную силу лыжника на склоне. Нормальная сила всегда перпендикулярна поверхности, а поскольку движение перпендикулярно поверхности отсутствует, нормальная сила должна равняться составляющей веса лыжника, перпендикулярной склону. (См. диаграмму «лыжник и свободное тело» на рис. 3.)
Рис. 3. Движение лыжника и трение параллельны склону, поэтому удобнее всего спроецировать все силы на систему координат, где одна ось параллельна склону, а другая перпендикулярна (оси показаны слева лыжника). Н (нормальная сила) перпендикулярна склону, а f (трение) параллельно склону, но w (вес лыжника) имеет компоненты по обеим осям, а именно w ⊥ 92)(0,906)}}\boldsymbol{=\:0,082. }[/latex]
}[/latex]Обсуждение
Этот результат немного меньше коэффициента, приведенного в табл. 1 для вощеной древесины на снегу, но все же разумно, так как значения коэффициентов трения могут сильно различаться. В подобных ситуациях, когда объект массой 90 228 90 198 м 90 199 90 229 скользит по склону, составляющему угол 90 228 90 198 θ 90 199 90 229 с горизонтом, трение определяется выражением 90 198 90 228 f 90 229 90 012 k = μ k мг cos θ
. В этих условиях все объекты будут скользить вниз по склону с постоянным ускорением. Доказательство этого оставлено для задач и упражнений этой главы.Мы обсудили, что когда объект лежит на горизонтальной поверхности, на него действует нормальная сила, равная по величине его весу. Кроме того, простое трение всегда пропорционально нормальной силе.
ИССЛЕДОВАНИЯ PHET: СИЛА И ДВИЖЕНИЕ
Узнайте, какие силы действуют, когда вы пытаетесь толкнуть картотечный шкаф. Создайте приложенную силу и посмотрите результирующую силу трения и общую силу, действующую на шкаф. Диаграммы показывают силы, положение, скорость и ускорение в зависимости от времени. Нарисуйте диаграмму всех сил свободного тела (включая силы тяжести и нормальные силы).
Создайте приложенную силу и посмотрите результирующую силу трения и общую силу, действующую на шкаф. Диаграммы показывают силы, положение, скорость и ускорение в зависимости от времени. Нарисуйте диаграмму всех сил свободного тела (включая силы тяжести и нормальные силы).
Рисунок 6. Силы и движение
Сила трения — определение, типы и проблемы
Сила трения
Силу трения можно определить как силу, противодействующую движению, когда поверхность тела соприкасается с поверхностью другого тела. Сила трения уменьшает механическое преимущество машины или уменьшает отношение выхода к входу. Около четверти своей энергии автомобиль использует для ограничения силы трения, но трение в шинах позволяет автомобилю оставаться на дороге, а трение в сцеплении дает нам возможность управлять автомобилем.
Сила трения уменьшает механическое преимущество машины или уменьшает отношение выхода к входу. Около четверти своей энергии автомобиль использует для ограничения силы трения, но трение в шинах позволяет автомобилю оставаться на дороге, а трение в сцеплении дает нам возможность управлять автомобилем.
От спичек до машин и молекулярных структур каждого простого и сложного объекта трение является одним из самых важных процессов в физическом мире. В этой статье будет подробно рассмотрена сила трения и ее виды.
Что такое сила трения?
Что такое сила трения? Сила, создаваемая двумя поверхностями двух тел, когда они соприкасаются и скользят друг относительно друга, называется силой трения. Факторы, влияющие на силу трения, включают:
Расчет силы трения
Что такое расчет силы трения? Максимальную силу трения, действующую на объект со стороны поверхности, можно легко рассчитать по следующей формуле:
Ffrict = µ • Fnorm
Ниже приведены систематические шаги, которые вы можете выполнить при расчетах, основанных на силе трения:
Определение нормальной силыНормальная сила, действующая на тело, находящееся в контакте с другим телом устойчивое тело является опорной силой, и в большинстве случаев ее можно просто описать следующей формулой силы трения:
Н = мг
гравитация
Если поверхность наклонена, сила силы уменьшается со степенью наклона; поэтому формула силы трения принимает вид:
Н = мг cos(θ)
Где
Угол наклона поверхности θ
Сила нормального типа 2-килограммового деревянного бруска, сидящего на поверхности, равна рассчитывается простым расчетом, как
Н = 2 кг × 9,8 Н/кг = 19,6 Н
Расчет силы трения
Формула силы трения определяется по формуле:
F = µN
Предположим, мы рассматриваем деревянный брусок весом 2 кг, лежащий на столе, который перемещают из состояния покоя. В этом случае мы рассматриваем коэффициент статического трения, который для дерева равен 0,5.
В этом случае мы рассматриваем коэффициент статического трения, который для дерева равен 0,5.
Нормальную силу можно рассчитать с учетом данных:
Н = 2 кг × 9,8 Н/кг = 19,6 Н
Поскольку теперь у нас есть значения коэффициента статического трения и нормальной силы, силу трения можно рассчитать как следующим образом:
F = 0,5 × 19,6 Н = 9,8 Н
Различаются ли силы трения?
Существуют различные типы сил трения, такие как кинетическая сила трения, статическая сила трения, сила трения скольжения и сила трения качения. Сила трения, возникающая между газами и жидкостями, называется жидкостным трением. Ниже приводится широкая классификация силы трения:
Реакция между двумя твердыми телами описывается сухим трением. Когда два твердых тела находятся в движении, их трение описывается как кинетическое трение. Когда они не находятся в движении, это можно описать как статическое трение. И кинетическая, и статическая силы трения пропорциональны нормальной силе между двумя твердыми телами.
Когда они не находятся в движении, это можно описать как статическое трение. И кинетическая, и статическая силы трения пропорциональны нормальной силе между двумя твердыми телами.
Различные коэффициенты трения моделируют взаимодействие различных веществ. Это означает, что одни вещества более сопротивляются движению по сравнению с другими, когда величина нормальной силы между ними одинакова. Значения каждого из них могут быть определены экспериментально.
Трение каченияТрение качения проявляется, когда шарик, колесо или цилиндр свободно катятся по поверхности, как в случае качения шарика и подшипника. Распределение энергии, связанной с скручиванием тел, является основной причиной трения при качении. Если мы катим твердый мяч по ровной поверхности, поверхность имеет углубления в точках соприкосновения, а мяч несколько уплотняется.
Сжатие или упругий изгиб, возникающий в основной точке контакта, является препятствием движению, которое не полностью компенсируется, поскольку вещества возвращаются к своей типичной форме на заднем участке. Внутренние потери в этих двух веществах аналогичны потерям, препятствующим отскоку мяча обратно на уровень его выброса. Коэффициенты трения скольжения обычно в 100-1000 раз выше, чем коэффициенты трения качения для соответствующих материалов.
Внутренние потери в этих двух веществах аналогичны потерям, препятствующим отскоку мяча обратно на уровень его выброса. Коэффициенты трения скольжения обычно в 100-1000 раз выше, чем коэффициенты трения качения для соответствующих материалов.
Трение качения — это тип динамического или кинетического трения, возникающего, когда один объект катится по другому. Например, когда круглый диск, кольцо, сфера или колесо катятся по поверхности, трение качения представляет собой силу, противодействующую их движению. Другие примеры трения качения:
Жидкостное трение
Сила, препятствующая потоку жидкости, называется жидкостным трением. В этой ситуации сопротивление обеспечивается жидкостью между двумя поверхностями. Если сопротивление оказывают обе поверхности, ее называют высокоплотной и в целом можно назвать жирной. Примеры жидкостного трения включают:
Проблемы с силой трения
Решение: Нормальная сила, действующая на объект, покоящийся на плоской поверхности, может быть определена по формуле N = mg. Это можно использовать для расчета силы трения следующим образом:
Это можно использовать для расчета силы трения следующим образом:
Ff = мкН
Ff = мкг
В приведенном выше уравнении, если мы подставим данные, мы получим:
Ff =0,05 × 300 кг × 9,8 м/ s2
147 кг-м/с2 или 147 Н.
Сила трения, действующая в противоположном направлении, когда мы тянем ледяную глыбу через озеро, равна 147 Н.
Решение: Нормальная сила, действующая на объект на плоской поверхности, равна N = мг.
Эту информацию можно использовать для расчета силы трения следующим образом:
F = мкН F = мкмг
Если подставить данные в формулу, то получится
F = (0,400)(40,0 кг)(9,80 м/с2)
F = 156,8 Н
Следовательно, сила трения, действующая на лодку, равна 156,8 Н.
Заключение
Если вы прошли Внимательно изучите всю дискуссию, большинство ваших сомнений по поводу силы трения рассеялись, и вы, надеюсь, сможете решить множество проблем, основанных на этой теме. Продолжайте практиковать различные типы задач, связанных с темой, чтобы получить фундаментальное понимание ее концепций.
Часто задаваемые вопросы (FAQ)
1.Что такое статическое трение?Сила трения возникает, когда мы пытаемся привести неподвижное тело в движение по поверхности, не вызывая относительного движения по поверхности, и это тело называется силой трения покоя.
2. Является ли сила трения скалярной или векторной величиной?Поскольку сила трения включает в себя как величину, так и направление, она является векторной величиной.
3.Как подобрать правильный коэффициент? Выбранный коэффициент зависит от объекта и конкретной ситуации. Коэффициент трения покоя используется, если объект не движется по поверхности, а коэффициент трения скольжения используется, если рассматриваемый объект движется. На коэффициент также влияет тип используемых материалов. Например, коэффициент равен 0,6, если на кирпичной поверхности лежит брусок, а на бруске из чистого дерева — от 0,25 до 0,5.
На коэффициент также влияет тип используемых материалов. Например, коэффициент равен 0,6, если на кирпичной поверхности лежит брусок, а на бруске из чистого дерева — от 0,25 до 0,5.
Экспериментальное исследование связи между силой трения и реальной площадью контакта
Abstract
Классические законы трения предполагают, что сила трения пропорциональна нормальной нагрузке и не зависит от номинальной площади контакта. В качестве большого улучшения в этом вопросе в настоящее время широко признано, что сила трения пропорциональна реальной площади контакта, и на основе этой гипотезы было проведено много исследований. В настоящем исследовании эта гипотеза будет тщательно пересмотрена путем измерения силы трения и реальной площади контакта на месте и в режиме реального времени как на стадиях нормальной загрузки, так и на стадии разгрузки. Наши эксперименты показывают, что между силой трения и нормальной нагрузкой всегда сохраняется линейная зависимость. Однако для отношения между силой трения и реальной площадью контакта линейность сохраняется только на этапе нагружения, а на этапе разгрузки нарушается. Это исследование может улучшить наше понимание происхождения трения.
Это исследование может улучшить наше понимание происхождения трения.
Введение
Приблизительно 20 процентов мирового потребления энергии связано с вредным трением 1 , и это имеет практическое значение для улучшения фундаментального понимания трения. Еще в 1493 году Леонардо да Винчи заметил, что сила трения между двумя твердыми телами пропорциональна приложенной нормальной нагрузке и не зависит от номинальной площади контакта 2 . Таким образом, пропорциональность была определена как коэффициент трения. Коэффициент трения может быть изменен скоростью относительного движения 3 , топография контактной поверхности 4 , толщина смазочной пленки 5 и т. д. Реальная площадь контакта стала одним из ключевых факторов, так как на нее приходится тангенциальное напряжение 6 . В качестве большого шага в понимании трения Боуден и Табор 7 утверждали, что тангенциальная сила, необходимая для скольжения каждого контактного соединения, пропорциональна площади соединения на критическую силу сдвига, что приводит к линейности между силой трения и реальной контактная площадка .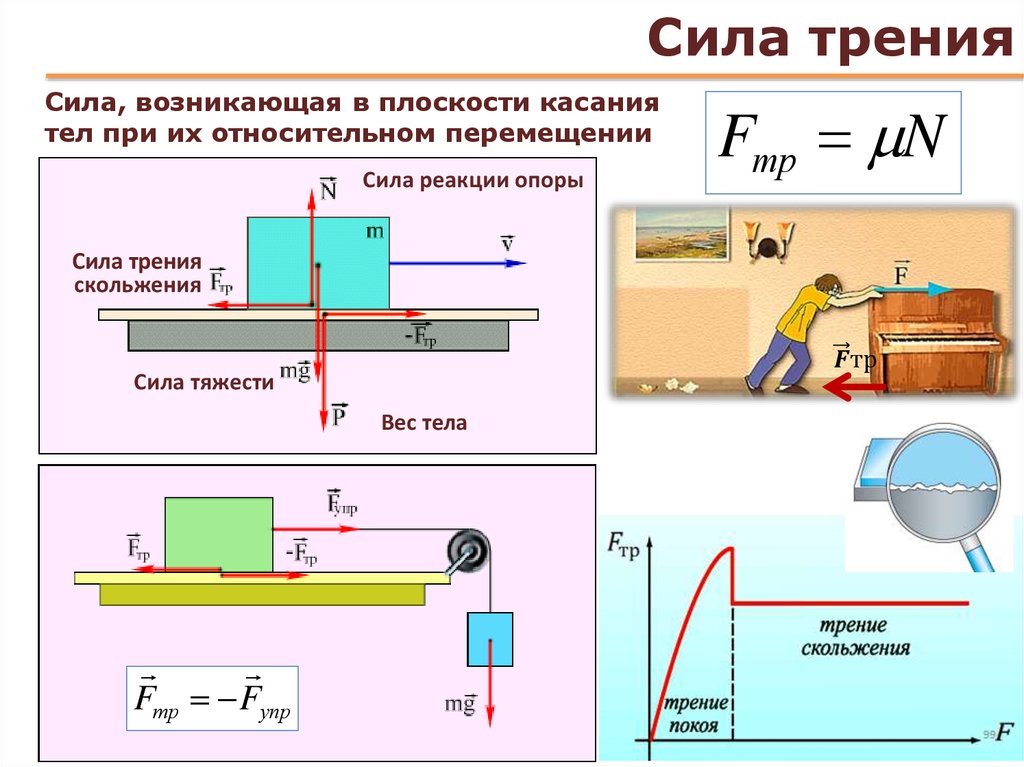 Эта концепция может объяснить происхождение древнего феноменологического закона трения, если соблюдается линейность между реальной площадью контакта и нормальной нагрузкой.
Эта концепция может объяснить происхождение древнего феноменологического закона трения, если соблюдается линейность между реальной площадью контакта и нормальной нагрузкой.
После работы Боудена и Табора исследование контакта шероховатых поверхностей получило дальнейшее развитие для определения соотношения между реальной площадью контакта и нормальной нагрузкой. Существуют модели с несколькими выступами 8,9,10 , фрактальные модели 11,12,13 , теория Перссона 14,15 и т.д. контактная фракция 16 . Такая линейность также была подтверждена с помощью анализа конечных элементов 17,18,19 и атомного моделирования 20,21 .
Кроме того, огромные усилия были затрачены на экспериментальные измерения реальной площади контакта 22 . Косвенные методы, такие как измерение теплового сопротивления 23 , электрического сопротивления 24 и ультразвукового отражения 25 , были приняты для оценки доли контакта. Для получения достаточно детальной картины контактных пятен применяют такие методы, как рентгеновская компьютерная томография 26 , оптическая интерференция 27,28,29 , флуоресцентные молекулярные зонды 30 и нарушенное полное внутреннее отражение 31,32,33 использовались для регистрации реальной площади контакта. Аналогично, почти все эксперименты 26,28,31,32,33 показали линейную зависимость реальной площади контакта от нормальной нагрузки.
Для получения достаточно детальной картины контактных пятен применяют такие методы, как рентгеновская компьютерная томография 26 , оптическая интерференция 27,28,29 , флуоресцентные молекулярные зонды 30 и нарушенное полное внутреннее отражение 31,32,33 использовались для регистрации реальной площади контакта. Аналогично, почти все эксперименты 26,28,31,32,33 показали линейную зависимость реальной площади контакта от нормальной нагрузки.
Принимая во внимание линейное соотношение нагрузки и площади в процессе непрерывного нагружения, очевидно, что существует линейность между любыми двумя величинами: силой трения, реальной площадью контакта и нормальной нагрузкой. Тем не менее, такая линейность отношения нагрузки к площади может нарушаться при некоторых обстоятельствах. Для контакта шара из вязкоупругой резины со стеклом был обнаружен явный гистерезис на кривых площади нагрузки во время цикла нагружения-разгрузки 9.0484 28 . Аналогичный гистерезис наблюдался при контакте шероховатого образца меди с гладким стеклом за счет пластической деформации 33 . В процессе разгрузки реальная площадь контакта уменьшается монотонно, но нелинейно по отношению к нормальной нагрузке, что может предоставить сценарий для проверки того, зависит ли сила трения исключительно линейно от площади контакта или нормальной нагрузки.
Аналогичный гистерезис наблюдался при контакте шероховатого образца меди с гладким стеклом за счет пластической деформации 33 . В процессе разгрузки реальная площадь контакта уменьшается монотонно, но нелинейно по отношению к нормальной нагрузке, что может предоставить сценарий для проверки того, зависит ли сила трения исключительно линейно от площади контакта или нормальной нагрузки.
В этом исследовании проводятся испытания на трение между медными образцами и стеклянным диском. Метод нарушенного полного внутреннего отражения применяется для измерения реальной площади контакта при различной внешней нормальной нагрузке и силе трения. Результаты подтверждают линейную зависимость силы трения как от нормальной нагрузки, так и от реальной площади контакта на стадии нормального нагружения. Тем не менее, для стадии разгрузки такая линейность между силой трения и нормальной нагрузкой сохраняется, тогда как наблюдается нелинейная связь между силой трения и площадью контакта.
Эксперимент
Подготовка образца
Три кубических образца из меди были приготовлены для контактных и фрикционных испытаний. Как показано на рис. 1, испытуемые поверхности сначала шлифовали наждачной бумагой, чтобы получить грубую топографию. Такая топография поверхности довольно обычна для пар трения. Номинальная площадь контакта поверхности каждого образца составляет 3 × 3 мм 2 . Перед контактно-фрикционными испытаниями было проведено стандартное испытание на растяжение, при котором модуль Юнга E меди , коэффициент Пуассона ν меди и предел текучести σ y меди были измерены как 125,3 ГПа и 2,24 ГПа соответственно.
Рисунок 1Поверхности тестовых образцов S1, S2 и S3.
Изображение полного размера
Экспериментальный прибор
Как схематично показано на рис. 2, был спроектирован и изготовлен новый прибор для одновременного измерения силы трения, реальной площади контакта и нормальной нагрузки. Аппарат состоит из трех основных частей: системы заряжания, системы освещения и системы фотосъемки.
Аппарат состоит из трех основных частей: системы заряжания, системы освещения и системы фотосъемки.
Схема экспериментального устройства (сгенерирована Microsoft PowerPoint & Visio 2016 MSO (16.0.4266.1001) 64 бита, http://www.microsoft.com).
Увеличить
Основным модулем нагрузочной системы является роликовый подшипник, внутреннее кольцо которого навинчено на верстак, а наружное кольцо установлено с диском из кварцевого стекла. Диск из кварцевого стекла имеет диаметр 200 мм и толщину 15 мм. Шаговый двигатель соединен с наружным кольцом подшипника через пару шестерен, и стеклянный диск может стабильно вращаться с передаваемым крутящим моментом. Испытуемый образец закрепляется на держателе образца, который приводится в движение шариковым винтом и синхронным двигателем. Во время контакта образец будет прижиматься к верхней поверхности кварцевого стекла на расстоянии около 40 мм от центра диска. При срабатывании шагового двигателя образец будет тереться о стеклянный диск, а сила сдвига и нормальная нагрузка регистрируются трехмерным датчиком силы, соединенным с держателем образца. Скорость загрузки держателя образца составляет 0,5 мм/мин, а скорость вращения стеклянного диска составляет 0,02 об/мин. Следовательно, когда происходит скольжение, относительную линейную скорость между образцом и стеклянным диском можно оценить как 0,042 мм/с. Скорость сбора данных датчика силы устанавливается равной 30 Гц.
Скорость загрузки держателя образца составляет 0,5 мм/мин, а скорость вращения стеклянного диска составляет 0,02 об/мин. Следовательно, когда происходит скольжение, относительную линейную скорость между образцом и стеклянным диском можно оценить как 0,042 мм/с. Скорость сбора данных датчика силы устанавливается равной 30 Гц.
Осветительная система построена на основе метода нарушенного полного внутреннего отражения. Монохроматическая фиолетовая светодиодная полоса обвивает стеклянный диск по окружности. Все огни падают на стеклянный диск сбоку. Световая полоса и край стеклянного диска вместе покрыты тканью блэкаут. Свет, падающий под углом, меньшим, чем критический угол полного отражения, поглощается тканью, в то время как другие остаются ограниченными стеклянным диском. Весь аппарат помещают в темную комнату, чтобы исключить помехи от других источников света.
Функция системы съемки камеры записывает эволюцию реальной площади контакта. Камера устройства с зарядовой связью (ПЗС) устанавливается под стеклянным диском и калибруется для фокусировки на верхней поверхности стеклянного диска.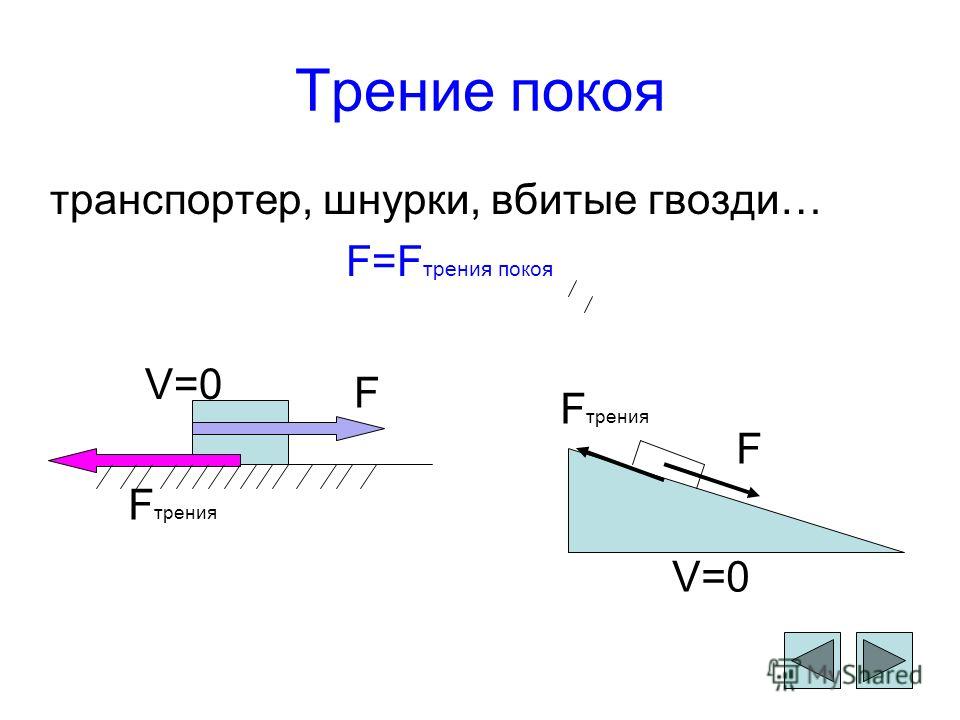 Поскольку стеклянный диск значительно тверже исследуемых образцов, его верхнюю поверхность можно рассматривать как жесткую плоскую плоскость, на которую легко ориентироваться при сжатии и трении. Когда испытуемый образец прижимается к поверхности стекла, условие полного внутреннего отражения будет нарушено в области тесного контакта, и свет будет рассеиваться поверхностью образца, а затем улавливаться ПЗС-камерой 9.0484 32,33 . В пределах бесконтактной области свет будет отражаться под углом, превышающим критический угол полного отражения, и все еще оставаться внутри стеклянного диска. После активации ПЗС-камера будет последовательно записывать изображения контактного интерфейса с постоянной скоростью 30 кадров в секунду. С объективом 1× , установленным на камере, каждый пиксель на изображении соответствует квадратной области 4,8 × 4,8 мкм 2 на контактном интерфейсе.
Поскольку стеклянный диск значительно тверже исследуемых образцов, его верхнюю поверхность можно рассматривать как жесткую плоскую плоскость, на которую легко ориентироваться при сжатии и трении. Когда испытуемый образец прижимается к поверхности стекла, условие полного внутреннего отражения будет нарушено в области тесного контакта, и свет будет рассеиваться поверхностью образца, а затем улавливаться ПЗС-камерой 9.0484 32,33 . В пределах бесконтактной области свет будет отражаться под углом, превышающим критический угол полного отражения, и все еще оставаться внутри стеклянного диска. После активации ПЗС-камера будет последовательно записывать изображения контактного интерфейса с постоянной скоростью 30 кадров в секунду. С объективом 1× , установленным на камере, каждый пиксель на изображении соответствует квадратной области 4,8 × 4,8 мкм 2 на контактном интерфейсе.
Приняв улучшенную технику Оцу 34 , исходные изображения могут быть преобразованы в бинарные изображения, где 1 соответствует точкам контакта, а 0 — точкам отсутствия контакта.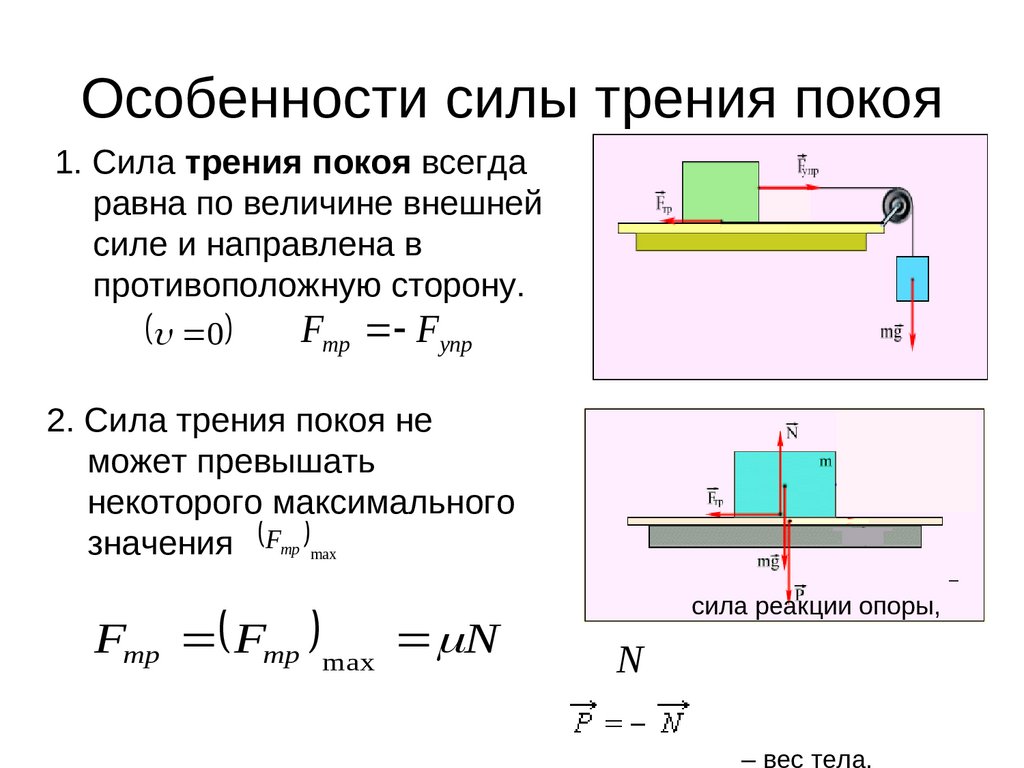 Следовательно, реальная площадь контакта получается как количество пятен контакта, умноженное на площадь одного пятна. Благодаря одновременному срабатыванию камеры и датчика силы реальная площадь контакта, сила трения и нормальная нагрузка измеряются и записываются синхронно.
Следовательно, реальная площадь контакта получается как количество пятен контакта, умноженное на площадь одного пятна. Благодаря одновременному срабатыванию камеры и датчика силы реальная площадь контакта, сила трения и нормальная нагрузка измеряются и записываются синхронно.
Методика эксперимента
Испытания на полную нормальную нагрузку-разгрузку были проведены на образцах S1, S2 и S3. Нормальная нагрузка P , сила трения F и реальная площадь контакта A r непрерывно измерялись и записывались на протяжении всего испытания. В качестве примера история нагружения образца S1 показана на рис. 3. На этапах нагружения образцы приводились в движение синхронным двигателем и приводились в контакт со стеклянным диском, при этом нормальная нагрузка P постепенно увеличивалась от 0 до 120 Н. Для достижения низкой скорости нагружения между синхронным двигателем и ШВП были установлены муфта и редуктор. Возможные промежутки между этими компонентами могут вызвать прекращение увеличения нормальной нагрузки на короткий промежуток времени, что приведет к небольшим плато при нормальной нагрузке (т.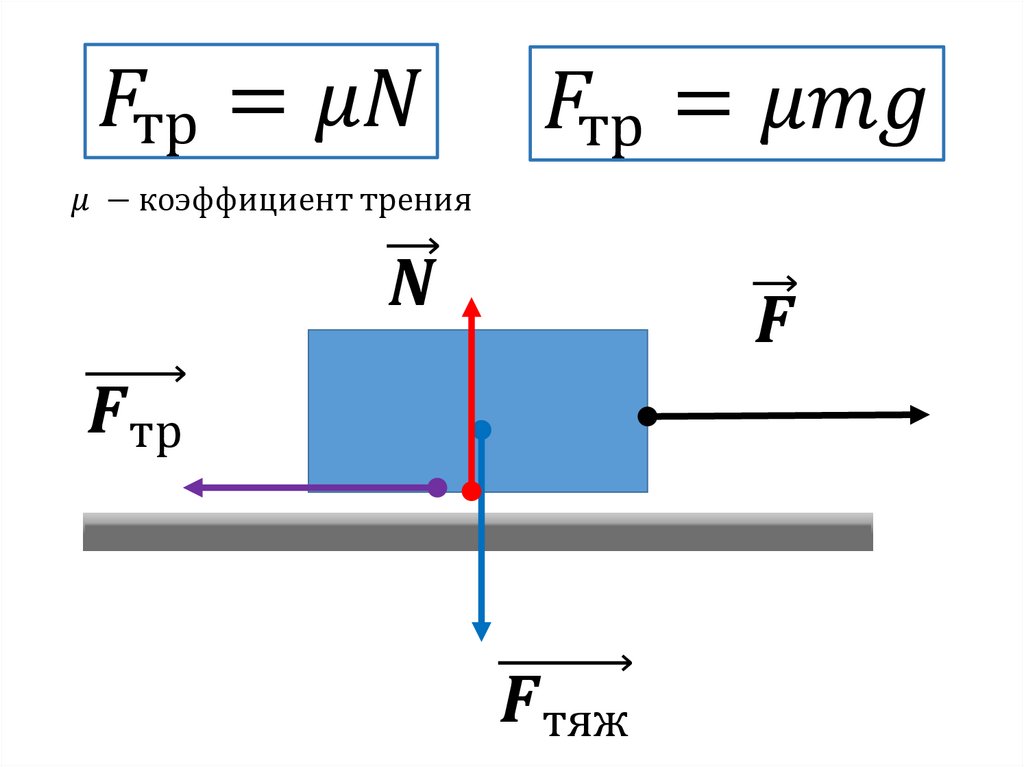 е. около P = 5 Н и 53 Н), но не повлияет на непрерывность процедур нагружения, а также правильность получения данных. Затем синхронный двигатель был реверсирован, после чего нормальная нагрузка P уменьшался до исчезновения. Во время цикла нагрузки-разгрузки для каждого образца выполнялась серия процессов трения путем вращения стеклянного диска при определенных нормальных нагрузках 20 Н, 40 Н, 60 Н, 80 Н и 100 Н.
е. около P = 5 Н и 53 Н), но не повлияет на непрерывность процедур нагружения, а также правильность получения данных. Затем синхронный двигатель был реверсирован, после чего нормальная нагрузка P уменьшался до исчезновения. Во время цикла нагрузки-разгрузки для каждого образца выполнялась серия процессов трения путем вращения стеклянного диска при определенных нормальных нагрузках 20 Н, 40 Н, 60 Н, 80 Н и 100 Н.
Эволюция реальной площади контакта A r , нормальной нагрузки P и силы трения F в зависимости от времени для образца S1.
Изображение в полный размер
Первый процесс натирания проводится примерно через 26 с. До этого момента сила трения остается почти нулевой, а реальная площадь контакта очень мала, поскольку нормальная нагрузка довольно мала. Видно, что процесс натирания состоит из двух стадий. Во-первых, сила трения претерпевает резкое увеличение до тех пор, пока не будет достигнут максимум, обычно известный как максимальная сила трения покоя 9.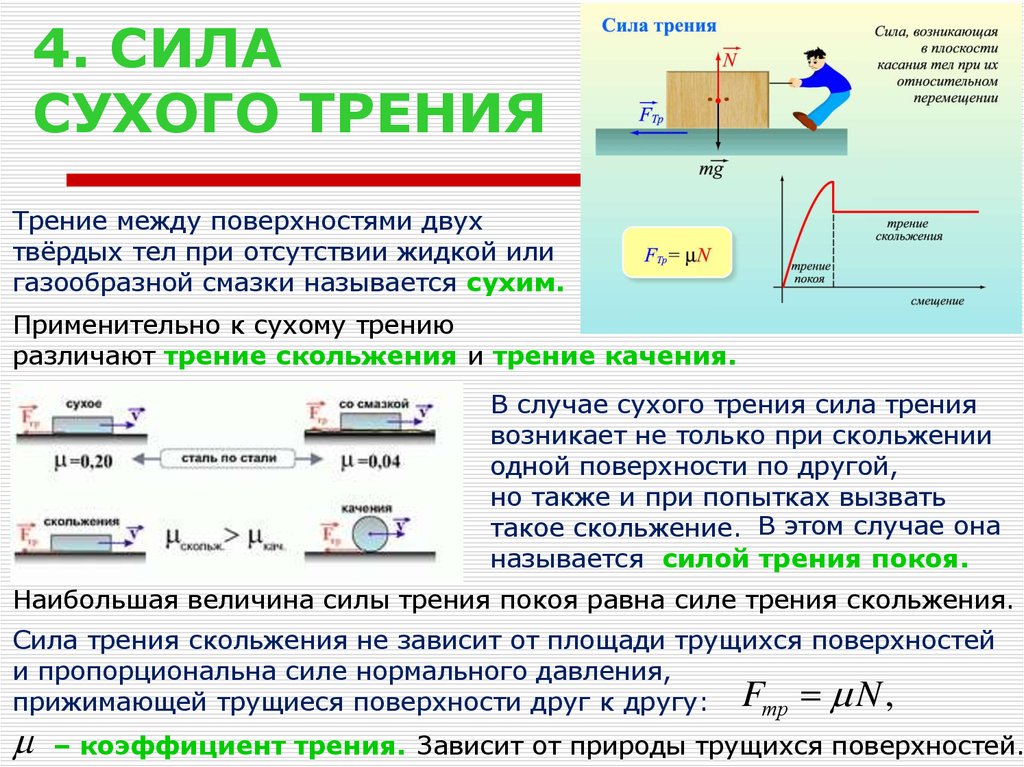 0055 Ф с . Как только достигается пиковое значение, сила трения быстро падает, приближаясь к стабильному значению, известному как кинетическая сила трения F k . В каждом процессе трения происходит небольшое увеличение площади контакта A r , что также было обнаружено в работе [1]. 35 . Чтобы избежать значительного увеличения площади контакта, вызванного длительным трением, вращение стеклянного диска немедленно останавливается, как только обнаруживается кинетическая сила трения. В этом случае каждый процесс трения длится около 5 с, а стеклянный диск будет поворачиваться на 0,6°. Для удобства сравнения P , F s and F k are normalized by E*A 0 , and A r normalized by A 0 , где E* = E медь /(1 − ν медь 2 ) — составной модуль упругости, а A 0 — номинальная площадь контакта.
0055 Ф с . Как только достигается пиковое значение, сила трения быстро падает, приближаясь к стабильному значению, известному как кинетическая сила трения F k . В каждом процессе трения происходит небольшое увеличение площади контакта A r , что также было обнаружено в работе [1]. 35 . Чтобы избежать значительного увеличения площади контакта, вызванного длительным трением, вращение стеклянного диска немедленно останавливается, как только обнаруживается кинетическая сила трения. В этом случае каждый процесс трения длится около 5 с, а стеклянный диск будет поворачиваться на 0,6°. Для удобства сравнения P , F s and F k are normalized by E*A 0 , and A r normalized by A 0 , где E* = E медь /(1 − ν медь 2 ) — составной модуль упругости, а A 0 — номинальная площадь контакта.
Результаты и обсуждение
На рис. 4 показано изменение доли контакта A r / A 0 по отношению к безразмерной нормальной нагрузке P /( E*A). На каждой кривой имеется пять небольших скачков при нагрузках, ведущих процессы трения, где реальная площадь контакта претерпевает небольшой прирост за счет трения. Для образца S1 при нагрузке P = 20 Н области контакта в начале и в конце истирания показаны на рис. 5а,б соответственно. После натирания некоторые контактные пятна увеличились, а также появились новые. В основном A R / A 0 увеличивается примерно линейно с P /( E*A 0 ) на загрузке и сгруппировании P) ( /) ( /) ( /) ( /). *A r ) для образцов S1, S2 и S3 лучше всего соответствуют 0,0053, 0,0035 и 0,0023 соответственно. Соответственно коэффициенты детерминации R 2 принимают 0,9965, 0,9925 и 0,9945, что свидетельствует об эффективности такой линейной арматуры. Однако, поскольку пластическая деформация, накопленная на этапе нагружения, не может быть восстановлена, реальная площадь контакта монотонно уменьшается при разгрузке, но нелинейно, вплоть до исчезновения.
Однако, поскольку пластическая деформация, накопленная на этапе нагружения, не может быть восстановлена, реальная площадь контакта монотонно уменьшается при разгрузке, но нелинейно, вплоть до исчезновения.
Эволюция контактной фракции A R / A 0 С уважением к безразмерной нормальной нагрузке P / ( E*a 0 P / ( E*a 0: / ( E*a 0 ). а ) образец S1, ( б ) образец S2, ( в ) образец S3. Рис. 5
Изображение в натуральную величину
Для различных нормальных нагрузок безразмерная максимальная сила трения покоя /( E*A 0 ) явно увеличивается по мере увеличения нормальной нагрузки. Для любой конкретной нормальной нагрузки как при загрузке, так и при разгрузке F s /( E*A 0 ) практически не различается между разными образцами.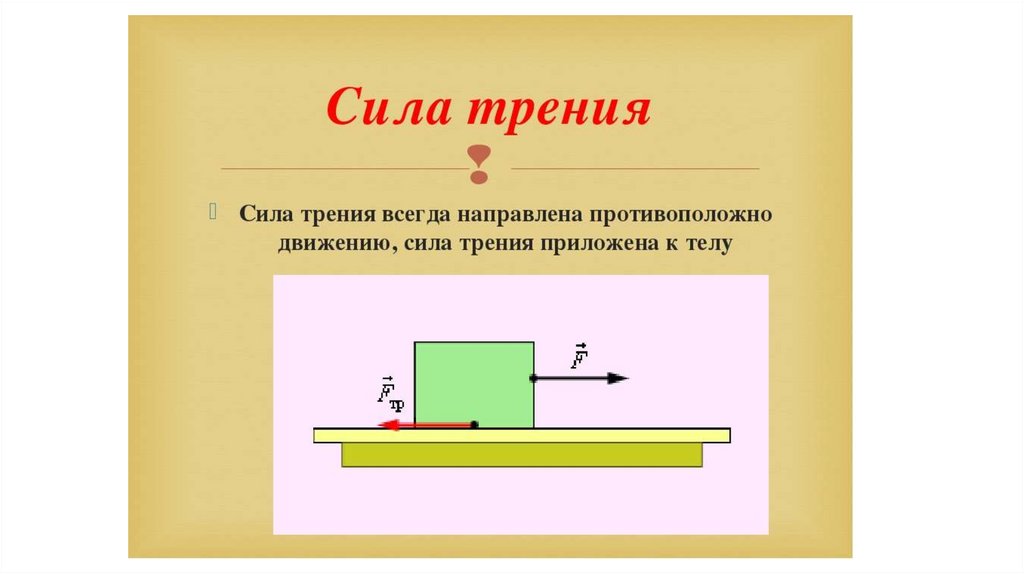 Оказывается, что как история нагружения, так и грубая топография образцов мало влияют на статическое трение. На рис. 7 показана безразмерная кинетическая сила трения 9.0055 F k /( E*A 0 ) относительно безразмерной нормальной нагрузки P /( E*A 0 ). Кинетическая сила трения F k демонстрирует такую же зависимость от нормальной нагрузки, как и статическая сила трения F s , за исключением того, что F k немного меньше 9 k F s при том же давлении.
Оказывается, что как история нагружения, так и грубая топография образцов мало влияют на статическое трение. На рис. 7 показана безразмерная кинетическая сила трения 9.0055 F k /( E*A 0 ) относительно безразмерной нормальной нагрузки P /( E*A 0 ). Кинетическая сила трения F k демонстрирует такую же зависимость от нормальной нагрузки, как и статическая сила трения F s , за исключением того, что F k немного меньше 9 k F s при том же давлении.
The dimensionless maximum static friction force F s /( E*A 0 ) at various dimensionless normal loads P /( E*A 0 ) .
Полноразмерное изображение
Рис. 7 Сила кинетического трения без размеров F K /( E*A 0 ) При различных безмерных нормальных нагрузках P /(5 E*5 E*.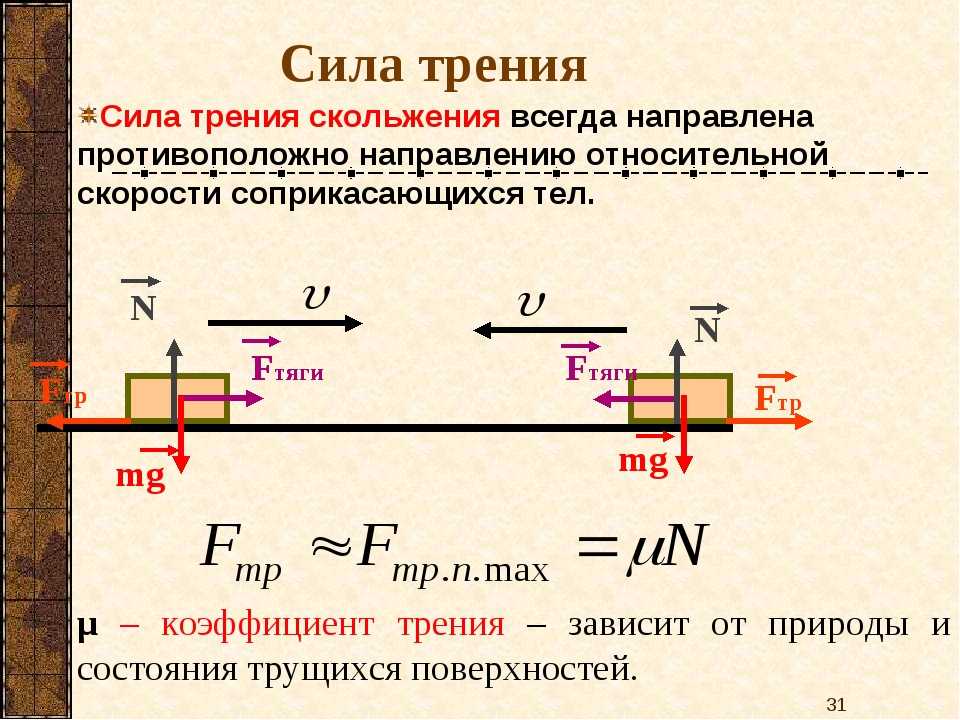 E* E* E* E*).0056 0 ).
E* E* E* E*).0056 0 ).
Изображение в натуральную величину
Для более ясного понимания взаимосвязи между силой трения и внешней нормальной нагрузкой коэффициент статического трения μ s и коэффициент кинетического трения μ 5 k 5 k 3 рассчитано, как показано на рис. 8. Видно, что как в процессе загрузки, так и в процессе разгрузки0013 остаются почти постоянными, что доказывает пропорциональность между силой трения и нормальной нагрузкой. Как для нагрузки, так и для разгрузки коэффициенты детерминации R 2 для линейной аппроксимации кривых F — P представлены в таблице 1. Для каждой кривой результирующий R 2 превышает 0,97, показывая надежность линейных зависимостей. Эволюция коэффициента трения по отношению к безразмерной нормальной нагрузке. Изображение в натуральную величину Full size table The evolutions of F s /( E*A 0 ) and F k /( E*A 0 ) versus доля контакта А r / А 0 показаны на рис. 9 и 10 соответственно. Обе силы трения изменяются по совершенно аналогичной схеме с изменением коэффициента контакта. При пяти удельных нагрузках в стадии нагружения сила трения в основном пропорциональна площади контакта. Такая линейность наблюдалась и в начале трения между ПДМС и стеклянной пластиной 9.0484 36 . Тем не менее, при той же нормальной нагрузке, то есть почти при одинаковой силе трения, наблюдается, что площадь контакта на стадии разгрузки намного больше, чем на стадии нагрузки. The dimensionless maximum static friction force F s /( E*A 0 ) under various contact fractions A r / A 0 . Полноразмерное изображение Сила кинетического трения без размеров F K / ( E*A 0 ) под различными контактными фракциями A 5513. 9555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555913. Безразмерные средние касательные напряжения как для статического, так и для кинетического трения0056 k /( GA r ) are calculated and denoted as τ s and τ k , respectively, with G = E /[2(1 + ν )] — модуль сдвига. На рисунке 11 показаны τ s и τ k при различных нормальных нагрузках как при загрузке, так и при разгрузке. Видно, что оба τ s и τ k незначительно изменяются при нагружении, а на этапах разгрузки монотонно уменьшаются. Эволюция безразмерного среднего касательного напряжения по отношению к безразмерной нормальной нагрузке. Полноразмерное изображение Также замечено, что τ s и τ k значительно различаются между разными образцами, что указывает на то, что даже при нагружении коэффициент пропорциональности между силой трения и реальной площадью контакта сильно зависит на неровных топографиях. Для контакта между металлами и стеклом гистерезис на кривых площади нагрузки во время цикла нагружения-разгрузки возникает из-за пластической деформации 33 . Адгезия является еще одним важным фактором при анализе контактных поверхностей 37 и может увеличить реальную площадь контакта для грубого контакта 38 . Поэтому стоит рассмотреть влияние сцепления на отношение площади трения. Настоящая работа представляет собой просто экспериментальное феноменологическое исследование, микромеханизм, лежащий в основе наблюдаемых результатов, все еще далек от полного понимания и нуждается в дальнейшем изучении. С помощью метода нарушенного полного внутреннего отражения был создан прибор для измерения силы трения, реальной площади контакта и внешней нормальной нагрузки на месте и в реальном времени. Нагрузочно-разгрузочные испытания проводятся на различных образцах меди. При нескольких заданных нормальных нагрузках образцы протираются в течение короткого промежутка времени как на этапах нагружения, так и на этапах разгрузки. Результаты эксперимента показывают, что сила трения примерно пропорциональна как нормальной нагрузке, так и реальной площади контакта при нагрузке. Такая линейность все еще сохраняется между силой трения и нормальной нагрузкой при разгрузке, в то время как связь между силой трения и реальной площадью контакта нарушается. Эти результаты показывают, что линейное предположение о силе трения на площади контакта не всегда выполняется. Хансен, Дж., Бьёрлинг, М. и Ларссон, Р. Формирование смазочной пленки в неконформных соединениях с шероховатой поверхностью, подверженных давлению в ГПа и высокому соотношению ползуна к валку. науч. Респ. 10 , 22250 (2020). ОБЪЯВЛЕНИЕ
КАС
Статья
Google ученый Carbone, G. & Bottiglione, F. Теории шероховатости контакта: предсказывают ли они линейность между площадью контакта и нагрузкой? Дж. Мех. физ. Твердые вещества 56 , 2555–2572 (2008). ОБЪЯВЛЕНИЕ
Статья
Google ученый Чжан Ф.К., Лю Дж.Х., Дин С.Ю. и Ван Р.Л. Экспериментальный и конечно-элементный анализ контактного поведения между непрозрачными шероховатыми поверхностями. Дж. Мех. физ. Твердые вещества 126 , 87–100 (2019). ОБЪЯВЛЕНИЕ
КАС
Статья
Google ученый Зугель, Б. Б. и Калин, М. Наблюдения на месте реальной контактной площадки с множеством неровностей в субмикронном масштабе. Стройнишки Вестн. Дж. Мех. англ. 63 , 351–362 (2017). Артикул
Google ученый Ссылки на скачивание Благодарим за поддержку Национального фонда естественных наук Китая (грант № 11525209). Авторы XML, YZX. Г. Ф. Ван. Авторы не заявляют об отсутствии конкурирующих интересов. Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности. Открытый доступ Эта статья находится под лицензией Creative Commons Attribution 4.0 International License, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате при условии, что вы укажете соответствующую ссылку на оригинальный автор(ы) и источник, предоставьте ссылку на лицензию Creative Commons и укажите, были ли внесены изменения. Перепечатка и разрешения Отправляя комментарий, вы соглашаетесь соблюдать наши Условия и правила сообщества. Если вы обнаружите что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неприемлемое. Когда тело движется через вязкий материал, такой как воздух или
воде или по бурной
поверхность, есть сопротивление ее движению; это сопротивление
называется
сила трения. Рассмотрим более простую систему; блок, лежащий на ровной поверхности. Как только f s достигнет своего максимума, любой
дальнейшее увеличение F приводит к
блок начинает скользить.
Из экспериментального наблюдения,
известно, что когда блок находится в движении, сила трения уменьшается.
Таким образом, сила сопротивления, когда блок неподвижен или статичен, больше, чем
что от того, когда блок движется или скользит.
Из-за этого,
необходимо различать силы трения в статике и
кинетические ситуации. Когда блок приходит в движение,
сила сопротивления называется силой кинетического трения
ф к . Момент после начала движения требует нескольких замечаний.
Для удержания тела в движении требуется гораздо меньше усилий.
чем это
инициировать это движение. Интересное поведение возникает в системе из-за
сумма так называемого
«избыточная» сила, которая присутствует после того, как блок начинает проскальзывать. Если цель
для получения постоянной скорости, то F должно быть резко уменьшено сразу же после того, как произойдет проскальзывание, чтобы
привести силы в равновесие. Если F не уменьшается,
затем он доминирует над гораздо более слабым f k , что приводит к
постоянное ускорение. Поскольку сила трения является резистивной,
вводится взаимодействием
двух поверхностей, то выражение для f следует полагаться на две взаимодействующие поверхности и количество
происходящее взаимодействие. Если самолет наклонен, нормальная сила уменьшается и
становится намного больше
интересно. Имейте в виду, что нормальная сила и вес противодействуют прижатию двух
поверхности вместе. Также стоит отметить, что слово «нормальный» означает
«перпендикуляр». Это означает, что все меньше и меньше
значения веса
действуют, чтобы прижать поверхности друг к другу. Должно быть ясно, что когда
поддержка
поверхность вертикальна, вес блока больше не влияет на
сила нормальная.
Поскольку вес блока является единственной содействующей силой в
нормальное направление, нормальная сила
равен нулю. Если сила трения прямо пропорциональна
нормальная сила и
нормальная сила равна нулю, делается вывод, что при опорной поверхности
вертикальный есть
отсутствие трения между поверхностями. В математике мы говорим, что величины пропорциональны, если существует
некоторое число, мультипликативный коэффициент,
что приведет к равенству в отношениях. Это означает, что там
существует постоянная
пропорциональности, при которой сила трения равна произведению
этой постоянной и Ф Н . Эта константа называется коэффициентом трения .
Ранее было сказано, что сила
трения каким-то образом уменьшается, когда тело находится в движении. Поскольку у нас есть
пришли к выводу, что
два фактора, которые создают силу трения, являются нормальной силой, и это
коэффициент
трения. Должно быть очевидно, что нормальная сила не собирается
уменьшаться, когда
блок начинает двигаться. Отсюда следует, что коэффициент трения должен
измениться, когда движение начинается. В очередной раз необходимо различать
эти величины в обозначениях: коэффициент
трения покоя с и коэффициент кинетического трения к ,
(это греческая буква Му и является общим символом для
коэффициент трения). Теперь рассмотрим бульдозер с гусеницами. Вес бульдозера придает ему большую
нормальная сила на любой поверхности. На мягких поверхностях, таких как грязь, шипы на
следы уходят на поверхность. Таким образом, коэффициент трения между
земля и бульдозер намного больше, чем один. Этот больший коэффициент трения
позволяет бульдозеру толкать объекты, которые в несколько раз превышают его собственный вес. Когда объект движется или покоится на поверхности или в среде, такой как воздух или вода, возникает сопротивление, которое противодействует его движению и стремится удерживать его в покое. Это сопротивление известно как трение . Трение играет жизненно важную роль в нашей повседневной жизни. Мы, например, можем ходить или водить машину благодаря наличию трения. Сила трения является результатом взаимодействия между атомами и молекулами. Иногда трение может быть нежелательным, и для его уменьшения используются смазочные материалы различных типов. Например, в машинах, где трение может изнашивать определенные детали, для его уменьшения используются смазочные материалы на масляной основе. Рис. 1. Визуальное представление взаимодействия двух поверхностей в микроскопическом масштабе. Источник: StudySmarter. Хотя две соприкасающиеся поверхности могут казаться очень гладкими, в микроскопическом масштабе имеется множество пиков и впадин, которые приводят к трению. На практике невозможно создать объект, имеющий абсолютно гладкую поверхность. Согласно закону сохранения энергии никакая энергия в системе никогда не исчезает. В этом случае трение производит тепловую энергию, которая рассеивается через среду и сами объекты. В системе, если все объекты неподвижны относительно внешнего наблюдателя, сила трения между объектами называется статической силой трения. Как следует из названия, это сила трения (fs), которая действует, когда взаимодействующие объекты статичны. Поскольку сила трения такая же, как и любая другая сила, она измеряется в ньютонах. Направление силы трения противоположно направлению приложенной силы. Рассмотрим брусок массы m и действующую на него силу F так, что брусок остается в покое. Рис. 2. Все силы, действующие на массу, лежащую на поверхности. Источник: StudySmarter. На объект действуют четыре силы: сила тяжести mg, нормальная сила N, сила трения покоя fs и приложенная сила величины F. Объект будет оставаться в равновесии до тех пор, пока величина приложенной силы не станет больше чем сила трения. Сила трения прямо пропорциональна нормальной силе, действующей на объект. Следовательно, чем легче объект, тем меньше трение. Чтобы убрать знак пропорциональности, мы должны ввести константу пропорциональности, известную как коэффициент трения покоя , обозначенный здесь как μ s . Однако в этом случае будет неравенство. Величина приложенной силы увеличится до точки, после которой объект начнет двигаться, и статического трения больше не будет. Таким образом, максимальное значение трения покоя составляет μ с ⋅Н, и любое значение меньше этого является неравенством. Это можно выразить следующим образом: Здесь нормальная сила равна N = мг. Как мы видели ранее, когда объект находится в состоянии покоя, действующая сила трения представляет собой трение покоя. Однако, когда приложенная сила больше, чем трение покоя, объект больше не является неподвижным. Когда объект движется из-за внешней неуравновешенной силы, сила трения, связанная с системой, известна как k инетическая сила трения . В точке, где приложенная сила превышает статическую силу трения, вступает в действие кинетическое трение. Как следует из названия, это связано с движением объекта. Кинетическое трение можно разделить на три типа: трение скольжения , трение качения и жидкостное трение . Когда объект может свободно вращаться вокруг оси (сфера на наклонной плоскости), действующая сила трения известна как трение качения . Когда объект движется в среде, такой как вода или воздух, среда вызывает сопротивление, известное как жидкостное трение . Под жидкостью здесь понимаются не только жидкости, поскольку газы также считаются жидкостями. Когда объект не является круглым и может совершать только поступательное движение (блок на поверхности), трение, возникающее при движении этого объекта, называется трение скольжения . Все три типа кинетического трения можно определить с помощью общей теории кинетического трения. Здесь μ k — коэффициент кинетического трения , а N — нормальная сила. Значения μ k и μ s зависят от характера поверхностей, причем μ k обычно меньше, чем μ s . Типичные значения находятся в диапазоне от 0,03 до 1,0. Важно отметить, что значение коэффициента трения никогда не может быть отрицательным. Может показаться, что объект с большей площадью контакта будет иметь больший коэффициент трения, но вес объекта распределен равномерно и поэтому не влияет на коэффициент трения. См. следующий список некоторых типичных коэффициентов трения. Surfaces Рассмотрим блок массой m на поверхности и внешнюю силу F, приложенную параллельно поверхности, которая постоянно увеличивается, пока блок не начнет двигаться. Мы видели, как вступают в действие статическое трение, а затем кинетическое трение. Представим силы трения графически как функцию приложенной силы. Рис. 3. Графическое представление статического и кинетического трения в зависимости от приложенной силы. Источник: StudySmarter. Как обсуждалось ранее, приложенная сила является линейной функцией статического трения и увеличивается до определенного значения, после чего вступает в действие кинетическое трение. До сих пор мы фокусировались на объектах на горизонтальной поверхности. Теперь рассмотрим объект, покоящийся на наклонной плоскости, которая образует с горизонтом угол θ. Рис. 4. Объект, покоящийся на наклонной поверхности со всеми действующими на него силами. Источник: StudySmarter. Учитывая все силы, действующие на объект, мы находим, что гравитационная сила, трение и нормальная сила — это все силы, которые необходимо принимать во внимание. Поскольку объект находится в равновесии, эти силы должны компенсировать друг друга. Мы можем рассматривать наши декартовы оси где угодно, чтобы сделать наши вычисления удобными. Представим оси вдоль наклонной плоскости, как показано на рисунке 4. Во-первых, сила тяжести действует вертикально вниз, поэтому ее горизонтальная составляющая будет равна mg sinθ, которая уравновешивает трение покоя, действующее в противоположном направлении. Когда угол наклона увеличивается до тех пор, пока блок не окажется на грани проскальзывания, сила трения покоя достигнет своего максимального значения μ s Н. Угол в этой ситуации называется критическим углом θ с . Подставляя это, мы получаем: Нормальная сила: Теперь у нас есть два уравнения. Так как мы ищем значение коэффициента трения, то берем соотношение обоих уравнений и получаем: Здесь θc — критический угол. Как только угол наклонной плоскости превысит критический угол, блок начнет двигаться. Итак, условие равновесия бруска: Когда наклон превысит критический угол, брусок начнет ускоряться вниз, и вступит в действие кинетическое трение. Отсюда видно, что значение коэффициента трения можно определить путем измерения угла наклона плоскости. Поскольку шайба начнет двигаться с немного большей силой, значение статического трения будет максимальным. Это дает нам: Подставляя все значения, мы получаем: Таким образом, мы определили силу трения, действующую на шайбу, когда она находится в состоянии покоя.

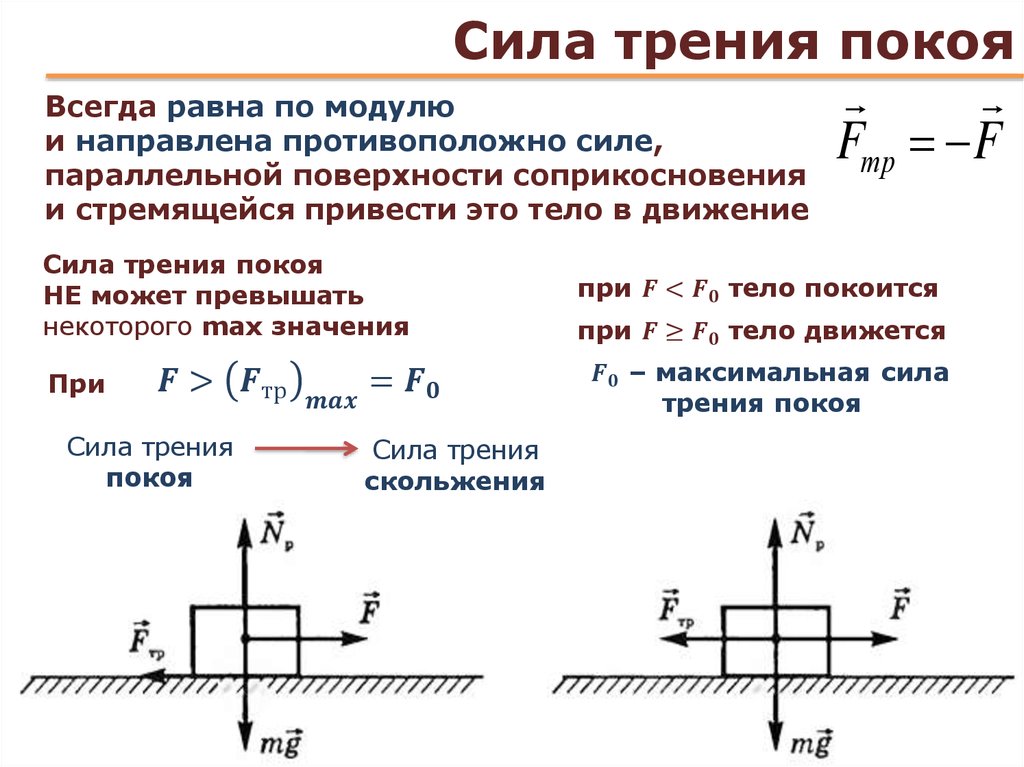 Наклон безразмерного среднего касательного напряжения по отношению к безразмерной нормальной нагрузке ступеней нагружения намного меньше, чем у участков разгрузки. Это говорит о том, что сила трения примерно пропорциональна реальной площади контакта на стадиях нагружения. Коэффициенты детерминации р 2 для линейного фитинга F — A r кривые также приводят к тем же выводам. Однако R 2 падает менее чем на 0,8 и даже до 0,5 для случаев разгрузки, что свидетельствует о нарушении линейности между силой трения и реальной площадью контакта.
Наклон безразмерного среднего касательного напряжения по отношению к безразмерной нормальной нагрузке ступеней нагружения намного меньше, чем у участков разгрузки. Это говорит о том, что сила трения примерно пропорциональна реальной площади контакта на стадиях нагружения. Коэффициенты детерминации р 2 для линейного фитинга F — A r кривые также приводят к тем же выводам. Однако R 2 падает менее чем на 0,8 и даже до 0,5 для случаев разгрузки, что свидетельствует о нарушении линейности между силой трения и реальной площадью контакта. Вероятным объяснением является то, что изменение шероховатой топографии приводит к изменению среднего давления на реальную площадь контакта, а среднее касательное напряжение пропорционально среднему давлению на коэффициент трения. В любом случае между силой трения и реальной площадью контакта не всегда существует линейная зависимость, учитывая тот факт, что одной и той же силе трения соответствуют два разных значения реальной площади контакта при нагрузке и разгрузке.
Вероятным объяснением является то, что изменение шероховатой топографии приводит к изменению среднего давления на реальную площадь контакта, а среднее касательное напряжение пропорционально среднему давлению на коэффициент трения. В любом случае между силой трения и реальной площадью контакта не всегда существует линейная зависимость, учитывая тот факт, что одной и той же силе трения соответствуют два разных значения реальной площади контакта при нагрузке и разгрузке.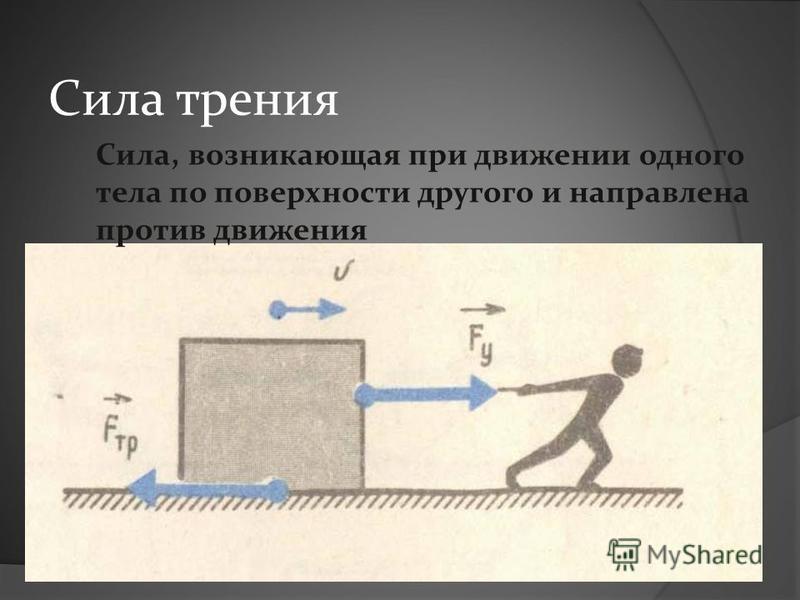
Выводы
Ссылки
Благодарности

Информация об авторе
Авторы и организации
Contributions
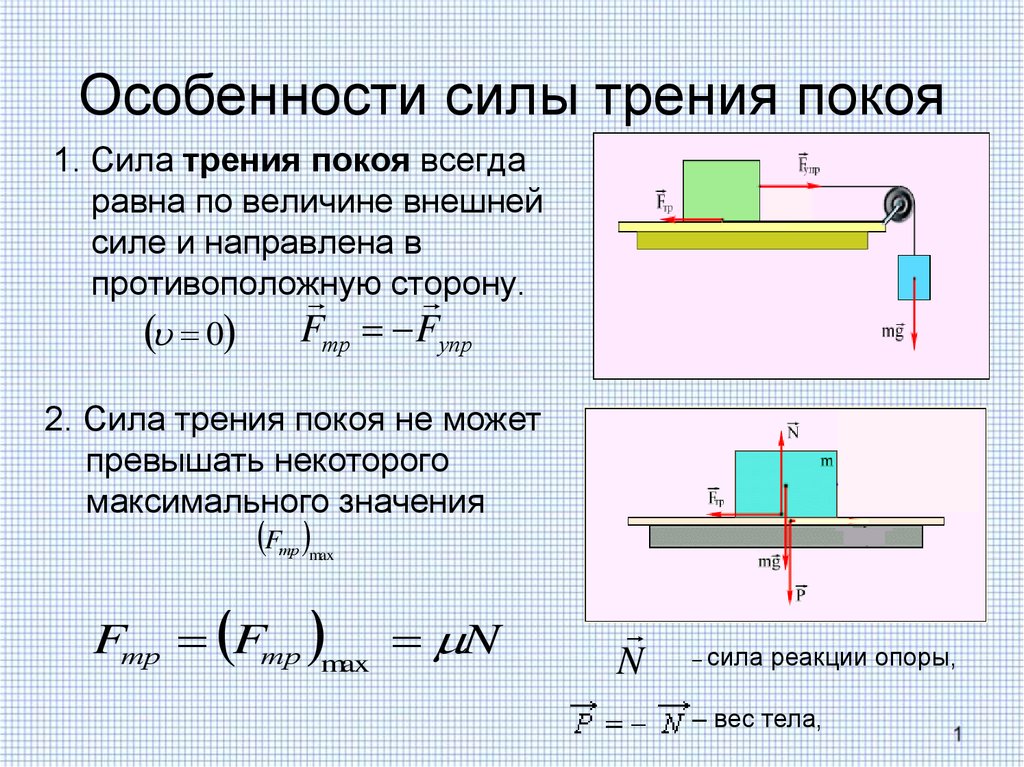 и Л.Т.Л. провел эксперимент и проанализировал данные. G.F.W разработал исследование. X.M.L., W.K.Y. и Г.Ф.В. написал рукопись. X.M.L. и Y.Z.X. в равной мере внесли свой вклад в эту работу.
и Л.Т.Л. провел эксперимент и проанализировал данные. G.F.W разработал исследование. X.M.L., W.K.Y. и Г.Ф.В. написал рукопись. X.M.L. и Y.Z.X. в равной мере внесли свой вклад в эту работу. Автор, ответственный за переписку
Заявление об этике
Конкурирующие интересы
Дополнительная информация
Примечание издателя
Права и разрешения
 Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на статью, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.
Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на статью, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/. Об этой статье
Комментарии
Трение — Фон
Трение — Фон
Фон Трение, возникающее в результате взаимодействия
тело и элементы, с которыми оно контактирует, играет очень важную роль во многих физических системах. Картина,
если хотите, система состояла из 100 студентов, пытающихся попасть в
класс без
трение между подошвой обуви и полом.
Трение также может быть помехой.
Возьмем, к примеру, двигатель автомобиля. В бензиновом двигателе искра
взрывает пары бензина
тем самым продвигая поршень вверх через цилиндр.
Стенка цилиндра должна плотно прилегать к поршню, чтобы усилие
взрыв не «просачивается» между поршнем и стенками цилиндра.
Очевидно, это приводит к трению поверхностей цилиндра и поршня.
вместе и благодаря
этот контакт, в системе существует трение. Побочный продукт
трение это тепло.
Тепло заставляет металл расширяться. Если поршень расширяется быстрее, чем
стенка цилиндра (это
делает), то трение увеличивается и может привести к повреждению. Это трение
сила в двигателе
уменьшается за счет использования смазки, такой как масло.
Трение, возникающее в результате взаимодействия
тело и элементы, с которыми оно контактирует, играет очень важную роль во многих физических системах. Картина,
если хотите, система состояла из 100 студентов, пытающихся попасть в
класс без
трение между подошвой обуви и полом.
Трение также может быть помехой.
Возьмем, к примеру, двигатель автомобиля. В бензиновом двигателе искра
взрывает пары бензина
тем самым продвигая поршень вверх через цилиндр.
Стенка цилиндра должна плотно прилегать к поршню, чтобы усилие
взрыв не «просачивается» между поршнем и стенками цилиндра.
Очевидно, это приводит к трению поверхностей цилиндра и поршня.
вместе и благодаря
этот контакт, в системе существует трение. Побочный продукт
трение это тепло.
Тепло заставляет металл расширяться. Если поршень расширяется быстрее, чем
стенка цилиндра (это
делает), то трение увеличивается и может привести к повреждению. Это трение
сила в двигателе
уменьшается за счет использования смазки, такой как масло.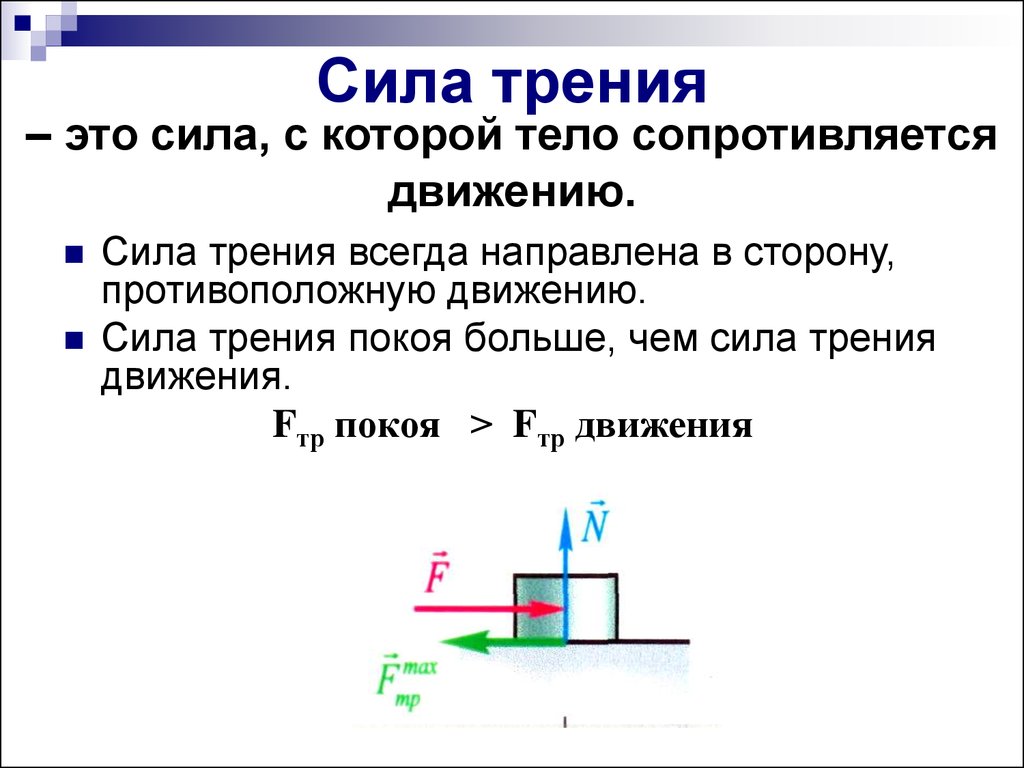 секунда Ньютона
закон гласит, что
если на блок не действует результирующая сила, то движение блока будет
оставаться в своем нынешнем
государство. Если мы начнем прикладывать силу к бруску параллельно плоскости (доске),
блок изначально остается
в состоянии покоя. Так как блок
не двигается,
на блок не действует результирующая сила. Это означает, что существует сила
действуя с величиной, равной величине нашего толчка, но в противоположном направлении, нейтрализуя прилагаемую нами силу.
Сила, удерживающая блок от движения, называется 9.0198 фрикционная
сила . Для этого обсуждения f будет использоваться для обозначения этой силы трения и F будет обозначать приложенную силу. Следует отметить, что как Ф увеличивается, как и f . Аналогично, как F убывает, f также уменьшается. Это потому, что f является силой сопротивления, а не активной силой. Так как блок еще не скользит,
мы звоним ф сила трения покоя ф с .
секунда Ньютона
закон гласит, что
если на блок не действует результирующая сила, то движение блока будет
оставаться в своем нынешнем
государство. Если мы начнем прикладывать силу к бруску параллельно плоскости (доске),
блок изначально остается
в состоянии покоя. Так как блок
не двигается,
на блок не действует результирующая сила. Это означает, что существует сила
действуя с величиной, равной величине нашего толчка, но в противоположном направлении, нейтрализуя прилагаемую нами силу.
Сила, удерживающая блок от движения, называется 9.0198 фрикционная
сила . Для этого обсуждения f будет использоваться для обозначения этой силы трения и F будет обозначать приложенную силу. Следует отметить, что как Ф увеличивается, как и f . Аналогично, как F убывает, f также уменьшается. Это потому, что f является силой сопротивления, а не активной силой. Так как блок еще не скользит,
мы звоним ф сила трения покоя ф с .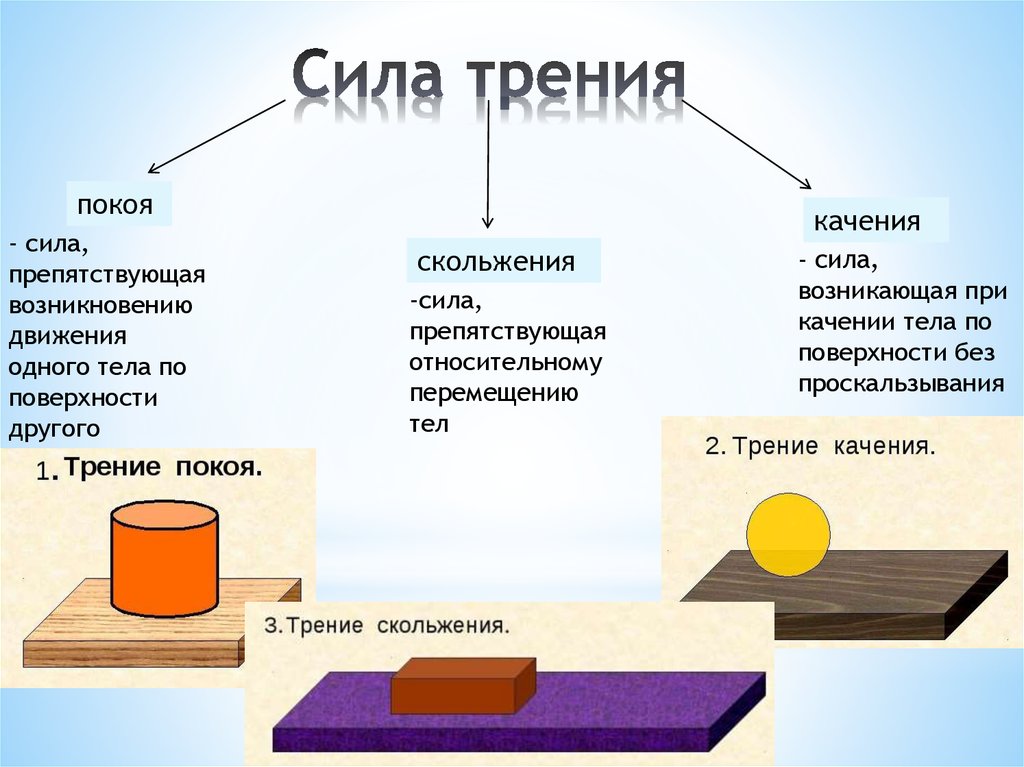 Должно
читателю должно быть очевидно, что если толкнуть блок достаточно сильно, он
в конце концов начинают скользить. Это говорит о том, что f s имеет
максимум. Говоря более формально, после F превышает определенное значение, блок будет проскальзывать. В точке, где
блок вот-вот соскользнет, f s на максимуме.
Должно
читателю должно быть очевидно, что если толкнуть блок достаточно сильно, он
в конце концов начинают скользить. Это говорит о том, что f s имеет
максимум. Говоря более формально, после F превышает определенное значение, блок будет проскальзывать. В точке, где
блок вот-вот соскользнет, f s на максимуме. Справедливо следующее неравенство:
Справедливо следующее неравенство: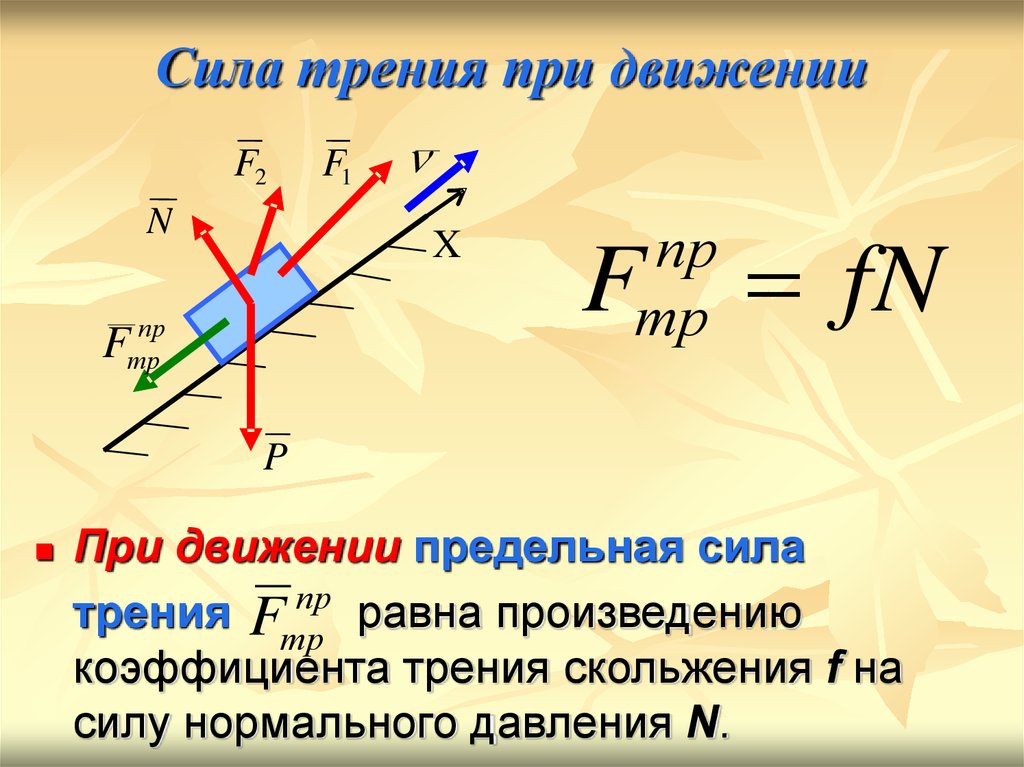 Экспериментально это было показано, чтобы быть правдой. (В ходе этого обсуждения мы сосредоточимся на
система
двух поверхностей, скользящих друг по другу.) Сила трения равна
прямо пропорциональный
к силе, прижимающей две поверхности друг к другу. Эта сила называется нормальное усилие, F N . Если поверхности горизонтальны,
нормальная сила равна
вес объекта, w . Это связано с тем, что вес является единственной силой, толкающей
поверхности вместе. Для ясности следует отметить, что нормальная сила
действует наоборот
направление веса. Другими словами, вес блока
пытаясь ускорить
блок к центру Земли, нижняя поверхность прикладывает
равная сила в
противоположное направление, удерживающее блок от падения (действие = противодействие).
Экспериментально это было показано, чтобы быть правдой. (В ходе этого обсуждения мы сосредоточимся на
система
двух поверхностей, скользящих друг по другу.) Сила трения равна
прямо пропорциональный
к силе, прижимающей две поверхности друг к другу. Эта сила называется нормальное усилие, F N . Если поверхности горизонтальны,
нормальная сила равна
вес объекта, w . Это связано с тем, что вес является единственной силой, толкающей
поверхности вместе. Для ясности следует отметить, что нормальная сила
действует наоборот
направление веса. Другими словами, вес блока
пытаясь ускорить
блок к центру Земли, нижняя поверхность прикладывает
равная сила в
противоположное направление, удерживающее блок от падения (действие = противодействие). Из этого следует что нормальную силу можно рассматривать как силу, действующую перпендикулярно
интерфейс
из двух поверхностей. По мере увеличения наклона сила веса блока
продолжает действовать «прямо вниз». В конце концов, когда плоскость достаточно наклонена, нормальная сила, а значит, и сила трения, уменьшается до точки, где максимальное статическое трение уже недостаточно велико, чтобы противостоять силе тяжести, действующей вдоль плоскости. Затем блок начинает скользить. Здесь необходимо отметить, что любая сила является
векторное количество. Это не будет подробно определено в этом проекте, но это
необходимо упомянуть несколько характеристик векторов, чтобы понять, как
силы в нашей системе меняются. Вектор — это величина, такая как сила или скорость,
полностью определяется величиной и направлением. Потому что направление
силы важны, нам нужен метод для описания того, какая сила
действуют в определенных направлениях. Используемое здесь соглашение — компоненты. Если
вектор направлен под углом, то он имеет горизонтальную составляющую и
вертикальная составляющая.
Из этого следует что нормальную силу можно рассматривать как силу, действующую перпендикулярно
интерфейс
из двух поверхностей. По мере увеличения наклона сила веса блока
продолжает действовать «прямо вниз». В конце концов, когда плоскость достаточно наклонена, нормальная сила, а значит, и сила трения, уменьшается до точки, где максимальное статическое трение уже недостаточно велико, чтобы противостоять силе тяжести, действующей вдоль плоскости. Затем блок начинает скользить. Здесь необходимо отметить, что любая сила является
векторное количество. Это не будет подробно определено в этом проекте, но это
необходимо упомянуть несколько характеристик векторов, чтобы понять, как
силы в нашей системе меняются. Вектор — это величина, такая как сила или скорость,
полностью определяется величиной и направлением. Потому что направление
силы важны, нам нужен метод для описания того, какая сила
действуют в определенных направлениях. Используемое здесь соглашение — компоненты. Если
вектор направлен под углом, то он имеет горизонтальную составляющую и
вертикальная составляющая.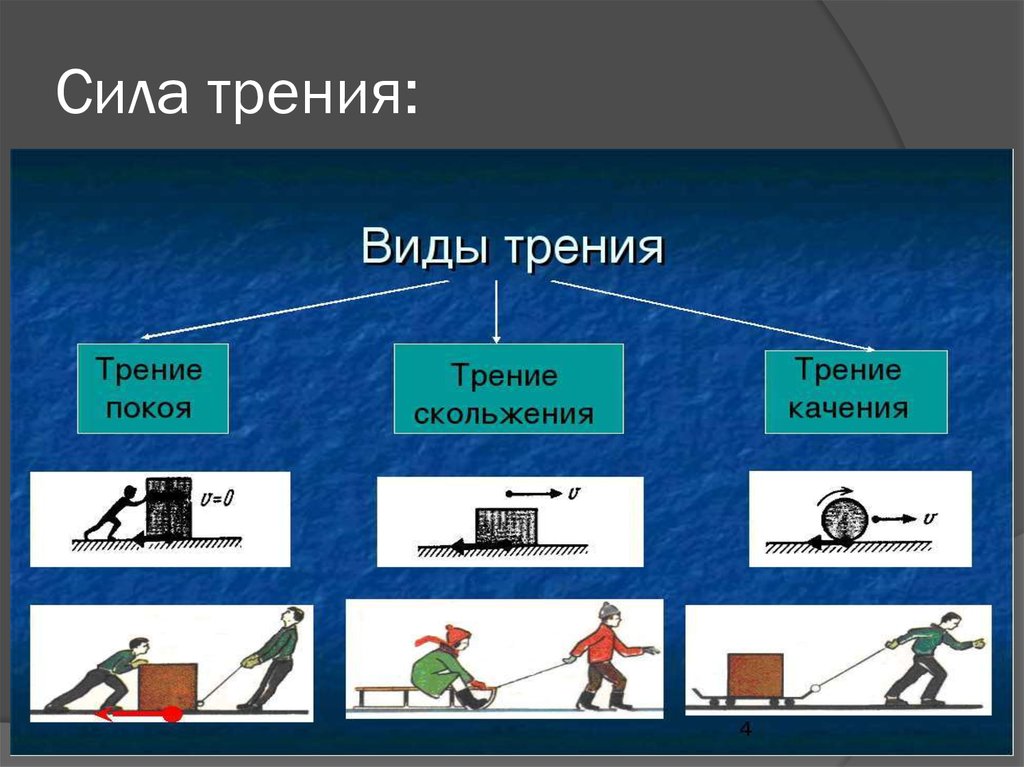 Когда доска выровнена, вся сила веса действует на
вертикальное направление. Следовательно, вертикальная составляющая силы веса равна силе веса, а горизонтальная составляющая силы веса равна
нуль. Когда доска наклонена, сила веса больше не состоит только из
вертикальный компонент, но вместо этого имеет как вертикальный, так и горизонтальный компоненты.
Так как нормальная сила действует с величиной, равной вертикальной
составляющая силы веса, по мере увеличения наклона доски нормальная
уменьшение силы.
Когда доска выровнена, вся сила веса действует на
вертикальное направление. Следовательно, вертикальная составляющая силы веса равна силе веса, а горизонтальная составляющая силы веса равна
нуль. Когда доска наклонена, сила веса больше не состоит только из
вертикальный компонент, но вместо этого имеет как вертикальный, так и горизонтальный компоненты.
Так как нормальная сила действует с величиной, равной вертикальной
составляющая силы веса, по мере увеличения наклона доски нормальная
уменьшение силы.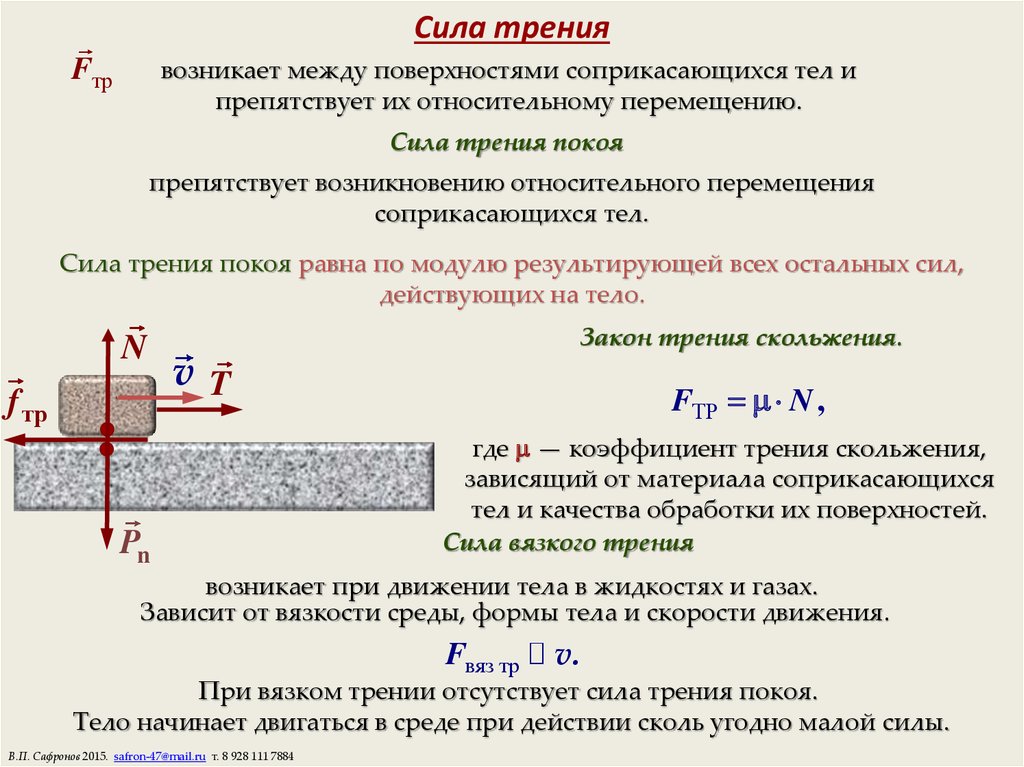
 Это также
случай, когда s > к .
Это также
случай, когда s > к . Сила трения = (коэффициент трения) x (нормальная сила) 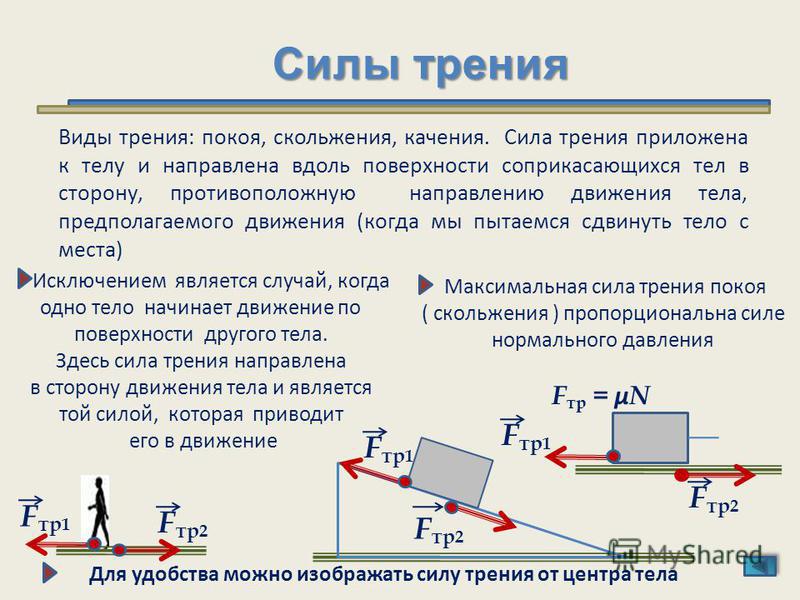
Назад в меню трения Определение, Формула, Сила, Пример, Причина
 На поверхности два объекта могут казаться очень гладкими, но на молекулярном уровне есть много шероховатых участков, вызывающих трение.
На поверхности два объекта могут казаться очень гладкими, но на молекулярном уровне есть много шероховатых участков, вызывающих трение. Статическая сила трения
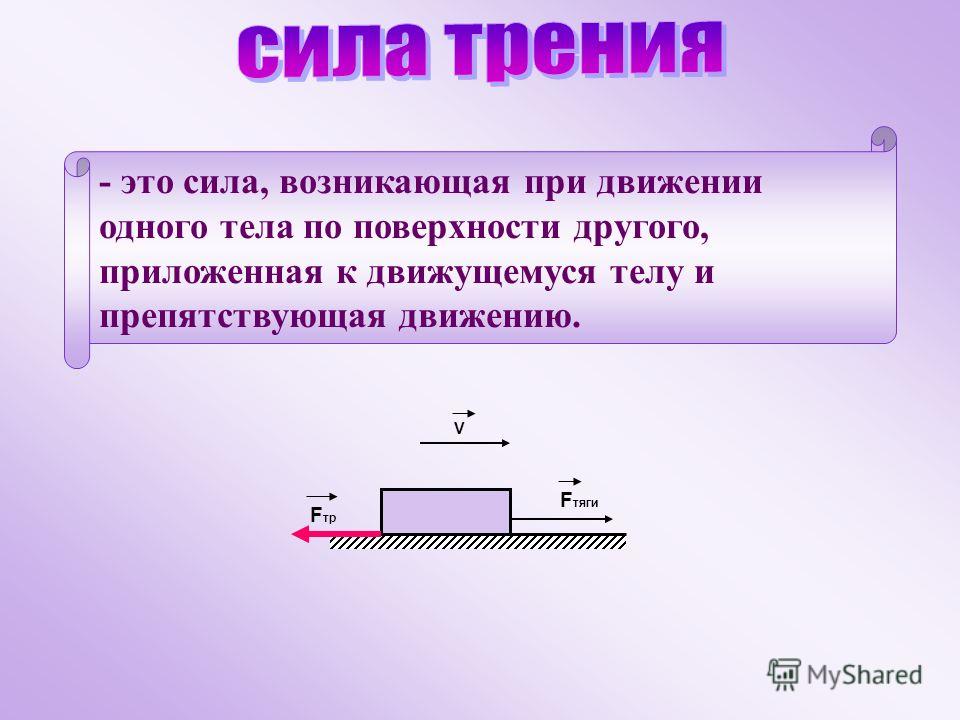
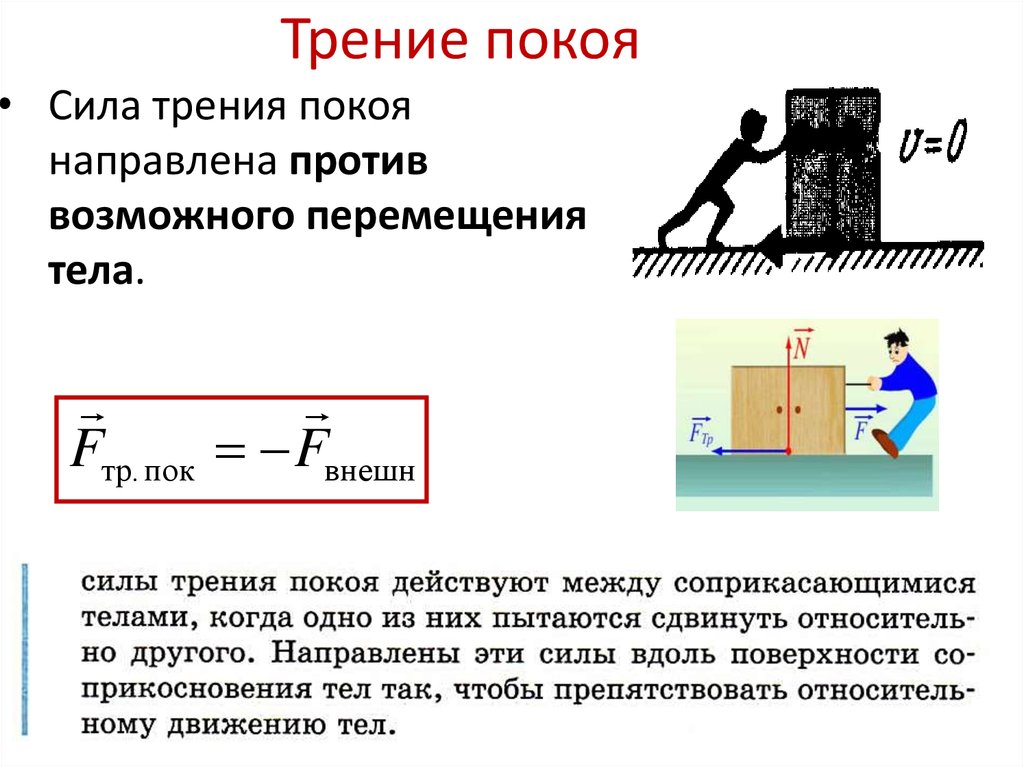
Кинетическая сила трения
 Кинетическое трение не увеличивается линейно с увеличением приложенной силы. Вначале кинетическая сила трения уменьшается по величине, а затем остается постоянной на всем протяжении.
Кинетическое трение не увеличивается линейно с увеличением приложенной силы. Вначале кинетическая сила трения уменьшается по величине, а затем остается постоянной на всем протяжении. Как и статическое трение, кинетическое трение также пропорционально нормальной силе. Константа пропорциональности в этом случае называется коэффициентом кинетического трения .
Как и статическое трение, кинетическое трение также пропорционально нормальной силе. Константа пропорциональности в этом случае называется коэффициентом кинетического трения . Rubber on concrete 0.  7
7 1.0 Steel on steel 0.57 0.74 Aluminium on steel 0.47 0,61 Стекло на стекле 0,40 0,94 Медь на стали 0,36 909 909 9028 013 0,530030 Геометрическая связь между статическим и кинетическим трением
 Величина кинетического трения уменьшается до тех пор, пока не будет достигнуто определенное значение. При этом значение трения остается почти постоянным с увеличением значения внешней силы.
Величина кинетического трения уменьшается до тех пор, пока не будет достигнуто определенное значение. При этом значение трения остается почти постоянным с увеличением значения внешней силы. Трение о наклонную плоскость
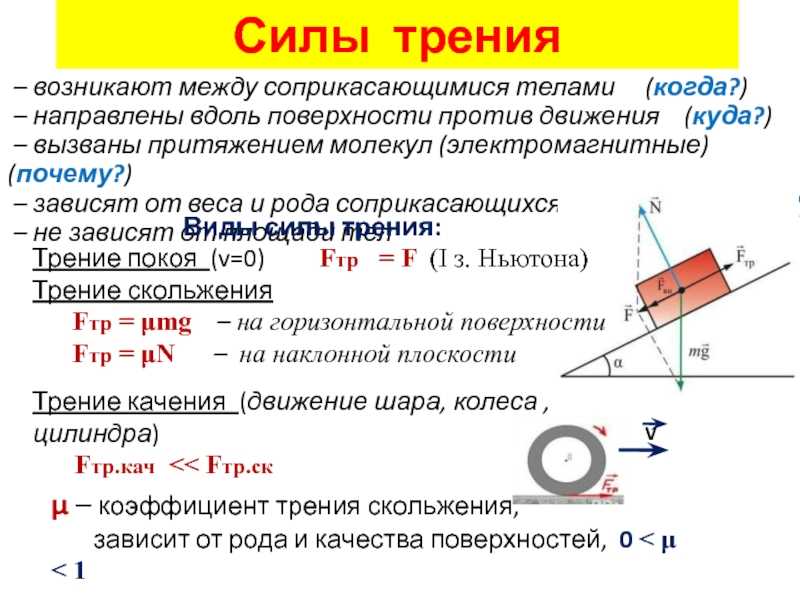 Вертикальная составляющая силы тяжести будет равна mg cosθ, что равно действующей на нее нормальной силе. Записав уравновешенные силы алгебраически, мы получим:
Вертикальная составляющая силы тяжести будет равна mg cosθ, что равно действующей на нее нормальной силе. Записав уравновешенные силы алгебраически, мы получим: 92).
92). Трение – основные выводы


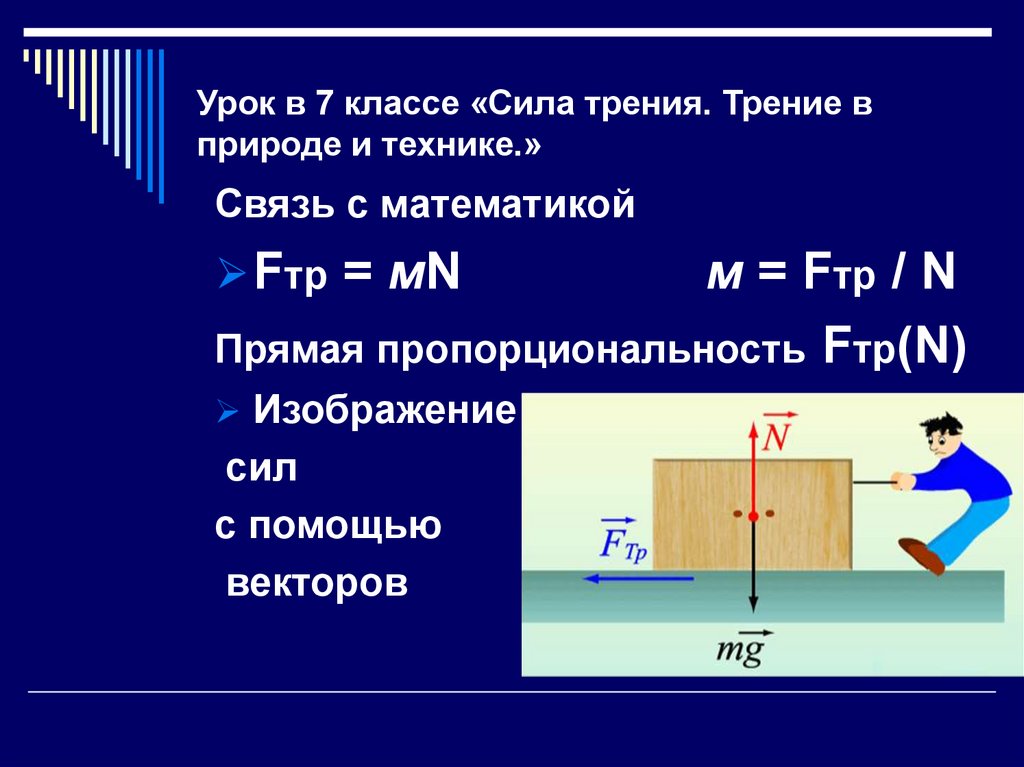 2$$
2$$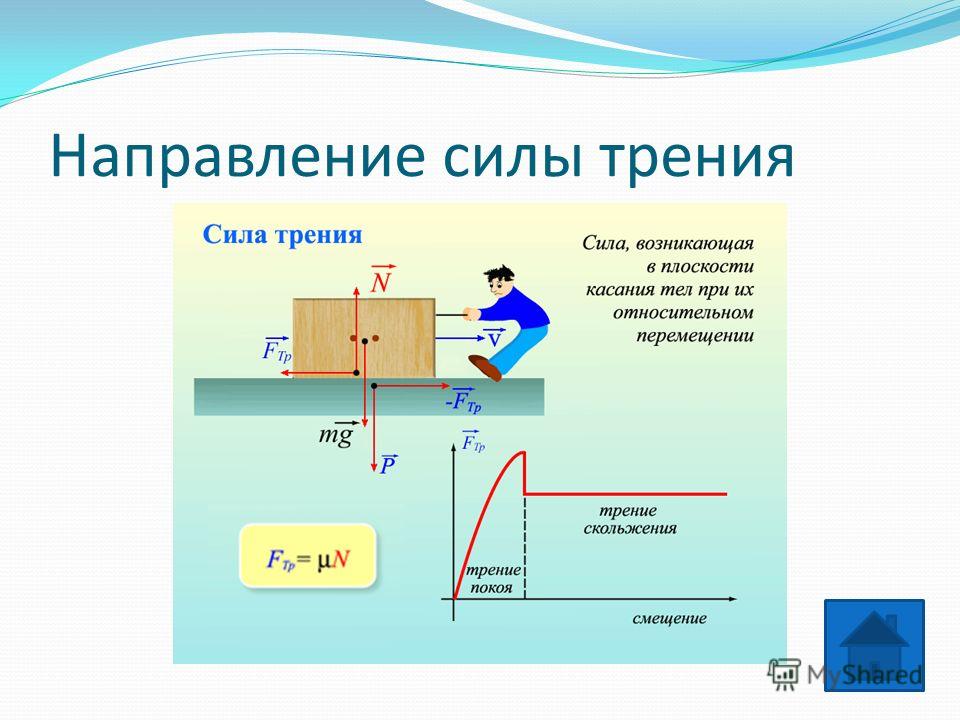 Модуль этой силы равен m · g.
Модуль этой силы равен m · g. Опыт показывает, что для поддержания неизменной скорости скольжения бруска по горизонтальной крышке стола необходимо продолжать действовать на брусок в направлении его движения определенной силой. Следовательно, и в этом случае на брусок со стороны стола в горизонтальном направлении действует сила, компенсирующая силу упругости. Эту силу называют силой сухого трения скольжения. Так как сумма силы сухого трения скольжения и силы упругости пружины равна нулю, брусок движется по поверхности стола равномерно. О том, как зависит сила сухого трения скольжения от скорости движения тела по опоре, мы поговорим в старших классах. Пока же будем считать, что
Опыт показывает, что для поддержания неизменной скорости скольжения бруска по горизонтальной крышке стола необходимо продолжать действовать на брусок в направлении его движения определенной силой. Следовательно, и в этом случае на брусок со стороны стола в горизонтальном направлении действует сила, компенсирующая силу упругости. Эту силу называют силой сухого трения скольжения. Так как сумма силы сухого трения скольжения и силы упругости пружины равна нулю, брусок движется по поверхности стола равномерно. О том, как зависит сила сухого трения скольжения от скорости движения тела по опоре, мы поговорим в старших классах. Пока же будем считать, что Поэтому модуль силы реакции стола N2 должен возрасти в два раза по сравнению с предыдущим случаем и стать равным 2m · g (сравните рис. 114 и 115).
Поэтому модуль силы реакции стола N2 должен возрасти в два раза по сравнению с предыдущим случаем и стать равным 2m · g (сравните рис. 114 и 115). Тогда μ = Fmax / N.
Тогда μ = Fmax / N. Этот факт был обнаружен еще нашими предками. Для перемещения тяжелых грузов они подкладывали под них катки (рис. 116). По этой же причине на транспорте используют колеса. Опыт показывает, что силы трения качения уменьшается с увеличением твердости катящегося тела и поверхности, по которой оно катится. Поэтому в подшипниках (рис. 117) используют шарики (1) или ролики (2), изготовленные из твердых сплавов. Подшипники получили широкое распространение в технике. Они позволяют заменить скольжение на качение и тем самым уменьшить силы трения.
Этот факт был обнаружен еще нашими предками. Для перемещения тяжелых грузов они подкладывали под них катки (рис. 116). По этой же причине на транспорте используют колеса. Опыт показывает, что силы трения качения уменьшается с увеличением твердости катящегося тела и поверхности, по которой оно катится. Поэтому в подшипниках (рис. 117) используют шарики (1) или ролики (2), изготовленные из твердых сплавов. Подшипники получили широкое распространение в технике. Они позволяют заменить скольжение на качение и тем самым уменьшить силы трения. Однако при возникновении такого движения силы вязкого трения увеличиваются по мере роста скорости. Этим объясняется, почему находящуюся на плаву многотонную баржу может стронуть с места один человек. Эту баржу может заставить двигаться и легкий ветерок.
Однако при возникновении такого движения силы вязкого трения увеличиваются по мере роста скорости. Этим объясняется, почему находящуюся на плаву многотонную баржу может стронуть с места один человек. Эту баржу может заставить двигаться и легкий ветерок.
 Какие способы уменьшения (увеличения) сил трения вы знаете?
Какие способы уменьшения (увеличения) сил трения вы знаете?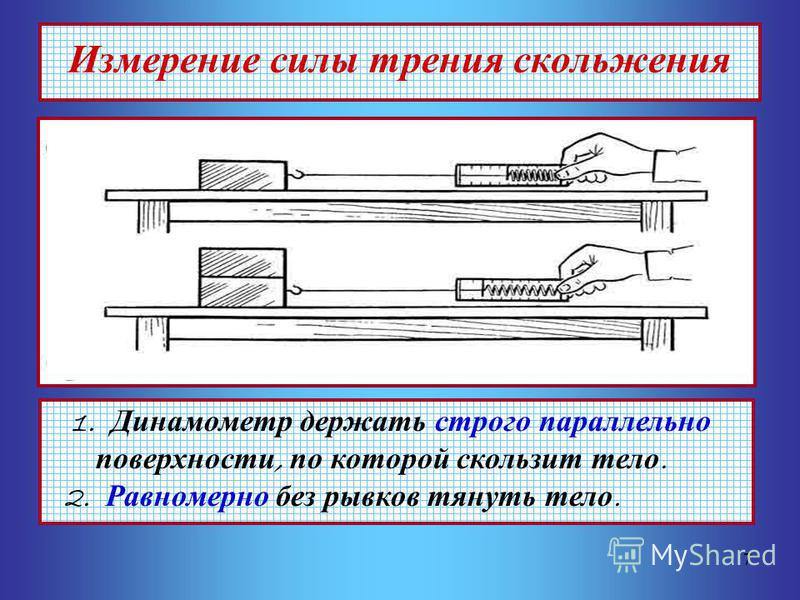 Для того чтобы сдвинуть его с места, потребовалось приложить к нему в горизонтальном направлении силу, модуль которой равен 200 Н. Определите массу ящика, если коэффициент трения ящика о пол равен 0,5.
Для того чтобы сдвинуть его с места, потребовалось приложить к нему в горизонтальном направлении силу, модуль которой равен 200 Н. Определите массу ящика, если коэффициент трения ящика о пол равен 0,5.

 Им осталось пройти совсем немного. Домик
совы был уже виден.
Им осталось пройти совсем немного. Домик
совы был уже виден.
 Почему? (вспомните строение
вещества)
Почему? (вспомните строение
вещества)

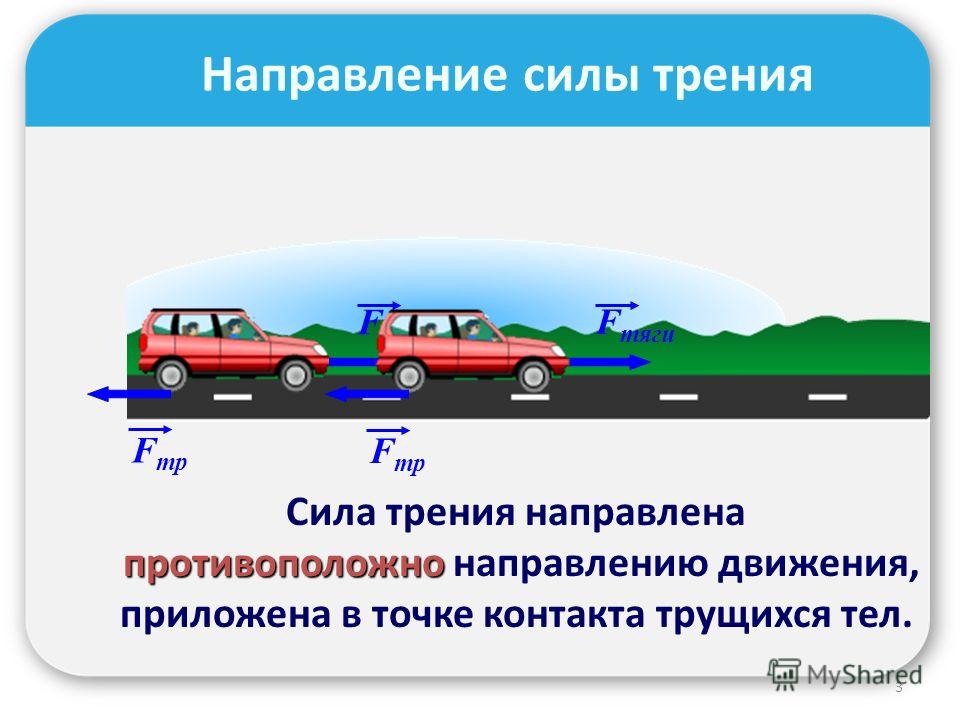
 Заметить показания динамометра в тот момент,
когда брусок сдвинется с места – это и будет сила
трения покоя (показания записать в таблицу)
Заметить показания динамометра в тот момент,
когда брусок сдвинется с места – это и будет сила
трения покоя (показания записать в таблицу) 1 Кинематика
1 Кинематика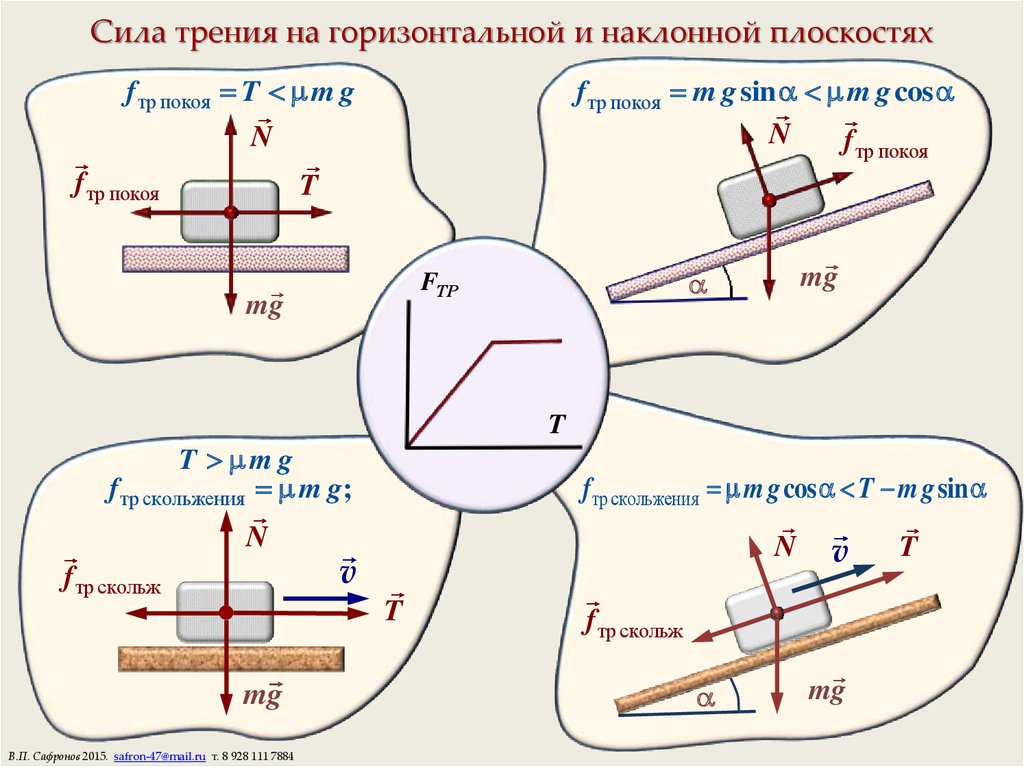 3 Магнетизм
3 Магнетизм Квантовая теория
Квантовая теория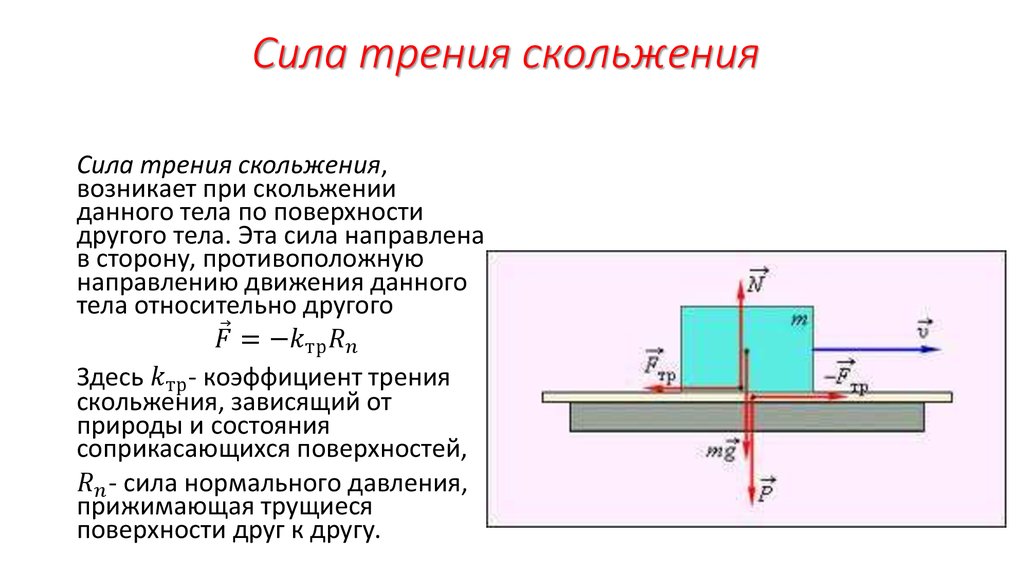 Тогда сила сопротивления трения может быть записана:
Тогда сила сопротивления трения может быть записана: На самом деле трение — очень сложное явление, которое нельзя представить простой моделью. Почти каждому простому утверждению, которое вы делаете о трении, можно противопоставить конкретные примеры обратного. Утверждение, что более шероховатые поверхности испытывают большее трение, звучит достаточно безопасно — два куска грубой наждачной бумаги, очевидно, будут труднее двигаться друг относительно друга, чем два куска мелкой наждачной бумаги. Но если два куска плоского металла делать все более гладкими, вы достигнете точки, в которой сопротивление относительному движению возрастет. Если вы сделаете их очень плоскими и гладкими и удалите все поверхностные загрязнения в вакууме, гладкие плоские поверхности фактически прилипнут друг к другу, образуя то, что называется «холодным сварным швом».
На самом деле трение — очень сложное явление, которое нельзя представить простой моделью. Почти каждому простому утверждению, которое вы делаете о трении, можно противопоставить конкретные примеры обратного. Утверждение, что более шероховатые поверхности испытывают большее трение, звучит достаточно безопасно — два куска грубой наждачной бумаги, очевидно, будут труднее двигаться друг относительно друга, чем два куска мелкой наждачной бумаги. Но если два куска плоского металла делать все более гладкими, вы достигнете точки, в которой сопротивление относительному движению возрастет. Если вы сделаете их очень плоскими и гладкими и удалите все поверхностные загрязнения в вакууме, гладкие плоские поверхности фактически прилипнут друг к другу, образуя то, что называется «холодным сварным швом».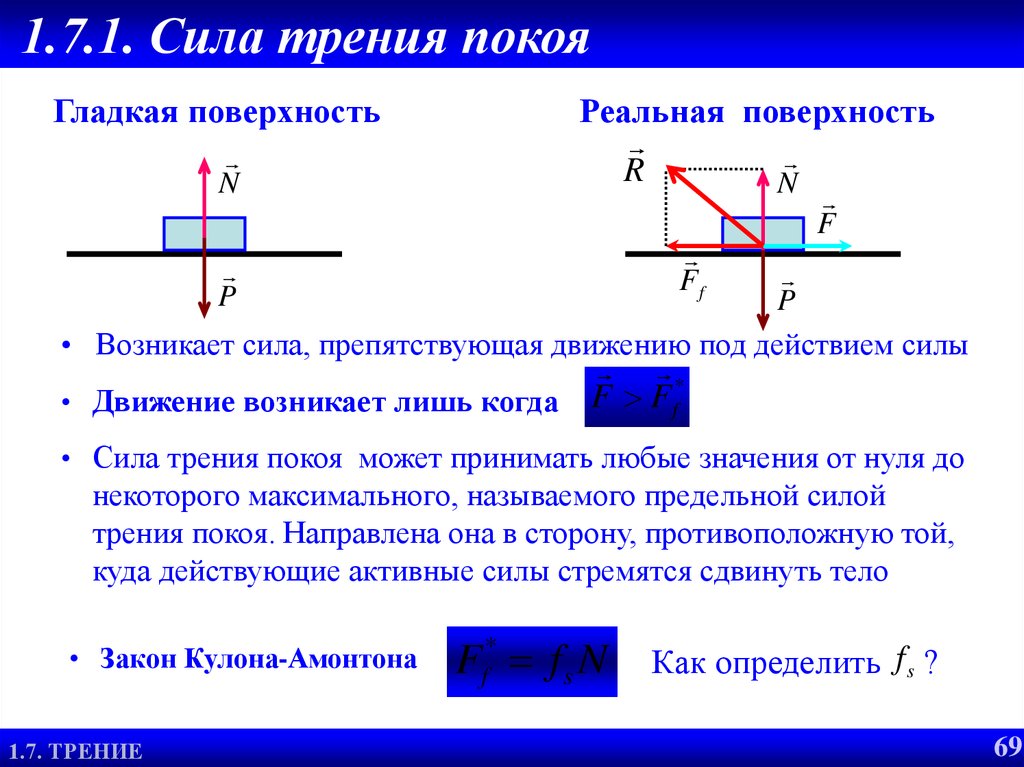
 Гладкие стеклянные пластины при контакте демонстрируют гораздо большее сопротивление трению относительному движению, чем более шероховатое матовое стекло.
Гладкие стеклянные пластины при контакте демонстрируют гораздо большее сопротивление трению относительному движению, чем более шероховатое матовое стекло.

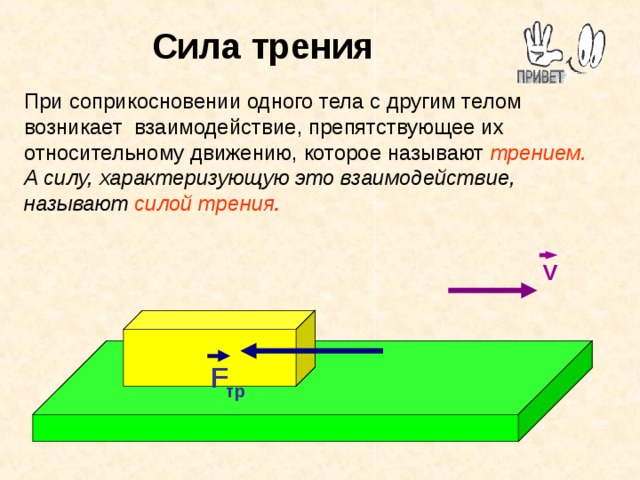
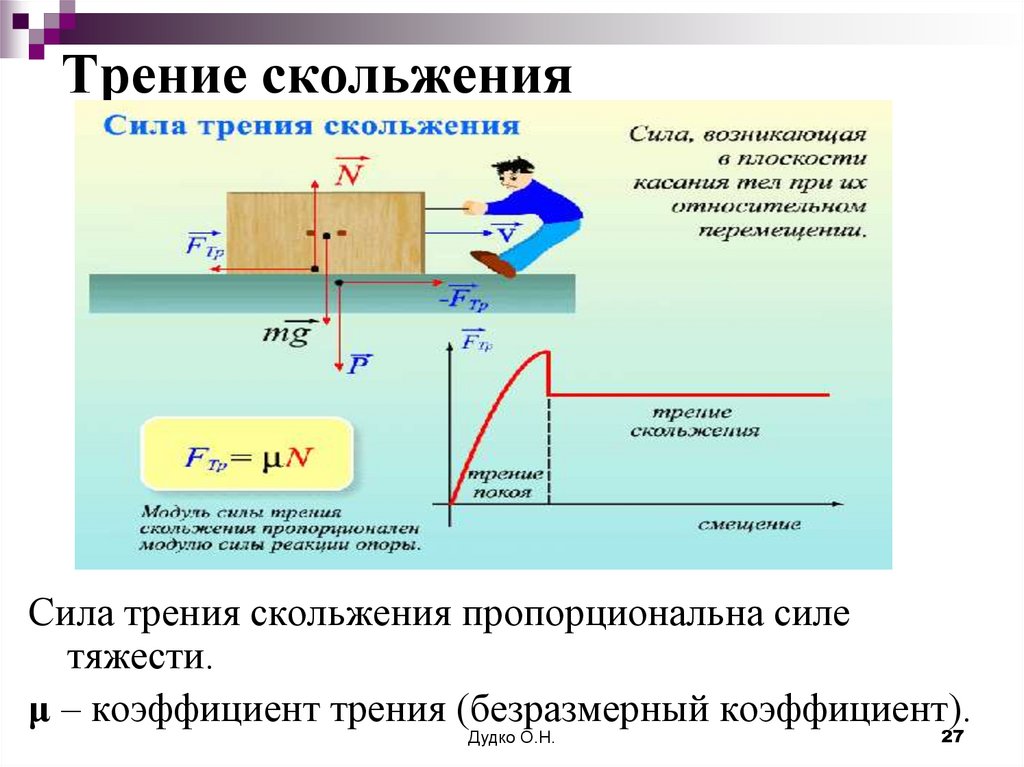

 Влияние трибологии на глобальное потребление энергии, затраты и выбросы. Трение 5 , 263–284 (2017).
Влияние трибологии на глобальное потребление энергии, затраты и выбросы. Трение 5 , 263–284 (2017). Проц. Р. Соц. Математика. физ. англ. науч. 243 , 190–205 (1957).
Проц. Р. Соц. Математика. физ. англ. науч. 243 , 190–205 (1957).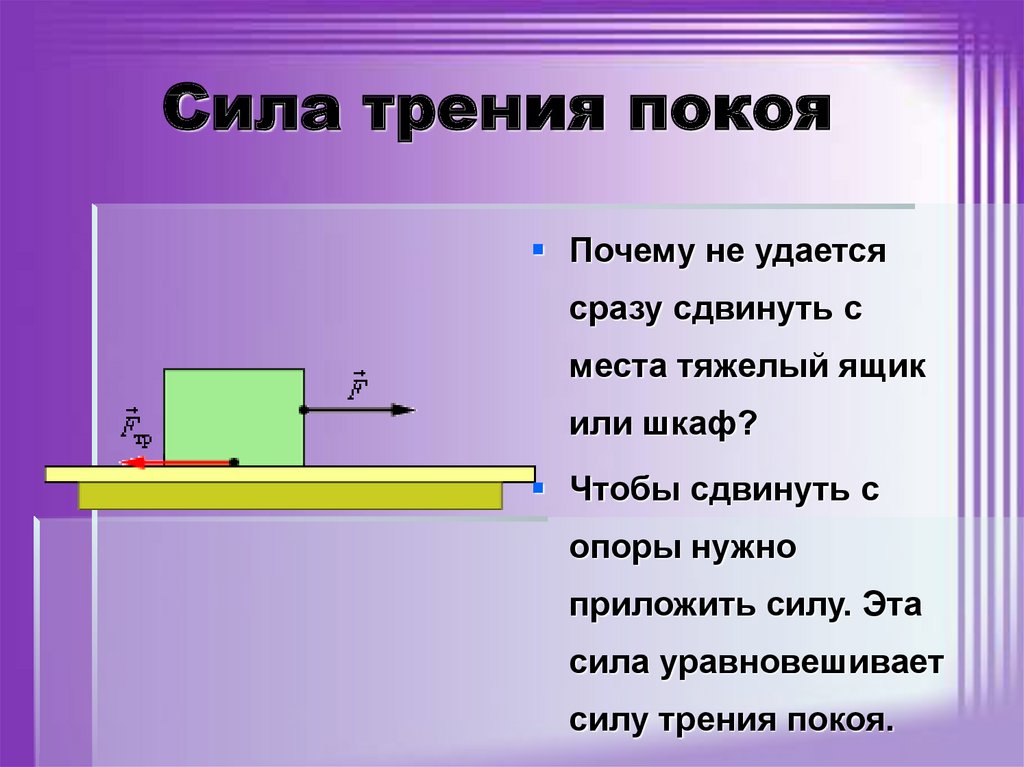 , Демелио, Г., Барбер, Дж. Р. и Джанг, Ю. Х. Линейный упругий контакт профиля Вейерштрасса. Проц. R Соц. Математика. физ. англ. науч. 456 , 387–405 (2000).
, Демелио, Г., Барбер, Дж. Р. и Джанг, Ю. Х. Линейный упругий контакт профиля Вейерштрасса. Проц. R Соц. Математика. физ. англ. науч. 456 , 387–405 (2000).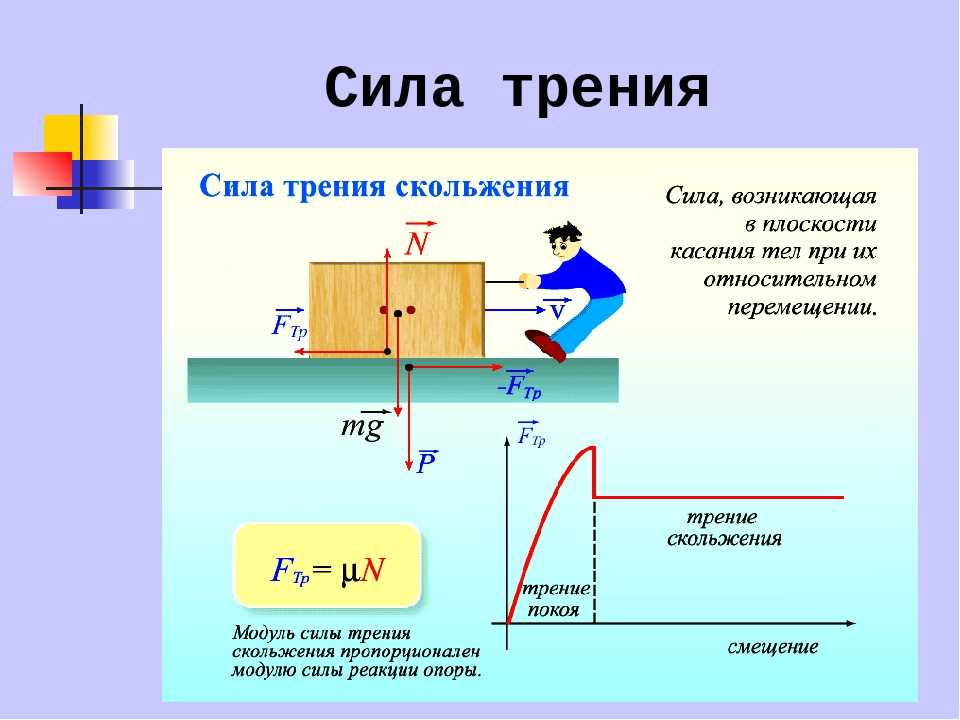 , Ван дер Гиссен, Э. и Лю, X. Анализ пластичности градиента деформации упругопластического контакта между шероховатыми поверхностями. Дж. Мех. физ. Solids 96 , 18–28 (2016).
, Ван дер Гиссен, Э. и Лю, X. Анализ пластичности градиента деформации упругопластического контакта между шероховатыми поверхностями. Дж. Мех. физ. Solids 96 , 18–28 (2016). Wear 58 , 331–340 (1980).
Wear 58 , 331–340 (1980).