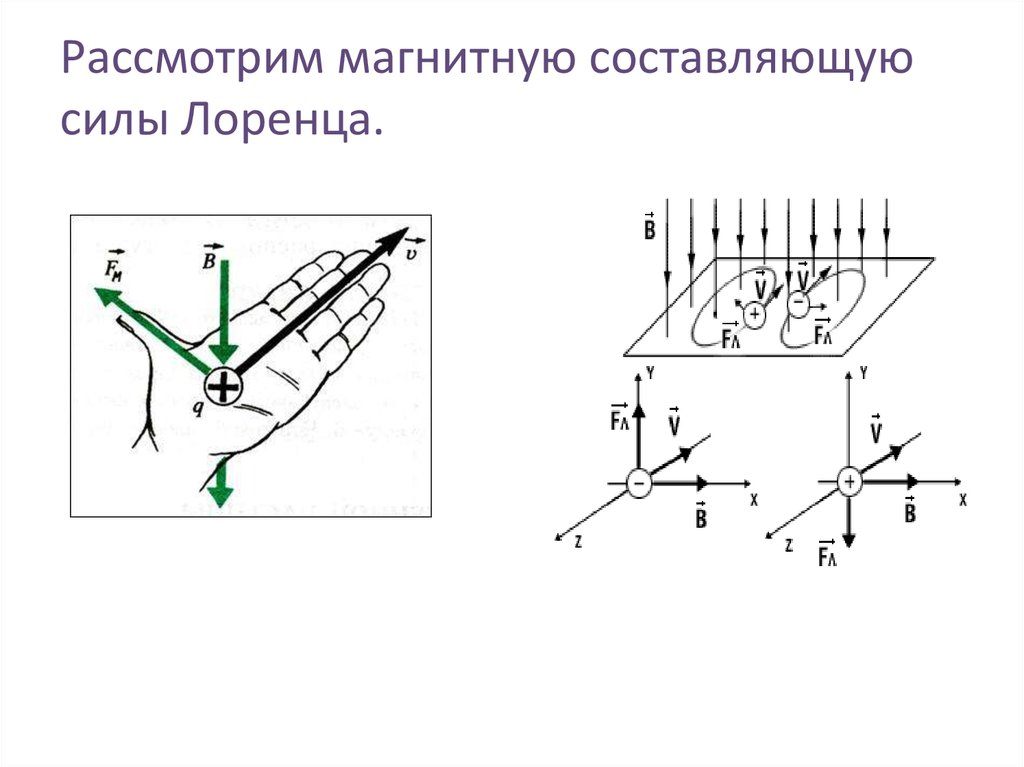
Вывести силу Лоренца из закона Максвелла, в котором частная производная от магнитного поля заменена на полную
%PDF-1.4 % 66 0 obj >/Metadata 65 0 R/PieceInfo>>>/Pages 12 0 R/PageLayout/OneColumn/StructTreeRoot 67 0 R/Type/Catalog/LastModified(D:20120804141326)/PageLabels 62 0 R/OutputIntents[64 0 R]>> endobj 65 0 obj >stream Acrobat Distiller 8.3.1 (Windows)HomeD:20120804111259Acrobat PDFMaker 8.1 for Word2012-08-04T14:13:26+03:002012-08-04T14:13:21+03:002012-08-04T14:13:26+03:00uuid:5c110c13-e87f-4e49-a7e2-f2f94188b133uuid:1af8b30d-a337-4a14-b1c3-d089448e6d52
Магнитометры силы Лоренца | АО СКАН
Рынок недорогих МЭМС-датчиков растет быстрыми темпами, частично благодаря экспоненциальному росту на смартфоны и систем помощи водителю. Компас или магнитометр является важным компонентом для использования в этих устройствах функции навигации и определения местоположения. В то время как магниторезистивные (MR) магнитометры и магнитометры на эффекте Холла являются доминирующими технологиями в существующих электронных компасах, магнитометры силы Лоренца имеют некоторые заметные преимущества, включая:
- Нет необходимости в каких-либо специализированных магнитных материалах
- Нет необходимости в магнитных концентраторах для измерения полей, параллельных устройству, и
- Простая интеграция с МЭМС гироскопами и акселерометрами, которые в настоящее время используются в бытовой электронике
Благодаря этим преимуществам увеличиваются научно-исследовательские работы по разработке практических магнитометров силы Лоренца на основе МЭМС.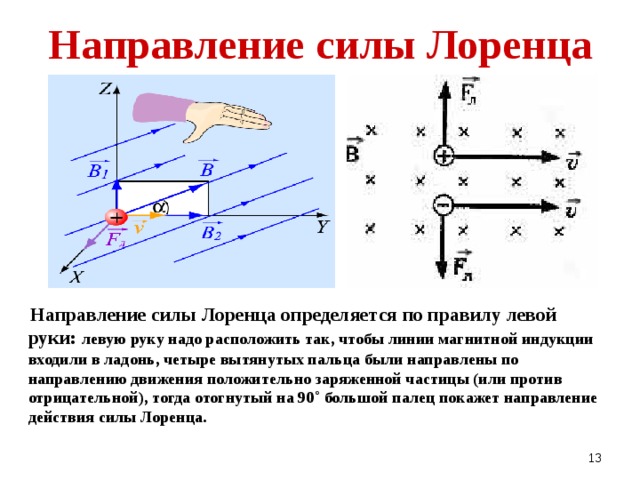
Работа в этой области направлена на снижение энергопотребления и шума [1], а также на интеграцию с монолитными инерциальными МЭМС с 9 степенями свободы [2].
Задачи проектирования
Чувствительность, шум, гистерезис, линейность, динамический диапазон, надежность и производительность — все это важные параметры для магнитометров на основе МЭМС. Инженеры-конструкторы должны оптимизировать работу устройства в соответствии с этими критериями, одновременно снижая стоимость, форм-фактор и время выхода на рынок.
Магнитометры силы Лоренца мультифизические по своей природе. Конструкция этих устройств должна включать анализ резонансных частот, силы Лоренца и емкостного выхода. Сопутствующая схема обычно требует точной модели магнитометра для того, чтобы спроектировать управление переменным током, усилитель измерения емкости, АЦП и обработку выходного сигнала. Конструкция системы может также включать в себя анализ шума для датчика и схемы, а также исследование температурной стабильности.
Рисунок 1: Изображение под микроскопом (слева), стрелками, указывающими ток возбуждения в направлении y+, и схемой измерения (справа) магнитометра силы Лоренца из [1]. Использовано повторно с разрешения автора.
Методология мультифизического проектирования
Частота срабатывания и приложение силы Лоренца
Магнитометр, показанный на Рисунке 1 (также называемый «магнитометр UC Davis»), использует микроструктуру, показанную на Рисунке 2, для измерения двухосного поля B. Переменный ток передается через структуру в направлении y+.
Рисунок 2: Модель MEMS+ магнитометра UC Davis (вверху), и сила Лоренца за счет взаимодействия тока управления и полей Bz (внизу слева), и Bx (внизу справа)
Для увеличения реакции, частоты сигнала переменного тока согласованы с частотами механических колебаний, соответствующими направлению x, движению в плоскости и направлению z, движению вне плоскости. Результаты модального анализа в MEMS + показаны на рисунке 3.
Рисунок 3: Модальный анализ MEMS+ для режима измерения Bz в плоскостном режиме на частоте 49,7 кГц (слева) и режима измерения Bx вне плоскостного режима на частоте 112 кГц (справа).
Емкостное измерение полей Bz и Bx
Измерение Bz обеспечивается дифференциальной емкостью между пальцами электростатической гребенки x + и x-, а измерение Bx обеспечивается емкостью на одном электроде под микроструктурой, как показано на рисунке 4.
Рисунок 4: Модель MEMS +, показывающая измерение дифференциальной емкости для Bz (слева, выделен только конденсатор x +) и измерение одиночной емкости для Bx через электрод под микроструктурой (справа).
Результаты измерения для полей Bz и Bx показаны на рисунке 5. Обратите внимание, что частота переменного тока для каждого поля измерения (слева) соответствует рассчитанной частоте для каждого режима измерения в модальном анализе MEMS+ (справа).
Рисунок 5: Емкостной выходной сигнал для Bz (слева) и Bx (справа), рассчитанный MEMS+
Источники
- Area-Efficient Three Axis MEMS Lorentz Force Magnetometer, V. Rouf et al, IEEE Sensors Journal, Vol 13, 2013.
- A Monolithic 9 Degree of Freedom (DOF) Capacitive Inertial MEMS Platform, I.
Источник: https://www.coventor.com/mems-solutions/magnetometers/
электромагнетизм — В чем разница между силой Лапласа и силой Лоренца?
спросил
Изменено 2 года, 8 месяцев назад
Просмотрено 4к раз
$\begingroup$
В настоящее время мы изучаем силу Лапласа, когда я искал, я нашел также силу Лоренца, и я сейчас потерялся, я пытался понять это, но не смог! $$F=I\vec l \клин \vec B$$ другого не понял!
- электромагнетизм
- силы
- терминология
$\endgroup$
3
$\begingroup$
Ну разница проста;
Сила Лапласа: сила, приложенная к проводнику, по которому проходит электрический ток и который находится в однородном магнитном поле.
Применим правило правой руки, чтобы определить его направление. Его интенсивность рассчитывается, как вы сказали, по следующему закону:
$$F=I\vec l \клин \vec B$$
Сила Лоренца: это сила, приложенная к электрическому заряду, движущемуся в электромагнитном поле, для определения направления мы снова используем правило правой руки, а ее интенсивность определяется как:
$$F=q\vec v \клин \vec B$$
Разница между этими силами очевидна, первая приложена к проволоке, по которой проходит электрический ток $I$, вторая носит более общий характер, и мы можем наблюдать, что электрический ток может быть преобразован в движение:
Давайте посчитаем: За время $t$ в этом проводе проходит заряд $q=It$, а скорость этих зарядов равна $\vec v=\frac{\vec l}{t}$
Перемножая $q$ и $\vec v $ получаем:
$$q\vec v= I\vec l$$
Вернемся к силе Лоренца; по определению это сила, приложенная к зарядам в электрическом или магнитном поле. Когда по проводнику проходит электрический ток, на электроны действует сила Лоренца, поэтому они могут перемещать провод, $$F=q\vec v \wedge \vec B = I(\vec l \wedge \vec B) = I.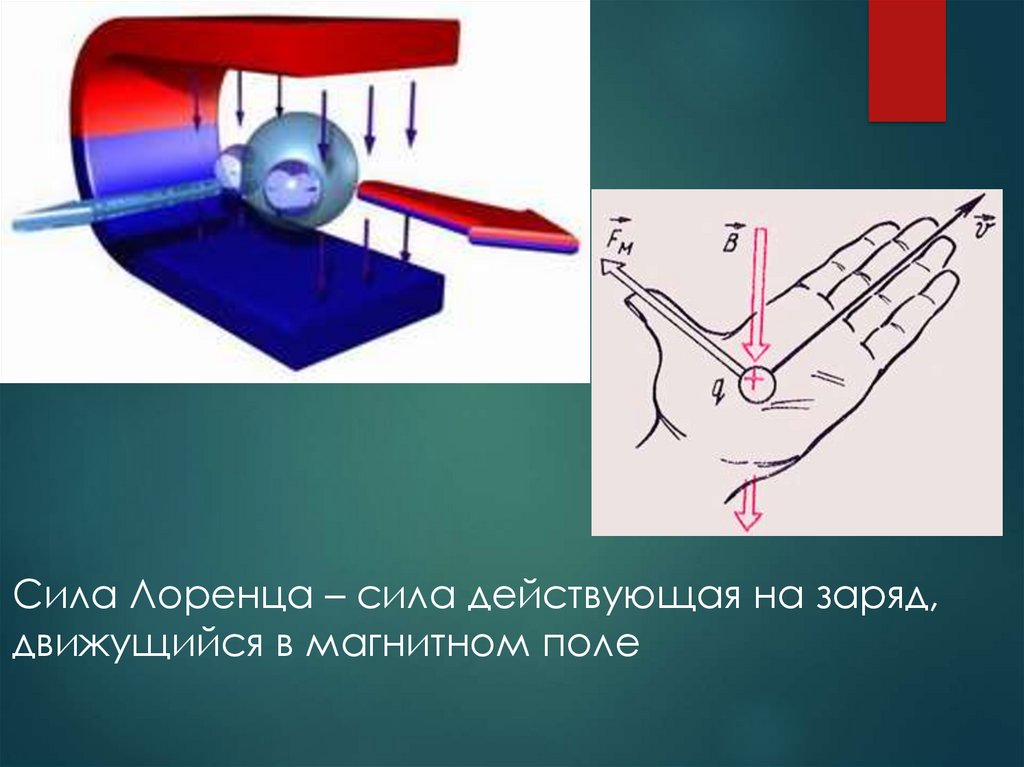
в заключение :
Сила Лапласа вызвана силой Лоренца, эта сила приложена к движущимся зарядам и вызывает движение любого провода в однородном магнитном поле.
Надеюсь, мое объяснение будет полезным, удачи!
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
сила Лоренца — ВикиЛекции
Спасибо за ваши комментарии.
Спасибо за рецензирование этой статьи.
Ваш отзыв не вставлен (допускается один отзыв на статью в день)!
Содержимое
- 1 Сила Лоренца
- 2 Заряженная частица в магнитном поле
- 2.1 Векторное представление
- 2.2 Расчет силы Лоренца
- 3 Использование
- 4 ссылки
- 4.1 Внешние ссылки
- 4.2 Ресурсы
Сила Лоренца F L — это сила, возникающая под действием магнитных и электростатических сил на заряженную частицу. Обычно только магнитная сила, действующая на движущуюся заряженную частицу v, называется силой магнитного поля Лоренца.
Хендрик Антон Лоренц[править | править источник]
Эйнштейн и Лоренц
(18. Червенце 1853 г. в Арнему – 4. Унора 1928 г. в Харлему)
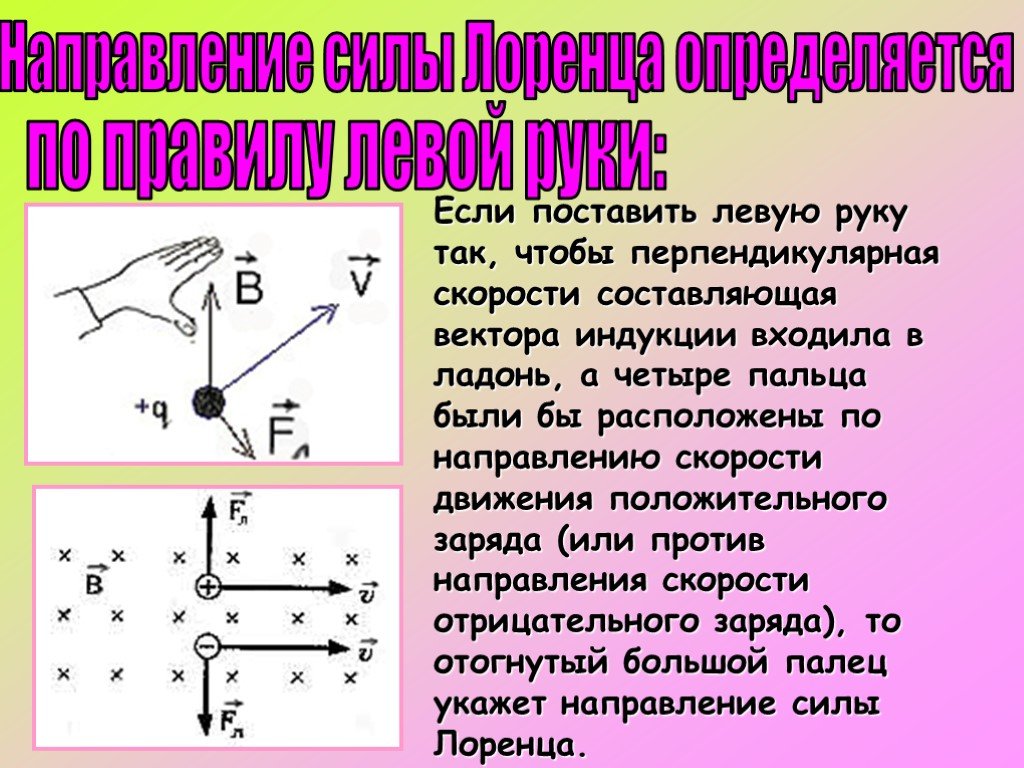Он получил эту премию вместе с Питером Зееманом за исследование влияния магнетизма на излучение. В возрасте 22 лет он защитил диссертацию в Лейденском университете. Работа имела такой успех, что в университете для него открылась новая кафедра теоретической физики. В течение своей жизни Хендрик Антон Лоренц занимался различными областями физики, такими как механика, термодинамика и исследования света. Его наиболее важные вклады относятся к области теории электронов, теории относительности и электромагнетизма.Заряженная частица в магнитном поле[править | править источник]
Траектории положительно, отрицательно и нейтрально заряженных частиц в однородном магнитном поле
Как положительно, так и отрицательно заряженные частицы, движущиеся в магнитном поле, которые встречаются отдельно или в проводнике , подвержены влиянию этого магнитного поля. Магнитное поле действует на них с магнитной силой, величина этой силы определяется соотношением:
Ф м = Bqv sin α
где:
- B – величина магнитной индукции (единица тесла Тл)
- q — величина заряда (единица кулон C) частица (единица м/с)
- sin α — угол, под которым направление движения частицы составляет с линиями магнитной индукции
На практике действие магнитной силы можно представить с помощью проводника с током и подковообразного магнита или в так называемой трубке Венельта.
