Дистанционный репетитор — онлайн-репетиторы России и зарубежья

КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?

Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!

КАК ВЫБРАТЬ репетитора

Выбрать репетитора самостоятельно

ИЛИ

Позвонить и Вам поможет специалист

8 (800) 333 58 91

* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК

ПОДАТЬ ЗАЯВКУ

Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41

Выбранные репетиторы

Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.

Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных

Вы также можете воспользоваться
расширенной формой подачи заявки

Как оплачивать и СКОЛЬКО ЭТО СТОИТ

от
800 до 5000 ₽

за 60 мин.

и зависит

ОТ ОПЫТА и
квалификации
репетитора

ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)

ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)

Оплата непосредственно репетитору, удобным для Вас способом

Почему я выбираю DisTTutor

БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД

ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА

ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ

НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.

ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА

ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО

376313 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА

уже сделали свой выбор

И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах

Владимир Александрович Кузьмин

«

Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить. Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии. Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.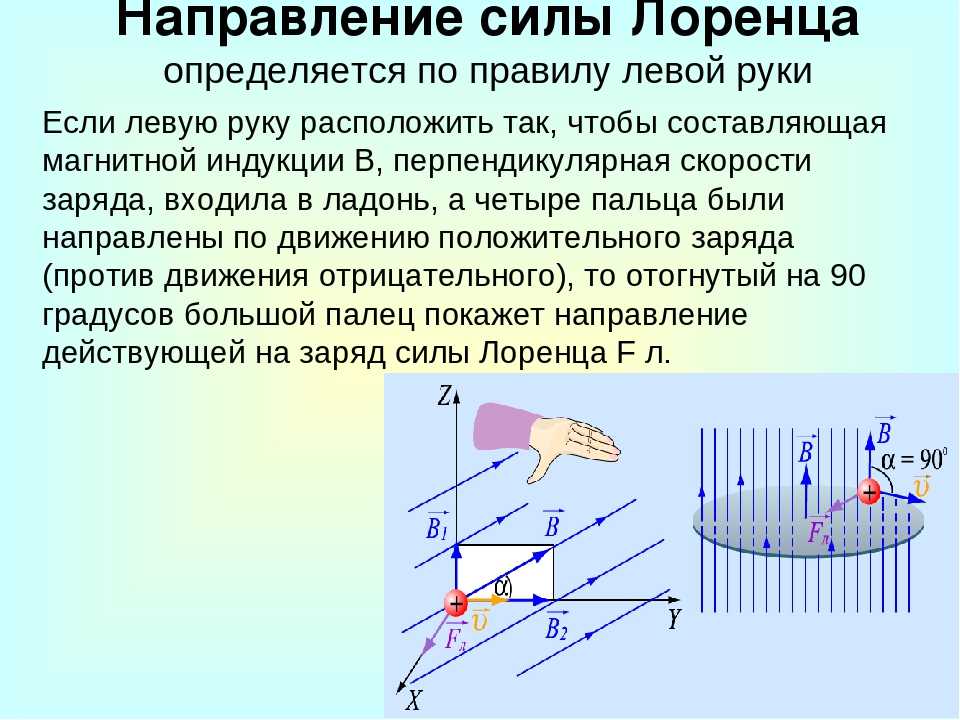

В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!

«

Вячеслав Юрьевич Матыкин

Чулпан Равилевна Насырова

«

Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!

«

Алина Крякина

Надежда Васильевна Токарева

«

Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания.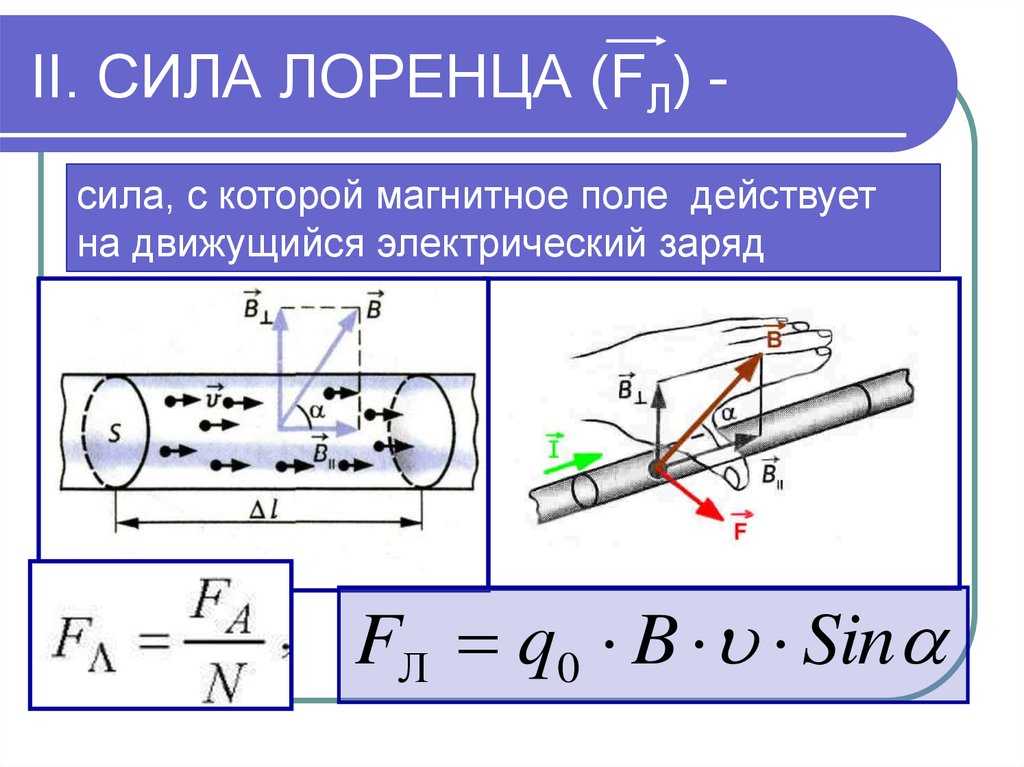

Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.

«

Эльмира Есеноманова

Ольга Александровна Мухаметзянова

«

Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.

«

Оксана Александровна

Клиентам

• Репетиторы по математике
• Репетиторы по русскому языку
• Репетиторы по химии
• Репетиторы по биологии
• Репетиторы английского языка
• Репетиторы немецкого языка

Репетиторам

• Регистрация
• Публичная оферта
• Библиотека
• Бан-лист репетиторов

Партнеры

• ChemSchool
• PREPY. RU
• Class

20.Сила Лоренца. Сила Ампера.

Сила ампера:

Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположном — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила , с которой магнитное поле действует на элемент объёма

dV проводника с током плотности , находящегося в магнитном поле с индукцией:

Элементарную силу взаимодействия   между элементамиипроводников, по которым протекают токиI₁ и I₂ можно определить из закона Ампера:

Сила Лоренца:

Выражение для силы, с которой магнитное поле действует на движущийся заряд, впервые получил голландский физик Хендрик Антон Лоренц (1895 г.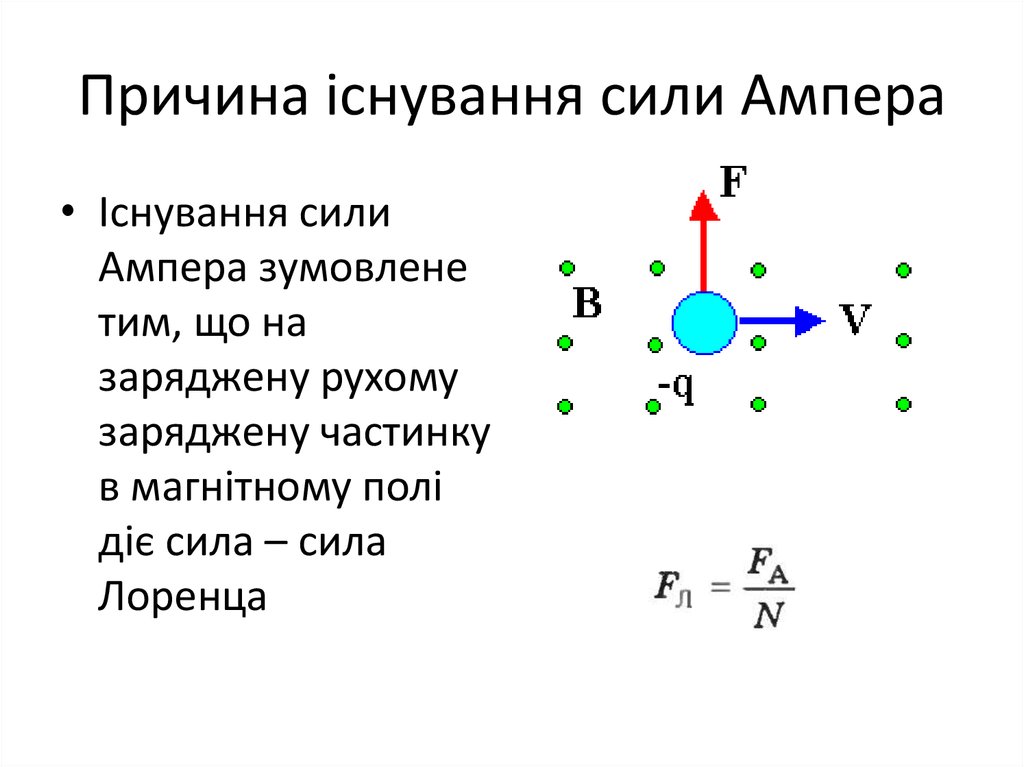 ). В его честь эта сила называется силой Лоренца.

Сила Лоренца — это сила, с которой магнитное поле действует на движущуюся в нем заряженную частицу.

Модуль силы Лоренца равен произведению модуля индукции магнитного поля B(вектор), в котором находится заряженная частица, модуля заряда q этой частицы, ее скорости υ и синуса угла между направлениями скорости и вектора индукции магнитного поля

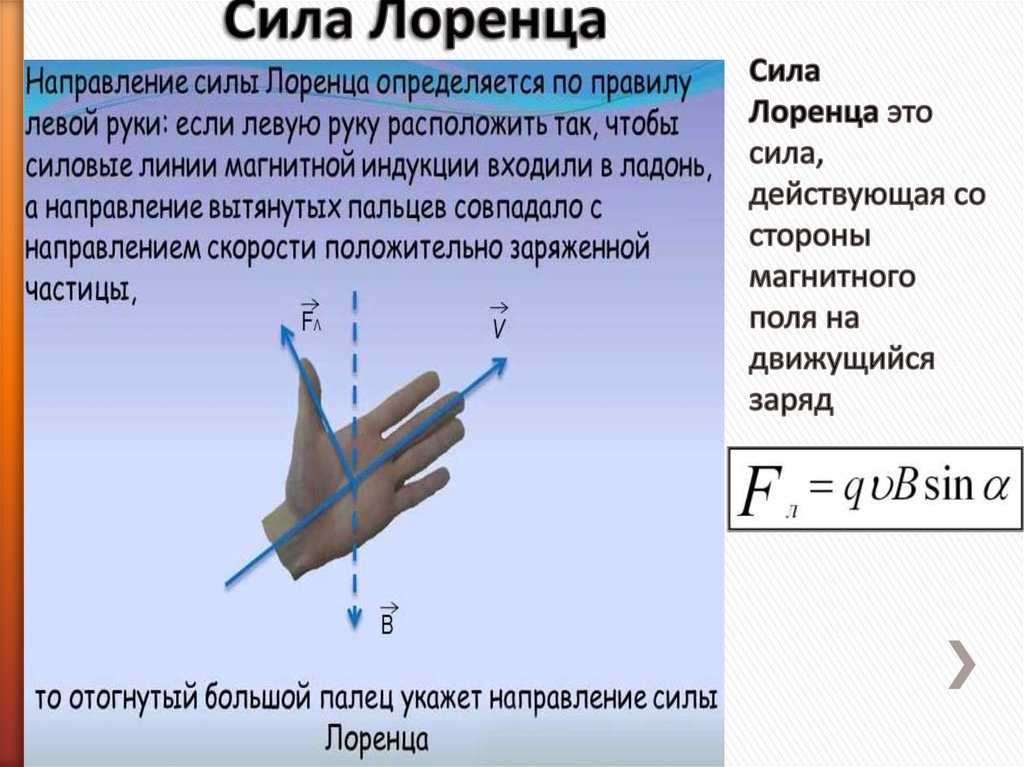
Для определения направления силы Лоренца применяют правило левой руки: если левую руку расположить так, чтобы вектор индукции магнитного поля () входил в ладонь, четыре вытянутых пальца указывали направления скорости движения положительно заряженной частицы (), тогда отогнутый на 90° большой палец укажет направление силы Лоренца () (рис. 3, а). Для отрицательной частицы четыре вытянутых пальца направляют против скорости движения частицы (рис. 3, б).

Поскольку величина B∙sin α представляет собой модуль компоненты вектора индукции, перпендикулярной скорости заряженной частицы, , то ориентацию ладони можно определять именно этой компонентой — перпендикулярная составляющая к скорости заряженной частицы должна входить в открытую ладонь левой руки.

Так как сила Лоренца перпендикулярна вектору скорости частицы, то она не может изменить значение скорости, а изменяет только ее направление и, следовательно, не совершает работы.

1. Если контур L с током I расположен таким образом, что вектор индукции однородного магнитного поля перпендикулярен плоскости этого контура, то сила действующая на элемент стремится его растянуть, тогда результирующая сила ровна 0.

Не будет иметь ни поступательного, ни вращательного движений.

2. Если вектор индукции однородного магнитного поля параллелен плоскости этого контура, то разделив площадь контура на маленькие участки шириной dZ, получим, что на элементы () контура будут действовать противоположные силы , в результате чего образуется элементарный вращающий момент .

Суммируя моменты для всех полосок, получим:

Из рассмотренных выше двух ситуаций следует, что вращающее действие оказывает только параллельная плоскости контура составляющая

Обобщая, можно записать:

Магнитное поле стремится повернуть контур с током так, чтобы и его потенциальная энергиябыла бы минимальной.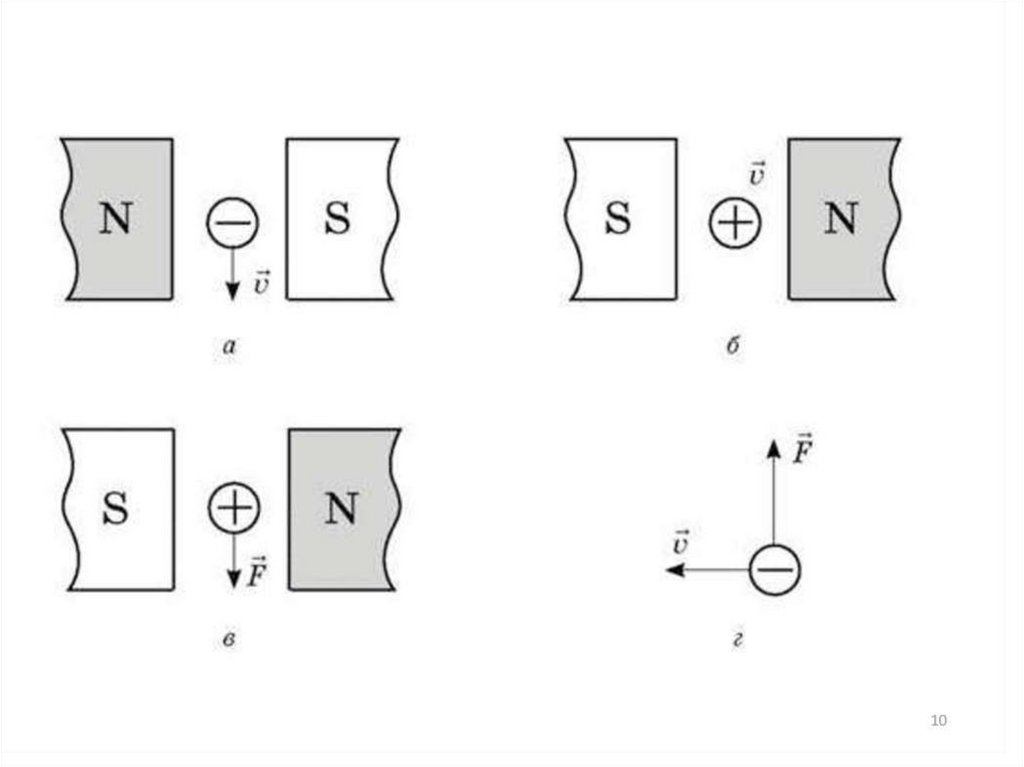 2\vec{F_{12}}$$

Где $i_2d\vec{\ell_2}$ и $i_1d\vec{\ell_1}$ — текущие элементы проводов. А круговой закон таков: $$\oint \vec B\cdot d\vec l=\mu_oI_{net}$$

Мой вопрос: какой закон был написан первым? Извлекает ли Ампер закон замыкания из приведенного выше уравнения силы? Является ли математическая форма уравнения магнитного поля исходной формой, которую написал Ампер, или она пришла позже других ученых, и если да, то какова исходная формулировка.

• электромагнетизм
• магнитные поля
• история

$\endgroup$

2

$\begingroup$

Насколько я знаю, Ампер пытался объяснить силу между проводниками по формуле, которую вы написали. Господствующим понятием того времени было действие на расстоянии, успешное как для гравитации, так и для электростатики.

Даже магнитные силы он объяснял как равнодействующую сил между микротоками в материалах.

Представление о магнитном поле, передающем силу между проводами, со временем возобладало, возможно, потому, что микротоки были слишком умозрительны, а железные пломбы Фарадея слишком убедительно доказывали существование магнитного поля.

$\endgroup$

0

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Закон силы Лоренца — изучите и поймите его онлайн

ЦЕРН — один из самых известных и крупнейших ускорителей частиц в мире. Эта лаборатория элементарных частиц была основана различными европейскими правительствами и стремится раскрыть больше секретов, скрытых в области физики элементарных частиц и стандартной модели. Большие ускорители частиц в центре работают, используя электрические и магнитные поля, чтобы воздействовать на частицы, разгоняя их до высоких скоростей и сталкивая частицы друг с другом. Это взаимодействие между заряженными частицами и электромагнитными полями называется сила Лоренца, , если вам интересно, как работает сила Лоренца и как она применяется в различных ситуациях, продолжайте читать!

Рис. 1 Невероятно сложное оборудование в центре ЦЕРН создано для использования силы Лоренца.

Определение закона силы Лоренца

Силу Лоренца можно определить следующим образом.

Сила Лоренца — это сила \(\vec{F}\) на заряженную частицу \(\vec{q}\), движущуюся со скоростью \(\vec{v}\) через магнитное поле \ (\vec{B}\) и электрическое поле \(\vec{E}\).

В частности, сила Лоренца учитывает действие и электрических и магнитных полей на заряженные частицы.

Уравнение закона силы Лоренца

Сила Лоренца принимает математическое уравнение

\[ \vec{F} = q\vec{E} + (q \vec{v} \times \vec{B} ),\]

где \(\vec{F}\) — вектор силы, действующей на заряженные частицы, измеренный в ньютонах \(\mathrm{N}\), \(q\) — заряд частиц, измеренный в кулонах \( \mathrm{C}\), \(\vec{v}\) — вектор скорости заряженной частицы, измеренный в \(\mathrm{\frac{m}{s}}\), \(\vec{B }\) — вектор магнитного поля, измеренный в теслах \(\mathrm{T}\), а \(\vec{E}\) — вектор электрического поля, измеренный в \(\mathrm{\frac{V}{m }}\).

Мы видим, что это уравнение состоит из двух компонентов; первый член в правой части представляет собой электрическую силу, тогда как второй член представляет собой магнитную силу.

Чтобы найти величину силы Лоренца, мы берем величину векторных величин, фигурирующих в приведенном выше уравнении. Для термина электрической силы это относительно просто, поскольку нам нужно только взять величину электрического поля \(|\vec{E}|\), умноженную на величину заряда \(q\).

С другой стороны, величина перекрестного произведения немного сложнее. Напомним, что при получении величины векторного произведения мы должны умножить величины двух векторов на синус угла между векторами. Это гарантирует, что мы берем перпендикулярные компоненты обоих векторов. Приходим к уравнению

\[ | \vec{a} \times \vec{b}| = |\vec{a}||\vec{b}| \sin(\theta),\]

где \(|\vec{a}|\) и \(|\vec{b}|\) — величины векторов \(\vec{a}\) и \(\vec{b}\) соответственно, а \(\theta\) — угол между двумя векторами.

Теперь мы можем применить это к нашему уравнению для силы Лоренца, чтобы найти, что величина силы Лоренца определяется выражением

\[ |\vec{F}| = q |\vec{E}|+ q|\vec{v}||\vec{B}|\sin(\theta),\]

, где \(\theta\) — угол между магнитным полем и скорость заряженной частицы, измеренная в радианах \(\mathrm{rad}\). Поскольку \(q\) является скалярной величиной, нам не нужно ничего с ней делать.

Вывод закона силы Лоренца

Одним из выводов, который можно сделать из определения силы Лоренца, является скорость заряженной частицы при движении в магнитном поле. Если мы предположим, что электрического поля нет, а есть только магнитное поле, мы можем видеть из векторного произведения, что результирующая сила Лоренца, действующая на заряженную частицу, всегда перпендикулярна направлению движения частицы. Следствием этого является кривизна траектории заряженной частицы. С какой силой мы уже встречались ранее, которая также действует в направлении, перпендикулярном движению объекта? 92}{r},\]

где \(F_{\mathrm{cent}}\) — центростремительная сила, измеряемая в ньютонах, \(\mathrm{N}\), \(m\) — масса объекта, измеренная в \(\mathrm{kg}\), \(v\) — скорость объекта, измеренная в \(\mathrm{\frac{m}{s}}\), а \(r\) — радиус вращения измеряется в \(\mathrm{м}\).

Теперь, когда мы знаем, что заряженная частица находится во вращательном движении, мы можем приравнять величину силы Лоренца и центростремительной силы, чтобы найти величину результирующей скорости из-за взаимодействия заряженной частицы с магнитным полем. Приравнивая и переставляя, находим 9{\bотмена{2}} \\v &= \frac{Bqr\sin(\theta)}{m}. \end{align}\]

При решении задач, связанных с любой из этих величин, мы можем изменить это уравнение, чтобы выделить величину, для которой нас интересует решение. Каково это количество, будет варьироваться от проблемы к проблеме.

Рис. 2. На электрон, движущийся в магнитном поле, действует сила Лоренца, вызывающая круговое движение.

Применение закона силы Лоренца

Во время экспериментов по физике в школе мы часто сталкиваемся с устройством, называемым электронно-лучевая трубка или электронная пушка. Эти устройства позволяют нам увидеть путь электронного луча, отклоняющегося из-за приложения внешнего электрического поля. Металлическая нить нагревается с одного конца, так что электроны в металле получают достаточную кинетическую энергию, чтобы вырваться на свободу. Поскольку электроны заряжены отрицательно, они притягиваются к положительно заряженному аноду на другом конце вакуумной трубки.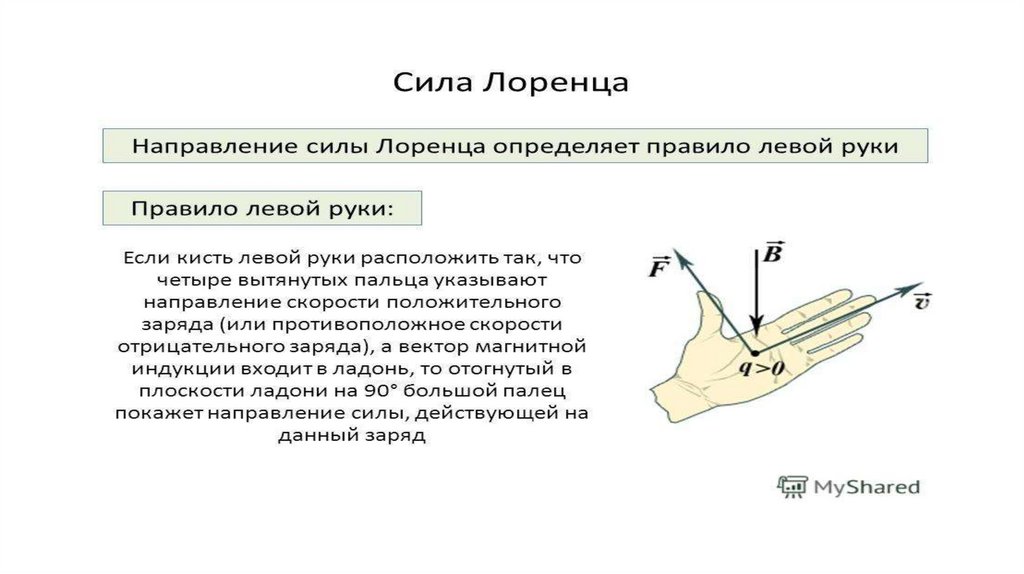 Кроме того, вакуумная камера, через которую проходят электроны, облицована флуоресцентным материалом, так что, когда электроны сталкиваются со стенками, они проявляются в виде света, видимого человеческим глазом. Наконец, искривление электронного пучка обусловлено взаимодействием силы Лоренца между заряженными электронами и окружающим электрическим полем. 9{-17} \, \mathrm{N} . \end{align} \]

Закон силы Лоренца – ключевые выводы

• Уравнение силы Лоренца задается выражением \(\vec{F} = q\vec{E} + (q \vec{v} \times \vec{B} ) \).

• Сила Лоренца учитывает действие как электрического, так и магнитного полей на заряженные частицы.

• Величина силы Лоренца определяется выражением \(|\vec{F}| = q |\vec{E}|+ q|\vec{v}||\vec{B}|\sin( \тета)\).

• Круговая скорость заряженной частицы, движущейся в магнитном поле, равна \(v = \frac{Bqr\sin(\theta)}{m}\).

• Сила Лоренца заставляет электронный пучок в электронно-лучевой пушке искривляться.