Физика. Понятия и определения.

 

 

 

 

 

 

 

Что такое сила?

Если тело ускоряется то на него что-то действует. А как найти это «что-то»? Например, что за силы действуют на тело вблизи поверхности земли? Это — сила тяжести, направленная вертикально вниз, пропорциональная массе тела и для высот, много меньших, чем радиус земли ${\large R}$, почти независящая от высоты; она равна

${\large F = \dfrac {G  \cdot m \cdot M}{R^2} = m \cdot g }$

где

${\large g = \dfrac {G  \cdot M}{R^2} }$

 

так называемое ускорение силы тяжести. В горизонтальном направлении тело будет двигаться с постоянной скоростью, однако движение в вертикальном направлении по второму закону Ньютона:

 

${\large m \cdot g = m \cdot \left ( \dfrac {d^2 \cdot x}{d \cdot t^2} \right ) }$

 

после сокращения ${\large m}$ получаем, что ускорение в направлении ${\large x}$ постоянно и равно ${\large g}$. Это хорошо известное движение свободно падающего тела, которое описывается уравнениями

${\large v_x = v_0 + g \cdot t}$

${\large x = x_0 + x_0 \cdot t  + \dfrac {1}{2} \cdot g \cdot t^2}$

 

 

В чем сила измеряется?

Во всех учебниках и умных книжках, силу принято выражать в Ньютонах, но кроме как в моделях которыми оперируют физики ньютоны ни где не применяются. Это крайне неудобно.

Ньютон newton (Н) — производная единица измерения силы в Международной системе единиц (СИ).
Исходя из второго закона Ньютона, единица ньютон определяется как сила, изменяющая за одну секунду скорость тела массой один килограмм на 1 метр в секунду в направлении действия силы.

Таким образом, 1 Н = 1 кг·м/с².   

Килограмм-сила (кгс или кГ) — гравитационная метрическая единица силы, равная силе, которая действует на тело массой один килограмм в гравитационном поле земли. Поэтому по определению килограмм-сила равна 9,80665 Н. Килограмм-сила удобна тем, что её величина равна весу тела массой в 1 кг.
1 кгс = 9,80665 ньютонов (примерно ≈ 10 Н)
1 Н ≈ 0,10197162 кгс ≈ 0,1 кгс

1 Н = 1 кг x 1м/с2.

 

 

 

Закон тяготения

Каждый объект Вселенной притягивается к любому другому объекту с силой, пропорциональной их массам и обратно пропорционально квадрату расстояния между ними.

${\large F = G  \cdot \dfrac {m \cdot M}{R^2}}$

 

Добавить можно, что любое тело реагирует на приложенную к нему силу ускорением в направлении этой силы, по величине обратно пропорциональным массе тела.

 ${\large G}$ — гравитационная постоянная

 ${\large M}$ — масса земли

 ${\large R}$ — радиус земли

 

${\large G = 6,67 \cdot {10^{-11}} \left ( \dfrac {m^3}{kg \cdot {sec}^2} \right ) }$

${\large M = 5,97 \cdot {10^{24}} \left ( kg \right ) }$

${\large R = 6,37 \cdot {10^{6}} \left ( m \right ) }$

 

В рамках классической механики, гравитационное взаимодействие описывается законом всемирного тяготения Ньютона, согласно которому сила гравитационного притяжения между двумя телами массы ${\large m_1}$ и ${\large m_2}$, разделённых расстоянием ${\large R}$ есть

${\large F = -G  \cdot \dfrac {m_1 \cdot m_2}{R^2}}$

Здесь ${\large G}$ — гравитационная постоянная, равная ${\large 6,673 \cdot {10^{-11}} m^3 / \left ( kg \cdot {sec}^2 \right ) }$. Знак минус означает, что сила, действующая на пробное тело, всегда направлена по радиус-вектору от пробного тела к источнику гравитационного поля, т.е. гравитационное взаимодействие приводит всегда к притяжению тел.
Поле тяжести потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность поля тяжести влечёт за собой закон сохранения суммы кинетической и потенциальной энергии, что при изучении движения тел в поле тяжести часто существенно упрощает решение.
В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал и сила зависят только от положения тела в данный момент времени.

 

 

Тяжелее — Легче

Вес тела ${\large P}$ выражается произведением его массы ${\large m}$ на ускорение силы тяжести ${\large g}$.

${\large P = m \cdot g}$

 

Когда на земле тело становится легче (слабее давит на весы), это происходит от уменьшения массы. На луне все не так, уменьшение веса вызвано изменением другого множителя — ${\large g}$, так как ускорение силы тяжести на поверхности луны в шесть раз меньше чем на земле.

 

масса земли = ${\large 5,9736 \cdot {10^{24}}\ kg }$

масса луны = ${\large 7,3477 \cdot {10^{22}}\ kg }$ 

 

ускорение свободного падения на Земле = ${\large 9,81\ m / c^2 }$ 

ускорение свободного падения на Луне = ${\large 1,62 \ m / c^2 }$ 

 

В результате произведение ${\large m \cdot g }$, а следовательно и вес уменьшаются в 6 раз.

Но нельзя обозначить оба эти явления одним и тем же выражением «сделать легче». На луне тела становятся не легче, а лишь менее стремительно падают они «менее падучи»))).

 

 

Векторные и скалярные величины

Векторная величина (например сила, приложенная к телу), помимо значения (модуля), характеризуется также направлением. Скалярная же величина (например, длина) характеризуется только значением. Все классические законы механики сформулированы для векторных величин.

 

 Рисунок 1.

 

На рис. 1 изображены различные варианты расположения вектора ${ \large \overrightarrow{F}}$ и его проекции ${ \large F_x}$ и ${ \large F_y}$ на оси ${ \large X}$ и ${ \large Y}$ соответственно:

• A.    величины ${ \large F_x}$ и ${ \large F_y}$ являются ненулевыми и положительными
• B.    величины ${ \large F_x}$ и ${ \large F_y}$ являются ненулевыми, при этом ${\large F_y}$ — положительная величина, а ${\large F_x}$ — отрицательная, т.к. вектор ${\large \overrightarrow{F}}$ направлен в сторону, противоположную направлению оси ${\large X}$ 
• C.    ${\large F_y}$ — положительная  ненулевая величина, ${\large F_x}$ равна нулю, т.к. вектор ${\large \overrightarrow{F}}$ направлен перпендикулярно оси ${\large X}$

 

Момент силы

Моментом силы называют векторное произведение радиус-вектора, проведённого от оси вращения к точке приложения силы, на вектор этой силы. Т.е. согласно классическому определению момент силы — величина векторная. В рамках нашей задачи, это определение можно упростить до следующего: моментом силы ${\large \overrightarrow{F}}$, приложенной к точке с координатой ${\large x_F}$, относительно оси, расположенной в точке ${\large x_0}$ называется скалярная величина, равная произведению модуля силы ${\large \overrightarrow{F}}$, на плечо силы — ${\large \left | x_F — x_0 \right |}$. А знак этой скалярной величины зависит от направления силы: если она вращает объект по часовой стрелке, то знак плюс, если против — то минус.

Важно понимать, что ось мы можем выбирать произвольным образом — если тело не вращается, то сумма моментов сил относительно любой оси равна нулю. Второе важное замечание — если сила приложена к точке, через которую проходит ось, то момент этой силы относительно этой оси равен нулю (поскольку плечо силы будет равно нулю). 

 

 

Проиллюстрируем вышесказанное примером, на рис.2. Предположим, что система, изображенная на рис. 2, находится в равновесии. Рассмотрим опору, на которой стоят грузы. На неё действуют 3 силы: ${\large \overrightarrow{N_1},\ \overrightarrow{N_2},\ \overrightarrow{N},}$ точки приложения этих сил

А, В и С соответственно. На рисунке также присутствуют силы ${\large \overrightarrow{N_{1}^{gr}},\ \overrightarrow{N_2^{gr}}}$. Эти силы приложены к грузам, и согласно 3-му закону Ньютона

 

${\large \overrightarrow{N_{1}} = — \overrightarrow{N_{1}^{gr}}}$

${\large \overrightarrow{N_{2}} = — \overrightarrow{N_{2}^{gr}}}$

Теперь рассмотрим условие равенства моментов сил, действующих на опору, относительно оси, проходящей через точку А (и, как мы договаривались ранее, перпендикулярную плоскости рисунка):

 

${\large N \cdot l_1 — N_2 \cdot \left ( l_1 +l_2 \right ) = 0}$

Обратите внимание, что в уравнение не вошёл момент силы ${\large \overrightarrow{N_1}}$, поскольку плечо этой силы относительно рассматриваемой оси равно ${\large 0}$. Если же мы по каким-либо причинам хотим выбрать ось, проходящую через точку С, то условие равенства моментов сил будет выглядеть так:

 

${\large N_1 \cdot l_1 — N_2 \cdot l_2  = 0}$

Можно показать, что с математической точки зрения два последних уравнения эквивалентны.

 

 

Центр тяжести

Центром тяжести механической системы называется точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю.

 

 

 

Центр масс

Точка центра масс замечательна тем , что если на частицы образующие тело (неважно будет ли оно твердым или жидким, скоплением звезд или чем то другим) действует великое множество сил (имеются ввиду только внешние силы, поскольку все внутренние силы компенсируют друг друга), то результирующая сила приводит к такому ускорению этой точки, как будто в ней вся масса тела ${\large m}$.

Положение центра масс определяется уравнением:

 

${\large R_{c.m.} = \frac{\sum m_i\, r_i}{\sum m_i}}$

 

Это векторное уравнение, т.е. фактически три уравнения — по одному для каждого из трех направлений. Но рассмотрим только ${\large x}$ направление.  Что означает следующее равенство?

 

${\large X_{c.m.} = \frac{\sum m_i\, x_i}{\sum m_i}}$

 

Предположим тело разделено на маленькие кусочки с одинаковой массой ${\large m}$, причем полная масса тела равна будет равна числу таких кусочков ${\large N}$, умноженному на массу одного кусочка, например 1 грамм. Тогда это уравнение означает, что нужно взять координаты ${\large x}$ всех кусочков, сложить их и результат разделить на число кусочков. Иными словами, если массы кусочков равны то ${\large X_{c.m.}}$ будет просто средним арифметическим ${\large x}$ координат всех кусочков.

 

 

центр масс сложного тела лежит на линии, соединяющей центры масс двух составляющих его частей

 

 

 

Масса и плотность

Масса — фундаментальная физическая величина. Масса характеризует сразу несколько свойств тела и сама по себе обладает рядом важных свойств.

 

• Масса служит мерой содержащегося в теле вещества.
• Масса является мерой инертности тела. Инертностью называется свойство тела сохранять свою скорость неизменной (в инерциальной системе отсчёта), когда внешние воздействия отсутствуют или компенсируют друг друга. При наличии внешних воздействий инертность тела проявляется в том, что его скорость меняется не мгновенно, а постепенно, и тем медленнее, чем больше инертность (т.е. масса) тела. Например, если бильярдный шар и автобус движутся с одинаковой скоростью и тормозятся одинаковым усилием, то для остановки шара требуется гораздо меньше времени, чем для остановки автобуса.
• Массы тел являются причиной их гравитационного притяжения друг к другу (см. раздел «Сила тяготения»).
• Масса тела равна сумме масс его частей. Это так называемая аддитивность массы. Аддитивность позволяет использовать для измерения массы эталон — 1 кг.
• Масса изолированной системы тел не меняется со временем (закон сохранения массы).
• Масса тела не зависит от скорости его движения. Масса не меняется при переходе от одной системы отсчёта к другой.
• Плотностью однородного тела называется отношение массы тела к его объёму:

 ${\large p = \dfrac {m}{V} }$

 

Плотность не зависит от геометрических свойств тела (формы, объёма) и является характеристикой вещества тела. Плотности различных веществ представлены в справочных таблицах. Желательно помнить плотность воды: 1000 кг/м3.

 

 

Второй и третий законы Ньютона

Взаимодействие тел можно описывать с помощью понятия силы. Сила — это векторная величина, являющаяся мерой воздействия одного тела на другое.
Будучи вектором, сила характеризуется модулем (абсолютной величиной) и направлением в пространстве. Кроме того, важна точка приложения силы: одна и та же по модулю и направлению сила, приложенная в разных точках тела, может оказывать различное воздействие. Так, если взяться за обод велосипедного колеса и потянуть по касательной к ободу, то колесо начнёт вращаться. Если же тянуть вдоль радиуса, никакого вращения не будет.

Второй закон Ньютона

Произведение массы тела на вектор ускорения есть равнодействующая всех сил, приложенных к телу:

${\large m \cdot \overrightarrow{a} = \overrightarrow{F} }$

Второй закон Ньютона связывает векторы ускорения и силы. Это означает, что справедливы следующие утверждения.

1. ${\large m \cdot a = F}$, где ${\large a}$ — модуль ускорения, ${\large F}$ — модуль равнодействующей силы.
2. Вектор ускорения имеет одинаковое направление с вектором равнодействующей силы, так как масса тела положительна.

Третий закон Ньютона

Два тела действуют друг на друга с силами, равными по модулю и противоположными по направлению. Эти силы имеют одну и ту же физическую природу и направлены вдоль прямой, соединяющей их точки приложения.

 

 

 

Принцип суперпозиции

Опыт показывает, что если на данное тело действуют несколько других тел, то соответствующие силы складываются как векторы. Более точно, справедлив принцип суперпозиции.
Принцип суперпозиции сил. Пусть на тело действуют силы ${\large \overrightarrow{F_1}, \overrightarrow{F_2},\ \ldots \overrightarrow{F_n}}$  Если заменить их одной силой ${\large \overrightarrow{F} =  \overrightarrow{F_1} + \overrightarrow{F_2} \ldots + \overrightarrow{F_n}}$, то результат воздействия не изменится.
Сила ${\large \overrightarrow{F}}$ называется

равнодействующей сил ${\large \overrightarrow{F_1}, \overrightarrow{F_2},\ \ldots \overrightarrow{F_n}}$ или результирующей силой.
 

 

 

Единица измерения силы, теория и онлайн калькуляторы

Одним из основных законов классической динамики является второй закон Ньютона. Он содержит две величины, которые нельзя выразить только при помощи кинематических величин. Этими величинами являются сила и масса. Данные величины равноправны. Каждую из них можно считать основной как силу, так и массу. Избрав для единицы одной из них эталон, получают единицу для другой, применяя второй закон Ньютона. Так можно получить две разные системы единиц, в одной из них (метрической) основными единицами служат единицы массы, а единицы силы считаются производными. Причиной выбора единиц массы как основным в первую очередь служит то, что для массы проще создать эталон.

Ньютон — единица измерения силы в системе СИ

На сегодняшний момент в физике используют Международную систему единиц (СИ) в которой ньютон — единица измерения силы. Один ньютон (1Н) — это сила, сообщающая телу, имеющему массу в 1 килограмм, ускорение равное 1 метру, деленному на секунду в квадрате в направлении действия силы:

\[1Н=1кг\cdot 1\frac{м}{с^2}.\]

Ньютон является производной единицей в СИ.

Первоначально единицу силы как сформулировано выше приняли для системы единиц МКС (метр-килограмм-секунда) в 1946 г. Немного позднее единицу силы назвали ньютоном (в 1948 г). В системе СИ ньютон — единица измерения силы с 1960 года. Очевидно, что свое имя единица силы получила в честь английского ученого И. Ньютона, основателя классической динамики. Ньютон в своих разработках не использовал единиц измерения силы, рассматривая ее как абстракцию.

При вычислениях часто используют кратные и дольные единицы силы, применяя стандартные приставки системы СИ, например: $1кН={10}^3Н;;\ 1нН={10}^{-9}Н;;\ 1МН={10}^6Н.$

Единицы измерения силы в других системах единиц

Долгое время, и иногда сейчас, в физике используют систему единиц, называемую СГС. В этой системе единицей длины является сантиметр (см), единицей массы — грамм (г), единицей времени стала секунда (с). В системе СГС единицей силы является дина (дин). Одна дина — это сила, сообщающая телу массой 1 г ускорение, равное 1$\frac{см}{с^2}$. Дина является очень маленькой единицей силы. Ньютон и дина соотносятся как:

\[1Н={10}^5дин.\]

В технических расчетах используют еще одну единицу измерения силы, которую называют килограмм — сила (кгс). 1 кгс — это сила, с которой Земля действует на эталонную массу в один килограмм, притягивая ее.

\[1Н\approx 0,10197162\ кгс.\]

В России килограмм-сила используется как внесистемная единица измерения силы, ее рекомендуют использовать там, где численные значения силы невозможно или нерационально выражать в СИ.

Примеры задач с решением

Пример 1

Задание. Тело падает на Землю с высоты $h$. Масса тела равна $m$. Удар длится время $\Delta t$. Какова с

Сила (физическая величина) — это… Что такое Сила (физическая величина)?

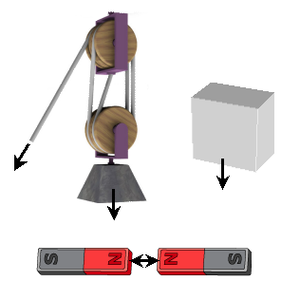
Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций.^[1]

Сила как векторная величина характеризуется модулем, направлением и «точкой» приложения силы. Последним параметром понятие о силе, как векторе в физике, отличается от понятия о векторе в векторной алгебре, где равные по модулю и направлению векторы, независимо от точки их приложения, считаются одним и тем же вектором . В физике эти векторы называются свободными векторами.В механике чрезвычайно распространено представление о связанных векторах, начало которых закреплено в определённой точке пространства или же может находиться на линии, продолжающей направление вектора (скользящие векторы). ^[2].

Также используется понятие линия действия силы, обозначающее проходящую через точку приложения силы прямую, по которой направлена сила.

Второй закон Ньютона гласит, что в инерциальных системах отсчета ускорение материальной точки по направлению совпадает с приложенной силой, а по модулю прямо пропорционально модулю силы и обратно пропорционально массе материальной точки. Или, что эквивалентно, в инерциальных системах отсчета скорость изменения импульса материальной точки равна приложенной силе.

При приложении силы к телу конечных размеров в нём возникают механические напряжения, сопровождающиеся деформациями.^[3][4][5][6]

С точки зрения Стандартной модели физики элементарных частиц фундаментальные взаимодействия (гравитационное, слабое, электромагнитное, сильное) осуществляются посредством обмена так называемыми калибровочными бозонами.^[3] Эксперименты по физике высоких энергий, проведённые в 70−80-х гг. XX в. подтвердили предположение о том, что слабое и электромагнитное взаимодействия являются проявлениями более фундаментального электрослабого взаимодействия.^[7]

Размерность силы — LMT⁻², единицей измерения в Международной системе единиц (СИ) является ньютон (N, Н), в системе СГС — дина.

История понятия

Понятие силы использовали ещё ученые античности в своих работах о статике и движении. Изучением сил в процессе конструирования простых механизмов занимался в III в. до н. э. Архимед.^[8] Представления Аристотеля о силе, связанные с фундаментальными несоответствиями, просуществовали в течение нескольких столетий. Эти несоответствия устранил в XVII в. Исаак Ньютон, используя для описания силы математические методы. Механика Ньютона оставалась общепринятой на протяжении почти трехсот лет.^[5] К началу XX в. Альберт Эйнштейн в теории относительности показал, что ньютоновская механика верна лишь в при сравнительно небольших скоростях движения и массах тел в системе, уточнив тем самым основные положения кинематики и динамики и описав некоторые новые свойства пространства-времени.

Ньютоновская механика

Исаак Ньютон задался целью описать движение объектов, используя понятия инерции и силы. Сделав это, он попутно установил, что всякое механическое движение подчиняется общим законам сохранения. В 1687 г. Ньютон опубликовал свой знаменитый труд «Математические начала натуральной философии», в котором изложил три основополагающих закона классической механики (знаменитые законы Ньютона).^[5][9]

Первый закон Ньютона

Первый закон Ньютона утверждает, что существуют системы отсчета, в которых тела сохраняют состояние покоя или равномерного прямолинейного движения при отсутствии действий на них со стороны других тел или при взаимной компенсации этих воздействий.^[9] Такие системы отсчета называются инерциальными. Ньютон предположил, что каждый массивный объект имеет определенный запас инерции, который характеризует «естественное состояние» движения этого объекта. Эта идея отрицает взгляд Аристотеля, который рассматривал покой «естественным состоянием» объекта. Первый закон Ньютона противоречит аристотелевской физике, одним из положений которой является утверждение о том, что тело может двигаться с постоянной скоростью лишь под действием силы. Тот факт, что в механике Ньютона в инерциальных системах отсчёта покой физически неотличим от равномерного прямолинейного движения, является обоснованием принципа относительности Галилея. Среди совокупности тел принципиально невозможно определить какие из них находится «в движении», а какие «покоятся». Говорить о движении можно лишь относительно какой-либо системы отсчета. Законы механики выполняются одинаково во всех инерциальных системах отсчета, другими словами все они механически эквивалентны. Последнее следует из так называемых преобразований Галилея.^[10]

Например, законы механики абсолютно одинаково выполняются в кузове грузовика, когда тот едет по прямому участку дороги с постоянной скоростью и когда стоит на месте. Человек может подбросить мячик вертикально вверх и поймать его через некоторое время на том же самом месте вне зависимости от того движется ли грузовик равномерно и прямолинейно или покоится. Для него мячик летит по прямой. Однако для стороннего наблюдателя, находящегося на земле, траектория движения мячика имеет вид параболы. Это связано с тем, что мячик относительно земли движется во время полета не только вертикально, но и горизонтально по инерции в сторону движения грузовика. Для человека, находящегося в кузове грузовика не имеет значения движется ли последний по дороге, или окружающий мир перемещается с постоянной скоростью в противоположном направлении, а грузовик стоит на месте. Таким образом, состояние покоя и равномерного прямолинейного движения физически неотличимы друг от друга.

Второй закон Ньютона

Второй закон Ньютона в современной формулировке звучит так: в инерциальной системе отсчета скорость изменения импульса материальной точки равна векторной сумме всех сил, действующих на эту точку.

где − импульс материальной точки, − суммарная сила, действующая на материальную точку. Второй закон Ньютона гласит, что действие несбалансированных сил приводит к изменению импульса материальной точки.^[9]

По определению импульса:

где − масса, − скорость.

По правилу нахождения производной произведения:

Если масса материальной точки остается неизменной, то производная по времени от массы равна нулю, и уравнение принимает вид:

Учитывая определение ускорения точки, второй закон Ньютона принимает вид:

Считается, что это «вторая самая известная формула в физике»^[11], хотя сам Ньютон никогда явным образом не записывал свой второй закон в этом виде.

Поскольку в любой инерциальной системе отсчёта ускорение тела одинаково и не меняется при переходе от одной системы к другой, то и сила инвариантна по отношению к такому переходу.

Во всех явлениях природы сила, независимо от своего происхождения, проявляется только в механическом смысле, то есть как причина нарушения равномерного и прямолинейного движения тела в инерциальной системе координат. Обратное утверждение, т.е установление факта такого движения, не свидетельствует об отсутствии действующих на тело сил, а лишь о том, что действия этих сил взаимно уравновешиваются. Иначе: их векторная сумма есть вектор с модулем, равным нулю. На этом основано измерение величины силы, когда она компенсируется силой, величина которой известна .

Второй закон Ньютона позволяет измерять величину силы. Например, знание массы планеты и ее центростремительного ускорения при движении по орбите позволяет вычислить величину силы гравитационного притяжения, действующую на эту планету со стороны Солнца.

Третий закон Ньютона

Для любых двух тел (назовем их тело 1 и тело 2) третий закон Ньютона утверждает, что сила действия тела 1 на тело 2, сопровождается появлением равной по модулю, но противоположной по направлению силы, действующей на тело 1 со стороны тела 2.

[12] Математически закон записывается так:

Этот закон означает, что силы всегда возникают парами «действие-противодействие».^[9] Если тело 1 и тело 2 находятся в одной системе, то суммарная сила в системе, обусловленная взаимодействием этих тел равна нулю:

Это означает, что в замкнутой системе не существует несбалансированных внутренних сил. Это приводит к тому, что центр масс замкнутой системы (то есть той, на которую не действуют внешние силы) не может двигаться с ускорением. Отдельные части системы могут ускоряться, но лишь таким образом, что система в целом остается в состоянии покоя или равномерного прямолинейного движения. Однако в том случае, если внешние силы подействуют на систему, то ее центр масс начнет двигаться с ускорением, пропорциональным внешней результирующей силе и обратно пропорциональным массе системы.

[3]

Фундаментальные взаимодействия

Все силы в природе основаны на четырех типах фундаментальных взаимодействий. Максимальная скорость распространения всех видов взаимодействия равна скорости света в вакууме. Электромагнитные силы действуют между электрически заряженными телами, гравитационные − между массивными объектами. Сильное и слабое проявляются только на очень малых расстояниях, они ответственны за возникновение взаимодействия между субатомными частицами, включая нуклоны, из которых состоят атомные ядра.

Интенсивность сильного и слабого взаимодействия измеряется в единицах энергии (электрон-вольтах), а не единицах силы, и потому применение к ним термина «сила» объясняется берущей из античности традицией объяснять любые явления в окружаемом мире действием специфических для каждого явления «сил».

Понятие силы не может быть применено по отношению к явлениям субатомного мира. Это понятие из арсенала классической физики, ассоциирующейся (пусть даже только подсознательно) с ньютоновскими представлениями о силах, действующих на расстоянии. В субатомной физике таких сил уже нет: их заменяют взаимодействия между частицами, происходящими через посредство полей, то есть каких-то других частиц. Поэтому физики высоких энергий избегают употреблять слово

сила, заменяя его словом взаимодействие.^[13]

Каждый вид взаимодействия обусловлен обменом соответствующих переносчиков взаимодействия: гравитационное − обменом гравитонов (существование не подтверждено экспериментально), электромагнитное − виртуальных фотонов, слабое − векторных бозонов, сильное − глюонов (и на больших расстояниях — мезонов). В настоящее время электромагнитное и слабое взаимодействия объединены в более фундаментальное электрослабое взаимодействие. Делаются попытки объединения всех четырех фундаментальных взаимодействие в одно (так называемая теория великого объединения).

Всё многообразие проявляющих себя в природе сил в принципе может быть сведено к этим четырем фундаментальным взаимодействиям. Например, трение − это проявление электромагнитных сил, действующих между атомами двух соприкасающихся поверхностей, и принципа запрета Паули,^[14] который не позволяет атомам проникать в область друг друга. Сила, возникающая при деформации пружины, описываемая законом Гука, также является результатом действия электромагнитных сил между частицами и принципа запрета Паули, заставляющих атомы кристаллической решетки вещества удерживаться около положения равновесия.^[3].

Однако на практике оказывается не только нецелесообразной, но и просто невозможной по условиям задачи подобная детализация рассмотрения вопроса о действии сил.

Гравитация

Гравитация (сила тяготения) — универсальное взаимодействие между любыми видами материи. В рамках классической механики описывается законом всемирного тяготения, сформулированным Исааком Ньютоном в его труде «Математические начала натуральной философии». Ньютон получил величину ускорения, с которым Луна движется вокруг Земли, положив при расчете, что сила тяготения убывает обратно пропорционально квадрату расстояния от тяготеющего тела. Кроме этого, им же было установлено, что ускорение, обусловленное притяжением одного тела другим, пропорционально произведению масс этих тел^[15]. На основании этих двух выводов был сформулирован закон тяготения: любые материальные частицы притягиваются по направлению друг к другу с силой , прямо пропорциональной произведению масс ( и ) и обратно пропорциональной квадрату расстояния между ними:

Здесь − гравитационная постоянная^[16], значение которой впервые получил в своих опытах Генри Кавендиш. Используя данный закон, можно получить формулы для расчета силы тяготения тел произвольной формы. Теория тяготения Ньютона хорошо описывает движение планет Солнечной системы и многих других небесных тел. Однако, в ее основе лежит концепция дальнодействия, противоречащая теории относительности. Поэтому классическая теория тяготения неприменима для описания движения тел, перемещающихся со скоростью, близкой к скорости света, гравитационных полей чрезвычайно массивных объектов (например, черных дыр), а также переменных полей тяготения, создаваемых движущимися телами, на больших расстояниях от них^[17].

Более общей теорией гравитации является общая теория относительности Альберта Эйнштейна. В ней гравитация не характеризуется инвариантной силой, не зависящей от системы отсчёта. Вместо этого свободное движение тел в гравитационном поле, воспринимаемое наблюдателем как движение по искривленным траекториям в трехмерном пространстве-времени с переменной скоростью, рассматривается как движение по инерции по геодезической линии в искривлённом четырехмерном пространстве-времени, в котором время в разных точках течет по-разному. Причем эта линия в некотором смысле «наиболее прямая» — она такова, что пространственно-временной промежуток (собственное время) между двумя пространственно-временными положениями данного тела максимален. Искривление пространства зависит от массы тел, а также от всех видов энергии, присутствующих в системе^[3].

Электромагнитное взаимодействие

Электростатическое поле (поле неподвижных зарядов)

Развитие физики после Ньютона добавило к трём основным (длина, масса, время) величинам электрический заряд с размерностью C. Однако, исходя из требований практики, основанных на удобствах измерения, вместо заряда нередко стал использоваться электрический ток с размерностью I, причём I = CT ^{− 1}. Единицей измерения величины заряда является кулон, а силы тока ампер.

Поскольку заряд, как таковой, не существует независимо от несущего его тела, то электрическое взаимодействие тел проявляется в виде той же рассматриваемой в механике силы, служащей причиной ускорения. Применительно к электростатическому взаимодействию двух «точечных зарядов» в вакууме используется закон Кулона:

где  — расстояние между зарядами, а ε₀ ≈ 8.854187817·10⁻¹² Ф/м. В однородном (изотропном) веществе в этой системе сила взаимодействия уменьшается в ε раз, где ε — диэлектрическая постоянная среды.

Направление силы совпадает с линией, соединяющей точечные заряды. Графически электростатическое поле принято изображать в виде картины силовых линий, представляющих собой воображаемые траектории, по которым бы перемещалась лишённая массы заряжённая частица. Эти линии начинаются на одном и заканчиваются на другом зарядах.

Электромагнитное поле (поле постоянных токов)

Существование магнитного поля признавалось ещё в средние века китайцами, использовавшим «любящий камень» — магнит, в качестве прообраза магнитного компаса. Графически магнитное поле принято изображать в виде замкнутых силовых линий, густота которых (так же, как и в случае электростатического поля) определяет его интенсивность. Исторически наглядным способом визуализации магнитного поля были железные опилки, насыпаемые, например, на лист бумаги, положенный на магнит.

Эрстед установил, что текущий по проводнику ток вызывает отклонение магнитной стрелки.

Фарадей пришёл к выводу, что вокруг проводника с током создаётся магнитное поле.

Ампер высказал гипотезу, признаваемую в физике, как модель процесса возникновения магнитного поля, заключающуюся в существовании в материалах микроскопических замкнутых токов, обеспечивающих совместно эффект естественного или наведённого магнетизма.

Ампером было установлено, что в находящейся в вакууме системе отсчёта, по отношению к которой заряд находится в движении, то есть ведёт себя как электрический ток, возникает магнитное поле, интенсивность которого определяется вектором магнитной индукции, лежащим в плоскости, расположенной перпендикулярно по отношению к направлению движения заряда.

Единицей измерения магнитной индукции является тесла: 1 Тл = 1 Т кг с⁻² А⁻²
Количественно задача была решена Ампером, измерявшим силу взаимодействия двух параллельных проводников с текущими по ним токами. Один из проводников создавал вокруг себя магнитное поле, второй реагировал на это поле сближением или удалением с поддающейся измерению силой, зная которую и величину силы тока можно было определить модуль вектора магнитной индукции.

Силовое взаимодействие между электрическими зарядами, не находящимися в движении относительно друг друга описывается законом Кулона. Однако заряды, находящиеся в движении относительно друг друга создают магнитные поля, посредством которых созданные движением зарядов токов в общем случае приходят в состояние силового взаимодействия.

Принципиальным отличием силы, возникающей при относительном движении зарядов от случая их стационарного размещения, является различие в геометрии этих сил. Для случая электростатики сил взаимодействия двух зарядов направлена по линии, их соединяющей. Поэтому геометрия задачи двумерна и рассмотрение ведётся в плоскости, проходящей через эту линию.

В случае токов сила, характеризующая магнитное поле, создаваемое током, расположена в плоскости, перпендикулярной току. Поэтому картина явления становится трёхмерной. Магнитное поле, создаваемое бесконечно малым по длине элементом первого тока, взаимодействуя с таким же элементом второго тока, в общем случае создаёт силу, действующую на него. При этом для обоих токов эта картина полностью симметрична в том смысле, что нумерация токов произвольна.

Закон взаимодействия токов используется для эталонирования постоянного электрического тока.

Сильное взаимодействие

Сильное взаимодействие — короткодействующие силы между адронами и кварками. В атомном ядре сильное взаимодействие удерживает вместе положительно заряженные (испытывающие электростатическое отталкивание) протоны, происходит это посредством обмена пи-мезонами между нуклонами (протонами и нейтронами). Пи-мезоны живут очень мало, времени жизни им хватает лишь на то, чтобы обеспечить ядерные силы в радиусе ядра, потому ядерные силы называют короткодействующими. Увеличение количества нейтронов «разбавляет» ядро, уменьшая электростатические силы и увеличивая ядерные, но при большом количестве нейтронов они сами, будучи фермионами, начинают испытывать отталкивание вследствие принципа Паули. Также при слишком сильном сближении нуклонов начинается обмен W-бозонами, вызывающее отталкивание, благодаря этому атомные ядра не «схлопываютс­я­».

Внутри самих адронов сильное взаимодействие удерживает вместе кварки — составные части адронов. Квантами сильного поля являются глюоны. Каждый кварк имеет один из трёх «цветовых» зарядов, каждый глюон состоит из пары «цвет»-«антицвет». Глюоны связывают кварки в т. н. «конфайнмент», из-за которого на данный момент свободные кварки в эксперименте не наблюдались. При отдалении кварков друг от друга энергия глюонных связей возрастает, а не уменьшается как при ядерном взаимодействии. Затратив много энергии (столкнув адроны в ускорителе) можно разорвать кварк-глюонную связь, но при этом происходит выброс струи новых адронов. Впрочем, свободные кварки могут существовать в космосе: если какому-то кварку удалось избежать конфайнмента во время Большого взрыва, то вероятность аннигилировать с соответствующим антикварком или превратиться в бесцветный адрон для такого кварка исчезающе мала.

Слабое взаимодействие

Слабое взаимодействие — фундаментальное короткодействующее взаимодействие. Радиус действия 10⁻¹⁸ м. Симметрично относительно комбинации пространственной инверсии и зарядового сопряжения. В слабом взаимодействии участвуют все фундаментальные фермионы (лептоны и кварки). Это единственное взаимодействие, в котором участвуют нейтрино (не считая гравитации, пренебрежимо малой в лабораторных условиях), чем объясняется колоссальная проникающая способность этих частиц. Слабое взаимодействие позволяет лептонам, кваркам и их античастицам обмениваться энергией, массой, электрическим зарядом и квантовыми числами — то есть превращаться друг в друга. Одно из проявлений — бета-распад.

Производные виды сил

Сила упругости — сила, возникающая при деформации тела и противодействующая этой деформации. В случае упругих деформаций является потенциальной. Сила упругости имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. Сила упругости направлена противоположно смещению, перпендикулярно поверхности. Вектор силы противоположен направлению смещения молекул.

Сила трения — сила, возникающая при относительном движении твёрдых тел и противодействующая этому движению. Относится к диссипативным силам. Сила трения имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. Вектор силы трения направлен противоположно вектору скорости.

Сила сопротивления среды — сила, возникающая при движении твёрдого тела в жидкой или газообразной среде. Относится к диссипативным силам. Сила сопротивления имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. Вектор силы сопротивления направлен противоположно вектору скорости.

Сила нормальной реакции опоры — сила упругости, действующая со стороны опоры на тело. Направлена перпендикулярно к поверхности опоры.

Силы поверхностного натяжения — силы, возникающие на поверхности фазового раздела. Имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. Сила натяжения направлена по касательной к поверхности раздела фаз; возникает вследствие нескомпенсированного притяжения молекул, находящихся на границе раздела фаз, молекулами, находящимися не на границе раздела фаз.

Осмотическое давление

Силы Ван-дер-Ваальса — электромагнитные межмолекулярные силы, возникающие при поляризации молекул и образовании диполей. Ван-дер-Ваальсовы силы быстро убывают с увеличением расстояния.

Сила инерции — фиктивная сила, вводимая в неинерциальных системах отсчёта для того, чтобы в них выполнялся второй закон Ньютона. В частности, в системе отсчёта, связанной с равноускоренно движущимся телом сила инерции направлена противоположно ускорению. Из полной силы инерции могут быть для удобства выделены центробежная сила и сила Кориолиса.

Равнодействующая

При расчёте ускорения тела все действующие на него силы заменяют одной силой, называемой равнодействующей. Это геометрическая сумма всех сил, действующих на тело. При этом действие каждой силы не зависит от действия других, то есть каждая сила сообщает телу такое ускорение, какое она сообщила бы в отсутствие действия других сил. Это утверждение носит название принципа независимости действия сил (принцип суперпозиции).

См. также

Источники

Примечания

1. ↑ Glossary. Earth Observatory. NASA. — «Сила — любой внешний фактор, который вызывает изменение в движении свободного тела или возникновение внутренних напряжений в зафиксированном теле.»  (англ.)
2. ↑ Бронштейн И. Н. Семендяев К. А. Справочник по математике. М.: Издательство «Наука» Редакция справочной физико-математической литературы.1964.
3. ↑ ^{1 2 3 4 5} Feynman, R. P., Leighton, R. B., Sands, M. Lectures on Physics, Vol 1 — Addison-Wesley, 1963.  (англ.)
4. ↑ Kleppner, D., Kolenkow, R. J. An introduction to mechanics — McGraw-Hill.  (англ.)
5. ↑ ^{1 2 3} University Physics, Sears, Young & Zemansky, pp. 18-38  (англ.)
6. ↑ Хайкин С. Э.Силы инерции и невесомость. Изд-во «Наука» М.,1967, с илл.
7. ↑ Weinberg, S. Dreams of a Final Theory — Vintage Books USA, 1994. — ISBN 0-679-74408-8.  (англ.)
8. ↑ Heath,T.L. The Works of Archimedes (1897). Archive.org. Архивировано из первоисточника 23 августа 2011. Проверено 14 октября 2007.  (англ.)
9. ↑ ^{1 2 3 4} Newton, I. The Principia Mathematical Principles of Natural Philosophy — University of California Press, 1999. — ISBN 0-520-08817-4.  (англ.)
10. ↑ Мултановский В. В. Курс теоретической физики. Классическая механика. Основы специальной теории относительности. Релятивистская механика — М.: Просвещение, 1988. — С. 80−81.
11. ↑ Принято не подчёркивать специально, что в такой формулировке Второй закон Ньютона годится только для наблюдателя, имеющего достаточные основания считать, что он находится в инерциальной системе отсчёта, из которой он и наблюдает движущееся под действием силы тело. Если же он сам находится в системе отсчёта, связанной с ускоряемым телом, в которой оно для него неподвижно, то в этой ситуации Второй закон Ньютона принимает вид: F − ma = 0 . Или F − F(i) = 0 , где F(i) есть сила инерции, действующей на ускоряемое тело, уравновешивающая по Третьему закону Ньютона действующее на него силу, что является причиной неподвижности этого тела в рассматриваемой неинерциальной системе отсчёта. Сила инерции фиктивна в том смысле, что причиной её возникновения не являются, в конечном итоге, ни силы гравитации, ни силы электромагнитного происхождения. Она появляется исключительно из-за неинерциальности движения системы наблюдателя.
12. ↑ Henderson, Tom Lesson 4: Newton’s Third Law of Motion. The Physics Classroom (1996-2007). Архивировано из первоисточника 23 августа 2011. Проверено 4 января 2008.  (англ.)
13. ↑ Капра, Фритьоф ДАО ФИЗИКИ. СПб.,»ОРИС»*»ЯНА-ПРИНТ». 1994 г. 304 с. ISBN 5-88436-021-5
14. ↑ Nave, R Pauli Exclusion Principle. HyperPhysics***** Quantum Physics. Архивировано из первоисточника 23 августа 2011. Проверено 2 января 2008.  (англ.)
15. ↑ University Physics, Sears, Young & Zemansky, pp. 59−82  (англ.)
16. ↑ Sir Isaac Newton: The Universal Law of Gravitation. Astronomy 161 The Solar System. Архивировано из первоисточника 23 августа 2011. Проверено 4 января 2008.  (англ.)
17. ↑ Статья И. Д. Новикова Физический энциклопедический словарь — М.: Советская энциклопедия, 1984. — С. 772−775.

Динамометр — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 июля 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 июля 2019; проверки требует 1 правка. Динамометр общего назначения на 400 кН

Динамо́ме́тр (от др.-греч. δύναμις — «сила» и μέτρεω — «измеряю») — прибор для измерения силы или момента силы, состоит из силового звена (упругого элемента) и отсчётного устройства. В силовом звене измеряемое усилие вызывает деформацию, которая непосредственно или через передачу сообщается отсчётному устройству. Существующими динамометрами можно измерять усилия от долей ньютонов (н, долей кгс) до 20 Мн (2000 тс). По принципу действия различают динамометры механические (пружинные или рычажные), гидравлические и электронные. Иногда в одном динамометре используют два принципа.

Пружинные весы Приборная доска самолёта Ан-140, самая верхняя пара приборов — ИКМ двигателей, 4 % — крутящий момент на минимальном режиме («Тихое руление»)

Первыми приборами для измерения силы стали весы, первое изображение которых было напечатано в 1726 году. Около 1830 года Сальтер предложил более удобное устройство: для измерения силы в нём использовалась пружина, которая растягивалась грузом. Ещё раньше Ренье изобрёл динамометр с циферблатом, в котором использовалась кольцеобразно-замкнутая пружина. Более поздними изобретениями являются нажим Прони и динамометры Томсона, Геффнер-Альтенека, Броуна и Межи^[1].

Существует несколько типов динамометров: механические динамометры (рычажные и пружинные), а также гидравлические и электрические.

Механический динамометр[править | править код]

Существует два вида механических динамометров: пружинный и рычажный. В пружинном динамометре сила или момент силы передаётся пружине, которая в зависимости от направления силы сжимается или растягивается. Величина упругой деформации пружины пропорциональна силе воздействия и регистрируется. В рычажном динамометре действие силы деформирует рычаг, величина деформации которого после регистрируется.

Гидравлический динамометр[править | править код]

Действие гидравлического динамометра основано на вымещении измеряемой силой жидкости из цилиндра. Под давлением жидкость поступает по трубке к записывающему аппарату или датчику и регистрируется. Гидравлический динамометр используется как измеритель крутящего момента (ИКМ) двигателя турбовинтового самолёта, его данные используются для оценки работы двигателя, а также для автоматического флюгирования винта при отказе двигателя. ИКМ может быть выполнен в виде нескольких цилиндров, удерживающих корпус планетарного редуктора винта от проворота — давление, требуемое для удержания, является функцией крутящего момента, такой ИКМ входит в состав редуктора двигателя АИ-20 и многих других. В редукторе же двигателя НК-12 бомбардировщика Ту-95 и транспортного самолёта Ан-22, приводящем соосные винты, разместить такой ИКМ негде, поэтому там ИКМ выполнен как щель в одном из валов, за счёт скручивания вала изменяется расход масла через щель, что и является исходной величиной для ИКМ.

Электрический динамометр[править | править код]

Электрический динамометр состоит из датчика, который преобразует деформацию от воздействия силы в электрический сигнал, и дополнительного датчика, который усиливает и записывает электрический сигнал первого датчика. Для преобразования силы или момента силы в деформацию используются индуктивные, пьезоэлектрические, тензорезисторные и вибрационно-частотные датчики сопротивления. Под действием силы датчик деформируется и токи моста сопротивления изменяются. Сила электрического сигнала прямо пропорциональна деформации элемента и в итоге силе воздействия. Второй датчик усиливает сигнал и записывает его для последующей обработки.

Примеры повседневного использования[править | править код]

В повседневной жизни прибор используется для измерения силы сжатия створок автоматически закрывающихся систем, таких как двери автобусов, трамваев, вагонов поездов, метро, а также двери пассажирских и грузовых лифтов, гаражные ворота, автомобильные окна, сдвигающиеся люки на крыше и так далее. Так как все эти системы могут в случае неправильной юстировки стать причиной травм, разработаны и внедрены технические нормы, определяющие предельные значения сил сжатия в закрывающихся системах. Данные нормы^[2] обязательны во всех странах Европейского союза, а также используются в США, Японии, Китае, Саудовской Аравии, Австралии и других странах мира.

Перевод единиц измерения Силы. Обозначения единиц измерения силы. Фунт-сила, грамм-сила, килограмм-сила, тонна-сила, Ньютон, дина, паундаль.

Перевод единиц измерения силы. Обозначения единиц измерения величины силы. Фунт-сила, грамм-сила, килограмм-сила, тонна-сила, Ньютон, дина, паундаль. фунтов , или фунт-сил (lbf) грамм — сил(gf) килограмм — сил (kgf) тонн — сил (tf) (СИ) Ньютонов (N) дина (dyn) паундаль (pdl) 1 фунт, он-же фунт-сила (lbf) это: 453,6 0,4536 4,536*10-4 4,448 32,174 1 грамм — сила (gf) это: 2,205*10-3 0,001 1*10-6 9,807*10-3 980,665 0,70932 1 килограмм — сила (kgf) это: 2,205 1000 0,001 9,807 980665 70,932 1 тонна — сила (tf) это: 2,205*103 1*106 1000 9,807*103 9,807*108 7,0932*104 (Единица СИ) 1 Ньютон (N) это: 0,2248 102,0 0,1020 1,020*10-4 1 (кг*м/с2) 105 7,2330 1 дина (dyn) это: 2,248*10-6 1,020*10-3 1,020*10-6 1,020*10-9 10-5 1 (г*см/с2) 7,233*10-5 1 паундаль (pdl) 0,03108 14,098 0,014098 1,4098*10-5

Дина (единица измерения) — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Дина.

Ди́на (от греч. δύναμις — сила, русское обозначение: дин, международное обозначение: dyn) — единица силы в системе единиц СГС. Одна дина численно равна силе, которая сообщает телу массой в 1 грамм ускорение в 1 см/с². 1 дин = 1 г·см/с² = 10^-5H = 1,0197·10^-6кгс^[1][2].

Кратные				Дольные
величина	название	обозначение		величина	название	обозначение
101 дин	декадина	дадин	dadyn	10−1 дин	децидина	ддин	ddyn
102 дин	гектодина	гдин	hdyn	10−2 дин	сантидина	сдин	cdyn
103 дин	килодина	кдин	kdyn	10−3 дин	миллидина	мдин	mdyn
106 дин	мегадина	Мдин	Mdyn	10−6 дин	микродина	мкдин	µdyn
109 дин	гигадина	Гдин	Gdyn	10−9 дин	нанодина	ндин	ndyn
1012 дин	терадина	Тдин	Tdyn	10−12 дин	пикодина	пдин	pdyn
1015 дин	петадина	Пдин	Pdyn	10−15 дин	фемтодина	фдин	fdyn
1018 дин	эксадина	Эдин	Edyn	10−18 дин	аттодина	адин	adyn
1021 дин	зеттадина	Здин	Zdyn	10−21 дин	зептодина	здин	zdyn
1024 дин	иоттадина	Идин	Ydyn	10−24 дин	иоктодина	идин	ydyn
применять не рекомендуется

Гравиметр — Википедия

CG-5 — один из самых популярных кварцевых гравиметров

Гравиметр (от лат. gravis «тяжёлый» + греч. μετρεω «измеряю») — прибор для высокоточного измерения силы тяжести; чаще всего применяется при поисках полезных ископаемых.

Следует заметить, что в конце XIX — начале XX века под этим термином понимался иной измерительный прибор. В частности, на страницах Энциклопедического словаря Брокгауза и Ефрона было дано следующее определение гравиметра: «прибор для определения гравиметрической плотности пороха»^[1].

Вдобавок, в некоторых^[2] источниках гравиметром назывался Гравитационный вариометр.

Предназначение прибора и применение[править | править код]

1. график силы тяжести
2. карстовая воронка
3. плотное рудное тело
4. вмещающая порода

Гравиметр, по своей сути, является многопрофильным прибором, применение которого возможно во многих областях. Однако на практике чуть ли не 100 % гравиметров используются в гравиразведочных работах, а именно — в поисках месторождений полезных ископаемых. Из-за этого сами гравиметры стали прочно ассоциироваться именно с ними. Благодаря гравиразведке можно прямо с земной поверхности определить наличие в недрах того или иного полезного ископаемого. Это позволяет существенно снизить количество дорогостоящего бурения скважин или строительства шахт.

Типичной иллюстрацией являются, например, карстовые воронки, над которыми сила тяжести меньше, поэтому показания гравиметров становятся ниже; над плотными породами руды показания гравиметров выше, так как над тяжёлыми объектами сила тяжести возрастает.

Следует отметить, что иногда гравиметры всё же используются археологами, палеонтологами, а также возможно применение в гидрологии, почвоведении, сельском хозяйстве, картировании и многих других областях. Гравиметры устанавливаются на автомобилях, судах, самолётах, космических спутниках и др., но более распространены переносимые вручную конструкции.

Любопытным фактом является то, что именно гравиметры нашли своё применение в одной из нестандартных областей — в навигации баллистических (в том числе ядерных) ракет. В основе системы ориентации ракеты применяется гравиметрия, так как именно гравитационное поле Земли является сильным и стабильным ориентиром: в отличие от ориентации по магнитному полю, либо наведения путём радиосигнала, гравитационное поле невозможно исказить или перехватить. По понятным причинам невозможно и «замаскировать» атакуемую цель искусственной гравитационной аномалией, так как для её создания потребуется быстрое и скрытное перемещения миллиардов тонн породы из одной точки планеты в другую.

Изначально в гравиразведке и гравиметрии для точных измерений поля силы тяжести применялись различные градиентометры и вариометры. Данные приборы позволяют измерить полные значения вторых производных потенциала, что достаточно информативно, но они имеют крайне низкую производительность — на одно измерение силы тяжести может уходить до 40 минут и более. Из-за этого распространение получили более простые, но в то же время более производительные гравиметры различных конструкций, которые измеряют только вертикальную производную потенциала — Δg{\displaystyle \Delta g}. В СССР к 1953 году был налажен выпуск собственных гравиметров и производство вариометрической аппаратуры резко снизилось, а к 1968 году прекратилось. В настоящее время градиентометры и вариометры используются лишь для высокоточных измерений поля силы тяжести (с их помощью возможны археологические изыскания, поиск крупных подземных помещений — галерей и бункеров), когда точности гравиметров не хватает.

Гравиметр представляет собой достаточно тонкий измерительный прибор, работа которого зависит от целого ряда мешающих факторов: температуры, давления, вибраций (всевозможные микросейсмы или тряска). Поэтому измерения проводят исключительно в покое, устанавливая гравиметр по очереди на каждом пикете заранее подготовленной сети. Чувствительная часть гравиметра помещена в защитный корпус, в котором поддерживаются постоянные температура и давление. Современные гравиметры уже достигли точности определения g{\displaystyle g} на уровне ~10⁻⁷—10⁻⁹ при относительных измерениях, а точность при абсолютных измерениях может составлять 0,03—0,07 мГал.

Существует много различных конструкций чувствительной системы, работа которой обусловлена влиянием силы тяжести на некое явление: свободное падение тел, колебание маятника (струны, мембраны), прецессия тяжёлого гироскопа, искривление поверхности вращающейся жидкости (или подъём жидкости в капилляре), левитация проводника с током или заряженной частицы в магнитном поле, а также равновесие какой-либо системы из весов (из рычагов или пружин).

Измеренные показания могут быть как абсолютными (измеряется сама величина силы тяжести, например, 981,2573 мГал), так и относительными (в этом случае измеряется разность силы тяжести в двух соседних пунктах). Также измерения могут проводиться в движении (на воде, а в последнее время «модной» становится авиагравиразведка), но чаще гравиметры неподвижно устанавливают на пункте измерения, и лишь после окончания измерений переносят на новый пункт.

Абсолютные измерения исторически появились раньше из-за того, что их грубое проведение возможно без специального оборудования. Например, в качестве измерительного прибора может быть большой маятник. Кроме того, оценку величины силы тяжести проводили бросая тяжёлые шары с высоких башен (в этом случае измерялось время падения шара на землю). Однако только с развитием современных технологий абсолютные измерения стали по-настоящему точными.

Маятниковые гравиметры абсолютных измерений[править | править код]

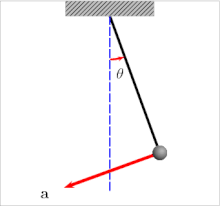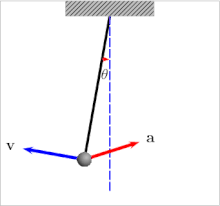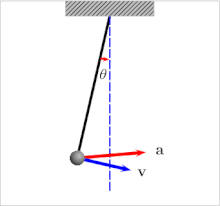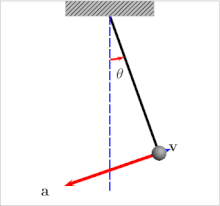Колебания маятника: стрелками показаны векторы скорости (v) и ускорения (a)

Измерение абсолютного значения силы тяжести основаны на том, что период колебаний T у маятника зависит от величины поля, в котором совершаются эти колебания. Математическим аппаратом, описывающим данную зависимость, является формула:

T=2πlg{\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}}

Для более точного вычисления можно воспользоваться более сложной моделью:

T=T0{1+(12)2sin2⁡(α2)+(1⋅32⋅4)2sin4⁡(α2)+⋯+[(2n−1)!!(2n)!!]2sin2n⁡(α2)+…}{\displaystyle T=T_{0}\left\{1+\left({\frac {1}{2}}\right)^{2}\sin ^{2}\left({\frac {\alpha }{2}}\right)+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}\sin ^{4}\left({\frac {\alpha }{2}}\right)+\dots +\left[{\frac {\left(2n-1\right)!!}{\left(2n\right)!!}}\right]^{2}\sin ^{2n}\left({\frac {\alpha }{2}}\right)+\dots \right\}}, где T0=2πlg{\displaystyle T_{0}=2\pi {\sqrt {\frac {l}{g}}}} — период малых колебаний, α{\displaystyle \alpha } — максимальный угол отклонения маятника от вертикали.

Однако на точность вычислений силы тяжести, в результате, будут оказывать влияние точность измерения длины маятника, а также масса груза. Для решения этой проблемы Ф. В. Бессель предложил измерять периоды колебаний T1{\displaystyle T_{1}} и T2{\displaystyle T_{2}} одного и того же маятника при разной длине нити l1{\displaystyle l_{1}} и l2{\displaystyle l_{2}}. Для расчётов необходимо использовать формулу:

g=4π2l1−l2T12−T22{\displaystyle g=4\pi ^{2}{\frac {l_{1}-l_{2}}{T_{1}^{2}-T_{2}^{2}}}}

Преимущество данного подхода заключается в том, что измерить разность длин маятников можно значительно точнее и проще, чем сами длины маятников. Точность измерения может составить 0,3 мГал.

Баллистические гравиметры[править | править код]

Измерение абсолютного значения силы тяжести основано на регистрации времени свободного падения некоторого пробного тела известной массы. Математическим аппаратом, описывающим данную зависимость, является формула:

z=z0+v0t+gt22{\displaystyle z=z_{0}+v_{0}t+{\frac {gt^{2}}{2}}}

Величины z0{\displaystyle z_{0}} — начальная высота, v0{\displaystyle v_{0}} — начальная скорость заранее известны, соответственно, измерив положение тела z и время t в нескольких положениях, можно составить систему уравнений:

{z1=z0+v0t1+gt122z2=z0+v0t2+gt222z3=z0+v0t3+gt322{\displaystyle \left\{{\begin{matrix}z_{1}=z_{0}+v_{0}t_{1}+{\frac {gt_{1}^{2}}{2}}\\z_{2}=z_{0}+v_{0}t_{2}+{\frac {gt_{2}^{2}}{2}}\\z_{3}=z_{0}+v_{0}t_{3}+{\frac {gt_{3}^{2}}{2}}\end{matrix}}\right.}

Измерения координаты тела осуществляется с помощью лазерного дальномера, а для увеличения точности вводят поправку на время запаздывания определения координат из-за физических процессов в приборе.

Для ещё большего увеличения точности могут усложнять математический аппарат, учитывая неоднородность самого гравитационного поля (свободно падающий груз меняет свою абсолютную высоту, а на разной высоте разное нормальное значения силы тяжести). Поэтому на практике распространена следующая формула:

zi=z0+v0ti+gti22+γv0ti36+γgti424{\displaystyle z_{i}=z_{0}+v_{0}t_{i}+{\frac {gt_{i}^{2}}{2}}+\gamma {\frac {v_{0}t_{i}^{3}}{6}}+\gamma {\frac {gt_{i}^{4}}{24}}}

где γ{\displaystyle \gamma } — вертикальный градиент силы тяжести на текущем пикете.

Фактически, в гравиметрах типа ГАБЛ-Э во время одного свободного падения измерений производят не три раза, а несколько сотен раз. Это позволяет статистическими методами определить наиболее вероятное значение силы тяжести. Для этого применяется следующая формула:

g=2Δ|N∑ti∑Si−16γ(v0ti3+14gti4)∑ti∑ti2∑[Si−16γ(v0ti3+14gti4)]ti∑ti2∑ti3∑[Si−16γ(v0ti3+14gti4)]ti2|{\displaystyle g={\frac {2}{\Delta }}{\begin{vmatrix}N&\sum t_{i}&\sum S_{i}-{\frac {1}{6}}\gamma (v_{0}t_{i}^{3}+{\frac {1}{4}}gt_{i}^{4})\\\sum t_{i}&\sum t_{i}^{2}&\sum \left[{S_{i}-{\frac {1}{6}}\gamma (v_{0}t_{i}^{3}+{\frac {1}{4}}gt_{i}^{4})}\right]t_{i}\\\sum t_{i}^{2}&\sum t_{i}^{3}&\sum \left[{S_{i}-{\frac {1}{6}}\gamma (v_{0}t_{i}^{3}+{\frac {1}{4}}gt_{i}^{4})}\right]t_{i}^{2}\end{vmatrix}}}

где N — количество измерений, а величина Δ{\displaystyle \Delta } определяется выражением:

Δ=|N∑ti∑ti2∑ti∑ti2∑ti3∑ti2∑ti3∑ti4|{\displaystyle \Delta ={\begin{vmatrix}N&\sum t_{i}&\sum t_{i}^{2}\\\sum t_{i}&\sum t_{i}^{2}&\sum t_{i}^{3}\\\sum t_{i}^{2}&\sum t_{i}^{3}&\sum t_{i}^{4}\end{vmatrix}}}

Визуально основная часть гравиметра представляет собой короткую трубку, из которой откачан воздух. Специальный механизм сверху вниз по трубке бросает шарик известной массы, а нижний механизм (так называемая «юбка») ловит шарик внизу, когда тот вылетает из трубки. Затем механизм возвращает шарик обратно к верхней части трубы и снова бросает. Во время падения лазерный луч многократно измеряет координаты шарика в трубе.

Квантовый гравиметр[править | править код]

Создан квантовый гравиметр размером в 1 см3{\displaystyle {\text{1 см}}^{3}} и основанный на использовании интерферометра Маха — Цендера^[3].

Относительное измерение силы тяжести[править | править код]

В отличие от абсолютных измерений, относительные характеризуются более высокой производительностью. Один и тот же прибор переносят между площадками, заранее выбранными из предположений более общего свойства, и, сравнивая результаты измерений, определяют конфигурацию гравитационного поля в данной области.

Маятниковые гравиметры для относительных измерений[править | править код]

Примерами данной конструкции являются гравиметры Штюкарта и комплекс «Агат» (ЦНИИГАиК). Приборы состоят из одного или нескольких комплектов маятников, в которых два маятника качаются в противофазе. Маятники помещаются в сосуд Дьюара, в котором поддерживается постоянная температура.

Измеряется отношение:

gagb=Tb2Ta2{\displaystyle {\frac {g_{a}}{g_{b}}}={\frac {T_{b}^{2}}{T_{a}^{2}}}}

Точность измерения может достигать 0,1 мГал.

Гравиметры на основе сейсмографа Голицына[править | править код]

В основе конструкции прибора лежит… сейсмограф.

Данный тип гравиметров, пожалуй, самый распространённый. Несмотря на кажущуюся грубоватость конструкции, именно кварцевые гравиметры (из кварца делают основной чувствительный элемент системы — сейсмограф Голицына) имеют оптимальное соотношение доступности и функционала. Чаще всего это относительно недорогие приборы небольшого веса и габаритов при хорошей точности измерений. Таковы, например, популярные канадские гравиметры CG-5 и отечественные ГНУ-К (ГНУ-КС, ГНУ-КВ).

Прообраз конструкции разработан великим отечественным геофизиком Б. Б. Голицыным.

Её основу составляет каркас чувствительного элемента в виде перевёрнутой П-образной рамки из кварца. Между верхними концами рамки натянута кварцевая нить, закрученная в двойную спираль. В середине спирали между витками вставлено тонкое кварцевое коромысло с платиновым грузом на конце. Груз на коромысле уравновешивает усилие раскручивания кварцевой нити.

Мерой силы тяжести в таком гравиметре является угол отклонения коромысла от положения при калибровке прибора. Угол измеряется оптической системой (визуально), впрочем, встречаются и другие схемы. Вся кварцевая конструкция с платиновым грузом помещается в термостат.

Отдельной ветвью эволюции кварцевых гравиметров являются гравиметры La Coste&Romberg аналогичного устройства, но чувствительная часть этих гравиметров выполнена не из кварца, а из металла. Стабильность системы так же обеспечивается термостатированием датчика.

Инерциальные гравиметры[править | править код]

Определение вектора ускорения силы тяжести с помощью инерциального гравиметра происходит по результатам измерений параметров инерциальной системы на подвижном носителе (чаще всего на флоте). Сама инерциальная система состоит из акселерометров, гироскопов и других устройств.

Теория инерциальной гравиметрии полностью совпадает с теорией инерциальной навигации, а основное уравнение имеет вид:

md2r→dt2=mg→+F→{\displaystyle m{\frac {d^{2}{\vec {r}}}{dt^{2}}}=m{\vec {g}}+{\vec {F}}}

где r→{\displaystyle {\vec {r}}} — радиус-вектор точечной пробной массы m, mg→{\displaystyle m{\vec {g}}} — вектор силы тяжести, а F→{\displaystyle {\vec {F}}} — сила воздействия опоры на пробную массу.

Инерциальная навигация — достаточно развитая наука, развившаяся ещё в 1930-х, и нашедшая применение во многих областях. Например, А. В. Тиль разработал быстродействующий морской гравиметр «Стен» с магнитным подвесом инерциального тела. С его помощью он реализовал возможность определения координат подводных лодок только по гравитационному полю Земли. Прибор прошёл испытания в 1982 году и его включили в состав комплекса навигации подлодок «Тайфун». В ходе этих испытаний Тиль выполнил и гравиразведку акватории Белого моря, где были выявлены аномалии, перспективные для дальнейшего поиска полезных ископаемых.

Подобный гравиметр состоит из трёх ортогональных акселерометров, положение которых непрерывно контролируется гироскопами. С помощью упомянутых акселерометров получают три составляющие вектора силы, действующей на пробную массу.

Криогенные гравиметры[править | править код]

Сверхпроводящую сферу помещают над кольцом, по которому циркулирует электрический ток, создающий внешнее магнитное поле, индуцирующее на поверхности сферы, магнитное поле которого противоположно приложенному извне и выталкивает сферу из внешнего поля, поэтому сфера парит (левитирует) над кольцом на высоте, определяемой силой тяжести. Измерение этой высоты и позволяет вычислить силу тяжести.

Отсутствие существенных преимуществ в сочетании с дороговизной ограничивает распространённость таких приборов единичными образцами.

Струнные гравиметры[править | править код]

Гравиметры струнного типа основаны на зависимости резонансной частоты струны от её натяжения подвешенным на струне грузом. Они практически безынерционны, имеют небольшие вес и габариты, поэтому подходят для измерений силы тяжести с самолёта. Также они характеризуются очень малым смещением нуля, высокой помехоустойчивостью и острой направленностью оси чувствительности. Идея гравиметров была предложена физиками Мандельштамом и Папалекси, но впервые реализована и испытана в Англии на подводной лодке в 1949 году. В СССР первый струнный гравиметр был разработан и испытан в 1956 году на надводном судне А. М. Лозинской в ВНИИГеофизике. Точность составила 1,2 мГал.

Технически гравиметр представляет собой медный груз, подвешенный в поле постоянных магнитов на струне из сплава с малым температурным коэффициентом. Эти магниты демпфируют вибрации в поперечной плоскости. Струна помещена между полюсами другого постоянного магнита и является частью цепи положительной обратной связи генератора. Когда генератор возбуждает струну, возникают незатухающие механические колебания с собственной частотой струны, зависящей от натяжения силой тяжести груза, следовательно, задача сводится к измерению отклонения этой частоты от эталонной. Уравнение движение струны имеет вид:

Mgdα−Sσdz∂2x∂t2=0{\displaystyle Mgd\alpha -S\sigma dz{\frac {\partial ^{2}x}{\partial t^{2}}}=0}

M — это масса груза, σ{\displaystyle \sigma } — плотность, α{\displaystyle \alpha } — крайне небольшой угол между векторами силы натяжения и силы тяжести.

Недостатком струнных гравиметров является восприимчивость к вибрациям.

1. ↑ Гравиметр // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
2. ↑ Федынский В. В. Советский гравиметр // Новости нефтяной техники. 1947. № 85. С. 3-5.
3. ↑ S. Abend, M. Gebbe, M. Gersemann, H. Ahlers, H. Müntinga, E. Giese, N. Gaaloul, C. Schubert, C. Lämmerzahl, W. Ertmer, W. P. Schleich, and E. M. Rasel Phys. Rev. Lett. 117, 203003 — Published 11 November 2016 Atom-Chip Fountain Gravimeter

• Гравиразведка
• Геофизика
• GRACE — международный проект по изучению гравитационного поля Земли, представляющих два идентичных спутника, летящими друг за другом по одной и той же орбите на расстоянии друг от друга.

• Лозинская А. М., Федынский В. В. Гравиметр-высотомер // Прикладная геофизика. 1953. Вып. 10. С. 3-28.
• Федынский В. В. О разработке аппаратуры для гравиметрических измерений в движении // Известия АН СССР. Сер. геофиз. 1959. № 1. С. 146—152.
• Федынский В. В. К вопросу о классификации гравиметрических работ и новая техническая инструкция по гравиметрической разведке // Геофизическая разведка. 1962. Вып. 8. С. 51-56.
• Гайнанов А. Г., Красный Л. И. Строев П. А., Федынский В. В. и др. Объяснительная записка к гравиметрической карте Тихого океана и Тихоокеанского подвижного пояса. — Л.: ВСЕГЕИ, 1979. — 60 с.
• Виноградов В. Б., Болотнова Л. А. Гравиметры. — Екатеринбург: Изд-во УГГУ, 2010. — 67 с. — 200 экз.
• Миронов В. С. Курс гравиразведки. — Л.: Недра, 1972. — 512 с.