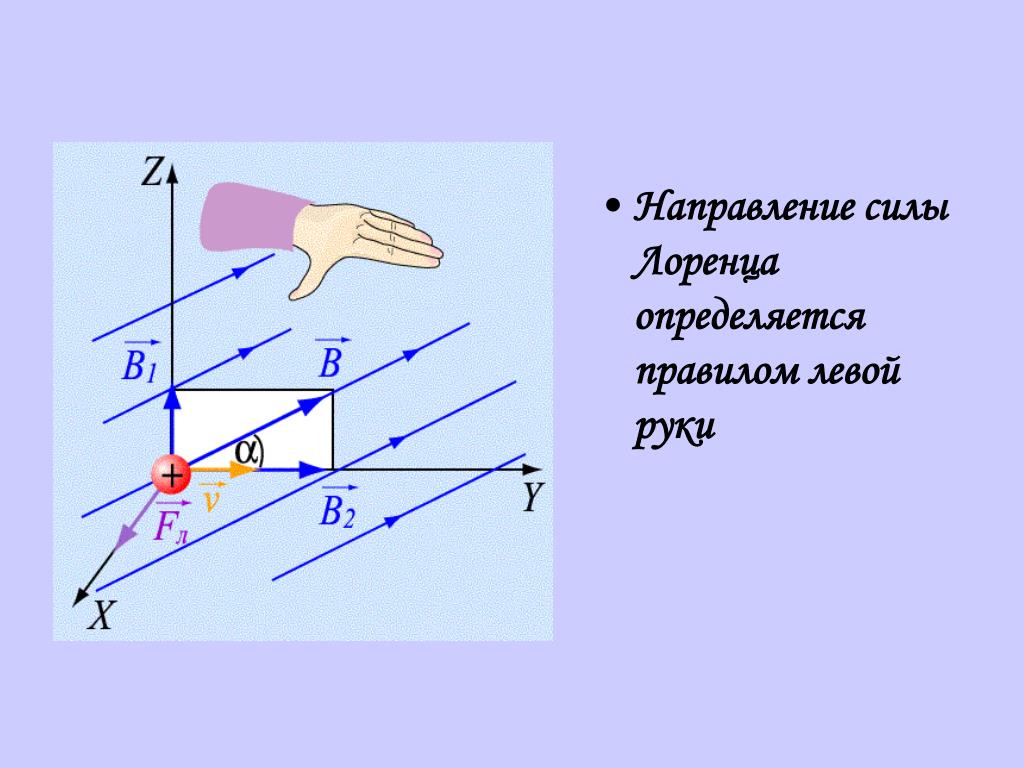
С использованием Л. с. были объяснены Холла эффект, нормальный Зеемана эффект, диамагнетизм и др. эффекты, связанные с взаимодействием в веществе движущихся зарядов и магнитного поля.
Вывести силу Лоренца из закона Максвелла, в котором частная производная от магнитного поля заменена на полную
%PDF-1.4 % 66 0 obj >/Metadata 65 0 R/PieceInfo>>>/Pages 12 0 R/PageLayout/OneColumn/StructTreeRoot 67 0 R/Type/Catalog/LastModified(D:20120804141326)/PageLabels 62 0 R/OutputIntents[64 0 R]>> endobj 65 0 obj >stream Acrobat Distiller 8.3.1 (Windows)HomeD:20120804111259Acrobat PDFMaker 8.1 for Word2012-08-04T14:13:26+03:002012-08-04T14:13:21+03:002012-08-04T14:13:26+03:00uuid:5c110c13-e87f-4e49-a7e2-f2f94188b133uuid:1af8b30d-a337-4a14-b1c3-d089448e6d52
Закон силы Лоренца (магнитные и смешанные поля)
июль Томас и Шравант С. внес
Содержание
- Физические эффекты на движение частицы
- Частица, циркулирующая в однородном магнитном поле
- Масс-спектрометр
- Рекомендации
[1]
По определению векторного произведения магнитная сила должна быть перпендикулярна как скорости, так и магнитному полю. В результате перпендикулярности скорости магнитное поле не может изменить скорость, а только направление скорости.
Следовательно, это всегда центростремительная сила. 92/r\]
\[r=\frac{mv}{qB}\]
Найдите радиус орбиты частицы с зарядом \(q=5\text{C}\) и массой \(m=20\text{кг}\), движущейся со скоростью \(v = 16\frac{\text{ m}}{\text{s}}\) через однородное магнитное поле \(B = 2\text{ T}.\) \[r=\frac{mv}{qB}=\frac{(20\text{кг})(16 \frac{\text{м}}{\text{s}})}{(5 \ текст{С})(2\текст{Т})}=32\текст{м}\]
Многие устройства используют круговое движение заряженной частицы, движущейся через однородное поле. Одним из таких устройств является масс-спектрометр , который сортирует ионы в образце в соответствии с отношением их массы к заряду.
Найдите отношение заряда к массе частицы, которая движется со скоростью \(v=4\text{м/с}\) через масс-спектрометр, настроенный на \(B=100\text{мТл}\) по орбите радиуса \(r = 20\text{см}.\)
Из \(r=\frac{mv}{qB},\) отношение заряда к массе равно \[\ frac {q} {m} = \ frac {v} {rB} = \ frac {4} {(0,20) (0,1)} = 200 \ frac {\ text {C}} {\ text {kg} }.
{-19}\text{C}.\)
Сила Лоренца — это сила, ощущаемая частицей заряда \(q\), движущейся со скоростью \(\vec{v}\) через область с электрическим поле \(\vec{E}\) и магнитное поле \(\vec{B}.\)
\[\vec{F}_{Лоренц} = q(\vec{E} + \vec{v }\times\vec{B})\]
Суммарная сила, действующая на частицу, движущуюся через область с электрическим и магнитным полями, представляет собой просто векторную сумму полей. \[\vec{F}_{Лоренц} = \vec{F}_E + \vec{F}_B=q\vec{E} + q\vec{v}\times\vec{B}=q(\ vec{E} + \vec{v}\times\vec{B})\]
Найдите результирующую силу, действующую на частицу \(3 \text{C}\), движущуюся со скоростью \(\vec{v} = 6\hat{x}\frac{\text{m}}{\text{s}} \) в области с электрическим полем \(\vec{E} = 5\hat{y}\frac{\text{N}}{\text{C}}\) и магнитным полем \(\vec{B} = 20\шляпа{г}\текст{Т}.\)
Лучше всего начать с оценки перекрестного произведения.
\[\vec{v}\times\vec{B} = (6\шляпа{x})\times(5\шляпа{z}) = -30\шляпа{y}\]
Теперь сила Лоренца равна. \[\vec{F}_{Лоренц} = q(\vec{E} + \vec{v}\times\vec{B}) = (3)(5\hat{y} — 30\hat{ у}) = -75\шляпа{у}\текст{N}.\]
Вдоль плоскости \(xz\) Вдоль плоскости \(yz\) Строго \(х\) Ни один из этих вариантов Строго \(у\) Вдоль плоскости \(xy\) Строго \(z\)
Позитрон движется через область, в которой электрические поля однородны в направлении \(x\) и магнитное поле однородно в направлении \(y\). Куда направлена конечная скорость позитрона?
- Индианфейс, ., & Примфак, . Действие силы Лоренца, искривляющей траекторию электрона в магнитном поле . Получено 4 мая 2016 г., от https://commons.wikimedia.org/wiki/File:Action_of_the_Lorentz_force_bending_the_path_of_an_electron_in_a_ Magnetic_field.
Процитировать как: Закон силы Лоренца (магнитные и смешанные поля).
Brilliant.org . Извлекаются из https://brilliant.org/wiki/lorentz-force-law-magnetic-fields/ электромагнетизм — Какова *причина* силы Лоренца
В чем причина силы Лоренца?
«Винтовая» природа электромагнетизма. Минковский упоминал об этом в «Пространстве и времени», как и Максвелл в «О физических силовых линиях: », «поступательное движение вдоль оси не может вызвать вращение вокруг этой оси, если оно не встречается с каким-то особым механизмом, например, с винтом» . . Вот почему правило правой руки применимо как к электромагнетизму, так и к резьбе. ИМХО, чтобы действительно «понять» это, вы должны принять к сведению классическую электродинамику Джексона:
«правильно следует говорить об электромагнитном поле Fμν, а не отдельно о E или B». Это упрощенно, но теперь вы начинаете понимать «спинорную» природу электрона. И если вы обратили внимание на заголовок страницы Максвелла, вы можете понять, что вихрей, вращающихся в противоположных направлениях, притягивают и 9 вихрей.0085 вращающиеся в одном направлении вихри отталкивают
. Хотя электрон не связан с каким-либо движением жидкости, существует вектор Пойнтинга и «циркулирующий поток энергии», так что аналогия работает. В результате, если вы поместите электрон рядом с позитроном, они будут двигаться навстречу друг другу по прямой линии. Но если бросить электрон мимо позитрона, они тоже будут двигаться вокруг друг друга, примерно так: Это то, что мы видим в позитронии, а теперь сила Лоренца $\mathbf{F} = q\left[\ mathbf{E} + (\mathbf{v} \times \mathbf{B})\right]$ выглядит очевидным.
Можно ли объяснить, что на самом деле вызывает силу, действующую на проводник с током в магнитном поле?
Да. Вы можете достаточно легко понять линейные и вращательные силы между заряженными частицами. Следующим шагом является понимание силы вращения заряженной частицы вблизи проводника с током. По сути, это неподвижный столб ионов металлов и движущийся столб электронов. Вы когда-нибудь читали, что Эйнштейн говорил о поле как о состоянии пространства? Хорошо, видите гравитомагнитное поле, которое автор НАСА Тони Филлипс описывает как «искривленное пространство»? Вы можете думать об электромагнитном поле как о чем-то подобном, но немного более интенсивном. Только если бы у вас было движение относительно него, вы могли бы подумать об этом как о «поворотном пространстве» и начать говорить о завитке, также известном как гниение, что является сокращением от ротора. ИМХО, это ключ к пониманию того, как работают магниты. Все электроны имеют отрицательное электромагнитное поле, а все ионы металлов имеют положительное электромагнитное поле с противоположной хиральностью.
Получается, что вы двигаетесь через один набор поворотных полей, но не через другой. И когда у вас есть движение относительно поля кручения, вы думаете о нем как о поле вращений, , и это то, что представляет собой магнитное поле . Итак, то, что вы «видите», — это остаточное магнитное поле вокруг провода. Электрон, брошенный мимо провода, движется по кругу не из-за какой-то магической силы, действующей на расстоянии, а потому, что это «динамический спинор в пространстве, затянутом системой отсчета».
Последний шаг — понять, почему два провода движутся вместе. Для этого вы можете представить себе, что ваш электрон заключен в соседний провод. Он движется вверх, и он движется по кругу. Это вращение означает, что остаточное поле поворота выглядит как поле закручивания, а поскольку вращения представляют собой противоположные вращения влево и вправо, вы снова находитесь в ситуации, когда вращающихся в противоположных направлениях вихрей притягивают .
{-19}\text{C}.\)
gif
Затем нужно изобразить Fμν для электрона. Один упрощенный способ сделать это — скомбинировать радиальные линии электрического поля с концентрическими линиями магнитного поля, например:
*$.
*$. Однако электроны движутся вверх по проводу:
