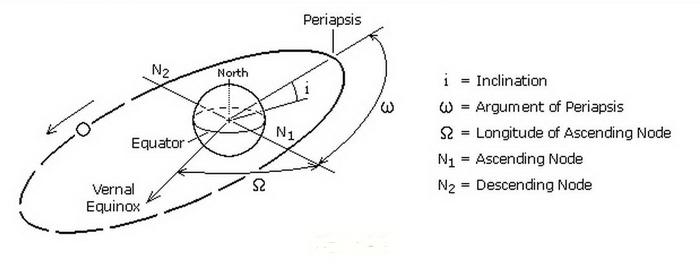
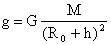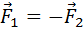Referat. Всемирное тяготение — PhysBook
Введение
Почему выпущенный из рук камень падает на Землю? Потому что его притягивает Земля, скажет каждый из вас. В самом деле, камень падает на Землю с ускорением свободного падения. Следовательно, на камень со сто-роны Земли действует сила, направленная к Земле. Согласно третьему закону Ньютона и камень действует на Землю с такой же по модулю силой, направленной к камню. Иными словами, между Землей и камнем действуют силы взаимного притяжения.
Ньютон был первым, кто сначала догадался, а потом и строго доказал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же. Это сила тяготения, действующая между любыми телами Вселенной. Вот ход его рассуждений, приведенных в главном труде Ньютона «Математические начала натуральной философии»:
«Брошенный горизонтально камень отклонится под действием тяжести от прямолинейного пути и, описав кривую траекторию, упадет наконец на Землю. Если его бросить с большей скоростью, то он упадет дальше» (рис. 1).
Рис. 1
Продолжая эти рассуждения, Ньютон приходит к выводу, что если бы не сопротивление воздуха, то траектория камня, брошенного с высокой горы с определенной скоростью, могла бы стать такой, что он вообще никогда не достиг бы поверхности Земли, а двигался вокруг нее «подобно тому, как планеты описывают в небесном пространстве свои орбиты».
Сейчас нам стало настолько привычным движение спутников вокруг Земли, что разъяснять мысль Ньютона подробнее нет необходимости.
Итак, по мнению Ньютона, движение Луны вокруг Земли или планет вокруг Солнца – это тоже свободное падение, но только падение, которое длится, не прекращаясь, миллиарды лет. Причиной такого «падения» (идет ли речь действительно о падении обычного камня на Землю или о движении планет по их орбитам) является сила всемирного тяготения. От чего же эта сила зависит?
Зависимость силы тяготения от массы тел
Галилей доказал, что при свободном падении Земля сообщает всем телам в данном месте одно и то же ускорение независимо от их массы. Но ускорение по второму закону Ньютона обратно пропорционально массе\[a = \frac {F}{m}\]. Как же объяснить, что ускорение, сообщаемое телу силой притяжения Земли, одинаково для всех тел? Это возможно лишь в том случае, если сила притяжения к Земле прямо пропорциональна массе тела. В этом случае увеличение массы т, например, вдвое приведет к увеличению модуля силы F тоже вдвое, а ускорение, которое равно \(a = \frac {F}{m}\), останется неизменным. Обобщая этот вывод для сил тяготения между любыми телами, заключаем, что сила всемирного тяготения прямо пропорциональна массе тела, на которое эта сила действует.
Но во взаимном притяжении участвуют по меньшей мере два тела. На каждое из них, согласно третьему закону Ньютона, действуют одинаковые по модулю силы тяготения. Поэтому каждая из этих сил должна быть пропорциональна как массе одного тела, так и массе другого тела. Поэтому сила всемирного тяготения между двумя телами прямо пропорциональна произведению их масс:
\(F \sim m_1 \cdot m_2\)Зависимость силы тяготения от расстояния между телами
Из опыта хорошо известно, что ускорение свободного падения равно 9,8 м/с
Чтобы выяснить, как влияет расстояние между телами на силу их вза-имного притяжения, нужно было бы узнать, каково ускорение тел, удаленных от Земли на достаточно большие расстояния. Однако наблюдать и изучать свободное падение тела с высоты в тысячи километров над Землей трудно. Но сама природа пришла здесь на помощь и дала возможность определить ускорение тела, движущегося по окружности вокруг Земли и обладающего поэтому центростремительным ускорением, вызванным, разумеется, той же силой притяжения к Земле. Таким телом является естественный спутник Земли – Луна. Если бы сила притяжения между Землей и Луной не зависела от расстояния между ними, то центростремительное ускорение Луны было бы таким же, как ускорение тела, свободно падающего близ поверхности Земли. В действительности же центростремительное ускорение Луны равно 0,0027 м/с
Докажем это. Обращение Луны вокруг Земли происходит под действием силы тяготения между ними. Приближенно орбиту Луны можно считать окружностью. Следовательно, Земля сообщает Луне центростремительное ускорение. Оно вычисляется по формуле \(a = \frac {4 \pi^2 \cdot R}{T^2}\), где
Найденное значение ускорения меньше ускорения свободного падения тел у поверхности Земли (9,8 м/с2) приблизительно в 3600 = 602 раз.
Таким образом, увеличение расстояния между телом и Землей в 60 раз привело к уменьшению ускорения, сообщаемого земным притяжением, а следовательно, и самой силы притяжения в 602 раз.
Отсюда вытекает важный вывод: ускорение, которое сообщает телам сила притяжения к Земле, убывает обратно пропорционально квадрату расстояния до центра Земли
\(F \sim \frac {1}{R^2}\).Закон всемирного тяготения
В 1667 г. Ньютон окончательно сформулировал закон всемирного тяготения:
\(F = G \cdot \frac {m_1 \cdot m_2}{R^2}.\quad (1)\)Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.
Коэффициент пропорциональности G называется гравитационной постоянной.
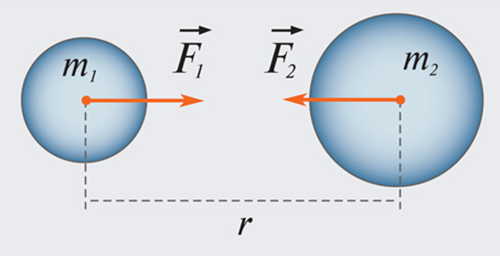
Закон всемирного тяготения справедлив только для таких тел, размеры которых пренебрежимо малы по сравнению с расстоянием между ними. Иначе говоря, он справедлив только для материальных точек. При этом силы гравитационного взаимодействия направлены вдоль линии, соединяющей эти точки (рис. 2). Подобного рода силы называются центральными.
Рис. 2
Для нахождения силы тяготения, действующей на данное тело со сто-роны другого, в случае, когда размерами тел пренебречь нельзя, поступают следующим образом. Оба тела мысленно разделяют на столь малые элементы, чтобы каждый из них можно было считать точечным. Складывая силы тяготения, действующие на каждый элемент данного тела со стороны всех элементов другого тела, получают силу, действующую на этот элемент (рис. 3). Проделав такую операцию для каждого элемента данного тела и сложив полученные силы, находят полную силу тяготения, действующую на это тело. Задача эта сложная.
Рис. 3
Есть, однако, один практически важный случай, когда формула (1) применима к протяженным телам. Можно доказать, что сферические тела, плотность которых зависит только от расстояний до их центров, при расстояниях между ними, больших суммы их радиусов, притягиваются с силами, модули которых определяются формулой (1). В этом случае R – это расстояние между центрами шаров.
И наконец, так как размеры падающих на Землю тел много меньше размеров Земли, то эти тела можно рассматривать как точечные. Тогда под R в формуле (1) следует понимать расстояние от данного тела до центра Земли.
Между всеми телами действуют силы взаимного притяжения, зависящие от самих тел (их масс) и от расстояния между ними.
Физический смысл гравитационной постоянной
Из формулы (1) находим
\(G = F \cdot \frac {R^2}{m_1 \cdot m_2}\).Отсюда следует, что если расстояние между телами численно равно единице (R = 1 м) и массы взаимодействующих тел тоже равны единице (m1 = m2 = 1 кг), то гравитационная постоянная численно равна модулю силы F. Таким образом (физический смысл),
гравитационная постоянная численно равна модулю силы тяготения, действующей на тело массой 1 кг со стороны другого тела такой же массы при расстоянии между телами, равном 1 м.
В СИ гравитационная постоянная выражается в
.Опыт Кавендиша
Значение гравитационной постоянной G может быть найдено только опытным путем. Для этого надо измерить модуль силы тяготения F, действующей на тело массой m1 со стороны тела массой m2 при известном расстоянии R между телами.
Первые измерения гравитационной постоянной были осуществлены в середине XVIII в. Оценить, правда весьма грубо, значение G в то время удалось в результате рассмотрения притяжения маятника к горе, масса которой была определена геологическими методами.
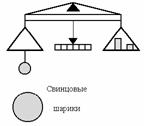
Точные измерения гравитационной постоянной впервые были проведены в 1798 г. английским физиком Г. Кавендишем с помощью прибора, называемого крутильными весами. Схематично крутильные весы показаны на рисунке 4.
Рис. 4
Кавендиш закрепил два маленьких свинцовых шара (диаметром 5 см и массой m1 = 775 г каждый) на противоположных концах двухметрового стержня. Стержень был подвешен на тонкой проволоке. Для этой проволоки предварительно определялись силы упругости, возникающие в ней при закручивании на различные углы. Два больших свинцовых шара (диаметром 20 см и массой m2 = 49,5 кг) можно было близко подводить к маленьким шарам. Силы притяжения со стороны больших шаров заставляли маленькие шары перемещаться к ним, при этом натянутая проволока немного закручивалась. Степень закручивания была мерой силы, действующей между шарами. Угол закручивания проволоки (или поворота стержня с малыми шарами) оказался столь малым, что его пришлось измерять с помощью оптической трубы. Результат, полученный Кавендишем, только на 1% отличается от значения гравитационной постоянной, принятого сегодня:
G ≈ 6,67∙10-11 (Н∙м2)/кг2Таким образом, силы притяжения двух тел массой по 1 кг каждое, находящихся на расстоянии 1 м друг от друга, по модулям равны всего лишь 6,67∙10-11 Н. Это очень малая сила. Только в том случае, когда взаимодействуют тела огромной массы (или по крайней мере масса одного из тел велика), сила тяготения становится большой. Например, Земля притягивает Луну с силой F ≈ 2∙1020 Н.
Гравитационные силы – самые «слабые» из всех сил природы. Это связано с тем, что гравитационная постоянная мала. Но при больших массах космических тел силы всемирного тяготения становятся очень большими. Эти силы удерживают все планеты возле Солнца.
Значение закона всемирного тяготения
Закон всемирного тяготения лежит в основе небесной механики – науки о движении планет. С помощью этого закона с огромной точностью определяются положения небесных тел на небесном своде на многие десятки лет вперед и вычисляются их траектории. Закон всемирного тяготения применяется также в расчетах движения искусственных спутников Земли и межпланетных автоматических аппаратов.
Возмущения в движении планет. Планеты не движутся строго по законам Кеплера. Законы Кеплера точно соблюдались бы для движения данной планеты лишь в том случае, когда вокруг Солнца обращалась бы одна эта планета. Но в Солнечной системе планет много, все они притягиваются как Солнцем, так и друг другом. Поэтому возникают возмущения движения планет. В Солнечной системе возмущения невелики, потому что притяжение планеты Солнцем гораздо сильнее притяжения другими планетами. При вычислении видимого положения планет приходится учитывать возмущения. При запуске искусственных небесных тел и при расчете их траекторий пользуются приближенной теорией движения небесных тел – теорией возмущений.
Открытие Нептуна. Одним из ярких примеров триумфа закона все-мирного тяготения является открытие планеты Нептун. В 1781 г. английский астроном Вильям Гершель открыл планету Уран. Была вычислена ее орбита и составлена таблица положений этой планеты на много лет вперед. Однако проверка этой таблицы, проведенная в 1840 г., показала, что данные ее расходятся с действительностью.
Ученые предположили, что отклонение в движении Урана вызвано притяжением неизвестной планеты, находящейся от Солнца еще дальше, чем Уран. Зная отклонения от расчетной траектории (возмущения движения Урана), англичанин Адаме и француз Леверрье, пользуясь законом всемирного тяготения, вычислили положение этой планеты на небе. Адаме раньше закончил вычисления, но наблюдатели, которым он сообщил свои результаты, не торопились с проверкой. Тем временем Леверрье, закончив вычисления, указал немецкому астроному Галле место, где надо искать неизвестную планету. В первый же вечер, 28 сентября 1846 г., Галле, направив телескоп на указанное место, обнаружил новую планету. Ее назвали Нептуном.
Таким же образом 14 марта 1930 г. была открыта планета Плутон. Оба открытия, как говорят, были сделаны «на кончике пера».
При помощи закона всемирного тяготения можно вычислить массу планет и их спутников; объяснить такие явления, как приливы и отливы воды в океанах, и многое другое.
Силы всемирного тяготения – самые универсальные из всех сил природы. Они действуют между любыми телами, обладающими массой, а массу имеют все тела. Для сил тяготения не существует никаких преград. Они действуют сквозь любые тела.
Литература
- Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. сред. шк. – М.: Просвещение, 1992. – 191 с.
- Физика: Механика. 10 кл.: Учеб. для углубленного изучения физики / М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др.; Под ред. Г.Я. Мякишева. – М.: Дрофа, 2002. – 496 с.
| ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ. | ||
Открыт Ньютоном в 1667 году на основе анализа движения планет (з-ны Кеплера) и, в частности, Луны. В этом же направлении работали Р.Гук (оспаривал приоритет) и Р.Боскович. |
| |
Все тела взаимодействуют друг с другом с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.
|
| |
Закон справедлив для:
Гравитационное взаимодействие существенно при больших массах. | Примеры: Притяжение электрона к протону в атоме водорода » 2×10-11 Н.
Тяготение между Землей и Луной» 2×1020 Н.
Тяготение между Солнцем и Землей » 3,5×1022 Н. | |
Применение:
| ||
Внимание!:
| ||
Анализ закона:
|
| |
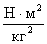 . . | G=6,67.10-11 | |
Впервые прямые измерения гравитационной постоянной провел Г. Кавендиш с помощью крутильных весов в 1798 г.
|
| |
Пусть m1=m2=1 кг, R=1 м, тогда: G=F (численно). Физический смысл гравитационной постоянной: гравитационная постоянная численно равна модулю силы тяготения, действующей между двумя точечными телами массой по 1 кг каждое, находящимися на расстоянии 1 м друг от друга. | ||
То, что гравитационная постоянная G очень мала показывает, что интенсивность гравитационного взаимодействия мала. |
| |
СИЛА ТЯЖЕСТИ | ||
Сила тяжести — это сила притяжения тел к Земле (к планете). |
|
|
| ||
| g0=9,81 м/с2 — на поверхности Земли | |
Если обозначить R0 радиус планеты, а |
| |
Ускорение силы тяжести зависит:
|
| |
Закон всемирного тяготения. Сила тяжести – FIZI4KA

1. Силы, с которыми все тела притягиваются друг к другу, называют силами всемирного тяготения или гравитационными силами.
Закон всемирного тяготения был установлен Ньютоном, и он утверждает, что тела притягиваются друг к другу с силой, модуль которой прямо пропорционален произведению их масс и обратно пропорционален квадрату расстояния между ними.
\( F=G\frac{m_1m_2}{r^2} \)
где \( m_1 \) и \( m_2 \) — массы тел, \( r \) — расстояние между телами, \( G \) — постоянная всемирного тяготения или гравитационная постоянная.
Значение гравитационной постоянной установлено опытным путём, оно равно \( G \) = 6,67·10-11 Нм2/кг2. Смысл её заключается в следующем: два тела, каждое массой 1 кг, находящиеся на расстоянии 1 м друг от друга, взаимодействуют с силой 6,67·10-11 Н.
Значение гравитационной постоянной свидетельствует о том, что силы тяготения между телами малы. Они становятся заметными при больших значениях масс взаимодействующих тел. Например, притяжение шарика к Земле можно наблюдать без специальных приборов, а притяжение Земли к такому же шарику мы не можем наблюдать непосредственно.
Закон всемирного тяготения справедлив для тел, размерами которых можно пренебречь по сравнению с расстоянием между ними (для материальных точек). Закон применим также к шарам, в этом случае расстоянием между телами является расстояние между центрами шаров.
2. Все тела притягиваются к Земле. Силу притяжения тела к Земле называют силой тяжести \( (F_т) \).
По второму закону Ньютона сила равна произведению массы тела и ускорения, с которым оно движется под действием этой силы. Ускорение, с которым движется тело под действием силы тяжести, называется ускорением свободного падения и обозначается буквой \( g \). Ускорение свободного падения не зависит от массы тела. Соответственно, сила тяжести рассчитывается но формуле: \( F_т=mg \).
3. Закон всемирного тяготения позволяет получить формулу для вычисления значения ускорения свободного падения. С одной стороны, сила тяжести равна \( F_т=mg \), с другой стороны, сила притяжения тела к Земле может быть вычислена, исходя из закона всемирного тяготения: \( F_т=G\frac{M_Зm}{R^2} \), где \( M_З \) — масса Земли, \( m \) — масса тела, \( r \) — радиус Земли. Приравнивая правые части записанных равенств, получим: \( mg=G\frac{M_Зm}{R^2} \) или \( g=G\frac{M_З}{R^2} \).
Полученная формула позволяет вычислить ускорение свободного падения тела, находящегося на поверхности Земли. Она наглядно показывает, что значение ускорения свободного падения зависит от расстояния тела до центра Земли. Именно поэтому оно на экваторе больше, чем на полюсах.
По этой формуле можно вычислить ускорение свободного падения на любой планете, подставив вместо массы Земли массу соответствующей планеты, а вместо радиуса
Земли радиус планеты.
4. Если тело находится на высоте \( h \) относительно поверхности Земли, то ускорение свободного падения определяется равенством \( g=G\frac{M_З}{(R_З+h)^2} \). Из приведенного равенства понятно, что чем дальше тело находится от центра Земли, тем меньше ускорение свободного падения. Например, на высоте 18 км, на которой летают современные истребители, оно равно 9,72 м/с2.
5. Пользуясь законом всемирного тяготения, можно вычислить скорость, которую необходимо сообщить телу для того, чтобы оно стало спутником Земли. Эта скорость
называется первой космической скоростью.
Центростремительное ускорение \( a \) спутнику массой \( m \) обеспечивает сила тяготения \( F_т \), которая по второму закону Ньютона равна \( F_т=ma \). Сила тяготения \( F_т=G\frac{M_Зm}{R^2} \), центростремительное ускорение равно \( a=\frac{v^2}{R} \), где \( v \) — линейная скорость спутника, \( R \) — радиус Земли. Откуда следует: \( G\frac{M_Зm}{R^2}=m\cdot\frac{v^2}{R} \) или \( g=\frac{v^2}{R} \). Отсюда \( v=\sqrt{gR} \), т.е. первая космическая скорость равна 7,9 км/с. Первый в мире искусственный спутник Земли был запущен в СССР в 1957 г.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Сила тяготения между двумя телами уменьшится в 2 раза, если массу каждого тела
1) увеличить в √2 раз
2) уменьшить в √2 раз
3) увеличить в 2 раза
4) уменьшить в 2 раза
2. Массу каждого из двух однородных шаров увеличили в 4 раза. Расстояние между ними тоже увеличили в 4 раза. Сила тяготения между ними
1) увеличилась в 64 раза
2) увеличилась в 16 раз
3) увеличилась в 4 раза
4) не изменилась
3. В вершинах прямоугольника расположены тела одинаковой массы. Со стороны какого тела на тело 1 действует наибольшая сила?
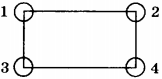

1) со стороны тела 2
2) со стороны тела 3
3) со стороны тела 4
4) со стороны всех тел одинаковая
4. Закон всемирного тяготения справедлив
A. Для всех тел
Б. Для однородных шаров
B. Для материальных точек
Правильный ответ
1) А
2) только Б
3) только В
4) и А, и Б
5. На ящик массой 5 кг, лежащий на полу лифта, движущегося с ускорением \( a \) вертикально вниз, действует сила тяжести
1) равная 50 Н
2) большая 50 Н
3) меньшая 50 Н
4) равная 5 Н
6. Сравните значения силы тяжести \( F_э \), действующей на груз на экваторе, с силой тяжести \( F_м \), действующей на этот же груз на широте Москвы, если груз находится на одной и той же высоте относительно поверхности Земли.
1) \( F_э=F_м \)
2) \( F_э>F_м \)
3) \( F_э<F_м \)
4) ответ может быть любым в зависимости от массы тел
7. Сила тяжести, действующая на космонавта на поверхности Луны,
1) больше силы тяжести, действующей на него на поверхности Земли
2) меньше силы тяжести, действующей на него на поверхности Земли
3) равна силе тяжести, действующей на него на поверхности Земли
4) больше силы тяжести, действующей на него на поверхности Земли на экваторе, и меньше силы тяжести, действующей на него, на поверхности Земли на полюсе
8. Сила тяжести, действующая на тело, зависит от
А. Географической широты местности
Б. Скорости падения тела на поверхность Земли
Правильный ответ
1) только А
2) только Б
3) ни А, ни Б
4) и А, и Б
9. Какое(-ие) из утверждений верно(-ы)?
Сила тяжести, действующая на тело у поверхности некоторой планеты, зависит от
А. Массы планеты.
Б. Массы тела.
1) только А
2) только Б
3) ни А, ни Б
4) и А, и Б
10. Первая космическая скорость зависит
A. От радиуса планеты
Б. От массы планеты
B. От массы спутника
Правильный ответ
1) только А
2) только Б
3) только А и Б
4) А, Б, В
11. Установите соответствие между физической величиной (левый столбец) и формулой, выражающей её взаимосвязь с другими величинами (правый столбец). В ответе запишите подряд номера выбранных ответов
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Сила тяжести
Б. Ускорение свободного падения на поверхности Земли
B. Закон всемирного тяготения
ФОРМУЛА
1) \( F=G\frac{m_1m_2}{r^2} \)
2) \( F_т=mg \)
3) \( g=G\frac{M_З}{(R_З+h)^2} \)
4) \( g=G\frac{M_З}{R^2} \)
12. Среди приведённых утверждений выберите два правильных и запишите их номера в таблицу
1) Гравитационная постоянная показывает, с какой силой притягиваются друг к другу два тела массой 1 кг.
2) Значение силы тяжести, действующей на тело, зависит от скорости его движения.
3) Ускорение свободного падения зависит от массы и радиуса планеты.
4) При увеличении расстояния между телами в 3 раза сила тяготения между ними уменьшается в 9 раз.
5) Изменение массы одного из взаимодействующих тел не влияет на значение силы тяготения.
Часть 2
13. Человек на Земле притягивается к ней с силой 700 Н. С какой силой он притягивался бы к Марсу, находясь на его поверхности, если радиус Марса в 2 раза меньше радиуса Земли, а масса в 10 раз меньше, чем масса Земли?
Ответы


Закон всемирного тяготения. Сила тяжести
ОценкаЗакон всемирного тяготения: физика :: SYL.ru
Закон всемирного тяготения открыл Ньютон в 1687 году при изучении движения спутника Луны вокруг Земли. Английский физик четко сформулировал постулат, характеризующий силы притяжения. Кроме того, анализируя законы Кеплера, Ньютон вычислил, что силы притяжения должны существовать не только на нашей планете, но и в космосе.
История вопроса
Закон всемирного тяготения родился не спонтанно. Издревле люди изучали небосвод, главным образом для составления сельскохозяйственных календарей, вычисления важных дат, религиозных праздников. Наблюдения указывали, что в центре «мира» находится Светило (Солнце), вокруг которого по орбитам вращаются небесные тела. Впоследствии догматы церкви не позволяли так считать, и люди утратили накапливавшиеся тысячелетиями знания.
В 16 веке, до изобретения телескопов, появилась плеяда астрономов, взглянувших на небосвод по-научному, отбросив запреты церкви. Т. Браге, многие годы наблюдая за космосом, с особой тщательностью систематизировал перемещения планет. Эти высокоточные данные помогли И. Кеплеру впоследствии открыть три своих закона.
К моменту открытия (1667 г.) Исааком Ньютоном закона тяготения в астрономии окончательно утвердилась гелиоцентрическая система мира Н. Коперника. Согласно ей, каждая из планет системы вращается вокруг Светила по орбитам, которые с приближением, достаточным для многих расчетов, можно считать круговыми. В начале XVII в. И. Кеплер, анализируя работы Т. Браге, установил кинематические законы, характеризующие движения планет. Открытие стало фундаментом для выяснения динамики движения планет, то есть сил, которые определяют именно такой вид их движения.
Описание взаимодействия
В отличие от короткопериодных слабых и сильных взаимодействий, гравитация и электромагнитные поля имеют свойства дальнего действия: их влияние проявляется на гигантских расстояниях. На механические явления в макромире воздействуют 2 силы: электромагнитная и гравитационная. Воздействие планет на спутники, полет брошенного или запущенного предмета, плавание тела в жидкости – в каждом из этих явлений действуют гравитационные силы. Эти объекты притягиваются планетой, тяготеют к ней, отсюда и название «закон всемирного тяготения».
Доказано, что между физическими телами безусловно действует сила взаимного притяжения. Такие явления, как падение объектов на Землю, вращение Луны, планет вокруг Солнца, происходящие под действием сил всемирного притяжения, называют гравитационными.
Закон всемирного тяготения: формула
Всемирное тяготение формулируется следующим образом: два любых материальных объекта друг к другу притягиваются с определенной силой. Величина этой силы прямо пропорциональна произведению масс этих объектов и обратно пропорциональна квадрату расстояния между ними:
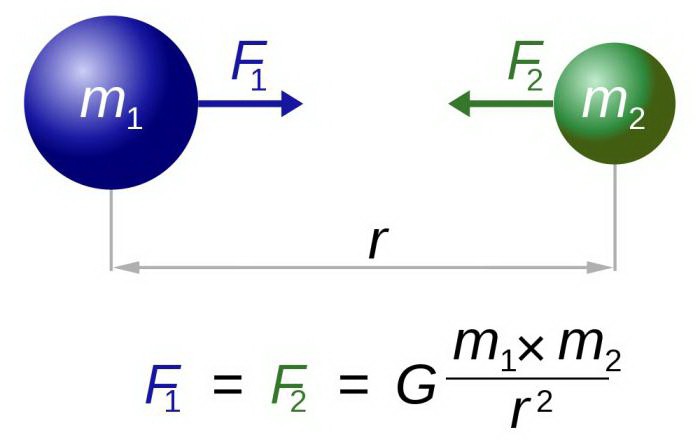
В формуле m1 и m2 являются массами исследуемых материальных объектов; r – расстояние, определяемое между центрами масс расчетных объектов; G – постоянная гравитационная величина, выражающая силу, с которой осуществляется взаимное притяжение двух объектов массой по 1 кг каждый, располагающихся между собой на расстоянии 1 м.
Гравитационная постоянная определена экспериментальным путем. Выполнить расчеты удалось британскому ученому Генри Кавендишу с помощью специального динамометра – крутильных весов. Выяснилось, что величина G=(6,673±0,003)·10-11Н·м2·кг—2 в МСЕ (Международной системе единиц).
Нюансы вычислений
Закон тяготения Исаака Ньютона относится к так называемой классической механике (традиционной физике) и не всегда точно отражает взаимодействия на микроуровне (в «новой» физике). Поэтому принято закон всемирного тяготения Ньютона применять только для материальных точек (объектов). Силу притяжения, возникающую между двумя объектами, можно определить по формуле, представленной выше, в следующих случаях:
- Если оба тела – однородные объекты, тогда r – известное расстояние между центрами объектов; m1, m2 – массы объектов.
- Одно из тел – материальная точка (объект), а второе – однородный шар, тогда m1 – масса точки, m2 – шара, r – известное расстояние между центрами масс.
Поле тяготения
Две силы взаимодействия, которые действуют на каждый из взаимодействующих объектов, одинаковы по величине, при этом противоположны по направлению в полном соответствии с 3 законом Ньютона (закон взаимодействия 2 материальных точек). Направлены силы вдоль прямой, которая соединяет обе материальные точки – их называют центральными. Гравитационное взаимодействие между этими объектами осуществляется полем тяготения. В каждой точке гравитационного поля на помещенный в него объект воздействует сила тяжести, пропорциональная массе этого объекта. Сила тяжести при этом не зависит от среды, в которой исследуемый объект (тело, точка) находится.
Поле тяготения имеет специфическое свойство – во время переноса объекта определенной массы (m) между различными точками поля тяготения действие силы тяжести не будет зависеть от траектории движения объекта, а будет зависеть исключительно от положения в гравитационном поле начальной и конечной точки перемещения объекта. Силы, обладающие подобными свойствами, назвали консервативными, а поле с действием таких сил – потенциальным.
Сила тяжести в космическом масштабе
Исаак Ньютон доказал, что закон всемирного тяготения, определение которого он дал для классической механики, также актуален при астрономических расчетах. Неотъемлемой характеристикой закона тяготения является понятие силы тяжести – та сила, с которой объект притягивается полем тяготения. Данное определение актуально для любых космических объектов.
Обычно сила тяжести (Ft) рассчитывается по простой формуле: Ft=mg, то есть масса объекта (m), поднятого над поверхностью Земли, умножается на коэффициент ускорения свободного падения (g). У поверхности Земли коэффициент g известен, если округлить, он равен 9,8 м/с². Но расчеты становятся неточными, если объект находится от плоскости Земли на значительном отдалении. В этой ситуации коэффициент g заранее не известен, и здесь приходит на помощь ньютоновская физика. Закон всемирного тяготения позволяет рассчитать силу тяжести даже для отдаленных объектов (например, Луны, спутников, метеоритов и т. д.), если известно расстояние между телом и Землей.
Пример расчетов
Разместим на высоте h над Землей, радиус которой — Rc, и масса — Mc, объект массой m. Между объектом и Землей действует все та же сила всемирного тяготения:
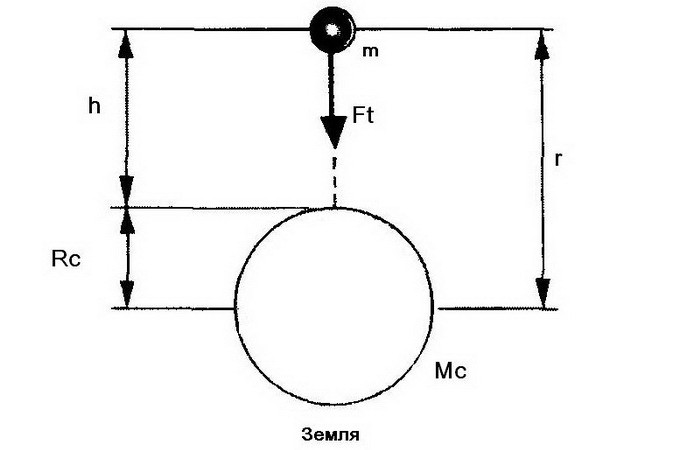 В этом случае Ft называется силой тяжести – силой притяжения исследуемого объекта Землей (точнее, составляющей этой силы). Эта сила придает объекту ускорение свободного падения. Рассчитать его можно так: Ft=G·(Mc·m/r²) , где r=Rc+h – это расстояние от объекта до центра Земли, G – гравитационная постоянная.
В этом случае Ft называется силой тяжести – силой притяжения исследуемого объекта Землей (точнее, составляющей этой силы). Эта сила придает объекту ускорение свободного падения. Рассчитать его можно так: Ft=G·(Mc·m/r²) , где r=Rc+h – это расстояние от объекта до центра Земли, G – гравитационная постоянная.Если изучить формулу, становится очевидным, что чем выше объект исследования над плоскостью планеты, тем сила тяжести меньше и меньше. То есть гравитационное поле планеты увеличивается при приближении к ее центру.
Особенности воздействия
Из-за суточного вращения Земли либо другой планеты вокруг оси сила притяжения и сила тяжести для одного и того же объекта отличаются между собой по модулю и направлению. Сила притяжения (гравитационная сила) всегда направлена по радиусу к центру Земли, сила тяжести Ft – по линии отвеса к центру Земли.
Сила притяжения зависит от значений географической широты. Причина такой зависимости заключается в том, что произвольное тело, которое находится в покое относительно Земли, участвует в ее суточном вращении, поэтому при движении вокруг оси по кругу на тело действует сила притяжения и сила реакции, направленная под определенным углом. Равнодействующая этих сил и придает телу центростремительное ускорение.
От чего зависит сила притяжения
Закон всемирного тяготения по-разному действует, в зависимости от региона. Так как сила притяжения зависит от значений широты на определенной местности, то аналогично ускорение свободного падения обладает разными значениями в разных местах. Максимальное значение сила тяжести и, соответственно, ускорение свободного падения имеют на полюсах Земли – сила тяжести в этих точках равна силе притяжения. Минимальными значения будут на экваторе.
Земной шар слегка сплюснут, его полярный радиус меньше экваториального примерно на 21,5 км. Однако эта зависимость менее существенная по сравнению с суточным вращением Земли. Расчеты показывают, что из-за сплюснутости Земли на экваторе величина ускорения свободного падения чуть меньше его значения на полюсе на 0,18%, а через суточное вращение – на 0,34%.
Впрочем, в одном и том же месте Земли угол между векторами направления мал, поэтому расхождение между силой притяжения и силой тяжести незначительно, и ею в расчетах можно пренебречь. То есть можно считать, что модули этих сил одинаковы – ускорение свободного падения около поверхности Земли везде одинаковое и равно приблизительно 9,8 м/с².
Вывод
Исаак Ньютон был ученым, который совершил научную революцию, полностью перестроил принципы динамики и на их основе создал научную картину мира. Его открытие повлияло на развитие науки, на создание материальной и духовной культуры. На судьбу Ньютона выпала задача пересмотреть результаты представления о мире. В XVII в. ученым завершена грандиозная работа построения фундамента новой науки – физики.
1.2.6 Закон всемирного тяготения. Сила тяжести. Зависимость силы тяжести от высоты над поверхностью планеты
Видеоурок: Закон всемирного тяготения
Лекция: Закон всемирного тяготения. Сила тяжести. Зависимость силы тяжести от высоты над поверхностью планеты
 Закон гравитационного взаимодействия
Закон гравитационного взаимодействияДо некоторого времени Ньютон не задумывался о том, что его предположения справедливы для всех тех, находящихся во Вселенной. Спустя некоторое время им были изучены законы Кеплера, а также законы, которых придерживаются тела, что свободно падают на поверхность Земли. Данные мысли не были зафиксированы на бумаге, а только остались заметки про яблоко, упавшее на Землю, а также о Луне, которая вращается вокруг планеты. Он считал, что
все тела рано или поздно упадут на Землю;
они падают с одинаковым ускорением;
Луна двигается по окружности с постоянным периодом;
размеры Луны практически в 60 раз меньше, чем у Земли.
В результате всего это был сделан вывод, что все тела притягиваются друг к другу. При этом, чем больше масса тела, тем с большей силой оно притягивает к себе окружающие объекты.
В результате этого был открыт закон всемирного притяжения:
Любые материальные точки притягиваются друг к другу с силой, увеличивающейся в зависимости от роста их масс, но при этом уменьшается в квадратной пропорциональности в зависимости от расстояния между этими телами.
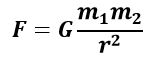
F – сила гравитационного притяжения
m1, m2 – массы взаимодействующих тел, кг
r – расстояние между телами (центрами масс тел), м
G – коэффициент (гравитационная постоянная) ≈ 6,67*10-11 Нм2/кг2
 Данный закон справедлив в том случае, когда тела можно принять за материальные точки, а вся их масса сконцентрирована в центре.
Данный закон справедлив в том случае, когда тела можно принять за материальные точки, а вся их масса сконцентрирована в центре.Коэффициент пропорциональности из закона всемирного тяготения был определен экспериментальным путем ученым Г.Кавендишем. Гравитационная постоянная равна силе, с которой притягиваются килограммовые тела на расстоянии одного метра:
G = 6,67*10-11 Нм2/кг2Взаимное притяжение тел объясняется гравитационным полем, подобным электрическому, которое находится вокруг всех тел.
 Сила тяжести
Сила тяжестиВокруг Земли также существует такое поле, его еще называют полем земного притяжения. Все тела, что находятся в местах его действия, притягиваются к Земле.
Сила тяжести — это равнодействующая гравитационной силы, а также центростремительной силы, направленной по оси вращения.
 Именно с такой силой все планеты притягивают к себе другие тела.
Именно с такой силой все планеты притягивают к себе другие тела.Характеристика силы тяжести:
1. Точка приложения: центр масс тела.
2. Направление: к центру Земли.
3. Модуль силы определяется по формуле:
Fтяж = gmg = 9,8 м/с2 — ускорение свободного падения
m — масса тела
Так как сила тяжести — это частный случай закона гравитационного взаимодействия, то ускорение свободного падения определяется по формуле:

g — ускорение свободного падения, м/с2
G — гравитационная постоянная, Нм2/кг2
M3 — масса Земли, кг
R3 — радиус Земли
Из этого можно сделать вывод:
чем больше масса космического объекта, тем больше ускорение свободного падения;
чем больше расстояние до космического объекта, тем меньше ускорение свободного падения.
Более того, на данную величину влияет и период вращения планеты вокруг оси.
Если тело находится на некотором расстоянии от поверхности Земли, то определить ускорение можно по следующей формуле:
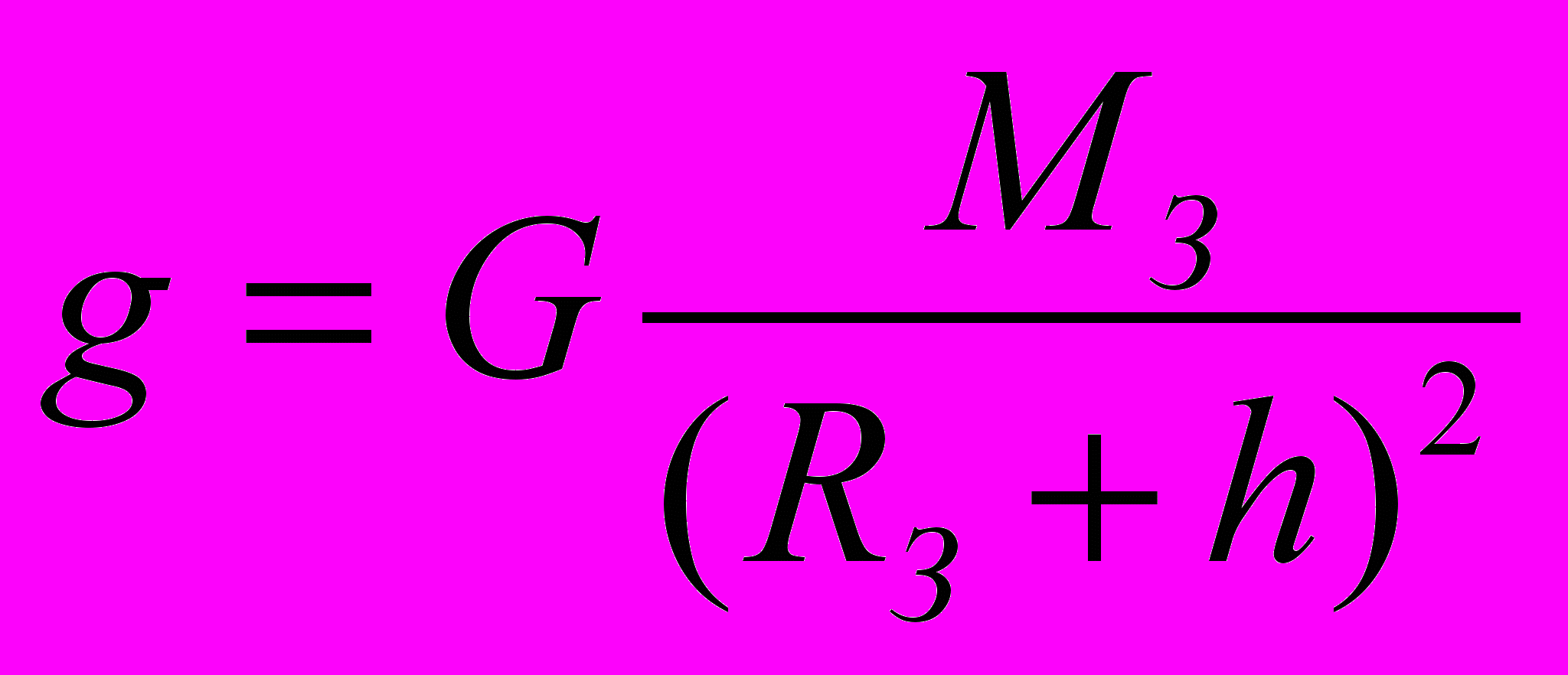
Если же с увеличением высоты уменьшается ускорение, то можно сделать вывод, что сила тяжести так же уменьшается.

Сила тяжести и сила всемирного тяготения
Сила тяжести и сила всемирного тяготения
«Физика — 10 класс»
Почему Луна движется вокруг Земли?
Что будет, если Луна остановится?
Почему планеты обращаются вокруг Солнца?
В главе 1 подробно говорилось о том, что земной шар сообщает всем телам у поверхности Земли одно и то же ускорение — ускорение свободного падения. Но если земной шар сообщает телу ускорение, то согласно второму закону Ньютона он действует на тело с некоторой силой. Силу, с которой Земля действует на тело, называют силой тяжести. Сначала найдём эту силу, а затем и рассмотрим силу всемирного тяготения.
Ускорение по модулю определяется из второго закона Ньютона:
В общем случае оно зависит от силы, действующей на тело, и его массы. Так как ускорение свободного падения не зависит от массы, то ясно, что сила тяжести должна быть пропорциональна массе:
= m (3.1)
Физическая величина — ускорение свободного падения, оно постоянно для всех тел.
На основе формулы F = mg можно указать простой и практически удобный метод измерения масс тел путём сравнения массы данного тела с эталоном единицы массы. Отношение масс двух тел равно отношению сил тяжести, действующих на тела:
Это значит, что массы тел одинаковы, если одинаковы действующие на них силы тяжести.
На этом основано определение масс путём взвешивания на пружинных или рычажных весах. Добиваясь того, чтобы сила давления тела на чашку весов, равная силе тяжести, приложенной к телу, была уравновешена силой давления гирь на другую чашку весов, равной силе тяжести, приложенной к гирям, мы тем самым определяем массу тела.
Сила тяжести, действующая на данное тело вблизи Земли, может считаться постоянной лишь на определенной широте у поверхности Земли. Если тело поднять или перенести в место с другой широтой, то ускорение свободного падения, а следовательно, и сила тяжести изменятся.
Сила всемирного тяготения.
Ньютон был первым, кто строго доказал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же. Это сила всемирного тяготения, действующая между любыми телами Вселенной.
Ньютон пришёл к выводу, что если бы не сопротивление воздуха, то траектория камня, брошенного с высокой горы (рис. 3.1) с определённой скоростью, могла бы стать такой, что он вообще никогда не достиг бы поверхности Земли, а двигался бы вокруг неё подобно тому, как планеты описывают в небесном пространстве свои орбиты.
Итак, по мнению Ньютона, движение Луны вокруг Земли или движение планет вокруг Солнца — это тоже свободное падение, которое длится, не прекращаясь, миллиарды лет. Причиной такого падения (идёт ли речь действительно о падении обычного камня на Землю или о движении планет по их орбитам) служит сила тяготения.
Земля сообщает Луне ускорение, которое не зависит от массы Луны и, как показали расчёты, в (60)2 раз меньше ускорения тел на Земле. Расстояние до Луны в 60 раз больше радиуса Земли. Отсюда Ньютон сделал вывод, что ускорение и соответственно сила притяжения тел к Земле обратно пропорциональны квадрату расстояния до центра Земли:
Также Ньютон установил, что Солнце сообщает всем планетам ускорение, обратно пропорциональное квадрату расстояния от планет до Солнца.
Закон всемирного тяготения.
Можно лишь догадываться о волнении, охватившем Ньютона, когда он пришёл к великому результату: одна и та же причина вызывает явления поразительно широкого диапазона — от падения брошенного камня на землю до движения огромных космических тел.
Ньютон нашёл эту причину и смог точно выразить её в виде одной формулы — закона всемирного тяготения.
Так как сила всемирного тяготения сообщает всем телам одно и то же ускорение независимо от их массы, то она должна быть пропорциональна массе того тела, на которое действует:
«Тяготение существует ко всем телам вообще и пропорционально массе каждого из них… все планеты тяготеют друг к другу…» И. Ньютон
Но поскольку, например, Земля действует на Луну с силой, пропорциональной массе Луны, то и Луна по третьему закону Ньютона должна действовать на Землю с той же силой. Причём эта сила должна быть пропорциональна массе Земли. Если сила тяготения является действительно универсальной, то со стороны данного тела на любое другое тело должна действовать сила, пропорциональная массе этого другого тела. Следовательно, сила всемирного тяготения должна быть пропорциональна произведению масс взаимодействующих тел. Отсюда вытекает формулировка закона всемирного тяготения.
Закон всемирного тяготения:
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними:
Коэффициент пропорциональности G называется гравитационной постоянной.
Гравитационная постоянная численно равна силе притяжения между двумя материальными точками массой 1 кг каждая, если расстояние между ними равно 1 м. Ведь при массах m1 = m2 = 1 кг и расстоянии r = 1 м получаем G = F (численно).
Нужно иметь в виду, что закон всемирного тяготения (3.4) как всеобщий закон справедлив для материальных точек. При этом силы гравитационного взаимодействия направлены вдоль линии, соединяющей эти точки (рис. 3.2, а).
Можно показать, что однородные тела, имеющие форму шара (даже если их нельзя считать материальными точками, рис. 3.2, б), также взаимодействуют с силой, определяемой формулой (3.4). В этом случае r — расстояние между центрами шаров. Силы взаимного притяжения лежат на прямой, проходящей через центры шаров. Такие силы называются центральными. Тела, падение которых на Землю мы обычно рассматриваем, имеют размеры, много меньшие, чем земной радиус (R ≈ 6400 км).
Такие тела можно, независимо от их формы, рассматривать как материальные точки и определять силу их притяжения к Земле с помощью закона (3.4), имея в виду, что r есть расстояние от данного тела до центра Земли.
Брошенный на Землю камень отклонится под действием тяжести от прямолинейного пути и, описав кривую траекторию, упадёт наконец на Землю. Если его бросить с большей скоростью, то он упадёт дальше». И. Ньютон
Определение гравитационной постоянной.
Теперь выясним, как можно найти гравитационную постоянную. Прежде всего заметим, что G имеет определённое наименование. Это обусловлено тем, что единицы (и соответственно наименования) всех величин, входящих в закон всемирного тяготения, уже были установлены ранее. Закон же тяготения даёт новую связь между известными величинами с определёнными наименованиями единиц. Именно поэтому коэффициент оказывается именованной величиной. Пользуясь формулой закона всемирного тяготения, легко найти наименование единицы гравитационной постоянной в СИ: Н • м2/кг2 = м3/(кг • с2).
Для количественного определения G нужно независимо определить все величины, входящие в закон всемирного тяготения: обе массы, силу и расстояние между телами.
Оцените силу гравитационного взаимодействия между вами и вашим соседом по парте. Считайте, что вы нахояитесь на расстоянии r = 0,5 м.
Трудность состоит в том, что гравитационные силы между телами небольших масс крайне малы. Именно по этой причине мы не замечаем притяжение нашего тела к окружающим предметам и взаимное притяжение предметов друг к другу, хотя гравитационные силы — самые универсальные из всех сил в природе. Два человека массами по 60 кг на расстоянии 1 м друг от друга притягиваются с силой всего лишь порядка 10-9 Н. Поэтому для измерения гравитационной постоянной нужны достаточно тонкие опыты.
Впервые гравитационная постоянная была измерена английским физиком Г. Кавендишем в 1798 г. с помощью прибора, называемого крутильными весами. Схема крутильных весов показана на рисунке 3.3. На тонкой упругой нити подвешено лёгкое коромысло с двумя одинаковыми грузиками на концах. Рядом неподвижно закреплены два тяжёлых шара. Между грузиками и неподвижными шарами действуют силы тяготения. Под влиянием этих сил коромысло поворачивается и закручивает нить до тех пор, пока возникающая сила упругости не станет равна гравитационной силе. По углу закручивания можно определить силу притяжения. Для этого нужно только знать упругие свойства нити. Массы тел известны, а расстояние между центрами взаимодействующих тел можно непосредственно измерить.
Из этих опытов было получено следующее значение для гравитационной постоянной:
G = 6,67 • 10-11 Н • м2/кг2.
Лишь в том случае, когда взаимодействуют тела огромных масс (или по крайней мере масса одного из тел очень велика), сила тяготения достигает большого значения. Например, Земля и Луна притягиваются друг к другу с силой F ≈ 2 • 1020 Н.
Зависимость ускорения свободного падения тел от географической широты.
Одна из причин увеличения ускорения свободного падения при перемещении точки, где находится тело, от экватора к полюсам, состоит в том, что земной шар несколько сплюснут у полюсов и расстояние от центра Земли до её поверхности у полюсов меньше, чем на экваторе. Другой причиной является вращение Земли.
Равенство инертной и гравитационной масс.
Самым поразительным свойством гравитационных сил является то, что они сообщают всем телам, независимо от их масс, одно и то же ускорение. Что бы вы сказали о футболисте, удар которого одинаково ускорял бы обыкновенный кожаный мяч и двухпудовую гирю? Каждый скажет, что это невозможно. А вот Земля является именно таким «необыкновенным футболистом» с той только разницей, что действие её на тела не носит характера кратковременного удара, а продолжается непрерывно миллиарды лет.
В теории Ньютона масса является источником поля тяготения. Мы находимся в поле тяготения Земли. В то же время мы также являемся источниками поля тяготения, но в силу того, что наша масса существенно меньше массы Земли, наше поле намного слабее и окружающие предметы на него не реагируют.
Необыкновенное свойство гравитационных сил, как мы уже говорили, объясняется тем, что эти силы пропорциональны массам обоих взаимодействующих тел. Масса тела, которая входит во второй закон Ньютона, определяет инертные свойства тела, т. е. его способность приобретать определённое ускорение под действием данной силы. Это инертная масса mи.
Казалось бы, какое отношение она может иметь к способности тел притягивать друг друга? Масса, определяющая способность тел притягиваться друг к другу, — гравитационная масса mr.
Из механики Ньютона совсем не следует, что инертная и гравитационная массы одинаковы, т. е. что
mи = mr. (3.5)
Равенство (3.5) является непосредственным следствием из опыта. Оно означает, что можно говорить просто о массе тела как о количественной мере как инертных, так и гравитационных его свойств.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Динамика — Физика, учебник для 10 класса — Класс!ная физика
Основное утверждение механики — Сила — Инертность тела. Масса. Единица массы — Первый закон Ньютона — Второй закон Ньютона — Принцип суперпозиции сил — Примеры решения задач по теме «Второй закон Ньютона» — Третий закон Ньютона — Геоцентрическая система отсчёта — Принцип относительности Галилея. Инвариантные и относительные величины — Силы в природе — Сила тяжести и сила всемирного тяготения — Сила тяжести на других планетах — Примеры решения задач по теме «Закон всемирного тяготения» — Первая космическая скорость — Примеры решения задач по теме «Первая космическая скорость» — Вес. Невесомость — Деформация и силы упругости. Закон Гука — Примеры решения задач по теме «Силы упругости. Закон Гука» — Силы трения — Примеры решения задач по теме «Силы трения» — Примеры решения задач по теме «Силы трения» (продолжение) —
Закон всемирного тяготения. Движение тел под действием силы тяжести
По второму закону Ньютона причиной изменения движения, т. е. причиной ускорения тел, является сила. В механике рассматриваются силы различной физической природы. Многие механические явления и процессы определяются действием сил тяготения.
Закон всемирного тяготения был открыт Исааком Ньютоном в 1682 году. Еще в 1665 году 23-летний Ньютон высказал предположение, что силы, удерживающие Луну на ее орбите, той же природы, что и силы, заставляющие яблоко падать на Землю. По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс (рис. 1.10.1). Понятие центра масс тела будет строго определено в 1.23.
У однородного шара центр масс совпадает с центром шара.
|
Рисунок 1.10.1. Гравитационные силы притяжения между телами.
|
В последующие годы Ньютон пытался найти физическое объяснение законам движения планет, открытых астрономом Иоганном Кеплером в начале XVII века, и дать количественное выражение для гравитационных сил. Зная как движутся планеты, Ньютон хотел определить, какие силы на них действуют. Такой путь носит название обратной задачи механики. Если основной задачей механики является определение координат тела известной массы и его скорости в любой момент времени по известным силам, действующим на тело, и заданным начальным условиям (прямая задача механики), то при решении обратной задачи необходимо определить действующие на тело силы, если известно, как оно движется. Решение этой задачи и привело Ньютона к открытию закона всемирного тяготения.
Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:
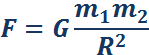
Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной
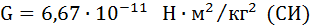
Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все они находят объяснение на основе закона всемирного тяготения и законов динамики.
Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если M – масса Земли, R – ее радиус, m – масса данного тела, то сила тяжести равна
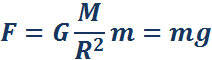
где g – ускорение свободного падения у поверхности Земли:
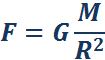
Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения.
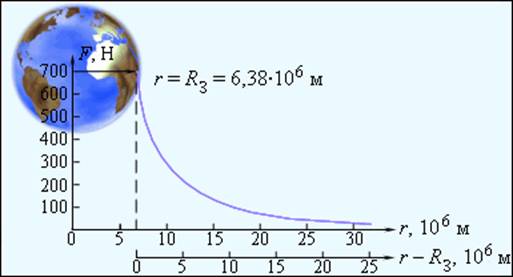
Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с2. Зная ускорение свободного падения и радиус Земли (R = 6,38·106 м), можно вычислить массу Земли М:
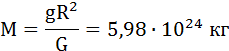
При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Рис. 1.10.2 иллюстрирует изменение силы тяготения, действующей на космонавта в космическом корабле при его удалении от Земли. Сила, с которой космонавт весом 71,5 кг (Гагарин) притягивается к Земле вблизи ее поверхности равна 700 Н.
|
Рисунок 1.10.2. Изменение силы тяготения, действующей на космонавта при удалении от Земли |
Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии rЛ = 3,84·106 м. Это расстояние приблизительно в 60 раз превышает радиус Земли RЗ. Следовательно, ускорение свободного падения aЛ, обусловленное земным притяжением, на орбите Луны составляет
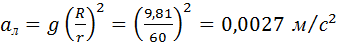
С таким ускорением, направленным к центру Земли, Луна движется по орбите. Следовательно, это ускорение является центростремительным ускорением. Его можно рассчитать по кинематической формуле для центростремительного ускорения:
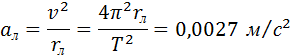
где T = 27,3 сут – период обращения Луны вокруг Земли. Совпадение результатов расчетов, выполненных разными способами, подтверждает предположение Ньютона о единой природе силы, удерживающей Луну на орбите, и силы тяжести.
Собственное гравитационное поле Луны определяет ускорение свободного падения gЛ на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли. Поэтому ускорение gЛ определится выражением:
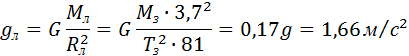

В условиях такой слабой гравитации оказались космонавты, высадившиеся на Луне. Человек в таких условиях может совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м, то на Луне он мог бы подпрыгнуть на высоту более 6 м.
Рассмотрим теперь вопрос об искусственных спутниках Земли. Искусственные спутники движутся за пределами земной атмосферы, и на них действуют только силы тяготения со стороны Земли. В зависимости от начальной скорости траектория космического тела может быть различной. Мы рассмотрим здесь только случай движения искусственного спутника по круговой околоземной орбите. Такие спутники летают на высотах порядка 200–300 км, и можно приближенно принять расстояние до центра Земли равным ее радиусу RЗ. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Обозначим скорость спутника на околоземной орбите через υ1. Эту скорость называют первой космической скоростью. Используя кинематическую формулу для центростремительного ускорения, получим:
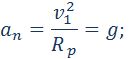
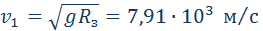
Двигаясь с такой скоростью, спутник облетал бы Землю за время
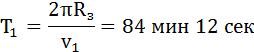
На самом деле период обращения спутника по круговой орбите вблизи поверхности Земли несколько превышает указанное значение из-за отличия между радиусом реальной орбиты и радиусом Земли.
Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли.
Для спутников, движущихся по круговым траекториям на значительном удалении от Земли, земное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Скорость спутника υ находится из условия

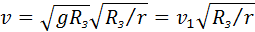
Таким образом, на высоких орбитах скорость движения спутников меньше, чем на околоземной орбите.
Период T обращения такого спутника равен

Здесь T1 – период обращения спутника на околоземной орбите. Период обращения спутника растет с увеличением радиуса орбиты. Нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6 RЗ, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6 RЗ называется геостационарной.


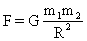
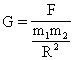
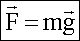
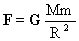 — из закона Всемирного тяготения. (где M — масса планеты, m — масса тела,
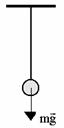
— из закона Всемирного тяготения. (где M — масса планеты, m — масса тела, 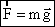 — сила тяжести из второго закона Ньютона (где m — масса тела, g — ускорение силы тяжести).
— сила тяжести из второго закона Ньютона (где m — масса тела, g — ускорение силы тяжести).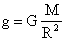 — ускорение силы тяжести не зависит от массы тела (опыты Галилея).
— ускорение силы тяжести не зависит от массы тела (опыты Галилея).