Сила тяжести — frwiki.wiki

Не следует путать с невесомостью или гравитацией .

Гравитационное поле является привлекательным поле, которое воздействует на любой орган, наделенный массой на Земле (или другой звезды ). Это поле из ускорения, который часто называют просто тяжесть или «г». Большая часть силы тяжести Земли обусловлена гравитацией, но отличается от нее осевым ускорением, вызванным вращением Земли над самой собой.

Серьезность вытекает из закона Ньютона всемирного тяготения из Ньютона, что все массивные тела, небесные тела и Земли оказывают поле тяготения, ответственного за силы притяжения на других массивных телах. В наземной системе отсчета, то вращательное движение вокруг оси полюсов индуцируют центробежный диск ускорение, который, в сочетании с силой тяжести, определяет силу тяжести. Это определение можно обобщить на другие небесные тела: тогда мы говорим, например, о гравитации Марса .

Сила, с которой тело подвергаются под действием силы тяжести называется весом этого тела и непосредственно связана с действием силы тяжести с помощью своей массы; его единицей измерения является ньютон, как и для любой силы.

Эта сила определяет вертикаль места, направление, в котором все свободные тела падают на землю в данном месте и которое можно измерить с помощью отвеса .

Сила тяжести Земли варьируется в зависимости от местоположения. Для практических целей, Генеральная конференция мер и весов, определенной в 1901 году в нормальное значение ускорения силы тяжести, отметил г ₀, равный 9.806 65 м / с ², или приблизительно 9,81 

м с ^-2 (или 9,81 Н / кг). Это значение соответствует силе тяжести на идеальном эллипсоиде, приближающемся к уровню моря и на 45 ° широты .

Диаграмма, показывающая скорость падения объекта как функцию времени, когда он испытывает ускорение свободного падения Земли (1  g ). Сопротивлением воздуха пренебрегаем и принимаем начальную скорость равной нулю. Скорость увеличивается каждую секунду на 9,81  

м / с .

Резюме

• 1 Серьезность
• 2 Гравитация
• 3 Вес
• 4 значение силы тяжести Земли
  • 4.1 Вариация по местоположению
  • 4.2 Нормальное значение
  • 4.3 Единица ускорения g
  • 4.4 Важность знания гравитационного поля
    • 4.4.1 Гравиметрия
  • 4.5 Движущийся объект
• 5 падающих тел
  • 5.1 Опыт Галилея
  • 5.2 Нападение Архимеда
  • 5.3 Сопротивление воздуха
• 6 Лунная гравитация
• 7 Примечания и ссылки
  • 7.1 Примечания
  • 7.2 Ссылки
• 8 См. Также
  • 8.1 Библиография
  • 8.2 Статьи по теме

Сила тяжести

Гравитация является основной составляющей силы тяжести. {2}}}}

G — универсальная постоянная гравитации . В системе СИ стоит:

G = 6,674 × 10 ⁻¹¹   м ³  кг ⁻¹  с ⁻²

Гравитационное поле подвержено пространственным диспропорциям из-за неоднородностей в составе и топографии небесного тела. Изучая аномалии траекторий спутников, вращающихся вокруг небесного тела, мы можем вывести внутреннее распределение масс, а также топографию тела, над которым происходит перелет.

Гравитация также меняется в зависимости от положения на Земле: она слабее на экваторе, чем на полюсах, из-за неодинаковой силы земных лучей, и она уменьшается с высотой. Со временем движение водных масс из-за приливов вызывает периодические изменения силы тяжести.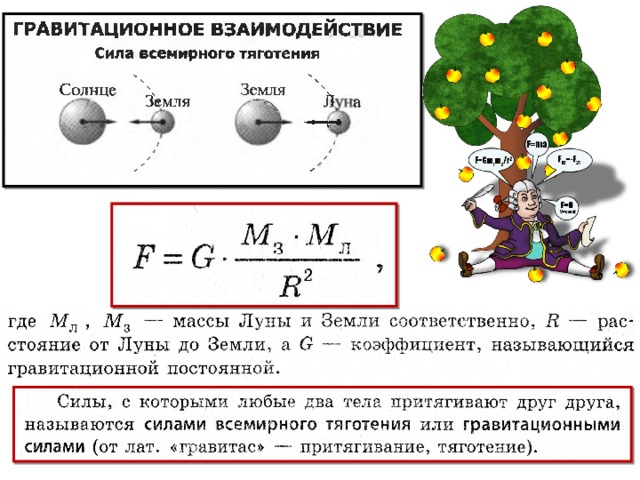

Сила тяжести

Гравитация — это реальное силовое поле, наблюдаемое на небесном теле. На объектах, связанных с вращающимся небесным телом, таких как Земля, он включает осевую силу инерции, которая противодействует силе тяжести (точнее, она добавляется к ней векторно ).

Гравитационное поле описывается векторным полем (отмечено ), направление которого указано отвесом, а норма (отмеченная ) может быть измерена путем вытягивания пружины известной жесткости или путем измерения периода тяжелого маятника. . грамм→{\ displaystyle {\ vec {g}}}‖грамм→‖{\ Displaystyle \ | {\ vec {g}} \ |}

Масса

На объект массы в месте, где имеет значение ускорение свободного падения, кажется, что он подвергается действию силы тяжести, называемой весом, значение которой равно . Эта сила действует вниз по вертикали места, в направлении, в котором все свободные тела падают на землю в данном месте и которое можно измерить с помощью отвеса . м{\ displaystyle m}грамм{\ displaystyle g}пзнак равномграмм{\ Displaystyle P = мг}

В 1903 году килограмм-сила или килограмм-вес был определен как единица измерения силы.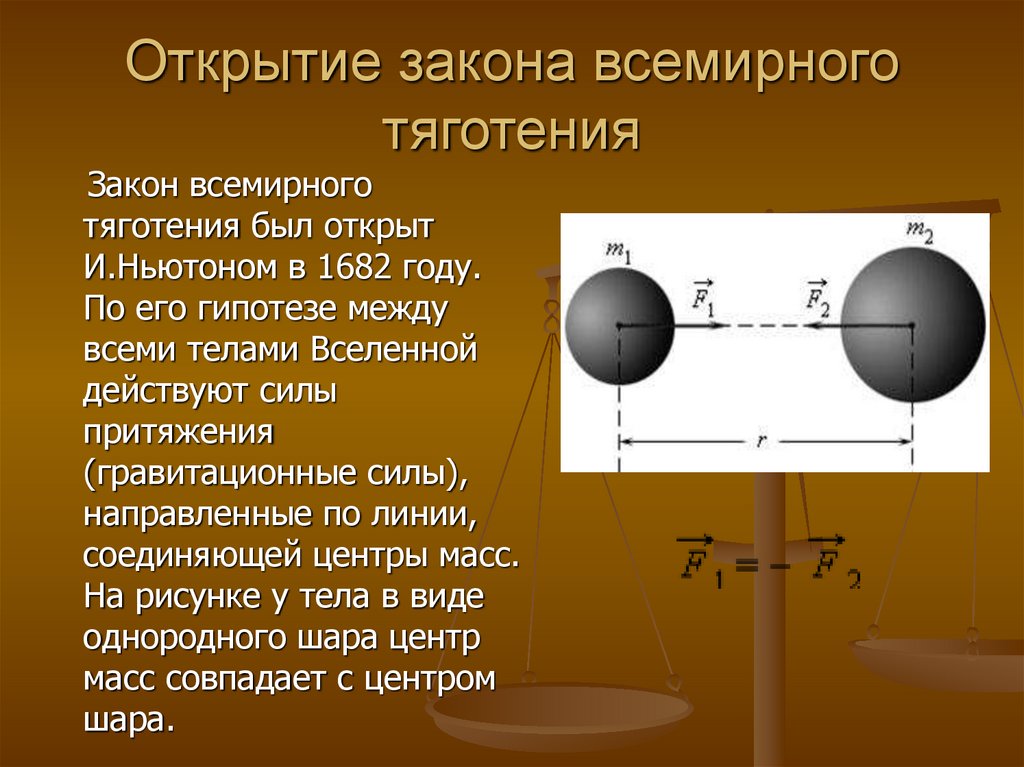 Это вес массы 1  кг в месте, где ускорение силы тяжести равно нормального значение ускорения силы тяжести, отметил

г _п и равный 9,806 65  м с ^-2 .

Кгс является устаревшей модуль, равный 9.806 65 ньютон по определению  .

Значение силы тяжести Земли

Во дворце открытий — вращающийся сад, демонстрирующий влияние силы тяжести на растения.

Вариация в зависимости от местоположения

Земли тяжести измеряется GRACE спутника из НАСА и космического агентства немецкого. На графике показаны отклонения от реальной силы тяжести к нормированной, связанные с теоретическим однородным эллипсоидом, моделирующим форму Земли.

Красные зоны — это те, где сила тяжести выше теоретической, а синие зоны — те, где она меньше, общая амплитуда изменения (от синего к красному) составляет 1 мм / с ² .

Земля вращается сама по себе и не является сферической и однородной звездой, ускорение свободного падения зависит от места и следующих факторов:

• земное вращение: вращение Земли само по себе приводит к поправке, состоящей в добавлении к ускорению силы тяжести ускорения осевого движения, направленного перпендикулярно оси полюсов и модуля: a = (2π / T ) ² d с T = 86 164,1  с и d расстояние в метрах между объектом и осью вращения Земли. Коррекция, нулевая на полюсах, достигает -0,3% на экваторе;
• Несферичность Земли: из-за уплощения Земли ускорение свободного падения зависит от широты  : на полюсах оно сильнее, чем на экваторе (разница 0,2%).
• высота: для изменения высоты h, малого перед R, относительное изменение ускорения свободного падения равно -2 h / R, то есть -3,139 × 10 ^-7 на метр на небольшом расстоянии от поверхности Земли. ;
• вариации плотности грунта: они приводят к локальным колебаниям силы тяжести, которые не учитываются в общих формулах из-за сложности их моделирования;
• силы прилива, особенно из-за Луны и Солнца . Соответствующая коррекция меняется в течение дня. Это порядка 2 × 10 ⁻⁷ на широте 45 °.
• движение тела в земной системе отсчета: если тело движется в земной системе отсчета, оно подвергается дополнительному ускорению, называемому ускорением Кориолиса, ответственным, в частности, за вращательное движение масс воздуха ( циклонов и антициклонов ) и вода океаническая ( спираль Экмана ). Вертикальная составляющая этого ускорения составляет силу Этвёша .

Следующая формула дает приблизительное значение нормального значения ускорения свободного падения в зависимости от широты и для небольшой высоты перед земным радиусом (обычно: несколько тысяч метров):

граммзнак равно9 780327×(1+5,3024×10-3×грех2⁡(ϕ)-5,8×10-6×грех2⁡(2×ϕ)-3,086×10-7×час){\ displaystyle g = 9 {,} 780 \, 327 \ times \ left (1 + 5 {,} 302 \, 4 \ times 10 ^ {- 3} \ times \ sin ^ {2} (\ phi) -5 {,} 8 \ times 10 ^ {- 6} \ times \ sin ^ {2} (2 \ times \ phi) -3 {,} 086 \ times 10 ^ {- 7} \ times h \ right)}

с участием:

• г в м / с ²  ;
• h, высота в м;
• ϕ, широта в радианах в геодезической системе GRS 80 (1980).

Нормальное значение

Для практических целей Генеральная конференция мер и весов определила в 1901 году нормальное значение ускорения свободного падения на высоте 0 на идеальном эллипсоиде, приближающемся к поверхности земли, для широты 45 °, равном 9,806 65  м / ев ², или 980.665  Gal (блок, полученный из старого РКИ измерительной системы, до сих пор иногда используется в гравиметрии, равный 1  см / с ² ).

Единица ускорения

g

На обыденном языке мы часто говорим о «  g  » как о единице силы тяжести, равной нормальному значению земной силы тяжести, то есть 9,806 65 м / с ² . Мы прочитаем, например, что лунная гравитация равна 0,16  g, т.е. в 0,16 раза больше нормальной земной силы тяжести, или что космонавт в центрифуге (или пилот истребителя в повороте) испытывает ускорение в 6  g — в шесть раз больше силы тяжести. земли.

Важность знания гравитационного поля

Важность знания гравитационного поля Земли для геодезистов легко понять, если мы знаем, что его направление в каждой точке, которое соответствует вертикали места, обозначенного отвесом, используется в качестве ориентира при настройке любого геодезического измерительный инструмент. Более подробно, интерес к познанию гравитационного поля можно понять по следующим причинам:

• его значения на поверхности и вблизи Земли используются в качестве эталона для большинства величин, измеряемых в геодезии . Фактически, необходимо знать гравитационное поле, чтобы преобразовать геодезические наблюдаемые в геометрически определенные системы;
• распределение значений силы тяжести на земной поверхности позволяет в сочетании с другими геодезическими измерениями определять форму этой поверхности;
• несферичность вызывает нарушения в орбитах спутников, точное наблюдение которых с точностью до нескольких сантиметров орбитографической системой DORIS дает ценную информацию об отклонениях от сферической формы;
• самая важная опорная поверхность для измерения высоты, называемая геоидом, представляет собой поверхность уровня гравитационного поля;
• Анализ внешнего гравитационного поля дает информацию о структуре и свойствах недр Земли. Делая эту информацию доступной, геодезия становится вспомогательной наукой геофизики. Это то, что ускорилось в последние десятилетия с появлением космической гравиметрии .

Гравиметрия

Сила тяжести — это мера изменений и неравномерностей силы тяжести; однако это не поддается непосредственному измерению: мы должны сначала измерить гравитацию и соотнести ее с необходимыми поправками, такими как эффекты из-за вращения Земли или эффекты, вызванные приливами — смещение масс воды вызывает периодические изменения силы тяжести. Гравиметрические измерения позволяют описать неравномерное распределение масс внутри Земли, которое вызывает неравномерность силы тяжести в зависимости от местоположения.

В общем, относительные вариации g более важны для геодезиста и геофизика, чем абсолютные значения; Действительно, дифференциальные измерения более точны, чем абсолютные.

Максимальное изменение g у поверхности Земли составляет приблизительно 5  галлонов (5 × 10 ^-2  м с ^-2 ) и связано с изменением g с широтой.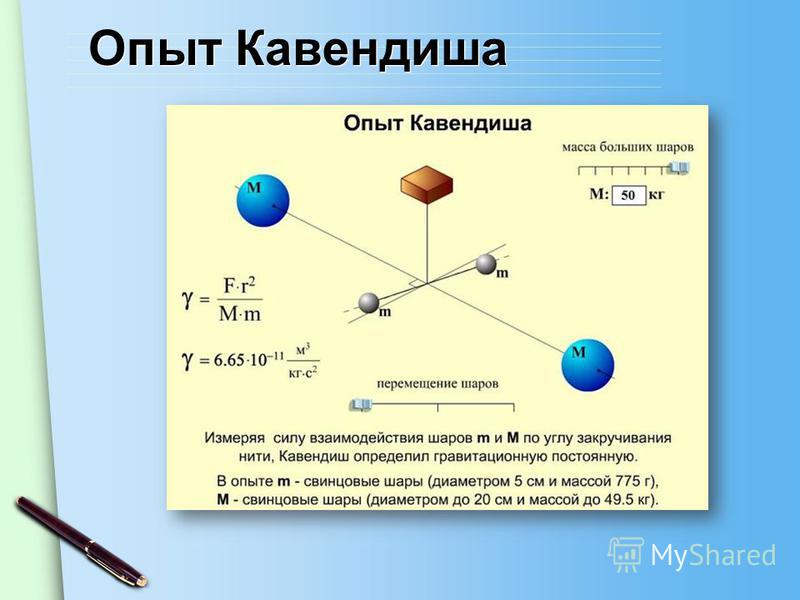 Вариации более коротких длин волн, известные как аномалии силы тяжести геоида, обычно составляют от нескольких десятых до нескольких десятков миллигал (мгал). В некоторых геодинамических явлениях, наблюдение которых стало возможным в последнее время благодаря прогрессу в геодезических инструментах, нас интересуют вариации g как функция времени, амплитуда которых достигает лишь нескольких микрогал (мкгал). Теоретические исследования ( моды ядра, вековая вариация g ) в настоящее время предусматривают вариации g, расположенные на уровне наногал (нгал).

При гравиметрической разведке и в гражданском строительстве значительные аномалии g обычно находятся в пределах от нескольких микрогалл до нескольких десятых миллигалла. Чтобы закрепить представление, когда на поверхности Земли человек поднимается на три метра, сила тяжести изменяется примерно на 1 мгал.

Движущийся объект

Если объект не неподвижен по отношению к Земле, ускорение Кориолиса, пропорциональное скорости объекта, добавляется к ускорению силы тяжести. Обычно он слишком слаб, чтобы оказывать заметное влияние, но играет важную роль в движении воздуха в атмосфере, в частности ветра .

Падающие тела

Даже с поправкой на влияние высоты и широты, а также суточного вращения, ускорение свободного падения недостаточно, чтобы полностью описать падение тел на Землю.

Опыт Галилея

Итальянский ученый Галилей (1564–1642) был одним из первых, кто описал и приблизительно количественно оценил гравитацию Земли. С помощью мифического эксперимента, проведенного с вершины Пизанской башни, он мог бы отметить, что тяжелые пули разного веса имеют одинаковое время падения, но, когда он объясняет в своем Диалоге о двух великих системах мира, почему это происходит. Таким образом, он находится в вакууме, он оправдывает мысленными экспериментами  : в частности, представляя два камня одинакового веса и формы, падающих одновременно и связанных или не связанных связью, таким образом образуя два отдельных тела одинакового веса или одно из двух вес, но во всех случаях имеющий одинаковую скорость падения.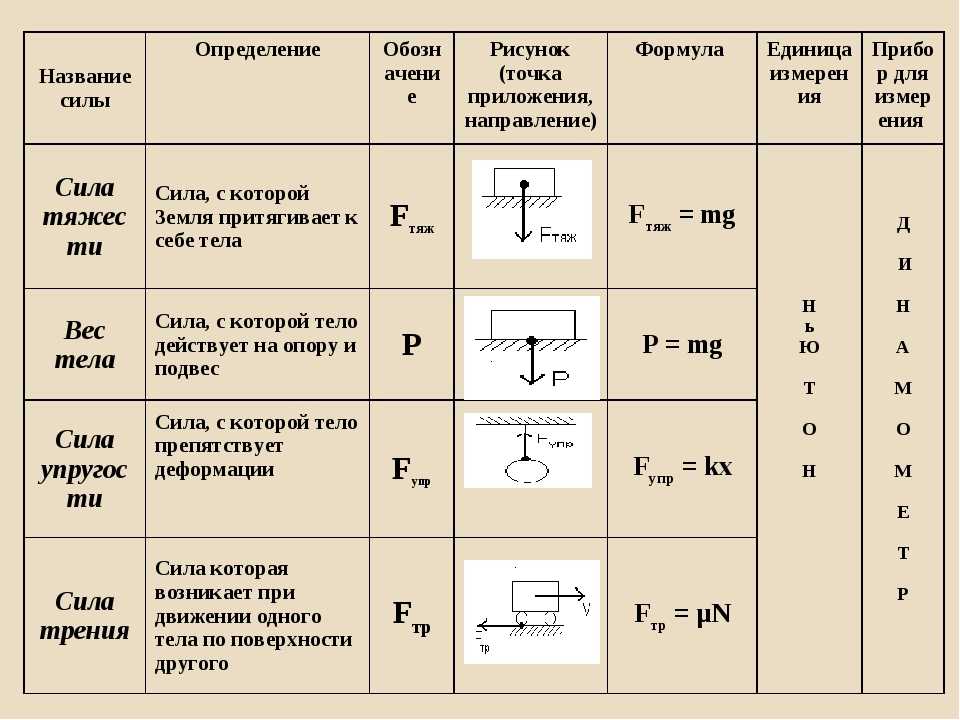

Примерно в 1604 году Галилей использовал наблюдение: объект в свободном падении имеет начальную скорость, равную нулю, но когда он достигает земли, его скорость… не равна нулю. Так что скорость меняется во время падения. Галилей предлагает простой закон: скорость будет непрерывно изменяться от 0 и пропорционально времени, прошедшему с начала падения. Итак: скорость = постоянная × прошедшее время .

Он приходит к выводу, что во время падения пройденное расстояние пропорционально квадрату прошедшего времени. Точнее: расстояние = 1/2 константы × прошедшее время ²  (с той же константой, что и выше). Его идея подтверждается экспериментом с материалом, созданным его рукой: наклонным желобом, вдоль которого расположены колокольчики, указывающие на прохождение мяча.

Выпад Архимеда

Если объект не взвешивается в вакууме, его  измеренный «  вес » равен весу, обусловленному его массой, за вычетом веса вытесненного объема воздуха ( тяга Архимеда ). Без этой поправки вес килограмма пера меньше веса килограмма свинца (потому что объем этого килограмма перьев больше, чем объем того же килограмма свинца, а тяга Архимеда равна поэтому важнее).

Сопротивление воздуха

Трение о воздухе вызывает аэродинамические силы и, в частности, сопротивление, которое противодействует движение, которое вызывает маленький шарик падать быстрее, чем большая одной из тех же массы .

Лунная гравитация

На Луне гравитация примерно в шесть раз меньше, чем на Земле (около 1,6 м / с ² против 9,8 м / с ² ), из-за меньшей массы Луны (в 81,3 раза меньше) и несмотря на ее меньший радиус (3,67 раза). меньше). Этим объясняются необыкновенные прыжки астронавтов американской космической программы « Аполлон » . Это явление было предвосхищено и популяризировано в альбоме Тинтина On a Marche sur la Lune .

Примечания и ссылки

Заметки

1. ↑ Можно считать, что масса небесного тела сосредоточена в точке, если выполняется одно из следующих трех условий:
   • расстояние достаточно велико, чтобы пренебречь размерами небесного тела;р{\ displaystyle \ scriptstyle R}
   • небесное тело однородно;
   • небесное тело состоит из однородных концентрических слоев.
2. ↑ Строго говоря, центробежная сила относится к точке: вектор силы коллинеарен линии, соединяющей центр вращения с точкой приложения силы. В случае вращения небесного тела вокруг оси сила инерции переносится линией, перпендикулярной оси вращения небесного тела и проходящей через точку приложения силы d ‘, где определитель daxifuge .
3. ↑ «Нормальный» здесь означает «нормализованный», а не «обычный».
4. ↑ Расчет выполнен с R = 6,371  км (среднее значение радиуса Земли ).
5. ↑ Сила тяжести на поверхности звезды пропорциональна ее массе и обратно пропорциональна квадрату ее радиуса.

Рекомендации

1. ↑ ^{a и b} Эли Леви, Физический словарь, Presses Universitaires de France, Париж, 1988, стр. 601.
2. ↑ ^{а и б} Третья Генеральная конференция мер и весов, Париж, 1901 г., CR 70.
3. ↑ ^{a и b} В 1901 году «Значение, принятое Международной службой мер и весов для стандартного ускорения свободного падения, составляет 980,665 см / с ², значение уже указано в законах некоторых стран» в BIPM: (en) Декларация об единице массы и об определении веса; условное значение g _n
4. ^ Taillet, Villain and Febvre 2018, sv gravity field, стр.  116, цв.  1 .
5. ↑ Комиссионные романы по математике, физике и химии, Формы и таблицы: Математика, Физика, Химия, Треугольник,2000 г., 278  с. ( ISBN  2-8293-0216-8 ), стр.  196
6. ↑ Международное гравиметрическое бюро / Международное гравиметрическое бюро, Определение нормальной силы тяжести (документ BGI): BGI_Formules_Pesanteur_Normale.pdf, 2  стр. ( читать онлайн ), стр.  1
7. ↑ Gravimetric Bureau International International Gravimetric Bureau, Прямое измерение гравитационного поля Земли: Гравиметрия: tutorial5. pdf 1,44 МБ, 30  стр. ( читать онлайн ), стр.  22
8. ↑ Александр Койре, исследование истории научной мысли, Gallimard, 1986 ( 1- ^е  издание) ( ISBN  2-07-070335-5 )  : статья « motu gravium of Galilee», основанная на обзоре истории наук и их приложений в PUF изд., 1960, с.197-245.

Смотрите также

Библиография

• (ru) В. А. Хейсканен и Х. Мориц, Physical Geodesy, WH Freeman and Company, 1967, Сан-Франциско и Лондон. ix + 364 стр., ( ISBN  978-0716702337 )
• (en) Б. Хофманн-Велленхорф и Х. Мориц, Физическая геодезия, Springer, 2005 г. ( ISBN  978-3-211-33544-4 )
• [Taillet, Villain and Febvre 2018] R. Taillet, L. Villain и P. Febvre, Словарь физики, Louvain-la-Neuve, De Boeck Sup. , кроме колл. ,Янв 2018, 4- ^е  изд. ( 1- ^е  изд. Май 2008 г.), 1  т. , X -956  с. , плохо. и рис. , 24  см ( ISBN  978-2-8073-0744-5, EAN  9782807307445, OCLC  1022951339, SUDOC  224228161, презентация онлайн, читать онлайн ).

Статьи по Теме

• Нормальное ускорение свободного падения
• Космонавтика
• Невесомость
• Небесная механика
• Ньютоновский потенциал
• Свойства ньютоновского потенциала
• Поверхностная гравитация

<img src=»https://fr. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

Ускорение силы тяжести – определение, формулы

3.9

Средняя оценка: 3.9

Всего получено оценок: 103.

3.9

Средняя оценка: 3.9

Всего получено оценок: 103.

Процесс изменения скорости при движении физического тела характеризуется ускорением. Ускорение силы тяжести (обозначается буквой g) возникает в результате влияния силы тяжести, которая действует на любое тело у поверхности Земли или другой планеты. Разберемся от чего зависит значение g и как его определяют.

Основные формулы для равноускоренного движения

Равноускоренное движение — самый простой вид неравномерного движения. Равноускоренным называется движение с ускорением, постоянным по модулю и направлению:

$ a = {Δv\over Δt} = const $ (1),

где:

Δv — изменение скорости (“дельта v “), м/с;

Δt — промежуток времени, (“дельта t “)за которое произошло изменение скорости, с.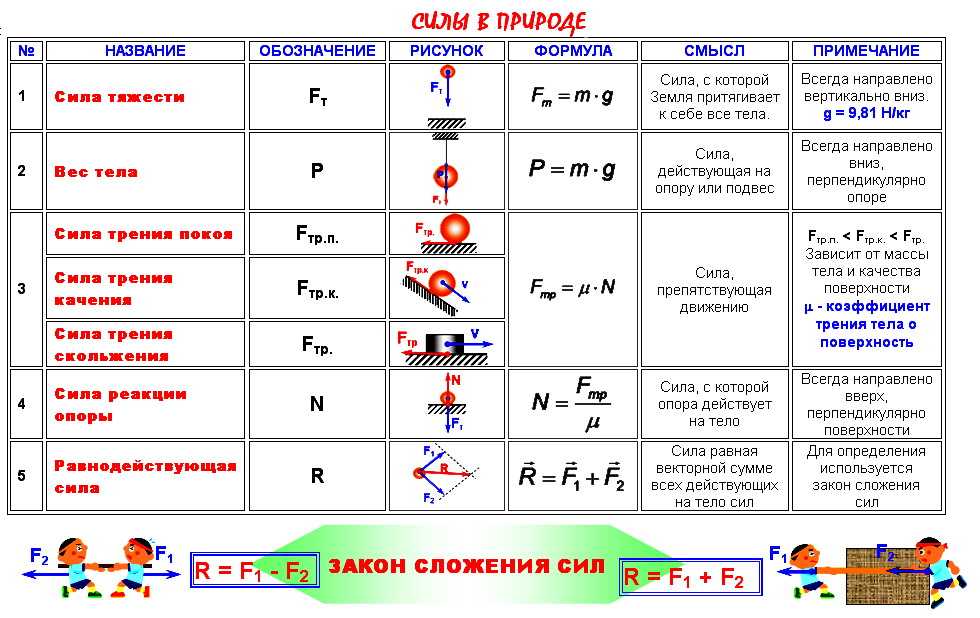 2 $ (2).

Второй закон Ньютона гласит:

$ F = m * a $ (3),

где:

F — сила, действующая на тело, Н;

m — масса тела, кг;

a — ускорение, м/с².

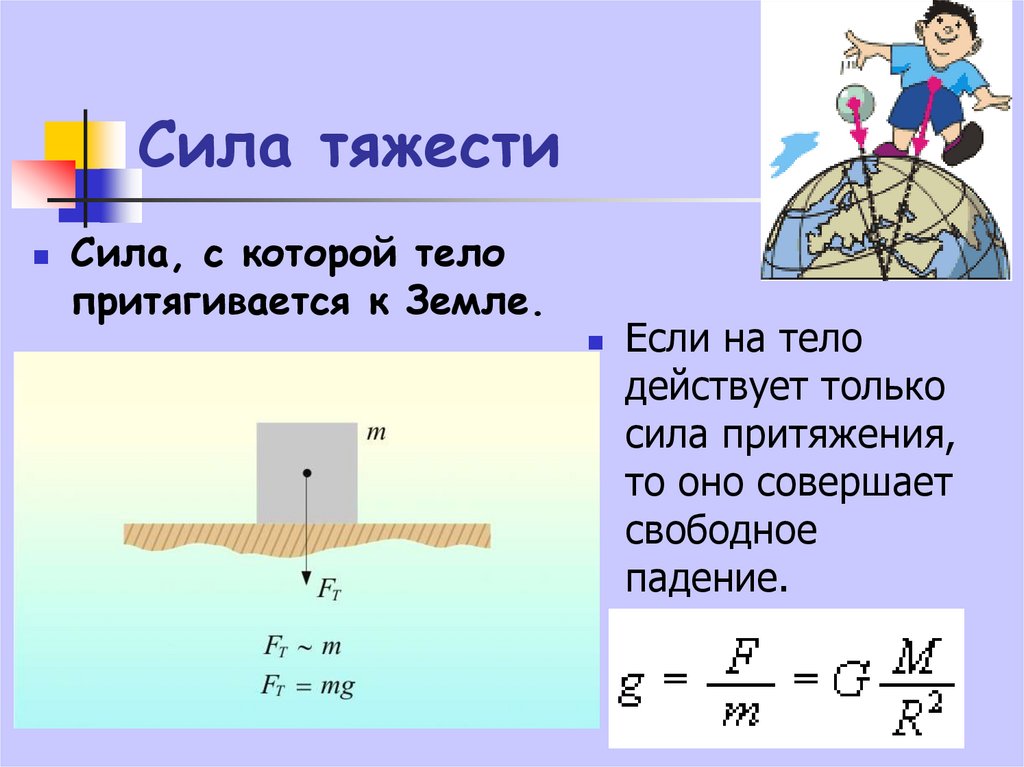
Сила тяжести и ускорение свободного падения

При свободном падении на Землю все тела, независимо от их массы, движутся одинаково. Свободное движение является равноускоренным движением. Ускорение, с которым падают на Землю тела в пустоте, называется ускорением свободного падения (или ускорением силы тяжести). Условие пустоты или, что тоже самое, вакуума, требуется для исключения влияния сопротивления атмосферного воздуха. Сила притяжения F_т со стороны Земли на тело массой m, называется силой тяжести:

$ F_т = m * g $ (4),

Определением ускорения силы тяжести впервые систематически занимался Галилео Галилей — итальянский математик, физик, астроном. Будучи профессором университета в городе Пиза, Галилей измерял время падения предметов с высоты местной, слегка наклонной, башни. 2} $ .

И хотя это открытие датировано 1589г., современное, общепринятое среднее значение g практически не отличается от этого значения. Когда от расчетов не требуется высокой точности, то принимают, что модуль g равен 10 м/с².

Последовавшие за Галилеем более точные измерения показали, что значение g не является абсолютной константой, а зависит от местоположения измерений в разных точках Земли. Ответ на этот вопрос нашел английский ученый Исаак Ньютон.

Закон всемирного тяготения

В 1682 г. Ньютон открыл закон всемирного тяготения, из которого следует:

• все тела притягиваются друг к другу;
• сила тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними;
• векторы сил тяготения направлены вдоль прямой, соединяющей тела.

Этот закон универсален, и для случая пары тел, одно из которых является произвольным телом массой m, а второй — Земля, в виде формулы выглядит так:

$ F_т = G * {{m * Mз }\over {(R_з + h)^2} } $ (5),

где:

M_з — масса Земли, кг;

R_з — радиус Земли, м;

h — высота, на которой находится тело, относительно поверхности Земли, м;

G — гравитационная постоянная, равная 6,6720 * 10^-11 Н*м² * кг^-2. 2 } }$ (6)

Из (6) следует, что ускорение силы тяжести будет зависеть от высоты h и величины радиуса Земли, который для обычных расчетов принимается равным примерно 6400 км. Но поскольку форма Земли не является идеальным шаром, а сплюснута к полюсам, то точные значения g будут отличаться от среднего значения в 9,81 м/с²:

• максимальное значение g_макс = 9,83 м/с² — на полюсах Земли, где R_з меньше;
• минимальное значение g_мин = 9,79 м/с² — на экваторе Земли, где R_з больше.

Рис. 2. Зависимость ускорения свободного падения на полюсах, экваторе и от вращения Земли.

Из формулы (6) также следует, что ускорение силы тяжести на других планетах, имеющих массу, отличающуюся от массы Земли, будет для космонавтов значительно отличаться от привычных земных условий. Так, например:

• На Марсе — g_Марса = 3,86 м/с²;
• На Меркурии — g_{Меркурия} = 3,7 м/с²;
• На Луне — g_Луны = 1,62 м/с²;
• На Нептуне — g_{Нептуна} = 11,0 м/с².

Как определяют ускорение силы тяжести

Для точного измерения силы тяжести, а значит, и ускорения, используется прибор, называемый гравиметром. Прибор применяется при поиске полезных ископаемых и для сбора информации археологами, палеонтологами, гидрологами и представителями других профессий, изучающих поверхность Земли.

Рис. 3. Гравиметры:.

Следует упомянуть еще два фактора, влияющих на значение ускорения свободного падения:

• Известно, что Земля вращается вокруг своей оси, имея при этом так называемое центростремительное ускорение, которое влияет на величину ускорения свободного падения;
• Масса Земли распределена неравномерно, например, в местах расположения больших месторождений металлических руд ускорение силы тяжести будет больше, а там, где есть пустоты (газовые месторождения) ускорение будет несколько меньше.

Эти факторы дают очень малые отклонения от средних значений g , но зато их регистрация позволяет, например, геологам находить новые месторождения полезных ископаемых.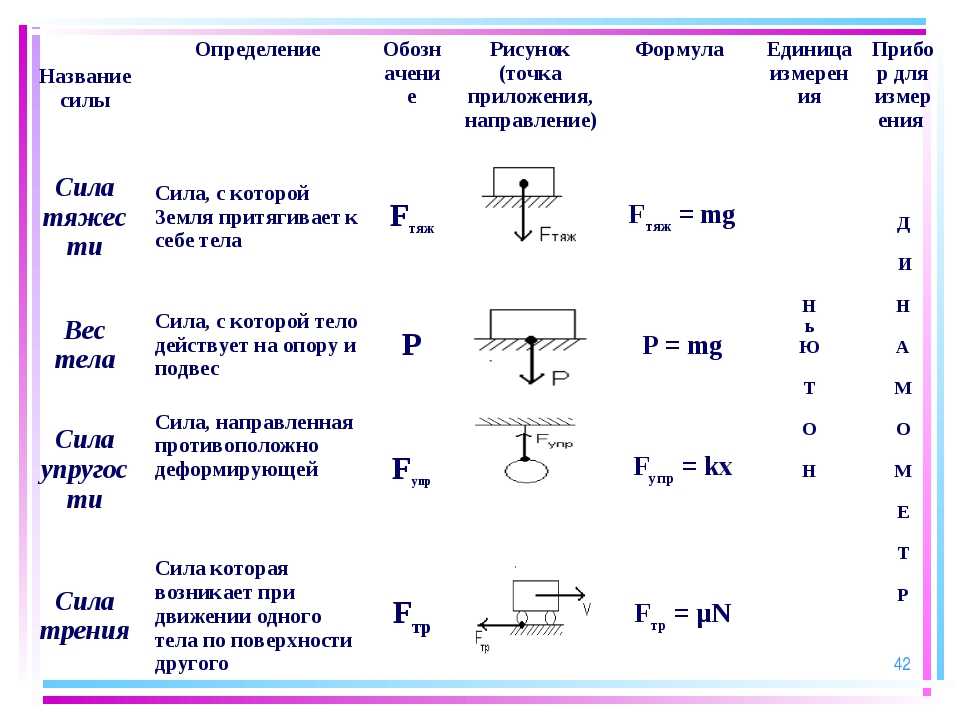

Что мы узнали?

Итак, мы узнали, что такое ускорение силы тяжести. Сила тяжести возникает вследствие действия силы гравитации, подчиняющейся закону Ньютона (формула (5)). На Земле среднее значение ускорения силы тяжести g_Земли равно 9,81 м/с². Для точного определения ускорения силы тяжести требуется использование современных приборов, называемых гравиметрами.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Александр Коновалов

  4/5

Оценка доклада

3.9

Средняя оценка: 3.9

Всего получено оценок: 103.

---

А какая ваша оценка?

Какова мера силы тяжести, действующей на объект?

Вы должны войти в систему, чтобы опубликовать ответ.

Баллы:	1

Какова мера силы тяжести, действующей на объект?

Ответы

3 Найдено ответов.

Баллы:	7 (₹ 6)

Что такое сила тяжести?

Сила, действующая со стороны Земли на объект, чтобы притянуть его к своему центру, называется силой тяжести. Сила тяжести всегда направлена ​​к центру земли. Он всегда действует через центр тяжести тела при свободном падении.

Сила тяжести есть произведение массы тела на его ускорение под действием силы тяжести.
При вертикальном движении предполагается, что сила тяжести, действующая на тело, везде одинакова, независимо от его высоты над землей. Здесь предполагалось, что изменение высоты не очень велико, поэтому значение ускорения свободного падения g остается постоянным. На самом деле значение «g» уменьшается с высотой, так что сила тяжести также будет меняться.

Единица измерения «г»

Единица СИ: Поскольку сила тяжести является силой, единицей измерения СИ является ньютон (Н).
1Н = 1 кг * 1 мс ^-2
Один ньютон можно определить как силу, действующую на тело массой 1 кг так, что оно приобретает ускорение 1 мс-2.

Гравитационные единицы

кгс и гс используются для измерения силы тяжести.

а) 1 кгс = 1 кг * г
= 1 кг * 9,8 мс ^-2
= 9,8 Н
Таким образом, 1 кгс — это сила, с которой Земля действует на тело массой 1 кг.

б) 1 гс = 1 г * г
= 1 г * 980 см ^-2
= 980 дин.
Приблизительно на нашу ладонь действует сила 10 Н, если мы держим на ней груз массой 1 кг.

---

С уважением,
Вивек
Редактор ISC.
Редактор Studyvillage.

Группа ослов во главе со львом может победить группу львов во главе с ослом.

Очки:	2

Сила гравитации есть не что иное, как притяжение объекта к центру Земли. Это зависит от массы и расстояния от объекта, которые к нему притягиваются.

Сила гравитации = масса, умноженная на ускорение свободного падения на Земле.

Если объект находится над или под землей, соответственно изменяется значение ускорения свободного падения и, следовательно, сила тяжести.

---

Доктор Пареш Б. Гуджарати.
Инженер-механик.
‘Я-совершенствование всегда начинается с «я».

Очки:	2 (₹ 1)

Это притяжение, которое испытывает тело из-за силы тяжести Земли ускорение силы тяжести земли=GMe/r2=90,8 м/с2 (постоянная): здесь Me-масса Земли G-универсальная гравитационная постоянная r2-квадрат радиуса Земли)
на каждой планете g отличается, поэтому w=(m)(geff), где m — масса body и geff — значение ускорения под действием силы тяжести на новой планете (любой) пример для земли geff=g)

Войдите, чтобы оставлять комментарии

Задайте вопрос

Вернуться к разделу «Спросить у экспертов»

Гравитация: определение, теория и уравнения

В известной истории говорится, что Исаак Ньютон открыл гравитацию, когда увидел, как яблоко падает с дерева. Однако главное, что он понял, это не то, почему яблоки падают с троек. Но тот факт, что яблоко падает по той же причине, по которой планеты вращаются вокруг Солнца! Спустя столетия его открытие до сих пор считается одним из самых замечательных вкладов в науку! Это позволило нам объяснить движение планеты и доставить нас на Луну. Эта статья расскажет вам об определении гравитации и о том, как измерить ее влияние путем расчета веса объектов в гравитационном поле Земли.

Определение гравитации

Гравитация — это сила притяжения между двумя телами, обусловленная их массой.

Гравитация, действующая на падающее яблоко, журнал Quant

Гравитация — это бесконтактная сила , , что означает, что она может действовать на два объекта, которые физически не соприкасаются, даже на больших расстояниях! Давайте посмотрим, как это работает, немного подробнее.

Теория гравитации

Чтобы понять, как работает гравитация, полезно ввести понятие центра масс.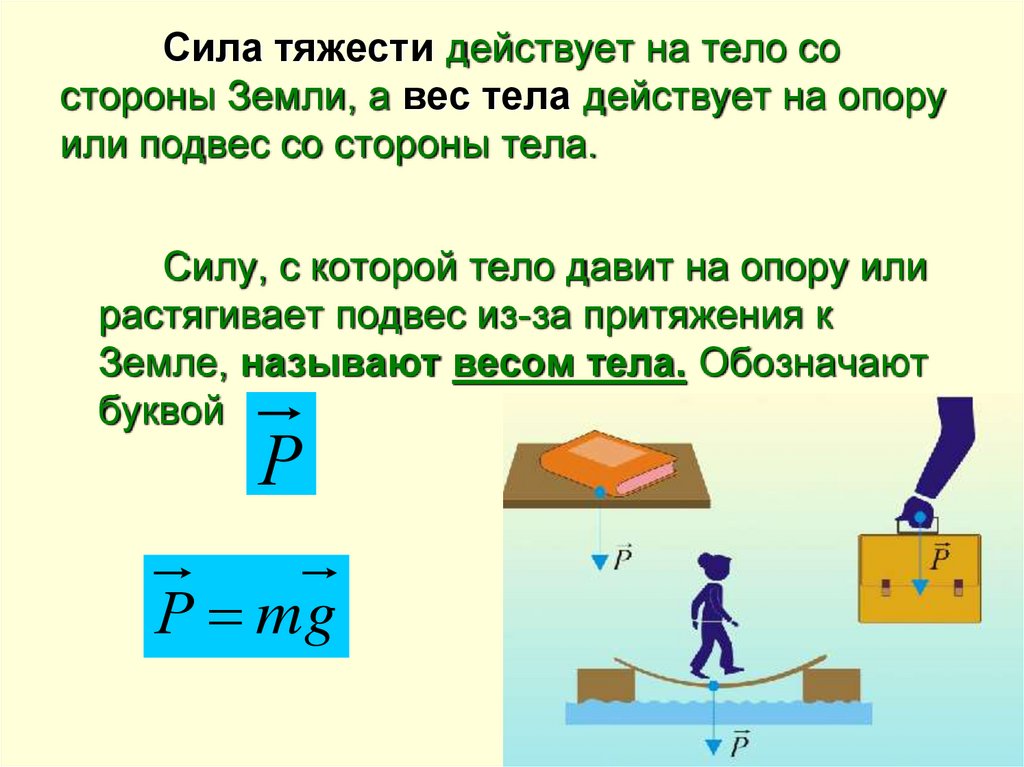

Можно предположить, что вся масса объекта находится в одной точке, называемой центром масс . Его расположение зависит от того, как распределена масса в объекте.

Центр масс шара расположен в его геометрическом центре. У среднего человека она находится чуть ниже пупка.

Теория гравитации утверждает, что каждая масса во Вселенной притягивает любой другой объект невидимой силой, действующей в направлении линии, соединяющей центры масс обоих объектов. Сила между двумя объектами зависит от их масс и расстояния между их центрами масс.

Сила притяжения между двумя массами, Звездный сад

Чем больше масса, тем сильнее сила. Мы не видим кучу карандашей на столе, прыгающих навстречу друг другу, потому что их гравитация слишком мала, чтобы ее можно было заметить, поскольку их масса очень мала. С другой стороны, этот эффект становится заметным для очень массивных объектов, таких как планеты и звезды в нашей Солнечной системе. Например, Луна держится на орбите вокруг Земли из-за гравитационной силы между ними.

Поскольку гравитация притягивает Луну к Земле, Луна описывает приблизительно круговую траекторию вокруг Земли, Encyclopædia Britannica, Inc.

Как упоминалось выше, расстояние между объектами также играет важную роль. Если расстояние увеличивается, величина гравитационной силы уменьшается. Подробнее об этом мы поговорим ниже.

Значение силы тяжести

Сила гравитационного поля измеряется в и обозначается символом . Это означает, что в гравитационном поле объект будет испытывать силу на каждые его массы. Силу гравитационного поля Земли можно считать постоянной, и она имеет приблизительное значение . Это означает, что мы испытываем силу на каждый килограмм массы нашего тела. Для сравнения, сила гравитационного поля Луны всего лишь примерно в шесть раз меньше. Поскольку сила на килограмм, которую мы почувствовали бы на Луне, меньше, на Луне все легче!

Сила гравитационного поля уменьшается по мере увеличения расстояния до центров масс. Тогда почему мы считаем постоянным на земле? не должно ли оно уменьшаться по мере того, как мы поднимаемся выше и удаляемся от его центра? Это правда. На самом деле она не постоянна и уменьшается с высотой. Однако мы должны были бы находиться на высоте примерно от поверхности земли, чтобы значение уменьшилось ровно на . Для высот ниже изменение меньше, чем. Поскольку вариация на более низких высотах весьма незначительна, значение принимается за константу.

Калиброванные пружинные весы, также известные как N эвтонометр, , можно использовать для непосредственного измерения веса. Он использует пружину, прикрепленную к крючку, чтобы удерживать предметы. Затем пружина удлиняется на длину, пропорциональную весу предмета. Весы в устройстве показывают вес в ньютонах.

Измеритель Ньютона использует калиброванную пружину для измерения веса объекта. Wikimedia commons

Уравнение гравитации

В нашей повседневной жизни очень часто говорят о весе или массе объекта, как если бы они были одним и тем же. Тем не менее, это очень разные вещи в физике.

Масса — это скалярная величина, которая относится к количеству материи объекта.

Поскольку масса объекта постоянна независимо от гравитационного поля , в котором он находится, масса космонавта на Луне такая же, как и на Земле.

Вес объекта — это сила, действующая на него из-за гравитационного поля, в котором он находится.

Вес — векторная величина, измеряемая в ньютонах.

Так как Луна и Земля имеют разные гравитационные поля, космонавт имеет разный вес на Луне по сравнению с Землей.

Вес объекта прямо пропорционален как силе гравитационного поля, в котором он находится, так и его массе. Вес объекта в гравитационном поле можно рассчитать, используя следующее уравнение:

или прописью:

, где вес в, масса в килограммах, а напряженность гравитационного поля в. в нескольких примерах, где это уравнение может быть использовано.

Квантовая гравитация — это теория, утверждающая, что гравитация — это сила, действующая через теоретическую частицу, называемую гравитоном . Эту теорию было трудно доказать, поскольку условия, необходимые для ее доказательства, недостижимы и ограничены современными технологиями.

Рассчитайте вес человека, масса которого, стоя на поверхности земли, где сила гравитационного поля. Каков был бы его вес, если бы он вместо этого оказался на Луне?

Шаг 1: Перечислите указанные количества.

Шаг 2: Рассчитайте вес на Земле.

Уравнение для расчета веса объекта в гравитационном поле имеет вид

Шаг 3: Рассчитайте вес на Луне.

Точно так же его вес на Луне определяется тем же уравнением, но мы меняем значение

Вес объекта на Луне меньше из-за относительно меньшей напряженности его гравитационного поля по сравнению с земля.

Давайте посмотрим на другой пример.

Если бы автомобиль имел вес на Луне. Рассчитайте его вес на Земле. Напряженность гравитационного поля на Земле равна и Напряженность гравитационного поля на Луне равна

Шаг 1: Перечислите заданные величины

Шаг 2: Уравнение для веса на Земле

Уравнение для расчета веса объекта в гравитационном поле определяется как

Шаг 3: Уравнение для веса на Луне

Точно так же вес на Луне равен

Шаг 4: Используйте тот факт, что масса не меняется

Поскольку масса постоянна независимо от гравитационных полей, мы можем переписать оба приведенных выше уравнения в виде выделить массы объекта и приравнять их.

Приравняем оба уравнения

Это даст нам вес объекта на Земле.

На этом мы подошли к концу этой статьи. Давайте пройдемся по тому, что мы узнали до сих пор.