Формула силы тяги в физике
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Содержание:
- Определение и формула силы тяги
- Единицы измерения силы тяги
- Примеры решения задач
В том случае, если тело при перемещении имеет ускорение, то на него кроме всех прочих обязательно действует некоторая сила, которая является силой тяги в рассматриваемый момент времени. В действительности, если тело движется прямолинейно и с постоянной скоростью, то сила тяги также действует, так как тело должно преодолевать силы сопротивления. Обычно силу тяги находят, рассматривая силы, действующие на тело, находя равнодействующую и применяя второй закон Ньютона. Жестко определенной формулы для силы тяги не существует.
Не следует считать, что сила тяги, например, транспортного средства действует со стороны двигателя, так как внутренние силы не могут менять
скорость системы как единого целого, что входило бы в противоречие с законом сохранения импульса.
$$P=\bar{F}_{T} \bar{v}(1)$$
Определение и формула силы тяги
Определение
Исходя из формулы (1) силу тяги можно определить через полезную мощность, и скорость транспортного средства (v):
$$F_{T}=\frac{P}{v}(2)$$
Для автомобиля, поднимающегося в горку, которая имеет уклон , масса автомобиля m сила тяги (FT) войдет в уравнение:
$$F_{T}-F_{s}-m g \sin \alpha=m a(3)$$
где a – ускорение, с которым движется автомобиль.
Единицы измерения силы тяги
Основной единицей измерения силы в системе СИ является: [FT]=Н
В СГС: [FT]=дин
Примеры решения задач
Пример
Задание. На автомобиль имеющий массу 1 т при его движении по горизонтальной поверхности, действует сила трения, которая равна $\mu$=0,1 от силы тяжести. Какой будет сила тяги, если автомобиль движется с ускорением 2 м/с?
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем второй закон Ньютона:
$$\bar{N}+m \bar{g}+\bar{F}_{t r}+\bar{F}_{T}=m \bar{a}(1.1)$$
Спроектируем уравнение (1.1) на оси X и Y:
$$ \begin{array}{c} X: F_{T}-F_{t r}=m a(1.2) \\ Y: m g=N(1.3) \end{array} $$
По условию задачи:
$$ F_{t r}=\mu \cdot m g (1.4) $$
Подставим правую часть выражения (1. {3}(H)$$
{3}(H)$$
Ответ. FT=2,98 кН
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. На гладкой горизонтальной поверхности лежит доска массой M. На доске находится тело массы m. Коэффициент трения тела о доску равен $\mu$ . К доске приложена сила горизонтальная сила тяги, которая зависит от времени как: F=At (где A=const). В какой момент времени доска начнет выскальзывать из-под тела?
Решение. Сделаем рисунок.
Для решения задачи нам потребуются проекции сил на осиX и Y, которые отличны от нуля. Для тела массы m:
$$
\begin{array}{c}
X: m a_{1}=F_{t r}(2.1) \\
Y: m g=N(2.2) \\
F_{t r}=\mu N=\mu m g \rightarrow m a_{1}=\mu m g \rightarrow a_{1}=\mu g(2. 3)
\end{array}
$$
3)
\end{array}
$$
Для тела массы M:
$$M a_{2}=F-F_{t r} \rightarrow M a_{2}=A t-F_{t r} \rightarrow a_{2}=\frac{A t-F_{t r}}{M}(2.2)$$
Обозначим момент времени, в который доска начнет выскальзывать из-под тела t
$$\mu g=\frac{A t_{0}-\mu m g}{M} \rightarrow t_{0}=\frac{m+M}{A} \mu g$$
Ответ. $t_{0}=\frac{m+M}{A} \mu g$
Читать дальше: Формула силы упругости.
Формула силы тяги при равномерном движении
Разберёмся в вопросе, что такое сила тяги. Как следует из самого названия – это сила, которую необходимо прикладывать к телу, чтобы оно находилось в состоянии постоянного движения.
Если её убрать, то тело, будь то автомобиль, электровоз, космическая ракета или санки, со временем остановится. Это произойдёт потому, что на тело всегда действуют силы, которые заставляют его стремиться к состоянию покоя:
- сопротивления воздуха (газа),
- сопротивления воды и др.

Первый и второй законы Ньютона
Обратимся к законам Ньютона, которые хорошо описывают механическое движение тел. Из школьной программы мы знаем, что есть первый закон Ньютона, который описывает закон инерции. Он гласит, что любое тело, если на него не действуют силы, или если их равнодействующая равна нулю, движется прямолинейно и равномерно, или же находится в состоянии покоя. Это означает, что тело, пока на него ничто не действует, будет двигаться с постоянной скоростью v=const или пребывать в состоянии покоя сколько угодно долго, пока какое-то внешнее воздействие не выведет тело из этого состояния. Это и есть движение по инерции.
Надо сказать, что этот закон справедлив лишь в так называемых инерциальных системах отсчёта. В неинерциальных системах отсчёта этот закон не действует и нужно использовать второй закон Ньютона. В таких системах отсчёта тело тоже будет двигаться по инерции, но оно будет двигаться с ускорением, стремясь сохранять своё движение, т. е. на него также не будут действовать никакие внешние силы, кроме силы инерции, стремящейся двигать тело в том направлении, в каком оно двигалось до воздействия. Тут мы приходим к рассмотрению второго закона Ньютона, который также справедлив в инерциальных системах отсчёта, т. е. в таких системах отсчёта, в которых тело движется с постоянной скоростью либо находится в покое.
е. на него также не будут действовать никакие внешние силы, кроме силы инерции, стремящейся двигать тело в том направлении, в каком оно двигалось до воздействия. Тут мы приходим к рассмотрению второго закона Ньютона, который также справедлив в инерциальных системах отсчёта, т. е. в таких системах отсчёта, в которых тело движется с постоянной скоростью либо находится в покое.
Этот закон утверждает, что для того, чтобы вывести тело из состояния покоя или равномерного движения, к нему необходимо приложить силу, равную F=m•a, где m — это масса тела, a — ускорение, сообщаемое телу. Зная эти законы, можно рассчитать силу тяги (двигателя автомобиля, ракетного двигателя или, например, лошади, тянущей нагруженную повозку).
Примеры из жизни
Насколько вы сильны?
Рассмотрим простейший пример. Ваш ребёнок сел на санки и просит вас его покатать. С какой силой вам нужно тянуть эти санки, чтобы ребёнок остался доволен быстрой ездой ? Пока санки с ребёнком остаются в состоянии покоя, все силы, действующие на них, уравновешены. Состояние покоя — это частный случай инерции. Здесь на санки действуют две силы: тяжести Fт = m•g, направленная вертикально вниз, и нормального давления N, направленная вертикально вверх. Поскольку санки не движутся, то N – m•g = 0. Тогда из этого равенства следует, что N = m•g.
Состояние покоя — это частный случай инерции. Здесь на санки действуют две силы: тяжести Fт = m•g, направленная вертикально вниз, и нормального давления N, направленная вертикально вверх. Поскольку санки не движутся, то N – m•g = 0. Тогда из этого равенства следует, что N = m•g.
Когда вы решили покатать своего ребёнка, вы прикладываете силу тяги (Fтяги) к санкам с ребёнком. Когда вы начинаете тянуть санки, возникает сопротивление движению, вызванное силой трения (Fтр.), направленной в противоположную сторону. Это так называемая сила трения покоя. Когда тело не движется, она равна нулю. Стоит потянуть за санки — и появляется сила трения покоя, которая меняется от нуля до некоторого максимального значения (Fтр. max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.
Чтобы найти Fтяги, применим второй закон Ньютона: Fтяги – Fтр.max = m•a, где a – ускорение, с которым вы тянете санки, m – масса санок с ребёнком. Допустим, вы разогнали санки до определённой скорости, которая не изменяется. Тогда a = 0 и вышеприведённое уравнение запишется в виде: Fтяги – Fтр. max = 0, или Fтяги = Fтр.max. Есть известный закон из физики, который устанавливает определённую зависимость для Fтр.max и N. Эта зависимость имеет вид: Fтр.max = fmax • N, где fmax – максимальный коэффициент трения покоя.
Тогда a = 0 и вышеприведённое уравнение запишется в виде: Fтяги – Fтр. max = 0, или Fтяги = Fтр.max. Есть известный закон из физики, который устанавливает определённую зависимость для Fтр.max и N. Эта зависимость имеет вид: Fтр.max = fmax • N, где fmax – максимальный коэффициент трения покоя.
Если в эту формулу подставить выражение для N, то мы получим Fтр.max = fmax•m•g. Тогда формула искомой силы тяги примет вид: Fтяги = fmax•m•g = fск•m•g, где fск = fmax – коэффициент трения скольжения, g – ускорение свободного падения. Допустим, fск = 0,7, m = 30 кг, g = 9,81 м/с², тогда Fтяги = 0,7 • 30 кг • 9,81 м/с² = 206,01 Н (Ньютона).
Насколько силён ваш автомобиль?
Рассмотрим ещё пример. У вас есть автомобиль, мощность двигателя которого N. вы едете со скоростью v. Как в этом случае узнать силу тяги двигателя вашего автомобиля ? Поскольку скорость автомобиля не меняется, то Fтяги уравновешена силами трения качения, лобового сопротивления, трения в подшипниках и т. д. (первый закон Ньютона). По второму закону Ньютона она будет равна Fтяги = m•a. Чтобы её вычислить, достаточно знать массу автомобиля m и ускорение a.
д. (первый закон Ньютона). По второму закону Ньютона она будет равна Fтяги = m•a. Чтобы её вычислить, достаточно знать массу автомобиля m и ускорение a.
Допустим, вы разогнали свой автомобиль до скорости v за какое-то время t, проехав расстояние s. Тогда Fтяги будет легко рассчитана по формуле: Fтяги = m•v/t. Как и в примере с санками, справедлива также такая формула: Fтяги = f•m•g, где f – коэффициент трения качения, который зависит от скорости автомобиля (чем больше скорость, тем меньше этот коэффициент).
Но что делать, если масса автомобиля m, коэффициент трения качения f и время разгона t неизвестны ? Тогда можно поступить по-другому. Двигатель вашего автомобиля при разгоне совершил работу A = Fтяги • s. Поскольку формула расстояния имеет вид s = v•t, то выражение для работы будет таким: A = Fтяги • v • t. Разделив обе части этого равенства на t, получим A/t = Fтяги • v. Но A/t = N – это мощность двигателя вашего автомобиля, поэтому N = Fтяги • v. Отсюда уже получим искомую формулу: Fтяги =N/v.
Допустим, вы разогнали свой автомобиль до скорости v = 180 км/ч, а мощность его двигателя N = 200 л. с. (лошадиных сил). Чтобы вычислить Fтяги двигателя, необходимо прежде перевести указанные единицы измерения в единицы СИ, т. е. международной системы измерения. Здесь 1 л. с. = 735,499 Вт, поэтому мощность двигателя составит N = 200 л. с. • 735,499 Вт/л. с. = 147099,8 Вт. Скорость в системе СИ будет равна v = 180 км/ч = 180 • 1000 м/3600 с = 50 м/с. Тогда искомое значение будет равно Fтяги = 147099,8 Вт/50 (м/с) = 2941,996 Н
2,94 кН (килоньютона).
Около 3 килоньютонов. Много это или мало ? Допустим, вы жмёте 100 килограммовую штангу. Чтобы её поднять, вам нужно преодолеть её вес, равный P = m•g = 100 кг • 9,81 м/с² = 981 Н (ньютон)
0,98 кН. Полученное для автомобиля значение Fтяги больше веса штанги в 2,94/0,98 = 3 раза. Это равносильно тому, что вы будете поднимать штангу массой в 300 кг. Такова сила тяги двигателя вашего автомобиля (на скорости 180 км/ч).
Таким образом, зная школьный курс физики, мы можем с лёгкостью вычислить силу тяги:
- человека,
- лошади,
- паровоза,
- автомобиля,
- космической ракеты и всех прочих видов техники.
В нашем видео вы найдете интересные опыты, поясняющие, что такое сила тяги и сила сопростивления.
Сила тяги при рассмотрении транспортных средств называется внешней силой, которая должна быть реализована с использованием машины или механизма для перемещения груза.
Сама по себе концепция «тяговой силы» имеет смысл только по отношению к любому транспортному средству, например, говорить о тяговой силе автомобиля, самолета, лошади, тянуть сани.
Единицей измерения силы является Н (Ньютон).
Очень заманчиво заключить, что источником тяги автомобиля является его двигатель. Однако это неверно. Внутренние силы одной части системы (двигателя), действующие на другую часть системы (колеса), не могут ускорить всю систему (весь автомобиль), так как это противоречит закону сохранения импульса. Источником тяги являются внешние воздействия. В случае с автомобилем это сила трения колес на поверхности дороги, в случае корабля – сила струи воды, выброшенной пропеллером.
Источником тяги являются внешние воздействия. В случае с автомобилем это сила трения колес на поверхности дороги, в случае корабля – сила струи воды, выброшенной пропеллером.
Нет единой универсальной формулы для расчета силы тяги. Сила тяги определяется конструкцией транспортного средства и физическими условиями проблемы.
Примеры решения проблем по теме «Тяга»
Автомобиль весом 4 тонны движется по ровной дороге с ускорением . Найдите силу тяги двигателя автомобиля, если коэффициент трения .
Мы делаем картину:
При движении по машине сила тяжести , сила реакции опоры , сила трения и тяговое усилие действуют. Под действием этих сил автомобиль движется с ускорением .
Согласно второму закону Ньютона:
Введем систему координат, как показано на рисунке, и запишем это векторное равенство в проекциях на оси координат.
Сила трения . Из второго уравнения . Поэтому мы можем написать ( . Замените значение силы трения в первом уравнении и определите силу тяги автомобильного двигателя:
Ускорение силы тяжести
Подставляя в формулу численные значения физических величин, вычисляем:
Двигатель двигателя тяги
Автомобиль весом 4 тонны движется в гору с наклоном 1 м на каждые 25 м пути с постоянной скоростью. Найдите силу тяги двигателя автомобиля, если коэффициент трения
Найдите силу тяги двигателя автомобиля, если коэффициент трения
Мы делаем картину:
В этом примере, как и в предыдущем, при движении автомобиля сила тяжести , сила реакции поддержки , сила трения и тяговое усилие действуют на автомобиль. И под влиянием этих сил автомобиль движется в гору с постоянной скоростью, то есть ускорение автомобиля .
Согласно второму закону Ньютона:
Запишем это векторное равенство в проекциях на оси координат:
Из второго уравнения и силы трения .
Подставляя значение силы трения в первое уравнение, мы определяем силу тяги:
Сила тяги: определение
Силой тяги называют силу, прикладываемую к телу для поддержании его в постоянном движении.
Прекращение действия силы тяги приводит к остановке вследствие трения, вязкости окружающей среды и других противодействующих движению сил.
Тело, на которое не действуют силы, движется с постоянной скоростью $v = const$ (первый закон Ньютона). Частным случаем такого движения является состояние покоя ($v = 0$). Движение с постоянной скоростью называют состоянием инерции. Чтобы вывести тело из такого состояния, нужно приложить к нему силу. Скорость тела в этом случае изменится, т.е. оно получит ускорение (либо замедление, которое можно считать отрицательным ускорением).
Движение с постоянной скоростью называют состоянием инерции. Чтобы вывести тело из такого состояния, нужно приложить к нему силу. Скорость тела в этом случае изменится, т.е. оно получит ускорение (либо замедление, которое можно считать отрицательным ускорением).
Величина ускорения обратнопропорциональна массе тела (чем оно массивнее, тем труднее его вывести из состояния инерции) и прямопропорциональна интенсивности приложенной силы. Таким образом:
Эта формула отражает Второй закон Ньютона.
Попробуй обратиться за помощью к преподавателям
Формулы для расчета
В качестве примера силы тяги, выводящей тело из состояния покоя, можно рассмотреть спортсмена, поднимающего штангу. В исходном состоянии штанга находится в состоянии инерции (остается неподвижной). Когда спортсмен отрывает ее от земли, его мышцы должны сокращаться с такой силой, чтобы она превысила вес штанги, т.е. силу, с которой ее притягивает гравитационное поле Земли. Если штангисту удастся оторвать штангу от пола – значит она переместится вверх на некоторое расстояние, т. е. получит ускорение. Т.е. силой тяги, двигающей данный снаряд, является сила сокращающихся мышц спортсмена. При этом должно соблюдаться условие:
е. получит ускорение. Т.е. силой тяги, двигающей данный снаряд, является сила сокращающихся мышц спортсмена. При этом должно соблюдаться условие:
$F_м$ > $F_т$, т.е. $F_м$ >$ m cdot g$,
где $F_м$ – сила мышц (в данном случае сила тяги), $F_т$ – сила тяжести (гравитация), $m$ – масса, $g$ – ускорение свободного падения.
Состояние движения по инерции следует отличать от равномерного движения, когда сила тяги уравновешивается противодействующими силами. Например, при движении автомобиля работающий двигатель через систему трансмиссии передает на колеса силу, преодолевающую силы трения внутри механизмов автомобиля, трения колес о поверхность дороги, сопротивления воздуха и т.д. Силу тяги можно в этом случае вычислить зная время разгона $t$ до нужной скорости $v$ и массу автомобиля $m$:
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Здесь ускорение выражено как частное от деления скорости на время разгона.
Силу тяги можно также выразить через мощность – способность некоторого источника энергии совершать работу. 2$, если его масса составляет 1,5 тонны, а сила трения – 10% от силы тяжести.
2$, если его масса составляет 1,5 тонны, а сила трения – 10% от силы тяжести.
Рассмотрим силу тяги как сумму двух сил:
- разгоняющей автомобиль с заданным ускорением: $F_1 = m cdot a$, где $m$ – масса, $a$ – ускорение;
- преодолевающей силу трения: $F_2 = mu cdot m cdot g$, где $mu$ – коэффициент силы трения, $g$ – ускорение свободного падения.
Подставив числовые значения в формулу
$F = F_1 + F_2 = m cdot a + mu cdot m cdot g$
получим, попутно переведя тонны в единицы СИ килограммы,
$F = 1500 cdot 3 + 0,1 cdot 9,8 cdot 1500 = 1500 cdot (3 + 0,98) = 5970$
Ответ: 5970 ньютонов.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
определение, формулы для вычисления и примеры из реальной жизни
Разберёмся в вопросе, что такое сила тяги. Как следует из самого названия – это сила, которую необходимо прикладывать к телу, чтобы оно находилось в состоянии постоянного движения.
Если её убрать, то тело, будь то автомобиль, электровоз, космическая ракета или санки, со временем остановится. Это произойдёт потому, что на тело всегда действуют силы, которые заставляют его стремиться к состоянию покоя:
- силы трения (покоя, качения, скольжения),
- сопротивления воздуха (газа),
- сопротивления воды и др.
Содержание:
- Первый и второй законы Ньютона
- Примеры из жизни
- Насколько вы сильны?
- Насколько силён ваш автомобиль?
Первый и второй законы Ньютона
Обратимся к законам Ньютона, которые хорошо описывают механическое движение тел. Из школьной программы мы знаем, что есть первый закон Ньютона, который описывает закон инерции. Он гласит, что любое тело, если на него не действуют силы, или если их равнодействующая равна нулю, движется прямолинейно и равномерно, или же находится в состоянии покоя. Это означает, что тело, пока на него ничто не действует, будет двигаться с постоянной скоростью v=const или пребывать в состоянии покоя сколько угодно долго, пока какое-то внешнее воздействие не выведет тело из этого состояния. Это и есть движение по инерции.
Это и есть движение по инерции.
Надо сказать, что этот закон справедлив лишь в так называемых инерциальных системах отсчёта. В неинерциальных системах отсчёта этот закон не действует и нужно использовать второй закон Ньютона. В таких системах отсчёта тело тоже будет двигаться по инерции, но оно будет двигаться с ускорением, стремясь сохранять своё движение, т.е. на него также не будут действовать никакие внешние силы, кроме силы инерции, стремящейся двигать тело в том направлении, в каком оно двигалось до воздействия. Тут мы приходим к рассмотрению второго закона Ньютона, который также справедлив в инерциальных системах отсчёта, т. е. в таких системах отсчёта, в которых тело движется с постоянной скоростью либо находится в покое.
Этот закон утверждает, что для того, чтобы вывести тело из состояния покоя или равномерного движения, к нему необходимо приложить силу, равную F=m•a, где m — это масса тела, a — ускорение, сообщаемое телу. Зная эти законы, можно рассчитать силу тяги (двигателя автомобиля, ракетного двигателя или, например, лошади, тянущей нагруженную повозку).
Примеры из жизни
Насколько вы сильны?
Рассмотрим простейший пример. Ваш ребёнок сел на санки и просит вас его покатать. С какой силой вам нужно тянуть эти санки, чтобы ребёнок остался доволен быстрой ездой ? Пока санки с ребёнком остаются в состоянии покоя, все силы, действующие на них, уравновешены. Состояние покоя — это частный случай инерции. Здесь на санки действуют две силы: тяжести Fт = m•g, направленная вертикально вниз, и нормального давления N, направленная вертикально вверх. Поскольку санки не движутся, то N – m•g = 0. Тогда из этого равенства следует, что N = m•g.
Когда вы решили покатать своего ребёнка, вы прикладываете силу тяги (Fтяги) к санкам с ребёнком. Когда вы начинаете тянуть санки, возникает сопротивление движению, вызванное силой трения (Fтр.), направленной в противоположную сторону. Это так называемая сила трения покоя. Когда тело не движется, она равна нулю. Стоит потянуть за санки — и появляется сила трения покоя, которая меняется от нуля до некоторого максимального значения (Fтр. max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.
max). Как только Fтяги превысит Fтр.max, санки с ребёнком придут в движение.
Чтобы найти Fтяги, применим второй закон Ньютона: Fтяги – Fтр.max = m•a, где a – ускорение, с которым вы тянете санки, m – масса санок с ребёнком. Допустим, вы разогнали санки до определённой скорости, которая не изменяется. Тогда a = 0 и вышеприведённое уравнение запишется в виде: Fтяги – Fтр. max = 0, или Fтяги = Fтр.max. Есть известный закон из физики, который устанавливает определённую зависимость для Fтр.max и N. Эта зависимость имеет вид: Fтр.max = fmax • N, где fmax – максимальный коэффициент трения покоя.
Если в эту формулу подставить выражение для N, то мы получим Fтр.max = fmax•m•g. Тогда формула искомой силы тяги примет вид: Fтяги = fmax•m•g = fск•m•g, где fск = fmax – коэффициент трения скольжения, g – ускорение свободного падения. Допустим, fск = 0,7, m = 30 кг, g = 9,81 м/с², тогда Fтяги = 0,7 • 30 кг • 9,81 м/с² = 206,01 Н (Ньютона).
Насколько силён ваш автомобиль?
Рассмотрим ещё пример.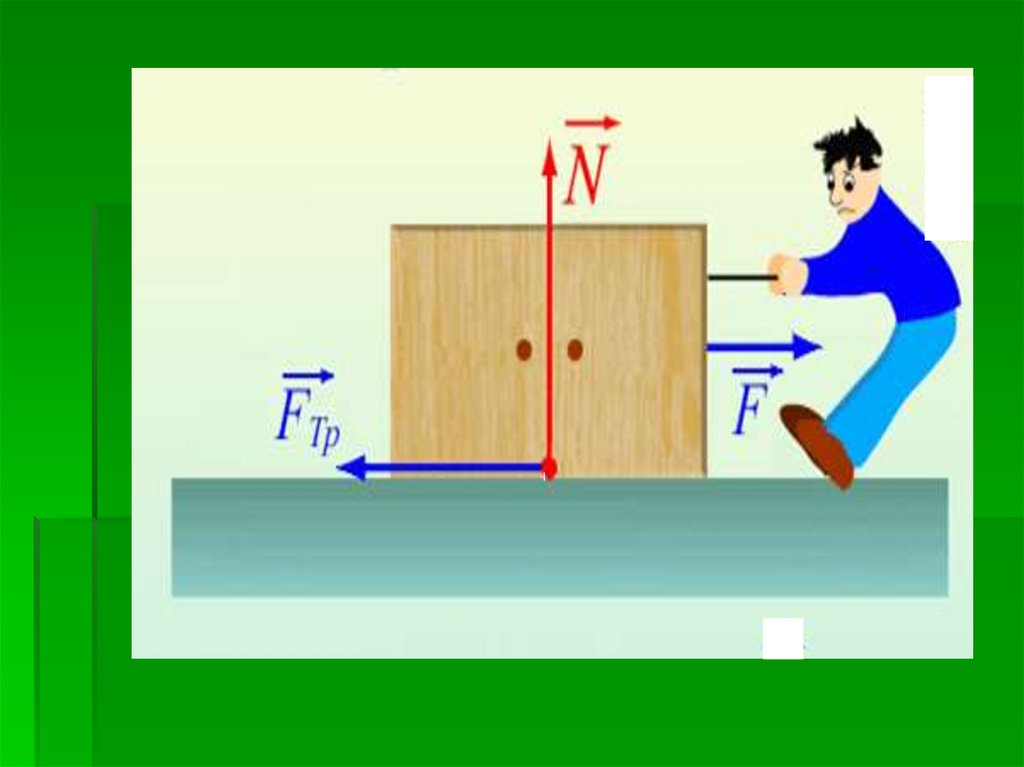 У вас есть автомобиль, мощность двигателя которого N. вы едете со скоростью v. Как в этом случае узнать силу тяги двигателя вашего автомобиля ? Поскольку скорость автомобиля не меняется, то Fтяги уравновешена силами трения качения, лобового сопротивления, трения в подшипниках и т. д. (первый закон Ньютона). По второму закону Ньютона она будет равна Fтяги = m•a. Чтобы её вычислить, достаточно знать массу автомобиля m и ускорение a.
У вас есть автомобиль, мощность двигателя которого N. вы едете со скоростью v. Как в этом случае узнать силу тяги двигателя вашего автомобиля ? Поскольку скорость автомобиля не меняется, то Fтяги уравновешена силами трения качения, лобового сопротивления, трения в подшипниках и т. д. (первый закон Ньютона). По второму закону Ньютона она будет равна Fтяги = m•a. Чтобы её вычислить, достаточно знать массу автомобиля m и ускорение a.
Допустим, вы разогнали свой автомобиль до скорости v за какое-то время t, проехав расстояние s. Тогда Fтяги будет легко рассчитана по формуле: Fтяги = m•v/t. Как и в примере с санками, справедлива также такая формула: Fтяги = f•m•g, где f – коэффициент трения качения, который зависит от скорости автомобиля (чем больше скорость, тем меньше этот коэффициент).
Но что делать, если масса автомобиля m, коэффициент трения качения f и время разгона t неизвестны ? Тогда можно поступить по-другому. Двигатель вашего автомобиля при разгоне совершил работу A = Fтяги • s. Поскольку формула расстояния имеет вид s = v•t, то выражение для работы будет таким: A = Fтяги • v • t. Разделив обе части этого равенства на t, получим A/t = Fтяги • v. Но A/t = N – это мощность двигателя вашего автомобиля, поэтому N = Fтяги • v. Отсюда уже получим искомую формулу: Fтяги =N/v.
Поскольку формула расстояния имеет вид s = v•t, то выражение для работы будет таким: A = Fтяги • v • t. Разделив обе части этого равенства на t, получим A/t = Fтяги • v. Но A/t = N – это мощность двигателя вашего автомобиля, поэтому N = Fтяги • v. Отсюда уже получим искомую формулу: Fтяги =N/v.
Допустим, вы разогнали свой автомобиль до скорости v = 180 км/ч, а мощность его двигателя N = 200 л. с. (лошадиных сил). Чтобы вычислить Fтяги двигателя, необходимо прежде перевести указанные единицы измерения в единицы СИ, т. е. международной системы измерения. Здесь 1 л. с. = 735,499 Вт, поэтому мощность двигателя составит N = 200 л. с. • 735,499 Вт/л. с. = 147099,8 Вт. Скорость в системе СИ будет равна v = 180 км/ч = 180 • 1000 м/3600 с = 50 м/с. Тогда искомое значение будет равно Fтяги = 147099,8 Вт/50 (м/с) = 2941,996 Н ~ 2,94 кН (килоньютона).
Около 3 килоньютонов. Много это или мало ? Допустим, вы жмёте 100 килограммовую штангу. Чтобы её поднять, вам нужно преодолеть её вес, равный P = m•g = 100 кг • 9,81 м/с² = 981 Н (ньютон)~0,98 кН. Полученное для автомобиля значение Fтяги больше веса штанги в 2,94/0,98 = 3 раза. Это равносильно тому, что вы будете поднимать штангу массой в 300 кг. Такова сила тяги двигателя вашего автомобиля (на скорости 180 км/ч).
Полученное для автомобиля значение Fтяги больше веса штанги в 2,94/0,98 = 3 раза. Это равносильно тому, что вы будете поднимать штангу массой в 300 кг. Такова сила тяги двигателя вашего автомобиля (на скорости 180 км/ч).
Таким образом, зная школьный курс физики, мы можем с лёгкостью вычислить силу тяги:
- человека,
- лошади,
- паровоза,
- автомобиля,
- космической ракеты и всех прочих видов техники.
Видео
В нашем видео вы найдете интересные опыты, поясняющие, что такое сила тяги и сила сопростивления.
Урок физики по теме «Сила трения»
Тип урока: изучение нового материала, используя деятельностный подход к обучению и усвоение знаний.
Образовательная цель: получить учащихся, усвоивших следующие знания:
- сила трения – это сила, которая возникает при соприкосновении одного тела с другим, препятствующая их относительному движению;
- причины возникновения силы трения: шероховатость поверхностей соприкасающихся тел и взаимное притяжение молекул соприкасающихся тел;
- способ увеличения силы трения – ввести между трущимися поверхностями смазку;
- виды силы трения: трения скольжения, качения и покоя;
- сила трения качения меньше силы трения скольжения и покоя;
- сила трения скольжения численно равна силе тяги, при равномерном движении тела;
- сила трения зависит от силы реакции опоры и коэффициента трения;
- коэффициент трения зависит от материала, из
которого изготовлены соприкасающиеся тела и от
качества обработки их поверхностей.

Цель урока по развитию учащихся: подготовить учащихся, овладевших следующими видами деятельности:
- называть причину действия силы трения;
- выделять причину возникновения силы;
- определять вид и значения силы трения;
- строить график;
- вычислять силу трения.
Задачи урока:
- сформировать представление о том, что такое сила трения, какова причина возникновения силы трения, какие виды силы трения существуют, как её измеряют;
- создать условия для развития личности учеников в процессе их деятельности;
- способствовать развитию практических навыков и умений;
- научить выделять главное, сравнивать, развивать способности к обобщению, систематизации полученных знаний. Формировать умение работать в паре
Формы организации познавательной деятельности: фронтальная, индивидуальная.
Методы: частично-поисковый,
исследовательский.
Оборудование: трибометр, брусок, динамометр, грузики.
Этапы проведения урока:
- Организационный момент.
- Актуализация ранее усвоенных знаний.
- Системная актуализация.
- Контроль и самопроверка знаний.
- Рефлексия.
Ход урока
1. Фронтальный опрос:
- Что называется силой?
- Какой прибор измеряет силу?
- Какие виды сил мы знаем?
- Что называется весом?
- Как можно рассчитать вес тела?
- Чем отличатся сила тяжести от веса тела?
2. Провести эксперимент и ответить на вопросы.
| Вопрос | Ответ |
| 1. Что будет наблюдаться, если толкнуть по столу брусок? | |
| 2. Как меняется скорость? | |
3. Почему изменяется скорость движения
бруска? Почему изменяется скорость движения
бруска? | |
| 4. Какие силы действуют на брусок? | |
| 5. Куда направлены силы? |
Сила трения — это_______________________________________
III. Прочитать в учебнике пункт 4-6 в параграфе 30 стр. 71 и выяснить причину возникновения силы трения и её записать.
1 причина_____________________________________________
2 причина_____________________________________________
IV. Прочитать в учебнике пункт 7 в §30 стр. 71 и выяснить, каким образом можно уменьшить силу трения.
______________________________________________________
V. Выполните эксперимент по алгоритму.
1. Прикрепите динамометр к бруску и двигайте брусок равномерно по трибометру при помощи горизонтально расположенного динамометра.
2. Измерьте силу, с которой динамометр действует
на брусок. Какую силу показывает динамометр? Чему
она равна?_________________________________________________
Какую силу показывает динамометр? Чему
она равна?_________________________________________________
3. Почему можно утверждать, что сила тяги, которую показывает динамометр, рана силе трения?________________________________________________
4. Положите на брусок груз. Измерьте силу тяги при равномерном движении бруска. Как она изменилась? ____________________________________________
5. Повторите опыт с двумя и тремя грузами. Заполните таблицу.
| № опыта | количество грузов | вес бруска с грузом | сила трения |
| 1 | 1 | ||
| 2 | 2 | ||
| 3 | 3 |
6.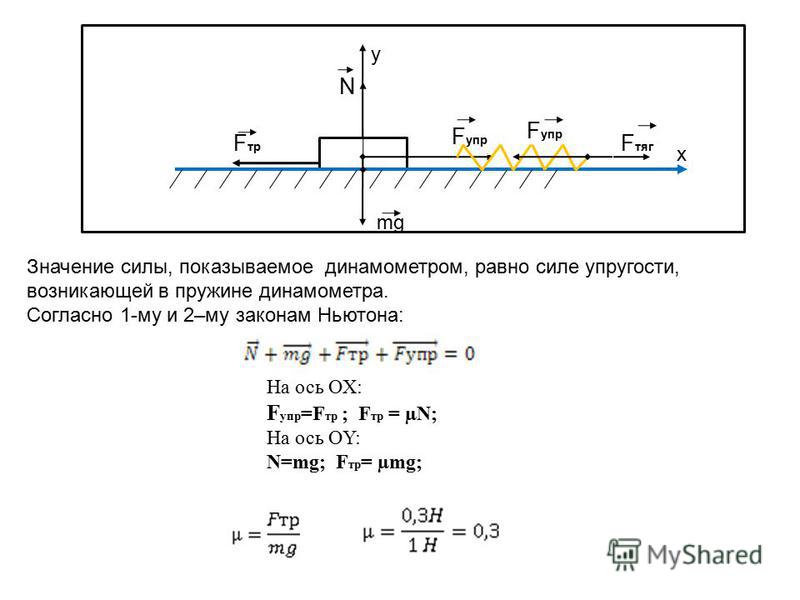 Сделайте вывод _____________________________________
Сделайте вывод _____________________________________
7. Расположите на столе два круглых карандаша. Поставьте на них брусок с грузами. Приведите брусок с грузами в движение при помощи динамометра. Измерьте силу трения качения.___________________________________________
8. Сравните силу трения качения с силой трения скольжения. Сделайте вывод. _________________________________________
9. Расположите брусок с тремя грузами на столе. Прикрепите динамометр к бруску. Начинайте тянуть брусок до тех пор, пока он не придет в движение, наблюдая при этом показания динамометра. Как меняется сила трения покоя? ________________________________
10. Какова максимальная сила трения покоя?__________________________________
11. Дайте сравнительную оценку силам трения покоя, скольжения и качения. ________________________________________
12. Постройте график зависимости Fтр от N
13. Какая зависимость между Fтр и N _____________________________________________
14. Запомните формулу вычисления силы трения.
Запомните формулу вычисления силы трения.
Fтр = µN, где µ — коэффициент трения, всегда меньше 1
N — сила реакции опоры.
µ зависит:
- от материала, из которого изготовлены соприкасающиеся тела;
- от качества обработки их поверхностей
µ не зависит:
- от площади их соприкосновения.
VI. Домашнее задание. Параграф 30,31,32.
По параграфу 30 заполнить схему:
VII. Самопроверка знаний:
1. Зачем зимой дорожки посыпаю песком? (Чтобы увеличить силу трения).
2. Зачем зимой на задние колеса автомобилей надевают цепи? (Чтобы увеличить силу трения).
3. Зачем на шины автомобилей наносят протектор? (Чтобы увеличить силу трения).
4. Зачем спортсмены-лыжники на лыжи наносят особою смазку? (Чтобы лыжи лучше скользили).
5. Готовь сани летом, а телегу зимой. Почему сани
лучше использовать зимой, а телегу летом? (Сила
трения скольжения полозьев о снег меньше, чем о
землю. Летом используют телегу, так как сила
трения качения колес по земле небольшая, а по
снегу — значительная).
Летом используют телегу, так как сила
трения качения колес по земле небольшая, а по
снегу — значительная).
6. Корабль спускают, так салазки салом подмазывают. А зачем при спуске кораблей салазки смазывают салом? (Для того чтобы уменьшить силу трения скольжения).
7. Вода близка, да гора склизка. Почему по скользкой горе трудно добираться до воды? (Так как трение между подошвами и горой мало, то и идти тяжело).
VIII. Подведение итогов. Рефлексия.
1. Что вы узнали нового при изучении темы урока?
2. Чему вы научились при изучении данной темы?
3. Что оказалось для вас самым главным?
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.
 3 Законы сохранения
3 Законы сохранения - 2.4 Статика
- 2.5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 5 Оптика.
 СТО
СТО- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Решение задач по теме «Механическая работа и мощность» 7 класс онлайн-подготовка на Ростелеком Лицей
Задача №1
К бруску прикрепили динамометр и переместили брусок на расстояние 30 см.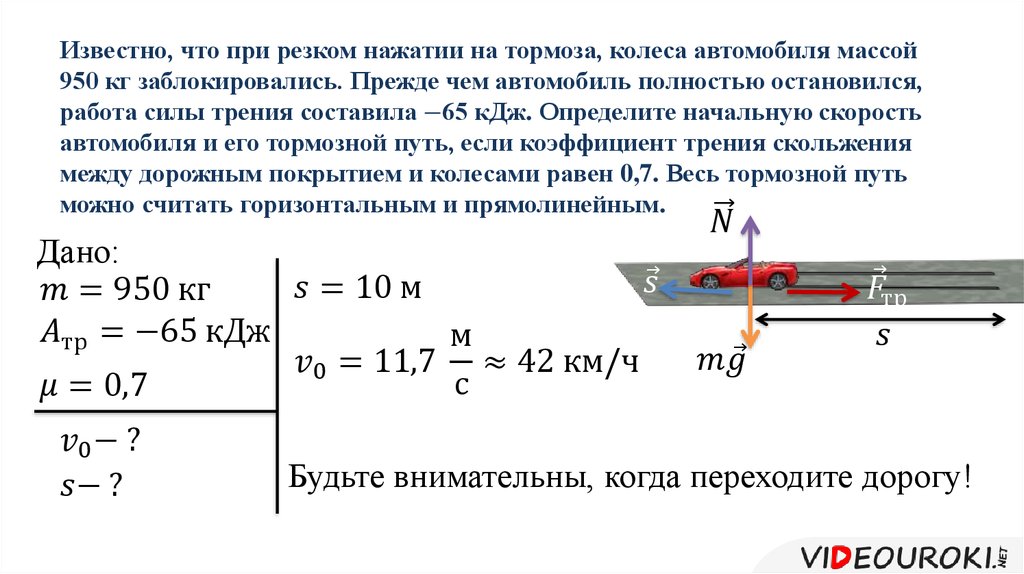 Показания динамометра равны 0,8 Н. Найти работу силы тяги по перемещению бруска (рис. 1).
Показания динамометра равны 0,8 Н. Найти работу силы тяги по перемещению бруска (рис. 1).
Рис. 1. К задаче №1
Прежде всего запишем краткое условие задачи и позаботимся, чтобы все данные были выражены в системе СИ (рис. 2).
Рис. 2. Краткое условие задачи №1
Для вычисления работы воспользуемся формулой
Полное решение задачи выглядит так (рис. 3).
Рис. 3. Полное решение задачи №1
Задача №2
Трактор перемещает платформу со скоростью 7,2 км/ч, развивая тяговое усилие в 25 кН. Какую работу совершит трактор за 10 мин (рис. 4)?
Рис. 4. К задаче №2
Запишем краткое условие задачи и переведем все единицы измерения в систему СИ (рис. 5).
Рис. 5. Краткое условие задачи №2
Для вычисления работы необходимо знать расстояние, пройденное телом. В условии задачи дана скорость движения трактора и время движения, поэтому воспользуемся формулой
которую подставим в выражение для работы и получим рабочую формулу
Подстановка данных из условия задачи дает
Рис. 6. Полное решение задачи №2
6. Полное решение задачи №2
Задача №3
Найдем работу силы тяжести при падении грузика.
Для решения задачи нам потребуется линейка и сам грузик. Измерим высоту, с которой будет падать грузик. Получаем 1 м. Масса грузика написана на нем самом и равна 100 г. Поднимем грузик на указанную высоту и отпустим его.
Краткое условие задачи будет выглядеть так (рис. 7):
Рис. 7. Краткое условие задачи №3
Для нахождения работы выразим силу тяжести через массу тела , и учтем, что расстояние, пройденное телом, равно высоте, с которой оно упало: .
Тогда
Подстановка чисел дает
Рис. 8. Полное решение задачи №3
Теперь у нас есть представление о том, насколько велика работа в 1 джоуль. Такая работа совершается при падении грузика массой 100 г со стола высотой 1 м.
Переходим к решению более сложных задач.
Задача №4
Со дна реки глубиной 4 м поднимают камень объемом 0,6 м3 на поверхность. Плотность камня 2500 кг/м3, плотность воды 1000 кг/м3. Найти работу по подъему камня.
Плотность камня 2500 кг/м3, плотность воды 1000 кг/м3. Найти работу по подъему камня.
Для решения задачи необходимо не только записать краткое условие задачи, но и сделать схематический рисунок и показать силы, действующие на камень. Это сила тяги Fт (работу именно этой силы мы будем находить), сила тяжести mg и сила Архимеда Fa. Кроме того, покажем высоту, на которую сила тяги перемещает камень (рис. 9).
Рис. 9. К решению задачи №4
Как видно из рисунка, искомая работа равна .
Для нахождения силы тяги воспользуемся условием равновесия тела: если оно неподвижно или движется с постоянной скоростью, то равнодействующая всех сил, приложенных к нему, равна нулю.
, откуда .
Массу камня выразим через плотность камня и его объем, а силу Архимеда – через плотность воды и объем погруженной части камня (в этом задаче он равен объему всего камня). Объем камня и ускорение выносим за скобки.
Остается подставить силу тяги в формулу для вычисления работы
Поскольку рабочая формула получилась более сложной, единицы измерения результата определим отдельно от расчета его численного значения.
Рис. 10. Полное решение задачи №4
Задача №5
Поршень двигателя перемещается на 20 см под давлением 800 кПа. Определите работу, совершаемую двигателем за один ход поршня, если площадь поршня 150 см2 (рис. 11).
Рис. 11. К задаче №5
Запишем краткое условие и выразим все единицы в системе СИ (рис. 12).
Рис. 12. Краткое условие задачи №5
В данной задаче работу выполняет сила давления газа в цилиндре двигателя. Для нахождения этой силы необходимо давление в цилиндре умножить на площадь поршня. Расстояние, пройденное поршнем, мы обозначили буквой l.
Единицы измерения результата:
Численное значение результата:
Рис. 13. Полное решение задачи №5
13. Полное решение задачи №5
Задача №6
Найти КПД (коэффициент полезного действия) наклонной плоскости (экспериментальная) (рис. 14).
Рис. 14. Груз поднимают вверх по наклонной плоскости
Поднимая груз по наклонной плоскости с помощью динамометра, измерим силу, которая для этого требуется. Она оказывается равной 2,2 Н. Расстояние, пройденное грузом вдоль плоскости, измеряем рулеткой. Оно составило 0,5 м. При этом груз поднялся над столом на высоту 20 см. Кроме того, известны масса бруска, равная 50 г, и общая масса трех поднимаемых грузов – 300 г.
Полученные опытные данные занесем в краткое условие задачи, выразим все величины в единицах системы СИ и сделаем схематический рисунок измерительной установки (рис. 15).
Рис. 15. Краткое условие задачи №6
Коэффициентом полезного действия механизма называется физическая величина, равная отношению полезной работы, совершенной механизмом, к работе, затраченной для приведения его в действие.
КПД также обозначают греческой буквой η (эта) и часто выражают в процентах.
В нашем случае механизмом является наклонная плоскость.
Полезная работа – эта работа, которую нужно совершить, чтобы поднять тело на высоту h.
Затраченная работа совершается силой тяги, то есть силой упругости пружины динамометра.
Тогда КПД равен
Определяем единицы измерения КПД
Такой результат означает, что КПД является безразмерной величиной (просто число без единиц измерения).
Его числовое значение
Обратите внимание, что коэффициент полезного действия не может быть больше единицы, поскольку полезная работа всегда меньше затраченной. Если у вас получилось наоборот, значит, либо при измерениях, либо в ходе вычислений допущена ошибка.
Рис. 16. Полное решение задачи №6
Задача №7
Трактор равномерно тянет плуг, прилагая силу в 10 кН. За 10 мин он проходит путь 1,2 км. Определить мощность, развиваемую трактором (рис. 17).
За 10 мин он проходит путь 1,2 км. Определить мощность, развиваемую трактором (рис. 17).
Рис. 17. К условию задачи №7
Запись краткого условия и перевод величин в систему СИ будет выглядеть так (рис. 18):
Рис. 18. Краткое условие задачи №7
Для нахождения мощности нужно работу, выполненную трактором, разделить на время ее выполнения. Работа вычисляется как произведение силы тяги трактора на пройденное трактором расстояние. Таким образом, получаем:
Рис. 19. Полное решение задачи №7
Задача №8
Поезд массой 600 тонн равномерно движется со скоростью 36 км/ч. Определить развиваемую тепловозом мощность, если сила трения составляет 0,002 веса поезда.
Рис. 20. К условию задачи №8
Запишем краткое условие задачи, выразим величины в единицах системы СИ, сделаем рисунок, на котором покажем силу тяги тепловоза и силу трения (рис. 21).
21).
Рис. 21. Краткое условие задачи №8
Поскольку по условию задачи скорость поезда не изменяется и равна 36 км/ч, сила тяги равна силе трения Вес в случае движения с постоянной скоростью равен силе тяжести Тогда сила тяги равна
Для вычисления мощности воспользуемся формулой откуда
Подстановка данных из условия дает
Рис. 22. Полное решение задачи №8
Список литературы
- Перышкин А. В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
- Перышкин А. В. Сборник задач по физике, 7–9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.
- Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7–9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.
Домашнее задание
- Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7–9 классов №675–683, 706–712.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Единая коллекция Цифровых Образовательных Ресурсов (Источник)
- Единая коллекция Цифровых Образовательных Ресурсов (Источник)
Что такое тяга, трение и сцепление с дорогой?
Независимо от того, управляете ли вы маленьким картингом или тяжелым самосвалом, вам необходимо иметь сцепление с дорогой, чтобы двигаться вперед. На самом деле, вы даже не можете ходить без него. Слово «тяга» часто используется, и многие считают, что это просто еще одно слово, обозначающее трение. Но так ли это на самом деле? Давайте подробнее рассмотрим трение и сцепление — что это такое и почему это так важно для безопасного вождения.
На самом деле, вы даже не можете ходить без него. Слово «тяга» часто используется, и многие считают, что это просто еще одно слово, обозначающее трение. Но так ли это на самом деле? Давайте подробнее рассмотрим трение и сцепление — что это такое и почему это так важно для безопасного вождения.
Всем нам знакомо чувство, когда шины теряют сцепление с дорогой и автомобиль начинает заносить. Контролируемое заносы на картинге могут быть забавными, но неожиданное заносы тяжелого автомобиля на дороге могут привести к очень опасной ситуации. Занос происходит из-за того, что автомобиль теряет сцепление с дорогой, и, очевидно, это связано с шинами и дорожным покрытием.
Во-первых, давайте углубимся в физику трения и добавим немного резины и асфальта. Трение как таковое не двигает автомобиль вперед. Трение — это сила сопротивления , которая сопротивляется относительному движению двух поверхностей. Проще говоря, при движении двигатель создает усилие на ведущие колеса, которое двигает автомобиль вперед.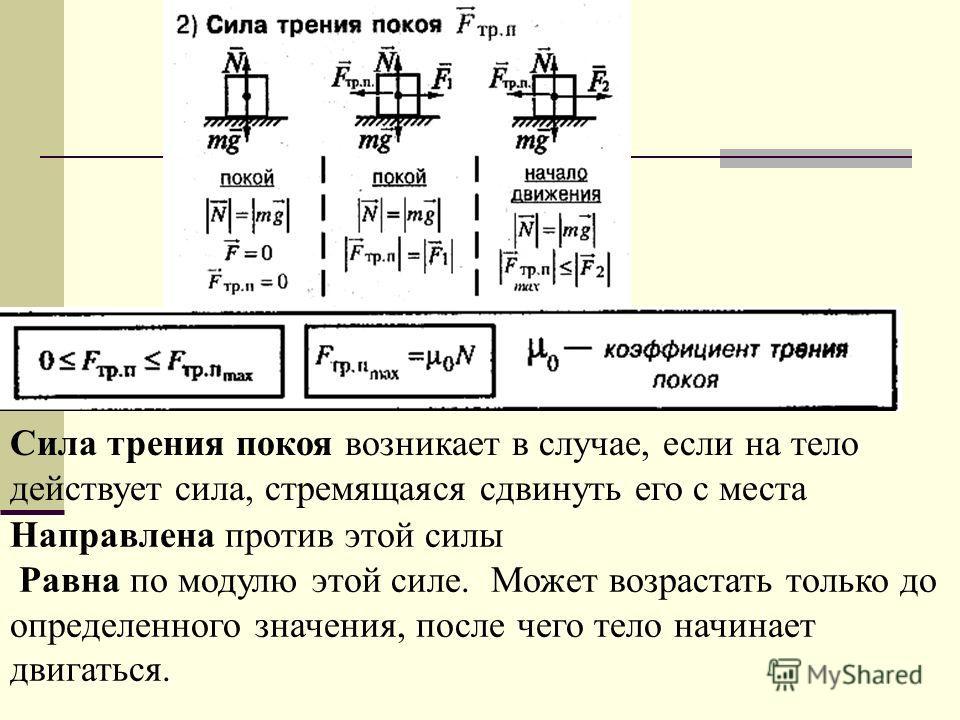 Трение – это сила, препятствующая скольжению резины шины по дорожному покрытию. Однако на самом деле все не так просто — нам нужно рассмотреть два разных трения; статическое и кинетическое трение.
Трение – это сила, препятствующая скольжению резины шины по дорожному покрытию. Однако на самом деле все не так просто — нам нужно рассмотреть два разных трения; статическое и кинетическое трение.
Статическое трение – сила трения между поверхностями, которые НЕ движутся относительно друг друга.
Кинетическое трение – сила трения между поверхностями, которые движутся относительно друг друга.
Но когда колеса катятся, разве это не кинетическое трение? Нет. При движении по сухой дороге, независимо от скорости автомобиля, статическое трение удерживает автомобиль на курсе. Если вы посмотрите на это в микроскоп — и в очень замедленной съемке — пятно контакта шины не двигается относительно дорожного покрытия. Просто постоянно новые части шины соприкасаются с дорогой, когда колесо катится.
Трение имеет решающее значение для маневрирования автомобиля Теперь вы знаете, что статическое трение удерживает автомобиль на правильном курсе при движении с постоянной скоростью. Но есть и другие ситуации, когда трение имеет основополагающее значение для того, чтобы заставить автомобиль вести себя так, как вы хотите:
Но есть и другие ситуации, когда трение имеет основополагающее значение для того, чтобы заставить автомобиль вести себя так, как вы хотите:
- При ускорении
- Когда тебе исполнится
- При торможении
В таких ситуациях очень важно, чтобы статическая сила трения превышала другие силы, например, кинетической энергии, которая может вывести автомобиль из-под контроля. В противном случае вы потеряете сцепление с дорогой. Итак, что повлияет на ваше сцепление с дорогой?
Сцепление с дорогой представляет собой сумму переменныхНа самом деле существует несколько факторов, влияющих на сцепление с дорогой. Некоторые из них являются критическими.
- Материал контактирующих поверхностей, т.е. качество резины и материал дорожного покрытия.
- Текстура этих материалов, то есть чем грубее текстура, тем лучше сцепление с дорогой.
- Сила, прижимающая поверхности друг к другу, т. е. вес автомобиля.

- Другие материалы между контактными поверхностями, напр. водой, льдом, гравием или разливом нефти.
В типичной дорожной ситуации первые три фактора довольно постоянны; наша машина имеет определенный вес и определенные шины, и мы едем по длинной дороге. Соответственно, мы адаптируем наш стиль вождения к этим заданным факторам. Но вдруг может пойти сильный дождь, и все изменится…
Статика может стать кинетикойВ определенных условиях между шиной и поверхностью дороги может появиться что-то другое, например, дождевая вода. Вода действует как смазка между резиной и асфальтом, в результате чего снижается статическое трение. Хуже того, дорога может быть ледяной.
Если при ускорении на льду приложенная сила (движущая сила на колесах) превышает трение покоя, колеса теряют сцепление с дорогой и начинают пробуксовывать.
Если при повороте или повороте центробежная сила превышает статическую силу трения, колеса теряют сцепление с дорогой, а кинетическая энергия заставляет автомобиль двигаться прямо вперед, несмотря на то, что вы поворачиваете рулевое колесо.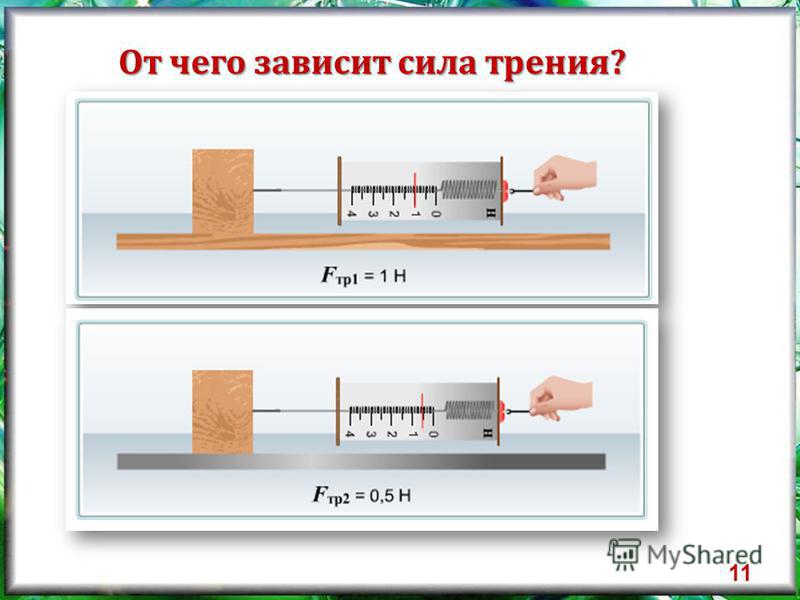
На самом деле здесь происходит то, что когда статическое трение превышено, начинает действовать другое трение; кинетическое трение, также известное как динамическое трение или трение скольжения. Транспортное средство будет скользить до тех пор, пока это кинетическое трение не заставит его остановиться.
В случае вращающихся колес они будут вращаться до тех пор, пока статическая сила трения не превысит кинетическую силу трения (достигается дросселированием) – тогда шины будут сцепляться.
Коэффициент тренияНасколько далеко будет скользить автомобиль и насколько скользкой будет дорога, определяется коэффициентом трения.
Различные материалы и текстуры обеспечивают разное трение. Коэффициент трения является мерой того, какое трение обеспечивает материал или текстура. Этот коэффициент пригодится ученым при разработке новых материалов для шин и дорожных покрытий, но для обычного водителя достаточно сделать вывод, что желательно высокое трение — оно устойчиво удерживает нас на дороге.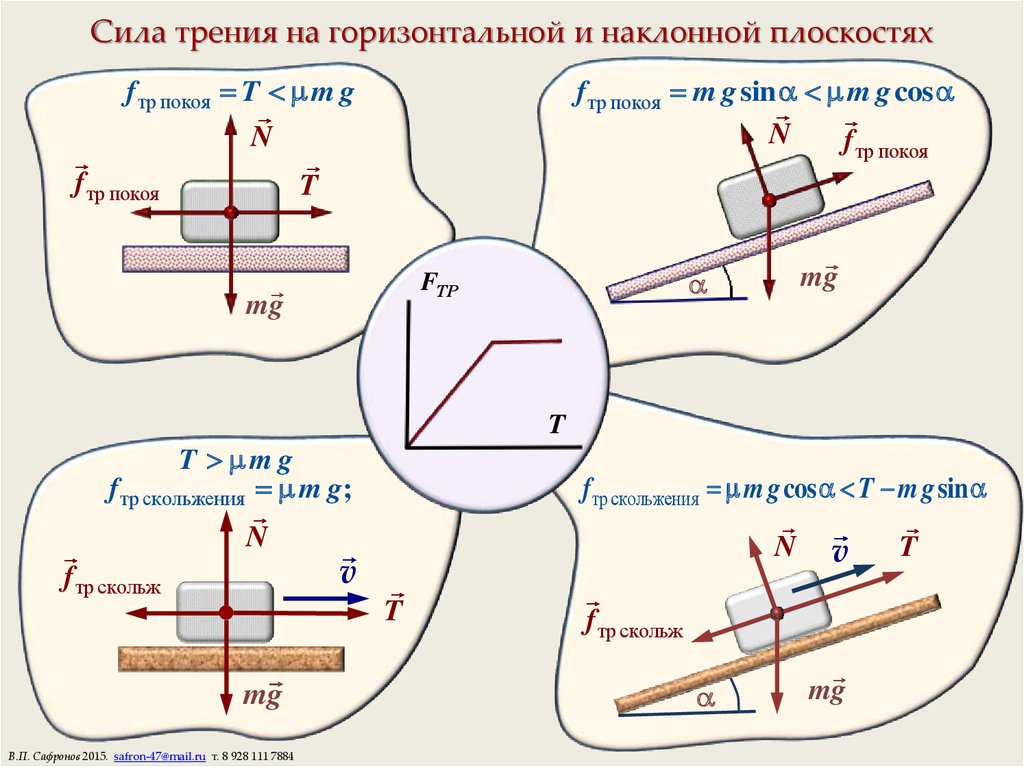
Хотя трение является общим физическим выражением, транспортное средство сцепление можно определить как трение между ведущим колесом и поверхностью дороги.
“ тяга – трение между ведущим колесом и поверхностью дороги. Если вы теряете сцепление с дорогой, вы теряете сцепление с дорогой».
Теперь вы знаете, что все сводится к трению. Вы также понимаете, что тягу как таковую нельзя увеличить с помощью электронных систем. Чтобы действительно увеличить сцепление, вам нужно физически ввести под шины что-то с более высоким коэффициентом трения. Собственно, это то, что вы делаете, когда шлифуете обледенелую дорогу или используете цепи противоскольжения — вы увеличиваете коэффициент трения. В конце концов, все дело в трении в этой небольшой области контакта между шиной и дорогой — и все это чистая физика.
Если ваше транспортное средство потеряло сцепление с дорогой, крайне важно восстановить его.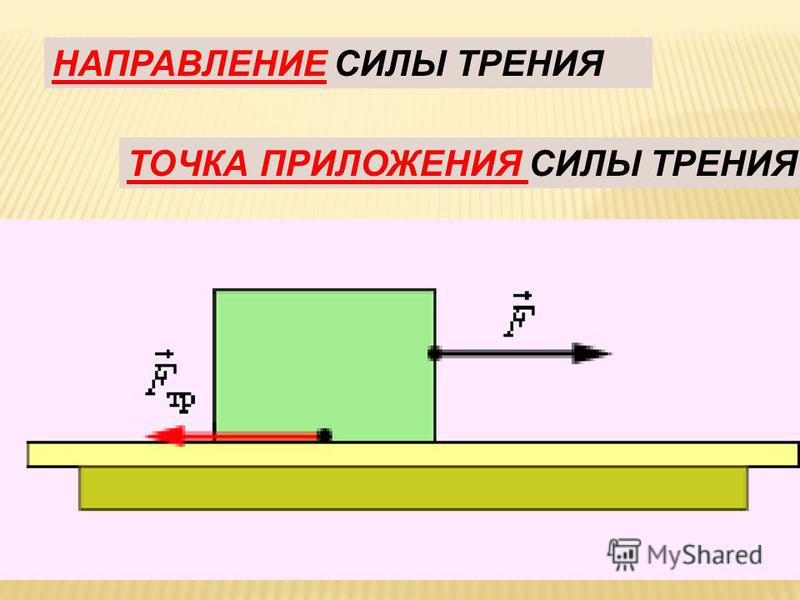 Ознакомьтесь с нашим руководством по основам тяги грузовых автомобилей «The Case for Onspot».
Ознакомьтесь с нашим руководством по основам тяги грузовых автомобилей «The Case for Onspot».
Загрузите наше руководство и узнайте, как повысить эффективность вождения на обледенелых дорогах.
Просмотрите наш бесплатный онлайн-ресурс Тяговые средства для тяжелых транспортных средств, чтобы узнать больше.
Ньютоновская механика — Статическое трение — Единственное, что может ускорить поезд?
спросил
Изменено 7 лет, 5 месяцев назад
Просмотрено 8к раз
$\begingroup$
Я компьютерный программист, который никогда не изучал физику в школе, и теперь она возвращается ко мне, чтобы немного укусить меня в некоторых вещах, которые меня просят программировать.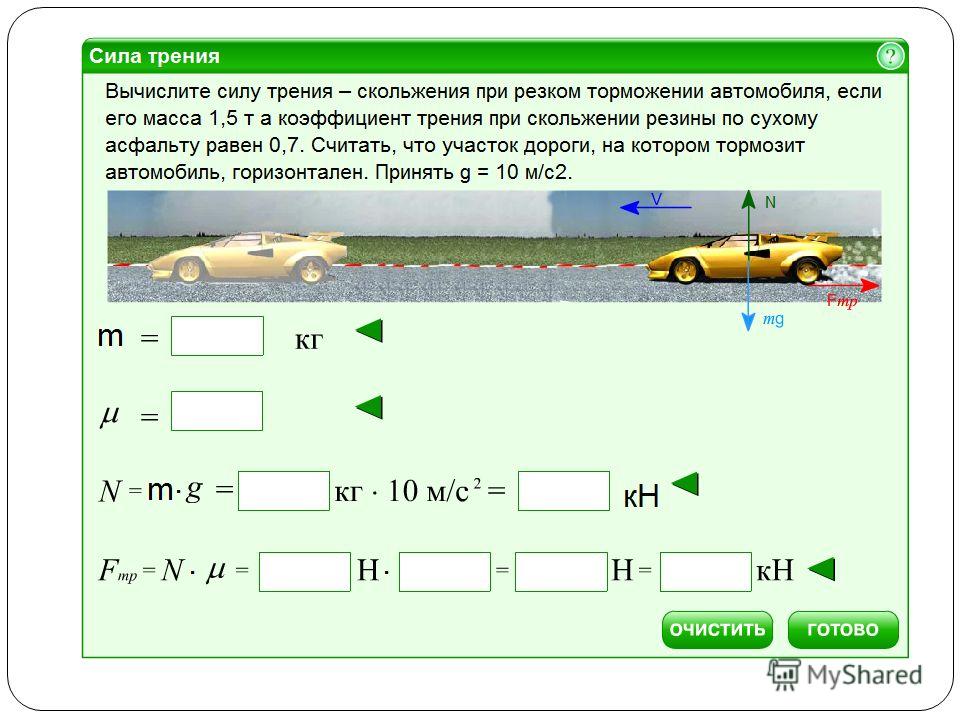 Я пытаюсь самостоятельно изучить физику, и у меня есть несколько вводных книг по физике с открытым исходным кодом, и я понимаю ее по большей части, но я немного сбит с толку этим утверждением, на которое я наткнулся в разделе о статическом трении.
Я пытаюсь самостоятельно изучить физику, и у меня есть несколько вводных книг по физике с открытым исходным кодом, и я понимаю ее по большей части, но я немного сбит с толку этим утверждением, на которое я наткнулся в разделе о статическом трении.
Формула статического трения уже прошлась и так далее. Он попадает в раздел, объясняющий, что вес поезда увеличивает статическое трение между колесами и гусеницами. Хорошо, имеет смысл. Но потом пишет так:
Причина, по которой локомотивы делаются такими тяжелыми, заключается в тяге. Восходящая нормальная сила рельсов на колесах, FN, компенсирует нисходящая сила тяжести, FW, поэтому игнорируя плюс и минус знаков, эти две силы равны по абсолютной величине, FN = FW. Учитывая это количество нормальной силы, максимальная сила статического трение равно Fs = sFN = sFW. Эта статическая сила трения, рельсы толкают колеса вперед, это единственная сила, которая может ускорить поезд, тянуть его в гору или компенсировать силу воздуха сопротивления при движении с постоянной скоростью.Коэффициент статическое трение стали о сталь составляет около 1/4, поэтому ни один локомотив не может тянуть с силой, превышающей примерно 1/4 собственного веса. Если двигатель способен развивать большее усилие, т. результатом будет просто нарушение статического трения и вращение колес.
— «Ньютоновская физика», Свет и материя — Книга 1, стр. 158 Б. Кроуэлл http://www.lightandmatter.com/bk1.pdf
Я не понимаю, почему только трение покоя может двигать поезд вперед. Я думал, что именно статическое трение удерживает его на месте в первую очередь. Есть еще одна сила, название которой я не могу вспомнить, но я где-то слышал, и я думал, что это больше похоже на то, что они описывают здесь, когда вес колес слегка давит вниз и вперед на гусеницы, вызывая гусеницы отодвинуть вверх и вперед (с противоположной стороны).
Кто-нибудь может мне объяснить, что это значит?
- ньютоновская механика
- трение
- кинематика
$\endgroup$
$\begingroup$
Это сложный (и запутанный, или просто запутанный) способ сказать, что если вы хотите, чтобы локомотив тянул поезд, вы не хотите, чтобы его колеса скользили. Именно трение предотвращает проскальзывание колес.
Именно трение предотвращает проскальзывание колес.
Я предлагаю вам просто удалить это предложение:
Эта статическая сила трения рельсов, толкающих колеса вперед, является единственной силой, которая может ускорить поезд, тянуть его в гору или нейтрализовать силу сопротивления воздуха при движении с постоянной скоростью.
Абзац без него имеет больше смысла. Автор пытается добраться до третьего закона Ньютона (равная и противоположная реакция), но такая формулировка дает больше путаницы, чем понимания.
$\endgroup$
5
$\begingroup$
Здесь вам нужно подумать о том, что колеса катятся .
Если бы не было трения между колесами и гусеницей, то при запуске локомотива его ведущее колесо просто пробуксовывало бы.
Трение предотвращает или препятствует относительному движению между двумя поверхностями. Итак, если на колеса действует крутящий момент, а точка контакта не может двигаться относительно рельса (именно там, где она касается) из-за статического трения, колесо может вращаться только тогда, когда поезд движется относительно колеса.
Итак, если на колеса действует крутящий момент, а точка контакта не может двигаться относительно рельса (именно там, где она касается) из-за статического трения, колесо может вращаться только тогда, когда поезд движется относительно колеса.
$\endgroup$
6
$\begingroup$
Возникает вопрос, что вы пытаетесь узнать о трении из этого запутанного примера. Что может немного сбить с толку, так это то, что существует два типа трения : статическое трение и кинетическое трение . Кинетическое трение — это трение, связанное со скольжением двух тел друг о друга, что может происходить только тогда, когда одно движется относительно другого. Следовательно, кинетическое трение связано с движением. Статическое трение — это трение, связанное с удержанием объекта в неподвижном состоянии. Однако, когда кто-то рассматривает движение катящегося колеса, трение катящегося колеса является статическим трением, несмотря на движение колеса, потому что колесо на самом деле никогда не скользит по дорожке (или, по крайней мере, не должно).
Сила, которую вы ищете в последнем абзаце, называется «Обычная сила». Посмотрите статью в Википедии о трении, если это поможет, так как она дает больше уравнений и диаграмм.
РЕДАКТИРОВАТЬ (после комментария ниже) Из исходного вопроса и комментариев видно, что дополнительным компонентом этого вопроса было лучшее понимание более сложного случая упругой деформации. Чтобы понять это, рассмотрим массивный предмет на пружинящем матраце: тогда в материале возникнет U- или V-образная деформация. Моделирование этого потребует некоторой математики, и закон Гука (F=-kx) покажется наиболее подходящим приближением. Теперь, если этот объект двигался вперед с некоторой скоростью v, то соответствующая деформация также будет двигаться с этой скоростью. Также было бы необходимо смоделировать поверхностное натяжение материала (которое может разорваться, если напряжение будет слишком большим). В совокупности все это вызовет опережающие и отстающие деформации (и, возможно, колебания) в материале.
Так как это для компьютерной модели, то мне не ясно, должна ли физика колебаний этого материала быть точно правильной в соответствии с некоторыми специфическими параметрами и уравнениями, или это просто эффект для демонстрации в какой-то компьютерной игре. В любом случае требуется дополнительное моделирование для определения уравнения такого движения на основе вышеизложенных принципов. Если мы имеем дело с движением автомобилей по дорогам или поездов по рельсам, то в этом дополнительном моделировании нет необходимости и такой упругой деформацией можно пренебречь.
$\endgroup$
6
$\begingroup$
Поскольку колеса пытаются катиться, они не могут катиться из-за силы трения, действующей в опп. направлении. Когда сила тяги превышает предельную силу трения, колесо начинает катиться вперед относительно рельсов.
Сила пытается вызвать относительное движение между колесами и рельсами. Поскольку рельсы не могут двигаться назад (из-за трения), колеса должны катиться вперед, чтобы вызвать относительное движение. Трение противодействует вращению колеса до предельного трения.
Поскольку рельсы не могут двигаться назад (из-за трения), колеса должны катиться вперед, чтобы вызвать относительное движение. Трение противодействует вращению колеса до предельного трения.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
3.1: Traction — Engineering LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 46845
- Николас М. Холден, Мэри Ли Вулф, Джэктон Арого Огеджо и Энда Дж. Камминс
- Университетский колледж Дублина и Технологический институт Вирджинии через Инициативу открытого образования Технических библиотек Вирджинии
Даниэль М. Кейрос
Кафедра сельскохозяйственной инженерии
Федеральный университет Викозы
Висоса, Минас-Жерайс, Бразилия
Джон К. Шуллер
Кафедра машиностроения и аэрокосмической техники
Университет Флориды
Гейнсвилл, Флорида, США
| Основные термины |
| Механика тяги | Тяговые устройства | Тракторы |
| Мощность двигателя | Транспортные устройства | Прицепное оборудование |
| Сила тяги |
Переменные
Введение
Тракторы были созданы для сокращения трудозатрат человека и животных и повышения эффективности и производительности растениеводства (Schueller, 2000). В основном тракторы используются для буксировки таких орудий, как почвообрабатывающие орудия, сеялки, культиваторы и комбайны, в поле и, в некоторой степени, на дороге (Renius, 2020). Чтобы эффективно тянуть навесное оборудование, трактор должен создавать сцепление между шинами и поверхностью почвы. Тяга — это способ, которым транспортное средство использует силу для движения по поверхности.
В основном тракторы используются для буксировки таких орудий, как почвообрабатывающие орудия, сеялки, культиваторы и комбайны, в поле и, в некоторой степени, на дороге (Renius, 2020). Чтобы эффективно тянуть навесное оборудование, трактор должен создавать сцепление между шинами и поверхностью почвы. Тяга — это способ, которым транспортное средство использует силу для движения по поверхности.
Уже на раннем этапе разработки тракторов прямая передача мощности от тракторов к орудиям стала возможной благодаря использованию коробок отбора мощности (ВОМ), которые передают мощность вращения на орудия и машины, а также благодаря использованию гидравлических систем для подъема и опускания навесного оборудования и перемещения части навесных машин. Тяговое орудие по-прежнему является наиболее распространенным применением мощности трактора. Полевая производительность сельскохозяйственных машин, т. е. площадь поля, которую можно обработать в единицу времени, обусловила разработку и применение более крупных орудий. Увеличенные размеры требуют большей тяги от тянущего трактора. Необходимы более эффективные системы для создания тягового усилия, чтобы обеспечить большие силы, необходимые для тяги этих орудий.
Увеличенные размеры требуют большей тяги от тянущего трактора. Необходимы более эффективные системы для создания тягового усилия, чтобы обеспечить большие силы, необходимые для тяги этих орудий.
Эффективность того, как тракторы преобразуют мощность, вырабатываемую двигателем, в мощность, необходимую для тяги навесного оборудования, зависит от многих переменных, связанных с трактором и состоянием почвы. Тяга особенно важна в сельском хозяйстве, так как полевые почвы не такие твердые, как дороги, по которым ездят легковые и грузовые автомобили. В этой главе представлены основные принципы тяги, применяемые к сельскохозяйственным машинам.
Результаты
Прочитав эту главу, вы сможете:
- • Объясните, как тракторы развивают тяговое усилие
- • Опишите влияние некоторых важных переменных на тяговое усилие
- • Рассчитайте, какую мощность трактор может развить при буксировке навесного оборудования
- • Рассчитайте требуемую мощность для согласования тракторов с навесным оборудованием
Концепции
Тяговые и транспортные устройства
Согласно Американскому обществу инженеров-агрономов и биологических инженеров (стандарты ASABE, 2018 г. ), существует два типа устройств поверхностного контакта, связанных с движением транспортного средства: тяговые устройства и транспортные устройства. Тяговое устройство получает мощность от двигателя и использует реакции сил опорной поверхности для движения транспортного средства, в то время как транспортное устройство не получает мощности, но необходимо для поддержания транспортного средства на поверхности при движении транспортного средства по этой поверхности. . Колеса, шины и гусеницы могут быть тяговыми устройствами, если они подключены к двигателю или другому источнику энергии; если они не подключены, они являются транспортными устройствами. Основные узлы сельскохозяйственного трактора представлены на рис. 3.1.1. В данном примере трактор двухколесный, поэтому большие задние колеса, получающие мощность от двигателя, являются тяговыми устройствами, а малые передние колеса — транспортными. Все колеса были бы тяговыми устройствами, если бы трактор был полноприводным. Двигатель соединен с тяговым устройством трансмиссией, часто состоящей из сцепления, трансмиссии, дифференциала, осей и других компонентов.
), существует два типа устройств поверхностного контакта, связанных с движением транспортного средства: тяговые устройства и транспортные устройства. Тяговое устройство получает мощность от двигателя и использует реакции сил опорной поверхности для движения транспортного средства, в то время как транспортное устройство не получает мощности, но необходимо для поддержания транспортного средства на поверхности при движении транспортного средства по этой поверхности. . Колеса, шины и гусеницы могут быть тяговыми устройствами, если они подключены к двигателю или другому источнику энергии; если они не подключены, они являются транспортными устройствами. Основные узлы сельскохозяйственного трактора представлены на рис. 3.1.1. В данном примере трактор двухколесный, поэтому большие задние колеса, получающие мощность от двигателя, являются тяговыми устройствами, а малые передние колеса — транспортными. Все колеса были бы тяговыми устройствами, если бы трактор был полноприводным. Двигатель соединен с тяговым устройством трансмиссией, часто состоящей из сцепления, трансмиссии, дифференциала, осей и других компонентов. (Привод в этой главе не рассматривается.) Дышло — это точка крепления, через которую трактор может передавать тяговое усилие на навесное оборудование.
(Привод в этой главе не рассматривается.) Дышло — это точка крепления, через которую трактор может передавать тяговое усилие на навесное оборудование.
Механика тяги
Самый простой способ анализа силы тяги, создаваемой тяговым устройством, таким как колесо или гусеница, заключается в рассмотрении сил трения, действующих при контакте тягового устройства с поверхностью, когда система находится в равновесии. Для упрощения предполагается, что машина движется с постоянной скоростью по неизменной поверхности (рис. 3.1.2). Тяговое устройство (далее упрощенное до наиболее распространенного варианта «колесо») имеет две основные функции: воспринимать нагрузку, действующую на ось колеса ( W ) и для создания чистой тяговой силы ( H ). Силу Вт обычно называют динамической нагрузкой, действующей на колесо. Динамическая нагрузка зависит от того, как вес трактора в этот момент времени распределяется на каждое колесо. Если система находится в равновесии, поверхность реагирует на W приложением к колесу вертикальной силы реакции ( R ). При контакте поверхности с колесом возникает сила трения ( F f ) генерируется. Чтобы сохранить равновесие в горизонтальном направлении, величина чистой силы тяги H равна величине силы трения F f . Чтобы создать результирующую силу тяги H , необходимо преодолеть силу трения. Это делается приложением крутящего момента ( T ) к оси колеса. Этот крутящий момент пропорционален крутящему моменту, создаваемому двигателем трактора в соответствии с трансмиссией, включая текущее передаточное число.
Если система находится в равновесии, поверхность реагирует на W приложением к колесу вертикальной силы реакции ( R ). При контакте поверхности с колесом возникает сила трения ( F f ) генерируется. Чтобы сохранить равновесие в горизонтальном направлении, величина чистой силы тяги H равна величине силы трения F f . Чтобы создать результирующую силу тяги H , необходимо преодолеть силу трения. Это делается приложением крутящего момента ( T ) к оси колеса. Этот крутящий момент пропорционален крутящему моменту, создаваемому двигателем трактора в соответствии с трансмиссией, включая текущее передаточное число.
ω = угловая скорость колеса
F f = сила трения
H = чистая тяговая сила
R = вертикальная сила реакции колеса
T = крутящий момент передается на ось колеса
v a = фактическая скорость колеса
Вт = динамическая нагрузка на колесо
При движении колесо (рисунок 3. 1.2) вращается с постоянной угловой скоростью ( ω ), причем эта угловая скорость пропорциональна скорости вращения двигателя и зависит от передаточного отношения в трансмиссии. Колесо имеет фактическую скорость v a , что равно угловой скорости, умноженной на радиус качения колеса, уменьшенный на проскальзывание (как обсуждается ниже). В равновесной ситуации ω и v и являются константами. Мощность, передаваемая на ось колеса ( P w ), может быть рассчитана как произведение крутящего момента ( T ) и угловой скорости ( ω ), как показано в уравнении 3.1.1. Тяговая мощность, развиваемая колесом ( P t ), является произведением чистой тяговой силы ( H ) и фактической скорости ( v a ), как показано в уравнении 3.1.2. Тяговый КПД колеса ( T E ) можно рассчитать как отношение тяговой мощности к мощности оси колеса, как показано в уравнении 3.
1.2) вращается с постоянной угловой скоростью ( ω ), причем эта угловая скорость пропорциональна скорости вращения двигателя и зависит от передаточного отношения в трансмиссии. Колесо имеет фактическую скорость v a , что равно угловой скорости, умноженной на радиус качения колеса, уменьшенный на проскальзывание (как обсуждается ниже). В равновесной ситуации ω и v и являются константами. Мощность, передаваемая на ось колеса ( P w ), может быть рассчитана как произведение крутящего момента ( T ) и угловой скорости ( ω ), как показано в уравнении 3.1.1. Тяговая мощность, развиваемая колесом ( P t ), является произведением чистой тяговой силы ( H ) и фактической скорости ( v a ), как показано в уравнении 3.1.2. Тяговый КПД колеса ( T E ) можно рассчитать как отношение тяговой мощности к мощности оси колеса, как показано в уравнении 3. 1.3.
1.3.
\[ P_{W}=T\omega \]
\[ P_{t}=H\nu_{a} \]
\[ T_{E}=\frac{P_{t}}{P_ {W}} \]
где P w = мощность, передаваемая на ось колеса (Вт)
T = крутящий момент, передаваемый на ось колеса (Н·м)
ω = угловая скорость колесо (рад с −1 )
P t = тяговая мощность, развиваемая колесом (Вт)
H = чистая тяговая сила (Н)
v a = фактическая скорость колеса )
T E = тяговое усилие колеса (безразмерное)
Сила трения ( F f на рис. 3.1.2) создается за счет взаимодействия колеса с поверхностью. Силу трения можно рассчитать, умножив силу реакции ( R ) на эквивалентный коэффициент трения ( μ ). В таблице 3.1.1 представлены некоторые типичные значения. Поскольку R равно динамической нагрузке, действующей на ось колеса ( W ), а чистая тяговая сила равна силе трения, тяговую силу можно рассчитать как произведение эквивалентного коэффициента трения и динамической нагрузка, как:
| Тип поверхности | Эквивалентный коэффициент трения ( μ )[a] |
|---|---|
Мягкий грунт | 0,26–0,31 |
Средний грунт | 0,40–0,46 |
Твердая почва | 0,43–0,53 |
Бетон | 0,91–0,98 |
[a] Эти значения были оценены на основе данных, представленных Kolator and Bialobrzewski (2011).
\[ H= \mu W \]
где μ = коэффициент трения (безразмерный).
Теоретическая скорость ( v t ) определяется скоростью вращения колеса ( ω ), умноженной на радиус качения ( r ), как показано в уравнении 3.1.5, но фактическая скорость колеса ( v a ) меньше из-за относительного движения на границе раздела между колесом и поверхностью. Это относительное движение является коэффициентом уменьшения хода, обычно называемым проскальзыванием, и определяется как отношение потери скорости колеса к теоретической скорости, то есть скорости, которую колесо имело бы, если бы не было потери. Уравнение 3.1.6 показывает, как можно оценить коэффициент уменьшения хода:
\[ \nu_{t} = \omega r \]
\[ s= \frac{\nu_{t}-\nu_{a}}{\nu_{t}} \]
, где v t = теоретическая скорость колеса (м с −1 )
r = радиус качения колеса (м с −1 )
s 90men, = коэффициент уменьшения хода Коэффициент уменьшения хода является важной переменной для анализа тягового усилия колес. Коэффициент уменьшения хода колеса может варьироваться от 0 до 1 в зависимости от состояния колеса и поверхности. Когда коэффициент уменьшения хода равен 0, относительное движение между периферией колеса и поверхностью отсутствует. Вращение колеса вызывает совершенное поступательное движение относительно поверхности. Однако опыт показал, что для того, чтобы колесо развивало тяговое усилие, должно быть относительное движение (скольжение) между колесом и поверхностью. Следовательно, колесо, создающее тяговое усилие, должно иметь передаточное отношение уменьшения хода больше нуля. Когда колесо создает большее тяговое усилие, коэффициент уменьшения хода увеличивается, а фактическая скорость колеса уменьшается. Когда коэффициент уменьшения хода равен 1, колесо не движется вперед при вращении. В моделях, используемых для расчета тяговой силы, в качестве одной из переменных обычно используется коэффициент уменьшения хода.
Коэффициент уменьшения хода колеса может варьироваться от 0 до 1 в зависимости от состояния колеса и поверхности. Когда коэффициент уменьшения хода равен 0, относительное движение между периферией колеса и поверхностью отсутствует. Вращение колеса вызывает совершенное поступательное движение относительно поверхности. Однако опыт показал, что для того, чтобы колесо развивало тяговое усилие, должно быть относительное движение (скольжение) между колесом и поверхностью. Следовательно, колесо, создающее тяговое усилие, должно иметь передаточное отношение уменьшения хода больше нуля. Когда колесо создает большее тяговое усилие, коэффициент уменьшения хода увеличивается, а фактическая скорость колеса уменьшается. Когда коэффициент уменьшения хода равен 1, колесо не движется вперед при вращении. В моделях, используемых для расчета тяговой силы, в качестве одной из переменных обычно используется коэффициент уменьшения хода.
ω = угловая скорость колеса
F = полная тяговая сила
H = чистая тяговая сила
R = вертикальная сила реакции колеса
r = радиус качения
T = крутящий момент передается на колесо
F r = сила сопротивления движению
v a = фактическая скорость колеса
Вт = динамическая нагрузка на колесо
Еще одним важным понятием при анализе процесса тяги движущегося колеса является сила сопротивления движению ( F r ) (рис. 3.1.3). Если колесо движется, колесо и поверхность деформируются. На эту деформацию тратится энергия. Сопротивление, создаваемое колесом, и деформации поверхности должны быть преодолены, чтобы колесо могло двигаться. Учитывая существование силы сопротивления движению, в контакте колеса с поверхностью необходимо создать силу трения большую, чем сила сопротивления движению в контакте колеса с поверхностью, чтобы создать тяговое усилие. Эта сила трения теперь называется общей силой тяги (обозначается 9).0346 Ф ). Таким образом, полная тяговая сила была бы чистой тяговой силой, создаваемой колесом, если бы не было сопротивления движению. Добавление понятий сопротивления движению и общей тяговой силы к рисунку 3.1.2 приводит к рисунку 3.1.3, который является улучшенным представлением сил, действующих на колесо.
3.1.3). Если колесо движется, колесо и поверхность деформируются. На эту деформацию тратится энергия. Сопротивление, создаваемое колесом, и деформации поверхности должны быть преодолены, чтобы колесо могло двигаться. Учитывая существование силы сопротивления движению, в контакте колеса с поверхностью необходимо создать силу трения большую, чем сила сопротивления движению в контакте колеса с поверхностью, чтобы создать тяговое усилие. Эта сила трения теперь называется общей силой тяги (обозначается 9).0346 Ф ). Таким образом, полная тяговая сила была бы чистой тяговой силой, создаваемой колесом, если бы не было сопротивления движению. Добавление понятий сопротивления движению и общей тяговой силы к рисунку 3.1.2 приводит к рисунку 3.1.3, который является улучшенным представлением сил, действующих на колесо.

Если колесо, представленное на рисунке 3.1.3, не движется в вертикальном направлении (ось z), то колесо находится в статическом равновесии в этом направлении. В этом состоянии сумма сил в направлении z (вертикальном) равна нулю. Следовательно,
\[ \sum F_{z} = 0 \]
\[ R-W=0 \]
\[ R=W \]
где F z = любая сила, приложенная к колесу в направлении z (Н)
R = вертикальная сила реакции колеса (Н)
Если фактическая скорость колеса, представленного на рис. 3.1.3, постоянна, то горизонтальные силы находятся в статическом равновесии в этом направлении и сумма горизонтальных сил равна нулю. Следовательно,
\[ \sum F_{x}=0 \]
где F x = любая сила, приложенная к колесу в направлении x (Н)
F = полная тяговая сила (Н)
F r = сила сопротивления движению (Н)
Исходя из уравнения 3.1.12, общая тяговая сила ( F ) должна быть чистой тяговой силой ( H ) плюс сила сопротивления движению ( F r ). Если обе части уравнения 3.1.12 разделить на динамическую нагрузку ( W ), действующую на колесо, то в уравнении 3.1.13 получится три безразмерных числа, т. е. , и ρ , создаются, как показано в уравнениях 3.1.15, 3.1.16 и 3.1.17. Первый – чистое передаточное отношение (μ N ), определяется как чистая тяговая сила, деленная на динамическую нагрузку. Второй — это общий коэффициент тяги ( μ г ), определяемый как общая тяговая сила, деленная на динамическую нагрузку. И третье — это коэффициент сопротивления движению ( μ ), определяемый как сила сопротивления движению, деленная на динамическую нагрузку.
Если обе части уравнения 3.1.12 разделить на динамическую нагрузку ( W ), действующую на колесо, то в уравнении 3.1.13 получится три безразмерных числа, т. е. , и ρ , создаются, как показано в уравнениях 3.1.15, 3.1.16 и 3.1.17. Первый – чистое передаточное отношение (μ N ), определяется как чистая тяговая сила, деленная на динамическую нагрузку. Второй — это общий коэффициент тяги ( μ г ), определяемый как общая тяговая сила, деленная на динамическую нагрузку. И третье — это коэффициент сопротивления движению ( μ ), определяемый как сила сопротивления движению, деленная на динамическую нагрузку.
\[ \frac{H}{W}=\frac{F}{W}-\frac{F_{r}}{W} \]
Уравнение 3.1.14 показывает, что μ n , мк g и ρ не являются независимыми. С помощью метода, называемого анализом размеров, были разработаны функции для прогнозирования изменения μ g и ρ в зависимости от переменных колес и сопротивления грунта. Этот анализ представлен Герингом и др. (2003) и выходит за рамки этой главы. Если известны μ g , ρ и W , тяговое усилие, создаваемое колесом, можно предсказать с помощью уравнения 3.1.18:
Этот анализ представлен Герингом и др. (2003) и выходит за рамки этой главы. Если известны μ g , ρ и W , тяговое усилие, создаваемое колесом, можно предсказать с помощью уравнения 3.1.18:
\[ H= (\mu_{g}-\rho)W \]
На точку, называемую центр сопротивления колеса. Эта точка не совпадает с направлением динамической нагрузки W , но немного опережает ее. Это горизонтальное расстояние называется горизонтальным смещением ( e ). Статический анализ буксируемого колеса (рис. 3.1.4) показывает, что центр сопротивления колеса не совпадает с направлением динамической нагрузки на колесо. В буксируемом колесе на его ось не действует крутящий момент. Реакция почвы ( G ) в центре сопротивления является равнодействующей сил R и F r . Направление силы G проходит через центр колеса. Для перемещения буксируемого колеса с постоянной фактической скоростью ( v a ) к колесу необходимо приложить результирующую тяговую силу ( H ), равную силе сопротивления движению ( F r ). Чтобы колесо сохраняло постоянную угловую скорость, сумма импульсов в центре колес должна равняться нулю. Геринг и др. (2003) показали, что горизонтальное смещение можно рассчитать с помощью уравнения 3.1.19.-3.1.21.
Чтобы колесо сохраняло постоянную угловую скорость, сумма импульсов в центре колес должна равняться нулю. Геринг и др. (2003) показали, что горизонтальное смещение можно рассчитать с помощью уравнения 3.1.19.-3.1.21.
\[ Re-F_{r}r = 0 \]
, где e = горизонтальное смещение (м).
Используя уравнение 3.1.18, можно предсказать силу тяги. Другой важной информацией в анализе тягового усилия колес является прогнозирование того, какой крутящий момент необходимо передать на ось колеса для создания тягового усилия ( H ). В уравнении 3.1.5 радиус колеса используется для преобразования угловой скорости вращения в теоретическую скорость колеса. Радиус колеса также можно использовать для расчета крутящего момента, необходимого для создания тягового усилия колеса. Крутящий момент ( T ), необходимое для поддержания постоянной угловой скорости колеса и получения полезной тяговой силы, представляет собой произведение общей тяговой силы и радиуса крутящего момента колеса, определяемое по формуле:
ω = угловая скорость колеса колесо
e = смещение по горизонтали
G = реакция почвы в центре сопротивления
H = чистая тяговая сила
R = вертикальная сила реакции колеса
r = радиус качения
F r = сила сопротивления движению
v a = фактическая скорость колеса
Вт = динамическая нагрузка на колесо
\[ T=Fr_{t} \]
, где r t = радиус крутящего момента колеса (м).
Радиус колеса, определенный в уравнении 3.1.5, отличается от радиуса крутящего момента колеса, определенного в уравнении 3.1.22, из-за взаимодействия колеса и поверхности, которое меняется на поверхности мягкого грунта. Как правило, используется радиус качения, основанный на расстоянии от центра оси колеса до твердой поверхности. Следовательно, уравнение 3.1.23 можно использовать для оценки крутящего момента, действующего на ось колеса:
\[ T=Fr \]
Мощность двигателя, необходимая для создания тягового усилия
Стандарты ASABE (2015 г.) представили диаграмму (рис. 3.1.5) приблизительного типичного соотношения мощности для сельскохозяйственных тракторов. Тракторы можно определить по полной номинальной мощности маховика двигателя ( P e ). Одним из стандартов, используемых для определения полной номинальной мощности маховика двигателя, является SAE J1995 (SAE, 1995). Номинальная мощность, определяемая этим стандартом, представляет собой механическую мощность, вырабатываемую двигателем без некоторых его аксессуаров (таких как генератор переменного тока, вентилятор радиатора и водяной насос). Следовательно, полная номинальная мощность маховика двигателя больше, чем полезная мощность, вырабатываемая двигателем. Приблизительную чистую мощность двигателя на маховике можно оценить, умножив полную мощность на маховике на 0,9.2. Мощность на ВОМ трактора примерно равна полной мощности на маховике двигателя, умноженной на 0,83, или полезной мощности на маховике двигателя, умноженной на 0,90.
Следовательно, полная номинальная мощность маховика двигателя больше, чем полезная мощность, вырабатываемая двигателем. Приблизительную чистую мощность двигателя на маховике можно оценить, умножив полную мощность на маховике на 0,9.2. Мощность на ВОМ трактора примерно равна полной мощности на маховике двигателя, умноженной на 0,83, или полезной мощности на маховике двигателя, умноженной на 0,90.
Мощность, которую трактор может генерировать для тяги навесного оборудования, часто называемая мощностью тягового стержня, поскольку к дышлу трактора прикреплено много навесного оборудования, зависит от типа трактора, т. е. привод на 2 колеса (2WD), механический привод на передние колеса (MFWD) , полноприводная (4WD), или гусеничная. Состояние поверхности, на которой используется трактор, имеет еще большее значение. Используя эти две части информации, коэффициенты, которые показывают оценку соотношения между мощностью тягового стержня и мощностью ВОМ, приведены на рис. 3.1.5.
Мощность тяги, необходимая для тяги орудия:
\[ P_{DB} = F_{i} \nu_{i} \]
где P DB = мощность тяги (Вт)
F i = сила, необходимая для тяги орудия (Н)
v i = скорость орудия (м с −1 )
Сила, необходимая для тяги орудия, зависит от орудия. Например, сила, необходимая для вытягивания сеялки F p — усилие, требуемое на ряд, умноженное на количество рядов:
Например, сила, необходимая для вытягивания сеялки F p — усилие, требуемое на ряд, умноженное на количество рядов:
\[ F_{p} = f_{r}n_{r} \]
, где f r = усилие, необходимое на ряд сеялки (Н ряд −1 )
n r = количество рядов
После определения требуемой мощности на дышле значения на рис. 3.1.5 можно использовать для расчета расчетной необходимой полной номинальной мощности на маховике трактора. тянуть орудие.
Приложения
Понятия тяги и мощности трактора необходимы для правильного согласования трактора с навесным оборудованием. Сельскохозяйственные операции нельзя выполнять, если трактор не может развить достаточную мощность или тягу для буксировки орудия. Поскольку размеры навесного оборудования с годами увеличились, необходимо, чтобы тракторы имели достаточную мощность и достаточное тяговое усилие для выполнения задач, которые они должны выполнять. Выбор слишком большого трактора отрицательно скажется на рентабельности сельского хозяйства, поскольку большие тракторы стоят дороже, чем маленькие. Негабаритный трактор также может увеличить расход топлива и выбросы выхлопных газов. Это важно, потому что даже самые эффективные тракторы получают менее 4 кВтч работы на литр дизельного топлива.
Негабаритный трактор также может увеличить расход топлива и выбросы выхлопных газов. Это важно, потому что даже самые эффективные тракторы получают менее 4 кВтч работы на литр дизельного топлива.
Тракторы сильно различаются по размеру (например, рис. 3.1.6). Например, один крупный современный производитель продает тракторы мощностью от 17 до 477 кВт. Вес трактора должен быть достаточным для создания достаточной силы тяги, как показано в уравнении 3.1.18. Однако, помимо затрат на добавление веса, дополнительный вес может увеличить уплотнение почвы и снизить урожайность. Поэтому необходимо понимать эти концепции для проектирования тракторов и навесного оборудования. Возможности двигателя трактора, элементов силовой передачи и колес необходимо соответствующим образом масштабировать. Необходимо найти компромисс между тем, чтобы сделать их большими и мощными, и сделать их компактными и недорогими. Приведенный выше анализ может быть использован для выбора и конструкции трактора.
Приведенный выше анализ может быть использован для выбора и конструкции трактора.
Эти концепции также применяются к другим типам сельскохозяйственной техники, например, к самоходным комбайнам и опрыскивателям. Чтобы эти машины могли выполнять свои задачи, они должны иметь возможность передвигаться по сельскохозяйственным землям. Те же расчеты можно использовать для определения достаточности мощности и для проектирования различных компонентов этих машин. Колеса, оси и компоненты силовой передачи должны выдерживать усилия, крутящие моменты и мощность во время использования машин.
Примеры
Пример \(\PageIndex{1}\)
Пример 1: Тяговое усилие 5 кН. Скорость колеса 2 м с −1 . Если коэффициент тяги равен 0,73, какая мощность должна быть передана на ось колеса?
Раствор
Примите эквивалентный коэффициент трения равным 0,48, среднее значение для твердого грунта представлено в таблице 3. 1.1. Рассчитайте тяговую силу, используя уравнение 3.1.4:
1.1. Рассчитайте тяговую силу, используя уравнение 3.1.4:
\( H= \mu W=0,48 \times 5 = 2,4 \text{ кН} \)
Теперь рассчитайте тяговую мощность колеса трактора, используя уравнение 3.1.2:
\( P_{t} = H\nu_{a} = 2,4 \times 2 = 4,8 \text{ кВт} \)
Рассчитайте мощность, которую необходимо передать на ось колеса, используя уравнение 3.1.3 при заданном коэффициенте тяги 0,73:
\( P_{W} = \frac{P_{t}}{T_{E}} = \frac{4.8}{0.73} = 6.58 \text{ кВт} \)
Это значение необходимой мощности можно использовать для проектировать различные компоненты силовой передачи. Потребляемая мощность также может быть использована для расчета мощности, необходимой для конечного источника энергии, возможно, двигателя, для расчета расхода топлива и, следовательно, затрат на конкретную операцию в полевых условиях.
Пример \(\PageIndex{2}\)
Пример 2: Коэффициент уменьшения крутящего момента и хода или скольжение
Проблема:
Колесо другого трактора получает 40 кВт от трансмиссии трактора. Колесо вращается со скоростью 25 об/мин, что соответствует угловой скорости ω, равной 2,62 рад с -1 . (Примечание: 2π рад × 25 об/мин/60 мин с −1 = 2,62 рад с −1 .) Если радиус качения колес равен 0,81 м, а скорость трактора равна 2 м с −1 , рассчитать крутящий момент, действующий на колесо, и коэффициент уменьшения хода (обычно известный как скольжение).
Колесо вращается со скоростью 25 об/мин, что соответствует угловой скорости ω, равной 2,62 рад с -1 . (Примечание: 2π рад × 25 об/мин/60 мин с −1 = 2,62 рад с −1 .) Если радиус качения колес равен 0,81 м, а скорость трактора равна 2 м с −1 , рассчитать крутящий момент, действующий на колесо, и коэффициент уменьшения хода (обычно известный как скольжение).
Решение
Рассчитайте крутящий момент, действующий на колесо T для мощности P w 40 кВт, используя уравнение 3.1.1:
\( T=}{\frac{P_{W} \omega} = \frac{40}{2,62} = 15,28 \text{ Нм} \)
Рассчитайте мощность, передаваемую колесу для создания тягового усилия 2,4 кН на расстоянии 2 м с −1 скорости колеса, используя Уравнение 3.1.3:
\( P_{W} = \frac{P_{t}}{T_{E}} = \frac{4,8}{0,73} =6,58 \text{кВт} \) 9{-1} \)
Поскольку фактическая скорость колеса составляет 2 м с −1 , что меньше теоретической скорости колеса, рассчитайте коэффициент уменьшения хода с , используя уравнение 3. 1.6:
1.6:
\(s= \frac{\nu_{t}-\nu_{a}}{\nu_{t}} = \frac{2.12-2.00}{2.12} = 0,057, \text{or} \ 5,7\% \ )
Помимо предоставления рекомендаций по конструкции сельскохозяйственной машины и ее потребляемой мощности, расчет проскальзывания полезен для определения скорости выполнения операции. Чрезмерное скольжение также может оказать неблагоприятное воздействие на структуру почвы и затормозить рост растений.
Пример \(\PageIndex{3}\)
Пример 3: Тяговая сила и мощность
Задача:
Рассмотрим колесо, которое работает с динамической нагрузкой 10 кН, коэффициентом сопротивления движению 0,08 и общий тяговый коэффициент 0,72. Найдите силу тяги, которую может развивать колесо. Если это колесо вращается со скоростью 40 об/мин, а радиус качения колеса равен 0,71 м, какая мощность необходима для перемещения этого колеса?
Решение
Рассчитайте общую тяговую силу, развиваемую колесом F , используя уравнение 3. 1.16:
1.16:
\( F= \mu_{g} W = 0,72 \times 10 = 7,2 \text{ кН} \)
Рассчитайте сопротивление движению F r этого колеса используя уравнение 3.1.17:
\( F_{r} = \rho W = 0,08 \times 10 = 0,80 \text{ кН} \)
Сила тяги H , развиваемая колесом, согласно уравнению 3.1. 12, есть разница между полной тяговой силой и сопротивлением движению:
\( H = F-F_{r} = 7,2 — 0,8 = 6,4 \text{ кН} \)
Рассчитайте крутящий момент, необходимый для перемещения этого колеса, используя уравнение 3.1.23:
\( T = Fr = 7,2 \times 0,71 = 5,11 \text{ кН·м} \)
Рассчитайте мощность P w необходимо чтобы повернуть колесо, используя уравнение 3.1.1:
\( P_{W} = T \omega = T \frac{2\pi N}{60} = 5.11 \times \frac{2 \times \pi \times 40 }{60} = 21,4 \text{ кВт} \)
Пример \(\PageIndex{4}\)
Пример 4: Полная мощность двигателя на маховике
Задача:
Рассчитайте необходимую мощность трактора MFWD для буксировки 30-рядной сеялки. Согласно стандартам ASABE (2015 г.), требуется усилие 900 Н на ряд, чтобы тянуть прицепную сеялку для пропашных культур, если она выполняет только операцию посева. Скорость трактора составит 8,1 км ч -1 (2,25 м с -1 ). Почва в распаханном состоянии. Учтите, что трактор должен иметь запас хода 20% для преодоления непредвиденных перегрузок.
Согласно стандартам ASABE (2015 г.), требуется усилие 900 Н на ряд, чтобы тянуть прицепную сеялку для пропашных культур, если она выполняет только операцию посева. Скорость трактора составит 8,1 км ч -1 (2,25 м с -1 ). Почва в распаханном состоянии. Учтите, что трактор должен иметь запас хода 20% для преодоления непредвиденных перегрузок.
Раствор
Рассчитайте силу тяги, необходимую для тяги сеялки, используя уравнение 3.1.25:
\( F_{p} = f_{r}n_{r} = 900 \times 30 = 27 000 \text{ N} \)
Рассчитайте мощность на дышле P DB , необходимую для тяги сеялки, используя уравнение 3.1.24:
\( P_{DB} = F_{p} \nu_{p} = 27 000 \times 2,25 = 60 750 \text{ Вт } \)
Следовательно, трактор должен выдавать тяговую мощность 60,75 кВт. Из рисунка 3.1.5 найдите, что коэффициент, связывающий мощность дышла с мощностью ВОМ трактора для трактора MFWD, работающего на вспаханной почве, равен 0,72. Таким образом, мощность ВОМ трактора P ВОМ должно быть:
\( P_{PTO} = \frac{P_{DB}}{0,72} = \frac{60,75}{0,72} = 84 \text{кВт} \)
Учитывая что коэффициент, связывающий мощность ВОМ с полной мощностью на маховике двигателя, равен 0,83 (рис. 3.1.5), полная мощность на маховике двигателя P e равна:
3.1.5), полная мощность на маховике двигателя P e равна:
\( P_{e} = \frac{P_{ ВОМ}}{0,83} = \frac{84,375}{0,83} = 102 \text{кВт} \)
Учитывая запас мощности 20% для преодоления непредвиденных перегрузок, выбранный трактор должен иметь полную мощность двигателя на маховике при как минимум на 20 % больше, чем требуется для тяги 30-рядной сеялки, или 1,2 × 102 кВт = 122 кВт.
Эти расчеты помогут управляющему фермой выбрать правильный трактор для работы.
Кредиты на изображения
Рис. 1. Queiroz, D. (CC By 4.0). (2020). Схематический вид двухколесного сельскохозяйственного трактора.
Рис. 2. Кейрос, Д. (CC By 4.0). (2020). Упрощенная диаграмма переменных, связанных с колесом, развивающим чистую тяговую силу.
Рис. 3. Кейрос, Д. (CC By 4.0). (2020). Диаграмма переменных, связанных с колесом, развивающим чистую тяговую силу ( H ), включая общую тяговую силу ( F ) и силу сопротивления движению ( F r ).
Рис. 4. Кейрос, Д. (CC By 4.0). (2020). Схема сил, действующих на буксируемое колесо.
Рис. 5. Стандарт ASABE ASAE D497.7 (CC By 4.0). (2020). Схема примерных соотношений мощностей сельскохозяйственных тракторов (типы указаны в основном тексте) и почвенных условий.
Рис. 6. Шуллер, Дж. (CC By 4.0). (2020). Типичные современные (а) малые и (б) большие тракторы.
Ссылки
Стандарты ASABE. (2018). ANSI/ASAE S296.5 DEC2003 (R2018): Общая терминология тяги сельскохозяйственных тягово-транспортных устройств и транспортных средств. Сент-Джозеф, Мичиган: ASABE.
Стандарты ASABE. (2015). ASAE D497.7 MAR 2011 (R2015): Данные по управлению сельскохозяйственной техникой. Сент-Джозеф, Мичиган: ASABE.
Геринг, К.Э., Стоун, М.Л., Смит, Д.В., и Тернквист, П.К. (2003). Тяговые и транспортные устройства. В Принципы проектирования внедорожников (стр. 351-382). Сент-Джозеф, Мичиган: ASAE.
351-382). Сент-Джозеф, Мичиган: ASAE.
Колатор, Б., и Бялобжевски, И. (2011). Имитационная модель производительности полноприводного трактора. Вычисл. Электрон. Агр. 76 (2): 231-239.
Рениус, К. Т. (2020). Основы конструкции трактора. Чам, Швейцария: Springer Nature.
SAE. (1995). SAE J1995_199506: Код проверки мощности двигателя — искровое зажигание и воспламенение от сжатия — номинальная полная мощность. Трой, Мичиган: SAE.
Шуллер, Дж. К. (2000). На службе изобилия: механизация сельского хозяйства обеспечила питание для необычайного роста 20-го века. Мех. англ. 122 (8):58-65.
Эта страница под названием 3.1: Traction распространяется под лицензией CC BY 4.0, ее авторами, ремиксами и/или кураторами являются Николас М. Холден, Мэри Ли Вулф, Джактон Арого Огеджо и Энда Дж. Камминс (Технологические библиотеки Вирджинии). Открытая образовательная инициатива) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Открытая образовательная инициатива) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Николас М. Холден, Мэри Ли Вульф, Джактон Арого Огеджо и Энда Дж. Камминс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- Инициатива открытого образования технических библиотек Вирджинии
- Метки
- мощность двигателя
- механика тяги
- навесное оборудование
- источник@https://vtechworks.
 lib.vt.edu/handle/10919/93254
lib.vt.edu/handle/10919/93254 - тяга
- тяговые устройства
- тяговое усилие
- тракторы
- транспортные устройства
ДИНАМИКА ТРАНСПОРТНОГО СРЕДСТВА
ДИНАМИКА ТРАНСПОРТНОГО СРЕДСТВА
Динамика транспортного средства представляет собой сложный аналитический и экспериментальная технология, которая используется для изучения и понимания ответов автомобиля в различных ситуациях движения. В области обучения водителей нет необходимости иметь дело с особенности этой технологии, а с некоторыми из основных физических принципов, задействованных в нем. в этом блоке будут обсуждаться следующие принципы.
И. Кинетическая энергия
II. Центробежная сила
Центробежная сила
III. Инерция
IV. Трение
В. Тяговый
Есть не намерен давать полное техническое определение каждого принципа, но представить их таким образом, который будет полезен для понимания того, почему транспортное средство действует так, как это делает.
Кинетическая энергия – это термин, описывающий энергию транспортное средство имеет из-за его массы и скорости. Его формула проста, но говорит о многом.
Кинетическая энергия = (масса) x (скорость) 2
Это показывает, что кинетическая энергия транспортного средства
возрастает пропорционально квадрату скорости.
Это означает, что если скорость удвоится, энергия увеличится в четыре раза.
раз. Это увеличение энергии не вызывает
проблема, если только она не должна быть быстро рассеяна или перенаправлена.
Один Способ, которым кинетическая энергия может рассеиваться очень быстро, — это когда транспортное средство сталкивается с твердый предмет. В этом случае, когда скорость удваивается, в четыре раза больше энергии доступно для повреждения транспортного средства и ранить своих пассажиров. кинетический энергия автомобиля массой 4000 фунтов, движущегося со скоростью 100 миль в час, равна 1,36 млн. футов достаточно, чтобы поднять человека весом 175 фунтов на 1,5 мили. Чтобы остановить это транспортное средство, необходима огромная энергия. быть рассеянным. Это может быть выполнено ударом или тормозом. Остановка расстояние связано с квадратом скорости; следовательно, для скорости 30 миль в час требуется четыре раз расстояние до остановки, чем 15 миль в час. Многие водители никогда не задумываются о последствиях увеличения скорости, но они должны быть осведомлены о связанных с этим рисках.
ЦЕНТРОБЕЖНАЯ СИЛА
Когда
автомобиль поворачивается, центробежная сила действует на автомобиль и пытается толкнуть его в
снаружи кривой. Формула
равно:
Формула
равно:
Центробежная сила = (масса) X (скорость) 2 / радиус поворота
Это показывает, что центробежная сила возрастает пропорционально квадрату скорости. Также при заданной скорости малый (узкий) радиус повороты производят больше силы, чем повороты большого радиуса. Большие количества центробежной силы требуют столь же больших количеств противодействующей силы от шин, если транспортное средство должно оставаться на Дорога. Шины можно рассматривать как струны от каждого конца транспортного средства к центру поворота. Если центробежная сила выше шины могут противодействовать, порвется одна или обе струны. После этого автомобиль выйдет из поворота.
ИНЕРЦИЯ
Инерция
сопротивление изменению направления или скорости тела в состоянии покоя
или в движении. В данном случае это
связанные с изменением курса или направления транспортного средства; то есть меняется
от движения прямо до поворота.
важность инерции и распределения веса, поскольку они связаны с вождением, заключается в том, что они влияют на количество времени, необходимое для перехода от прямого к поворот или наоборот. Хотя эти изменения при обычной загрузке автомобиля невелики, водитель должен распознавать необычную загрузку транспортного средства, например, размещение большого груза на задней двери универсала (или добавление тяжелого груза на крыша автомобиля) вызовет изменения в способе вождения автомобиля и регулировки должны быть сделаны в вождении соответственно.
С
инерция диктует, что движущееся тело будет продолжать двигаться прямолинейно
линии, необходимо приложить силу, чтобы заставить транспортное средство повернуться. Эта сила называется Центростремительная сила ,
и является результатом того, что шины растягиваются, чтобы увести автомобиль с прямого пути. Центростремительная сила должна превышать центробежную
усилие , чтобы автомобиль повернулся.
МОМЕНТЫ ИНЕРЦИИ:
А. Шаг силы, ощущаемой при ускорении или торможении вокруг (Горизонтальная ось) автомобиля
B. Сила качения, ощущаемая при прохождении поворотов, движение из стороны в сторону (Боковое оси) автомобиля
C. Рыскание сила, ощущаемая при вращении вокруг (вертикальной оси) транспортное средство
ПОЛЯРНЫЙ МОМЕНТ ИНЕРЦИИ
Очень важная концепция обращения, которая диктует
готовность автомобиля изменить направление движения, если это называется полярным моментом
инерции. Полюса инерции просто
другой способ сказать центр концентрации веса. Момент в этом понятии определяется
по передне-заднему расположению центра тяжести. Автомобиль поворачивает (меняет направление) вокруг своей оси.
центр тяжести в углу поэтому дальше центры тяжести
концентрации расположены от центра тяжести (что является их общим
центре), тем больше момент.
Высокий полярный момент инерции присутствует, когда массовые концентрации тяжелые и далеко друг от друга. Малый полярный момент инерции находится при весе концентрации легкие и близки друг к другу. Другими словами, легче управлять транспортным средством с низкой полярностью. момент инерции.
Транспортное средство с малым полярным моментом инерции дает быстрая реакция на команды руля. А транспортное средство с высоким полярным моментом обладает высокой курсовой устойчивостью (т. сопротивляется изменению направления).
Трение определяется как сопротивление движению между двумя поверхностями. Различают четыре основных типа трения.
А. Статическая удерживающая сила между двумя покоящимися поверхностями
B. Скольжение сопротивления движению между двумя поверхностями, движущиеся поперек друг друга
С. Сопротивление качению катящегося объекта, такого как мяч,
цилиндр или колесо
Сопротивление качению катящегося объекта, такого как мяч,
цилиндр или колесо
D. Внутреннее сопротивление движению внутри упругих объектов (шины получают нагреваются от внутреннего трения при изгибании)
величина трения между двумя поверхностями зависит от:
1) субстанция материала
2) шероховатость поверхностей
3) количество силы, прижимающей поверхности друг к другу
4) наличие смазочных материалов
величина трения между двумя поверхностями называется коэффициентом трения .
КОЭФФИЦИЕНТ ТРЕНИЯ
Коэффициент трения определяется как максимальная сила, которую может создать шина на данном дорожном покрытии состоянии, деленное на вес на шине. Its formula is:
Maximum Force Available
Coefficient of Friction = Weight on the Tire
OR
Максимальная доступная сила = коэффициент трения X вес колесной нагрузки
Таким образом, маневренность автомобиля на сухом
дорога зависит в первую очередь от дорожного покрытия и веса автомобиля. На мокрой дороге другие факторы, такие как шина
состояние тоже надо учитывать.
На мокрой дороге другие факторы, такие как шина
состояние тоже надо учитывать.
По мере ускорения или замедления автомобиля больше быстро или по мере того, как автомобиль поворачивает на более высоких скоростях, требуется большее силы тяги от комбинации шина-дорога. Комбинация шины и дороги создаст эти силы вплоть до предел трения.
Тяга определяется как адгезионное трение шины о дорожное покрытие. Существует три силы тяги:
1) Приводная тяга Для ускорения автомобиля
2) Торможение Тяга Для замедления или остановки автомобиля
3) Сцепление на поворотах Для поворота автомобиля
В всякий раз, когда сила тяги становится больше, чем коэффициент трения автомобиль выйдет из-под контроля.
А
водитель имеет потенциал для приложения трех сил. Для любой конкретной ситуации существует уровень трения
(коэффициент), доступный для приложения этих сил и, следовательно, для маневрирования
автомобиль. Когда водитель напрягается
тормозную или ускоряющую силу, в то же время оказывая
угловая сила, вы должны добавить силы при рассмотрении доступного
трение. Другими словами, сумма
тяга при движении или торможении и тяга на поворотах должна быть , а не превышают
предел трения, иначе транспортное средство выйдет из-под контроля. По возможности избегайте торможения или
ускорение в поворотах. Этот
позволяет использовать все доступное трение в поворотах.
Для любой конкретной ситуации существует уровень трения
(коэффициент), доступный для приложения этих сил и, следовательно, для маневрирования
автомобиль. Когда водитель напрягается
тормозную или ускоряющую силу, в то же время оказывая
угловая сила, вы должны добавить силы при рассмотрении доступного
трение. Другими словами, сумма
тяга при движении или торможении и тяга на поворотах должна быть , а не превышают
предел трения, иначе транспортное средство выйдет из-под контроля. По возможности избегайте торможения или
ускорение в поворотах. Этот
позволяет использовать все доступное трение в поворотах.
А вращающаяся шина не может обеспечить полное сцепление с дорогой при ускорении. Если водитель вызывает пробуксовку ведущего колеса при на повороте автомобиль может выйти из-под контроля.
А
заблокированная шина обеспечивает нет сцепление на поворотах и снижение торможения
тяга. Когда водитель запирает
колеса в повороте, не будет реакции на рулевое управление . При торможении максимальный коэффициент
трение; следовательно, максимальная тормозная способность достигается, когда водитель применяет
тормоза на уровне 15% пробуксовки.
При торможении максимальный коэффициент
трение; следовательно, максимальная тормозная способность достигается, когда водитель применяет
тормоза на уровне 15% пробуксовки.
Основы физики
Джим Роал
Основы двигателей и номинальные характеристики
Мощность двигателя — это оценка того, насколько быстро может быть выполнена работа. Работа есть мера силы, умноженная на расстояние. Если вы поднимаете объект весом 550 фунтов на 1 фут, вы выполнили работу в 550 фут-фунтов (не путать с крутящим моментом в футо-фунтах, который представляет собой силу, а не работу). Это игнорирует эффекты инерции, которые были бы очень большими в этом примере. Если вы выполняете эту работу за одну секунду, вы только что применили одну лошадиную силу (или 746 Вт). Соотношение между крутящим моментом двигателя и мощностью:
1HP = ((крутящий момент в футо-фунтах)x(об/мин))/5252
Если у вас есть измерение мощности или крутящего момента, а также число оборотов в минуту, вы можете рассчитать другое. Если у вас есть только измерение крутящего момента, но нет числа оборотов в минуту, при которых создается этот крутящий момент, вы не можете рассчитать ускорение. Однако, если у вас есть только номинальная мощность, вы можете рассчитать ускорение, хотя бы в точке этого рейтинга. Если вы действительно хотите понять потенциал ускорения двигателя, вам нужно посмотреть на кривую мощности в диапазоне оборотов, в котором двигатель будет работать при ускорении.
Если у вас есть только измерение крутящего момента, но нет числа оборотов в минуту, при которых создается этот крутящий момент, вы не можете рассчитать ускорение. Однако, если у вас есть только номинальная мощность, вы можете рассчитать ускорение, хотя бы в точке этого рейтинга. Если вы действительно хотите понять потенциал ускорения двигателя, вам нужно посмотреть на кривую мощности в диапазоне оборотов, в котором двигатель будет работать при ускорении.
Крутящий момент — это номинальное или крутящее усилие. Фут-фунт крутящего момента равен 1 фунту силы, приложенной перпендикулярно валу на расстоянии 1 фута от осевой линии вала. Крутящий момент может быть приложен без движения. Сам по себе номинальный крутящий момент говорит вам кое-что о двигателе, но не говорит вам, какую работу двигатель может выполнить за заданное время.
Мощность (л.с. или кВт) — это оценка объема работы, которая может быть выполнена за заданное время. Мощность — это показатель, который вам нужен, чтобы определить, насколько быстро вы можете двигаться, как быстро вы можете разогнаться или любой другой аспект производительности транспортного средства, лодки или любой другой машины.
В зубчатой передаче сохраняется мощность, за исключением некоторой потери из-за трения. Однако крутящий момент умножается или делится в зубчатой передаче. Если у вас передаточное число 4:1, вы умножите свой крутящий момент на 4. Применение крутящего момента в 200 футо-фунтов приведет к 800 футо-фунтам на выходе. Однако, если вы подаете 200 л.с. на вход, вы все равно получаете 200 л.с. (за вычетом некоторых потерь на трение), но обороты вашего выходного вала составляют 1/4 от того, что было на входе.
Двигатели с высоким номинальным крутящим моментом и низкой номинальной мощностью — это двигатели, которые создают мощность при низких оборотах, но быстро падают при высоких оборотах. Эти двигатели обычно имеют широкий, постоянный диапазон мощности. Они хороши для буксировки, когда вам нужно подавать мощность на каждой передаче в течение длительного времени.
Двигатели с высокой мощностью и низким крутящим моментом являются двигателями с более высокими оборотами. Эти двигатели работают лучше с более высокими скоростями трансмиссии и более высокими передаточными числами главной передачи. Их диапазон мощности обычно не плоский, а имеет наклон вверх к пику, а затем падает. Если вы запускаете эти двигатели намного ниже пиковой мощности RPM, мощность будет намного ниже, чем пиковая мощность. Если вы можете сохранить тот же номинальный пиковый крутящий момент, но удвоить число оборотов в минуту, при которых достигается пиковый крутящий момент, вы удвоите мощность.
Эти двигатели работают лучше с более высокими скоростями трансмиссии и более высокими передаточными числами главной передачи. Их диапазон мощности обычно не плоский, а имеет наклон вверх к пику, а затем падает. Если вы запускаете эти двигатели намного ниже пиковой мощности RPM, мощность будет намного ниже, чем пиковая мощность. Если вы можете сохранить тот же номинальный пиковый крутящий момент, но удвоить число оборотов в минуту, при которых достигается пиковый крутящий момент, вы удвоите мощность.
Принимая во внимание, что мощность и крутящий момент — это просто измерения характеристик двигателя, а мощность — это измерение того, насколько быстро может быть выполнена работа (например, ускорение транспортного средства), чтобы действительно понять характеристики двигателя, вы должны действительно учитывать все кривая мощности во всем диапазоне оборотов двигателя. Часто люди спорят о том, что важнее, крутящий момент или мощность, но, честно говоря, это неправильный аргумент. Более актуальным является обсуждение того, насколько широка кривая мощности двигателя. Это часто называют «мощность под кривой» и относится к площади под кривой мощности двигателя.
Это часто называют «мощность под кривой» и относится к площади под кривой мощности двигателя.
Динамика автомобиля
Закон Ньютона гласит, что сила равна массе, умноженной на ускорение (F=ma). Это уравнение можно решить для ускорения, чтобы показать, что ускорение равно массе, деленной на силу (a=F/m). Ускорение — это скорость изменения скорости, выраженная в единицах длины на квадрат времени (обычно футы на секунду в квадрате). Если пренебречь такими вещами, как тяга, удвоение силы приведет к удвоению ускорения. Мощность требуется для приложения силы со скоростью, достаточной для выполнения работы по ускорению транспортного средства. Удвоение ускорения сократит время, необходимое для достижения заданной скорости, вдвое. Сокращение массы вдвое имеет тот же эффект, что и удвоение мощности. Итог: если вы хотите улучшить ускорение, уменьшение массы (веса) или транспортного средства будет иметь тот же эффект, что и увеличение мощности (силы).
Вес — это просто произведение массы на ускорение, эквивалентное силе тяжести (32,2 фута в секунду в квадрате). Если вы разделите вес автомобиля в фунтах на 32,2, вы получите массу в единицах слизняков. Если вы разделите вес в ньютонах на 9,81, вы получите массу в килограммах (кг).
Если вы разделите вес автомобиля в фунтах на 32,2, вы получите массу в единицах слизняков. Если вы разделите вес в ньютонах на 9,81, вы получите массу в килограммах (кг).
В мощных транспортных средствах тяга обычно является фактором, ограничивающим ускорение. Сцепление — это сила, с которой шины могут прикладываться к дорожному покрытию. Реакция представляет собой равную и противоположную силу, приложенную к транспортному средству, тем самым ускоряя его. Он управляется трением. Есть 2 меры трения: кинетическая (относительное движение между поверхностями) и статическая (относительное движение отсутствует). Если ваши шины скользят по асфальту, вы используете кинетическое трение. Если шины не скользят, у вас есть статическое трение. Автомобиль, движущийся по дороге с постоянной скоростью, использует статическое трение между дорогой и шинами. Статическое трение больше кинетического. Другими словами, когда вы пробуксовываете шины, вы теряете тяговое усилие и, следовательно, теряете ускорение. Сцепление равно весу, приложенному к шине (нормальная сила), умноженному на коэффициент трения. Коэффициент статического трения больше, чем коэффициент кинетического трения. Увеличение веса шины увеличит сцепление с дорогой, а также увеличит коэффициент трения. Шины будут иметь меньшее сцепление при проскальзывании.
Сцепление равно весу, приложенному к шине (нормальная сила), умноженному на коэффициент трения. Коэффициент статического трения больше, чем коэффициент кинетического трения. Увеличение веса шины увеличит сцепление с дорогой, а также увеличит коэффициент трения. Шины будут иметь меньшее сцепление при проскальзывании.
Для внедорожников необходимо учитывать еще один фактор, а именно инерцию. На мягком грунте, таком как мягкий песок, трение очень мало. Когда шина катится, песок просто перемещается под ней. Чтобы продвинуть транспортное средство через эту среду, вы можете вытеснить достаточное количество песка, чтобы заставить транспортное средство двигаться вперед. Это больше похоже на лодку. Лодка движется вперед, толкая воду назад. Внедорожник просто продвигает песок вместо воды. Вот почему шины лопастного типа используются на очень мягком грунте.
Гравитация так же влияет на массу, как и ускорение. Когда автомобиль находится в состоянии покоя, на автомобиль действует только ускорение из-за силы тяжести, создающее вес (силу). Когда автомобиль ускоряется, требуется вторая сила, чтобы вызвать ускорение. Эти две силы называются векторами (каждая из которых имеет направление и величину). Линейная алгебра используется для объединения векторов в один результирующий вектор. Этот эффект обычно называют сдвигом веса. На самом деле это означает, что результирующее направление векторной суммы двух векторов силы больше не перпендикулярно центру Земли (только сила тяжести).
Когда автомобиль ускоряется, требуется вторая сила, чтобы вызвать ускорение. Эти две силы называются векторами (каждая из которых имеет направление и величину). Линейная алгебра используется для объединения векторов в один результирующий вектор. Этот эффект обычно называют сдвигом веса. На самом деле это означает, что результирующее направление векторной суммы двух векторов силы больше не перпендикулярно центру Земли (только сила тяжести).
Центр масс автомобиля будет расположен в точке, называемой центром масс. Эта точка отличается от геометрического центра, но обычно находится недалеко от геометрического центра транспортного средства. Поскольку сила ускорения действует прямо на шины и параллельна поверхности дороги, центр тяжести массы всегда располагается выше вектора силы тяги. Это заставляет автомобиль приподниматься спереди и приседать сзади, независимо от того, является ли он передним, задним или полноприводным, во время ускорения вперед. Это будет иметь тот же эффект, что и перенос веса с передней части автомобиля на заднюю. Когда это произойдет, на задние шины будет воздействовать более высокая нормальная сила (приложенный вес), а на передние шины — меньшая. Это называется переносом веса.
Когда это произойдет, на задние шины будет воздействовать более высокая нормальная сила (приложенный вес), а на передние шины — меньшая. Это называется переносом веса.
Если вы правильно спроектируете автомобиль, учитывая имеющийся у вас потенциал ускорения, вы настроите его так, чтобы передние колеса едва отрывались от тротуара при максимальном ускорении. Это перенесет весь вес автомобиля на задние колеса, что увеличит сцепление с дорогой до максимума. Добавление веса к транспортному средству уменьшит ускорение так же, как и уменьшение мощности. Чтобы оптимизировать перенос веса, вы можете переместить центр масс вверх. Другими словами, увеличить высоту автомобиля. Если вы слишком увлечетесь, вы слишком сильно поднимете передние колеса при ускорении и потеряете контроль. Если это так, опустите центр масс.
Как видите, передний привод — это последнее, что вам нужно для дрэг-рейсинга. Из-за эффекта переноса веса вы теряете сцепление с дорогой при увеличении ускорения на переднеприводном автомобиле. Автомобиль с задним приводом увеличивает тягу при ускорении.
Автомобиль с задним приводом увеличивает тягу при ускорении.
Тяговое усилие на шинах всегда параллельно поверхности дороги, независимо от того, ускоряетесь вы или поворачиваете. На самом деле повороты — это просто еще одна форма ускорения. Любое изменение скорости есть ускорение. Скорость также является вектором. Это означает, что она имеет определенное направление и величину. Скорость имеет величину, но не конкретное направление. Если вы меняете направление движения, вы меняете скорость (но не обязательно скорость), таким образом, вы ускоряетесь. При прохождении поворотов действуют силы точно так же, как при ускорении вперед. Однако для прохождения поворотов вы хотите максимально снизить центр тяжести массы, чтобы уменьшить крен кузова и сохранить более равномерный вес на всех шинах, но, что более важно, уменьшить склонность к опрокидыванию.
Когда-нибудь, когда у меня будет время, мне нужно будет добавить к этому больше…..
Трение как функция площади — Общий форум
rbayer
#1
Вот вопрос, с которым я недавно столкнулся, пытаясь научить сборщиков всему, что им нужно знать…
На уроках физики нас учат, что сила трения f определяется выражением f=uN, и мы даже проверили это экспериментально.
Очевидно, что это уравнение не включает площадь, и наши лабораторные результаты также показали, что площадь не имеет значения. Однако, как только две поверхности «слипаются», площадь начинает играть роль.
Мой вопрос: какое уравнение связывает площадь, u и N? Это просто f=uNA? Однако единицы измерения здесь неверны. Кроме того, как определить, является ли А фактором? Например, горячая резина (такая как шины Indy Car), кажется, заботится, а холодная резина — нет.
Гаджет470 92; P = 20
Когда вы увеличиваете площадь, вы также уменьшаете давление
f = uN эквивалентно f = u (P * A), потому что нормальная сила = давление * площадь
Adam_Y
#3
Упс, мы одновременно ответили на вопрос. Хе-хе. В любом случае, он думал о тяге, которая зависит от площади поверхности.
Сцепление в шинах отличается от стандартной силы трения, о которой говорится в большинстве учебников по физике. В автомобильных шинах края протектора являются основным фактором предотвращения скольжения. На их долю приходится гораздо большее сцепление или трение, чем коэффициент трения резины о дорожное покрытие. Конечно, более широкая шина обычно имеет больше протекторов, чем тонкая.
Причина, по которой они делают гоночные шины горячими, заключается в том, что они должны стать липкими, иначе есть только сцепление с краями шины.
Сунит
#4
Например, кажется, что горячая резина (такая как шины Indy car) заботится, а холодная резина — нет.
Я думаю, что это так, потому что теплопроводность напрямую зависит от площади контакта, а шины настолько широкие, что они остаются холоднее (не плавятся).
Я действительно не думаю, что вам нужно беспокоиться о площади при работе с трением… Если поле состоит из песка в этом сезоне (например), нам нужно беспокоиться о давлении, чтобы колеса не утопали в песке. , но я думаю, что вы беспокоитесь только о давлении на подобные вещи.
Хе-хе, вопросы и ответы работают, не допуская дополнительных обсуждений, пока мод не ответит. Тогда вы получите дополнительную ссылку. Итак, сначала квалифицированный ответ
SlamminSammy
#5
*Первоначально опубликовано Gadget470 *
**f = uN эквивалентно f = u (P * A), поскольку нормальная сила = давление * площадь **
Ну, я никогда не любил давления, так что я буду использовать свою собственную формулу. 2, единицы измерения сокращаются. Моя формула кажется логичной, но я не несу ответственности за какие-либо травмы, полученные в результате неправильной формулы :p.
2, единицы измерения сокращаются. Моя формула кажется логичной, но я не несу ответственности за какие-либо травмы, полученные в результате неправильной формулы :p.
рбайер
#6
Для уточнения:
f=uN для простых поверхностей. Это не касается площади. Однако, во-первых, площадь имеет значение. Например, попробуйте протащить шину шириной 1 мм по ковру, а затем попробуйте полосу шириной 1 м. Предполагая, что оба имеют одинаковую массу или, по крайней мере, одинаковую результирующую силу, действующую на ковер, тянуть шириной 1 м будет труднее. Мой вопрос, почему.
To wysywig: мне не очень понятна разница между сцеплением и трением. Если тяга не от трения, то откуда берется сила? Силы не могут появиться из ниоткуда. Что касается ребра, вы говорите, что каждое ребро обеспечивает небольшую часть чистой силы, поэтому чем больше ребер, тем больше чистая сила? В этом случае площадь имеет значение, так как края — это не что иное, как площадь.
Адам_Y
#7
Я не уверен, но почему бы не использовать исходное уравнение, потому что его площадь поверхности и трение не зависят друг от друга. Я понимаю, что протекторы дают шине сцепление с дорогой, включая силу трения резины. Широкие шины = больше протектора, следовательно, больше сцепления. http://www.physlink.com/Education/AskExperts/ae200.cfm Лол, поиск сцепления и площади поверхности привел к этому. http://www.wheelchairjunkie.com/traction.html
система
#8
Mu в качестве коэффициента трения применим к двум гладким поверхностям, взаимодействующим друг с другом. Для наших целей, при рассмотрении силы, с которой колеса инвалидной коляски воздействуют на ковер, F=uN подходит.
Для наших целей, при рассмотрении силы, с которой колеса инвалидной коляски воздействуют на ковер, F=uN подходит.
Однако, как утверждает Мэтт Лиз в этой теме, сцепление может увеличиться, когда две поверхности зацепляются друг с другом. В таких случаях это происходит из-за того, что между поверхностями возникает контакт, перпендикулярный направлению движения.
Подумайте о наборе цилиндрических шестерен, если хотите. Их способность передавать крутящий момент не ограничивается трением, возникающим между этими двумя поверхностями, потому что они зацепляются друг с другом.
На наших роботах ремни или картотеки или другие неровные поверхности часто служат той же цели. В прошлом сезоне наш робот имел гусеницы площадью более 1 кв. фута, соприкасающиеся с ковром. Поскольку ковер сделан из небольших петель волокна, а наш ленточный материал был сделан из аналогичных крючков из ПВХ, материалы сцеплялись, обеспечивая нам превосходное сцепление.
К сожалению, я не знаю, существует ли единая универсальная формула, применимая к силе, которую две сцепленные поверхности могут испытывать перед скольжением. Я бы предположил, что, как и мю, он зависит от некоторой экспериментально полученной константы, которая меняется с каждой поверхностью.
Я бы предположил, что, как и мю, он зависит от некоторой экспериментально полученной константы, которая меняется с каждой поверхностью.
Извините, больше ничем помочь не могу.
Сунит
#9
* Первоначально опубликовано rbayer *
**Для уточнения:
f=uN для простых поверхностей. Это не касается площади. Однако, во-первых, площадь имеет значение. Например, попробуйте протащить шину шириной 1 мм по ковру, а затем попробуйте полосу шириной 1 м. Предполагая, что оба имеют одинаковую массу или, по крайней мере, одинаковую результирующую силу, действующую на ковер, тянуть шириной 1 м будет труднее. Мой вопрос, почему. **
Гуман. Если я правильно понимаю, две полоски будут иметь одинаковое сопротивление скользящему движению, вызванному трением, до тех пор, пока пара поверхностей состоит из одних и тех же материалов, а нормальная сила между полосой и землей равна . Шина толщиной 1 мм и полоса шириной 1 м не имеют одинаковых нормальных сил с ковром. Если бы вы сделали это, поместив полосы разной ширины под одинаковые грузы и перетащив груз так, чтобы только полоса соприкасалась с землей, сила трения была бы одинаковой в обоих случаях.
Шина толщиной 1 мм и полоса шириной 1 м не имеют одинаковых нормальных сил с ковром. Если бы вы сделали это, поместив полосы разной ширины под одинаковые грузы и перетащив груз так, чтобы только полоса соприкасалась с землей, сила трения была бы одинаковой в обоих случаях.
Гаджет470
#10
Внизу быстрый mspaint, объясняющий, что я имею в виду, разницу между сцеплением и трением.
Черным цветом: гусеницы колеса
Красным цветом: Поверхность, такая как ковер, который можно формовать под давлением
Зеленым цветом: Точки приложения силы трения 8. При приложении силы давления ковер прилегает к ступеням.
На верхних рисунках показана ситуация с нулевым весом, когда колеса едва касаются ковра и прилагается сила трения. На центральном изображении показано, как при приложении веса колеса «въезжают» в ковер. Точки, где ковер сжимается, теперь находятся на ступенях. На нижнем рисунке видно, что точек трения становится больше даже после приложения давления.
Точки, где ковер сжимается, теперь находятся на ступенях. На нижнем рисунке видно, что точек трения становится больше даже после приложения давления.
Вот чем «Тяга» отличается от «Трения» Тяга — это трение в разных плоскостях.
рбайер
#11
*Первоначально отправлено Suneet *
**Humn. Если я правильно понимаю, две полоски будут иметь одинаковое сопротивление скользящему движению, вызванному трением, до тех пор, пока пара поверхностей состоит из одних и тех же материалов, а нормальная сила между полосой и землей равна . Шина толщиной 1 мм и полоса шириной 1 м не имеют одинаковых нормальных сил с ковром. Если бы вы сделали это, поместив полосы разной ширины под одинаковые грузы и перетащив груз так, чтобы только полоса соприкасалась с землей, сила трения была бы одинаковой в обоих случаях.**
Да, есть. Если вы посмотрите на мой пост, я указал, что они имеют одинаковую массу, а значит, одинаковую нормальную силу. (Пожалуйста, не говорите, что это неправда. N=мг).
В любом случае, есть причина, по которой я написал в Q&A: никакая информация здесь не является чем-то новым для меня. Я спрашиваю, как увеличение нашей площади поверхности увеличит наше сцепление/трение/как бы вы это ни называли. Например, если мы удвоим ширину нашего колеса, удвоится ли наша тяга? Поднимается ли он на root 2? Кубический корень из 2? Или нельзя посчитать?
система
#12
* Первоначально опубликовано rbayer *
** В любом случае, есть причина, по которой я разместил сообщение в разделе «Вопросы и ответы»: никакая информация здесь не является для меня чем-то новым.Я спрашиваю, как увеличение нашей площади поверхности увеличит наше сцепление/трение/как бы вы это ни называли. Например, если мы удвоим ширину нашего колеса, удвоится ли наша тяга? Поднимается ли он на root 2? Кубический корень из 2? Или нельзя посчитать? **
Если ваше колесо имеет гладкую поверхность (например, алюминий, два колеса для инвалидных колясок), удвоение площади никак не улучшит сцепление с дорогой. Он увеличится в 1,9 раза.0003
Если материал на вашем колесе не имеет гладкой поверхности и взаимодействует с волокнами ковра, ваше сцепление с дорогой увеличится. Не существует установленного фактора, определяющего, насколько это эффективно.
В то время как гладкая поверхность колеса инвалидной коляски приводит в движение робота за счет трения, неровная поверхность, сцепляющаяся с волокнами ковра, приводит в движение робота за счет как трения (сила скольжения между гладкими частями колеса и ковром), так и крутящего момента (контакт между двумя поверхностями, перпендикулярными направлению движения)
Опять же, подумайте о двух зубчатых колесах, сцепленных вместе. Предположим, что верхнее колесо — это ваше колесо, а нижнее — ковер. Если бы у каждой «шестерни» не было зубьев, передача мощности происходила бы за счет трения между двумя поверхностями. Когда вы добавляете зубья к каждой шестерне, трение по поверхности шестерни не имеет значения. Вместо этого сила передается от поверхности одного зуба одной шестерни к поверхности зуба второй шестерни через крутящий момент.
Предположим, что верхнее колесо — это ваше колесо, а нижнее — ковер. Если бы у каждой «шестерни» не было зубьев, передача мощности происходила бы за счет трения между двумя поверхностями. Когда вы добавляете зубья к каждой шестерне, трение по поверхности шестерни не имеет значения. Вместо этого сила передается от поверхности одного зуба одной шестерни к поверхности зуба второй шестерни через крутящий момент.
Когда двигатели выдают крутящий момент, превышающий силу трения между двумя гладкими поверхностями, поверхности скользят. Когда те же самые поверхности зацеплены, они не могут скользить, поэтому мощность передается более эффективно (или ломаются зубья).
Шестеренки — это упрощенный пример явления, которое происходит, когда объекты неправильной формы взаимодействуют с ковром. Поскольку материалы ковров и лент являются гибкими и неравномерными, соотношение похоже, но не совсем то же самое.
РЕДАКТИРОВАТЬ: Итак, чтобы действительно ответить на ваш вопрос; Нет, уравнение, которое вы привели, неверно. На самом деле нет никакого простого уравнения, чтобы охарактеризовать это поведение, потому что контактные поверхности меняются при любом заданном движении бесчисленным множеством способов, включая, среди прочего, площадь и угол контактной поверхности. Если бы определение математической взаимосвязи между ячеистыми сервисами было абсолютной необходимостью, я бы провел эксперименты и определил «мю», понимая, что мы имеем дело вовсе не с трением. Вместо этого вы инкапсулируете взаимодействие многих лиц в одну систему и относитесь к этой системе как к трению. Однако это не трение. Надеюсь, это поможет.
На самом деле нет никакого простого уравнения, чтобы охарактеризовать это поведение, потому что контактные поверхности меняются при любом заданном движении бесчисленным множеством способов, включая, среди прочего, площадь и угол контактной поверхности. Если бы определение математической взаимосвязи между ячеистыми сервисами было абсолютной необходимостью, я бы провел эксперименты и определил «мю», понимая, что мы имеем дело вовсе не с трением. Вместо этого вы инкапсулируете взаимодействие многих лиц в одну систему и относитесь к этой системе как к трению. Однако это не трение. Надеюсь, это поможет.
Адам_Y
№13
Это совершенно сбивает с толку. Слышишь, это я понимаю. Трение не зависит от площади поверхности, почти на каждом веб-сайте это написано. Но другие веб-сайты, которые я искал, описывают площадь поверхности как способ улучшить сцепление. Очевидно, сцепление и трение — это не одно и то же, так что же такое сцепление?
Но другие веб-сайты, которые я искал, описывают площадь поверхности как способ улучшить сцепление. Очевидно, сцепление и трение — это не одно и то же, так что же такое сцепление?
система
№14
* Первоначально отправлено wysiswyg *
** Это совершенно сбивает с толку. Слышишь, это я понимаю. Трение не зависит от площади поверхности, почти на каждом веб-сайте это написано. Но другие веб-сайты, которые я искал, описывают площадь поверхности как способ улучшить сцепление. Очевидно, сцепление и трение — это не одно и то же, так что же такое сцепление? **
Тяга — это слово. Не существует физических единиц, связанных с тягой так же, как с трением, или массой, или скоростью (т. е. трение измеряется в ньютонах, но тяга не измеряется ни в чем. )
)
Сила трения, напротив, измеряется в ньютонах. Это происходит между двумя поверхностями, скользящими вместе.
Хорошая «тяга» достигается за счет оптимального использования выходного крутящего момента наших двигателей и редукторов. Это означает, по сути, что мы пытаемся максимизировать силу, которая используется для движения робота по полу, избегая при этом двух ситуаций — остановки двигателей или проскальзывания колес.
Адам_Y
№15
Неважно, что вы ответили на вопрос со сценарием снаряжения. Чем больше у вас площадь поверхности, тем больше места у вас есть, чтобы сцепиться с крошечными неровностями на земле. Хе-хе, между прочим, я нашел эту небольшую интересную информацию о резиновых шинах.
Шинына самом деле являются наиболее цепкими, когда проскальзывание составляет около 5%.
VanWEric
№16
Существует три основных типа трения: кинетическое статическое и трение качения. Когда вы двигали блоки массы в физике, вы изучали кинетическое и статическое трение, и вся эта ерунда с F=µN была правдой.
Роб говорит о трении качения. Все формы трения зависят от площади поверхности, но в кинетическом и статическом — очень незначительно. Сила, зависящая от площади, на несколько порядков слабее силы µN, поэтому формула Ff = µN + действительно очень малое число. Трение качения почти полностью зависит от слабых сил. Это связано с тем, что шина технически не движется против дороги. Если бы это было так, это было бы заносом. Понаблюдайте за тем, как колесо какое-то время движется — точка соприкосновения с дорогой остается на том же участке дороги, пока ее не оторвут от нее. Поэтому, когда ваши шины начинают вращаться, вы теряете эффект дополнительной площади.
Поэтому, когда ваши шины начинают вращаться, вы теряете эффект дополнительной площади.
Сегодня вечером я посмотрю свой новый учебник по физике. Может быть, я смогу это прояснить. И если я ошибаюсь, что, вероятно, так и есть, прошу прощения. Но я считаю, что вам нужно учитывать разницу между кинетическим трением и трением качения.
Взгляните на эти сайты.
http://www.school-for-champions.com/science/frictionrolling2.htm
http://hyperphysics.phy-astr.gsu.edu/hbase/frict2.html
Gary_Dillard
# 17
*Первоначально написал М. Красс *
**
Если материал на вашем колесе не имеет гладкой поверхности, в том смысле, что он взаимодействует с волокнами ковра, ваше сцепление с дорогой увеличится. Не существует установленного фактора, определяющего, насколько это эффективно.В то время как гладкая поверхность колеса инвалидной коляски приводит в движение робота за счет трения, неровная поверхность, которая зацепляется с волокнами ковра, приводит в движение робота за счет как трения (сила скольжения между гладкими частями колеса и ковром), так и крутящего момента ( контакт между двумя поверхностями, перпендикулярными направлению движения)
**
ОК — Завтра вечером, когда моя дочь (IBApril180 на этой доске) закончит работу, мы опубликуем здесь результаты ее научного эксперимента, что, признаться, меня удивило. Используя ремни Brecoflex и ковровое покрытие FIRST spec, сцепление увеличилось за счет УМЕНЬШЕНИЯ площади контакта! По-видимому, это связано с тем, что влияние дополнительной деформации ковра из-за более высокого местного давления было эффектом более высокого порядка, чем дополнительное количество «выступов», взаимодействующих с ковром. Это бросило нашу F = mu N + nu Гипотеза за окном. Следите за обновлениями.
Адам_Y
# 18
ОК — Завтра вечером, когда моя дочь (IBApril180 на этой доске) закончит работу, мы опубликуем здесь результаты ее научного эксперимента, который, должен признаться, меня удивил. Используя ремни Brecoflex и ковровое покрытие FIRST spec, сцепление увеличилось за счет УМЕНЬШЕНИЯ площади контакта! По-видимому, это связано с тем, что влияние дополнительной деформации ковра из-за более высокого местного давления было эффектом более высокого порядка, чем дополнительное количество «выступов», взаимодействующих с ковром. Это бросило нашу F = mu N + nu Гипотеза за окном. Следите за обновлениями.
Этого не может быть. Формула неверна, но есть некоторая корреляция между площадью поверхности и сцеплением. Ах, я вижу, если у вас есть два объекта с одинаковым давлением, тот, у которого больше площадь поверхности, будет иметь большее сцепление, чем тот, у которого нет. Вот почему танковые гусеницы работают, и вам нужны тележки в гусеницах, чтобы давление на гусеницу было на всем протяжении.
Ах, я вижу, если у вас есть два объекта с одинаковым давлением, тот, у которого больше площадь поверхности, будет иметь большее сцепление, чем тот, у которого нет. Вот почему танковые гусеницы работают, и вам нужны тележки в гусеницах, чтобы давление на гусеницу было на всем протяжении.
система
# 19
Первоначально отправлено Гэри Диллардом *
**ОК — Завтра вечером, когда моя дочь (IBApril180 на этой доске) закончит, мы опубликуем здесь результаты ее научного эксперимента, который, должен признать, меня удивил. Используя ремни Brecoflex и ковровое покрытие FIRST spec, сцепление увеличилось за счет УМЕНЬШЕНИЯ площади контакта! По-видимому, это связано с тем, что влияние дополнительной деформации ковра из-за более высокого местного давления было эффектом более высокого порядка, чем дополнительное количество «выступов», взаимодействующих с ковром.Это бросило нашу F = mu N + nu*A гипотеза в окно. Следите за обновлениями. **
Оооо. Принесите его по номеру
Ваша дочь может иметь на руках белую бумагу. Я с нетерпением жду, чтобы прочитать это, и это как раз вовремя.
Вы уверены, что нет характеристик ремня, которые могли бы способствовать этому открытию так, как другие материалы не могли бы? Справедливы ли результаты, например, для колес инвалидных колясок?
Джим_Мейер
#20
В прошлом году мы провели аналогичный тест с неопреновым материалом прокладки (доступен в spi). Наш тест немного отличался тем, что у нас было два колеса, покрытых этим материалом, а также большая пластина, покрытая тем же материалом. Мы использовали около 70 фунтов собственного веса и немного ковра FIRST.



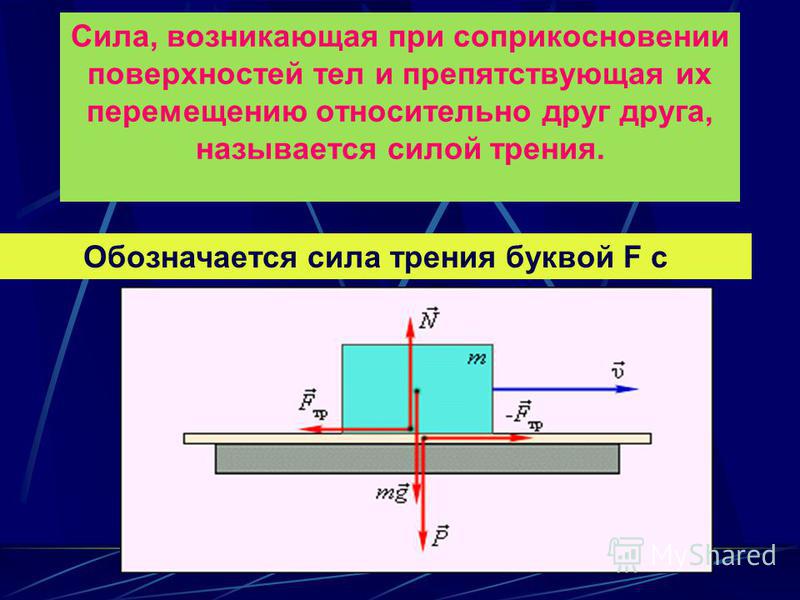
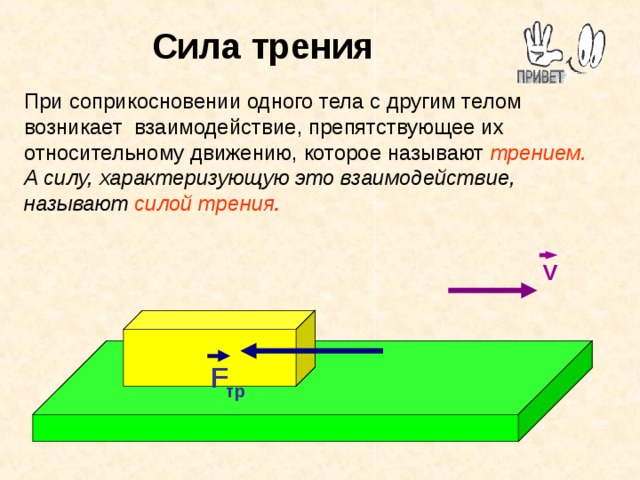 3 Законы сохранения
3 Законы сохранения СТО
СТО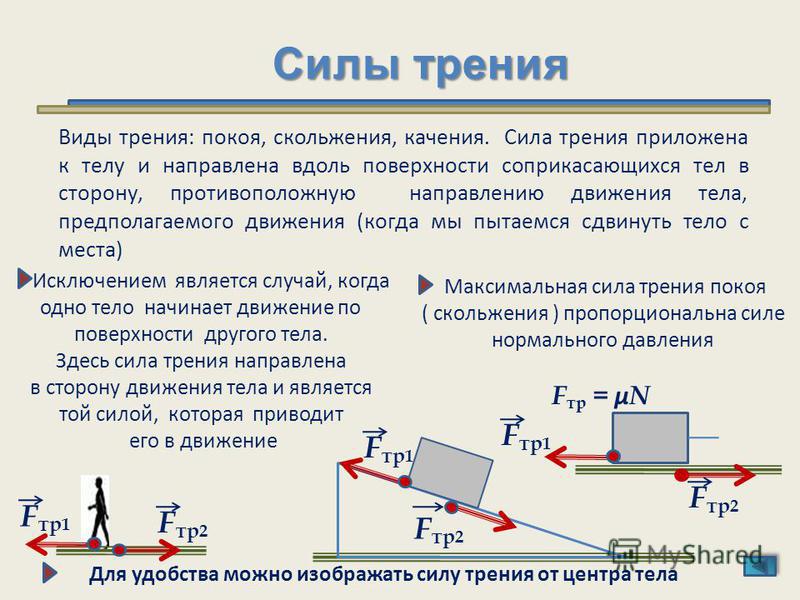
 Коэффициент
статическое трение стали о сталь составляет около 1/4, поэтому ни один локомотив не может
тянуть с силой, превышающей примерно 1/4 собственного веса. Если
двигатель способен развивать большее усилие, т.
результатом будет просто нарушение статического трения и вращение колес.
Коэффициент
статическое трение стали о сталь составляет около 1/4, поэтому ни один локомотив не может
тянуть с силой, превышающей примерно 1/4 собственного веса. Если
двигатель способен развивать большее усилие, т.
результатом будет просто нарушение статического трения и вращение колес.