Сила трения | ЕГЭ по физике
Основные понятия и законы кинематики
Часть механики, в которой изучают движение, не рассматривая причины, вызывающие тот или иной характер движения, называют кинематикой.
Механическим движением называют изменение положения тела относительно других тел
Системой отсчёта называют тело отсчёта, связанную с ним систему координат и часы.
Телом отсчёта называют тело, относительно которого рассматривают положение других тел.
Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.
Траекторией называют мысленную линию, которую при своём движении описывает материальная точка.
По форме траектории движение делится на:
а) прямолинейное — траектория представляет собой отрезок прямой;
б) криволинейное — траектория представляет собой отрезок кривой.
Путь — это длина траектории, которую описывает материальная точка за данный промежуток времени.
Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).
Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение — это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось). А путь — это, наборот, скалярная величина, отражающая длину пройденной траектории.
Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения
Скоростью равномерного прямолинейного движения
Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:
Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.
Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину
Ускорением называют отношение изменения мгновенной скорости тела ко времени, за которое это изменение произошло:
Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x0 + Vxt, где x0 — начальная координата тела, Vx — скорость движения.
Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с2, не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.
Скорость при свободном падении рассчитывается по формуле:
Перемещение по вертикали рассчитывается по формуле:
Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость).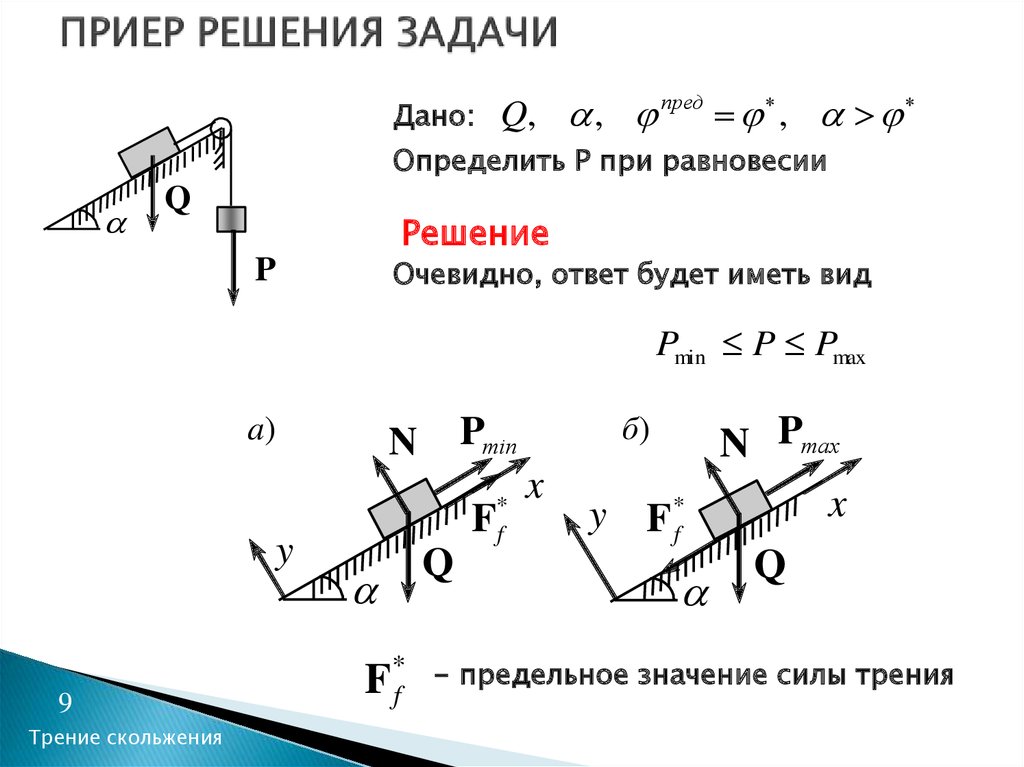 Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название
Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название
Угловая скорость связана с линейной скоростью соотношением
где r — радиус окружности.
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду — частота обращения — ν
Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением, оно направлено по радиусу к центру окружности:
Основные понятия и законы динамики
Часть механики, изучающая причины, вызвавшие ускорение тел, называется
Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией. Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.
Принцип относительности Галилея:
во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законам
Масса — это мера инертности тела
Сила — это количественная мера взаимодействия тел.
Второй закон Ньютона:
Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F↖{→} = m⋅a↖{→}$
Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.
Третий закон Ньютона:
Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело
A (см. рис.).
Если тело A действует на тело B, то и тело B действует на тело
A (см. рис.).
Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.
Закон Гука записывают в виде
где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.
При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения подсчитывается по формуле
где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.
Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значения
Гравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.
Закон всемирного тяготения:
любые два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
Здесь R — расстояние между телами. Закон всемирного тяготения в таком виде справедлив либо для материальных точек, либо для тел шарообразной формы.
Весом тела называют силу, с которой тело давит на горизонтальную опору или растягивает подвес.
Сила тяжести — это сила, с которой все тела притягиваются к Земле:
При неподвижной опоре вес тела равен по модулю силе тяжести:
Если тело движется по вертикали с ускорением, то его вес будет изменяться.
При движении тела с ускорением, направленным вверх, его вес
Видно, что вес тела больше веса покоящегося тела.
При движении тела с ускорением, направленным вниз, его вес
В этом случае вес тела меньше веса покоящегося тела.
Невесомостью называется такое движение тела, при котором его ускорение равно ускорению свободного падения, т.е. a = g. Это возможно в том случае, если на тело действует только одна сила — сила тяжести.
Искусственный спутник Земли — это тело, имеющее скорость V1, достаточную для того, чтобы двигаться по окружности вокруг Земли
На спутник Земли действует только одна сила — сила тяжести, направленная к центру Земли
Первая космическая скорость — это скорость, которую надо сообщить телу, чтобы оно обращалось вокруг планеты по круговой орбите.
где R — расстояние от центра планеты до спутника.
Для Земли, вблизи её поверхности, первая космическая скорость равна
1.3. Основные понятия и законы статики и гидростатики
Тело (материальная точка) находится в состоянии равновесия, если векторная сумма сил, действующих на него, равна нулю. Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное. Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это устойчивое равновесие. Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это неустойчивое положение; если никаких сил не возникает — безразличное (см. рис. 3).
Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное. Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это устойчивое равновесие. Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это неустойчивое положение; если никаких сил не возникает — безразличное (см. рис. 3).
Когда речь идёт не о материальной точке, а о теле, которое может иметь ось вращения, то для достижения положения равновесия помимо равенства нулю суммы сил, действующих на тело, необходимо, чтобы алгебраическая сумма моментов всех сил, действующих на тело, была равна нулю.
Здесь d —плечо силы. Плечом силы d называют расстояние от оси вращения до линии действия силы.
Условие равновесия рычага:
алгебраическая сумма моментов всех вращающих тело сил равна нулю.
Давлением называют физическую величину, равную отношению силы, действующей на площадку, перпендикулярную этой силе, к площади площадки:
Для жидкостей и газов справедлив закон Паскаля:
давление распространяется по всем направлениям без изменений.
Если жидкость или газ находятся в поле силы тяжести, то каждый вышерасположенный слой давит на нижерасположенные и по мере погружения внутрь жидкости или газа давление растёт. Для жидкостей
где ρ — плотность жидкости, h — глубина проникновения в жидкость.
Однородная жидкость в сообщающихся сосудах устанавливается на одном уровне. Если в колена сообщающихся сосудов залить жидкость с разными плотностями, то жидкость с большей плотностью устанавливается на меньшей высоте. В этом случае
Высоты столбов жидкости обратно пропорциональны плотностям:
Гидравлический пресс представляет собой сосуд, заполненный маслом или иной жидкостью, в котором прорезаны два отверстия, закрытые поршнями. Поршни имеют разную площадь. Если к одному поршню приложить некоторую силу, то сила, приложенная ко второму поршню, оказывается другой.
Таким образом, гидравлический пресс служит для преобразования величины силы. Поскольку давление под поршнями должно быть одинаковым, то
Тогда A1 = A2.
На тело, погружённое в жидкость или газ, со стороны этой жидкости или газа действует направленная вверх выталкивающая сила, которую называют силой Архимеда
Величину выталкивающей силы устанавливает закон Архимеда: на тело, погружённое в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости или газа, вытесненного телом:
где ρжидк — плотность жидкости, в которую погружено тело; Vпогр — объём погружённой части тела.
Условие плавания тела — тело плавает в жидкости или газе, когда выталкивающая сила,действующая на тело, равна силе тяжести, действующей на тело.
1.4. Законы сохраненияИмпульсом тела называют физическую величину, равную произведению массы тела на его скорость:
Импульс — векторная величина. [p] =кг·м/с. Наряду с импульсом тела часто пользуются импульсом силы. Это произведение силы на время её действия
Изменение импульса тела равно импульсу действующей на это тело силы. Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется закон сохранения импульса: сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется закон сохранения импульса: сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Механической работой называют физическую величину, которая равна произведению силы, действующей на тело, на перемещение тела и на косинус угла между направлением силы и перемещения:
Мощность — это работа, совершённая в единицу времени:
Способность тела совершать работу характеризуют величиной, которую называют энергией. Механическую энергию делят на кинетическую и потенциальную. Если тело может совершать работу за счёт своего движения, говорят, что оно обладает кинетической энергией. Кинетическая энергия поступательного движения материальной точки подсчитывается по формуле
Если тело может совершать работу за счёт изменения своего положения относительно других тел или за счёт изменения положения частей тела, оно обладает потенциальной энергией. Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле
Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле
где h — высота подъёма
Энергия сжатой пружины:
где k — коэффициент жёсткости пружины, x — абсолютная деформация пружины.
Сумма потенциальной и кинетической энергии составляет механическую энергию. Для изолированной системы тел в механике справедлив закон сохранения механической энергии: если между телами изолированной системы не действуют силы трения (или другие силы, приводящие к рассеянию энергии), то сумма механических энергий тел этой системы не изменяется (закон сохранения энергии в механике). Если же силы трения между телами изолированной системы есть, то при взаимодействии часть механической энергии тел переходит во внутреннюю энергию.
1.5. Механические колебания и волныКолебаниями называются движения, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
Гармоническими колебаниями называются такие колебания, в которых колеблющаяся физическая величина x изменяется по закону синуса или косинуса, т.е.
Величина A, равная наибольшему абсолютному значению колеблющейся физической величины
x, называется амплитудой колебаний. Выражение α = ωt + ϕ определяет значение x в данный момент времени и называется фазой колебаний. Периодом T называется время, за которое
колеблющееся тело совершает одно полное колебание. Частотой периодических колебаний называют число полных колебаний, совершённых за единицу времени:
Частота измеряется в с-1. Эта единица называется герц (Гц).
Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости.
Если один конец пружины закрепить неподвижно, а к другому её концу прикрепить некоторое тело массой m, то при выведении тела из положения равновесия пружина растянется и возникнут колебания тела на пружине в горизонтальной или вертикальной плоскости. Такой маятник называется пружинным.
Такой маятник называется пружинным.
Период колебаний математического маятника определяется по формуле
где l — длина маятника.
Период колебаний груза на пружине определяется по формуле
где k — жёсткость пружины, m — масса груза.
Распространение колебаний в упругих средах.
Среда называется упругой, если между её частицами существуют силы взаимодействия. Волнами называется процесс распространения колебаний в упругих средах.
Волна называется поперечной, если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны.
Длиной волны называется расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе:
где v — скорость распространения волны.
Звуковыми волнами называют волны, колебания в которых происходят с частотами от 20 до 20 000 Гц.
Скорость звука различна в различных средах. Скорость звука в воздухе равна 340 м/c.
Ультразвуковыми волнами называют волны, частота колебаний в которых превышает 20 000 Гц. Ультразвуковые волны не воспринимаются человеческим ухом.
Молекулярная теория трения
Автор(ы): Бондарев Олег Викторович
Рубрика: Технические науки
Журнал: «Евразийский Научный Журнал №11 2017» (ноябрь, 2017)
Количество просмотров статьи: 3484
Показать PDF версию Молекулярная теория трения
Бондарев Олег Викторович
инженер
Как свидетельствуют различные публикации на тему исследований трения скольжения [1,4; 2,5], явной связи сил и коэффициентов трения с физическими свойствами тел и состоянием их поверхностей установить не удалось. Это позволило сделать вывод, что такая связь отсутствует.
Рассмотрим тела, являющиеся упругими монолитами, имеющие шероховатые поверхности с хаотически выступающими неровностями. Схематично эти поверхности изображены на рис.1.
Схематично эти поверхности изображены на рис.1.
Из рисунка видно, что для горизонтального перемещения тела в данном случае необходимо приложить силу для его подъема на имеющиеся неровности, пусть микроскопические, но буквально в то же время, затраченная на такой микроподъем энергия, будет возвращена скатыванием в микроскопические углубления. В случае хаотического расположения неровностей на поверхностях в условиях их упругих деформаций, потери энергии, и ее возврат при движении будут происходить фактически одновременно, не требуя приложения силы на перемещение тела. Таким образом, влияния таких шероховатостей на силу трения скольжения нет, такие шероховатости могут влиять только на, так называемую, силу трения покоя, требуя приложения силы в момент начала движения, для первоначального подъема тела на микро выступы.
Как известно [3,207; 3,255; 4,8; 4,45], между всеми молекулами действуют межмолекулярные силы притяжения и отталкивания. Суммарное их действие в зависимости от расстояния между молекулами показано на графике (рис. 2).
Суммарное их действие в зависимости от расстояния между молекулами показано на графике (рис. 2).
Силы притяжения проявляют себя на всех расстояниях между молекулами и прекращают свое действие лишь на бесконечном удалении молекул друг от друга, а силы отталкивания становятся значительно слабее сил притяжения и практически прекращают проявлять себя на расстояниях более r0. Соответственно на расстояниях менее r0 доминируют силы отталкивания, которые здесь превышают силы притяжения, а на расстоянии r = r0 силы отталкивания и притяжения равны между собой. Если нет действия внешних сил сжимающих или растягивающих тело, его молекулы за счет имеющейся внутренней энергии колеблются относительно r0, при этом расстояние между ними попеременно изменяется от r = rmin до r = rmax, в точках rmin и rmax кинетическая энергия колебаний равна нулю, а потенциальная максимальна, а в точке r = r0 наоборот кинетическая энергия максимальна, а потенциальная равна нулю.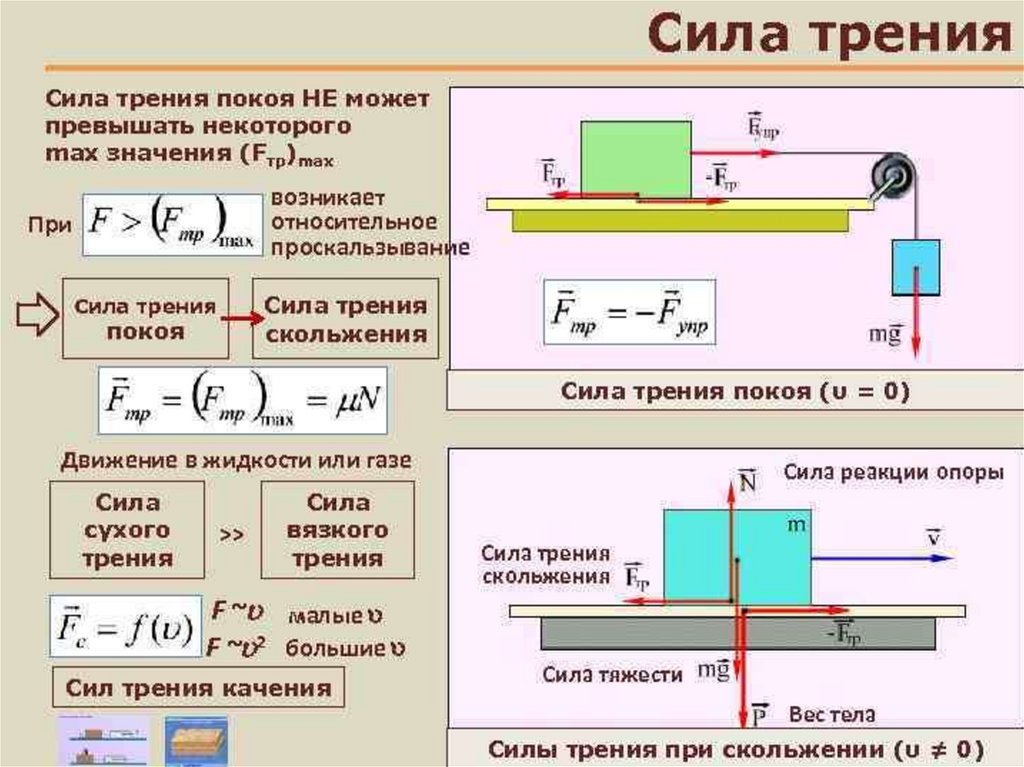 В случае действия сжимающих внешних сил, центр колебаний смещается в зону r < r0 (здесь r — среднее расстояние между молекулами) и действие внешних сил компенсируется внутренними межмолекулярными силами отталкивания. При растяжении центр колебаний смещается в зону r > r0 и внешним силам противодействуют силы межмолекулярного притяжения.
В случае действия сжимающих внешних сил, центр колебаний смещается в зону r < r0 (здесь r — среднее расстояние между молекулами) и действие внешних сил компенсируется внутренними межмолекулярными силами отталкивания. При растяжении центр колебаний смещается в зону r > r0 и внешним силам противодействуют силы межмолекулярного притяжения.
При рассмотрении действия внешних сил на молекулы можно оперировать смещением r относительно r0, а именно величиной Dr=r0-r (1). Для упрощения понимания влияния внешних сил на межмолекулярные силы, можно использовать модель, где между молекулами присутствуют некие межмолекулярные «пружины». Не принимая во внимание амплитуду и частоту имеющихся колебаний молекул под действием тепловой энергии, силу, действующую между молекулами, можно выразить как f=k.Dr (2), где k — коэффициент жесткости межмолекулярной пружины. Согласно рис.2 зависимость между f и Dr близка к линейной. Значения k могут быть вычислены для различных материалов, исходя, например, из модулей упругости, если таковые известны, в других случаях могут быть определены экспериментально. Для материалов, у которых усредненное значение k сильно зависит от температуры (амплитуды колебаний молекул), может быть определен набор коэффициентов k соответствующих каждый своей температуре.
Для материалов, у которых усредненное значение k сильно зависит от температуры (амплитуды колебаний молекул), может быть определен набор коэффициентов k соответствующих каждый своей температуре.
Так как силы притяжения проявляют себя на расстояниях более r0 вплоть до бесконечности, то действуя со всех сторон на перемещаемое тело, они, как при его движении, так и в состоянии его покоя, будут уравновешивать друг друга, тем самым не создавая никаких препятствий и сопротивлений его перемещению. Таким образом, силы притяжения не являются причиной потерь энергии на трение. На межмолекулярном уровне, если молекулы электрически нейтральны, действуют только силы межмолекулярного притяжения и отталкивания [4, 8,9], следовательно, единственной оставшейся причиной возникновения трения для упругих монолитов являются силы межмолекулярного отталкивания.
Происходит это следующим образом: под действием своего веса или какой-либо другой силы тело прижимается к поверхности, что вызывает некоторую, пусть незначительную, деформацию (появление Dr), как между молекулами перемещаемого тела, так и поверхности по которой оно перемещается, расстояние между молекулами становится меньше r0, между ними начинают преобладать силы отталкивания.
Если представить ранее предложенную модель, где между молекулами имеются некие «пружины», то в данном случае эти «пружины», пусть на очень малую величину, сжимаются. При перемещении тела относительно поверхности вертикально вверх, перпендикулярно поверхности, межмолекулярные «пружины», разжимаясь, отдают запасенную под силой давления в себе энергию в полезную сторону, внося свой вклад в работу по подъему тела. При горизонтальном же перемещении тела, т. е. при перемещении тела по поверхности (см. рис. 3), «пружины» сжатые перпендикулярно поверхности, распрямляясь, перемещению тела никакой энергии не добавляют, а отдают, запасенную в себе под действием веса тела или другой силы прижимающей тело к поверхности, энергию находящимся на их концах молекулам, повышая их кинетическую энергию и, как следствие, температуру тела и поверхности, увеличивая их амплитуду колебаний. Причина потерь энергии на трение скольжения в том, что при разрыве связи, установленной силами отталкивания, «пружины» крайних молекул, потеряв противодействие, разжимаются в направлении перпендикулярном направлению движения, повышая амплитуду колебаний как самих этих молекул, так и молекул соседних с ними, повышая тем самым их тепловую энергию.
Определяющим для величины силы трения является взаимодействие молекул находящихся на поверхности тел.
Учитывая сложную структуру веществ тела и поверхности, уместно предположить, что при упомянутой выше деформации будет иметь место сжатие межмолекулярных «пружин», как в вертикальной, так и в горизонтальной (параллельной поверхности перемещения) плоскости, но при перемещении тела равновесие «пружин», сжатых в горизонтальном направлении, не нарушается и сжатие «пружин» со стороны направления движения компенсируется распрямлением «пружин» с противоположной стороны и на увеличение внутренней энергии (температуры тел) они не работают, так как возвращают свою потенциальную энергию сжатых «пружин» на совершение работы по перемещению тела, компенсируя затраты энергии на такое же сжатие таких же пружин с противоположной его стороны.
Рис.3
На рис. 3 схематично показаны: М1 — молекулы поверхности по которой происходит перемещение; М2 — молекулы перемещаемого тела.
В случае неупругих деформаций вероятно следует учитывать дополнительные затраты энергии на соответствующие изменения формы тела или структуры вещества. А для сыпучих веществ на перемещаемую массу сыпучего вещества.
Количественное выражение для трения скольжения выведем исходя из работы, затрачиваемой на сжатие межмолекулярных «пружин» в направлении перпендикулярном направлению движения.
Если для определения силы и величины сжатия межмолекулярных «пружин», как было сказано выше, колебания молекул под действием тепловой энергии учитывать необходимости нет, то для определения работы по сжатию межмолекулярных «пружин». важна величина амплитуды этих колебаний. Расстояние между точками r0 и rmin (см. рис.2) являющееся амплитудой колебаний можно обозначить как Ar. При сравнительно больших Ar, имеющих место при наиболее часто встречающихся температурах Dr <<< Ar, так как сжимающее усилие обычно распределено на очень огромное число молекул. Исходя из того, что колебания являются гармоническими, или, по крайней мере, очень близки к гармоническим, величину увеличения потенциальной энергии молекул от сжатия внешней силой межмолекулярных «пружин» можно записать, как DPpot = F. Ar.2/p (формула 3), где F- внешняя сжимающая сила. В случаях, когда температура будет близка к абсолютному нулю и Ar будет очень и очень мала Ar <<< Dr, будет правильным выражение DPpot = F. Dr /2 (формула 4).
Исходя из того, что колебания являются гармоническими, или, по крайней мере, очень близки к гармоническим, величину увеличения потенциальной энергии молекул от сжатия внешней силой межмолекулярных «пружин» можно записать, как DPpot = F. Ar.2/p (формула 3), где F- внешняя сжимающая сила. В случаях, когда температура будет близка к абсолютному нулю и Ar будет очень и очень мала Ar <<< Dr, будет правильным выражение DPpot = F. Dr /2 (формула 4).
При перемещении тела на величину r0 (среднее расстояние между молекулами) вся энергия DPpot выделится, перейдя в тепловую, так как при таком перемещении разорвутся установившиеся связи («пружинки») между молекулами перемещаемого тела и молекулами поверхности перемещения. Выделившаяся энергия равна работе силы трения. В результате можно записать, что fтр..r0 = DPpot1 + DPpot2 , где fтр. — сила трения; DPpot1 и DPpot2 — приращения внутренней потенциальной энергии соответственно перемещаемого тела и поверхности перемещения, вызванные давлением тела на поверхность. Таким образом, величина силы трения скольжения равна fтр. = (DPpot1 + DPpot2) / r0, а с учетом формулы 3 fтр. = F. (Ar1 + Ar2).2/p.r0 (формула 5). Выражение (Ar1 + Ar2).2/p.r0 является коэффициентом трения скольжения, т.е. kтр. = (Ar1 + Ar2).2/p.r0 (формула 6), величина r0 должна приниматься наименьшей из двух вариантов (поверхность, тело), при этом для материалов сложной структуры и смешанного химического состава, входящие в формулу 6 величины могут приниматься средневзвешенными с учетом процентного содержания всех компонентов.
— сила трения; DPpot1 и DPpot2 — приращения внутренней потенциальной энергии соответственно перемещаемого тела и поверхности перемещения, вызванные давлением тела на поверхность. Таким образом, величина силы трения скольжения равна fтр. = (DPpot1 + DPpot2) / r0, а с учетом формулы 3 fтр. = F. (Ar1 + Ar2).2/p.r0 (формула 5). Выражение (Ar1 + Ar2).2/p.r0 является коэффициентом трения скольжения, т.е. kтр. = (Ar1 + Ar2).2/p.r0 (формула 6), величина r0 должна приниматься наименьшей из двух вариантов (поверхность, тело), при этом для материалов сложной структуры и смешанного химического состава, входящие в формулу 6 величины могут приниматься средневзвешенными с учетом процентного содержания всех компонентов.
Величины Ar1 и Ar2 , зная величину внутренней энергии приходящейся на одну межмолекулярную «пружину» (Епр.), можно определить из формулы Ar2=2.Епр./k [3, 267; 3,274]
Для случаев, когда справедлива формула 4 сила трения составит fтр. = F. Drср./ 2r0 (формула 7). Так как величина Dr в свою очередь зависит от величины сжимающей силы то приходящееся на одну молекулу Dr = F/(kж.N), где kж — коэффициент жесткости межмолекулярной «пружины» в области низких температур, N — количество пар молекул сжимаемых под действием внешней силы. Величина Drср. (для формулы 7) будет равна Drср. = F(kж1.N1 + kж2.N2)/ kж1.N1.kж2.N2. С малой степенью погрешности при определении N можно учитывать только молекулы находящиеся на поверхностях в пятне контакта тел, фактически важно их соотношение (соотношение плотностей). Для определения силы трения в этом случае будет справедлива формула: fтр. = F2(kж1.N1 + kж2.N2)/ (kж1.N1.kж2.N2.2r0) (формула 8). N, как правило, является очень большой величиной, практически стремящейся к бесконечности, и при близких по значению величинах N1 и N2 сила fтр. в рассматриваемом случае при росте количества N стремится к нулю.
Для определения силы трения в этом случае будет справедлива формула: fтр. = F2(kж1.N1 + kж2.N2)/ (kж1.N1.kж2.N2.2r0) (формула 8). N, как правило, является очень большой величиной, практически стремящейся к бесконечности, и при близких по значению величинах N1 и N2 сила fтр. в рассматриваемом случае при росте количества N стремится к нулю.
При качении также происходит сжатие межмолекулярных «пружин» под действием сил прижимающих тела друг к другу, но в отличие от скольжения энергия этого сжатия почти полностью возвращается перекатываемому телу. При качении молекулы колеса от молекул поверхности отрываются не по циклоиде, чем больше диаметр (радиус) колеса, тем больше в траектории движения молекул (в пределах деформации в месте контакта колеса и поверхности) вертикальной составляющей и меньше составляющей горизонтальной, порождающей трение аналогично скольжению. Таким образом, величина трения качения кроме величины силы F и коэффициента трения зависит также от диаметра колеса, чем больше диаметр — меньше трение, чем меньше диаметр больше трение. Кроме того, при качении за счет деформации колеса и поверхности, отталкивание молекул колеса от молекул поверхности начинается не в нижней точке циклоиды, где скорость встречи колеса с поверхностью равна нулю, а раньше, где, особенно в случаях больших деформаций, скорость имеет существенную величину, увеличивая прижимающую колесо к поверхности силу и, тем самым, дополнительно потери энергии на трение. Таким образом, трение качения зависит еще и от скорости, чем выше скорость, тем больше потери энергии на трение.
Таким образом, величина трения качения кроме величины силы F и коэффициента трения зависит также от диаметра колеса, чем больше диаметр — меньше трение, чем меньше диаметр больше трение. Кроме того, при качении за счет деформации колеса и поверхности, отталкивание молекул колеса от молекул поверхности начинается не в нижней точке циклоиды, где скорость встречи колеса с поверхностью равна нулю, а раньше, где, особенно в случаях больших деформаций, скорость имеет существенную величину, увеличивая прижимающую колесо к поверхности силу и, тем самым, дополнительно потери энергии на трение. Таким образом, трение качения зависит еще и от скорости, чем выше скорость, тем больше потери энергии на трение.
Аналогично рассмотренным выше случаям трения упругих монолитов, от сжатия межмолекулярных «пружин» зависят и величины гидродинамических и аэродинамических сопротивлений, имеющих место в жидких и газообразных средах. В виду обширности материала по этой теме их описание в объем настоящей статьи не вошло.
Литература.
- Заднепровский Р. П. Теория трения скольжения. Волгоград; издательство «Офсет». 2005 г.
- Каржавин В. В., Зимин А. И. Трение, износ и смазочные материалы. Учеб. пособие. Екатеринбург; РГППУ. 2003 г.
- Зисман Г. А., Тодес О. М. Курс общей физики. Том 1. М.; издательство «Наука». 1969 г.
- Малеев А. В. Лекции по физике твердого тела. Владимир; ВлГУ. 2015 г.
Силы трения и Специальная теория относительности
Реферат
- формат ppt
- размер 9.54 МБ
- добавлен 11 апреля 2011 г.
Издательство: ФизФак МГУ. Год: 2010-2011. Представлены очень
интересные презентации с лекций Физфака МГУ по следующим темам:
Силы трения и Специальная теория относительности.
Энергия, Работа, Мощность.
Сохранение импульса. Момент сил, Силы инерции.
Момент инерции, Теорема Штейнера.
Поверхностное натяжение, Уравнение Бернулли.
Колебания
Волны
Основные положения, Идеальный газ.
++++Обновление++++
Кинематика
Динамика
Вязкость, число Рейнольдса, Физика дождя, Капилярные явления
Распределения Максвелла, Больцмана, внутренняя энергия
1-е начало термодинамики, Теплоемкость, Работа
2-е начало термодинамики
Реальные газы
Похожие разделы
- Абитуриентам и школьникам
- ВНО / ЗНО
- ЗНО по физике
- Абитуриентам и школьникам
- ЕГЭ
- ЕГЭ по физике
- Абитуриентам и школьникам
- ОГЭ / ГИА / ДПА
- ОГЭ / ГИА / ДПА по физике
- Абитуриентам и школьникам
- Физика
- Академическая и специальная литература
- Механика
- Механика жидкостей и газов
- Академическая и специальная литература
- Педагогика
- Методики преподавания
- Методика преподавания физики
- Академическая и специальная литература
- Радиоэлектроника
- Антенная и СВЧ техника
- Электромагнитные поля и волны
- Академическая и специальная литература
- Радиоэлектроника
- Радиофизика
- Учебные планы, программы и нормативная документация
- Для средней школы
- Физика
- Учебные планы, программы и нормативная документация
- Физика
Смотрите также
Презентация
- формат ppt
- размер 1.
 4 МБ
4 МБ - добавлен 09 июня 2011 г.
Для понимания студентами и учениками основ динамики. В работу входят: Инерциальные системы отсчета Масса. Сила. Инертность Принцип суперпозиции сил Законы Ньютона Закон всемирного тяготения Сила тяжести Ускорение свободного падения 1я, 2-я и 3-я космические скорости Вес тела невесомость Сила упругости. Закон Гука Сила трения. Способы уменьшения. Увеличения силы трения.
Реферат
- формат doc
- размер 20.48 КБ
- добавлен 11 сентября 2010 г.
1. Введение. 2. Открытия Галилея в области астрономии. 3. Другие открытия Галилея. 4. Теория относительности. 5. Заключение.
- формат doc
- размер 62.
 13 КБ
13 КБ - добавлен 13 марта 2011 г.
Классификация сил, приложенных к частицам жидкости. Напряжения. Тензор напряжений. Все силы, приложенные к данной частице жидкости, можно разбить на два класса: 1) силы объёмные, то есть такие, которые действуют не только на поверхности жидкости, но и на внутренние части жидкости, заключенные в данном объёме, как например, силы веса, в известном условном смысле фиктивные силы инерции и другие (иногда ещё объёмные силы называют массовыми силами)…
- формат doc
- размер 863 КБ
- добавлен 23 января 2010 г.
Биография. Рождение теории относительности. Преобразования Лоренца. Закон взаимосвязи массы и энергии. Значение теории относительности.
- формат doc
- размер 245 КБ
- добавлен
01 марта 2010 г.

Введение. Основные законы механики. Первый закон Ньютона. Второй закон Ньютона. Третий закон Ньютона. Силы трения. Реализация основных законов механики. Общие сведения о подъемных установках. Продолжительность подъемной операции. Динамика подъемных систем. Нагрузки подъемного двигателя. Коэффициент полезного действия подъемной установки и машины. Выводы. Использованная литература.
- формат doc
- размер 139 КБ
- добавлен 21 октября 2008 г.
Введение. Принцип относительности Галилея Постулат относительности. Постулат постоянства скорости света. Теория Ритца и родственные теории. Относительность одновременности. Вывод преобразований Лоренца из обоих постулатов. Аксиоматика преобразований Лоренца. Лоренцево сокращение и замедление времени. Теорема сложения скоростей Эйнштейна. Аберрация. Коэффициент увеличения. Релятивистский импульс. Зависимость массы от скорости. Релятивистская энерг…
Аберрация. Коэффициент увеличения. Релятивистский импульс. Зависимость массы от скорости. Релятивистская энерг…
Реферат
- формат doc
- размер 201 КБ
- добавлен 20 апреля 2011 г.
Реферат 17листов Введение 1. Принцип и понятие эйнштейновской теории гравитации 2. Экспериментальная проверка общей теории относительности Проверка принципа эквивалентности Проверка постоянной тяготения Отклонение луча света в поле Солнца Изменение частоты в поле тяготения Запаздывание сигнала в поле Солнца Смещение перигелия Гравитационное линзирование Гравитационное излучение Заключение Список литературы Вуз — РГТЭУ ВФ специальность — экономика…
- формат doc
- размер 50 КБ
- добавлен
13 мая 2009 г.

Рождение теории относительности, Специальная теория относительности. 6 стр.
Реферат
- формат ppt
- размер 3.01 МБ
- добавлен 06 октября 2011 г.
Жизнь Альберта Эйнштейна Закон внешнего фотоэффекта Формула связи массы тела при излучении энергии Постуланы специальной теории Выводы из специальной теории Преобразования Лоренца Выводы из общей теории относительности Взгляды Пуанкаре Принцип относительности Пуанкаре и его лекция в США Доклад Пуанкре Сравнение теории Пуанкре и Эйнштейна Проверка теории относительности
Презентация
- формат ppt
- размер 6.
 41 МБ
41 МБ - добавлен 09 января 2011 г.
Презентация к докладу «Теория относительности и Альберт Эйнштейн». Уровень: вуз (для студентов не физических специальностей).
Сила трения в природе интересные факты. История возникновения силы трения
Наука
Европейские ученые предоставили современное объяснение происхождения трения скольжения между твердыми предметами. Несмотря на тот факт, что трение – это одно из основополагающих явлений современной прикладной физики, данный феномен не прекращают изучать уже на протяжении многих веков . Вплоть до наших дней считалось, что механическая износоустойчивость и наличие (или отсутствие) жидкой смазки являются одними из основных факторов, влияющих на трение, однако фундаментальные причины трения скольжения оставались неизвестными.
Доктор Лэйси Макконен, старший научный сотрудник Технического исследовательского центра в Финляндии, представил собственное объяснение происхождения трения скольжения между твердыми предметами. Его теория полностью подтверждает тот факт , что величина трения зависит также от так называемой поверхностной энергии рассматриваемых материалов. При этом трение оказывает значительный эффект на многие явления, с которыми мы сталкиваемся каждый раз (такие как, к примеру, поглощение энергии).
Его теория полностью подтверждает тот факт , что величина трения зависит также от так называемой поверхностной энергии рассматриваемых материалов. При этом трение оказывает значительный эффект на многие явления, с которыми мы сталкиваемся каждый раз (такие как, к примеру, поглощение энергии).
Новая термодинамическая модель, созданная Макконеном, является первой в своем роде, которая дает возможность определить количественные параметры коэффициента трения материалов с учетом поверхностной энергии материалов. Модель, фактически, показывает, что трение возникает при соприкосновении материалов на наноразмерном уровне , являясь следствием формирования новых связей на атомном уровне. Данная теория дополняет объяснение происхождения силы трения и наличия фрикционного нагрева при сухом трении. Ее также можно применить для более точного расчета коэффициентов трения комбинаций различных материалов.
Построенная модель также дает возможность более точно управлять процессами трения посредством выбора определенной поверхности материалов или посредством использования смазочных слоев, учитывая наличие поверхностной энергии между ними . Примечательно, что данная теория подтверждает мнения многих физиков о том, что во всем известных таблицах с представленными в них коэффициентами трения для различных материалов (особенно для однородных) присутствуют заметные неточности.
Примечательно, что данная теория подтверждает мнения многих физиков о том, что во всем известных таблицах с представленными в них коэффициентами трения для различных материалов (особенно для однородных) присутствуют заметные неточности.
Ответ оставил Гость
Силы трения, сопровождая нас повсюду, играют огромную роль в нашей жизни. Правда, мы не замечаем этого за повседневными заботами и чаще всего стремимся свести действие трения к минимуму. Подшипники, смазочные материалы, обтекаемые формы — все это и многое другое позволяет вести успешную борьбу с различными видами трения. На это уходит много сил и средств, благодаря чему сложилось мнение о вреде трения, о том, что если бы трение вдруг исчезло, то человек остался бы только в выигрыше. Но так ли это? Это далеко не так, ведь трение — и наш враг, и наш союзник. В каких-то случаях отсутствие трения грозит большими неприятностями (например, торможение автомобилей происходит только за счет сил трения, возникающих между колодками и барабаном), а в каких-то случаях даже минимальные силы трения оказывают самое вредное воздействие (например, в механических часах и тонких научных приборах). Однако, чтобы понять все значение трения, необходимо его «выключить» и проследить за будущими событиями. Итак, каким будет мир без сухого и вязкого трения всех видов? Мы не сможем ни ходить, ни передвигаться никаким другим способом. Ведь во время ходьбы подошвы наших ног испытывают трение с полом, а без трения мы будем чувствовать себя хуже, чем на самом гладком льду в самой скользкой обуви. Ни один предмет (в том числе и мы) не сможет находиться на одном месте. Ведь все, что лежит на столе, полу или просто земле, удерживается трением покоя. А что же будет происходить? Все тела начнут двигаться, стремясь достичь самой низкой точки. На Земле почти невозможно создать идеально горизонтальную поверхность, даже ровные лабораторные столы или станины станков имеют уклоны в тысячные доли градуса. Но в мире без трения тела придут в движение даже на таких плоскостях. Понятно, что о транспорте и вообще о работе любых механизмов и говорить не приходится. Тормозные колодки, шкивы и ремни, шины и дорога — ничего из этого не будет испытывать взаимное трение, а значит, и не будет работать.
Однако, чтобы понять все значение трения, необходимо его «выключить» и проследить за будущими событиями. Итак, каким будет мир без сухого и вязкого трения всех видов? Мы не сможем ни ходить, ни передвигаться никаким другим способом. Ведь во время ходьбы подошвы наших ног испытывают трение с полом, а без трения мы будем чувствовать себя хуже, чем на самом гладком льду в самой скользкой обуви. Ни один предмет (в том числе и мы) не сможет находиться на одном месте. Ведь все, что лежит на столе, полу или просто земле, удерживается трением покоя. А что же будет происходить? Все тела начнут двигаться, стремясь достичь самой низкой точки. На Земле почти невозможно создать идеально горизонтальную поверхность, даже ровные лабораторные столы или станины станков имеют уклоны в тысячные доли градуса. Но в мире без трения тела придут в движение даже на таких плоскостях. Понятно, что о транспорте и вообще о работе любых механизмов и говорить не приходится. Тормозные колодки, шкивы и ремни, шины и дорога — ничего из этого не будет испытывать взаимное трение, а значит, и не будет работать. Да и самих-то машин не станет — из них выкрутятся все болты и открутятся все гайки, так как они удерживаются только благодаря силам трения в резьбе. Исчезни вдруг трение, наши дома в мгновение ока рассыплются — раствор не будет больше держать кирпичи, вбитые гвозди вылезут из досок, ведь они держатся там только за счет трения! Целыми останутся только сварные или клепаные металлические конструкции. Без трения исчезнут и многие другие привычные нам вещи. Из веревок нельзя будет вязать узлы — они будут расползаться. Все тканые материалы разойдутся на отдельные нити, а нити распадутся на составляющие их мельчайшие волокна. Такая судьба ожидает также металлические и веревочные сетки. Катастрофические изменения ждут природу — сам облик Земли изменится до неузнаваемости. Волны, возникающие в океане, никогда не утихнут, а в атмосфере будут дуть постоянные ветры страшной силы — ведь трения между отдельными слоями воды и воздуха нет, а значит, ничто не мешает им очень быстро двигаться относительно друг друга.
Да и самих-то машин не станет — из них выкрутятся все болты и открутятся все гайки, так как они удерживаются только благодаря силам трения в резьбе. Исчезни вдруг трение, наши дома в мгновение ока рассыплются — раствор не будет больше держать кирпичи, вбитые гвозди вылезут из досок, ведь они держатся там только за счет трения! Целыми останутся только сварные или клепаные металлические конструкции. Без трения исчезнут и многие другие привычные нам вещи. Из веревок нельзя будет вязать узлы — они будут расползаться. Все тканые материалы разойдутся на отдельные нити, а нити распадутся на составляющие их мельчайшие волокна. Такая судьба ожидает также металлические и веревочные сетки. Катастрофические изменения ждут природу — сам облик Земли изменится до неузнаваемости. Волны, возникающие в океане, никогда не утихнут, а в атмосфере будут дуть постоянные ветры страшной силы — ведь трения между отдельными слоями воды и воздуха нет, а значит, ничто не мешает им очень быстро двигаться относительно друг друга. Реки выйдут из своих берегов, и их воды понесутся с большой скоростью по равнинам. Горы и холмы начнут рассыпаться на отдельные глыбы и песок. Деревья, корни которых держатся в земле только из-за трения, сами по себе начнут выкорчевываться и поползут в поисках самой низкой точки. Да, нашему взору предстанет страшная картина: горы, деревья, огромные глыбы, да и сама почва будут ползти, перемешиваясь, до тех пор, пока не найдут точку равновесия. Если пропадет сила трения, то наша планета станет гладким шариком, на котором не будет ни гор, ни впадин, ни рек, ни океанов — все это сломается, вытечет, перемешается и свалится в одну кучу. А сильные, ни на минуту не утихающие ветры будут подхватывать пыль и носить ее над планетой. Жизнь в таких условиях вряд ли будет возможна… Поэтому нельзя говорить о трении как о вредном физическом явлении. Да, часто просто жизненно необходимо свести трение к минимуму, но нередко нужны и максимально возможные силы трения, потому что трение — одновременно и враг, и друг.
Реки выйдут из своих берегов, и их воды понесутся с большой скоростью по равнинам. Горы и холмы начнут рассыпаться на отдельные глыбы и песок. Деревья, корни которых держатся в земле только из-за трения, сами по себе начнут выкорчевываться и поползут в поисках самой низкой точки. Да, нашему взору предстанет страшная картина: горы, деревья, огромные глыбы, да и сама почва будут ползти, перемешиваясь, до тех пор, пока не найдут точку равновесия. Если пропадет сила трения, то наша планета станет гладким шариком, на котором не будет ни гор, ни впадин, ни рек, ни океанов — все это сломается, вытечет, перемешается и свалится в одну кучу. А сильные, ни на минуту не утихающие ветры будут подхватывать пыль и носить ее над планетой. Жизнь в таких условиях вряд ли будет возможна… Поэтому нельзя говорить о трении как о вредном физическом явлении. Да, часто просто жизненно необходимо свести трение к минимуму, но нередко нужны и максимально возможные силы трения, потому что трение — одновременно и враг, и друг.
Выпуск 19
В видеоуроке физики от Академии занимательных наук профессор Даниил Эдисонович расскажет о силе трения. Оказывается, есть разные виды силы трения. И действуют они по-разному. В знакомых нам явлениях мы научимся различать действие этих сил, а значит сможем их использовать при необходимости.
Виды силы трения
Взаимодействие, которое возникает в месте соприкосновения двух тел и препятствует их движению относительно друг друга, называют трением. А силу, которая характеризует это взаимодействие, называют силой трения. Когда мы, делая уборку, попытаемся сдвинуть тяжелый шкаф, то сразу почувствуем, как что-то мешает этому. А мешать движению будет работа силы трения. С трением мы сталкиваемся на каждом шагу, причём буквально. Ведь без трения мы и шагу ступить не сможем. Именно силы трения удерживают наши ноги на поверхности земли. Каждый знает, что ходить по скользкой поверхности (например, по льду) — занятие не из лёгких. Это говорит о том, что сила трения может быть очень полезной штукой. Силу трения различают по причинам возникновения силы трения. Первая причина — это шероховатость поверхности. Это хорошо понятно на примере досок пола или поверхности Земли. А если поверхность более гладкая, например, поверхность льда, то шероховатости почти не видны, но они всё-таки имеются. Эти шероховатости и неровности цепляются друг за друга и мешают движению (скольжению). первым видом силы трения всё ясно. Вторая причина возникновения силы трения — это межмолекулярное притяжение, которое действует в местах контакта трущихся тел. Вторая причина проявляется, в основном, лишь в случае очень хорошо отполированных тел. А чаще всего мы имеем дело с первой причиной возникновения сил трения. При необходимости, чтобы уменьшить силу трения, применяют смазку. Слой смазки, чаще всего жидкий, разъединяет трущиеся поверхности, и трутся между собой слои жидкости, сила трения в которых в разы меньше. Какие же существуют виды силы трения? Всего различают три вида силы трения: трение скольжения, трение покоя и трение качения.
Силу трения различают по причинам возникновения силы трения. Первая причина — это шероховатость поверхности. Это хорошо понятно на примере досок пола или поверхности Земли. А если поверхность более гладкая, например, поверхность льда, то шероховатости почти не видны, но они всё-таки имеются. Эти шероховатости и неровности цепляются друг за друга и мешают движению (скольжению). первым видом силы трения всё ясно. Вторая причина возникновения силы трения — это межмолекулярное притяжение, которое действует в местах контакта трущихся тел. Вторая причина проявляется, в основном, лишь в случае очень хорошо отполированных тел. А чаще всего мы имеем дело с первой причиной возникновения сил трения. При необходимости, чтобы уменьшить силу трения, применяют смазку. Слой смазки, чаще всего жидкий, разъединяет трущиеся поверхности, и трутся между собой слои жидкости, сила трения в которых в разы меньше. Какие же существуют виды силы трения? Всего различают три вида силы трения: трение скольжения, трение покоя и трение качения. Когда мы пытались сдвинуть шкаф с места, его удерживала сила трения покоя. Трение покоя удерживает вбитые в стену гвозди, мешает самопроизвольно развязываться шнуркам, а также держит на месте наш шкаф. Сила трения скольжения, как и сила трения покоя, направлена в сторону, противоположную приложенному воздействию. В случае, когда тело не скользит по поверхности, а катится, то, возникающее в месте контакта трение, называют трением качения. Катящееся колесо немного вдавливается в дорогу, и перед ним образуется небольшой бугорок, который приходится преодолевать. Именно этим и обусловлено трение качения. Чем тверже дорога, тем меньше трение качения. Именно поэтому ехать по шоссе намного легче, чем по песку. Трение качения в подавляющем большинстве случаев ощутимо меньше трения скольжения. Именно поэтому повсеместно применяют колеса, подшипники и так далее.
Когда мы пытались сдвинуть шкаф с места, его удерживала сила трения покоя. Трение покоя удерживает вбитые в стену гвозди, мешает самопроизвольно развязываться шнуркам, а также держит на месте наш шкаф. Сила трения скольжения, как и сила трения покоя, направлена в сторону, противоположную приложенному воздействию. В случае, когда тело не скользит по поверхности, а катится, то, возникающее в месте контакта трение, называют трением качения. Катящееся колесо немного вдавливается в дорогу, и перед ним образуется небольшой бугорок, который приходится преодолевать. Именно этим и обусловлено трение качения. Чем тверже дорога, тем меньше трение качения. Именно поэтому ехать по шоссе намного легче, чем по песку. Трение качения в подавляющем большинстве случаев ощутимо меньше трения скольжения. Именно поэтому повсеместно применяют колеса, подшипники и так далее.
Если вы попробуете сдвинуть тяжелый шкаф, полный вещей, то как-то сразу станет понятно, что не так все просто, и что-то явно мешает благому делу наведения порядка.
- И мешать движению будет не что иное, как работа силы трения , которую изучают в курсе физики седьмого класса.
С трением мы сталкиваемся на каждом шагу. В прямом смысле этого слова. Вернее было бы сказать, что без трения мы и шагу ступить не можем, так как именно силы трения удерживают наши ноги на поверхности.
Любой из нас знает, что такое ходить по очень скользкой поверхности — по льду, если этот процесс вообще можно назвать ходьбой. То есть, мы сразу видим очевидные плюсы силы трения. Однако, прежде чем говорить о пользе или вреде сил трения, рассмотрим для, начала, что такое сила трения в физике.
Сила трения в физике и ее виды
Взаимодействие, которое возникает в месте соприкосновения двух тел и препятствует их относительному движению, называют трением. А силу, которая характеризует это взаимодействие, называют силой трения.
- Различают три вида трения: трение скольжения, трение покоя и трение качения.
Трение покоя
В нашем случае, когда мы пытались сдвинуть шкаф с места, мы пыхтели, толкали, краснели, но не сдвинули шкаф ни на дюйм. Что удерживает шкаф на месте? Сила трения покоя. Теперь другой пример: если мы положим руку на тетрадь и будем двигать ее по столу, то тетрадь будет двигаться вместе с нашей рукой, удерживаемая все той же силой трения покоя.
Что удерживает шкаф на месте? Сила трения покоя. Теперь другой пример: если мы положим руку на тетрадь и будем двигать ее по столу, то тетрадь будет двигаться вместе с нашей рукой, удерживаемая все той же силой трения покоя.
Трение покоя удерживает вбитые в стену гвозди, мешает самопроизвольно развязываться шнуркам, а также держит на месте наш шкаф, чтобы мы, случайно опершись на него плечом, не задавили любимого кота, который вдруг улегся подремать в тишине и покое между шкафом и стеной.
Трение скольжения
Вернемся к нашему пресловутому шкафу. Мы, наконец, сообразили, что сдвинуть его в одиночку нам не удастся и позвали на помощь соседа. В конце концов, исцарапав весь пол, вспотев, напугав кота, но, так и не выгрузив вещи из шкафа, мы передвинули его в другой угол.
Что мы обнаружили, кроме клубов пыли и не обклеенного обоями куска стены? Что, когда мы приложили силу, превышающую силу трения покоя, шкаф не просто сдвинулся с места, но и (с нашей помощью, естественно) продолжил двигаться дальше, до нужного нам места. И усилия, которые приходилось затрачивать на его передвижение, были примерно одинаковы на всем протяжении пути.
И усилия, которые приходилось затрачивать на его передвижение, были примерно одинаковы на всем протяжении пути.
- В данном случае нам мешала сила трения скольжения . Сила трения скольжения, как и сила трения покоя, направлена в сторону, противоположную приложенному воздействию.
Трение качения
В случае, когда тело не скользит по поверхности, а катится, то, возникающее в месте контакта трение, называют трением качения. Катящееся колесо немного вдавливается в дорогу, и перед ним образуется небольшой бугорок, который приходится преодолевать. Именно этим и обусловлено трение качения.
Чем тверже дорога, тем меньше трение качения. Именно поэтому ехать по шоссе намного легче, чем по песку. Трение качения в подавляющем большинстве случаев ощутимо меньше трения скольжения. Именно поэтому повсеместно применяют колеса, подшипники и так далее.
Причины возникновения сил трения
Первая — это шероховатость поверхности. Это хорошо понятно на примере досок пола или поверхности Земли. В случае же более гладких поверхностей, например, льда или покрытой металлическими листами крыши, шероховатости почти не видны, но это не значит, что их нет. Эти шероховатости и неровности цепляются друг за друга и мешают движению.
В случае же более гладких поверхностей, например, льда или покрытой металлическими листами крыши, шероховатости почти не видны, но это не значит, что их нет. Эти шероховатости и неровности цепляются друг за друга и мешают движению.
Вторая причина — это межмолекулярное притяжение, которое действует в местах контакта трущихся тел. Однако, вторая причина проявляется, в основном, лишь в случае очень хорошо отполированных тел. В основном же, мы имеем дело с первой причиной возникновения сил трения. И в таком случае, чтобы уменьшить силу трения, часто применяют смазку.
- Слой смазки, чаще всего жидкий, разъединяет трущиеся поверхности, и трутся между собой слои жидкости, сила трения в которых в разы меньше.
Сочинение на тему «Сила трения»
В курсе физики седьмого класса школьникам дают задание написать сочинение на тему «Сила трения». Примером сочинения на эту тему может служить примерно такая фантазия:
«Допустим, решили мы на каникулах съездить к бабушке в гости на поезде. И не в курсе того, что как раз в это время вдруг, ни с того ни с сего, пропала сила трения. Проснулись, встаем с кровати и падаем, так как силы трения между полом и ногами нет.
И не в курсе того, что как раз в это время вдруг, ни с того ни с сего, пропала сила трения. Проснулись, встаем с кровати и падаем, так как силы трения между полом и ногами нет.
Начинаем обуваться, и не можем завязать шнурки, которые не держатся из-за отсутствия силы трения. С лестницей вообще туго, лифт не работает — он уже давно лежит в подвале. Пересчитав копчиком абсолютно все ступени и доползя как-то до остановки, обнаруживаем новую беду: ни один автобус не остановился на остановке.
Чудом сели в поезд, думаем, какая красота — тут хорошо, топлива уходит меньше, так как потери на трение сведены к нулю, быстрее доедем. Но вот в чём беда: силы трения между колёсами и рельсами нету, а, значит, и оттолкнуться поезду не от чего! Так что, в общем, как-то и не судьба съездить к бабушке без силы трения.»
Польза и вред силы трения
Конечно же, это фантазия, и она полна лирических упрощений. В жизни все немного по-другому. Но, по сути, несмотря на то, что есть очевидные минусы силы трения, которые создают для нас ряд сложностей в жизни, очевидно, что без существования сил трения, проблем было бы куда как побольше. Так что нужно говорить, как о вреде сил трения, так и о пользе все тех же сил трения.
Так что нужно говорить, как о вреде сил трения, так и о пользе все тех же сил трения.
Примерами полезных сторон сил трения можно назвать то, что мы можем ходить по земле, что наша одежда не разваливается, так как нитки в ткани удерживаются благодаря все тем же силам трения, что насыпав на обледеневшую дорогу песок, мы улучшаем сцепление с дорогой, дабы избежать аварии.
Ну а вредом силы трения является проблема перемещения больших грузов, проблема изнашивания трущихся поверхностей, а также невозможность создания вечного двигателя, так как из-за трения любое движение рано или поздно останавливается, требуя постоянного стороннего воздействия.
Люди научились приспосабливаться и уменьшать, либо увеличивать силы трения , в зависимости от необходимости. Это и колеса, и смазка, и заточка, и многое другое. Примеров масса, и очевидно, что нельзя однозначно сказать: трение — это хорошо или плохо. Но оно есть, и наша задача — научиться использовать его на пользу человека.
Нужна помощь в учебе?
Предыдущая тема: Связь между силой тяжести и массой тела: динамометр.
Следующая тема:   Трение в природе, быту и технике: еще больше ПРИМЕРОВ
Сила трения скольжения
Оглавление:
- Плоская система активных сил действует на тело, касаясь поверхности другого тела, где тело находится в равновесии и является связью рассматриваемого тела. Если поверхность контактирующего объекта идеально гладкая и объект полностью твердый, то реакция связанной поверхности направлена перпендикулярно общей касательной в точке контакта, и направление реакции в этом случае не зависит от действующей на объект активной силы. Только численное значение силы реакции зависит от активного force. Дело в том, что здесь нет идеально гладких поверхностей и абсолютно твердых предметов. Все поверхности тела были огрублены до некоторой степени и все тела deformable.
В связи с этим сила реакции шероховатой поверхности при равновесии а Тела зависит от рабочей силы не только по модулю, но и по направлению рис.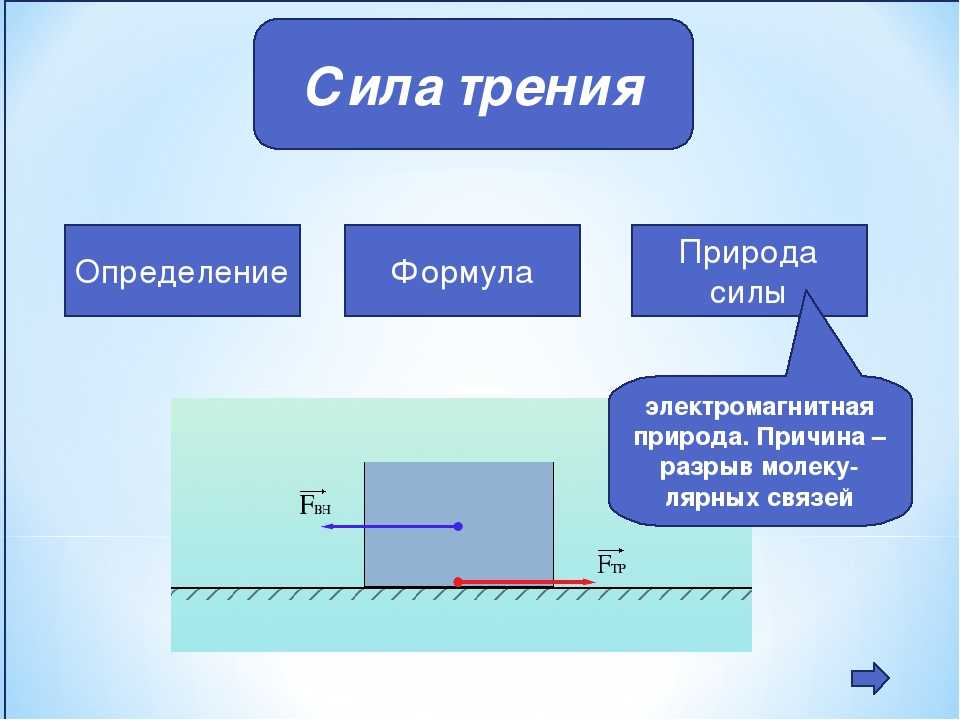 58. Если реактивная сила R шероховатой поверхности разложена на составляющие, 1 N из которых направлена вдоль линии общего закона контактной поверхности, а другая 1 g находится в касательной плоскости этих поверхностей, то компонент реактивной силы F является силой трения. Скольжение, а компоненты N нормальная реакция. В теории механики Сухое трение между поверхностями корпуса, то есть трение при отсутствии смазки между bodies.
58. Если реактивная сила R шероховатой поверхности разложена на составляющие, 1 N из которых направлена вдоль линии общего закона контактной поверхности, а другая 1 g находится в касательной плоскости этих поверхностей, то компонент реактивной силы F является силой трения. Скольжение, а компоненты N нормальная реакция. В теории механики Сухое трение между поверхностями корпуса, то есть трение при отсутствии смазки между bodies.
Проекция угловой скорости тела y как на движущуюся, так и на неподвижную оси также может найти Эйлеров угол как функцию времени, и положение тела относительно неподвижной системы координат может быть вычислено. Людмила Фирмаль
В случае сухого трения необходимо различать трение скольжения в покое или при равновесии тела, а также трение скольжения, когда один объект движется по поверхности другого с определенной относительной скоростью. В состоянии покоя сила трения зависит только от активного force. In направление касательной выбирается в точке соприкосновения поверхности тела, сила трения рассчитывается по формуле: Аналогично, для выбранного направления нормали нормальная сила реакции выражается в терминах данной силы В 1781 году кулоном был установлен основной закон приближения для сухого трения скольжения. Позже закон Кулона неоднократно проверялся другими исследователями.
Позже закон Кулона неоднократно проверялся другими исследователями.
Однако эти законы подтвердились, когда поверхности предметов не были вдавлены друг в друга, и шероховатость была не так велика. Вы можете установить закон Кулона на устройстве. Схема показана на рисунке. 59.In это устройство, изменяя массу массы груза, позволяет изменять нормальное давление P или нормальную реакцию N, равную ему между трущимися поверхностями. Вы можете изменить силу Q, изменив вес груза Q. It имеет тенденцию перемещать тело по поверхности другого тела, которое является соединительным. Очевидно, что в случае силы 6 = 0 объект находится в равновесии, а сила трения F равна нулю.
При увеличении силы 2 Если тело не скользит по поверхности
и находится в равновесном состоянии равновесное состояние вызывает силу
трения, F. Другая сторона активной силы Q. нормальная реактивная сила N
равна нормальному давлению P. увеличение силы Q при таком же нормальном
давлении P также может привести к незначительному увеличению силы Q, что
нарушает равновесие тела и приводит к скользящему положению вдоль
суставной поверхности. Четко достигнут Рис. 59 предельное положение для
максимальной силы трения Вы можете сбалансировать силу Q и ее increase.
By изменяя силу нормального давления P, можно видеть, как изменяется
конечная сила трения Fm.
Четко достигнут Рис. 59 предельное положение для
максимальной силы трения Вы можете сбалансировать силу Q и ее increase.
By изменяя силу нормального давления P, можно видеть, как изменяется
конечная сила трения Fm.
Вы можете. Он также исследует влияние таких факторов, как конечная сила трения на площадь контакта объекта, а также материал объекта, характер обработки поверхности, при сохранении нормального давления. Такие эксперименты позволяют проверить закон сухого трения скольжения кулона. закон Кулона 1.Сила трения скольжения расположена на общей касательной плоскости контактной поверхности объекта и направлена в противоположном направлении к возможному или фактическому направлению скольжения объекта под действием приложенной силы.
Статическая сила трения зависит от активной силы, ее модуль находится
между нулем и максимальным значением, которого тело достигает в момент
выхода из равновесного положения. 2.При прочих равных условиях
максимальная сила трения скольжения не зависит от площади контакта
поверхности трения. Из этого закона, например, чтобы сдвинуть кирпич,
необходимо приложить ту же силу, независимо от ширины грани, которая
размещена на поверхности. 3.Максимальная сила трения скольжения
пропорциональна нормальному давлению нормальная реакция. Lpah = М0 Здесь
безразмерный коэффициент называется коэффициентом скольжения friction.
It не зависит от обычного давления.
Из этого закона, например, чтобы сдвинуть кирпич,
необходимо приложить ту же силу, независимо от ширины грани, которая
размещена на поверхности. 3.Максимальная сила трения скольжения
пропорциональна нормальному давлению нормальная реакция. Lpah = М0 Здесь
безразмерный коэффициент называется коэффициентом скольжения friction.
It не зависит от обычного давления.
Коэффициент трения скольжения зависит от физического состояния материала и поверхности трения, а именно от величины и характера шероховатости, влажности, температуры. И другие условия. Коэффициент трения скольжения устанавливается экспериментально, в зависимости от различных conditions. So, коэффициент трения бетонных кирпичей равен 0,76.Для стали на стали 0,15 дуба дуба поперек волокон 0,54 дуба дуба вдоль волокон 0,62 Эксперименты показывают, что при скольжении одного объекта по поверхности другого с определенной относительной скоростью возникает сила трения скольжения, равная максимальной.
Только в этом случае коэффициент трения скольжения изменяется
незначительно в зависимости от скольжения speed. In в большинстве
материалов она уменьшается с увеличением скорости скольжения,
но в некоторых материалах, наоборот, увеличивается трение кожи о металл.
В приближенных технических расчетах обычно считается, что коэффициент
трения скольжения не зависит от относительной скорости скольжения.
В отличие от сухого трения, когда между поверхностями имеется смазочный
слой, трение определяется распределением относительной скорости
скольжения этого слоя. layer. In в этом случае прицел возникает не между
поверхностью объекта, а между слоями смазки.
In в большинстве
материалов она уменьшается с увеличением скорости скольжения,
но в некоторых материалах, наоборот, увеличивается трение кожи о металл.
В приближенных технических расчетах обычно считается, что коэффициент
трения скольжения не зависит от относительной скорости скольжения.
В отличие от сухого трения, когда между поверхностями имеется смазочный
слой, трение определяется распределением относительной скорости
скольжения этого слоя. layer. In в этом случае прицел возникает не между
поверхностью объекта, а между слоями смазки.
В механике жидкости рассматривается теория трения слоев смазочной
жидкости. Угол и конус трения Многие проблемы с равновесием объектов
на шероховатой поверхности, то есть наличием сил трения, решаются
геометрически и удобно. Для этого введем понятие угла и конусов трения.
Твердое тело под действием активной силы помещается на шероховатую
поверхность в ограниченном состоянии равновесия, то есть там, где сила
трения достигает своего максимального значения при заданном значении
нормального противодействия рис. 60. в этом случае полная реакция
шероховатой поверхности L отклоняется от нормали общей касательной
плоскости натираемой поверхности на максимальный угол.
60. в этом случае полная реакция
шероховатой поверхности L отклоняется от нормали общей касательной
плоскости натираемой поверхности на максимальный угол.
- Этот максимальный угол между полной реакцией, основанной на максимальной силе трения данной нормальной реакции и нормальным направлением реакции p, называется углом трения. Угол трения p зависит от коэффициента трения. тг р = Макс переменного тока Но Третий закон Кулона, Fma,= lg Результат. То есть тангенс угла трения равен коэффициенту трения. Диаграмма 60 Конус трения это конус, который описывается полной реакцией, построенной на основе максимальной силы трения нормального направления реакции.
Это может быть достигнуто путем изменения активной силы так, что
объект на шероховатой поверхности находится в критическом положении
равновесия и пытается выйти из равновесия во всех возможных направлениях
на общей касательной плоскости контактной поверхности. Если коэффициент
трения во всех направлениях одинаков, то конус трения является
круговым. Если они не совпадают, например, конусы трения не являются
круговыми, если характеристики контактных поверхностей различны
из за специфического направления волокон или если плоскость
обрабатывается в зависимости от направления обработки поверхности
объекта.
Если они не совпадают, например, конусы трения не являются
круговыми, если характеристики контактных поверхностей различны
из за специфического направления волокон или если плоскость
обрабатывается в зависимости от направления обработки поверхности
объекта.
Это положение установлено для случая двух вращений, поэтому для его установления в общем случае, если оно верно для N-1 вращений, оно не верно для n вращений. Людмила Фирмаль
Баланс тела на шероховатой поверхности Когда сила, действующая
на твердое тело в равновесии с шероховатой поверхностью,
уравновешивается, на шероховатой поверхности возникает еще более
неизвестная реактивная сила, или сила трения surface. In в случае
окончательного равновесия сила трения достигает своего максимального
значения и выражается обычной реакцией по Формуле 1. в случае общего
равновесия сила трения находится между нулем и ее максимальным
значением. Таким образом, соответствующие условия равновесия, включая
силу трения после замены силы трения на максимальную величину,
становятся неравенствами. Затем мы находим неизвестное, решая уравнения
и неравенства совместно.
Затем мы находим неизвестное, решая уравнения
и неравенства совместно.
Для всех неизвестных или их части они получают решение в виде неравенства. Некоторые задачи равновесия удобно решать, используя конус трения геометрически, с учетом силы трения. Используя конусы трения, можно сформулировать условия равновесия для объекта на шероховатой поверхности. Если действующая на объект эффективная сила сводится к равнодействующей силе RM, то при уравновешивании объекта на шероховатой поверхности равнодействующая сила эффективной силы R п, согласно аксиоме равновесия 2 сил, приложенных к твердому телу, равновесие принимается полной реакцией R шероховатой поверхности рис. 61.
Очевидно, что при изменении равнодействующей силы объект находится
в равновесии до тех пор, пока составляющая равнодействующей силы в общей
контактной плоскости контактной плоскости больше не превысит максимума
силы трения Fmax. Рисунок 61: 62 Предельное положение равновесия тела
это когда сила Q равна силе Fmax. In в этом случае результат эффективной
силы L o получается из шины фрикционного конуса.
In в этом случае результат эффективной
силы L o получается из шины фрикционного конуса.
Это происходит потому, что результирующая составляющая эффективной силы в нормальном направлении P уравновешивается нормальной реакцией N, если только эффективная сила не отделяет объект от шероховатой поверхности. Таким образом, условие равновесия объекта на шероховатой поверхности можно сформулировать следующим образом: для равновесия объекта на шероховатой поверхности необходимо и достаточно, чтобы линия эффективной силы, действующей в результате воздействия на объект, проходила через вершину либо внутри фрикционного конуса, либо вдоль его втулок рис.62. Если линия действия проходит через конус трения, активная сила по модулю не приведет к нарушению равновесия тела.
Если результирующая линия эффективной силы не проходит внутри
фрикционного конуса или вдоль его шины, то объект на шероховатой
поверхности не будет находиться в равновесии рис. 63. Пример 1.An
объект, сила тяжести которого равна P = 100H, уравновешивается силой T
на шероховатой наклонной поверхности с углом наклона. Диаграмма 64
Диаграмма 63 Наклон a = 45 рис. 64.Коэффициент трения скольжения между
объектом и плоскостью f = 0,6.Сила Т действует на объект под углом р =
15 относительно линии максимального наклона. Определите величину силы T
при равновесии объекта на неровной наклонной плоскости. Решение. Сила I,
P, T и сила трения F приложены к телу.
Диаграмма 64
Диаграмма 63 Наклон a = 45 рис. 64.Коэффициент трения скольжения между
объектом и плоскостью f = 0,6.Сила Т действует на объект под углом р =
15 относительно линии максимального наклона. Определите величину силы T
при равновесии объекта на неровной наклонной плоскости. Решение. Сила I,
P, T и сила трения F приложены к телу.
Предельное равновесие тела имеет 2 случая, поэтому в зависимости от направления скольжения вверх и вниз существует 2 предельных значения силы т в 2 направлениях силы трения вдоль наклонной плоскости, и целесообразно ввести FKF, fc = + L. Для обоих предельных случаев условие равновесия строится в виде суммы проекций сил на координатные оси. У нас есть 7cosP F Psina = 0 Tsinp + jV Pcosa = 0. Согласно закону кулона Отсюда Три Ф = ф Если мы получим эти уравнения относительно t, Т = п синоу + с Коза б + Ят НИИЯФ МГУ.
Следовательно, сила т в равновесном состоянии тела должна удовлетворять условию 35 7 102 Н. Пример 2.Равномерный, тяжелый стержень АВ длиной опирается на гладкую вертикальную стенку ребра A, а другой B поддерживается с помощью грубой вертикальной стене рис.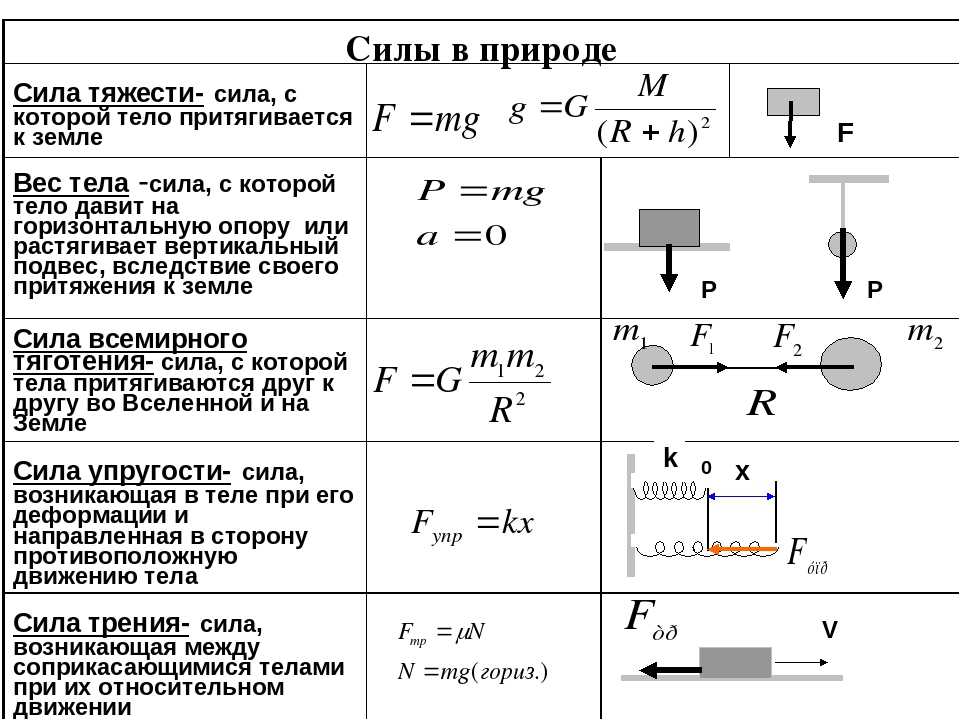 65.Расстояние между стенами. Определите коэффициент трения стенки f, способной уравновешивать стержень. Решение. Рассмотрим случай, когда точка A находится выше точки B. сила тяжести P, добавленная к середине стержня, нормальная реакция гладкой стенки и реакция грубой стенки q разлагается на нормальную реакцию NB и силу трения FB, которая действует на стержень.
65.Расстояние между стенами. Определите коэффициент трения стенки f, способной уравновешивать стержень. Решение. Рассмотрим случай, когда точка A находится выше точки B. сила тяжести P, добавленная к середине стержня, нормальная реакция гладкой стенки и реакция грубой стенки q разлагается на нормальную реакцию NB и силу трения FB, которая действует на стержень.
Составлено условие равновесия плоской силовой системы. F F,, = 0 NA Nt = 0 Ф = 0 ФБ Р = 0 Mb P, = 0 P NAlsma = 0. К этим условиям Диаграмма 65 Нам нужно добавить неравенство. ФБ ФНБ. Из уравнения равновесия мы видим N4 = Nb = N , Fb = P, N = NB = Ph 2 sina. Итак, для силы трения FB существуют следующие уравнения и неравенства: ПВ = п. г За исключением ила 1, который является силой трения FB, после уменьшения P получается 1 UA 2×2 A2.
Смотрите также:
Задачи по теоретической механике
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.
Сила трения и СТО.
 (Лекция 4)
(Лекция 4)Лекция 4
Силы трения и СТО
Профессор А.М.Тишин
2. Силы трения
Есть две силы: химическая иотносительно дальнодействующая Ван дер ВаальсаСуществует
Отталкива
ние ~10-6
Притяжение
начинается в
контактном
режиме
N
Fтр
N=mg Рис. 13
сухое и вязкое трение. Законы трения
установлены Леонардом да Винчи около 5 веков
назад. Сила F уравновешивается равной ей по
величине и противоположно направленной силой,
которая и есть сила трения покоя Fтр. Сила трения
покоя может быть меньше по величине и для
данных поверхностей их много, но макс. сила
только одна Fтр. max= Fтр. cк. и именно через нее и
определяется безразмерным коэфф. пропорц.
называемым коэфф. трения скольжения μ. Закон
Амонтона-Кулона(1699 ): модуль вектора Fтр.ск.
линейно пропорц. нагрузке (или реакции опоры
N ) и практически не зависит от модуля скорости
тела, но направлен противоположно скорости.
F
μ
Fтр max
N
Fтр.
 ск
скN
F тр.ск
N
v
v
Точно равно если пренебречь Ван-дер-Ваальсом
4. Сила трения? Это много или мало?
Если сил трения нет?Человек не мог бы ходить!
Чтобы космическому спутнику массой 650 кг
поменять орбиту, нужен двигатель, дающий в
импульсе дополнительную «эффективную»
массу 5 гр (если она изменилась из-за трения
об остатки атмосферы)
5. Сила трения сухого трения
NF
Fтр
Рис. 13
N=mg
x
Если горизонтальная поверхность т.е. =0 ? проекция mg на
горизонтальную ось x равна 0 и при начале скольжения
max= F-Fтр=F–μmg=0 или для баланса сил и обеспечения
хотя бы нулевого ускорения (не нулевой начальной
скорости) a=(F/m- μ g) =0 или F/m=μg или F= μmg. Сила
F линейна пропорциональна массе тела. Сила с которой
надо тянуть на санях одного и двух студентов отличаются
в два раза. А для троих надо тройку запрягать!
Но из опыта: Fтр не зависит от площади соприкосновения. Посмотрим на
трибометр.
 Почему? Fтр определяется химией поверхностей и силой, которая их
Почему? Fтр определяется химией поверхностей и силой, которая ихсдавливает и зависит от истинной площади! Чем меньше площадь при той же
величине силы сдавливания, тем больше давление на 1 мм кв. и больше атомов входят в
химическое взаимодействие. Посмотрим трибометр с двумя брусками. Сила возросла
в 2 раза! Противоречие? Т.е. для начала движения надо чтобы mgsin μmgcos =mg(sin — μcos )=0 или μ =tg ! Т.е. угол наклона доски в момент сползания
бруска определяется только величиной μ, а не m. А почему нет зависимости от
скорости? Так как короткодейтвие (химия). Сила действует только на маленьком
расстоянии. При малых скоростях с какой скоростью она создавалась не важно.
Важно, что в один и тот же момент времени есть определенное количество молекул
состоящих в химической связи. Химия в 10 раз сильнее Ван-дер-Ваальсовых сил.
6. Сила трения
Брусок на столе и шарик. Не путать коэфф. трение скольжения(безразмерен) и качения (определяемого как отношение момента силы
трения качения к нормальной силе и имеющего размерность длины).
 То,
То,что коэфф. трения качения очень мал используется в подшипниках.
Трение качения ничтожно мало и резко возрастает только при скоростях,
сравнимых со скоростью распространения деформации в теле тогда
лучше переходить на трение скольжения.
Автомобилистам: Кинетическая энергия в результате действия сил
трения переходит в тепловую и энергию деформации (поэтому
тормозные диски и колодки на машинах в основном греются (при
плавном торможении ) и изнашиваются (при резком) . Насколько чаще
надо менять тормозные колодки у внедорожника в сравнению с Ладой ?
Направление силы трения между ведущими (связанными с двигателем) и
ведомыми колесами прямо противоположны. На полном приводе в одну.
Опыта с двумя тележками уже нет ;-(
Однако до 2009 года предсказать реальный коэфф. трения было
невозможно, точнее связать его со свойствами материала
7. Трения в макро- и наномире похожи
Законы трения для наноструктур не отличаютсяот классических законов.
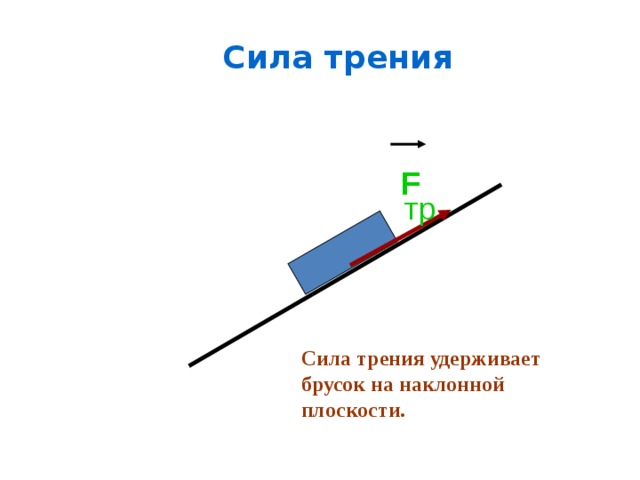 Если говорить просто,
Если говорить просто,то сухое трение создается неровностями
данных поверхностей, которые зацепляются
друг за друга и дают большее колличество
взаимодействующих атомов, из которых
состоят поверхности. Для наноповерхностей
(совокупность молекул) рассчитывались силы
межмолекулярного взаимодействия.
Установлено, что сила трения прямо
пропорциональна количеству химически
взаимодействующих атомов — аналогу
истинной (реальной) площади соприкосновения
макрообъектов. Сила трения прямо
пропорциональна истинной площади (ее не
следует путать с обычной площадью
соприкосновения поверхностей тел). Трущиеся
наноповерхности можно рассматривать в рамках
классических теорий трения поверхностей.
8. Трение или адгезия ? близкодействие или дальнодействие?
В чем принципиальное отличие сил трения от сил адгезии?В том, что в трении участвуют только близкодействующие силы (химия),
а Ван-дер-Ваальс не участвует ? В адгезии работают обе силы? или нет?
Трение, обусловленное близкодействием (химическим взаимодействием),
линейно зависит от веса тела, а трение с учетом Ван-дер-Ваальса
(«дальнодействующая адгезия») сублинейно.

Правильно ли говорить , что адгезия включает и
короткодействующие силы (химию) и Ван-дер-Ваальсовы?
Да, это так. Только короткодействующие силы, связанные с трением и
такие же, связанные с адгезией, различаются (вторые можно устранить,
например, пассивацией с помощью водорода, а первые, нет).
9. Силы трения в животном мире
Когда миллионы волосковгеккона (А) вступают в
контакт с поверхностью (В),
они все вместе создают
мощную связь, которая в
тысячу раз сильнее, чем та
сила, которая нужна геккону,
чтобы висеть на вертикальной
стене.
Ящерицы способны прочно прилипать к поверхности. И это тот
механизм, который исследователям во всем мире еще только предстоит
воспроизвести.
Полипропиленовые
микроволокна
(0.6-5) х20 микрон гораздо
лучше контактируют со
стеклом, чем гладкая
поверхность и коэффициент
трения на порядок больше чем
у объемного полипропилена.
Площадь не важна. Важно
качество контакта со
стеклом (физические
свойства микроволокон).

Адгезию измеряли, ее нет т.е.
все без клея.
11. Факультативно: Исключения бывают! Анизотропное трение на наноуровне
Измерение сила трения между иглой АСМ и боковой поверхностьюмногослойной углеродной нанотрубки показало, что линейная
зависимость Fтр не выполняется, а вместо этого Fтр ~ N2/3.
Выяснилось, что для нанотрубок диаметром менее 10 нм величина
трения различается при движении иглы перпендикулярно и
параллельно оси нанотрубки. Моделирование взаимодействия иглы
с нанотрубкой показало, что более сильное трение в
перпендикулярном направлении связано с возникновением мягкой
моды колебаний, которая эффективно “забирает” энергию
поступательного движения иглы. Т.е. дополнительно тратится энергия
на деформацию поверхности. Конечно, надо изучать, как влияют
конкретная форма иглы, поверхностные дефекты и другие факторы.
M.Lucas et al., Nature Mater. 8, 876 (2009). ПерсТ, 2009, т.16, вып. 22
12. Движении твердого тела в жидкой среде.
 На тело в жидкости или газе действует сила сопротивления (F //v и
На тело в жидкости или газе действует сила сопротивления (F //v иобусловлена вязким трением) и подъемная сила (F v и ≠0 при
отсутствие симметрии тела относительно линии движения) .
• Если в жидкость привести в движение, то оно со временем затухнет!
Значит, между слоями есть трение. Назовем его силами внутреннего
трения или силами вязкости, а — коэфф. внутреннего трения или
динамической вязкости. Кстати, поток газа тоже затухнет. Слои
жидкости или газа, соприкасающиеся с телом, «прилипают» к нему и
двигаются вместе с телом, вовлекая другие слои за счет сил вязкости.
Возникает вязкое трение между этими слоями и остальными.
• Давление на разные участки тела разное. Результирующая сил давления
направлена противоположно v, по модулю равна силе сопротивления
(силе вязкого трения) и существенно зависит от скорости движения.
• Ньютон установил для двух слоев жидкости с разными скоростями
(dv/dh≠0) разделенных тонкой площадкой ∆S :
dv
ΔFтр ηΔS
dh
Движении твердого тела в жидкой среде (верно и для газа).

• При малых скоростях коэфф. внутреннего трения , а также форма,
размеры, шероховатость тела и определяют коэфф вязкого трения b :
Fтр.ж. = -bv для шарика b=6 r
• При больших v по модулю Fтр.ж.= -b1v2 или векторно Fтр.ж. = -b1vv .
При дальнейшем увеличении скорости b1 может измениться. Какой b1 у
катера мчащегося с V=100 км/ч ? Должен быть минимален!
• При больших скоростях и размерах позади тела возникает
турбулентность, приводящая к дополнительной разнице давлений, и сила
сопротивления среды может превосходить силу вязкого трения. Т.е.
правильно говорить о силе вязкого трения + силе сопротивления среды.
Отметим, что при отклонении v от оси симметрии тела возникает
подъемная сила. Т.е. это верно и для газа. Пример, взлетающий самолет
(благодаря отсутствию симметрии он и взлетает).
Вязкого трения покоя не существует. Если скорость v=0
то Fтр.ж. =0 и огромный корабль сдвигаем с места пальцем!
К сожалению, как только он тронулся, сразу появляется сила трения
Микрокапли отказались подчиняться законам трения!
14.
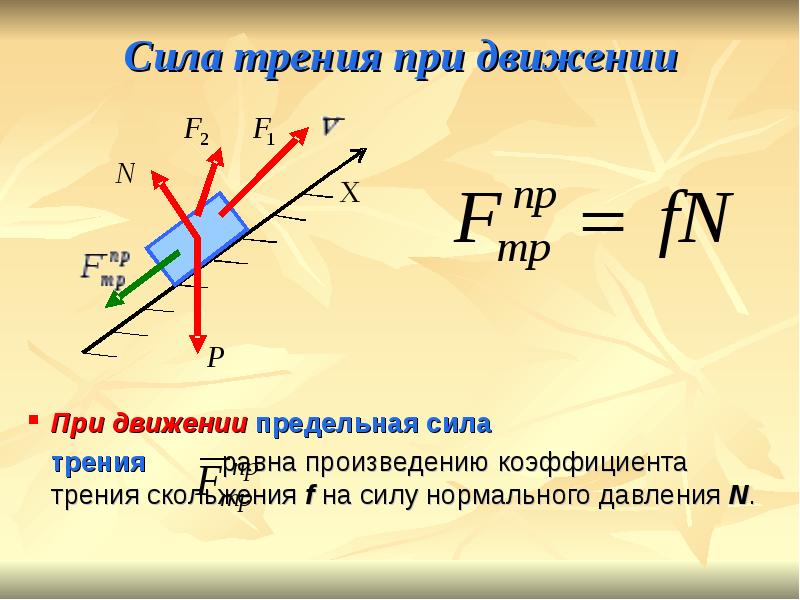 Факультативно: «Вязкое» трение – в реальном компьютереКогда диск (темно-синего
Факультативно: «Вязкое» трение – в реальном компьютереКогда диск (темно-синегоцвета) двигается навстречу
ползунку (зеленого цвета)
записывающей/считывающей
головки (а), то
образуется мениск из смазочной жидкости. Но он
достаточно маленький, и потому не вносит значительного
вклада в общую силу трения. Но если диск движется от
ползунка (б), то возле него смазка скапливается в большом
количестве и, следовательно, оказывает большее влияние.
Кто-то хочет сухое или вязкое трение уменьшить, а ктото увеличить (покрышки)! Эффект водяного клина.
15. Факультативно: трибология и сверхпроводимость
Бесконтактное трение возникает при конечном (нанометры) расстоянии междудвижущимися относительно друг друга объектами (существует как у металлов, так
и у диэлектриков, и обусловлено как электронными возбуждениями, так и фононами,
возникающими при взаимодействии соприкасающихся и/или почти
соприкасающихся поверхностей). Как отделить электронный вклад
от фононного? В 2011 ученые измерили силу, действующую на иглу кантилевера на
расстоянии 3 нм от поверхности ленки ниобия при его осцилляциях вдоль пленки.

Трение в сверхпроводящем состоянии резко уменьшалось (вклад в трение электронов в
сверхпроводящем состоянии сильно подавлен так как нет электронных возбуждений с
энергией, меньшей сверхпроводяшей щели). Сверхпроводящий наноподшипник?
Перст, 2011, том 18, вып 4, M.Kisiel et al., Nature Mater. 10, 119 (2011).
16. Теперь поговорим об относительности, больших расстояниях и скоростях.
Вселенная – это весь мир, безграничный во времени ипространстве. Доступна изучению астрономическими
средствами только часть Вселенной. Эта часть обычно
называется Метагалактикой.
Только в 30-х годах XX века удалось установить размеры
и основные черты строения нашей Галактики, в которую
входит Солнце. Поперечник Галактики примерно 30 000
парсек или около 100 000 световых лет.
1 парсек (пк) = 3,26 светового года = 3,08 1016 м.
17. Галактики
В галактику входит более 100 млрд. звезд ирасположены они в слое диска толщиной в несколько
сотен парсек, следовательно толщина диска намного
меньше его диаметра.
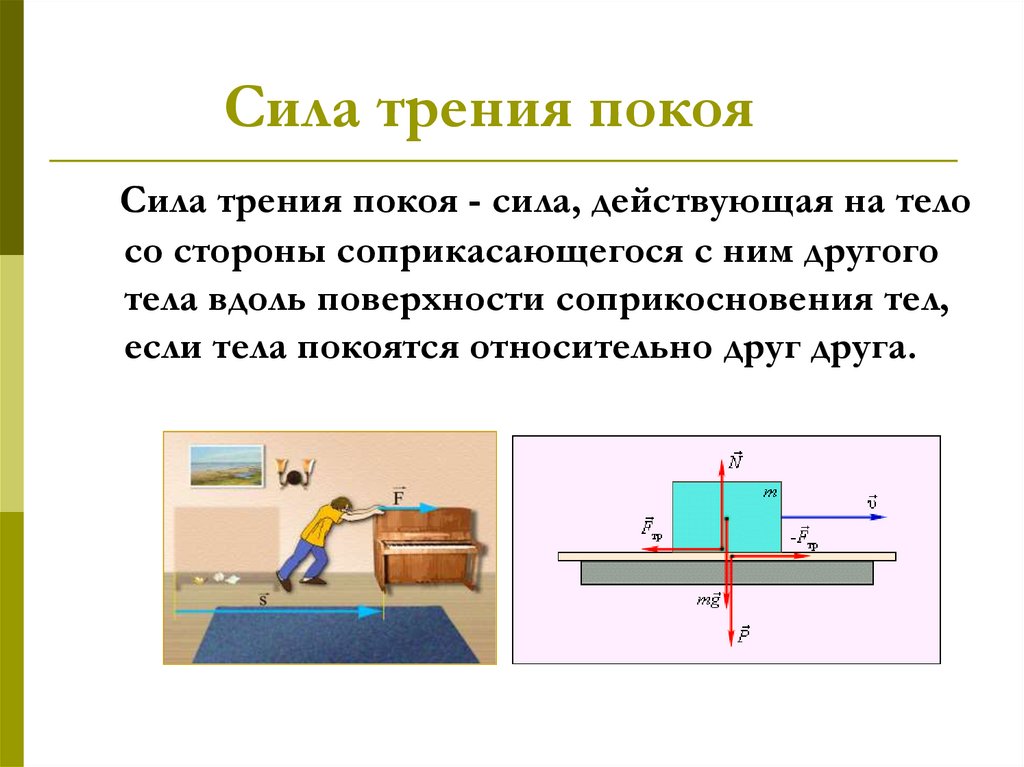 Средний возраст галактик
Средний возраст галактикприблизительно 10 млрд. лет.
Все галактики Хаббл разбил на три основных типа:
эллиптические, спиральные и неправильные.
Общее число звезд в Метагалактике – более 1019.
Предельный стабильный размер звезды до 62 Мс.
Плотность от 1.41 (у Солнца) до 1014-15 г/см3 (у нейтронных
звезд).
Т.е. масса распределена очень не равномерно,
кстати, также как и в Земле (средняя плотность
5.5 г/см3).
18. Пространственная структура Вселенной
Вселенная расширяется. Скорость разлета галактикпрямо пропорциональна расстоянию от нашей
Галактики.
Факт разлета галактик подтверждается “красным
смещением” вследствие известного в физике эффекта
Доплера.
Экстраполяция
расширяющейся
Вселенной
в
обратную временную сторону приводит к выводу, что
все началось с большого взрыва около 15 млрд. лет
назад, что и считают возрастом Вселенной.
19. Солнце
Солнце- газовый (68% водорода, 30 % гелия) или плазменный шар возраста 4. 6
6миллиарда лет на расстоянии 1 а.е. (астрономическая единица ≈1.5 108 км). Радиус R≈7
108м (в 109 раз больше Земли), М≈2 1033 кг (в 333000? больше Земли и около 99.866 %
массы солнечной системы). Плотность ρ= 1.41 г/см3 (0.256 от плотности Земли),
gС=271 м/с2 (в 27,5 раз больше чем на Земле). Температура на поверхности Т=5830 К, а
внутри 16 миллионов К. Мощность излучения –светимость 3.85 1033 эрг/с=3.86 1026 Вт.
Идет ядерная реакция синтеза гелия из водорода. Из-за многократного поглощения и
переизлучения от центра Солнца эл.-маг. излучение (рентгеновский диапазон) идет до
поверхности очень долго. А от Солнца до Земли за 8 мин.
При прохождении к поверхности спектр эл.-маг. излучения существенно меняется и
наблюдаемое излучение в оптическом диапазоне формируется в тонком
поверхностном слое –фотосфере толщиной около 350 км. Оно тепловое и хорошо
описывается в видимой и ИК области спектра .
Солнечная постоянная – полное количество лучистой энергии Солнца , доходящее
до 1 м2 Земли вне атмосферы 1369 Вт/м2 (H≈1000 км над поверхностью Земли) из них
основная часть в диапазоне 0.
 1-4 мкм. Только 336 Вт/м2 доходит до Земли. В
1-4 мкм. Только 336 Вт/м2 доходит до Земли. Вклиматологии из нулевого уравнения теплового баланса Земли следует, что
поглощается Землей тепло 157 Вт/м2, 80 Вт/м2 поглощается облаками, аэрозолями и
газами. А еще есть в диапазоне 3-45 мкм. В этом диапазоне обратно в космос уходит
235 Вт/м2. Ежедневно на поверхность Земли от Солнца приходит 10 18 Вт.
20. Принцип относительности Галилея
Рассмотримдве
инерциальные системы
отсчета, одна из которых
покоится,
а
другая
движется по отношению
к ней с постоянной
скоростью v0,
направленной вдоль оси х. Чтобы системы как-то
различать в подвижной системе будем все символы
обозначать с индексом т.е., например, v
21. Преобразованиями Галилея
Связь междукоординатами x, y, z
некоторой точки P в
первой системе и
координатами x , y , z той
же точки в второй системе
можно записать как:
Совокупность уравнений — преобразования
Галилея. 1-е и 4-е уравнения справедливы
только для классической механики, то есть
при V0<<c.
 При V0 сравнимых со скоростью
При V0 сравнимых со скоростьюсвета
с
преобразования
Галилея
заменяются
на
более
общие
преобразования Лоренца.
x = x’ + V0t ‘
y= y
z = z’
t=t
‘
‘
22. Правилом сложения скоростей
Продифференцируемкоординатные соотношения
по времени и найдем связь
между скоростями:
x x V0
y y
Vx Vx V0
или
Vy Vy
Vz Vz
z z
Эти три скалярных соотношения эквивалентны одному
векторному:
V V V
0
23. Принципом относительности Галилея
Продифференцируем по времени выражение учтя при этом,что V0= const:
V V V0
V V
или
a = a
Ускорение тела во всех инерциальных системах отсчета
оказывается одинаковым. Масса в классической
механике постоянна, то умножив обе части последнего
уравнения на m получим:
ma = ma
или
F F
24. Принцип относительности Галилея
Уравнения механики инвариантны (латинское invariantsнеизменяющийся) по отношению к преобразованиям Галилея.
Это принцип относительности Галилея
Все механические явления в различных инерциальных
системах отсчета протекают одинаково, вследствие чего
никакими механическими опытами невозможно установить,
покоится данная система отсчета или движется
прямолинейно и равномерно. Время идет одинаково в обоих
системах t=t’
Галилей «……..В закрытой каюте корабля двигающегося
прямолинейно и равномерно ….полет мухи, …длина прыжка,
падение капли воды …….все одинаково как и в покоящейся»
25. Преобразования Галилея
• Но так как V V V0 то скорость, кинетическая энергияи импульс – вариантные величины.
• Сила, потенциальная энергия, масса –инварианты
• Уравнения, вид которых не изменяется при переходе к
другой системе отсчета тоже инварианты. Сами величины
входящие в уравнение могут меняться, а формулы, их
связывающие, неизменны.
• Закон сохранения количества движения и энергии
справедливы во всех инерциальных системах отсчета.

• Т.е. если энергия в какой-то инерциальной системе
сохраняется, то в любой другой инерциальной системе она
тоже сохраняется.
• Все три закона Ньютона справедливы во всех инерциальных
системах отсчета.
1905 г. – опираясь на работы Галилея, Эйнштейн совместно
с Лоренцем и Пуанкаре и другими учеными создает СТО
1916 г. — Эйнштейн создал также ОТО — классическую (не
квантовую) релятивистскую теорию гравитации.
Он распространяет механический принцип относительности
Галилея на все остальные физические явления: Законы
всей природы (а не только механики) одинаково
формулируются для всех инерциальных СО. В основе
теории: принцип относительности, принцип постоянства
скорости света и изотропность пространства.
Показал, что преобразования Галилея надо заменить на
более общие преобразования Лоренца
27. Принцип постоянства скорости света.
• Скорость света в вакууме c=2.997 108 м/c не зависит от движенияисточников света и, следовательно, одинакова во всех инерциальных
системах отсчета (инвариантна) и является предельной скоростью
распространения взаимодействий в природе.
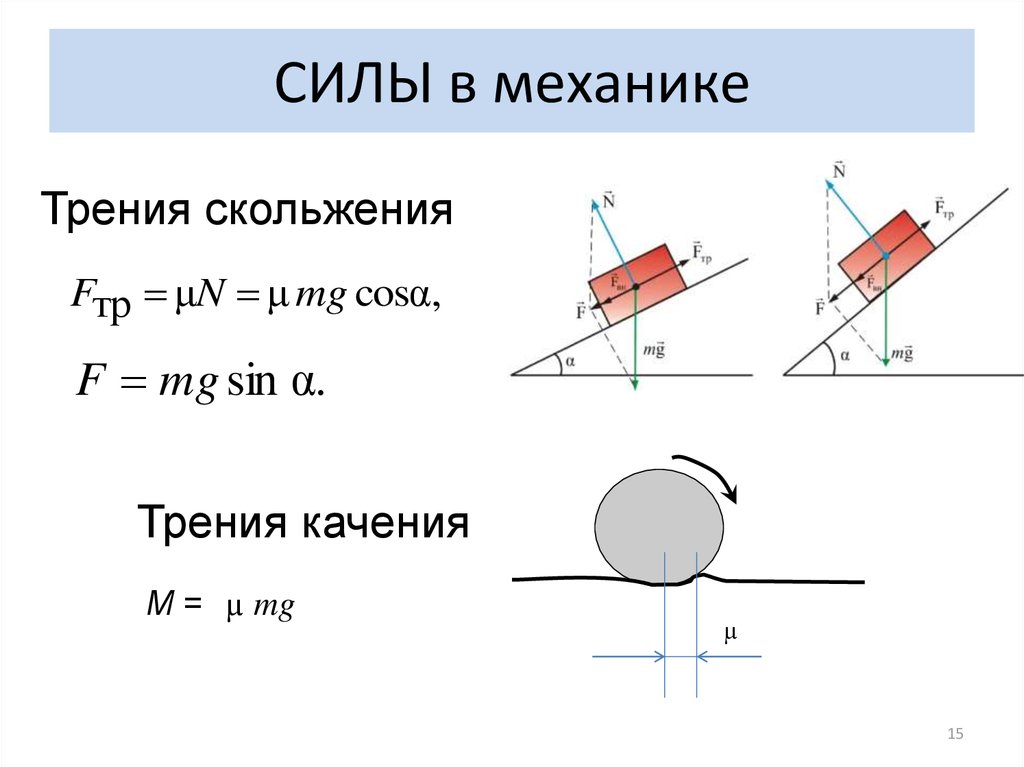 Не зависит от движения
Не зависит от движенияисточника. Постулат является следствием опытных фактов (показано
ранее в 1887 г. Майкельсоном и Морли).
•Относительная скорость материальных тел не может быть больше
скорости света. То есть предельная скорость для материальных тел и
любых физических воздействий.
•В отличии от вакуума, в среде появляются групповая и фазовые
скорости, которые отличаются. И групповая, и фазовая скорости в среде
могут быть больше скорости света в вакууме. Если групповая скорость
больше, то она не есть скорость передачи энергии. Если фазовая больше –
ничего страшного, так как она не соответствует движению физических
объектов. А что случится если свет пройдет сквозь пары натрия при
низкой температуре ?!
28. Факультативно : С чем сравнить скорость света? Это мало или много?
p r2
2
r
2
me
— радиус атома Н
Соотношение
неопределенности
p
e
V e
1
V
m mr
c c
137
2
2
Получаем по порядку величины скорость атомного электрона в
основном состоянии в 137 раз меньше скорости света
29.
 Время в разных системах отсчетаПонятие одновременности, считавшееся в ньютоновской механике
Время в разных системах отсчетаПонятие одновременности, считавшееся в ньютоновской механикеабсолютным, в действительности относительно. Пусть из середины
равномерно движущегося поезда испускается в обоих направлениях
световой сигнал. Пассажир поезда увидит, что сигнал достиг головы и
Y
y’
1
2
x’
X
хвоста поезда одновременно. А
дежурный на станции, что сигнал достиг
хвоста поезда раньше, чем головы,
так как точка 1 движется навстречу сигналу, а точку 2 свету надо
догонять. Пространство и время оказываются взаимосвязанными, образуя
единое четырехмерное пространство-время. Принципиально то, что
они из разных систем отсчета наблюдают! Одно и тоже событие в
инерциальных системах отсчета может иметь разные пространственные
координаты и происходить в разные моменты времени. То как, это
происходит для двух инерциальных систем отсчета, показал Хендрик
Антон Лоренц (1853-1928). В его преобразованиях координаты и время
перемешаны.
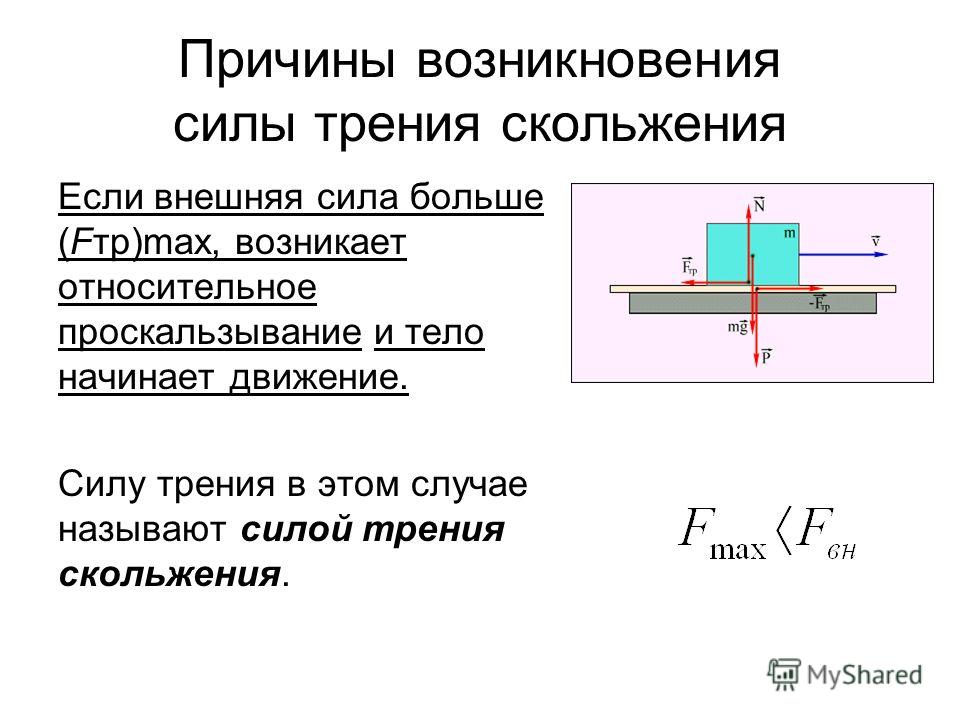
30. Принцип относительности Эйнштейна.
При переходе из одной инерциальной системы отсчета вдругую надо пользоваться преобразованиями Лоренца:
x vt
x
2
1
y y
z z
, где
v
t 2 x
c
t
2
1
v
c
Уравнения, выражающие законы природы, инвариантны
по отношению к преобразованиям Лоренца.
При V<<c превращаются в преобразования Галилея
31. Физики снова подтвердили теорию относительности
Принцип лоренц-инвариантности постулирует, что все физическиезаконы действуют одинаково вне зависимости от положения и
ориентации лаборатории в пространстве и от момента времени и, в
частности, неизменность физических процессов при повороте системы на
произвольный угол. Так, поворот лаборатории вместе с поверхностью
Земли в ходе суточного вращения планеты не должен влиять на
процессы. И днем и ночью результат должен быть одинаков.
Для проверки физики использовали нейтрино — частицы с очень высокой
проникающей способностью.
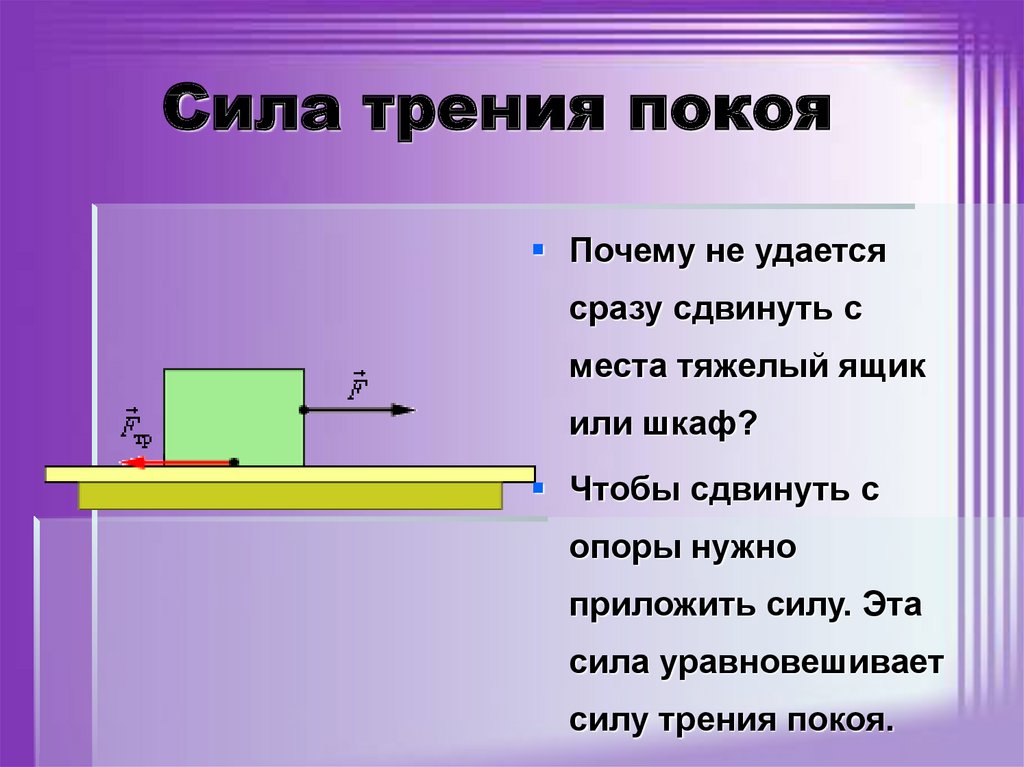 Нейтрино, получаемые при облучении
Нейтрино, получаемые при облученииуглеродной мишени на ускорителе заряженных частиц, направлялись
через слой грунта на расположенный в нескольких сотнях метров
детектор, который регистрировал количество и энергию частиц.
Зависимости результата от времени суток не обнаружилось. Пучок ведет
себя одинаково при любом положении в пространстве и все
направления оказываются для него одинаковы: принцип
инвариантности работает. Равноправие направлений в пространстве
очевидно. Но существует ряд теорий, в которых выделенное направление
существует и играет важную роль в формировании Вселенной.
32. Относительность времени
Время между событиями 0, в неподвижной системе отчета(относительно наблюдателя с часами, которые измеряют этот интервал)
Часто 0 называется собственным временем. Собственное время
является минимальным временем, в движущихся относительно часов
системах отсчета оно будет больше. Пусть
— время между теми
же событиями в системе отсчета, движущейся со скоростью v
относительно первой системы.
 Тогда
Тогда0
1 2
v
c
Так как > 0 то в движущихся системах время течет медленнее.
Проявляется заметным образом лишь при скоростях движения, близких к
скорости света с.
33. Замедление времени
• Парадокс близнецов. Один на земле а второй летит в космос с большойскорость. Кто их близнецов старше? В действительности для парадокса
близнецов принципиально важно чтобы один близнец находился в
инерциальной системе отсчета (на Земле, например), а второй в
неинерциальной системе отсчета которая движется с ускорением (в
ракете в космосе). С другой стороны, каждый из близнецов находится в
совершенно одинаковой ситуации относительно другого и должен быть
старше другого.
• Среднее время жизни нестабильной частицы мезона ~10-6 сек, и он не
мог бы долететь до Земли с высоты 10-20 км, если бы для него не
замедлялось время вследствие движения со скоростью близкой к с
• Но если между событиями имеется причинная связь, то событиепричина во всех системах отсчета предшествует событию-следствию.
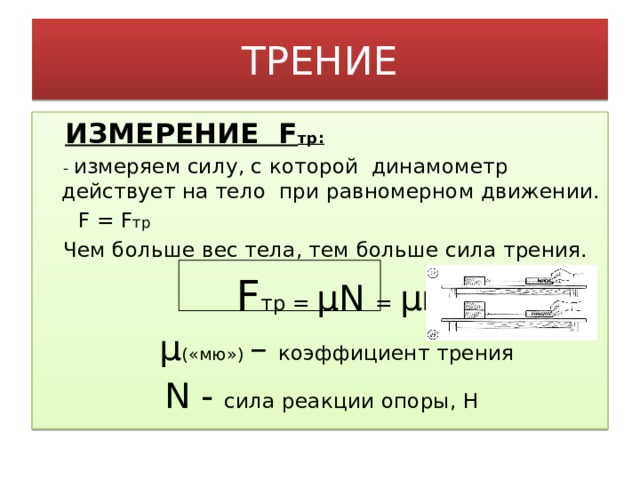
Сын не рождается раньше отца .
Качественное решение : Братья не являются равноправными. Один из них (путешественник)
испытывал этапы ускоренного движения, которые необходимы для его возвращения на Землю
Более сложное: тот кто изменяет свою систему отсчёта, тот и оказывается моложе.
34. Замедление времени — реальность!
в 2010 году физики экспериментально подтвердилизамедление времени. Использование сверхточных атомных
часов показало замедления времени вблизи массивных
объектов (правда это уже ОТО, которая учитывает кривизну
пространства-времени, а не СТО). Студенту, который
находится дальше от объекта, будет казаться, что часы его
сокурсника, который стоит ближе к объекту, идут
медленнее.
Показано, что с точки зрения неподвижного студента
«стрелки» на атомных часах движущегося коллеги будут
перемещаться медленнее (замедление хода часов при
движении).
35. Реальное применение!
Автомобильная система навигации, которой мы свами пользуемся сегодня, определяет
местонахождения транспорта с точностью до
нескольких метров, основываясь именно на теории
относительности Эйнштейна.

36. Факультативно ОТО
37. Относительность расстояния
yK
z
y’
K’
z’
l0
v0
v0
x, x’
Пусть относительно штрихованной
системы нештрихованная будет
подвижной! Стержень собственной
длины l0 относительно
неподвижный “штриховой” системы
отсчета K’, движется вдоль оси X со
скоростью vo
Длина стержня l в подвижной системе отсчета K равна:
l l0 1
1
l 0
2
38. Сложение скоростей
Пусть частица движется вдоль осей x и x’в направлениискорости Vo движущейся системы отсчета. Пусть V —
скорость в системе K, V’— скорость в системе K’. Тогда
v v0
v
v0v
1 2
c
Те связь скоростей не так как у Галилея. Можно утверждать,
что пространство и время неотделимы и представляют
единую 4-х мерную СК.
39. Зависимость массы от скорости
• Инертная масса от скорости не зависит!!!• Релятивистская масса зависит от скорости как
m
m0
1
2
При увеличении V ? при V→c m →∞.

Ни одно тело при m>0 не может достигнуть c.
При V→c m →∞, а l →0. Материальная точка?
При использовании данной формулы возникает ряд теоретических
противоречий. Сейчас научное сообщество отказалось от введения
зависимости массы от скорости. Во новых учебниках этой формулы
нет! Применяются формулы для импульса и энергии!
40. Второй закон Ньютона
Выражение для импульса частицы в теорииотносительности имеет вид:
P
mV
1
2
Основное уравнение релятивистской динамики
материальной точки :
d mV
F
dt 1 2
41. Энергии свободной частицы
Полная энергия свободной частицы, движущейся соскоростью v:
2
E
mc
1 2
Свободной называют частицу, на которую не действуют
никакие силы. Неподвижная частица обладает энергией
E0 mc2
Энергия Eo называется энергией покоя и представляет
собой внутреннюю энергию частицы. Т.е. тело с
инертной массой покоя m обладает определенным запасом
энергии пропорциональным m.
 1 моль вещества
1 моль веществасодержит энергию около 9 1013 Дж
42. Факультативно Настоящее оказалось переходным звеном между квантовым будущим и классическим прошлым
Физики предложили новую модель Вселенной, в рамках которой квантовоебудущее приводит к своего рода «кристаллизации» классического прошлого
через настоящее.
По аналогии с ОТО ученые рассматривали Вселенную в качестве
четырехмерного куска пространства-времени с фиксированными
границами. При этом выделенного момента времени никакого не вводится.
Пока этот кусок относится к будущему, его природа исключительно
квантовая. В будущем с разной степенью вероятности могут присутствовать
одновременно несколько возможных событий.
Прошлое подчиняется классическим законам физики, то есть все
физические величины однозначно определены.
Течение времени — эволюцию законов пространства-времени. Настоящее в
этом случае — это момент перехода от квантовых законов к классическим
[PDF] Трение резины: сравнение теории с экспериментом
- title={Резиновое трение: сравнение теории с экспериментом},
автор = {Б.
 Лоренц и Б. Н. Дж. Перссон, Сабина Дилувейт и Тошио Тада},
journal={Европейский физический журнал E},
год = {2011},
объем = {34},
страницы={1-11}
}
Лоренц и Б. Н. Дж. Перссон, Сабина Дилувейт и Тошио Тада},
journal={Европейский физический журнал E},
год = {2011},
объем = {34},
страницы={1-11}
} - Б. Лоренц, Б. Перссон, Т. Тада
- Опубликовано 6 декабря 2011 г.
- Материаловедение
- The European Physical Journal E
Мы измерили силу трения, действующую на резиновый блок, скользящий по бетонной поверхности. Мы использовали как ненаполненный, так и наполненный (сажей) стирол-бутадиеновый (SB) каучук и варьировали температуру от -10 ° C до 100 ° C и скорость скольжения от 1 мкм / с до 1000 мкм / с. Мы обнаружили, что экспериментальные данные при различных температурах могут быть сдвинуты в гладкую эталонную кривую, используя коэффициенты температурно-частотного сдвига, полученные из измерений объемного вязкоупругого модуля.
View on Springer
multiscaleconsulting.comТрение резины о дорожное покрытие: Эксперимент и теория для низких скоростей скольжения.
Важный вклад в трение резины вносят процессы сдвига в области контакта, которые могут возникать из-за того, что молекулы резины (или участки резины) подвергаются циклам склеивания-растяжения-разрыва, как обсуждалось в классической статье Шалламаха.

Прогнозирование коэффициента трения скольжения наполненной резины по сухим и мокрым поверхностям с самоаффинной большой шероховатостью
- Hiro Tanaka, Kimiyasu Yoshimura, H. Kadowaki
Материаловедение
- 2016
Трение резины с наполнителем по шероховатой поверхности в основном определяется может быть представлена спектральной мощностью…
Теоретическое и экспериментальное исследование вязкоупругих контактов качения с учетом тепловых эффектов
- К. Путиньяно, Ж. Ле Рузик, Т. Реддихофф, Г. Карбоне, Д. Дини
Машиностроение, материаловедение
- 2014
Вязкоупругие контакты присутствуют в бесчисленных промышленных компонентах, включая шины, амортизаторы и резиновые уплотнения. Эффективный дизайн таких компонентов требует полного знания вязкоупругих…
Трение резины с поверхностями с жесткими сферическими неровностями
- Д. Т. Нгуен, С. Рамакришна, К.
 Фретиньи, Н. Спенсер, Ю. Ле Шенадек, А. Шатоминуа
Фретиньи, Н. Спенсер, Ю. Ле Шенадек, А. Шатоминуа Engineering
Tribology Letters
- 2012
В данной статье сообщается о фрикционных свойствах гладких резиновых подложек, скользящих по жестким поверхностям, покрытым коллоидными наночастицами различной плотности (средний диаметр 77 нм).…
Вязкоупругое трение эластомеры с шероховатой поверхностью в условиях контакта при кручении.
- M. Trejo, C. Fretigny, A. Chateauminois
Engineering
Физический обзор. E, Статистическая, нелинейная физика и физика мягкого вещества
- 2013
Сравнение между k(v) и напряжением трения гладких контактов показывает, что диссипативные процессы нанометрового масштаба, происходящие на границе раздела, преобладают над вязкоупругой диссипацией на микронеровностях.
Гистерезисный вклад трения полированной резины о бетонную поверхность
- Фешанджерди М.
 , Хоррами М., Масуди А., Кашани М.
, Хоррами М., Масуди А., Кашани М. Физико-технические науки
- 2017
Трение резины для состава протектора шины на дорожном покрытии
Измеряется эффективный модуль вязкоупругости резины при больших деформациях, рассчитывается коэффициент трения резины и вклад в трение от площади реального контакта интерпретируется как обусловленный сдвигом очень тонкая замкнутая резиновая мазковая пленка.
Влияние трибомодифицированного поверхностного слоя на трение в эластомерных контактах
- М. Мохтари
Материаловедение
- 2015
Трение резины о встречную поверхность интересовало многих исследователей из-за его огромной практической значимости. Резиновые компоненты применяются в различных отраслях промышленности, таких как шины,…
Адгезия: роль объемной вязкоупругости и шероховатости поверхности и γeff(v,T) имеет вклад одинаковой величины как от рассеяния объемной вязкоупругой энергии вблизи вершины трещины, так и от процесса разрыва связи в вершине трещины.

О трение углеродных чернокожих и эластомеров, армированных BR и S-SBR,
- M. Mokhtari, D. Schipper, T. Tolpekina
Материалогические науки
Письма Tribology
- 2014
- Б. Перссон, А. Волокитин
Инженерия, физика
Европейский физический журнал. E, Мягкая материя
- 2006
- Б. Перссон
Физика, инженерия
Журнал физики. Конденсированное вещество : журнал Института физики
- 2006
- André Le Gal, Xin Yang, M. Klüppel
Материаловедение, инженерия
Журнал химической физики
- 2005
- Д. Т. Нгуен, П. Паолино, Э. Бартель
Машиностроение
- 2011
2020. Экспериментально и теоретически исследовано трение эластомеров, армированных техническим углеродом и диоксидом кремния, с использованием модели Перссона. Влияние армирующих наполнителей на эластичность было…
ПОКАЗАНЫ 1-10 ИЗ 44 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантностьНаиболее влиятельные статьиНедавность
Трение резины о гладкие поверхности
Разработана детальная модель, учитывающая влияние термических флуктуаций на депиннинг небольших пятен контакта на границе резина-подложка, предсказывающая, что зависимость макроскопического напряжения сдвига от скорости имеет колоколообразную форму и что низкоскоростная сторона демонстрирует ту же температурную зависимость, что и объемный вязкоупругий модуль.

Трение резины: роль температуры вспышки
Исследовано влияние локального нагрева на трение резины и показано, что в типичном случае повышение температуры приводит к уменьшению трения резины с увеличением скольжения. скорость для v>0,01 м с (-1).
Оценка трения скольжения и контактной механики эластомеров на основе динамо-механического анализа.
вклад в трение резины на сухих и смазанных шероховатых поверхностях, и установлено, что в данном диапазоне скоростей на шероховатых сухих поверхностях доминирующую роль играет адгезионная формула.
Взаимосвязь между трением и вязкоупругими свойствами резины
В этой статье описано исследование трения нескольких типов резины о твердые поверхности в широком диапазоне температур и скоростей скольжения.
 Наибольшая скорость не превышала нескольких…
Наибольшая скорость не превышала нескольких…Поля поверхностного давления и касательного напряжения в контакте трения на резине
В статье рассматривается вопрос определения распределения напряжения трения по инверсии измеренного поля перемещений поверхности для поверхностей скольжения между стеклянной линзой и…
Инженерия, физика
- 1998
Влияние молекулярного веса и температуры на кинетическое трение силиконовых каучуков
- К. Форволакос, М. Чаудхури
Материаловедение
- 2003
Напряжения трения поли(диметилсилоксановых) эластомеров различной молекулярной массы измерялись относительно нанесенного монослоя гексадецилсилоксана и тонкой пленки полистирола в зависимости от модели каучука…
Исследования и исследования стационарное трение на шероховатых поверхностях
- A.
 Le Gal, M. Klüppel
Le Gal, M. Klüppel Материаловедение, машиностроение
- 2007
В этой статье представлены новые аспекты физически мотивированного моделирования стационарного трения резины скольжения по шероховатым поверхностям. Описание динамического контакта рассматривается в…
Теория трения резины и контактная механика
- Б. Перссон
Инженерия, физика
- 2001
При скольжении резины по шероховатой поверхности, неровности подложки воздействуют на поверхность резины колебательными силами, что приводит к «рассеиванию» энергии за счет внутреннего трения…
Адгезия и трение упругого полупространства, находящегося в контакте со слегка волнистой твердой поверхностью по теории контактов | Дж. Трибол.
Пропустить пункт назначения навигации
Научно-исследовательские работы
Цзяньвэй Ву,
Хуэй Ван,
Тяньфэн Чен,
Яруи Ма,
Дживен Цуй,
Цзюбин Тан
Информация об авторе и статье
Электронная почта: wujianwei@hit. edu.cn
edu.cn
Электронная почта: [email protected]
Электронная почта: 93
[email protected]Электронная почта: [email protected]
Электронная почта: [email protected]
Электронная почта: [email protected]
Предоставлено отделом трибологии ASME для публикации в Journal of Tribology.
Дж. Трибол . Февраль 2022 г., 144(2): 021501 (10 страниц)
Номер статьи: ТРИБ-20-1422 https://doi.org/10.1115/1.4050901
Опубликовано онлайн: 6 мая 2021 г.
История статьи
Получен:
15 сентября 2020 г.
Пересмотренный:
24 января 2021
Принято:
25 января 2021
Опубликовано:
май 6, 2021
- .
 Просмотры
Просмотры- Содержание артикула
- Рисунки и таблицы
- Видео
- Аудио
- Дополнительные данные
- Экспертная оценка
- Делиться
- MailTo
- Твиттер
Иконка Цитировать Цитировать
Разрешения
- Поиск по сайту
Citation
Ву Дж. , Ван Х., Чен Т., Ма Ю., Цуй Дж. и Тан Дж. (6 мая 2021 г.). «Механизм трения и характеристики сетки на основе теории контакта». КАК Я. Дж. Трибол . февраль 2022 г.; 144(2): 021501. https://doi.org/10.1115/1.4050901
, Ван Х., Чен Т., Ма Ю., Цуй Дж. и Тан Дж. (6 мая 2021 г.). «Механизм трения и характеристики сетки на основе теории контакта». КАК Я. Дж. Трибол . февраль 2022 г.; 144(2): 021501. https://doi.org/10.1115/1.4050901
Скачать файл цитаты:
- Рис (Зотеро)
- Менеджер ссылок
- EasyBib
- Подставки для книг
- Менделей
- Бумаги
- КонецПримечание
- РефВоркс
- Бибтекс
- Процит
- Медларс
Расширенный поиск
Abstract
С развитием интегральных схем структура микросхем становится все более и более сложной, и соответственно увеличивается стоимость обработки. Для повышения производительности литографии необходимо увеличить ускорение столика сетки, чтобы сократить время позиционирования. Однако увеличение ускорения вызовет относительное скольжение между сеткой и вакуумным патроном, что серьезно повлияет на точность и выход продукта литографии. Для подавления проскальзывания в этой статье исследуются механизм трения и характеристики между сеткой и патроном. Во-первых, на основе модели контакта Когута-Эциона и модели фрактального контакта Маджумдара-Бхушана (МБ) была установлена модель максимального коэффициента статического трения между наноразмерными поверхностями. Затем с помощью сканирования атомно-силовой микроскопии (АСМ) были получены параметры морфологии поверхности сетки и адсорбционной поверхности патрона. Наконец, эксперименты с максимальной статической силой трения показывают, что модель MB больше подходит для изучения механизма трения между сеткой и вакуумным патроном, а модель более информативна для подавления проскальзывания сетки.
Однако увеличение ускорения вызовет относительное скольжение между сеткой и вакуумным патроном, что серьезно повлияет на точность и выход продукта литографии. Для подавления проскальзывания в этой статье исследуются механизм трения и характеристики между сеткой и патроном. Во-первых, на основе модели контакта Когута-Эциона и модели фрактального контакта Маджумдара-Бхушана (МБ) была установлена модель максимального коэффициента статического трения между наноразмерными поверхностями. Затем с помощью сканирования атомно-силовой микроскопии (АСМ) были получены параметры морфологии поверхности сетки и адсорбционной поверхности патрона. Наконец, эксперименты с максимальной статической силой трения показывают, что модель MB больше подходит для изучения механизма трения между сеткой и вакуумным патроном, а модель более информативна для подавления проскальзывания сетки.
Раздел выдачи:
Контактная механика
Ключевые слова:
литография, сетка, трение, соскальзывать, фрактал, адгезия, шероховатости и неровности поверхности, поверхности
Темы:
Деформация, фракталы, Трение, Стикшн, Шероховатость поверхности, Вакуум, Адгезия, Литография, Стресс
Список литературы
1.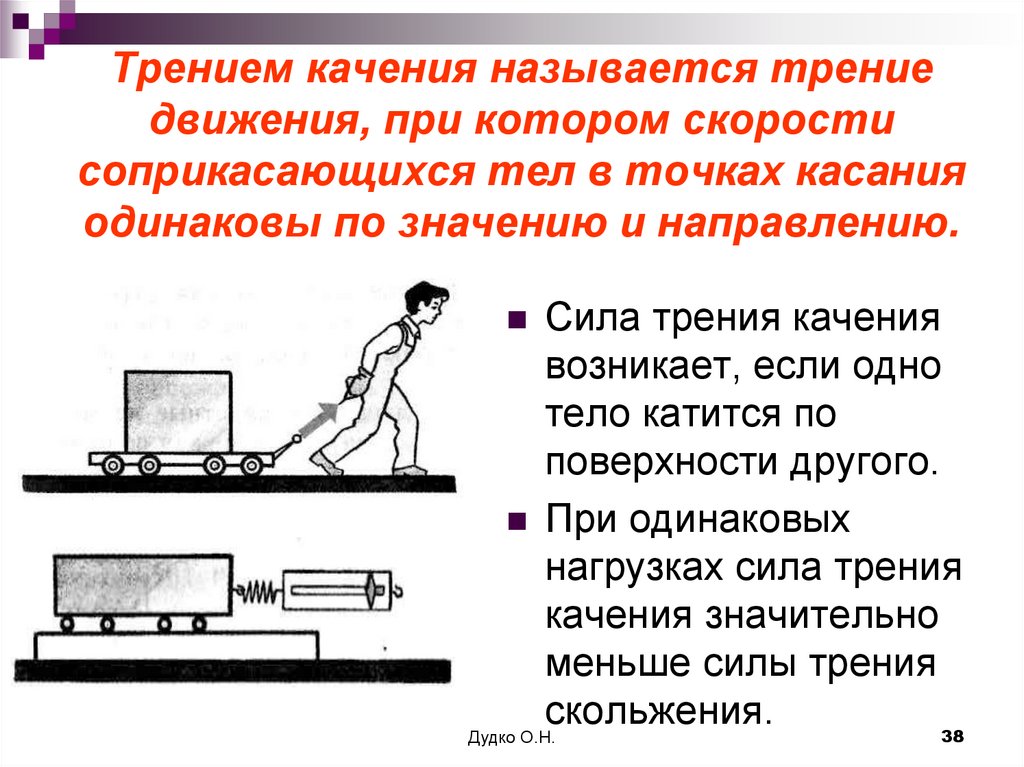
MOORE
,
G. E.
,
2006
, «
Прогресс в цифровой интегрированной Electronics
,
. Франциско, Калифорния
,
11–13 декабря
.
2.
Банерджи
,
С.
,
Агарвал
,
K. B.
и
Orshansky
,
M.
,
2011
, «
Simultage OPC и декорация для двойного воздействия
11202020202020202020202020202020202020202020202020202020202020202020202020202020202020202020202.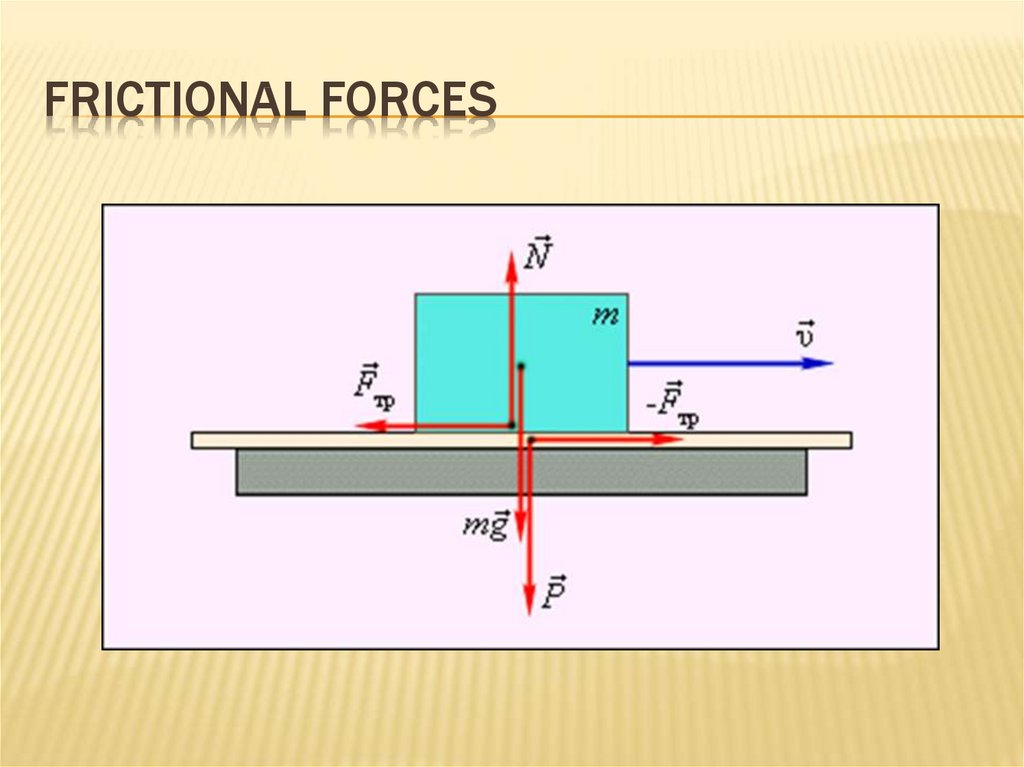 SPIE
SPIE
,
7973
, стр.
298
–
306
.
3.
Яэгаси
,
Х.
,
Ояма
,
K.
,
Hara
,
A.
,
Natori
,
S.
,
Yamauchi
,
S.
, and
Yamato
,
M.
,
2013
,
Advanced Etch Technology for Nanopatterning II
, Y. Zhang, G. S. Oehrlein, and.
Zhang, G. S. Oehrlein, and.
8685
,
Spie-Int Soc Optical Engineering
,
Bellingham
, p.
86850М
.
4.
Lai
,
K.
,
Erdmann
,
A.
,
Ma
,
X.
,
Gao
,
J.
,
Han
,
C.
и
Li
,
Y.
,
2014
, “
Efficient Source Polarization Optimization for Robust Optical Lithography
,”
SPIE
,
9052
, p.
.
5.
NAAIJKENS
,
G. J. P.
,
Conley
,
W.
,
Roselel
,
.0021
и
Steinbuch
,
M.
,
2013
, «
Mask Swiping Walling
,
SPIE Adv. литогр.
,
8683
, с.
86832I
.
6.
Amin-Shahidi
,
D.
, and
Trumper
,
D.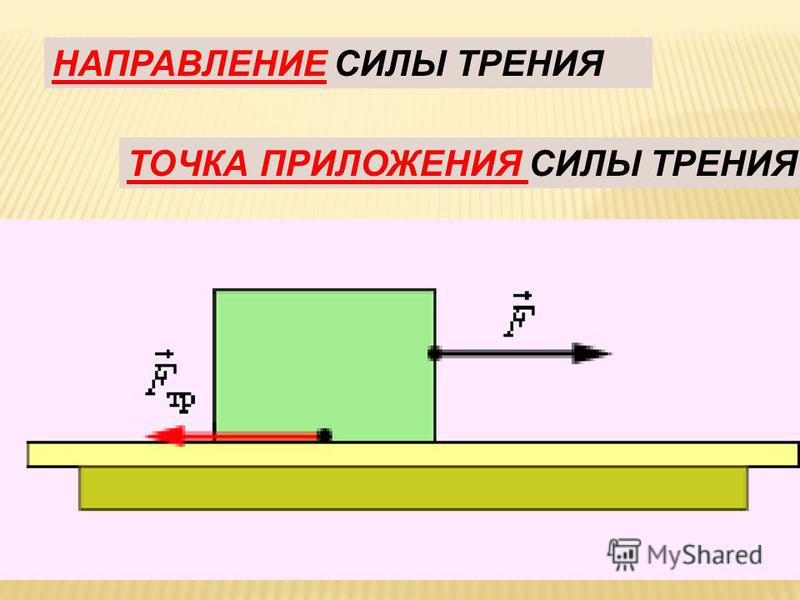 L.
L.
,
2014
, “
Проектирование и контроль пьезоэлектрического приготовления сетки для профилактики скольжения сетки в литографических системах
, ”
Mechatronics
,
24
(
6
), PP. –
571
.
7.
Герц
,
H.
,
1881
, “
О контакте упругих тел1 9002
021
J. Fur Die Reine Und Angewandte Mathematik
,
92
, стр.
156
–
171
1 .
8.
Johnson
,
K. L.
,
Kendall
,
K.
, and
Roberts
,
A. D.
,
1971
, “
Поверхностная энергия и контакт упругих тел
”,
Proc. Р. Соц. Лондон А: математика. физ. науч.
,
324
(
1588
), стр.
301
–
313
.
9.
Derjaguin
,
B. V.
,
Muller
,
V.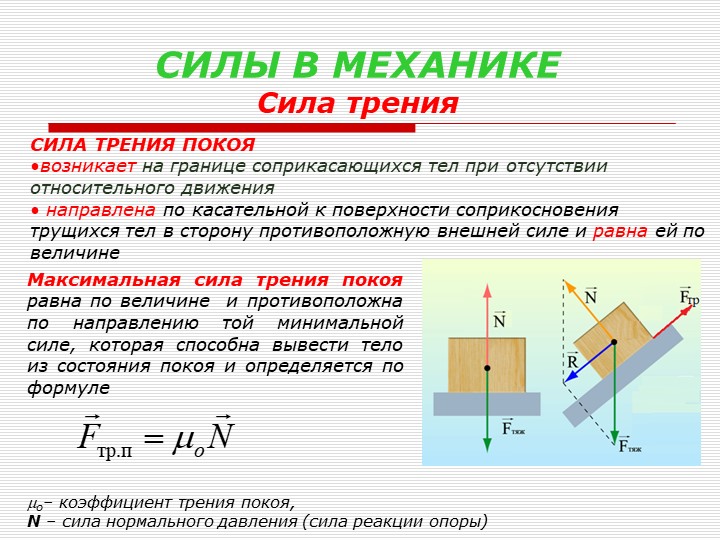 M.
M.
, and
Toporov
,
Y. P.
,
1975
, “
Влияние контактных деформаций на адгезию частиц
»,
J. Colloid Interface Sci.
,
53
(
2
), с.
10.
Lior
,
K.
, and
Izhak
,
E.
,
2002
, “
Elastic-Plastic Contact Analysis of a Sphere and a Жесткая плоская
»,
ASME J. Appl. мех.
,
69
(
5
), с.
11.
Lior
,
K.
, and
Izhak
,
E.
,
2003
, “
A Finite Element Based Elastic-Plastic Model for the Контакт шероховатых поверхностей
»,
Трибол. Транс.
,
46
(
3
), с.
12.
Lior
,
K.
и
Izhak
,
E.
,
2004
,
,
2004
,
,
2004
,
,
2004
,
,
2004
,
,
2004
,
.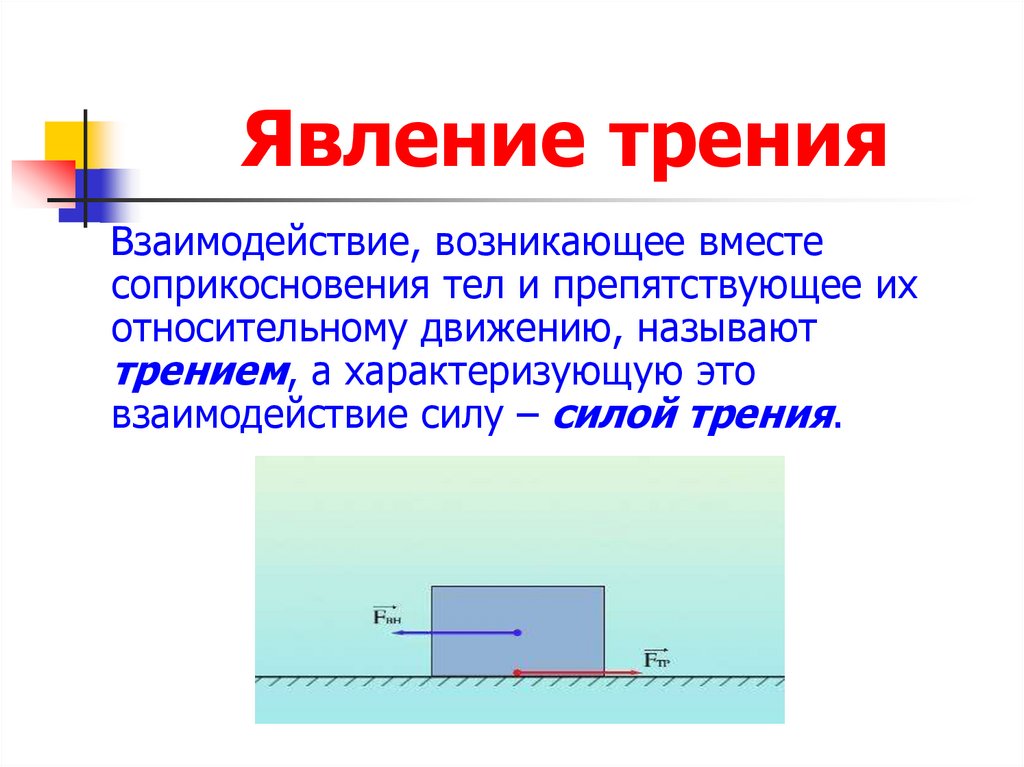 Поверхности
Поверхности
”,
ASME J. Tribol.
,
126
(
1
), стр.
34
–
40
.
13.
Majumdar
,
A. A.
, and
Bhushan
,
B.
,
1990
, “
Role of Fractal Geometry in Roughness Characterization and Contact Mechanics of Поверхности
”,
ASME J. Tribol.
,
112
(
2
), стр.
205
–
216
.
14.
Majumdar
,
A. A.
, and
Bhushan
,
B.
,
1991
, “
Fractal Model of Elastic-Plastic Contact Between Rough Surfaces
»,
ASME J. Tribol.
,
113
(
1
), стр.
1
–
11
.
15.
Xu
,
K.
,
Yuan
,
Y.
, and
Chen
,
J.
,
2018
, «
Влияние функций распределения размеров на контакт между фрактальными шероховатыми поверхностями
»,
AIP Adv.
,
8
(
7
), с.
075317
.
16.
Yuan
,
Y.
,
Li
,
G.
,
Kai
,
L.
, and
Xiaohui
,
Y.
,
2017
, “
Модель упругопластической контактной механики шероховатой поверхности на основе теории фракталов
”,
Китай. Дж. Мех. англ.
Дж. Мех. англ.
,
30
(
1
), с.
17.
Greenwood
,
J. A.
, and
Williamson
,
J. B. P.
,
1966
, “
Contact of Nominally Flat Surfaces
,”
Proc . Р. Соц. Математика. физ. англ. науч.
,
295
(
1442
), стр.
300
–
319
18.
Sayles
,
R. S.
, and
Thomas
,
T. R.
R.
,
1978
, “
Surface Topography as a Nonstationary Random Process
,”
Природа
,
271
(
5644
), стр.
431
–
434
.
19.
Мандельброт
,
Б.
,
1967
, “
Какова длина побережья Британии? Статистическое самопоклонность и дробное размер
, ”
Science
,
156
(
3775
), стр.
636
–
), стр.
636
–
), с..0026 .
20.
Wang
,
S.
, and
Komvopoulos
,
K.
,
1994
, “
A Fractal Theory of the Interfacial Temperature Distribution in the Режим медленного скольжения: Часть i — Анализ упругого контакта и теплопередачи
»,
ASME J. Tribol.
,
116
(
4
), стр.
812
–
822
.
21.
Kogut
,
L.
, and
Etsion
,
I.
,
2003
, “
A Semi-Analytical Solution for the Sliding Inception of a Сферический контакт
»,
ASME J. Tribol.
,
125
(
3
), стр.
499
–
506
.
22.
Ganti
,
S.
, and
Bhushan
,
B.
,
1995
, “
Generalized Fractal Analysis and Its Applications to Engineering Surfaces
, ”
Wear
,
180
(
1–2
), стр.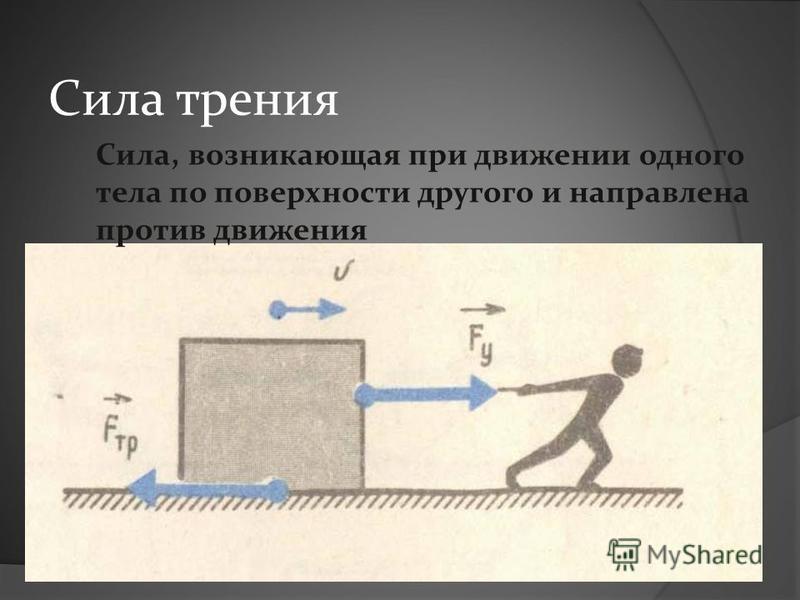
17
—
34
.
23.
Wu
,
J. J.
,
2001
, “
Структурная функция и спектральная плотность фрактальных профилей
,
12
(
13
), стр.
2481
–
2492
.
24.
Цзи
,
К. С.
,
Чжу
,
Ч.
,
Jiang
,
W.
, and
Lu
,
B.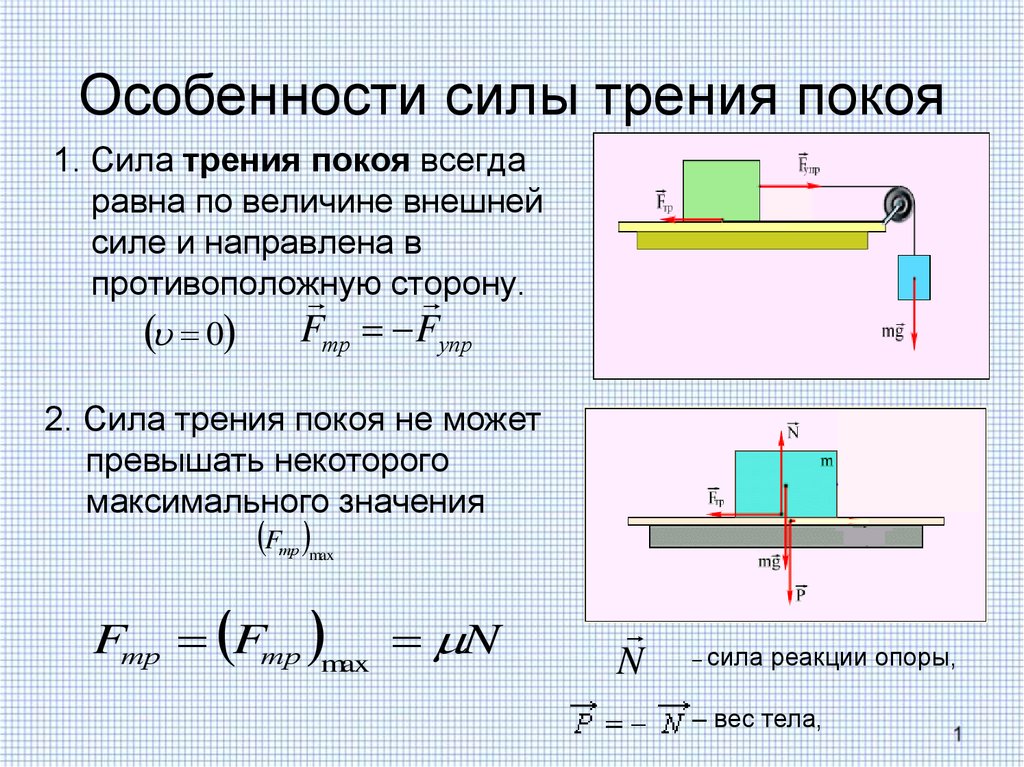 B.
B.
,
2010
, “
Running-In Test and Fractal Methodology for Worn Surface Topography Characterization
”,
Китай. Дж. Мех. англ.
,
23
(
5
), стр.
600
–
605
1 900
25.
Morag
,
Y.
, and
Etsion
,
I.
,
2007
, “
Resolving the Contradiction of Asperities Plastic to Elastic Mode Transition in Current Contact Models of Fractal Rough Surfaces
,”
Wear
,
262
(
5–6
), pp.
624
–
629
.
26.
Liou
,
J. L.
,
Lin
,
J. F.
,
Liou
,
J. L.
, and
Lin
,
J. F.
,
2010
, “
Модифицированная фрактальная микроконтактная модель, разработанная для шероховатостей с переменными параметрами морфологии
”,
Износ
,
0020 268
(
1
), стр.
133
–
144
.
27.
Stronge
,
W. J.
,
2000
,
Влияние в механических системах
,
B.
20202020202020202021,
, ED.551
,
Springer
,
Берлин, Гейдельберг
, стр.
189
–
234
.
28.
LIU
,
W.
,
Ян
,
J.
,
,
,
,
,
.
J.
, и
Li
,
L.
,
2015
, “
Параметр, основанный на теории нормального интерфейса0021
»,
J. Доп. мех. Дес. Сист. Произв.
,
9
(
5
), с.
JAMDSM0070
.
29.
Hamilton
,
G. M.
, and
Goodman
,
L. E.
,
1966
, “
The Stress Field Created by a Circular Sliding Contact
, ”
ASME J. Appl. мех.
Appl. мех.
,
33
(
2
), стр.
371
–
376
30.
Spittel
,
M.
, and
Spittel
,
T.
,
2011
, “
AlZn5.5MgCu
,”
Landolt Бернштейн.
,
2
, с.
480
.
31.
Данные
,
2020
, https://www.makeitfrom.com/material-properties/EN-1. 8509-41CrAlMo7-10-Nitriding-Steel, по состоянию на август 2020 г. 9020. в настоящее время имеют доступ к этому контенту.
8509-41CrAlMo7-10-Nitriding-Steel, по состоянию на август 2020 г. 9020. в настоящее время имеют доступ к этому контенту.
25,00 $
Покупка
Товар добавлен в корзину.
Проверить Продолжить просмотр Закрыть модальный режимТрение | Трибология в малых масштабах: современный учебник по трению, смазке и износу
Фильтр поиска панели навигации Oxford Academic Трибология в малых масштабах: современный учебник по трению, смазке и износу (2-е изд.) Атомная, молекулярная и оптическая физикаФизика конденсированного состоянияКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации
Oxford Academic Трибология в малых масштабах: современный учебник по трению, смазке и износу (2-е изд. ) Атомная, молекулярная и оптическая физикаФизика конденсированного состоянияКнигиЖурналы
Термин поиска на микросайте
) Атомная, молекулярная и оптическая физикаФизика конденсированного состоянияКнигиЖурналы
Термин поиска на микросайте
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
Ссылка
Мейт, К. Мэтью и Роберт В. Карпик,
«Трение»
,
Трибология в малых масштабах: современный учебник по трению, смазке и износу
, 2-е изд.
Оксфордский выпускной Texts
(
Oxford,
2019;
online edn,
Oxford Academic
, 24 Oct. 2019
2019
), https://doi.org/10.1093/oso/9780199609802.003.0004,
по состоянию на 30 сентября 2022 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford Academic Трибология в малых масштабах: современный учебник по трению, смазке и износу (2-е изд.) Атомная, молекулярная и оптическая физикаФизика конденсированного состоянияКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford Academic Трибология в малых масштабах: современный учебник по трению, смазке и износу (2-е изд.) Атомная, молекулярная и оптическая физикаФизика конденсированного состоянияКнигиЖурналы Термин поиска на микросайте
Advanced Search
Abstract
В этой главе рассказывается о трениях, которые проявляются в повседневной жизни. Глава начинается с закона Амонтона (1699) что трение пропорционально силе нагрузки между контактирующими поверхностями (константа пропорциональности называется коэффициентом трения ). Двумя основными механизмами трения без смазки являются адгезионное трение и трение вспашки, причем преобладающим механизмом обычно является адгезионное трение. Адгезионное трение пропорционально реальной площади контакта; для шероховатых поверхностей эта площадь контакта пропорциональна силе нагрузки, что обеспечивает физическое обоснование закона Амонтона. Такие процессы, как наноразмерный поток атомов и молекул вокруг точек контакта, приводят к тому, что сила, необходимая для индукции скольжения (статическое трение), превышает силу, необходимую для поддержания скольжения (кинетическое трение). Трение, уменьшающееся с увеличением скорости, приводит к прерывистому движению поверхностей скольжения, где расстояние скольжения может быть таким же коротким, как расстояние между атомами.
Глава начинается с закона Амонтона (1699) что трение пропорционально силе нагрузки между контактирующими поверхностями (константа пропорциональности называется коэффициентом трения ). Двумя основными механизмами трения без смазки являются адгезионное трение и трение вспашки, причем преобладающим механизмом обычно является адгезионное трение. Адгезионное трение пропорционально реальной площади контакта; для шероховатых поверхностей эта площадь контакта пропорциональна силе нагрузки, что обеспечивает физическое обоснование закона Амонтона. Такие процессы, как наноразмерный поток атомов и молекул вокруг точек контакта, приводят к тому, что сила, необходимая для индукции скольжения (статическое трение), превышает силу, необходимую для поддержания скольжения (кинетическое трение). Трение, уменьшающееся с увеличением скорости, приводит к прерывистому движению поверхностей скольжения, где расстояние скольжения может быть таким же коротким, как расстояние между атомами.
Ключевые слова: Закон Амонтона, трение, коэффициент трения, адгезионное трение, трение вспашки, трение покоя, кинетическое трение, прерывистое скольжение, трение кожи человека, рост соединения
Тема
Физика конденсированного состояния Атомная, молекулярная и оптическая физика
В настоящее время у вас нет доступа к этой главе.
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic.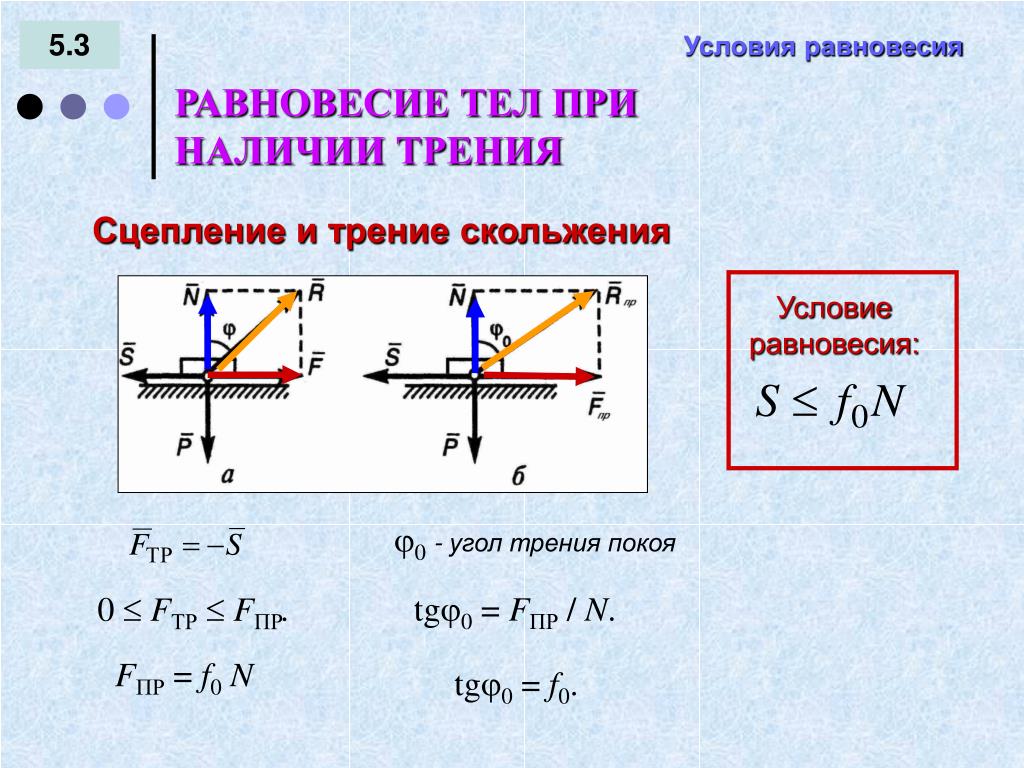 Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.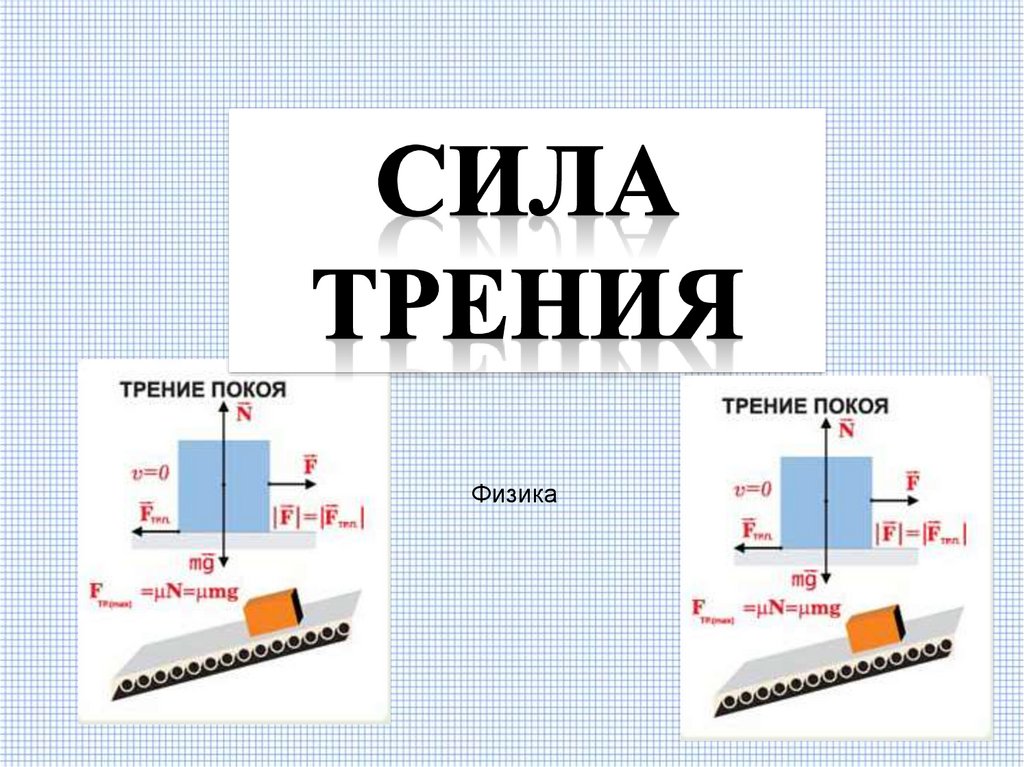
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи, в которой выполнен вход, и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
д.
Покупка
Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.
Информация о покупке
Приложения теории твердого, статического и кинетического трения
Когда человек идет по дороге, ему или ей не дает поскользнуться сила трения о землю. При отсутствии трения, например, на обледенелой поверхности, ботинок человека будет скользить, если поставить его на землю. Сила трения всегда противодействует движению обуви.
Силу трения между поверхностью стола и деревянным бруском А можно исследовать, прикрепив один конец веревки к А, а другой — к чаше весов S. Нить проходит по неподвижному желобковому колесу B. При добавлении к S небольших грузов блок не двигается. Таким образом, сила трения между блоком и столом равна общему весу S вместе с весом S. Когда добавляется больше грузов, A не перемещается, показывая, что сила трения увеличилась, но по мере дальнейшего увеличения веса , А вдруг начинает буксовать. Сила трения, существующая теперь между поверхностями, называется предельной силой трения, и говорят, что мы достигли предельного трения. Предельная сила трения – это максимальная сила трения между поверхностями.
Сила трения, существующая теперь между поверхностями, называется предельной силой трения, и говорят, что мы достигли предельного трения. Предельная сила трения – это максимальная сила трения между поверхностями.
Коэффициент статического трения
Нормальная реакция R стола на A равна весу A. Помещая на A различные веса, чтобы изменить величину R, мы можем найти, как предельная сила трения F зависит от R в соответствии с только что описанным экспериментом. Результаты показывают, что приблизительно
, а µ известен как коэффициент статического трения между двумя поверхностями. Величина µ зависит от характера двух поверхностей; например, оно составляет от 0,2 до 0,5 для дерева к дереву и от 0,2 до 0,6 для дерева к металлам. Эксперимент также показывает, что предельная сила трения остается той же, если брусок А на рис. контакт, когда нормальная реакция такая же.
Коэффициент статического трения µ также можно найти, поместив блок A на поверхность S, а затем плавно наклонив S до тех пор, пока A не окажется в точке соскальзывания вниз по плоскости, рис. **** Сила статического трения F равна тогда равна mg sin o, где o угол наклона плоскости к горизонту, нормальная реакция R равна mg cos0
**** Сила статического трения F равна тогда равна mg sin o, где o угол наклона плоскости к горизонту, нормальная реакция R равна mg cos0
Кинетическое трение. Коэффициент кинетического (динамического) трения
При торможении велосипеда между движущимися колесами и тормозными колодками возникает сила трения. В отличие от случая статического трения, когда один из тел находится на грани проскальзывания, сила трения между движущимся колесом и тормозными колодками называется кинетической (или динамической) силой трения. Таким образом, между двумя поверхностями, которые имеют относительное движение, возникает кинетическое трение. Коэффициент кинетического (динамического) трения µ между двумя поверхностями определяется соотношением
Где F’ — сила трения, когда объект движется с постоянной скоростью, а R’ — нормальная реакция между поверхностями. На чашу весов добавляются гири, и каждый раз А слегка толкается. На одном этапе А продолжает двигаться с постоянной скоростью, и тогда кинетическая сила трения F равна общему весу в чаше весов вместе с весом последнего. При делении F на вес A можно вычислить коэффициент. Эксперимент показывает, что, когда на А помещаются грузы для изменения нормальной реакции R, величина отношения F’/R остается приблизительно постоянной. Результаты также показывают, что коэффициент кинетического трения между двумя данными поверхностями меньше, чем коэффициент статического трения между теми же поверхностями, и что коэффициент кинетического трения между двумя данными поверхностями приблизительно не зависит от их относительной скорости.
При делении F на вес A можно вычислить коэффициент. Эксперимент показывает, что, когда на А помещаются грузы для изменения нормальной реакции R, величина отношения F’/R остается приблизительно постоянной. Результаты также показывают, что коэффициент кинетического трения между двумя данными поверхностями меньше, чем коэффициент статического трения между теми же поверхностями, и что коэффициент кинетического трения между двумя данными поверхностями приблизительно не зависит от их относительной скорости.
Законы трения твердых тел
Экспериментальные результаты по трению твердых тел обобщены в законах трения, которые гласят:
- Сила трения между двумя поверхностями противодействует их относительному движению.
- Сила трения не зависит от площади контакта данных поверхностей, когда нормальная реакция постоянна.
- Предельная сила трения пропорциональна9 нормальной реакции для случая трения покоя. Сила трения пропорциональна нормальной реакции для случая кинетического (динамического) трения и не зависит от относительной скорости поверхностей.

Теория трения твердых тел
Законы трения твердых тел были известны сотни лет назад, но они были объяснены лишь сравнительно недавно, главным образом Ф. П. Боуденом и его сотрудниками. Чувствительные методы, основанные на измерении электропроводности, показывают, что истинная площадь контакта между двумя поверхностями чрезвычайно мала, возможно, одна десятитысячная площади, фактически совмещенной для стальных поверхностей. Это объясняется фотографиями, на которых видно, что некоторые атомы металла немного выступают над поверхностью, образуя ряд гребней или горбов». Как заявил Боуден: «Лучшее зеркало, плоское с точностью до миллионной доли сантиметра, для любого человека размером с атом скорее будет похоже на Саут-Даунс — долину и холмистую местность высотой в сотню или более атомов». на проекции друг друга при размещении друг на друге.
Поскольку площадь фактического контакта чрезвычайно мала, давление в точках контакта очень велико, возможно, 100 миллионов кгс на м 2 для стальных поверхностей. Выступы немного сливаются под высоким давлением, создавая сцепление или «сварку» в точках, и поэтому получается сила, противодействующая движению. Это объясняет закон 1 законов твердого трения. Когда один из объектов переворачивается так, что другому объекту оказывается меньшая или большая поверхность, измерения показывают, что небольшая площадь фактического контакта остается постоянной. Таким образом, сила трения не зависит от площади поверхностей, что объясняет закон 2. Когда нагрузка увеличивается, крошечные выступы сжимаются огромным давлением, пока новая площадь контакта не станет достаточно большой, чтобы выдержать нагрузку. Чем больше нагрузка, тем больше площадь фактического контакта, и, таким образом, сила трения приблизительно пропорциональна нагрузке, что объясняет закон 3.9.0021
Выступы немного сливаются под высоким давлением, создавая сцепление или «сварку» в точках, и поэтому получается сила, противодействующая движению. Это объясняет закон 1 законов твердого трения. Когда один из объектов переворачивается так, что другому объекту оказывается меньшая или большая поверхность, измерения показывают, что небольшая площадь фактического контакта остается постоянной. Таким образом, сила трения не зависит от площади поверхностей, что объясняет закон 2. Когда нагрузка увеличивается, крошечные выступы сжимаются огромным давлением, пока новая площадь контакта не станет достаточно большой, чтобы выдержать нагрузку. Чем больше нагрузка, тем больше площадь фактического контакта, и, таким образом, сила трения приблизительно пропорциональна нагрузке, что объясняет закон 3.9.0021
6.1: Сухое трение — Инженерные тексты
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 50594
- Джейкоб Мур и участники
- Пенсильванский государственный университет Мон-Альто через карту механики
Сухое трение — это сила, противодействующая скольжению одной твердой поверхности по другой твердой поверхности.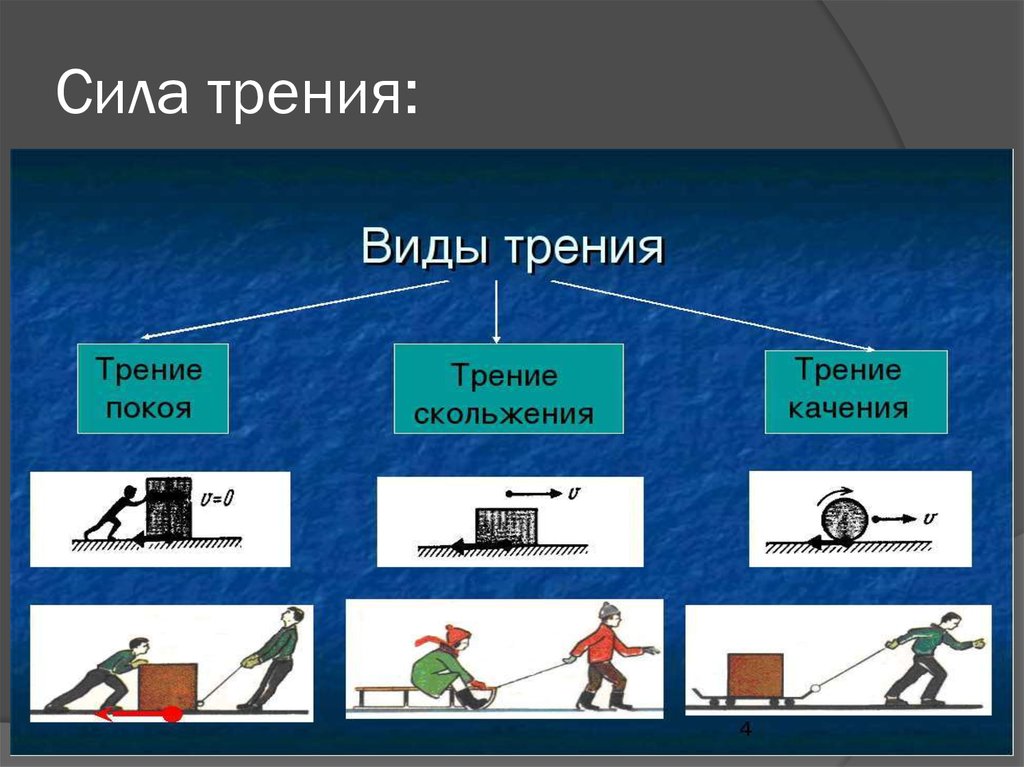 Сухому трению всегда противодействует скольжение поверхностей друг относительно друга, и оно может иметь эффект как противодействующего движения, так и вызывающего движение тел.
Сухому трению всегда противодействует скольжение поверхностей друг относительно друга, и оно может иметь эффект как противодействующего движения, так и вызывающего движение тел.
Наиболее часто используемой моделью для сухого трения является кулоновое трение . Этот тип трения можно разделить на статическое трение и кинетическое трение. Эти два типа трения показаны на диаграмме ниже. Во-первых, представьте себе коробку, стоящую на поверхности. Сила толкания прикладывается параллельно поверхности и постоянно увеличивается.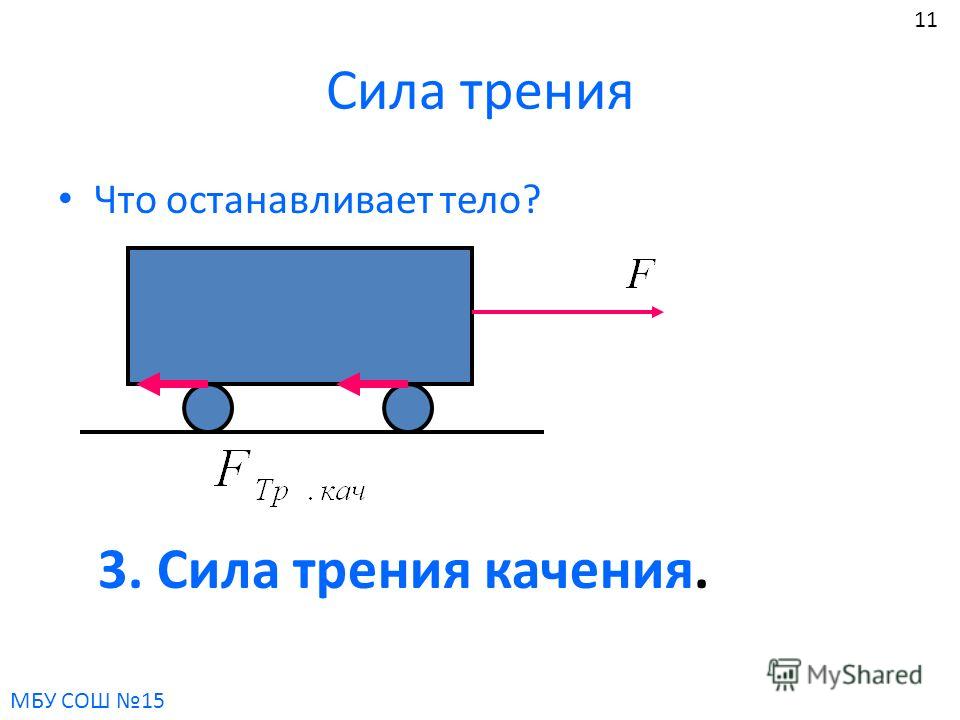 На ящик действуют также сила тяжести, нормальная сила и сила трения.
На ящик действуют также сила тяжести, нормальная сила и сила трения.
Статическое трение возникает до проскальзывания и перемещения коробки. В этой области сила трения будет равна по величине и противоположна по направлению самой толкающей силе. По мере увеличения величины толкающей силы увеличивается и величина силы трения.
Если величина толкающей силы продолжает расти, в конце концов коробка начнет скользить. Когда ящик начинает скользить, тип трения, противодействующего движению ящика, меняется со статического трения на то, что называется кинетическим трением. Точка непосредственно перед тем, как коробка соскользнет, известна как 9.2116 предстоящее движение .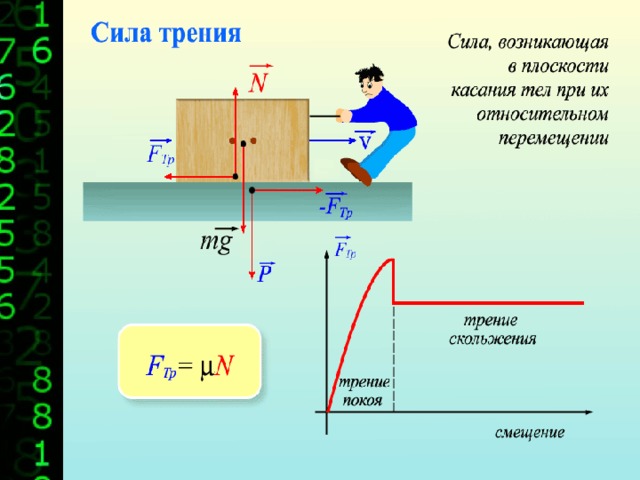 Это также можно рассматривать как максимально возможную силу статического трения перед проскальзыванием. Величина максимальной статической силы трения равна статическому коэффициенту трения, умноженному на нормальную силу, существующую между коробкой и поверхностью. Этот коэффициент трения является свойством, которое зависит от обоих материалов и обычно может быть найдено в таблицах.
Это также можно рассматривать как максимально возможную силу статического трения перед проскальзыванием. Величина максимальной статической силы трения равна статическому коэффициенту трения, умноженному на нормальную силу, существующую между коробкой и поверхностью. Этот коэффициент трения является свойством, которое зависит от обоих материалов и обычно может быть найдено в таблицах.
Кинетическое трение возникает за точкой предстоящего движения, когда ящик скользит. При кинетическом трении величина силы трения, противодействующей движению, будет равна произведению кинетического коэффициента трения на нормальную силу между коробкой и поверхностью. Кинетический коэффициент трения также зависит от двух контактирующих материалов, но почти всегда будет меньше статического коэффициента трения.
Видеолекция по этому разделу, прочитанная доктором Джейкобом Муром.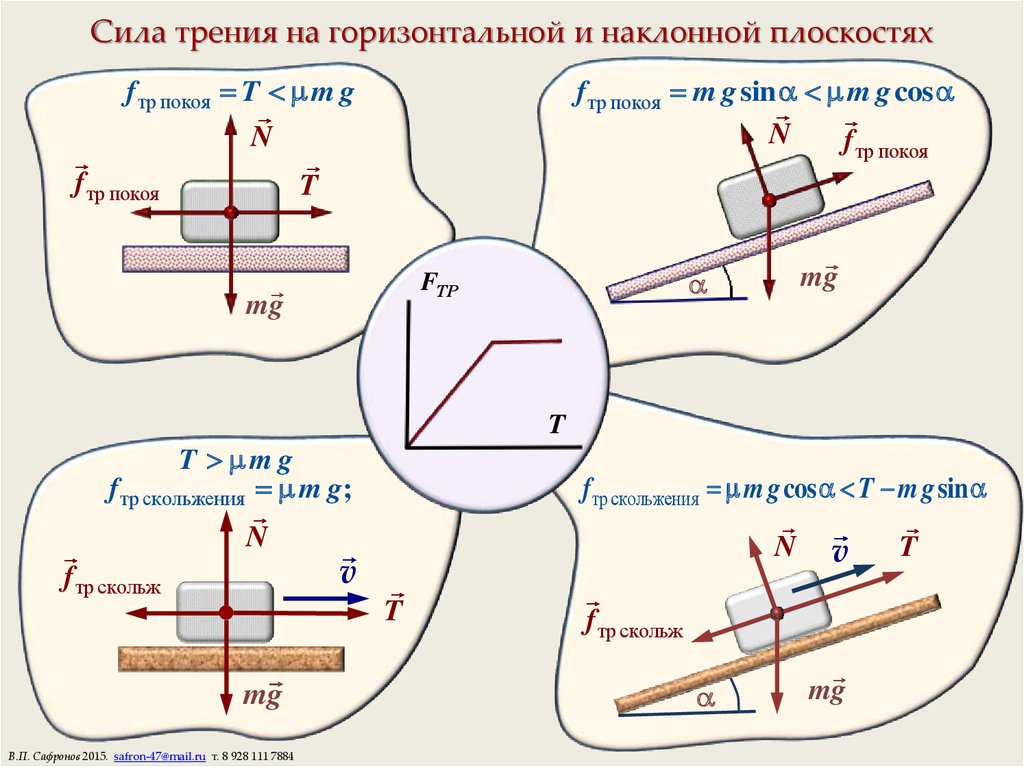 Источник на YouTube: https://youtu.be/OPRc38nDpKo.
Источник на YouTube: https://youtu.be/OPRc38nDpKo.Пример \(\PageIndex{1}\)
Ящик весом 500 фунтов стоит на бетонном полу. Если статический коэффициент трения равен 0,7, а кинетический коэффициент трения равен 0,6:
- Чему равна сила трения, если сила тяги равна 150 фунтам?
- Какое тяговое усилие потребуется, чтобы сдвинуть коробку?
- Какая минимальная сила требуется, чтобы удерживать коробку в движении после того, как она начала двигаться?
- Раствор
- Видео \(\PageIndex{2}\): рабочее решение примера проблемы \(\PageIndex{1}\), предоставленное доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/7R7kvKBxUjw.
Пример \(\PageIndex{2}\)
30-фунтовые сани тянут вверх по обледенелому склону 25 градусов. Если статический коэффициент трения между льдом и санями равен 0,4, а кинетический коэффициент трения равен 0,3, то какая сила тяги необходима, чтобы сани продолжали двигаться с постоянной скоростью?
Если статический коэффициент трения между льдом и санями равен 0,4, а кинетический коэффициент трения равен 0,3, то какая сила тяги необходима, чтобы сани продолжали двигаться с постоянной скоростью?
- Раствор
- Видео \(\PageIndex{3}\): рабочее решение примера проблемы \(\PageIndex{2}\), предоставленное доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/oPMx-SZyiy4.
Пример \(\PageIndex{3}\)
Пластиковый ящик стоит на стальной балке. Один конец стальной балки медленно поднимают, увеличивая угол поверхности до тех пор, пока коробка не начнет скользить. Если коробка начинает скользить, когда балка находится под углом 41 градус, каков статический коэффициент трения между стальной балкой и пластиковой коробкой?
Рисунок \(\PageIndex{6}\): схема проблемы для примера \(\PageIndex{3}\). Коробка на стальной балке, левый конец которой поднят до угла 41° над горизонталью.
Коробка на стальной балке, левый конец которой поднят до угла 41° над горизонталью.- Раствор
- Видео \(\PageIndex{4}\): рабочее решение примера проблемы \(\PageIndex{3}\), предоставленное доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/ShGP5rzIHN4.
Эта страница под названием 6.1: Dry Friction распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Джейкобом Муром и участниками (Mechanics Map) с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Джейкоб Мур и авторы
- Лицензия
- СС BY-SA
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
- сухое трение
- предстоящее движение
- кинетическое трение
- источник@http://mechanicsmap.
 psu.edu
psu.edu - статическое трение
- статья
Рациональная теория сцепления шин с дорожным покрытием
Настоящее исследование включает полевые испытания теории сцепления с дорожным покрытием, основанной на нагрузке на шины, вместо традиционного коэффициента трения. Связанная с этим гипотеза касается указанного существования четвертой резиновой силы, гистерезиса поверхностной деформации, которая, как предполагается, не зависит от нагрузки на шину во время скольжения шины.
1. Предыстория проекта NCITEC, цели и исследовательские задачи
Управление по исследованиям и инновационным технологиям (RITA) Министерства транспорта США (DOT) в 2012 году выделило финансирование Национальному центру интермодальных перевозок для обеспечения экономической конкурентоспособности (NCITEC) при Университете Миссисипи для проведения исследований. Общая тема проекта заключается в содействии развитию интегрированной, экономически конкурентоспособной, эффективной, безопасной, надежной и устойчивой национальной интермодальной транспортной сети путем интеграции всех видов транспорта как для грузовых, так и для пассажирских перевозок.
Общая тема проекта заключается в содействии развитию интегрированной, экономически конкурентоспособной, эффективной, безопасной, надежной и устойчивой национальной интермодальной транспортной сети путем интеграции всех видов транспорта как для грузовых, так и для пассажирских перевозок.
(1) Общие сведения о свойствах сцепления шин с дорожным покрытием . В соответствии с целью проекта CAIT-NCITEC 2012-27 по повышению безопасности на транспорте, в этом проекте оценивается новый подход к пониманию сцепления с дорогой и взлетно-посадочной полосой аэропорта путем сосредоточения внимания на силах трения, возникающих при скольжении частей шины по асфальтовым и бетонным покрытиям в как во влажных, так и в сухих условиях. Связанная с этим гипотеза касается указанного существования четвертой силы трения резины, гистерезиса поверхностной деформации (), которая теоретически не зависит от нагрузки на шину во время такого скольжения. В 1966, Куммер предложил [1] единую инженерную теорию трения шины скольжения как сумму сцепления шины с дорожным покрытием, или , макрогистерезисной объемной деформации протектора шины на неровной дороге, или , и физического износа шины, или . Эта теория будет дополнена термином.
Эта теория будет дополнена термином.
Несмотря на то, что введение пассажирских автоматических антиблокировочных тормозных систем (ABS) с допустимым коэффициентом проскальзывания в диапазоне примерно от 0,10 до 0,30 значительно уменьшило проскальзывание при торможении в этих транспортных средствах, в заторможенных коммерческих транспортных средствах часто происходит проскальзывание шин. Кроме того, изменения углов автоматического рулевого управления (скольжения) во время обычных поворотов могут привести к возникновению боковых сил трения. Относительно сегментов протектора шины, подвергающихся такому скольжению, Хейни [2] утверждает следующее:
При более высоких углах скольжения части заплаты шины скользят, и вы можете получить меньшее увеличение поперечной силы с увеличением угла скольжения… После пика [a]… боковые силы могут упасть на 30% в течение нескольких градусов дополнительный угол скольжения. При таких больших углах скольжения большая часть пятна контакта скользит, что приводит к сильному нагреву и износу.
(стр. 94)
Таким образом, значительное проскальзывание шины в пятне контакта при повороте транспортного средства является обычным явлением, и возникающие силы трения следует понимать как можно тщательнее.
В дополнение к этому вопросу также рассматриваются аспекты безопасности взаимодействия дорожного покрытия и шины, выявленные с помощью подхода, основанного на нагрузке на шину, в качестве выгодной замены традиционному использованию коэффициента трения (CoF) и числа скольжения (SN). CoF не является характеристикой материала резины и, как иногда полагают, не всегда остается постоянным при различных нагрузках на шины. Количественное определение фактических сил трения, возникающих в заданных условиях, должно помочь в определении адекватности принимаемых в настоящее время коэффициентов безопасности.
(2) Цель исследования . Целями данного исследования являются (1) обзор и обсуждение измерения традиционного коэффициента трения и теории, основанной на переменной нагрузке, для определения характеристик сцепления шины с дорожным покрытием, (2) проведение программы полевых испытаний для проверки переменной нагрузки.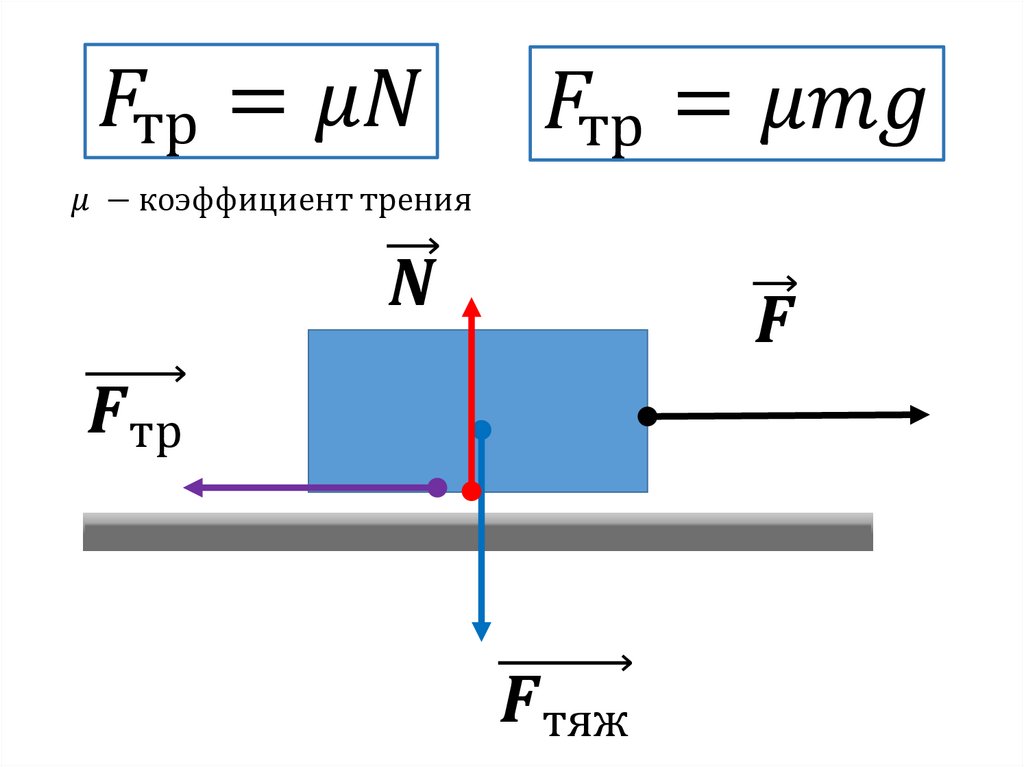 на основе теории, (3) оценить результаты полевых испытаний, используя анализ данных на основе нагрузки, и сравнить их с результатами традиционных параметров сцепления шин с дорожным покрытием, (4) и предложить использование индекса трения скольжения (SFI) в качестве замена использования коэффициента трения и числа скольжения.
на основе теории, (3) оценить результаты полевых испытаний, используя анализ данных на основе нагрузки, и сравнить их с результатами традиционных параметров сцепления шин с дорожным покрытием, (4) и предложить использование индекса трения скольжения (SFI) в качестве замена использования коэффициента трения и числа скольжения.
Испытание на занос с заблокированным колесом используется в полевых испытаниях для проверки теории, основанной на нагрузке, и иллюстрации использования соответствующего подхода к анализу данных.
(3) Исследования . Как обсуждалось в книге автора Анализ трения при проектировании резиновых изделий и их парных поверхностей [3], использование подхода CoF возникло во время важных исследований металлического оборудования в промышленности. Первоначальное научное исследование было сосредоточено на контакте с металлическими поверхностями. Принятая в настоящее время теория металлического трения, разработанная на основе исследований, начатых в 19 в. 40-х и 1950-х годов. Вводные курсы физики в технических институтах использовали CoF для иллюстрации практических приложений теории трения металлов. Однако, к сожалению для инженеров, во многих таких курсах не подчеркивалось, что CoF (определяемый как , где равна общей развиваемой силе трения и равен приложенной вертикальной нагрузке) не применим к резине, поскольку это не свойство материала эластомеров. Точно так же не действует и номер скида (SN), который определяется как значение, умноженное на 100.
40-х и 1950-х годов. Вводные курсы физики в технических институтах использовали CoF для иллюстрации практических приложений теории трения металлов. Однако, к сожалению для инженеров, во многих таких курсах не подчеркивалось, что CoF (определяемый как , где равна общей развиваемой силе трения и равен приложенной вертикальной нагрузке) не применим к резине, поскольку это не свойство материала эластомеров. Точно так же не действует и номер скида (SN), который определяется как значение, умноженное на 100.
(4) Задачи консультанта . В задачи консультанта входило (i) разработка плана полевых испытаний, включающих как асфальтовые, так и бетонные дорожные покрытия, (ii) выявление и привлечение компетентной и хорошо оснащенной организации для испытаний дорожных покрытий, (iii) проведение измерений сцепления на сухих и мокрых бетонных и асфальтовых покрытиях. (iv) интерпретация результатов как относящихся к гипотезе, основанной на нагрузке, и сравнение их с традиционными значениями CoF и SN.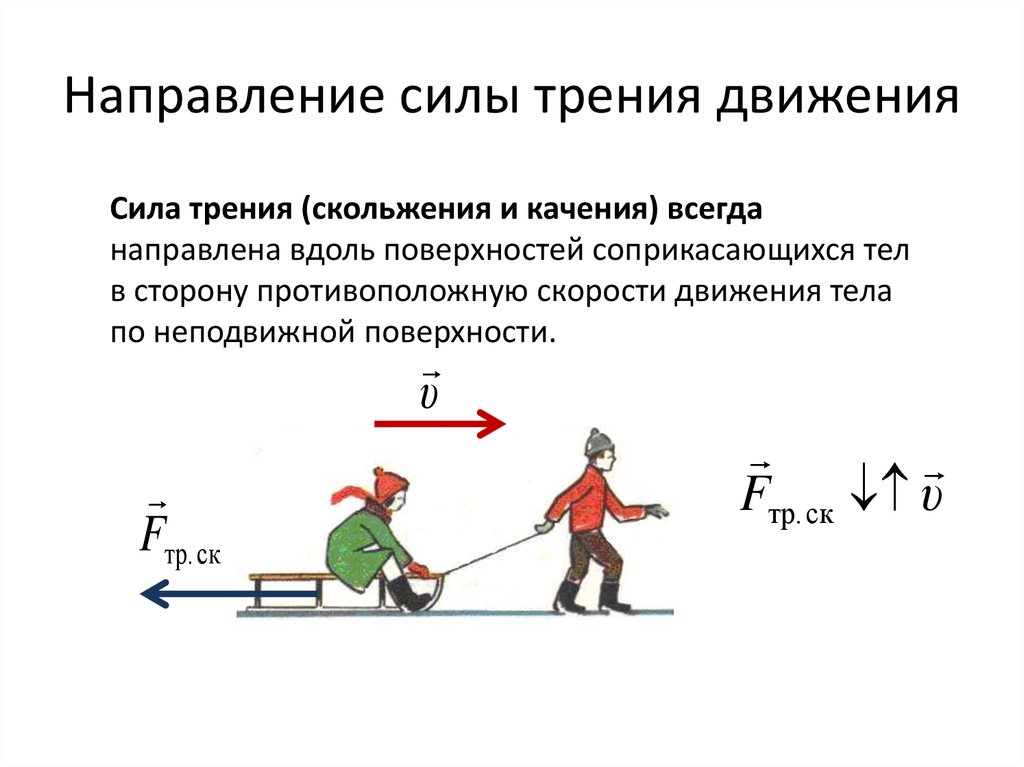 Каждое испытание проводилось на стандартной скорости с использованием восьми нагрузок (883, 930, 984, 1034, 1084, 1132, 1188 и 1242 фунта). Были зарегистрированы температуры испытанных покрытий.
Каждое испытание проводилось на стандартной скорости с использованием восьми нагрузок (883, 930, 984, 1034, 1084, 1132, 1188 и 1242 фунта). Были зарегистрированы температуры испытанных покрытий.
Применение теоретических соображений в анализе данных на основе переменной нагрузки и результатов связанных полевых исследований позволяет специалистам по управлению транспортными средствами и проектировщикам дорог лучше понять механизмы трения, возникающие в пятне контакта шины с дорожным покрытием. В следующем разделе будут показаны и обсуждены ограничения традиционных терминов и терминов SN. Конкретные рекомендации по применению результатов исследования и заявление о реализации представлены в Разделе 8.5.
2. Альтернативная теория и технология испытаний, применимая к исследовательскому подходу
Если взглянуть на результаты стандартных испытаний на скольжение способом, отличным от традиционного подхода CoF, можно лучше понять механизмы трения резины. План полевых испытаний предусматривал использование тестера трения шины/дорожного покрытия, способного производить и контролировать скольжение полноразмерной шины, необходимой для иллюстрации этих механизмов. Это скользящее требование было продемонстрировано в книге Смита 2008 г. [3] по Analyzing Friction и статью [8] в соавторстве со Смитом и Нойбертом, в которой подробно описывается подход, основанный на нагрузке на шины и дорожное покрытие. Подход и теория, подробно изложенные в документе Analyzing Friction [3], основаны на анализе более 100 испытаний на трение сухой и мокрой резины, проведенных другими исследователями на макроскопически гладких и шероховатых поверхностях. Большая часть этих тестов проводилась учеными в контролируемых лабораторных условиях, что продемонстрировало точность данных за счет повторяемости результатов. В настоящем исследовании была получена сила микрогистерезисного трения резины при использовании стандартной ребристой шины ASTM в натуральную величину при испытаниях с заблокированным колесом [4], что указывает на ее существование в пределах инженерной точности.
Это скользящее требование было продемонстрировано в книге Смита 2008 г. [3] по Analyzing Friction и статью [8] в соавторстве со Смитом и Нойбертом, в которой подробно описывается подход, основанный на нагрузке на шины и дорожное покрытие. Подход и теория, подробно изложенные в документе Analyzing Friction [3], основаны на анализе более 100 испытаний на трение сухой и мокрой резины, проведенных другими исследователями на макроскопически гладких и шероховатых поверхностях. Большая часть этих тестов проводилась учеными в контролируемых лабораторных условиях, что продемонстрировало точность данных за счет повторяемости результатов. В настоящем исследовании была получена сила микрогистерезисного трения резины при использовании стандартной ребристой шины ASTM в натуральную величину при испытаниях с заблокированным колесом [4], что указывает на ее существование в пределах инженерной точности.
Статья Смита и Нойберта 2011 года [8] служит кратким изложением той части книги Смита [3] 2008 года, посвященной анализу трения , которая применима к текущему исследованию сцепления шин с дорожным покрытием, а также иллюстрирует ряд методов, иллюстрирующих как рассчитать силы трения скольжения, возникающие, когда шины нагружаются до значений, превышающих те, которые используются в настоящих испытаниях.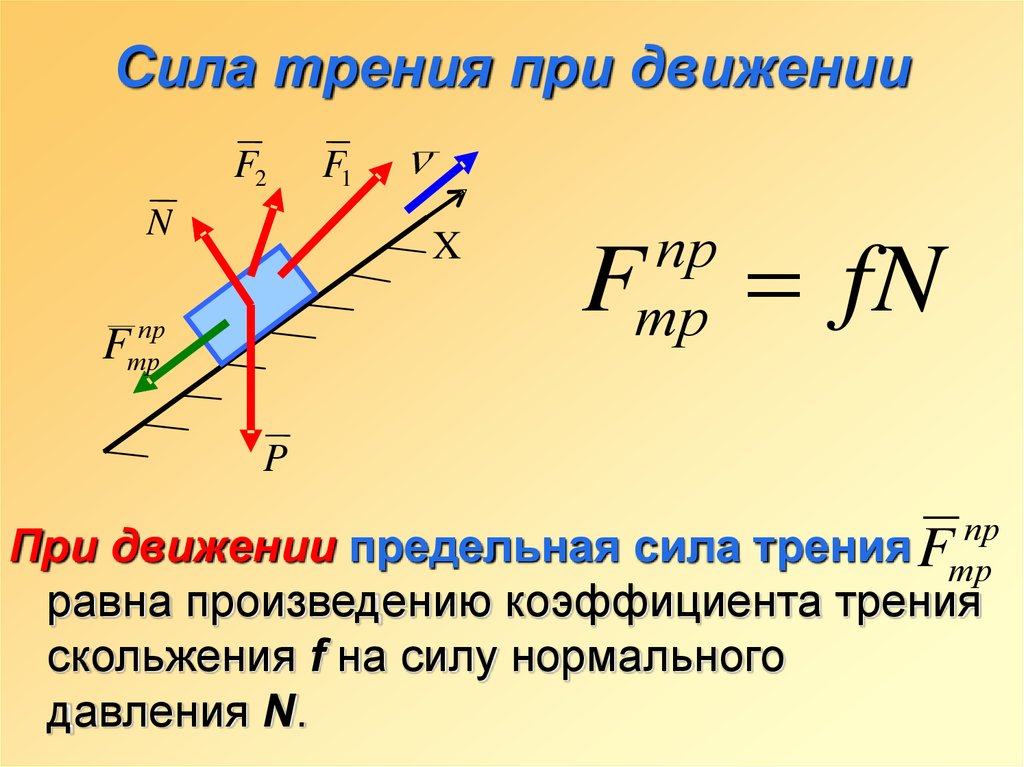
2.1. Генерация микрогистерезисной силы трения резины в испытаниях на занос с заблокированными колесами
Создание микрогистерезисной силы трения можно проиллюстрировать на примере анализа ранее проведенных испытаний с заблокированным колесом. В 1974 году Совет по транспортным исследованиям (TRB) опубликовал результаты [4] своего обширного исследования, касающегося корреляции и калибровки испытаний дорожного покрытия с заблокированными колесами во влажных условиях. Из примерно 70 цифр, представленных в отчете TRB, одна касалась последствий нагрузки испытательного колеса. В отчете говорится, что «прямое влияние изменений нагрузки испытательного колеса на сопротивление скольжению относительно невелико… Это было подтверждено в недавних испытаниях, и на рис. среднее из 10 блокировок». Были применены нагрузки 800 фунтов, 1000 фунтов и 1200 фунтов.
На рисунке 1 представлен график данных TRB Рисунок A-41 [4], иллюстрирующий подход, основанный на нагрузке, в котором ось ординат представляет общую измеренную силу трения () в фунт-силах, а ось абсцисс представляет нормальную нагрузку () в фунтах, применительно к шине.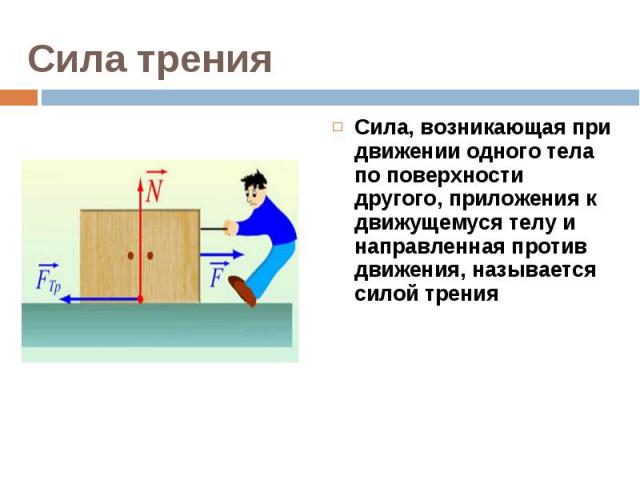 Показаны три точки данных TRB. Можно заметить, что эти точки соединяет прямая. Когда эта прямая экстраполируется на ось, отображается значение точки пересечения 150 lbf.
Показаны три точки данных TRB. Можно заметить, что эти точки соединяет прямая. Когда эта прямая экстраполируется на ось, отображается значение точки пересечения 150 lbf.
Кроме того, видно, что график рис. 1 соответствует элементарному алгебраическому выражению , где «» — значение ординаты, «» — значение абсциссы, «» — наклон прямой, а «» — угол наклона прямой. постоянная составляющая во всех значениях, охватываемых диапазоном тестирования. Считается, что значение « » количественно определяет величину , 150 фунтов силы.
Предполагается, что возникновение гистерезиса деформации поверхности происходит, когда скользящая резина самоадгезивно обволакивает, по крайней мере, часть микрошероховатости жесткой контактирующей подложки. Эта микрошероховатость характеризуется глубиной микротекстуры и свободной энергией поверхности дорожной одежды ( γ ). Показано, что механизм сцепления возникает из-за комбинированной свободной поверхностной энергии ( γ ) дорожного покрытия и контактирующего с ним протектора шины. Как показано в Analyzing Friction [4] и статье Смита/Нойберта [8], если суммарная свободная поверхностная энергия ( γ ) недостаточны для создания хотя бы некоторого охвата контактирующих микронеровностей, не развивается.
Как показано в Analyzing Friction [4] и статье Смита/Нойберта [8], если суммарная свободная поверхностная энергия ( γ ) недостаточны для создания хотя бы некоторого охвата контактирующих микронеровностей, не развивается.
На рис. 2 показано средство проверки наличия и точности определенной силы: путем вычитания количественного значения, в данном случае [4] 150 lbf, из связанных значений. Нанесение результирующих значений в зависимости от тех же приложенных нагрузок, что и на рис. 1, должно дать прямую линию, которая экстраполируется до начала координат, как показано на рис. 2.
2.2. Научные данные, подтверждающие существование микрогистерезисной силы трения резины
Механизм создания микрогистерезисной силы трения резины (т. е. с участием микротекстуры жесткой поверхности в паре со скользящей резиной) был теоретизирован Перссоном в 1998 г. [5]. Хотя Перссон не полагал, что эта сила будет постоянной при различных приложенных нагрузках, ее характеристики, по-видимому, согласуются с теми, которые демонстрирует постоянное значение, как показано на рисунке 1 и показано позже в настоящих результатах испытаний.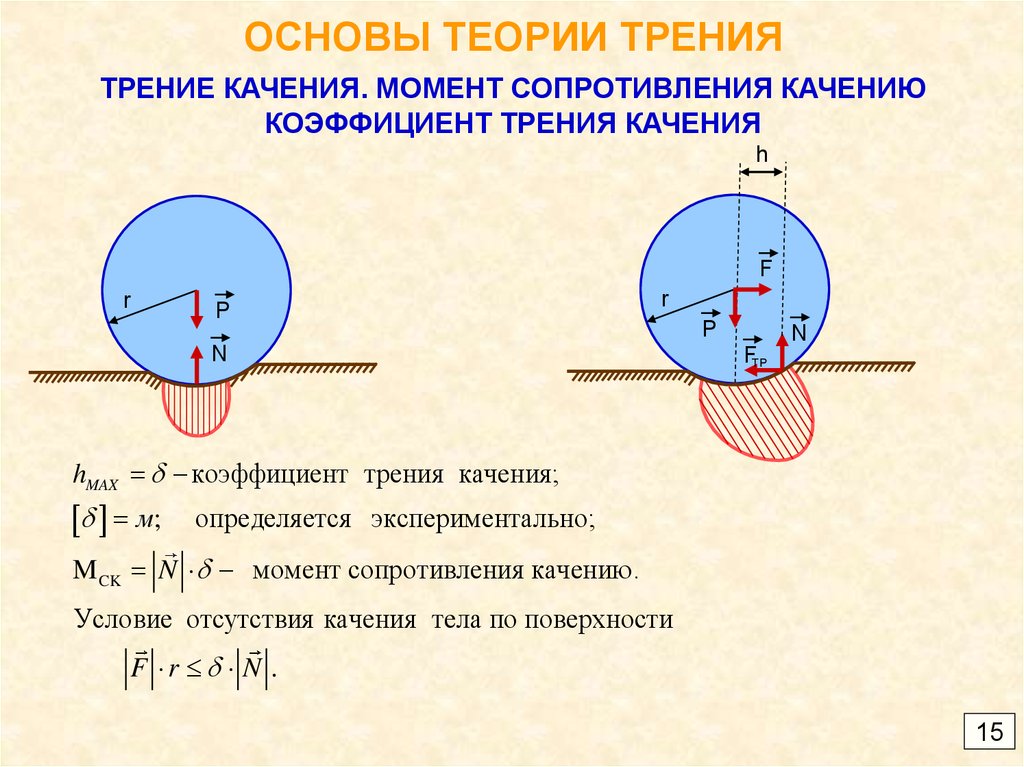
Перссон [5] применил теорию вязкоупругости к скольжению каучука с малой скоростью () по чистой, твердой, макроскопически шероховатой подложке с микротекстурой на поверхности примерно 100 Å. Учитывая свободные поверхностные энергии ( γ ) парных материалов, Перссон пришел к выводу, что при комнатной температуре и при достаточном комбинированном значении γ поверхность резины может деформироваться и самоадгезивно покрывать контактирующие микрошероховатости с скользящей резиной. Далее Перссон подсчитал, что микрошероховатость, приближающаяся к 1000 Å, может быть покрыта этим механизмом.
На рис. 3 показано скольжение каучука со скоростью по листовому стеклу, которое обычно имеет микрошероховатость около 100 Å. Эластомер сжимается в микротекстуру и уплотняется приложенной нормальной нагрузкой . Механизм Перссона [5] также работает и считается, что слой резины самоприлипает к частям поверхности стекла и тем самым создает отчетливую силу сопротивления трения.
Дальнейшее научное подтверждение существования силы можно увидеть в лабораторных испытаниях, основанных на опыте, полученном во время Второй мировой войны с использованием шин из синтетического каучука. Стало понятно, что такие шины с большей вероятностью будут скользить по льду, чем шины из натурального каучука (NR). Pfalzner [6] провел воспроизводимые лабораторные испытания в холодной комнате, сравнивая сопротивление трению скольжения NR с составами синтетических Hycar (акрилонитрилбутадиен) и GR-S (стиролбутадиен). Пфальцнер подготовил 1 дюйм 2 × 0,25 дюйма и приложили к ним обычные нагрузки в диапазоне от 42 до 100 фунтов на квадратный дюйм, установив их на покрытом льдом поворотном столе с электрическим приводом, вращающемся с постоянной скоростью 50 об/мин. Испытания проводились при температуре 20°F. Замораживание для производства льда производилось таким образом, чтобы он был одновременно сухим и макроскопически гладким. На рис. 4 представлены результаты тестирования Пфальцнера [6].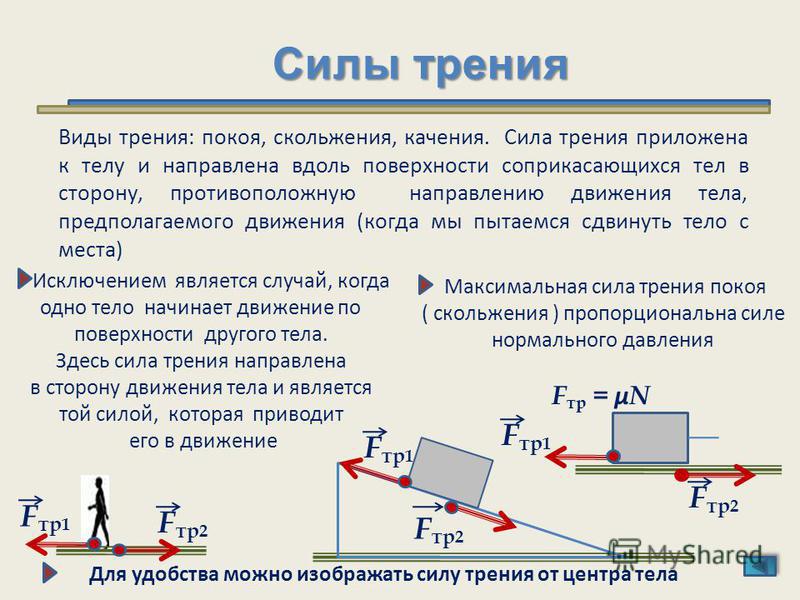
Возникновение микрогистерезисной силы трения в натуральном каучуке величиной около 0,6 фунт-силы показано на рис. 4 в результате испытаний Пфальцнера [6]. Графики GR-S и Hycar указывают на генерацию силы, имеющей величину приблизительно 0,30 фунт-силы и 0,25 фунт-силы соответственно. Эти результаты согласуются с наблюдениями за скользкостью шин, сделанными во время Второй мировой войны. В дополнение к указанию на существование, результаты испытаний показывают, что его вклад в сопротивление скольжению на льду не следует упускать из виду.
Исследование Mori et al., проведенное в 1994 г. [7] также поддерживает существование . Их контролируемые в лаборатории исследования были сосредоточены на выяснении роли свободной поверхностной энергии ( γ ) в силах сцепления, возникающих в конфигурации скольжения, когда резина соединяется с различными, макроскопически гладкими поверхностями при различной приложенной нагрузке. Вулканизированные образцы формовали в специально изготовленных формах, которые обладали различной свободной поверхностной энергией, тем самым сообщая поверхности резиновых образцов разную свободную поверхностную энергию. Этот метод позволил каждому образцу сохранить присущие объемному материалу деформационные свойства. Различные протестированные образцы включали стирол-бутадиеновый каучук (SBR), который был сформован таким образом, чтобы он обладал поверхностями как с высокой, так и с низкой адгезией. SBR был соединен с макроскопически гладким тефлоном.
Этот метод позволил каждому образцу сохранить присущие объемному материалу деформационные свойства. Различные протестированные образцы включали стирол-бутадиеновый каучук (SBR), который был сформован таким образом, чтобы он обладал поверхностями как с высокой, так и с низкой адгезией. SBR был соединен с макроскопически гладким тефлоном.
Один образец SBR был сформован на макроскопически гладком тефлоне для получения материала с низкой поверхностной свободной энергией. Другой образец SBR был отлит из макроскопически гладкого хрома, чтобы получить SBR с высокой свободной поверхностной энергией. Оба они находились в скользящем контакте с тефлоновой поверхностью и прикладывались к нагрузке.
На рис. 5 представлены Mori et al. [7] результаты, построенные в соответствии с теорией, основанной на нагрузке, для выявления признаков микрогистерезисной силы трения резины, если она присутствует. Видно, что экстраполяция графика пары SBR-Teflon с высокой адгезией (хромированная форма) свидетельствует о создании силы, имеющей величину приблизительно 0,2 фунт-силы. Однако график пары SBR-Teflon с низкой адгезией экстраполируется на исходную точку, указывая на отсутствие .
Однако график пары SBR-Teflon с низкой адгезией экстраполируется на исходную точку, указывая на отсутствие .
3. Пересмотр коэффициента трения и числа скольжения
3.1. В отчете TRB 1974 г.
В отчете TRB 1974 г. [4] говорится, что «прямое влияние изменений нагрузки испытательного колеса на сопротивление скольжению относительно невелико… Это было подтверждено в недавних испытаниях, и на Рисунке A-41 (Рисунок 6) показана зависимость от нагрузки. сопротивление скольжению, рассчитанное на основе семи испытаний на разных покрытиях, каждое из которых является средним значением 10 блокировок». Однако со ссылкой на фиг.1 видно, что, вопреки заявленному мнению, прямое влияние изменения нагрузки на колесо при скольжении шины является значительным, как показано на оси. Самая большая сила создавалась самой большой нагрузкой. Увеличение может увеличить реальную площадь контакта шины с дорожным покрытием. Такой рост контакта может вызвать большее сцепление [3], основную силу трения между шиной и дорожным покрытием. Более сильное сцепление может также увеличить площадь контакта шины с макрошероховатостью дорожного покрытия, увеличивая макрогистерезисное () развитие силы трения за счет большей объемной деформации протектора шины.
Более сильное сцепление может также увеличить площадь контакта шины с макрошероховатостью дорожного покрытия, увеличивая макрогистерезисное () развитие силы трения за счет большей объемной деформации протектора шины.
На рис. 6 показана зависимость SN от приложенной нормальной нагрузки. Видна умеренно убывающая гиперболическая кривая для трех приложенных нагрузок 800 фунтов, 1000 фунтов и 1200 фунтов, что указывает на то, что сопротивление трения уменьшается с увеличением нагрузки, когда верно обратное. Применение подхода, основанного на переменной нагрузке, при анализе данных трения скольжения может улучшить интерпретацию результатов испытаний на скольжение.
3.2. Использование CFME для оценки сцепления с покрытием аэропорта
Сцепление с покрытием аэропорта также оценивается с использованием CoF. В настоящее время общепринятой практикой для этой цели являются так называемые CFME, или оборудование для измерения непрерывного трения [8]. Такое оборудование одобрено Федеральным управлением гражданской авиации (FAA) и может включать автомобили с приборами, пикапы или прицепы. Эти испытания гладких шин проводятся при фиксированном процентном проскальзывании, а не при проскальзывании заблокированных колес. Их проводят в соответствии со стандартом ASTM [10]. Поскольку эти тесты включают проскальзывание, теоретическая сила микрогистерезисного трения не генерируется. Как следствие, вклад микрогистерезисного трения в тяговое усилие не определяется.
Эти испытания гладких шин проводятся при фиксированном процентном проскальзывании, а не при проскальзывании заблокированных колес. Их проводят в соответствии со стандартом ASTM [10]. Поскольку эти тесты включают проскальзывание, теоретическая сила микрогистерезисного трения не генерируется. Как следствие, вклад микрогистерезисного трения в тяговое усилие не определяется.
На Рисунке 7 представлены результаты таких испытаний CFME, проведенных в 2009 г. на «почти полированной», бетонной рулежной дорожке без нарезов в сухих условиях при 17-процентном проскальзывании шин с использованием буксируемого прицепа с испытательной шиной в прямолинейном режиме на скорости скорость 30 миль в час при температуре окружающей среды 86°F. Точки данных CoF были получены путем изменения нагрузок, приложенных к шине. Как показано, график экстраполируется в исходную точку, что указывает на то, что сила не создавалась.
3.3. Изучение заявленных результатов программы СТАРТ
Ягер и др. [9] сообщили о результатах, полученных в рамках программы Surface Traction and Radial Tire (START), проводимой американской авиационной промышленностью, Национальным управлением по аэронавтике и исследованию космического пространства (NASA) и FAA. Особое внимание в программе уделялось оценке сопротивления качению шин, торможению и прохождению поворотов в сухих условиях на бетонном покрытии. Были исследованы три типа полноразмерных шин для коммерческих самолетов — с радиальным кордом, с диагональным расположением слоев и Н-типа.
[9] сообщили о результатах, полученных в рамках программы Surface Traction and Radial Tire (START), проводимой американской авиационной промышленностью, Национальным управлением по аэронавтике и исследованию космического пространства (NASA) и FAA. Особое внимание в программе уделялось оценке сопротивления качению шин, торможению и прохождению поворотов в сухих условиях на бетонном покрытии. Были исследованы три типа полноразмерных шин для коммерческих самолетов — с радиальным кордом, с диагональным расположением слоев и Н-типа.
Исследования проводились в центре NASA Langley Aircraft Landing Dynamics Facility, который предоставил тестовую взлетно-посадочную полосу из текстурированного бетона длиной 2800 футов. Макротекстура взлетно-посадочной полосы была измерена с использованием методики проб смазки НАСА [11], и было установлено, что ее средняя толщина составляет 0,0051 дюйма. Прохождение поворотов оценивалось с использованием 60-тонного шасси с шинами, работающего со скоростью 100 узлов и приложенного к нормальным нагрузкам ( ) на свободно вращающихся шинах весом до 25 000 фунтов.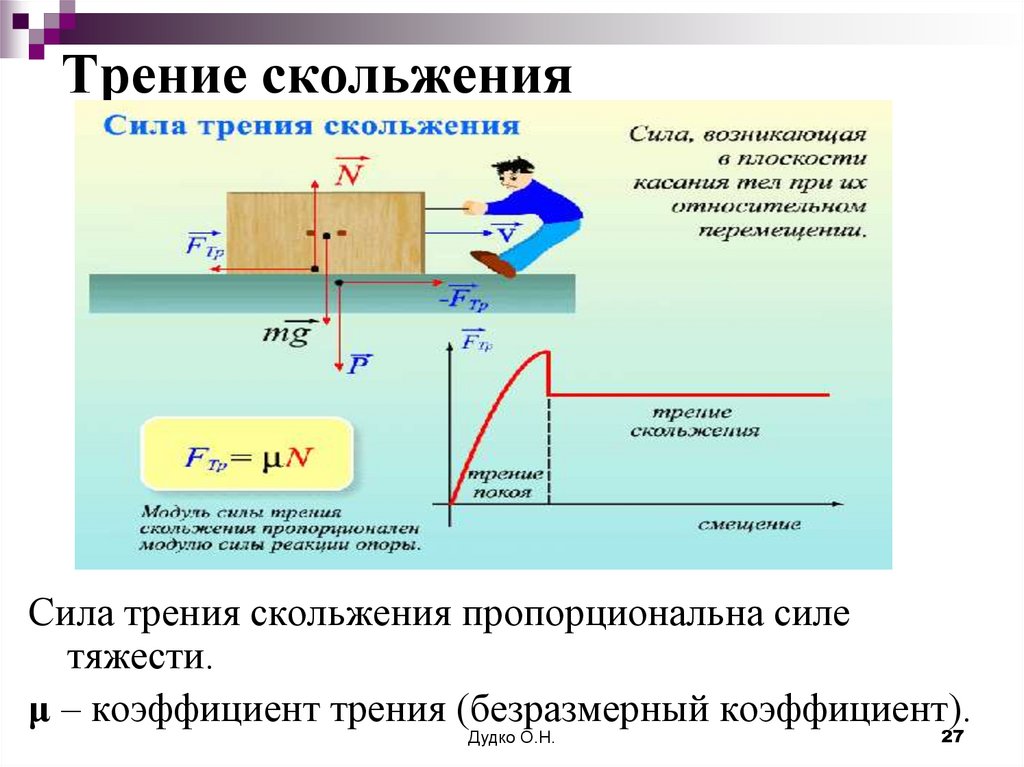 На тележке были установлены приборы для измерения общей силы бокового трения , создаваемой при различных интересующих углах скольжения шины, и сообщались значения коэффициента бокового трения .
На тележке были установлены приборы для измерения общей силы бокового трения , создаваемой при различных интересующих углах скольжения шины, и сообщались значения коэффициента бокового трения .
На рис. 8 представлены результаты измерения бокового коэффициента трения (), полученные в [9] по программе START для диагональной шины, испытанной при пяти интересующих углах скольжения. Видно, что каждый график представляет собой прямую линию с ярко выраженным нисходящим уклоном. Традиционная интерпретация коэффициентов трения резины заключалась бы в том, что боковое сопротивление скольжению уменьшалось с увеличением при всех углах скольжения. Однако, как видно на рисунке 9, на котором те же данные нанесены в соответствии с подходом, основанным на нагрузке (ранее объясненным на рисунке 1), для количественной оценки значений, сила бокового трения увеличивается. Это еще один пример улучшенной интерпретации данных для анализа коэффициента трения. В таблице 1 представлены приблизительные значения силы при каждом угле скольжения шины.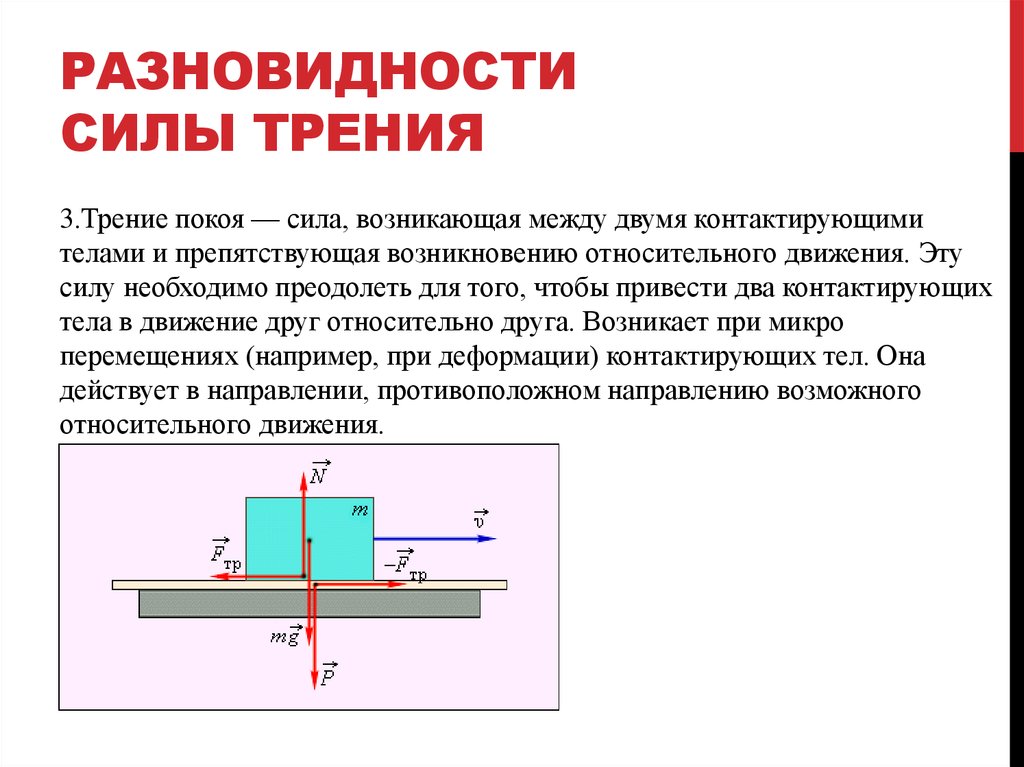
На рисунках 8 и 9 результаты испытаний на боковое трение на покрытии испытательной трассы, похожей на аэропорт, указывают на возникновение сил при всех углах скольжения. Эти силы возникают из-за хорошей глубины микротекстуры дорожного покрытия и достаточной суммарной поверхностной свободной энергии шины и дорожного покрытия. Традиционная количественная оценка значений сопротивления скольжению, выраженная в виде бокового CoF, показана в таблице 1. Ее использование просто игнорирует эти силы, возникающие в пятне контакта шины, и наличие микротекстуры на поверхности дорожного покрытия.
4. Методология и факторы для полевых испытаний в текущем исследовании
В текущем проекте NCITEC 2012-27 управляемые испытания на трение асфальта и бетонного покрытия со скольжением шин проводились с использованием устройства прицепа с заблокированными колесами, оснащенного стандартным, полноразмерная шина. Однако вместо обычного испытания с одинарной нагрузкой и заблокированным колесом к шине, скользящей как по асфальтовым, так и по бетонным покрытиям во влажных и сухих условиях, прикладывались восемь различных нагрузок, как описано в Разделе 1(4).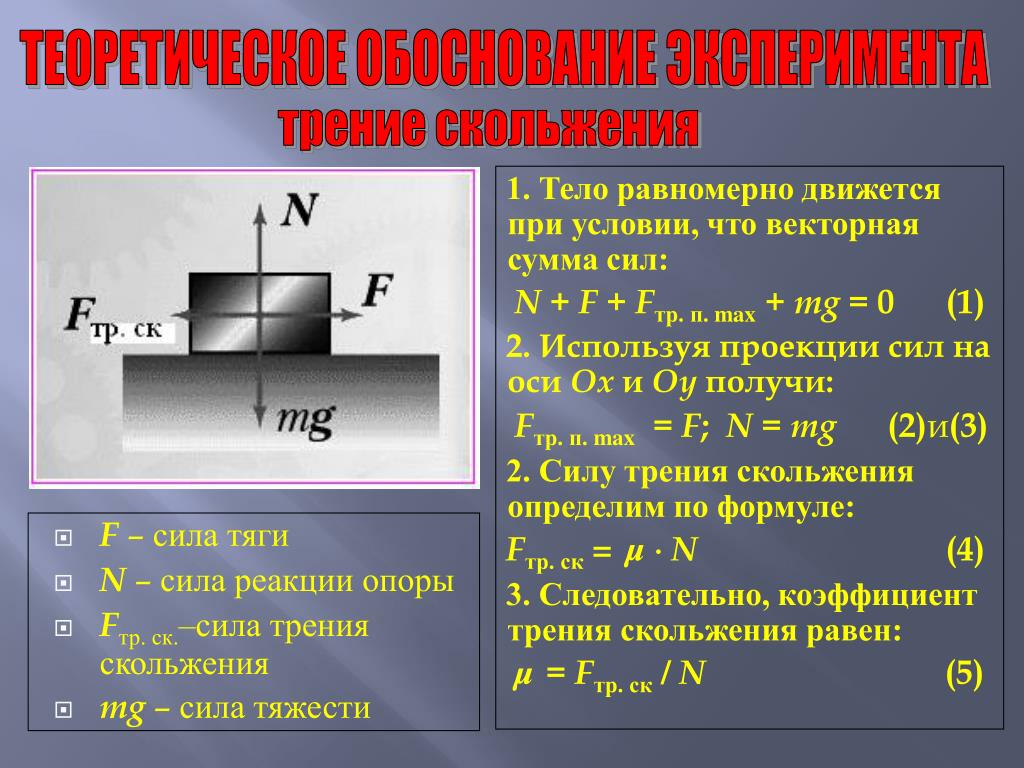
4.1. Оборудование и стандарты для испытаний на сцепление с дорожным покрытием
Испытания на трение между шинами и дорожным покрытием проводились с использованием приборного устройства с блокировкой колес, предоставленного и эксплуатируемого Международной кибернетической корпорацией (ICC) из Ларго, Флорида. Этот тестер способен создавать и контролировать скольжение предварительно кондиционированной стандартной ребристой шины в натуральную величину (ASTM E501-08) [12] при измерении создаваемой общей силы трения. Он эксплуатировался в соответствии с ASTM E274/E274M-11 [13], действующим стандартом для таких испытаний, за исключением того, что указанная стандартом приложенная нагрузка в 1085 ± 15 фунтов была заменена нагрузками, перечисленными в Разделе 1(4). Отдельные ровные испытательные участки дорожного покрытия имели одинаковый возраст, состав материала и степень износа, не имели крупных дефектов и явных поверхностных загрязнений. ICC обслуживает государственных и консалтинговых клиентов с 19 лет. 75 и получил контракты на испытания из США и всего мира. Он поставляет как аппаратное, так и программное обеспечение для удовлетворения потребностей в сборе и анализе данных испытаний на трение.
75 и получил контракты на испытания из США и всего мира. Он поставляет как аппаратное, так и программное обеспечение для удовлетворения потребностей в сборе и анализе данных испытаний на трение.
4.2. Факторы и переменные программы испытаний
При проведении полевых испытаний учитывались следующие два фактора: (1) тип дорожного покрытия на двух уровнях (дорожные покрытия с асфальтовым и бетонным покрытием) и (2) состояние поверхности дорожного покрытия (сухое и мокрое). Оба типа покрытий были испытаны с использованием восьми нагрузок, перечисленных в Разделе 1(4). Для каждой загрузки в сухом состоянии выполняли пять блокировок. Было выполнено пять наборов из трех блокировок для каждой различной нагрузки на шины во влажных условиях. Эта выборка привела к четырем наборам тестовых данных, собранных при каждой из восьми нормальных тестовых нагрузок.
В соответствии со стандартом ASTM E274/E274M-11 [13] испытатель с заблокированным колесом скользил по испытательной шине с постоянной скоростью 40 ± 1 миль в час.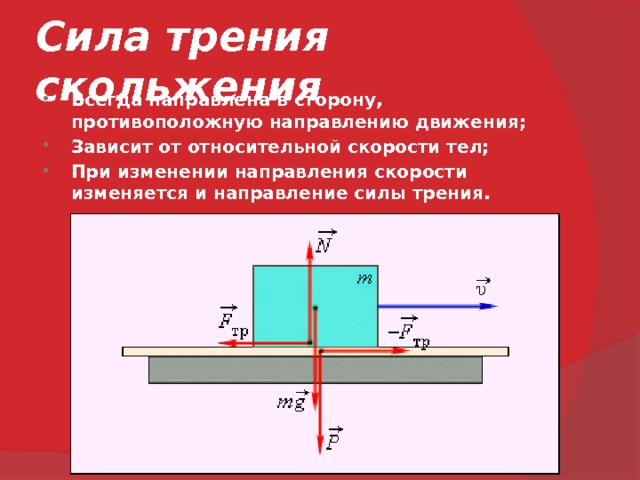 Восемь различных вертикальных нагрузок в диапазоне от 883 до 1242 фунтов были приложены к центральной линии шины в различных условиях испытаний. В соответствии с разделом этого стандарта, касающимся смачивания дорожного покрытия [13], количество воды, подаваемой в моделируемых мокрых испытаниях при скорости 40 ± 1 миль в час, составляло 4,0 галлона ± 10%/мин·дюйм. смоченной ширины, составляющей 28 галлонов в минуту.
Восемь различных вертикальных нагрузок в диапазоне от 883 до 1242 фунтов были приложены к центральной линии шины в различных условиях испытаний. В соответствии с разделом этого стандарта, касающимся смачивания дорожного покрытия [13], количество воды, подаваемой в моделируемых мокрых испытаниях при скорости 40 ± 1 миль в час, составляло 4,0 галлона ± 10%/мин·дюйм. смоченной ширины, составляющей 28 галлонов в минуту.
4.3. Сбор данных и интерпретация результатов
В каждом из четырех испытаний с блокировкой колес при скольжении было получено восемь средних значений измеренной силы трения в зависимости от приложенной нормальной нагрузки для асфальтовых и бетонных покрытий во влажных и сухих условиях. Эти результаты были нанесены на график в обычных прямоугольных координатах, обеспечивающих визуальное представление изменений величины возникающих сил трения при изменении нагрузки на шину.
Восемь различных нагрузок на шины, использованные при испытаниях асфальта и бетона, были получены путем помещения отдельных грузов из стальных плит в грузовой ящик, расположенный в задней части испытательного прицепа. Нагрузка, приложенная к шине, контролировалась выбранными грузами, помещенными в этот ящик.
Нагрузка, приложенная к шине, контролировалась выбранными грузами, помещенными в этот ящик.
5. Проверка блокировки колес
5.1. Испытания сухого асфальтового покрытия
Сухие испытания асфальта с использованием тестера ICC, которым всегда управляет один и тот же опытный инженер, начались на Белчер-роуд в Ларго, Флорида, 18 марта и завершились 22 марта 2013 г. в светлое время суток. Движение на Белчер-роуд было умеренным; при тестировании на скорости 40 ± 1 миль в час значительных помех движению не было. На рис. 10 показана начальная точка этих тестов. Несмотря на наличие некоторых облаков, во время исследования сухого асфальта дождя не было.
Асфальтовое покрытие в возрасте от 18 до 20 месяцев без значительной полировки. На рис. 11 изображен крупный план дорожного покрытия Белчер-Роуд, на котором проводились испытания на скольжение. Четверть США, размещенная на тротуаре, была включена, чтобы помочь изобразить отсутствие полировки.
Использовалась новая, обкатанная полноразмерная ребристая шина ASTM E501-08, установленная на левой стороне испытательного стенда, со стандартным давлением накачки 24 ± 0,5 psi.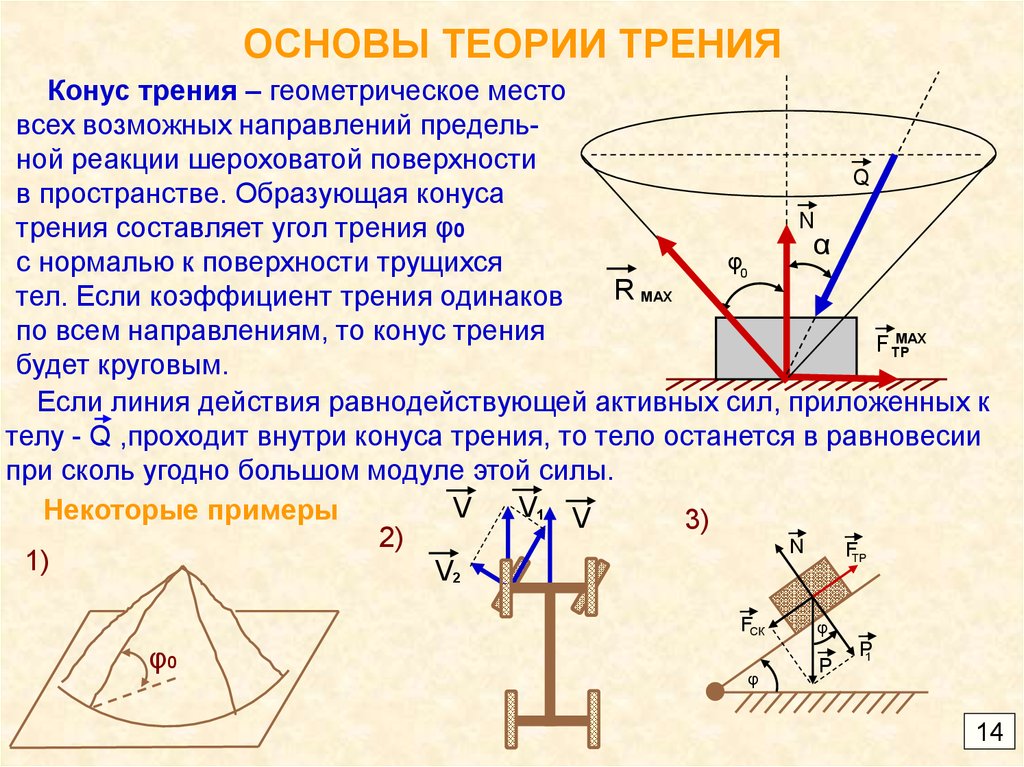 В целях контроля качества были выполнены три предварительные блокировки с одинаковой нагрузкой на шины.
В целях контроля качества были выполнены три предварительные блокировки с одинаковой нагрузкой на шины.
Для каждой из восьми приложенных нагрузок было выполнено пять циклов блокировки из пяти отдельных испытаний. Результаты усреднялись для получения среднего значения общей измеренной силы трения, создаваемой каждой нагрузкой. Эти тестовые данные всегда были получены в одном и том же боковом положении на одной и той же рабочей полосе, записанные в течение 1 с. На рисунке 12 представлены результаты сухой дороги Белчер, построенные в соответствии с подходом, основанным на нагрузке. По сравнению с графиком CoF в зависимости от нагрузки, представленным на рис. 6, графики тестовых данных дают лучшее представление о механизмах, создающих трение, действующих в пятне контакта шины с дорожным покрытием. В таблице 2 представлены нормальные нагрузки и связанные с ними значения силы трения.
Видно, что шесть из восьми значений, соединенных прямой линией и экстраполированных на ось, указывают на возникновение микрогистерезисной силы трения, имеющей величину около 140 lbf. Однако нанесенные на график точки для двух приложенных нагрузок, 984 фунта и 1034 фунта, считаются выбросами. Это может быть связано с клубами белого дыма, которые исходили из пятна контакта шины с дорожным покрытием во время всех сухих блокировок.
Однако нанесенные на график точки для двух приложенных нагрузок, 984 фунта и 1034 фунта, считаются выбросами. Это может быть связано с клубами белого дыма, которые исходили из пятна контакта шины с дорожным покрытием во время всех сухих блокировок.
Осмотр дорожного покрытия в местах сухой блокировки показал, что на шине образовались мягкие пятна, о чем свидетельствуют черные полосы резины на поверхности дорожного покрытия. Дымообразование могло быть вызвано наличием механизма, характерного для шин при посадке самолетов. Тепловая деструкция шин и испарение резины могут привести к образованию белого дыма. Профессиональный коммерческий пилот заявил [14], что «дым возникает из-за того, что колесо, которое не вращается в полете, соприкасается со стационарной взлетно-посадочной полосой. Колесо должно очень быстро разгоняться до посадочной скорости. Во время этого ускорения есть короткое время, когда шина скользит, что приводит к дыму».
В то время как размягчение шин происходило во время всех случаев блокировки всухую в результате трения, при испытаниях под нагрузкой 984 фунта и 1034 фунта на Белчер-Роуд также наблюдались самые высокие непрерывные температуры дорожного покрытия, вызванные солнечным излучением, что может привести к дополнительному размягчению шины с последующим снижением в создаваемой силе трения. Температура дорожного покрытия во время этих двух циклов испытаний составляла 119°F. Температура дорожного покрытия во время применения других шести приложенных нагрузок в среднем постоянно составляла 82°F.
Температура дорожного покрытия во время этих двух циклов испытаний составляла 119°F. Температура дорожного покрытия во время применения других шести приложенных нагрузок в среднем постоянно составляла 82°F.
5.2. Испытания мокрого асфальтового покрытия
Мокрые испытания одного и того же асфальтового покрытия с использованием тестера ICC, всегда управляемого одним и тем же опытным инженером, начались на Белчер-роуд в Ларго, Флорида, 18 марта 2013 г. и были завершены 22 марта 2013 г. оба в светлое время суток. Движение на Белчер-роуд было умеренным; при тестировании на скорости 40 ± 1 миль в час значительных помех дорожному движению не было.
График результатов испытаний, основанный на нагрузке, представлен на рис. 13. Указано создание силы трения около 220 фунтов силы. В Таблице 3 представлены отдельные использованные веса и полученные связанные с ними значения.
Использовалась новая, обкатанная полноразмерная ребристая шина ASTM E501-08, установленная на левой стороне испытательного стенда, со стандартным давлением накачки 24 ± 0,5 psi [4].
Для каждой из восьми приложенных нагрузок было выполнено пять циклов блокировки из трех отдельных испытаний. Результаты усреднялись для получения среднего значения общей измеренной силы трения, создаваемой каждой нагрузкой. Эти тестовые данные всегда были получены в одном и том же боковом положении на одной и той же рабочей полосе, записанные в течение 1 с.
Видно, что семь значений лежат на прямой линии или очень близко к ней, что при экстраполяции указывает на возникновение микрогистерезисной силы трения, имеющей величину около 220 lbf. Однако точка данных 1188 фунтов, которая находится немного ниже прямой линии, может считаться выбросом. Основываясь на опыте ICC в ходе их обычных испытаний с заблокированными колесами во влажных условиях, вероятно, было выявлено очевидное несоответствие. Данные о трении для нагрузок 1188 фунтов и 1242 фунта были собраны через три дня после данных о трении для других нагрузок. Было замечено, что данные о сцеплении, полученные в разные дни, могут давать такие разные результаты, что, вероятно, связано с колебаниями температуры дорожного покрытия в такие периоды.
5.3. Испытание бетонного покрытия в сухом состоянии
Испытание бетонного покрытия в сухом состоянии с использованием тестера ICC, которым всегда управляет один и тот же опытный инженер, началось на бульваре Тайрон в Сент-Питерсберге, штат Флорида, 18 марта 2013 г. и завершилось 22 марта 2013 г. оба в светлое время суток. Движение на бульваре Тайрон было умеренным; никакого существенного взаимодействия между ним и тестером не произошло на скорости 40 ± 1 миль в час. На рис. 14 показана начальная точка этих испытаний, а также грузовик и прицеп ICC. Несмотря на наличие некоторых облаков, дождя во время исследования сухого бетона не было.
На рис. 15 представлен крупный план полированного тротуара Tyrone Boulevard. На тротуаре была помещена монета в десять центов США, чтобы помочь изобразить состояние поверхности и ее обработку. Департамент транспорта Флориды требует, чтобы все бетонные дороги подвергались тонировке — процессу, при котором металлические штыри протаскивают по полузатвердевшему бетону для создания поперечных или продольных канавок [15].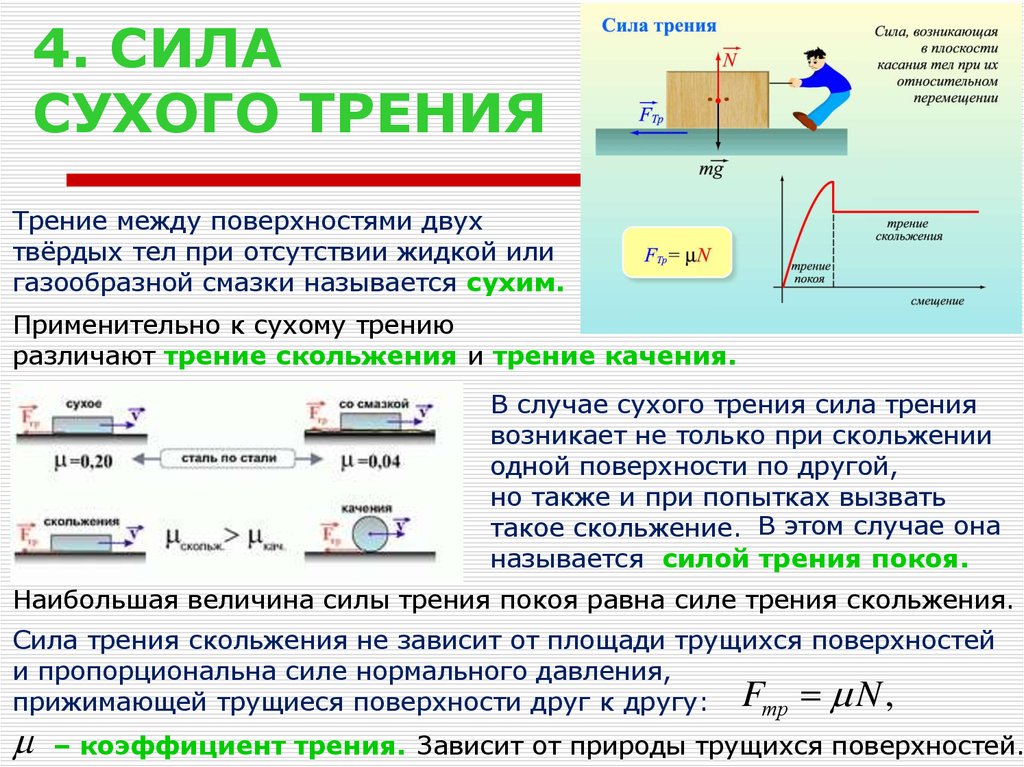 Продольные канавки на полированном в других отношениях дорожном покрытии Tyrone Boulevard в зоне проведения испытаний хорошо видны. На рис. 16 представлены результаты испытаний на бульваре Тайрон в сухом состоянии.
Продольные канавки на полированном в других отношениях дорожном покрытии Tyrone Boulevard в зоне проведения испытаний хорошо видны. На рис. 16 представлены результаты испытаний на бульваре Тайрон в сухом состоянии.
Видно, что семь из восьми значений, соединенных прямой линией и экстраполированных на ось, указывают на возникновение микрогистерезисной силы трения, имеющей величину около 200 lbf. Однако, как и при испытаниях на сухом асфальте, присутствует выброс, в данном случае при нагрузке 883 фунта. Непрерывная температура дорожного покрытия при испытаниях с нагрузкой 883 фунта составляла 116°F, в то время как температура дорожного покрытия во время испытаний при других нагрузках составляла в среднем 74°F. Во время испытаний сухого бетона также наблюдались клубы дыма, исходящие из пятна контакта шины с дорожным покрытием. Как сообщается, эти условия соответствуют большему размягчению шины и уменьшенному значению при нагрузке 883 фунта. Было измерено значение 200 фунтов силы. В таблице 4 представлены приложенные нагрузки и соответствующие значения.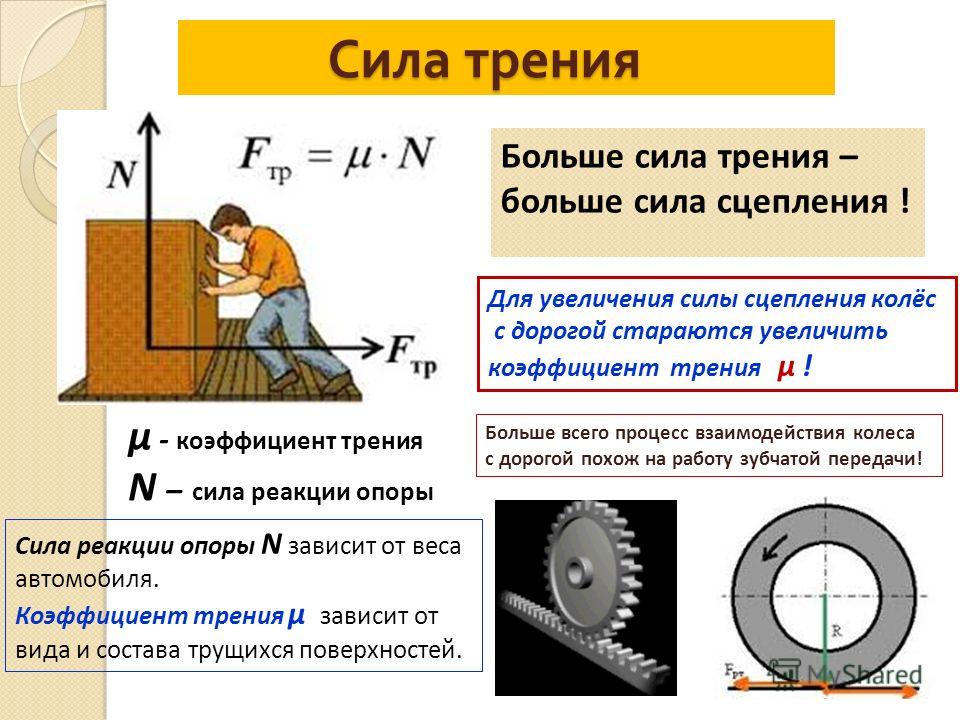
5.4. Испытание мокрого бетонного покрытия
Испытание мокрого бетона с использованием тестера ICC, которым всегда управляет один и тот же опытный инженер, началось на бульваре Тайрон в Санкт-Петербурге, Флорида, 18 марта 2013 г. и завершилось 22 марта 2013 г. в светлое время суток. Движение на бульваре Тайрон было умеренным; никакого существенного взаимодействия между ним и испытанием на скорости 40 ± 1 миль в час не произошло.
Использовалась новая, обкатанная полноразмерная ребристая шина ASTM E501-08, установленная на левой стороне испытательного стенда, со стандартным давлением накачки 24 ± 0,5 psi.
Для каждой из восьми приложенных нагрузок было выполнено пять циклов блокировки из трех отдельных испытаний. Результаты усреднялись для получения среднего значения для каждой нагрузки. Эти тестовые данные всегда были получены одним и тем же инженером в одном и том же боковом положении на одной и той же рабочей полосе, записанные в течение 1 с. На рис. 17 представлены результаты мокрого бульвара Тайрон. В таблице 5 представлены нормальные нагрузки на шины и соответствующие им значения.
В таблице 5 представлены нормальные нагрузки на шины и соответствующие им значения.
Видно, что семь значений лежат на прямой линии или касаются ее, что при экстраполяции указывает на возникновение микрогистерезисной силы трения, имеющей величину около 60 lbf.
Однако значение 1188 фунтов можно считать выбросом. Опыт ICC с их обычными испытаниями с заблокированными колесами во влажных условиях в разные дни, вероятно, объясняет расхождение.
5.5. Сводка результатов испытаний и предлагаемые значения индекса трения скольжения
В таблице 6 приведены результаты интерпретации на основе нагрузки со значениями для всех четырех наборов данных испытаний на трение. Более высокие значения микрогистерезисной силы для неполированного асфальта указывают на превосходные характеристики микротекстуры во время испытаний по сравнению с полированным бетонным покрытием.
Используя подход, основанный на нагрузке, «индекс трения скольжения» (SFI) предлагается в качестве улучшенного показателя для расчета трения шины скольжения на основе переменных значений, представленных в разделе 8. 3.
3.
5.6. Значения коэффициента трения для всех четырех испытаний с блокировкой колес
В таблице 7 представлены значения для всех четырех результатов испытаний с блокировкой колес. Они приведены здесь для сравнения с использованием подхода, основанного на нагрузке на шину, который позволяет проводить отдельную количественную оценку силы. В каждом расчете использовалось среднее значение соответствующего измерения, и он неизбежно содержал силовую составляющую.
6. Унифицированная инженерная теория трения шины о дорожное покрытие, основанная на нагрузке
Как уже говорилось, Куммер предложил [1] единую теорию трения скольжения шины о дорожное покрытие в 1966 г., выражая общую силу трения, создаваемую как сумму его компоненты. К ним относятся адгезия, связанная с комбинированной свободной поверхностной энергией парных материалов. Он считал, что объемная деформация протектора шины на неровных покрытиях вносит вклад макрогистерезисного трения . Он также включил износ шин или потерю сцепления. Целью предложенной Куммером теории было «улучшить фрикционное сцепление между шинами и мокрым дорожным покрытием, особенно на высоких скоростях».
Целью предложенной Куммером теории было «улучшить фрикционное сцепление между шинами и мокрым дорожным покрытием, особенно на высоких скоростях».
Основываясь на подходе Куммера, была предложена расширенная, унифицированная, основанная на нагрузке инженерная теория трения шины о дорожное покрытие [3, 8]. Теория включает в себя микрогистерезисную силу трения резины, доказательство которой было подтверждено испытаниями на заблокированных колесах: парных материалов, представляет собой объемную деформацию протектора шины, представляет собой составляющую потери сцепления из-за износа шины и представляет собой вклад постоянной микрогистерезисной силы трения.
Следует отметить, что Куммер [1] включил термин для полноты, но высказал мнение, что его величина в конкретных краткосрочных обстоятельствах может быть незначительной. Следует также отметить, что и не обязательно являются независимыми. Адгезионный макрогистерезис может в некоторых случаях увеличить развитие силы за счет более плотного прилипания резины шины к шероховатой поверхности дорожного покрытия [3].
7. Практическое применение подхода, основанного на нагрузке
7.1. Вклад в анализ динамики транспортных средств
Как показано на Рисунке 1 и других графиках, представляющих результаты испытаний, представленных здесь, в сравнении с , увеличение приложенной нормальной нагрузки увеличивает результирующую силу трения между шиной и дорожным покрытием. Как обсуждалось в Разделе 3, использование коэффициента трения и количества заносов может непреднамеренно привести к неправильной интерпретации разработанных оценок силы трения. Это можно проиллюстрировать, рассмотрев простой пример из динамики транспортных средств.
При торможении двухосного транспортного средства при прямолинейном торможении на горизонтальном дорожном покрытии может произойти передача динамической нагрузки с задней оси на переднюю ось. Во время этого процесса нагрузки на задние шины уменьшаются, а на передние колеса нагрузка может возрастать. Поскольку CoF, как правило, не является постоянным при переменной нагрузке, более высокий коэффициент, по-видимому, может применяться к задним шинам, когда автомобиль замедляется, в то время как меньший коэффициент трения, по-видимому, будет связан с передними шинами, напротив показаний фактического образования силы трения.
Использование подхода, основанного на нагрузке, позволяет рассчитать фактические силы, возникающие при заданных углах скольжения и интересующих значениях. Когда водители совершают обычные повороты на перекрестках или регулируют рулевое управление, чтобы следовать кривизне проезжей части, возникают силы бокового трения. Знание таких данных может оказаться ценным для специалистов по динамике транспортных средств для использования при количественной оценке сопротивления боковому скольжению, необходимого для преодоления инерционных сил, возникающих во время таких маневров, что позволяет удерживать транспортные средства на дороге.
7.2. Мониторинг изменения глубины микротекстуры поверхностей дорожного покрытия
Ранее было признано, что исследование сцепления шин должно включать микротекстуру дорожного покрытия. Бонд и др. провели исследования важности микротекстуры мокрого дорожного покрытия, о которых сообщалось в 1974 году [16]. Они обнаружили, что микрошероховатость играет значительную роль в сцеплении шин с дорогой во влажных условиях. Их исследование охватило вопросы сезонности и обнаружило, что сцепление на мокрой дороге увеличивается до максимума зимой и снижается до минимума летом. Изучение микрофотографий дорожных одежд, находящихся в эксплуатации, показало, что микрошероховатость дорожных одежд максимально увеличивалась в зимний период из-за мороза и других естественных атмосферных воздействий на дорожное покрытие в этот период. Также было установлено, что в летнее время доминирует транспортная полировка, в результате чего в значительной степени удаляется микротекстура заполнителя. Эти результаты хорошо коррелируют с частотой дорожно-транспортных происшествий, меньше зимой и больше летом.
Их исследование охватило вопросы сезонности и обнаружило, что сцепление на мокрой дороге увеличивается до максимума зимой и снижается до минимума летом. Изучение микрофотографий дорожных одежд, находящихся в эксплуатации, показало, что микрошероховатость дорожных одежд максимально увеличивалась в зимний период из-за мороза и других естественных атмосферных воздействий на дорожное покрытие в этот период. Также было установлено, что в летнее время доминирует транспортная полировка, в результате чего в значительной степени удаляется микротекстура заполнителя. Эти результаты хорошо коррелируют с частотой дорожно-транспортных происшествий, меньше зимой и больше летом.
Бонд и др. [16] далее определили, что сцепление на мокром покрытии, которое, как было указано, обеспечивается микронеровностями дорожного покрытия, было минимальным, если только топографическая глубина заполнителей не превышала критического значения, порядка 1,95 × 10 −4 дюймов. -сопротивление скольжению на проезжей части резко возросло.
Компания Williams провела обзор [17] современного состояния сцепления шин с дорожным покрытием в 1992 г., уделив особое внимание способности шины держать дорогу во влажных условиях. Признавая важность адекватной микротекстуры дорожного покрытия, он заявил следующее:
Не существует замены для соответствующего уровня микротекстуры заполнителей в новом и пройденном состоянии. Наиболее желательный уровень микротекстуры связан с его способностью удалять оставшуюся тонкую пленку воды для создания реальных областей контакта с резиновой смесью протектора. Уровни микротекстуры ниже этого минимума не могут обеспечить высокий уровень мокрого трения. (стр. 132)
На рисунках 13 и 17 представлены результаты испытаний, позволяющие количественно определить микрогистерезисную силу трения резины во влажных условиях, полученную при обычном использовании испытательного стенда с заблокированными колесами. Измерения неполированной дороги Белчер-роуд (220 фунтов силы) и полированной улицы Тайрон-Бульвар (60 фунтов силы) согласуются с выводами Bond et al. [16] и Уильямс [17]. Эти результаты, полученные за несколько дней испытаний, показывают существенные различия в величинах соответствующих сил. Возможность обычных испытаний с заблокированными колесами, на результаты которых, вероятно, повлияли, по крайней мере частично, характеристики микротекстуры дорожного покрытия, позволяет предположить, что более высокое сопротивление трению измеряется на покрытиях с большей глубиной микротекстуры. Усовершенствованная интерпретация данных, основанная на нагрузке, использовалась для разработки «индекса трения скольжения», обсуждаемого ниже в разделе 7.5. Сезонные испытания и испытания на других дорожных покрытиях с различными характеристиками микротекстуры должны помочь продемонстрировать широкую применимость предложенной модели индекса трения. Это обеспечило бы надежное указание на изменение индекса трения в результате изменения .
[16] и Уильямс [17]. Эти результаты, полученные за несколько дней испытаний, показывают существенные различия в величинах соответствующих сил. Возможность обычных испытаний с заблокированными колесами, на результаты которых, вероятно, повлияли, по крайней мере частично, характеристики микротекстуры дорожного покрытия, позволяет предположить, что более высокое сопротивление трению измеряется на покрытиях с большей глубиной микротекстуры. Усовершенствованная интерпретация данных, основанная на нагрузке, использовалась для разработки «индекса трения скольжения», обсуждаемого ниже в разделе 7.5. Сезонные испытания и испытания на других дорожных покрытиях с различными характеристиками микротекстуры должны помочь продемонстрировать широкую применимость предложенной модели индекса трения. Это обеспечило бы надежное указание на изменение индекса трения в результате изменения .
7.3. Используемый в настоящее время тестер бокового трения
Расследование показало, что по крайней мере одно мобильное устройство бокового трения находится в постоянном использовании — парк тестеров SCRIM®, которым управляет Лаборатория транспортных исследований (TRL) в Великобритании. Машина для рутинных исследований коэффициента боковой силы, или SCRIM, измеряет боковое трение, создаваемое в контролируемых условиях влажной среды, с помощью свободно вращающейся гладкой резиновой шины, закрепленной под углом 20° к направлению движения испытуемого автомобиля. Хотя в настоящее время это не используется в соответствии с подходом, основанным на нагрузке на шину, графическое представление отчетных данных показано на рисунке 9.выявит истинное отношение к соотношению и определит количественно значение .
Машина для рутинных исследований коэффициента боковой силы, или SCRIM, измеряет боковое трение, создаваемое в контролируемых условиях влажной среды, с помощью свободно вращающейся гладкой резиновой шины, закрепленной под углом 20° к направлению движения испытуемого автомобиля. Хотя в настоящее время это не используется в соответствии с подходом, основанным на нагрузке на шину, графическое представление отчетных данных показано на рисунке 9.выявит истинное отношение к соотношению и определит количественно значение .
Использование данных SCRIM при угле скольжения 20° таким образом подходит для мониторинга изменения глубины микротекстуры поверхностей дорожного покрытия, что обсуждалось в разделе 7.2. Фактически, заявленная цель испытаний SCRIM состоит в том, чтобы «определить необходимость обработки [испытательного] участка для восстановления сопротивления скольжению».
7.4. Альтернативный подход к коэффициенту трения в геометрическом расчете дорог
В разделе 3 обсуждалось и иллюстрировалось (рис.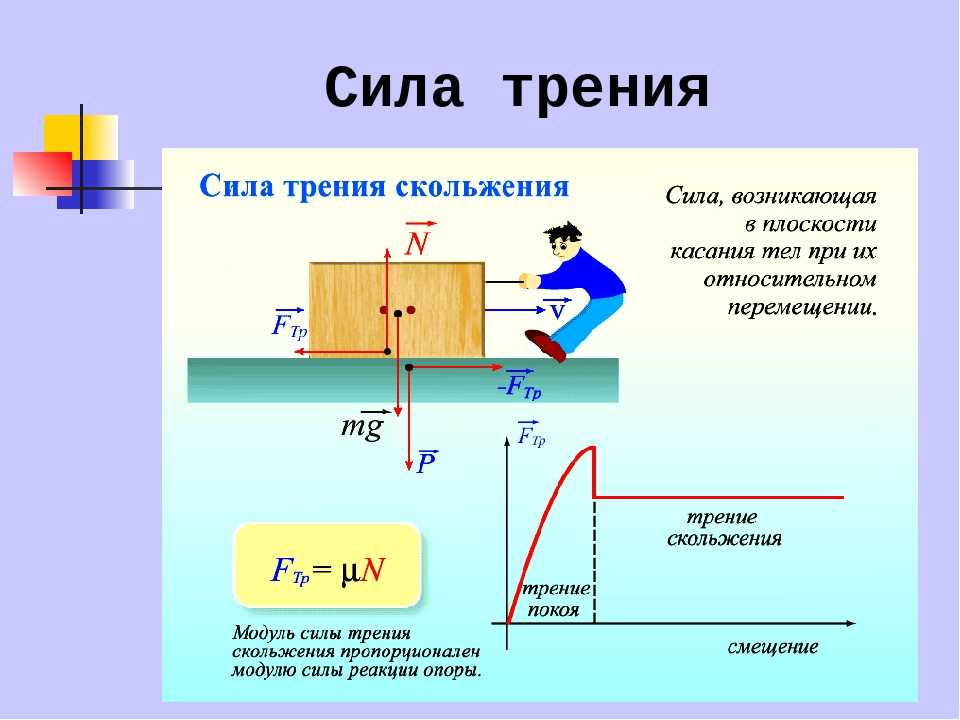 1 и 6), как использование коэффициента трения и количества заносов может привести к непреднамеренным ошибкам в оценке при анализе результатов испытаний с блокировкой колес. В настоящее время не существует общепринятой, поддающейся проверке, всеобъемлющей и рациональной теории трения резины, включающей термин CoF, который сам по себе не является свойством эластомеров. Из соображений безопасности вместо этого рекомендуется применять проверенный подход, основанный на нагрузке на шины, и индекс трения скольжения в соответствующих транспортных сегментах.
1 и 6), как использование коэффициента трения и количества заносов может привести к непреднамеренным ошибкам в оценке при анализе результатов испытаний с блокировкой колес. В настоящее время не существует общепринятой, поддающейся проверке, всеобъемлющей и рациональной теории трения резины, включающей термин CoF, который сам по себе не является свойством эластомеров. Из соображений безопасности вместо этого рекомендуется применять проверенный подход, основанный на нагрузке на шины, и индекс трения скольжения в соответствующих транспортных сегментах.
Коэффициент трения, обозначаемый как , широко используется в уравнениях, представленных в «Зеленой книге» [18], основном американском руководстве по геометрическому проектированию дорог. Это руководство, постоянно разрабатываемое в течение многих десятилетий с участием многочисленных квалифицированных инженеров и опытных конструкторов, внесло огромный и долговременный вклад в практику обеспечения безопасности и эффективности транспорта [18]. Однако практика при использовании не учитывает вклад микрогистерезисной силы (), возникающей в результате контакта шины скольжения с микротекстурой дорожного покрытия.
Однако практика при использовании не учитывает вклад микрогистерезисной силы (), возникающей в результате контакта шины скольжения с микротекстурой дорожного покрытия.
7.5. Индекс трения скольжения
Допуская существование микрогистерезисной силы трения () и учитывая ее при анализе испытаний с заблокированными колесами, можно получить рациональное число, определяющее переменное сопротивление скольжению трения, возникающее при различных значениях применяемой шины. load() используются в таком тестировании.
Процесс включает вычитание постоянного значения из общей измеренной силы трения (), создаваемой каждой такой приложенной нагрузкой. Это можно проиллюстрировать, используя данные испытаний с заблокированными колесами, опубликованные Советом по исследованиям в области транспорта [4] в 1919 г.74 и показан на рисунке 1, где сила в 150 фунтов создавалась с использованием трех различных приложенных нагрузок в 800 фунтов, 1 000 фунтов и 1 200 фунтов. В этом испытании соответствующие значения были 350 фунтов, 400 фунтов и 450 фунтов, соответственно.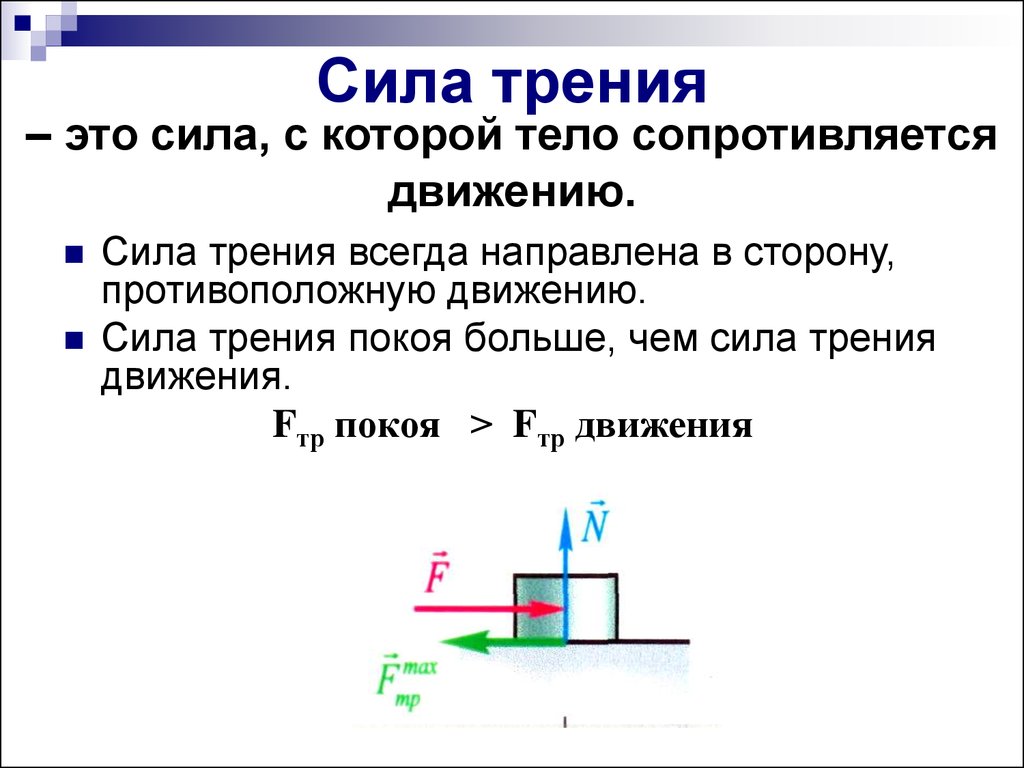 В таблице 8 представлены соответствующие расчеты. Видно, что вычитание силы в 150 фунтов силы из трех значений дает 200 фунтов силы, 250 фунтов силы и 300 фунтов силы соответственно. Разделение этих равнодействующих на их соответствующие количества дает значение безразмерного индекса трения скольжения (SFI), равное 0,25 для всех трех нагрузок. Фигуры 18, 19, 20 и 21 представляют значения SFI для настоящих результатов испытаний на мокрой и сухой дороге с заблокированными колесами. Значения выбросов не были включены в эти расчеты SFI.
В таблице 8 представлены соответствующие расчеты. Видно, что вычитание силы в 150 фунтов силы из трех значений дает 200 фунтов силы, 250 фунтов силы и 300 фунтов силы соответственно. Разделение этих равнодействующих на их соответствующие количества дает значение безразмерного индекса трения скольжения (SFI), равное 0,25 для всех трех нагрузок. Фигуры 18, 19, 20 и 21 представляют значения SFI для настоящих результатов испытаний на мокрой и сухой дороге с заблокированными колесами. Значения выбросов не были включены в эти расчеты SFI.
8. Выводы
8.1. Роль микротекстуры дорожного покрытия в сопротивлении скольжению
Важность микротекстуры дорожного покрытия обсуждалась в разделе 7.2. Это было реализовано в 1974 г. [16] в результате испытаний на эксплуатируемых дорогах, на которых микрошероховатость дорожного покрытия играет существенную роль в сцеплении шин во влажных условиях. Эти дороги включали те, которые были сильно отполированы летом, и другие, которые испытали усиление микрошероховатости из-за зимних морозов.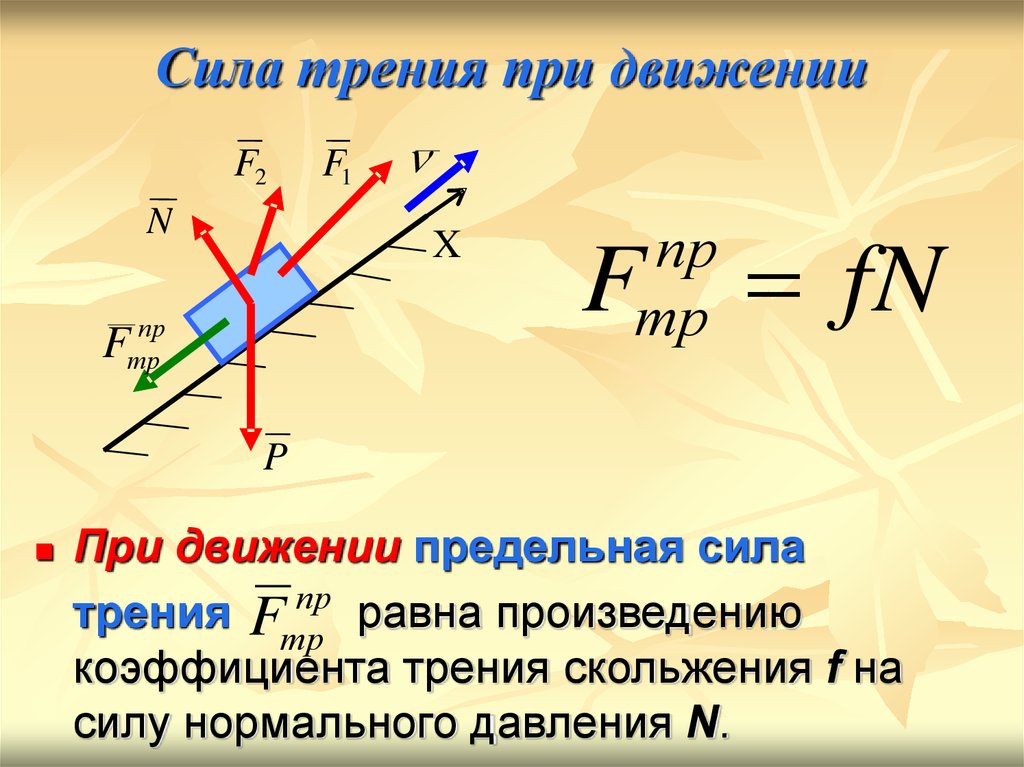 Фотомикрографические исследования показали, что полезность микротекстуры дорожного покрытия во влажных условиях минимальна, если только она не превышает примерно 1,9.5 × 10 −4 дюймов в глубину. Эти результаты хорошо коррелируют с частотой дорожно-транспортных происшествий, меньше зимой и больше летом.
Фотомикрографические исследования показали, что полезность микротекстуры дорожного покрытия во влажных условиях минимальна, если только она не превышает примерно 1,9.5 × 10 −4 дюймов в глубину. Эти результаты хорошо коррелируют с частотой дорожно-транспортных происшествий, меньше зимой и больше летом.
Впоследствии было обнаружено [17], что адекватная глубина микротекстуры дорожного покрытия играет роль в улучшении сцепления шины с дорогой во влажных условиях. Наиболее желательной шероховатостью микротекстуры является та, которая помогает шине удалить любую присутствующую поверхностную водяную пленку, чтобы создать реальные области контакта с протектором.
На рисунках 13 и 17 представлены результаты испытаний на мокром покрытии, полученные при обычном использовании устройства для испытаний с заблокированными колесами, что позволяет количественно определить микрогистерезисную силу трения резины в качестве показателя для оценки микрошероховатости дорожного покрытия и вклада ее составляющих в общую потенциально доступную силу вдоль с компонентом нагрузки на шины.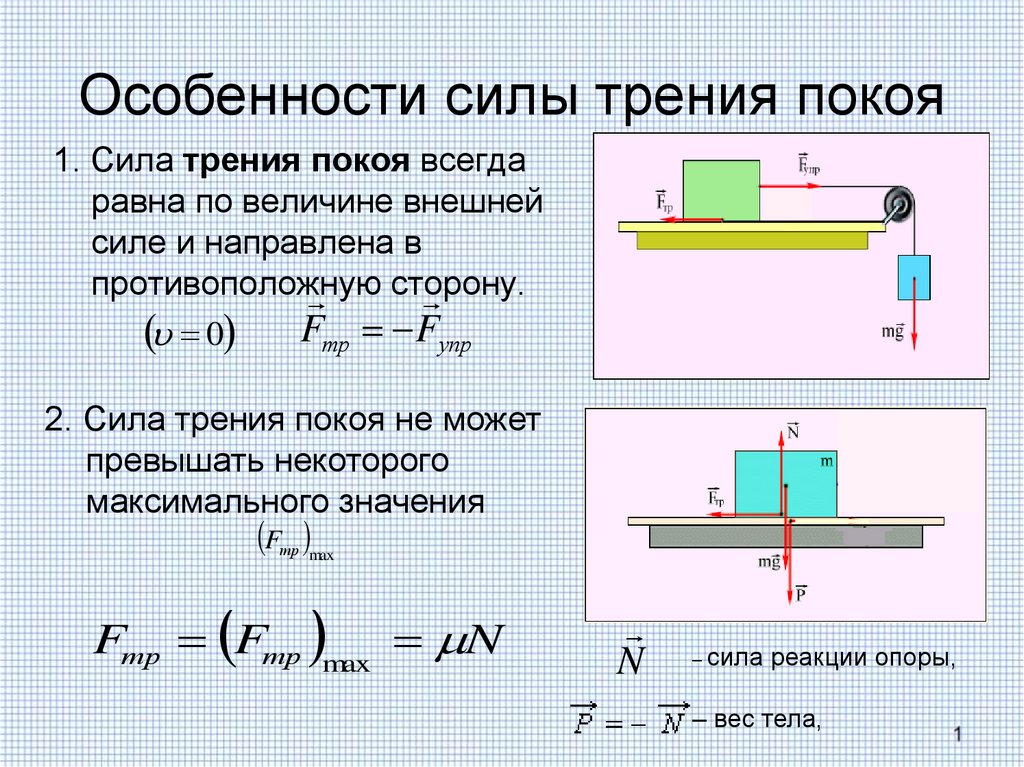
В качестве примера в этом отношении можно использовать размеры неполированного покрытия Белчер-Роуд (220 фунтов) и полированного Тайрон-Бульвар (60 фунтов). Идентичные нагрузки составили в среднем 52 процента от общего значения Belcher Road, в то время как компонент в тестировании Tyrone Boulevard внес в среднем 17 процентов от общего значения. Известно, что алмазная шлифовка бетонного покрытия увеличивает макротекстуру поверхности. Чтобы определить, улучшается ли также микротекстура поверхности, потребуется испытание ASTM с заблокированным колесом. Испытание асфальтового покрытия после фрезерования также потребовало бы такого испытания с той же целью.
Вкратце, примите во внимание следующее: (i) Обычные испытания с заблокированными колесами могут использоваться для количественной оценки стоимости сегмента проезжей части. (ii) значения могут использоваться в качестве показателя для оценки микрошероховатости дорожного покрытия. (iii) Заблокированные колеса Потребуется испытание бетонного покрытия с алмазным шлифованием, чтобы определить, увеличилось ли оно.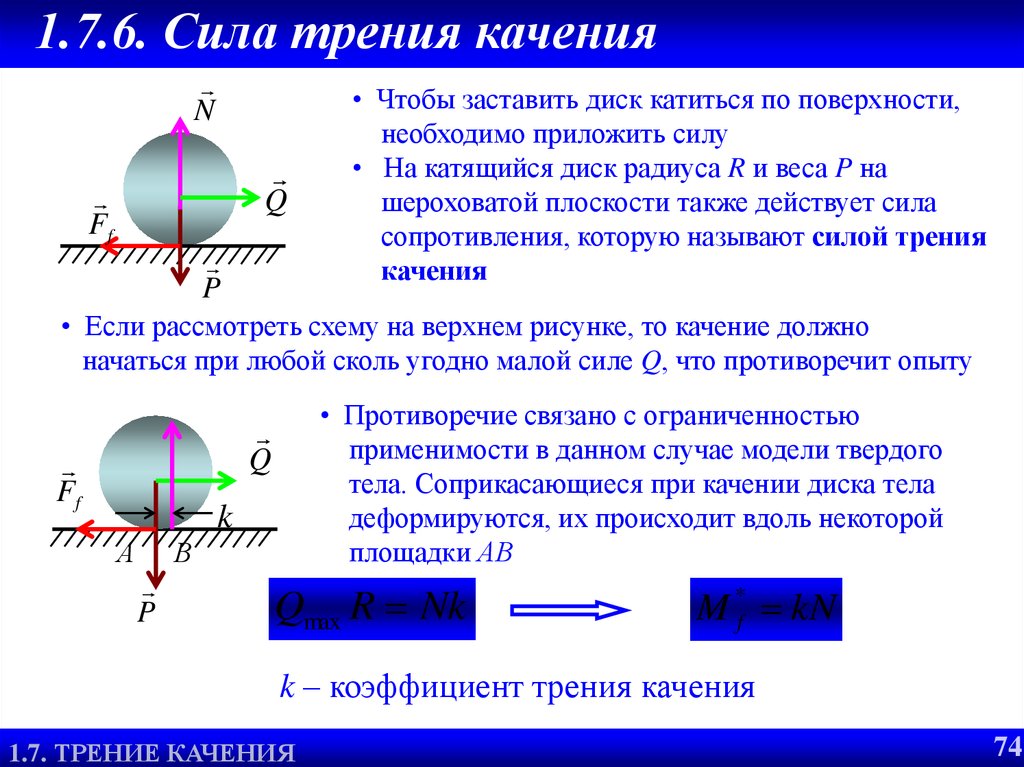 (iv) Для той же цели потребуется испытание асфальтового покрытия с заблокированным колесом после фрезерования.
(iv) Для той же цели потребуется испытание асфальтового покрытия с заблокированным колесом после фрезерования.
8.2. Индекс трения скольжения при практическом применении данных испытаний с заблокированными колесами
Значение индекса трения скольжения (SFI) обсуждалось в разделе 7.5. Измерение значений силы может быть легко выполнено с помощью стандартного испытания ASTM с заблокированным колесом. Вычитание этих значений из общей измеренной силы трения () дает количественную оценку сопротивления скольжению, вызванного приложением нагрузки на шину, . Этот метод позволяет определить безразмерный SFI, который точно определяет количество этого второго, отдельного компонента нагрузки .
8.3. Двусторонний подход, необходимый для использования общей силы сопротивления скольжению, измеренной в стандартном испытании ASTM с заблокированным колесом
Поскольку значение SFI зависит от нагрузки на шину, а сила не зависит от нагрузки на шину, необходим двусторонний подход для применения этих двух различных сил трения скольжения, измеренных в стандартном испытании ASTM с заблокированными колесами. Это может быть легко достигнуто с помощью простого уравнения сочетания сил: где — общая сила сопротивления трению скольжению, измеренная в ходе стандартного испытания ASTM с заблокированным колесом, полученная с использованием подхода, основанного на нагрузке, для количественной оценки путем экстраполяции прямолинейных данных. график по оси -, выраженный в фунт-силах, представляет собой значение микрогистерезисной силы, измеренное в ходе стандартного испытания ASTM с заблокированным колесом, выраженное в фунтах-силах, представляет собой расчетное значение SFI, полученное по результатам стандартного испытания ASTM с заблокированным колесом, умноженное на приложенная интересующая нагрузка на шину, выраженная в фунт-силах.
Это может быть легко достигнуто с помощью простого уравнения сочетания сил: где — общая сила сопротивления трению скольжению, измеренная в ходе стандартного испытания ASTM с заблокированным колесом, полученная с использованием подхода, основанного на нагрузке, для количественной оценки путем экстраполяции прямолинейных данных. график по оси -, выраженный в фунт-силах, представляет собой значение микрогистерезисной силы, измеренное в ходе стандартного испытания ASTM с заблокированным колесом, выраженное в фунтах-силах, представляет собой расчетное значение SFI, полученное по результатам стандартного испытания ASTM с заблокированным колесом, умноженное на приложенная интересующая нагрузка на шину, выраженная в фунт-силах.
Следующая часть иллюстрирует применение уравнения сочетания сил к данным испытаний мокрого и сухого асфальта и бетона при значении 1242 фунта. Можно отметить, что значение силы на мокрой дороге Белчер-Роуд было значительно больше (220 фунтов силы). чем значение сухой силы Белчер-Роуд (140 фунтов силы).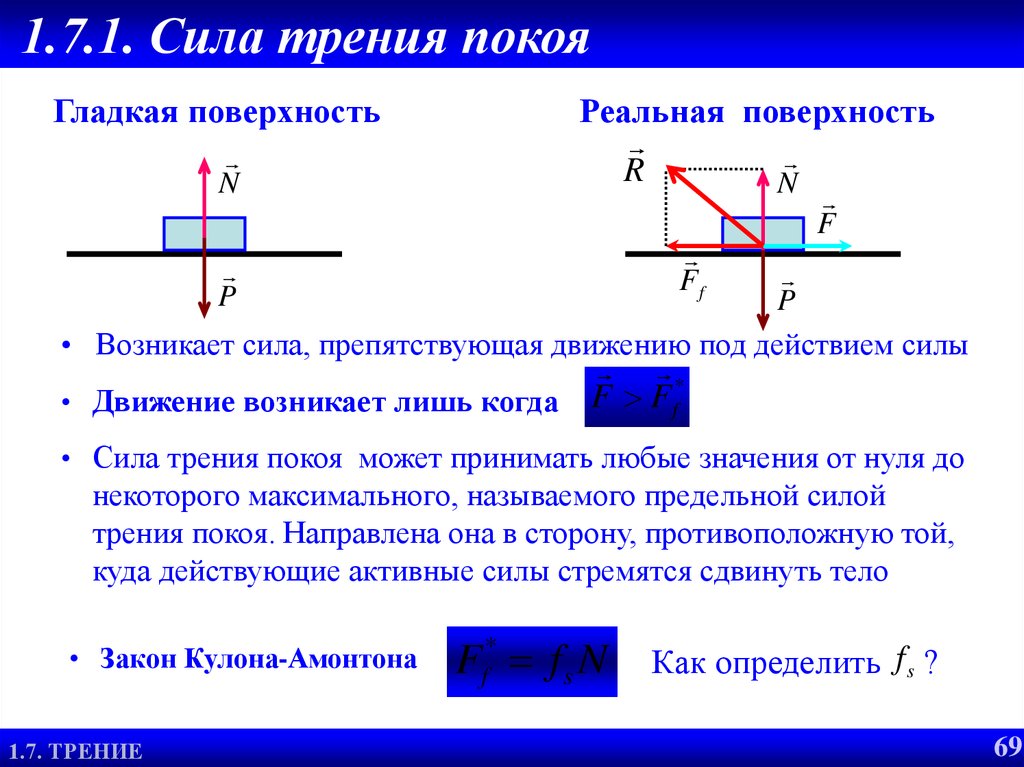 Напомним, что при тестировании сухого асфальта наблюдалось задымление. Уменьшенное значение кажется совместимым с этим образованием дыма. Возможно, тепло, связанное с дымом, также уменьшило жесткость микротекстуры асфальта и/или привело к уменьшению глубины во время процедуры блокировки колес.
Напомним, что при тестировании сухого асфальта наблюдалось задымление. Уменьшенное значение кажется совместимым с этим образованием дыма. Возможно, тепло, связанное с дымом, также уменьшило жесткость микротекстуры асфальта и/или привело к уменьшению глубины во время процедуры блокировки колес.
Расчет значений уравнения объединения сил . Учтите следующее:
8.4. Использование уравнения сочетания сил для прогнозирования сопротивления скольжению и тормозного пути
Разработка базы данных испытаний, включающей типичные значения асфальта и бетона и значения SFI, полученные в ходе стандартных испытаний ASTM с заблокированными колесами и проанализированные с использованием уравнения сочетания усилий в комбинации с испытанием тормозного пути потребуется, чтобы обеспечить надежное прогнозирование сопротивления скольжению и тормозного пути.
Вкратце, примите во внимание следующее: (i) Обычное использование испытаний с заблокированными колесами позволяет измерять значения на интересующих участках дорожного покрытия.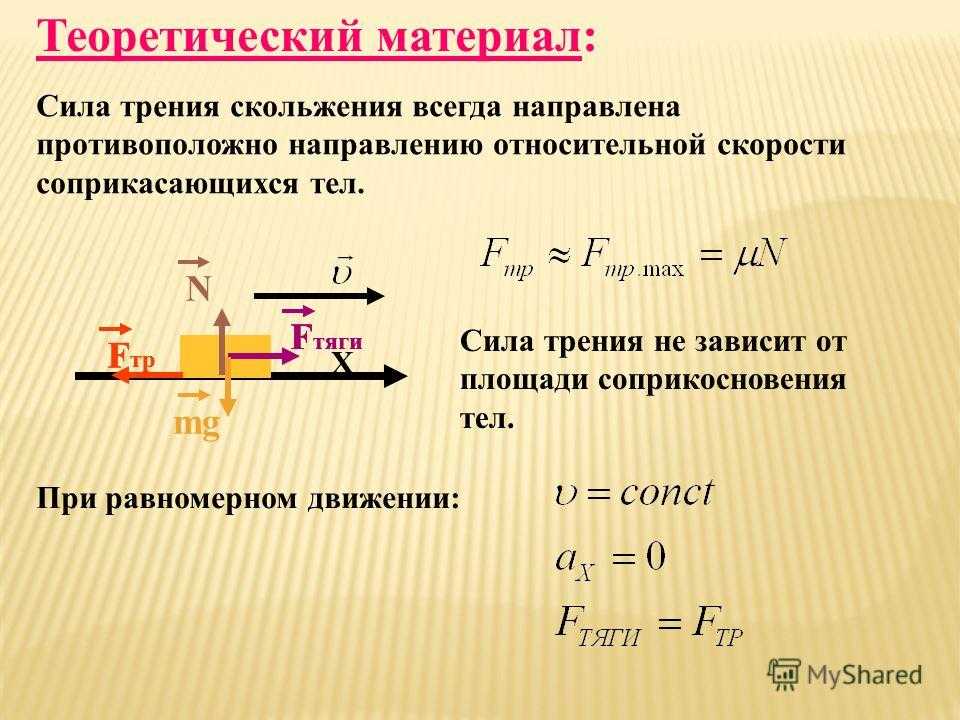 нагрузка на шину. (iii) Использование подхода, основанного на нагрузке, для анализа данных испытаний ASTM с заблокированными колесами позволяет измерить силу, приписываемую микрошероховатости дорожного покрытия, свободную энергию поверхности дорожного покрытия и свободную поверхностную энергию протектора скользящей шины.
нагрузка на шину. (iii) Использование подхода, основанного на нагрузке, для анализа данных испытаний ASTM с заблокированными колесами позволяет измерить силу, приписываемую микрошероховатости дорожного покрытия, свободную энергию поверхности дорожного покрытия и свободную поверхностную энергию протектора скользящей шины.
8.5. Заявление о внедрении
Принимая во внимание доказательства, полученные в результате анализа результатов испытаний, включающих данные как о мокром, так и о сухом асфальте и бетонных покрытиях, а также о вспомогательных материалах, рассмотренных выше, рекомендуется пересмотреть использование числа салазок и коэффициента трения.
9. Необходимые исследования
Как показано на рис. 2 на прямолинейном графике, когда сила вычитается из , соответствующие значения CoF прямо пропорциональны приложенной нагрузке в обычно используемом диапазоне блокировки колес. Как показано прямолинейными графиками на рисунках 18, 19, 20 и 21 — когда точки выбросов игнорируются — значения индекса трения скольжения также прямо пропорциональны приложенной нагрузке. Необходимы дальнейшие исследования, чтобы понять основной механизм, порождающий эту прямо пропорциональную характеристику. Такие знания могут оказаться полезными при практическом применении индекса трения скольжения.
Необходимы дальнейшие исследования, чтобы понять основной механизм, порождающий эту прямо пропорциональную характеристику. Такие знания могут оказаться полезными при практическом применении индекса трения скольжения.
Арчард [19, 20] научно исследовал проблему прямой пропорциональности, используя макроскопически гладкие материалы, скользящие по макроскопически гладким поверхностям. При использовании этого подхода генерируются только силы трения. Арчард исследовал пары гладкой латуни и пары гладкого неэластомерного пластика, полиметилметакрилата или полиметилметакрилата, все в диапазоне упругих нагрузок. Он обнаружил, что по мере увеличения могут устанавливаться новые реальные области контакта между парными поверхностями. Он предположил, что создаваемые дополнительные силы трения будут прямо пропорциональны увеличению нагрузки, если основным результатом такой нагрузки является создание новых реальных областей контакта. Недавно Перссон пересмотрел [21] теорию Арчарда и согласился с ней.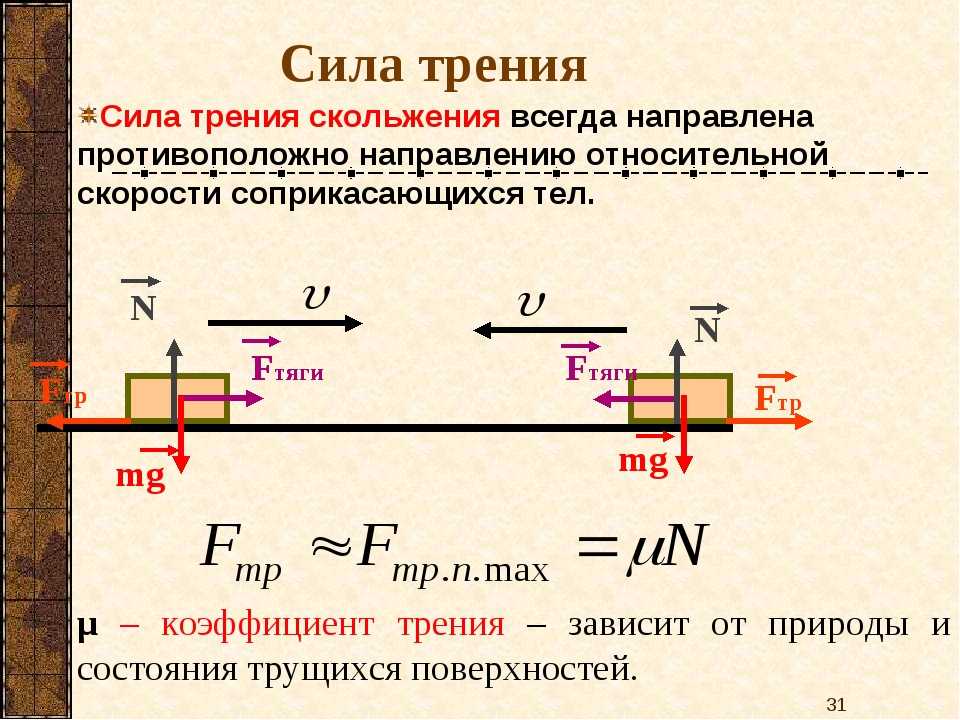


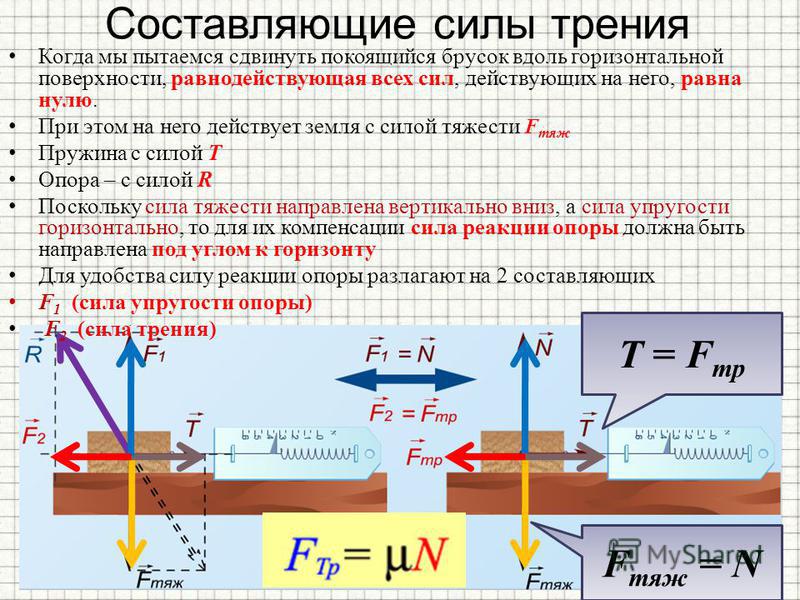 13 КБ
13 КБ

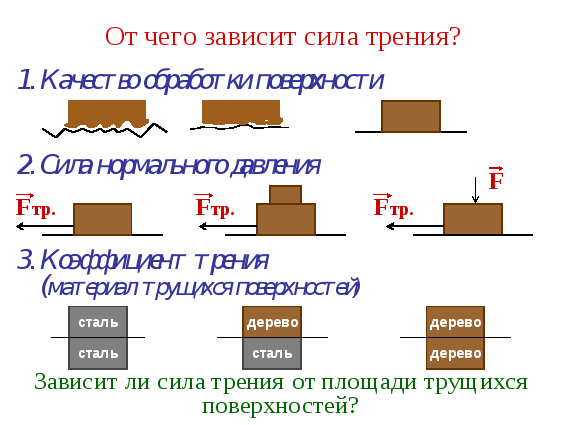 41 МБ
41 МБ Лоренц и Б. Н. Дж. Перссон, Сабина Дилувейт и Тошио Тада},
journal={Европейский физический журнал E},
год = {2011},
объем = {34},
страницы={1-11}
}
Лоренц и Б. Н. Дж. Перссон, Сабина Дилувейт и Тошио Тада},
journal={Европейский физический журнал E},
год = {2011},
объем = {34},
страницы={1-11}
} 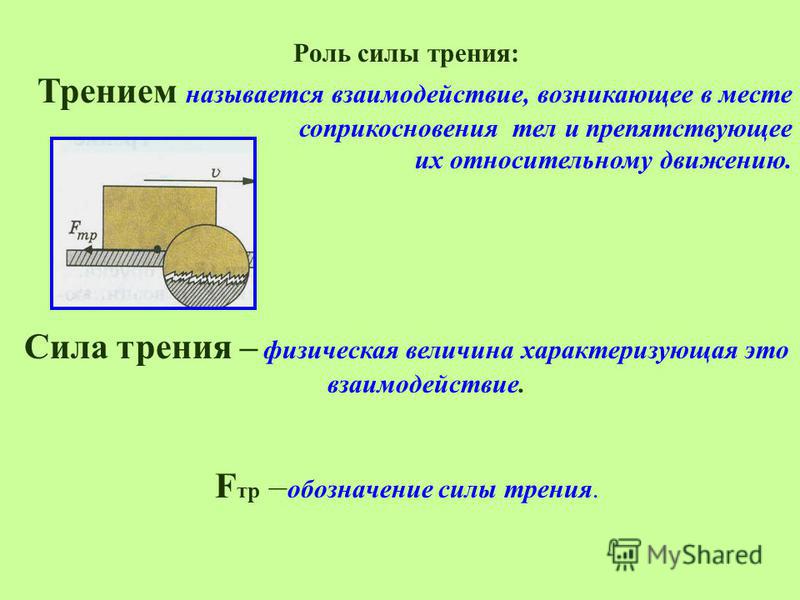
 Фретиньи, Н. Спенсер, Ю. Ле Шенадек, А. Шатоминуа
Фретиньи, Н. Спенсер, Ю. Ле Шенадек, А. Шатоминуа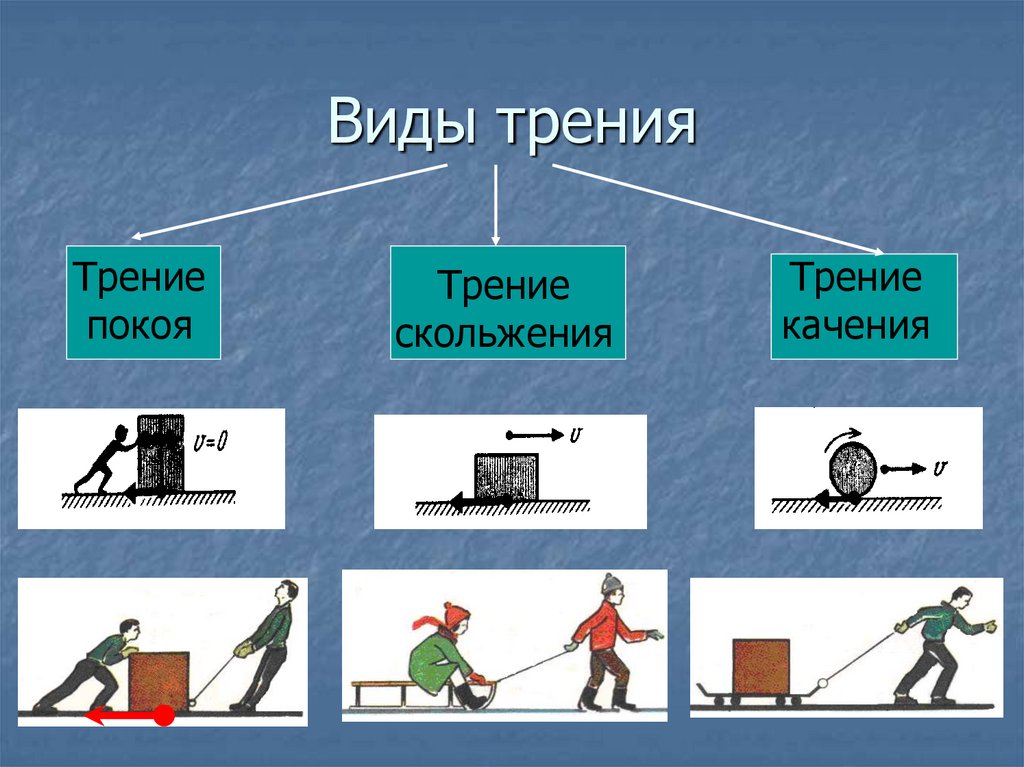 , Хоррами М., Масуди А., Кашани М.
, Хоррами М., Масуди А., Кашани М.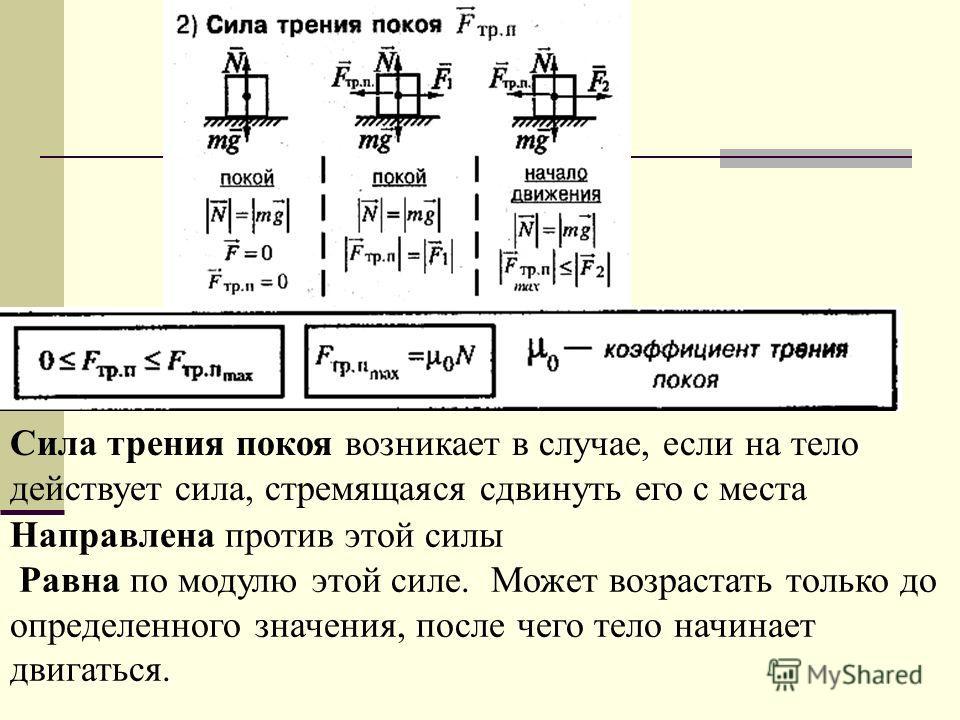
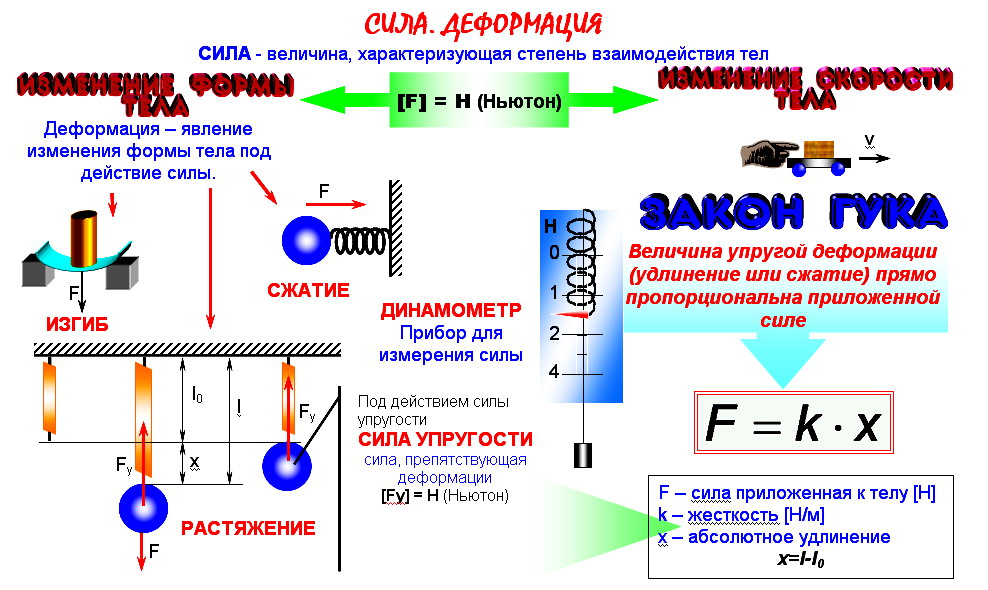
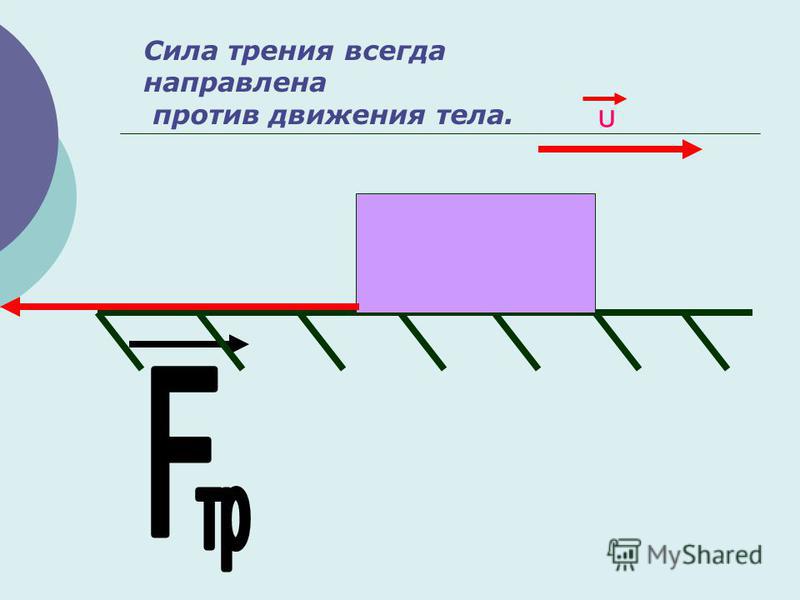 Наибольшая скорость не превышала нескольких…
Наибольшая скорость не превышала нескольких… Le Gal, M. Klüppel
Le Gal, M. Klüppel Просмотры
Просмотры
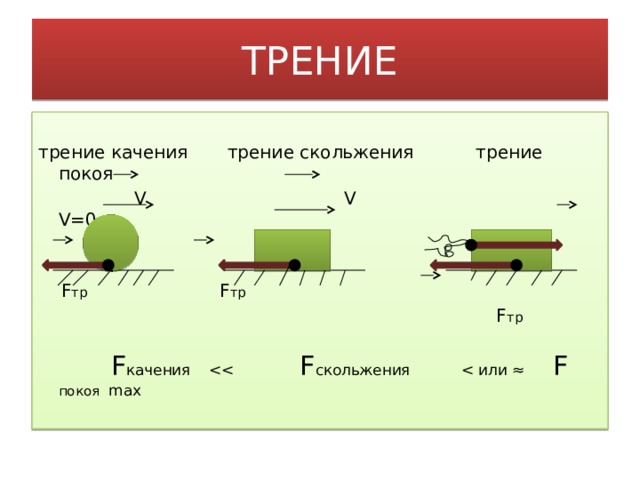 psu.edu
psu.edu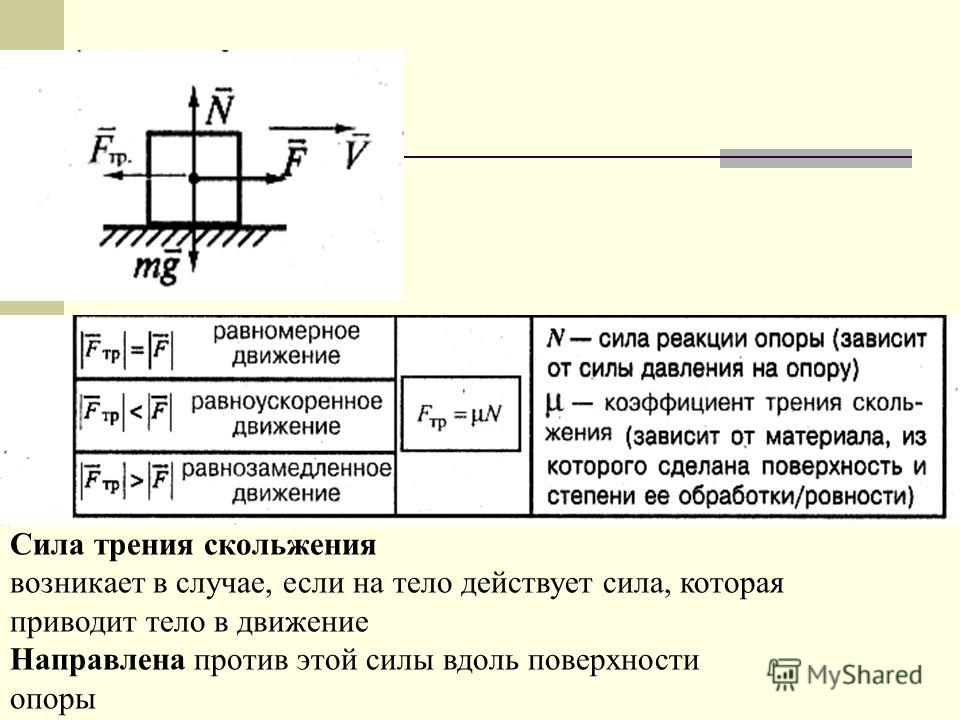 (стр. 94)
(стр. 94)