Молекулярная теория трения

Автор(ы): Бондарев Олег Викторович
Рубрика: Технические науки
Журнал: «Евразийский Научный Журнал №11 2017»  (ноябрь, 2017)
Количество просмотров статьи: 3726
Показать PDF версию Молекулярная теория трения

Бондарев Олег Викторович
инженер

Как свидетельствуют различные публикации на тему исследований трения скольжения [1,4; 2,5], явной связи сил и коэффициентов трения с физическими свойствами тел и состоянием их поверхностей установить не удалось. Это позволило сделать вывод, что такая связь отсутствует.

Рассмотрим тела, являющиеся упругими монолитами, имеющие шероховатые поверхности с хаотически выступающими неровностями. Схематично эти поверхности изображены на рис.1.

Из рисунка видно, что для горизонтального перемещения тела в данном случае необходимо приложить силу для его подъема на имеющиеся неровности, пусть микроскопические, но буквально в то же время, затраченная на такой микроподъем энергия, будет возвращена скатыванием в микроскопические углубления.

В случае хаотического расположения неровностей на поверхностях в условиях их упругих деформаций, потери энергии, и ее возврат при движении будут происходить фактически одновременно, не требуя приложения силы на перемещение тела. Таким образом, влияния таких шероховатостей на силу трения скольжения нет, такие шероховатости могут влиять только на, так называемую, силу трения покоя, требуя приложения силы в момент начала движения, для первоначального подъема тела на микро выступы.

Как известно [3,207; 3,255; 4,8; 4,45], между всеми молекулами действуют межмолекулярные силы притяжения и отталкивания. Суммарное их действие в зависимости от расстояния между молекулами показано на графике (рис. 2).

Силы притяжения проявляют себя на всех расстояниях между молекулами и прекращают свое действие лишь на бесконечном удалении молекул друг от друга, а силы отталкивания становятся значительно слабее сил притяжения и практически прекращают проявлять себя на расстояниях более r₀. Соответственно на расстояниях менее r₀ доминируют силы отталкивания, которые здесь превышают силы притяжения, а на расстоянии r = r

0 силы отталкивания и притяжения равны между собой. Если нет действия внешних сил сжимающих или растягивающих тело, его молекулы за счет имеющейся внутренней энергии колеблются относительно r₀, при этом расстояние между ними попеременно изменяется от r = r_min до r = r_max, в точках r_min и r_max кинетическая энергия колебаний равна нулю, а потенциальная максимальна, а в точке r = r₀ наоборот кинетическая энергия максимальна, а потенциальная равна нулю. В случае действия сжимающих внешних сил, центр колебаний смещается в зону r < r₀ (здесь r — среднее расстояние между молекулами) и действие внешних сил компенсируется внутренними межмолекулярными силами отталкивания. При растяжении центр колебаний смещается в зону r > r ₀ и внешним силам противодействуют силы межмолекулярного притяжения.

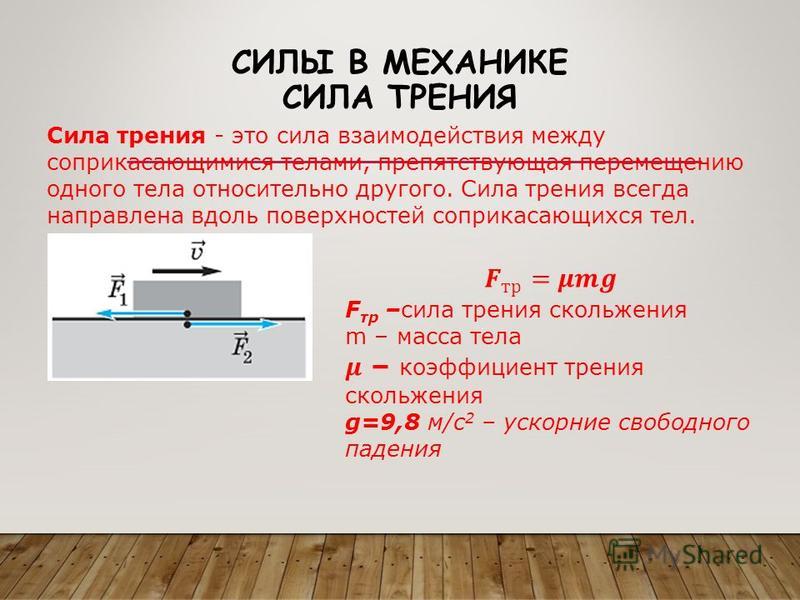
При рассмотрении действия внешних сил на молекулы можно оперировать смещением r относительно r_0, а именно величиной Dr=r₀-r (1). Для упрощения понимания влияния внешних сил на межмолекулярные силы, можно использовать модель, где между молекулами присутствуют некие межмолекулярные «пружины». Не принимая во внимание амплитуду и частоту имеющихся колебаний молекул под действием тепловой энергии, силу, действующую между молекулами, можно выразить как f=k

.Dr (2), где k — коэффициент жесткости межмолекулярной пружины. Согласно рис.2 зависимость между f и Dr близка к линейной. Значения k могут быть вычислены для различных материалов, исходя, например, из модулей упругости, если таковые известны, в других случаях могут быть определены экспериментально. Для материалов, у которых усредненное значение k сильно зависит от температуры (амплитуды колебаний молекул), может быть определен набор коэффициентов k соответствующих каждый своей температуре.

Так как силы притяжения проявляют себя на расстояниях более r

0 вплоть до бесконечности, то действуя со всех сторон на перемещаемое тело, они, как при его движении, так и в состоянии его покоя, будут уравновешивать друг друга, тем самым не создавая никаких препятствий и сопротивлений его перемещению. Таким образом, силы притяжения не являются причиной потерь энергии на трение. На межмолекулярном уровне, если молекулы электрически нейтральны, действуют только силы межмолекулярного притяжения и отталкивания [4, 8,9], следовательно, единственной оставшейся причиной возникновения трения для упругих монолитов являются силы межмолекулярного отталкивания.

Происходит это следующим образом: под действием своего веса или какой-либо другой силы тело прижимается к поверхности, что вызывает некоторую, пусть незначительную, деформацию (появление Dr), как между молекулами перемещаемого тела, так и поверхности по которой оно перемещается, расстояние между молекулами становится меньше r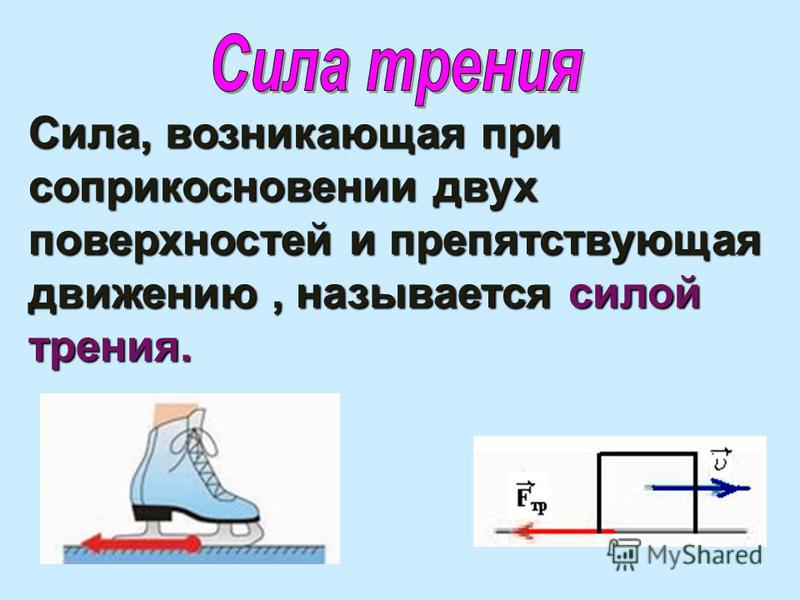

0, между ними начинают преобладать силы отталкивания.

Если представить ранее предложенную модель, где между молекулами имеются некие «пружины», то в данном случае эти «пружины», пусть на очень малую величину, сжимаются. При перемещении тела относительно поверхности вертикально вверх, перпендикулярно поверхности, межмолекулярные «пружины», разжимаясь, отдают запасенную под силой давления в себе энергию в полезную сторону, внося свой вклад в работу по подъему тела. При горизонтальном же перемещении тела, т. е. при перемещении тела по поверхности (см. рис. 3), «пружины» сжатые перпендикулярно поверхности, распрямляясь, перемещению тела никакой энергии не добавляют, а отдают, запасенную в себе под действием веса тела или другой силы прижимающей тело к поверхности, энергию находящимся на их концах молекулам, повышая их кинетическую энергию и, как следствие, температуру тела и поверхности, увеличивая их амплитуду колебаний. Причина потерь энергии на трение скольжения в том, что при разрыве связи, установленной силами отталкивания, «пружины» крайних молекул, потеряв противодействие, разжимаются в направлении перпендикулярном направлению движения, повышая амплитуду колебаний как самих этих молекул, так и молекул соседних с ними, повышая тем самым их тепловую энергию.

Определяющим для величины силы трения является взаимодействие молекул находящихся на поверхности тел.

Учитывая сложную структуру веществ тела и поверхности, уместно предположить, что при упомянутой выше деформации будет иметь место сжатие межмолекулярных «пружин», как в вертикальной, так и в горизонтальной (параллельной поверхности перемещения) плоскости, но при перемещении тела равновесие «пружин», сжатых в горизонтальном направлении, не нарушается и сжатие «пружин» со стороны направления движения компенсируется распрямлением «пружин» с противоположной стороны и на увеличение внутренней энергии (температуры тел) они не работают, так как возвращают свою потенциальную энергию сжатых «пружин» на совершение работы по перемещению тела, компенсируя затраты энергии на такое же сжатие таких же пружин с противоположной его стороны.

Рис.3

На рис. 3 схематично показаны: М1 — молекулы поверхности по которой происходит перемещение; М2 — молекулы перемещаемого тела.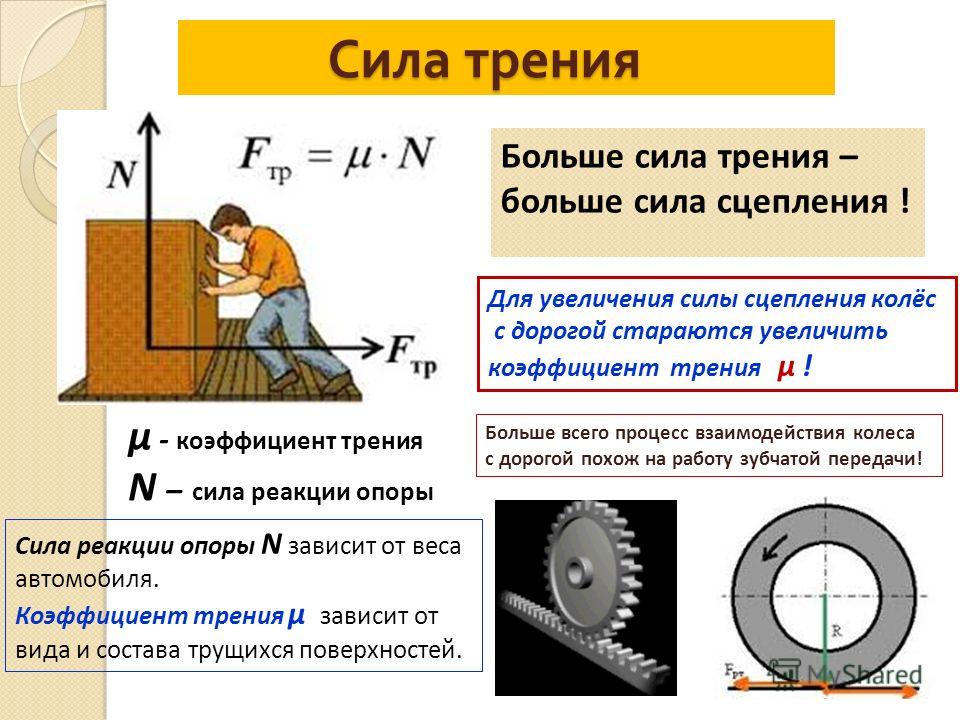

В случае неупругих деформаций вероятно следует учитывать дополнительные затраты энергии на соответствующие изменения формы тела или структуры вещества. А для сыпучих веществ на перемещаемую массу сыпучего вещества.

Количественное выражение для трения скольжения выведем исходя из работы, затрачиваемой на сжатие межмолекулярных «пружин» в направлении перпендикулярном направлению движения.

Если для определения силы и величины сжатия межмолекулярных «пружин», как было сказано выше, колебания молекул под действием тепловой энергии учитывать необходимости нет, то для определения работы по сжатию межмолекулярных «пружин». важна величина амплитуды этих колебаний. Расстояние между точками r

0 и r_min (см. рис.2) являющееся амплитудой колебаний можно обозначить как A_r. При сравнительно больших A_r, имеющих место при наиболее часто встречающихся температурах Dr <<< A_r, так как сжимающее усилие обычно распределено на очень огромное число молекул. Исходя из того, что колебания являются гармоническими, или, по крайней мере, очень близки к гармоническим, величину увеличения потенциальной энергии молекул от сжатия внешней силой межмолекулярных «пружин» можно записать, как DP _pot = F^. A_r^.2/p (формула 3), где F- внешняя сжимающая сила. В случаях, когда температура будет близка к абсолютному нулю и A_r будет очень и очень мала A_r <<< Dr, будет правильным выражение DP_pot = F^. Dr /2 (формула 4).

При перемещении тела на величину r₀ (среднее расстояние между молекулами) вся энергия DP_pot выделится, перейдя в тепловую, так как при таком перемещении разорвутся установившиеся связи («пружинки») между молекулами перемещаемого тела и молекулами поверхности перемещения. Выделившаяся энергия равна работе силы трения. В результате можно записать, что f_тр.^.r₀ = DP_pot1 + DP_pot2 , где f_тр. — сила трения; DP_pot1 и DP_pot2 — приращения внутренней потенциальной энергии соответственно перемещаемого тела и поверхности перемещения, вызванные давлением тела на поверхность. Таким образом, величина силы трения скольжения равна f_тр. = (DP_pot1 + DP_pot2) / r₀, а с учетом формулы 3 f_тр. = F^. (A_r1 + A_r2)^.2/p^.r₀ (формула 5). Выражение (A_r1 + A_r2)^.2/p^.r₀ является коэффициентом трения скольжения, т.е. k_тр. = (A_r1 + A_r2)^.2/p^.r₀ (формула 6), величина r₀ должна приниматься наименьшей из двух вариантов (поверхность, тело), при этом для материалов сложной структуры и смешанного химического состава, входящие в формулу 6 величины могут приниматься средневзвешенными с учетом процентного содержания всех компонентов.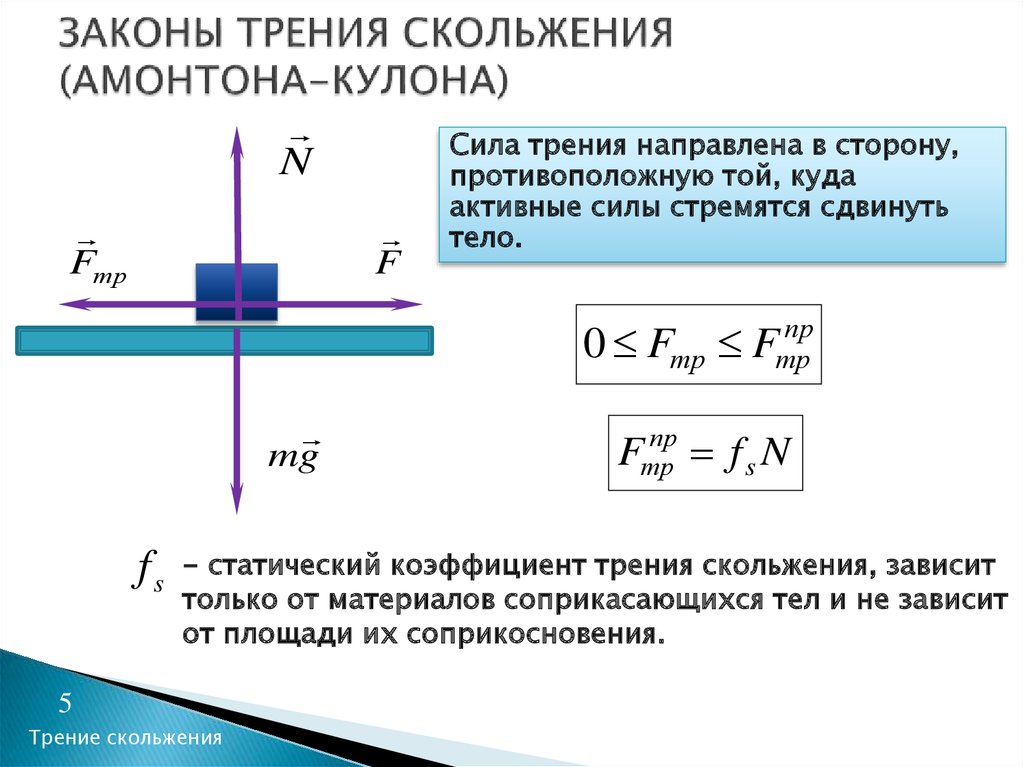

Величины A_r1 и A_r2 , зная величину внутренней энергии приходящейся на одну межмолекулярную «пружину» (Е_пр.), можно определить из формулы A_r²=2^.Е_пр./k [3, 267; 3,274]

Для случаев, когда справедлива формула 4 сила трения составит f_тр. = F^. Dr_ср./ 2r₀ (формула 7). Так как величина Dr в свою очередь зависит от величины сжимающей силы то приходящееся на одну молекулу Dr = F/(k_ж^.N), где k_ж — коэффициент жесткости межмолекулярной «пружины» в области низких температур, N — количество пар молекул сжимаемых под действием внешней силы. Величина Dr_ср. (для формулы 7) будет равна Dr_ср. = F(k_ж1^.N₁ + k_ж2^.N₂)/ k_ж1^.N₁^.k_ж2^.N₂. С малой степенью погрешности при определении N можно учитывать только молекулы находящиеся на поверхностях в пятне контакта тел, фактически важно их соотношение (соотношение плотностей). Для определения силы трения в этом случае будет справедлива формула: f_тр. = F²(k_ж1^.N₁ + k_ж2^.N₂)/ (k_ж1^.N₁^.k_ж2^.N₂^.2r₀) (формула 8). N, как правило, является очень большой величиной, практически стремящейся к бесконечности, и при близких по значению величинах N₁ и N₂ сила f_тр. в рассматриваемом случае при росте количества N стремится к нулю.

При качении также происходит сжатие межмолекулярных «пружин» под действием сил прижимающих тела друг к другу, но в отличие от скольжения энергия этого сжатия почти полностью возвращается перекатываемому телу. При качении молекулы колеса от молекул поверхности отрываются не по циклоиде, чем больше диаметр (радиус) колеса, тем больше в траектории движения молекул (в пределах деформации в месте контакта колеса и поверхности) вертикальной составляющей и меньше составляющей горизонтальной, порождающей трение аналогично скольжению. Таким образом, величина трения качения кроме величины силы F и коэффициента трения зависит также от диаметра колеса, чем больше диаметр — меньше трение, чем меньше диаметр больше трение. Кроме того, при качении за счет деформации колеса и поверхности, отталкивание молекул колеса от молекул поверхности начинается не в нижней точке циклоиды, где скорость встречи колеса с поверхностью равна нулю, а раньше, где, особенно в случаях больших деформаций, скорость имеет существенную величину, увеличивая прижимающую колесо к поверхности силу и, тем самым, дополнительно потери энергии на трение. Таким образом, трение качения зависит еще и от скорости, чем выше скорость, тем больше потери энергии на трение.

Аналогично рассмотренным выше случаям трения упругих монолитов, от сжатия межмолекулярных «пружин» зависят и величины гидродинамических и аэродинамических сопротивлений, имеющих место в жидких и газообразных средах. В виду обширности материала по этой теме их описание в объем настоящей статьи не вошло.

Литература.

1. Заднепровский Р. П. Теория трения скольжения. Волгоград; издательство «Офсет». 2005 г.
2. Каржавин В. В., Зимин А. И. Трение, износ и смазочные материалы. Учеб. пособие. Екатеринбург; РГППУ. 2003 г.
3. Зисман Г. А., Тодес О. М. Курс общей физики. Том 1. М.; издательство «Наука». 1969 г.
4. Малеев А. В. Лекции по физике твердого тела. Владимир; ВлГУ. 2015 г.

Курс общей физики, Т.1

Курс общей физики, Т.1

Савельев И. В. Курс общей физики, т. 1. Механика. Молекулярная физика: Учебное пособие.— 2-е изд., перераб.—М.: Наука. Главная редакция физико-математической литературы, 1982.— 432 с. Книга представляет собой первый том трехтомного курса общей физики, созданного заведующим кафедрой общей физики Московского инженерно-физического института, заслуженным деятелем науки и техники РСФСР, лауреатом Государственной премии, профессором И. В. Савельевым. Главная цель книги—познакомить студентов с основными идеями и методами физики. Особое внимание обращено на разъяснение смысла физических законов и на сознательное применение их. Данный курс предназначен в первую очередь для втузов с расширенной программой по физике. Однако изложение построено так, что, опустив отдельные места, эту книгу можно использовать в качестве учебного пособия для втузов с обычной программой. Оглавление ПРЕДИСЛОВИЕ МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ВВЕДЕНИЕ ЧАСТЬ 1. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ § 1. Механическое движение § 2. Некоторые сведения о векторах § 3. Скорость § 4. Ускорение § 5. Кинематика вращательного движения ГЛАВА II. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ § 6. Классическая механика. Границы ее применимости § 7. Первый закон Ньютона. Инерциальные системы отсчета § 8. Масса и импульс тела § 9. Второй закон Ньютона § 10. Единицы и размерности физических величин § 11. Третий закон Ньютона § 12. Принцип относительности Галилея § 13. Силы § 14. Упругие силы § 15. Силы трения. § 16, Сила тяжести и вес § 17. Практическое применение законов Ньютона ГЛАВА III. ЗАКОНЫ СОХРАНЕНИЯ § 18. Сохраняющиеся величины § 19. Кинетическая энергия § 20. Работа § 21. Консервативные силы § 22. Потенциальная энергия во внешнем поле сил § 23. Потенциальная энергия взаимодействия § 24. Закон сохранения энергии § 25. Энергия упругой деформации § 26. Условия равновесия механической системы § 27. Закон сохранения импульса § 28. Соударение двух тел § 29. Закон сохранения момента импульса § 30. Движение в центральном поле сил § 31. Задача двух тел ГЛАВА IV. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА § 32. Силы инерции § 33. Центробежная сила инерции § 34. Сила Кориолиса § 35. Законы сохранения в неинерциальных системах отсчета ГЛАВА V. МЕХАНИКА ТВЕРДОГО ТЁЛА § 36. Движение твердого тела § 37. Движение центра масс твердого тела § 38. Вращение тела вокруг неподвижной оси § 39. Момент инерции § 40. Понятие о тензоре инерции § 41. Кинетическая энергия вращающегося твердого тела § 42. Кинетическая энергия тела при плоском движении § 43. Применение закона динамики твердого тела § 44. Гироскопы ГЛАВА VI. ВСЕМИРНОЕ ТЯГОТЕНИЕ § 45. Закон всемирного тяготения § 46. Гравитационное поле § 47. Принцип эквивалентности § 48. Космические скорости ГЛАВА VII. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ § 49. Общие сведения о колебаниях § 50. Малые колебания § 51. Комплексные числа § 52. Линейные дифференциальные уравнения § 53. Гармонические колебания § 54. Маятник § 55. Векторная диаграмма § 56. Биения § 57. Сложение взаимно перпендикулярных колебаний § 58. Затухающие колебания § 59. Автоколебания § 60. Вынужденные колебания § 61. Параметрический резонанс ГЛАВА VIII. РЕЛЯТИВИСТСКАЯ МЕХАНИКА § 62. Специальная теория относительности § 63. Преобразования Лоренца § 64. Следствия из преобразований Лоренца § 65. Интервал § 66. Преобразование и сложение скоростей § 67. Релятивистское выражение для импульса § 68. Релятивистское выражение для энергии § 69. Преобразования импульса и энергии § 70. Взаимосвязь массы и энергии § 71. Частицы с нулевой массой покоя ГЛАВА IX. ГИДРОДИНАМИКА § 72. Линии и трубки тока. Неразрывность струи § 73. Уравнение Бернулли § 74. Истечение жидкости из отверстия § 75. Силы внутреннего трения § 76. Ламинарное и турбулентное течения § 77. Течение жидкости в круглой трубе § 78. Движение тел в жидкостях и газах ЧАСТЬ 2. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА § 79. Статистическая физика и термодинамика § 80. Масса и размеры молекул § 81. Состояние системы. Процесс § 82. Внутренняя энергия системы § 83. Первое начало термодинамики § 84. Работа, совершаемая телом при изменениях объема § 85. 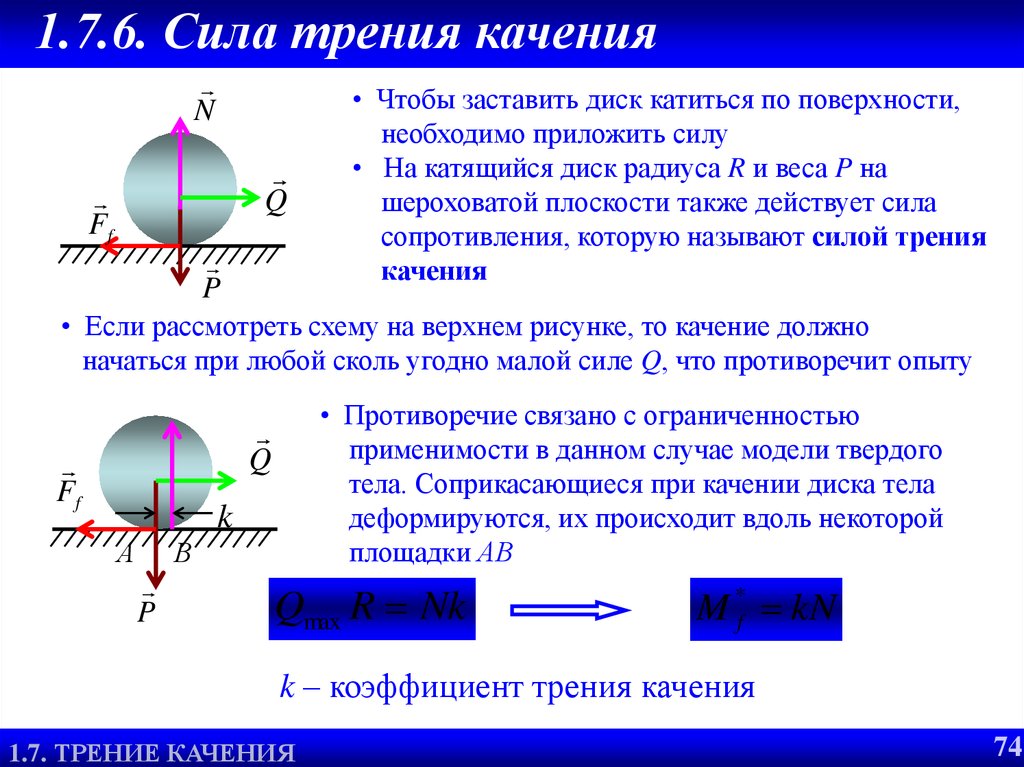Температура § 86. Уравнение состояния идеального газа § 87. Внутренняя энергия и теплоемкость идеального газа § 88. Уравнение адиабаты идеального газа § 89. Политропические процессы § 90. Работа, совершаемая идеальным газом при различных процессах § 91. Ван-дер-ваальсовский газ § 92. Барометрическая формула ГЛАВА XI. СТАТИСТИЧЕСКАЯ ФИЗИКА § 93. Некоторые сведения из теории вероятностей § 94. Характер теплового движения молекул § 95. Число ударов молекул о стенку § 96. Давление газа на стенку § 97. Средняя энергия молекул § 98. Распределение Максвелла § 99. Экспериментальная проверка закона распределения Максвелла § 100. Распределение Больцмана § 101. Определение Перреном числа Авогадро § 102. Макро- и микросостояния. Статистический вес § 103. Энтропия ГЛАВА XII. ТЕРМОДИНАМИКА § 104. Основные законы термодинамики § 105. Цикл Карно § 106. Термодинамическая шкала температур § 107. Примеры на вычисление энтропии § 108. Некоторые применения энтропии § 109. Термодинамические потенциалы ГЛАВА XIII. КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ § 110. Отличительные черты кристаллического состояния § 111. Классификация кристаллов § 112. Физические типы кристаллических решеток § 113. Дефекты в кристаллах § 114. Теплоемкость кристаллов ГЛАВА XIV. ЖИДКОЕ СОСТОЯНИЕ § 115. Строение жидкостей § 116. Поверхностное натяжение § 117. Давление под изогнутой поверхностью жидкости § 118. Явления на границе жидкости и твердого тела § 119. Капиллярные явления ГЛАВА XV. ФАЗОВЫЕ РАВНОВЕСИЯ И ПРЕВРАЩЕНИЯ § 121. Испарение и конденсация § 122. Равновесие жидкости и насыщенного пара § 123. Критическое состояние § 124. Пересыщенный пар и перегретая жидкость § 125. Плавление и кристаллизация § 126. Уравнение Клапейрона—Клаузиуса § 127. Тройная точка. Диаграмма состояния ГЛАВА XVI. ФИЗИЧЕСКАЯ КИНЕТИКА § 128. Явления переноса § 129. Средняя длина свободного пробега § 130. Диффузия в газах § 131. Теплопроводность газов § 132. Вязкость газов § 133. Ультраразреженные газы § 134. Эффузия ПРИЛОЖЕНИЯ I. Вычисление некоторых интегралов II. Формула Стирлинга III. Симметричные тензоры второго ранга

Возвращение к Да Винчи — ScienceDaily

Новости науки

от исследовательских организаций

---

Дата:

1 марта 2018 г.

Источник:

Университет Амстердама (UVA)

Резюме:

На долю трения приходится около двадцати процентов мирового потребления энергии. Основная причина этого заключается в том, что силы трения замедляют движение соприкасающихся поверхностей: подумайте о движущихся частях автомобильного двигателя. Более пятисот лет назад Леонардо да Винчи был первым, кто систематически изучал трение. Главный результат да Винчи до сих пор используется многими инженерами: трение пропорционально нормальной силе.

Поделиться:

Фейсбук Твиттер Пинтерест LinkedIN Электронная почта

ПОЛНАЯ ИСТОРИЯ

---

На трение приходится около двадцати процентов мирового потребления энергии. Основная причина этого заключается в том, что силы трения замедляют движение соприкасающихся поверхностей: подумайте о движущихся частях автомобильного двигателя. Более пятисот лет назад Леонардо да Винчи был первым, кто систематически изучал трение. Главный результат да Винчи до сих пор используется многими инженерами: трение пропорционально нормальной силе. То есть: когда два предмета прижимаются друг к другу в два раза сильнее, трение также удваивается. Исследователи из Института физики Университета штата Калифорния, Института молекулярных наук имени Вант-Гоффа Университета штата Калифорния, Центра микротрибологии µTC во Фрайбурге и Технологического института Карлсруэ теперь более тщательно изучили эту пропорциональность между трением и нормальной силой, используя молекулы, которые люминесцируют под давлением. .

реклама

---

В понимании трения ключевую роль играет понятие шероховатости поверхности. В молекулярном масштабе почти все поверхности шероховатые: вблизи такая поверхность выглядит как горный пейзаж. Трение возникает только в тех местах, где самые высокие вершины холмов на двух скользящих поверхностях соприкасаются друг с другом.

Чтобы детально изучить этот процесс, исследователи разработали модельный эксперимент, в котором шероховатая сферическая поверхность контактировала с плоской стеклянной поверхностью. Особенностью этого эксперимента было то, что на поверхность стекла наносился один слой контактно-чувствительных молекул красителя. Эти молекулы излучают флуоресцентный свет, когда на них оказывается давление. Это позволило исследователям очень точно определить, где шероховатая сферическая поверхность соприкасалась с плоской стеклянной поверхностью (см. рисунок 1), и как изменился контакт при приложении большего давления.

При приложении большей нормальной силы (давления) «вершины холмов» на сферической поверхности становятся более плоскими, что приводит к увеличению площади контакта между сферой и стеклянной пластиной. Обычная интерпретация пропорциональности Да Винчи между трением и нормальной силой состоит в том, что обе силы пропорциональны этой площади контакта: приложение двойного давления приводит к удвоению площади контакта и, следовательно, к удвоению трения. Несколько теорий предсказывают связь между площадью контакта и нормальной силой, но до сих пор эти теории не могли быть проверены с высокой точностью. Теперь исследователи показывают, что существующие теории не оправдывают ожиданий: трение пропорционально площади контакта, как и ожидалось, но площадь контакта оказывается непропорциональной нормальной силе.

Результаты исследований показывают, что для лучшего понимания трения требуются изменения в существующих моделях, чтобы можно было воспроизвести измеренное соотношение между площадью контакта и нормальной силой. Результаты были опубликованы на этой неделе в Nature Communications.

реклама

---

История Источник:

Материалы предоставлены Universiteit van Amsterdam (UVA) . Примечание. Содержимое можно редактировать по стилю и длине.

---

Ссылка на журнал :

1. Б. Вебер, Т. Сухина, Т. Юнге, Л. Пастевка, А. М. Брауэр, Д. Бонн. Молекулярные зонды выявляют отклонения от закона Амонтона в фрикционных контактах с множеством шероховатостей . Nature Communications , 2018; 9 (1) DOI: 10.1038/s41467-018-02981-y

---

Цитировать эту страницу :

• MLA
• АПА
• Чикаго

Университет Амстердама (UVA). «Трение: новый взгляд на да Винчи». ScienceDaily. ScienceDaily, 1 марта 2018 г. .

Университет Амстердама (UVA). (2018, 1 марта). Трение: новый взгляд на да Винчи. ScienceDaily . Получено 7 марта 2023 г. с сайта www.sciencedaily.com/releases/2018/03/180301091836.htm

Universiteit van Amsterdam (UVA). «Трение: новый взгляд на да Винчи». ScienceDaily. www.sciencedaily.com/releases/2018/03/180301091836.htm (по состоянию на 7 марта 2023 г.).

Узнать больше

от ScienceDaily

---

ПОХОЖИЕ ИСТОРИИ

---

реклама

---

Трение — О трибологии

Что такое трение?

Трение Определение

Трение – это сила, действующая против направления относительного движения. Трение возрастает на границе раздела тел, но может развиваться и внутри тела. Примеры последнего включают воздушное и гидродинамическое трение, когда трение возрастает между слоями жидкости. Трение — это не фундаментальная сила, а скорее проявление электромагнитных и гравитационных сил. Источников трения много: деформация поверхностей, адгезия, капиллярные силы, силы Ван-дер-Ваальса, химическая связь и др. Сила трения неконсервативна, и энергия, затрачиваемая на преодоление трения, теряется. Потери на трение снижают энергоэффективность многих механических устройств. В недавнем отчете о потреблении энергии из-за потерь на трение в легковых автомобилях указано, что только 21,5% потенциальной энергии топлива используется для движения автомобиля, тогда как прямые потери на трение составляют 33% (28%, если исключить поломку). Из этих потерь 35 % идет на преодоление трения шины о дорогу, 35 % — на преодоление трения двигателя, 15 % — на трение в трансмиссии и 15 % — на контактное трение тормозов. Таким образом, одной из основных задач современной трибологии является поиск новых технологий для снижения трения и повышения энергоэффективности.

Обычно трение может быть сухим или смазанным. Для подавляющего большинства поверхностей, встречающихся в природе и используемых в промышленности, источником сухого трения являются несовершенства поверхностей. Оказывается, даже зеркально блестящие поверхности на самом деле не плоские, по крайней мере, на микро- и наномасштабах, а содержат холмы и долины. Эти дефекты называются шероховатостью поверхности. Типичный профиль поверхности гладкой чистой стеклянной пластины, измеренный атомно-силовой микроскопией, показан ниже. Профиль высоты АСМ и поперечное сечение чистой стеклянной пластины

Когда эту шероховатую поверхность тянут по другой шероховатой поверхности, эти долины и холмы будут сцепляться друг с другом, деформироваться и, следовательно, препятствовать движению. Классическим примером блокировки являются поверхности типа застрявших картонных коробок для яиц, которые трудно скользить друг относительно друга (из-за высокого трения), как показано на рисунке ниже. Сила, необходимая для преодоления этой блокировки, называется трением. Поверхности типа яичного картона. Источник: https://en.wikipedia.org/wiki/Superlubricity

В то же время создание атомарно-плоских поверхностей не решает проблему снижения трения. На самом деле уменьшение шероховатости до атомарно-плоского уровня для технических материалов, таких как, например, стали, приводит к гораздо более высокому сухому трению! И происходит это за счет увеличения сил сцепления (ван-дер-ваальсовых взаимодействий, капиллярных сил и т. д. ).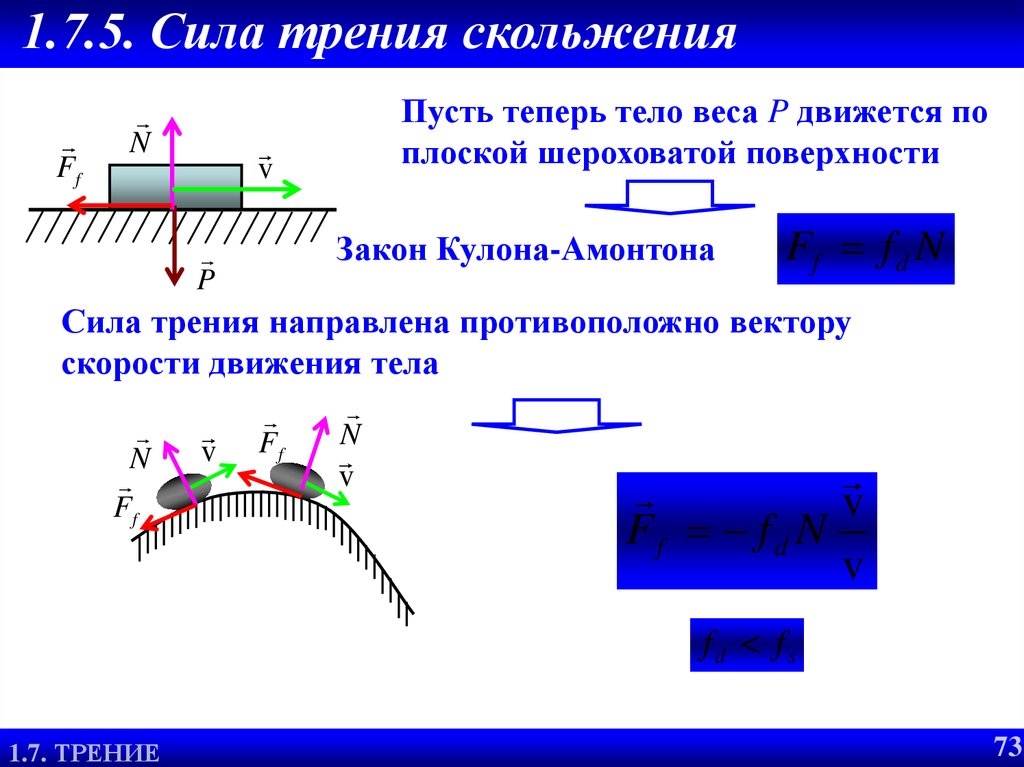

Для уменьшения трения используется теория смазки (гидродинамическая или упругогидродинамическая). Этот подход создает смазочную пленку между шероховатыми поверхностями, и прямой контакт между шероховатыми поверхностями либо устраняется, либо сводится к минимуму. Трение в этом случае определяется главным образом сдвигом слоев смазки, а не сдвигом твердых тел, как показано на рисунке ниже:

Смазочная пленка (из: Lubrication for Industry, Ken Bannister, Industrial Press)

В этом случае эффекты блокировки и адгезии уменьшаются. Для большинства технических материалов сухое трение больше, чем трение со смазкой, поскольку прочность твердых тел на сдвиг обычно больше. Однако теория достигла своего фундаментального предела (коэффициент трения 0,01-0,04) и не может быть использована для дальнейшего снижения трения. Поэтому исследователи ищут другие способы уменьшить трение, и недавно было сообщено о нескольких случаях сверхсмазывающей способности (коэффициент трения значительно ниже 0,01) (см.