воздействуем с силой, направленной под углом
В этой статье силу, с которой воздействуют на тело, раскладывают на проекции по координатным осям. Выбирать направления осей удобно так, чтобы раскладывать приходилось одну-две силы, то есть чтобы большинство векторов сил были бы коллинеарны осям.
Задача 1. Коэффициент трения скольжения ящика массой 100 кг о пол равен 0,2. Ящик тянут за веревку, проходящую через его центр тяжести. Веревка образует угол  с горизонтом. Какую силу надо прикладывать, чтобы ящик двигался равномерно? Какова при этом сила трения скольжения?
с горизонтом. Какую силу надо прикладывать, чтобы ящик двигался равномерно? Какова при этом сила трения скольжения?

Введем систему координат: ось  направим горизонтально, а ось
направим горизонтально, а ось  – вертикально вверх. Запишем уравнения по осям по второму закону:
– вертикально вверх. Запишем уравнения по осям по второму закону:
По оси  :
:
![Rendered by QuickLaTeX.com \[F\cos{\alpha}-F_{tr}=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-149e84b968b7993458762f9d3cdcfb60_l3.png)
По оси  :
:
![Rendered by QuickLaTeX.com \[F\sin{\alpha}+N-mg=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-87fb295df88a1bf8f9aab3ef0192b7be_l3.png)
Из второго уравнения найдем силу реакции опоры:
![Rendered by QuickLaTeX.com \[N=mg- F\sin{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c2c47116cfe9ce720347fc9ce5e5ead6_l3.png)
Сила трения равна
![Rendered by QuickLaTeX.com \[F_{tr}= \mu N=\mu (mg- F\sin{\alpha})\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-20eb0303629863bf6dedb82294bda414_l3.png)
С другой стороны,
![Rendered by QuickLaTeX.com \[F_{tr} = F\cos{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-131b4adf46568f4aa28272dc453cb867_l3.png)
Приравняв, можем найти силу  :
:
![Rendered by QuickLaTeX.com \[F\cos{\alpha}=\mu (mg- F\sin{\alpha})\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b6636148ad7fe0db951fa9466c6cacb9_l3.png)
![Rendered by QuickLaTeX.com \[F\cos{\alpha}=\mu mg- \mu F\sin{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f48fbfa9bf378ddd19297d71eec407ea_l3.png)
![Rendered by QuickLaTeX.com \[F\cos{\alpha}+ \mu F\sin{\alpha}=\mu mg\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-965508c5340a43c504906c25d4936a8a_l3.png)
![Rendered by QuickLaTeX.com \[F(\cos{\alpha}+ \mu\sin{\alpha})=\mu mg\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-129a38cd677e425601b8ffca5a70c507_l3.png)
![Rendered by QuickLaTeX.com \[F=\frac{\mu mg }{\cos{\alpha}+ \mu\sin{\alpha}}=\frac{0,2\cdot 100\cdot 9,8}{\frac{\sqrt{3}}{2}+ 0,2\cdot\frac{1}{2}}}=\frac{196}{0,965}=203\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6864426086fc9e8705be57bac8589458_l3.png)
Определим силу трения:
![Rendered by QuickLaTeX.com \[F_{tr} = F\cos{\alpha}=203 \cdot \frac{\sqrt{3}}{2}=175,6\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b71f09bd5c7d0fc2f7ac6b44b8df5676_l3.png)
Ответ:  Н,
Н,  Н.
Н.
Задача 2. Тело массой 10 кг тянут по горизонтальной поверхности, прикладывая силу 50 Н, направленную под углом  к горизонту. Ускорение тела равно 3,5 м/с
к горизонту. Ускорение тела равно 3,5 м/с . Найдите коэффициент трения между телом и поверхностью.
. Найдите коэффициент трения между телом и поверхностью.
Введем систему координат: ось  направим горизонтально, а ось
направим горизонтально, а ось  – вертикально вверх. Запишем уравнения по осям по второму закону:
– вертикально вверх. Запишем уравнения по осям по второму закону:
По оси  :
:
![Rendered by QuickLaTeX.com \[F\cos{\alpha}-F_{tr}=ma\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a2115b070e0e646f01b568c161bd5c1c_l3.png)
По оси  :
:
![Rendered by QuickLaTeX.com \[F\sin{\alpha}+N-mg=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-87fb295df88a1bf8f9aab3ef0192b7be_l3.png)
Из второго уравнения найдем силу реакции опоры:
![Rendered by QuickLaTeX.com \[N=mg- F\sin{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c2c47116cfe9ce720347fc9ce5e5ead6_l3.png)
Сила трения равна
![Rendered by QuickLaTeX.com \[F_{tr}= \mu N=\mu (mg- F\sin{\alpha})\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-20eb0303629863bf6dedb82294bda414_l3.png)
С другой стороны,
![Rendered by QuickLaTeX.com \[F_{tr} = F\cos{\alpha}-ma\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7b1df4e82b02bc297843fe8d6e61e006_l3.png)
Приравняв, можем найти силу коэффициент трения:
![Rendered by QuickLaTeX.com \[F\cos{\alpha}-ma=\mu (mg- F\sin{\alpha})\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-09387571835fd00b4ca553981a01ee10_l3.png)
![Rendered by QuickLaTeX.com \[\mu=\frac{ F\cos{\alpha}-ma }{ mg- F\sin{\alpha}}=\frac{50 \cdot\sqrt{3}}{2}-10\cdot 3,5}{10\cdot 9,8-50\cdot\frac{1}{2}}=0,11\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-64053066f25ccf7bf13a1ad8f5169e35_l3.png)
Ответ:  .
.
Задача 3. Тело массой  прижимают к потолку с силой
прижимают к потолку с силой  , направленной под углом
, направленной под углом  к горизонту. При этом тело неподвижно. Чему равен коэффициент трения между телом и потолком?
к горизонту. При этом тело неподвижно. Чему равен коэффициент трения между телом и потолком?

Введем систему координат: ось  направим горизонтально, а ось
направим горизонтально, а ось  – вертикально вверх. Запишем уравнения по осям по второму закону:
– вертикально вверх. Запишем уравнения по осям по второму закону:
По оси  :
:
![Rendered by QuickLaTeX.com \[F\cos{\alpha}-F_{tr}=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-149e84b968b7993458762f9d3cdcfb60_l3.png)
По оси  :
:
![Rendered by QuickLaTeX.com \[F\sin{\alpha}- mg -N=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d199a65804f367bdaef3b4fa39251e1d_l3.png)
Вспомним, что  . Силу реакции найдем из второго уравнения:
. Силу реакции найдем из второго уравнения:
![Rendered by QuickLaTeX.com \[N= F\sin{\alpha}- mg\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b4e938305e363663aa3b7a421689dab6_l3.png)
![Rendered by QuickLaTeX.com \[F_{tr}=\mu (F\sin{\alpha}- mg)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9f4d67717816d9f146de3c7724ffd0a7_l3.png)
С другой стороны,
![Rendered by QuickLaTeX.com \[F_{tr} = F\cos{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-131b4adf46568f4aa28272dc453cb867_l3.png)
Приравняв, можем найти силу коэффициент трения:
![Rendered by QuickLaTeX.com \[F\cos{\alpha}=\mu (F\sin{\alpha}- mg)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-72e989016fe99f308191f456818f1cf6_l3.png)
![Rendered by QuickLaTeX.com \[\mu=\frac{ F\cos{\alpha} }{ F\sin{\alpha- mg }}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-11fd2d5d13bdcff67b21faac53aa4397_l3.png)
Ответ: 
определение, формулы – простое и доходчивое объяснение
Определение силы тренияСила трения возникает из соприкосновения поверхностей двух физических тел, пребывающих в движении по отношению друг к другу. Теория трения издревле волновала умы человечества, древние инженеры: строители Египетских пирамид, Стоунхенджа в Англии или таинственных каменных истуканов на острове Пасхе, все они (как впрочем, и их современные коллеги) решали насущную проблему, связанную с трением и тем как его максимально уменьшить. Ведь именно сила трения делает трудным перемещение тяжелых грузов по земле (тех же камней для пирамид или Стоунхенджа), и чтобы облегчить эту задачу, нашими далекими предками было придумано такое полезное изобретение как колесо и сделано множество других важных открытий. В нашей статье мы посмотрим на силу трения в физическом аспекте, разберем, как действует она на те или иные тела, какие есть ее виды и формулы расчета.
Определение силы трения
Что такое сила трения? Классическое определение звучит так: сила трения – это сила, появляющаяся при соприкосновении двух тел во время движения и препятствующая этому самому движению. Иными словами, чем больше сила трения между телами, тем труднее их двигать относительно друг друга. Что же касается самой физической природы трения, то оно появляется как результат взаимодействия между атомами и молекулами тел, соприкасающихся между собой.
Также стоит заметить, что при трении двух тел на них действует третий закон Ньютона: сила трения, действующая на первое тело (тело А), равна силе трения, действующей на второе тело (тело Б), только по модулю эти силы имеют противоположное направление.

На этой картинке, сила трения, действующая на холодильник, равна силе трения, действующей на пол, но направлены эти силы в противоположные стороны.
Виды силы трения
В зависимости от характера движения тел различают такие виды сил трения как:
- Покоя. Сила трения покоя возникает при соприкосновении двух тел, которые, однако, не движутся относительно друг друга, и имеет нулевое значение.
- Скольжения. Сила трения скольжения – наиболее классическая иллюстрация действия трения, возникает при скольжении тел относительно друг друга. На ее величину влияет масса тела (чем она больше, тем больше сила трения), характер поверхности (разумеется, при скольжении по льду сила трения будет в разы меньше чем при скольжении по земле).
- Качения. Сила трения качения появляется, когда одно тело катится по поверхности другого, например, при езде на велосипеде или автомобиле. При качении сила трения гораздо меньше, чем при скольжении. Это опытным, эмпирическим путем установили еще те далекие наши предки, которые изобрели колесо – величайшее изобретение в истории науки и техники.
- Верчения. Сила трения верчения проявляется при вращении одного тела по поверхности другого.

Что же касается самого трения то и оно бывает нескольких видов:
- Сухое – проявляется при соприкосновении твердых поверхностей.
- Вязкое, также подобное трение называют жидкостным, появляется при соприкосновении твердого тела c жидкостью либо газом. Например, на корабль, плывущий по воде, как и на поверхность воды, действует вязкое (жидкостное) трение. Сила вязкого трения обычно гораздо меньше силы сухого трения.
- Смешанное, возникает, когда между поверхностями, которые соприкасаются, есть слой смазки.
Интересный факт: при осаде Константинополя в 1453 году турки, чтобы обойти специальную цепь, преграждающую путь турецким кораблям в залив Золотой Рог перетянули их по суше. А для того, чтобы уменьшить силу трения при перемещении больших тяжелых военных кораблей сделали настил из деревянных рельсов, который обильно смазали салом. Таким образом, благодаря смазке и смешанному трению, сила которого гораздо меньше, чем при трении сухом, турки удачно воплотили свой замысел, приведя защитников Константинополя в подлинное смятение.

Султан Мехмед II наблюдает за перевозкой своих судов.
Как видите, знание законов физики и механики не раз и не два находило свое практическое воплощение в реальной жизни.
Но вернемся от истории снова к физике, трение также разделяют на внешнее и внутреннее. Внешнее трение характерно для взаимодействия исключительно твердых тел. Внутреннее трение характеризуется вязкостью и возникает при взаимодействии жидкостей или газов, а такое взаимодействие может происходить внутри условно одного тела. Например, в водах мирового океана есть разные течения, с более холодной или более теплой водой, при взаимодействии этих течений между ними и возникает внутреннее трение.
Как найти силу трения?
Чтобы рассчитать силу трения необходимо знать коэффициент трения k, который зависит от характера поверхности. Коэффициент трения – постоянная величина и его значение можно узнать из специальной таблицы.

Помимо коэффициента трения необходимо знать силу реакцию опоры N, которая, по сути, равна силе тяжести (гравитации) зависящей от массы тела (m) и ускорения свободного падения. Ее формула будет иметь следующий вид:
N = m * g
Где m – масса тела, а g – ускорение свободного падения, это постоянная величина равная 9,8 м/с2.
Формула силы трения
Сила трения высчитывается путем произведения реакции опоры N и коэффициента трения k. Формула силы трения будет иметь следующий вид:
Fтр = k * N.
В некоторых формулах коэффициент трения k обозначается символом µ.
Написанные выше расчеты справедливы в самом простом случае, когда тело лежит на строго горизонтальной поверхности.

Если же движение происходит по наклонной плоскости, то расчеты силы трения несколько усложняются. На тело, как и раньше, действует сила гравитации и реакция опоры поверхности, но не в одном направлении.

Таким образом, формула силы трения для тела, которое движется по наклонной поверхности, будет иметь следующий вид:
Fтр = k * m * g * cosα.
Где k – коэффициент трения, m – масса тела, g гравитационная постоянная (помним, что она равна 9,8 м/с2), cosα – отношение катета, прилежащего к углу, к гипотенузе треугольника (косинус).

При определении силы трения на наклонных поверхностях ярко проявляется связь между физикой и геометрией.
Рекомендованная литература и полезные ссылки
- Сила трения. ЗФТШ, МФТИ. Дата обращения 14 февраля 2019.
- Енохович А. С. Справочник по физике. — Просвещение, 1978. — С. 85. — 416 с.
- Зайцев А. К. Основы учения о трении, износе и смазке машин. Часть 1. Трение в машинах. Теория, расчет и конструкция подшипников и подпятников скольжения. Машгиз. М.-Л. — 1947. 256 с.
- Bowden F. P., Tabor D. The Friction and Lubrication of Solids. Oxford University Press, 2001.
Persson Bo N. J.: Sliding Friction. Physical Principles and Applications. Springer, 2002. - Popov V. L. Kontaktmechanik und Reibung. Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation, Springer, 2009.
- Rabinowicz E. Friction and Wear of Materials. Wiley-Interscience, 1995.
Сила трения, видео
И в завершении образовательное видео по теме нашей статьи.

Автор: Павел Чайка, главный редактор журнала Познавайка
При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту [email protected] или в Фейсбук, с уважением автор.
Решение задач на движение тел по наклонной плоскости. Видеоурок. Физика 11 Класс
Мы ежедневно сталкиваемся с движением по наклонной плоскости, когда транспорт едет с горы или в гору, при проведении лабораторных работ, и сегодня мы рассмотрим, как решаются задачи на движение тел по наклонной плоскости.
Брусок находится на наклонной плоскости и может скользить вниз при наличии трения, на него будут действовать сила притяжения к земле, сила реакции опоры и сила трения (Рис. 1).
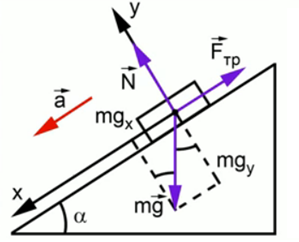
Рис. 1. Получение стандартного уравнения движения тел по наклонной плоскости
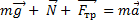
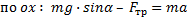
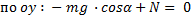
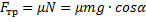
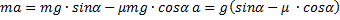
Векторная сумма этих трех сил будет равна произведению массы на ускорение. Координатная ось 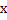
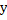 будет перпендикулярна оси х, соответственно, она совпадает по направлению с силой реакции опоры.
будет перпендикулярна оси х, соответственно, она совпадает по направлению с силой реакции опоры.Тогда в проекциях на ось 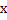
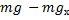 противолежащая углу
противолежащая углу 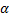 , как мы помним, углы со взаимно перпендикулярными сторонами равны,
, как мы помним, углы со взаимно перпендикулярными сторонами равны, 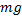
По оси 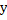 проецируются две силы:
проецируются две силы: 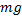
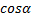 со знаком «минус», так как проекция направлена против оси
со знаком «минус», так как проекция направлена против оси 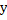 , и сила реакции опоры.
, и сила реакции опоры.Находим силу трения через произведение коэффициента трения и силы реакции опоры, которую находим из второго уравнения.
Подставляя это выражение силы трения в уравнение по оси 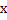
Тело скользит равномерно по наклонной плоскости с углом наклона 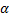 . Чему равен коэффициент трения?
. Чему равен коэффициент трения?
1. 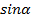 2.
2. 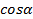 3.
3. 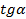 4.
4. 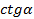
Составляем краткую запись условия задачи и решаем:
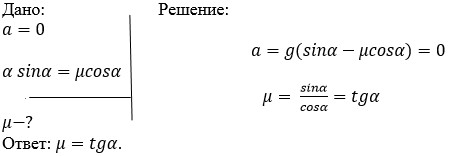
Записываем стандартное уравнение движения тела по наклонной плоскости, ускорение в данном случае будет равно нулю, так как тело движется равномерно по наклонной плоскости. Так как 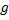 у нас не может быть равно нулю, значит, нулю будет равна разность в скобочках, отсюда мы и находим коэффициент трения, который будет равен
у нас не может быть равно нулю, значит, нулю будет равна разность в скобочках, отсюда мы и находим коэффициент трения, который будет равен 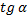 , по выборке это ответ 3.
, по выборке это ответ 3.
Троллейбус массой 12 т движется равномерно под гору с уклоном 0,05 рад при силе тяги 4 кН. Определить силу сопротивления движению.
Записываем краткое условие задачи и выполняем поясняющий чертеж (рис. 2):
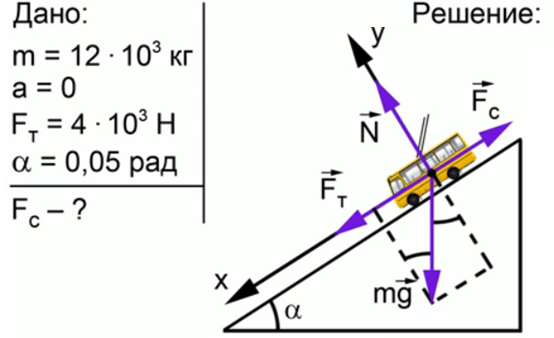
Рис. 2. Решение задачи 2
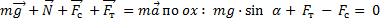 при
при 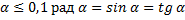
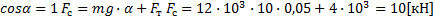
Ответ: 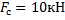 .
.
Запишем общее уравнение динамики по второму закону Ньютона и в проекции ох, необходимо помнить, что если угол α меньше или равен 0,1 рад, то в задачах по физике можно применять равенство, где угол 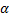 численно равен
численно равен 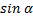 и равен
и равен 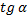 , а
, а 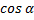 равен единице. В таком случае мы можем выразить силу сопротивления через уравнение и, подставив значения, получим, что
равен единице. В таком случае мы можем выразить силу сопротивления через уравнение и, подставив значения, получим, что 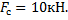
На наклонной плоскости с углом 300 находится брусок массой m, на который воздействует горизонтальная сила, равная mg/2, прижимающая брусок к поверхности плоскости. С каким ускорением будет двигаться брусок при коэффициенте трения, равном 0,065?
Запишем краткое условие задачи и поясняющий чертеж (рис. 3):
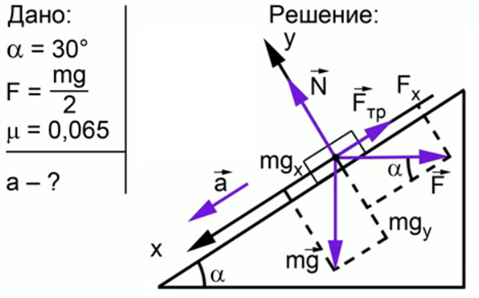
Рис. 3. Решение задачи 3
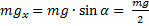 ;
; 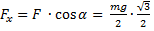 ;
; 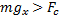
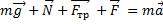
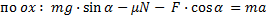
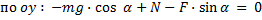
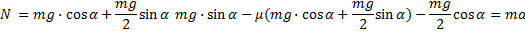
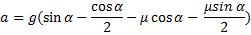
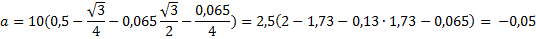
Ответ : 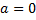 .
.
К бруску приложено несколько сил. Горизонтальная сила, прижимающая брусок к плоскости, направлена в одну сторону, сила тяжести действует так, что брусок должен двигаться в другую сторону, поэтому необходимо вычислить силы, которые могут подействовать на брусок, сдвинув его с места. Сила 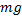 имеет проекцию
имеет проекцию 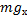 , которая будет равна
, которая будет равна 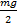 , так как
, так как 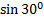 равен
равен  . Сила
. Сила 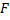 пытается сдвинуть брусок вверх по наклонной плоскости, но она имеет проекцию
пытается сдвинуть брусок вверх по наклонной плоскости, но она имеет проекцию 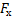 , которая, в свою очередь, равна произведению
, которая, в свою очередь, равна произведению 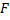 на
на 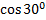 , который меньше единицы. В таком случае
, который меньше единицы. В таком случае 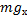 будет больше силы, действующей на тело, это означает, что брусок будет двигаться вниз и сила трения будет направлена вверх. Применив уравнение динамики по второму закону Ньютона и спроецировав его на координатные оси, мы выразим силу реакции опоры и подставим в уравнение по оси
будет больше силы, действующей на тело, это означает, что брусок будет двигаться вниз и сила трения будет направлена вверх. Применив уравнение динамики по второму закону Ньютона и спроецировав его на координатные оси, мы выразим силу реакции опоры и подставим в уравнение по оси 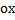 , откуда и получим выражение для ускорения.
, откуда и получим выражение для ускорения.
Подставляя числовые значения, определим, что ускорение будет отрицательным. Это значит, что тело не может двигаться вниз по наклонной плоскости, но и при наличии силы притяжения и силы, прижимающей брусок, тело не может двигаться вверх по наклонной плоскости. Это говорит о том, что ускорение равно нулю, то есть тело могло бы двигаться вниз, но силе тяжести не удается преодолеть возникающую при этом силу трения. Сила трения не будет достигать своего максимального значения, будет принимать несколько меньшее значение, а ускорение тела будет равно нулю.
Мы разобрали основные типы задач на движение тел по наклонной плоскости, использование основных законов механики для различных способов решения задач не только на уроках физики, но даже в практической и повседневной жизни.
Список литературы
- Тихомирова С.А., Яворский Б.М. Физика (базовый уровень) – М.: Мнемозина, 2012.
- Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. – М.: Мнемозина, 2014.
- Кикоин И.К., Кикоин А.К. Физика-9. – М.: Просвещение, 1990.
Домашнее задание
- Каким законом мы пользуемся при составлении уравнений?
- Какое равенство используется при решении задач, когда угол меньше или равен 0,1 рад?
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Dist-tutor.info (Источник).
- Интернет-портал Repetitors.info (Источник).
- Интернет-портал Bambookes.ru (Источник).
Трение и движение по окружности
В этой статье собраны задачи, затрагивающие одновременно как тему “сила трения”, так и тему “движение по окружности”, придется вспомнить, что такое центробежная сила и как рассчитывается нормальное ускорение.
Задача 1. На горизонтальной дороге автомобиль делает поворот радиусом 16 м. Какова наибольшая скорость, которую может развить автомобиль, чтобы его не занесло, если коэффициент трения скольжения колес о дорогу равен 0,4? Во сколько раз изменится эта скорость зимой, когда коэффициент трения станет меньше в 4 раза?

К задаче 1
Чтобы автомобиль не занесло, необходимо чтобы сила трения была не меньше, чем центробежная сила. Поэтому
![Rendered by QuickLaTeX.com \[F_{n}=\frac{m \upsilon^2}{R}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-18dde7fffe4ba06def4a39a165225d24_l3.png)
![Rendered by QuickLaTeX.com \[F_{tr}=\mu m g\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a26c8cb9b04618750bdd8d9278ffe82b_l3.png)
Приравняем:
![Rendered by QuickLaTeX.com \[\frac{m \upsilon^2}{R}=\mu m g\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-98609f8f7daea6af7bf6f1efef18384c_l3.png)
Откуда скорость:
![Rendered by QuickLaTeX.com \[\upsilon^2=\mu g R\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3d433f64163ac98e4f7559398d1eecf0_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon=\sqrt{\mu g R }=\sqrt{0,4 \cdot 9,8 \cdot 16}=7,9\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-fc75c74c2aabe564121eb95c61e1fb70_l3.png)
Если коэффициент трения уменьшится вчетверо, скорость придется уменьшить вдвое:  м/с.
м/с.
Ответ:  м/с,
м/с,  м/с.
м/с.
Задача 2. Горизонтально расположенный диск проигрывателя вращается с частотой 78 об/мин. На него поместили небольшой предмет. Расстояние от оси вращения до предмета составляет 7 см. На этом расстоянии предмет удерживается на диске. Каков коэффициент трения между предметом и диском?
Необходимо, чтобы сила трения была не меньше, чем центробежная сила. Поэтому
![Rendered by QuickLaTeX.com \[F_{n}=\frac{m \upsilon^2}{R}=m \omega^2 R\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-fbb2a8e06f110d32648417dc99bcd997_l3.png)
![Rendered by QuickLaTeX.com \[F_{tr}=\mu m g\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a26c8cb9b04618750bdd8d9278ffe82b_l3.png)
Приравняем:
![Rendered by QuickLaTeX.com \[m \omega^2 R =\mu m g\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a8188b2aab7fe188f1c6971df575b2b9_l3.png)
![Rendered by QuickLaTeX.com \[\omega^2 R =\mu g\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0c48c90d0c261b1a3c6048f12b5f1261_l3.png)
![Rendered by QuickLaTeX.com \[4 \pi^2 \nu^2 R=\mu g\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e4b306467930ad25d0386c9ca3ff1aae_l3.png)
Зная частоту вращения, определим коэффициент трения:
![Rendered by QuickLaTeX.com \[\mu=\frac{4 \pi^2 \nu^2 R }{g}=\frac{4 \cdot 3,14^2 \cdot1,3^2 \cdot 0,07 }{9,8}=0,48\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-57cf2cb2c0b866593ea48d75146ce00a_l3.png)
Ответ:  .
.
Задача 3. Определите, какого радиуса круг может описать велосипедист, если он едет со скоростью 25 км/ч, а предельный угол наклона велосипедиста к земле равен  ?
?

К задаче 3
Чтобы велосипедиста не занесло, необходимо чтобы сила трения была не меньше, чем центробежная сила. Но колесо наклонено под углом  , поэтому введем систему координат (ось
, поэтому введем систему координат (ось  – горизонтальна, ось
– горизонтальна, ось  – направлена вертикально вверх):
– направлена вертикально вверх):
![Rendered by QuickLaTeX.com \[N=mg\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8ff39fc4dae72e75ebafeb897ad91d5f_l3.png)
![Rendered by QuickLaTeX.com \[\operatorname{ctg}{\alpha}=\frac{ F_{tr}}{N}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ac123e97130305a46a2224b49fe69da7_l3.png)
Следовательно, так как по определению  , то
, то
![Rendered by QuickLaTeX.com \[\mu=\operatorname{ctg}{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a32cfaa0554278c85d85b29c5764c2df_l3.png)
Теперь определим радиус из условия равенства силы трения и центробежной силы:
![Rendered by QuickLaTeX.com \[F_{n}=F_{tr}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6682a9dc38178039ee722e7a1cafa914_l3.png)
Приравняем:
![Rendered by QuickLaTeX.com \[\frac{m \upsilon^2}{R}= mg \operatorname{ctg}{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3ef36b2dba04342ee2871f5ddb2758fe_l3.png)
![Rendered by QuickLaTeX.com \[R=\frac{ \upsilon^2}{ g \operatorname{ctg}{\alpha}}=\frac{ \upsilon^2\operatorname{tg}{\alpha}}{ g }=\frac{ 25000^2\cdot \sqrt{3}}{ 9,8\cdot 3600^2 }=8,51\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5f888898f6545ed8d7df3774bbbe3c26_l3.png)
Ответ: 8,5 м
Задача 4. Описывая окружность радиусом 30 м, конькобежец наклонился в сторону поворота на угол  к горизонту. С какой скоростью двигался конькобежец? Каков коэффициент трения коньков о лед?
к горизонту. С какой скоростью двигался конькобежец? Каков коэффициент трения коньков о лед?
Введем систему координат и разложим силу реакции опоры на проекции на оси:
![Rendered by QuickLaTeX.com \[N\sin{\alpha}=mg\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ad23bcb02c451947135d75002ce394f3_l3.png)
![Rendered by QuickLaTeX.com \[N\cos{\alpha}= F_{tr}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2eae9fc7c441360470fc1d32626d7a22_l3.png)
Найдем силу реакции опоры:
![Rendered by QuickLaTeX.com \[N=\frac{ mg }{\sin{\alpha}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f3fadd5bc0f69e67f7c752868b5ce7c5_l3.png)
Найдем  :
:
![Rendered by QuickLaTeX.com \[F_{tr}=\frac{ mg\cos{\alpha} }{\sin{\alpha}}=mg \operatorname{ctg}{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1fd8df54a34b622e3399766b06170774_l3.png)
Теперь определим скорость:
![Rendered by QuickLaTeX.com \[F_{n}=\frac{m \upsilon^2}{R}=F_{tr}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4b1fb274553cbe7f175d875a15784192_l3.png)
![Rendered by QuickLaTeX.com \[\frac{m \upsilon^2}{R}= mg \operatorname{ctg}{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3ef36b2dba04342ee2871f5ddb2758fe_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon^2= g R\operatorname{ctg}{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ae70bf680ea21b5eea20265d502c8480_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon=\sqrt{ g R\operatorname{ctg}{\alpha}}=\sqrt{ 9,8 \cdot 30 \cdot0,325=9,77\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4266381be675949a4d56626a789a0cb5_l3.png)
Определим коэффициент трения:
![Rendered by QuickLaTeX.com \[F_{tr}=\mu mg =\frac{m \upsilon^2}{R}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9499ab437324eb45b9cbe53488898bbe_l3.png)
![Rendered by QuickLaTeX.com \[\mu=\frac{\upsilon^2}{gR}=0,32\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-25fb36237399cb5b4d2ccea6a928f8f6_l3.png)
Ответ:  м/с,
м/с,  .
.
Наклонная плоскость — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 июня 2013; проверки требуют 36 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 12 июня 2013; проверки требуют 36 правок.
Наклонная плоскость — это плоская поверхность, установленная под углом к горизонтали. Наклонная плоскость является одним из простых механизмов. Она позволяет поднимать груз вверх, прикладывая к нему усилие, заметно меньшее, чем сила тяжести, действующая на этот груз.
Примерами наклонных плоскостей служат пандусы и трапы. Принцип наклонной плоскости можно видеть также в таких колющих и режущих инструментах, как стамеска, топор, плуг, клин, винт.
здесь μ{\displaystyle \mu } — коэффициент трения тела о поверхность, θ{\displaystyle \theta } — угол наклона плоскости.
Предельным является случай, когда угол наклона плоскости α{\displaystyle \alpha } равен 90°, a=g{\displaystyle a=g} и тело падает вдоль стены. Другим предельным случаем является ситуация, когда угол наклона плоскости равен 0° и плоскость параллельна земле; в этом случае тело не может ускоренно двигаться без приложения внешней силы.
Характер движения тела, лежащего на наклонной плоскости, зависит от величины критического угла. Тело покоится, если угол наклона плоскости меньше критического угла, покоится или движется равномерно, если угол наклона плоскости равен критическому углу, и движется равноускоренно, если угол наклона плоскости больше критического угла.
Видеоурок: наклонная плоскость
