Практикум по решению задач на тему «Сила трения»

Занятие 1. Сила трения

Трение – физическое явление, сопровождающее всякое движение на Земле. При любом механическом движении тела соприкасаются либо друг с другом, либо с окружающей их сплошной жидкой или газообразной средой. В результате соприкосновения возникает сила трения, которая препятствует движению. Трение может быть полезно, и тогда мы стремимся его увеличить. В случаях, когда трение вредно, принимаются меры для его уменьшения.

История открытия. Свой вклад в попытки объяснить природу трения внесли многие ученые, начиная с Аристотеля, Леонардо да Винчи, Амонтона, Леонарда Эйлера, Кулона. Дальнейший вклад в теорию трения сделали Майер, Джоуль, Гельмгольц, Кузнецов, Дерягин, Томлинсон, Рейнольдс, Штрибек, Боуден и другие.

Различают следующие виды трения:

1. сухое;

2. жидкое (вязкое).

Сухое трение бывает трех видов:

1. трение покоя;

2. трение скольжения;

3. трение качения.

Причины возникновения силы трения:

1. шероховатость поверхностей соприкасающихся тел.

2. взаимное притяжение молекул соприкасающихся тел.

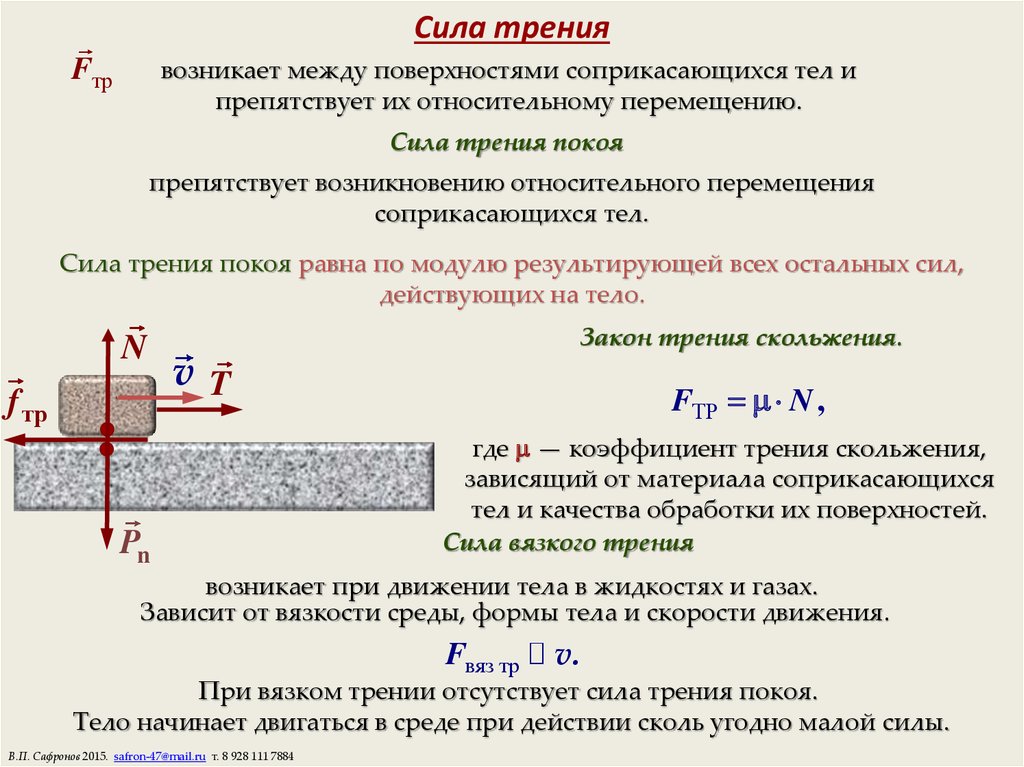
Сухое трение − трение, возникающее при соприкосновении двух твердых тел при отсутствии между ними жидкой или газообразной прослойки. Силы сухого трения всегда направлены по касательной к соприкасающимся поверхностям.

Сухое трение, возникающее при относительном покое тел, называют трением покоя.

Сухое трение, возникающее при относительном движении тел, называют трением скольжения.

Трение качения возникает, когда одно тело катится по поверхности другого тела.

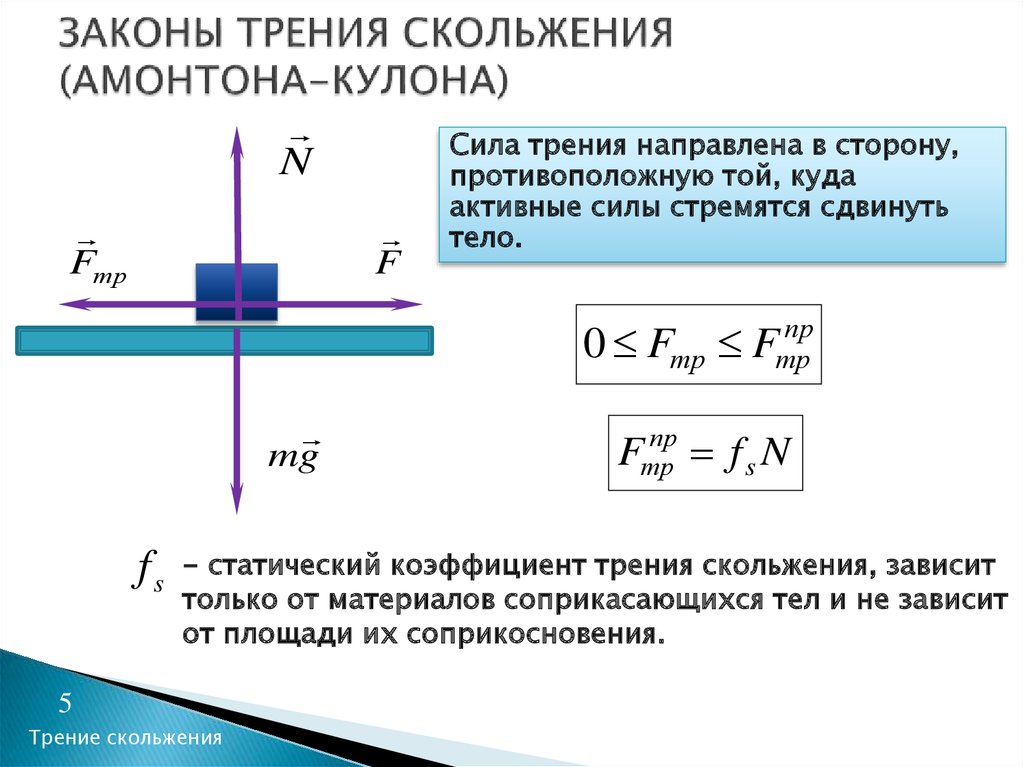
Закон, выражающий зависимость максимального значения модуля силы трения покоя от модуля силы нормальной реакции опоры впервые экспериментально установил французский военный инженер и учёный-физик Шарль Огюстен де Кулон. Согласно этому закону, максимальное значение модуля силы трения покоя прямо пропорционально модулю силы нормальной реакции опоры

F_{тр.макс} = µN,

где F_{тр.макс} — модуль максимальной силы трения покоя, µ- коэффициент пропорциональности, называемый коэффициентом трения покоя.

Коэффициент трения µ характеризует обе трущиеся поверхности и зависит не только от материала этих поверхностей, но и от качества их обработки. Коэффициент трения определяется экспериментально.

Трение скольжения. Сила трения скольжения также направлена вдоль поверхности соприкосновения тел, но в отличие от силы трения покоя, которая противоположна внешней силе, стремящейся сдвинуть тело, сила трения скольжения всегда направлена противоположно относительной скорости.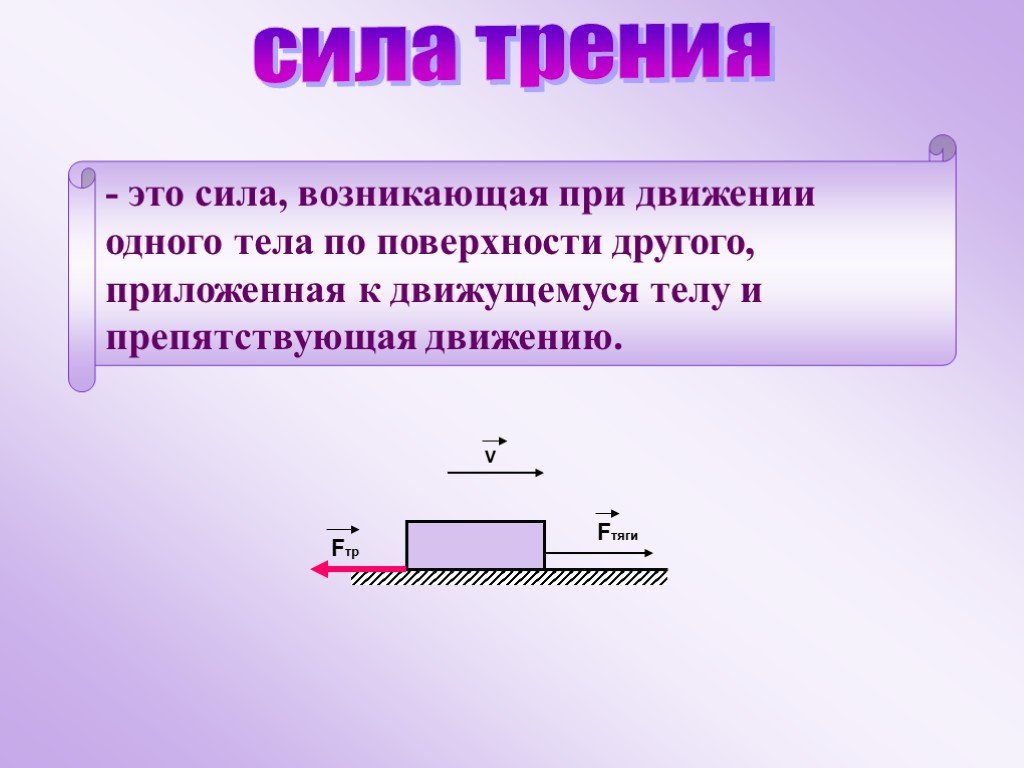 Модуль силы трения скольжения, как и максимальной силы трения покоя, тоже пропорционален прижимающей силе, а значит, нормальной силе реакции опоры:

При не слишком больших относительных скоростях движения сила трения скольжения мало отличается от максимальной силы трения покоя. Поэтому приближенно можно считать ее постоянной и равной максимальной силе трения покоя:

F_тр ≈ F_{тр.макс} = µN.

Важно! Сила трения зависит от относительной скорости движения тел. В этом ее главное отличие от сил тяготения и упругости, зависящих только от расстояний.

При движении твердого тела в жидкости или газе возникает силa жидкого (вязкого) трения. Сила жидкого трения значительно меньше силы сухого трения. Эта сила направлена против скорости тела относительно среды и тормозит движение.

Главная особенность силы сопротивления состоит в том, что она появляется только при наличии относительного движения тела и окружающей среды.  Сила трения покоя в жидкостях и газах полностью отсутствует. Поэтому усилием рук можно сдвинуть тяжелую баржу в воде, а сдвинуть поезд усилием рук невозможно.

Итак, основными особенностями силы сопротивления, действующей на тело, являются:

1) отсутствие силы трения покоя; 2) зависимость от относительной скорости движения.

Примеры и разбор решения заданий

1. Какая сила не позволяет человеку сдвинуть с места дом?

1. Силы трения скольжения;

2. сила трения покоя;

3. сила тяжести.

Ответ: 2) Сила трения покоя.

2. Деревянный ящик равномерно движется по поверхности длинного стола. Сила давления ящика на поверхность равна 30 Н, сила трения 6 Н. Найдите коэффициент трения скольжения.

Решение.

Воспользуемся формулой, которая связывает силу давления на плоскость, силу трения и коэффициент трения F_тр = µP. Из этой формулы легко получить формулу для расчёта коэффициента трения µ = F_тр / P. Подставляя в неё численные значения, получаем:

µ = F_тр / P = 6Н/30Н = 0,2.

Ответ: 0,2.

3. Кубик из детского конструктора покоится на наклонной плоскости, образующей угол α = 40° с горизонтом. Сила трения покоя равна 0,32 Н. Определите значение силы тяжести, которая действует на кубик.

Решение.

По условию задачи кубик покоится. Следовательно, сумма всех действующих на него сил равна нулю. В проекции на ось, идущей вдоль склона плоскости, получаем соотношение: mg sin α – F_{тр =} 0. Из него выражаем формулу для расчета силы тяжести, действующей на кубик

Ответ: 0,5 Н.

Задание ЕГЭ

1. На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 10 Н. Чему будет равна сила трения скольжения после уменьшения массы тела в 2 раза, если коэффициент трения не изменится? (Ответ дайте в ньютонах.)

Решение.

Сила трения скольжения связана с коэффициентом трения и силой реакции опоры соотношением   Для бруска, движущегося по горизонтальной поверхности, по второму закону Ньютона, 

Таким образом, сила трения скольжения пропорциональна произведению коэффициента трения и массы бруска. Если коэффициент трения не изменится, то после уменьшения массы тела в 2 раза, сила трения скольжения также уменьшится в 2 раза и окажется равной

 Ответ: 5 Н.

2. На горизонтальном полу стоит ящик массой 10 кг. Коэффициент трения между полом и ящиком равен 0,25. К ящику в горизонтальном направлении прикладывают силу 16 Н. Какова сила трения между ящиком и полом? Ответ выразите в ньютонах.

Решение.

Определим, какую величину имеет сила трения скольжения:

Поскольку сила трения скольжения превосходит по величине силу   с которой ящик толкают в горизонтальном направлении, ящик останется стоять на месте. Следовательно, согласно второму закону Ньютона, сила трения между ящиком и полом будет равняться по модулю силе 

 Ответ: 16.

3. Два спортсмена разной массы на одинаковых автомобилях, движущихся со скоростью   и   стали тормозить, заблокировав колеса. Каково отношение   тормозных путей их автомобилей при одинаковом коэффициенте трения колес о землю?

Решение.

При торможении на автомобили действует сила трения скольжения, которая и останавливает их. Величина силы трения скольжения определяется выражением   где   — сила реакции опоры, которую можно найти, выписав второй закон Ньютона в проекции на вертикальную ось: 

Вычислим теперь ускорение, с которым тормозит каждый из спортсменов. Второй закон Ньютона в проекции на горизонтальную ось даёт   (здесь m — масса автомобиля вместе со спортсменом). Поскольку ускорение не зависит от массы, заключаем, что оба автомобиля тормозят с одинаковым ускорением.

Тормозной путь можно найти по формуле   где    — начальная скорость. Следовательно, отношение тормозных путей равно

Ответ: 0,25.

4.

Брусок массой 20 кг равномерно перемещают по горизонтальной поверхности, прикладывая к нему постоянную силу, направленную под углом 30° к поверхности. Модуль этой силы равен 75 Н. Определите коэффициент трения между бруском и плоскостью. Ответ округлите до десятых долей.

Решение.

Запишем второй закон Ньютона, учитывая, что тело движется равномерно, то есть ускорение бруска равно нулю:   Вспомним, что сила трения и сила реакции опоры связаны соотношением:   Запишем это уравнение в проекции на горизонтальную и вертикальную оси:

Таким образом, получаем: 

Ответ: 0,4.

5. На горизонтальной поверхности лежит деревянный брусок массой 1 кг. Для того чтобы сдвинуть этот брусок с места, к нему нужно приложить горизонтально направленную силу 3 Н. Затем на эту же поверхность кладут стальной брусок массой 5 кг. Коэффициент трения для стали о данную поверхность в 2 раза больше, чем для дерева. Какую горизонтально направленную силу нужно приложить к стальному бруску для того, чтобы сдвинуть его с места?

Решение.

Для момента начала движения:   где   — приложенная сила. Распишем силы, которые действуют на деревянный брусок —   на стальной —   Следовательно, 

Ответ: 30.

6. Брусок массой 5 кг покоится на шероховатом горизонтальном столе. Коэффициент трения между поверхностью бруска и поверхностью стола равен 0,2. На этот брусок действуют горизонтально направленной силой 2,5 Н. Чему равна по модулю возникающая при этом сила трения?

Решение.

Максимально возможная сила трения равна   Поскольку внешняя сила меньше, значит, тело будет покоиться, сила трения будет уравновешивать внешнюю силу и, соответственно, равняться 2,5 Н.

 Ответ: 2,5

7.

Брусок массой 1 кг лежит на горизонтальной шероховатой поверхности. К нему прикладывают силу   направленную под углом 60° к горизонту. Модуль этой силы равен 4 Н. Коэффициент трения между бруском и поверхностью равен 0,6. Чему равен модуль силы трения, действующей со стороны поверхности на брусок? Ответ приведите в ньютонах.

Решение.

Запишем второй закон Ньютона в проекции на вертикальную ось:   Откуда   Заметим, что горизонтальная проекция силы   меньше силы трения скольжения:   Следовательно, тело останется в покое.

Тело осталось неподвижным, поэтому искомая сила трения — сила трения покоя. Запишем второй закон Ньютона в проекции на горизонтальную ось: 

 Ответ: 2.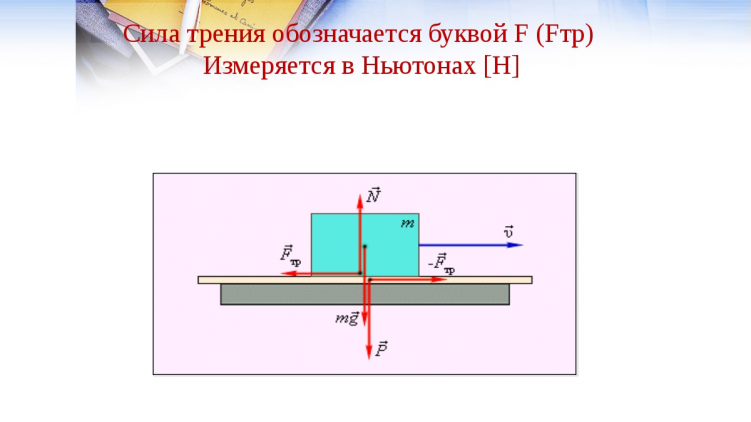  

Примечание.

Если вы попытаетесь вычислить силу трения исходя из предположения, что тело движется, получится иррациональный ответ — это ещё одна подсказка, которая указывает, что необходимо обратить внимание на то, что тело покоится.

Ответ: 2

8.

Брусок покоится на наклонной плоскости, образующей угол 30° с горизонтом. Сила трения покоя равна 0,5 Н. Определите силу тяжести, действующую на тело.

Решение.

Поскольку брусок покоится сумма всех действующих на него сил равна нулю. В проекции на ось, идущей вдоль склона плоскости, получаем 

Ответ: 1.

9. Мальчик скатился с горки высотой 10 метров и проехал путь 50 метров по горизонтальному участку дороги. Чему равен коэффициент трения? Трением на горке пренебречь.

Решение.

По закону сохранения энергии:

где   — высота горки.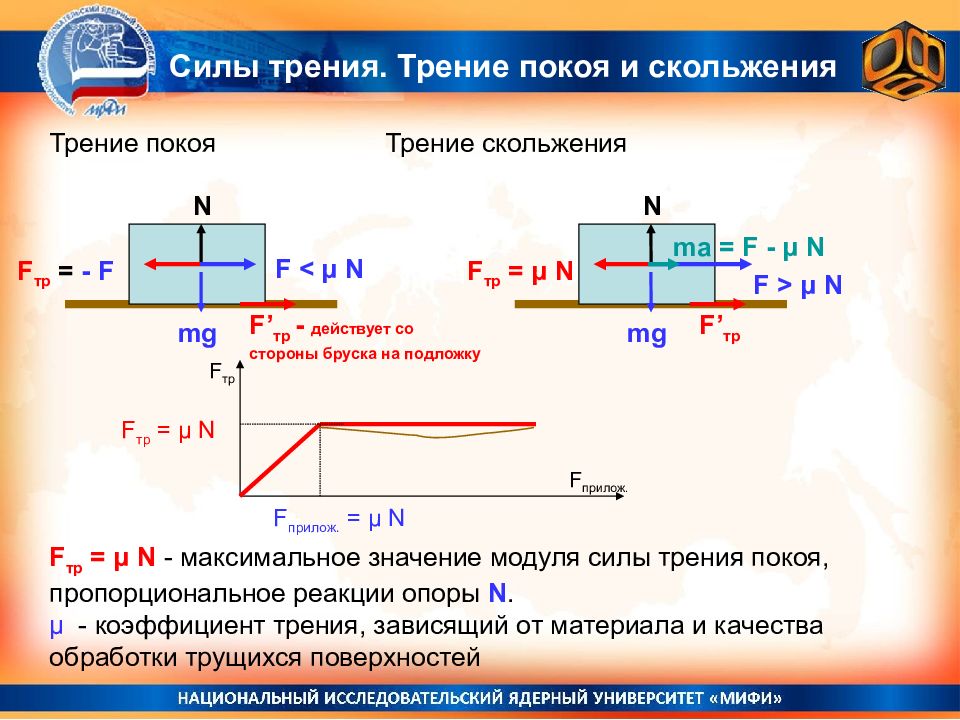

На горизонтальном участке мальчик имеет ускорение, направленное против его движения

По второму закону Ньютона:

Отсюда

Ответ: 0,2.

10.

На графике приведена зависимость модуля силы трения скольжения от модуля силы нормального давления. Каков коэффициент трения?

Решение.

Сила трения скольжения связана с силой нормального давления соотношением   где   — коэффициент трения. Из графика видно, что   Значит, 

Ответ: 0,125

11. Шайбе массой 100 г, находящейся на наклонной плоскости, сообщили скорость 4 м/с, направленную вверх вдоль наклонной плоскости. Шайба остановилась на расстоянии 1 м от начала движения. Угол наклона плоскости 30°. Чему равна сила трения шайбы о плоскость? Ответ укажите в ньютонах с точностью до одного знака после запятой.

Решение.

1 способ:

Запишем закон сохранения энергии. Кинетическая энергия шайбы переходит в его потенциальную энергию и в тепло, которое выделяется за счет работы силы трения шайбы о наклонную плоскость:   Поскольку шайба проехала вдоль склона   а угол наклона плоскости   она поднялась на высоту   В итоге, для модуля силы трения имеем:

2 способ:

Определим сперва величину ускорения шайбы, используя так называемую формулу для пути без времени:   Знак минус у ускорения возник, так как тело тормозит и ускорение направлено вниз по склону, чтобы дальше не запутаться, будем в последующих формулах считать, что   а знак минус учитывать при проектировании уравнений.

Второй закон Ньютона в проекции на ось, направленную вниз вдоль плоскости:   Отсюда для силы трения имеем:

 Ответ: 0,3.

12. Лыжник массой 60 кг спустился с горы высотой 20 м. Какой была сила сопротивления его движению по горизонтальной лыжне после спуска, если он остановился, проехав 200 м? Считать, что по склону горы он скользил без трения. Ответ приведите в ньютонах.

Решение.

Выпишем закон сохранения энергии: потенциальная энергия лыжника перешла в тепло, которое выделилось за счет работы силы трения при движении по горизонтальному участку,   Таким образом, величина силы трения равна 

 Ответ: 60 Н.

13.  Груз массой 1 кг, находящийся на столе, связан лёгкой нерастяжимой нитью, переброшенной через идеальный блок, с другим грузом. На первый груз действует горизонтальная постоянная сила   равная по модулю 10 Н (см. рисунок). Второй груз движется из состояния покоя с ускорением 2  направленным вверх. Коэффициент трения скольжения первого груза по поверхности стола равен 0,2. Чему равна масса второго груза?

Решение.

Запишем второй закон Ньютона для двух тел в проекциях на направленную влево горизонтальную ось и направленную вверх вертикальную ось:

где   — сила натяжения нити. Ускорения у грузов одинаковы, поскольку соединяющая их нить нерастяжима. С учётом того, что   получаем:

 

Ответ: 0,5 кг.

14. Брусок равномерно двигают по горизонтальной поверхности. В процессе движения по этой поверхности он проходит два участка одинаковой длины с различными коэффициентами трения. Известно, что на первом участке модуль работы силы трения 2,5 Дж, а на втором участке модуль работы силы трения 7,5 Дж. При этом на втором участке коэффициент трения на 0,4 больше, чем на первом. Определите, чему равен коэффициент трения на втором участке.

Решение.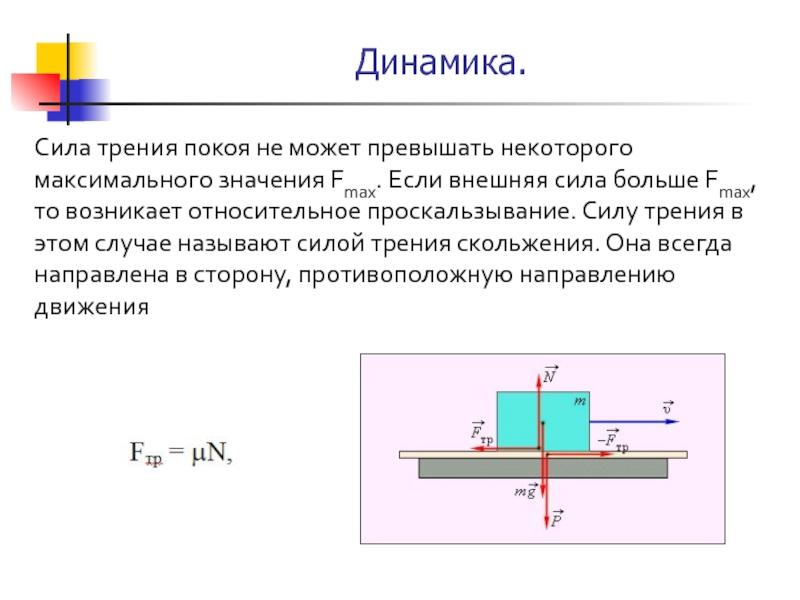

При движении бруска по шероховатой поверхности будет возникать сила трения, равная

Модуль работы силы трения равен

Найдем отношение работ сил трения при прохождении двух различных участков

По условию   Тогда 

 Ответ: 0,6.

Как найти силу натяжения с трением: шаги, примеры задач —

Обычно мы предполагаем поверхность без трения и невесомую веревку при расчете натяжения. В этой статье описывается, как найти силу натяжения с учетом трения.

Всякий раз, когда возникает контакт между поверхностью и объектом, возникает трение. Всегда будет небольшая сила кинетического трения или трения покоя, а сила натяжения определяется приравниванием сил, которые уравновешивают друг друга (используя второй и третий законы движения Ньютона).

Будет сила из-за кинетического трения, если какой-либо объект, соприкасающийся с поверхностью, находится в движении, а если нет движения, будет сила из-за статического трения.

Подробнее о Как рассчитать силу натяжения: Exhaustive InsightСила натяжения в перетягивании каната
Кредиты на изображения: Wikimedia Commons

Шаги о том, как найти силу натяжения с трением

1. Отдельный блок

Напряжение для одного блока

Рассмотрим блок массы M тянут с ускорением a, как показано на рисунке. Сила натяжения T будет развиваться в веревке. Поскольку блок находится в движении, будет возникать трение из-за движения, известного как кинетическое трение между поверхностью и блоком.

Сначала постройте диаграмму свободного тела и найдите все силы, действующие на блок.

Диаграмма свободного тела

В данном конкретном случае силы, действующие на блок, представляют собой силу натяжения, силу трения и результирующую силу ускорения.

Выражение для кинетического трения имеет вид

F_k=му_k * М * г

где му_k это коэффициент кинетики трение.

Используя третий закон Ньютона и второй закон движения, мы получаем,

F_сеть= ТФ_k

М*а=Т-мю_k * М * г

Т = М* а + мю_k * М * г

Т = М(а+мю_k * грамм)

Это выражение силы натяжения для одиночного блока, тянущего с ускорением по поверхности, где существует трение.

Подробнее о том, как рассчитать натяжение между двумя объектами: исчерпывающая информация

• Два блока соединены веревкой

Натяжение в случае двух блоков, соединенных веревкой

Предположим, два блока масс m₁ и m₂ соответственно связаны веревкой и один из блоков тянется с силой F как показано на рисунке.

Суммарное трение в системе определяется выражением 

F_Knet=му_k * грамм

F_Knet=му_k * (м1+м2) * г

Теперь ускорение системы определяется выражением

а = F_сеть/Общая масса

F_сеть= ФФ_сеть

а=F₁ — мю_k * (м1+м2)

Теперь найдем силу натяжения каждого блока.

Для первого блока массы m₁, построить диаграмму свободного тела.Свободная диаграмма тела m₁

Сила трения и сила натяжения являются силами, действующими на этот брусок.

F_сеть = Т-трение

Т = F_сеть + трение

Т = м₁*а + мю_k * м₁ * грамм

Для второго блока массы m₂ также построить диаграмму свободного тела.Свободная диаграмма тела m₂

На этот блок действуют сила трения, натяжение и приложенная сила.

Следовательно, F_сеть=FT-трение

Т = ФФ_сеть-трение

Т= Ф – м₂* а-му_k*m₂*g

Следовательно, можно получить силу натяжения для отдельных блоков.

Подробнее о Является ли напряжение контактной силой: почему, как, подробные факты

Задачи на нахождение силы натяжения с учетом трения

Проблема 1

Безмассовая веревка тянет по горизонтали брусок массой 2 кг с силой 50 Н, как показано на рисунке. Найти величину натяжения каната, если коэффициент трения между поверхностью и блоком равен 0.35.

Рисунок для задачи 1

Решение:

Дано, масса блока m = 2 кг

Сила применена F = 50 Н

Коэффициент трения мю_k= 0.35

напряжение T знак равно

Рисуется схема свободного тела блока.Бесплатная диаграмма тела для блока

Силы, действующие на блок, представляют собой трение вследствие движения, т. е. кинетическое трение и силу 50 Н. 

Сила трения определяется выражением 

F_k=му_k*м*г

F_k= 0.35*2*9.8=6.86 Н

Теперь, применяя законы движения Ньютона, 

Ф=ТФ_k

Т=Ж+Ж_k

Т=50+6.86=56.86Н

Отсюда и напряжение 56.86 N.

Подробнее о Является ли напряжение консервативной силой: Exhaustive Insight

Проблема 2

На изображенном рисунке два блока масс m₁ = 2 кг и m₂= 4 кг прикреплены безмассовым стержнем. Стержень параллелен поверхности наклона, по которому оба блока скользят и движутся вниз по наклонной плоскости с m₁ задний m₂. Известно, что угол наклонной плоскости равен θ = 60°. Коэффициент трения между m₁ а наклонная плоскость = 0.4, а между m₂ а наклон равен µ₂ = 0.25. Найди сила натяжения развивается в стержне, соединяющем m1 и m2.Рисунок для задачи 2

Решение:

Данный m₁ = 2 кг; m₂ = 4 кг, θ = 60°

Также µ₁ = 0.4; µ₂ = 0.25

Теперь можно получить общее ускорение системы:

a=Общая сила/Общая масса

Суммарная сила F = м₁ gsinθ +m₂ gsinθ -трение на m₁ И м₂

Ф =m₁ + m₂ gsinθ -(m₁µ₁+m₂µ₂)gcosθ

Следовательно, ускорение,

a=6* 9. 8*sin 60-(2*0.4+4*0.25)*9.8*cos 60(2+4)

а=7.02 м/с²

Рассмотрим движение m₂, Позволять T — натяжение стержня, связывающего m₁ И м₂.

Следовательно, используя второй и третий законы движения Ньютиона,

m₂ gsinθ -(T+µ₂m₂ gcosθ)=m₂a

T=m₂ gsinθ-µ₂m₂ gcosθ-м₂a

T=4*9.8*sin (60-0.25)* 4*9.8*cos(60-4)*7.02

Т=0.97 Н

Отсюда величина натяжения в стержневых связях масс m_{1и m2 is 0.97 N.}

Подробнее о Является ли трение консервативной силой: исчерпывающий анализ

Кинетическое трение: определение, взаимосвязь и формулы

Вы когда-нибудь задумывались, почему во время дождя дороги становятся скользкими, что затрудняет остановку автомобиля? Оказывается, это прямое следствие кинетической силы трения, так как сухой асфальт обеспечивает лучшее сцепление шины с дорогой, чем мокрый асфальт, что сокращает время остановки автомобиля.

Кинетическое трение — это сила трения, которая почти неизбежна в нашей повседневной жизни. Иногда это остановка, а иногда необходимость. Он присутствует, когда мы играем в футбол, пользуемся смартфонами, гуляем, пишем и занимаемся многими другими обычными делами. В сценариях реальной жизни, когда бы мы ни рассматривали движение, ему всегда будет сопутствовать кинетическое трение. В этой статье мы лучше поймем, что такое кинетическое трение, и применим эти знания к различным примерам задач.

Кинетическое трение Определение

Когда вы пытаетесь толкнуть коробку, вам нужно будет приложить определенное усилие. Как только коробка начинает двигаться, легче поддерживать движение. По опыту, чем легче ящик, тем легче его передвигать.

Представим себе тело, лежащее на плоской поверхности. Если одна контактная сила \(\vec{F}\) приложена к телу горизонтально, мы можем определить четыре составляющие силы, перпендикулярные и параллельные поверхности, как показано на рисунке ниже.

Рис. 1 — Если объект положить на горизонтальную поверхность и приложить к нему горизонтальную силу, то кинетическая сила трения возникнет в направлении, противоположном движению, и будет пропорциональна нормальной силе.

Нормальная сила, \(\vec{F_\mathrm{N}}\), перпендикулярна поверхности, а сила трения, \(\vec{F_\mathrm{f}}\),

равна параллельно поверхности. Сила трения направлена ​​против движения.

Кинетическое трение — это тип силы трения, которая действует на движущиеся объекты.

Обозначается \(\vec{F_{\mathrm{f, k}}}\), а его величина пропорциональна величине нормальной силы.

Это отношение пропорциональности интуитивно понятно, как мы знаем из опыта: чем тяжелее объект, тем труднее заставить его двигаться. На микроскопическом уровне большая масса равна большему гравитационному притяжению; поэтому объект будет ближе к поверхности, увеличивая трение между ними.

Формула кинетического трения

Величина кинетической силы трения зависит от безразмерного коэффициента кинетического трения \(\mu_{\mathrm{k}}\) и нормальной силы \(\vec{F_\mathrm{N}} \) измеряется в ньютонах (\(\mathrm{N}\)). Эту связь можно показать математически

$$ \vec{F}_{\mathrm{f,k}}=\mu_{\mathrm{k}} \vec{F_\mathrm{N}}.$$

Кинетический коэффициент трения

Отношение кинетической силы трения контактирующих поверхностей к нормальной силе известно как коэффициент кинетического трения . Обозначается \(\mu_{\mathrm{k}}\). Его величина зависит от того, насколько скользкой является поверхность. Поскольку это отношение двух сил, коэффициент кинетического трения безразмерен. В таблице ниже мы можем видеть приблизительные коэффициенты кинетического трения для некоторых распространенных комбинаций материалов.

0

Материалы	Коэффициент кинетического трения, \(\mu_{\mathrm{k}}\)
Сталь по стали	\ (0,57 \)
Алюминий на стали	\ (0,47 \)
Медная на стали	\ (0,36 \)
Glass	\	\	9141414142	\	\	92	\	\	rlase	.
Copper on glass	\(0.53\)
Teflon on Teflon	\(0.04\)
Teflon on steel	\(0.04\)
Rubber on concrete (dry )	\(0,80\)
Резина на бетоне (мокром)	\(0,25\)

Теперь, когда мы знаем уравнение для расчета кинетической силы трения и познакомились с коэффициентом кинетического трения, давайте применим это знание к некоторым примерным задачам. !

Примеры кинетического трения

Для начала давайте рассмотрим простой случай непосредственного применения уравнения кинетического трения!

Автомобиль движется с постоянной скоростью с нормальной силой \(2000 \, \mathrm{N}\). Если кинетическое трение, приложенное к этому автомобилю, равно \(400 \, \mathrm{N}\). Тогда вычислите коэффициент кинетического трения, связанного с этим?

Решение

В примере даны величины нормальной силы и кинетической силы трения.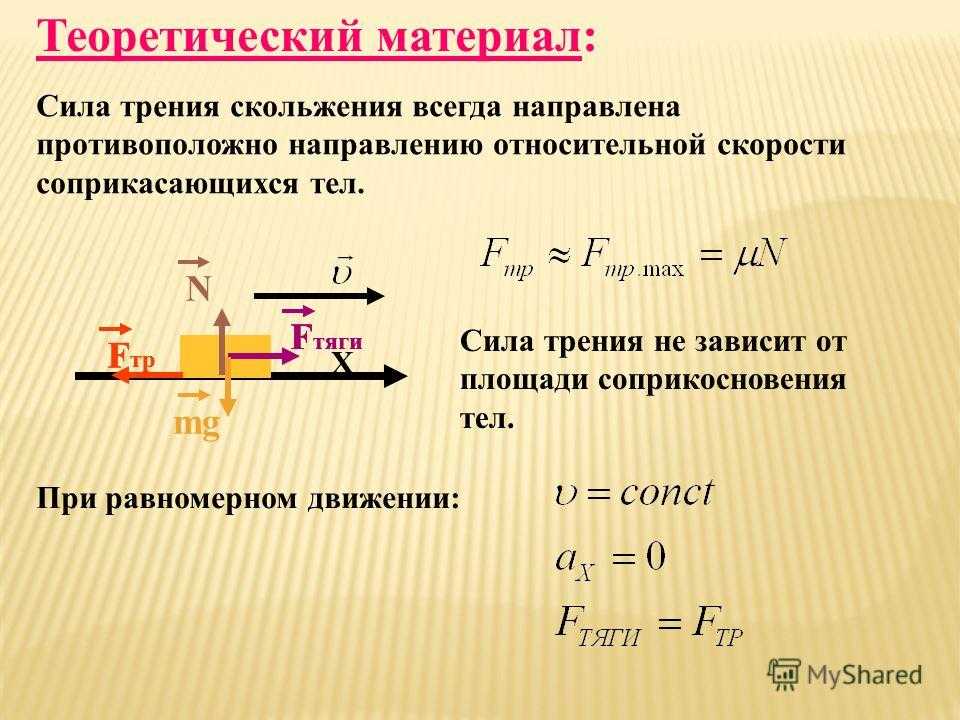 Итак, \(\vec{F}_{\mathrm{f,k}}=400 \, \mathrm{N}\) и \(F_\mathrm{N}= 2000 \, \mathrm{N}\) . Если мы подставим эти значения в формулу кинетического трения

$$ \vec{F}_{\mathrm{f,k}}=\mu_{\mathrm{k}} \vec{F_\mathrm{N}}, $$

получаем следующее выражение

$$400 \, \mathrm{N} =\mu_{\mathrm{k}} \cdot 2000 \, \mathrm{N}, $$

которое можно преобразовать в найти коэффициент трения 9{\circ}\) к горизонтальной поверхности. Кинетическая сила трения направлена ​​противоположно силе.

Решение

В примере сказано, что мы хотим поддерживать постоянную скорость. Постоянная скорость означает, что объект находится в состоянии равновесия (т.е. силы уравновешивают друг друга). Давайте нарисуем диаграмму свободного тела, чтобы лучше понять силы, и посмотрим на горизонтальную и вертикальную составляющие.

Рис. 3 — Свободная схема коробки. Силы действуют как в горизонтальном, так и в вертикальном направлении.

Когда мы смотрим на перпендикулярные компоненты силы, направленные вверх силы должны быть равны по величине направленным вниз силам.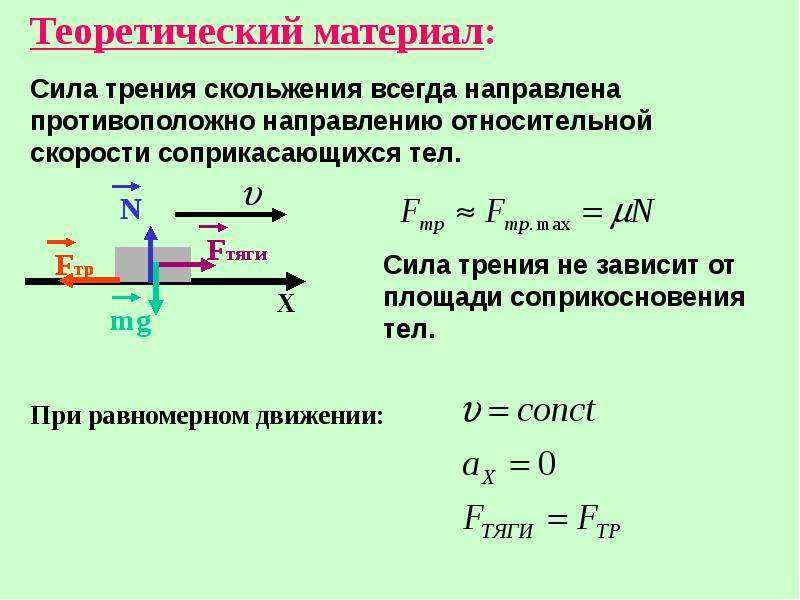 {\ circ} = F _ {\ mathrm {f, k}} = \ mu _ {\ mathrm {k}} F_ \ mathrm {N}. $ $ 9{\circ}} \\ T &= \frac{0,5000 \cdot 200,0 \, \mathrm{N}}{0,87 + 0,5000 \cdot 0,5} \\ T &= 89,29 \, \mathrm{N}. \end{align}$$

Наконец, давайте рассмотрим аналогичный пример, только на этот раз ящик расположен на наклонной плоскости.

Коробка скользит вниз с постоянной скоростью с наклонной плоскости, составляющей угол \(\alpha\) с горизонтом. Поверхность имеет коэффициент кинетического трения \(\mu_{\mathrm{k}}\). Если вес коробки равен \(w\), найдите угол \(\alpha\).

Рис. 4. Коробка, скользящая по наклонной плоскости. Он движется с постоянной скоростью.

Давайте посмотрим на силы, действующие на коробку на рисунке ниже.

Рис. 5 — Все силы, действующие на коробку, скользящую по наклонной плоскости. Мы можем применить новую систему координат, чтобы написать соответствующие уравнения.

Если мы получим новые координаты (\(x\) и \(y\)), то увидим, что в направлении \(x\) действуют кинетическая сила трения и горизонтальная составляющая веса.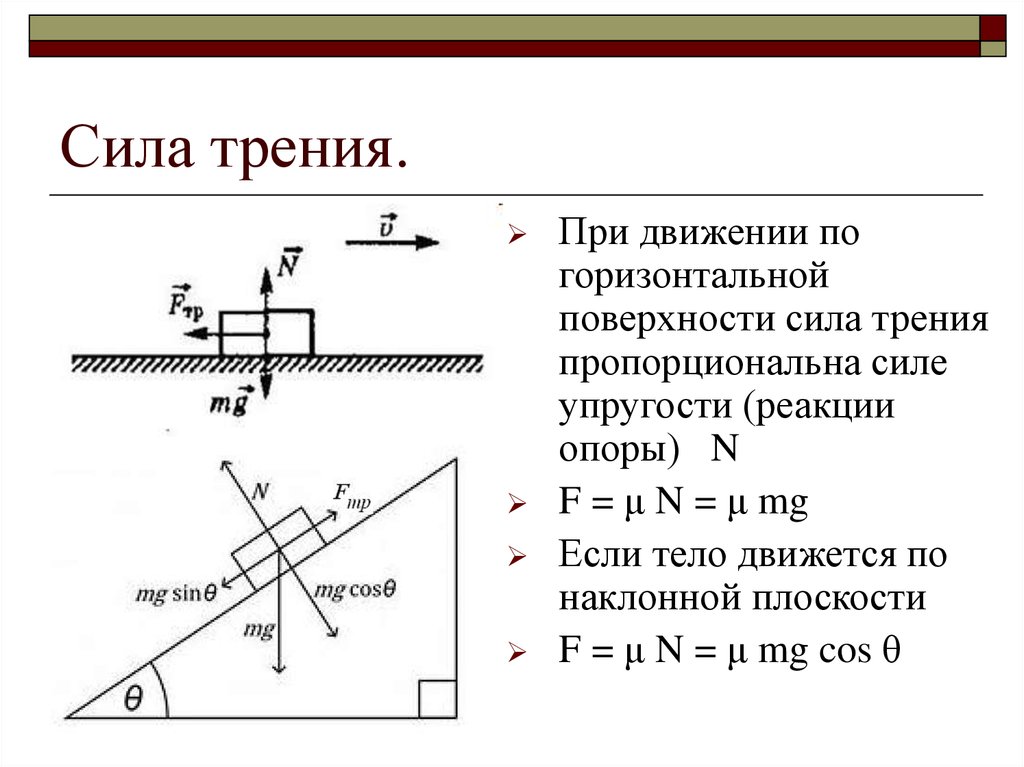 В направлении \(y\) действуют нормальная сила и вертикальная составляющая веса. Поскольку ящик движется с постоянной скоростью, он находится в равновесии.

1. Для направления \(x\): \(w\cdot\sin\alpha=F_\mathrm{f,k} = \mu_{\mathrm{k}}F_\mathrm{N}\)
2. Для \(y\)-направления: \(F_\mathrm{N}=w\cdot\cos\alpha\)

Мы можем вставить второе уравнение в первое уравнение:

$$ \begin{align} w \cdot \sin\alpha & =\mu_\mathrm{k}w \cdot \cos\alpha \\ \cancel{w}\cdot\sin\alpha & =\mu_\mathrm{k} \cancel{w} \cdot \cos\alpha \\ \mu_\mathrm{k} & = \tan\alpha \end{align}$$

Тогда угол \(\alpha\) равен

$$ \alpha = \arctan\mu_\mathrm{k}.$$

Статическое трение против кинетического трения

В целом коэффициент трения может принимать две формы, и кинетическое трение является одной из них. Другой тип известен как статическое трение . Как мы уже установили, кинетическая сила трения является разновидностью силы трения, действующей на движущиеся объекты.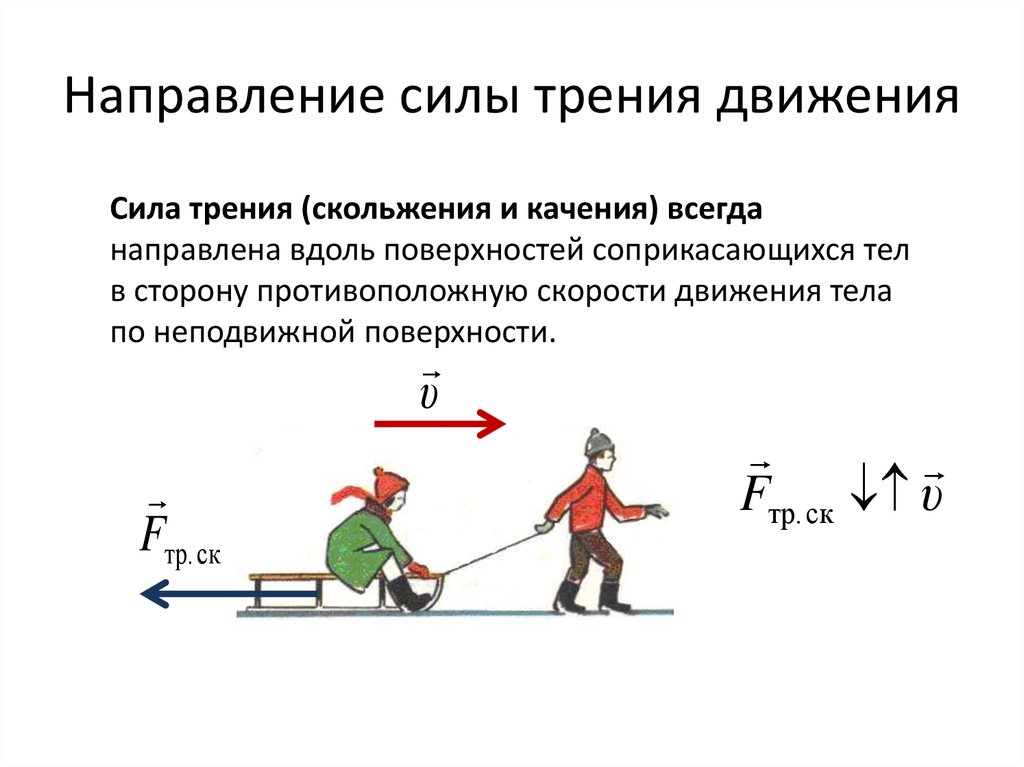 Итак, в чем же разница между статическим трением и кинетическим трением?

Статическое трение — это сила, обеспечивающая неподвижность объектов, покоящихся друг относительно друга.

Другими словами, кинетическое трение относится к движущимся объектам, тогда как статическое трение относится к неподвижным объектам.

Разницу между двумя типами можно запомнить прямо из словаря. В то время как статика означает отсутствие движения, кинетика означает отношение к движению или его следствие!

Математически статическое трение \(F_\mathrm{f,s}\) очень похоже на кинетическое трение,

$$ F_\mathrm{f,s} = \mu_\mathrm{s}F_\mathrm{N}$$

, где единственным отличием является использование другого коэффициента \(\mu_\mathrm{s} \), который является коэффициентом статического трения.

Давайте рассмотрим пример, когда объект испытывает оба типа трения.

Тяжелая коробка лежит на столе и остается неподвижной до тех пор, пока не будет приложена некоторая сила в горизонтальном направлении, чтобы сдвинуть ее по столу. Поскольку поверхность стола довольно неровная, изначально коробка не движется, несмотря на приложенную силу. В результате коробку толкают еще сильнее, пока, в конце концов, она не начнет двигаться по столу. Объясните различные этапы сил, действующих на коробку, и постройте график зависимости трения от приложенной силы.

Решение

• Сначала к ящику не приложены никакие силы, поэтому он испытывает только гравитационное притяжение вниз и нормальную силу от стола, толкающую его вверх.
• Затем к коробке горизонтально прикладывается некоторая толкающая сила \(F_\mathrm{p}\). В результате возникнет сопротивление в противоположном направлении, известное как трение \(F_\mathrm{f}\).
• Учитывая, что коробка тяжелая, а поверхность стола неровная, коробка не будет легко скользить, так как обе эти характеристики влияют на трение.

Нормальная сила и шероховатость/гладкость задействованных поверхностей являются основными факторами, влияющими на трение.

• Итак, в зависимости от величины приложенной силы коробка будет оставаться неподвижной за счет трения покоя \(F_\mathrm{f,s}\).
• С увеличением приложенной силы, в конце концов, \(F_\mathrm{p}\) и \(F_\mathrm{f,s}\) будут иметь одинаковую величину. Эта точка известна как порог движения, 9После достижения 0020 и коробка начнет двигаться.
• Как только коробка начнет двигаться, сила трения, влияющая на движение, будет равна кинетическому трению \(F_\mathrm{f,k}\). Поддерживать его движение станет легче, так как коэффициент трения у движущихся объектов обычно меньше, чем у неподвижных.

Графически все эти наблюдения можно увидеть на рисунке ниже.

Рис. 6 – График зависимости трения от приложенной силы.

Кинетическое трение — основные выводы

• Кинетическая сила трения — это тип силы трения, действующей на движущиеся объекты.
• Величина кинетической силы трения зависит от коэффициента кинетического трения и нормальной силы.
• Отношение кинетической силы трения контактирующих поверхностей к нормальной силе называется коэффициентом кинетического трения.
• Для расчета коэффициента трения используется уравнение \(\mu_{\mathrm{k}} = \frac{\vec{F}_{\mathrm{f,k}}}{\vec{F}_ \mathrm{N}}\).
• Коэффициент кинетического трения зависит от того, насколько скользкой является поверхность.
• Нормальная сила не всегда равна весу.
• Статическое трение — тип трения, применяемого к неподвижным объектам.

Нахождение ускорения

Как уже говорилось ранее в уроке 3 (а также в уроке 2), результирующая сила представляет собой векторную сумму всех отдельных сил. На уроке 2 мы узнали, как определить результирующую силу, если известны величины всех отдельных сил. На этом уроке мы научимся определять ускорение объекта, если известны величины всех отдельных сил. Три основных уравнения, которые будут полезны, — это уравнение для результирующей силы (F _нетто = м•а), уравнение для гравитационной силы (F _грав = м•г) и уравнение для силы трения (F _трение = μ • F _норма ).

Процесс определения ускорения объекта требует, чтобы были известны масса и результирующая сила. Если масса (м) и результирующая сила (F _net ) известны, то ускорение определяется с помощью уравнения.

а = F _нетто / м

 

Ваша очередь попрактиковаться

Таким образом, задание включает в себя использование приведенных выше уравнений, предоставленной информации и вашего понимания законов Ньютона для определения ускорения. Чтобы почувствовать, как применяется этот метод, попробуйте решить следующие практические задачи. После того, как вы решили задачи, нажмите кнопку, чтобы проверить свои ответы.

 

Практика №1

Приложенная сила в 50 Н используется для ускорения объекта вправо по поверхности трения. Объект сталкивается с силой трения 10 Н. Используйте диаграмму, чтобы определить нормальную силу, результирующую силу, массу и ускорение объекта.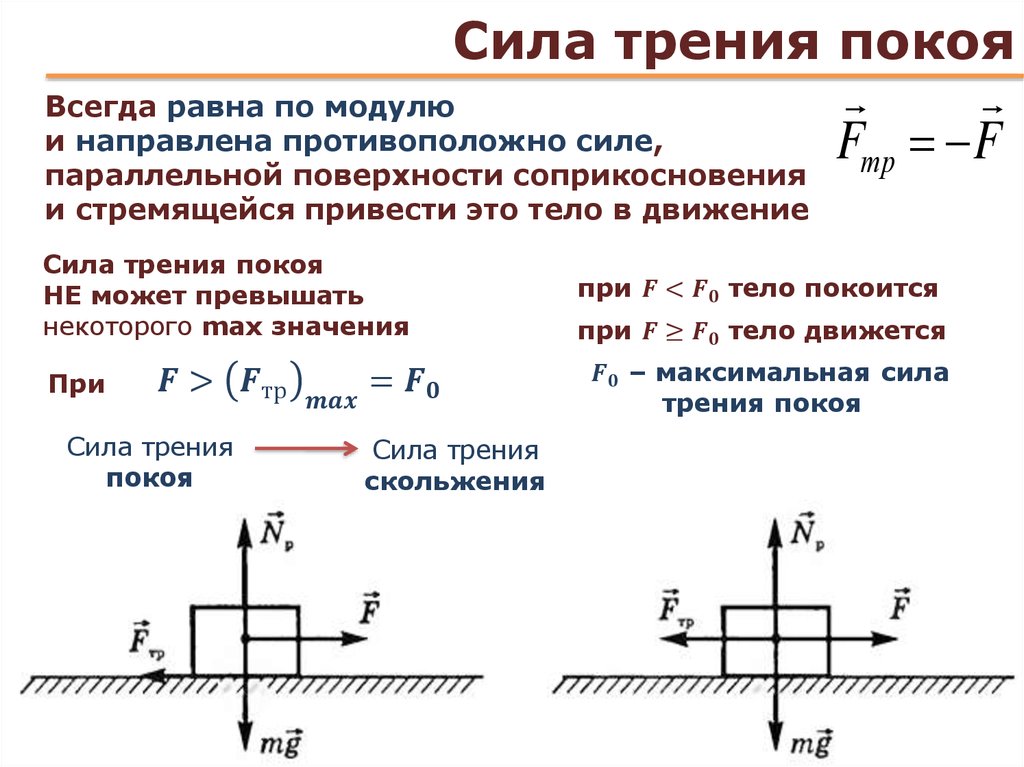 (Сопротивлением воздуха пренебречь.)

 

 

 

Практика №2

Приложенная сила в 20 Н используется для ускорения объекта вправо по поверхности трения. Объект сталкивается с силой трения 10 Н. Используйте диаграмму, чтобы определить нормальную силу, результирующую силу, коэффициент трения (μ) между объектом и поверхностью, массу и ускорение объекта. (Сопротивлением воздуха пренебречь.)

 

 

 

 

Практика №3

Объект массой 5 ​​кг скользит вправо и сталкивается с силой трения, которая замедляет его. Коэффициент трения (μ) между объектом и поверхностью равен 0,1. Определить силу тяжести, нормальную силу, силу трения, результирующую силу и ускорение. (Сопротивлением воздуха пренебречь. )

 

 

Ниже приведены еще несколько практических задач. Вы должны приложить усилия, чтобы решить как можно больше задач без помощи заметок, решений, учителей и других учеников. Посвятите себя индивидуальному решению проблем. Между тем, стоит упомянуть важное предостережение:

Избегайте форсирования проблемы в виде ранее решенной проблемы. Проблемы в физике редко выглядят одинаково. Вместо решения проблем наизусть или путем имитации ранее решенной проблемы, используйте свое концептуальное понимание законов Ньютона для поиска решений проблем. Используйте свое понимание веса и массы, чтобы найти m или Fgrav в задаче. Используйте свое концептуальное понимание результирующей силы ( векторная сумма всех сил ), чтобы найти значение Fnet или значение отдельной силы. Не отделяйте решение физических задач от понимания физических концепций. Если вы не можете решить физические задачи, подобные приведенным выше, это не обязательно означает, что у вас проблемы с математикой. Вполне вероятно, что у вас возникли трудности с понятиями физики.

 

 

Мы хотели бы предложить …

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Force Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Force Interactive позволяет учащимся исследовать влияние изменений приложенной силы, результирующей силы, массы и трения на ускорение объекта.

Посетите:  Force

 

Проверьте свое понимание  

1. Эдвардо прикладывает направленную вправо силу 4,25 Н к книге весом 0,765 кг, чтобы ускорить ее перемещение по поверхности стола.