Задача 5: сила трения и график зависимости ускорения от силы
К бруску массой 10 кг, находящемуся на горизонтальной поверхности, приложена сила. Учитывая, что коэффициент трения равен 0,7, определите:
- силу трения для случая, если F = 50 Н и направлена горизонтально;
- силу трения для случая, если F = 80 Н и направлена горизонтально;
- построить график зависимости ускорения бруска от горизонтально приложенной силы;
- с какой минимальной силой нужно тянуть за веревку, чтобы равномерно перемещать брусок?
Решение:
1. Определим максимальную силу трения покоя. Она будет равна:
| μmg = 0,7×10×10 = 70 (H). |
Приложенной силы будет недостаточно для того, чтобы сдвинуть тело. По третьему закону Ньютона F = Fmp= 50 H.
2. В случае приложенной силы F = 80 Н тело приобретает ускорение, равное:
| a = | = 1 м/с2. | |
| m |
3. Для построения зависимости a(F) воспользуемся функцией:
| a = | F − Fmp | = | F − μmg | = | F | − μg. (1) |
| m | m | m |
Из уравнения (1) можно сделать вывод, что зависимость ускорения от горизонтально приложенной силы линейная.
При F = 0 a = −μg, а при a = 0 F = μmg. Построим график зависимости a(F), см. рисунок.
4. Запишем уравнение движения санок в проекциях на горизонтальное и вертикальное направления:
| −Fmp + F cos α = 0 |
и
| −mg + N + F sin α = 0, |
где α — угол между веревкой и горизонтом, а сила трения равна Fmp= μN. Из записанных уравнений найдем силу натяжения веревки:
| F = | μmg | . (2) |
| cos α + μ • sin α |
Ее значение зависит от угла
Таким образом, на результат влияют два конкурирующих фактора. Для выяснения, при каких α превалирует первый из них, а при каких — второй, представим зависимость
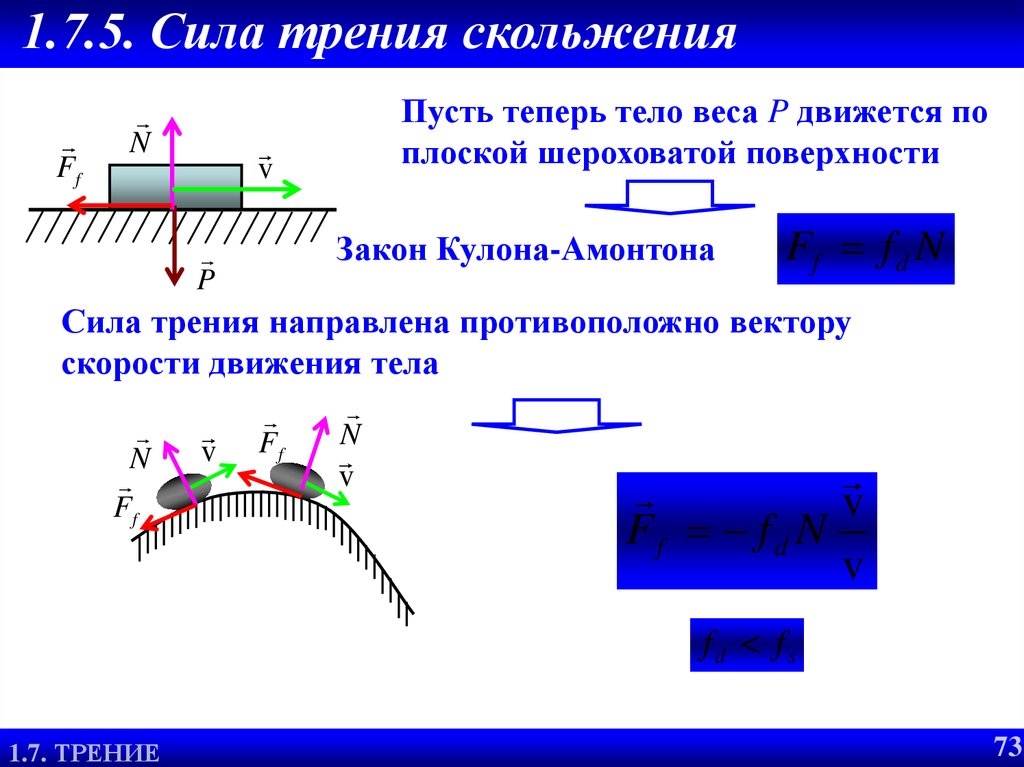Функция (2) минимальна, когда знаменатель максимален. Обозначим знаменатель буквой y. Найдем производную y’ по α и приравняем ее к нулю:| y’ = −sin α + μ cos α = 0. |
Отсюда, обозначив соответствующий угол как
| tg αо = μ |
и
| αо + arctg μ = 35°. |
Тогда:
| Fmin = | μmg | . |
| cos αo + μsin αo |
Используя тригонометрические соотношения и предыдущее равенство, найдем:
| cos αo = | 1 | = | 1 | , |
| √(tg2αo + 1) | √(μ2 + 1) |
| sin αo = | tg αo | = | μ | . |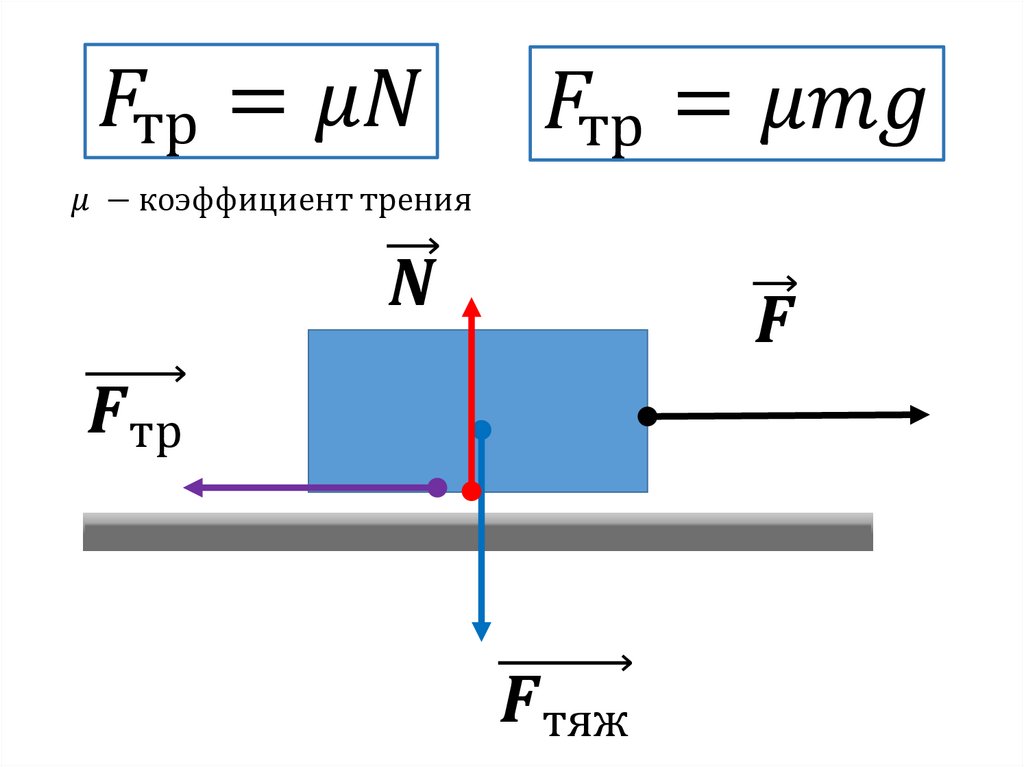
| √(tg2αo + 1) | √(μ2 + 1) |
Следовательно:
| Fmin= | μmg | = 56 H. |
| √(μ2 + 1) |
Далее: зависимость потока воды от температуры [тема: графическое решение задач по физике]
1.Сравните силу трения скольжения и силу трения покоя:что у них общего и чем они различаются?…
При соприкосновении тел между ними наблюдается взаимодействие. Силу, характеризующую это взаимодействие, называют силой реакции поверхности, обозначают как и представляют в виде суммы сил, составляющих ее:, где–сила нормальной реакции поверхности, направленная перпендикулярно этой поверхности,–сила трения, направленная вдоль этой поверхности.
При контакте гладких поверхностей Fтр= 0 и.
Простейшее соотношение между модулями сил, составляющих силу реакции поверхности, формулируется в виде закона сухого трения:
При скольжении модуль силы трения прямопропорционален модулю силы нормальной реакции:
Коэффициент пропорциональности –коэффициент трения скольженияне зависит ни от площади соприкасающихся поверхностей, ни от скорости их относительного движения.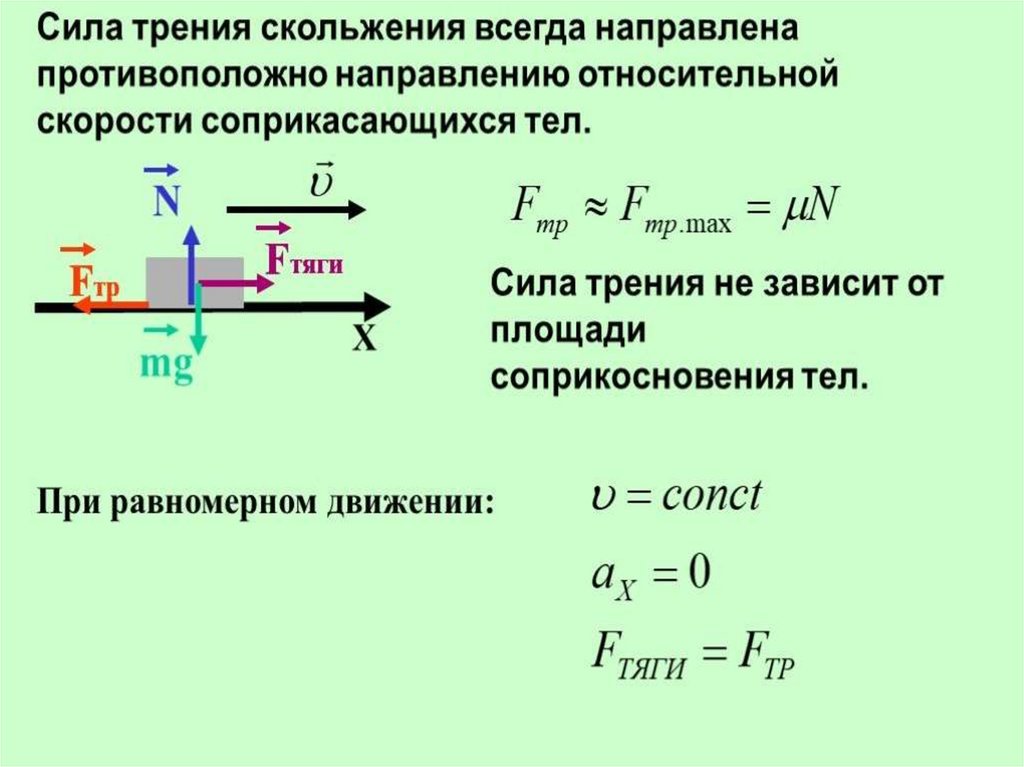
Если скольжение не происходит, то максимально возможное значение силы трения покоя равно значению силы трения скольжения:
Значение и направление силы трения покоя отыскиваются из услови неподвижности тела относительно опоры.
При постепенном увеличении (со временем) силы , приложенной вдоль трущихся поверхностей, происходит аналогичный рост силы трения покоя (рис. 9). Силы, действующие вдоль поверхности, скомпенсированы, поэтому тело покоится. Когда модуль силыдостигнет значенияN, модуль силы трения покоя достигает своего максимального значения, а затем сила трения уже не уравновешивает внешнюю силу, и тело начинает скользить, разгоняясь (рис. 9).
Рис. 9
В реальных экспериментах закон сухого трения выполняется приближенно.
9. Закон всемирного тяготения. Гравитационное поле. Невесомость
Закон всемирного тяготения – сила гравитационного притяжения любых двух материальных точек прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.
Рис. 3
Рис. 4
Гравитационную массу m1(илиm2) определяют сравнением ее с массой эталонного тела – цилиндра из платино-иридиевого сплава, масса которого принята за 1 кг (рис. 3). Процесс сравнения масс на рычажных весах называется взвешиванием (рис. 4). Гравитационная постояннаяG= 6,67·10–11Н.м2/кг2впервые была измерена английским физиком Кавендишем в 1798 году.
Закон всемирного тяготения сформулирован для материальных точек. Если его применять к протяженному телу, то это тело следует разбить на малые части, а затем использовать принцип суперпозиции сил.
Ньютон доказал, что закон можно применять для расчета сил взаимодействия между симметричными сферическими телами, если считать, что r– это расстояние между их центрами (рис. 5).
Рис. 5
Для расчета силы притяжения между двумя телами произвольной формы (например, два куба) закон всемирного тяготения в таком виде неприменим.
Силу всемирного тяготения называют силой тяжести, если рассматривают притяжение к Земле тел, которые достаточно малы по сравнению с размером самой Земли.
Для тел массой m, расположенных близко к поверхности Земли, установлено, что сила притяжения примерно равна:
где g9,8 м/с2– ускорение свободного падения. При точном измеренииgдолжно зависеть от распределения пород на Земле, места расположения тела на Земле и от высоты над уровнем моря.
На полюсах Земли ускорение свободного падения больше, так как Земля сплюснута с полюсов.
Рис. 6
Вес тела– это сила, с которой тело вследствие притяжения Земли давит на горизонтальную опору или растягивает вертикальный подвес. Таким образом, если на чаше весов стоит гиря, то вес – это сила, действующая не на гирю, а на чашу весов (рис. 6). Вес тела действует на подставку (опору) или подвес. При взвешивании в системе отсчета, покоящейся относительно Земли, вес неподвижного тела и сила тяжести совпадают, если не учитывать малые поправки, связанные с вращением Земли. Если весы движутся с ускорением, то вес может быть и больше, и меньше силы тяжести. Так, точные пружинные весы показывают вес тела, а не силу притяжения к Земле.
На экваторе или в лифте, движущемся с ускорением, направленным вниз, вес тела меньше силы тяжести.
Если тело не давит на опору или не натягивает подвес, то говорят, что тело находится в состоянии невесомости. Если лифт и весы падают с ускорением свободного падения независимо друг от друга, то груз не давит на чашу, поэтому вес груза равен нулю, т.е. груз находится в состоянии невесомости.
Приложенная сила и трение | Класс физики
Теперь, когда мы разобрались с основами, давайте перейдем к более сложным силам.
Приложенная сила
Приложенная сила особенная, поскольку представляет собой обобщенную и упрощенную форму множества различных сил. По сути, приложенная сила представляет собой механическую силу, приложенную к объекту другим объектом. Например, человек, прилагающий силу 10 Н, чтобы толкнуть коробку, считается приложенной силой.
Примеры:
- Автомобильный двигатель прилагает силу, чтобы заставить автомобиль двигаться вперед
- Двигатель лифта прилагает усилие для перемещения лифта вверх
- Вы ударили по шайбе клюшкой
- Вы бросаете мяч рукой
***В примере двигателя лифта, тянущего лифт вверх, какова нормальная сила, действующая на людей, стоящих внутри лифта? Ответ (выделите, чтобы прочитать): Ноль, потому что нормальная сила — это ленивая реакционная сила и действует на объекты только тогда, когда это необходимо.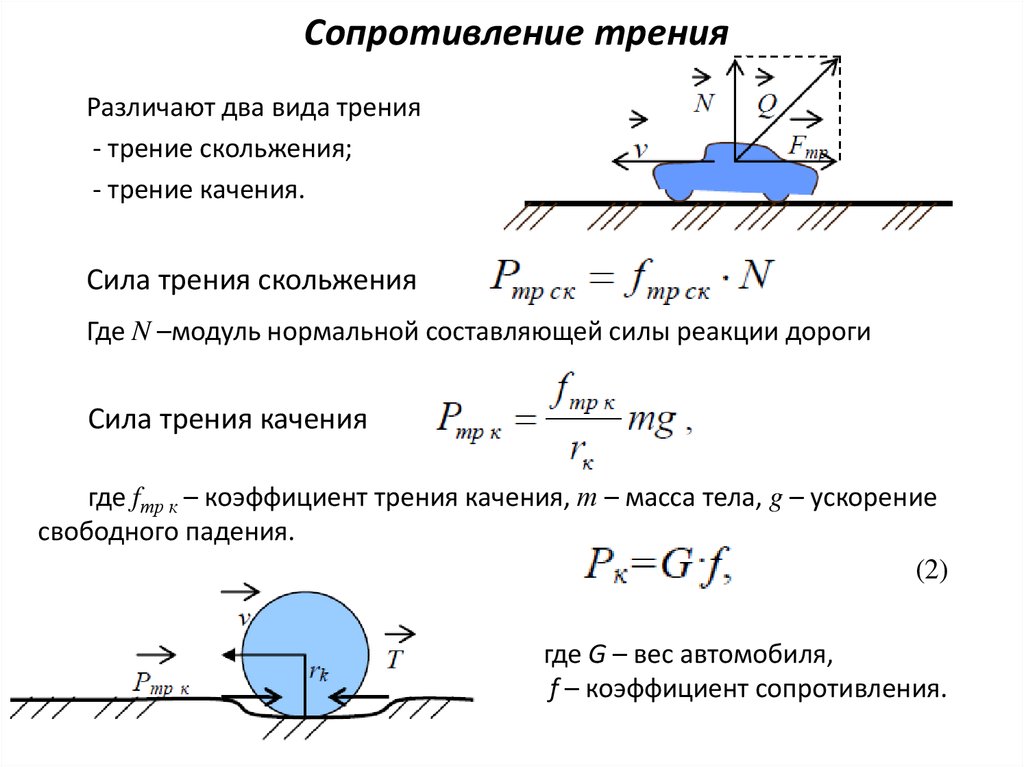
Сила трения
Название этой силы дает большую часть ее определения. Сила трения — еще одна реактивная сила, возрастающая в зависимости от массы объекта и поверхности, по которой происходит трение. Давайте снова возьмем пример сверху.
Человек толкает коробку. Однако земля покрыта льдом. Ожидаете ли вы, что этот объект будет легче или труднее толкать, чем если бы он шел по бетонной поверхности? Правильно, лед обеспечивает меньшее трение и позволяет меньше трения и, следовательно, его легче толкать. В качестве альтернативы, если есть два ящика, которые нужно толкать, и один из них весит 10 кг, а другой 1000 кг, что будет труднее толкать? Тяжелее, это точно! Помните, что в этих случаях сила трения противоположна приложенной силе. Или еще лучше, сила трения всегда противоположна направлению движения.
Рассмотрим математическое представление трения:
Где:
- Ff сила трения (в ньютонах)
- μ — коэффициент трения (без единиц)
- Fn — нормальная сила (в ньютонах)
Коэффициент трения — положительное рациональное число, указывающее на шероховатость трения. Например, если стул с войлочным дном волочится по скользкому деревянному полу, коэффициент трения будет относительно ниже, чем если бы этот же стул волочили по ковру.
Статическое и кинетическое трение
Вы когда-нибудь замечали, что когда вы пытаетесь толкнуть что-то очень тяжелое, но как только вы немного сдвинули его с места, остальная часть толчка требует значительно меньших усилий? Вы не сумасшедший! Существует два типа трения, статическое трение и кинетическое трение, и почти всегда статическое трение выше, чем кинетическое трение.
Статическое трение относится к силе трения, необходимой для преодоления стоящего объекта, а кинетическое трение — к силе трения, необходимой для преодоления движущегося объекта. Таким образом, чтобы заставить объект двигаться, вам нужно учитывать статическое трение, а чтобы ускорить или замедлить объект, уже находящийся в движении, вам нужно учитывать кинетическое трение.
Ниже вы можете найти графическое представление статического и кинетического трения в зависимости от времени при попытке переместить неподвижный объект.
Начальный горб — это величина статического трения, необходимая для перемещения объекта, а последующее плато — это величина трения, присутствующая, когда объект уже находится в движении.
Для расчета статического и кинетического трения вам нужно всего лишь применить приведенную выше формулу, используя либо коэффициент статического трения, либо коэффициент кинетического трения.
Нравится:
Нравится Загрузка…
Применение трех законов Ньютона: силы трения
Другой довольно распространенной силой является сила трения. Как обычно
сила, это вызвано непосредственным контактом между поверхностями. Однако пока
нормальная сила всегда перпендикулярна поверхности, сила трения
сила всегда параллельна поверхности. Чтобы полностью описать
Причина трения требует знаний, выходящих за рамки классического
механика. Для наших целей достаточно знать, что трение возникает
электрическим взаимодействием между двумя поверхностями на микроскопическом
уровень.
Статические силы трения
Рассмотрим пример двух блоков, один из которых лежит поверх другого. Если
присутствует трение, требуется определенная минимальная горизонтальная сила, чтобы
переместить верхний блок. Если горизонтальная сила меньше этой минимальной силы
приложенная к верхнему блоку, должна действовать сила, противодействующая приложенной силе
и держать блок в покое. Эта сила называется силой трения покоя.
сила, и она изменяется в зависимости от величины силы, приложенной к
блокировать. Если сила не приложена, очевидно, что статическое трение отсутствует.
сила. Чем больше прилагается сила, тем больше статическая сила трения.
пока не достигнет определенного максимального значения; как только горизонтальная сила
превышает максимальную силу трения, блок начинает двигаться. сила трения, определяемая как F s max удобно пропорциональна
нормальная сила между двумя поверхностями:
| F с макс = μ с F N | 8888
Константа пропорциональности μ с называется коэффициентом статическое трение, и является свойством материалов, которые взаимодействуют (т.е. два взаимодействующих необработанных материала будут иметь более высокое значение мк с чем два гладких материала).
Это уравнение для максимальной статической силы трения содержит много информации, и необходимо сделать несколько пояснений.
- Похоже, что уравнение связывает два вектора: F s max и F N .
Это соотношение справедливо только для величин векторов, а не
направление.
На самом деле два вектора всегда будут перпендикулярны. - Уравнение вводит понятие коэффициента статики трение. Эта константа варьируется от материала к материалу, но не не зависит от ориентации материала на поверхности. За например, если деревянный брусок поставить на бетонную платформу, μ s не зависит от того, находится ли блок на боку, спереди или сверху. Другими словами, коэффициент , а не изменяется в зависимости от площадь поверхности контакта.
- Поскольку в уравнении не указано направление силы трения, необходимо констатировать и понять, что сила трения всегда действует в направление, противоположное силе, приложенной к объекту.
- Это
жизненно важно помнить, что это уравнение дает только максимальная сила статического трения , что соответствует максимальному
сила, которую можно приложить к телу до его движения. Если меньше
к телу приложена сила, сила трения меньше максимальной
сила противодействует первоначальной силе.
Хотя довольно удивительно, что сила трения и нормальная сила связаны таким простым образом, физическая интуиция подсказывает нам, что они должны быть связаны напрямую. Рассмотрим снова деревянный брусок на бетонном Платформа. Нормальная сила определяется весом дерева. Если к древесине прилагается дополнительная направленная вниз сила (производящая большее нормальная сила) поверхности на самом деле находятся в более тесном контакте, чем они были раньше, и результирующие электрические взаимодействия сильнее. Таким образом, интуитивно большая нормальная сила дает большую силу трения. Наша интуиция согласна с уравнением.
Кинетические силы трения
Как только к объекту приложена сила, превышающая F s max , объект
начинает двигаться, и статические силы трения больше не действуют. Перемещение
объект по-прежнему испытывает силу трения, но другой
природа. Мы называем эту силу кинетической силой трения. кинетический
сила трения всегда противодействует движению тела и равна
независимо от скорости. Независимо от скорости объекта (пока v ≤ 0) на него действует та же сила трения. Также для того же
причинам, как объясняется статическим трением, кинетическая сила трения равна
пропорциональна нормальной силе:
| F k = μ k F N |
Это уравнение имеет тот же вид, что и уравнение для максимального статического трения.
сила и определяет коэффициент кинетического трения, μ k , что
имеет те же свойства, что и μ s , но другое значение. мк к есть
свойство взаимодействующих материалов и, как и μ s , не зависит
ориентации предметов. Единственная существенная разница между
двух уравнений трения заключается в том, что первое измеряет трение между
два неподвижных объекта, и его значение зависит от силы, приложенной к
один, а второй измеряет силу трения, которая существует только тогда, когда один из
объекты движутся и не зависят от силы, приложенной к
блокировать.
