Сила трения покоя — определение термина

это сила, возникающая между двумя телами, соприкасающимися своими поверхностями, в том случае, когда тела покоятся друга относительно друга.

Научные статьи на тему «Сила трения покоя»

тел, называется силой трения покоя….
Причины силы трения покоя такие же, как у силы трения скольжения….
Сила трения покоя возникает, когда пытаются сдвинуть стоящее тело….
Замечание 2 В большинстве случаев максимальная сила трения покоя немного превосходит силу трения…
покоя равна силе трения скольжения; абсолютная величина силы трения скольжения прямо пропорциональна

Статья от экспертов

Приведены результаты разработанной автором динамической теории предельного трения, содержащей механическую модель динамического взаимодействия пары трения, а также аналитические законы, устанавливающие зависимость силы трения от времени остановки и от скорости тангенциального нагружения фрикционного контакта и указывающие на существование в природе новых универсальных физических констант в виде предельно возможных коэффициентов, сил и углов трения покоя и движения.

Приведена расчетная сводная диаграмма перехода тела от покоя к движению, охватывающая фазы предварительного смещения и возникновения фрикционных автоколебаний, а также режимы сухого, смешанного и жидкостного трения.

Creative Commons

Научный журнал

заметим максимальное значение силы трения покоя….
трения покоя….
Опыт показывает, что модуль силы трения скольжения $F_{mp} $, как и модуль максимальной силы трения покоя…
, пропорционален модулю силы реакции опоры: \[F_{mp} =\mu N.\] Максимальное значение силы трения покоя…
примерно равно силе трения скольжения, приближенно равны также коэффициенты трения покоя и скольжения

Статья от экспертов

В статье рассмотрено влияние сил трения в узлах уплотнений на динамические характеристики регуляторов давления газа.

Разработана математическая модель регулятора давления газа с учетом сил сухого трения. Выявлено негативное влияние на устойчивость системы автоматического регулирования с регуляторами давления газа разницы между силой трения покоя и движения. Представлены результаты проведенных экспериментов, которые подтверждают адекватность разработанной математической модели.

Creative Commons

Научный журнал

Повышай знания с онлайн-тренажером от Автор24!

1. Напиши термин
2. Выбери определение из предложенных или загрузи свое
3. Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных карточек

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2. 1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3.2 Термодинамика
• 4 Электродинамика
  • 4. 1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5.3 Фотометрия
  • 5.4 Квантовая оптика
  • 5. 5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

2.8: Трение — Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

46158

• OpenStax
• OpenStax

Цели обучения

• Обсудите общие характеристики трения.
• Описать различные виды трения.
• Объясните влияние трения на движение.

Трение  – это сила, постоянно присутствующая вокруг нас, которая противодействует относительному движению между контактирующими системами, но также позволяет нам двигаться (что вы обнаружили, если когда-либо пытались ходить по льду). Хотя трение является обычной силой, поведение трения на самом деле очень сложное и до сих пор полностью не изучено. Мы должны в значительной степени полагаться на наблюдения для любого понимания, которое мы можем получить. Однако мы все еще можем иметь дело с его более элементарными общими характеристиками и понять обстоятельства, в которых он ведет себя.

Определение: ТРЕНИЕ

Трение – это сила, противодействующая относительному движению между контактирующими системами.

Одной из самых простых характеристик трения является то, что оно параллельно поверхности контакта между системами и всегда в направлении, противодействующем движению или попытке движения систем друг относительно друга. Если две системы находятся в контакте и движутся друг относительно друга, то трение между ними называется кинетическим трением . Например, трение замедляет скольжение хоккейной шайбы по льду. Но когда объекты неподвижны,

статическое трение  может действовать между ними; статическое трение обычно больше, чем кинетическое трение между объектами.

Определение: КИНЕТИЧЕСКОЕ ТРЕНИЕ

Если две системы находятся в контакте и движутся друг относительно друга, то трение между ними называется кинетическим трением.

Представьте, например, что вы пытаетесь сдвинуть тяжелый ящик по бетонному полу — вы можете давить на ящик все сильнее и сильнее и не двигать его вообще. Это означает, что статическое трение реагирует на то, что вы делаете — оно увеличивается, чтобы быть равным вашему толчку и в противоположном направлении. Но если вы, наконец, нажмете достаточно сильно, ящик, кажется, внезапно соскользнет и начнет двигаться. Находясь в движении, его легче поддерживать в движении, чем было запустить, что указывает на то, что кинетическая сила трения меньше, чем статическая сила трения. Если вы добавляете массу к ящику, скажем, кладете на него коробку, вам нужно давить еще сильнее, чтобы он начал двигаться, а также чтобы он продолжал двигаться. Кроме того, если вы смазаете бетон маслом, вам будет легче запустить ящик и поддерживать его в рабочем состоянии (как и следовало ожидать).

На рисунке \(\PageIndex{1}\) грубо показано, как возникает трение на границе раздела двух объектов. При ближайшем рассмотрении этих поверхностей видно, что они шероховатые. Поэтому, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет прыгать вместе с ударами только кончиками поверхности, отламывать точки или делать и то, и другое. Значительной силе можно сопротивляться трением без видимого движения. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик кладут еще одну коробку), тем больше усилий требуется для их перемещения. Часть трения обусловлена ​​силами сцепления между поверхностными молекулами двух объектов, которые объясняют зависимость трения от природы веществ. Адгезия зависит от контактирующих веществ и представляет собой сложный аспект физики поверхности. Когда объект движется, становится меньше точек соприкосновения (меньше прилипающих молекул), поэтому для удержания объекта в движении требуется меньшее усилие. При малых, но отличных от нуля скоростях трение почти не зависит от скорости.

Рисунок \(\PageIndex{1}\): Силы трения, такие как \(f\), всегда препятствуют движению или попытке движения между соприкасающимися объектами. Трение возникает отчасти из-за шероховатости соприкасающихся поверхностей, как видно на увеличенном виде. Для того чтобы объект двигался, он должен подняться туда, где пики могут проскакивать по нижней поверхности. Таким образом, сила требуется только для того, чтобы привести объект в движение. Некоторые из пиков будут сломаны, что также потребует силы для поддержания движения. На самом деле большая часть трения возникает из-за сил притяжения между молекулами, составляющими два объекта, так что даже идеально гладкие поверхности не лишены трения. Такие силы сцепления также зависят от веществ, из которых сделаны поверхности, что объясняет, например, почему обувь с резиновой подошвой скользит меньше, чем обувь с кожаной подошвой.

Величина силы трения имеет две формы: одна для статических ситуаций (статическое трение), другая для случая движения (кинетическое трение).

Когда между объектами нет движения, величина трения покоя f _s  равна

\[f_{\mathrm{s}} \leq \mu_{\mathrm{s}} N, \nonumber \]

, где \(\mu_{\mathrm{s}}\) – коэффициент трения покоя, а  N  – величина нормальной силы (силы, перпендикулярной поверхности).

ВЕЛИЧИНА СТАТИЧЕСКОГО ТРЕНИЯ

Величина статического трения \(f_{\mathrm{s}}\) равна

\[f_{\mathrm{s}} \leq \mu_{\mathrm{s}} N, \ nonumber\]

, где \(\mu _{\mathrm{s}}\) – коэффициент трения покоя, а N – величина нормальной силы.

Символ ≤ означает, что меньше или равно , подразумевая, что трение покоя может иметь минимальное и максимальное значение \(\mu_{\mathrm{s}} Н\). Статическое трение — это реактивная сила, которая увеличивается, чтобы быть равной и противоположной любой приложенной силе, вплоть до своего максимального предела. Как только приложенная сила превысит \(f_{\mathrm{s}(\max)}\), объект начнет двигаться. Таким образом

\[f_{\mathrm{s}(\max)}=\mu_{\mathrm{s}} N. \nonumber \]

Когда объект движется, величина кинетического трения \(f_{\mathrm{k}}\) определяется как

\[\mathrm{f}_{\mathrm{k}}=\mu_{\mathrm{k}} N, \nonumber \]

, где \(\mu_{\mathrm{k}}\) – коэффициент кинетического трения. Система, в которой \(\mathrm{f}_{\mathrm{k}}=\mu_{\mathrm{k}} N\) описывается как система, в которой трение ведет себя просто .

ВЕЛИЧИНА КИНЕТИЧЕСКОГО ТРЕНИЯ

Величина кинетического трения \(f_{\mathrm{k}}\) определяется как

\[f_{\mathrm{k}}=\mu_{\mathrm{k}} N, \nonumber\]

, где \(\mu_{\mathrm{k}}\) – коэффициент кинетического трения.

Как видно из Таблицы \(\PageIndex{1}\), коэффициенты кинетического трения меньше, чем их статические аналоги. То, что значения \(\mu\) в Таблице \(\PageIndex{1}\) выражаются только одной или, самое большее, двумя цифрами, указывает на приблизительное описание трения, данное двумя приведенными выше уравнениями.

Таблица \(\PageIndex{1}\): коэффициенты статического и кинетического трения

Система	Статическое трение \(\mu_{\mathrm{s}}\)	Кинетическое трение \(\mu_{\mathrm{k}}\)
Резина на сухом бетоне	1,0	0,7
Резина на мокром бетоне	0,7	0,5
Дерево на дереве	0,5	0,3
Вощеная древесина на мокром снегу	0,14	0,1
Металл на дереве	0,5	0,3
Сталь по стали (сухая)	0,6	0,3
Сталь по стали (промасленный)	0,05	0,03
Тефлон на стали	0,04	0,04
Кость, смазанная синовиальной жидкостью	0,016	0,015
Туфли на дереве	0,9	0,7
Обувь для льда	0,1	0,05
Лед на льду	0,1	0,03
Сталь на льду	0,4	0,02

Приведенные ранее уравнения включают зависимость трения от материалов и нормальной силы. Направление трения всегда противоположно движению, параллельно поверхности между объектами и перпендикулярно нормальной силе. Например, если ящик, который вы пытаетесь толкнуть (с силой, параллельной полу), имеет массу 100 кг, то нормальная сила будет равна его весу, \(W=m g=(100 \mathrm{~kg })\влево(9{2}\right)=980 \mathrm{~N}\), перпендикулярно полу. Если коэффициент статического трения равен 0,45, вам придется приложить силу, параллельную полу, большую, чем )(980 \mathrm{~N})=440 \mathrm{~N}\), чтобы переместить ящик. Когда есть движение, трение меньше, а коэффициент кинетического трения может быть 0,30, так что сила всего 290 Н (\(f _ {\ mathrm {k}} = \ mu _ {\ mathrm {k}} Н = ( 0,30)(980 \mathrm{~N})=290 \mathrm{~N}\)) будет поддерживать постоянную скорость. Если пол смазан, оба коэффициента значительно меньше, чем без смазки. Коэффициент трения – это безразмерная величина, величина которой обычно находится в диапазоне от 0 до 1,0. Коэффициент трения зависит от двух соприкасающихся поверхностей.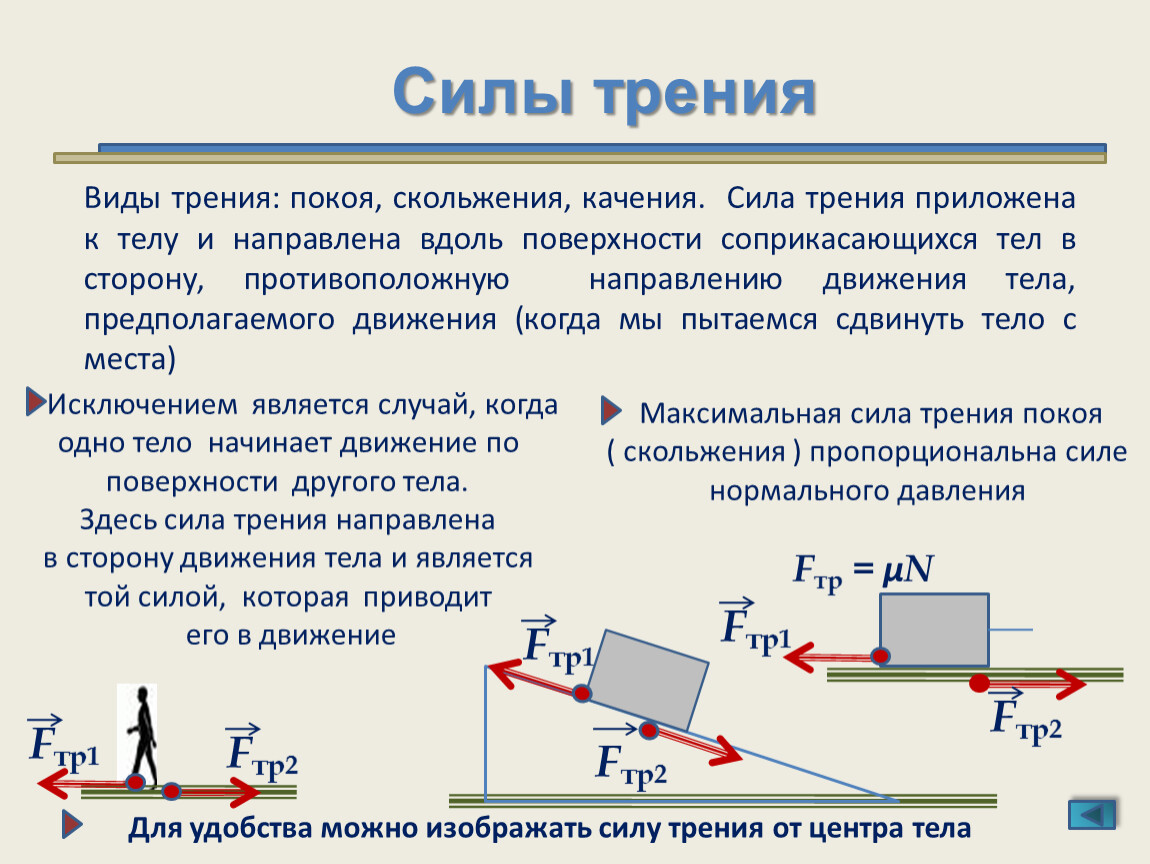

ЭКСПЕРИМЕНТ ДЛЯ ДОМА

Найдите небольшой пластиковый предмет (например, пищевой контейнер) и поставьте его на кухонный стол, слегка постукивая по нему. Теперь распылите воду на стол, имитируя легкий дождь. Что происходит теперь, когда вы нажимаете на объект того же размера? Теперь добавьте несколько капель масла (растительного или оливкового) на поверхность воды и дайте такой же кран. Что происходит сейчас? Эта последняя ситуация особенно важна для водителей, особенно после небольшого дождя. Почему?

Многие люди испытывают скользкость при ходьбе по льду. Однако многие части тела, особенно суставы, имеют гораздо меньший коэффициент трения — часто в три-четыре раза меньше, чем лед. Сустав образован концами двух костей, которые соединены толстыми тканями. Коленный сустав образован костью голени (голенью) и бедренной костью (бедренной костью). Тазобедренный сустав представляет собой шаровидный (на конце бедренной кости) и впадинный (часть таза) сустав. Концы костей в суставе покрыты хрящом, что обеспечивает гладкую, почти стекловидную поверхность. Суставы также вырабатывают жидкость (синовиальную жидкость), которая уменьшает трение и износ. Поврежденный или пораженный артритом сустав можно заменить искусственным суставом (рис. \(\PageIndex{2}\)). Эти заменители могут быть изготовлены из металлов (нержавеющая сталь или титан) или пластмассы (полиэтилен), также с очень низкими коэффициентами трения.

Рисунок \(\PageIndex{2}\): Искусственная замена коленного сустава — это процедура, которая проводится уже более 20 лет. На этом рисунке мы видим послеоперационные рентгеновские снимки замены правого коленного сустава. (Фото: Майк Бэрд, Flickr)

Другие природные смазки включают слюну, вырабатываемую во рту, чтобы помочь в процессе глотания, и скользкую слизь, находящуюся между органами в теле, позволяющую им свободно перемещаться друг мимо друга во время сердцебиения, во время дыхания, и когда человек двигается. Искусственные смазки также распространены в больницах и поликлиниках. Например, при ультразвуковой визуализации гель, соединяющий датчик с кожей, также служит для смазывания поверхности между датчиком и кожей, тем самым снижая коэффициент трения между двумя поверхностями. Это позволяет датчику свободно перемещаться по коже.

Мы обсудили, что когда объект лежит на горизонтальной поверхности, на него действует нормальная сила, равная по величине его весу. Кроме того, простое трение всегда пропорционально нормальной силе.

СОЗДАНИЕ СОЕДИНЕНИЙ: СУБМИКРОСКОПИЧЕСКОЕ ОБЪЯСНЕНИЕ ТРЕНИЯ

Более простые аспекты трения, с которыми мы имели дело до сих пор, — это его макроскопические (крупномасштабные) характеристики. За последние несколько десятилетий были достигнуты большие успехи в объяснении трения на атомном уровне. Исследователи обнаружили, что атомарная природа трения, по-видимому, имеет несколько фундаментальных характеристик. Эти характеристики не только объясняют некоторые из более простых аспектов трения, они также несут в себе потенциал для разработки сред, почти свободных от трения, которые могли бы сэкономить сотни миллиардов долларов энергии, которая в настоящее время преобразуется (без необходимости) в тепло.

Рисунок \(\PageIndex{3}\) иллюстрирует одну макроскопическую характеристику трения, которая объясняется микроскопическими (мелкомасштабными) исследованиями. Мы заметили, что трение пропорционально нормальной силе, но не площади контакта, что несколько противоречит здравому смыслу. Когда соприкасаются две шероховатые поверхности, фактическая площадь контакта составляет крошечную часть от общей площади, поскольку соприкасаются только высокие точки. Когда действует большая нормальная сила, фактическая площадь контакта увеличивается, и оказывается, что трение пропорционально этой площади.

Рисунок \(\PageIndex{3}\): Две соприкасающиеся шероховатые поверхности имеют гораздо меньшую площадь фактического контакта, чем их общая площадь. Когда имеется большая нормальная сила в результате большей приложенной силы, площадь фактического контакта увеличивается, как и трение.

Но представление в атомном масштабе обещает объяснить гораздо больше, чем более простые особенности трения. В настоящее время определяется механизм образования тепла. Другими словами, почему поверхности нагреваются при трении? По сути, атомы связаны друг с другом, образуя решетки.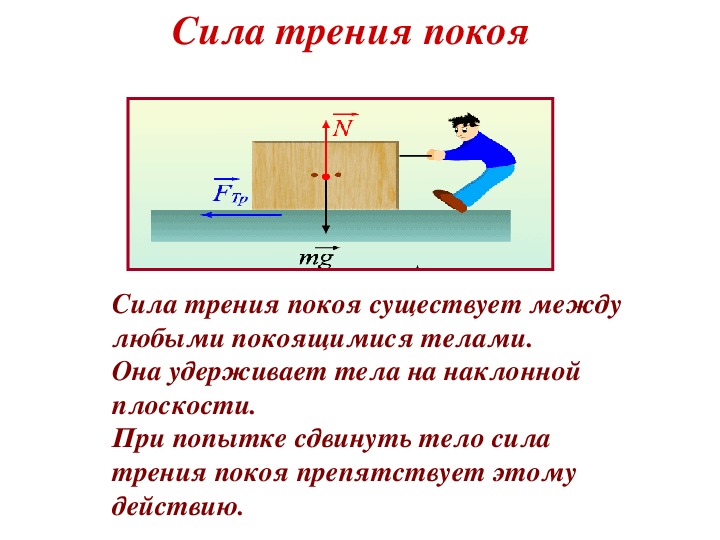 {12}\)) , и его трудно предсказать теоретически, но напряжение сдвига дает фундаментальное понимание крупномасштабного явления, известного с древних времен, — трения.

Рисунок \(\PageIndex{4}\): Наконечник зонда деформируется вбок под действием силы трения, когда зонд тащит по поверхности. Измерения того, как сила меняется для разных материалов, дают фундаментальное представление об атомной природе трения.

Резюме раздела

• Трение — это контактная сила между системами, которая препятствует движению или попытке движения между ними. Простое трение пропорционально нормальной силе Н , толкающей системы друг к другу. (Нормальная сила всегда перпендикулярна поверхности контакта между системами.) Трение зависит от обоих задействованных материалов. Величина статического трения \(f_{\mathrm{s}}\) между системами, стационарными друг относительно друга, определяется выражением

  \[f_{\mathrm{s}} \leq \mu_{\mathrm{s}} N, \nonumber\]

  где \(\mu_{\mathrm{s}}\) – коэффициент статического трения, зависящий от обоих материалов.
• Кинетическая сила трения \(f_{\mathrm{k}}\) между системами, движущимися относительно друг друга, определяется выражением

  \[f_{\mathrm{k}}=\mu_{\mathrm{k}} N, \nonumber\]

  где \(\mu_{\mathrm{k}}\) – коэффициент кинетического трения, который также зависит от обоих материалов.

Глоссарий

трение

сила, противодействующая относительному движению или попыткам движения между системами, находящимися в контакте

кинетическое трение

сила, противодействующая движению двух систем, находящихся в контакте и движущихся относительно друг друга

статическое трение

сила, противодействующая движению двух систем, находящихся в контакте и не движущихся относительно друг друга

величина трения покоя

\(f_{\mathrm{s}} \leq \mu_{\mathrm{s}} N\), где \(\mu_{\mathrm{s}}\)  – коэффициент трения покоя, а \(N \) есть величина нормальной силы

величина кинетического трения

\(f_{\mathrm{k}}=\mu_{\mathrm{k}} N\), где \(\mu_{\mathrm{k}}\) — коэффициент кинетического трения

---

Эта страница под названием 2. 8: Friction распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

2. Теги

   На этой странице нет тегов.

Статическое трение: определение, взаимосвязь и формулы

Трение очень важно в нашей повседневной жизни, так как помогает предотвратить скольжение автомобильных шин по льду зимой и позволяет автомобилю остановиться при торможении.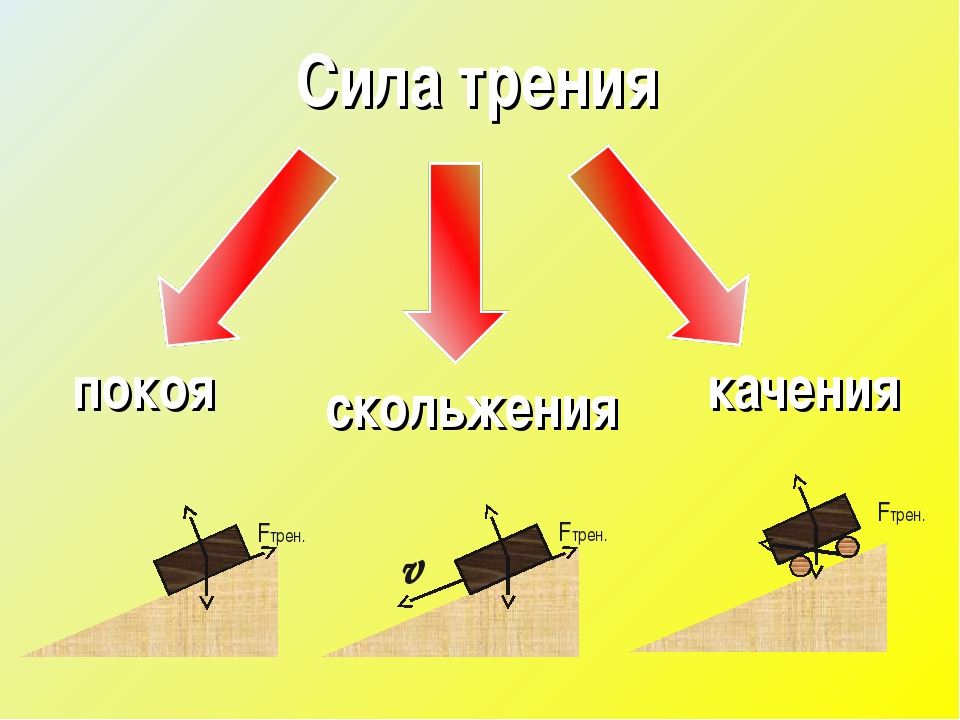 Человек, прыгающий с парашютом при спуске, ощущает сопротивление воздуха, представляющее собой силу жидкостного трения, оказываемую воздухом на движущееся тело. Кроме того, мяч, катящийся по земле, будет замедляться до тех пор, пока в конечном итоге не остановится из-за трения качения, оба из которых являются примерами контактных сил.

Рис. 1. Люди пытаются преодолеть силу трения покоя, чтобы столкнуть заглохший автомобиль с дороги.

Если два тела касаются друг друга напрямую, они соприкасаются. Контактные силы используются для объяснения взаимодействия между двумя телами. Некоторые примеры контактных сил включают нормальную силу и силу трения. Есть два основных типа сил трения, в которые попадают все остальные; статическое и кинетическое трение. В этой статье мы сосредоточимся на силе трения покоя и объясним ее математическое представление. Мы также обсудим различия между статическим и кинетическим трением.

Статическое трение: определение

Если у нас есть коробка на полу, и мы пытаемся толкнуть ее с некоторой силой, коробка может просто стоять на месте и не двигаться.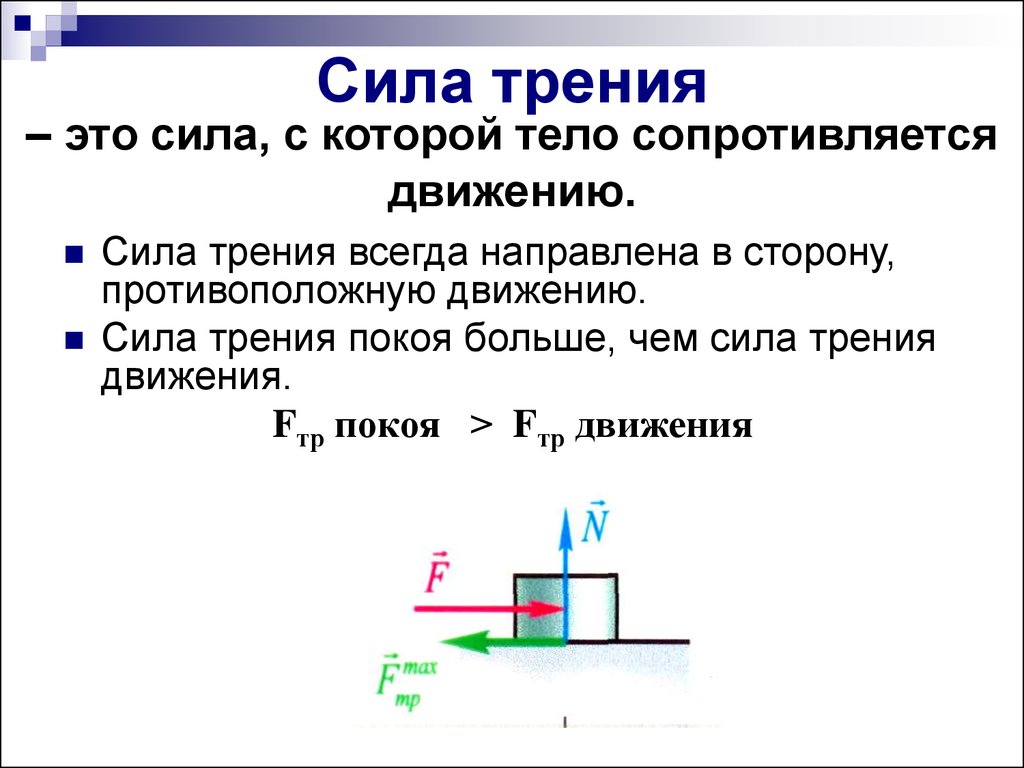 Это происходит из-за силы статического трения . Статическая сила трения возникает, когда объект и поверхность покоятся друг относительно друга. Нет движения одного относительно другого. Из-за статического трения объект будет оставаться неподвижным на поверхности, не скользя. На пол действует сила статического трения, равная по величине и противоположная по направлению приложенной силе, пока приложенная сила не превысит максимальную силу статического трения. Сила трения покоя может быть представлена ​​как \(\overset\rightharpoonup{f_{\mathrm s}}\).

Важно отметить, что это не имеет никакого отношения к третьему закону Ньютона, так как пара сила-противодействие всегда действует на разные объекты.

Рис. 2. Коробка, изначально находящаяся в состоянии покоя, испытывает приложенную силу \(\overset\rightharpoonup F\) для преодоления силы трения покоя.

На рисунке выше мы видим коробку, которая изначально находится в состоянии покоя. Нормальная сила \(\overset\rightharpoonup N\) направлена ​​вверх и действует на коробку со стороны пола, а вес \(\overset\rightharpoonup W\) действует вниз.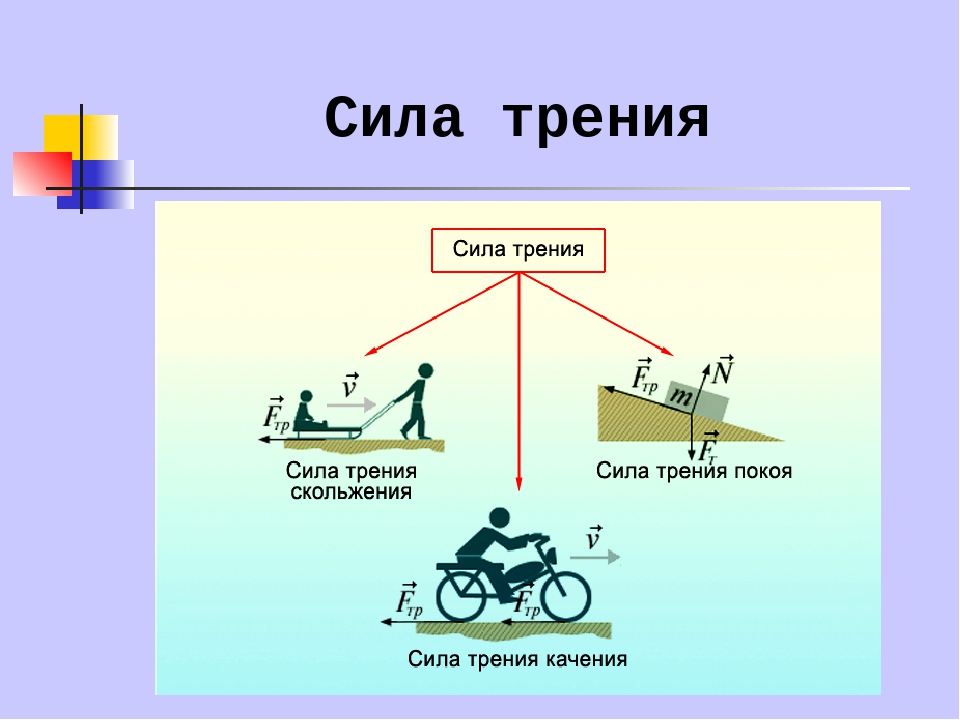 Поскольку ящик находится в равновесии, величины нормальной силы и веса равны.

Затем к ящику прикладывается сила \(\overset\rightharpoonup F\), которая тянет его вправо, со временем величина этой приложенной силы постепенно увеличивается. Коробка некоторое время будет находиться в состоянии покоя. Это связано с тем, что даже если сила увеличивается, сила трения покоя также увеличивается, чтобы уравновесить величину с силой \(\overset\rightharpoonup F\).

Сила, необходимая для перемещения ящика, равна и противоположна максимальной силе статического трения. Максимальное значение силы статического трения показано как \({(f _ {\mathrm s})}_\max\), и оно пропорционально величине нормальной силы. Коэффициент пропорциональности отображается как \(\mu_{\mathrm s}\) и называется коэффициент трения покоя . Как только максимальная сила статического трения будет преодолена, коробка начнет скользить вправо.

Статическое трение: формула

Реальное значение статического трения может варьироваться от нуля (когда на объект не действует сила) до максимального значения, которое математически представляется как

$$f_s\leq{(f_s) }_{max}=\mu_sN. $$

Согласно математическому представлению, отношение статического трения находится между величинами, так как величина статического трения пропорциональна как величине нормальной силы, так и шероховатости между двумя поверхностями в контакт. Следовательно, направления не имеют значения, как в векторных отношениях.

Итак, что означает эта формула?

• Когда приложенная сила \(\overset\rightharpoonup F\) равна значению, при котором начинается движение, можно использовать формулу для расчета величины силы трения покоя.
• Если сила \(\overset\rightharpoonup F\) не заставляет объект двигаться, то величина силы трения покоя должна быть меньше \(\mu_sN\). В этом случае величина силы трения покоя будет просто равна величине приложенной силы \(\overset\rightharpoonup F\).

Предельное трение

Мы упоминали, что существует предел, при котором сила \(\overrightarrow F\) превышает максимальное значение силы статического трения. Если предел превышен, коробка начинает двигаться. Когда сила статического трения максимальна и движение вот-вот начнется, сила трения называется ограничивающим трением . Когда движение начинается, объект больше не будет испытывать статическое трение. Вместо этого объект испытывает силу кинетического трения.

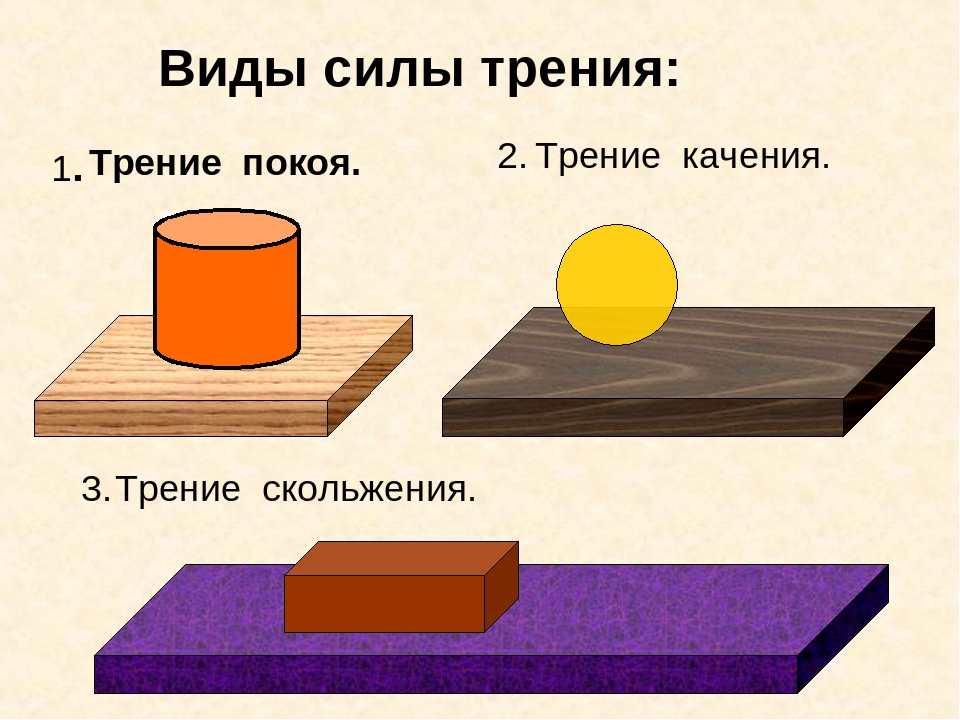
Рис. 3. Диаграмма, показывающая, как силы статического и кинетического трения изменяются с увеличением приложенной силы.

Если мы посмотрим на приведенный выше график, мы увидим, что с увеличением приложенной силы \(\overset\rightharpoonup F\) величина силы статического трения также начинает увеличиваться, пока не достигнет пика, где величина равна величине предельное трение. После этого объект начинает двигаться, и действует уже не статическая сила трения, а кинетическая сила трения.

Примеры статического трения

Теперь давайте рассмотрим несколько примеров, связанных с силой статического трения.

Рис. 4 – Ящик в покое. Приложенная сила недостаточно велика, чтобы преодолеть силу трения покоя. 2}\))

Решения

а) Когда объект находится в состоянии покоя и к нему приложена сила, величина силы равна величине силы трения покоя. Поскольку приложена сила \(10\,\mathrm N\), величина силы трения покоя также равна \(10\,\mathrm N\).

б) Величина максимальной силы трения покоя равна \(\mu_{\mathrm s}N\).

Поскольку значение максимальной силы трения покоя равно \(20\,\mathrm N\), его можно вставить вместо \({\left(f_s\right)}_\max\). Также указана масса объекта. Итак, мы можем рассчитать вес. 92\right),\\\mathrm W&=40\,\mathrm N.\end{align*}$$

Поскольку вес и нормальная сила имеют одинаковую величину, мы можем определить коэффициент трения покоя \(\ му _ {\ mathrm s} \).

$$\begin{align*}f _{\mathrm s}&=\mu _{\mathrm s}N,\\\mu _{\mathrm s}&=\frac{{\mathrm f}_{\mathrm s}}{\mathrm N},\\\mu _{\mathrm s}&=\frac{20\,\mathrm N}{40\,\mathrm N},\\\mu _{\mathrm s}&= 0.5.\end{align*}$$

Статическое трение против кинетического трения

Итак, что такое разница между статическим трением и кинетическим трением?

Различия между силами статического трения и кинетического трения можно обобщить следующим образом:

1. Статическое трение применяется только тогда, когда объект неподвижен, а кинетическая сила трения применяется, когда объект движется. (Способ запомнить ключевое различие между ними состоит в том, чтобы критически подумать об их определениях. В то время как статика означает отсутствие движения, кинетика означает отношение к движению или результат его действия.)
2. Максимальное значение силы статического трения всегда больше величины кинетической силы трения, потому что объекту всегда легче поддерживать движение, чем начать движение из состояния покоя.
3. Величина силы кинетического трения о сухую поверхность практически постоянна, независимо от скорости объекта. В то время как величина статического трения увеличивается с приложенной силой, пока не достигнет предельного трения.

Статическое трение — основные выводы

• Сила трения покоя прикладывается, когда объект находится в состоянии покоя.

• Когда приложенная сила \(\overset\rightharpoonup F\) достигает значения, при котором начинается движение, можно использовать формулу для расчета величины силы трения покоя.