Сила трения: введение

Эта статья открывает целый блок статей, связанных с определением силы трения в разных ситуациях. Для начала нужно четко себе представить, что, пока тело неподвижно, сила трения равна той силе, с которой воздействуют на тело, и только после того, как  тело сдвинется с места, сила трения больше не изменяется. Также помним обязательно тот факт, что произведение коэффициента трения на силу реакции опоры – это сила трения скольжения, и работает эта формула только когда тело уже движется.

Задача 1. На тело массой кг, лежащее на горизонтальной поверхности, начинает действовать сила . Коэффициент трения между телом и поверхностью . Определить ускорение тела, если модуль силы равен: а) 0,5 Н; б) 2Н; в) 2,5 Н. Построить график зависимости силы трения от силы . Считать м/с.

К задаче 1

Составим уравнение по второму закону, направив ось горизонтально вправо. Тогда

   

   

   

Ускорение тела равно:

   

Подставим численные данные, при Н получим:

   

Сила F и сила трения

Но ведь так не бывает, чтобы сила действовала в одну сторону, а ускорение тела было бы направлено в другую (об этом вроде бы свидетельствует минус)! То есть такой величины силы нам не хватит, чтобы сдвинуть тело с места. Тогда .

При Н получим:

   

Тело покоится или движется равномерно, .

При Н получим:

   

Сила трения равна Н.

 

Построим теперь график зависимости силы трения от силы :

Зависимость силы трения от приложенной силы

 

Задача 2. На тело массой кг начинает действовать горизонтальная сила, модуль которой линейно зависит от времени:  , где Н/с. Построить график зависимости модуля силы трения от времени, если коэффициент трения . Определить момент времени, когда тело стронется с места.

Тело стронется с места, когда величина силы станет равной силе трения. Сила трения скольжения равна Н.

Тогда момент трогания найдем из равенства:

   

   

   

График будет выглядеть точь-в-точь как в первой задаче.

Задача 3. Если к телу приложить силу Н под углом к горизонту, то тело будет двигаться равномерно. С каким ускорением будет двигаться тело, если ту же силу приложить под углом к горизонту? Масса тела 25 кг.

К задаче 3

Сначала разберемся с ситуацией 1: тело движется равномерно, сила направлена под углом к горизонту. Следовательно, горизонтальная проекция силы, с которой на него воздействуют, равна силе трения.

   

По вертикальной оси уравнение будет выглядеть так (силу реакции опоры не изобразила):

   

Найдем отсюда силу реакции опоры, которая позволит нам определить силу трения:

   

   

Таким образом, мы определили силу трения с двух различных сторон, и, приравняв эти выражения, сможем теперь определить коэффициент трения, который не был нам известен:

   

   

Теперь, зная коэффициент трения, рассмотрим ситуацию 2:  на тело воздействует сила под углом к горизонту.  Снова запишем все уравнения:

   

   

   

   

   

Тогда ускорение равно:

   

Когда задача в общем виде решена, давайте подставим числовые данные:

   

Ответ: 1 м/с.

 

Задача 4. С какой наименьшей силой нужно толкать перед собой тележку, масса которой кг, для того чтобы сдвинуть ее с места? Сила направлена вдоль ручки тележки и составляет с горизонтом угол , а коэффициент трения между полом и тележкой ?

К задаче 4

Горизонтальная проекция силы, с которой воздействуют на тележку, равна силе трения.

   

По вертикальной оси уравнение будет выглядеть так:

   

Найдем отсюда силу реакции опоры, которая позволит нам определить силу трения:

   

Тогда

   

Найдем отсюда :

   

   

   

Подставим числа:

   

Ответ: 72 Н

Задача 5: сила трения и график зависимости ускорения от силы

К бруску массой 10 кг, находящемуся на горизонтальной поверхности, приложена сила. Учитывая, что коэффициент трения равен 0,7, определите:

1. силу трения для случая, если F = 50 Н и направлена горизонтально;
2. силу трения для случая, если F = 80 Н и направлена горизонтально;
3. построить график зависимости ускорения бруска от горизонтально приложенной силы;
4. с какой минимальной силой нужно тянуть за веревку, чтобы равномерно перемещать брусок?

Решение:

1. Определим максимальную силу трения покоя. Она будет равна:

μmg = 0,7×10×10 = 70 (H).

Приложенной силы будет недостаточно для того, чтобы сдвинуть тело. По третьему закону Ньютона F = F_mp = 50 H.

2. В случае приложенной силы F = 80 Н тело приобретает ускорение, равное:

a =	F − Fmp	= 1 м/с2.
	m

3. Для построения зависимости

a(F) воспользуемся функцией:

a =	F − Fmp	=	F − μmg	=	F	− μg.     (1)
	m		m		m

Из уравнения (1) можно сделать вывод, что зависимость ускорения от горизонтально приложенной силы линейная.
При F = 0   a = −μg, а при a = 0   F = μmg. Построим график зависимости a(F), см. рисунок.

4. Запишем уравнение движения санок в проекциях на горизонтальное и вертикальное направления:

и

−mg + N + F sin α = 0,

где α — угол между веревкой и горизонтом, а сила трения равна F_mp = μN. Из записанных уравнений найдем силу натяжения веревки:

F =	μmg	.     (2)
	cos α + μ • sin α

Ее значение зависит от угла α. Проанализируем эту зависимость. Тело будет двигаться равномерно, если горизонтальная составляющая силы натяжения веревки Fcos α равна силе трения F_mp. Поэтому для обеспечения минимальной силы F веревку, казалось бы, надо тянуть горизонтально, т. е. под углом α = 0°. Но с другой стороны, желательно, чтобы угол α был побольше, так как в этом случае за счет увеличения вертикальной составляющей

Fsin α, стремящейся приподнять санки, уменьшается их давление на опору, и соответственно уменьшается сила трения.

Таким образом, на результат влияют два конкурирующих фактора. Для выяснения, при каких α превалирует первый из них, а при каких — второй, представим зависимость F = F(α) в виде графика. Из него видно, что исследуемая функция при α = α_о имеет минимум. Для нахождения значений α_о и F_min воспользуемся аналитическим методом. Функция (2) минимальна, когда знаменатель максимален. Обозначим знаменатель буквой

y. Найдем производную y’ по α и приравняем ее к нулю:

y’ = −sin α + μ cos α = 0.

Отсюда, обозначив соответствующий угол как α_о, получим: и Тогда:

Fmin =	μmg	.
	cos αo + μsin αo

Используя тригонометрические соотношения и предыдущее равенство, найдем:

cos αo =	1	=	1	,
	√(tg2αo + 1)		√(μ2 + 1)

sin αo =	tg αo	=	μ	.
	√(tg2αo + 1)		√(μ2 + 1)

Следовательно:

Fmin=	μmg	= 56 H.
	√(μ2 + 1)

Далее: зависимость потока воды от температуры   [тема: графическое решение задач по физике]

---

Глава 4. Сила трения

Сила трения возникает при скольжении шероховатых тел по шероховатым поверхностям, или при попытке сдвинуть такие тела вдоль поверхностей. Чтобы сформулировать основные законы, которым подчиняется сила трения, рассмотрим несколько случаев.

Тело аккуратно положили на горизонтальную поверхность, а затем подействовали на него горизонтальной силой , которую в дальнейшем мы будем называть сдвигающей. Очевидно, что если сдвигающая сила не достаточна, чтобы сдвинуть тело, то сила трения равна силе (в частности, при нулевой внешней силе сила трения равна нулю — шероховатости тела и опоры «не зацепляются»).

Поскольку тело, свободно лежащее на какой-то поверхности, можно сдвинуть, прикладывая к нему достаточно большую сдвигающую силу, то сила трения между телом и этой поверхностью не может превышать некоторого максимального значения, которое, как это следует из опыта, определяется соотношением

(4.1)

где — некоторое число, называемое коэффициентом трения, — сила нормальной реакции, действующая между телом и поверхностью. Если тело скользит по поверхности, то, как это также следует из опыта, на тело действует сила трения, равная своему максимальному значению (4.1).

Из этого краткого обзора свойств силы трения следуют правила анализа этой силы. Если в условии задачи говорится, что тело движется по некоторой поверхности, то для силы трения следует использовать закон (4.1) с силой реакции, которую можно найти из проекции второго закона Ньютона на ось, перпендикулярную этой поверхности. Далее с помощью второго закона Ньютона можно исследовать движение тела. Если же задача поставлена так, что тело кладут на поверхность и действуют на него какими-нибудь силами, причем неизвестно, сдвигают эти силы тело, или нет, то требуется дополнительный анализ силы трения. Необходимо сравнить сдвигающую силу (которой является проекция суммарной силы на ось, параллельную поверхности) и максимальную силу трения (4.1). Если сдвигающая сила меньше максимальной силы трения, тело будет покоиться, а сила трения равняться сдвигающей силе. Если сдвигающая сила больше максимальной силы трения (4.1), тело будет двигаться, а действующая на него сила трения будет определяться формулой (4.1). Разберем эти и другие свойства силы трения на примере решения задач.

Очевидно, коэффициент трения — безразмерная величина. Действительно, в формуле (4.1) и , и имеют размерность силы, поэтому коэффициент трения — безразмерный (задача 4.1.1 — ответ 4).

В задаче 4.1.2 тело не движется, и никакие силы не стремятся его сдвинуть. Поэтому шероховатости тела и опоры «не зацепляются» и сила трения равна нулю (ответ 2).

В задаче 4.1.3 тело движется по шероховатой горизонтальной поверхности, поэтому сила трения определяется формулой (4.1) и равна (ответ 1).

Из условия задачи 4.1.4 не ясно, будет двигаться данное тело, или нет. Сравнение сдвигающей силы и максимальной силы трения показывает, что данной сдвигающей силы не достаточно, чтобы сдвинуть тело. Следовательно, тело будет покоиться, а сила трения равняться сдвигающей силе (ответ 2). Из этого анализа следует также, что сдвинуть данное тело может минимальная горизонтальная сила (задача 4.1.5 — ответ 3).

Аналогичный анализ необходимо выполнить, когда исследуется поведение тела на наклонной плоскости (задача 4.1.6). Если тело аккуратно положить на плоскость, то в зависимости от коэффициента трения и угла наклона плоскости оно может как покоиться, так и скользить. Очевидно, для тела на наклонной плоскости сдвигающей силой является составляющая силы тяжести, параллельная плоскости, т.е.

(см. рисунок). Сила реакции плоскости компенсирует составляющую силы тяжести, перпендикулярную плоскости, и потому равна (параллельная и перпендикулярная плоскости составляющие силы тяжести показаны на рисунке пунктирными стрелками). Поэтому телу будет двигаться, если

(4.2)

или (ответ 2). Или (задача 4.1.7 — ответ 1). Ускорение тела, соскальзывающего с наклонной плоскости, можно найти из второго закона Ньютона (задача 4.1.8)

Для наклонной плоскости высотой 3 и длиной 5 м , . Отсюда находим, что (ответ 2).

В задачах 4.1.9 и 4.1.10 необходимо выразить коэффициент трения между телом и поверхностью через кинематические характеристики движения тела по этой поверхности. Основная идея решения заключается в том, чтобы из кинематических характеристик найти ускорение тела, а затем из второго закона Ньютона — силу и коэффициент трения. Из законов равноускоренного движения (2.2) и (2.3) находим связь времени движения до остановки и пройденного расстояния

Отсюда получаем . С другой стороны из второго закона Ньютона для тела, движущегося по шероховатой горизон — тальной поверхности, следует, что . Поэтому (задача 4.1.9 — ответ 3).

Аналогично в задаче 4.1.10 из закона равноускоренного движения для скорости ( — начальная скорость, — время движения до остановки) и второго закона Ньютона получаем (ответ 1).

В нескольких следующих задачах также необходимо исследовать возможность движения тела под действием тех или иных сдвигающих сил. В задаче 4.2.1 сдвигающей силой является сила тяжести, а сила реакции и сила трения возникают благодаря прижиманию тела к стенке внешней силой (см. рисунок). Поэтому . Отсюда заключаем, что брусок будет покоиться, пока сила тяжести будет меньше максимальной силы трения . Или (ответ 3).

В задаче 4.2.2 сдвигающей силой является горизонтальная составляющая внешней силы , т.е. . Сила реакции поверхности, как это следует из проекции второго закона Ньютона на вертикальное направление, равна . Поэтому тело начнет двигаться, если . Или

(ответ 1).

Согласно второму закону Ньютона при действии на тело двух взаимно перпендикулярных горизонтальных сил и , сдвигающая сила равна . Поскольку по условию задачи 4.2.3 при и тело движется с пренебрежимо малым ускорением, то . Откуда получаем (ответ 4).

В задаче 4.2.4 цепочка начинает соскальзывать со стола, когда сила тяжести, действующая на свисающий со стола конец цепочки ( ) , сравнивается с максимальной силой трения, действующей на ее часть, лежащую на столе ( ) . Поэтому (ответ 2).

График зависимости силы трения от сдвигающей силы (задача 4.2.5) строится следующим образом. При малых значениях сдвигающей силы тело покоится, а сила трения равна сдвигающей силе. Когда же сдвигающая сила превосходит максимальную силу трения , то сила трения не зависит от сдвигающей силы:

График, правильно представляющий эту зависимость, дан на рисунке 4.

Аналогичные рассуждения позволяют построить график зависимости ускорения тела от сдвигающей силы (задача 4.2.6). Для значений сдвигающей силы, не превосходящих максимальную силу трения, тело покоится и его ускорение равно нулю. Если сдвигающая сила превосходит максимальную силу трения , ускорение тела находится из второго закона Ньютона: . Правильный график приведен на рисунке 1.

На тело со стороны наклонной плоскости в задаче 4.2.7 действуют перпендикулярная плоскости сила реакции и сила трения, направленная вверх вдоль плоскости, причем поскольку тело движется, сила трения достигает своего максимального значения. Чтобы найти направление вектора суммы этих сил заметим, что поскольку первоначально тело покоилось на плоскости, то в этом положении сумма силы нормальной реакции и силы трения, которая меньше максимальной, направлена вертикально вверх. Поэтому правильный ответ для направления суммы сил трения и реакции в случае движения тела вниз по плоскости дает рисунок 2.

Движение тела в задаче 4.2.8 в системе отсчета, связанной с лентой, происходит следующим образом. На покоящуюся ленту попадает тело, имеющее скорость , замедляется под действием силы трения, а затем останавливается. При этом пока тело перемещается относительно ленты, на него действует постоянная сила трения . Поэтому ускорение тела постоянно и равно . Применяя закон равноускоренного движения для скорости (2.3) к моменту остановки тела относительно ленты

где — время, прошедшее от начала движения тела по ленте до его остановки, получаем (ответ 2).

Очевидно, правильным графиком зависимости скорости от времени в задаче 4.2.9 является график 1. Действительно, после остановки в верхней точке тело начнет соскальзывать по плоскости вниз, так как (задача 4.1.6). Следовательно, график 3. не подходит. При движении тела вниз проекция его скорости на ось отрицательна, поэтому не подходит и график 4. А поскольку ускорение тела при его движении вверх больше ускорения при движении вниз , наклон второй части графика зависимости скорости от времени должен быть меньше его наклона при движении вниз.

При движении тела по доске в задаче 4.2.10 на доску в горизонтальном направлении действуют силы трения со стороны тела и со стороны поверхности , направленные так, как показано на рисунке. Это значит, что сила трения, действующая на доску со стороны тела, стремится заставить ее двигаться, со стороны поверхности — не дать доске двигаться. Поэтому поведение доски определяется сравнением этих сил. А поскольку сила трения между доской и телом равна ( — масса тела, сила трения выражена в Ньютонах), максимальная сила трения между доской и поверхностью — ( — масса доски, сила трения также выражена в Ньютонах), то доска будет двигаться (ответ 1).

План-конспект урока физики по теме «Силы трения»

Инфоурок › Физика ›Конспекты›План-конспект урока физики по теме «Силы трения»

Курс повышения квалификации

Курс повышения квалификации

Курс повышения квалификации

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: 351236

Похожие материалы

Оставьте свой комментарий

Урок 09. Лабораторная работа № 01. Исследование движения тела под действием постоянной силы (отчет)

Лабораторная работа №1

Исследование зависимости силы трения скольжения от веса тела

   Цель работы: 1. выяснить, зависит ли сила трения скольжения от силы нормального давления, если зависит, то как.

                           2. Определить коэффициент трения дерева по дереву.

   Приборы и материалы: динамометр, деревянный брусок, деревянная линейка или деревянная плоскость, набор грузов по 100 г.

 Выполнение работы.

1. Определили цену деления шкалы динамометра.

Цена деления динамометра: 

(2H-1H)/10 дел = 0,1Н/дел

2. Определили массу бруска. Сначала подвесив брусок к динамометру нашли вес бруска   Pбруска=0,7Н

Зная, что  P=mg  и   g=10м/с²   получим m_бруска=P/g 

m_бруска=0,7Н/10м/с²=0,07кг

Определяем общий вес тела (силу нормального давления по формуле:

Р=N=(m1+m2)∙g

1.Р=N=(0,07кг+0,1кг)∙10м/с2=1,7Н

2.Р=N=(0,07кг+0,2кг)∙10м/с2=2,7Н

3.Р=N=(0,07кг+0,3кг)∙10м/с2=3,7Н

4.Р=N=(0,07кг+0,4кг)∙10м/с2=4,7Н

5.Р=N=(0,07кг+0,5кг)∙10м/с2=5,7Н

Провели измерения силы трения.

5. Подготовили таблицу для записи результатов измерений и вычислений:

№ опыта	Масса бруска, m1 , кг	Масса груза, m2 , кг	Общий вес тела  (сила нормального давления), Р=N=(m1+m2)g, Н	Сила трения, Fтр, Н	Коэффициент трения, μ	Среднее значение коэффициента трения, μср
1	0,07	0,1	1,7	0,4
2		0,2	2,7	0,6
3		0,3	3,7	0,8
4		0,4	4,7	1
5		0,5	5,7	1,2

6. Из опыта видим, что сила трения зависит от силы нормального давления прямо пропорционально(т.е. чем больше сила нормального давления, тем больше сила трения)

7. В каждом опыте рассчитали коэффициент трения по формуле: . 

μ=0,4Н/1,7Н=0,235

μ=0,6Н/2,7Н=0,222

μ=0,8Н/3,7Н=0,216

μ=1,0Н/4,7Н=0,213

μ=1,2Н/5,7Н=0,211

Результаты расчётов занесли в таблицу.

8. По результатам измерений построили график зависимости силы трения от силы нормального давления: 

Определили по графику средние значения силы трения и силы нормального давления:

N=3Н

Fтр=0,68Н

Вычислили среднее значение коэффициент трения:

μ_ср=0,68Н/3Н=0,227

Вывод: мы определили, что сила трения зависит от силы нормального давления прямо пропорционально(т.е. чем больше сила нормального давления, тем больше сила трения). Коэффициент трения дерева по дереву получился равен 0,227

Ответы на контрольные вопросы.

1. Что называется силой трения?

Сила трения – это сила, которая возникает в том месте, где тела соприкасаются друг с другом, и препятствует перемещению тел.

2. Какова природа сил трения?

Сила трения — это сила электромагнитной природы.

3. Назовите основные причины, от которых зависит сила трения?

Возникновение силы трения объясняется двумя причинами:

   1) Шероховатостью поверхностей
   2) Проявлением сил молекулярного взаимодействия.

4. Перечислите виды трения.

Силы трения подразделяются на силы трения покоя, скольжения, качения.

5. Можно ли считать явление трения вредным? Почему?

 

Урок 09. Лабораторная работа № 01. Исследование движения тела под действием постоянной силы (отчет)

Лабораторная работа №1

Исследование зависимости силы трения скольжения от веса тела

   Цель работы: 1. выяснить, зависит ли сила трения скольжения от силы нормального давления, если зависит, то как.

                           2. Определить коэффициент трения дерева по дереву.

   Приборы и материалы: динамометр, деревянный брусок, деревянная линейка или деревянная плоскость, набор грузов по 100 г.

 Выполнение работы.

1. Определили цену деления шкалы динамометра.

Цена деления динамометра: 

(2H-1H)/10 дел = 0,1Н/дел

2. Определили массу бруска. Сначала подвесив брусок к динамометру нашли вес бруска   Pбруска=0,7Н

Зная, что  P=mg  и   g=10м/с²   получим m_бруска=P/g 

m_бруска=0,7Н/10м/с²=0,07кг

Определяем общий вес тела (силу нормального давления по формуле:

Р=N=(m1+m2)∙g

1.Р=N=(0,07кг+0,1кг)∙10м/с2=1,7Н

2.Р=N=(0,07кг+0,2кг)∙10м/с2=2,7Н

3.Р=N=(0,07кг+0,3кг)∙10м/с2=3,7Н

4.Р=N=(0,07кг+0,4кг)∙10м/с2=4,7Н

5.Р=N=(0,07кг+0,5кг)∙10м/с2=5,7Н

Провели измерения силы трения.

5. Подготовили таблицу для записи результатов измерений и вычислений:

№ опыта	Масса бруска, m1 , кг	Масса груза, m2 , кг	Общий вес тела  (сила нормального давления), Р=N=(m1+m2)g, Н	Сила трения, Fтр, Н	Коэффициент трения, μ	Среднее значение коэффициента трения, μср
1	0,07	0,1	1,7	0,4
2		0,2	2,7	0,6
3		0,3	3,7	0,8
4		0,4	4,7	1
5		0,5	5,7	1,2

6. Из опыта видим, что сила трения зависит от силы нормального давления прямо пропорционально(т.е. чем больше сила нормального давления, тем больше сила трения)

7. В каждом опыте рассчитали коэффициент трения по формуле: . 

μ=0,4Н/1,7Н=0,235

μ=0,6Н/2,7Н=0,222

μ=0,8Н/3,7Н=0,216

μ=1,0Н/4,7Н=0,213

μ=1,2Н/5,7Н=0,211

Результаты расчётов занесли в таблицу.

8. По результатам измерений построили график зависимости силы трения от силы нормального давления: 

Определили по графику средние значения силы трения и силы нормального давления:

N=3Н

Fтр=0,68Н

Вычислили среднее значение коэффициент трения:

μ_ср=0,68Н/3Н=0,227

Вывод: мы определили, что сила трения зависит от силы нормального давления прямо пропорционально(т.е. чем больше сила нормального давления, тем больше сила трения). Коэффициент трения дерева по дереву получился равен 0,227

Ответы на контрольные вопросы.

1. Что называется силой трения?

Сила трения – это сила, которая возникает в том месте, где тела соприкасаются друг с другом, и препятствует перемещению тел.

2. Какова природа сил трения?

Сила трения — это сила электромагнитной природы.

3. Назовите основные причины, от которых зависит сила трения?

Возникновение силы трения объясняется двумя причинами:

   1) Шероховатостью поверхностей
   2) Проявлением сил молекулярного взаимодействия.

4. Перечислите виды трения.

Силы трения подразделяются на силы трения покоя, скольжения, качения.

5. Можно ли считать явление трения вредным? Почему?

 

Силы трения | Физика

1. Сила трения скольжения

Поставим опыт

Толкнем лежащий на столе брусок, сообщив ему некоторую начальную скорость. Мы увидим, что брусок скользит по столу и его скорость уменьшается до полной остановки (на рисунке 17.1 показаны последовательные положения бруска через равные промежутки времени). Как вы уже знаете из курса физики основной школы, тормозит брусок силы трения скольжения, действующая на него со стороны стола.
Силы трения скольжения действуют на каждое из соприкасающихся тел, когда они движутся друг относительно друга.

Эти силы действуют на каждое из соприкасающихся тел (рис. 17.2). Они равны по модулю и противоположны по направлению, потому что связаны третьим законом Ньютона.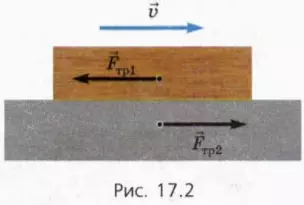

Когда брусок скользит по столу, мы не замечаем силу трения скольжения, действующую на стол со стороны бруска, потому что стол прикреплен к полу (или на стол со стороны пола действует довольно большая сила трения покоя, речь о которой пойдет далее).

Если же толкнуть брусок, лежащий на тележке, то под действием силы трения скольжения, действующей на тележку со стороны бруска, тележка станет двигаться с ускорением, а скорость бруска относительно тележки будет уменьшаться.

? 1. Во сколько раз ускорение бруска относительно стола в этом опыте больше, чем ускорение тележки относительно стола, если масса бруска 200 г, а масса тележки 600 г? Трением между тележкой и столом можно пренебречь.

Силы трения скольжения направлены вдоль поверхности соприкосновения тел. Действующая на каждое тело сила трения направлена противоположно скорости этого тела относительно другого тела.

Силы трения скольжения обусловлены главным образом зацеплением и разрушением неровностей соприкасающихся тел (эти неровности на рисунке 17.3 для наглядности преувеличены). Поэтому обычно чем более гладкие поверхности соприкасающихся тел, тем меньше силы трения между ними.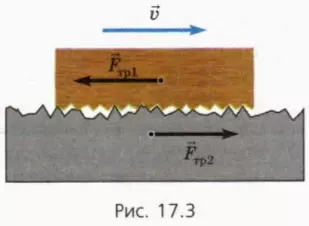

Однако если сделать соприкасающиеся поверхности очень гладкими (например, отшлифовать их), то сила трения скольжения может увеличиться вследствие действия сил межмолекулярного притяжения.

Выясним, от чего зависит сила трения скольжения.

От чего зависит сила трения скольжения?

Поставим опыт
Будем с помощью динамометра тянуть брусок по столу с постоянной скоростью (рис. 17.4, а), прикладывая к нему горизонтально направленную силу 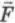_упр.

При движении с постоянной скоростью ускорение бруска равно нулю. Следовательно, силу трения скольжения, действующую на брусок со стороны стола, уравновешивает сила упругости, действующая на брусок со стороны динамометра. Значит, эти силы равны по модулю, то есть динамометр показывает модуль силы трения.

Повторим опыт, положив на брусок другой такой же брусок (рис. 17.4, б). Мы увидим, что сила трения скольжения увеличилась в 2 раза. Заметим теперь, что в этом опыте (по сравнению с опытом с одним бруском) сила нормальной реакции тоже увеличилась в 2 раза.

Изменяя силу нормальной реакции, можно убедиться, что модуль силы трения скольжения Fтр пропорционален модулю силы нормальной реакции N:

F_тр.ск = μN.     (1)

Как показывает опыт, сила трения скольжения практически не зависит от относительной скорости движения соприкасающихся тел и от площади их соприкосновения.

Коэффициент пропорциональности μ называют коэффициентом трения. Его определяют из опыта (см. лабораторную работу 4). Он зависит от материала и качества обработки соприкасающихся поверхностей. На форзаце задачника (под обложкой) приведены приближенные значения коэффициента трения для некоторых видов поверхностей.

Коэффициент трения шин по мокрому асфальту или по льду в несколько роз меньше коэффициента трения шин по сухому асфальту. Поэтому тормозной путь автомобиля значительно увеличивается во время дождя или гололеда. О скользкой дороге водителей предупреждает дорожный знак (рис. 17.5).

? 2. Тело массой m движется по горизонтальной поверхности. Коэффициент трения между телом и поверхностью μ.
а) Чему равна сила трения скольжения?
б) С каким по модулю ускорением движется тело, если на него действуют только сила тяжести, сила нормальной реакции и сила трения скольжения?

? 3. Лежащему на столе бруску сообщили скорость 2 м/с, и он прошел до остановки 1 м (тормозной путь). Чему равен коэффициент трения между бруском и столом?

? 4. Можно приближенно считать, что на автомобиль при торможении действует сила трения скольжения. Оцените, чему равен тормозной путь автомобиля на сухом асфальте и на льду при начальной скорости 60 км/ч; 120 км/ч. Сравните найденные значения с длиной классной комнаты.

Полученные ответы удивят вас. Наверное, вы станете осторожнее на дороге во время дождя и особенно гололеда.

2. Сила трения покоя

Поставим опыт
Попробуйте сдвинуть с места шкаф (рис. 17.6). Он будет оставаться в покое, даже если прикладывать к нему довольно большую силу.

Какая же сила уравновешивает горизонтально направленную силу, приложенную вами к шкафу? Это сила трения покоя, действующая на шкаф со стороны пола.

Силы трения покоя возникают при попытке сдвинуть одно из соприкасающихся тел относительно другого в том случае, когда тела остаются в покое друг относительно друга. Эти силы препятствуют относительному движению тел.

? 5. Действует ли сила трения покоя на пол со стороны шкафа (рис. 17.6)?

Причины возникновения силы трения покоя сходны с причинами возникновения силы трения скольжения: наличие неровностей на соприкасающихся поверхностях тел и действие сил межмолекулярного притяжения.

Будем постепенно увеличивать приложенную к шкафу горизонтальную силу. При достижении некоторого ее значения шкаф сдвинется с места н начнет скользить по полу. Следовательно, модуль силы трения покоя Fтр.пок не превышает некоторого предельного значения, называемого максимальной силой трения покоя.

Опыт показывает, что максимальная сила трения покоя немного больше силы трения скольжения. Однако для упрощения решения школьных задач принимают, что максимальная сила трения покоя равна силе трения скольжения:

F_тр.пок ≤ μN.      (2)

Если тело покоится, то сила трения покоя 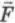_тр.пок уравновешивает силу 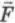, направленную вдоль поверхности соприкосновения тел и стремящуюся сдвинуть тело.
Следовательно, в этом случае

F_тр.пок = F.     (3)

Обратите внимание: сила трения покоя удовлетворяет двум соотношениям – неравенству (4) и равенству (5). Из них следует неравенство для силы 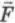, которая не может сдвинуть тело:

F ≤ μN.     (4)

Если же F > μN, то тело начнет скользить, и на него будет действовать сала трения скольжения. В таком случае

F_тр = F_тр.ск = μN.

Соотношения (3) и (5) иллюстрирует график зависимости силы трения Fтр от приложенной к телу силы F (рис. 17.7).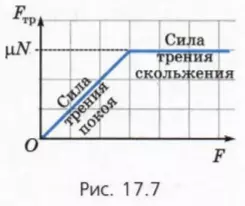

? 6. К лежащему на столе бруску массой 1 кг прикладывают горизонтальную силу, равную по модулю F. Коэффициент трения между бруском и столом равен 0,3. Чему равна действующая на брусок со стороны стола сила трения, если F = 2 Н? F = 5 Н?

? 7. Тягач тянет по горизонтали связку бревен массой 10 т с силой 40 кН. Чему равно ускорение связки, если коэффициент трения между бревнами и дорогой равен 0,3? 0,5?

? 8. Находящийся на столе брусок массой 1 кг тянут горизонтальной пружиной жесткостью 100 Н/м. Коэффициент трения 0,3. Каково удлинение x пружины, если брусок покоится? движется со скоростью 0,5 м/с?

Может ли сила трение быть движущей силой?

Делая шаг, человек толкает дорогу назад, действуя на нее силой трения покоя 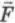_тр1: ведь подошва во время толчка покоится относительно дороги (на это иногда указывает четкий отпечаток подошвы) (рис. 17.8, а). Согласно третьему закону Ньютона, со стороны дороги на человека действует такая же по модулю сила трения покоя 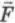_тр2, направленная вперед.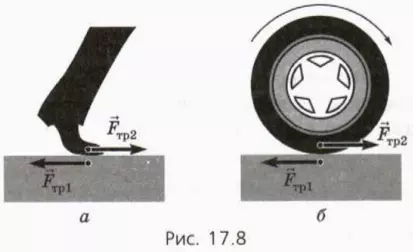

Сила трения покоя разгоняет и автомобиль (рис. 17.8, б). Когда колесо катится без проскальзывания, его нижняя точка покоится относительно дороги. Ведущее колесо автомобиля (приводимое во вращение двигателем) толкает дорогу назад, действуя на нее силой трения покоя 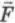_тр1. Согласно третьему закону Ньютона, дорога при атом толкает колесо (а вместе с ним и автомобиль) вперед силой трения покоя 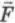_тр2. Именно эту силу и называют часто силой тяги.

? 9. С какой целью локомотивы (электровозы и тепловозы) делают очень массивными?

? 10. Коэффициент трения между шинами ведущих колес автомобиля и дорогой равен 0,5. Считайте, что сопротивлением воздуха можно пренебречь.
а) С каким максимально возможным ускорением может двигаться автомобиль, если все его колеса – ведущие?
б) Увеличилось бы или уменьшилось максимально возможное ускорение автомобиля, если ведущими были бы только передние или только задние колеса? Обоснуйте свой ответ.

Подсказки. Ускорение автомобиля обусловлено действием силы трения покоя со стороны дороги.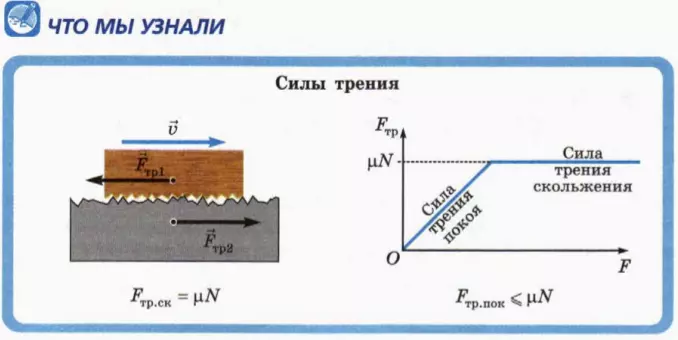

Дополнительные вопросы и задания

11. На рисунке 17.9 приведены графики зависимости силы трения скольжения от силы нормальной реакции при движении по столу трех разных брусков. Между каким бруском и столом коэффициент трения наибольший? Чему он равен?

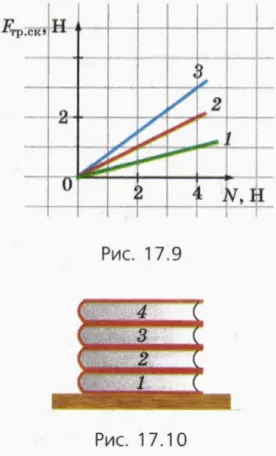
12. На столе лежит стопка из четырех одинаковых книг массой 500 г каждая (рис. 17.10). Коэффициент трения между обложками книг равен 0,4. Какую горизонтально направленную силу надо приложить, чтобы, придерживая остальные книги:
а) сдвинуть книгу 4?
б) сдвинуть книги 3 и 4 вместе?
в) вытащить книгу 3?
г) вытащить книгу 2?

13. Оцените, до какой скорости может разогнаться за 2 с автомобиль на мокром асфальте. Все его колеса ведущие.

Сила трения | Типы силы трения

Сила трения — это сила, создаваемая двумя поверхностями, которые контактируют и скользят друг относительно друга. Эти силы в основном зависят от текстуры поверхности и количества силы, требующей их вместе. Угол и положение объекта влияют на величину силы трения. Основная причина возникновения трения между объектами связана с силами притяжения, известными как адгезия, между точками контакта областей поверхностей, которые всегда незначительно неровны.Трение возникает из-за срезания этих «плавленых» стыков и из-за воздействия неровностей более твердой поверхности на более мягкую поверхность. (Изображение будет загружено в ближайшее время) Если объект помещен напротив объекта, сила трения будет такой же. как вес объекта. Если объект прижат к поверхности, сила трения возрастет и станет больше веса объекта. Полную силу трения, которую поверхность может приложить к объекту, можно легко измерить с помощью данной формулы: Ffrict _{= \ [\ mu.F_ {norm} \]}

Два основных экспериментальных факта описывают трение скользящих твердых тел. Во-первых, величина трения практически не зависит от площади контакта. Если кирпич тянут по столу, сила трения одинакова, лежит ли кирпич ровно или стоит дыбом. Во-вторых, трение прямо пропорционально весу, прижимающему поверхности друг к другу. Если по столу тянут груз из трех кирпичей, трение будет в три раза больше, чем если тянут один кирпич. Таким образом, отношение трения F к нагрузке L одинаково.Это постоянное отношение называется коэффициентом трения и обычно обозначается греческой буквой мю (μ).

Математически μ = F / L. Поскольку трение и нагрузка рассчитываются в единицах силы (например, фунтах или ньютонах), коэффициент трения безразмерен. Значение коэффициента трения для случая, когда один или несколько кирпичей скользят по чистому деревянному столу, составляет около 0,5, что указывает на то, что сила, равная половине веса кирпичей, требуется только для преодоления трения и удержания кирпичей в движении. вперед с постоянной скоростью.Сила трения направлена ​​противоположно движению объекта. Поскольку до сих пор описанное трение возрастает между поверхностями при относительном движении, это называется кинетическим трением.

Типы сил трения

Трение — это сила, которая конкурирует с движением между любыми поверхностями, которые соприкасаются с основанием. Между твердыми поверхностями возникает статическое, кинетическое трение, трение скольжения и качения. Трение жидкости имеет место в жидкостях и газах. Все четыре типа трения описаны ниже

1.Сухое трение

(a) Статическое трение
(b) Кинетическое трение
(c) Трение качения
(d) Трение скольжения

Сухое трение — это сила, которая конкурирует с одной твердой поверхностью, скользящей по другой твердой поверхности. Сухое трение всегда противопоставляет скользящие поверхности друг другу и может иметь эффект любого встречного движения или вызывать движение тел. Для сухого трения чаще всего используется кулоновское трение. Этот вид трения можно далее разделить на трение покоя и кинетическое трение.Эти два типа трения поясняются на схеме ниже. Сначала представьте коробку на поверхности. Толкающая сила прилагается параллельно поверхности и медленно увеличивается. На коробку также действуют гравитационная сила, нормальная сила и сила трения.

(изображение будет загружено в ближайшее время)

(a) Статическое трение

Статическое трение возникает раньше, когда коробка скользит и перемещается. В этой области сила трения будет равна по масштабу и противоположна по направлению самой толкающей силе.По мере того, как увеличивается сила толкания, увеличивается и сила трения. Если величина толкающей силы продолжает расти, в конечном итоге коробка начнет соскальзывать. Когда коробка начинает скользить, тип трения, препятствующего движению коробки, изменяется от статического трения до того, что называется кинетическим трением. Точка перед проскальзыванием коробки называется препятствующим движением. Это также можно принять за максимальную силу трения покоя перед проскальзыванием. Сумма максимальной силы статического трения равна статическому коэффициенту трения, умноженному на нормальную силу, существующую между коробкой и поверхностью.Этот коэффициент трения — это свойство, которое зависит от обоих материалов, и его обычно можно найти в таблицах.

(b) Кинетическое трение

Кинетическое трение возникает за пределами точки приближающегося движения, когда коробка скользит. При кинетическом трении величина силы трения, противоположной движению, будет такой же, как кинетический коэффициент трения, умноженный на нормальную силу между коробкой и поверхностью. Кинетический коэффициент трения также зависит от двух соприкасающихся предметов, но почти всегда будет меньше статического коэффициента трения.

(c) Трение качения

(изображение будет скоро загружено)

Трение качения происходит, когда колесо, шарик или цилиндр свободно катятся по поверхности, как в шариковых и роликовых подшипниках. Основная причина трения при качении, по-видимому, заключается в распределении энергии, участвующей в скручивании объектов. Если твердый шарик катится по ровной поверхности, он несколько набит, а на ровной поверхности в местах соприкосновения есть неровности. Упругий изгиб или сжатие, возникающие в передней части соприкасающейся детали, является препятствием для движения, которое не полностью компенсируется, поскольку вещества возвращаются к типичной форме в задней части.Внутренние потери в двух веществах параллельны потерям, которые не позволяют мячу отскочить обратно на уровень, с которого он выпущен. Коэффициенты трения скольжения обычно в 100-1000 раз больше, чем коэффициенты трения качения для соответствующих материалов. Трение скольжения — это трение, которое действует на предметы, когда они скользят по поверхности. Трение скольжения слабее, чем трение покоя. Вот почему легче сдвинуть оборудование по полу после того, как вы начали двигаться, чем заставить его двигаться в первую очередь.Трение скольжения может быть ценным. Например, вы используете трение скольжения, когда пишете пером. Ручка «острие» легко скользит по бумаге, но трение между ручкой и бумагой достаточно, чтобы оставить след.

1. Трение жидкости

(изображение будет скоро загружено)

Трение жидкости происходит между слоями жидкости, которые движутся навстречу друг другу. Этот внутренний конфликт с потоком называется вязкостью. В повседневных терминах вязкость жидкости называется ее «толщиной».Все жидкости обладают некоторым сопротивлением сдвигу и поэтому являются вязкими. Очень полезно использовать концепцию идеальной жидкости, не имеющей сопротивления сдвигу и, следовательно, не вязкой.

Примеры трения жидкости.

• Если между двумя тонкими стеклянными пластинами есть влажная поверхность, вы увидите, что пластины застревают, а нижняя пластина не падает, если вы держите только верхнюю.

Как рассчитать силу трения : Рассчитайте силу трения по формуле:

F = μn

Где N — нормальная сила, а μ — коэффициент трения для ваших инструментов и независимо от того, неподвижны они или перемещение.Нормальная сила эквивалентна весу объекта, поэтому это также можно записать как:

Дано m — масса объекта, а g — ускорение свободного падения. Трение препятствует движению объекта.

Расчет силы трения : «Нормальная» сила определяет силу, с которой поверхность, опирающаяся на объект, действует на объект. Для неподвижного объекта на плоской поверхности сила должна точно противостоять силе гравитации, в противном случае объект будет двигаться в соответствии с законами движения Ньютона.«Нормальная» сила (Н) — это сила, которая это делает. Она постоянно действует перпендикулярно поверхности. Это означает, что на неровной поверхности нормальная сила по-прежнему будет направлена ​​прямо от поверхности, а сила тяжести будет направлена ​​прямо вниз.
Нормальную силу в большинстве случаев можно просто определить следующим образом:

N = mg

Здесь m обозначает массу объекта, а g обозначает ускорение свободного падения, которое составляет 9,8 м / с ² . Это просто соответствует «весу» объекта.Для неровных поверхностей сила нормальной силы минимизируется, чем больше наклонена поверхность, поэтому формула принимает следующий вид:

N = mg cos (θ)

С θ обозначает угол, к которому наклонена поверхность.
Для простого расчета случая рассмотрим плоскую поверхность с лежащим на ней деревянным бруском весом 2 кг. Нормальная сила будет направлена ​​прямо вверх (чтобы выдержать вес блока), и вы должны измерить: N = 2 кг × 9,8 Н / кг = 19,6 Н. Найдите правильный коэффициент. Коэффициент зависит от объекта и конкретной ситуации, в которой вы находитесь. повторно работаем с.Если объект еще не движется по поверхности, вы используете коэффициент трения покоя μ _static , но если он движется, вы будете использовать коэффициент трения скольжения μ _slide .
Обычно коэффициент трения скольжения меньше коэффициента трения покоя. Другими словами, легче сдвинуть то, что уже скользит, чем что-то неподвижное. Природа материала также влияет на коэффициент. Например, если раньше деревянный брусок лежал на кирпичной поверхности, коэффициент будет равен 0.6, но для чистого дерева он может быть где-то от 0,25 до 0,5. Статический коэффициент трения льда о лед составляет 0,1. Опять же, коэффициент скольжения уменьшается еще больше, до 0,03 для льда по льду и 0,2 для дерева по дереву. Формула силы трения указывает:
F = μN Например, рассмотрим деревянный блок массой 2 кг на деревянном столе. , выталкивается из неподвижности. В этом случае вы можете использовать статический коэффициент с μ _static = от 0,25 до 0,5 для древесины. Принимая μ _static = 0,5, чтобы в полной мере использовать потенциальный эффект трения, и помня о N = 19.6 Н, как было сказано ранее, сила составляет:
F = 0,5 × 19,6 Н = 9,8 Н. Помните, что трение предлагает только силу для сопротивления движению, поэтому, если вы начнете слегка толкать его и станете сильнее, сила трения возрастет до максимального значения, что вы только что рассчитали. Физики иногда отмечают F _max , чтобы прояснить эту точку. Как только блок находится в движении, вы используете μ _slide = 0,2, в данном случае:

= 0,2 × 19,6 N = 3,92 N

Проблемы на Сила трения: Задача 1 — К 6-килограммовому ящику прилагается сила 50 Н.Если коэффициент трения 0, 3, рассчитать ускорение коробки? Решение 1 — F _{нормальное} = 60 Н — 40 Н = 20 Н
Сила трения составляет — F _трение = µ.F _{нормальное} = 0, 3.20N = 6N
Чистая сила в диапазоне от –Y до Y = ноль,
Но в направлении –X + X чистая сила не равна нулю
F _net = ma
F _net = ma

F _x — F _трение = ma
F _x — F _трение = ma
30 Н — 6 Н = 6 a
a = 4 м / с²

Задача 2 — Блок массой M = 10 кг помещается на поверхность, наклоненную под углом θ = 45 °.
Отметим, что μ _s = 0,5 — это коэффициент статического трения между блоком и поверхностью.

• Какое будет минимальное усилие F, необходимое для предотвращения скольжения?

• Какая максимальная сила F может быть приложена, не вызывая скольжения блока?

Решение 2 -Минимальная сила, необходимая для предотвращения скольжения, — это минимальная сила, которая не даст блоку соскользнуть вниз по склону.
F _мин = 10 g sin (45 °) —10 g cos (45 °) x 0.5.
Максимальная сила, которая может быть приложена, не вызывая скольжения блока, — это максимальная сила, которая может быть приложена, не вызывая скольжения блока вверх по склону.
F _макс. = 10 г sin (45 °) + 10 г cos (45 °) x 0,5.
F _мин. = 34,65 Н, F _макс. = 103,94 Н

,

Сила трения

Трение определяется как противодействующая сила, которая пытается сопротивляться скорости тела. Она возникает из-за контакта двух или более тел друг с другом.

Когда мы пытаемся скользить по поверхности тела, движению тела препятствует сила, называемая силой трения. Сила трения возникает из-за межмолекулярного взаимодействия.

Когда тело покоится на поверхности и не применяется внешняя сила, трение отсутствует.В этом случае нормальная реакция R уравновешивает вес Mg, т.е. для вертикального равновесия R = Mg и силы трения = 0

Без трения

Когда внешняя сила (F) применяется для перемещения тела, а тело не движется, тогда сила трения действует противоположно приложенной силе F и равна приложенной силе, то есть F — f = 0 сила трения, f = приложенная сила F. Когда тело остается в покое, сила трения называется трением покоя. Статическое трение — это саморегулирующаяся сила.

Статическое трение

Когда внешняя сила F увеличивается, наступает стадия, когда тело находится на грани движения. На этом этапе сила трения максимальна и называется предельным трением . Экспериментально установлено, что предельная сила трения

где называется коэффициентом статического трения. Это безразмерная постоянная, но зависит от природы контактирующих поверхностей.

Таким образом, трение покоя представляет собой саморегулирующуюся силу, и тело находится в состоянии покоя,

статическое трение = приложенная сила.

Предельное трение

Кинетическое трение:

При дальнейшем увеличении приложенной силы (сверх предельной силы трения) тело начинает двигаться, тогда сила, противодействующая движению, называется кинетическим трением или трением скольжения. Кинетическое трение меньше предельного трения. Сила кинетического трения R где называется коэффициентом кинетического трения.

Кинетическая сила трения между двумя поверхностями остается неизменной, независимо от того, движется ли тело с постоянной скоростью или ускорением.

График между приложенной силой и силой трения:

Если график построен между приложенной силой и силой трения, то он представляет собой прямую линию. Это говорит о том, что

Сила трения = приложенная сила.

График приложенной силы и силы трения

Когда приложенная сила увеличивается сверх определенного значения, сила трения внезапно падает и становится равной R, которая остается постоянной.

Трение качения:

Когда тело катится по поверхности, сопротивление, оказываемое поверхностью, называется трением качения. Трение качения меньше статического или кинетического трения. Коэффициент трения качения обозначается

.

Угол трения:

Когда блок массы M помещают на горизонтальную поверхность и тянут вправо внешней силой, равной предельной силе трения; затем результат нормальной реакции и предельной силы трения.Угол, образованный равнодействующей силой с нормалью, называется углом трения.

Угол трения

……………………. (1)

А коэффициент трения покоя

Как

…………………… .. (2)

Сравнение (1) и (2),

Сила трения на велосипеде в движении:

Колесо вращается вокруг своей оси:

Когда колесо вращается вокруг своей оси без скольжения, сила трения, действующая на него, является трением качения, и оно действует противоположно направлению движения точек его контакта с поверхностью.Например, на рис. колесо вращается по часовой стрелке, сила трения, действующая на него, будет направлена ​​вперед.

Колесо вращается вокруг своей оси

(ii) При педалировании велосипеда:

Сила, прилагаемая к заднему колесу через систему оси педаль-цепь, направлена ​​в обратном направлении, поэтому сила трения на заднем колесе действует в прямом направлении. Переднее колесо велосипеда движется само по себе в прямом направлении, поэтому сила трения на переднем колесе действует в обратном направлении.

(iii) Если на велосипеде нет педалей:

Никакая внешняя сила не применяется; оба колеса движутся сами по себе в прямом направлении, и поэтому сила трения на обоих колесах действует в обратном направлении.
Кузов на наклонной плоскости; Угол естественного откоса

Угол естественного откоса

Предположим, что тело расположено на наклонной плоскости под углом наклона, тогда силы, действующие на тело, равны

(i) Его вес Mg (вертикально вниз),

(ii) Нормальная реакция R

(iii) Сила трения, действующая параллельно плоскости вверх

Если разрешить вес Mg, нормальный и параллельный плоскости, то для положения равновесия перпендикулярно плоскости

…………………………….. (1)

и для положения равновесия параллельно плоскости.

………………………………. (2)

т.е. если тело покоится на наклонной плоскости

сила трения, f =

Если угол наклона плоскости увеличивается, то увеличивается Mg sin и, следовательно, увеличивается и сила трения. На одном этапе тело как раз на грани скольжения; на этом этапе сила трения максимальна, а угол наклона плоскости называется углом естественного откоса. Таким образом, угол естественного откоса — это такой угол наклона плоскости, при котором установленный на ней блок только начинает скользить.

Таким образом,

Также

или

Как

Так

Ясно, что угол естественного откоса равен его углу трения

Похожие сообщения:

1. Межмолекулярная сила Межмолекулярная сила. Межмолекулярная сила между атомами, молекулами …
2. Рабочий лист электродвижущей силы Краткая форма электродвижущей силы — ЭДС.Согласно …
3. Спонтанность, случайность и природа движущей силы Спонтанность и случайность Тщательное изучение показывает, что в каждом из …
4. Альфа, Бета, Гамма Введение, соотношение и т. Д. Альфа — это первый греческий первый алфавит ….
5. Математические формулы для физики Математические формулы для физики. Список математических формул, используемых в …

.

КОЭФФИЦИЕНТЫ СТАТИЧЕСКОГО И ДИНАМИЧЕСКОГО ТРЕНИЯ

В этом эксперименте мы определим коэффициенты при кинетическое и статическое трение деревянного блока о деревянную доску, а статическое коэффициенты трения для стекла и других материалов. Мы также проверим гипотезу о том, что сила трения не зависит от площади поверхности в контакт.

Когда две поверхности соприкасаются, они прикладывают силу к каждой. Другой. Конечный источник этих поверхностные или «контактные» силы — это электрическое притяжение или отталкивание между заряженные частицы — электроны и протоны — из которых состоит вся материя.Векторная сумма всех субмикроскопических сил между частицами в поверхности — это макроскопическая сила, которую мы можем измерить в лаборатории.

На диаграмме 1 показаны две соприкасающиеся поверхности. Каждая поверхность проявляет равные, но противоположные направленная сила на другой. Общая сила, F ₁₂ , эта поверхность 2 воздействует на поверхность 1 в некоторых произвольное направление пространства, как показано. F ₁₂ для удобства разбиваем на компоненты параллельно и перпендикулярно поверхности. Мы называем перпендикулярный компонент нормальной силой ( F _N на схеме) и параллельная составляющая сила трения ( f ).

Нормальная сила имеет тенденцию разделять две поверхности: сопротивляется вдавливанию поверхности 1 в поверхность 2. Сила трения сопротивляется любому относительному движению между поверхностями. и всегда направлен против этого движения, если поверхности движутся, или противоположно любому потенциальному движению, если поверхности неподвижны.

Статическое и кинетическое трение

Силы трения бывают двух типов, в зависимости от того, не поверхности движутся относительно друг друга.

Статическое трение действует, когда две поверхности находятся на отдыхают друг относительно друга и сопротивляются скольжению. Статическое трение ( f _s ) сила сцепления, которая пытается удерживать поверхности вместе. Направление f _s противоположна любой внешней силе, которая пытается заставить поверхности двигаться.вверх до определенного предела величина f _s равна внешней силы, так что результирующая сила на поверхности остается нулевой, а поверхность не двигается. Статическое трение таким образом, переменная сила, принимающая любое значение, необходимое для удержания поверхности в равновесие.

Однако f _s не может превышать определенного максимальное значение. Когда внешняя сила превышает это максимальное значение, поверхностное соединение между материалами нарушается и начинается скольжение.Максимальное значение f _s зависит от химического состава поверхностей и должен быть определяется экспериментально.

После начала скольжения кинетическое трение ( f _k ) берет на себя. Кинетическое трение направлено противоположной относительной скорости между двумя поверхностями, сопротивляясь движение и замедление его скорости. кинетический трение примерно постоянно при нормальных условиях. Как и статическое трение, его величина зависит от на задействованных поверхностях и должен быть определен экспериментально.

Коэффициент трения

Экспериментально мы обнаружили, что как статические, так и кинетические силы трения в хорошем приближении пропорциональны нормальному сила между поверхностями. Соотношение сила трения к нормальной силе называется коэффициентом трение, ( м ):

(1)

Mu — это число без единицы измерения и обычно меньше одного дюйма. стоимость.

Для любой данной поверхности коэффициенты статики и кинетическое трение разные, поэтому мы должны различать м _с (для статического трения) и м _k (для кинетического трения).Если мы знаем коэффициенты и нормальный силы, то мы можем вычислить силы трения:

(2)

(где неравенство отражает тот факт, что f _s переменная; максимальное значение f _s дается равным знак;)

(3)

Обычно м _с больше м _k , поэтому максимальная сила статического трения больше, чем сила кинетической трение.

Определение силы трения

В нашем эксперименте сначала определим коэффициенты статического и кинетического трения между двумя деревянными поверхностями (деревянным блоком и деревянная доска). Диаграмма 2 иллюстрирует настройка, которую мы будем использовать. Блок ( М ₁ ) кладется на горизонтальную планку и привязан веревкой к грузу ( M ₂ ), который подвешивается вертикально с помощью шкива. Чтобы определить величину кинетического трения, мы вешаем на струна так, что если блок приводится в движение, он скользит с постоянной скорость.(Сначала мы должны привести его в движение слегка толкнув его, иначе статическое трение будет удерживать его место.)

Поскольку ускорение блока равно нулю как в в горизонтальном и вертикальном направлениях, второй закон движения Ньютона говорит нам, что сумма сил в каждом из этих направлений должна быть равна нулю. В горизонтальном направлении напряжение в веревка (которая равна весу подвешенной массы) тянет блок и кинетическое трение сопротивляется натяжению. В в вертикальном направлении, собственный вес блока тянет вниз, а нормальная сила толкает вверх.Каждая из этих пар сил должны быть равны и противоположны, поэтому у нас должно быть:

(4) и

где Вт ₂ — вес подвешенной массы. и W ₁ — вес блока (и любая масса поверх Это). Поскольку мы знаем массы, мы можем рассчитать силы трения и нормальные силы.

Мы можем определить коэффициент кинетического трения по формуле Проведение нескольких испытаний и расчет соотношения масс для каждого испытания:

(5)

Коэффициент трения покоя можно определить во многих так же.В этом случае оставляем блок в состоянии покоя и ищите ту висящую массу, которая только начинает блок скольжения. Когда блок только начинает слайд у нас

(6) и

как и в кинетическом случае. Мы определим м _с , построив график f _с как функция F _N . наклон графика м _с .

Трение и площадь поверхности

Поскольку силы трения возникают, когда две поверхности находятся в контакта друг с другом, может показаться разумным ожидать, что величина силы трения будет уменьшаться по мере увеличения площади соприкасающейся поверхности уменьшается.Однако мы находим, что силы трения практически не зависят от размера области контакта.

В качестве объяснения этого предположим, что вес блок одинаков, независимо от того, опирается ли на него широкая или узкая грань доска. Для узкого лица у нас есть та же сила (вес блока), давящая на меньшую площадь дощечки. Это означает, что давление больше (давление — это сила, разделенная на площадь), и поверхности сжаты вместе более плотно.Это увеличивает сила трения в той же пропорции, что и площадь поверхности уменьшилось. Результатом является то, что величина силы трения такая же, как и у широкого лица вниз. Мы проверим эту идею повторное выполнение нашего эксперимента для кинетического трения, используя узкую грань блокировать и сравнивать результаты в двух случаях.

Предельный угол естественного откоса

Есть второй способ определения коэффициента статическое трение. См. Диаграмму 3.Ставим блок на доску и приподнимите один конец планки так, чтобы он составлял угол q с горизонтальный. Когда угол большой достаточно, блок соскользнет вниз по склону.

Под углом непосредственно перед тем, как блок начинает скользить (так называемый предельный угол естественного откоса ), силы по-прежнему уравновешены, и мы есть:

и

Соотношение этих двух уравнений дает нам м _с :

(7)

,

Кинетическое трение — широкая грань блока

1. Взвесьте блок и запишите его массу.

2. Протрите поверхности планки и замазать влажным бумажным полотенцем. Убедитесь, что на обоих нет грязи и песка.

3. Зажим шкив на конце доски и поместите доску на край лаборатории стол. Поместите блок в дальний конец планку и прикрепите к ней шнурок. Натяните шнур на шкив и повесьте подвеску груза на конец.Строка должна быть достаточно короткой так, чтобы блок мог скользить по длине доски до того, как грузоподъемник ударится этаж.

4. Определите, какой вес нужно добавить к подвеска так, чтобы система (блок, веревка и подвеска с массой) двигалась на постоянная скорость:

· Добавьте немного массы на вешалку. Слегка подтолкните блок, чтобы запустить его перемещение. Если блок ускоряется (скорости вверх), снимите немного массы и попробуйте еще раз. Если блок замедляется (тормозит), добавьте еще немного массы и попробуйте очередной раз.(Примечание: если блок ускоряется от веса одну вешалку, положите 20 или около того граммов на верхнюю часть блока и обработайте это масса в составе блока.)

· Если блок перемещает длину доски на примерно одинаковая скорость, вы нашли необходимую массу.

· Запишите общую подвешенную массу и ее вес. Вес подвешенной массы эквивалентно силе трения на блоке (см. уравнение 4 выше).

· Запишите общую массу и на блоке и его вес.Вес на блоке составляет эквивалент нормальной силы, F _N .

6. Повторите описанный выше процесс, добавляя 100 грамм вершина блока для каждого нового испытания, всего шесть испытаний.

Кинетическое трение — узкая грань блока

7. Для проверки гипотезы о том, что сила трение не зависит от площади соприкасающейся поверхности, повторите описанный выше эксперимент. используя узкую грань блока:

• комплект блок в конце планки на ее узкой поверхности и повторно соедините шнур к нижнему крючку так, чтобы тетива располагалась горизонтально.
• Определить количество подвешиваемой массы, необходимое для поддержания постоянного движения блока скорость после начального толчка. Делать это для 0–500 грамм, помещенных на блок, с шагом 100 грамм, для всего шесть испытаний.

Анализ

1. Рассчитайте нормальная сила F _n и сила трения f _k , для каждого испытания. Обратите внимание, что нормальные силы одинаковы для широких и узких лиц.

2. Рассчитайте коэффициент трения μ _k для каждого испытания.

3. Найдите среднее значения, отклонения и стандартное отклонение для обоих наборов данных.

4. Рассчитайте процентная разница между средними значениями для широкого и узкого лиц.

5. Вопросы:

а) При определении кинетической силы трения, f , почему это было необходимо, чтобы блок двигался с постоянной скоростью? б) Используя законы Ньютона, покажите, как можно измерить μ _k для ускоряющего блока.

Статическое трение — плоская доска

1. Используйте ту же настройку, что и при кинетическом трении. эксперименты, широкой лицевой стороной вниз. На этот раз, однако, определите, какая висячая масса необходима, чтобы начать движение блока без толчка.

2. Испытайте пять разных масс на блоке, начиная с отсутствия массы на блоке и добавляя по 100 грамм для каждой новой попытки. Определите среднюю массу подвешивания , необходимую для начала движения системы. от покоя для каждого набора массы.Сделать в не менее 3 испытаний для каждого набора масс по следующей процедуре:

· Сначала снова протрите планку сухой тканью или бумажное полотенце.

· Для каждого нового испытания снимайте всю массу с массы вешалка. Поднимите блок с доски и надежно установите его на доску в том же исходном положении.

· Наращиваем массу на вешалке с помощью массы увеличивается так, чтобы блок скользил после того, как вы положили максимум 5-граммовый кусок на вешалке.Это означает, что вы будете сначала нужно найти общий диапазон масс, в котором будет скользить блок. Затем переходите к скользящей массе, используя небольшой приращения массы. Если блок скользит после того, как вы положили, например, 10 грамм на вешалку, не используйте это испытание: вы промахнулись. В идеале, вы хотите, чтобы последняя масса, помещенная на вешалку, была 1- или 2-граммовая штука.

Эта процедура необходима, потому что блок имеет тенденцию чтобы «приварить» к доске, пока вы медленно добавляете массу вешалка.Вы, несомненно, заметите это эффект при проведении эксперимента. Таким образом, каждое испытание согласуется с другими.

1. Запишите общую массу на блоке ( м ₁ ) и подвесной массы, включая подвес ( м ₂ ), для каждого пробный.

Анализ

1. Рассчитайте средняя висячая масса для каждой нормальной силы и, следовательно, средний максимум сила статического трения для каждого набора масс.

2.Изобразите график сила трения как функция нормальной силы. Предположим, что если нормальная сила равна нулю (a безмассовый блок), сила трения также будет равна нулю, поэтому используйте начало координат (0,0) как первая точка графика. Используя линейку, нарисуйте лучшую линию, которую вы можете определить по origin и через точки данных.

3. Возьмите склон график и запишите уравнение графика. Наклон — это ваше экспериментальное значение для коэффициент статического трения.

4. Вопрос: При определении силы трения покоя для блок на доске, если на вешалку было помещено слишком много массы, блок внезапно дрочит. Используйте ваш результаты для μ _k и μ _s для объяснения Зачем.

Статическое трение: предельный угол Отдых

1. Прикрепите угловой зажим к столу стоять. Вставьте металлический стержень в отверстие в боковой части планки и зажмите конец стержня под прямым углом зажим.Поднимая и опуская зажимом, вы можете увеличить или уменьшить угол, который планка образует с горизонтальный. Начните с доски все вниз (почти горизонтально).

2. Снимите веревку с блока и поместите блок на доске возле зажима.

3. Медленно поднимите зажим (и планку), пока блок начинает скользить. Затяните зажим как только начинается скольжение.

4. С помощью инклинометра измерьте угол планка делается с горизонталью.Это предельный угол естественного откоса блока. Запишите угол в таблице 4.

5. Повторите вышеуказанное еще два раза, чтобы у вас три отдельных измерения предельного угла. Каждый раз начинайте с планки горизонтально.

6. Выполните описанные выше процедуры трижды, используя плита из стекла или других предоставленных материалов. Запишите предельные углы в таблице 4.

1. Найдите среднее из трех записанных углов. Это q _L , предельный угол естественного откоса.2. Найдите отклонения от среднего для каждого пробный.

3. Рассчитайте коэффициент трения покоя для каждого материала с использованием q _L уравнение (7).

4. Найдите погрешность коэффициента, Δμ _с , используя среднее отклонение в предельный угол как Δ q _L . (См. Раздел во введении, Расчет с ошибками , если необходимо.)

5. Взять процент разница между μ _с для блока, найденного здесь и найденного методом плоских досок.

6. Вопрос: Рассчитать ускорение блока на наклон после начала движения. использование ваше значение μ _k из Части 1 и средний угол естественного откоса.

,

Line Graphs, Elastic Force, and Frictional Force Quiz скачать ppt

Презентация на тему: «Тесты на линейные графики, упругую силу и силу трения 2» — стенограмма презентации:

1 Линейные графики, упругая сила и сила трения: тест 2

2 Урок 3: Сила упругости Два типа силы упругости — это растяжение и сжатие.Сила упругости резинки прямо пропорциональна расстоянию растяжения. — Приблизительно сила упругости удваивается, когда расстояние растяжения удваивается. — Следовательно, если на 2 см сила упругости составляет 1,0 Н, то на 4 см вы можете оценить, что сила упругости будет 2,0 Н.

3 Упругая сила и третий закон движения Ньютона Третий закон движения Ньютона: на каждое действие существует равное и противоположное противодействие.- Резинка является примером третьего закона движения Ньютона, потому что, когда резинка растягивается (действие), она оттягивает пружинную шкалу, создавая силу (противодействие).

4 Урок 4: Сила трения Статическое трение — трение между двумя неподвижными объектами. — Пример: когда вы впервые пытаетесь протянуть блок по поверхности, кажется, что он застрял. Это из-за статического трения.Чтобы преодолеть статическое трение, требуется определенное усилие. Несбалансированная сила — когда две силы, действующие на объект, не равны по размеру. — Несбалансированные силы заставляют неподвижный объект двигаться. движущийся объект для ускорения или замедления, движущийся объект для остановки, движущийся объект для изменения направления.

5 Урок 4: Несбалансированная сила Примером неуравновешенной силы из урока 4 была сила, с которой ваша рука тянула блок, которая была сильнее силы трения.Двумя силами были сила руки, тянущей блок, и сила трения.

6 Что вызывает изменение трения? Изменение поверхностей Изменение типа поверхности, на которой находится блок, изменит силу трения. — У столешницы было наименьшее трение, а у наждачной бумаги — наибольшее. Изменение площади поверхности Изменение стороны блока, контактирующей с поверхностью, НЕ изменило силу трения.

7 Изменение веса Изменение веса блока (добавление большего количества блоков) действительно изменило силу трения. — Вес блока прямо пропорционален силе трения. — Удвоение веса (количество блоков) увеличивает вдвое силу трения.

8 Графики: оси Ось x находится внизу.Ось y (y к небу) находится сбоку. Независимая переменная (то, что вы меняете) идет по оси абсцисс. Зависимая переменная (определяемая экспериментом) идет по оси ординат.

9 Графики: маркировка Каждая ось должна включать метку с единицами измерения в скобках. Например, «Расстояние растяжения» — это метка, а «(см)», обозначающее сантиметры, — это единицы измерения в скобках.- Обычно вы можете найти метки и единицы измерения как метки столбцов таблицы данных. В верхней части графика должен быть заголовок, объясняющий, что изображено на графике.

10 Графики: равномерный масштаб Каждая ось должна иметь набор чисел, начинающийся с 0. В зависимости от данных, каждая ось должна идти только на 1 или 2 числа выше, чем наивысшая точка. — Например, если данные идут только до 14, тогда масштаб оси должен увеличиваться примерно до 16.На каждой оси должны быть числа, распределенные вдоль оси. На каждой оси должен быть узор. Например: 0,5, 1,0, 1,5, 2,0, 2,5.

11 Построение графика: линия Прямая линия должна проходить через большинство, если не все точки. Вы НЕ должны соединять точки, а проведите через них прямую линию.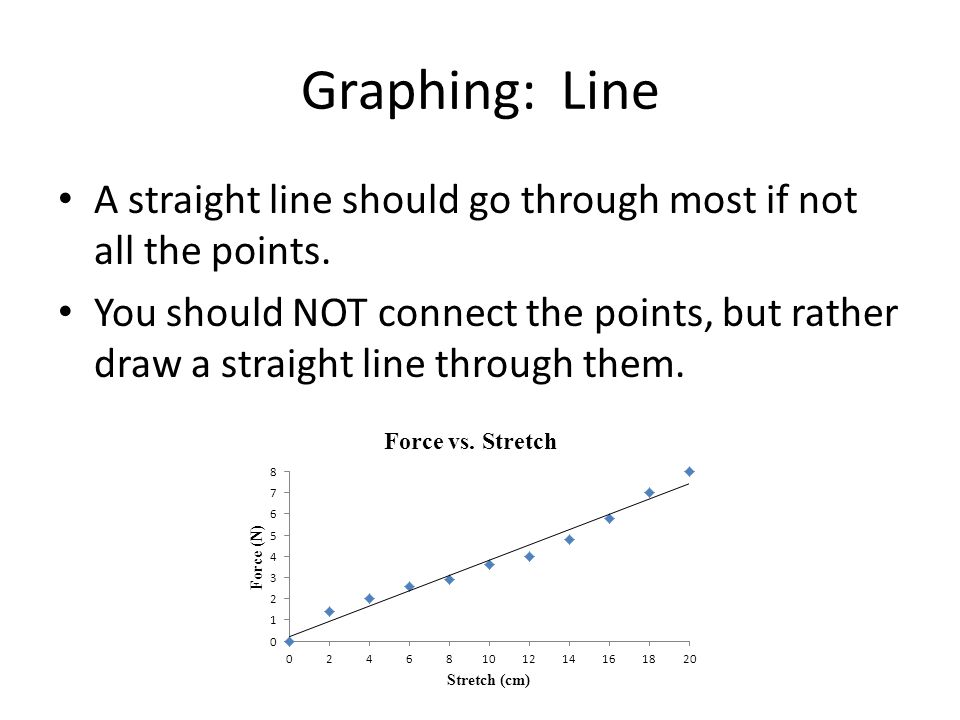

12 Словарь для изучения экстраполяции Прямая пропорция Независимая переменная Зависимая переменная трение Статическое трение Несбалансированная сила

.