Закон Ома для замкнутой цепи
Закон Ома для замкнутой цепи часто находит применение в работе с электричеством. Благодаря закономерности, найденной немецким физиком Георгом Омом, сегодня мы можем рассчитать величину тока, протекающего в проводе или необходимую толщину провода для подключения к сети.
История открытия
Будущий ученый с малых лет интересовался природой электрического тока. Он провел множество испытаний, связанных с измерением напряжения и силы тока. Ввиду несовершенства измерительных приборов того времени, первые результаты исследований были ошибочны и препятствовали дальнейшему развитию вопроса. Георг опубликовал первую научную работу, в которой описывал возможную связь между напряжением и силой тока. Последующие его работы подтвердили предположения, и Ом сформулировал свой знаменитый закон. Все труды были внесены в доклад 1826 года, но научное сообщество не заметило труды молодого физика.
Через пять лет, когда известный французский учёный Пулье пришел к такому же выводу, Георга Ома наградили медалью Копли, за внесение большого вклада в развитии физика как науки.
Сегодня закон Ома используется по всему миру, признанный истинным законом природы. .
Детальное описание
Закон Георга показывает значение электричества в определенной сети, имеющее зависимость от сопротивления к нагрузке и внутренним элементам источника питания. Рассмотрим это детально.
Условное устройство, использующее электроэнергию (например, звуковой динамик) при подключении к источнику питания образует замкнутую цепь (рисунок 1). Подсоединим динамик к аккумулятору. Следующий через динамик ток тоже следует через источник питания. Поток заряженных частиц встретит сопротивление провода и внутренней электроники устройства, а также сопротивление аккумулятора (электролит внутри банки оказывает определенное воздействие на электрический ток). Исходя из этого, значение сопротивления закрытой сети складывается из сопротивления:
- Источника питания;
- Электрического устройства.
Подключение условного электрического прибора (динамика) к источнику питания (автомобильному аккумулятору)
Первый параметр называют внутренним, второй – внешним сопротивлением. Противодействие источника электричества маркируется символом r.
Представим, что по сети источник питания/электрическое устройство проходит определённый ток T. Для сохранения стабильного значения электричества внешней сети, в соответствии с законом, на её окончаниях должна наблюдаться потенциальная разность, которая равна R*T. Ток такой же величины проходит и внутри цепи. Вследствие этого – сохранение постоянного значения электричества внутри сети требует потенциальной разности на окончаниях сопротивления r. Она, согласно закону, должна равняться T*r. При сохранении стабильного тока в сети, значение электродвижущей силы равно:
E=T*r+T*R
Из формулы следует, что ЭДС равна сумме падения напряжений во внутренней и внешней сети. Если вынести значение T за скобки, получим:
Е=T(r+R)
или
T=E/(r+R)
Примеры задач на применение закона для соединенной сети
1) К источнику ЭДС 15 В и сопротивлением 2 Ом подсоединен реостат с сопротивлением 5 Ом. Задача – вычислить силу тока и напряжение на зажимах.
Вычисление
- Представим закон Ома для соединенной сети: T=E/(r+R).
- Снижение напряжения вычислим по формуле: U= E-Tr=ER/(R+r).
- Подставим имеющиеся значения в формулу: T= (15 В)/((5+2) Ом) = 2.1 А, U=(15 В* 5 Ом)/(5+1) Ом = 12.5 В
Ответ: 2.1 А, 12.5 В.
2) При подсоединении к гальваническим элементам резистора с сопротивлением 30 Ом, сила тока в сети приняла значение в 1.5 А, а при подсоединении такого же элемента с сопротивлением 15 Ом сила тока стала 2.5 А. Задача – узнать значение ЭДС и внутреннее сопротивление цепи из гальванических элементов.
Вычисление
- Запишем закон Георга Ома для соединённой сети: T=E/(r+R).
- Из него выведем формулы для внутреннего и внешнего сопротивления: E=T_1 R_1+T_1 r, E= T_2 R_2 + T 2r.
- Приравняем части формулы и вычислим внутреннее сопротивление: r=(T_1 R_1-T_2 R_2)/(T_2-T_1 ).
- Полученные значения подставим в закон: E=(T_1 T_2 (R_2-R_1))/(T_2-T_1 ).
- Проведем вычисления: r=(1.5 А∙30 Ом-2.5А∙15 Ом)/(2,5-1,5)А=7.5 Ом, E=(1.5 А∙2.5А(30-15)Ом)/((2.5-1.5)А)=56 В.
Ответ: 7.5 Ом, 56 В.
Сфера применения закона Ома для замкнутой цепи
Закон Ома – универсальный инструмент электрика. Он позволяет правильно рассчитать силу тока и напряжение в сети. В основе принципа работы некоторых устройств лежит закон Ома. В частности, предохранителей короткого замыкания.
Короткое замыкание – случайное замыкание двух участков сети, не предусмотренное конструкцией оборудования и приводящее к неисправностям. Для предотвращения таких явлений используют специальные устройства, отключающие питание сети.
Если произойдет случайное замыкание цепи с большой перегрузкой, устройство автоматически прекратит подачу тока.
Закон Ома в данном случае находит место на участке цепи постоянного тока. В полной схеме процессов может быть гораздо больше. Многие действия при построении электрической сети или ее ремонте следует проводить с учетом закона Георга Ома.
Для полного изучения соотношения параметров тока в проводниках представлены формулы: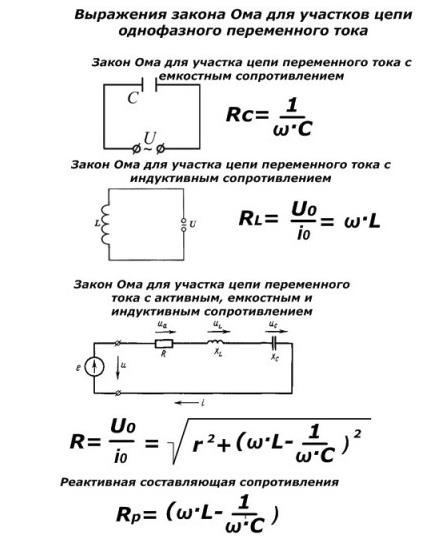
Более сложное выражение закона для практического применения:
Сопротивление представлено отношением напряжения к силе тока в цепи. Если напряжение увеличить в n раз, значение тока также увеличится в n раз.
Не менее известны в электротехнике труды Густава Киргофа. Его правила находят применения в расчетах разветвленных сетей. В основе этих правил лежит закон Ома для электрической цепи.
Труды ученого нашли применение при изобретении многих повседневных вещей, таких как лампы накаливания и электрические плиты. Современные достижения в электронике многим обязаны открытиям 1825 года.
Поделиться ссылкой:
Похожее
формула и определение, источник ЭДС
Взаимозависимость параметров системы в физике принято называть законом.
В электротехнике таковых было открыто несколько и один из главнейших — закон Ома для замкнутой цепи.
В данной статье он и все связанные с ним понятия рассматриваются подробно.
Закон Ома для замкнутой цепи
Какова причина их движения? Объяснить его действием электростатического поля нельзя: работа последнего при перемещении заряженной частицы по закольцованному контуру, как известно, равна нулю, а между тем в электросети в момент протекании тока явно совершается некая отличная от нуля работа — выделяется тепло, горит свет либо возникает магнитное поле.
Следовательно, должны быть какие-то иные силы, обуславливающие данное движение. Их называют сторонними (СС), а компонент электросхемы, в котором они проявляются, — источником тока (ИТ или двухполюсником). СС, преодолевая силы электростатического поля, «растаскивают» минусовые и плюсовые заряды в разные части ИТ (они называются полюсами), создавая разность потенциалов, и далее те движутся по сети под действием электростатического поля.
Аналогично подъемник «заряжает» потенциальной энергией поднимаемый груз, преодолевая силу гравитации, а циркуляционный насос — кинетической энергией частицы воды, создавая разность давлений. Электрическую сеть, включающую ИТ, называют полной или замкнутой. В противоположность ей, сеть вне двухполюсника называют внешней.
В разных ИТ сторонние силы создаются следующими способами:
- фотонным. Разность потенциалов возникает при взаимодействии фотонов (из этих частиц состоит свет) с полупроводниковыми материалами. Действующие по такому принципу ИТ называют солнечными батареями;
- химическим. На этом принципе основано действие гальванических элементов — батареек и аккумуляторов. К примеру, химическое разделение зарядов возникает при погружении в серную кислоту медного и цинкового электродов. Кислота изымает из каждого металла положительно заряженные ионы, но цинк отдает их легче и потому принимает относительно меди отрицательный заряд. Медный же электрод становится положительным полюсом, и если теперь соединить его с цинковым электродом проволокой, по ней потечет ток;
- электромагнитным. СС вызываются воздействием на проводник переменного магнитного поля. Изменение его параметров, то есть его «переменность», достигается за счет движения относительно него проводника: тот совершает обороты в поле либо, наоборот, магнит вращают вокруг проводника. На этом принципе основана работа электрогенераторов (в обиходе называются динамо-машинами).
Возникновение электротока в проводнике под действием переменного электромагнитного поля, называется электромагнитной индукцией. Двигая заряды q по сети, СС совершают некую работу А. Она, очевидно, пропорциональна величине перемещаемого q, а значит, при любой величине А и Q их соотношение остается константой и может выступать характеристикой двухполюсника. Ее называют электродвижущей силой (ЭДС).
Электродвижущая сила источника тока
Математическое выражение ЭДС, обозначенной буквой Ԑ, записывается так: Ԑ = А/q. Измеряют ЭДС в тех же единицах, что и напряжение — в вольтах (В). Из последнего выражения работа СС записывается как А = Ԑ * q. С другой стороны, работа СС, согласно закону сохранения энергии, должна равняться действию электрического тока. Последняя состоит в выделении тепла (рассматривается сеть постоянного тока с активным сопротивлением).
Выделяемое тепло, в соответствии с законом Дж.-Ленца, вычисляется как произведение квадрата силы тока и электросопротивления. Последняя характеристика присуща как внешней цепи — она обозначается через R, так и ИТ (сопротивление обмоток генератора или электролита, обозначаемое через r).
Математическая запись вышесказанного:
- теплота, выделяющаяся во внешней сети: Q1 = I2 * R * t;
- теплота, выделяющаяся в ИТ: Q2 = I2 * r * t;
- работа СС: А = Ԑ * q = I2 * R * t + I2 * r * t.
Силой тока I, как известно, называют количество заряда, пересекающее поперечное сечение проводника за единицу времени: I = q / t. Значит, q = I * t, соответственно, Ԑ * q = E * I * t. Тогда получим: А = Е * q = Ԑ * I * t = I2 * R * t + I2 * r * t. Сократив обе части равенства на I * t, получим: Ԑ = I * R + I * r. Откуда I = Ԑ / (R + r).
Последнее выражение представляет собой математическую запись закона Ома для замкнутой (полной) электросхемы. Сила тока в сети находится в прямой зависимости от ЭДС его источника и в обратной – от полного сопротивления. Как ясно из определения, сумму сопротивлений внешней цепи и ИТ (R + r) называют ее полным сопротивлением.
Таким образом, закон Ома для участка сети, выражаемый формулой I = U / R, является частным случаем закона для полной цепи, в котором двухполюсник во внимание не берут. Из него следует, что U = I * R. Возвращаясь к записи Ԑ = I *R + I * r, можно Заменить I * R на U, и тогда получится: Ԑ = U + I * r.
Формула закона Ома для замкнутой цепи
Поскольку через R обозначалось сопротивление всех наружных проводников, U в данном выражении определяет напряжение на ее концах, то есть на клеммах ИТ. После переноса слагаемого из одной части равенства в другую, получим: U = Ԑ – I * r.
Напряжение на клеммах двухполюсника зависит от протекающего в сети тока. Когда электросеть разомкнута и сила тока равна нулю, U = Ԑ. При коротком замыкании (КЗ), когда ток приобретает максимально возможное значение, U = 0.
Коэффициент полезного действия
Любое устройство или механизм сообщенную ему извне энергию частично расходует на всевозможные потери, а ее оставшееся количество преобразует в работу. Она именуется полезной (Апол). Отношение полезной работы к общим затратам энергии, говорит об эффективности устройства. Такую характеристику называют коэффициентом полезного действия (КПД): КПД = Апол / А.
Коэффициент полезного действия источника тока
В электротехнике «полезной» называют работу тока во внешней цепи. В самом простом случае (постоянный ток, активное сопротивление) она равна количеству тепловыделения, то есть: Апол = Qвнеш = I2 * R * t. Выше было показано, что совокупная работа СС А = I2 * R * t + I2 * r * t, следовательно: КПД = Апол / А = I2 * R * t / (I2 * R * t + I2 * r * t) = R / (R + r).
Приведенная формула позволяет определить КПД ИТ. В соответствии с законом сохранения энергии, он не может быть больше единицы. Принято КПД указывать в процентах. Так, при его значении, к примеру равному 0,95, говорят, что КПД составляет 95%.
Источник ЭДС
Выше было показано, что в реальном ИТ, напряжение на клеммах U зависит от силы тока в электросети. Источник ЭДС — это идеальный, теоретический ресурс напряжения (ИН) с отсутствующим внутренним сопротивлением (r = 0), то есть напряжение U на его контактах и ЭДС равны. Сила тока здесь на это равенство не влияет.
Идеальный источник напряжения
При КЗ ток становится теоретически бесконечно большим. В самом деле, если в выражении закона Ома для полной цепи: I = Ԑ / (R + r) Если полное сопротивление приравнять к нулю, сила тока I достигает бесконечности.
Поэтому источник ЭДС представляет собой теоретический бесконечный источник мощности. В реальности подобное невозможно, так как при КЗ ток в электросети ограничивается сопротивлением двухполюсника (обмоток генератора или электролита гальванического элемента).
Реальный ИН представляет собой источник конечной мощности. На схемах его обозначают как идеальный ИН с подключенным к нему последовательно элементом, соответствующим сопротивлению ИТ.
Соединение источников тока
Если одного ИТ для работы устройства недостаточно, их устанавливают несколько. Характер работы такой группы зависит от способа соединения отдельных источников.
Есть три варианта:
- последовательное;
- параллельное;
- смешанное.
При последовательном подключении ИТ выстраивают в ряд, соединяя «плюсом» к «минусу». При этом заряды проходят по порядку через все источники, воспринимая энергию от каждого из них.
Следовательно, совокупные:
- ЭДС группы равна алгебраической сумме этих характеристик всех ИТ;
- сопротивления группы двухполюсников равно сумме соответствующих параметров каждого из них.
Если соединены n идентичных ИТ с ЭДС, равным Ԑ, и сопротивлением r, то эти параметры для группы окажутся, соответственно: Ԑ гр = n * E; Rгр = n * r. Тогда закон Ома для замкнутой цепи записывается в такой форме: I = (n * Ԑ) / (R + n * r).
Последовательное и параллельное соединение источников
Если направление от «минуса» к «плюсу» в источнике совпадает с движением часовой стрелки, то его ЭДС считается положительной. Электродвижущая сила, направленная в противоположную сторону, отрицательна.
Если внутреннее сопротивление источников в сравнении с R цепи пренебрежимо мало, а надо увеличить U на наружной сети, ИТ соединяют последовательно.
«Плюсы» ИТ, установленных параллельно, подсоединяются к одному концу системы проводников, а все «минусы» — к другому, при этом:
- каждый заряд набирает энергию только в одном ИТ, потому ЭДС группы равна одноименному параметру одного двухполюсника: Ԑ гр = Ԑ;
- через отдельно взятый ИТ протекает только доля потока, потому совокупное внутреннее сопротивление группы ниже внутреннего одного элемента в n раз: rгр = r / n. Здесь n — число ИТ в группе.
Здесь также рассматривается случай с одинаковыми ИТ. Закон Ома для полной цепи примет следующую форму: I = Ԑ / (R + (r / n)). Как видно, замена одного ИТ группой параллельно подключенных, приводит к увеличению I во внешней сети.
Соответственно, такой способ подключения применяют при необходимости повысить силу тока в электросети без увеличения напряжения, и сопротивление наружной сети соизмеримо с аналогичным параметром одного двухполюсника.
Видео по теме
Объяснение закона Ома для замкнутой цепи в видео:
Как видно, закон Ома для замкнутой электросхемы соотносит главные «электрические» параметры: силу тока, ЭДС источника напряжения и сопротивление. Потому его следует знать и понимать любому, кто стремится освоить электротехнику.
Закон Ома для замкнутой цепи. Напряжение. — Студопедия.Нет
Замкнутая (полная) электрическая цепь состоит из источника тока и сопротивления.
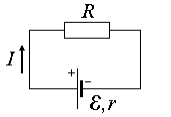
Источник тока имеет ЭДС (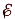 
) и сопротивление (r), которое называют внутренним. ЭДС (электродвижущая сила) — работа сторонних сил по перемещению положительного заряда по замкнутой цепи (физический смысл аналогичен напряжению, потенциалу). Полное сопротивление цепи — R+r.
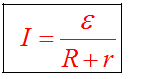
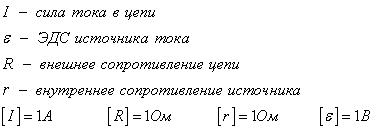
1) Напряжение на зажимах источника, а соответственно и во внешней цепи
,
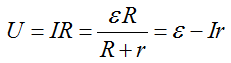где величина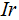 
— падение напряжения внутри источника тока.
2) Если внешнее сопротивление замкнутой цепи равно нулю, то такой режим источника тока называется коротким замыканием.
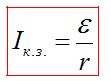
Работа и мощность тока. КПД источника тока. Закон Джоуля–Ленца.
Рассмотрим однородный участок 1−2 проводника, к которому приложена разность потенциалов ϕ2 − ϕ1. Если по проводнику течет ток I, то за время dt через поперечное сечение его будет перенесен заряд dq = Idt.
Следовательно, силы поля совершат элементарную работу
δA = dq(ϕ2− ϕ1) = I(ϕ2 − ϕ1)dt = IUdt.
Полезная работа на всем участке 1− 2
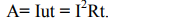
Если электрическая цепь замкнута и содержит источника с ЭДС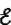 
, то вся затраченная источником тока работа АЗ = АП + АВНУТ, где АЗ = I 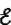t, АП = IURt, АВНУТ = IUrt. Тогда
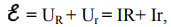
где UR − напряжение на внешнем сопротивлении, Ur − напряжение на внутреннем сопротивлении источника тока.
Мощность тока можно найти по формуле
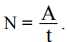
Развиваемая источником тока затраченная мощность
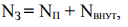
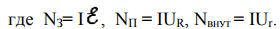
КПД источника тока можно найти по формуле
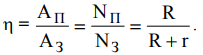
Затраченная источником тока мощность
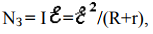
гдеI = 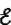/(R + r).
Полезная мощность, выделяемая во внешнем участке цепи
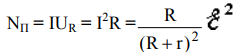
Следовательно, затраченная и полезная мощности являются функциями от
внешнего сопротивления. Если R→ 0, то NП → 0; R→ ∞, то NП → 0. В этом случае функция NП = f2 (R) имеет один максимум. Найдем условие, при котором полезная мощность максимальна, т. е. NП = NП, МАХ. Для этого производную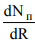 
приравняем нулю,
т. е.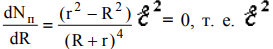 
, т. е.
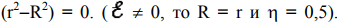
Вывод: Если R = r , то полезная мощность максимальна, а КПД источника тока равно 50%.
Тепловое действие тока. Закон Джоуля-Ленца.
При прохождении тока по проводнику происходит его нагревание, т. е. выделяется некоторое количество теплоты Q.
Для определения выделяющегося количества теплоты за единицу времени рассмотрим однородный участок проводника, к которому приложена разность потенциалов ϕ1 − ϕ2.
На основании закона сохранения энергии эта работа переходит во внутреннюю (тепловую) энергию, в результате чего проводник нагревается.
Действительно, в металлах электроны проводимости (носители тока) под действием сил поля получают дополнительную кинетическую энергию, которая расходуется на возбуждение колебаний кристаллической решетки при взаимодействии электронов с ее узлами.
Так как при прохождении тока в металлических проводниках не происходит изменение внутренней структуры металла, то вся работа сторонних сил идет на выделение тепла, т. е. δА = δQ.
На основании закона Ома для однородного участка проводника U = IR и формулы (19) получаем закон Джоуля−Ленца:
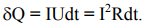
Если на участке цепи выделить некоторый объем dV, то с учетом формул (2) и (9) последняя формула примет вид
Если в последнем выражении левую и правую части разделить на dVdt, то получим удельную тепловую мощность:
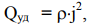(26)
т. е. удельная тепловая мощность определяет количество теплоты, которое выделяется в единице объема проводника за единицу времени, и численно равна произведению удельного сопротивления проводника на квадрат плотности тока.
Формула (26) применима к любым проводникам, не зависит от их формы, однородности и природы сил, возбуждающих электрический ток.
Если на заряды проводника действуют только электрические силы, то на основании закона Ома (11) имеем
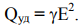
Если участок цепи неоднородный, то выделяемое количество теплоты по закону сохранения энергии будет равно алгебраической сумме работ кулоновских и сторонних сил. Действительно, умножив правую и левую части формулы (16) на силу тока I получим
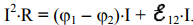(28)
Следовательно, из уравнения (28) следует, что тепловая мощность
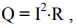(29)
выделяемая на участке цепи 1−2, равна алгебраической сумме мощностей кулоновских и сторонних сил. Если цепь замкнута, то затраченная мощность
N =I ⋅ 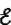. (30)
Таким образом, общее количество теплоты, выделяемой за единицу времени во всей цепи, равно мощности только сторонних сил.
Электрическое же поле только перераспределяет теплоту по различным участкам цепи. Закон Джоуля−Ленца справедлив и для электролитов, так как работа электрического поля в них не расходуется на образование ионов, которые возникают при диссоциации молекул в результате растворения.
Высокая электропроводность и теплопроводность металлов объясняется наличием в них «свободных» электронов.
Пожалуйста запишите закон Ома для замкнутой цепи, очень надо тт. тт
Замкнутая цепь состоит из двух частей — внутренней и внешней. Внутренняя часть цепи представляет собой источник тока, обладающий внутренним сопротивлением r; внешняя — различные потребители, соединительные провода, приборы и т. д. Общее сопротивление внешней части обозначается R. Тогда полное сопротивление цепи равно r + R. Рис. 2 По закону Ома для внешнего участка цепи 1 → 2 имеем: φ 1− φ 2=IR. Внутренний участок цепи 2 → 1 является неоднородным. Согласно закону Ома, φ 2− φ 1+ε=Ir. Сложив эти равенства, получим ε=IR+Ir.(1) Отсюда I=ε R+r .(2) Последняя формула представляет собой закон Ома для замкнутой цепи постоянного тока. Сила тока в цепи прямо пропорциональна ЭДС источника и обратно пропорциональна полному сопротивлению цепи. Так как для однородного участка цепи разность потенциалов есть напряжение, то φ 1− φ 2=IR=U и формулу (1) можно записать: ε=U+Ir⇒U=ε−Ir. Из этой формулы видно, что напряжение на внешнем участке уменьшается с увеличением силы тока в цепи при ε = const. Подставим в последнюю формулу силу тока (2), получим U=ε(1−r R+r ). Проанализируем это выражение для некоторых предельных режимов работы цепи. а) При разомкнутой цепи (R → ∞) U = ε, т. е. напряжение на полюсах источника тока при разомкнутой цепи равно ЭДС источника тока. На этом основана возможность приблизительного измерения ЭДС источника тока с помощью вольтметра, сопротивление которого много больше внутреннего сопротивления источника тока ( R v≫r). Для этого вольтметр подключают к клеммам источника тока. б) Если к клеммам источника тока подключить проводник, сопротивление которого R≪r, то R + r ≈ r, тогда U=ε(1−r r )=0, а сила тока I=ε r — достигает максимального значения. Подключение к полюсам источника тока проводника с ничтожно малым сопротивлением называется коротким замыканием, а максимальную для данного источника силу тока называют током короткого замыкания: I kz= ε r . У источников с малым значением r (например, у свинцовых аккумуляторов r = 0,1 — 0,01 Ом) сила тока короткого замыкания очень велика. Особенно опасно короткое замыкание в осветительных сетях, питаемых от подстанций (ε > 100 В) , Ikz может достигнуть тысячи ампер. Чтобы избежать пожаров, в такие цепи включают предохранители. Запишем закон Ома для полной цепи в случае последовательного и параллельного соединения источников тока в батарею. При последовательном соединении источников «-» одного источника соединяется с «+» второго, «-» второго с «+» третьего и т. д. (рис. 3, а) . Если ε1 = ε2 = ε3 а r1 = r2 = r3 то εb = 3ε1, rb = 3r1. В этом случае закон Ома для полной цепи имеет вид I=ε b R+r b = 3ε 1 R+3r 1 , или для n одинаковых источников I=nε 1 R+nr 1 . Рис. 3 Последовательное соединение применяют в том случае, когда внешнее сопротивление R≫nr 1, тогда I=nε 1 R и батарея может дать силу тока, в n раз большую, чем сила тока от одного источника. При параллельном соединении источников тока все «+» источников соединены вместе и «-» источников — также вместе (рис. 3, б) . В этом случае ε b= ε 1; r b= r 1 3 . Откуда I=ε 1 R+r 1 3 . Для n одинаковых источников I=ε 1 R+r 1 n . Параллельное соединение источников тока применяют тогда, когда нужно получить источник тока с малым внутренним сопротивлением или когда для нормальной работы потребителя электроэнергии в цепи должен протекать ток. больший, чем допустимый ток одного источника. Параллельное соединение выгодно, когда R невелико по сравнению с r. Иногда применяют смешанное соединение источников. —ИЗУЧАЙ
