2. Закон изменения тока в цепи при подключении
и отключении источника.
Применение закона для определения индуктивности
Найдем изменение тока в цепи, состоящей из последовательно соединенных соленоида, индуктивность которой равна , и резистора, активное сопротивление которого.
Если внешнее магнитное поле отсутствует или постоянно, а контур неподвижен, то индукционные явления обусловлены только самоиндукцией.
Из закона Ома для замкнутой цепи, в которой действует источник ЭДС , а общее активное сопротивление, сила тока равна
Для нахождения зависимости силы тока от времени разделим переменные
.
Полагая постоянными и интегрируя, получаем
где
–
постоянная интегрирования, значение
которой определяется начальными
условиями решаемой задачи.
Выразив силу тока, получим
(15.5)
Из этой общей формулы можно получить зависимость силы тока от времени при замыкании цепи. В этом случае начальный ток равен нулю и выражение (15.5) приобретает вид
(15.6)
Из этой формулы видно, что сила тока при замыкании цепи постепенно увеличивается, стремясь к , соответствующей величине постоянного тока (рис. 15.1). Нарастание тока происходит тем медленнее, чем меньше отношениев показателе степени экспоненты или больше обратное отношение, физический смысл которого обсуждается ниже.
Если же в момент времени при силе токаисточник ЭДС отключить (), сохранив замкнутость цепи, то из формулы (15.5), получим следующую зависимость силы тока от времени:
(15.
7)
В этом случае сила тока в цепи постепенно уменьшается от начального значения , стремясь к нулю. При этом за время(время релаксации) сила тока изменяется в раза.
Рис. 15.1
Следует заметить, что в опыте удобнее снимать вместо зависимости силы тока в цепи от времени зависимость напряжения на некотором известном активном сопротивлении, последовательно включенном в цепь, от времени. Напряжение в этом случае будет пропорционально силе тока.
Из сказанного ясно, что, измерив силу токов (или напряжения) в некоторые моменты времени ,и зная, кроме того, величину общего активного сопротивления контура, можно с помощью зависимостей (15.6) или (15.7) определить индуктивность контура.
Особенно просто, зная активное сопротивление цепи , определить её индуктивность, измерив время релаксации,
(15.8)
их применение для измерения индуктивности
Рассмотрим
контур, состоящий из последовательно
соединенных конденсатора емкостью
,
активного сопротивленияи соленоида индуктивностью.
Для получения незатухающих электромагнитных колебаний необходимо включить в контур источник тока с периодически изменяющейся ЭДС (рис. 15.2).
Рис. 15.2
В этом случае колебания в контуре являются вынужденными.
Пусть внешняя ЭДС изменяется по гармоническому закону
.
Тогда, используя закон Ома, можно получить следующее дифференциальное уравнение вынужденных электромагнитных колебаний
и, решив это уравнение, найти для установившихся вынужденных колебаний связь амплитудных значений силы тока и внешней ЭДС
(15.9)
где величина называется полным сопротивлением электрической цепи переменного тока.
В
нее входят активное
сопротивление контура, емкостное
сопротивление и индуктивное
сопротивление .
Если электрическая емкость контура стремится к бесконечности , то есть емкостное сопротивление к нулю, то формула (15.9) упрощается
(15.10)
Используя это выражение, получаем рабочую формулу для экспериментального определения индуктивности соленоида. При этом учтем, что амплитуда падения напряжения на активном сопротивлении R связана с амплитудой силы тока в цепи формулой
(15.11)
Из выражений (15.10) и (15.11) получим
(15.12)
Расчет тока короткого замыкания — журнал IAEI
Одним из наиболее фундаментальных расчетов, выполняемых в системе распределения электроэнергии, является расчет доступного тока короткого замыкания. В выпуске журнала IAEI за сентябрь–октябрь 2012 г. была опубликована статья под названием «Переход к основам, максимальный ток короткого замыкания», в которой затрагивалась эта тема, но не вдавались в математику.
С тех пор я получил много просьб заняться математикой. Я надеюсь, что эта статья удовлетворит пытливые умы подробностями расчета доступного тока короткого замыкания и предоставит некоторые уравнения для изучения студентом.
Доступный ток короткого замыкания
Максимально доступный ток короткого замыкания является важным параметром для каждой системы распределения электроэнергии, поскольку он обеспечивает точку данных, необходимую для обеспечения того, чтобы оборудование применялось в пределах его номинальных характеристик, а система работала в соответствии с ожиданиями. Доступный ток короткого замыкания также используется во многих других приложениях.
Национальный электротехнический кодекс требует эту точку данных для обеспечения соблюдения таких разделов, как 110.9, Номинальные параметры прерывания; 110.10 Полное сопротивление цепи, номинальные токи короткого замыкания и другие характеристики; и 110.24 Доступный ток отказа. Независимо от того, являетесь ли вы проектировщиком, установщиком или инспектором, в какой-то момент своей карьеры вы столкнетесь с расчетом доступного тока короткого замыкания.
Понимание математики, лежащей в основе этого, и того, как используются расчетные токи короткого замыкания, может только расширить знания и понимание. Это также может помочь нам осознать, что эти расчеты должен производить квалифицированный специалист. Итак, ради понимания, я предлагаю эту статью, чтобы помочь вам.
Основы расчета тока короткого замыкания
Все, что вам нужно знать о расчете тока короткого замыкания, вы узнали на уроках схем 101, тригонометрии и базовых математических дисциплин. На рис. 1 показана простая однолинейная схема, которая вполне может быть вашим основным служебным входом для коммерческой или промышленной установки.
Рисунок 1. Однолинейная схема Рисунок 2 представляет собой базовую принципиальную схему того, что представлено на рисунке 1, и которая будет использоваться для расчета доступного тока короткого замыкания в любой точке приведенной выше простой однолинейной схемы. Инженеры назовут то, что вы видите на Рисунке 2, диаграммой импеданса, поскольку она в основном преобразует каждый компонент на Рисунке 1 выше в значения импеданса.
Для тех из вас, кто знаком со схемой 101, то, что вы видите ниже, когда все импедансы сложены вместе, представляет собой схему «эквивалента Thevanin», которая включает в себя импеданс и источник напряжения. Эта базовая схема будет использоваться на протяжении всей этой статьи.
Для расчетов и упрощения нашей работы над этим документом необходимо сделать допущения.
Предположения для трансформатора, который будет использоваться как часть примера для этой статьи, будут включать следующее. Эта информация должна быть доступна при чтении паспортной таблички трансформатора.
Трансформатор кВА 1500
Первичное напряжение 4 160 В
Вторичное напряжение 480 В
% Полное сопротивление 5,75 %
Предположение относится к доступному току короткого замыкания электросети. Для этого упражнения будет использовано 50 000 ампер. Перед проведением исследования с коммунальным предприятием связываются для получения этой информации.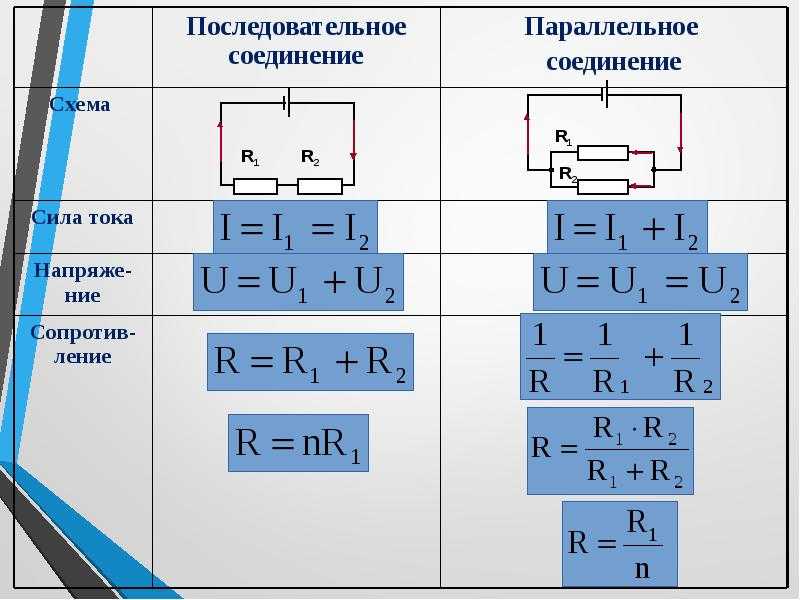
Они могут обеспечить доступный ток короткого замыкания одним из нескольких различных способов. Наиболее простыми и, вероятно, наиболее часто встречающимися данными от утилиты будет доступный ток короткого замыкания в кА. Некоторые утилиты вместо этого могут предоставлять данные в виде короткого замыкания MVA. В этой статье будут представлены уравнения для обеих форм входа, но с расчетом на допустимый ток короткого замыкания 50 кА.
Что касается импеданса проводника, то в следующих расчетах сопротивление проводника игнорируется, а используется только реактивное сопротивление. Это сделает две вещи ради этой статьи. Во-первых, это приведет к более высокому току короткого замыкания, чем было бы рассчитано, если бы мы приняли во внимание как сопротивление, так и реактивное сопротивление. Во-вторых, это упростит математику. В заключительном разделе этой статьи будут представлены результаты анализа, включающие сопротивление и реактивное сопротивление проводников и электросети. Используемые методы повторяют методы, используемые такими программами, как SKM Systems Analysis A-Fault.
В этой статье также не предполагается участие двигателя. Максимально доступный ток короткого замыкания должен включать все источники короткого замыкания. Мы не включаем этот вклад в эту работу для простоты.
Основные расчеты трансформатора
| FLA вторичный | = кВА |
| (√3)×(кВсек) |
| FLA вторичный | = 1500 |
| [(√3)×(0,480)] = 1804 Ампер |
Этот трансформатор мощностью 1500 кВА имеет вторичную полную нагрузку 1804 ампер. Этот параметр необходим для выбора вторичных проводников для данного трансформатора.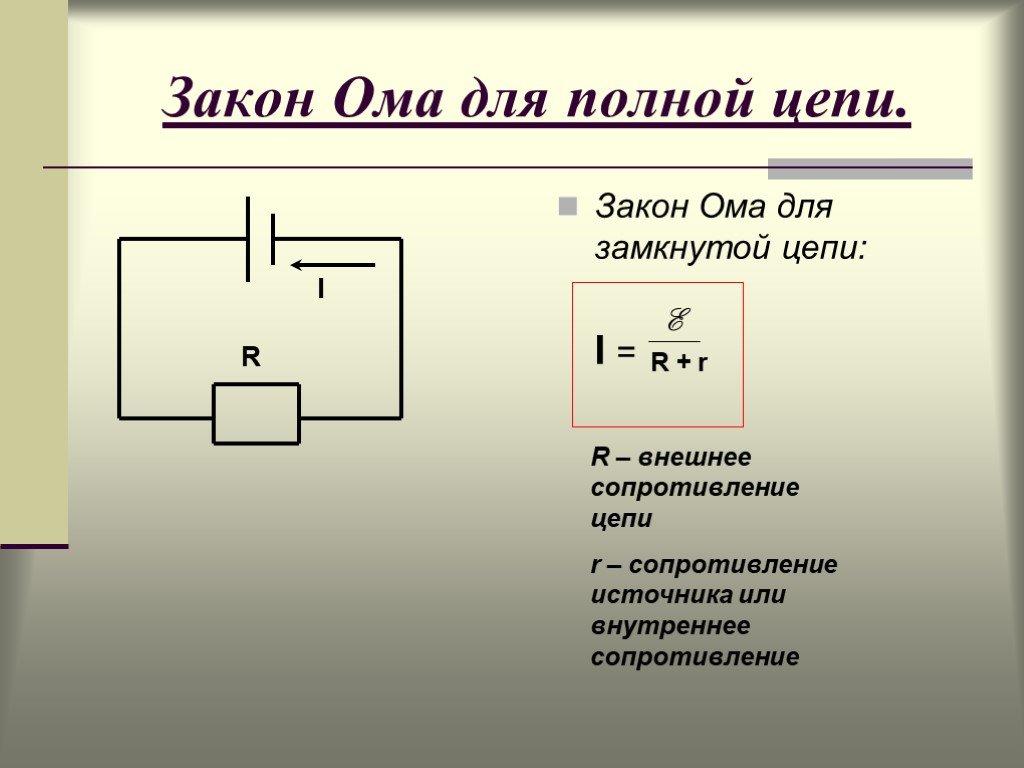
Расчет тока короткого замыкания на вторичной обмотке главного трансформатора
Существует два подхода к расчету доступного тока короткого замыкания на вторичной обмотке трансформатора. Мы можем рассчитать максимальное количество, которое пропускает трансформатор, как если бы установка по производству электроэнергии была подключена непосредственно к стороне линии трансформатора, или мы можем рассчитать доступный ток короткого замыкания, учитывая предоставленный доступный ток короткого замыкания от коммунальной службы. Первый подход, который приводит к максимальной величине тока короткого замыкания, который пропускает трансформатор, называется расчетом «бесконечной шины». Цепь на рис. 2 можно перерисовать, включив в нее нулевой импеданс для коммунальной сети, что снизит общий импеданс цепи и, таким образом, увеличит значение расчетного тока короткого замыкания.
На рис. 3 представлен только импеданс трансформатора. Уравнение для расчета максимально доступного тока короткого замыкания, который может обеспечить трансформатор, выглядит следующим образом:
| Isc | = ( Трансформатор кВА) × 100 |
| (√3)×(Вторичное кВ)×(%Z трансформатор) |
Используя приведенную выше информацию для трансформатора мощностью 1500 кВА, максимально допустимый ток короткого замыкания, который пропускает этот конкретный трансформатор, составляет 31 378 ампер и рассчитывается следующим образом:
| Искр | = 1500 × 100 |
| (√3)×(0,480)×(5,75) = 31 378 ампер |
Это говорит нам о том, что вторичная обмотка трансформатора не может подвергаться большему току короткого замыкания, чем мы рассчитали.
НИКАКИХ изменений на стороне электросети, которые могут повлиять на этот доступный ток короткого замыкания до точки, где он превысит 31 378 ампер. Единственный способ, которым эта услуга будет потреблять более 31 378 ампер, — это если мы заменим трансформатор, и новый трансформатор, который предположительно будет таким же по всем остальным характеристикам, будет иметь другой % импеданса. На рис. 4 представлена таблица, включающая результаты изменения импеданса рассматриваемого трансформатора на +/- 20 % с шагом 5 % по сравнению со значением импеданса 5,75 %, используемым в этом примере. Это показывает, как изменение импеданса трансформатора повлияет на максимально допустимый ток короткого замыкания, который он может пропустить.
Как показано на рис. 4, замена трансформатора и изменение его импеданса могут оказать существенное влияние на систему. Если бы я рискнул предположить, то сказал бы, что в большинстве случаев коммунальная служба, меняющая служебный трансформатор, будет распознаваться предприятием.
В этом расчете не учитывается импеданс источника электросети и не учитываются какие-либо проводники на стороне нагрузки. Теперь давайте рассмотрим влияние добавления в сеть доступного тока короткого замыкания.
Расчет тока короткого замыкания, включая доступный ток неисправности сети
Как и в большинстве ситуаций, мы используем консервативные методы, консервативные с точки зрения безопасности, до тех пор, пока не возникнут ситуации, требующие углубления в детали. Приведенный выше способ расчета тока короткого замыкания является консервативным, поскольку в нем НЕ учитывался доступный ток короткого замыкания, который дает максимальное значение.
При рассмотрении отключающих и других подобных номиналов устройства и оборудование, которые могут выдерживать это консервативное значение тока короткого замыкания, не требуют дальнейшего изучения. Когда новое или существующее оборудование не может справиться с этим консервативно высоким доступным током короткого замыкания, может быть проведен дальнейший подробный анализ или оборудование может быть заменено или подобрано соответствующим образом. Далее будет рассмотрено добавление утилиты при наличии доступного тока короткого замыкания. В частности, 50 кА доступны от утилиты. Это показывает, что таким образом можно уменьшить расчетные 31 378 ампер.
Ниже приведены два уравнения, которые относятся к случаям, когда доступно значение kA и когда доступно короткое замыкание MVA. Для этого примера мы будем использовать приведенное ниже уравнение, которое предполагает, что коммунальная служба предоставила вам доступный ток короткого замыкания в кА.
Принципиальная схема теперь выглядит так, как показано на рис.
5.
В первую очередь требуется преобразовать предоставленную коммунальным предприятием доступную информацию о токе короткого замыкания (50 кА) в импеданс источника.
Когда кА предоставляется коммунальным предприятием:
| %Z Коммунальное предприятие | = трансформатор кВА × 100 |
| (Isc Utility) × (√3) × (кВ Первичная) |
Когда короткое замыкание MVA предоставляется коммунальной службой:
| %Z коммунальная служба | = кВА Трансформатор |
| Короткое замыкание кВА инженерной системы |
Для заданного допустимого тока утечки 50 кА %Z сети рассчитывается следующим образом
| %Z Утилита | = 1500 × 100 |
| (50 000) × (√3) × (4,160) = 0,420 |
На рис.
6 приведены значения импеданса источника электросети для различных доступных токов короткого замыкания сети для этого конкретного примера. Как отмечалось выше, ключевую роль в этих значениях будут играть кВА трансформатора и первичное напряжение.
Уравнение для расчета доступного тока короткого замыкания на вторичной обмотке трансформатора, которое включает импеданс сети, выглядит следующим образом:
| Isc | = (Трансформатор кВА) × 100) |
| (√3) × (Вторичный KV) × [(%Zтрансформатор)+(%Z Утилита)] |
Вводя все известные переменные, новый доступный ток короткого замыкания рассчитывается следующим образом:
| Искр | = 1500 × 100 |
| (√3)×(0,480)×[(5,75)+(0,4164)] = 29 259 Ампер |
Если мы сравним расчет бесконечной шины и расчет, который включал импеданс источника (доступный ток короткого замыкания 50 000 ампер), мы увидим, что доступный ток короткого замыкания снизился с 31 378 ампер до 29 259 ампер, т.
е. снижение на 6,8%. в доступном токе короткого замыкания (2119 ампер).
Влияние переменного доступного тока короткого замыкания показано на рис. 7. В этой таблице показано, как расчетный доступный ток короткого замыкания изменяется при изменении значений тока короткого замыкания в сети. В качестве значения, с которым сравниваются изменения, используется доступный ток короткого замыкания 50 кА. Интересно отметить, что увеличение доступного тока короткого замыкания от сети, при начальной точке 50 кА, не имеет такого большого влияния, как можно было бы подумать. Например, удвоение допустимого тока короткого замыкания от сети с 50 кА до 100 кА увеличивает доступный вторичный ток короткого замыкания трансформатора только на 3%, или 1022 ампера. Для большинства применений устройств защиты от перегрузки по току это изменение не должно быть значительным. Я слышал, что некоторые говорят, что мы не должны маркировать оборудование служебного входа, потому что утилита может внести изменения в переключение на стороне линии, что повлияет на номер на этикетке.
Рисунок 7 — хороший пример, показывающий, что даже если бесконечная шина не использовалась, изменения на стороне электросети не оказывают такого значительного влияния на ток короткого замыкания, как можно было бы подумать.
Следующее, что мы должны рассмотреть, это проводник на вторичной обмотке трансформатора. Это еще больше снизит доступный ток короткого замыкания.
Расчет – После длины проводника
Проводники могут оказывать значительное влияние на доступный ток короткого замыкания. Давайте продолжим анализ этого примера трансформатора мощностью 1500 кВА, добавив параллельные проводники 500MCM на стороне нагрузки.
Эквивалентная схема уже представлена на рисунке 1. Теперь давайте рассмотрим влияние длины проводника на доступный ток короткого замыкания. Нам нужно следующее уравнение:
Данные, необходимые для этого примера, получены из Национального электротехнического кодекса .
Из таблицы 9 стандарта NEC 2014 для проводника сечением 500 мкм в стальном кабелепроводе Xl (реактивное сопротивление) составляет 0,048 Ом/1000 футов. Для этого примера, как указано ранее, мы используем только значение реактивного сопротивления, что приведет к несколько более высоким значениям тока короткого замыкания и сделает математические расчеты для этой публикации более приемлемыми. Для трансформатора мощностью 1500 кВА с током полной нагрузки 1804 ампер нам понадобится 5-500 мкМ проводников, соединенных параллельно на фазу. Расчет производится следующим образом:
уравнение для расчета доступного тока короткого замыкания выглядит следующим образом:
Введя все известные переменные, мы рассчитали ISC следующим образом: , выглядит следующим образом:
Подводя итог,
Как видно здесь, включение большего количества деталей снижает доступный ток короткого замыкания. В этом случае ток короткого замыкания был снижен с 31 378 ампер до 26 566 ампер, примерно на 15,3%.
Окончательная калибровка
Итак, мы выполнили расчет доступного тока короткого замыкания для оборудования ввода в эксплуатацию. Мы показали, как короткие замыкания приводят к консервативным доступным токам короткого замыкания, которые с целью оценки номиналов отключения и / или номиналов SCCR обеспечивают коэффициент безопасности для конструкции. Мы также показали, как можно снизить доступные токи короткого замыкания с помощью более подробного анализа, но это требует больше усилий и опыта. Давайте посмотрим на приведенный выше пример с точки зрения других инструментов, которые могут быть доступны.
В нашем распоряжении есть различные инструменты для расчета доступного тока короткого замыкания. Некоторые из них довольно дороги, и для их использования требуются обученные специалисты. К ним относятся такие программные приложения, как инструменты системного анализа SKM.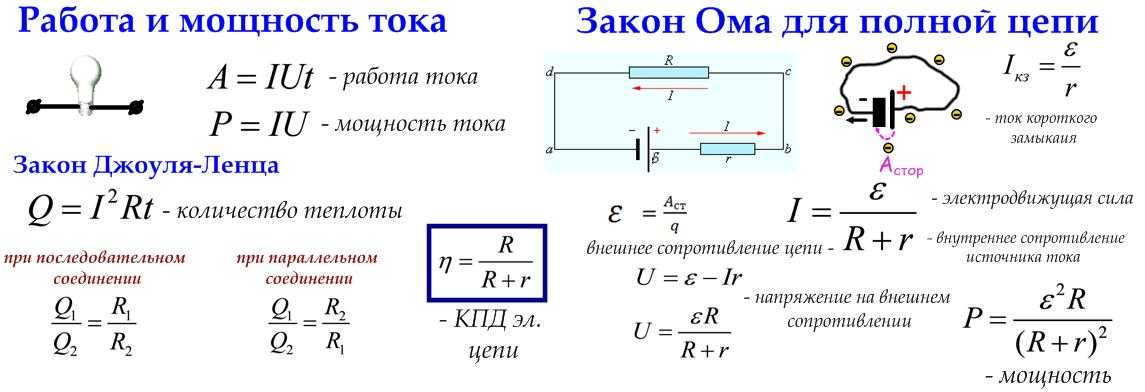
Эти приложения действительно очень тщательны и производят очень подробные отчеты. Существуют также бесплатные инструменты, такие как калькулятор короткого замыкания Eaton Bussmann FC2. На рис. 8 показано, что мы сделали выше, И дано сравнение с SKM и приложением Bussmann FC2. Калькулятор Bussmann FC2 бесплатен и доступен в Интернете или для любого IPHONE или ANDROID через любой из продуктов App Store. Посетите сайт www.cooperbussmann.com/fc2 для получения дополнительной информации. Вы заметите, что результат программного обеспечения SKM использует как реальный, так и реактивный компонент проводника. Значения импеданса были взяты прямо из таблицы 9.в NEC 2014 для медных проводников в стальных кабелепроводах.
Опять же, ни один из примеров, приведенных выше и включенных в эту статью, не учитывает моторный вклад. Это упражнение предназначалось для того, чтобы дать некоторую основу для обсуждения токов короткого замыкания, поэтому простота была нашим другом. Вклад двигателя может быть очень важным для этих расчетов.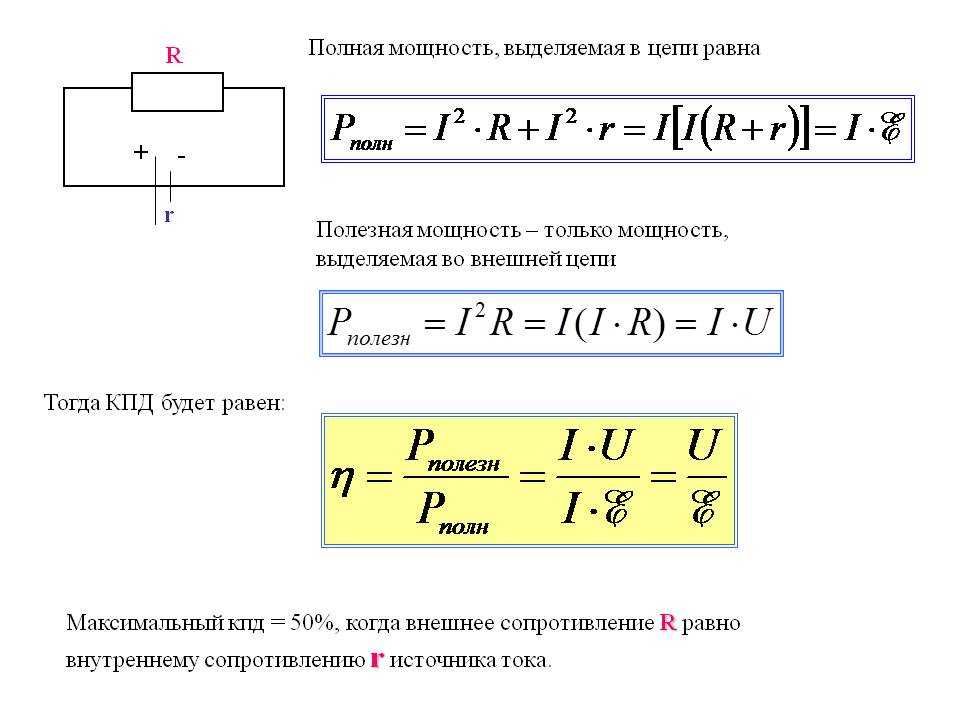
С точки зрения математики и/или системной схемы, когда вы включаете вклад двигателя, импеданс параллелен импедансу источника питания, импедансу трансформатора и импедансу проводника. Это снижает общий импеданс в цепи на рис. 2 и, следовательно, увеличивает расчетный ток короткого замыкания. Сброс остается за учеником. (Я всегда хотел это сказать.)
Заключение
Доступный ток короткого замыкания является очень важным параметром, который необходимо учитывать при проектировании, установке и проверке. На рынке доступны инструменты, которые помогают рассчитать доступный ток короткого замыкания. Используйте эти ресурсы для выполнения требований стандарта NEC и применения продукта.
Как всегда, ставьте безопасность на первое место и убедитесь, что вы и окружающие вас люди доживут до нового дня.
Уравнения цепи RLC серии— Ness Engineering Inc.
С избыточным демпфированием
С критическим демпфированием
Формулы на этой странице связаны с последовательным разрядом цепи RLC, поскольку это основная модель для большинства разрядных цепей высокого напряжения и импульсной мощности.
Каждый из следующих графиков сигналов можно щелкнуть, чтобы открыть полноразмерный график в отдельном окне.
С недостаточным демпфированием
Уравнение состояния цепи с недостаточным демпфированием RLC
Схема цепи для случая с недостаточным демпфированием показана ниже. В этой конкретной модели сопротивление на порядок (в 10 раз) меньше, чем значение, необходимое для цепи с критическим демпфированием.
Схематическая диаграмма для моделирования цепи RLC серии с недостаточным демпфированием
Результаты модели цепи показаны ниже. V(1) — напряжение на конденсаторе емкостью 1 мФ при его колебательном разряде. V(3) — это напряжение на нагрузочном резисторе, в данном случае значение 0,2 Ом. Ток цепи показан на втором, нижнем графике и достигает своего пикового значения почти при t=p/2w 0 .
Осциллограммы цепи для моделирования цепи RLC с недостаточным демпфированием
Уравнение для частоты колебаний серии RLC | Омега | L — индуктивность цепи (Гн) C — емкость цепи (Ф) R — сопротивление цепи (Вт).  |
Уравнение для серии RLC с недостаточным демпфированием: ток в зависимости от времени | Текущий | В 0 начальное напряжение на емкости (В) |
Уравнение для пикового тока в цепи разряда серии RLC с недостаточным демпфированием | Пиковый ток | То же, что и выше |
С избыточным демпфированием
RLC Уравнение состояния цепи с избыточным демпфированием
Схема цепи для случая с избыточным демпфированием показана ниже. В этой конкретной модели сопротивление на порядок (в 10 раз) больше, чем значение, необходимое для цепи с критическим демпфированием.
Схематическая диаграмма для моделирования цепи серии RLC с избыточным демпфированием
Результаты модели цепи показаны ниже. V(1) представляет собой напряжение на конденсаторе емкостью 1 мФ при его разрядке в режиме простого RC-распада.
V(3) — это напряжение на нагрузочном резисторе, в данном случае значение 20 Ом. В этом случае, как только переключатель замыкается и напряжение на нагрузочном резисторе возрастает, чтобы соответствовать напряжению на конденсаторе, обе формы волны затем по существу перекрываются и затухают с одинаковой скоростью, поскольку напряжение на катушке индуктивности минимально. Ток цепи показан на втором, нижнем графике.
Формы сигналов цепи для моделирования цепи RLC серии с избыточным демпфированием
| Уравнение цепи RLC серии с избыточным демпфированием для Omega | Омега | L — индуктивность цепи (Гн) C — емкость цепи (Ф) R — сопротивление цепи (Вт). |
Уравнение для серии RLC с избыточным демпфированием в зависимости от времени | Текущий | В 0 — начальное напряжение на конденсаторе (В) |
С критическим демпфированием
RLC Уравнение состояния цепи с критическим демпфированием
Схема цепи для случая с критическим демпфированием показана ниже.
В этой конкретной модели сопротивление точно равно значению, необходимому для цепи с критическим демпфированием.
Схематическая диаграмма для моделирования цепи серии RLC с критическим демпфированием
Результаты модели цепи показаны ниже. V(1) — это напряжение на конденсаторе емкостью 1 мФ, когда он разряжается до нуля без выброса напряжения. V(3) — это напряжение на нагрузочном резисторе, в данном случае значение 20 Ом. Видно, что напряжение на резисторе также не зашкаливает. Ток цепи показан на втором, нижнем графике и достигает своего пикового значения при t = 2L/R. Эта схема часто желательна (если возможно) с высоковольтными конденсаторами, аккумулирующими энергию, поскольку реверсирование напряжения может часто сокращать срок службы конденсатора. .
Осциллограммы цепи для моделирования цепи серии RLC с критическим демпфированием
Уравнение для серии RLC с критическим демпфированием: ток в зависимости от времени | Текущий | В 0 — начальное напряжение на конденсаторе (В) L — индуктивность цепи (Гн) R — сопротивление цепи (Вт). 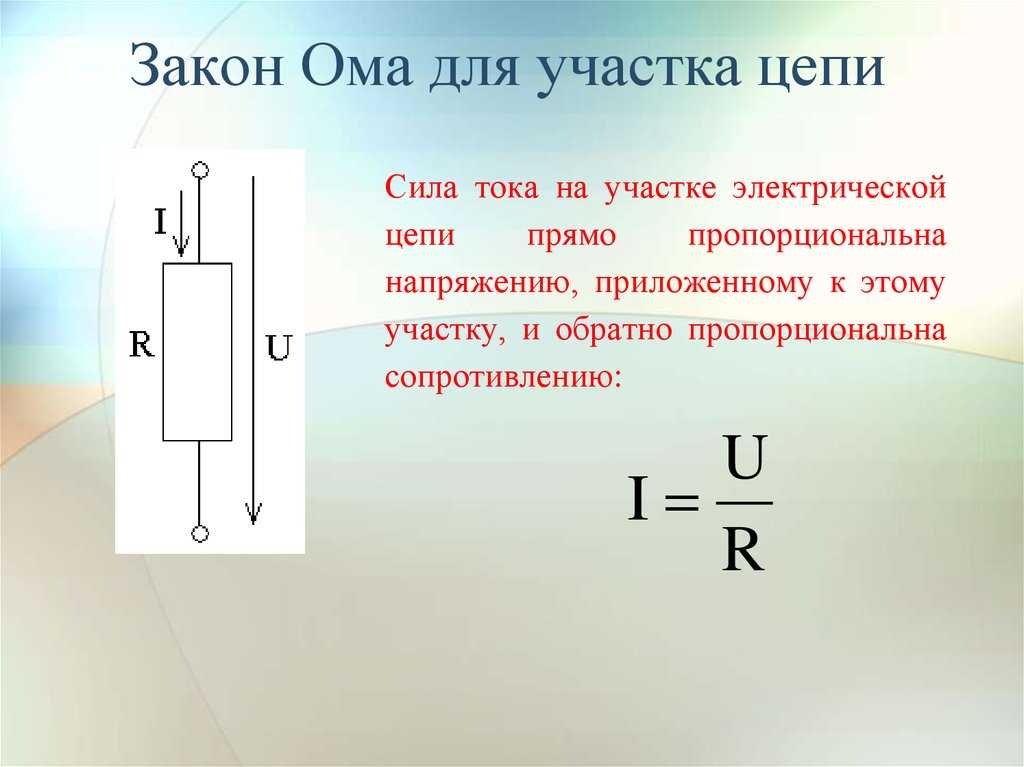  |