Переменный ток. ЭДС, напряжение, сила тока, заряд. Амплитудные

Ранее мы познакомились с постоянным электрическим током — направленным движением зарядов, для которого сила тока постоянна. В случае, если значение силы тока непостоянно, тогда ток будем называть переменным.

Для школьной физики переменный ток рассматривается в двух, в общем-то, похожих случаях:

• вынужденные колебания (на вход цепи подаётся внешняя разность потенциалов/ток, которые изменяются гармонически).
• колебания в LC (состоящем из катушек индуктивности и конденсаторов) или LCR (состоящем их катушек индуктивности, конденсаторов и сопротивлений) контурах.

Рассмотрение свободных колебаний в случае переменного тока аналогично постоянному. Точно так же существует закон Ома для цепи переменного тока, рассчитываются мощности и энергии (работы) для такого случая.

Для школы характерно описание переменного тока через гармонические законы. Переменными параметрами в цепи могут быть ЭДС (

), напряжение на элементе (), сила тока (), заряд конденсатора (). Рассмотрим ЭДС источника гармонический колебаний:

(1)

• где
  • — текущее значение ЭДС (в момент времени ),
  • — амплитудное (максимальное) значение ЭДС,
  • — циклическая частота колебания,
  • — момент времени, в который изучается значение ЭДС,
  • — начальная фаза колебания.

Аналогичным образом можно ввести колебания напряжения 

на элементе:

(2)

• где
  • — текущее значение напряжения (в момент времени ),
  •  — амплитудное (максимальное) значение напряжения,
  • — циклическая частота колебания,
  • — момент времени, в который изучается значение напряжения,
  • — начальная фаза колебания.

Таким же образом вводится и колебание силы тока:

(3)

• где
  • — текущее значение силы тока (в момент времени ),
  • — амплитудное (максимальное) значение силы тока,
  • — циклическая частота колебания,
  • — момент времени, в который изучается значение силы тока,
  • — начальная фаза колебания.

И, аналогично, заряд на конденсаторе:

(4)

• где
  • — текущее значение заряда конденсатора (в момент времени ),
  • — амплитудное (максимальное) значение заряда на конденсаторе,
  • — циклическая частота колебания,
  • — момент времени, в который изучается значение заряда конденсатора,
  • — начальная фаза колебания.

Важно: нужно помнить, что тригонометрически можно превратить синус в косинус:

(5)

• где
  • — новая начальная фаза колебания.

Вывод

: таким образом, рассмотрение переменного тока в случае формульных задач, связанных с соотношениями (1) — (4), касается анализа сомножителей и слагаемых, входящих в само соотношение.

Понравилось это:

Нравится Загрузка…

Сила тока в цепи переменного тока

Напряжение в цепи переменного тока меняется по гармоническому закону:

Сила тока в цепи переменного тока меняется по гармоническому закону:

Действующим значением силы переменного тока именуют величину неизменного тока, действие которого произведёт такую же работу , что и переменный ток:

Действующее значение напряжения переменного тока:

Средняя мощность переменного тока на конденсаторе и катушке индуктивности равна нулю, на резисторе определяется через действующие значения:

При последовательном соединении резистора, конденсатора и катушки индуктивности сила тока этих частей одинакова, а напряжение отличается по фазе от силы тока.
Если сила тока меняется по закону:

То на резисторе напряжение меняется синхронно с силой тока:

На конденсаторе напряжение отстает от силы тока на :

На катушке индуктивности напряжение опережает силу тока на :

З-н Ома для резистора :

З-н Ома для конденсатора :

где емкостное сопротивление назад пропорционально частоте и емкости конденсатора:

З-н Ома для катушки индуктивности :

где индуктивное сопротивление прямо пропорционально частоте и индуктивности катушки:

Трансформатор представляет собой две катушки с общим сердечником. При подаче переменного напряжения на первичную обмотку во вторичной появляется напряжение .

Мощность безупречного трансформатора на входе равна мощности на выходе :

Коэффициент трансформации :

Амплитуда силы тока во всей последовательной цепи находится в зависимости от частоты и определяется по формуле:

Переменный электрический ток. Действующее значение силы тока и напряжения.

Закон Ома для цепи переменного тока.

Переменный электрический ток – это ток, изменяющийся с течением времени по гармоническому закону (по величине и направлению):

Действующее значение силы тока:

Действующее значение напряжения:

Закон Ома для цепи переменного тока: «Амплитудное (действующее) значение силы тока в цепи переменного тока равно отношению амплитудного (действующего) значения напряжения на концах этой цепи к его полному сопротивлению»:

где – активное сопротивление, Ом;

– индуктивное сопротивление, Ом;

– повторяющаяся частота переменного тока, рад/с;

– индуктивность, Гн;

– емкостное сопротивление, Ом;

– емкость переменного тока, Ф;

– полное сопротивление, Ом;

– амплитудное значение силы тока, А, и напряжения, В.

Свободные электромагнитные колебания в колебательном контуре.

Повторяющиеся колебания электрических зарядов и токов, электрических и магнитных полей именуются электромагнитными колебаниями.

Электрическая цепь, в какой могут происходить электромагнитные колебания, именуется колебательным контуром. Простой закрытый колебательный контур – это соединённые между собой конденсатор и катушка индуктивности.

Дабы в контуре появились электромагнитные колебания, контур нужно вывести из состояния равновесия. Для этого довольно зарядить конденсатор либо возбудить ток в контуре.

В колебательном контуре временами меняются (колеблются) следующие физические величины: q – заряд на обкладках конденсатора; U – разность потенциалов на конденсаторе и, поэтому, на концах катушки; i – ток в катушке; и – напряжённость электрического и индукция магнитного поля; и – энергия электрического и магнитного полей.

Заряд на обкладках конденсатора меняется по гармоническому закону.

Собственные незатухающие колебания:

где – заряд, Кл;

– амплитудное значение заряда, Кл;

– исходная фаза;

– угловая частота колебаний (собственная частота), рад/с;

– время, с;

– фаза гармонических колебаний.

Период собственных колебаний контура:

где – индуктивность, Гн;

– емкость, Ф.

Частота собственных колебаний:

Собственные затухающие колебания не являются гармоническими:

где – исходная амплитуда заряда, Кл.

– коэффициент затухания.

:

где – активное сопротивление, Ом.

Логарифм отношений 2-ух последующих амплитуд, отличающихся на период, именуется логарифмическим декрементом затухания:

Время релаксации затухающих колебаний – время, в течение которого амплитуда колебаний миниатюризируется в e раз:

Коэффициент затухания – это величина, оборотная времени, в течение которого амплитуда колебаний миниатюризируется в e раз.

Логарифмический декремент затухания – это величина, оборотная числу колебаний, совершаемых за время релаксации:

Добротность контура есть умноженное на π число полных колебаний, по истечении которых амплитуда миниатюризируется в e раз:

Механическое удерживание земельных масс: Механическое удерживание земельных масс на склоне обеспечивают контрфорсными сооружениями разных конструкций.

Папиллярные узоры пальцев рук — маркер спортивных возможностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не меняются в течение жизни.

Опора древесной одностоечной и методы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на нужной высоте над землей, водой.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особенное значение присваивают эстетическим.

Действующее значение силы тока и напряжения

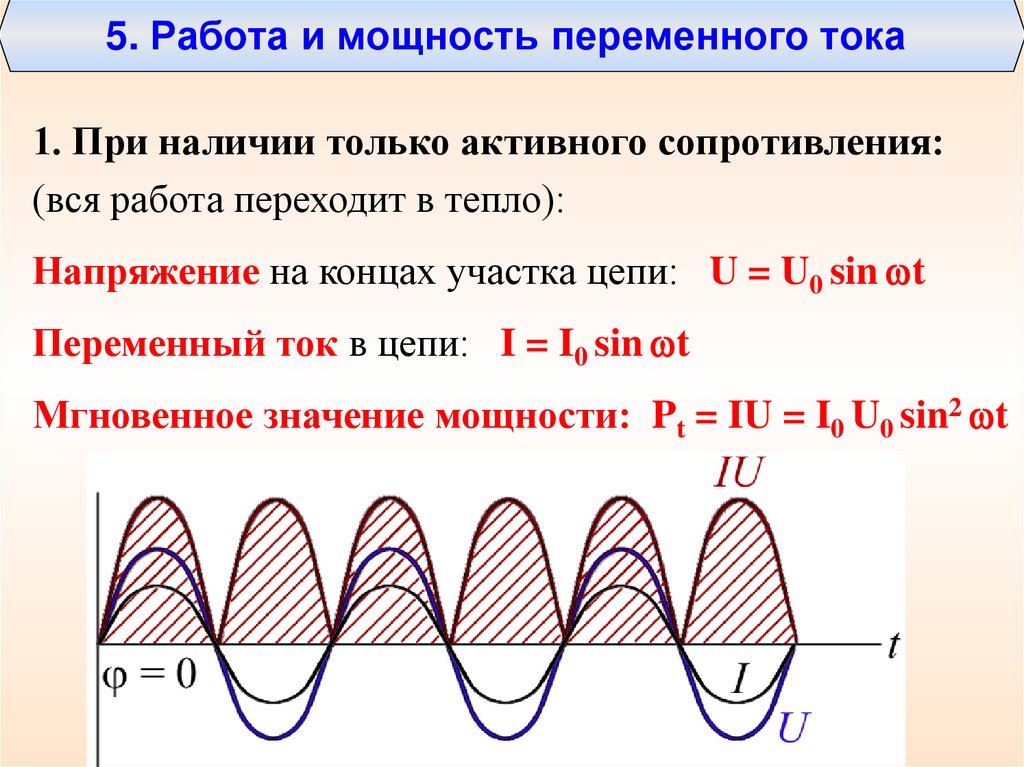
включающая сопротивление подводящих проводов. В цепи с активной нагрузкой — резистором — колебания силы тока, э.д.с. и напряжения происходят в одной фазе [см. (14.1) и (14.2)]. Моментальная мощность (мощность в каждый данный момент времени) [см. (9.30)]

График этой функции показан на рис. 14.3. Для сопоставления тут же штрихом изображен график силы тока. Амплитуда мощности

2. Вычислим среднюю мощность переменного тока за период времени

Т. Для этого следует работу, совершенную током за этот период времени (по другому — выделившуюся за этот период времени джоулеву теплоту), поделить на период. Для вычисления работы воспользуемся рис. 14.3.

Из определения мощности следует, что простая работа ЪА = pAt, а полная работа изображается площадью под графиком. Из характеристики синусоиды следует, что площадь, заштрихованная под кривой, равна площади прямоугольника, основание которого равно периоду, а высота — половине амплитуды мощности. Итак, за период Т работа

Средняя мощность [см. (9.29)]

• 3. Сравнив выражение (14.6) с формулой для вычисления мощности неизменного тока P=I [1][2] R [см. (9.30)], получим
• 1 / [2]

I [2] R = -I [2] UR. Отсюда следует, что / [2] = и

Поэтому, переменный ток с амплитудой /м по собственному термическому (либо механическому) действию эквивалентен неизменному току -рг.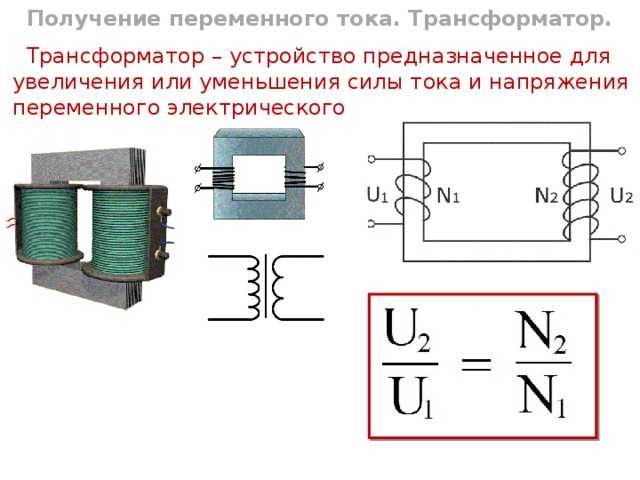 Данную величину именуют действующим значени-

ем силы переменного тока. Соответственно величины

именуют действующими значениями э.д.с. и напряжения.

Большая часть электроизмерительных устройств, применяемых для измерений в цепях переменного тока, градуируют так, что они демонстрируют действующие значения измеряемых величин.

Цепи переменного тока с индуктивностью и электроемкостью

Соединим последовательно резистор — лампу накаливания сопротивлением R, конденсатор емкостью С и катушку большой индуктивности L (рис. 14.4). Если данную цепь присоединить к зажимам генератора переменного тока, то лампа зажгется, что свидетельствует о наличии электрического тока в цепи, невзирая на разрыв, имеющийся между изолированными друг от друга обкладками конденсатора. Для переменного тока это разъясняется следующим образом.

В данной цепи действует переменная, сделанная наружным источником — генератором, э.д.с. ? = ?м sin со/. Дальше действует

э.

д.с. самоиндукции ?? =—[см. (12.8)]. В конце концов, действует

переменная разность потенциалов ф, -ф2 = Q [см. (8.19)], возникающая за счет зарядов, скапливающихся на пластинках конденсатора.

На базе закона Ома для неоднородного участка цепи (9.18) имеем

Данное выражение можно конвертировать к виду

тут разность потенциалов на резисторе с активным сопротивлением

на конденсаторе на катушке индуктивности

Итак, секундное значение наружной э.д.с. равно моментальному значению результирующей разности потенциалов, колеблющейся с частотой наружной э.д.с.:

2. Выражение (14.8) показывает на то, что в цепях переменного тока заместо 1-го резистора с активным сопротивлением мы рассматриваем действие одной наружной э.д.с. на три сопротивления: активное

R и два так именуемых реактивных — емкостное Хс и индуктивное XL, которые, как будет показано ниже, коренным образом отличаются как друг от друга, так и от активного сопротивления. Таковой подход к анализу явлений в цепях переменного тока очень комфортен. Его обширно используют в электротехнике.

Если подключить вертикально отклоняющие пластинки осциллографа к резистору, конденсатору и катушке, то можно следить гармонические колебания разности потенциалов на их концах. Как свидетельствует опыт, фазы колебаний на отдельных участках отличаются друг от друга. Разность фаз 2-ух колебаний именуют сдвигом фаз. Изучим несколько подробнее каждый участок цепи в отдельности.

• 3. Поначалу разглядим цепь, в какой падением напряжения на конденсаторе и катушке можно пренебречь по сопоставлению с падением напряжения на резисторе (т. е. Uc « UR и UL « UR). Тогда выражение (14.8) воспримет вид ё = IR, т. е. мы вернемся к соотношению (14.2). А это означает, что колебания силы тока и напряжения (э.д.с.) в цепи с активным сопротивлением, как это уже было отмечено, происходят в одной и той же фазе.
• * 4. Величины, изменяющиеся по синусоидальному закону, можно изображать при помощи графиков, как мы это делали выше. Но в теории колебаний и в электротехнике обширно используют и другой, очень обычной и приятный метод изображения гармонических функций, получивший название способа векторных диаграмм. Суть этого способа состоит в следующем. Амплитуды (либо действующие значения) величин условно считают векторами и строят эти векторы так, дабы углы между ними, отсчитанные против часовой стрелки, были равны сдвигам фаз между колебаниями значений соответственных величин.

Какой из векторов принять за базовый (т. е. таковой, относительно которого отсчитываются фазы колебаний), находится в зависимости от условия определенной задачи. К примеру, если сила тока во всех участках цепи одинакова (при последовательном соединении), то в качестве базового выбирают вектор силы тока. Если же на всех участках цепи одинаковы напряжения (параллельное соединение), то в качестве базового выбирают вектор напряжения.

Ниже мы увидим необыкновенную ценность способа векторных диаграмм при суммировании колебаний с равными частотами, но отличающихся фазами, так как суммирование осуществляется по правилу сложения векторов.

Для цепи с активным сопротивлением графики силы тока и напряжения и соответственная векторная диаграмма показаны на рис. 14.5,

а, б соответственно. *

5. Сейчас соберем цепь, аналогичную изображенной на рис. 14.4, в какой нет катушки (UL = 0), а емкость батареи конденсаторов и сопротивление лампы накаливания подобраны так, что Uc» UR. Мы получим цепь с емкостным сопротивлением. Опыты демонстрируют, что колебания силы тока в цепи с емкостным сопротивлением представляют собой гармонические колебания с частотой, равной частоте вынуждающей э.д.с. Но в отличие от цепи с активным сопротивлением, где фазы колебаний силы тока и э.д.с. совпадают, тут наблюдается сдвиг по фазе между колебаниями наружной э.д.с. и силы тока: в цепи с емкостным сопротивлением колебания силы тока опережают колебания наружной э.д.с. по фазе на к/2.

Естественно, точно так же можно утверждать, что колебания э.д.с. отстают от колебаний силы тока по фазе на тот же угол. Временная и векторная диаграммы для данного варианта приведены на рис.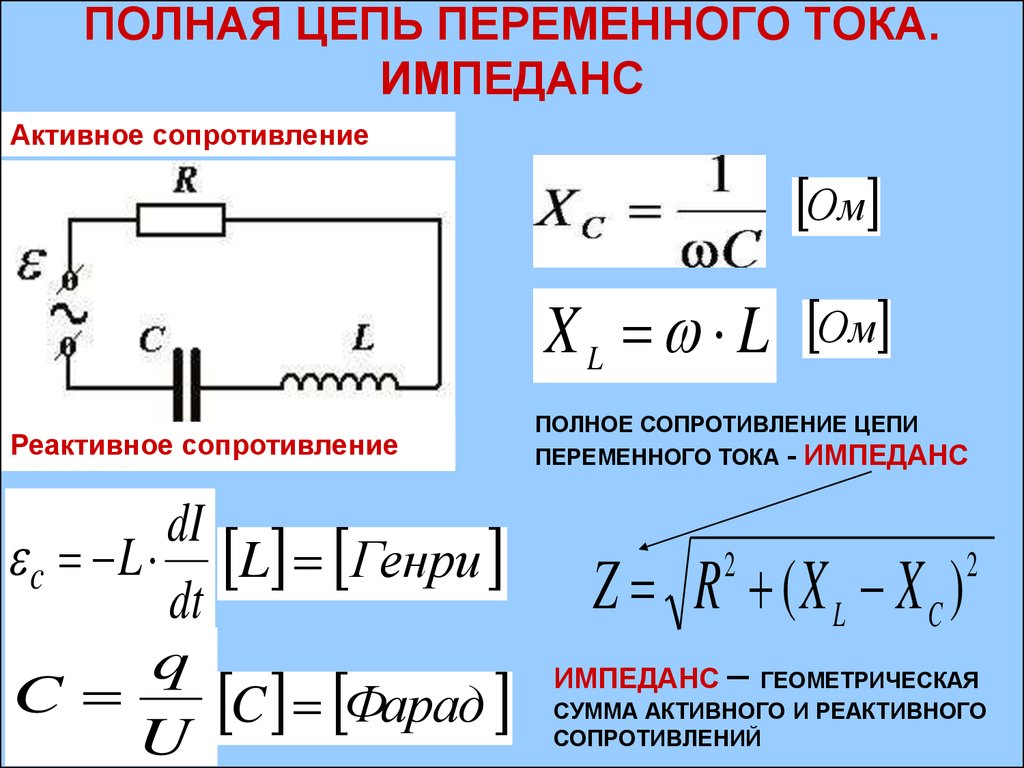 14.6, а, б соответственно.

Опыт указывает также, что конденсатор ведет себя в цепи переменного тока как некоторое сопротивление, ограничивающее амплитуду (и действующее значение) силы тока. Емкостное сопротивление

где С — электроемкость конденсатора, а со — радиальная частота переменного тока.

* 6. Выражение для емкостного сопротивления несложно вывести.

Опыт указывает, что сила тока и напряжение изменяются по закону синуса и смещены по фазе на п/2. Если так, то, как было установлено выше [см. (13.11)], /м = соCUM. Отсюда емкостное сопротивление

7. Соберем цепь, аналогичную изображенной на рис. 14.4, но без конденсатора, а активное сопротивление и индуктивность катушки подберем такими, дабы UL » UR. Мы получим цепь с индуктивным сопротивлением.

Опыт указывает, что колебания силы тока в цепи с индуктивным сопротивлением представляют собой гармонические колебания с частотой, равной частоте вынуждающей э. д.с., точь-в-точь как в цепи с активным и емкостным сопротивлениями. Итак, мы получаем общий вывод: частота принужденных колебаний тока равна частоте вынуждающей э.д.с. независимо от параметров электрической цепи. Этим обязанные колебания принципно отличаются от свободных колебаний и автоколебаний (см. гл. 13).

Заметим, что данное свойство принужденных колебаний справедливо не только лишь для электрических цепей, но и для механических колебательных систем.

Опыт также указывает, что в цепи с индуктивным сопротивлением колебания силы тока отстают по фазе на к/2 от колебаний наружной э.д.с., либо, что то же самое, колебания э.д.с. опережают колебания силы тока на тот же угол. Для данного варианта на рис. 14.7, а, б изображены соответственно временная и векторная диаграммы.

В конце концов, из опыта следует, что катушка с индуктивностью L ведет себя в цепи переменного тока с радиальный частотой со как некоторое сопротивление, ограничивающее амплитуду (и действующее значение) силы тока. . В связи с этим опять, как и ранее, воспользуемся тем, что формула ускорения

[см. (13.5)] подобна формуле

Тут изменение силы тока аналогично изменению скорости. Но, как мы установили ранее, /м = со0м. Подставив это в предшествующее выражение, имеем

Видео: Конденсатор в цепи переменного тока

Переменный ток | Сеансы ланчбоксов

Справка

• Определить переменный ток (AC)
• Объяснить временные параметры переменного тока
• Определить параметры амплитуды переменного тока
• Объяснить значение среднеквадратичного значения

) , который течет только в одном направлении, переменный ток (AC) течет то в одну, то в другую сторону, постоянно изменяясь по величине и меняя направление.

В результате переменное напряжение также постоянно изменяется (чередуется) между положительной (+) и отрицательной (-) полярностью, а его амплитуда меняется со временем.

При построении во времени сигнал переменного тока принимает форму синусоиды, пересекающей нулевую линию при каждом изменении направления тока.

Сигнал переменного тока не всегда имеет форму синусоиды.

Например, сигнал переменного тока может иметь форму треугольника или прямоугольной формы.

Цикл — это однократное повторение движения переменного тока «туда-сюда».

Время, необходимое для одного полного цикла сигнала переменного тока, называется периодом.

Единицей измерения периода являются секунды (с).

Частота сигнала переменного тока – это количество циклов в одну секунду.

Частота измеряется в герцах (Гц).

В Северной Америке частота сети электропитания составляет 60 циклов в секунду или 60 Гц.

В остальном мире более распространена частота 50 Гц.

И если мы знаем частоту, мы можем вернуться назад и рассчитать период.

Например, используя 60 Гц…

Амплитуда — это измерение интенсивности сигнала переменного тока, которое используется для определения напряжения сигнала.

Амплитуда определяется высотой пика сигнала.

Это значение известно как пиковое или пиковое значение сигнала переменного тока и обычно отображается как (V _pk ).

Другим способом измерения амплитуды является измерение общей высоты между противоположными пиками.

Это значение известно как размах сигнала переменного тока и обычно отображается как (V _стр. ).

На практике как пиковые (или пиковые), так и размаховые формы измерения амплитуды используются редко.

Почти всегда напряжение переменного тока выражается в среднеквадратических значениях (СКЗ) или (В _СКЗ ).

В _{среднеквадратичное значение} сообщает нам, каким будет напряжение постоянного тока, эквивалентное нашему существующему сигналу тока переменного тока.

Мощность или энергия сигнала может быть представлена ​​на графике.

На графике вы видите представление AC Vrms (эквивалент постоянного тока).

Но каково соотношение между напряжением V _pk и V _rms ?

Этот расчет применим только к наиболее распространенным синусоидальным сигналам переменного тока.

Среднеквадратичное значение для других сигналов будет другим и зависит от формы этого сигнала.

10 В _ОБС

5 A _{ОБЗА.0056}

2 Ом

50 Вт

Эти две лампы имеют одинаковое сопротивление (2 Ом), рассеивают одинаковую мощность в виде тепла (50 Вт) и излучают одинаковое количество света.

Одна лампа питается от переменного тока, а другая от постоянного.

Поскольку источник переменного напряжения эквивалентен 10-вольтовой батарее постоянного тока, мы назвали бы его источником переменного тока «10 вольт» RMS.

Если V

_pk формы сигнала составляет 55 В, каким будет V _pp ?

110 В _размах

100 В _размах

70 В _размах

55 В _размах

Какая частота показанного переменного тока?

4 Гц 1 В 4 В 1 Гц

Что представляет этот график?

Переменный ток Постоянный ток

• Переменный ток меняет направление своего течения
• Частота, измеряемая в герцах, представляет собой количество циклов за одну секунду
• Амплитуда определяет напряжение сигнала переменного тока.

Мы надеемся, что вам понравилось

Чередовый ток (AC)

Нагрузка

Вакуумное давление

Давление дренажа

Низкое давление

Среднее давление

Высокое давление

Ground

Lowest Lowest Lowest

. Напряжение

Максимальное напряжение

Магнитное поле

Проверьте свою консоль

20.5: Переменный ток в сравнении с постоянным током

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2683

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Объяснять различия и сходства между переменным и постоянным током.
• Рассчитать среднеквадратичное значение напряжения, тока и средней мощности.
• Объясните, почему переменный ток используется для передачи энергии.

Переменный ток

Большинство рассмотренных выше примеров, особенно те, в которых используются батареи, имеют источники постоянного напряжения. Как только ток установлен, он, таким образом, также является постоянным. Постоянный ток (DC) представляет собой поток электрического заряда только в одном направлении. Это устойчивое состояние цепи постоянного напряжения. Однако в большинстве известных приложений используется источник переменного напряжения. Переменный ток (AC) представляет собой поток электрического заряда, который периодически меняет направление на противоположное. Если источник периодически меняется, особенно синусоидально, цепь известна как цепь переменного тока. Примеры включают коммерческую и жилую энергию, которая удовлетворяет многие из наших потребностей. На рисунке \(\PageIndex{1}\) показаны графики зависимости напряжения и тока от времени для типичного питания постоянного и переменного тока. Напряжение и частота переменного тока, обычно используемые в домах и на предприятиях, различаются по всему миру.

Рисунок \(\PageIndex{1}\): (a) Напряжение постоянного тока и ток постоянны во времени после установления тока. (b) График зависимости напряжения и тока от времени для сети переменного тока с частотой 60 Гц. Напряжение и ток синусоидальны и находятся в фазе для простой цепи сопротивления. Частоты и пиковые напряжения источников переменного тока сильно различаются.

На рисунке \(\PageIndex{2}\) показана схема простой цепи с источником переменного напряжения. Напряжение между клеммами колеблется, как показано, с напряжением переменного тока определяется как \[V = V_{0} sin 2 \pi ft, \label{20.6.1}\], где \(V\) — напряжение в момент времени \(t\), \(V_{0}\ ), \(V_{0}\) — пиковое напряжение, а \(f\) — частота в герцах. Для этой простой цепи сопротивления \(I = V/R\), поэтому переменный ток равен

\[I = I_{0} sin 2 \pi ft, \label{20.6.2}\]

, где \(I\) — ток в момент времени \(t\), а \(I_{0} = V_{0} / R\) — пиковый ток. В этом примере говорят, что напряжение и ток совпадают по фазе, как показано на рисунке \(\PageIndex{1b}\).

Рисунок \(\PageIndex{2}\): Разность потенциалов \(В\) между клеммами источника переменного напряжения колеблется, как показано. Математическое выражение для \(V\) задается как \(V = V_{0} sin 2 \pi ft\).

Ток в резисторе колеблется туда-сюда точно так же, как управляющее напряжение, поскольку \(I = V / R\). Например, если резистор представляет собой люминесцентную лампочку, она становится ярче и тускнеет 120 раз в секунду, поскольку ток многократно проходит через ноль. Мерцание с частотой 120 Гц слишком быстрое для ваших глаз, но если вы будете махать рукой туда-сюда между лицом и флуоресцентным светом, вы увидите стробоскопический эффект, свидетельствующий о переменном токе. {2}2\pi ft\), как показано на рисунке \(\PageIndex{3}\).

Рисунок \(\PageIndex{3}\): Мощность переменного тока как функция времени. Поскольку здесь напряжение и ток совпадают по фазе, их произведение неотрицательно и колеблется между нулем и \(I_{0}V_{0}\). Средняя мощность равна \( \left( 1/2 \right) I_{0} V_{0}\).

Установление связей: домашний эксперимент — освещение переменного/постоянного тока

Проводите рукой вперед-назад между лицом и флуоресцентной лампочкой. Наблюдаете ли вы то же самое с фарами на вашем автомобиле? Объясните, что вы наблюдаете. Предупреждение: Не смотрите прямо на очень яркий свет.

Чаще всего нас интересует средняя мощность, а не ее колебания — например, 60-ваттная лампочка в вашей настольной лампе потребляет в среднем 60 Вт. Как показано на рисунке 3, средняя мощность \(P_{ave}\) равна \[P_{ave} = \frac{1}{2}I_{0}V_{0}. \label{20.6.3}\] Это видно из графика, так как площади выше и ниже линии \(\left(1/2\right)I_{0}V_{0}\) равны, но это также можно доказать с помощью тригонометрических тождеств. Точно так же мы определяем среднее или среднеквадратичное значение тока \(I_{rms}\) и среднее или среднеквадратичное значение напряжения \(V_{rms}\) должно быть, соответственно,

\[I_{rms} = \frac{I_{0}}{ \sqrt{2}}\label{20.6.4}\]

и

\[V_{rms} = \frac{V_{0}}{\sqrt{2}}.\label{20.6.5} \]

, где rms означает среднеквадратичное значение, особый тип среднего значения. В общем, для получения среднеквадратичного корня конкретную величину возводят в квадрат, находят ее среднее (или среднее) и извлекают квадратный корень. Это полезно для переменного тока, так как среднее значение равно нулю. Теперь \[P_{ave} = I_{rms}V_{rms}, \label{20.6.6}\], что дает

\[P_{ave} = \frac{I_{0}}{\sqrt{2}} \cdot \frac{V_{0}}{\sqrt{2}} = \frac{1}{2} I_{0}V_{0}, \label{20.6.7}\]

, как указано выше. Стандартной практикой является указывать \(I_{rms}\), \(V_{rms}\) и \(P_{ave}\), а не пиковые значения. Например, в большинстве бытовых электросетей напряжение переменного тока составляет 120 В, а это означает, что \(V_{rms}\) равно 120 В. Обычный автоматический выключатель на 10 А отключит устойчивое напряжение \(I_{rms}\), превышающее 10 А. Ваша микроволновая печь мощностью 1,0 кВт потребляет \(P_{ave} = 1,0 кВт\) и так далее. Вы можете думать об этих среднеквадратичных и средних значениях как об эквивалентных значениях постоянного тока для простой резистивной цепи. 9{2}_{rms}R.\label{20.6.11}\]

Пример \(\PageIndex{1}\): Пиковое напряжение и мощность для переменного тока

(a) Каково значение пикового напряжения для сети переменного тока 120 В?

Стратегия

Нам говорят, что \(V_{rms}\) равно 120 В, а \(P_{ave}\) равно 60,0 Вт. Мы можем использовать \(V_{rms} = \frac{V_{0 }}{\sqrt{2}}\), чтобы найти пиковое напряжение, и мы можем манипулировать определением мощности, чтобы найти пиковую мощность из заданной средней мощности.

Решение
Решение уравнения \(V_{rms}=\frac{V_{0}}{\sqrt{2}}\) для пикового напряжения \(V_{0}\) и подстановка известного значения для \(V_{rms}\) дает \[V_{0} = \sqrt{2} V_{rms} = 1,414\left(120 V\right) = 170 V. \]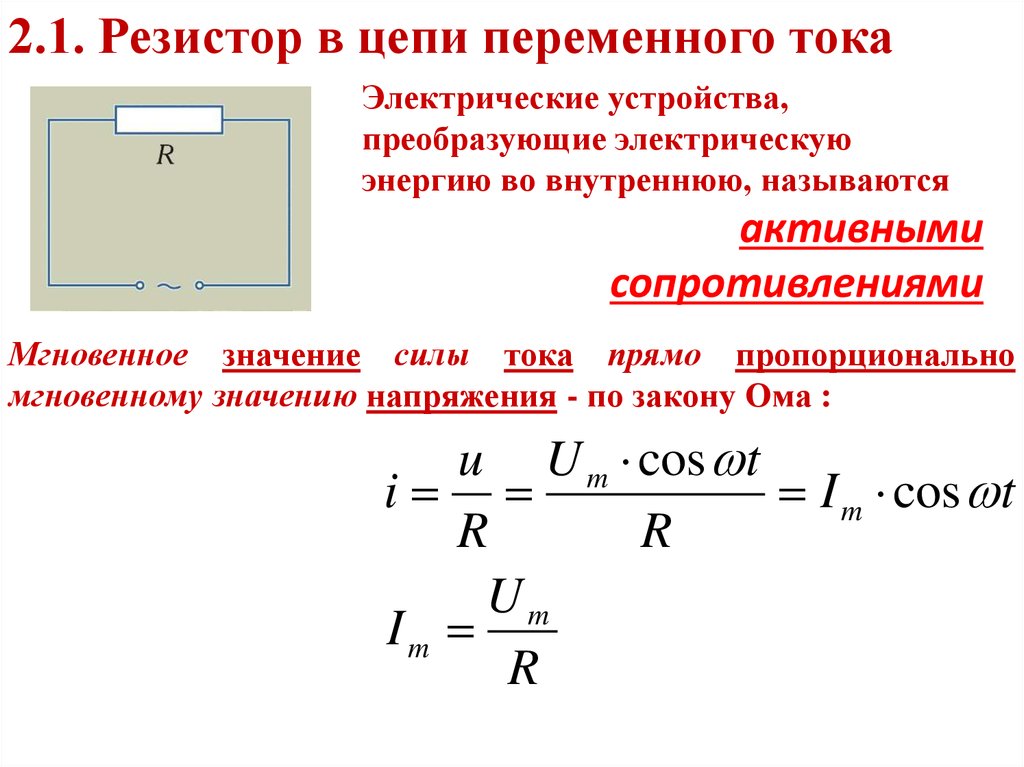

Обсуждение

Это означает, что переменное напряжение колеблется от 170 В до \(-170 В\) и обратно 60 раз в секунду. Эквивалентное постоянное напряжение равно 120 В.

(b) Какова пиковая потребляемая мощность лампочки переменного тока мощностью 60,0 Вт?

Решение

Пиковая мощность представляет собой произведение пикового тока на пиковое напряжение. Таким образом, \[P_{0} = I_{0}V_{0} = 2\left(\frac{1}{2} I_{0} V_{0} \right) = 2P_{ave}.\] Мы известно, что средняя мощность равна 60,0 Вт, поэтому \[P_{0} = 2\left(60,0 Вт\right) = 120 Вт.\]

Обсуждение

Итак, мощность колеблется от нуля до 120 Вт сто двадцать раз в секунду (дважды за цикл), а средняя мощность составляет 60 Вт.

Зачем использовать переменный ток для распределения электроэнергии?

Большинство крупных систем распределения электроэнергии работают на переменном токе. Кроме того, мощность передается при гораздо более высоких напряжениях, чем 120 В переменного тока (240 В в большинстве стран мира), которые мы используем дома и на работе. Экономия на масштабе делает строительство нескольких очень крупных электростанций дешевле, чем строительство множества мелких. Это требует передачи энергии на большие расстояния, и, очевидно, важно, чтобы потери энергии в пути были сведены к минимуму. Как мы увидим, высокие напряжения могут передаваться с гораздо меньшими потерями мощности, чем низкие напряжения. (См. рис. 4.) Из соображений безопасности напряжение у пользователя снижено до привычных значений. Решающим фактором является то, что переменное напряжение намного проще увеличивать и уменьшать, чем постоянное, поэтому переменный ток используется в большинстве крупных систем распределения электроэнергии.

Рисунок \(\PageIndex{4}\): Энергия распределяется на большие расстояния при высоком напряжении для уменьшения потерь мощности в линиях передачи. Напряжения, генерируемые на электростанции, повышаются пассивными устройствами, называемыми трансформаторами (см. Трансформаторы), до 330 000 вольт (или более в некоторых местах по всему миру). В точке использования трансформаторы снижают напряжение

Пример \(\PageIndex{2}\): Потери мощности меньше при высоковольтной передаче

(a) Какой ток необходим для передачи 100 МВт мощности при 200 кВ ? 9{2} \left(1.00 \Omega\right) = 250 кВт.\]

(c) Какой процент мощности теряется в линиях электропередачи?

Решение

Потери в процентах представляют собой отношение этой потерянной мощности к общей или потребляемой мощности, умноженное на 100: \[% потерь = \frac{250kW}{100 МВт} \times 100 = 0,250 %.\ ]

Обсуждение

Одна четвертая процента — допустимая потеря. Заметим, что если бы передавалось 100 МВт мощности при напряжении 25 кВ, то понадобился бы ток 4000 А. Это приведет к потере мощности в линиях 16,0 МВт, или 16,0%, а не 0,250%. Чем ниже напряжение, тем больше требуется тока и тем больше потери мощности в линиях передачи с фиксированным сопротивлением. Конечно, можно построить линии с меньшим сопротивлением, но для этого нужны более крупные и дорогие провода. Если бы сверхпроводящие линии можно было производить экономично, то в линиях передачи вообще не было бы потерь. Но, как мы увидим в одной из последующих глав, в сверхпроводниках также существует предел тока. Короче говоря, высокое напряжение более экономично для передачи мощности, а напряжение переменного тока гораздо легче повышать и понижать, поэтому переменный ток используется в большинстве крупномасштабных систем распределения электроэнергии.

Широко известно, что высокое напряжение представляет большую опасность, чем низкое. Но на самом деле некоторые высокие напряжения, например, связанные с обычным статическим электричеством, могут быть безвредными. Так что не только напряжение определяет опасность. Не так широко признано, что разряды переменного тока часто более вредны, чем аналогичные разряды постоянного тока. Томас Эдисон считал, что удары переменного тока более вредны, и в конце 1800-х годов создал систему распределения электроэнергии постоянного тока в Нью-Йорке. Были ожесточенные споры, в частности, между Эдисоном и Джорджем Вестингаузом и Николой Теслой, которые выступали за использование переменного тока в первых системах распределения электроэнергии.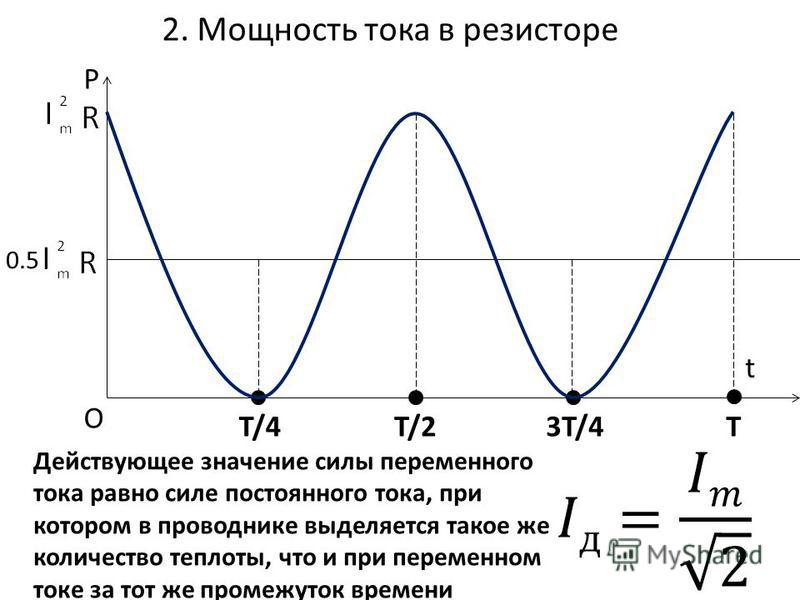 Переменный ток преобладает во многом благодаря трансформаторам и меньшим потерям мощности при передаче высокого напряжения.

ИССЛЕДОВАНИЯ PHET: ГЕНЕРАТОР

Генерировать электричество с помощью стержневого магнита! Откройте для себя физику этого явления, исследуя магниты и то, как вы можете использовать их, чтобы зажечь лампочку.

Рисунок \(\PageIndex{5}\): Генератор

Резюме

• Постоянный ток (DC) представляет собой поток электрического тока только в одном направлении. Это относится к системам, в которых напряжение источника постоянно.
• Источник напряжения системы переменного тока (AC) выдает \(V= V_{0} \sin{2\pi} ft\), где \(V\) — напряжение в момент времени \(t\), \(V_{0}\) — пиковое напряжение, а \(f\) — частота в герцах.
• В простой цепи \(I = V/R\), а переменный ток равен \(I = I_{0} \sin{2\pi}ft\), где \(I\) — ток в момент времени \ (t\), а \(I_{0} = V_{0}/R\) — пиковый ток.
• Средняя мощность переменного тока равна \(P_{ave} = \frac{1}{2} I_{0}V_{0}\).
• Средний (среднеквадратический) ток \(I_{rms}\) и среднее (среднеквадратичное) напряжение \(V_{rms}\) и \(I_{rms} = \frac{I_{0}}{\sqrt{2} }\) и \(V_{rms} = \frac{V_{0}}{\sqrt{2}}\), где rms обозначает среднеквадратичное значение.
• Таким образом, \(P_{ave} = I_{rms} V_{rms}\). 9{2}R\), аналогично выражениям для цепей постоянного тока.

Глоссарий

постоянный ток

(DC) поток электрического заряда только в одном направлении

переменный ток

(AC) поток электрического заряда, который периодически меняет направление на противоположное

Напряжение переменного тока

напряжение, которое синусоидально колеблется во времени, выражается как В = В ₀ sin 2 πft , где В — напряжение в момент времени t, В ₀ — пиковое напряжение, а f — частота в герцах

Переменный ток

ток, синусоидально колеблющийся во времени, выраженный как I = I ₀ sin 2 πft , где I — ток в момент времени t, I ₀ — пиковый ток2, а f — пиковый ток2.