Переменный ток. Формулы и параметры

Переменный ток

(AC — Alternating Current) — электрический ток, меняющий свою величину и направление с течением времени.

Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток. Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока. Такой вариант можно представить как переменный ток AC

с постоянной составляющей
DC
. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.

DC

— Direct Current — постоянный ток, не меняющий своей величины и направления.

В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC

) для периодически меняющегося электрического тока любой формы. Тогда величина
DC
будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей
AC
.

При синусоидальной форме тока, например в электросети, постоянная составляющая DC

равна нулю.

Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка. Запись AC+DC

в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности. Величина тока будет равна квадратному корню из суммы квадратов двух величин — значения постоянной составляющей
DC
и среднеквадратичного значения переменной составляющей
AC
.

Термины AC

и
DC
применимы как для тока, так и для напряжения.

Переменный электрический ток

В механической системе вынужденные колебания возникают при действии на нее внешней периодической силы. Аналогично этому вынужденные электромагнитные колебания в электрической цепи происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения.

Вынужденные электромагнитные колебания в электрической цепи представляют собой переменный электрический ток

.

• Переменный электрический ток
  — это ток, сила и направление которого периодически меняются.

Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω

по синусоидальному или косинусоидальному закону:
\(~u = U_m \cdot \sin \omega t\) или \(~u = U_m \cdot \cos \omega t\) ,
где u

– мгновенное значение напряжения,
U
m – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае
\(~i = I_m \cdot \sin (\omega t + \varphi_c)\) ,
где φc – разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Исходя из этого можно дать еще такое определение:

• Переменный ток
  – это электрический ток, который изменяется с течением времени по гармоническому закону.

Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.

Нелинейные элементы и цепи

Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников. Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы. Такие элементы и цепи, в которых они используются, называют нелинейными.

Генератор переменного тока

Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими гармонические колебания.

• Генератором переменного тока
  называется электротехническое устройство, предназначенное для преобразования механической энергии в энергию переменного тока.

ЭДС индукции генератора изменяется по синусоидальному закону

\(e={\rm E}_{m} \cdot \sin \omega \cdot t,\)

где \({\rm E}_{m} =B\cdot S\cdot \omega\) — амплитудное (максимальное) значение ЭДС. При подключении к выводам рамки нагрузки сопротивлением R

, через нее будет проходить переменный ток. По закону Ома для участка цепи сила тока в нагрузке

\(i=\dfrac{e}{R} =\dfrac{B \cdot S \cdot \omega }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\)

где \(I_{m} = \dfrac{B\cdot S\cdot \omega }{R}\) — амплитудное значение силы тока.

Основными частями генератора являются (рис. 1):

• индуктор
  — электромагнит или постоянный магнит, который создает магнитное поле;
• якорь
  — обмотка, в которой индуцируется переменная ЭДС;
• коллектор со щетками
  — устройство, посредством которого снимается с вращающихся частей или подается по ним ток.

Рис. 1
Неподвижная часть генератора называется статором

, а подвижная —
ротором
. В зависимости от конструкции генератора его якорь может быть как ротором, так и статором. При получении переменных токов большой мощности якорь обычно делают неподвижным, чтобы упростить схему передачи тока в промышленную сеть.

На современных гидроэлектростанциях вода вращает вал электрогенератора с частотой 1-2 оборота в секунду. Таким образом, если бы якорь генератора имел только одну рамку (обмотку), то получался бы переменный ток частотой 1-2 Гц. Поэтому, для получения переменного тока промышленной частоты 50 Гц якорь должен содержать несколько обмоток, позволяющих увеличить частоту вырабатываемого тока. Для паровых турбин, ротор которых вращается очень быстро, используют якорь с одной обмоткой. В этом случае частота вращения ротора совпадает с частотой переменного тока, т.е. ротор должен делать 50 об/с.

Мощные генераторы вырабатывают напряжение 15-20 кВ и обладают КПД 97-98 %.

Из истории

. Первоначально Фарадей обнаружил лишь едва заметный ток в катушке при движении вблизи нее магнита. «Какая от этого польза?» — спросили его. Фарадей ответил: «Какая может быть польза от новорож­денного?» Прошло немногим более половины столетия и, как сказал американский физик Р. Фейнман, «бесполезный новорожденный превратился в чудо-богатыря и изменил облик Земли так, как его гордый отец не мог себе и представить».

*Принцип действия

Принцип действия генератора переменного тока основан на явлении электромагнитной индукции.

Пусть проводящая рамка площадью S

вращается с угловой скоростью ω вокруг оси, расположенной в ее плоскости перпендикулярно однородному магнитному полю индукцией \(\vec{B}\) (см. рис. 1).

При равномерном вращении рамки угол α между направлениями вектора индукции магнитного поля \(\vec{B}\) и нормали к плоскости рамки \(\vec{n}\) меняется со временем по линейному закону. Если в момент времени t

= 0 угол α0 = 0 (см. рис. 1), то

\(\alpha = \omega \cdot t = 2\pi \cdot \nu \cdot t,\)

где ω — угловая скорость вращения рамки, ν — частота ее вращения.

В этом случае магнитный поток, пронизывающий рамку будет изменяться следующим образом

\(\Phi \left(t\right)=B\cdot S\cdot \cos \alpha =B\cdot S\cdot \cos \omega \cdot t.\)

Тогда согласно закону Фарадея индуцируется ЭДС индукции

\(e=-\Phi ‘(t)=B\cdot S\cdot \omega \cdot \sin \omega \cdot t = {\rm E}_{m} \cdot \sin \omega \cdot t.\)

Подчеркнем, что ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное, которое также остается неизменным в течение следующего полуоборота.

Закон Джоуля-Ленца

Закон Джоуля — Ленца гласит: количество теплоты, выделяемое в проводнике на участке электрической цепи с сопротивлением $R$ при протекании по нему постоянного тока $I$ в течение времени $t$ равно произведению квадрата тока на сопротивление и время:

$Q=I^2Rt$

Закон был установлен в 1841 г. 2t}/{R}$

Следовательно, на проводнике с меньшим сопротивлением будет выделяться больше тепла.

Если в формуле ($A=IUt$) выразить $U$ через $IR$, воспользовавшись законом Ома, получим закон Джоуля-Ленца. Это лишний раз подверждает тот факт, что работа тока расходуется на выделение тепла на активном сопротивлении в цепи.

Действующие значения силы тока и напряжения

Пусть источник тока создает переменное гармоническое напряжение

\(u=U_{m} \cdot \sin \omega \cdot t.\;\;\;(1)\)

Согласно закону Ома, сила тока в участке цепи, содержащей только резистор сопротивлением R

, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:

\(i = \dfrac{u}{R} =\dfrac{U_{m} }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\;\;\; (2)\)

где \(I_m = \dfrac{U_{m}}{R}.\) Как видим, сила тока в такой цепи также меняется с течением времени по синусоидальному закону. Величины Um

,
Im
называются
амплитудными значениями напряжения и силы тока
. Зависящие от времени значения напряжения
u
и силы тока
i
называют
мгновенными
.

Кроме этих величин используются еще одна характеристика переменного тока: действующие (эффективные) значения силы тока и напряжения

.

• Действующим (эффективным) значением силы
  переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.

Обозначается буквой I

.

• Действующим (эффективным) значением напряжения
  переменного тока называется напряжение такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.

Обозначается буквой U

.

Действующие (I, U

) и амплитудные (
Im, Um
) значения связаны между собой следующими соотношениями:

\(I = \dfrac{I_{m} }{\sqrt{2}}, \; \; \; U =\dfrac{U_{m} }{\sqrt{2}}. {2}}{R}, \;\;\; U=\dfrac{U_{m}}{\sqrt{2}}.\)

Закон Ома для цепи

Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).

Итак, закон Ома для рассматриваемого участка цепи имеет вид:

φ1-φ2=I*R, где

• I – ток, протекающий по участку цепи.
• R – сопротивление этого участка.
• φ1-φ2 – разность потенциалов между точками 1-2.

Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).

В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:

• U1=I*R1
• U2=I*R2
• Un=I*Rn
• U=I*(R1+R2+…+Rn

Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:

U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn

Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.

Закон Ома для участка цепи.

Для ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит: Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.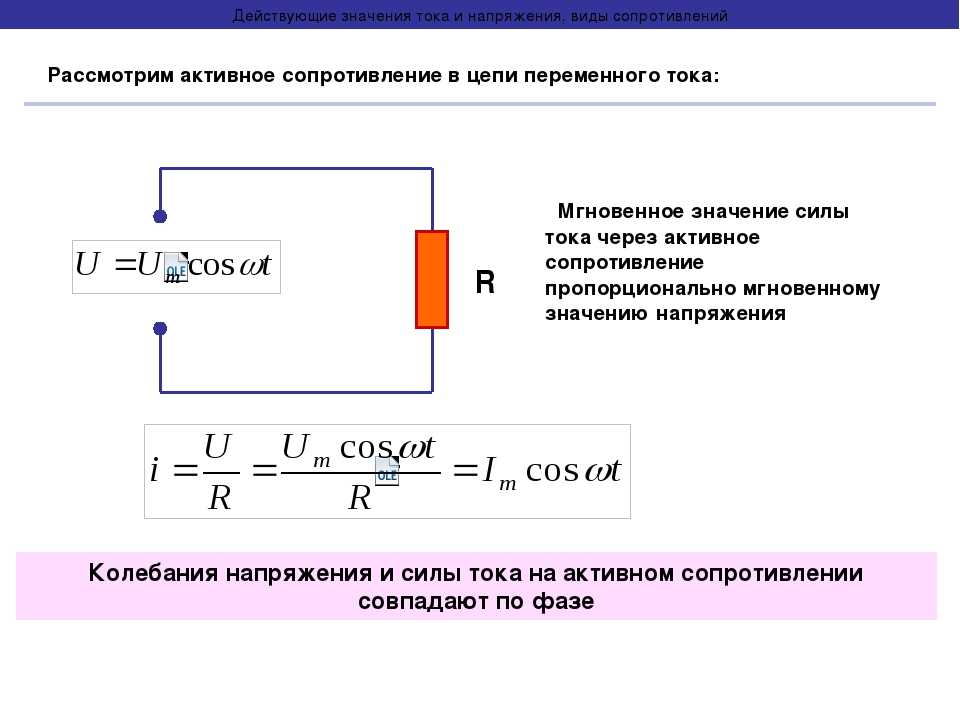

Для полной цепи

Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.

Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.

Полноценную цепь составляет уже участок (участки), а также источник ЭДС.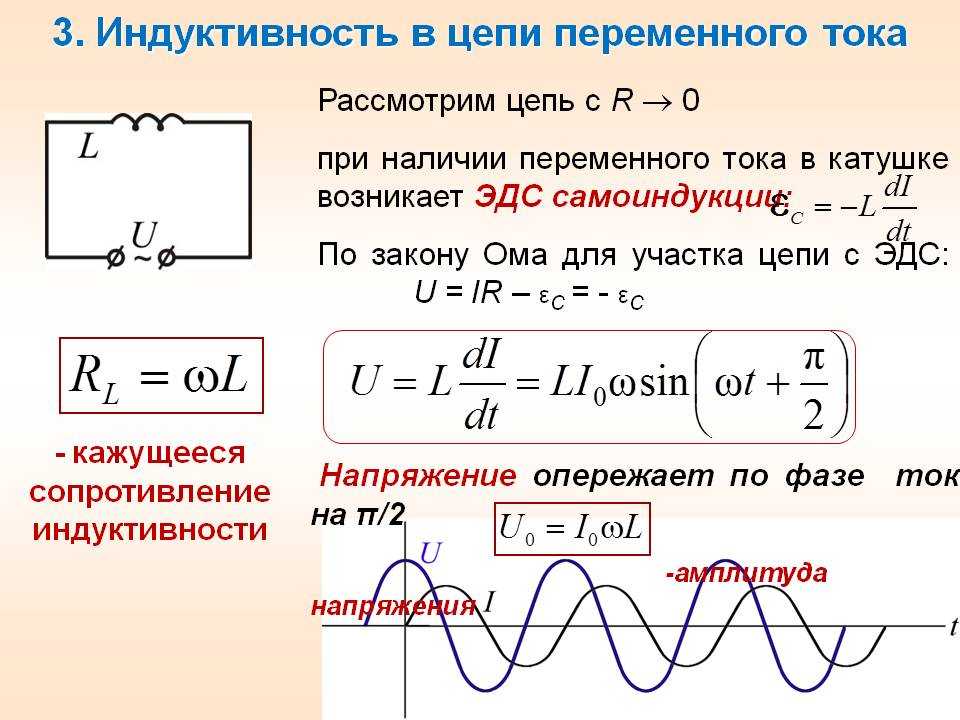 То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:

I = U / (R + r)

Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.

Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.

Значение Закона Ома

Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.

Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.

Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:

Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.

Задача 1.1

Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм2, если к концам провода приложено напряжение 12 B.

Задачка простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.

Переменный электрический ток | СПАДИЛО

теория по физике 🧲 колебания и волны

Свободные электромагнитные колебания в контуре быстро затухают. Поэтому они практически не используются. Наиболее важное практическое значение имеют незатухающие вынужденные колебания.

Определение

Переменный ток — вынужденные электромагнитные колебания.

Ток в осветительной сети квартиры, ток, применяемый на заводах и фабриках, представляет собой переменный ток. В нем сила тока и напряжение изменяются со временем по гармоническому закону. Колебания легко обнаружить с помощью осциллографа. Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять сбой синусоиду:

Зная скорость движения луча в горизонтальном направлении (она определяется частотой пилообразного напряжения), можно определить частоту колебаний.

Определение

Частота переменного тока — это количество колебаний за 1 с.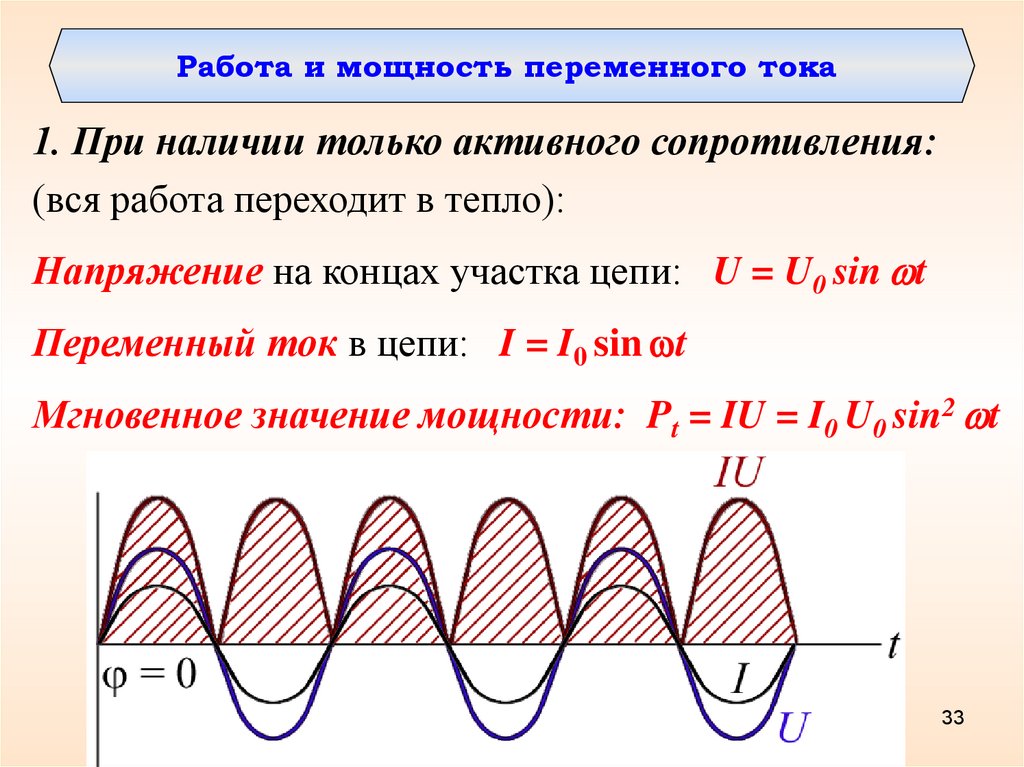

Стандартная частота переменного промышленного тока составляет 50 Гц. Это значит, что на протяжении 1 секунды ток 50 раз течет в одну сторону и 50 раз — в другую. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц.

Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводника будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц, и, следовательно, гармонические колебания силы тока.

Внимание!

При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменение поля происходит с большой скоростью, но она не бесконечно большая. Она равна скорости света (3∙10⁸ м/с).

Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока (см. рисунок ниже).

Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью

S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции.

Численно магнитный поток определяется формулой:

Φ=BScos.α

При равномерном вращении рамки угол α увеличивается пропорционально времени:

α=2πnt

где n — частота вращения. Поэтому поток магнитной индукции меняется гармонически:

Φ=BScos.2πnt

Здесь множитель 2πn представляет собой число колебаний магнитного потока за 2π секунд. Это не что иное, как циклическая частота колебаний:

ω=2πn

Следовательно:

Φ=BScos.ωt

Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «минус» скорости изменения потока магнитной индукции, т.е. производной потока магнитной индукции по времени:

e=−Φ´=−BS(cos.ωt)´=BSωsin.ωt=εmaxsin.ωt

εmax — амплитуда ЭДС индукции, равная:

εmax=BSω

Напряжение в цепи переменного тока может меняться по закону синуса или по закону косинуса:

u=Umaxsin. ωt

u=Umaxcos.ωt

где Umax — амплитуда напряжения (максимальное по модулю значение напряжения).

Сила тока меняется с той частотой, что и напряжение — ω. Но колебания тока необязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока

i в любой момент времени определяется по формуле:

i=Imaxsin.(ωt+φс)

где Imax — амплитуда силы тока (максимальное по модулю значение силы тока), φс — разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Пример №1. Найти напряжение в цепи переменного тока в момент времени t = π, если циклическая частота электромагнитных колебаний равна 300,25 Гц, а амплитуда напряжения составляет 12В. Считать, что напряжения меняется по закону косинуса.

u=Umaxcos.ωt=12cos.300,25π=12√22..≈8,5 (В).

Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (см. рисунок ниже).

Внимание!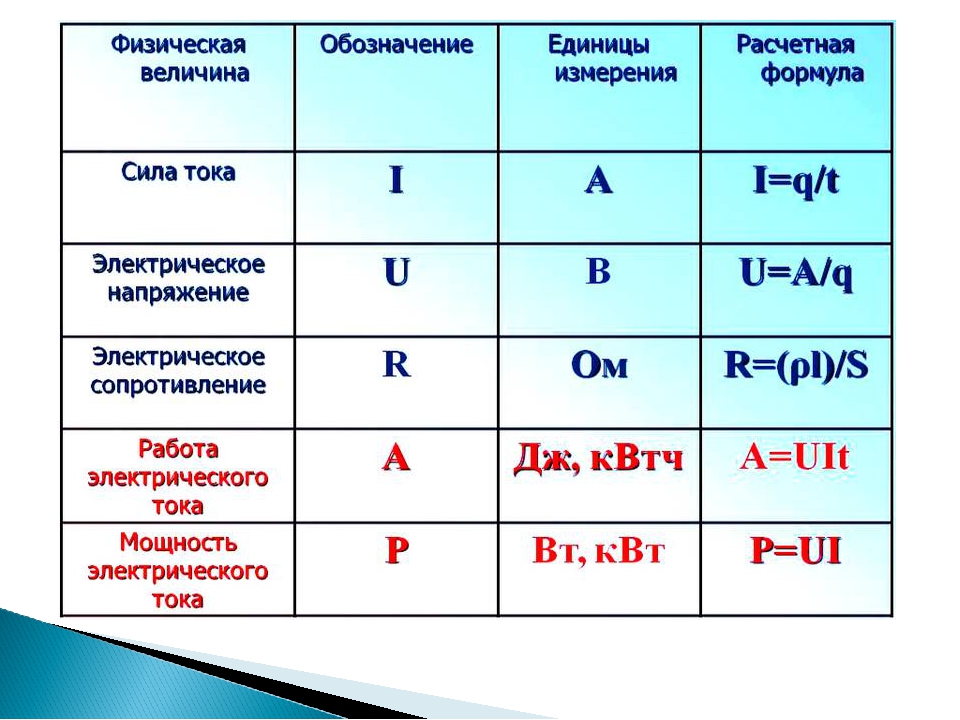

Ранее под величиной R мы понимали электрическое сопротивление. Но правильно его называть сопротивлением активным. Дело в том, что в цепи переменного тока могут быть сопротивления иного характера. Сопротивление же R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.

Будем считать, что напряжение на зажимах цепи меняется по закону косинуса:

u=Umaxcos.ωt

Для нахождения мгновенного значения силы тока мы можем воспользоваться законом Ома, так как эта величина прямо пропорционально мгновенному значению напряжения:

i=uR..=Umaxcos.ωtR..=Imaxcos.ωt

В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:

Imax=UmaxR..

Мощность в цепи с резистором

В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.

Определение

Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.

Мощность постоянного тока определяется формулой:

P=I2R

Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:

p=i2R

Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:

p=(Imaxcos.ωt)2R

Вспомним из курса математики:

cos2.α=1+cos.2α2..

Отсюда:

p=I2max2..R(1+cos.2ωt)=I2maxR2..+I2maxR2..cos.2ωt

График зависимости мгновенной мощности от времени:

На протяжении первой четверти периода, когда cos.2ωt>0, мощность в любой момент времени больше величины I2maxR2… На протяжении второй четверти периода, когда cos. 2ωt<0, мощность в любой момент времени меньше этой величины. Среднее за период значение cos.2ωt=0, следовательно, средняя за период мощность равна I2maxR2…

Средняя мощность −p равна:

−p=I2maxR2..=−i2R

Пример №2. Сила переменного тока в цепи меняется по закону i=Imaxcos.ωt. Определить мгновенную мощность в момент времени t = 1 с, если циклическая частота колебаний ω = 100π Гц при сопротивлении

R = 10 Ом. Амплитуда силы тока равна 1 А.

p=(Imaxcos.ωt)2R=10(1·cos.(100π·1)2=10 (Дж)

Действующие значения силы тока и напряжения

Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:

−i2=I2max2..

Определение

Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.

I=√−i2=Imax√2

Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.

Аналогично определяется действующее значение напряжения U:

U=√−u2=Umax√2..

Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:

P=I2R=UI

Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.

P=I2R

I=Imax√2..

P=(Imax√2..)2R=I2max2..R=222..·5=10 ⎛⎝Дж⎞⎠

Задание EF22720

В идеальном колебательном контуре (см. рисунок) напряжение между обкладками конденсатора меняется по закону U_C = U₀cos ωt, где U₀

 = 5 В, ω = 1000π с^–1. Определите период колебаний напряжения на конденсаторе.

---

Алгоритм решения

1.Записать исходные данные.

2.Записать формулу Томсона.

3.Вычислить искомую величину, подставив известные данные.

Решение

Запишем исходные данные:

• Закон изменения напряжения между обкладками конденсатора: UC=U0cos. ωt.

• Амплитуда напряжения: U0=5 В.

• Циклическая частота колебаний: ω = 1000π с^–1.

Запишем формулу Томсона:

T=2πω..=2π1000π..=21000..=0,002 (с)

Ответ: 0,002

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18735

В электрической цепи, показанной на рисунке, ключ К длительное время замкнут, E=6 В, r = 2 Ом, L = 1 мГн. В момент t = 0 ключ К размыкают. Амплитуда напряжения на конденсаторе в ходе возникших в контуре электромагнитных колебаний равна ЭДС источника. В какой момент времени напряжение на конденсаторе в первый раз достигнет значения E? Сопротивлением проводов и активным сопротивлением катушки индуктивности пренебречь. Ответ запишите в мкс.

---

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения в СИ.

2.Описать, что происходит в момент замыкания и размыкания цепи.

3.Выполнить решение задачи в общем виде.

4.Вычислить искомую величину, подставив известные данные.

Решение

Запишем исходные данные:

• ЭДС источника тока: ε=5 В.

• Амплитуда колебаний напряжения на конденсаторе: UCmax=5 В.

• Сопротивление ЭДС источника тока: r = 2 Ом.

• Индуктивность катушки: L = 1 мГн.

1 мГн = 10^–3 Гн

Перед размыканием ключа К ток через конденсатор не идет, по катушке течёт ток:

I0=εr..

Напряжение на конденсаторе в начальный момент времени равно нулю, так как оно равно нулю на катушке: U0C=0 В.

После размыкания ключа К в контуре возникают гармонические колебания напряжения между обкладками конденсатора и тока в контуре. Благодаря начальному условию (U0C=0 В) потенциал верхней обкладки конденсатора относительно нижней начинает меняться по закону:

u=−UCmaxsin.ωt

Знак «–» в формуле связан с тем, что сразу после размыкания ключа К ток приносит положительный заряд на нижнюю обкладку конденсатора.

Циклическую частоту выразим из формулы Томсона:

ω=2πT..=1√LC..

Энергия электромагнитных колебаний в контуре сохраняется. Она определяется формулой:

W=Li22..+Cu22..=CU2Cmax2..=LI202..

Выразим максимальное напряжение на конденсаторе:

CU2Cmax=LI20

UCmax=I0√LC..

Учтем, что амплитуда напряжения на конденсаторе равна напряжению источника тока, а I0=εr… Тогда получим:

UCmax=ε=I0r=I0√LC..

Отсюда:

√LC..=r

C=Lr2..

Период колебаний в контуре определим через формулу Томсона:

T=2π√LC=2π√LLr2..=2πLr..

Вспомним зависимость напряжения от времени:

u=−UCmaxsin.ωt

Подставим известные данные для искомого момента времени:

.5=−5sin.ωt

Синус должен быть равен «–1» Это возможно, если с начального момента времени пройдет четверть периода:

t=T4..=2π4..Lr..=π2..10−32..≈7,85·10−6(с)=7,85 (мкс)

Ответ: 7,85

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18116

Ученик изучает зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Какие два контура он должен выбрать для этого исследования?

---

Алгоритм решения

1. Выделить цель эксперимента.
2. Установить, какие величины для достижения цели эксперимента должны меняться, а какие — оставаться постоянными.
3. Выбрать верную пару контуров

Решение

Цель эксперимента — изучить зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Следовательно, емкости конденсатора должна быть единственной меняющейся величиной. При этом все другие величины должны оставаться постоянными. Поэтому катушки индуктивности должны быть одинаковыми, но конденсаторы — разные. Этому условию соответствует рисунок «а».

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18656

На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре.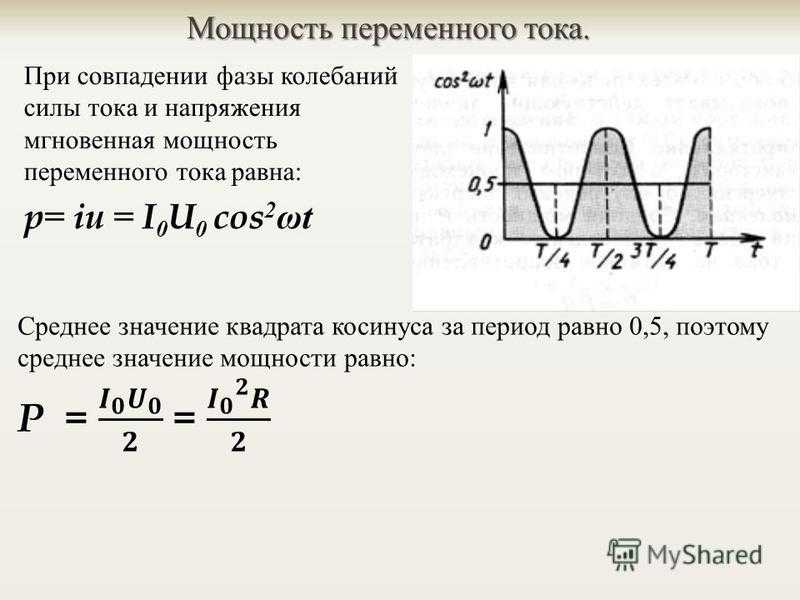 Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.

---

Алгоритм решения

1.Записать исходные данные (определить по графику начальный период колебаний).

2.Перевести единицы измерения величин в СИ.

3.Записать формулу Томсона.

4.Выполнить решение в общем виде.

5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.

Решение

Запишем исходные данные:

• Период колебаний (определяем по графику): T = 4 мкс.

• Емкость конденсатора в первом опыте: C₁ = 4C.

• Емкость конденсатора во втором опыте: C₂ = C.

4 мкс = 4∙10^–6 с

Запишем формулу Томсона:

T=2π√LC

Применим формулу для обоих опытов и получим:

T1=2π√L4C=4π√LC

T2=2π√LC

Поделим первый период на второй:

T1T2. .=4π√LC2π√LC..=2

Отсюда:

T2=T12..=4·10−62..=2·10−6 (с)=2 (мкс)

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 4.5k | Оценить:

Переменный электрический ток. Индуктивность в цепи переменного тока. Закон Ома для последовательного участка цепи

Физика \ Физика

Страницы работы

22 страницы (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

 41. ПЕРЕМЕННЫЙЭЛЕКТРИЧЕСКИЙТОК

Пусть электрический генератор создает напряжение £/(/)= l/₀sin ш*.

Согласно закону Ома сила тока в цепи, содержащей только резистор сопротивлением R, изменяется со временем также по синусоидальному закону

/о sin (о/,

=                        =.          Si,,

где 1₀ = -£- — амплитудное значение тока в цепи. «

Переменным током называется электрический ток, который изменяется   с  течением   времени   по   гармоническому  закону.

Величины U₀, 1₀ = -£ называются амплитудными значениями

н

напряжения и силы тока. Значения напряжения U (t) и силы тока I (t), зависящие от времени, называют мгновенными (рис. 129).

Зная  мгновенные значения   U (t) и I (t), можно вычислить мгновенную  мощность  Р (t)= U (t) I (t),  которая,  в  отличие  от цепей постоянного тока, изменяется с течением времени. Таким образом, тепловая мощность, рассеиваемая   на   резисторе, определяется по формуле

/>(/)= t/(0-/(0=

= I²(t)R = /lRsm²ut.

Поскольку    мгновенная мощность меняется со времеРис.  129. Зависимость напряжения, си-—*-» лы тока и мощности от времени   в цепи с активным сопротивлением

183

нем, то использовать эту величину в качестве характеристики длительно протекающих процессов на практике крайне неудобно.

Перепишем формулу для мощности иначе:

= UI=U₀I₀sin² co* =    £/₀/о(1 -cos 2«0=-Г-Первая составляющая мощности не зависит от времени и представляет собой постоянную часть мгновенной мощности за сколь угодно длительный промежуток времени. Вторая составляющая — переменная — есть функция косинус удвоенного угла, и ее среднее значение за период колебаний равно нулю (см. рис. 129).

Таким образом, среднее значение мощности переменного электрического тока за длительный промежуток времени определяется по формуле

Это выражение позволяет ввести действующее (эффективное) значение силы тока и напряжения, которое используется в качестве основных характеристик переменного тока.

Действующим (эффективным) значением переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделил бы в единицу времени такое же количество теплоты, что и данный переменный ток.

Для   переменного  тока   действующее   значение   силы   тока

/„ = — Д=т. Аналогично можно ввести действующее (эффективное)

V2

11         ^U° значение и для напряжения  и_я = —;=.

Таким образом, выражения для мощности постоянного тока остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:

имеют одинаковые  начальные фаз*ы, т.  е.  совпадают по фазе (см. рис.  129).

|    Электричество широко применяется в медицинских процедурах,  таких,  как  высокочастотное  прогревание, статический душ, электроанестезия, электросон и др. Электрический ток опасен для жизни!

При силе тока около 1 мА большинство людей уже его ощущают, а при силе тока выше 5 мА — чувствуют боль. Ток свыше 10 мА вызывает резкое сокращение мышц, при этом может произойти остановка дыхания, при токе выше 15 мА теряется контроль над мышцами. При прохождении тока свыше 70 мА в области сердца начинается беспорядочное сокращение (фибрилляция) сердца, которая может привести к смерти. Сила тока зависит от электрического сопротивления тела человека. При сухой коже сопротивление тела составляет от 10⁴ до 10⁶ Ом. Влажная кожа уменьшает сопротивление до 10³ Ом и меньших величин. Поэтому при хорошем контакте с поверхностью земли через тело человека, дотронувшегося до провода, находящегося под напряжением 120 В, пройдет ток 120 мА, что может оказаться смертельным. В связи с этим будьте осторожны при работе с цепями, питающимися переменным током.

Р    1. Какой ток называют переменным?

2.  Какое значение переменного тока называют мгновенным? амплитудным?

3.  Что   называется   действующим   значением   переменного тока?

4.  Почему неудобно характеризовать переменный ток с по мощью мгновенного значения мощности?

5.

г =/²/?

д      *д^а

и²-.

~ /? ‘

Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R, выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и тока вследствие того, что их колебания

184

Упражнение 30

1. Напряжение в цепи переменного тока изменяется по закону U = 200 sin 5(Ш. Чему равна частота v колебаний напряжения в цепи, его амплитудное U₀ и действующее U_{flзначения? На какое напряжение U должна быть рассчитана изоляция проводов?}

185

2.  Зависимостьсилытокаотвременивцепиимеетвид 1 = = 300 sinЮОлт. ₀ввитке.

Похожие материалы

Информация о работе

Скачать файл

Калькулятор мощности переменного тока

Создано Adena Benn

Отзыв от Dominik Czernia, PhD и Стивена Вудинга

Последнее обновление: 22 января 2022 г.

Содержание:

• мы его используем?
• Что нужно знать для расчета мощности переменного тока?
• Как рассчитать мощность в вольтах и ​​амперах, используя однофазный переменный ток
• Как рассчитать мощность в ваттах, используя трехфазный переменный ток для междуфазного напряжения
• Как рассчитать мощность, используя трехфазный переменный ток для напряжения фаза-нейтраль

Калькулятор мощности переменного тока преобразует однофазное и трехфазное напряжение в ватты. Наш инструмент позволяет вам вводить информацию, которую вы хотите преобразовать, и возвращает ответ, не зная ни одной формулы. Однако, если вам интересно, как мы получаем эти ответы, у нас также есть формулы, используемые в нашем калькуляторе мощности переменного тока ниже, с четкими пояснениями о том, как использовать каждую из них.

Для всех тех, кто находит электрические термины запутанными, эта статья также отвечает на вопросы:

• Что означает переменный ток?
• Что означает мощность для домовладельца?
• Как рассчитать мощность из вольт и ампер?

Если вы изучаете физику, вас также может заинтересовать наш калькулятор закона Ома.

Определение термина мощность

Являются ли эти электрические термины постоянной загадкой? Вы студент и хотите ответить на вопрос, что означает мощность? Большинство из нас слышали это слово, но его точное значение может быть полной загадкой.

Мощность в ваттах — это количество электроэнергии, необходимое для работы электроприбора. Единицей измерения мощности является ватт, который имеет аббревиатуру Вт .

Итак, что означает мощность для домовладельца? Каждый электроприбор имеет определенную мощность. На устройстве обычно указана мощность. Таким образом, если лампочка имеет маркировку 25 Вт, эта лампочка вносит 25 ватт-часов (или 0,025 киловатт-часа) в счет за электричество в час.

Что означает AC и где мы его используем?

Существует два разных типа питания: переменный и постоянный.

AC — сокращение от переменного тока. Это тип тока, направление которого меняет на противоположное с определенной частотой. Мы используем переменный ток для передачи электрического тока на большие расстояния.

Мы рассчитываем переменный ток по-разному в зависимости от того, используем ли мы однофазное, трехфазное линейное или трехфазное линейное напряжение.

Все еще не уверены, что можете ответить на вопрос что означает AC? Переменный ток, или переменный ток, движется волнами, амплитуда которых периодически увеличивается и уменьшается. Переменный ток — это тип электричества, который поступает в наши дома, школы и предприятия.

Постоянный ток (DC) протекает в одном направлении и не изменяется во времени. Мы используем его только на коротких дистанциях для запуска наших устройств.

Что нужно знать для расчета мощности переменного тока?

Чтобы рассчитать мощность переменного тока (в ваттах), сначала необходимо определить, используете ли вы однофазный или трехфазный ток. Если вы используете трехфазный ток, вам также необходимо знать его тип. Существует два типа трехфазного питания: фаза-фаза и фаза-нейтраль.

Мы рассчитываем мощность из вольт и ампер. Чтобы найти мощность, нам нужно:

• Узнать количество ампер и вольт, которые использует устройство.
• Получите коэффициент мощности. Проверьте наш калькулятор электрической мощности, чтобы узнать больше об этом.
• Затем, используя соответствующую формулу, подставьте значения и рассчитайте. Наши формулы ниже покажут вам, как рассчитать мощность из вольт и ампер.

🙋 Попробуйте наш калькулятор вольт в электрон-вольт, если вы хотите узнать больше о преобразованиях с использованием вольт.

Ниже приведена формула расчета однофазного переменного тока в ваттах, используемая нашим калькулятором мощности переменного тока:

• P = PF × I × U

где:

• P – Мощность или мощность;
• PF – Коэффициент мощности;
• I – Электрический ток; и
• U – Напряжение.

Эта формула означает, что мощность равна коэффициенту мощности, умноженному на ток, умноженному на напряжение. Измеряем ток в амперах ( А ) и напряжение в вольтах ( В ).

Коэффициент мощности варьируется от 0 до 1. Единица представляет наиболее эффективное использование мощности, а 0 означает обратное. Коэффициент мощности в нашем калькуляторе установлен на 0,9.5 по умолчанию.

Давайте рассмотрим пример, используя эту формулу расчета однофазной мощности переменного тока в амперах:

Рассчитайте ватты от 24 вольт и 3,75 ампер с коэффициентом мощности 0,5. Используя формулу мощности переменного тока, мы имеем:

• P = 0,5 × 3,75 × 24 = 45 Вт

Теперь, если вы заинтересованы в расчете потребления электроэнергии бытовой техникой в ​​вашем доме, вам нужен наш калькулятор мощности бытовой техники.

🔎 Трехфазное питание — это когда три линии электропередач чередуются, чтобы подать ток в ваш дом. Каждая из этих строк меняет свою силу в разное время . Только одна из трех линий будет максимальной в любой момент времени.

Как рассчитать мощность, используя трехфазный переменный ток для междуфазного напряжения

При работе с трехфазным током мы должны сначала определить, является ли это напряжение между фазами или между фазами. Только тогда мы знали бы, как правильно рассчитать мощность. Приведенная ниже формула предназначена строго для междуфазного напряжения:

• P = √3 × PF × I × V

Эта формула означает, что мощность равна квадратному корню из трех, умноженному на коэффициент мощности, ток и напряжение. Напряжение В на этот раз относится к линейному напряжению.

Вот пример, в котором используется эта формула мощности переменного тока:

Рассчитайте мощность в ваттах при 120 вольтах и ​​5 амперах с коэффициентом мощности 0,8:

P = √3 × 0,8 × 5 × 120 = 890,38 Вт .

Как рассчитать мощность при трехфазном переменном токе для фазного напряжения

Следующая формула используется для фазного напряжения

• P = 3 × PF × I × V

Эта формула означает, что мощность равна двум, умноженным на коэффициент мощности, ток и фазное напряжение.

Ниже мы рассмотрим задачу, чтобы увидеть применение этой формулы. Рассчитайте ватты от 12 вольт и 0,125 ампер с коэффициентом мощности 0,2:

P = 3 × 0,2 × 0,125 × 12 = 0,9 Вт

Если вы нашли этот калькулятор полезным, вам также может понравиться этот калькулятор стоимости электроэнергии.

Adena Benn

ТИПА ТИПА

Напряжение

Ток

Коэффициент мощности

По мощность

Проверьте 85 аналогичных кальцираторов электромагнетизма 🧲

Указывают частицы в электрическом поэтапном разбилке. Формулы физики

Электродвижущая сила переменного тока

Находить

Известно, что:

εBSω =

Рассчитать 'ε'

Электродвижущая сила переменного тока

Находить

Известно, что:

eε_msinωt =

Рассчитать e

Максимальная сила переменного тока

Находить

Известно, что:

I_mε_mR =

Расчет 'I_m'

Действующее значение силы переменного тока

Находить

Известно, что:

I_efI_m =

Рассчитать I_ef

Средняя мощность переменного тока

Находить

Известно, что:

p_avgI_mR =

Расчет 'p_avg'

Действующее значение напряжения переменного тока

Находить

Известно, что:

U_efU_m =

Расчет 'U_ef'

Напряжение переменного тока

Находить

Известно, что:

UU_mcosωt =

Рассчитать 'U'

Максимальная сила переменного тока

Находить

Известно, что:

I_mU_mCω =

Расчет 'I_m'

Емкостное реактивное сопротивление

Находить

Известно, что:

X_cCω =

Расчет 'X_c'

Сила и емкостное сопротивление переменного тока

Находить

Известно, что:

IUX_c =

Рассчитать I

Сила и индуктивное сопротивление переменного тока

Находить

Известно, что:

IUX_L =

Расчет I

Индуктивное сопротивление

Находить

Известно, что:

X_LωL =

Расчет 'X_L'

Закон Ома для цепи переменного тока

Находить

Известно, что:

XRX_LX_C =

Рассчитать «X»

Закон Ома для цепи переменного тока

Находить

Известно, что:

XRωLC =

Рассчитать «X»

Разность фаз между током и напряжением переменного тока (AC)

Находить

Известно, что:

φX_LX_CR =

Рассчитать 'φ'

Резонанс в цепи переменного тока (AC)

Находить

Известно, что:

УИЛК =

Вычислить 'U'

Первая формула трансформатора: напряжение

Находить

Известно, что:

U1U2N1N2 =

Расчет 'U1'

Вторая формула трансформатора: сила тока

Находить

Известно, что:

I1I2N2N1 =

Расчет 'I1'

Переменный ток и ЭДС: определение, формула и объяснение

Переменный ток

Мы уже знали, что постоянный ток (DC) создается источником напряжения, полюса которого не меняют своей полярности со временем. Следовательно, направление потока постоянного тока не меняется со временем.

С другой стороны, переменный ток создается источником напряжения, полярность клемм которого постоянно меняется со временем, т. е. клемма, которая была положительной в один момент времени, через какое-то время становится отрицательной, и наоборот.

Из-за изменения полярности источника напряжения направление протекания тока также продолжает меняться.

В этой главе «Переменный ток и электрические машины» мы узнаем, как напряжение и ток, изменяющиеся во времени, связаны друг с другом в различных цепях с компонентами, а именно резисторами, конденсатором и катушкой индуктивности.

Переменный ток Определение

Переменный ток – это ток, величина которого постоянно меняется со временем, а направление периодически меняется на противоположное.

Переменный ток – это ток, величина которого изменяется по синусоидальному закону во времени. Таким образом, переменный ток определяется как
$$I=I_0sin\left(\omega t\right)\tag{1}$$ Или это также может быть представлено уравнением
$$I=I_0cos\left(\omega t\right)$$ Где
$I_0=$ амплитуда тока или пиковое значение переменного тока.
Оба эти представления приводят к одному и тому же результату.

Если $T$ — период переменного тока, а $f$ — частота, то
$$\omega=\frac{2\pi}{T}=2\pi f \tag{2}$$ Где $\omega$ называется угловой частотой переменного тока, а $\phi$ называется фазовой постоянной. Полный набор изменений тока за один период времени T называется цикл .

Вместо функции синуса AC также может быть представлен функцией косинуса, и каждое представление приводит к одинаковым результатам. Мы обсудим схемы с синусоидальным представлением переменного тока

. На приведенном ниже рисунке показан контраст между переменным и постоянным током. Он показывает изменение переменного и постоянного тока во времени.

Переменный ток, меняющийся во времени по синусоидальному закону.

Эта цифра представляет изменение переменного тока во времени.

Из этого рисунка ясно видно, что переменный ток возрастает от 0 до максимума в одном направлении, затем падает до нуля в момент Т/2, затем возрастает от 0 до максимума в противоположном направлении и снова падает до нуля в момент времени Т, заканчивая один полный цикл.

Здесь важно отметить, что
Поскольку переменный ток положительный в одной половине цикла и отрицательный в другой, его среднее значение за весь цикл равно нулю. Это будет доказано в следующем разделе статьи.

Что такое переменная ЭДС?

Полная форма переменной ЭДС – переменная электродвижущая сила. Давайте теперь поймем значение переменной ЭДС, сначала определив ее.

Определение переменной ЭДС

ЭДС или напряжение, величина которого изменяется синусоидально со временем, известна как переменная ЭДС и представлена ​​соотношением
$$E=E_0sin\left(\omega t\right)\tag{3}$$ Или это также может быть представлено
$$E=E_0cos\left(\omega t\right)$$ где $E_0$ — пиковое значение переменной ЭДС.
Вышеупомянутое уравнение представляет мгновенное значение переменной ЭДС.

Так вот, например, величина ЭДС меняется со временем и ее направление периодически меняется на противоположное.

Важные термины, относящиеся к AC

Давайте начнем наше обсуждение с того, что сначала посмотрим, как генерируется переменная ЭДС? При вращении катушки в магнитном поле возникает переменная ЭДС. Соотношение (1) и (3) дает нам соотношение для переменного тока и переменной ЭДС и показывает нам, как они меняются со временем.

Теперь предположим, что эта ЭДС приложена к электрической цепи сопротивлением $R$. Тогда ток, протекающий по этой цепи, будет $$I=\frac{E}{R}=\frac{E_0}{R}sin\left(\omega t\right)$$ Или же, $$I=I_0sin\влево(\омега т\вправо)$$ Как мы знаем, это соотношение для переменного тока в цепи. Это уравнение представляет мгновенное значение переменного тока.
Здесь
$I= $ мгновенное значение переменного тока
$I_0=\frac{E_0}{R}=$ пиковое или максимальное значение переменного тока, также известное как амплитуда тока.

Амплитуда переменного тока

Это максимальное значение, достигаемое переменным током в любом направлении. Оно также известно как пиковое значение тока и обозначается $I_0$.

Формула амплитуды тока

Он определяется соотношением $$I_0=\frac{E_0}{R}$$

Время Период переменного тока

Время, за которое переменный ток совершает один цикл своих изменений, называется его периодом времени и обозначается $T$.