Конденсатор в цепи переменного тока
Положим теперь, что участок цепи содержит конденсатор емкости C, причем сопротивлением и индуктивностью участка можно пренебречь, и посмотрим, по какому закону будет изменяться напряжение на концах участка в этом случае. Обозначим напряжение между точками а и b через u и будем считать заряд конденсатора q и силу тока i положительными, если они соответствуют рис.4. Тогда
,
и, следовательно,
.
Если сила тока в цепи изменяется по закону
, (1)
то заряд конденсатора равен
.
Постоянная интегрирования q0 здесь обозначает произвольный постоянный заряд конденсатора, не связанный с колебаниями тока, и поэтому мы положим . Следовательно,
. (2)
Рис. | Рис.5. Зависимости тока через конденсатор и напряжения от времени |
Сравнивая (1) и (2), мы видим, что при синусоидальных колебаниях тока в цепи напряжение на конденсаторе изменяется также по закону косинуса. Однако колебания напряжения на конденсаторе отстают по фазе от колебаний тока на /2. Изменения тока и напряжения во времени изображены графически на рис.5. Полученный результат имеет простой физический смысл. Напряжение на конденсаторе в какой-либо момент времени определяется существующим зарядом конденсатора. Но этот заряд был образован током, протекавшим предварительно в более ранней стадии колебаний. Поэтому и колебания напряжения запаздывают относительно колебаний тока.
Формула (2) показывает, что амплитуда напряжения на конденсаторе равна
.
Сравнивая это выражение с законом Ома для участка цепи с постоянным током (), мы видим, что величина
играет
роль сопротивления участка цепи, она
получила название емкостного сопротивления. Емкостное сопротивление зависит от
частоты и
при высоких частотах даже малые емкости
могут представлять совсем небольшое
сопротивление для переменного тока.
Емкостное сопротивление зависит от
частоты и
при высоких частотах даже малые емкости
могут представлять совсем небольшое
сопротивление для переменного тока.
Мгновенная мощность переменного тока
меняется со временем по синусоидальному закону с удвоенной частотой. В течение времени от 0 до T/4 мощность положительна, а в следующую четверть периода ток и напряжение имеют противоположные знаки и мощность становится отрицательной. Поскольку среднее значение за период колебаний величины равно нулю, то средняя мощность переменного тока на конденсаторе.
Рассмотрим, наконец, третий частный случай, когда участок цепи содержит только индуктивность. Обозначим по-прежнему через
 6). При наличии переменного тока в
катушке индуктивности возникнет ЭДС
самоиндукции, и поэтому мы должны
применить закон Ома для участка цепи,
содержащего эту ЭДС:
6). При наличии переменного тока в
катушке индуктивности возникнет ЭДС
самоиндукции, и поэтому мы должны
применить закон Ома для участка цепи,
содержащего эту ЭДС:.
В нашем случае R = 0, а ЭДС самоиндукции
.
Поэтому
. (3)
Если сила тока в цепи изменяется по закону
,
то
. (4)
Рис.6. Катушка индуктивности в цепи переменного тока | Рис.7. Зависимости тока через катушку индуктивности и напряжения от времени |
Видно,
что колебания напряжения на индуктивности
опережают по фазе колебания тока на
/2.
Когда сила тока, возрастая, проходит
через нуль, напряжение уже достигает
максимума, после чего начинает уменьшаться;
когда сила тока становится максимальной,
напряжение проходит через нуль, и т.
Из (4) следует, что амплитуда напряжения равна
,
и , следовательно, величина
играет ту же роль, что сопротивление участка цепи. Поэтому называют индуктивным сопротивлением. Индуктивное сопротивление пропорционально частоте переменного тока, и поэтому при очень больших частотах даже малые индуктивности могут представлять значительное сопротивление для переменных токов.
Мгновенная мощность переменного тока
также, как и в случае идеальной емкости, меняется со временем по синусоидальному закону с удвоенной частотой. Очевидно, что средняя за период мощность равна нулю.
Таким образом, при протекании переменного тока через идеальные емкость и индуктивность обнаруживается ряд общих закономерностей:
Колебания тока и напряжения происходят в различных фазах — сдвиг по фазе между этими колебаниями равен /2.
Амплитуда переменного напряжения на емкости (индуктивности) пропорциональна амплитуде протекающего через этот элемент переменного тока
где X — реактивное (емкостное или индуктивное
сопротивление).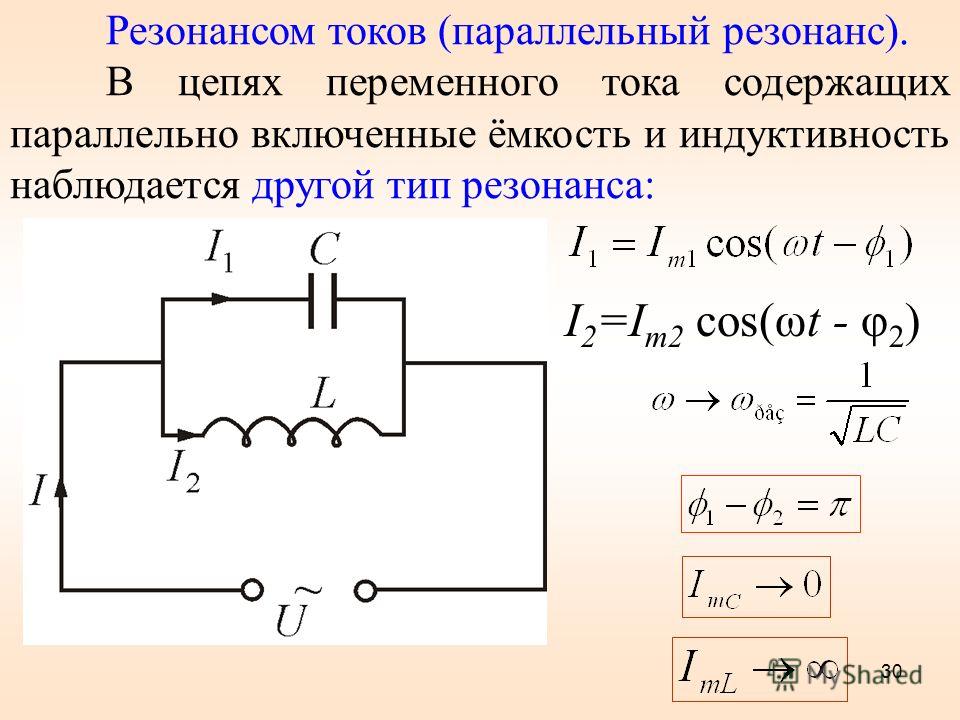
На реактивном сопротивлении не рассеивается мощность (в среднем за период колебаний), это означает, что, например, через конденсатор может протекать переменный ток очень большой амплитуды, но тепловыделение на конденсаторе будет отсутствовать. Это является следствием фазового сдвига между колебаниями тока и напряжения на реактивных элементах цепи (индуктивности и емкости).
Резистивный элемент, который описывается в рассматриваемом частотном диапазоне законом Ома для мгновенных токов и напряжений
,
называют омическим или активным сопротивлением. На активных сопротивлениях происходит выделение мощности.
Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.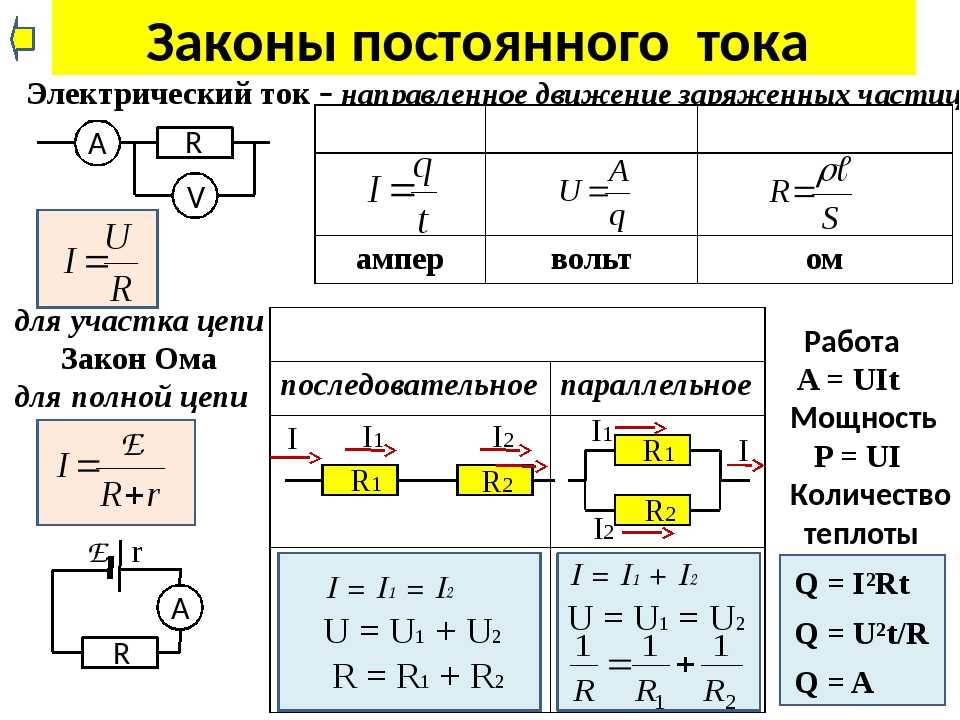
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.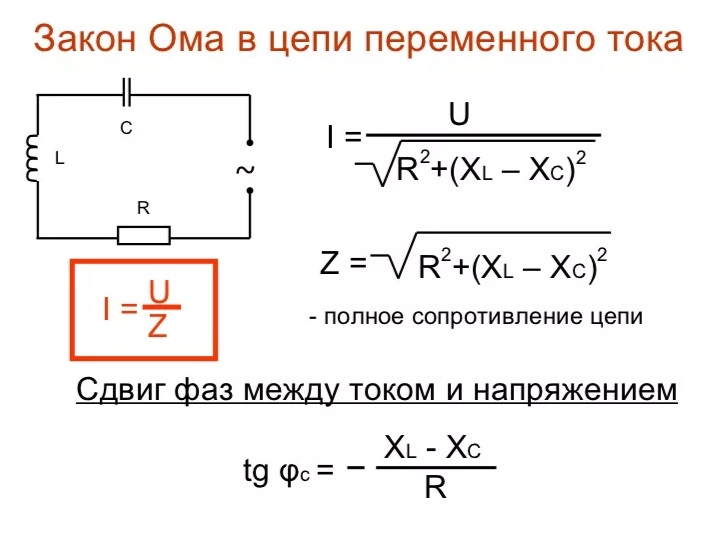
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
376045 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype. В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
 RU
RU
- Class
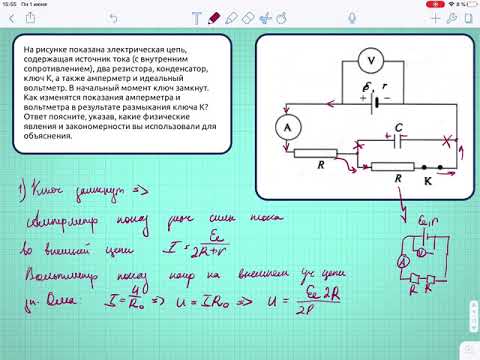
Цепи переменного тока
Цепи переменного токаДалее: Линии электропередач Вверх: Магнитная индукция Предыдущий: Магнитная энергия Цепи переменного тока (AC) состоят из э.д.с. источники и три различные типы пассивных элементов: резисторы, катушки индуктивности, и конденсаторы, резисторы удовлетворяют закону Ома:
| (968) |
где — сопротивление, ток, протекающий через резистор, и падение напряжения на резисторе (в направлении, в котором ток течет). Катушки индуктивности удовлетворяют
| (969) |
где индуктивность.
 Наконец, конденсаторы подчиняются
Наконец, конденсаторы подчиняются | (970) |
где — емкость, — заряд, накопленный на пластине с наибольшим положительный потенциал, а для . Обратите внимание, что любой пассивный компонент реального электрического Цепь всегда можно представить как комбинацию идеальных резисторов, катушек индуктивности и конденсаторы.
Рассмотрим классическую схему LCR, состоящую из катушки индуктивности,
конденсатор , и резистор , соединенные последовательно с ЭДС источник,
. Уравнение схемы получается путем установки входного напряжения равным
сумма падений напряжения на трех пассивных элементах цепи.
Таким образом,
| (971) |
Это интегро-дифференциальное уравнение, которое, вообще говоря, довольно сложно решить.
 решать. Предположим, однако, что и напряжение, и ток
колебаться с некоторой фиксированной угловой частотой, так что
решать. Предположим, однако, что и напряжение, и ток
колебаться с некоторой фиксированной угловой частотой, так что | (972) | |||
| (973) |
где под физическим решением понимается действительная часть приведенные выше выражения. Предполагаемое поведение напряжения и тока явно относится к электрике схемы питаются от сетевого напряжения (которое колеблется с частотой 60 герц).
Уравнения (971)–(973) дают результат
| (974) |
давать
| (975) |
Полезно определить импеданс схемы:
| (976) |
Импеданс является обобщением понятия сопротивления.
 В общем случае импеданс
цепи переменного тока составляет сложных величин.
В общем случае импеданс
цепи переменного тока составляет сложных величин. Средняя выходная мощность Э.Д.С. источник
| (977) |
где среднее значение берется за один период колебаний. Давайте, прежде всего, вычислить мощность, используя реальные (а не комплексные) напряжения и токи. Мы можем написать
| (978) | |||
| (979) |
где — фазовое отставание тока по отношению к напряжению.
 Это следует из того
Это следует из того | (980) |
давать
| (981) |
поскольку а также . В комплексном представлении напряжение и ток записываются
| (982) | |||
| (983) |
Обратите внимание, что
| (984) |
Это следует из того
| (985) |
Используя уравнение (976), мы находим, что
| (986) |
Обратите внимание, что рассеиваемая мощность связана с действительной частью импеданса.
 Для частного случая схемы LCR,
Для частного случая схемы LCR, | (987) |
Понятно, что только резистор рассеивает энергию в этой цепи. Индуктор и конденсатор накапливает энергию, но в конечном итоге возвращает ее в цепь без рассеивания.
Согласно уравнению. (976), амплитуда тока, протекающего в цепи LCR
для заданной амплитуды входного напряжения
данный
| (988) |
Ответ цепи четко резонансный , достигая пика в , и достижение пикового значения в (при условии, что ). На самом деле схемы LCR используются в радиотюнерах для фильтрации сигналы, частоты которых выходят за пределы заданного диапазона.
Отставание по фазе тока по отношению к напряжению определяется выражением
| (989) |
Отставание по фазе изменяется от для частот значительно ниже резонансной частоты, к нулю на резонансной частоте ( ), к для частот значительно выше резонансной частоты.

Понятно, что в обычных цепях переменного тока уравнение цепи сводится к простое алгебраическое уравнение, и поведение схемы суммируется по комплексному импедансу. Действительная часть говорит нам о мощности, рассеиваемой в цепи, величина дает отношение пикового тока к пиковое напряжение, а аргумент дает отставание по фазе тока относительно напряжения.
Далее: Линии электропередач Вверх: Магнитная индукция Предыдущий: Магнитная энергия Ричард Фицпатрик 2006-02-02
ЭМ колебания — Анализ цепи переменного тока
ЭМ колебания — Анализ цепи переменного тока — Физика 299 » Знаете, то, что только что сказал Эйнштейн, не так уж и глупо »
- Мы видели, что в управляемой цепи LCR ток в
схема колеблется с частотой возбуждения (частотой
генератор).
 Это ток Переменный
Текущий. В реальных приложениях многие
цепи будут иметь характеристическую индуктивность (L), сопротивление
(R) и емкость (C), так что при наличии
генератор переменного тока источник тока/напряжения ток в
схема будет описываться решением задачи
дифференциальное уравнение в ведомой секции LCR.
Это ток Переменный
Текущий. В реальных приложениях многие
цепи будут иметь характеристическую индуктивность (L), сопротивление
(R) и емкость (C), так что при наличии
генератор переменного тока источник тока/напряжения ток в
схема будет описываться решением задачи
дифференциальное уравнение в ведомой секции LCR.
- Вместо решения дифференциальных уравнений
инженеры (?) придумали альтернативный способ анализа этих
цепи переменного тока с помощью вращающихся векторов, называемых векторами .
- Вектор — это вектор, который вращается против часовой стрелки вокруг начала с частотой генератора, величина которой максимальное значение тока или напряжения. Проекция по оси Y представляет мгновенное значение тока или Напряжение.
П, С и Л Векторы
- Ток и напряжение на каждом из элементов, R, C и
L в схеме может быть представлен определенными векторами.

- Сопротивление
В цепи, где только генератор переменного тока обеспечивает напряжение, В(t) = В Rm sinωt, а сопротивление, R, напряжение и ток на резисторе определяются по формулеОбратите внимание, что векторы тока и напряжения фазы, как показано на диаграмме справа.
Обратите внимание, что на всех векторных диаграммах величина векторов максимальное значение ток или напряжение, обозначенные как V Rm и I Rm .
- Емкость
С генератором и емкость, у нас есть,
, где называется
емкостная реактивное сопротивление .
Обратите внимание, что в этом случае вектор тока опережает вектор напряжения на 90 0 .
- Индуктивность
Только с генератором и индуктивностью имеем
где называется
индуктивная реактивное сопротивление.
90 0 .
Обратите внимание, что в этом случае текущий вектор отстает от вектор напряжения на9Цепи LCR серии 0374
- Сочетание этих три элемента — сопротивление, емкость и индуктивность — в последовательной (LCR) цепи мы можем написать
Теперь, рассматривая эти потенциалы как векторы (фазоры), используя комбинированную векторную диаграмму ниже у нас есть
, где я м является максимальным ток, обеспечиваемый генератором и Z, называется импеданс, который играет аналогичную роль к сопротивлению в постоянном токе схемы.
С точки зрения сопротивление, емкость и индуктивность импеданс можно записать,
- Обратите внимание, что на векторной диаграмме выше общий вектор напряжения опережает вектор тока на угол θ, называемый фазой постоянный. То есть мы можем написать для напряжение как функция времени. От фазора схема,
- Когда V L > V C цепь более индуктивная, чем емкостный. В этом случае X L > X C и tanθ > 0. X C > X L и tanθ < 0 для более емкостных цепей.
- При резонансе, когда
, х C = X L так что
tanθ = 0 (θ = 0) и Z = R.
 То есть,
цепь чисто резистивная с током
и напряжение в фазе.
То есть,
цепь чисто резистивная с током
и напряжение в фазе.
Рассеиваемая мощность
- В цепи LCR энергия, подаваемая генератор переменного тока либо,
- хранится в магнитном поле индуктивность,
- хранится в электрическом поле емкость или
- рассеивается в виде тепловой энергии в сопротивление.
Как мы видели в простая LC-цепь индуктивность (L) и емкость (C) не рассеивает энергию. Энергия просто колеблется от магнитной к электрический без ограничений.Итак, в LCR энергия цепи может рассеиваться (теряться) только в сопротивление (R). Мощность рассеивается дано,
- Усредненная по времени мощность рассеяния P av дано,
где находится «среднеквадратичное» максимума Текущий.
Обратите внимание, что если мы используем среднеквадратичное значение тока выражение для рассеивания мощности в приложениях переменного тока то же самое, что и «стандартное» выражение используется для приложений постоянного тока.Переменный ток и напряжение измерительные приборы обычно калибруются для чтения среднеквадратичных значений.
На самом деле 110 вольт в розетке на самом деле среднеквадратичное значение. Максимальное напряжение определяется как 110 x √2 = 170 В.
- В цепи серии LCR имеем видел, что V макс. = i макс. Z так что V СКЗ = i СКЗ Z. Следовательно,
где из векторной диаграммы LCR мы видим что cosθ = R/Z.
- Cosθ называется Power
Фактор из
схема.

Максимальное рассеивание мощности когда cosθ = 1 или R = Z — цепь чисто резистивная.
- Есть два способа сделать Цепь LCR чисто резистивная
- Обеспечение резонанса, X C = X L или
- марка (X C — X L ) как можно меньше — это
есть, маленькая L и большая C.
Известные физики на вечеринке : Вольт считал, социалка имела большой потенциал.


 4. Конденсатор
в цепи переменного тока
4. Конденсатор
в цепи переменного тока RU
RU
 Это ток Переменный
Текущий. В реальных приложениях многие
цепи будут иметь характеристическую индуктивность (L), сопротивление
(R) и емкость (C), так что при наличии
генератор переменного тока источник тока/напряжения ток в
схема будет описываться решением задачи
дифференциальное уравнение в ведомой секции LCR.
Это ток Переменный
Текущий. В реальных приложениях многие
цепи будут иметь характеристическую индуктивность (L), сопротивление
(R) и емкость (C), так что при наличии
генератор переменного тока источник тока/напряжения ток в
схема будет описываться решением задачи
дифференциальное уравнение в ведомой секции LCR.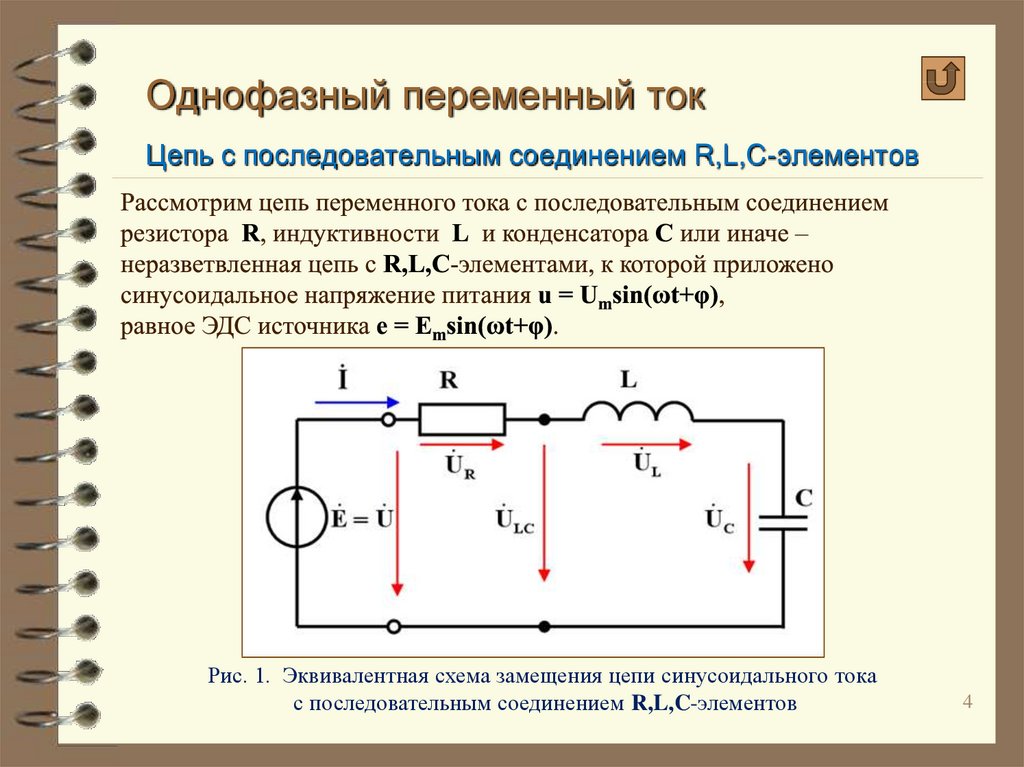

 С точки зрения
сопротивление, емкость и индуктивность
импеданс можно записать,
С точки зрения
сопротивление, емкость и индуктивность
импеданс можно записать, То есть,
цепь чисто резистивная с током
и напряжение в фазе.
То есть,
цепь чисто резистивная с током
и напряжение в фазе. Итак, в LCR
энергия цепи может рассеиваться (теряться) только в
сопротивление (R). Мощность рассеивается
дано,
Итак, в LCR
энергия цепи может рассеиваться (теряться) только в
сопротивление (R). Мощность рассеивается
дано,  На самом деле
110 вольт в розетке на самом деле
среднеквадратичное значение. Максимальное напряжение
определяется как 110 x √2 = 170 В.
На самом деле
110 вольт в розетке на самом деле
среднеквадратичное значение. Максимальное напряжение
определяется как 110 x √2 = 170 В. 
