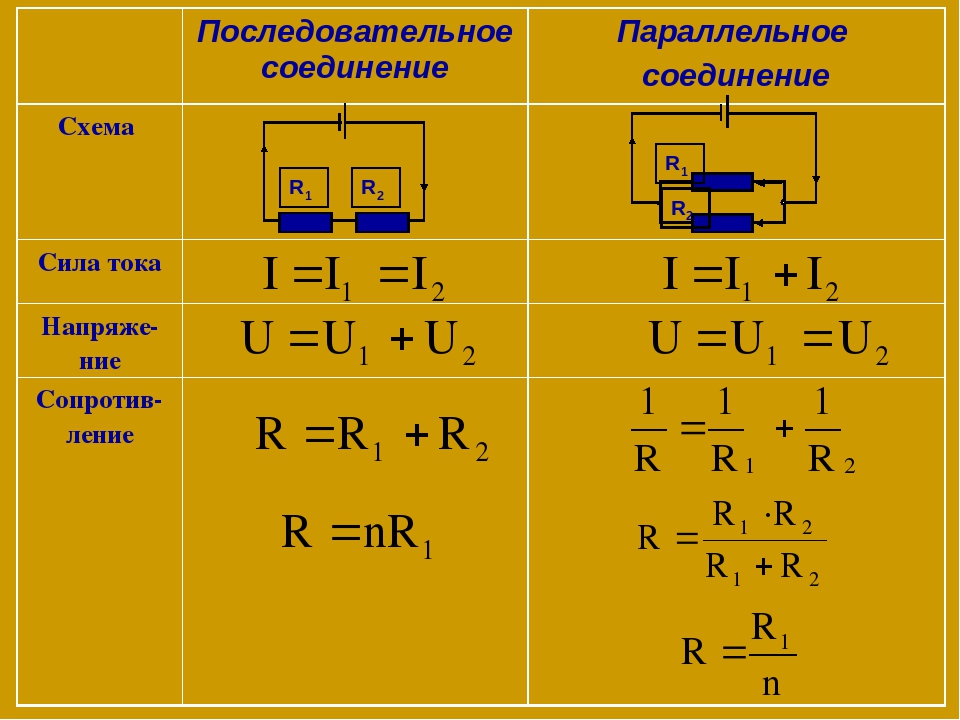
Сила тока

680 Во сколько раз возрастет сила тока через переход…

Прямое напряжение U, приложенное к р-n-переходу, равно 2 В. Во сколько раз возрастет сила тока через переход, если изменить температуру от Т₁ = 300 К до Т₂ = 273 К?

475 Определить среднее значение ЭДС самоиндукции…

Соленоид содержит \(N = 800\) витков. Сечение сердечника (из немагнитного материала) \(S = 10\) см². По обмотке течет ток, создающий поле с индукцией \(B = 8\) мТл. Определить среднее значение э. д. с.

476 Определить среднее значение ЭДС самоиндукции в контуре…

По катушке индуктивностью \(L = 8\) мкГн течет ток силой \(I = 6\) А. Определить среднее значение э. д. с. самоиндукции, возникающей в контуре, если сила тока изменится практически до нуля за время \(\Delta t = 5\) мс.

477 Определить силу тока в цепи через время…

В электрической цепи, содержащей сопротивление \(R = 20\) Ом и индуктивность \(L = 0,06\) Гн, течет ток силой \(I = 20\) А. Определить силу тока \(I\) в цепи через \(\Delta t = 0,2\) мс после ее размыкания.

478 Определить сопротивление катушки индуктивности…

Цепь состоит из катушки индуктивностью \(L = 0,1\) Гн и источника тока. Источник тока можно отключать, не разрывая цепь. Время, по истечении которого сила тока уменьшится до 0,001 первоначального значения, равно \(t = 0,07\) с. Определить сопротивление катушки.

480 Определить индуктивность катушки…

Источник тока замкнули на катушку сопротивлением \(R = 20\) Ом. По истечении времени \(t = 0,1\) с сила тока \(I\) замыкания достигла 0,95 предельного значения. Определить индуктивность \(L\) катушки.

411 Определить силу взаимодействия проводов…

По двум параллельным проводам длиной \(S = 3\) м каждый текут одинаковые токи \(I = 500\) А. Расстояние \(L\) между проводами равно 10 см. Определить силу \(F\) взаимодействия проводов.

412 Вычислить для каждого из проводов отношение силы к длине…

По трем параллельным прямым проводам, находящимся на одинаковом расстоянии \(R = 20\) см друг от друга, текут одинаковые токи \(I = 400\) А. В двух проводах направления токов совпадают. Вычислить для каждого из проводов отношение силы, действующей на него, к его длине.

413 Определить силу действующую на рамку…

Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводом так, что две ее стороны параллельны проводу. По рамке и проводу текут одинаковые токи силой \(I = 200\) А.

414 Найти магнитный момент катушки…

Короткая катушка площадью поперечного сечения \(S = 250\) см², содержащая \(N = 500\) витков провода, по которому течет ток силой \(I = 5\) А, помещена в однородное магнитное поле напряженностью \(H = 1000\) А/м Найти: 1) магнитный момент \({P_m}\) катушки; 2) вращающий момент \(M\), д

416 Найти силу взаимного отталкивания…

Шины генератора длиной \(l = 4\) м находятся на расстоянии \(L = 10\) cм друг от друга. Найти силу взаимного отталкивания шин при коротком замыкании, если ток \(I\) короткого замыкания равен 5 кА.

417 Определить изменение потенциальной энергии контура. ..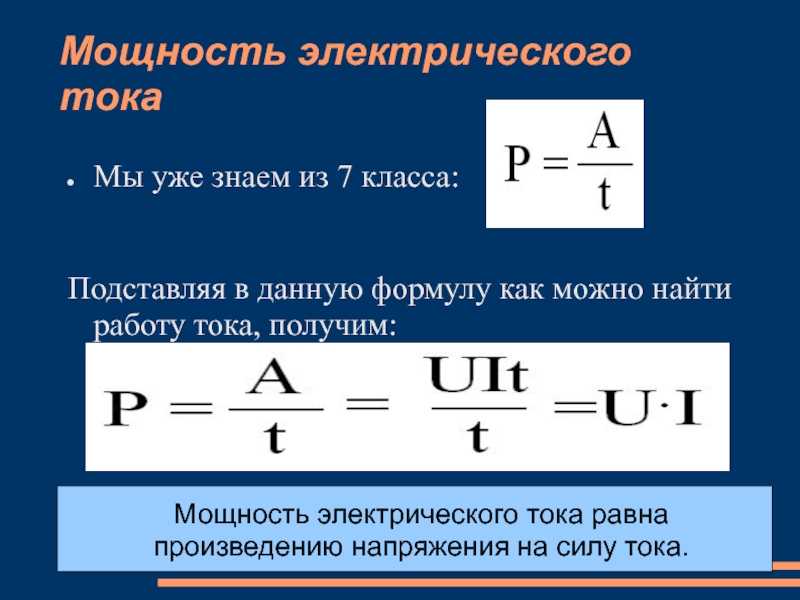

Квадратный контур со стороной \(d = 10\) см, по которому течет ток \(I = 50\) А, свободно установился в однородном магнитном поле (\(B = 10\) мТл).

418 Найти силу растягивающую кольцо…

Тонкое проводящее кольцо с током \(I = 40\) А помещено в однородное магнитное поле (\(B = 80\) мТл). Плоскость кольца перпендикулярна линиям магнитной индукции. Радиус \(R\) кольца равен 20 см. Найти силу \(F\), растягивающую кольцо.

419 Определить угол на который отклонилась рамка от вертикали…

Квадратная рамка из тонкого провода может свободно вращаться вокруг горизонтальной оси, совпадающей с одной из сторон. Масса \(m\) рамки равна 20 г. Рамку поместили в однородное магнитное поле (\(B = 0,1\) Тл), направленное вертикально вверх.

420 Определить изменение потенциальной энергии контура при повороте…

По круговому витку радиусом \(R = 5\) см течет ток \(I = 20\) А. Виток расположен в однородном магнитном поле (\(B = 40\) мТл) так, что нормаль к плоскости контура составляет угол \(\theta = \pi /6\) с вектором \(B\). \circ \).

457 Какую работу нужно совершить для того чтобы повернуть виток…

Виток, в котором поддерживается постоянная сила тока \(I = 60\) А, свободно установился в однородном магнитном поле (\(B = 20\) мТл). Диаметр витка \(d = 10\) см.

459 Определить работу совершаемую силами поля при повороте контура…

Плоский контур с током \(I = 50\) А расположен в однородном магнитном поле (\(B = 0,6\) Тл) так, что нормаль к контуру перпендикулярна линиям магнитной индукции.

362 Определить силу тока в цепи и напряжение…

ЭДС батареи \(\varepsilon = 80\) В, внутреннее сопротивление \(r = 5\) Ом. Внешняя цепь потребляет мощность \(P = 100\) Вт. Найти силу тока в цепи \(I\), напря­жение \(U\), под которым находится внешняя цепь, и ее сопротивление \(R\).

364 Определить силу тока короткого замыкания источника ЭДС…

При внешнем сопротивлении \({R_1} = 8\) Ом сила тока в цепи \({I_1} = 0,8\) А, при сопротивлении \({R_2} = 15\) Ом сила тока \({I_2} = 0,5\) А. Опре­делить силу тока короткого замыкания источника э. д. с.

365 Определить максимальную мощность которая может выделяться…

ЭДС батареи \(\varepsilon = 24\) В. Наибольшая сила тока, которую может дать батарея, \({I_{\max }} = 10\) А. Определить максимальную мощ­ность \({P_{\max }}\), которая может выделяться во внешней цепи.

368 Определить мощность потребляемую мотором и его КПД…

При включении электромотора в сеть с напряже­нием \(U = 220\) В он потребляет ток \(I = 5\) А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление \(R\) обмотки мотора равно 6 Ом.

370 Определить внутреннее сопротивление батареи…

ЭДС батареи \(\varepsilon = 12\) В. При силе тока \(I = 4\) А к. п. д. ба­тареи \(\eta = 0,6\). Определить внутреннее сопротивление \(r\) батареи.

371 Определить скорость нарастания силы тока…

За время \(t = 20\) с при равномерно возрастающей силе тока от нуля до некоторого максимума в проводнике сопро­тивлением \(R = 5\) Ом выделилось количество теплоты \(Q = 4\) кДж. { — 2}}\) с.

373 Определить количество теплоты выделившееся за это время в проводнике…

Сила тока в проводнике сопротивлением \(R = 10\) Ом за время \(t = 50\) с равномерно нарастает от \({I_1} = 5\) А до \({I_2} = 10\) А. Определить количество теплоты \(Q\), выделившееся за это время в проводнике.

374 Найти сопротивление R проводника…

В проводнике за время \(t = 10\) с при равномерном возрастании силы тока от \({I_1} = 1\) А до \({I_2} = 2\) А выдели­лось количество теплоты \(Q = 5\) кДж. Найти сопротив­ление \(R\) проводника.

375 Найти заряд проходящий через поперечное сечение проводника…

Сила тока в проводнике изменяется со временем по закону \(I = {I_0}\sin \omega t\). Найти заряд \(Q\), проходящий через поперечное сечение проводника за время \(t\), равное поло­вине периода \(T\), если начальная сила тока \({I_0} = 10\) А, цик­лическая частота \(\omega = 50\pi \) с-1.

376 Определить среднюю силу тока в проводнике…

За время \(t = 10\) с при равномерно возрастающей силе тока от нуля до некоторого максимума в проводнике выделилось количество теплоты \(Q = 40\) кДж.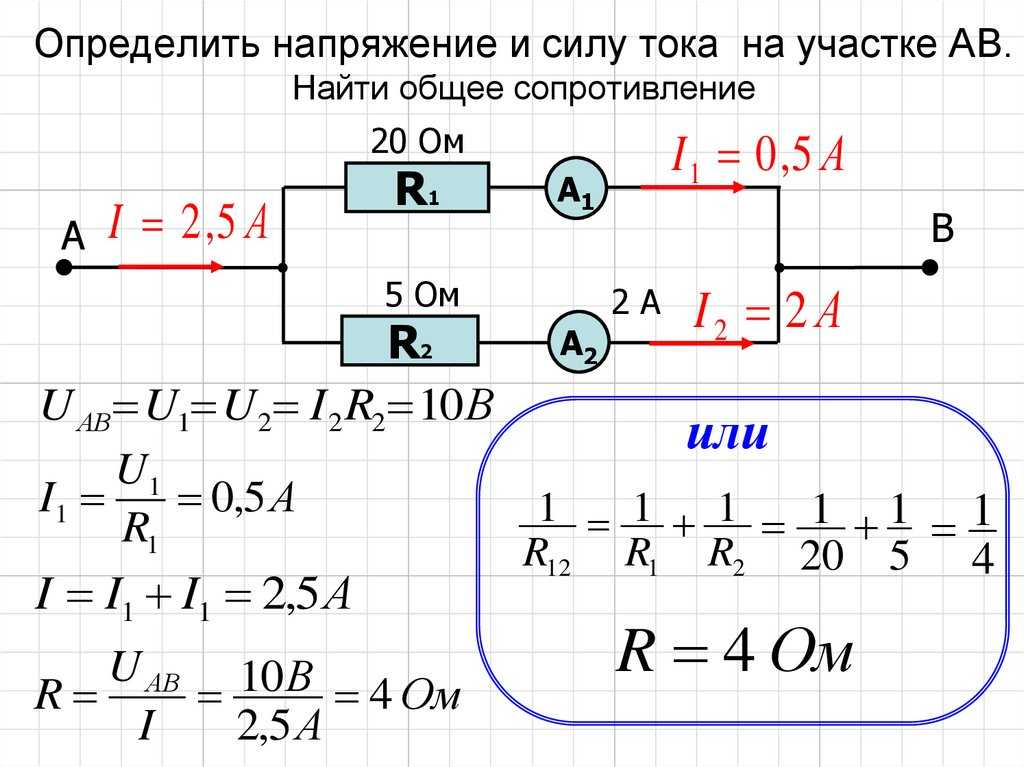 Определить среднюю силу тока \(\left\langle I \right\rangle \) в проводнике, если его сопро­тивление \(R = 25\) Ом.

377 Определить заряд проходящий в проводнике если сила тока…

За время \(t = 8\) с при равномерно возраставшей силе тока в проводнике сопротивлением \(R = 8\) Ом выде­лилось количество теплоты \(Q = 500\) Дж. Определить за­ряд \(q\), проходящий в проводнике, если сила тока в на­чальный момент времени равна нулю.

378 Определить количество теплоты Q выделившееся за время…

Определить количество теплоты \(Q\), выделившееся за время \(t = 10\) с в проводнике сопротивлением \(R = 10\) Ом, если сила тока в нем, равномерно уменьшаясь, изменилась от \({I_1} = 10\) А до \({I_2} = 0\).

379 Определить количество теплоты которое выделится в проводнике…

Сила тока в цепи изменяется по закону \(I = {I_0}\sin \omega t\). Определить количество теплоты, которое вы­делится в проводнике сопротивлением \(R = 10\) Ом за вре­мя, равное четверти периода (от \({t_1} = 0\) до \({t_2} = T/4\), где \(T = 10\) c). { — \alpha t}}\). Опреде­лить количество теплоты, которое выделится в проводнике сопротивлением \(R = 20\) Ом за время, в течение которого ток уменьшится в \(e\) раз.

401 Определить магнитную индукцию B в точке…

Бесконечно длинный провод с током \(I = 100\) А изогнут так, как это показано на рисунке. Определить магнитную индукцию \(B\) в точке \(O\). Радиус дуги \(R = 10\) см.

403 Определить магнитную индукцию в точке…

По двум скрещенным под прямым углом бесконечно длинным проводам текут токи \(I\) и \(2I\) (\(I = 100\) А). Определить магнитную индукцию \(B\) в точке \(A\). Расстояние \(d = 10\) см.

405 Определить магнитную индукцию B на оси кольца…

По тонкому кольцу радиусом \(R = 20\) см течет ток \(I = 100\) А. Определить магнитную индукцию \(B\) на оси кольца в точке \(A\). Угол \(\alpha = \pi /3\).

408 Определить магнитную индукцию в точке равноудаленной от точек кольца…

По тонкому кольцу течет ток \(I = 80\) А. Определить магнитную индукцию \(B\) в точке \(A\), равноудаленной от точек кольца на расстояние \(r = 10\) см.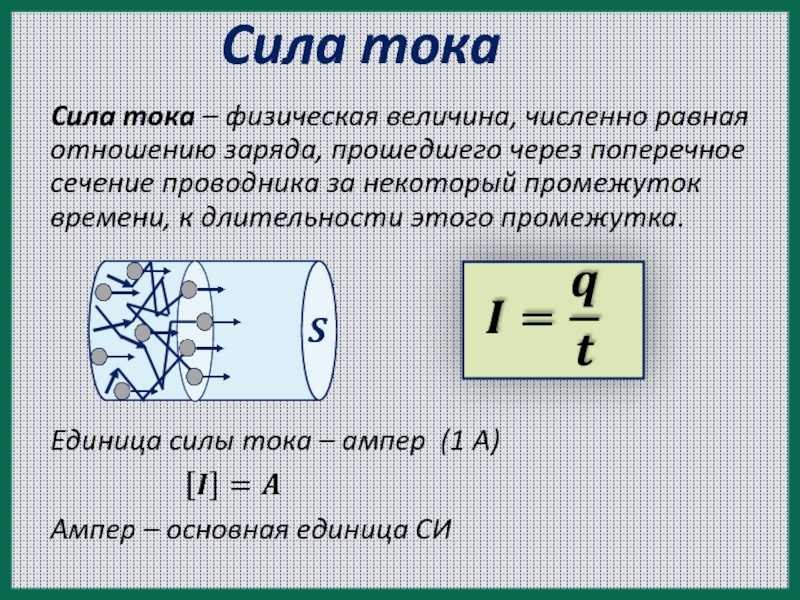 Угол \(\beta = \pi /6\).

409 Определить магнитную индукцию в точке равноудаленной от проводов на расстояние…

По двум бесконечно длинным, прямым параллельным проводам текут одинаковые токи \(I = 60\) А. Определить магнитную индукцию \(B\) в точке \(B\), равноудаленной от проводов на расстояние \(L = 10\) см. Угол \(\beta = \pi /3\).

410 Определить магнитную индукцию в точке лежащей на биссектрисе…

Бесконечно длинный провод с током \(I = 50\) А изогнут так, как это показано на рисунке. Определить магнитную индукцию \(B\) в точке \(A\), лежащей на биссектрисе прямого угла на расстоянии \(d = 10\) cм от его вер­шины.

Как найти силу в магнитном поле?

Статьи › Магнит › Сила Магнита в чем измеряется

Сила, действующая на проводник с током в магнитном поле, равна произведению модуля магнитной индукции, силы тока, длины проводника и синуса угла между вектором магнитной индукции и направлением тока: где α — угол между вектором B и направлением тока.

Сила, действующая на ток в магнитном поле, определяется по следующей формуле: q*|v|*|B|*sin a (произведение заряда магнитного поля, модули скорости этой же частицы, вектора индукции поля и синуса угла между их направлениями).

1. Как найти силу магнитного поля?
2. Какая сила В магнитном поле?
3. Как найти силу тока В магнитном поле?
4. Что такое F В магнитном поле?
5. В чем измеряется сила магнита?
6. Что такое сила тока формула?
7. Как рассчитать силу Ампера?
8. Чему равна работа В магнитном поле?
9. Что такое N В магнитном поле?
10. Как найти силу тока зная U и R?
11. Чему равно ню 0?
12. В чем измеряется B?
13. Как найти силу F В физике?
14. В чем измеряется сила?
15. Что такое H В магнитном поле?
16. Как можно найти силу тока?
17. Как определить магнитное поле?
18. Что такое B В физике?
19. Чему равно Q В силе Лоренца?
20. Какая сила действует на заряд В магнитном поле?
21. Как рассчитать силу Лоренца?
22. Как найти длину В силе Ампера?
23. Какие две силы действуют В магнитном поле?
24. Как найти ЭДС В магнитном поле?
25. Что означает буква R В физике?
26. Что означает буква H В физике?
27. Что означает буква W В физике?
28. Как найти силу тока через формулу энергии магнитного поля?
29. Как найти силу индукции магнитного поля?
30. Как найти силу тока В однородном магнитном поле?
31. Какая сила действует на ток В магнитном поле?
32. Чему равна сила действующая на проводник?
33. Что вращается В магнитном поле?
34. В чем измеряется Тесла?
35. Как найти работу магнитного поля?
36. Что означает буква N в физике?
37. Чему равно число е в физике?
38. Что означает буква Ф в физике?
39. Как найти силу магнитной индукции?
40. Как найти силу тока зная?

Как найти силу магнитного поля?

• Сила Ампера F = B·I·ℓ, где F — сила Ампера, Н В — индукция магнитного поля, Тл I — сила тока в проводнике, А ℓ — активная длина проводника, м Направление силы Ампера определяется по правилу «левой руки».
• 1) — + + +
• N. S. _ +
• + — + —
• ? — +
• N. S. I. B.
• 3)… I…
• N. + _ S.

Какая сила В магнитном поле?

Сила Ампера

Если металлический проводник с током поместить в магнитное поле, то на этот проводник со стороны магнитного поля будет действовать сила, которая называется силой Ампера.

Как найти силу тока В магнитном поле?

Fа = B * I * l * sinα, где Fа — действующая сила Ампера (Fа = 70 Н), B — значение индукции магнитного поля (B = 7 Тл), l — длина проводника (l = 25 см; 1 м = 100 см и 25 см = 0,25 м), так как угол между вектором магнитной индукции и направлением тока в проводнике не указан, считаем sinα = 1 (α = 90º).

Что такое F В магнитном поле?

Энергия магнитного поля

Где Ф — магнитный поток, I — ток, L — индуктивность катушки или витка с током.

В чем измеряется сила магнита?

Тесла — единица измерения индукции магнитного поля в СИ, численно равная индукции такого однородного магнитного поля, в котором на 1 метр длины прямого проводника, перпендикулярного вектору магнитной индукции, с током силой 1 ампер действует сила 1 ньютон.

Что такое сила тока формула?

Сила тока \(I\) — скалярная величина, равная отношению заряда \(q\), прошедшего через поперечное сечение проводника, к промежутку времени \(t\), в течение которого шёл ток. I = q t, где \(I\) — сила тока, \(q\) — заряд, \(t\) — время.

Как рассчитать силу Ампера?

Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником: F=B.I.ℓ. sin α — закон Ампера.

Чему равна работа В магнитном поле?

Таким образом,. Работа по перемещению замкнутого контура с током в МП равна произведению силы тока в контуре на приращение магнитного потока, сцепленного с контуром.

Что такое N В магнитном поле?

Индукция магнитного поля численно равна силе, с которой действует магнитное поле на единичный элемент тока (i*Dl = 1), расположенный перпендикулярно к направлению поля. Индукция магнитного поля — величина векторная.

Как найти силу тока зная U и R?

Сила тока на участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению участка цепи: I = U R, где I — сила тока, U — напряжение, R — сопротивление.

Чему равно ню 0?

В Международной системе единиц

С учётом определения ампера из этого соотношения следует точное равенство: μ0 = 4π · 10−7 Гн/м.

В чем измеряется B?

Единица магнитной индукции ($\overline{B}$) в международной системе единиц (СИ) называется тесла (Тл), по имени сербского ученого Н. Тесла, который успешно работал в области радиотехники и электроники.

Как найти силу F В физике?

Формула архимедовой силы:

Fa = ρ × g × V, где ρ — плотность жидкости, V — объем погруженной части тела, g — ускорение 9,8 м/с2.

В чем измеряется сила?

Ньютон.

Размерность силы

Единицей измерения в СИ является ньютон (русское обозначение: Н; международное: N), в системе СГС — дина (русское обозначение: дин, международное: dyn).

Что такое H В магнитном поле?

Электромагнитное поле характеризуется четырьмя векторными величинами (едини- цы измерения даны в системе СИ): B — вектор магнитной индукции (ед. измерения — Тл), • H — вектор напряженности магнитного поля (ед.

Как можно найти силу тока?

Через мощность и напряжение

В паспорте электроприбора обычно указывается его номинальная мощность и параметры электрической сети, для работы с которой он предназначен. Имея в распоряжении эти данные, можно вычислить силу тока по формуле: I = P/U. Данное выражение вытекает из формулы для расчета мощности: P = IU.

Как определить магнитное поле?

Обнаружить магнитное поле можно по действию на движущийся электрический заряд (или проводник с током) с некоторой силой; магнитное поле распространяется в пространстве с конечной скоростью, равной скорости света в вакууме.

Что такое B В физике?

Вектор магнитной индукции B является важнейшей характеристикой магнитного поля. Линии магнитной индукции — это линии, касательные к которым направлены так же, как и вектор В в данной точке.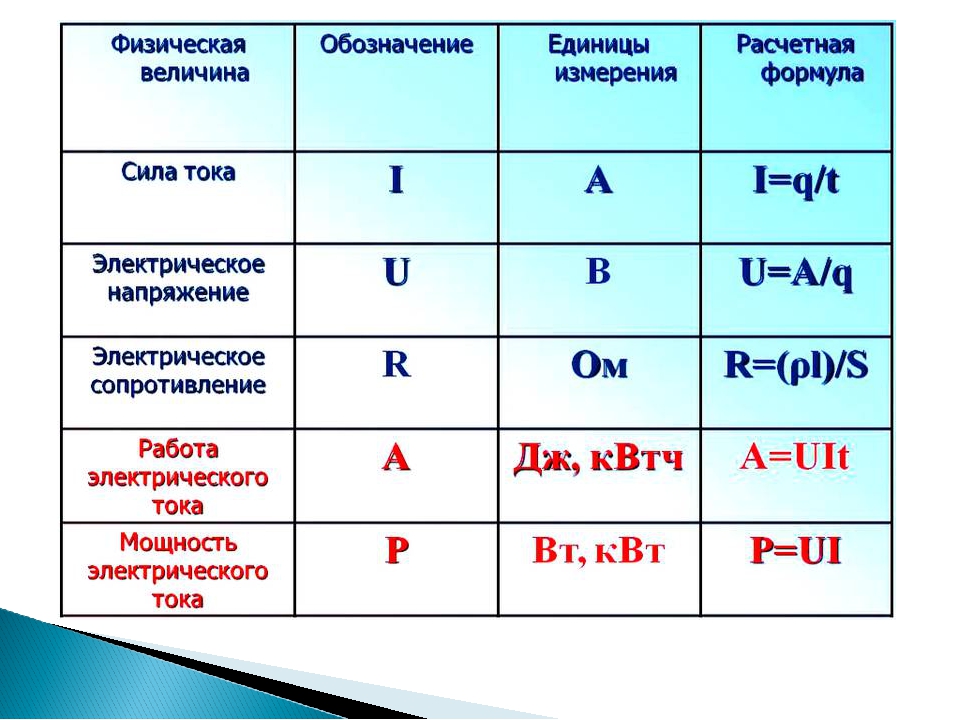 В отличие от силовых линий электростатического поля, линии магнитной индукции замкнуты. Магнитное поле является вихревым.

Чему равно Q В силе Лоренца?

Весьма нередко силой Лоренца называют лишь магнитную составляющую этого поля. Формула для определения: F = q(E+vB), где q — заряд частицы; Е — напряжённость электрического поля; B — магнитная индукция поля; v — скорость частицы.

Какая сила действует на заряд В магнитном поле?

Закон Ампера: на элемент dl проводника с током I действует сила Сила Лоренца действует на заряженные частицы, движущиеся в магнитном поле.

Как рассчитать силу Лоренца?

F = eE + . Здесь е — заряд частицы, Е — напряжённость электрического поля, В — магнитная индукция, u — скорость заряженной частицы относительно системы координат, в которой вычисляются величины F, Е, В, а с — скорость света в вакууме. Формула справедлива при любых значениях скорости заряженной частицы.

Как найти длину В силе Ампера?

На проводник с током в магнитном поле действует сила Ампера Fа, значение которой определяется формулой: Fа = I *B *L *sinα, где I — сила тока в проводнике, B — магнитная индукция магнитного поля, L — длина проводника, ∠α — угол между направлением тока и магнитной индукцией B. L = Fа /I *B *sinα.

Какие две силы действуют В магнитном поле?

Магнитная индукция. Силы Лоренца и Ампера Если заряд движется, то наряду с электрическим полем он создает еще одно поле — магнитное, которое действует на другие движущиеся заряды. В результате возникает дополнительное (наряду с кулоновским) взаимодействие движущихся электрических зарядов, которое называется магнитным.

Как найти ЭДС В магнитном поле?

Согласно закону электромагнитной индукции Фарадея, ЭДС прямо пропорциональна скорости изменения магнитного потока ΔФ: ЭДС = ΔФ / t. Магнитный поток Ф определяется формулой: Ф = B * S * cosα, где B — магнитная индукция, S — площадь контура, ∠α — угол между перпендикуляром к площади S и вектором магнитной индукции B.

Что означает буква R В физике?

R — в физике: обозначение электрического сопротивления.

Что означает буква H В физике?

H — постоянная Планка. ħ — редуцированная постоянная Планка (постоянная Дирака). h — гелион. Н — напряжённость магнитного поля.

Что означает буква W В физике?

W — обозначение ватта (единицы измерения мощности). W — один из вариантов обозначения механической работы в физике.

Как найти силу тока через формулу энергии магнитного поля?

Wм = L * I² / 2, где Wм — энергия магнитного поля (Wм = 6 Дж), L — индуктивность катушки (L = 3 Гн), I — сила тока в катушке (А). Выразим и рассчитаем силу тока в катушке: Wм = L * I² / 2.

Как найти силу индукции магнитного поля?

Индукция магнитного поля В на оси соленоида определяется формулой: В = μ0 * I * n / L, где μ0 — магнитная постоянная, I — сила тока в обмотке соленоида, n — количество витков соленоида, L — длина соленоида.

Как найти силу тока В однородном магнитном поле?

ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ СОЛЕНОИДА

Проверка справедливости формулы силы, действующей на проводник с током в однородном магнитном поле, — силы Ампера: F = I ·∙ l ·∙ B.

Какая сила действует на ток В магнитном поле?

Силу, действующую на проводник с током в магнитном поле, называют силой Ампера.

Чему равна сила действующая на проводник?

Для нахождения действующей на указанный проводник силы Ампера, воспользуемся формулой: Fa = B * I * l (sinα = 1, так как указанный проводник перпендикулярен линям магнитной индукции).

Что вращается В магнитном поле?

Обычно под вращающимся магнитным полем понимается магнитное поле, вектор магнитной индукции которого, не изменяясь по модулю, вращается с постоянной угловой скоростью.

В чем измеряется Тесла?

Тесла (единица измерения)

Тесла
Тл, T
Величина	индукция магнитного поля
Система	СИ
Тип	производная

Как найти работу магнитного поля?

Экспериментально выведена формула энергии магнитного поля катушки с током: E m = L I 2 2, где \(L\) — индуктивность катушки (Гн), \(I\) — сила тока в катушке (А). Энергия магнитного поля равна половине произведения индуктивности катушки на квадрат силы тока в ней. » («умножить на десять в степени») в записи вида «15e6».

Что означает буква Ф в физике?

В физике буквой F обозначают силу и оптический фокус. Также — постоянная Фарадея, свободная энергия Гельмгольца. На компьютерной клавиатуре: буквой F обозначены 12 функциональных клавиш.

Как найти силу магнитной индукции?

На проводник длиной L, по которому протекает ток с силой тока I, в магнитном поле индукцией В действует сила Ампера Fамп, значение которой определяется формулой: Fамп = I * B * L * sinα, где ∠α — угол между направлением тока в проводнике и вектором магнитной индукции В. В = Fамп / I * L * sinα.

Как найти силу тока зная?

Через мощность и напряжение

Имея в распоряжении эти данные, можно вычислить силу тока по формуле: I = P/U. Данное выражение вытекает из формулы для расчета мощности: P = IU.

Видео с вопросами

: Расчет силы тока в прямом проводе с учетом напряженности магнитного поля

Прямой провод в электрической цепи несет постоянный ток 𝐼 А. Результирующее магнитное поле на перпендикулярном расстоянии 18 мм от этого провода измеряется как 1,2 × 10⁻⁴ Тл. Рассчитайте 𝐼 с точностью до ампера. Используйте 4𝜋 × 10⁻⁷ Т⋅м/А для значения 𝜇₀.

Стенограмма видео

Прямой провод в электрической цепи несет постоянный ток 𝐼 ампер. Результирующее магнитное поле на перпендикулярном расстоянии 18 миллиметров от этого провода измеряется как 1,2, умноженное на 10 с отрицательными четырьмя теслами. Рассчитайте 𝐼 с точностью до ампера. Используйте четыре 𝜋, умноженные на 10, с отрицательными семью тесла-метрами на ампер для значения 𝜇 ноль.

Начнем с рисования схемы. Вот участок провода, по которому, как мы знаем, проходит ток 𝐼 ампер. Это создает магнитное поле с напряженностью 𝐵, измеренной на перпендикулярном расстоянии 𝑑 от провода. В этом вопросе магнитное поле измерялось на расстоянии 18 миллиметров от провода. Так что это наша ценность 𝑑. Мы также знаем, что сила магнитного поля 𝐵 измеряется как 1,2 умножить на 10 в минус четыре тесла.

Конечно, мы еще не знаем значения тока в проводе, но можем вспомнить формулу, связывающую 𝐼 с уже известными нам значениями. Это формула для силы магнитного поля, создаваемого током в прямом проводе, которая гласит: 𝐵 равно 𝜇 нулю, умноженному на 𝐼, деленное на два 𝜋𝑑.

Мы можем использовать эту формулу для определения значения тока в проводе. Но сначала нам нужно переставить его, чтобы сделать 𝐼 предметом. Начнем с копирования формулы. А затем мы умножим обе части на два 𝜋𝑑, деленное на 𝜇 ноль, чтобы все эти члены могли сократиться в правой части выражения, оставив 𝐼 отдельно. Теперь, перевернув это в другую сторону и написав немного более аккуратно, мы имеем 𝐼 равно двум 𝜋, умноженным на 𝑑, умноженным на 𝐵, деленным на 𝜇 ноль. И поскольку нам уже сказали значение 𝜇 равно нулю, а также 𝑑 и 𝐵, давайте продолжим и подставим их в уравнение.

Хорошо, у нас все подключено. Но прежде чем мы будем считать, давайте подумаем о единицах измерения. Обратите внимание, что значения для 𝜇 ноль и 𝐵 полностью выражены в основных единицах СИ, но значение расстояния указано в миллиметрах. Итак, давайте конвертируем его в простые метры. Для этого следует вспомнить, что приставка милли- означает 10 в отрицательной тройке. Таким образом, мы можем по существу отменить этот префикс, переместив десятичную точку значения миллиметра на три позиции влево. Таким образом, 18 миллиметров становятся 0,018 метра.

Теперь легче увидеть, что метры и тесла в числителе сокращаются с метрами и теслами в знаменателе, так что единственной единицей, связанной с этим выражением, является обратный ампер в знаменателе или просто ампер в числителе, т.е. хороший знак, потому что, в конце концов, мы ищем значение тока.

Наконец, давайте подключим это к калькулятору и получим результат 10,8 ампер. Теперь округлив до ближайшего целого числа, мы нашли, что сила тока в проводе составляет 11 ампер. Чтобы получить окончательный ответ на этот вопрос, вспомним, что нам сказали, что по проводу течет ток 𝐼 ампер. Мы должны быть осторожны, чтобы не спутать это 𝐼 с 𝐼, с которым мы столкнулись в формуле для магнитного поля.

Целью этого вопроса было вычислить 𝐼. Но важно понимать, что здесь 𝐼 выступает в качестве заполнителя числа в значении 𝐼 ампер. Так как мы обнаружили, что 𝐼 ампер составляет 11 ампер, мы обнаружили, что 𝐼 равно 11. Это наш окончательный ответ.

Как рассчитать и решить напряженность магнитного поля | Магнитные свойства

Сила магнитного поля показана на изображении ниже.

Для расчета напряженности магнитного поля необходимы три основных параметра, а именно: Количество катушек, расположенных близко друг к другу (N), Величина тока (I) и Длина катушки (L).

Формула для расчета напряженности магнитного поля:

H =  ^NI / _L

Где:

H = напряженность магнитного поля
N = количество катушек, расположенных близко друг к другу
I = величина тока
L = длина катушки

3 данный пример 900;
Найдите напряженность магнитного поля, если количество катушек, расположенных близко друг к другу, равно 4, сила тока равна 8, а длина катушки равна 10.

Отсюда следует, что;

N = количество катушек, расположенных близко друг к другу = 4
I = величина тока = 8
L = Length of Coil = 10

H =  ^NI / _L
H =  ⁽⁴⁾⁽⁸⁾ / ₁₀
H =  ³² / ₁₀
H = 3.2

Следовательно, напряженность магнитного поля составляет 3,2 А/м.

Расчет количества катушек, расположенных близко друг к другу, когда известны напряженность магнитного поля, величина тока и длина катушки.

N = ^HL / _I

Где:

N = количество катушек, расположенных близко друг к другу
H = напряженность магнитного поля
I = величина тока
L = длина катушки

Давайте решим пример;
Найдите количество катушек, расположенных близко друг к другу, когда напряженность магнитного поля равна 10, величина тока равна 5, а длина катушки равна 2.

Отсюда следует, что;

H = напряженность магнитного поля = 10
I = величина тока = 5
L = длина катушки = 2

n = ^HL / _I

n = ^{(10) (2)} / ₅
n = ²⁰ / ₅
n = 4

. С. близко друг к другу равно 4.

Вычисление величины тока, когда известны напряженность магнитного поля, количество катушек, расположенных близко друг к другу, и длина катушки.

I = ^HL / _N

Где:

I = величина тока
H = напряженность магнитного поля
N = количество катушек, расположенных близко друг к другу
L = длина катушки

Давайте решим пример;
Найдите величину тока, когда напряженность магнитного поля равна 18, количество катушек, расположенных близко друг к другу, равно 12, а длина катушки равна 14.

Отсюда следует, что;

H = напряженность магнитного поля = 18
N = количество катушек, расположенных близко друг к другу = 12
L = длина катушки = 14

I = ^HL / _N
I = ^{(18) (14)} / ₁₂
I = ²⁵² / ₁₂
I = 21

. Следовательно, Matderting Magnity . is  21.

Расчет длины катушки при заданной напряженности магнитного поля, количестве катушек, расположенных близко друг к другу, и величине тока.

L = ^NI / _H

Где:

L = длина катушки
H = напряженность магнитного поля
N = количество катушек, расположенных близко друг к другу
I = величина тока

Давайте решим пример;
Найдите длину катушки, если напряженность магнитного поля равна 5, количество катушек, расположенных близко друг к другу, равно 12, а сила тока равна 10.

Отсюда следует, что;

H = напряженность магнитного поля = 5
N = количество катушек, расположенных близко друг к другу = 12
I = величина тока = 10

L = ^Ni / _H
L = ^{(12) (10)} / ₅
L = ¹²⁰ / ₅
L = 24

С. 24.

Калькулятор Nickzom –  Энциклопедия калькулятора способна рассчитать напряженность магнитного поля.

Чтобы получить ответ и вычислить напряженность магнитного поля, используйте калькулятор Nickzom – The Calculator Encyclopedia. Во-первых, вам нужно получить приложение.

Вы можете получить это приложение любым из следующих способов:

Интернет  – https://www.nickzom.org/calculator-plus

Чтобы получить доступ к профессиональной версии через Интернет, вам необходимо  зарегистрируйтесь и подпишитесь , чтобы иметь полный доступ ко всем функциям.
Вы также можете попробовать демо-версию через https://www.nickzom.org/calculator

Android (платная)  – https://play.google.com/store/apps/details?id=org .nickzom.nickzomcalculator
Android (бесплатно)  – https://play. google.com/store/apps/details?id=com.nickzom.nickzomcalculator

Apple (платно)  – https://itunes.apple.com/ us/app/nickzom-calculator/id1331162702?mt=8
После того, как вы получили приложение энциклопедии калькулятора, перейдите к карте калькулятора , , затем нажмите Materials and Metallurgical в разделе Engineering .

Теперь нажмите на Магнитные свойства Под Материалами и металлургическим

Теперь нажмите на Magnetic Field Pellow под Магнитная собственность

. напряженность магнитного поля в соответствии с соответствующим параметром, который представляет собой Количество катушек, расположенных близко друг к другу (N), Величина тока (I) и Длина катушки (L).

Теперь введите соответствующие значения для параметров в соответствии с требованиями Количество витков, расположенных близко друг к другу (N)  –  4 Длина катушки (L) составляет 10 .