Как найти силу тока в цепи — Инженерные технологии Коломна

Одной из основных характеристик электрической цепи является сила тока. Она измеряется в амперах и определяет нагрузку на токопроводящие провода, шины или дорожки плат. Эта величина отражает количество электричества, которое протекло в проводнике за единицу времени. Определить её можно несколькими способами в зависимости от известных вам данных. Соответственно студенты и начинающие электрики из-за этого часто сталкиваются с проблемами при решении учебных заданий или практических ситуаций. В этой статье мы и расскажем, как найти силу тока через мощность и напряжение или сопротивление.

Если известна мощность и напряжение

Допустим вам нужно найти силу тока в цепи, при этом вам известны только напряжение и потребляемая мощность. Тогда чтобы её определить без сопротивления воспользуйтесь формулой:

P=UI

После несложных мы получаем формулу для вычислений

I=P/U

Следует отметить, что такое выражение справедливо для цепей постоянного тока. Но при расчётах, например, для электродвигателя учитывают его полную мощность или косинус Фи. Тогда для трёхфазного двигателя его можно рассчитать так:

Находим P с учетом КПД, обычно он лежит в пределах 0,75-0,88:

Р1 = Р2/η

Здесь P2 – активная полезная мощность на валу, η – КПД, оба этих параметра обычно указывают на шильдике.

Находим полную мощность с учетом cosФ (он также указывается на шильдике):

S = P1/cosφ

Определяем потребляемый ток по формуле:

Iном = S/(1,73·U)

Здесь 1,73 – корень из 3 (используется для расчетов трёхфазной цепи), U – напряжение, зависит от включения двигателя (треугольник или звезда) и количества вольт в сети (220, 380, 660 и т.д.). Хотя в нашей стране чаще всего встречается 380В.

Если известно напряжение или мощность и сопротивление

Но встречаются задачи, когда вам известно напряжение на участке цепи и величина нагрузки, тогда чтобы найти силу тока без мощности воспользуйтесь законом Ома, с его помощью проводим расчёт силы тока через сопротивление и напряжение.

I=U/R

Но иногда случается так, что нужно определить силу тока без напряжения, то есть когда вам известна только мощность цепи и её сопротивление. В этом случае:

P=UI

При этом согласно тому же закону Ома:

U=IR

То:

 P=I2*R

Значит расчёт проводим по формуле:

I2=P/R

Или возьмем выражение в правой части выражения под корень:

I=(P/R)1/2

Если известно ЭДС, внутреннее сопротивление и нагрузка

Ко студенческим задачам с подвохом можно отнести случаи, когда вам дают величину ЭДС и внутреннее сопротивление источника питания. В этом случае вы можете определить силу тока в схеме по закону Ома для полной цепи:

I=E/(R+r)

Здесь E – ЭДС, r – внутреннее сопротивление источника питания, R – нагрузки.

Закон Джоуля-Ленца

Еще одним заданием, которое может ввести в ступор даже более-менее опытного студента – это определить силу тока, если известно время, сопротивление и количество выделенного тепла проводником. Для этого вспомним закон Джоуля-Ленца.

Его формула выглядит так:

Q=I2Rt

Тогда расчет проводите так:

I2=QRt

Или внесите правую часть уравнения под корень:

I=(Q/Rt)1/2

Несколько примеров

В качестве заключения предлагаем закрепить полученную информацию на нескольких примерах задач, в которых нужно найти силу тока.

1 задача: Рассчитать I в цепи из двух резисторов при последовательном соединении и при параллельном соединении. R резисторов 1 и 2 Ома, источник питания на 12 Вольт.

Из условия ясно, что нужно привести два варианта ответа для каждого из вариантов соединений. Тогда чтобы найти ток при последовательном соединении, сначала складывают сопротивления схемы, чтобы получить общее.

R1+R2=1+2=3 Ома

Тогда рассчитать силу тока можно по закону Ома:

I=U/R=12/3=4 Ампера

При параллельном соединении двух элементов Rобщее можно рассчитать так:

Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67

Тогда дальнейшие вычисления можно проводить так:

I=12*0,67=18А

2 задача: рассчитать ток при смешанном соединении элементов.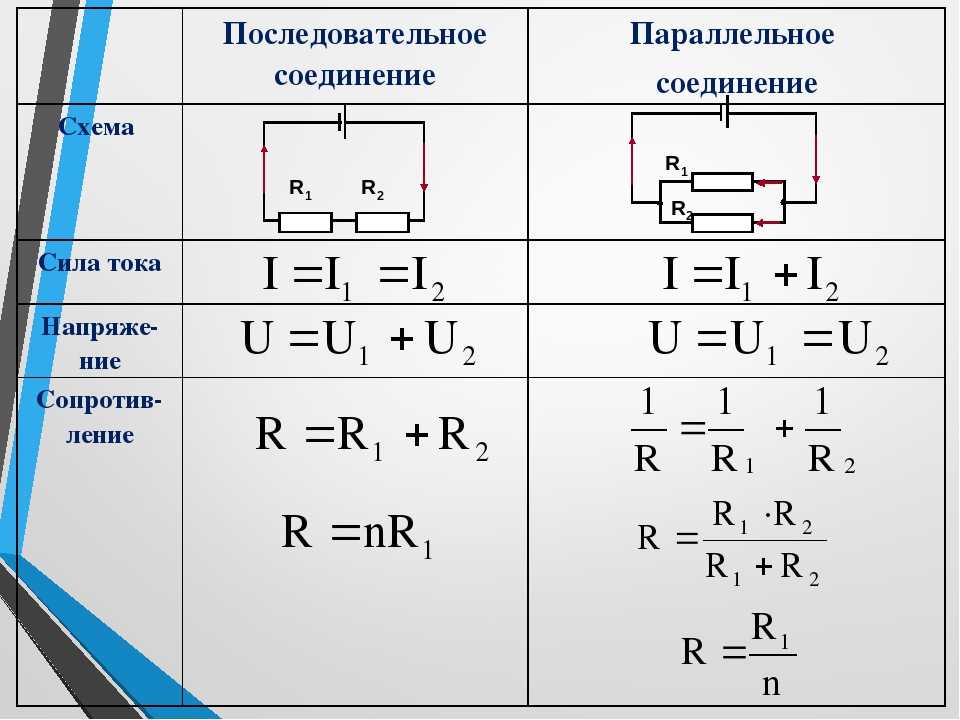 На выходе источника питания 24В, а резисторы на: R1=1 Ом, R2=3 Ома, R3=3 Ома.

В первую очередь нужно найти R общее параллельно соединенных R2 и R3, по той же формуле, что мы использовали выше.

Rприв=(R2*R3)/(R2+R3)=(3*3)|(3+3)=9/6=3/2=1,5 Ома

Теперь схема примет вид:

Далее находим ток по тому же закону Ома:

I=U/(R1+Rприв)=24/(1+1,5)=24/2,5=9,6 Ампер

Теперь вы знаете, как найти силу тока, зная мощность, сопротивление и напряжение. Надеемся, предоставленные формулы и примеры расчетов помогли вам усвоить материал!

Наверняка вы не знаете:

Источник

советов по поиску тока в цепи | Блог Advanced PCB Design

 

 

Одна из моих предыдущих поездок за границу едва не закончилась катастрофой. Как дотошный человек, я всегда держал свой паспорт рядом с собой. Прежде чем вы зададитесь вопросом, нет, я потерял не паспорт, а квитанцию ​​о прибытии, которую я должен был вернуть в иммиграционную службу перед посадкой на рейс.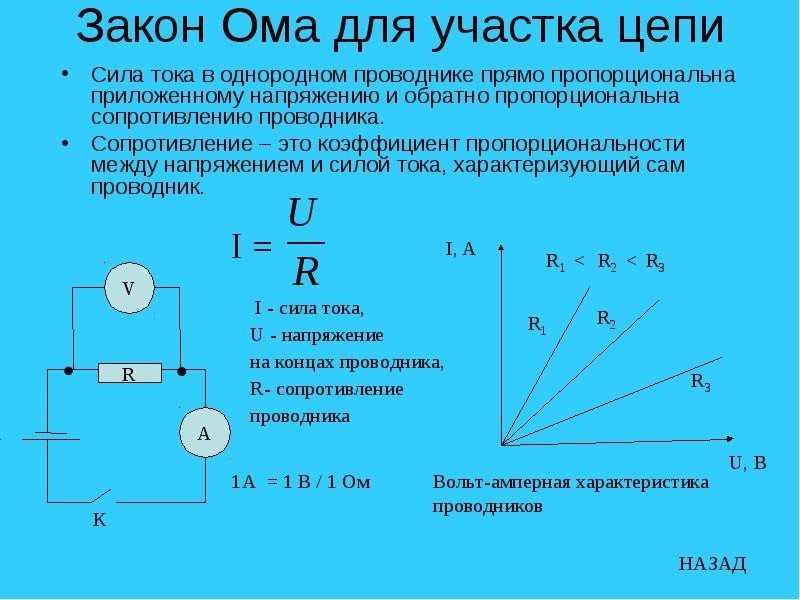

Мне потребовалось 30 минут лихорадочных поисков, прежде чем я нашел листок в куче квитанций. Я понятия не имею, как это закончилось среди квитанций, и как я закончил тем, что потратил почти все свои деньги, что привело к этой толстой стопке квитанций.

К счастью, мне не пришлось проходить многочасовые допросы в иммиграционном отделе. Точно так же у вас могут возникнуть различные проблемы, если вы забудете рассчитать ток в своей цепи, особенно когда это имеет решающее значение для функциональности конструкции.

Нельзя обсуждать расчет силы тока, не упомянув самые основные законы электроники: закон Ома. Закон Ома обозначает соотношение между напряжением, током и сопротивлением. Вы должны быть знакомы с уравнением V = IR.

Из уравнения можно легко получить значение тока, разделив напряжение на сопротивление или: 

I = V/R.

Это базовая электроника, которую вы должны знать еще до того, как начнете чертить схему. Расчет выглядит простым, когда у вас есть простая схема с одним элементом напряжения и резистором. В более сложной схеме, где у вас есть набор последовательных и параллельных конфигураций, вам необходимо проанализировать схему между узлами.

Расчет делителя напряжения будет полезен при определении напряжения, которое падает между двумя узлами. Это также помогает понять, что электрический ток разделяется на разные ветви в зависимости от сопротивления отдельной ветви.

Расчет тока для конденсатора и катушки индуктивности

Как бы ни был полезен закон Ома, он применим только к резистивным нагрузкам в цепи. Если у вас есть конденсатор и катушка индуктивности, вам нужно будет по-другому подойти к анализу схемы. В цепи постоянного тока, где источником напряжения является сигнал постоянного тока, применяются следующие правила:

Однако приведенные выше допущения перестают быть верными, когда сигналы переменного тока подаются на конденсаторы и катушки индуктивности.

Ток, протекающий через конденсатор от синусоидального напряжения, накапливается в виде заряда и определяется по следующей формуле:

I = C (dv/dt)

Из уравнения видно, что конденсатор проходит непрерывную серию зарядов и разрядов при подаче переменного напряжения.

 

Конденсаторы ведут себя по-разному при анализе постоянного и переменного тока.

 

Что касается катушки индуктивности, расчет несколько сложнее из-за характеристики компонента. Катушки индуктивности создают силу, противодействующую протекающему через них току, и ток рассчитывается по формуле:

I = 1/L ∫vdt

При построении графиков зависимости тока от напряжения для конденсаторов и катушек индуктивности вы заметите, что оба параметра не совпадают по фазе на 90 градусов.

Определение тока для нелинейных цепей

Было бы ошибкой упускать из виду расчет тока для нелинейных компонентов.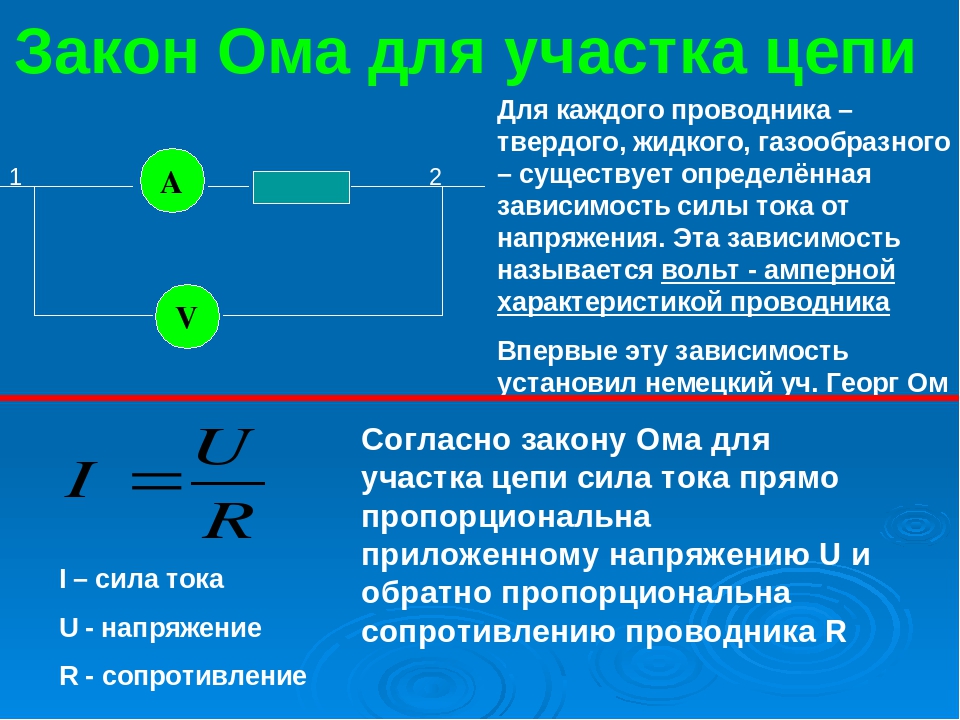

Резисторы, конденсаторы и катушки индуктивности являются линейными компонентами, что означает, что результирующий ток пропорционален приложенному напряжению.

Нелинейные компоненты имеют непропорциональную ВАХ, в которой нельзя определить значение тока по одной формуле. Например, диод является нелинейным компонентом, поскольку через него проходит очень небольшой ток, когда напряжение на нем меньше, чем его прямое напряжение (Vf). Когда напряжение превышает Vf, прямой ток резко возрастает и ограничивается только максимальным пределом компонента.

 

Диоды представляют собой нелинейные компоненты, в которых ток не пропорционален приложенному напряжению.

 

Транзисторы, варисторы и стабилитроны являются некоторыми примерами нелинейных компонентов. Когда эти компоненты помещаются в цепь, вам необходимо учитывать, как нелинейная кривая ВАХ повлияет на протекание тока к другим компонентам.

Важно знать силу тока, протекающего в цепи, если вы работаете с печатной платой. Величина тока будет определять толщину и ширину дорожки печатной платы. Это очень важно, когда вы имеете дело с мощными конструкциями.

Работа с набором инструментов компоновки и опций анализа от Cadence поможет решить любую из ваших текущих задач проектирования на одном дыхании. Однако расчет тока вручную может быть утомительным, и даже опытные проектировщики допускают ошибки. Поэтому полезно, если вы используете программное обеспечение для печатных плат, такое как OrCAD PCB Designer, которое оснащено симулятором SPICE. Проверка расчетов сведет к минимуму ошибки.

Если вы хотите узнать больше о том, какое решение у Cadence есть для вас, обратитесь к нам и нашей команде экспертов.

Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты.

Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.

Подпишитесь на Linkedin Посетить сайт Больше контента от Cadence PCB Solutions

УЧИТЬ БОЛЬШЕ 9Цепи постоянного тока серии 0000 — цепи постоянного тока

Цепи постоянного тока

Цепь серии определяется как цепь, содержащая только один путь для текущего потока. Чтобы сравнить базовую схему и более сложная последовательная цепь, на рисунке ниже показаны две цепи. Основная схема имеет только одна лампа, а в последовательной цепи три лампы соединены последовательно.

Сравнение основных и последовательных схем.

Сопротивление в последовательной цепи

Ссылаясь на рисунок выше, ток в последовательной цепи должен протекать через каждая лампа для завершения электрического пути в цепи. Каждая дополнительная лампа оказывает дополнительное сопротивление. В последовательной цепи

полное сопротивление цепи R _t равно сумме индивидуальные сопротивления .

В виде уравнения:

Примечание. Нижний индекс n обозначает любое количество дополнительных сопротивлений, может быть в уравнении.

Пример: На рисунке ниже показана последовательная цепь, состоящая из трех резисторов: показаны один из 10 Ом, один из 15 Ом и один из 30 Ом. Источник напряжения дает 110 В. Чему равно полное сопротивление?

Нахождение полного сопротивления в последовательной цепи.

Дано:
R ₁ = 10 Ом, R ₂ = 15 Ом, R

₃ = 30 Ом

Решение:

В некоторых схемах общее сопротивление известно, а значение необходимо определить один из резисторов цепи. Уравнение R _t = R ₁ + R ₂ + R ₃ можно транспонировать, чтобы найти значение неизвестного сопротивления.

Пример:
На рисунке ниже полное сопротивление цепи с тремя резисторами составляет 40 Ом. Два резистора цепи 10 Ом каждый. Рассчитайте значение третьего резистора ( R ₃ ).

Расчет значения одного сопротивления в последовательной цепи.

Дано:
R _t = 40 Ом, R ₁ = 10 Ом, R ₂ = 10 Ом, Ч ₃ = ?

Решение:

Вычитание ( R ₁ + R ₂ ) с обеих сторон уравнение

Ток в последовательной цепи

Так как в последовательной цепи ток проходит только один путь, то один и тот же ток должен протекать через каждый компонент цепи. Чтобы определить ток в последовательной цепи, только ток через один из компоненты должны быть известны.

Тот факт, что один и тот же ток протекает через каждый компонент серии цепь можно проверить, вставив счетчики в цепь в различных точках, как показано на рисунке ниже.

Если бы это было сделано, каждый метр окажется, что они указывают на одно и то же значение тока.

Ток в последовательной цепи.

Напряжение в последовательной цепи

Падение напряжения на резисторе в цепи, состоящей из одного резистор и источник напряжения — это общее напряжение в цепи, равное равно приложенному напряжению. Полное напряжение в последовательной цепи, которое состоит из более чем одного резистора и равно приложенному напряжению, но состоит из суммы падений напряжения на отдельных резисторах. В любой серии цепи сумма падений напряжения на резисторе должна равняться напряжению источника. Это утверждение может быть подтверждено исследованием схемы, показанной на рис. рисунок ниже.

Расчет отдельных падений напряжения в последовательной цепи.

В этой цепи сброшен потенциал источника ( В _t ) 20 В. через последовательную цепь, состоящую из двух резисторов по 5 Ом. Общая сопротивление цепи ( R _t ) равно сумме два отдельных сопротивления или 10 Ом.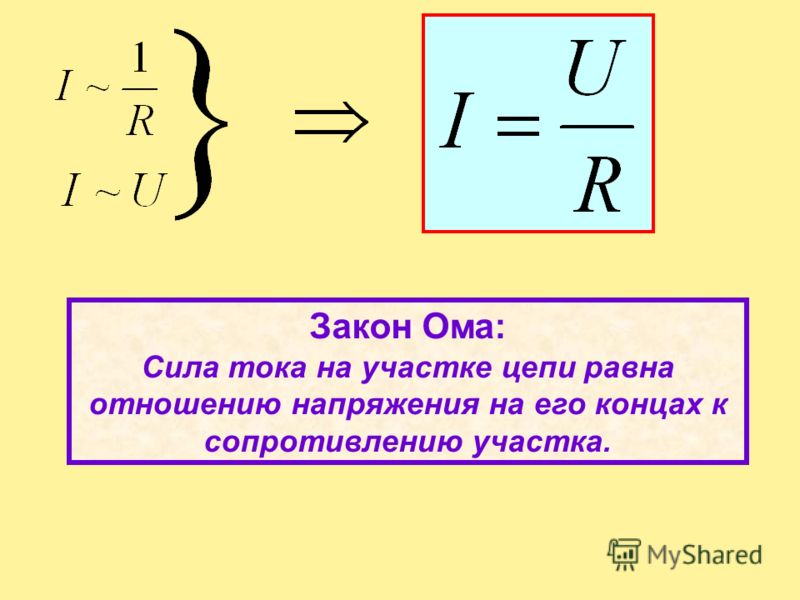 По закону Ома схема ток можно рассчитать следующим образом:

Дано: В _t = 20 В, R _t = 10 Ом
Решение:

Поскольку известно, что номинал резисторов равен 5 Ом каждый, а ток через резисторы равен 2 А, напряжение на них падает резисторы можно рассчитать. Напряжение ( В ₁ ) через R ₁ поэтому:

Дано: I ₁ = 2 А, R ₁ = 5 Ом
Решение:

Осмотрев схему, можно увидеть, что R ₂ то же омическое значение как R ₁ и несет такой же ток. Напряжение падение на R ₂ поэтому также равно 10 В. Сложение этих двух 10-вольтовых падений вместе дает общее падение 20 В, точно равно приложенному напряжению. Тогда для последовательной цепи:

Пример: Последовательная цепь состоит из трех резисторов со значениями 20 Ом, 30 Ом и 50 Ом соответственно. Найдите прикладной напряжение, если ток через резистор 30 Ом равен 2 А.

Для решения задачи сначала рисуется и маркируется принципиальная схема (рисунок ниже).

Решение для приложенного напряжения в последовательной цепи.

Дано: R ₁ = 20 Ом, R ₂ = 30 Ом, R ₃ = 50 Ом, I = 2 А

Решение: поскольку задействованная цепь представляет собой последовательную цепь, те же 2 А ток течет через каждый резистор. По закону Ома напряжение падает на каждый из трех резисторов может быть рассчитан и составляет:

Когда известны отдельные капли, их можно сложить, чтобы найти общее количество. или приложенное напряжение:

Примечание: Когда вы используете закон Ома, количество для уравнения должно быть взято из той же части схемы . В приведенном выше примере напряжение на R ₂ было рассчитано с использованием тока через р ₂ и сопротивление р ₂ .