10.Электрический ток — MAPHY.COM

Электрический ток. Сила тока. Сопротивление

В проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов, хотя в большинстве случае движутся электроны – отрицательно заряженные частицы.

Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда q, переносимого через поперечное сечение проводника за интервал времени t, к этому интервалу времени:

Если ток не постоянный, то для нахождения количества прошедшего через проводник заряда рассчитывают площадь фигуры под графиком зависимости силы тока от времени.

Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Сила тока измеряется амперметром, который включается в цепь последовательно. В Международной системе единиц СИ сила тока измеряется в амперах [А]. 1 А = 1 Кл/с.

Средняя сила тока находится как отношение всего заряда ко всему времени (т.е. по тому же принципу, что и средняя скорость или любая другая средняя величина в физике):

Если же ток равномерно меняется с течением времени от значения I1 до значения I2, то можно значение среднего тока можно найти как среднеарифметическое крайних значений:

Плотность тока – сила тока, приходящаяся на единицу поперечного сечения проводника, рассчитывается по формуле:

При прохождении тока по проводнику ток испытывает сопротивление со стороны проводника. Причина сопротивления – взаимодействие зарядов с атомами вещества проводника и между собой. Единица измерения сопротивления 1 Ом. Сопротивление проводника R определяется по формуле:

где: l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника (будьте внимательны и не перепутайте последнюю величину с плотностью вещества), которое характеризует способность материала проводника противодействовать прохождению тока. То есть это такая же характеристика вещества, как и многие другие: удельная теплоемкость, плотность, температура плавления и т.д. Единица измерения удельного сопротивления 1 Ом·м. Удельное сопротивление вещества – табличная величина.

Сопротивление проводника зависит и от его температуры:

где: R0 – сопротивление проводника при 0°С, t – температура, выраженная в градусах Цельсия, α – температурный коэффициент сопротивления. Он равен относительному изменению сопротивления, при увеличении температуры на 1°С. Для металлов он всегда больше нуля, для электролитов наоборот, всегда меньше нуля.

Диод в цепи постоянного тока

Диод – это нелинейный элемент цепи, сопротивление которого зависит от направления протекания тока. Обозначается диод следующим образом:

Стрелка в схематическом обозначении диода показывает, в каком направлении он пропускает ток. В этом случае его сопротивление равно нулю, и диод можно заменить просто на проводник с нулевым сопротивлением. Если ток течет через диод в противоположном направлении, то диод обладает бесконечно большим сопротивлением, то есть не пропускает ток совсем, и является разрывом в цепи. Тогда участок цепи с диодом можно просто вычеркнуть, так как ток по нему не идет.

 

Закон Ома. Последовательное и параллельное соединение проводников

Немецкий физик Г.Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (то есть проводнику, в котором не действуют сторонние силы) сопротивлением R, пропорциональна напряжению U на концах проводника:

Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Это соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.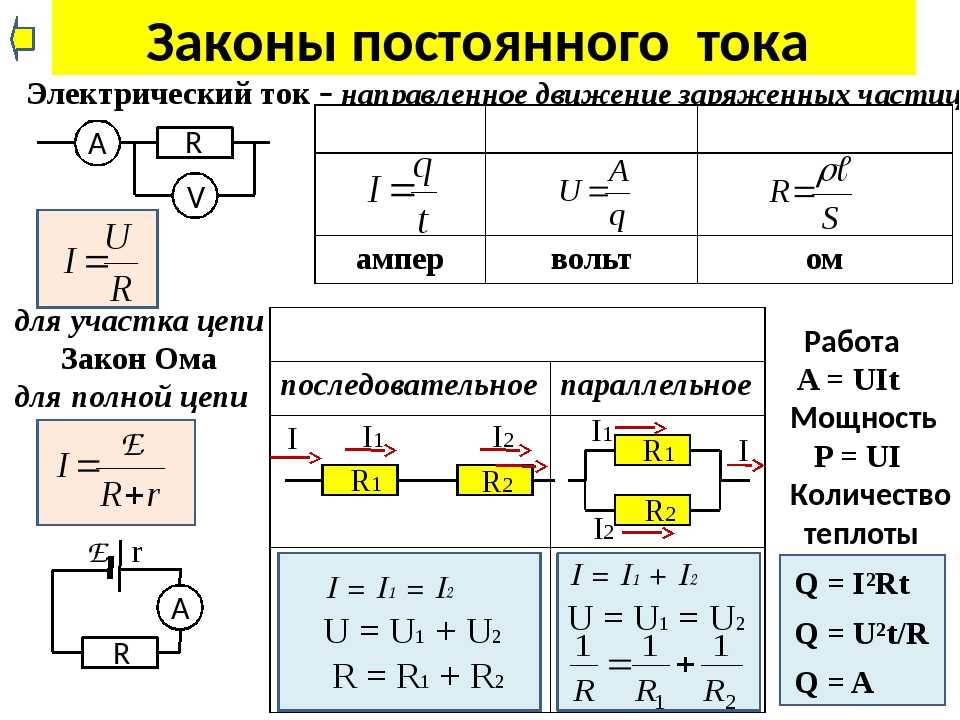

Проводники, подчиняющиеся закону Ома, называются линейными. Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками, сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при достаточно больших токах наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.

Проводники в электрических цепях можно соединять двумя способами: последовательно и параллельно. У каждого способа есть свои закономерности.

1. Закономерности последовательного соединения:

Формула для общего сопротивления последовательно соединенных резисторов справедлива для любого числа проводников. Если же в цепь последовательно включено n одинаковых сопротивлений R, то общее сопротивление R0 находится по формуле:

2. Закономерности параллельного соединения:

Формула для общего сопротивления параллельно соединенных резисторов справедлива для любого числа проводников. Если же в цепь параллельно включено n одинаковых сопротивлений R, то общее сопротивление R0находится по формуле:

Электроизмерительные приборы

Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры.

Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением RB. Для того чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен.

Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением RA. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи.

 

ЭДС. Закон Ома для полной цепи

Для существования постоянного тока необходимо наличие в электрической замкнутой цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.

Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.

При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу. Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):

Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).

Закон Ома для полной (замкнутой) цепи: сила тока в замкнутой цепи равна электродвижущей силе источника, деленной на общее (внутреннее + внешнее) сопротивление цепи:

Сопротивление r – внутреннее (собственное) сопротивление источника тока (зависит от внутреннего строения источника). Сопротивление R – сопротивление нагрузки (внешнее сопротивление цепи).

Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):

Важно понять и запомнить: ЭДС и внутреннее сопротивление источника тока не меняются, при подключении разных нагрузок.

Если сопротивление нагрузки равно нулю (источник замыкается сам на себя) или много меньше сопротивления источника, то тогда в цепи потечет ток короткого замыкания:

Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой ε и внутренним сопротивлением r. У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик, и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.

Несколько источников ЭДС в цепи

Если в цепи присутствует несколько ЭДС подключенных последовательно, то:

1. При правильном (положительный полюс одного источника присоединяется к отрицательному другого) подключении источников общее ЭДС всех источников и их внутреннее сопротивление может быть найдено по формулам:

Например, такое подключение источников осуществляется в пультах дистанционного управления, фотоаппаратах и других бытовых приборах, работающих от нескольких батареек.

2. При неправильном (источники соединяются одинаковыми полюсами) подключении источников их общее ЭДС и сопротивление рассчитывается по формулам:

В обоих случаях общее сопротивление источников увеличивается.

При параллельном подключении имеет смысл соединять источники только c одинаковой ЭДС, иначе источники будут разряжаться друг на друга. Таким образом суммарное ЭДС будет таким же, как и ЭДС каждого источника, то есть при параллельном соединении мы не получим батарею с большим ЭДС. При этом уменьшается внутреннее сопротивление батареи источников, что позволяет получать большую силу тока и мощность в цепи:

В этом и состоит смысл параллельного соединения источников. В любом случае при решении задач сначала надо найти суммарную ЭДС и полное внутреннее сопротивление получившегося источника, а затем записать закон Ома для полной цепи.

 

Работа и мощность тока. Закон Джоуля-Ленца

Работа A электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в теплоту Q, выделяющееся на проводнике. Эту работу можно рассчитать по одной из формул (с учетом закона Ома все они следуют друг из друга):

Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э.Ленцем и носит название закона Джоуля–Ленца. Мощность электрического тока равна отношению работы тока A к интервалу времени Δt, за которое эта работа была совершена, поэтому она может быть рассчитана по следующим формулам:

Работа электрического тока в СИ, как обычно, выражается в джоулях (Дж), мощность – в ваттах (Вт).

 

Энергобаланс замкнутой цепи

Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой ε и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. В этом случае полезная мощность или мощность, выделяемая во внешней цепи:

Максимально возможная полезная мощность источника достигается, если R = r и равна:

Если при подключении к одному и тому же источнику тока разных сопротивлений R1 и R2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:

Мощность потерь или мощность внутри источника тока:

Полная мощность, развиваемая источником тока:

КПД источника тока:

 

Электролиз

Электролитами принято называть проводящие среды, в которых протекание электрического тока сопровождается переносом вещества. Носителями свободных зарядов в электролитах являются положительно и отрицательно заряженные ионы. К электролитам относятся многие соединения металлов с металлоидами в расплавленном состоянии, а также некоторые твердые вещества. Однако основными представителями электролитов, широко используемыми в технике, являются водные растворы неорганических кислот, солей и оснований.

Прохождение электрического тока через электролит сопровождается выделением вещества на электродах. Это явление получило название электролиза.

Электрический ток в электролитах представляет собой перемещение ионов обоих знаков в противоположных направлениях. Положительные ионы движутся к отрицательному электроду (катоду), отрицательные ионы – к положительному электроду (аноду). Ионы обоих знаков появляются в водных растворах солей, кислот и щелочей в результате расщепления части нейтральных молекул. Это явление называется электролитической диссоциацией.

Закон электролиза был экспериментально установлен английским физиком М.Фарадеем в 1833 году. Закон Фарадея определяет количества первичных продуктов, выделяющихся на электродах при электролизе. Итак, масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:

Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:

где: n – валентность вещества, NA – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:

 

Электрический ток в газах и в вакууме

Электрический ток в газах

В обычных условиях газы не проводят электрический ток. Это объясняется электрической нейтральностью молекул газов и, следовательно, отсутствием носителей электрических зарядов. Для того чтобы газ стал проводником, от молекул необходимо оторвать один или несколько электронов. Тогда появятся свободные носителя зарядов — электроны и положительные ионы. Этот процесс называется ионизацией газов.

Ионизировать молекулы газа можно внешним воздействием — ионизатором. Ионизаторами может быть: поток света, рентгеновские лучи, поток электронов или α-частиц. Молекулы газа также ионизируются при высокой температуре. Ионизация приводит к возникновению в газах свободных носителей зарядов — электронов, положительных ионов, отрицательных ионов (электрон, объединившийся с нейтральной молекулой).

Если создать в пространстве, занятом ионизированным газом, электрическое поле, то носители электрических зарядов придут в упорядоченное движение – так возникает электрический ток в газах. Если ионизатор перестает действовать, то газ снова становится нейтральным, так как в нем происходит рекомбинация – образование нейтральных атомов ионами и электронами.

Электрический ток в вакууме

Вакуумом называется такая степень разрежения газа, при котором можно пренебречь соударением между его молекулами и считать, что средняя длина свободного пробега превышает линейные размеры сосуда, в котором газ находится.

Электрическим током в вакууме называют проводимость межэлектродного промежутка в состоянии вакуума. Молекул газа при этом столь мало, что процессы их ионизации не могут обеспечить такого числа электронов и ионов, которые необходимы для ионизации. Проводимость межэлектродного промежутка в вакууме может быть обеспечена лишь с помощью заряженных частиц, возникших за счет эмиссионных явлений на электродах.

20.1 Ток – Колледж физики

Глава 20 Электрический ток, сопротивление и закон Ома

Резюме

• Определение электрического тока, силы тока и скорости дрейфа
• Опишите направление потока заряда в обычном токе.
• Использовать скорость дрейфа для расчета тока и наоборот.

Электрический ток определяется как скорость, с которой течет заряд. Большой ток, например, используемый для запуска двигателя грузовика, перемещает большое количество заряда за короткое время, в то время как слабый ток, например, используемый для работы ручного калькулятора, перемещает небольшое количество заряда в течение короткого времени. длительный период времени. В форме уравнения электрический ток [латекс]{I}[/латекс] определяется как

[латекс] {I =} [/ латекс] [латекс] {\ гидроразрыва {\ Delta Q} {\ Delta t}} [/ латекс]

, где [латекс]{\Delta Q}[/латекс] — количество заряда, проходящего через данную область за время [латекс]{\Delta t}[/латекс]. (Как и в предыдущих главах, начальное время часто принимается равным нулю, и в этом случае [латекс] {\ дельта t = t} [/латекс].) (См. рис. 1.) Единица СИ для тока — ампер . (A), названный в честь французского физика Андре-Мари Ампера (1775–1836). Поскольку [latex]{I = \Delta Q / \Delta t}[/latex], мы видим, что ампер равен одному кулону в секунду:

[латекс]{1 \;\textbf{A} = 1 \;\text{C} / \text{s}}[/latex]

В амперах (или амперах) указаны не только предохранители и автоматические выключатели, но и многие электроприборы.

Рисунок 1. Скорость потока заряда текущая. Ампер — это поток в один кулон через площадь за одну секунду.

Пример 1: Расчет токов: ток в аккумуляторной батарее грузовика и портативном калькуляторе

(a) Какой ток возникает, когда аккумуляторная батарея грузового автомобиля приводится в движение с зарядом 720 Кл за 4,00 с при запуске двигателя? б) Сколько времени потребуется заряду 1,00 Кл, чтобы пройти через карманный калькулятор, если через него протекает ток 0,300 мА?

Стратегия

Мы можем использовать определение тока в уравнении [латекс]{I = \Delta Q / \Delta t}[/латекс], чтобы найти ток в части (а), так как заряд и время данный. В части (b) мы меняем определение тока и используем заданные значения заряда и тока, чтобы найти требуемое время.

Решение для (a)

Ввод заданных значений заряда и времени в определение тока дает

[латекс]\begin{array}{r @{{}={}} l} {I} & {\ frac {\ Delta Q} {\ Delta t} = \ frac {720 \; \ text {C}} {4,00 \; \ text {s}} = 180 \; \ text {C} / \ text { s}} \\[1em] & {180 \;\textbf{A}}. \end{массив}[/латекс]

Обсуждение для (a)

Это большое значение тока иллюстрирует тот факт, что большой заряд перемещается за небольшой промежуток времени. Токи в этих «стартерах» довольно велики, поскольку при приведении чего-либо в движение необходимо преодолевать большие силы трения.

Решение для (b)

Решение соотношения [латекс]{I = \Delta Q / \Delta t}[/latex] для времени [латекс]{\Delta t}[/латекс] и ввод известные значения заряда и тока дают 93 \;\текст{ы}}. \end{array}[/latex]

Обсуждение для (b)

Это время чуть меньше часа. Небольшой ток, используемый ручным калькулятором, требует гораздо больше времени для перемещения меньшего заряда, чем большой ток стартера грузовика. Так почему же мы можем работать с нашими калькуляторами всего через несколько секунд после их включения? Это потому, что калькуляторы требуют очень мало энергии. Такие малые требования к току и энергии позволяют портативным калькуляторам работать от солнечных батарей или работать много часов от небольших батарей.

Помните, что в калькуляторах нет движущихся частей, как в двигателе грузовика с цилиндрами и поршнями, поэтому технология требует меньших токов.

На рис. 2 показана простая схема и стандартное схематическое представление батареи, проводящего пути и нагрузки (резистора). Схемы очень полезны для визуализации основных особенностей схемы. Одна схема может отображать множество ситуаций. Схема на рис. 2(b), например, может представлять что угодно: от аккумулятора грузовика, подключенного к фаре, освещающей улицу перед грузовиком, до небольшой батареи, подключенной к фонарику-ручке, освещающему замочную скважину в двери. Такие схемы полезны, потому что анализ одинаков для самых разных ситуаций. Нам нужно понять несколько схем, чтобы применить концепции и анализ ко многим другим ситуациям.

Рис. 2. (а) Простая электрическая цепь. Замкнутый путь для протекания тока обеспечивается проводящими проводами, соединяющими нагрузку с клеммами батареи. (b) На этой схеме батарея представлена ​​двумя параллельными красными линиями, проводники показаны прямыми линиями, а зигзаг представляет собой нагрузку.

Схема представляет большое разнообразие подобных схем.

Обратите внимание, что направление тока на рис. 2 — от положительного к отрицательному. Направление обычного тока — это направление, в котором будет течь положительный заряд . В зависимости от ситуации могут перемещаться положительные заряды, отрицательные заряды или и то, и другое. В металлических проводах, например, ток переносится электронами, то есть движутся отрицательные заряды. В ионных растворах, таких как соленая вода, движутся как положительные, так и отрицательные заряды. Это верно и для нервных клеток. Генератор Ван де Граафа, используемый для ядерных исследований, может производить ток чисто положительных зарядов, таких как протоны. Рисунок 3 иллюстрирует движение заряженных частиц, составляющих ток. Тот факт, что обычный ток считается направленным в сторону положительного заряда, можно проследить до американского политика и ученого Бенджамина Франклина в 1700-х годах. Он назвал тип заряда, связанного с электронами, отрицательным задолго до того, как стало известно, что они несут ток во многих ситуациях.

Франклин, по сути, совершенно не знал о мелкомасштабной структуре электричества.

Важно понимать, что в проводниках, ответственных за производство тока, существует электрическое поле, как показано на рисунке 3. В отличие от статического электричества, где проводник, находящийся в равновесии, не может иметь в себе электрического поля, проводники, по которым течет ток, имеют электрическое поле. поле и не находятся в статическом равновесии. Электрическое поле необходимо для подачи энергии для перемещения зарядов.

Установление связей: домашнее исследование — иллюстрация электрического тока

Найдите соломинку и горошины, которые могут свободно перемещаться в соломе. Положите соломинку на стол и наполните ее горошком. Когда вы вставляете одну горошину с одного конца, другая горошина должна выскочить с другого конца. Эта демонстрация представляет собой аналогию электрического тока. Определите, что сравнивается с электронами и что сравнивается с запасом энергии. Какие еще аналогии вы можете найти для электрического тока?

Обратите внимание, что движение гороха основано на физическом столкновении горошин друг с другом; электроны текут за счет взаимно отталкивающих электростатических сил.

Рис. 3. Ток I — это скорость, с которой заряд проходит через площадь A , такую ​​как поперечное сечение провода. Условный ток определен для движения в направлении электрического поля. (а) Положительные заряды движутся в направлении электрического поля и в том же направлении, что и обычный ток. б) Отрицательные заряды движутся в направлении, противоположном электрическому полю. Обычный ток направлен в сторону, противоположную движению отрицательного заряда. Поток электронов иногда называют электронным потоком.

Пример 2: Расчет количества электронов, проходящих через калькулятор

Если ток 0,300 мА через калькулятор, упомянутый в примере 1, переносится электронами, сколько электронов в секунду проходит через него?

Стратегия

Ток, рассчитанный в предыдущем примере, был определен для потока положительного заряда. Для электронов величина такая же, но знак противоположный,

[латекс]{I_{\text{электроны}} = -0,300 \times 10^{-3} \;\text{C} / \text {s}}[/латекс]. {-19-}{\text{s}}} \end{array}[/latex]

Дискуссия

Заряженных частиц, движущихся даже в малых течениях, так много, что отдельные заряды не замечаются, как отдельные воды молекулы не замечаются в потоке воды. Еще более удивительно то, что они не всегда продолжают двигаться вперед, как солдаты на параде. Скорее они похожи на толпу людей с движением в разных направлениях, но общей тенденцией двигаться вперед. В металлической проволоке происходит множество столкновений с атомами и, конечно же, с другими электронами. 9{-4} \;\text{m} / \text{s}}[/latex]. Как нам согласовать эти две скорости и что это говорит нам о стандартных проводниках?

Высокая скорость электрических сигналов обусловлена ​​тем, что сила между зарядами быстро действует на расстоянии. Таким образом, когда свободный заряд попадает в провод, как на рис. 4, входящий заряд отталкивает другие заряды впереди себя, которые, в свою очередь, отталкивают заряды дальше по линии. Плотность заряда в системе нельзя легко увеличить, поэтому сигнал передается быстро. Возникающая в результате ударная волна электрического тока движется по системе почти со скоростью света. Точнее, этот быстро движущийся сигнал или ударная волна представляет собой быстро распространяющееся изменение электрического поля.0005 Рисунок 4. Когда заряженные частицы попадают в этот объем проводника, такое же количество быстро вынуждено покинуть его. Отталкивание между одноименными зарядами затрудняет увеличение количества зарядов в объеме. Таким образом, как только входит один заряд, другой почти сразу уходит, быстро перенося сигнал вперед.

Хорошие проводники имеют большое количество свободных зарядов. В металлах свободными зарядами являются свободные электроны. На рис. 5 показано, как свободные электроны движутся по обычному проводнику. Расстояние, которое может пройти отдельный электрон между столкновениями с атомами или другими электронами, весьма мало. Таким образом, траектории электронов кажутся почти случайными, как движение атомов в газе. Но в проводнике есть электрическое поле, которое заставляет электроны дрейфовать в указанном направлении (противоположном полю, поскольку они отрицательны). скорость дрейфа [латекс]{v_d}[/латекс] — средняя скорость свободных зарядов. Скорость дрейфа довольно мала, поскольку так много свободных зарядов. Если у нас есть оценка плотности свободных электронов в проводнике, мы можем рассчитать скорость дрейфа для данного тока. Чем больше плотность, тем ниже скорость, необходимая для данного тока.

Рис. 5. Свободные электроны, движущиеся в проводнике, совершают много столкновений с другими электронами и атомами. Показан путь одного электрона. Средняя скорость свободных зарядов называется скоростью дрейфа v _d , а для электронов — в направлении, противоположном электрическому полю. Столкновения обычно передают энергию проводнику, что требует постоянной подачи энергии для поддержания постоянного тока.

Проводимость электричества и тепла

Хорошие электрические проводники часто также являются хорошими проводниками тепла. Это связано с тем, что большое количество свободных электронов может переносить электрический ток и переносить тепловую энергию.

Столкновения свободных электронов передают энергию атомам проводника. Электрическое поле выполняет работу по перемещению электронов на расстояние, но эта работа не увеличивает кинетическую энергию (и, следовательно, скорость) электронов. Работа передается атомам проводника, возможно повышая температуру. Таким образом, для поддержания протекания тока требуется непрерывная потребляемая мощность. Исключение, конечно, составляют сверхпроводники по причинам, которые мы рассмотрим в одной из последующих глав. Сверхпроводники могут иметь постоянный ток без постоянного источника энергии — большая экономия энергии. Напротив, подача энергии может быть полезной, например, в нити накала лампочки. Подача энергии необходима для повышения температуры вольфрамовой нити, чтобы нить накала светилась.

Установление связей: домашнее расследование — Наблюдение за нитью

Найдите лампочку с нитью накала. Посмотрите внимательно на нить и опишите ее структуру. К каким точкам присоединяется нить?

Мы можем получить выражение для зависимости между током и скоростью дрейфа, рассмотрев количество свободных зарядов в отрезке провода, как показано на рисунке 6. {-19} \;\text{C}}[/latex].) Ток – это заряд, перемещаемый в единицу времени; таким образом, если все первоначальные заряды перемещаются из этого сегмента за время [латекс] {\ дельта t} [/латекс], ток равен

[латекс] {I =} [/ латекс] [латекс] {\ гидроразрыва {\ Delta Q} {\ Delta t}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва { qnAx}{\Delta t}}.[/latex]

Обратите внимание, что [latex]{x / \Delta t}[/latex] представляет собой величину скорости дрейфа, [latex]{v_{\textbf{d}}}[/latex], поскольку заряды перемещаются на среднее расстояние [латекс]{х}[/латекс] за время [латекс]{\Delta t}[/латекс]. Перестановка терминов дает

[латекс] {I = nqAv _ {\ textbf {d}}} [/латекс],

где [латекс]{I}[/латекс] — ток через провод с поперечным сечением [латекс]{А}[/латекс], изготовленный из материала с плотностью свободного заряда [латекс]{n}[/ латекс]. Каждый из носителей тока имеет заряд [латекс]{q}[/латекс] и движется с дрейфовой скоростью величины [латекс]{v_{\textbf{d}}}[/латекс].

Рис. 6. Все заряды в заштрихованном объеме этой проволоки удаляются за время t , имея скорость дрейфа величиной v _d = x/t . См. текст для дальнейшего обсуждения.

Обратите внимание, что простая скорость дрейфа — это еще не все. Скорость электрона намного больше скорости его дрейфа. Кроме того, не все электроны в проводнике могут двигаться свободно, а те, которые могут двигаться, могут двигаться несколько быстрее или медленнее скорости дрейфа. Так что же мы подразумеваем под свободными электронами? Атомы в металлическом проводнике упакованы в виде решетчатой ​​структуры. Некоторые электроны находятся достаточно далеко от ядер атомов, поэтому они не испытывают притяжения ядер так сильно, как внутренние электроны. Это свободные электроны. Они не связаны ни с одним атомом, а вместо этого могут свободно перемещаться среди атомов в «море» электронов. Эти свободные электроны реагируют ускорением при приложении электрического поля. Конечно, когда они движутся, они сталкиваются с атомами в решетке и другими электронами, выделяя тепловую энергию, и проводник нагревается. В изоляторе организация атомов и структура не допускают таких свободных электронов. 98 \;\text{m} / \text{s}}[/latex]), чем несущие его заряды.

• Электрический ток [латекс]{I}[/латекс] – это скорость, с которой течет заряд, определяемая выражением

  [латекс] {I = \frac{\Delta Q}{\Delta t}},[/latex]

  , где [latex]{\Delta Q}[/latex] — количество заряда, проходящего через площадь во времени [latex]{\Delta t}[/latex].

• Направление обычного тока принимается за направление, в котором движется положительный заряд.
• Единицей силы тока в системе СИ является ампер (А), где [латекс]{1 \;\textbf{A} = 1 \;\text{C} / \text{s}}[/latex].
• Ток — это поток свободных зарядов, таких как электроны и ионы.
• Скорость дрейфа [латекс]{v_{\textbf{d}}}[/латекс] — это средняя скорость, с которой движутся эти заряды.
• Текущий [латекс]{I}[/латекс] пропорционален скорости дрейфа [латекс]{v_{\textbf{d}}}[/латекс], что выражается соотношением [латекс]{I = nqAv_{\textbf {d}}}[/латекс]. Здесь [латекс]{I}[/латекс] — ток через провод с площадью поперечного сечения [латекс]{А}[/латекс]. Материал проволоки имеет плотность свободного заряда [латекс]{n}[/латекс], а каждый носитель имеет заряд [латекс]{q}[/латекс] и скорость дрейфа [латекс]{v _{\textbf{d} }}[/латекс]. 9{12}}[/latex] раз больше дрейфовой скорости свободных электронов.

Задачи и упражнения

1: Какова сила тока в миллиамперах, создаваемая солнечными элементами карманного калькулятора, через который проходит заряд 4,00 Кл за 4,00 ч?

2: Всего через фонарь проходит заряд 600 Кл за 0,500 ч. Какой средний ток?

3: Какова сила тока, когда типичный статический заряд [латекс]{0,250 \;\mu \text{C}}[/latex] перемещается с вашего пальца на металлическую дверную ручку в [латексе]{1,00 \ ;\mu \text{s}}[/латекс]?

4: Найдите силу тока, когда 2,00 нКл прыгает между расческой и волосами за интервал времени 0,500 – [латекс]\мю\текст{с}[/латекс]. 2 R}[/латекс].)

Рисунок 7. Конденсатор в дефибрилляторе пропускает ток через сердце пациента

8: Во время операции на открытом сердце дефибриллятор может быть использован для выведения пациента из состояния остановки сердца. Сопротивление пути составляет [латекс]{500 \;\Омега}[/латекс], и необходим ток 10,0 мА. Какое напряжение должно быть подано?

9: (а) Дефибриллятор пропускает ток силой 12,0 А через туловище человека за 0,0100 с. Сколько заряда перемещается? б) Сколько электронов проходит по проводам, подсоединенным к пациенту? (См. рисунок две проблемы выше.) 9{++}}[/latex] ядра поражают цель?

14: Повторите приведенный выше пример на Примере 3, но для проволоки из серебра и данного на один атом серебра приходится один свободный электрон.

15: Используя результаты приведенного выше примера на Примере 3, найти скорость дрейфа в медной проволоке двойного диаметра и несущей ток 20,0 А.

16: 1,628 мм. Ток какой величины протекает при скорости дрейфа 1,00 мм/с? (Полезную информацию см. выше в примере 3.)

17: SPEAR, накопительное кольцо диаметром около 72,0 м в Стэнфордском линейном ускорителе (закрыто в 2009 г.), имеет циркулирующий пучок электронов силой 20,0 А, которые движутся почти со скоростью света. (См. рис. 8.) Сколько электронов находится в пучке?

Рис. 8. Электроны, циркулирующие в накопительном кольце SPEAR, образуют ток силой 20,0 А. Поскольку они движутся со скоростью, близкой к скорости света, каждый электрон совершает множество оборотов в секунду.

электрический ток

скорость, с которой течет заряд, I = Δ Q / Δ t

ампер

(ампер) единица силы тока в системе СИ; 1 А = 1 Кл/с

скорость дрейфа

средняя скорость, с которой свободные заряды текут в ответ на электрическое поле

 

электричество — Определение электрического тока

спросил 1 год, 4 месяца назад

Изменено 1 год, 4 месяца назад

Просмотрено 1к раз

$\begingroup$

Я пытаюсь понять электрический ток. Некоторые ресурсы говорят, что это поток заряда, а другие говорят, что это количество заряда, которое проходит через площадь поперечного сечения за определенный период времени. Это смущает меня, потому что я не уверен, является ли это количеством (количеством заряда) или действием (потоком заряда). Не могли бы вы дать мне окончательное определение?

• электрические цепи
• электричество
• электрический ток
• заряд
• проводники

$\endgroup$

3

$\begingroup$

Проще говоря, ток — это просто поток заряда. Если, однако, вы хотите измерить и количественно определить количество тока, количество тока — это количество заряда, проходящего через точку в течение определенного периода времени.

Первый оператор определяет ток, а второй определяет его измерение.

$\endgroup$

5

$\begingroup$

Вероятно, вы можете найти различные определения, поэтому я не уверен, что существует какое-то единственное «окончательное» определение электрического тока.

Но как инженер я использую определение из справочного руководства для экзамена по основам для того, чтобы стать профессиональным инженером в США, следующим образом: 92$ определяется как $\vec J$.»

Надеюсь, это поможет.

$\endgroup$

2

$\begingroup$

Ваша путаница с терминами связана с использованием терминов на английском языке. Существует явление заряда, протекающего по проводу, и физическая величина, которая используется для измерения этого потока. Это два разных объекта, и их можно назвать двумя разными словами. Это делается на французском, итальянском, румынском и, возможно, на других языках, которых я не знаю. Таким образом, явление представляет собой «электрический ток», а величина, представляющая скорость протекания заряда, представляет собой «интенсивность электрического тока». Намек на это — обычная буква, используемая для обозначения «I», а не «C» (от текущего).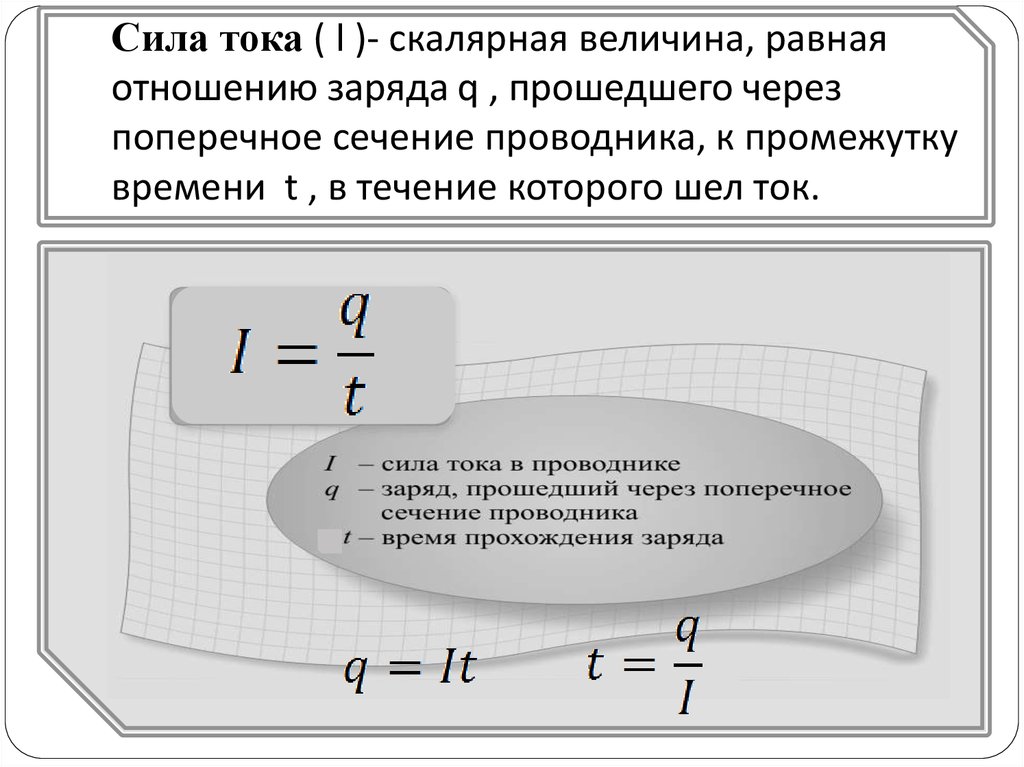 «Интенсивность тока» можно сократить до «тока», что может привести к путанице с термином, используемым для обозначения явления. В английском языке это настолько распространено, что даже в учебниках по физике количество называется «текущим», хотя имеется в виду сила тока. На румынском языке, например, я узнал о «силе тока» в школе, и именно так мы называли это в классе, но люди в электротехнической промышленности и торговле также называют это «током» или даже эквивалентом силы тока, как и в английском, мы используем напряжение для разности потенциалов. Во французских и итальянских текстах по физике я вижу, что они также используют эквивалент «интенсивности тока», поэтому, я полагаю, здесь меньше путаницы, чем в английском.

$\endgroup$

2

$\begingroup$

Bob D и SomeUser, соответственно, объяснили, что ток — это движение заряда в единицу времени, $$ I = \frac{\partial Q_\Omega}{\partial t},$$ и интеграл плотности тока по площади поперечного сечения, $$ I = \int_{\partial\Omega} \text{d}\mathbf{S} \cdot \mathbf{J}.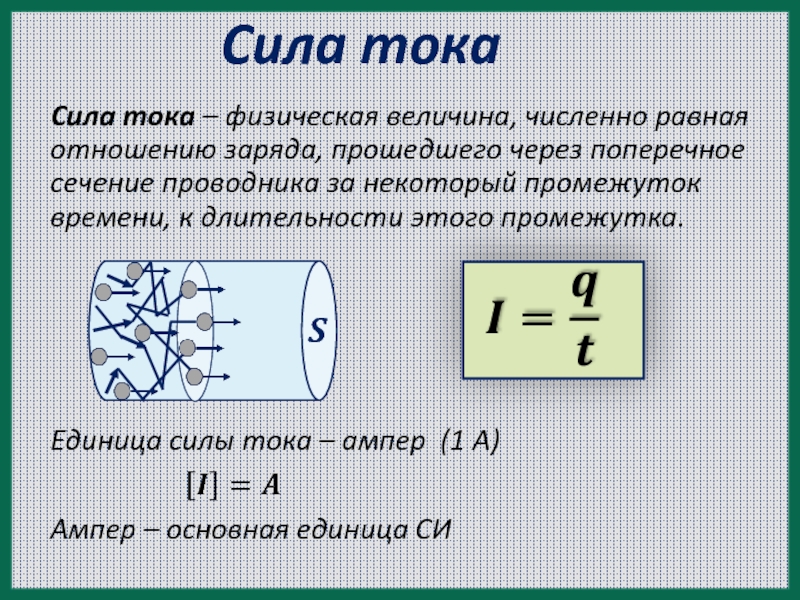 $$ Добавлю, что эти две величины одинаковы из-за сохранение заряда . Действительно, стандартными рассуждениями (см. Гриффитс, Электродинамика) можно записать следующее уравнение $$\frac{\partial \rho}{\partial t} + \nabla\cdot \mathbf{J} = 0.\qquad\qquad(*)$$ Первый член описывает изменение плотности заряда во времени в некоторой области $\Omega$, а второй описывает направленный наружу поток плотности тока в той же области. Действительно, мы видим приведенные выше величины после интегрирования по области $\Omega$, $$\int \text{d}V ~\frac{\partial \rho}{\partial t} = \frac{\partial Q}{\partial t}, \quad\text{and} \quad \int_\ Омега \text{d}V~ \nabla \cdot \mathbf{J} = \int_{\partial\Omega}\text{d}\mathbf{S}\cdot \mathbf{J},$$ где мы использовали теорему о расходимости для второго равенства. 9\mu= 0$ эквивалентно сохранению заряда. Подробнее см. здесь.

$\endgroup$

$\begingroup$

Электрический ток $I$ через поперечное сечение проводника равен: $$\lim_{\Delta t \to 0} \frac{\Delta q}{\Delta t}$$, где $\Delta q$ — количество заряда, прошедшего через это сечение за период времени длиной $\Delta t$.

Следовательно, это скалярная величина.

В качестве альтернативы, если площадь поперечного сечения $S$, количество заряда на единицу объема проводника равно $n=\frac{N}{V}$ ($N$ — количество заряженных частиц в объем $V$) и $v_d$ средняя скорость дрейфа в направлении электрического поля, то количество заряда, прошедшего через это сечение за время $\Delta t$, равно $\Delta q=q_0 \times n \ раз S \times v_d \times \Delta t$ ($q_0$ — элементарный заряд одиночной частицы).

Это связано с тем, что весь заряд, прошедший за этот период, находится внутри цилиндра высотой $v_d \Delta t$ и объемом $V=Sv_d \Delta t$, который содержит ровно $\Delta N=nV=nSv_d \Delta t$ заряженных частиц.

Отсюда ток $I_S$ в этом поперечном сечении будет равен $$\lim_{\Delta t \to 0} \frac{\Delta q}{\Delta t}=\lim_{\Delta t \to 0 } \frac{q_0nSv_d \Delta t}{\Delta t}=\lim_{\Delta t \to 0} q_0nSv_d=q_0nSv_d$$.

В общем, это скалярная величина, которая описывает количество заряда, протекающего через поверхность в течение определенного периода времени. Единицы измерения: $\frac{Кулоны}{секунды} \эквив Ампер$.

$\endgroup$

$\begingroup$

Я предпочитаю определять его как \begin{уравнение} I = \iint_{S} \mathbf{J} \cdot \, d\mathbf{S} \end{equation}

, которое можно переписать как \начать{выравнивать} I &= \frac{\iint_{S} \rho \mathbf{v} dt \cdot \, d\mathbf{S}}{dt} \\ \end{выравнивание} Плотность заряда интегрируется по поверхности и некоторой толщине, определяемой скоростью (на самом деле, просто скоростью в направлении, перпендикулярном $S$) зарядов: если заряды движутся быстрее, дальнейшие заряды достигнут поверхности за то же время. время $дт$. Вы можете видеть, что единицы совпадают. \начать{выравнивать} &= \frac{\iint_{S} \rho d\mathbf{r} \cdot \, d\mathbf{S}}{dt} \\ &= \frac{\iint_{S} \rho \,dr_{\perp} \,dS}{dt} \\ \end{выравнивание} По сути, числитель — это общее количество заряда, которое пройдет через $S$ за $dt$.