Формула силы тока через количество электронов

Определение и формула силы тока

Определение

Электрическим током

называют упорядоченное движение носителей зарядов. В металлах таковыми являются электроны, отрицательно заряженные частицы с зарядом, равным элементарному заряду. Направлением тока считают направление движения положительно заряженных частиц.

Силой тока (током) через некоторую поверхность S называют скалярную физическую величину, которую обозначают I, равную:

$$I=\frac{d q}{d t}$ (1)$

где q – заряд, проходящий сквозь поверхность S, t – время прохождения заряда. Выражение (1) определяет величину силы тока в момент времени t (мгновенное значение величины силы тока).

Физические проявления

Физически ощутить проявления электричества человеку можно только опосредованно. Если попробовать на язык батарейку — можно почувствовать пощипывание. Это следствие протекания малого тока через организм. Чувствительная слизистая языка уже ощущает это раздражение. Можно увидеть искры статического электричества между двумя заряженными объектами, например, синтетическими тканями, или в школьном опыте с динамо-машиной. Все это следствие накопления заряда или потенциального напряжения.

Протоны и нейтроны находятся в ядре атома. Электроны же, напротив, располагаются далеко от ядра и движутся вокруг него по орбитам, сходным с орбитами планет солнечной системы. Чем дальше находится электрон от ядра, тем меньше его связь с центром атома, и тем проще он может потеряться. В различных материалах электроны ведут себя по-разному.

В металлах они слабо связаны с ядром и свободно перемещаются внутри вещества. Однако их общее количество в предмете с нейтральным зарядом всегда должно соответствовать количеству протонов.

Если электроны вследствие каких-то действий покидают вещество, они уносят с собой заряд. Соответственно, заряд, оставшийся в протонах вещества, будет накоплен этим веществом. Электроны могут унести заряд в случаях:

• Трения двух веществ друг о друга.
• Воздействия ультрафиолета или радиации.
• Быстрого перепада температур.

Таким образом, между предметами возникает разность потенциалов, или напряжение, способное вызвать искру. А искра — это уже проявление электрического тока. Заряды разного знака всегда притягиваются друг к другу. Если электроны перешли с одного материала на другой, то один материал накопил положительный заряд, а другой — отрицательный.

Некоторые виды силы тока

Ток носит название постоянного, если его сила и направление с течением времени не изменяются, тогда:

$$I=\frac{q}{t}(2)$$

Формула (2) показывает, что сила постоянного тока равна заряду, который проходит сквозь поверхность S в единицу времени.

Если ток является переменным, то выделяют мгновенную силу тока (1), амплитудную силу тока и эффективную силу тока. Эффективной величиной силы переменного тока (Ieff) называют такую силу постоянного тока, которая выполнит работу равную работе переменного тока в течение одного периода (T):

$$I_{e f f}=\sqrt{\frac{1}{T} \int_{0}^{T} I^{2} d t}(3)$$

Если переменный ток можно представить как синусоидальный:

$$I=I_{m} \sin \omega t$$

то Im – амплитуда силы тока ($\omega$ – частота силы переменного тока).

Дополнительные единицы

На практике для удобства записи, для очень маленьких или очень больших токов, часто применяют кратные и дольные единицы от основной. Напомним, что кратными называют единицы намного больше основной, а дольными — намного меньше основной:

• Наноампер — 1 нА = 0,000000001=1,0*10 -9 А;
• Микроампер — 1 мкА = 0,000001 А;
• Миллиампер — 1 мА = 0,001 А;
• Килоампер — 1 кА = 1000 А;
• Мегаампер — 1МА = 1000000 А= 1,0*10 6 А.

Международное бюро мер и весов (находится в г. Севр, Франция), которое отвечает за обеспечение существования системы СИ, в 2021 г. планирует введение некоторых изменений в определениях основных единиц. Изменения будут внесены в определения кельвина, килограмма, моля и ампера. Эта реформа не повлияет на жизнь большинства людей. Необходимость этого мероприятия вызвана требованиями повышения точности в научных экспериментах и приборостроении. На основании опубликованных документов будут разработаны и утверждены государственные стандарты в странах, использующих систему СИ. На следующем этапе будут внесены корректировки в школьных и вузовских учебниках физики. Пока действующим является определение ампера, утвержденное в 1948 году.

Рис. 3. Примеры амперметров

Измерение тока в электрических цепях производится с помощью амперметров. Для калибровки шкал этих приборов (стрелочных и цифровых) очень важное значение имеет универсальность и точность самой единицы измерения — ампера.

Плотность тока

Распределение электрического тока по сечению проводника характеризуют при помощи вектора плотности тока ($\bar{j}$). При этом:

$$j_{n}=j \cos \alpha=\frac{d I}{d S}(5)$$

где $\alpha$ – угол между векторами $\bar{j}$ и $\bar{n}$ ( $\bar{n}$ – нормаль к элементу поверхности dS), jn – проекция вектора плотности тока на направление нормали ($\bar{n}$).

Сила тока в проводнике определяется при помощи формулы:

$$I=\int_{S} j d S(6)$$

где интегрирование в выражении (6) проводится по всему поперечному сечению проводника S ($\alpha \equiv 0$)

Для постоянного тока имеем:

$I = jS (7)$

Если рассматривать два проводника с сечениями S1 и S2 и постоянными токами, то выполняется соотношение:

$$\frac{j_{1}}{j_{2}}=\frac{S_{2}}{S_{1}}(8)$$

Практический расчёт

Например, пусть понадобится узнать, на какой ток необходимо приобрести устанавливаемый на участок цепи автоматический выключатель. При этом известно, что в линию, на которой он будет установлен, одновременно будут включаться холодильник с максимальной мощностью потребления энергии один киловатт, бойлер (два киловатта) и люстра, потребляющая 90 ватт. В месте установки используется однофазная сеть, рассчитанная на рабочее напряжение 220 вольт.

Советуем изучить — Режимы работы синхронных генераторов, рабочие характеристики генераторов

На первом этапе расчёта понадобится суммировать всю мощность подключаемых к линии электроприборов. Так, P общ. = 1000 + 2000 + 90 +220 = 3310 Вт. Используя формулу P = I*U, находится необходимое значение тока: I = P/U = 3310/220 = 15,04 А.

Из стандартного ряда выключателей наиболее близкое значение имеет автомат на 16 А. Поскольку необходимо покупать устройство защиты с небольшим запасом, то для рассматриваемого примера подойдёт выключатель, рассчитанный на 20 ампер.

С помощью закона Джоуля-Ленца

Некоторые затрудняются определять силу тока, если есть:

• Время;
• Значение сопротивления;
• Кол-во выделяемого тепла от проводника.

С помощью решения задачи, нужно воспользоваться законом Джоуля-Ленца: Q=I2Rt

Исходя из этой формулы, расчет нужно построить так: I2=QRt

Либо так: I=(Q/Rt)1/2

Модель электрической цепи

Лучше понять физический смысл рассматриваемой величины можно на примере механической модели электрической цепи. В качестве ее возьмем водопроводную сеть частного дома.

Для того, чтобы вода начала поступать в водопровод из скважины или колодца необходим насос. Поэтому его можно рассматривать в качестве аналога батареи или иного источника тока. Он создает в системе давление, которое и приводит воду в движение. Соответственно трубы выступают роли проводников, молекулы воды — электронов, а краны — электрических переключателей.

Чем сильнее напор в водопроводной системе, тем большее количество воды, а вернее ее молекул, протекает через поперечное сечение трубы за каждую секунду. Отсюда можно сделать вывод, что чем больше сила тока, тем сильнее и его действие.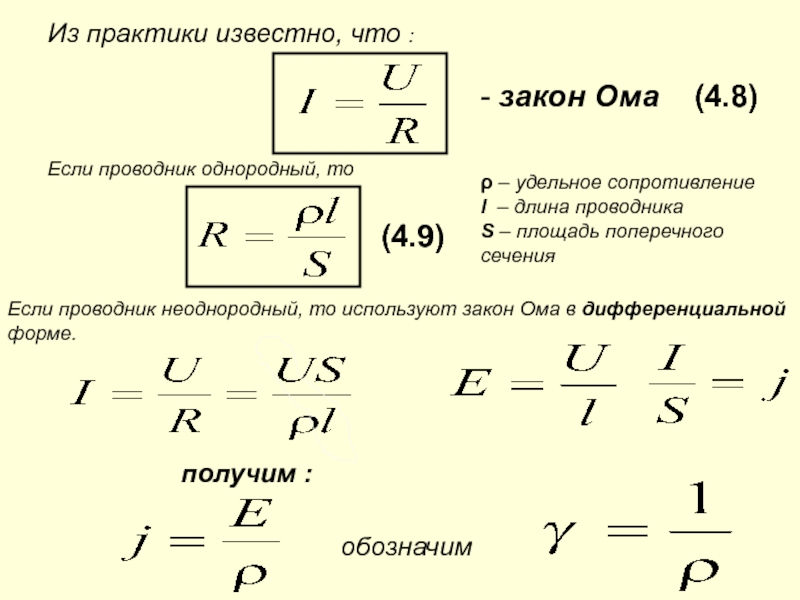

Теория к заданию 14 из ЕГЭ по физике

Закон Кулона

Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.

Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела.

В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.

Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.

В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.

Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.

Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.

В аналитическом виде закон Кулона имеет вид:

С помощью напряжения или мощности и сопротивления

Бывает и так, что для расчета силы электрического тока нужно задействовать напряжение с определённого участка или величину нагрузки. Тогда проще всего применить закон Ома, который знает каждый, кто немного разбирается в физике.

Если же напряжение Вам неизвестно, но вы знаете значение мощности и сопротивления, проводите расчет по следующей формуле: P=UI

Снова применяя закон Ома, можно получить следующее: U=IR

В таком случае: P=I2*R

Получаем следующую формулу: I2=P/R

Кроме того, можно применить следующий расчет, исходя из этих же формул и значений: I=(P/R)1/2

С помощью электродвижущей силы, внутреннего сопротивления и нагрузки

В некоторых студенческих учебниках встречаются так называемые задачки с подвохом. К ним относятся и те, где есть электродвижущая сила и значение внутреннего сопротивления.

Вспоминая закон Ома, силу электрического тока можно получить следующим образом: I=E/(R+r)

Здесь Е будет электродвижущей силой, а r будет внутренним сопротивлением. R представляет собой нагрузку.

Закон Ома для участка цепи формула. Законы Ома и их качественное объяснение.

Первоначальная и современная формулировка

Этот, на первый взгляд, простой закон был сформулирован немецким физиком Георгом Омом в 1826 году. Соответствующую научную статью он опубликовал в следующем году.

Интересно отметить, что появление этой работы не вызвало ажиотажа. Научная общественность оценила открытие Ома лишь после публикации работ физика Пулье аналогичного содержания в 1830 году. В 1833 Ом получил степень доктора в Нюрнбергском университете. В 1872 году единица измерения сопротивления стала называться Омом. В самой простой форме закон для участка цепи звучит так:

Закон носит эмпирический характер, так как он выражает обобщенный анализ большого количества опытных данных.

Сейчас формула закона Ома для полной электрической цепи имеет следующий вид:

I = ℰ / (R+r).

Здесь:

• ℰ — ЭДС источника напряжения, В;
• I — сила тока в цепи, А.
• R — общее сопротивление всех внешних элементов цепи, Ом;
• r — внутреннее сопротивление источника напряжения, Ом.

Закон Ома для полной цепи учитывает полное сопротивление, которое представляет собой сумму сопротивления цепи R и внутреннего сопротивления источника тока r.

Георг Ом первоначально сформулировал его по-другому. Закон Ома для замкнутой цепи выглядел так:

X = a / ( b + l ), где

• a — величина, характеризующая источник тока. Сейчас говорят, что это электродвижущая сила источника тока;
• b представляет собой свойство электрической установки, которое теперь рассматривается в качестве внутреннего сопротивления источника тока;
• l — величина, зависящая от длины используемых проводов (в современных терминах она соответствует сопротивлению электрической цепи).

Как видно, закон Ома, применяемый для полной электрической цепи, в обоих вариантах имеет одинаковую формулировку.

Также применяется закон Ома в дифференциальной форме. В данном случае рассматриваются очень малые величины. Но это позволяет применять интегральное и дифференциальное исчисление для сложных случаев.

Закон Ома для участка цепи

Со школьного курса физики всем хорошо известна классическая трактовка Закона Ома:

Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению.

I = U/R

Это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер.

Отсюда следуют ещё два полезных соотношения:

Если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения).

U = IR

Если на концах проводника есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.

R = U/I

Вышеописанные формулы в таком виде могут быть применимы для переменного тока лишь в том случае, если цепь состоит только из активного сопротивления R. Кроме того, следует помнить, что Закон Ома справедлив только для линейных элементов цепи.

Как звучит закон Ома для участка цепи

Есть говорить об официальной формулировке, то закон Ома можно озвучить так:

Сила тока имеет прямую зависимость от напряжения и обратную от сопротивления. Это высказывание справедливо для участка цепи с каким-то определенным и стабильным сопротивлением.

Формула этой зависимости на рисунке. Тут I — это сила тока, U — напряжение, R — сопротивление.

Формула закона Ома

• Чем больше напряжение, тем больше ток.
• Чем больше сопротивление, тем ток меньше.

Не так легко представить себе смысл этого выражения. Ведь электричество нельзя увидеть. Мы только приблизительно знаем что это такое. Попытаемся уяснить себе смысл этого закона при помощи аналогий.

Формула закона Ома

Легко и быстро находить нужные вам значения по этой формуле помогают такие вот подсказки, основанные на «магическом треугольнике».

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной  , и внутренним сопротивлением подключён к резистору
(который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. Полная цепь

Наша задача — найти силу тока
в цепи и напряжение
на резисторе .

За время по цепи проходит заряд .

Согласно формуле (1) источник тока совершает при этом работу:

(2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях
и r.

Данное количество теплоты определяется законом Джоуля–Ленца:

(3)

Итак, , и мы приравниваем правые части формул (2) и (3):

После сокращения на получаем:

Вот мы и нашли ток в цепи:

(4)

Формула называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе  с помощью закона Ома для участка цепи:

(5)

Это напряжение является разностью потенциалов между точками   и (рис). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки  равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет  — ведь   умножается на дробь, меньшую единицы. Но есть два случая, когда .

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При
формула (5) даёт .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина   неотличима от , и формула (5) снова даёт нам .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

Закон Ома в интегральной форме

Схема, иллюстрирующая три составляющие закона Ома
Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления

Закон Ома для участка электрической цепи имеет вид:

U = RI

где:

• U — напряжение или разность потенциалов,
• I — сила тока,
• R — сопротивление.

Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:

где:

• 
  — ЭДС цепи,
• I — сила тока в цепи,
• R — сопротивление всех элементов цепи,
• r — внутреннее сопротивление источника питания.

Закон Ома в дифференциальной форме

Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

• 
  — вектор плотности тока,
• σ — удельная проводимость,
• 
  — вектор напряжённости электрического поля.

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1).

Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Если цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), а ток является синусоидальным с циклической частотой ω, то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

• U = U0eiωt — напряжение или разность потенциалов,
• I — сила тока,
• Z = Re—iδ — комплексное сопротивление (импеданс),
• R = (Ra2+Rr2)1/2 — полное сопротивление,
• Rr = ωL — 1/ωC — реактивное сопротивление (разность индуктивного и емкостного),
• Rа — активное (омическое) сопротивление, не зависящее от частоты,
• δ = —arctg Rr/Ra — сдвиг фаз между напряжением и силой тока.

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведен взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, U = U0sin(ωt + φ) подбором такой
что
. Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо.

Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.

Как понять закон Ома?

Чтобы интуитивно понять закон Ома, обратимся к аналогии представления тока в виде жидкости. Именно так думал Георг Ом, когда проводил опыты, благодаря которым был открыт закон, названный его именем.

Представим, что ток – это не движение частиц-носителей заряда в проводнике, а движение потока воды в трубе.  Сначала воду насосом поднимают на водокачку, а оттуда, под действием потенциальной энергии, она стремиться вниз и течет по трубе. Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.

Отсюда следует вывод, что скорость потока воды (сила тока в проводе) будет тем больше, чем больше потенциальная энергия воды (разность потенциалов)

«Сила тока прямо пропорциональна напряжению»

Теперь обратимся к сопротивлению. Гидравлическое сопротивление – это сопротивление трубы, обусловленное ее диаметром и шероховатостью стенок. Логично предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество воды (больший ток) протечет через ее сечение.

«Сила тока обратно пропорциональна сопротивлению»

Такую аналогию можно проводить лишь для принципиального понимания закона Ома, так как его первозданный вид – на самом деле довольно грубое приближение, которое, тем не менее, находит отличное применение на практике.

В действительности, сопротивление вещества обусловлено колебанием атомов кристаллической решетки, а ток – движением свободных носителей заряда. В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.

Ток в проводнике

В данной статье мы постарались дать простое объяснение закона Ома. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Конечно, мы привели его простейшую формулировку закона Ома и не будем сейчас лезть в дебри высшей физики, разбираясь с активным и реактивным сопротивлениями и прочими тонкостями.

Если у Вас возникнет такая необходимость, Вам с удовольствием помогут сотрудники нашего  студенческого сервиса . А напоследок предлагаем Вам посмотреть интересное видео про закон Ома. Это действительно познавательно!

Формулировка и объяснение закона Ома

Закон немецкого учителя Георга Ома очень прост.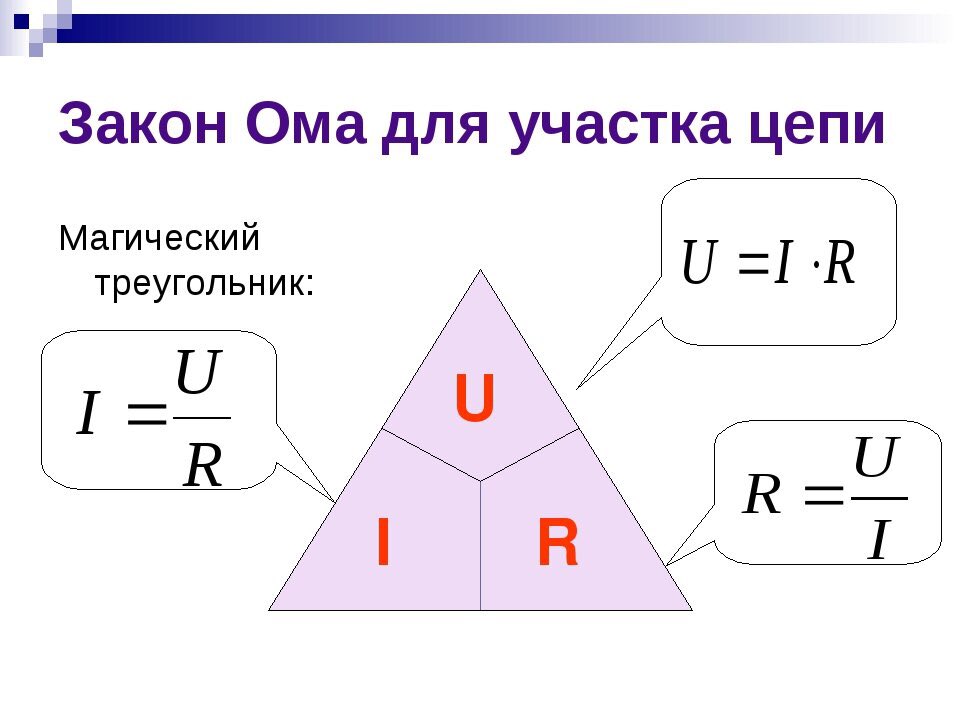 Он гласит:

Сила тока на участке цепи прямо пропорционально напряжению и обратно пропорциональна сопротивлению.

Георг Ом вывел этот закон экспериментально (эмпирически) в 1826 году. Естественно, чем больше сопротивление участка цепи, тем меньше будет сила тока. Соответственно, чем больше напряжение, тем и ток будет больше.

Данная формулировка закона Ома – самая простая и подходит для участка цепи. Говоря «участок цепи» мы подразумеваем, что это однородный участок, на котором нет источников тока с ЭДС. Говоря проще, этот участок содержит какое-то сопротивление, но на нем нет батарейки, обеспечивающей сам ток.

Если рассматривать закон Ома для полной цепи, формулировка его будет немного иной.

Пусть  у нас есть цепь, в ней есть источник тока, создающий напряжение, и какое-то сопротивление.

Закон запишется в следующем виде:

Объяснение закона Ома для полой цепи принципиально не отличается от объяснения для участка цепи. Как видим, сопротивление складывается из собственно сопротивления и внутреннего сопротивления источника тока, а вместо напряжения в формуле фигурирует электродвижущая сила источника.

Сфера применения

Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:

• Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
• В сверхпроводниках;
• Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
• В вакуумных и газовых радиолампах;
• В диодах и транзисторах.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

• I = I1= I2 ;
• U = U1+ U2 ;
• R = R1+ R2

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

• I = I1+ I2 … ;
• U = U1= U2 … ;
• 1 / R = 1 / R1+ 1 / R2 + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Анализ простых схем с помощью закона Ома

Давайте посмотрим, как эти формулы работают, чтобы помочь нам анализировать простые схемы:

Рисунок 1 – Пример простой схемы

В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применить закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.

В этом первом примере мы вычислим величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):

Рисунок 2 – Пример 1. Известны напряжение источника и сопротивление лампы

Какая величина тока (I) в этой цепи?

[I = frac{E}{R} = frac{12 В}{3 Ом} = 4 А]

Во втором примере мы вычислим величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):

Рисунок 3 – Пример 2. Известны напряжение источника и ток в цепи

Какое сопротивление (R) оказывает лампа?

[R = frac{E}{I} = frac{36 В}{4 А} = 9 Ом]

В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):

Рисунок 4 – Пример 3. Известны ток в цепи и сопротивление лампы

Какое напряжение обеспечивает батарея?

[E = IR = (2 А)(7 Ом) = 14 В]

Метода треугольника закона Ома

Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:

Рисунок 5 – Треугольник закона Ома

Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:

Рисунок 6 – Закон Ома для определения R

Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:

Рисунок 7 – Закон Ома для определения I

Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:

Рисунок 8 – Закон Ома для определения E

В конце концов, вам придется научиться работать с формуми, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!

Формула Закона Джоуля-Ленца

Величину резистора для изготовления блока нагрузки для блока питания компьютера мы рассчитали, но нужно еще определить какой резистор должен быть мощности? Тут поможет другой закон физики, который, независимо друг от друга открыли одновременно два ученых физика. В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь – Закон Джоуля-Ленца.

Потребляемая нагрузкой мощность прямо пропорциональна приложенной величине напряжения и протекающей силе тока. Другими словами, при изменении величины напряжения и тока будет пропорционально будет изменяться и потребляемая мощность.

где P – мощность, измеряется в ваттах и обозначается Вт;U – напряжение, измеряется в вольтах и обозначается буквой В;I – сила ток, измеряется в амперах и обозначается буквой А.

Зная напряжения питания и силу тока, потребляемую электроприбором, можно по формуле определить, какую он потребляет мощность. Достаточно ввести данные в окошки ниже приведенного онлайн калькулятора.

Закон Джоуля-Ленца позволяет также узнать силу тока, потребляемую электроприбором зная его мощность и напряжение питания. Величина потребляемого тока необходима, например, для выбора сечения провода при прокладке электропроводки или для расчета номинала.

Например, рассчитаем потребляемый ток стиральной машины. По паспорту потребляемая мощность составляет 2200 Вт, напряжение в бытовой электросети составляет 220 В. Подставляем данные в окошки калькулятора, получаем, что стиральная машина потребляет ток величиной 10 А.

Еще один пример, Вы решили в автомобиле установить дополнительную фару или усилитель звука. Зная потребляемую мощность устанавливаемого электроприбора легко рассчитать потребляемый ток и правильно подобрать сечение провода для подключения к электропроводке автомобиля. Допустим, дополнительная фара потребляет мощность 100 Вт (мощность установленной в фару лампочки), бортовое напряжение сети автомобиля 12 В. Подставляем значения мощности и напряжения в окошки калькулятора, получаем, что величина потребляемого тока составит 8,33 А.

Разобравшись всего в двух простейших формулах, Вы легко сможете рассчитать текущие по проводам токи, потребляемую мощность любых электроприборов – практически начнете разбираться в основах электротехники.

Преобразованные формулы Закона Ома и Джоуля-Ленца

Встретил в Интернете картинку в виде круглой таблички, в которой удачно размещены формулы Закона Ома и Джоуля-Ленца и варианты математического преобразования формул. Табличка представляет собой не связанные между собой четыре сектора и очень удобна для практического применения

По таблице легко выбрать формулу для расчета требуемого параметра электрической цепи по двум другим известным. Например, нужно определить ток потребления изделием по известной мощности и напряжению питающей сети. По таблице в секторе тока видим, что для расчета подойдет формула I=P/U.

А если понадобится определить напряжение питающей сети U по величине потребляемой мощности P и величине тока I, то можно воспользоваться формулой левого нижнего сектора, подойдет формула U=P/I.

Подставляемые в формулы величины должны быть выражены в амперах, вольтах, ваттах или Омах.

Таблица-шпаргалка

Используя закон Ома для участка цепи, а также формулу для мощности электрического тока: P = U*I — я подготовил для вас полезную таблицу-шпаргалку, которая позволяет соотносить между собой сопротивление (R), силу тока (I), напряжение (U) и мощность электрического тока (P). Будет точно полезно не только школьникам!

Известные величины	R (сопротивление)	I (сила тока)	U (напряжение)	P (мощность)
Ток и сопротивление			U = I × R	P = I2 × R
Напряжение и ток	R = U / I			P = U × I
Мощность и ток	R = P / I2		U = P / I
Напряжение и сопротивление		I = U / R		P = U2 / R
Мощность и сопротивление		I = P / R
Напряжение и мощность	R = U2 / R	I = P / U

Источники

• https://ProFazu. ru/knowledge/electrical/zakon-oma.html
• https://electric-220.ru/kak-ponyat-zakon-oma-prostoe-obyasnenie
• https://fishki.net/2315059-razjasnjaem-zakon-oma-bukvalyno-na-palycah-i-kartinkah.html
• https://ege-study.ru/ru/ege/materialy/fizika/eds-zakon-oma-dlya-polnoj-cepi/
• https://dic.academic.ru/dic.nsf/ruwiki/1075882
• https://Zaochnik.ru/blog/zakon-oma-dlya-chajnikov/
• https://dzen.ru/a/YmN-B6Fw1EvrDJu4
• https://www.asutpp.ru/zakon-oma-dlya-uchastka-tsepi.html

 

Как вам статья?

Павел

Бакалавр «210400 Радиотехника» – ТУСУР. Томский государственный университет систем управления и радиоэлектроники

Написать

Пишите свои рекомендации и задавайте вопросы

Как рассчитать ток двигателя с сопротивлением обмотки

Обновлено 03 ноября 2020 г.

Автор Chris Deziel

Согласно закону Ома, ток (I) через проводящий провод прямо пропорционален приложенному напряжению (V) и сопротивлению провода (R). Это соотношение не изменится, если проволока намотана на сердечник, образуя ротор электродвигателя. В математической форме закон Ома выглядит так:

V=IR

или, если поставить ток и сопротивление по разные стороны от знака равенства:

I=\frac{V}{R}

Сопротивление провода зависит от его диаметра, длины, проводимости и температуры окружающей среды. Медная проволока используется в большинстве двигателей, и медь имеет одну из самых высоких электропроводностей среди всех металлов.

TL;DR (слишком длинный; не читал)

Закон Ома говорит вам, что ток через провод — даже длинный провод, намотанный на соленоид двигателя — равен напряжению, деленному на сопротивление. Вы можете определить сопротивление катушки двигателя, если знаете сечение провода, радиус соленоида и количество витков.

Сопротивление провода

Закон Ома говорит вам, что вы можете рассчитать ток через обмотку двигателя, если знаете напряжение и сопротивление провода. Напряжение легко определить. Вы можете подключить вольтметр к клеммам источника питания и измерить его. Определение другой переменной, сопротивления провода, не так просто, потому что оно зависит от четырех переменных.

Сопротивление провода обратно пропорционально диаметру провода и проводимости, а это означает, что оно тем больше, чем меньше эти параметры. С другой стороны, сопротивление прямо пропорционально длине провода и температуре — оно увеличивается с увеличением этих параметров. Что еще более усложняет ситуацию, так это то, что сама проводимость изменяется с температурой. Однако, если вы проводите измерения при определенной температуре, например при комнатной температуре, и температура, и проводимость становятся постоянными, и вам нужно учитывать только длину провода и его диаметр для расчета сопротивления провода. Сопротивление (R) становится равным константе (k), умноженной на отношение длины провода (l) к диаметру (d):

R=k\frac{l}{d}

Длина провода и сечение провода

Для расчета сопротивления необходимо знать как длину провода, намотанного на соленоид двигателя, так и его диаметр. Однако, если вы знаете калибр проволоки, вы знаете и диаметр, потому что вы можете найти его в таблице. Некоторые таблицы помогают еще больше, указывая сопротивление на стандартную длину для проводов всех калибров. Например, диаметр провода 16-го калибра составляет 1,29 мм или 0,051 дюйма, а сопротивление на 1000 футов составляет 4,02 Ом.

В конце концов, все, что вам действительно нужно измерить, это длину провода, если вы знаете сечение провода. В соленоиде двигателя провод несколько раз обмотан вокруг сердечника, поэтому для расчета его длины вам нужны две части информации: радиус сердечника (r) и количество витков (n). Длина одной обмотки равна длине окружности сердечника — 2πr, поэтому общая длина провода равна 2πrn. Используйте это выражение для расчета длины провода, и как только вы его узнаете, вы сможете экстраполировать сопротивление из таблицы сопротивлений.

Рассчитать ток

Зная приложенное напряжение и рассчитав сопротивление провода, у вас есть все, что вам нужно, чтобы применить закон Ома для определения тока, протекающего через катушку.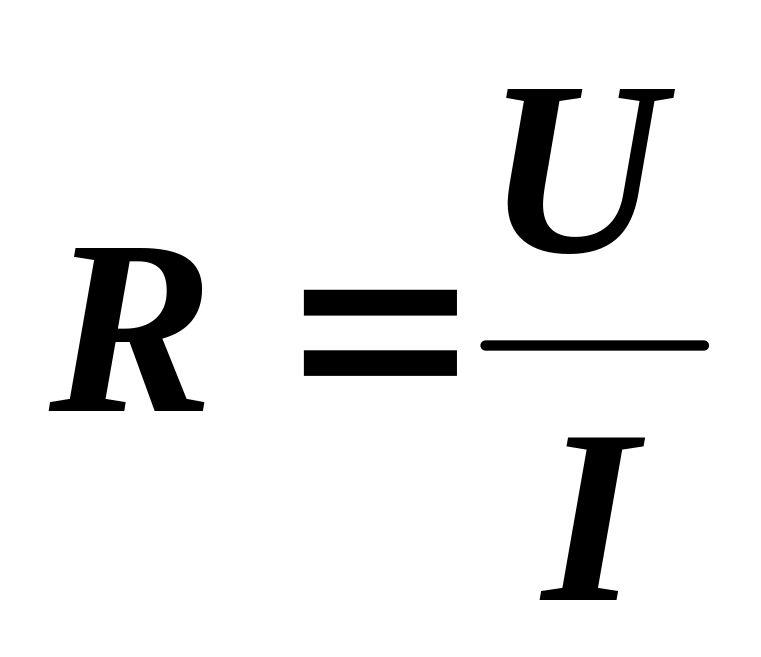 Поскольку сила тока определяет силу индуцированного магнитного поля катушки, эта информация позволяет количественно определить мощность двигателя.

Электрическое сопротивление | Расчет тока, напряжения и сопротивления

Центр знаний » GCSEs » GCSE Physics » Электрическое сопротивление

17 августа 2022 г.

В этом посте

Все компоненты, имеющие цепь, имеют определенное сопротивление. Это связано с тем, что каждый компонент в определенной степени сопротивляется потоку электричества. Величина сопротивления зависит от толщины или длины провода в самом компоненте. Чем толще провод, тем меньше сопротивление, чем длиннее провод, тем выше сопротивление.

Электрическое сопротивление — это мера трудности, с которой электричество может проходить через какой-либо конкретный компонент цепи. Сопротивление измеряется в омах (Ом) и зависит от величины напряжения, действующего на него, и тока, протекающего через него. Связь между этими тремя факторами показана уравнением:

   

В = разность потенциалов и измеряется в вольтах (В)

I = ток в амперах (А)

R = сопротивление в омах (Ом)

Вы должны знать и уметь переставлять уравнение, так как оно не будет представлено на экзамене.

Это уравнение показывает, что при постоянном сопротивлении существует прямо пропорциональная зависимость между напряжением и током. С увеличением напряжения увеличивается и ток. Увеличение напряжения означает, что электроны, движущиеся по цепи, получают больший «толчок». Они будут двигаться быстрее, и большее их число будет проходить одну и ту же точку каждую секунду. Это увеличивает ток.

Затем уравнение можно изменить, чтобы найти сопротивление:

   

Пример

Если ток 6 А протекает через чайник на 900 В, каково сопротивление чайника?

Помните, что сопротивление — это напряжение (измеряется в вольтах), деленное на силу тока (измеряется в амперах). Мы знаем, что напряжение составляет 900 В и что через него протекает ток 6 А. Мы используем следующее уравнение: R = V ÷ I

   

   

Уравнение также можно изменить, чтобы найти ток в цепи по заданным значениям сопротивления и напряжения, как показано ниже:

   

Как видно из уравнения, ток зависит от величины напряжения и сопротивления. Если напряжение остается постоянным, а сопротивление увеличивается, ток, измеряемый через компонент, также увеличивается. Если сопротивление увеличивается, электричеству становится труднее проходить через компонент, и поэтому скорость потока электричества (то есть тока) уменьшается. Если сопротивление уменьшается, электричеству становится легче течь, и скорость потока увеличивается. Следовательно, если сопротивление уменьшается, ток увеличивается.

Расчет тока, напряжения и сопротивления в последовательной цепи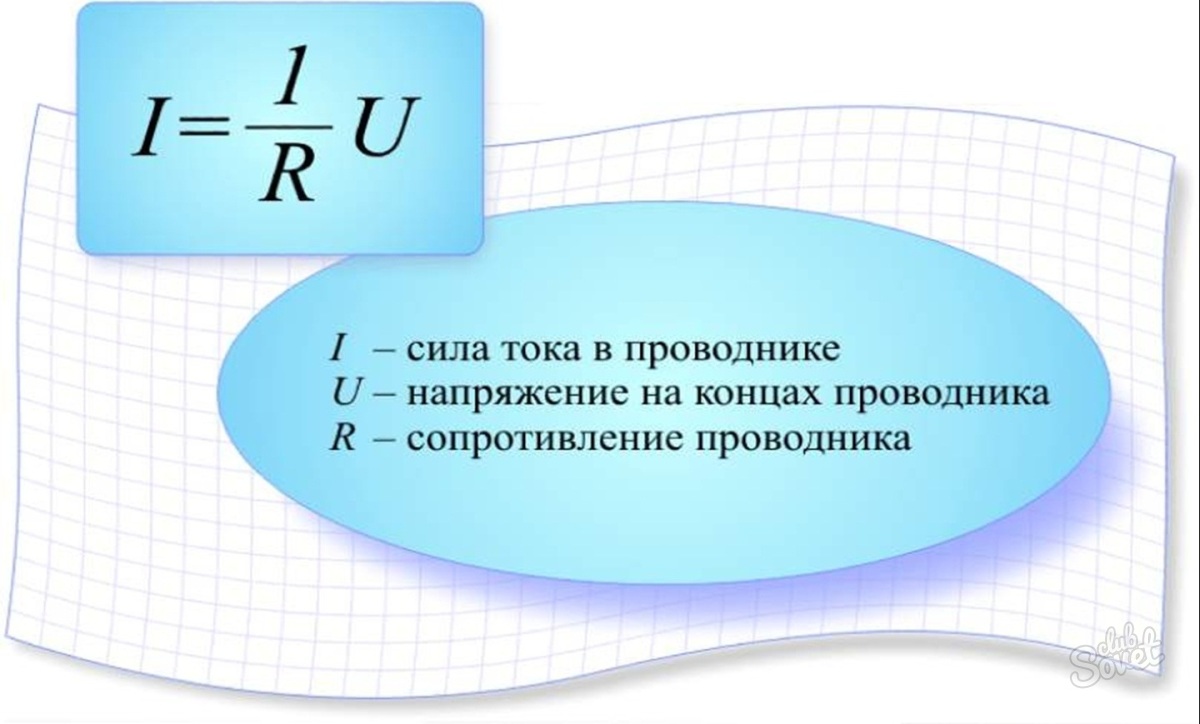

Общее сопротивление двух резистивных компонентов, соединенных в последовательную цепь, можно рассчитать как сумму их сопротивлений. Например, если резисторы 3 Ом и 4 Ом соединены последовательно, общее сопротивление, рассчитанное для цепи, будет: 3 Ом + 4 Ом = 7 Ом. Напряжение на резисторе связано с сопротивлением уравнением:

   

Добавление в цепь дополнительного резистора увеличивает сопротивление цепи. При увеличении сопротивления ток уменьшается. Равное увеличение сопротивления и уменьшение тока приводит к тому, что напряжение остается постоянным. Напряжение равномерно распределяется между всеми резисторами, присутствующими в цепи. В примере схемы, содержащей резисторы 3 Ом и 4 Ом, при подаче напряжения 40 В каждый резистор будет иметь напряжение 20 В. Ток для той же цепи, содержащей резистор 3 Ом и резистор 4 Ом, используя уравнение I = V ÷ R.

Общее сопротивление (R) = 7 Ом
Напряжение = 40 В
Ток = 40 В ÷ 7 Ом
Ток = 5,71 А

Электрические цепи часто также включают в себя компоненты, которые играют определенную роль в качестве типов резисторов. Эти специальные резисторы включают постоянные и переменные резисторы, диоды, термисторы и светочувствительные резисторы.

• Постоянные резисторы используются в цепях для управления величиной тока и напряжения, чтобы гарантировать, что правильное напряжение подается на лампу и что через нее протекает правильный ток. Без резистора напряжение на лампе может быть настолько большим, что вызовет внезапный скачок протекающего через нее тока, что приведет к разрыву нити накала.
• Переменные резисторы можно использовать для управления силой тока, протекающего через лампочку. Переменный резистор ведет себя как диммер. Если бы сопротивление было уменьшено, лампочка светила бы ярче, так как через цепь протекает больший ток. Переменные резисторы также можно использовать для управления такими переменными, как громкость или яркость.
• Диоды представляют собой особый тип резисторов, пропускающих ток только в одном направлении. Если направление тока было изменено на противоположное, высокое сопротивление диода потоку электричества означает, что через него может протекать очень небольшой ток. Диоды можно использовать для предотвращения повреждения других компонентов схемы из-за изменения направления напряжения из-за неправильного размещения ячеек.
• Термисторы — это резисторы, зависящие от температуры. Они часто изготавливаются из полупроводниковых материалов, таких как кремний. Их сопротивление меняется в зависимости от температуры. Если повысить температуру, сопротивление уменьшится. Если температура снижается, сопротивление увеличивается. Термисторы часто используются в чувствительных к температуре устройствах, таких как датчики температуры и нагревательные термостаты.
• Светозависимые резисторы (LDR) — это резисторы, работа которых зависит от интенсивности света. В условиях низкой освещенности сопротивление увеличивается, а при высокой освещенности сопротивление уменьшается. LDR имеют множество различных применений, включая наружное освещение, системы охранной сигнализации и автоматические системы освещения.

Использование передачи энергии в резисторе

Когда электрический ток протекает через резистор, часть электрической энергии преобразуется в тепловую энергию.