Что значит сила тока — Значения слов

Сила тока
Электрическая мощность
Электрическое сопротивление Сила тока — физическая величина I, равная отношению количества заряда ΔQ, прошедшего через некоторую поверхность за время Δt, к величине этого промежутка времени:

$I=\frac{\Delta Q}{\Delta t}.$

В качестве рассматриваемой поверхности часто используется поперечное сечение проводника .

Обычно обозначается символом I, от .

Сила тока в Международной системе единиц измеряется в амперах (русское обозначение: А; международное: A), ампер является одной из семи основных единиц СИ . 1 А = 1 Кл / с .

По закону Ома сила тока I для участка цепи прямо пропорциональна приложенному напряжению U к участку цепи и обратно пропорциональна сопротивлению R проводника этого участка цепи:

$I = \frac{U}{R}.$

По закону Ома для полной цепи

$I = \frac{\varepsilon}{R+r}$

Носителями заряда, движение которых приводит к возникновению тока, являются заряженные частицы, в роли которых обычно выступают электроны , ионы или дырки . Сила тока зависит от заряда q этих частиц, их концентрации n, средней скорости упорядоченного движения частиц $\vec {v_{cp}}$, а также площади S и формы поверхности, через которую течёт ток.

Если n и $\vec {v_{cp}}$ постоянны по объёму проводника, а интересующая поверхность плоская, то выражение для силы тока можно представить в виде

I = qnvcosαS, 

где α

— угол между скоростью частиц и вектором нормали к поверхности.

В более общем случае, когда сформулированные выше ограничения не выполняются, аналогичное выражение можно записать только для силы тока dI, протекающего через малый элемент поверхности площадью dS:

dI = qnvcosαdS.

Тогда выражение для силы тока, протекающего через всю поверхность, записывается в виде интеграла по поверхности

$I = \int \limits_S q n v_{cp} \cos \alpha dS.

$

В металлах заряд переносят электроны, соответственно в этом случае выражение для силы тока имеет вид

$I = \int \limits_S e n v_{cp} \cos \alpha dS.$

где e — элементарный электрический заряд .

Вектор $q n \vec {v_{cp}}$ называют плотностью электрического тока . Как следует из сказанного выше, его величина равна силе тока, протекающей через малый элемент поверхности единичной площади, расположенный перпендикулярно скорости $\vec {v_{cp}}$, а направление совпадает с направлением упорядоченного движения заряженных частиц.

Для измерения силы тока используют специальный прибор — амперметр (для приборов, предназначенных для измерения малых токов, также используются названия миллиамперметр, микроамперметр, гальванометр ). Его включают в разрыв цепи в том месте, где нужно измерить силу тока. Основные методы измерения силы тока: магнитоэлектрический , электромагнитный и косвенный (путём измерения вольтметром напряжения на известном сопротивлении).

В случае переменного тока различают мгновенную силу тока, амплитудную силу тока и эффективную силу тока .

Физика — 8

6.5. Сила тока и ее измерение

При сравнении рек Кура и Велвели, впадающих в Каспийское море, легко можно определить, что количество воды, проходящее через их поперечное сечение за один и тот же отрезок времени, разное. Аналогично этому различается и количество заряда, проходящее через поперечное сечение спирали лампы и нагревателя в единицу времени.

• Можно ли определить количество электрического заряда, проходящего через поперечное сечение проводника в единицу времени? В какой степени важно это знать?

ИССЛЕДОВАНИЕ-1

• В чем причина различия в свечении электрических ламп?

Оборудование: источник тока, ключ, разные лампы (2 шт.), соединительные провода.

Ход работы:

1. Соберите электрическую цепь на основании данной схемы (a).
2. Замкните ключ, пронаблюдайте за свечением ламп (b).

Обсудите результаты:

• Почему разные лампы, подключенные к одному и тому же источнику тока, светятся с разной яркостью?
• К какому выводу можно прийти из опыта? Каковы ваши предложения?

Для сравнения и вычисления количества электрического заряда, проходящего через поперечное сечение проводника за данный промежуток времени, используется физическая величина, называемая

силой тока:

Формула	Единица измерения
I = q t, где I — сила тока, q — количество заряда, проходящего через поперечное сечение провода, t — время, затраченное на прохождение этого заряда.	[I] = 1[q] [t] = 1Кл с = 1A. Единица измерения силы тока в системе СИ ампер (1A).
Определение	Определение
Сила тока — это скалярная величина, численно равная количеству электрического заряда, проходящего через поперечное сечение проводника за одну секунду.	Ампер — есть сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м друг от друга, вызвал бы на каждом участке проводника длиной 1 м силу взаимодействия, равную 2· 10-7 Н.

20.1 Ток – Колледж физики

Глава 20 Электрический ток, сопротивление и закон Ома

Резюме

• Определение электрического тока, силы тока и скорости дрейфа
• Опишите направление потока заряда в обычном токе.
• Использовать скорость дрейфа для расчета тока и наоборот.

Электрический ток определяется как скорость, с которой течет заряд. Большой ток, например, используемый для запуска двигателя грузовика, перемещает большое количество заряда за короткое время, в то время как слабый ток, например, используемый для работы ручного калькулятора, перемещает небольшое количество заряда в течение короткого времени. длительный период времени. В форме уравнения

электрический ток [латекс]{I}[/латекс] определяется как

[латекс] {I =} [/ латекс] [латекс] {\ гидроразрыва {\ Delta Q} {\ Delta t}} [/ латекс]

, где [латекс]{\Delta Q}[/латекс] — количество заряда, проходящего через данную область за время [латекс]{\Delta t}[/латекс]. (Как и в предыдущих главах, начальное время часто принимается равным нулю, и в этом случае [латекс] {\ дельта t = t} [/латекс].) (См. рис. 1.) Единица СИ для тока — ампер . (A), названный в честь французского физика Андре-Мари Ампера (1775–1836). Поскольку [latex]{I = \Delta Q / \Delta t}[/latex], мы видим, что ампер равен одному кулону в секунду:

[латекс]{1 \;\textbf{A} = 1 \;\text{C} / \text{s}}[/latex]

В амперах (или амперах) указаны не только предохранители и автоматические выключатели, но и многие электроприборы.

Рисунок 1. Скорость потока заряда текущая. Ампер — это поток в один кулон через площадь за одну секунду.

Пример 1: Расчет токов: ток в аккумуляторной батарее грузовика и портативном калькуляторе

(a) Какой ток возникает, когда аккумуляторная батарея грузового автомобиля приводится в движение с зарядом 720 Кл за 4,00 с при запуске двигателя? б) Сколько времени потребуется заряду 1,00 Кл, чтобы пройти через карманный калькулятор, если через него протекает ток 0,300 мА?

Стратегия

Мы можем использовать определение тока в уравнении [латекс]{I = \Delta Q / \Delta t}[/латекс], чтобы найти ток в части (а), так как заряд и время данный.

В части (b) мы меняем определение тока и используем заданные значения заряда и тока, чтобы найти требуемое время.

Решение для (a)

Ввод заданных значений заряда и времени в определение тока дает

[латекс]\begin{array}{r @{{}={}} l} {I} & {\ frac {\ Delta Q} {\ Delta t} = \ frac {720 \; \ text {C}} {4,00 \; \ text {s}} = 180 \; \ text {C} / \ text { s}} \\[1em] & {180 \;\textbf{A}}. \end{массив}[/латекс]

Обсуждение для (a)

Это большое значение тока иллюстрирует тот факт, что большой заряд перемещается за небольшой промежуток времени. Токи в этих «стартерах» довольно велики, поскольку при приведении чего-либо в движение необходимо преодолевать большие силы трения.

Решение для (b)

Решение соотношения [латекс]{I = \Delta Q / \Delta t}[/latex] для времени [латекс]{\Delta t}[/латекс] и ввод известные значения заряда и тока дают 93 \;\текст{ы}}. \end{array}[/latex]

Обсуждение для (b)

Это время чуть меньше часа. Небольшой ток, используемый ручным калькулятором, требует гораздо больше времени для перемещения меньшего заряда, чем большой ток стартера грузовика. Так почему же мы можем работать с нашими калькуляторами всего через несколько секунд после их включения? Это потому, что калькуляторы требуют очень мало энергии. Такие малые требования к току и энергии позволяют портативным калькуляторам работать от солнечных батарей или работать много часов от небольших батарей. Помните, что в калькуляторах нет движущихся частей, как в двигателе грузовика с цилиндрами и поршнями, поэтому технология требует меньших токов.

На рис. 2 показана простая схема и стандартное схематическое представление батареи, проводящего пути и нагрузки (резистора). Схемы очень полезны для визуализации основных особенностей схемы. Одна схема может отображать множество ситуаций. Схема на рис. 2(b), например, может представлять что угодно: от аккумулятора грузовика, подключенного к фаре, освещающей улицу перед грузовиком, до небольшой батареи, подключенной к фонарику-ручке, освещающему замочную скважину в двери.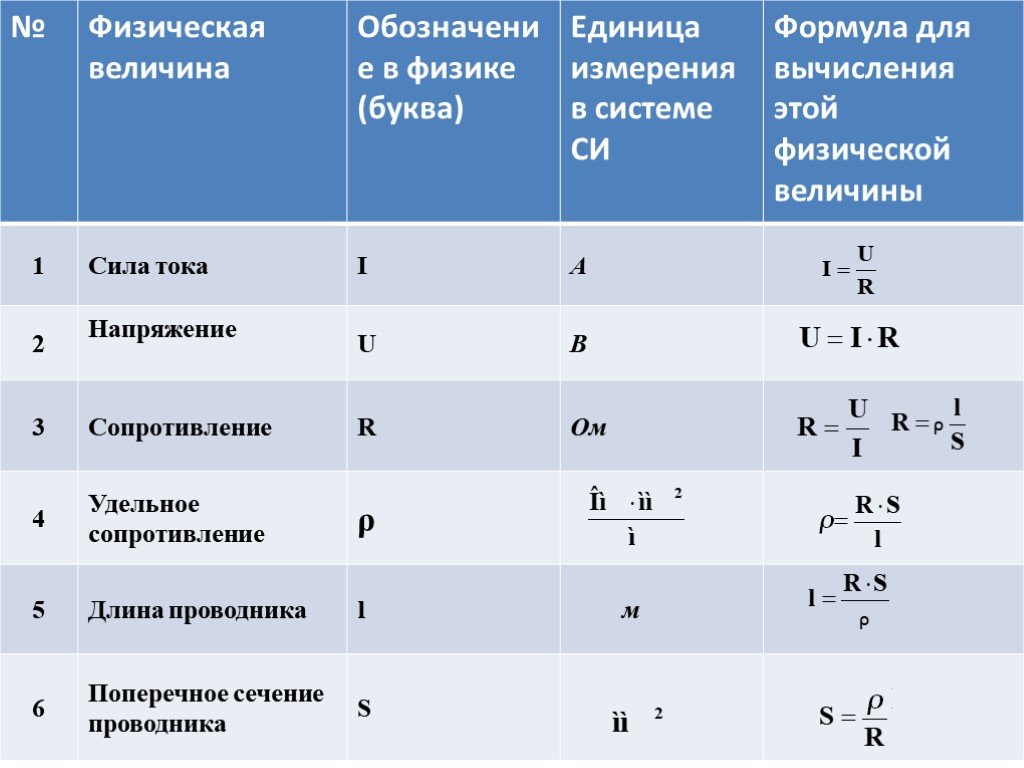 Такие схемы полезны, потому что анализ одинаков для самых разных ситуаций. Нам нужно понять несколько схем, чтобы применить концепции и анализ ко многим другим ситуациям.

Рис. 2. (а) Простая электрическая цепь. Замкнутый путь для протекания тока обеспечивается проводящими проводами, соединяющими нагрузку с клеммами батареи. (b) На этой схеме батарея представлена ​​двумя параллельными красными линиями, проводники показаны прямыми линиями, а зигзаг представляет собой нагрузку. Схема представляет большое разнообразие подобных схем.

Обратите внимание, что направление тока на рис. 2 — от положительного к отрицательному. Направление обычного тока — это направление, в котором будет течь положительный заряд . В зависимости от ситуации могут перемещаться положительные заряды, отрицательные заряды или и то, и другое. В металлических проводах, например, ток переносится электронами, то есть движутся отрицательные заряды. В ионных растворах, таких как соленая вода, движутся как положительные, так и отрицательные заряды. Это верно и для нервных клеток. Генератор Ван де Граафа, используемый для ядерных исследований, может производить ток чисто положительных зарядов, таких как протоны. Рисунок 3 иллюстрирует движение заряженных частиц, составляющих ток. Тот факт, что обычный ток направлен в направлении, в котором будет течь положительный заряд, можно проследить до американского политика и ученого Бенджамина Франклина в 1700-х годах. Он назвал тип заряда, связанного с электронами, отрицательным задолго до того, как стало известно, что они несут ток во многих ситуациях. Франклин, по сути, совершенно не знал о мелкомасштабной структуре электричества.

Важно понимать, что в проводниках, ответственных за производство тока, существует электрическое поле, как показано на рисунке 3. В отличие от статического электричества, где проводник, находящийся в равновесии, не может иметь в себе электрического поля, проводники, по которым течет ток, имеют электрическое поле. поле и не находятся в статическом равновесии. Электрическое поле необходимо для подачи энергии для перемещения зарядов.

Установление связей: домашнее исследование — иллюстрация электрического тока

Найдите соломинку и горошины, которые могут свободно перемещаться в соломе. Положите соломинку на стол и наполните ее горошком. Когда вы вставляете одну горошину с одного конца, другая горошина должна выскочить с другого конца. Эта демонстрация представляет собой аналогию электрического тока. Определите, что сравнивается с электронами и что сравнивается с запасом энергии. Какие еще аналогии вы можете найти для электрического тока?

Обратите внимание, что движение гороха основано на физическом столкновении горошин друг с другом; электроны текут за счет взаимно отталкивающих электростатических сил.

Рис. 3. Ток I — это скорость, с которой заряд проходит через площадь A , такую ​​как поперечное сечение провода. Условный ток определен для движения в направлении электрического поля. {-19-}{\text{s}}} \end{array}[/latex]

Обсуждение

Заряженных частиц, движущихся даже в малых течениях, так много, что отдельные заряды не замечаются, как отдельные воды молекулы не замечаются в потоке воды. Еще более удивительно то, что они не всегда продолжают двигаться вперед, как солдаты на параде. Скорее они похожи на толпу людей с движением в разных направлениях, но общей тенденцией двигаться вперед. В металлической проволоке происходит множество столкновений с атомами и, конечно же, с другими электронами. 9{-4} \;\text{m} / \text{s}}[/latex]. Как нам согласовать эти две скорости и что это говорит нам о стандартных проводниках?

Высокая скорость электрических сигналов обусловлена ​​тем, что сила между зарядами быстро действует на расстоянии. Таким образом, когда свободный заряд попадает в провод, как на рис. 4, входящий заряд отталкивает другие заряды впереди себя, которые, в свою очередь, отталкивают заряды дальше по линии. Плотность заряда в системе нельзя легко увеличить, поэтому сигнал передается быстро. Возникающая в результате ударная волна электрического тока движется по системе почти со скоростью света. Точнее, этот быстро движущийся сигнал или ударная волна представляет собой быстро распространяющееся изменение электрического поля.0005 Рисунок 4. Когда заряженные частицы попадают в этот объем проводника, такое же количество быстро вынуждено покинуть его. Отталкивание между одноименными зарядами затрудняет увеличение количества зарядов в объеме. Таким образом, как только входит один заряд, другой почти сразу уходит, быстро перенося сигнал вперед.

Хорошие проводники имеют большое количество свободных зарядов. В металлах свободными зарядами являются свободные электроны. На рис. 5 показано, как свободные электроны движутся по обычному проводнику. Расстояние, которое может пройти отдельный электрон между столкновениями с атомами или другими электронами, весьма мало. Таким образом, траектории электронов кажутся почти случайными, как движение атомов в газе. Но в проводнике есть электрическое поле, которое заставляет электроны дрейфовать в указанном направлении (противоположном полю, поскольку они отрицательны). скорость дрейфа [латекс]{v_d}[/латекс] — средняя скорость свободных зарядов. Скорость дрейфа довольно мала, поскольку так много свободных зарядов. Если у нас есть оценка плотности свободных электронов в проводнике, мы можем рассчитать скорость дрейфа для данного тока. Чем больше плотность, тем ниже скорость, необходимая для данного тока.

Рис. 5. Свободные электроны, движущиеся в проводнике, совершают много столкновений с другими электронами и атомами. Показан путь одного электрона. Средняя скорость свободных зарядов называется скоростью дрейфа v _d , а для электронов — в направлении, противоположном электрическому полю. Столкновения обычно передают энергию проводнику, что требует постоянной подачи энергии для поддержания постоянного тока.

Проводимость электричества и тепла

Хорошие электрические проводники часто также являются хорошими проводниками тепла. Это связано с тем, что большое количество свободных электронов может переносить электрический ток и переносить тепловую энергию.

Столкновения свободных электронов передают энергию атомам проводника. Электрическое поле выполняет работу по перемещению электронов на расстояние, но эта работа не увеличивает кинетическую энергию (и, следовательно, скорость) электронов. Работа передается атомам проводника, возможно повышая температуру. Таким образом, для поддержания протекания тока требуется непрерывная потребляемая мощность. Исключение, конечно, составляют сверхпроводники по причинам, которые мы рассмотрим в одной из последующих глав. Сверхпроводники могут иметь постоянный ток без постоянного источника энергии — большая экономия энергии. Напротив, подача энергии может быть полезной, например, в нити накала лампочки. Подача энергии необходима для повышения температуры вольфрамовой нити, чтобы нить накала светилась.

Установление связей: домашнее расследование — Наблюдение за нитью

Найдите лампочку с нитью накаливания. Посмотрите внимательно на нить и опишите ее строение. К каким точкам присоединяется нить?

Мы можем получить выражение для зависимости между током и скоростью дрейфа, рассмотрев количество свободных зарядов в отрезке провода, как показано на рисунке 6. {-19} \;\text{C}}[/latex].) Ток – это заряд, перемещаемый в единицу времени; таким образом, если все первоначальные заряды перемещаются из этого сегмента за время [латекс] {\ дельта t} [/латекс], ток равен

[латекс] {I =} [/ латекс] [латекс] {\ гидроразрыва {\ Delta Q} {\ Delta t}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва { qnAx}{\Delta t}}.[/latex]

Обратите внимание, что [latex]{x / \Delta t}[/latex] представляет собой величину скорости дрейфа, [latex]{v_{\textbf{d}}}[/latex], поскольку заряды перемещаются на среднее расстояние [латекс]{х}[/латекс] за время [латекс]{\Delta t}[/латекс]. Перестановка терминов дает

[латекс] {I = nqAv _ {\ textbf {d}}} [/латекс],

где [латекс]{I}[/латекс] — ток через провод с площадью поперечного сечения [латекс]{А}[/латекс], изготовленный из материала с плотностью свободного заряда [латекс]{n}[/ латекс]. Каждый из носителей тока имеет заряд [латекс]{q}[/латекс] и движется с дрейфовой скоростью величины [латекс]{v_{\textbf{d}}}[/латекс].

Рис. 6. Все заряды в заштрихованном объеме этой проволоки удаляются за время t , имея дрейфовую скорость v _d = x/t . См. текст для дальнейшего обсуждения.

Обратите внимание, что простая скорость дрейфа — это еще не все. Скорость электрона намного больше скорости его дрейфа. Кроме того, не все электроны в проводнике могут двигаться свободно, а те, которые могут двигаться, могут двигаться несколько быстрее или медленнее скорости дрейфа. Так что же мы подразумеваем под свободными электронами? Атомы в металлическом проводнике упакованы в виде решетчатой ​​структуры. Некоторые электроны находятся достаточно далеко от ядер атомов, поэтому они не испытывают притяжения ядер так сильно, как внутренние электроны. Это свободные электроны. Они не связаны ни с одним атомом, а вместо этого могут свободно перемещаться среди атомов в «море» электронов. Эти свободные электроны реагируют ускорением при приложении электрического поля. Конечно, когда они движутся, они сталкиваются с атомами в решетке и другими электронами, выделяя тепловую энергию, и проводник нагревается. В изоляторе организация атомов и структура не допускают таких свободных электронов. 98 \;\text{m} / \text{s}}[/latex]), чем несущие его заряды.

• Электрический ток [латекс]{I}[/латекс] – это скорость, с которой течет заряд, определяемая выражением

  [латекс] {I = \frac{\Delta Q}{\Delta t}},[/latex]

  , где [latex]{\Delta Q}[/latex] — количество заряда, проходящего через площадь во времени [latex]{\Delta t}[/latex].

• Направление обычного тока принимается за направление, в котором движется положительный заряд.
• Единицей силы тока в системе СИ является ампер (А), где [латекс]{1 \;\textbf{A} = 1 \;\text{C} / \text{s}}[/latex].
• Ток — это поток свободных зарядов, таких как электроны и ионы.
• Скорость дрейфа [латекс]{v_{\textbf{d}}}[/латекс] — это средняя скорость, с которой движутся эти заряды.
• Текущий [латекс]{I}[/латекс] пропорционален скорости дрейфа [латекс]{v_{\textbf{d}}}[/латекс], что выражается соотношением [латекс]{I = nqAv_{\textbf {d}}}[/латекс]. Здесь [латекс]{I}[/латекс] — ток через провод с площадью поперечного сечения [латекс]{А}[/латекс]. Материал проволоки имеет плотность свободного заряда [латекс]{n}[/латекс], а каждый носитель имеет заряд [латекс]{q}[/латекс] и скорость дрейфа [латекс]{v _{\textbf{d} }}[/латекс]. 9{12}}[/latex] раз больше дрейфовой скорости свободных электронов.

Задачи и упражнения

1: Какова сила тока в миллиамперах, создаваемая солнечными элементами карманного калькулятора, через который проходит заряд 4,00 Кл за 4,00 ч?

2: Всего через фонарь проходит заряд 600 Кл за 0,500 ч. Какой средний ток?

3: Какова сила тока, когда типичный статический заряд [латекс]{0,250 \;\mu \text{C}}[/latex] перемещается с вашего пальца на металлическую дверную ручку в [латексе]{1,00 \ ;\mu \text{s}}[/латекс]?

4: Найдите силу тока, когда 2,00 нКл прыгает между расческой и волосами за интервал времени 0,500 – [латекс]\мю\текст{с}[/латекс]. 2 R}[/латекс].)

Рисунок 7. Конденсатор в дефибрилляторе пропускает ток через сердце пациента

8: Во время операции на открытом сердце дефибриллятор может быть использован для выведения пациента из состояния остановки сердца. Сопротивление пути составляет [латекс]{500 \;\Омега}[/латекс], и необходим ток 10,0 мА. Какое напряжение должно быть подано?

9: (а) Дефибриллятор пропускает ток силой 12,0 А через туловище человека за 0,0100 с. Сколько заряда перемещается? б) Сколько электронов проходит по проводам, подсоединенным к пациенту? (См. рисунок две проблемы выше.) 9{++}}[/latex] ядра поражают цель?

14: Повторите приведенный выше пример на Примере 3, но для проволоки из серебра и данного на один атом серебра приходится один свободный электрон.

15: Используя результаты приведенного выше примера на Примере 3, найти скорость дрейфа в медной проволоке двойного диаметра и несущей ток 20,0 А.

16: 1,628 мм. Ток какой величины протекает при скорости дрейфа 1,00 мм/с? (Полезную информацию см. выше в примере 3.)

17: SPEAR, накопительное кольцо диаметром около 72,0 м в Стэнфордском линейном ускорителе (закрыто в 2009 г.), имеет циркулирующий пучок электронов силой 20,0 А, которые движутся почти со скоростью света. (См. рис. 8.) Сколько электронов находится в пучке?

Рис. 8. Электроны, циркулирующие в накопительном кольце SPEAR, образуют ток силой 20,0 А. Поскольку они движутся со скоростью, близкой к скорости света, каждый электрон совершает множество оборотов в секунду.

электрический ток

скорость, с которой течет заряд, I = Δ Q / Δ t

ампер

(ампер) единица силы тока в системе СИ; 1 А = 1 Кл/с

скорость дрейфа

средняя скорость, с которой свободные заряды текут в ответ на электрическое поле

 

17.

2 Текущий | Электрические цепи

Предыдущий 17.1 Разность потенциалов и ЭДС

Следующий 17.3 Сопротивление

17.2 Текущий (ESAFD)

Поток заряда (ESAFE)

Когда мы говорим о токе, мы говорим о том, сколько зарядов проходит мимо фиксированной точки цепи за одну секунду. Подумайте о зарядах, переносимых батареей по цепи, в проводах есть заряды, но если их нет. это батарея, которую они не будут двигаться.

Когда один заряд перемещается, заряды рядом с ним также перемещаются. Они сохраняют расстояние, как если бы у вас была трубка с шариками. как на этой картинке или посмотрел на поезд и его вагоны.

Если вы втолкнете один шарик в трубу, один должен выйти с другой стороны, если локомотив поезда перемещает все вагоны движутся немедленно, потому что они соединены. Это похоже на заряды в проводах цепи.

Идея состоит в том, что если батарея начала управлять зарядом в цепи, все заряды начинают двигаться мгновенно.

Бенджамин Франклин сделал предположение о направлении потока заряда при натирании гладкого воска грубой шерстью. Он считал, что заряды перетекают от воска к шерсти (то есть от положительного к отрицательному), что было противоположно к реальному направлению. Из-за этого говорят, что электроны имеют отрицательных зарядов и поэтому объекты, которые Бен Франклин назвал «отрицательным» (имея в виду недостаток заряда) действительно наличие избытка электронов. К тому времени, когда было обнаружено истинное направление потока электронов, условность «положительного» и «отрицательный» уже был настолько хорошо принят в научном мире, что не было предпринято никаких усилий, чтобы Измени это.

Медная проволока

Фотография на Flickr.com

Текущий

Ток — это скорость, с которой заряды перемещаются мимо фиксированной точки в цепи. Единицы тока ампер (А), который определяется как один кулон в секунду.

Количество: Текущий (I)         Название единицы: ампер        Обозначение единицы измерения: A

9{-1}$}\)).

\[I = \frac{Q}{\Delta t}\]

Когда в цепи течет ток, мы показываем это на диаграмме, добавляя стрелки. Стрелки показывают направление течь в цепи. Условно мы говорим, что заряд течет от положительной клеммы батареи к отрицательный терминал.

Если напряжение достаточно высокое, ток может проходить почти через все. В примере с плазменным шаром на слева создается напряжение, достаточно высокое, чтобы заряд протекал через газ в шаре. напряжение очень высокое, но результирующий ток очень низкий. Это делает его безопасным для прикосновения.

временный текст

Амперметр (ESAFF)

Амперметр — это прибор, используемый для измерения скорости электрического тока в цепи. Так как один заинтересован в измерении тока, протекающего через компонент цепи, амперметр должен быть подключен в серии с измеренным компонентом цепи.

Амперметр

Построение схем

Построить схемы для измерения ЭДС и разности потенциалов на клеммах аккумулятора. Некоторые общие элементы (компоненты), встречающиеся в электрических цепях, включают лампочки, аккумуляторы, соединительные провода, переключатели, резисторы, вольтметры и амперметры. О многих из них вы уже узнали. Ниже приведен таблица с предметами и их обозначениями:

Компонент	Символ	Применение
лампочка		светится, когда через него проходит заряд
батарея		обеспечивает энергию для заряда для перемещения
переключатель		позволяет разомкнуть или замкнуть цепь
резистор		сопротивляется потоку заряда
	ИЛИ
вольтметр 903:50		измеряет разность потенциалов
амперметр		измеряет ток в цепи
соединительный провод		соединяет элементы схемы вместе

Поэкспериментируйте с различными комбинациями компонентов в цепях.

В таблице ниже приведены сведения об использовании каждого из рассмотренных нами измерительных приборов и о том, как это должно быть. подключен к компоненту цепи.

Аккумулятор не производит одинакового тока независимо от того, что к нему подключено. В то время как напряжение, создаваемое батареей, является постоянным, количество подаваемого тока зависит от того, что находится в схема.

Инструмент	Измеренное количество	Правильное соединение
Вольтметр	Напряжение	Параллельно 903:50
Амперметр	Текущий	В серии

Использование счетчиков

Если возможно, подключите счетчики к цепям, чтобы привыкнуть к использованию счетчиков для измерения электрических величин. Если счетчики имеют более одной шкалы, всегда подключайтесь к первой, чтобы счетчик не был поврежден необходимости измерять значения, выходящие за его пределы.

Рабочий пример 1: расчет тока I

Количество заряда, равное \(\text{45}\) \(\text{C}\), проходит мимо точки цепи в \(\text{1}\) \(\text{секунда}\), какова сила тока в цепи?

Проанализируйте вопрос

Нам дают количество заряда и время и просят рассчитать ток. Мы знаем, что ток скорость, с которой заряд проходит мимо фиксированной точки в цепи, поэтому у нас есть вся необходимая информация. У нас есть уже в правильных единицах. 9{-1}$} \\ Я & = \текст{45}\текст{ А} \конец{выравнивание*}

Укажите окончательный результат

Текущий результат равен \(\text{45}\) \(\text{A}\).

Рабочий пример 2: расчет тока II

Количество заряда, равное \(\text{53}\) \(\text{C}\), перемещается мимо фиксированной точки цепи в \(\text{2}\) \(\text{s}\), какова сила тока в цепи?

Проанализируйте вопрос

Нам дают количество заряда и время и просят рассчитать ток. Мы знаем, что ток скорость, с которой заряд проходит мимо фиксированной точки в цепи, поэтому у нас есть вся необходимая информация. У нас есть уже в правильных единицах. 9{-1}$} \\ I & = \text{26,5}\text{ А} \конец{выравнивание*}

Укажите окончательный результат

Текущий результат равен \(\text{26,5}\) \(\text{A}\).

Рабочий пример 3: расчет тока III

95 электронов проходят мимо фиксированной точки цепи за одну десятую секунды, какова сила тока в цепи? схема?

Проанализируйте вопрос

Нам дано количество заряженных частиц, которые проходят мимо фиксированной точки, и время, за которое это происходит. Мы знаем что ток — это скорость, с которой заряд проходит мимо фиксированной точки в цепи, поэтому мы должны определить заряжать. В предыдущей главе мы узнали, что заряд, переносимый электроном, равен \(\text{1,6} \times \текст{10}^{-\текст{19{-\text{16}}\) \(\text{A}\).