Помощь студентам в учёбе от Людмилы Фирмаль
Здравствуйте!
Я, Людмила Анатольевна Фирмаль, бывший преподаватель математического факультета Дальневосточного государственного физико-технического института со стажем работы более 17 лет. На данный момент занимаюсь онлайн обучением и помощью по любыми предметам. У меня своя команда грамотных, сильных бывших преподавателей ВУЗов. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И не важно: она по объёму на две формулы или огромная сложно структурированная на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.
Срок выполнения разный: возможно онлайн (сразу пишите и сразу помогаю), а если у Вас что-то сложное – то от двух до пяти дней.
Для качественного оформления работы обязательно нужны методические указания и, желательно, лекции. Также я провожу онлайн-занятия и занятия в аудитории для студентов, чтобы дать им более качественные знания.
Моё видео:
youtube.com/embed/4sKc0lcxi7g» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Вам нужно написать сообщение в Telegram . После этого я оценю Ваш заказ и укажу срок выполнения. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за заказ, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл заказа в личные сообщения.
Сколько может стоить заказ?Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа?Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Сначала пришлите задание, я оценю, после вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Какие гарантии и вы исправляете ошибки?В течение 1 года с момента получения Вами заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Качественно сфотографируйте задание, или если у вас файлы, то прикрепите методички, лекции, примеры решения, и в сообщении напишите дополнительные пояснения, для того, чтобы я сразу поняла, что требуется и не уточняла у вас. Присланное качественное задание моментально изучается и оценивается.
Теперь напишите мне в Telegram или почту и прикрепите задания, методички и лекции с примерами решения, и укажите сроки выполнения. Я и моя команда изучим внимательно задание и сообщим цену.
Если цена Вас устроит, то я вышлю Вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Мы приступим к выполнению, соблюдая указанные сроки и требования. 80% заказов сдаются раньше срока.
После выполнения отправлю Вам заказ в чат, если у Вас будут вопросы по заказу – подробно объясню. Гарантия 1 год. В течении 1 года я и моя команда исправим любые ошибки в заказе.
youtube.com/embed/g4ioDc7sLwU» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
youtube.com/embed/zW5JhiZ4140″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Можете смело обращаться к нам, мы вас не подведем. Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
В заключение хочу сказать: если Вы выберете меня для помощи на учебно-образовательном пути, у вас останутся только приятные впечатления от работы и от полученного результата!
Жду ваших заказов!
С уважением
Пользовательское соглашение
Политика конфиденциальности
Задачи на закон Ома для полной цепи
Репетитор
по физике
916 478 1032
Репетитор
по алгебре
916 478 1032
Задачи на закон Ома для полной цепи .
\( I= \dfrac{\varepsilon }{R+r} \)
\(I\)- Сила тока цепи
\(\varepsilon \) — ЭДС источника питания, [Вольт]
\(r \)- внутреннее сопротивление источника, [Ом]
\(R \) -сопротивление внешней цепи [Ом]
Чаще всего на схемах внутреннее сопротивление источника тока не изображается отдельно от источника, считаю что это усложняет понимание данной темы и провоцирует ошибки для осваивающих тему: «Закон Ома для полной цепи»
Мы всегда будем изображать внутреннее сопротивление источника рядом с ним
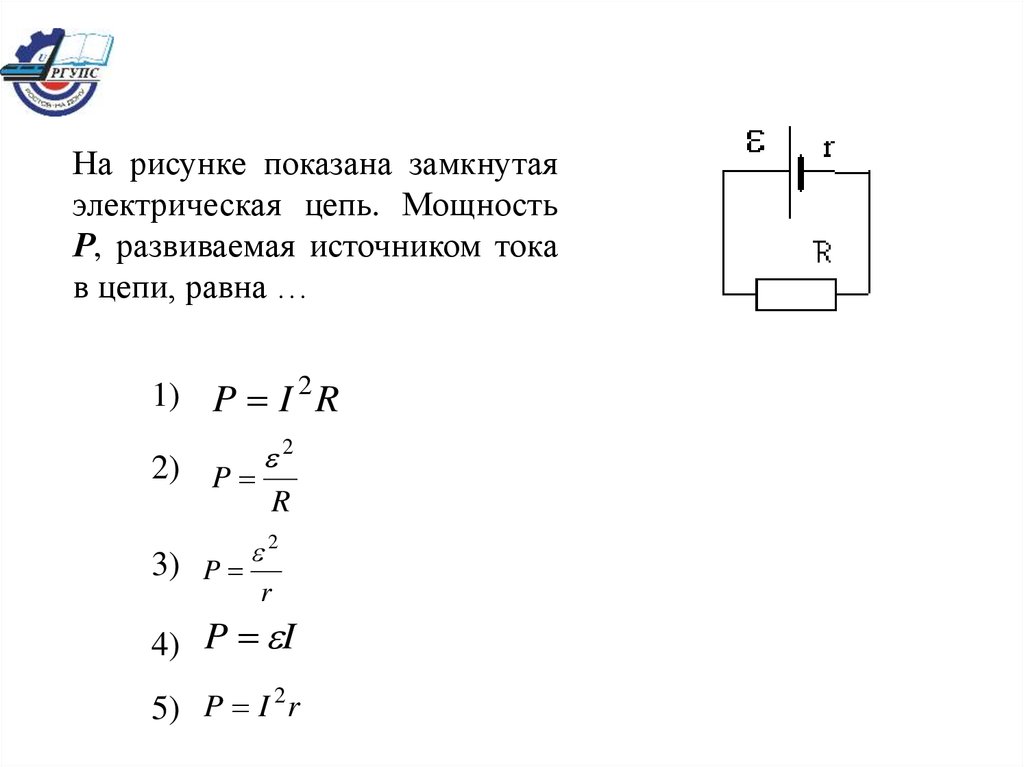
Задача 1.
На схеме, изображенной на рисунке ЭДС источника тока \(\varepsilon=12 Вольт \), внутреннее сопротивление
источника тока \(r=2 Ом\), сопротивление внешней цепи \(R=22 Ом\)
Вычислить силу тока цепи.
Показать ответ Показать решение Видеорешение
Ответ: \( I= 0,5 A \)
Дано:
\( r=2 Ом \)
\( R=22 Ом \)
\(\varepsilon=12 Вольт \)
\(I-?\)
\( I= \dfrac{\varepsilon }{R+r} \) \( I= \dfrac{ 12 В }{22 Ом +2 Ом}= 0,5 A \)
Ответ: \( I= 0,5 A \)
Задача 2. (закон Ома для полной цепи)
Сила тока в электрической цепи, изображенной на рисунке равна 2 Ампера, внутреннее
сопротивление батареи \(r=1 Ом\), сопротивление внешней цепи \(R=19 Ом\)
Найти ЭДС батареи \(\varepsilon \)
Показать ответ Показать решение Видеорешение
Ответ: \( \varepsilon=40 Вольт \)
Запишем закон Ома для полной цепи,
после чего умножим обе части уравнения на \((R+r)\)
Дано:
\( r=1 Ом \)
\( R=19 Ом \)
\(I=2А \)
\(\varepsilon-?\)
\( I= \dfrac{\varepsilon }{R+r} \) \(I(R+r)=\dfrac{\varepsilon }{(R+r)}\cdot (R+r) \)
\(I(R+r)=\varepsilon \)
\( \varepsilon=I(R+r) \)
\( \varepsilon=2А \cdot (19 Ом+1 Ом)=40 Вольт \)
Ответ: \( \varepsilon=40 Вольт \)
Ниже приведено решение этой задачи для «ленивых»
Задача 2.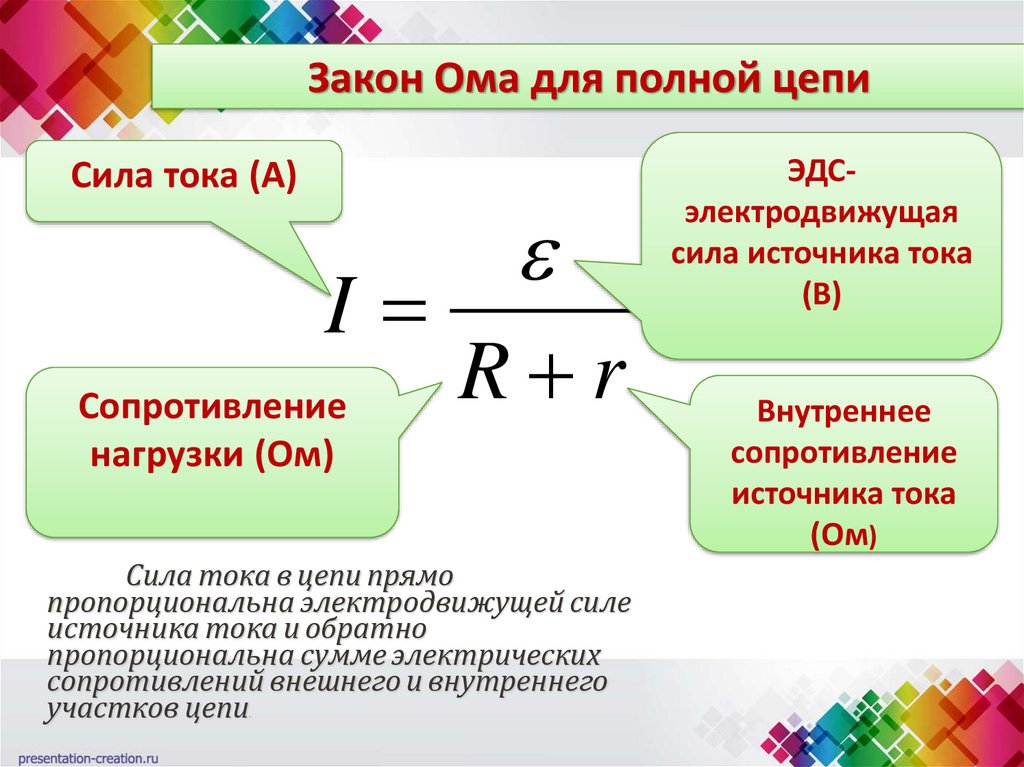 (Решение для ленивых)
(Решение для ленивых)
Сила тока в электрической цепи, изображенной на рисунке равна 2 Ампера, внутреннее
сопротивление батареи \(r=1 Ом\), сопротивление внешней цепи \(R=19 Ом\)
Найти ЭДС батареи \(\varepsilon \)
Показать ответ Показать решение Видеорешение
Ответ: \( \varepsilon=40 Вольт \)
Запишем закон Ома для полной цепи,
после чего просто вставим числа:
Дано:
\( r=1 Ом \)
\( R=19 Ом \)
\(I=2А \)
\(\varepsilon-?\)
\( I= \dfrac{\varepsilon }{R+r} \) \(2=\dfrac{\varepsilon }{19+1} \)
\(2=\dfrac{\varepsilon }{20} \)
\(2 \cdot 20=\varepsilon \)
\( \varepsilon=40 Вольт \)
Ответ: \( \varepsilon=40 Вольт \)
Задача 3. (закон Ома для полной цепи)
(закон Ома для полной цепи)
ЭДС источника тока в цепи, изображенной на рисунке \(\varepsilon=6 Вольт \), сила тока в этой
цепи составляет 3 Ампера, внутреннее сопротивление источника \(r=0,5 Ом .\)
Найти сопротивление внешней цепи \(R\)
Показать ответ Показать решение Видеорешение
Ответ: \( R=1,5 Ом \)
Запишем закон Ома для полной цепи,
после чего умножим обе части уравнения на \((R+r)\)
Дано:
\( r=0,5 Ом \)
\( \varepsilon =6 Вольт \)
\(I=3 А \)
\(R-?\)
\( I= \dfrac{\varepsilon }{R+r} \) \(I(R+r)=\dfrac{\varepsilon }{(R+r)}\cdot (R+r) \)
\(I(R+r)=\varepsilon \)
\(IR+Ir=\varepsilon \)
\(IR=\varepsilon-Ir \)
\(R=\dfrac{\varepsilon-Ir}{I} \)
\(R=\dfrac{6В-3А \cdot 0,5 Ом}{3А}=1,5 Ом \)
Ответ: \(R=1,5 Ом \)
Ниже приведено решение этой задачи для «ленивых»
Задача 3. (решение для ленивых)
(решение для ленивых)
ЭДС источника тока в цепи, изображенной на рисунке \(\varepsilon=6 Вольт \), сила тока в этой
цепи составляет 3 Ампера, внутреннее сопротивление источника \(r=0,5 Ом .\)
Найти сопротивление внешней цепи \(R\)
Показать ответ Показать решение Видеорешение
Ответ: \( R=1,5 Ом \)
Запишем закон Ома для полной цепи,
после чего просто вставим числа
Дано:
\( r=0,5 Ом \)
\( \varepsilon =6 Вольт \)
\(I=3 А \)
\(R-?\)
\( I= \dfrac{\varepsilon }{R+r} \) \( 3= \dfrac{6 }{R+0,5} \)
\( 3(R+0,5)= 6 \)
\( 3R+1,5= 6 \)
\( 3R= 6-1,5 \)
\( 3R= 4,5 \)
\( R= 4,5:3 \)
\(R=1,5 Ом\)
Ответ: \(R=1,5 Ом \)
Задача 7.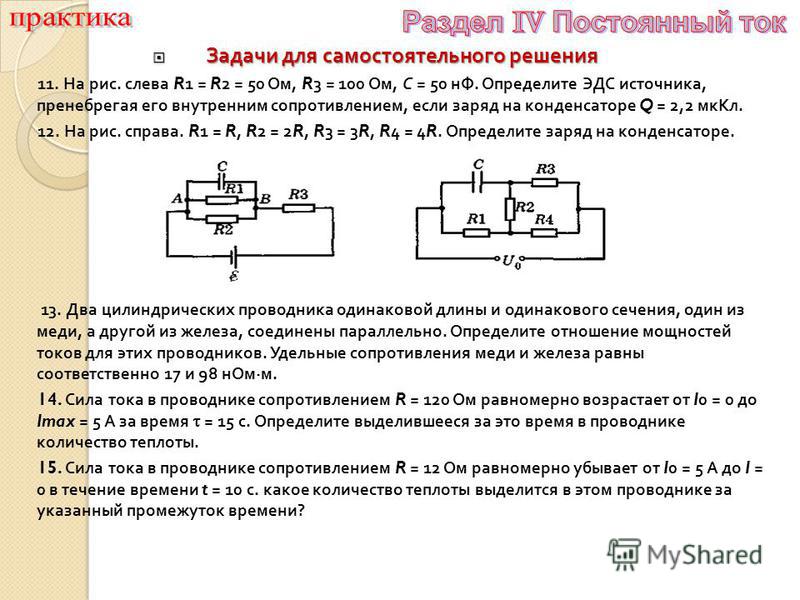 (закон Ома для полной цепи)
(закон Ома для полной цепи)
ЭДС батареи в электрической цепи, изображенной на рисунке \(\varepsilon=6 Вольт \), сила тока в этой
цепи составляет 3 Ампера,
внутреннее сопротивление батареи \(r=0,5 Ом .\)
Найти показания вольтметра
Показать ответ Показать решение Видеорешение
Ответ: \( U= 4,5 Вольт \)
Вольтметр показывает напряжение на резисторе \(R\) Зная силу тока цепи и сопротивление \(R\) сможем найти напряжение на резисторе \(R\) по закону Ома \(U=IR\) Запишем закон Ома для полной цепи,
Дано:
\( r=0,5 Ом \)
\( \varepsilon =6 Вольт \)
\(I=3 А \)
\(U-?\)
\( I= \dfrac{\varepsilon }{R+r} \) \(I(R+r)=\dfrac{\varepsilon }{(R+r)}\cdot (R+r) \)
\(I(R+r)=\varepsilon \)
\(IR+Ir=\varepsilon \)
\(IR=\varepsilon-Ir \)
\(U=\varepsilon-Ir \)
\(U=6В-3А \cdot 0,5 Ом=4,5 Вольт \)
Ответ: \(U= 4,5 Вольт \)
Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса — ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший «Салат из свеклы с чесноком» Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т. Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. |
Лабораторная работа №8 Изучение закона Ома для участка цепи Цель работы: изучить зависимость силы тока на участке цепи от напряжения, приложенного к его концам, и сопротивления. Оборудование: источник постоянного тока, амперметр, вольтметр, реостат, ключ, соединительные провода, набор резисторов. Содержание и метод выполнения работы
Напряжение, сила тока и сопротивление — физические величины, характеризующие явления, происходящие в электрических цепях. Эти величины связаны между собой. Эту связь впервые изучил немецкий физик Ом. Закон Ома звучит так: сила тока на участке цепи прямо пропорциональна напряжению на этом участке (при заданном сопротивлении) и обратно пропорциональна сопротивлению участка (при заданном напряжении). Работа заключается в проверке этих утверждений. Меняя напряжение, приложенное к концам участка цепи заданного сопротивления, можно отследить изменение силы тока и сделать вывод от зависимости . Изменяя сопротивление участка цепи при заданном напряжении на его концах можно сделать вывод о зависимости .
Порядок выполнения работы 1. 2. Соберите цепь по рисунку и схеме (используйте резистор 5 Ом). Измерьте силу тока: I1 = _________ 3. К концам исследуемого проводника присоедините вольтметр и измерьте напряжение:U1 = ________ 4. С помощью реостата измените силу тока и напряжение и снимите показания с амперметра и вольтметра: I2 = ________ U2 = ________ 5. Вновь с помощью реостата измените силу тока и напряжение и снимите показания с амперметра и вольтметра: I3 = ________ U3 = ________ 6. Результаты измерений занесите в таблицу.
7. 8. Сделайте вывод о зависимости силы тока в проводнике от напряжения на его концах при постоянном сопротивлении. ____________________________________________________________________________________________________________________________________________________________________________ 9. Исследуйте зависимость силы тока на участке цепи от сопротивления (реостат исключить из цепи): включайте в цепь поочередно несколько резисторов с известным сопротивлением и снимайте показания амперметра. Результаты занесите в таблицу:
10.
11. Сделайте вывод о зависимости силы тока в проводнике от его сопротивления при постоянном напряжении на его концах. ____________________________________________________________________________________________________________________________________________________________________________ Вывод: ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Контрольные вопросы:
1. Что такое сила тока? По какой формуле ее можно вычислить? 2. Каковы максимальные значения силы тока и напряжения, безопасные для человека? 3. 4. Сформулируйте закон Ома для участка цепи. 5. Какой формулой выражается зависимость сопротивления проводника от температуры?
Оценка:__________________________ Лабораторная работа №10 Измерение ЭДС и внутреннего сопротивления источника тока Цель работы: вычислить ЭДС и внутреннее сопротивление источника постоянного тока по результатам измерений силы тока в цепи и напряжения на участке цепи. Оборудование: амперметр, вольтметр, два резистора, соединительные провода, источник тока.
Содержание и метод выполнения работы Согласно закону Ома для полной цепи ЭДС источника, его внутреннее сопротивление, сила тока в цепи и сопротивление внешней цепи связаны соотношением:
Если к исследуемому источнику тока подключать поочередно два резистора с разными сопротивлениями, то, измеряя при этом силу тока в обоих случаях, можно записать два уравнения, из которых легко вычислить ЭДС и внутреннее сопротивление источника: и Решая совместно два уравнения получим: ; ; и подставляя найденное значение r в одно из выражений: или получим значение ЭДС. Порядок выполнения работы
1. Подготовьте таблицу для отчета по работе:
2. Соберите электрическую цепь с резистором R1 по схеме: Измерьте силу тока: ________ 3. Замените резистор R1 на R2 и вновь измерить силу тока: ________ 4. Подставляя найденные значения для силы тока и внешнего сопротивления, в закон Ома для полной цепи, получите систему из двух уравнений с двумя неизвестными, решая которую, определите ЭДС источника и его внутреннее сопротивление: _________ =________ 5. __________ 6. Рассчитайте погрешности измерений: =____________ =______________ Вывод: ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Контрольные вопросы:
1. Дайте определение сторонним силам. 2. Что такое ЭДС в каких единицах она измеряется? 3. Сформулируйте закон Ома для полной цепи. 4. По какой формуле вычисляется сила тока короткого замыкания? 5. Какое значение будет принимать сила тока в разомкнутой цепи? Оценка:__________________________ Доверь свою работу ✍️ кандидату наук! Имя Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности |
А батарея Э.Д.С. 2 В, а внутреннее сопротивление заряжается током 5 А. В каком направлении будет течь ток внутри батареи? Чему равна разность потенциалов между двумя выводами батареи? : Кейсонс Образование
Видеолекции
Доступ к более чем 500 часам видеолекций в режиме 24/7, охватывающих полную программу подготовки к ЕГЭ.
Онлайн-поддержка
Отработайте более 30000+ вопросов, начиная с базового уровня и заканчивая продвинутым уровнем JEE.
Сеанс устранения сомнений в реальном времени
Задавайте свои сомнения в прямом эфире каждый день. Присоединяйтесь к нашему сеансу устранения сомнений в прямом эфире, проводимому нашими экспертами.
Национальные пробные тесты
Проведите тесты, чтобы проанализировать свой прогресс и оценить, на каком уровне вы находитесь с точки зрения подготовки к ЕГЭ.
Организованное обучение
Правильное планирование завершения учебного плана является ключом к получению достойного рейтинга в JEE.
Серия тестов/Ежедневные задания
Проведите тесты, чтобы проанализировать свой прогресс и оценить, на каком уровне вы находитесь с точки зрения подготовки к ЕГЭ.
ПОГОВОРИТЬ С КОНСУЛЬТАНТОМ? НАЖМИТЕ ЗДЕСЬ
Загрузить вопросник и решение JEE Загрузить Важные вопросы JEE Загрузить полную программу по математике, физике и химии
Батарея Э.Д.С. 2 В и внутреннее сопротивление заряжается током 5 А. В каком направлении будет течь ток внутри батареи? Чему равна разность потенциалов между двумя выводами батареи?
2,5 В
2,6 В
2,7 В
2,9 В
легкий
Раствор
Правильный вариант
2,5 В
Ток будет течь от положительной клеммы к отрицательной клемме в аккумуляторе. Во время зарядки разность потенциалов = В + Ir = 2 + 5 0,1 = 2,5 В.
Загрузить вопросник и решение JEE Загрузить Важные вопросы JEE Загрузить Полный курс по математике, физике, химии
ПОХОЖИЕ ВОПРОСЫ
Q1
Определить токи I 1 , I 2 и I 3 для показанной ниже сети
а. I 1 = ––, b. I 2 = ––, c. I 3 = ––
I 1 = ––, b. I 2 = ––, c. I 3 = ––
средний Посмотреть решение
Q2
Найдите ток, обеспечиваемый источником на рис. Резисторы установлены вокруг в цилиндрической форме.
легкий Посмотреть решение
3 квартал
Параллельная комбинация резистора и неизвестного резистора R соединена последовательно с резистором и батареей. Затем эту схему разбирают и три резистора соединяют последовательно друг с другом и с одной и той же батареей. В обоих случаях ток через резистор одинаков. Какое неизвестное сопротивление R ?
средний Посмотреть решение
4 квартал
Для цепи резисторов, показанной на рис., падение потенциала между a и b составляет 12 В. Найдите
а. Ток через сопротивление –––––.
б. Ток через сопротивление –––––.
в. Ток через сопротивление 8 ––––.
легкий Посмотреть решение
Q5
Для цепи на рис.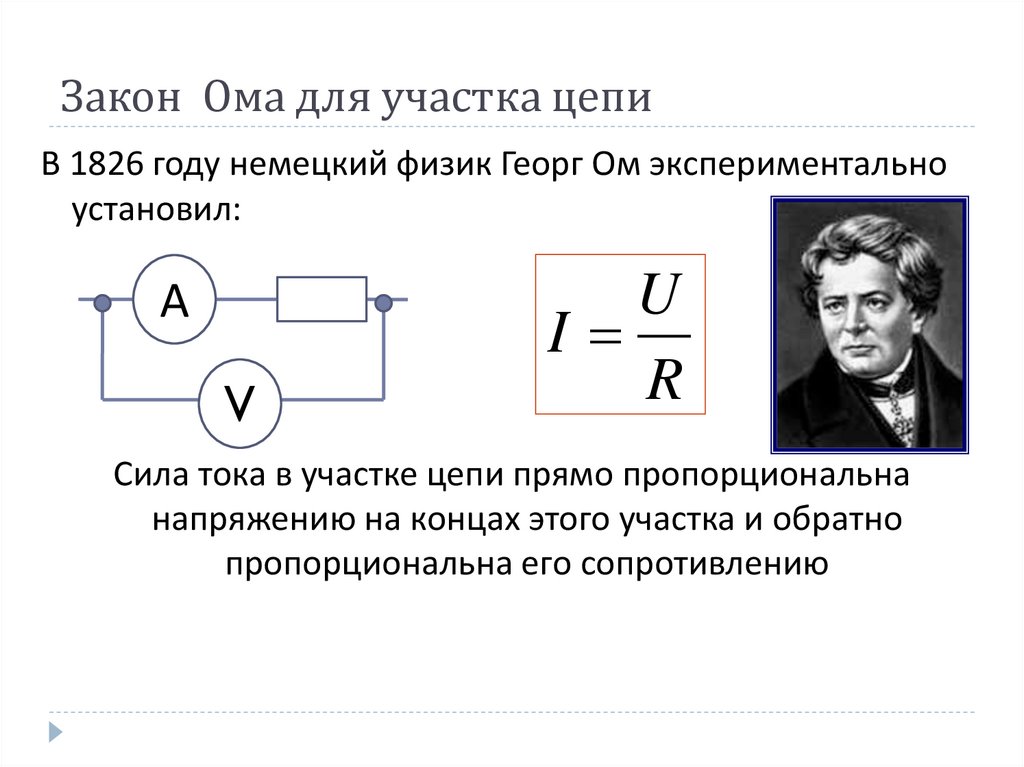 найти разность потенциалов между точками а и b .
найти разность потенциалов между точками а и b .
легкий Посмотреть решение
Q6
Найти ток в каждом резисторе цепи, изображенной на рис.
а. Ток через сопротивление –––––.
б. Ток через сопротивление –––––.
в. Ток через сопротивление –––––.
д. Ток через сопротивление –––––.
легкий Посмотреть решение
Q7
Учитывая, что по ответвлению от 9 проходит 5,0 Аот 0073 C до B на рис. Какое напряжение в точках A , D и G ?
а. В А = — б. V D = –– c. В Г = ––
трудный Посмотреть решение
Q8
Рассчитайте ток через сопротивление, соединенное между МН и , и ток, отдаваемый каждой из батарей по принципиальной схеме, показанной на рис. 9.0005
легкий Посмотреть решение
Q9
Если каждое сопротивление в показанной сети равно R , то каково сопротивление между A и B.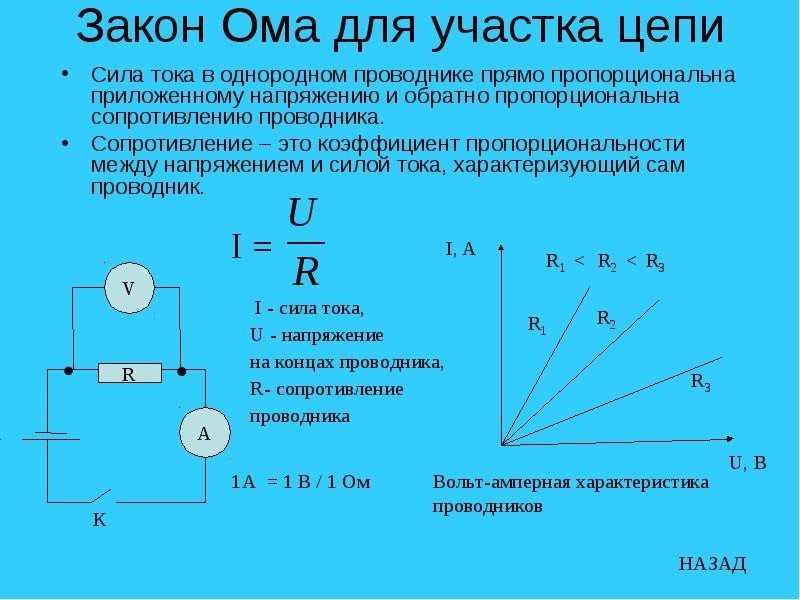
easy Посмотреть решение
Q10
Найдите Э.Д.С. ( В ) и внутреннее сопротивление ( r ) of a single battery which is equivalent to a parallel combination of two batteries of e.m.f.s V 1 and V 2 and internal resistance r 1 and r 2 , соответственно, с полярностью, как показано на рис.
трудный Посмотреть решение
Почему напряжение на клеммах меньше ЭДС при разрядке аккумулятора?
Эквивалентная схема батареи приведена ниже. Источник напряжения можно представить как источник ЭДС с внутренним последовательным сопротивлением.
При отсутствии нагрузки ток, протекающий через аккумулятор или элемент, равен нулю, а напряжение на клеммах точно равно ЭДС элемента или аккумулятора.
Когда элемент или батарея подключены к нагрузке, батарея подает ток на нагрузку. Теперь, если мы измерим напряжение на нагрузке (то есть в той же точке на клеммах батареи), измеренное напряжение будет несколько меньше, чем ЭДС батареи. Измеренное напряжение на выводе батареи, когда батарея подает ток на нагрузку, называется напряжение на клеммах.
Теперь, если мы измерим напряжение на нагрузке (то есть в той же точке на клеммах батареи), измеренное напряжение будет несколько меньше, чем ЭДС батареи. Измеренное напряжение на выводе батареи, когда батарея подает ток на нагрузку, называется напряжение на клеммах.
В чем причина снижения напряжения батареи? Внутри батареи должно быть некоторое падение напряжения. Да, падение напряжения происходит внутри элемента из-за внутреннего сопротивления батареи. Внутреннее сопротивление источника напряжения равно нулю для идеального источника напряжения. Однако источник напряжения никогда не может быть идеальным источником, и его внутреннее сопротивление не может быть равно нулю. Внутреннее сопротивление батареи или элемента можно свести к минимуму, выбрав соответствующую металлургию для материалов батареи.
Источник напряжения имеет некоторое внутреннее сопротивление, которое вызывает падение напряжения при разрядке батареи, а напряжение на клеммах будет меньше, чем ЭДС батареи во время разрядки. Одинаково ли напряжение на клеммах для всех типов нагрузок? Нет, это зависит от величины нагрузки. Чем выше значение нагрузки, тем больше будет ток от батареи и, следовательно, напряжение на клеммах будет меньше. Поясним это явление с помощью закона напряжения Кирхгофа.
Одинаково ли напряжение на клеммах для всех типов нагрузок? Нет, это зависит от величины нагрузки. Чем выше значение нагрузки, тем больше будет ток от батареи и, следовательно, напряжение на клеммах будет меньше. Поясним это явление с помощью закона напряжения Кирхгофа.
В приведенной выше схеме нагрузка бесконечна, а ток, протекающий через батарею, равен нулю. Падение напряжения на внутреннем сопротивлении I L R s равно нулю, поскольку I L равно нулю, и в этом состоянии говорят, что батарея разомкнута. В разомкнутом состоянии напряжение на клеммах батареи равно ЭДС батареи.
Напряжение ячейки с ЭДС V подключено к нагрузке R L . Ячейка подает ток I L в нагрузку. По закону напряжения Кирхгофа сумма падений потенциала в замкнутой электрической цепи равна нулю.
V = I L R s + I L R L
V = I L R s + (V T /R L ) R L
V = I L R s + V T
Если батарея разомкнута, I L = 0
R 8 L 0087 S + I L R L
V = 0 x R S + (V T /R L ) R L
V = 0+ V T 8
V = 0+ V T
999999999999797979999999799799999999999999999999999999999999999999999999999999999999999999999999999999999999999999 99988 8 9.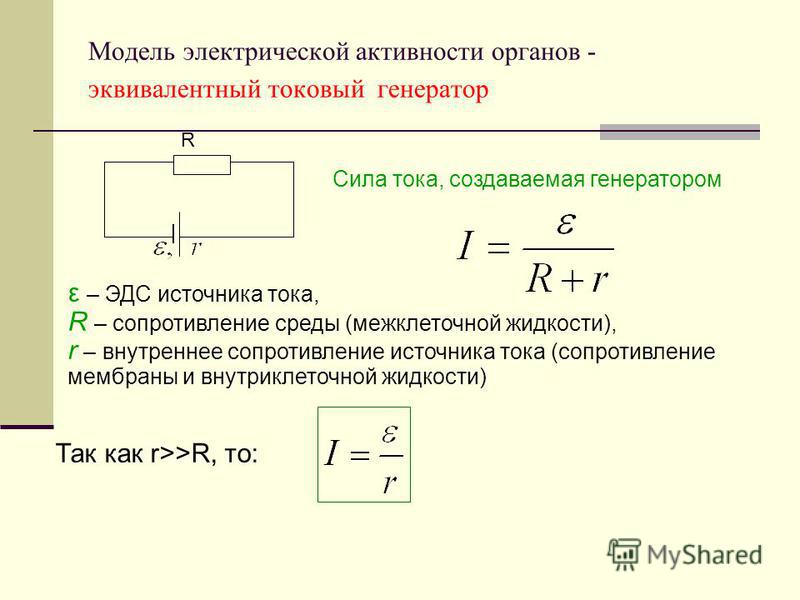 9. . T =V
9. . T =V
Когда батарея не подключена к нагрузке, ток нагрузки равен нулю, а ЭДС батареи равна напряжению на клеммах.
Теперь, если нагрузка подключена к батарее, батарея начинает подавать ток на нагрузку.
В = I Л Р s + I L R L
V = I L R s + (V T /R L ) R L
V = I L R s + V T
V T = V- I L R s
Из приведенного выше видно, что напряжение на клемме V T меньше, чем ЭДС батареи. Причиной меньшего напряжения на клеммах, когда батарея находится под нагрузкой, является падение напряжения внутри батареи, вызванное внутренним сопротивлением батареи R с .
Напряжение на клеммах дополнительно зависит от величины нагрузки. Ток нагрузки зависит от значения сопротивления нагрузки. Меньшее значение сопротивления нагрузки приводит к тому, что батарея потребляет больше тока, и, следовательно, больше падение напряжения происходит внутри батареи, и напряжение на клеммах будет меньше. Давайте разберемся в этом на наглядном примере.
Меньшее значение сопротивления нагрузки приводит к тому, что батарея потребляет больше тока, и, следовательно, больше падение напряжения происходит внутри батареи, и напряжение на клеммах будет меньше. Давайте разберемся в этом на наглядном примере.
Когда через батарею не протекает ток, напряжение на клеммах равно ЭДС батареи. ЭДС батареи равно 9.вольт, а напряжение на клеммах равно ЭДС батареи, равной 9 вольтам.
Случай 2: Когда батарея находится под нагрузкой – нагрузка равна 9 ОмКогда батарея на 9 В ЭДС подключена к сопротивлению 9 Ом, батарея будет подавать ток 1,49 А. ток в цепи и напряжение на клеммах 8,94 вольта. Падение напряжения на внутреннем сопротивлении батареи составляет 0,015 вольта.
Случай 3: Когда батарея находится под нагрузкой – нагрузка 6 Ом Когда батарея 9вольт ЭДС подключен к сопротивлению 6 Ом, батарея будет подавать 0,99 ампер. ток в цепи и напряжение на клеммах 8,91 вольт. Падение напряжения на внутреннем сопротивлении батареи 0,001 вольт.
ток в цепи и напряжение на клеммах 8,91 вольт. Падение напряжения на внутреннем сопротивлении батареи 0,001 вольт.
Из приведенного выше видно, что падение напряжения на внутреннем сопротивлении увеличивается с увеличением тока.
Когда через батарею не протекает ток, напряжение на клеммах равно ЭДС батареи. ЭДС батареи составляет 9 вольт, а напряжение на клеммах равно ЭДС батареи, то есть 9 вольт.вольт.
Напряжение на клеммах уменьшается с увеличением тока нагрузки или тока через аккумулятор. График, показывающий взаимосвязь между напряжением и током, показан ниже.
Наглядный пример: Батарея имеет ЭДС 9 вольт и внутреннее сопротивление 0,1 Ом. Вычислите
а) Рассчитайте напряжение на клеммах батареи, когда она подключена к нагрузке 15 Ом.
b) Напряжение на клеммах при подключении к нагрузке 1,0 Ом.
б) При подключении батареи к нагрузке 1,0 Ом
Статьи по теме :
- Что такое аккумуляторная кислота? Его композиция и роли
- батарея VRLA — регулируемый клапан свинцовой кислотной батареи
- Преимущества батарей с капустами и батареей
- .
 и таких как мы:
и таких как мы:Внутреннее сопротивление клетки — Наука A-Level
- Поиск
- Присоединяйтесь к более чем 1,2 миллионам студентов каждый месяц
- Ускорьте свое обучение на 29%
- Неограниченный доступ всего от 6,99 фунтов стерлингов в месяц
Выдержки из этого документа…
Тема: Внутреннее сопротивление элемента
Цель: Измерение внутреннего сопротивления и ЭДС (разности потенциалов на источнике напряжения, когда ток отсутствует) и наблюдение за комбинацией элементов
Гипотеза: ЭДС старого элемента меньше, чем ЭДС нового элемента, но внутреннее сопротивление старого элемента намного больше, чем нового элемента.
Введение:
Сопротивление электричеству, свойство электрической цепи или части цепи, преобразующее электрическую энергию в тепловую энергию при противодействии электрическому току. Сопротивление связано со столкновениями заряженных частиц, несущих ток, с неподвижными частицами, составляющими структуру проводников. Сопротивление часто считают локализованным в таких устройствах, как лампы, нагреватели, резисторы, в которых оно преобладает, хотя оно свойственно каждому участку цепи, в том числе соединительным проводам и линиям электропередач. (Британника.2006)
Сопротивление связано со столкновениями заряженных частиц, несущих ток, с неподвижными частицами, составляющими структуру проводников. Сопротивление часто считают локализованным в таких устройствах, как лампы, нагреватели, резисторы, в которых оно преобладает, хотя оно свойственно каждому участку цепи, в том числе соединительным проводам и линиям электропередач. (Британника.2006)Рассеивание электрической энергии в виде тепла, хотя и небольшое, влияет на величину электродвижущей силы или управляющего напряжения, необходимого для создания заданного тока в цепи. Фактически, электродвижущая сила V (измеряемая в вольтах) в цепи, деленная на силу тока I (ампер) в этой цепи, количественно определяет величину электрического сопротивления R. А именно, R = V/I. Таким образом, если 12-вольтовая батарея постоянно пропускает ток силой 2 ампера по длине провода, провод имеет сопротивление 6 вольт на ампер, или 6 Ом. Ом — общепринятая единица электрического сопротивления, эквивалентная одному вольту на ампер и обозначаемая заглавной греческой буквой омега, Ом.
 Сопротивление провода прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения. Сопротивление также зависит от материала проводника. Зеесопротивление.
Сопротивление провода прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения. Сопротивление также зависит от материала проводника. Зеесопротивление.Сопротивление проводника или элемента цепи обычно увеличивается с повышением температуры. При охлаждении до предельно низких температур некоторые проводники имеют нулевое сопротивление. В этих веществах, называемых сверхпроводниками, продолжают течь токи после устранения приложенной электродвижущей силы.
Величина, обратная сопротивлению 1/R, называется проводимостью и выражается в единицах обратного ома, называемых мОм. (Encarta.2006)
…подробнее.
1,4 вольта
1,49 вольта
Эта схема предназначена, когда элементы
расположены «параллельно» «b», потому что значение ЭДС увеличивается по сравнению с одиночной ячейкой, а ее напряжения увеличиваются больше всего при объединении двух ячеек
Обозначение комбинации ячеек
Комбинация последовательностей Параллельная комбинация0005
(b) (c) (c)
(c)
Результаты старой и новой батареи
Старая батарея
напряжение и токи
Voltage (Volts)
Voltage (Volts)
Voltage (Volts)
(Volts)
±0.
 05
05CURRENTS ( amps)
±0.05
1.30
0.00
1.19
0.10
1.09
0.20
0.97
0.30
0.85
0.40
0.75
0.50
0.60
0.60
Новый аккумулятор
Напряжение и ток
8 VOL0005 ±0.
 05
05CURRENT (I)
±0.05
1.50
0.00
1.49
0.10
1.45
0.20
1.40
0.30
1.39
0.40
1.35
0.50
1.30
0.60
1.20
0.
 70
701.10
0.80
1.09
0,90
1,05
1,00
1,02
11111111111111111111111111111111111111111111111111 год 1,02
9000 1,1099 9000 2,02 1,10980005 1,01
1,20
Две приведенные выше таблицы были получены после того, как токи от реостата были скорректированы, поэтому напряжение зависело от нас. реостат увеличивал напряжение уменьшалось
Графики результатов двух ячеек (старой и новой)
Приведенные выше графики были получены из предыдущей таблицы; он показал ЭДС и внутренние сопротивления двух батарей вместе.
 Самые верхние графики были новой ячейкой, а старая ячейка содержала нижнюю часть сетки.
Самые верхние графики были новой ячейкой, а старая ячейка содержала нижнюю часть сетки.Страница расчета для старого элемента:
Старый аккумулятор
A) Координата линии наилучшего соответствия:
= (0,00, 1,31) и (0,60, 0,62)
Наклон = внутреннее сопротивление (-r)
…читать дальше.
Лучшая комбинация, которую мы нашли после практических экспериментов, была в букве «b», соединенной последовательно, поскольку она удваивала напряжение каждой ячейки.
Величина ЭДС нового элемента составила 1,54 вольта при внутреннем сопротивлении -0,49Ом, а значение ЭДС старого элемента было 1,31 вольта при внутреннем сопротивлении -1,15 Ом
Итак, это выглядит так; сначала новая ячейка богата разностью потенциалов, но со временем внутреннее сопротивление нарастает, что означает, что она переживает свои разности потенциалов (плоская), а затем становится как старая ячейка, потому что ее ЭДС меньше, чем раньше, а внутреннее сопротивление увеличивается
Библиография:
- P.
 Howison, 1999, Physics year 13, ESA Publications (NZ) Ltd, Сингапур
Howison, 1999, Physics year 13, ESA Publications (NZ) Ltd, Сингапур
- Encarta 2006, внутреннее сопротивление, Microsoft Corporation
- Britannica 2006, внутреннее сопротивление, Britannica Corporation
- G.Alex, 23 мая, внутреннее сопротивление, www. battery.com,
Приложение: 1
Фото практического использования старой батареи
На приведенном выше рисунке показаны компоненты батареи вместе с лампочкой
Установка аппарат для новой камеры
…читать дальше.
Эта письменная работа студента является одной из многих, которые можно найти в разделе «Электрофизика и теплофизика» уровня AS и A.
Нашли то, что искали?
Вот что учитель думает об этом сочинении
5 звезд
Это 5-звездочная работа по исследованию ЭДС и внутреннего сопротивления старого и нового элемента. Он также исследует влияние различных комбинаций ячеек на получение максимального напряжения.
 Отличное введение и отличные научные знания и понимание, демонстрируемые повсюду. Хороший четкий план работы и выдвинутые гипотезы. Отличные результаты, но без повторов для надежности. Хорошие графики и анализ результатов с использованием подходящих точных уравнений. В целом отличная работа с хорошими результатами. Логический порядок, которому легко следовать.
Отличное введение и отличные научные знания и понимание, демонстрируемые повсюду. Хороший четкий план работы и выдвинутые гипотезы. Отличные результаты, но без повторов для надежности. Хорошие графики и анализ результатов с использованием подходящих точных уравнений. В целом отличная работа с хорошими результатами. Логический порядок, которому легко следовать.Отмечено учителем Патрисия МакХью 05.13.2013
Не тот? Найдите название своего сочинения…
- Присоединяйтесь к более чем 1,2 миллионам студентов каждый месяц
- Ускорьте свое обучение на 29%
- Неограниченный доступ всего от 6,99 фунтов стерлингов в месяц
Посмотреть связанные эссе
3 звезды
Переключатель S был замкнут, а реостат отрегулирован так, чтобы ячейка пропускала через цепь небольшой ток.
Внутреннее сопротивление является мерой противодействия потоку заряда в источнике питания, таком как сухой элемент в эксперименте.
 Когда электроны проходят через часть внутреннего сопротивления, они должны выделять энергию. Из данных, полученных в эксперименте, мы можем узнать
Когда электроны проходят через часть внутреннего сопротивления, они должны выделять энергию. Из данных, полученных в эксперименте, мы можем узнать
в поисковой катушке, а также магнитное поле вокруг прямого провода. 5. Повторялись шаги 2-4 с другими значениями тока (I) от генератора сигналов с шагом 0,1А. Затем результаты были сведены в таблицу.
1,89 9,96 22,0 8 1,89 9,94 25,0 9 1,89 9,93 27,0 10 1,87 9,90 28,0 11 1,87 9,91 30,0 12 1,88 9,92 31,0 13 1,89 9,94 33,0 14 1,88 9,90 34,0 14 м. 39S 1.88 9,90 34,5 188 9,90 34,0 14 м. 14 м 30,39 с, когда мы достигли нашей целевой температуры.
I0 — первичный ток холостого хода, он включает реактивную или намагничивающую составляющую I0r, которая создает поток, и активную или силовую составляющую I0a, которая компенсирует потери и находится в фазе с V1. Ток холостого хода и коэффициент мощности равны соответственно I0 = V(I0a)2 + (I0r)2 и cos ?0
Другими источниками ошибок могли быть наши показания термометра.



 Как компании прогнозируют привычки и манипулируют ими
Как компании прогнозируют привычки и манипулируют ими д.
д.
 Начертите схему цепи.
Начертите схему цепи.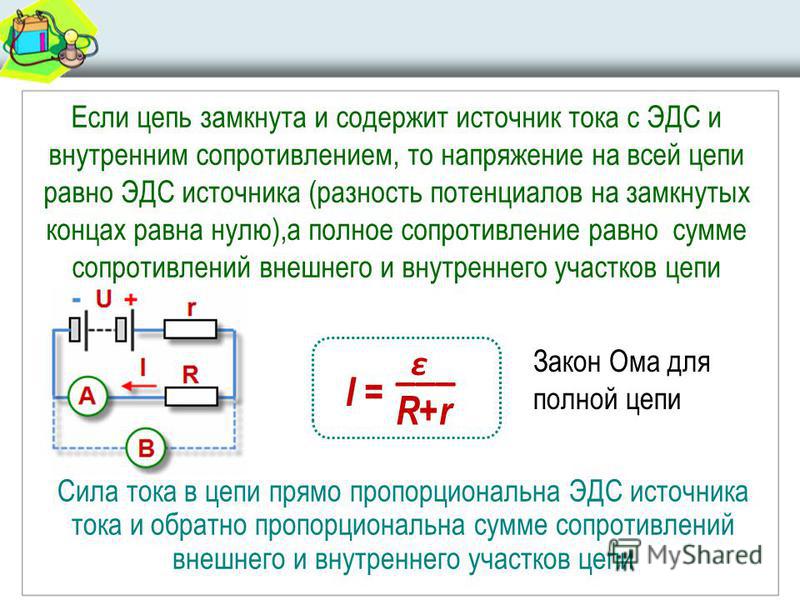 По данным таблицы постройте вольтамперную характеристику резистора I (U).
По данным таблицы постройте вольтамперную характеристику резистора I (U). Постройте график зависимости I(R).
Постройте график зависимости I(R). Какой формулой выражается зависимость сопротивления проводника от его геометрических размеров и вещества, из которого он состоит?
Какой формулой выражается зависимость сопротивления проводника от его геометрических размеров и вещества, из которого он состоит?
 Отключите от источника тока резистор и амперметр. Подключите вольтметр к источнику тока и снимите его показания:
Отключите от источника тока резистор и амперметр. Подключите вольтметр к источнику тока и снимите его показания: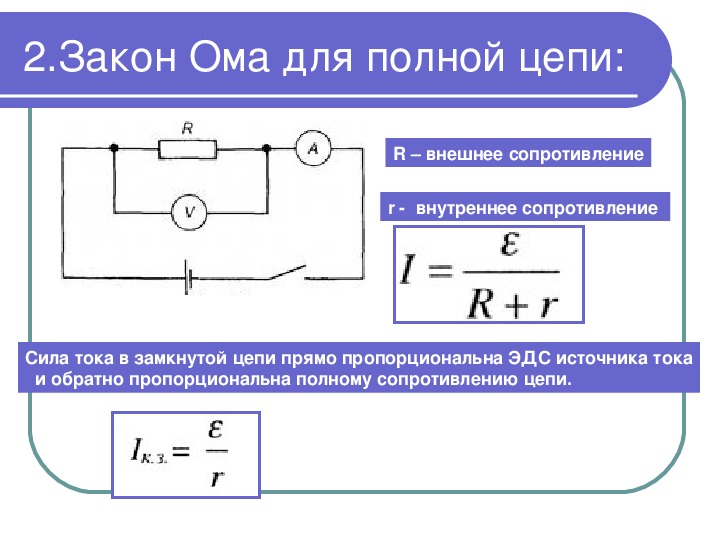 ru Все права принадлежат авторам размещенных материалов. Обратная связь…
ru Все права принадлежат авторам размещенных материалов. Обратная связь… и таких как мы:
и таких как мы: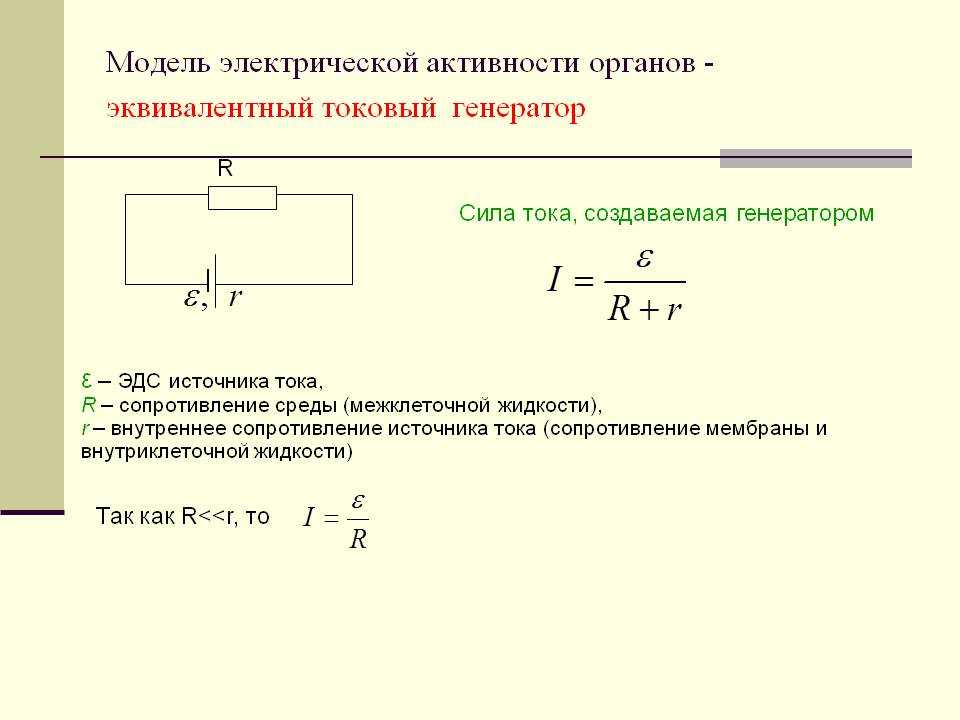 Сопротивление связано со столкновениями заряженных частиц, несущих ток, с неподвижными частицами, составляющими структуру проводников. Сопротивление часто считают локализованным в таких устройствах, как лампы, нагреватели, резисторы, в которых оно преобладает, хотя оно свойственно каждому участку цепи, в том числе соединительным проводам и линиям электропередач. (Британника.2006)
Сопротивление связано со столкновениями заряженных частиц, несущих ток, с неподвижными частицами, составляющими структуру проводников. Сопротивление часто считают локализованным в таких устройствах, как лампы, нагреватели, резисторы, в которых оно преобладает, хотя оно свойственно каждому участку цепи, в том числе соединительным проводам и линиям электропередач. (Британника.2006) Сопротивление провода прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения. Сопротивление также зависит от материала проводника. Зеесопротивление.
Сопротивление провода прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения. Сопротивление также зависит от материала проводника. Зеесопротивление. 05
05 05
05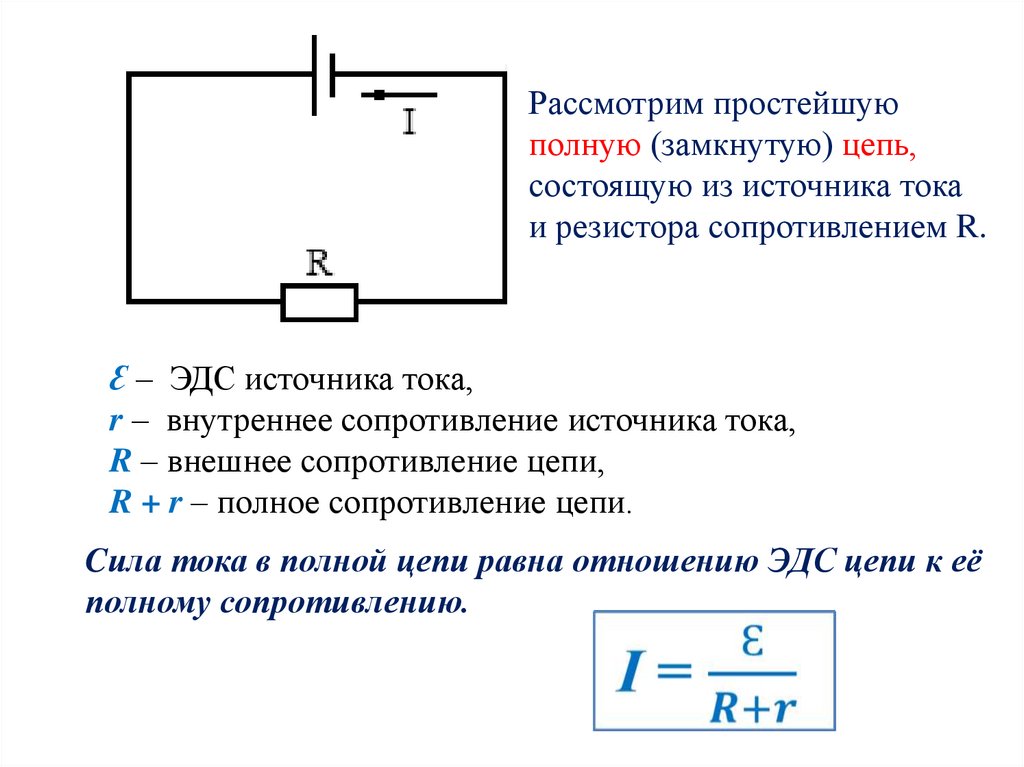 70
70 Самые верхние графики были новой ячейкой, а старая ячейка содержала нижнюю часть сетки.
Самые верхние графики были новой ячейкой, а старая ячейка содержала нижнюю часть сетки. Howison, 1999, Physics year 13, ESA Publications (NZ) Ltd, Сингапур
Howison, 1999, Physics year 13, ESA Publications (NZ) Ltd, Сингапур Отличное введение и отличные научные знания и понимание, демонстрируемые повсюду. Хороший четкий план работы и выдвинутые гипотезы. Отличные результаты, но без повторов для надежности. Хорошие графики и анализ результатов с использованием подходящих точных уравнений. В целом отличная работа с хорошими результатами. Логический порядок, которому легко следовать.
Отличное введение и отличные научные знания и понимание, демонстрируемые повсюду. Хороший четкий план работы и выдвинутые гипотезы. Отличные результаты, но без повторов для надежности. Хорошие графики и анализ результатов с использованием подходящих точных уравнений. В целом отличная работа с хорошими результатами. Логический порядок, которому легко следовать. Когда электроны проходят через часть внутреннего сопротивления, они должны выделять энергию. Из данных, полученных в эксперименте, мы можем узнать
Когда электроны проходят через часть внутреннего сопротивления, они должны выделять энергию. Из данных, полученных в эксперименте, мы можем узнать