Курс физики (Грабовский Р.И.)
Курс физики (Грабовский Р.И.)
ОглавлениеПредисловиеВведение § 1. Предмет физики. Связь физики с другими науками и производством § 2. О единицах измерения и размерности физических величин § 3. О некоторых математических понятиях и символах 1. Физические основы механики § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения § 5. Прямолинейное движение материальной точки § 6. Движение материальной точки по окружности Глава II. Основные законы динамики § 7. Законы Ньютона. Масса и сила § 8. Закон изменения количества движения (импульса) § 9. Закон сохранения количества движения в изолированной системе § 11. Силы трения § 12. Силы тяготения (гравитационные силы) § 13. Центростремительная сила § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции § 15. Вес тел. Ускорение силы тяжести. Невесомость Глава III.  Работа и энергия Работа и энергия§ 16. Работа и мощность § 17. Энергия § 18. Закон сохранения и превращения энергии § 19. О космических скоростях § 20. Границы применимости классической механики Глава IV. Вращательное движение твердого тела § 21. Основной закон динамики вращения § 22. Моменты инерции некоторых тел Глава V. Движение жидкости § 24. Основные определения. Уравнение неразрывности § 25. Уравнение Бернулли § 26. О некоторых приложениях уравнения Бернулли Глава VI. Колебания и волны § 27. Гармоническое колебание и его характеристики § 28. Сложение гармонических колебаний § 29. Динамика колебательного движения. Маятник § 30. О затухающих и вынужденных колебаниях § 31. Волновой процесс § 32. Уравнение волны. Интенсивность волны § 33. Интерференция волн. Стоячие волны § 34. Фронт волны. Принцип Гюйгенса-Френеля § 35.  Основные положения молекулярно-кинетической теории Основные положения молекулярно-кинетической теории§ 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории § 37. О теплоте и температуре § 38. О предмете и методах молекулярной физики Глава VIII. Газы § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная § 41. Основное уравнение кинетической теории идеального газа § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям § 46. Средняя длина свободного пробега молекул § 47. Явления переноса в газах. Уравнение переноса § 48. Диффузия § 49. Теплопроводность § 50.  Внутреннее трение (вязкость) Внутреннее трение (вязкость)Глава IX. Жидкости и твердые тела § 51. Особенности строения жидкостей и твердых тел § 52. Деформация твердого тела § 54. Теплоемкость твердых и жидких тел § 55. Диффузия в жидких и твердых телах § 56. Осмос § 57. Теплопроводность жидких и твердых тел § 58. Вязкость жидкости. Турбулентное движение жидкости § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа § 61. Капиллярные явления; формула Жюрена Глава X. Изменение агрегатного состояния вещества (фазовые превращения) § 62. Понятие о фазовых превращениях и диаграмме состояний вещества § 63. Реальный газ. Уравнение Ван-дер-Ваальса § 64. Опыт Эндрюса. Критическая температура § 66. Испарение и конденсация. Кипение § 67.  Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором§ 68. Плавление и затвердевание (кристаллизация). Возгонка Глава XI. Основы термодинамики § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы § 71. Цикл Карно. Второе начало термодинамики § 72. Энтропия § 73. О статистическом смысле энтропии и второго начала термодинамики § 74. Электризация тел. Электрический заряд § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность § 76 Электрический диполь. Поле диполя § 77. Теорема Остроградского-Гаусса и ее приложения § 78. Работа перемещения заряда в электрическом поле. Потенциал § 79. О неустойчивости статических систем электрических зарядов § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника § 81. Диэлектрики в электрическом поле.  Поляризация диэлектриков Поляризация диэлектриков§ 83. Конденсатор. Энергия электрического поля Глава XIII. Постоянный электрический ток § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока § 86. Разветвленная электрическая цепь. Правила Кирхгофа § 87. Контактная разность потенциалов. Термоэлектрические явления § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды § 93. Типы самостоятельного газового разряда Глава XIV. Электромагнетизм § 94. Постоянный магнит и круговой ток.  Магнитные поля магнитов и токов Магнитные поля магнитов и токов§ 95. Магнитное взаимодействие токов в вакууме; закон Ампера § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа § 97. Некоторые приложения закона Био-Савара-Лапласа § 98. Магнитные поля соленоида и тороида § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях Глава XV. Электромагнитная индукция и переменный ток § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко § 104. Взаимная индукция и самоиндукция § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла § 106.  § 107. Емкостное и индуктивное сопротивления § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи § 109. Понятие о трехфазном токе Глава XVI. Электрические колебания и электромагнитные волны § 110. Электромагнитные волны § 111. Закрытый колебательный контур § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн § 113. Радиосвязь 4. Оптика и атомная физика § 114. Природа света § 115. Отражение и преломление света. Полное отражение § 117. Тонкие линзы. Микроскоп § 118. Глаз как оптическая система. Спектральная чувствительность глаза § 119. Основные фотометрические характеристики § 120. Поглощение света. О физиологическом действии света Глава XVIII. Волновые свойства света § 121. Интерференция света. Интерферометр § 122.  Об интерференции света, отраженного от прозрачных пленок Об интерференции света, отраженного от прозрачных пленок§ 123. Дифракция света. Разрешающая способность оптических приборов § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов § 126. О дифракции микрочастиц и волнах де-Бройля § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя 129. Вращение плоскости колебаний поляризованного света. Поляриметр Глава XIX. Квантовые свойства света и строение атома § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора § 133. Квантовая теория строения атома водорода (по Бору).  Объяснение спектров излучения и поглощения водорода Объяснение спектров излучения и поглощения водорода§ 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света Глава XX. Атомное ядро и внутриядерные процессы § 138. Общие сведения об атомных ядрах. Изотопы § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада § 140. О методах наблюдения и регистрации микрочастиц § 141. Ядерные реакции. Искусственная радиоактивность § 142. Энергия связи и дефект массы атомного ядра § 143. Реакция деления. Цепная реакция. Ядерный реактор § 144. Реакция синтеза (термоядерная реакция). Энергия звезд § 145. Космические лучи. Элементарные частицы § 146. Об использовании ядерной энергии |
8.
 Электрический ток. Сила тока. Плотность тока. Эдс источника тока.
Электрический ток. Сила тока. Плотность тока. Эдс источника тока.Электрический ток — это упорядоченное движение заряженных частиц в проводнике. Чтобы он возник, следует предварительно создать электрическое поле, под действием которого вышеупомянутые заряженные частицы придут в движение.
Первые
сведения об электричестве, появившиеся
много столетий назад, относились к
электрическим «зарядам», полученным
посредством трения. Уже в глубокой
древности люди знали, что янтарь, потертый
о шерсть, приобретает способность
притягивать легкие предметы. Но только
в конце XVI века английский врач Джильберт
подробно исследовал это явление и
выяснил, что точно такими же свойствами
обладают и многие другие вещества. Тела,
способные, подобно янтарю, после натирания
притягивать легкие предметы, он назвал
наэлектризованными. Это слово образовано
от греческого электрон — «янтарь». В
настоящее время мы говорим, что на телах
в таком состоянии имеются электрические
заряды, а сами тела называются
«заряженными».
Электрические заряды всегда возникают при тесном контакте различных веществ. Если тела твердые, то их тесному соприкосновению препятствуют микроскопические выступы и неровности, которые имеются на их поверхности. Сдавливая такие тела и притирая их друг к другу, мы сближаем их поверхности, которые без нажима соприкасались бы только в нескольких точках. В некоторых телах электрические заряды могут свободно перемещаться между различными частями, в других же это невозможно. В первом случае тела называют «проводники», а во втором — «диэлектрики, или изоляторы». Проводниками являются все металлы, водные растворы солей и кислот и др. Примерами изоляторов могут служить янтарь, кварц, эбонит и все газы, находящиеся в нормальных условиях.
Тем
не менее нужно отметить, что деление
тел на проводники и диэлектрики весьма
условно. Все вещества в большей или
меньшей степени проводят электричество.
Электрические заряды бывают положительными
и отрицательными. Такого рода ток
просуществует недолго, потому что в
наэлектризованном теле кончится заряд. Для продолжительного существования
электрического тока в проводнике
необходимо поддерживать электрическое
поле. Для этих целей используются
источники электротока. Самый простой
случай возникновения электрического
тока — это когда один конец провода
соединен с наэлектризованным телом, а
другой — с землей.
Для продолжительного существования
электрического тока в проводнике
необходимо поддерживать электрическое
поле. Для этих целей используются
источники электротока. Самый простой
случай возникновения электрического
тока — это когда один конец провода
соединен с наэлектризованным телом, а
другой — с землей.
Электрические цепи, подводящие ток к осветительным лампочкам и электромоторам, появились лишь после изобретения батарей, которое датируется примерно 1800 годом. После этого развитие учения об электричестве пошло так быстро, что менее чем за столетие оно стало не просто частью физики, но легло в основу новой электрической цивилизации.
Сила тока — скалярная физическая величина, равная отношению заряда, прошедшего через проводник, ко времени, за которое этот заряд прошел.
где I —
сила тока, q — величина
заряда (количество электричества), t —
время прохождения заряда.
Плотность тока — векторная физическая величина, равная отношению силы тока к площади поперечного сечения проводника.
где j —плотность тока, S — площадь сечения проводника.
Направление вектора плотности тока совпадает с направлением движения положительно заряженных частиц.
Электродвижущей силой источника тока называют отношение работы сторонних сил к величине положительного заряда, переносимого от отрицательного полюса источника тока к положительному.
Если
изолированный проводник поместить в
электрическое поле
то
на свободные заряды q в проводнике будет
действовать сила
В
результате в проводнике возникает
кратковременное перемещение свободных
зарядов. Этот процесс закончится тогда,
когда собственное электрическое поле
зарядов, возникших на поверхности
проводника, не скомпенсирует полностью
внешнее поле. Результирующее
электростатическое поле внутри проводника
равно нулю (см. § 4.5). Однако, в
проводниках может при определенных
условиях возникнуть непрерывное
упорядоченное движение свободных
носителей электрического заряда.
Результирующее
электростатическое поле внутри проводника
равно нулю (см. § 4.5). Однако, в
проводниках может при определенных
условиях возникнуть непрерывное
упорядоченное движение свободных
носителей электрического заряда.
Такое движение называется электрическим током. За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле. Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда Δq, переносимого через поперечное сечение проводника (рис. 4.8.1) за интервал времени Δt, к этому интервалу времени:
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным.
1 |
Упорядоченное
движение электронов в металлическом
проводнике и ток I. |
В Международной системе единиц СИ сила тока измеряется в амперах (А). Единица измерения тока 1 А устанавливается по магнитному взаимодействию двух параллельных проводников с током (см. § 4.16). Постоянный электрический ток может быть создан только в замкнутой цепи, в которой свободные носители заряда циркулируют по замкнутым траекториям. Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю (см. § 4.4).
Поэтому
для существования постоянного тока
необходимо наличие в электрической
цепи устройства, способного создавать
и поддерживать разности потенциалов
на участках цепи за счет работы сил
неэлектростатического происхождения.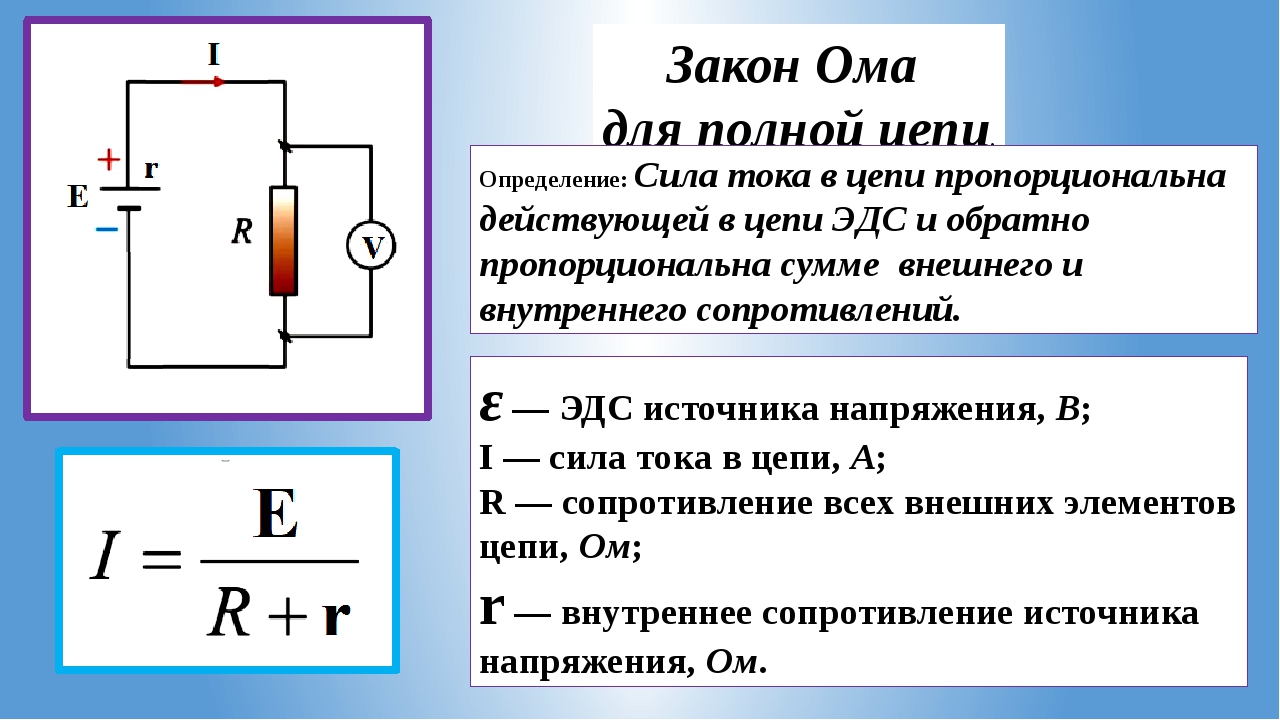 Такие устройства называются источниками
постоянного тока. Силы
неэлектростатического происхождения,
действующие на свободные носители
заряда со стороны источников тока,
называютсясторонними
силами. Природа
сторонних сил может быть различной. В
гальванических элементах или аккумуляторах
они возникают в результате электрохимических
процессов, в генераторах постоянного
тока сторонние силы возникают при
движении проводников в магнитном поле.
Источник тока в электрической цепи
играет ту же роль, что и насос, который
необходим для перекачки жидкости в
замкнутой гидравлической системе.
Такие устройства называются источниками
постоянного тока. Силы
неэлектростатического происхождения,
действующие на свободные носители
заряда со стороны источников тока,
называютсясторонними
силами. Природа
сторонних сил может быть различной. В
гальванических элементах или аккумуляторах
они возникают в результате электрохимических
процессов, в генераторах постоянного
тока сторонние силы возникают при
движении проводников в магнитном поле.
Источник тока в электрической цепи
играет ту же роль, что и насос, который
необходим для перекачки жидкости в
замкнутой гидравлической системе.
Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток. При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу. Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):
Таким
образом, ЭДС определяется работой,
совершаемой сторонними силами при
перемещении единичного положительного
заряда.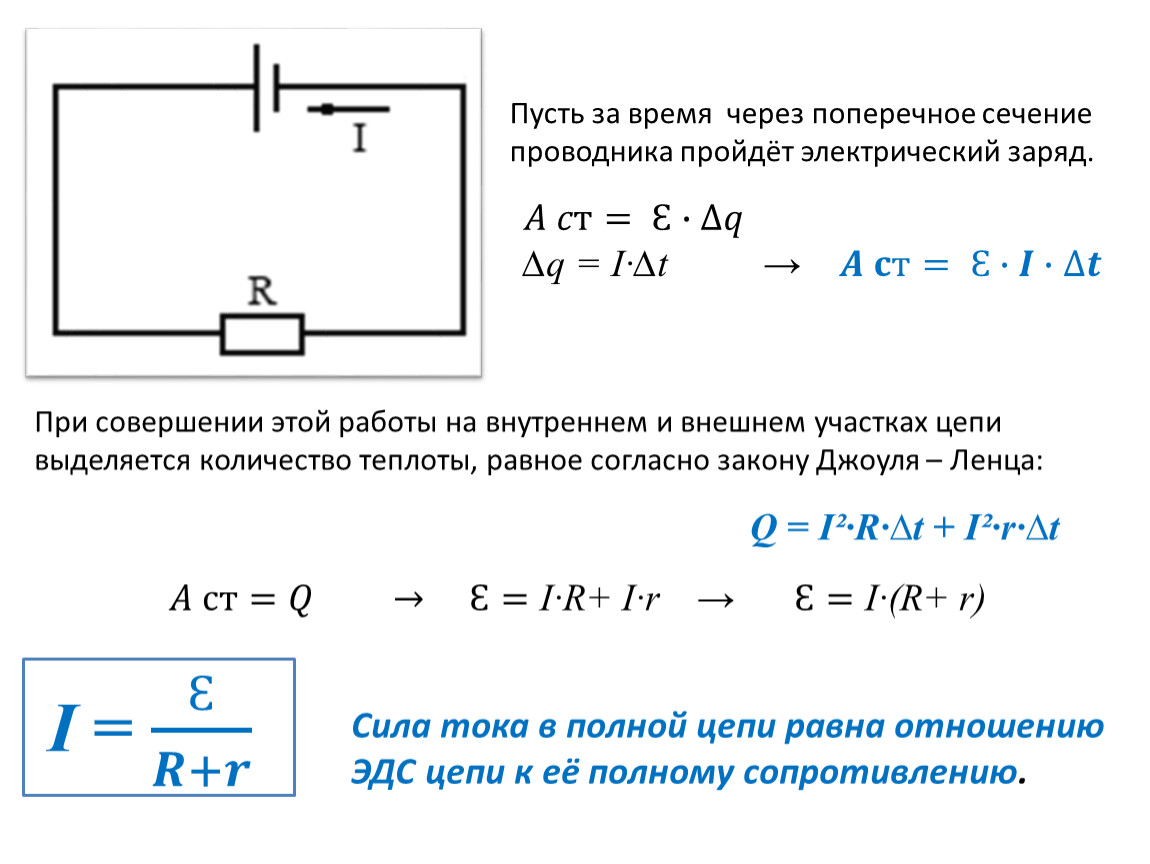 Электродвижущая сила, как и
разность потенциалов, измеряется
в вольтах (В).
При перемещении единичного положительного
заряда по замкнутой цепи постоянного
тока работа сторонних сил равна сумме
ЭДС, действующих в этой цепи, а работа
электростатического поля равна нулю.
Цепь постоянного тока можно разбить на
определенные участки. Те участки, на
которых не действуют сторонние силы
(то есть участки, не содержащие источников
тока), называются однородными.
Участки, включающие источники тока,
называются неоднородными.
При перемещении единичного положительного
заряда по некоторому участку цепи работу
совершают как электростатические
(кулоновские), так и сторонние силы.
Работа электростатических сил равна
разности потенциалов Δφ12 = φ1 – φ2
между начальной (1) и конечной (2) точками
неоднородного участка. Работа сторонних
сил равна по определению электродвижущей
силе
12,
действующей на данном участке. Поэтому
полная работа равна
U12 = φ1 – φ2 +
12.
Электродвижущая сила, как и
разность потенциалов, измеряется
в вольтах (В).
При перемещении единичного положительного
заряда по замкнутой цепи постоянного
тока работа сторонних сил равна сумме
ЭДС, действующих в этой цепи, а работа
электростатического поля равна нулю.
Цепь постоянного тока можно разбить на
определенные участки. Те участки, на
которых не действуют сторонние силы
(то есть участки, не содержащие источников
тока), называются однородными.
Участки, включающие источники тока,
называются неоднородными.
При перемещении единичного положительного
заряда по некоторому участку цепи работу
совершают как электростатические
(кулоновские), так и сторонние силы.
Работа электростатических сил равна
разности потенциалов Δφ12 = φ1 – φ2
между начальной (1) и конечной (2) точками
неоднородного участка. Работа сторонних
сил равна по определению электродвижущей
силе
12,
действующей на данном участке. Поэтому
полная работа равна
U12 = φ1 – φ2 +
12.
Величину
U12 принято называть напряжением на
участке цепи 1–2. В случае однородного
участка напряжение равно разности
потенциалов:
U12 = φ1 – φ2.
В случае однородного
участка напряжение равно разности
потенциалов:
U12 = φ1 – φ2.
Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (то есть проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
где R = const. Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Это соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. В СИ единицей электрического сопротивления проводников служит ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А. Проводники, подчиняющиеся закону Ома, называются линейными.
Графическая
зависимость силы тока I от напряжения
U (такие графики называются вольт-амперными
характеристиками,
сокращенно ВАХ) изображается прямой
линией, проходящей через начало координат. Следует отметить, что существует много
материалов и устройств, не подчиняющихся
закону Ома, например, полупроводниковый
диод или газоразрядная лампа. Даже у
металлических проводников при достаточно
больших токах наблюдается отклонение
от линейного закона Ома, так как
электрическое сопротивление металлических
проводников растет с ростом температуры.
Для участка цепи, содержащего ЭДС, закон
Ома записывается в следующей форме:
IR = U12 = φ1 – φ2 +
= Δφ12 +
.
Следует отметить, что существует много
материалов и устройств, не подчиняющихся
закону Ома, например, полупроводниковый
диод или газоразрядная лампа. Даже у
металлических проводников при достаточно
больших токах наблюдается отклонение
от линейного закона Ома, так как
электрическое сопротивление металлических
проводников растет с ростом температуры.
Для участка цепи, содержащего ЭДС, закон
Ома записывается в следующей форме:
IR = U12 = φ1 – φ2 +
= Δφ12 +
.
Это соотношение принято называть обобщенным законом Ома. На рис. 4.8.2 изображена замкнутая цепь постоянного тока. Участок цепи (cd) является однородным.
2 |
Рисунок 4.8.2. Цепь постоянного тока. |
По закону Ома, IR = Δφcd.
Участок (ab) содержит источник тока с ЭДС, равной . По закону Ома для неоднородного участка, Ir = Δφab + .
Сложив
оба равенства, получим:
I(R + r) = Δφcd + Δφab +
.
Но Δφcd = Δφba = – Δφab. Поэтому
Эта формула выражет закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.Сопротивление r неоднородного участка на рис. 4.8.2 можно рассматривать как внутреннее сопротивление источника тока. В этом случае участок (ab) на рис. 4.8.2 является внутренним участком источника. Если точки a и b замкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (R << r), тогда в цепи потечет ток короткого замыкания
Сила
тока короткого замыкания – максимальная
сила тока, которую можно получить от
данного источника с электродвижущей
силой
и
внутренним сопротивлением r. У источников
с малым внутренним сопротивлением ток
короткого замыкания может быть очень
велик и вызывать разрушение электрической
цепи или источника. Например, у свинцовых
аккумуляторов, используемых в автомобилях,
сила тока короткого замыкания может
составлять несколько сотен ампер. Особенно опасны короткие замыкания в
осветительных сетях, питаемых от
подстанций (тысячи ампер). Чтобы избежать
разрушительного действия таких больших
токов, в цепь включаются предохранители
или специальные автоматы защиты сетей.
Особенно опасны короткие замыкания в
осветительных сетях, питаемых от
подстанций (тысячи ампер). Чтобы избежать
разрушительного действия таких больших
токов, в цепь включаются предохранители
или специальные автоматы защиты сетей.
В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику подсоединяется некоторое внешнее балластное сопротивление. Тогда сопротивление r равно сумме внутреннего сопротивления источника и внешнего балластного сопротивления. Если внешняя цепь разомкнута, то Δφba = – Δφab = , то есть разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС. Если внешнее нагрузочное сопротивление R включено и через батарею протекает ток I, разность потенциалов на ее полюсах становится равной Δφba = – Ir.
На
рис. 4.8.3 дано схематическое изображение
источника постоянного тока с ЭДС
равной
и
внутренним сопротивлением r в трех
режимах: «холостой ход», работа на
нагрузку и режим короткого замыкания
(к. з.). Указаны напряженность
электрического
поля внутри батареи и силы, действующие
на положительные заряды:
–
электрическая сила и
–
сторонняя сила.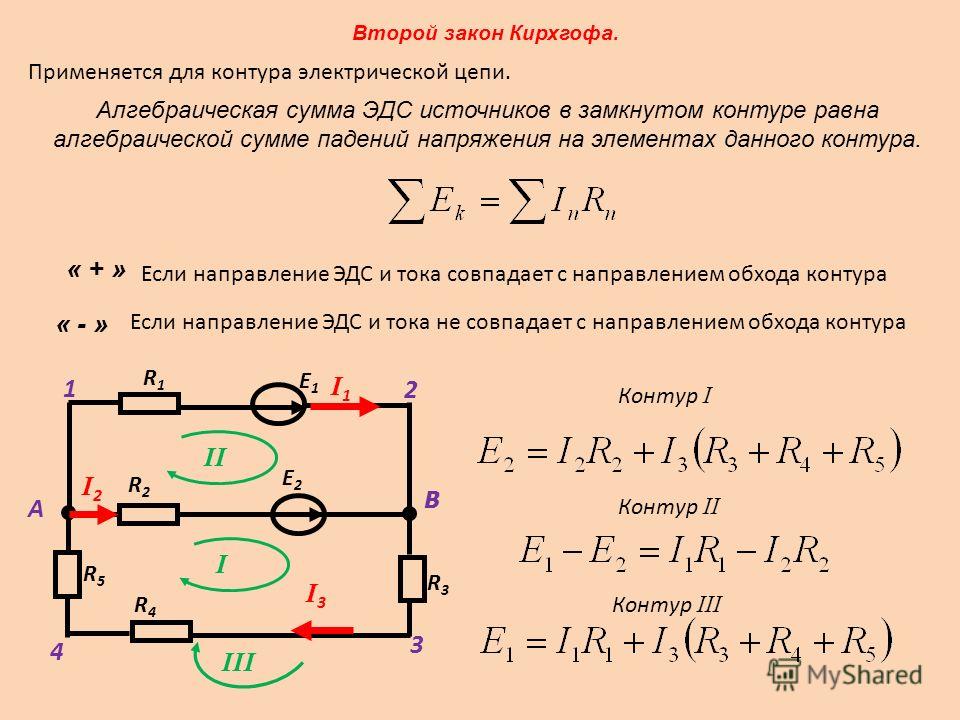 В режиме короткого
замыкания электрическое поле внутри
батареи исчезает.
В режиме короткого
замыкания электрическое поле внутри
батареи исчезает.
3 |
Схематическое изображение источника постоянного тока: 1 – батарея разомкнута; 2 – батарея замкнута на внешнее сопротивление R; 3 – режим короткого замыкания. |
Для
измерения напряжений и токов в
электрических цепях постоянного тока
используются специальные приборы
– вольтметры и амперметры. Вольтметр предназначен
для измерения разности потенциалов,
приложенной к его клеммам. Он
подключается параллельно участку
цепи, на котором производится измерение
разности потенциалов. Любой вольтметр
обладает некоторым внутренним
сопротивлением RB. Для того, чтобы
вольтметр не вносил заметного
перераспределения токов при подключении
к измеряемой цепи, его внутреннее
сопротивление должно быть велико по
сравнению с сопротивлением того участка
цепи, к которому он подключен. Для цепи,
изображенной на рис. 4.8.4, это условие
записывается в виде: RB >> R1
Для цепи,
изображенной на рис. 4.8.4, это условие
записывается в виде: RB >> R1
Это условие означает, что ток IB = Δφcd / RB, протекающий через вольтметр, много меньше тока I = Δφcd / R1, который протекает по узмеряемому участку цепи. Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение. Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением RA. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Для цепи на рис. 4.8.4 сопротивление амперметра должно удовлетворять условию RA << (r – R1 + R2),
чтобы при включении амперметра ток в
цепи не изменялся. Измерительные
приборы – вольтметры и амперметры –
бывают двух видов: стрелочные (аналоговые)
и цифровые. Цифровые электроизмерительные
приборы представляют собой сложные
электронные устройства. Обычно цифровые
приборы обеспечивают более высокую
точность измерений.
Цифровые электроизмерительные
приборы представляют собой сложные
электронные устройства. Обычно цифровые
приборы обеспечивают более высокую
точность измерений.
4 |
Включение амперметра (А) и вольтметра (В) в электрическую цепь. |
Как ЭДС ячейки не зависит от внешнего сопротивления (сопротивления цепи) и потребляемого тока?
$\begingroup$ЭДС — это работа, совершаемая для перемещения заряда по всей цепи. Если у меня есть резистор, не увеличится ли работа, проделанная для перемещения единичного заряда?
- электрические цепи
- электрические токовые
- электрические сопротивления
Как ЭДС ячейки не зависит от внешнего сопротивления (сопротивления цепь) и потребляемый ток?
ЭДС клетки представляет собой электрический потенциал (напряжение), возникающий внутри клетки в результате электрохимических реакций. Он идеально не зависит от внешнего сопротивления цепи и потребляемого тока. Напряжение на клеммах ячейки, $V_T$, не равно. Это потому, что все настоящие батареи имеют внутреннее сопротивление $r_b$. Когда ток потребляется цепью, происходит падение напряжения на внутреннем сопротивлении, что приводит к более низкому напряжению на клеммах.
Он идеально не зависит от внешнего сопротивления цепи и потребляемого тока. Напряжение на клеммах ячейки, $V_T$, не равно. Это потому, что все настоящие батареи имеют внутреннее сопротивление $r_b$. Когда ток потребляется цепью, происходит падение напряжения на внутреннем сопротивлении, что приводит к более низкому напряжению на клеммах.
На верхней диаграмме ниже показана «идеальная» батарея, то есть батарея с нулевым внутренним сопротивлением. Напряжение на клеммах $V_T$ равно ЭДС внутренней батареи независимо от сопротивления внешней нагрузки $R_L$ и потребляемого тока.
На нижней диаграмме показана «настоящая» батарея с внутренним сопротивлением $r_b$. Когда потребляется ток $I$, происходит падение напряжения $Ir_b$ на внутреннем сопротивлении, что приводит к более низкому напряжению на клеммах батареи. Аккумулятор должен совершить внутреннюю работу, чтобы преодолеть свое внутреннее сопротивление.
Надеюсь, это поможет.
$\endgroup$ $\begingroup$ ЭДС идеальной батареи постоянна, произойдет то, что ток через резистор уменьшится.
Если V=IR — это p.d на резисторе, то это то же самое для ЭДС $\epsilon=IR$, если только резистор подключен к батарее и в идеальных условиях. Если мы знаем, что ЭДС постоянна, то закон Ома говорит нам, что ток должен уменьшаться. Так что нет, работа, совершаемая для перемещения единичного заряда, не меняется. Я думаю, полезно сравнить с гравитацией, если вы прыгаете с дерева, количество потенциальной энергии, которое у вас есть наверху (например, ЭДС в клетке), будет потеряно к тому времени, когда вы упадете на землю.
$\endgroup$Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и парольОпубликовать как гость
Электронная почтаТребуется, но никогда не отображается
Опубликовать как гость
Электронная почтаТребуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
электрических цепей — Путаница в определении ЭДС
Утверждение второго закона Кирхгофа, наиболее близкое к тому, что вы процитировали, это
Вокруг любого замкнутого контура алгебраическая сумма разностей потенциалов равна нулю. $$\sum \Delta V=0$$
Это можно переформулировать как
Суммарная работа, выполненная электростатическими силами на «пробном заряде», совершаемом по любому замкнутому контуру (считая работу, выполненную против электростатических сил, как отрицательный) равен нулю.
Ключевое слово здесь «электростатический». Стационарные (или фактически стационарные) заряды создают консервативные электрические поля. Чистая работа, выполненная таким электрическим полем над пробным зарядом, равна нулю вокруг любого замкнутого контура.
Какое отношение это имеет к электрической цепи? Внутри батареи химические процессы работают на зарядах. Работа, совершаемая этими процессами на единицу заряда, равна Э. Д.С. . Результатом этой работы является перераспределение заряда в цепи. Отрицательная клемма батареи получает избыток электронов, а положительная клемма — недостаток. Таким образом, теперь у нас есть разность потенциалов. По мере того, как заряд (скажем, положительный) переходит от положительного к отрицательному выводу через внешнюю цепь, его потенциал падает. Но когда он достигает отрицательного полюса батареи и проталкивается через него химическими процессами, его потенциал повышается. В целом, когда он проходит через полную цепь, потенциал не меняется.
Д.С. . Результатом этой работы является перераспределение заряда в цепи. Отрицательная клемма батареи получает избыток электронов, а положительная клемма — недостаток. Таким образом, теперь у нас есть разность потенциалов. По мере того, как заряд (скажем, положительный) переходит от положительного к отрицательному выводу через внешнюю цепь, его потенциал падает. Но когда он достигает отрицательного полюса батареи и проталкивается через него химическими процессами, его потенциал повышается. В целом, когда он проходит через полную цепь, потенциал не меняется.
Другая версия второго закона К, возможно, более полезная:
Сумма ЭДС в любом замкнутом контуре цепи равна сумме падений потенциала. $$\sum \mathscr E =\sum Δ𝑉_\text{drop}$$
Здесь «капли» означают капли, а не алгебраические суммы подъемов и падений. Таким образом, мы приравниваем энергию на единицу заряда, придаваемую пробному заряду неэлектростатическими процессами, такими как химические реакции и электромагнитная индукция, с падением на единицу заряда приобретаемой электростатической энергии заряда по мере его прохождения по остальной части цепи.
Примечания
• Я говорил о зарядах (или тестовых зарядах), проходящих по полным циклам, чтобы попытаться дать читателю более живое представление о том, что происходит. Однако пурист будет настаивать на том, что потенциальные различия существуют между точками в цепи независимо от того, действительно ли присутствуют пробные заряды, чтобы «испытывать» их.
• Настоящие батареи и генераторы — это не просто источники ЭДС. Например, в аккумуляторе на электродах создается ЭДС, а на самом деле существует потенциал капают в электролит, когда мы проходим через батарею от отрицательного электрода к положительному электроду, когда заряд течет через батарею в этом направлении. Но это падение меньше суммы потенциалов подъемов за счет ЭДС на электродах. Обычно говорят, что падение потенциала происходит из-за внутреннего сопротивления , r . Таким образом, применяя второй закон К к батарее с pd V на клеммах, мы получаем любимое уравнение старшеклассника
$$V=\mathscr E — Ir.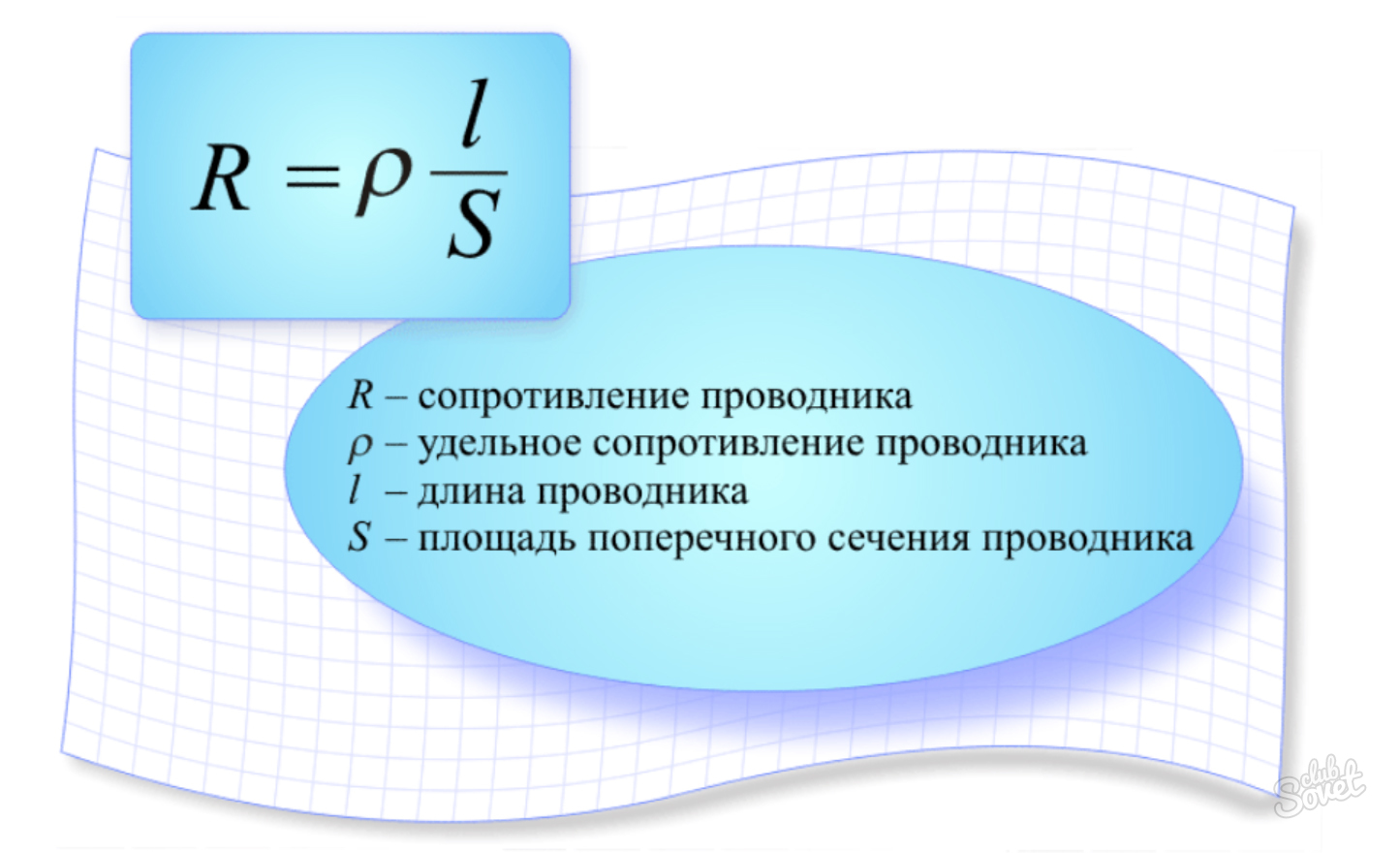



 S – площадь
поперечного сечения проводника,
–
электрическое поле.
S – площадь
поперечного сечения проводника,
–
электрическое поле.