Физические основы механики
Рассмотрим теперь плоское движение твердого тела, то есть движение, при котором точки тела описывают траектории, лежащие в параллельных плоскостях. Пример такого движения — вращение колеса автомобиля при его движении по прямой. Можно взять любую точку 0 тела и мысленно провести через нее ось вращения перпендикулярно плоскостям, в которых лежат траектории точек тела. Тогда ось вращения будет двигаться поступательно, оставаясь все время параллельной самой себе.
Видео 7.2. Плоское движение твердого тела в однородном поле тяжести. Полет плоской картонной фигуры
Соответственно, скорость элементарной массы твердого тела складывается из скорости поступательного движения точки 0 и линейной скорости вращения вокруг связанной с ней (мысленно проведенной) оси:
где — радиус-вектор, определяющий положение элементарной массы по отношению к точке 0.
Кинетическая энергия элементарной массы равна тогда:
Векторное произведение
имеет модуль, равный , где — расстояние массы от оси вращения. Следовательно, третье слагаемое в скобках равно . Второе слагаемое, представляющее собой смешанное произведение векторов, не меняется при циклической перестановке сомножителей:
Следовательно, третье слагаемое в скобках равно . Второе слагаемое, представляющее собой смешанное произведение векторов, не меняется при циклической перестановке сомножителей:
В результате получим для кинетической энергии элемента твердого тела следующее выражение
Для нахождения кинетической энергии тела просуммируем по всем элементарным массам:
Сумма элементарных масс
есть масса твердого тела. Выражение
где — радиус-вектор центра масс тела относительно точки 0.
Наконец,
— есть момент инерции тела относительно оси вращения. Поэтому для кинетической энергии твердого тела можно записать формулу:
Поскольку выбор мысленной оси вращения всецело в нашей власти, мы упростим полученное выражение, взяв в качестве точки 0 центр масс тела. Тогда = 0 и кинетическая энергия тела при плоском движении равна
Здесь — скорость движения центра масс, a — момент инерции относительно оси, проходящей через центр масс и ортогональной плоскости, где лежат траектории точек тела. Таким образом, кинетическая энергия твердого тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости центра масс и энергии вращения вокруг оси, проходящей через центр масс тела.
Таким образом, кинетическая энергия твердого тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости центра масс и энергии вращения вокруг оси, проходящей через центр масс тела.
Движение твердого тела определяется действующими на тело внешними силами и моментами этих сил
Индекс в обозначениях для момента внешней силы означает проекцию момента на ось вращения.
В следующих примерах мы имеем дело с плоским движением.
Видео 7.3. Зависимость поведения цилиндров на наклонной плоскости от характера распределение массы по их объему
Пример 1. Круглое однородное тело (обруч, цилиндр, шар) радиусом и массой скатывается без скольжения по наклонной плоскости под углом к горизонту с высоты (рис. 7.12). Начальная скорость тела равна нулю. Найдем скорость центра масс каждого тела в конце спуска.
Рис. 7.12. Скатывание тела с наклонной плоскости
Рассмотрение данной задачи можно вести двумя способами.
1-й способ. По условию тело катится без проскальзывания. Это условие используется у нас дважды. Сила трения между телом и плоскостью действует в точке соприкосновения и в отсутствие скольжения не превышает своего максимального значения:
где — коэффициент трения скольжения.
Оси координат удобно направить следующим образом: ось х — вдоль движения, ось у — перпендикулярно наклонной плоскости. Тело движется под действием трех сил: силы тяжести , силы трения и силы нормального давления , так что уравнение поступательного движения центра инерции тела имеет вид:
Вдоль оси у тело не движется. Проецируя уравнение движения центра масс на ось у, получаем для силы нормального давления соотношение:
Проекция уравнения движения на ось х дает:
Так как линейная скорость точек соприкосновения цилиндра с наклонной плоскостью равна нулю (опять используем условие отсутствия проскальзывания), то скорость (ускорение) поступательного движения связаны с угловой скоростью (угловым ускорением) тела обычными соотношениями:
Кроме поступательного движения, тело еще и вращается.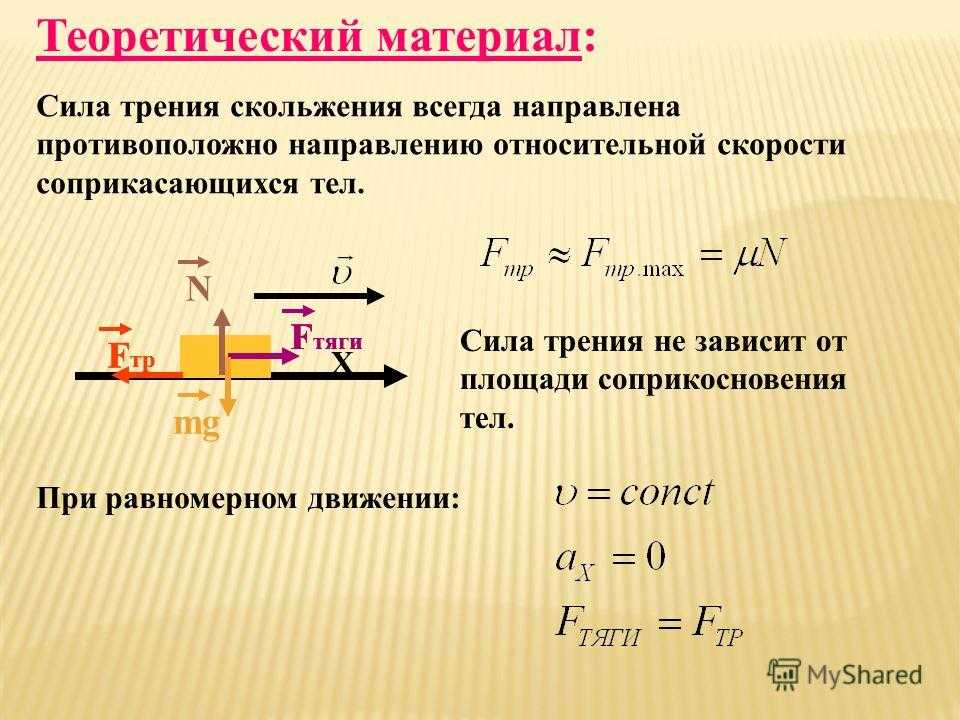
Выбор этот обусловлен тем, что линии действия силы тяжести и силы нормального давления плоскости проходят через ось вращения и, следовательно, моменты этих сил равны нулю. Таким образом, цилиндр вращается только под действием силы трения, и уравнение вращательного движения имеет вид:
Таким образом, получается система 4-х уравнений, описывающих поступательное и вращательное движение с дополнительным неравенством, выражающим закон трения. Решая систему уравнений, находим:
Чем больше момент инерции относительно оси, проходящей через центр масс, тем меньше ускорение тела. Мы уже получили ответ на один из вопросов задачи: шар будет двигаться быстрее цилиндра, а цилиндр — быстрее обруча. Подставляя решение для силы трения в неравенство, выражающее закон трения, находим условие, при котором будет отсутствовать проскальзывание:
Смысл этого условия прост: наклон не должен быть слишком крут.
Итак, центр масс тела движется вдоль плоскости с постоянным ускорением a, так что зависимость пройденного пути и скорости от времени имеет вид:
Отсюда следует связь скорости и пройденного пути:
К концу спуска тело проходит путь
так что его скорость достигает величины
Подставляя сюда моменты инерции обруча (), цилиндра () и шара (), находим соответственно:
2-й способ. Используем закон сохранения полной энергии. В конце спуска тело приобретает кинетическую энергию
Эта кинетическая энергия приобретена за счет потенциальной энергии . Отсюда следует найдено выше выражение для скорости тела в конце спуска. Такой способ намного короче, но он не позволяет узнать детали процесса: действующие на тело силы и т.п.
В рассмотренном выше примере мы считали примере мы имели дело со случаем, когда проскальзывание отсутствовало. Это позволило утверждать простую связь () между угловой и линейной скоростями тела и его радиусом.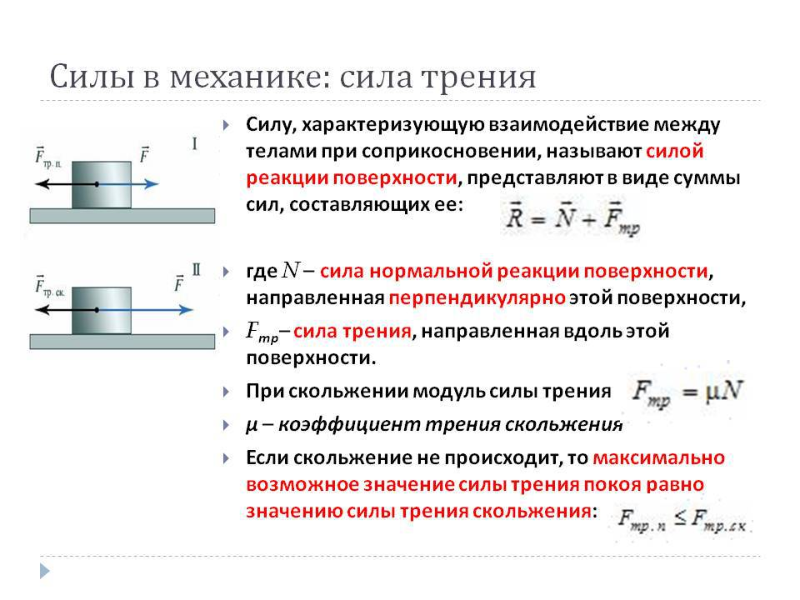 Сила трения покоя находилась при этом в результате решения уравнений движения. В случае, когда тело движется с проскальзыванием, заранее известной связи между линейной и угловой скоростями нет. Зато мы заранее знаем силу трения: раз точка соприкосновения тела с поверхностью скользит по поверхности, сила трения есть сила трения скольжения,модуль которой связан с силой нормального давления законом Амонтона — Кулона.
Сила трения покоя находилась при этом в результате решения уравнений движения. В случае, когда тело движется с проскальзыванием, заранее известной связи между линейной и угловой скоростями нет. Зато мы заранее знаем силу трения: раз точка соприкосновения тела с поверхностью скользит по поверхности, сила трения есть сила трения скольжения,модуль которой связан с силой нормального давления законом Амонтона — Кулона.
Силы трения, как уже говорилось, направлены так, чтобы препятствовать относительному проскальзыванию соприкасающихся тел. Часто путают это возможное проскальзывание с осуществляемым поступательным движением. Необходимо четко понимать, что не редки случаи, когда сила трения не тормозит, но ускоряет тело, то есть направлена по его движению. Самый известный пример — трогание автомобиля с места. Колеса начинают вращаться и проскальзывают по земле назад. Соответственно, сила трения направлена вперед, и именно она заставляет автомобиль трогаться. Чтобы ближе познакомиться с подобными случаями, рассмотрим пример.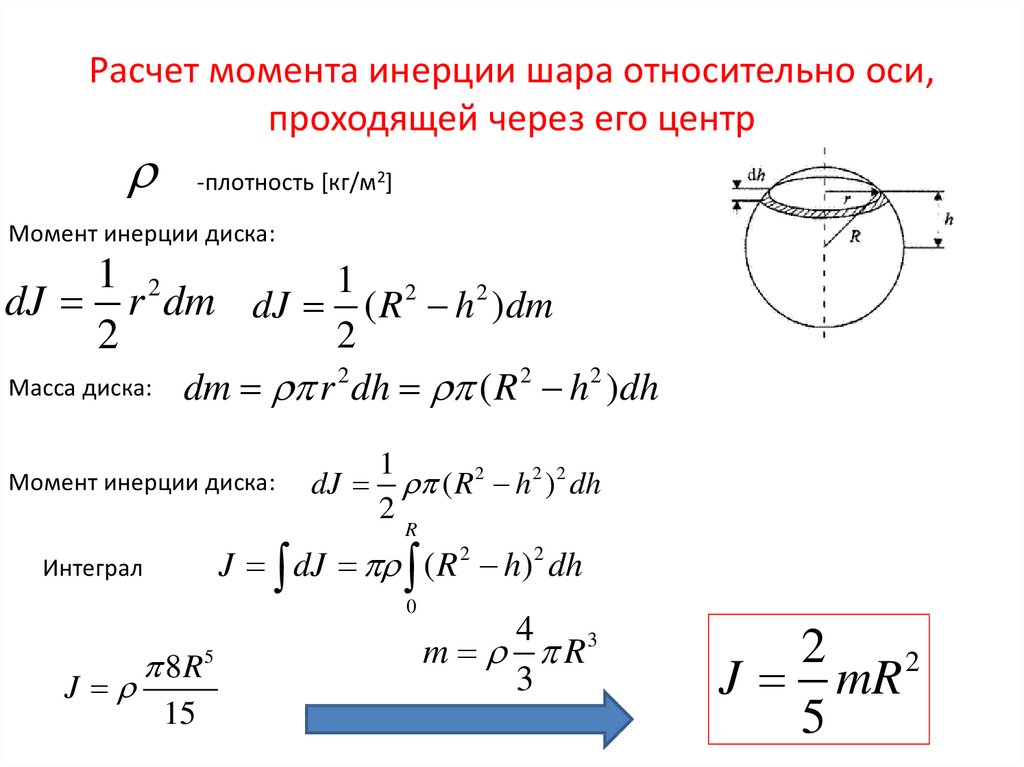
Пример 2. Цирковой артист бросает на арену обруч массой и радиусом , который начинает катиться в горизонтальном направлении со скоростью (рис. 7.13). При этом обручу придано обратное вращение с угловой скоростью . Найдем, при какой угловой скорости обруч после остановки покатится назад к артисту, а также конечную скорость поступательного движения обруча.
Рис. 7.13. Движение обруча с обратным вращением
При обратном вращении обруча точка его касания с ареной движется вперед как из-за вращения, так и из-за поступательного движения обруча. Поэтому неизбежно существует проскальзывание и, значит, сила трения достигает своего максимального значения. Она тормозит как поступательное движение, так и вращение обруча. Может случиться так, что поступательное движение обруча будет остановлено в тот момент, когда он еще сохраняет обратное вращение. Далее сила трения начнет ускорять обруч по направлению к артисту. Ускорение это прекратится, когда исчезнет тенденция к проскальзыванию, после чего обруч покатится назад равномерно с некоторой установившейся скоростью .
Направим ось ОХ направо (в направлении красной стрелки на рис. 7.13), ось вращения ОZ направим на нас (см. следующий пример, там эту ось удобнее направить от нас, то есть за чертеж), то есть в направлении «обратного» вращения, ось OY направим как обычно, вверх. Плоское движение обруча представим как суперпозицию его поступательного движения вместе с центром масс (геометрическим центром, поскольку обруч предполагается однородным). Спроектируем линейные и угловые скорости на соответствующие оси. Тогда, до тех пор, пока сила трения есть сила трения скольжения и направлена она налево, уравнения движения имеют вид
(7.3.1)
(7.3.2)
Уравнение (7.3.1) описывает движение центра масс обруча, а уравнение (7. 3.2) его вращение вокруг оси проходящей через центр масс в той системе отсчета, в которой она покоится (системе центра масс). В (7.3.2) учтено, что момент инерции однородного обруча относительно его оси симметрии равен . После элементарного интегрирования получаем
3.2) его вращение вокруг оси проходящей через центр масс в той системе отсчета, в которой она покоится (системе центра масс). В (7.3.2) учтено, что момент инерции однородного обруча относительно его оси симметрии равен . После элементарного интегрирования получаем
(7.3.3)
(7.3.4)
Поступательное движение прекратится, то есть станет равным нулю, в момент времени
(7.3.5)
Вращение прекратится, то есть станет равным нулю,в момент времени
(7.3.6)
Их отношение
(7.3.7)
может быть любым ввиду независимости начальных скоростей поступательного и вращательного движений.
Для дальнейшего анализа введем в рассмотрение скорость нижней точки обруча — той его точки, которая касается поверхности арены. Отметим уже здесь, что условием исчезновения проскальзывания является обращение в ноль скорости именно этой точки, потому что скорость соответствующей точки на поверхности арены (той, которой касается обруч) очевидным образом в нашей системе отсчета, где арена неподвижна, равна нулю. Отсутствие проскальзывания это и есть неподвижность этих двух точек относительно друг друга. При выбранном направлении осей OZ и OX, имеем
Отсутствие проскальзывания это и есть неподвижность этих двух точек относительно друг друга. При выбранном направлении осей OZ и OX, имеем
(7.3.8)
Если , то первым прекратится поступательное движение обруча. В момент времени скорости (7.3.3) и (7.3.8) будут иметь значения
Нижняя точка обруча, за счет продолжающегося вращения, будет по-прежнему скользить относительно арены направо (направо на рисунке 7.13), сила трения скольжения сохранит свою величину и направление налево. Соответственно, центр обруча начнет ускорятся налево, то есть станет меньше нуля и начнет расти по модулю, вращение против часовой стрелки (на рисунке 7.13) будет продолжать замедлятся. Другими словами, при обруч в момент времени (7.3.5) начинает возвращаться к бросившему его артисту.
Как следует из (7.3.8), в момент времени
(7.3.9)
скорость нижней точки обруча из (7.3.8) обращается в ноль, проскальзывание прекращается, сила трения скольжения скачком сменяется равной нулю силой трения покоя (силой трения качения пренебрегаем) и обруч начинает катится к артисту с постоянной скоростью движения центра масс
(7. 3.10)
3.10)
вращаясь против часовой стрелки с постоянной угловой скоростью
(7.3.11)
Если , то первым, в момент времени (7.3.6), прекратится вращение обруча. В момент времени скорость (7.3.8) нижней точки обруча будет равна скорости его центра и положительна:
(7.3.12)
Скольжение остается, сила трения скольжения сохраняет свою величину и направление налево, но обруч под действием этой силы трения скольжения начинает вращаться по часовой стрелке (напоминаем: налево, направо, по или против часовой стрелки — на рисунке 10). В результате этого скорость центра масс (центра обруча) будет уменьшаться, скорость вращения увеличиваться, в момент времени
(7.3.13)
проскальзывание обруча прекратится и обруч начнет равномерно удаляться от артиста со скоростью центра (7.3.10) и угловой скоростью вращения (7.3.11). Напомним, что в этом случае , так что а
Таким образом, ответ на вопрос: «Вернется обруч или укатится?» определяется начальными условиями, а конкретнее величиной параметра , который имеет простой физический смысл: это отношение модуля
скорости любой точки обруча за счет его поступательного движения вместе с центром масс к модулю скорости той же точки за счет вращения обруча вокруг оси, проходящей через его центр масс, в начальный момент времени.
Пример 3. Описать движение обруча (см. предыдущий пример), если ему придано прямое вращение (рис. 7.14). Поскольку обруч вращается теперь на рис. 7.14 по часовой стрелке, направим ось вращения OZ от нас, то есть за чертеж — в отличие от предыдущего случая.
Рис. 7.14. Движение обруча с прямым вращением: 1 – ; 2 –
Начальная скорость нижней точки обруча складывается из скорости поступательного движения и линейной скорости за счет вращения, направленной в противоположную сторону. В связи с этим надо различать два случая.
1 случай или . Тогда начальная скорость нижней точки обода положительна, то есть, направлена в ту же сторону, что и скорость . Значит, сила трения f направлена в противоположную сторону, как показано на рис. 11–1. В связи с изменением положительного направления оси вращения необходимо лишь изменить знак перед вторым слагаемым в уравнении (7.3.4). Решение уравнений движения в рассматриваемом случае имеют вид
(7. 3.14)
3.14)
(7.3.15)
При новом выборе направления оси вращения скорость нижней точки обруча записывается в виде
(7.3.16)
Момент исчезновения проскальзывания определится из того же соотношения равенства нулю скорости нижней точки обруча или равенства по модулю противоположно направленных скоростей этой точки за счет поступательного движения вместе с центром масс и вращательного движение вокруг оси, проходящей через центр масс:
откуда находим:
Скорость поступательного движения обруча в этот момент становится равной
и остается потом неизменной. Эта скорость меньше начальной скорости поступательного движения обруча.
2 случай или . В этом случае скорость нижней точки обода отрицательна, направлена против скорости . Значит, сила трения направлена по (см. рис.11-2).
Соответственно, в уравнениях движения и их решениях (7.3.14) и (7.3.15) надо изменить знаки на противоположные перед вторыми слагаемыми, содержащими изменившую направление силу трения, получаем:
(7.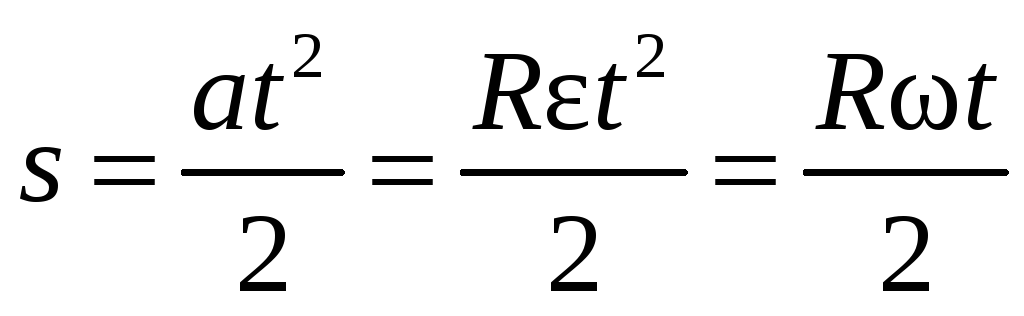 3.17)
3.17)
(7.3.18)
Соответственно, выражение для скорости нижней точки обруча приобретает вид:
(7.3.19)
Момент прекращения проскальзывания определяется аналогично и оказывается равным:
а для скорости установившегося движения получается вновь выражение
но в данном случае она будет больше () начальной скорости поступательного движения.
Объединяя оба случая в один, записываем окончательный результат:
Дополнительная информация
http://www.plib.ru/library/book/14978.html Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 256 (§ 48, задача 9): рассмотрено движение маятника Максвелла, включая силу натяжения нитей подвеса в нижней точке.
http://kvant.mirror1.mccme.ru/pdf/1997/04/kv0497khorozov.pdf — журнал «Квант» — решение задачи об отскоке вращающегося мяча от плоской стенки (С. Хорозов).
http://kvant.mirror1.mccme.ru/pdf/1998/04/kv0498chernoutsan.pdf — журнал «Квант» — применение законов динамики твердого тела в задаче о падении вертикальной палочки на горизонтальный стол (А. Черноуцан).
Черноуцан).
http://kvant.mirror1.mccme.ru/pdf/1999/02/kv0299chernoutsan.pdf — журнал «Квант» — продолжение задачи о падении вертикальной палочки на горизонтальный стол (А. Черноуцан).
Помогите решить / разобраться (Ф)
| propagator |
| ||
16/11/14 |
| ||
| |||
| profrotter |
| |||||
16/02/11 |
| |||||
| ||||||
| rustot |
| |||
29/11/11 |
| |||
| ||||
| Xey |
| |||
07/07/09 |
| |||
| ||||
| rustot |
| |||
29/11/11 |
| |||
| ||||
| propagator |
| ||
16/11/14 |
| ||
| |||
| rustot |
| |||
29/11/11 |
| |||
| ||||
| propagator |
| ||
16/11/14 |
| ||
| |||
| rustot |
| |||
29/11/11 |
| |||
| ||||
| svv |
| |||
23/07/08 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 10 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Расчет надлежащего сопротивления качению: более безопасное перемещение при погрузочно-разгрузочных работах | Машиностроение
Трение играет важную роль в промышленном мире, а также в повседневной жизни.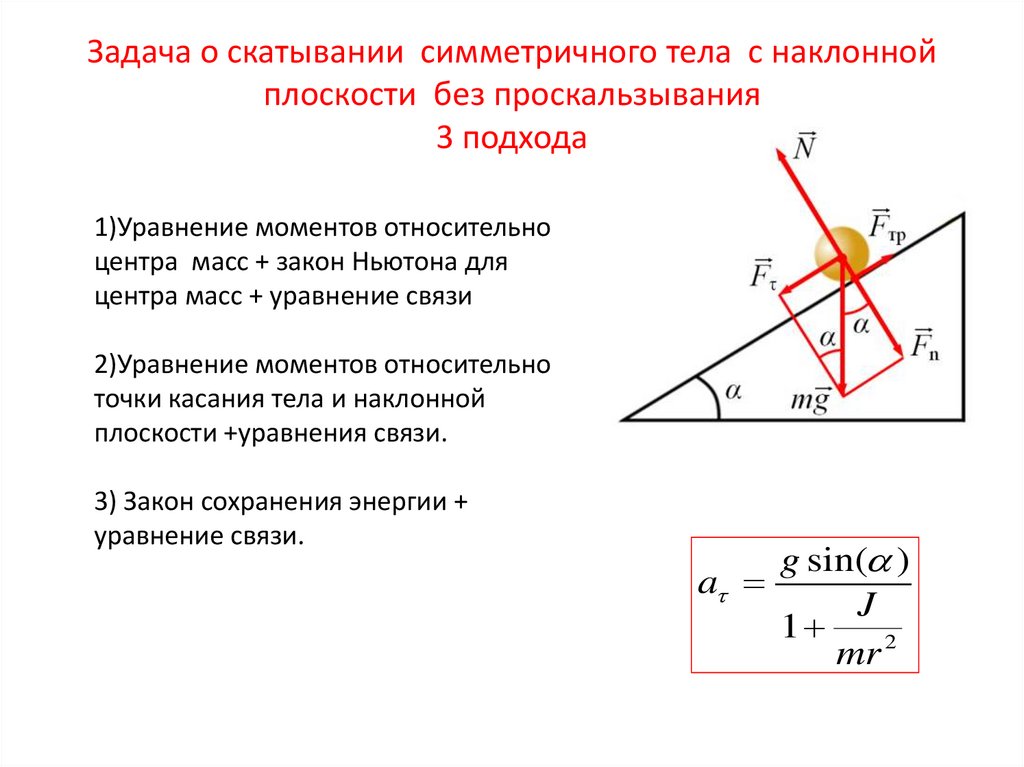 Трение — это сопротивление скольжению, качению или плавному движению объекта из-за его контакта с другим объектом. Это может быть как полезно (когда мы тормозим машину, чтобы остановиться), так и вредно (когда мы пытаемся ехать одной ногой на педали тормоза). В этой статье основное внимание будет уделено сопротивлению качению, важному аспекту промышленных колес.
Трение — это сопротивление скольжению, качению или плавному движению объекта из-за его контакта с другим объектом. Это может быть как полезно (когда мы тормозим машину, чтобы остановиться), так и вредно (когда мы пытаемся ехать одной ногой на педали тормоза). В этой статье основное внимание будет уделено сопротивлению качению, важному аспекту промышленных колес.
Сопротивление качению – это мера тормозящего действия поверхности пола на поверхности контакта колес с протектором. Обычно он выражается в фунтах и является мерой энергии, рассеиваемой на единицу пройденного пути. Рассмотрим шину, катящуюся по ровной поверхности. Шина будет до некоторой степени деформироваться, и эта деформация вызовет некоторое сопротивление движению качения. Плоская поверхность также может деформироваться, особенно если она относительно мягкая. Песок является хорошим примером мягкой, устойчивой к качению поверхности. Ехать на велосипеде по асфальтированной дороге гораздо проще, чем по белому песчаному пляжу.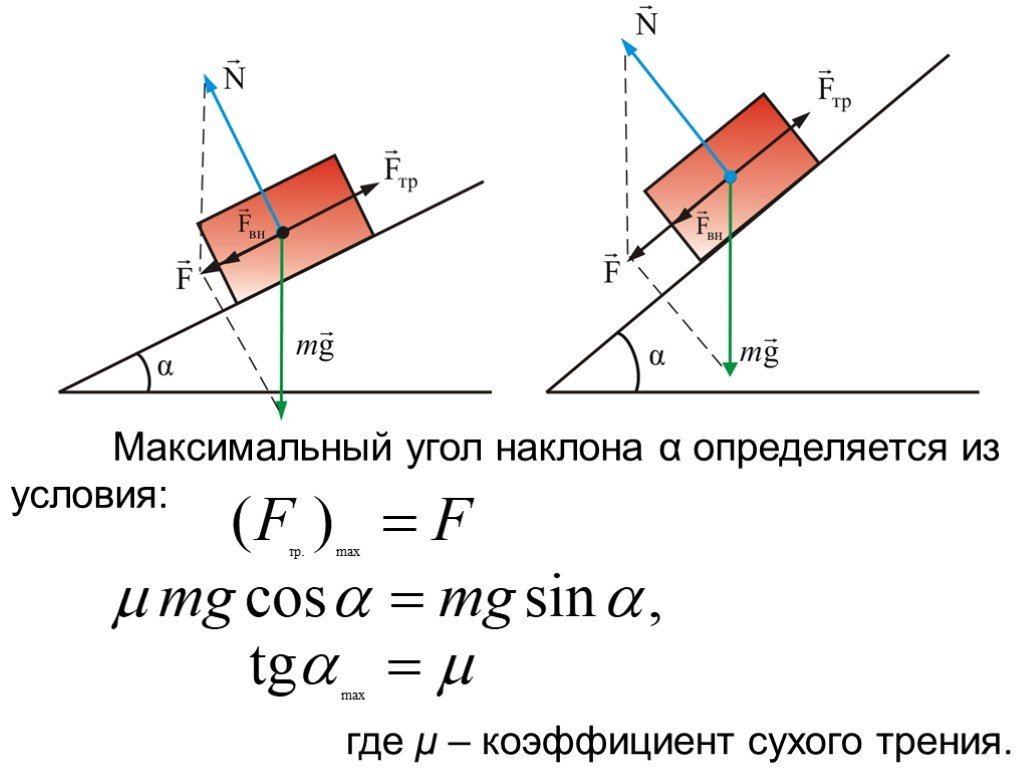 Сопротивление качению измеряет потерю энергии, когда что-то катится на определенное расстояние.
Сопротивление качению измеряет потерю энергии, когда что-то катится на определенное расстояние.
В мире промышленных колес контакт качения в идеале не должен оказывать сопротивления движению (за исключением случаев, когда мы хотим, чтобы что-то оставалось на месте). Но реальность так не работает. Энергия рассеивается:
- Из-за трения на поверхности контакта
- Из-за упругих свойств материалов
- Из-за шероховатости поверхности качения.
Как можно видеть на этом преувеличенном изображении, и колеса, и поверхность подвергаются деформации в степени, определяемой упругими свойствами двух поверхностей.
Сравнение трения качения и трения скольжения
Коэффициент трения качения не следует путать с коэффициентом трения скольжения или, как его часто называют, коэффициентом трения. Коэффициент трения (скольжения) — безразмерное число, описывающее отношение силы трения между двумя телами к силе, прижимающей их друг к другу. Коэффициент трения (скольжения) зависит от используемых материалов; например, сталь на льду имеет низкий коэффициент трения, а резина на дорожном покрытии имеет высокий коэффициент трения.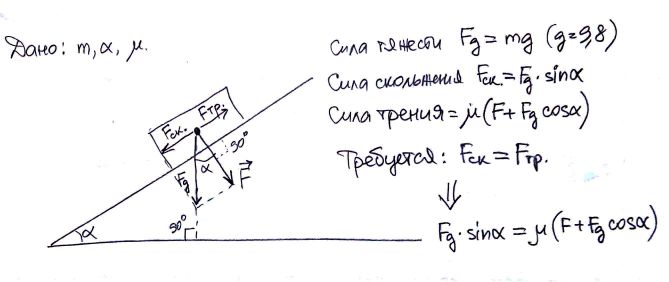
На приведенной ниже диаграмме рассматривается трение скольжения. Представьте себе силу, необходимую для того, чтобы толкнуть тяжелую коробку по полу. Статическое трение требует определенной приложенной силы, чтобы заставить коробку двигаться. После движения динамическое трение требует относительно постоянной силы для поддержания этого движения. В этом примере толкающий человек создает «приложенную силу», а коробка весом «N» и пол создают «силу трения», которая стремится сопротивляться этому движению.
Причина, по которой мы используем колеса для погрузочно-разгрузочных работ, заключается в том, что для перемещения объекта требуется значительно меньшее усилие (сила). Представьте, что вы толкаете холодильник или пианино без колес! Кроме того, подумайте, насколько легче было бы толкать коробку (упомянутую ранее) по полу, если бы она была на колесах.
Сила, необходимая для толкания/тяги колесного оборудования, всегда максимальна в начале, непосредственно перед началом движения. Эргономисты называют эту силу начальной или стартовой силой. К счастью, первоначальные силы обычно действуют лишь короткое время и падают до уровней устойчивых сил, как только начинается ускорение и преодолеваются любые механические помехи в начале движения. При движении с относительно постоянной скоростью требуемая сила обычно ниже. Эта сила называется устойчивой или катящейся силой.
Эргономисты называют эту силу начальной или стартовой силой. К счастью, первоначальные силы обычно действуют лишь короткое время и падают до уровней устойчивых сил, как только начинается ускорение и преодолеваются любые механические помехи в начале движения. При движении с относительно постоянной скоростью требуемая сила обычно ниже. Эта сила называется устойчивой или катящейся силой.
Для облегчения качения
Чтобы уменьшить усилие, необходимое для преодоления сопротивления качению колеса, можно выбрать колесо с более низким коэффициентом сопротивления качению (например, колесо из кованой стали имеет коэффициент сопротивления качению 0,019 дюйма) или использовать колесо большего диаметра. Оптимизируйте, выполнив и то, и другое — используйте колесо самого большого практического диаметра с самым низким коэффициентом сопротивления качению.
Выбор ступичного подшипника с точки зрения сопротивления качению не так важен, как материал и диаметр колеса. Антифрикционные подшипники не так сильно влияют на сопротивление качению, как такие факторы, как материал и диаметр колеса.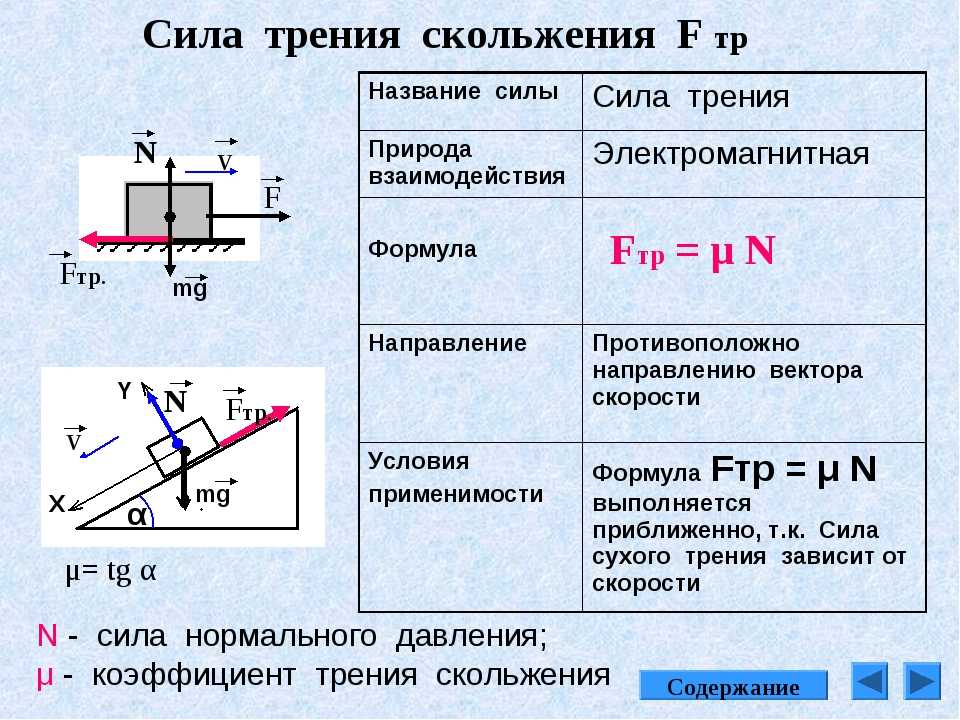 Однако выбор подшипника может быть очень важен по другим причинам, таким как грузоподъемность, ручное или буксируемое управление, наличие ударных нагрузок или боковых нагрузок, а также необходимость технического обслуживания. Как можно предположить, более мягкий материал протектора колеса обычно приводит к большему сопротивлению качению, чем очень прочный/твердый материал протектора колеса.
Однако выбор подшипника может быть очень важен по другим причинам, таким как грузоподъемность, ручное или буксируемое управление, наличие ударных нагрузок или боковых нагрузок, а также необходимость технического обслуживания. Как можно предположить, более мягкий материал протектора колеса обычно приводит к большему сопротивлению качению, чем очень прочный/твердый материал протектора колеса.
Основные факторы сопротивления качению
Наиболее важными факторами, которые следует учитывать, являются:
- Нагрузка
- Диаметр колеса
- Материал/твердость протектора
- Материал/покрытие пола
- Состояние пола (шероховатость, чистота и т. д.) .).
Факторы, которыми обычно можно пренебречь при расчетах:
- Тип подшипника
- Консистентная смазка или влияние смазки
- Температура окружающей среды
- Пробуксовка колес.
Рекомендации по эргономике
Общие рекомендации по эргономике для максимального (ручного) толкающего усилия можно найти в интерактивных таблицах в разделе Liberty Mutual Manual Material Handling на веб-сайте.
Использование калькулятора, представленного на этом веб-сайте, даст результаты, предлагающие процент населения (мужчины или женщины могут быть указаны), которые могут безопасно выполнять задачу толкания или тяги. Переменные включают силу толкания или тяги (которая исходит из расчетов, описанных в этой статье), высоту, на которой прикладывается сила, продолжительность толкания или тяги и частоту.
В целом любой результат, превышающий 75% женского населения, будет приемлемым с точки зрения безопасности. В частности, использование этого в качестве руководства в значительной степени предотвратит травмы поясницы. Конечно, никогда не бывает гарантии предотвращения травм спины.
Общие рекомендации для ручных и механических операций:
- Выберите подходящее колесо/протектор, исходя из максимальной нагрузки и состояния пола.
- При выборе эластичного протектора, как правило, для защиты пола, необходимо учитывать:
- Диапазон температур
- Ударопрочность
- Влага и вода
- Стойкость к свету, химическим веществам
- Отскок.

- Выберите максимально возможный/практичный диаметр колеса.
- Выберите колесо с наименьшим коэффициентом сопротивления качению.
- Рассчитайте сопротивление качению (имейте в виду, что при запуске усилие будет в 2-2,5 раза выше).
- Используйте коэффициент запаса при расчете требуемой мощности для привода.
- Не забудьте учесть любой уклон (a°). Рассчитанное сопротивление качению будет увеличиваться вверх по склону и уменьшаться вниз по склону (F = Fx/cosa). Например, наклон 10° увеличит требуемую силу (F = Fx/cos10° = Fx/0,9848 = 1,015Fx). Если угол наклона увеличить до 30°, требуемая сила существенно возрастет, с 1,015Fx до 1,155Fx (приблизительно 14%).
- Выбор ступичного подшипника очень важен для буксировки! Обязательно выбирайте подшипники, которые выдержат высокие скорости, боковые нагрузки и непрерывную работу.
Сопротивление качению играет важную роль при обработке материалов. Независимо от того, будут ли грузы буксироваться или толкаться вручную, правильный выбор колес существенно повлияет на результаты. Использование описанных здесь принципов позволит сделать правильный выбор.
Использование описанных здесь принципов позволит сделать правильный выбор.
Дэйв Липперт — вице-президент по маркетингу, а Джефф Спектор — технический директор Hamilton Caster. С ними можно связаться по адресу [email protected] и [email protected].
Расчет силы прокатки
Для количественной оценки сопротивления качению промышленных колес используется «коэффициент трения качения». Это число, которое было определено эмпирически для различных материалов и может варьироваться в зависимости от скорости колеса, нагрузки на колесо и материала, с которым колесо соприкасается. На приведенной ниже диаграмме неудивительно, что самый мягкий материал протектора (резина) имеет самый высокий коэффициент трения, а самый твердый материал (кованая сталь) — самый низкий.
*Полиуретан имеет диапазон значений коэффициента в зависимости от выбранного поли материала.
Допущения
Общая нагрузка:
- 1200 фунтов
Материал пола: Сталь
Шип
F = сила, необходимая для преодоления трения качения
f = коэффициент трения качения (единицы измерения должны совпадать с R (радиус))
W = нагрузка на колесо
R = радиус колеса
Пример
Найдите усилие, необходимое для перемещения 4800-фунтового прицепа, оснащенного 8-дюймовыми колесами. полиуретановые колеса диаметром 85А на ровном стальном полу.
полиуретановые колеса диаметром 85А на ровном стальном полу.
Шаг 1: На основе данной нагрузки мы можем определить нагрузку на колесо «W».
W = 4800 фунтов/4 (колеса) = 1200 фунтов на каждое колесо
Шаг 2: Из приведенной таблицы найдите коэффициент сопротивления качению «f».
f = 0,047 (дюйма) [Примечание: полиуретан имеет диапазон значений коэффициента в зависимости от выбранного материала.]
Шаг 3: Мы знаем, что радиус составляет ½ 8 дюймов. диаметр колеса.
R = 4 дюйма
Шаг 4: Рассчитайте силу «F», необходимую для преодоления трения качения колеса.
F = 0,047 x 1200/4 = 14,1 фунта (Примечание: это для каждого отдельного колеса).
Сопротивление на колесо составляет 14,1 фунта. Поскольку у грузовика четыре колеса, общая сила, необходимая для перемещения (продолжительного движения) грузовика, составляет 14,1 х 4 = 56,4 фунта.
Диаметр колеса играет важную роль в силе, необходимой для перемещения груза. В примере выше, используя 16-дюймовый. диаметр колеса (радиусом 8 дюймов) уменьшил бы требуемую силу вдвое. На самом деле, это закономерность, установленная уравнением. Каждое удвоение диаметра колеса приводит только к половине силы, необходимой для перемещения колеса или поддержания движения.
В примере выше, используя 16-дюймовый. диаметр колеса (радиусом 8 дюймов) уменьшил бы требуемую силу вдвое. На самом деле, это закономерность, установленная уравнением. Каждое удвоение диаметра колеса приводит только к половине силы, необходимой для перемещения колеса или поддержания движения.
Сила начала (инициации) движения обычно в 2-2,5 раза превышает поддерживающую силу. В приведенном выше примере начальное усилие составляет приблизительно 115 фунтов.
Есть ли у вас опыт и знания по темам, упомянутым в этом содержании? Вам следует подумать о том, чтобы внести свой вклад в нашу редакционную команду CFE Media и получить признание, которого вы и ваша компания заслуживаете. Нажмите здесь, чтобы начать этот процесс.
Расчет силы прокатки
Опубликовано: 26 марта 2020 г., доктор Тимоти Клемсон
При производстве листового проката важно понимать усилие прокатки. Это потому, что вам нужно установить соответствующий зазор между валками на стане с учетом растяжения клети.
Прогнозирование силы прокатки может быть сложной задачей из-за большого количества взаимосвязанных переменных процесса. Однако многолетний опыт работы с прокатными станами позволил нам создать Инновационную модель прокатки, которая дает точные прогнозы усилия прокатки.
Факторы, влияющие на усилие прокатки
Предел текучести
Основным фактором, влияющим на усилие прокатки, необходимое для уменьшения толщины полосы в прокатном стане, является предел текучести прокатываемого материала. Расчет предела текучести зависит от множества факторов. Это:
- состав
- предыдущая работа, выполненная с материалом
- термическая история
- скорость прокатки
- изменение толщины
Мы используем так называемое определяющее уравнение для расчета предела текучести материала или напряжения течения. В академической литературе встречается много форм этих уравнений, и в основе большинства из них лежит физическая металлургия. Однако в целом все эти уравнения имеют одинаковую форму:
Однако в целом все эти уравнения имеют одинаковую форму:
Предел текучести = (Коэффициент упрочнения при деформации) x (Коэффициент упрочнения при скорости деформации) x (Коэффициент термического размягчения)
При прокатке алюминия деформационное упрочнение обычно преобладает при низких температурах. С другой стороны, скорость деформации и температура более важны при горячей прокатке. Легирующие элементы и состояние, в котором они находятся в материале, влияют на каждый из этих факторов. Следовательно, хорошее понимание термической истории и результирующих металлургических свойств необходимо для прогнозирования предела текучести.
Рис. 1. Испытательное напряжение (предел текучести при деформации 0,2 %) для различных сплавов во время прокатки (кредит: Alcoa)Трение
Мы можем рассчитать результирующее давление на валки от деформируемого материала после того, как мы рассчитали напряжение течения в заданной точке в пределах захвата валков. Однако трение между двумя поверхностями также играет роль, особенно при холодной прокатке.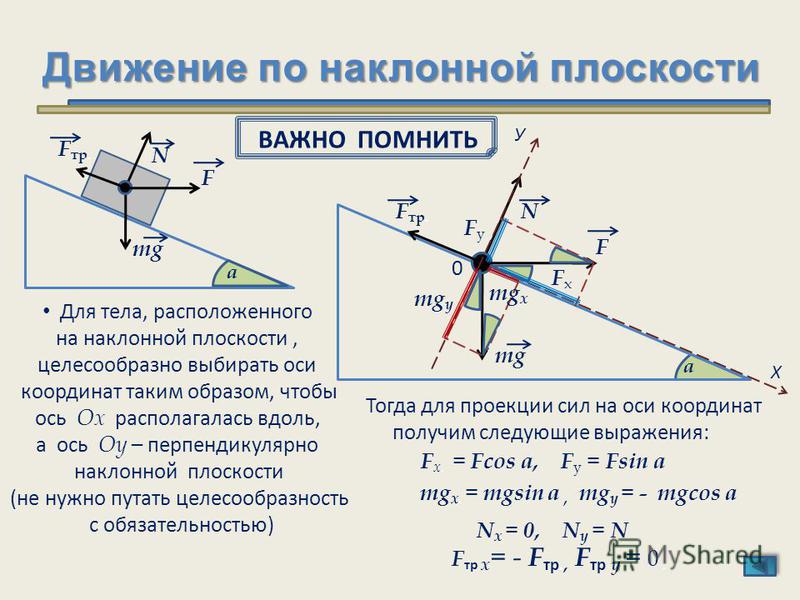 Следовательно, мы должны понимать микроскопические взаимодействия между смазкой, валками и материалом. Это означает знание шероховатости поверхностей и соотношения температуры и вязкости смазки.
Следовательно, мы должны понимать микроскопические взаимодействия между смазкой, валками и материалом. Это означает знание шероховатости поверхностей и соотношения температуры и вязкости смазки.
Нейтральная точка
Рис. 2: Диаграмма давления при прокатке через стык валковПри стандартной холодной прокатке давление, возникающее в стыке валков, увеличивается к середине стыка от входа и выхода. Они достигают пика в точке, известной как нейтральная точка, где скорость валков точно соответствует скорости материала. Расположение этой точки определяет общее усилие прокатки и сильно зависит от натяжения полосы по обе стороны от зацепа. Чтобы найти его местоположение, нам нужно рассчитать давление качения от входа и выхода до тех пор, пока их значения не совпадут в какой-то точке в пределах зацепа.
При очень тонкой толщине нейтральная точка расплывается в нейтральную зону, и валок сплющивается, принимая более сложную форму, что требует альтернативных расчетов. При очень толстых калибрах ситуация тоже иная.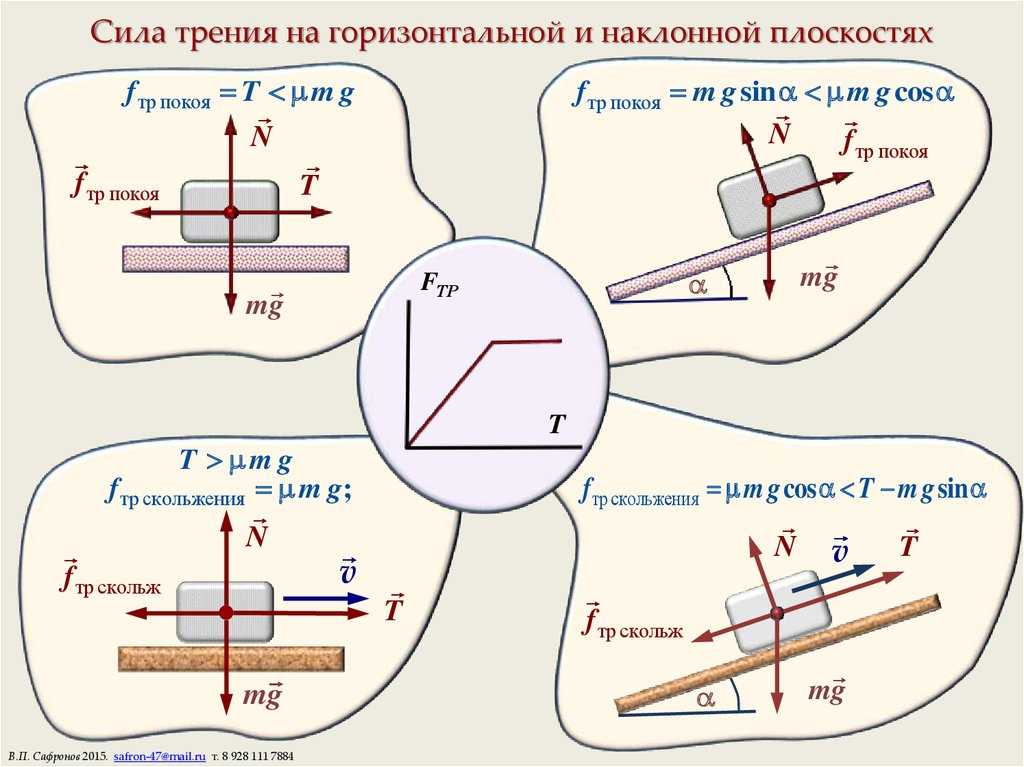 Эффекты сквозного потока становятся более важными и требуют третьего подхода к расчету нагрузки при прокатке.
Эффекты сквозного потока становятся более важными и требуют третьего подхода к расчету нагрузки при прокатке.
Натяжение
Натяжение, прикладываемое к полосе, также влияет на давление прокатки, возникающее в месте прихвата. Более высокое натяжение на входе снижает начальную точку на холме трения, и поэтому его необходимо учитывать в модели качения.
Дополнительное обучение
Таким образом, расчет силы прокатки является сложным и междисциплинарным расчетом. Изменения одной переменной процесса неизбежно влияют на другие, и последствия часто могут быть нелогичными. По этим причинам Innoval Rolling Model является бесценным инструментом в нашем повседневном консультационном бизнесе. Его также можно приобрести, что позволяет уточнять технологические графики и моделировать потенциальные новые продукты и оборудование.
Все эти и многие другие темы мы обсуждаем на нашем курсе «Технология алюминиевого проката».



 И это не зависит от того как именно частицы системы взаимодействуют между собой, составляют ли они твердое тело или вообще никак не взаимодействуют
И это не зависит от того как именно частицы системы взаимодействуют между собой, составляют ли они твердое тело или вообще никак не взаимодействуют 05.2016, 19:19
05.2016, 19:19 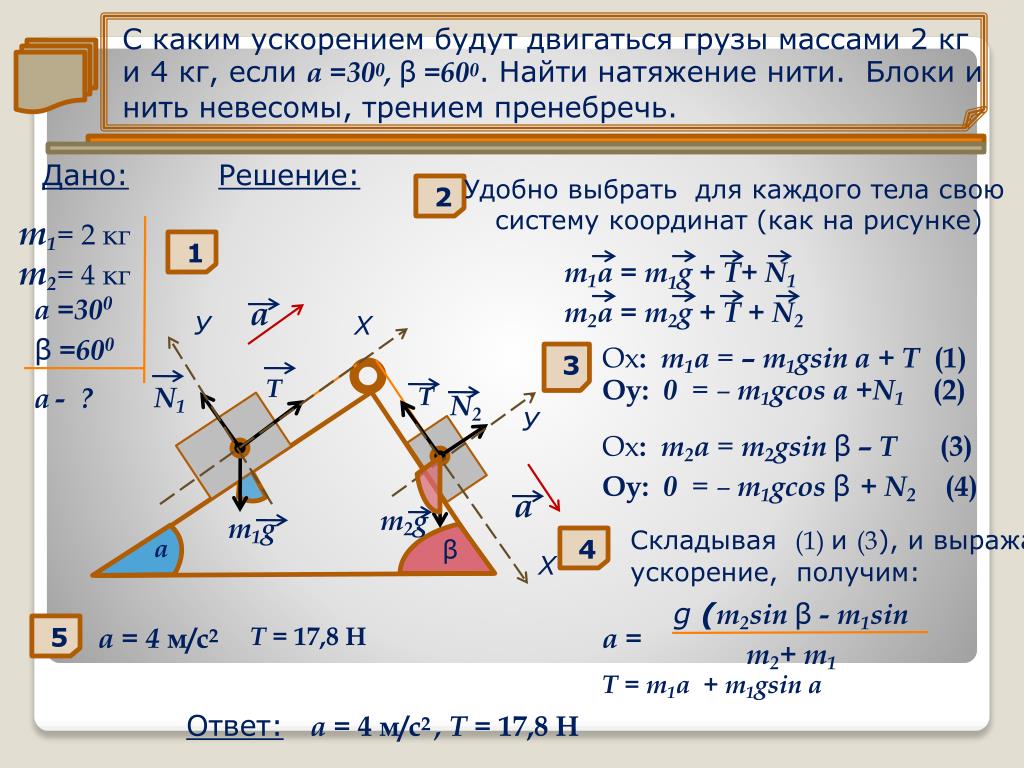 05.2016, 19:39
05.2016, 19:39 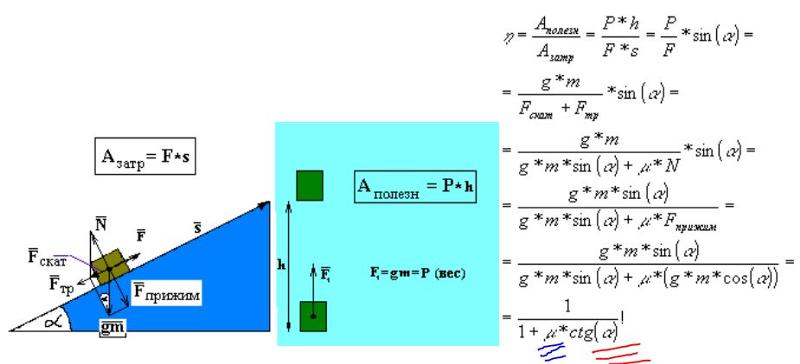 05.2016, 20:46
05.2016, 20:46  Тем более, в курсе, который читается, студентам дается детсадовское объяснение понятия угловой скорости, так что вывод вышеприведенной формулы им вообще не под силу.
Тем более, в курсе, который читается, студентам дается детсадовское объяснение понятия угловой скорости, так что вывод вышеприведенной формулы им вообще не под силу.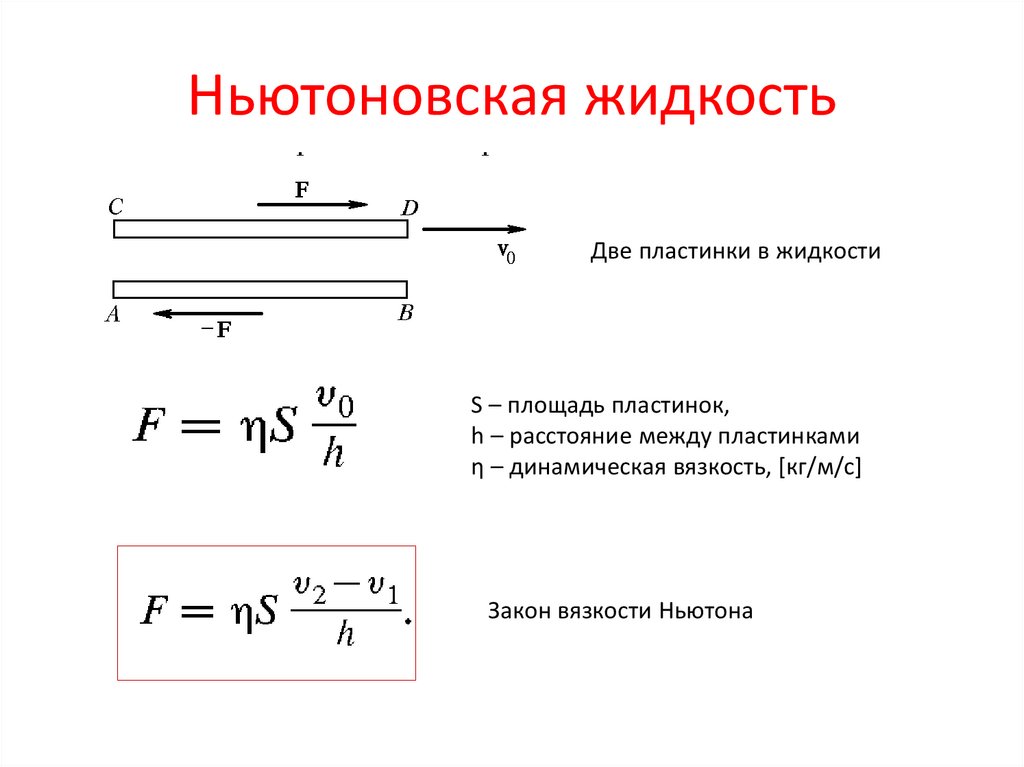 Тогда как через понятия кинетической и внутренней энергий системы это работает всегда, форму вращения или нет примет внутренняя энергия — неважно, даже для системы из двух невзаимодействующих частиц это работает
Тогда как через понятия кинетической и внутренней энергий системы это работает всегда, форму вращения или нет примет внутренняя энергия — неважно, даже для системы из двух невзаимодействующих частиц это работает В этом случае я действительно не вижу никакой выгоды через задний ход доказывать то, что очевидно по определению.
В этом случае я действительно не вижу никакой выгоды через задний ход доказывать то, что очевидно по определению.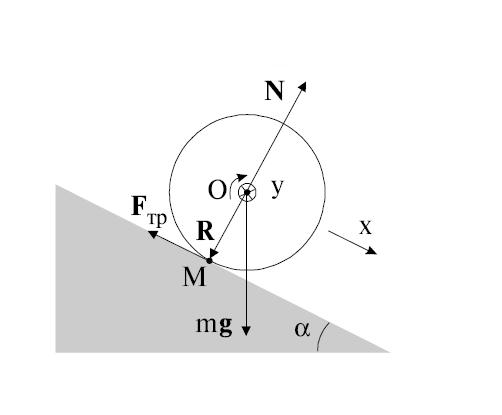 Если БЫ вместо цилиндра была одна бесструктурная частица той же массы и к ней были бы приложены той же величины силы и тяжести и трения, то ее поведение было бы точно таким же как и у центра масс цилиндра. Если мы дополнительно получаем информацию что на самом деле одна из сил приложена к неподвижной части системы и работы не совершает (тогда как по предыдущему расчету для материальной точки эта работа не была нулевой) значит мы имеет дополнительную информацию о том как меняется внутренняя энергия системы
Если БЫ вместо цилиндра была одна бесструктурная частица той же массы и к ней были бы приложены той же величины силы и тяжести и трения, то ее поведение было бы точно таким же как и у центра масс цилиндра. Если мы дополнительно получаем информацию что на самом деле одна из сил приложена к неподвижной части системы и работы не совершает (тогда как по предыдущему расчету для материальной точки эта работа не была нулевой) значит мы имеет дополнительную информацию о том как меняется внутренняя энергия системы 05.2016, 00:37
05.2016, 00:37 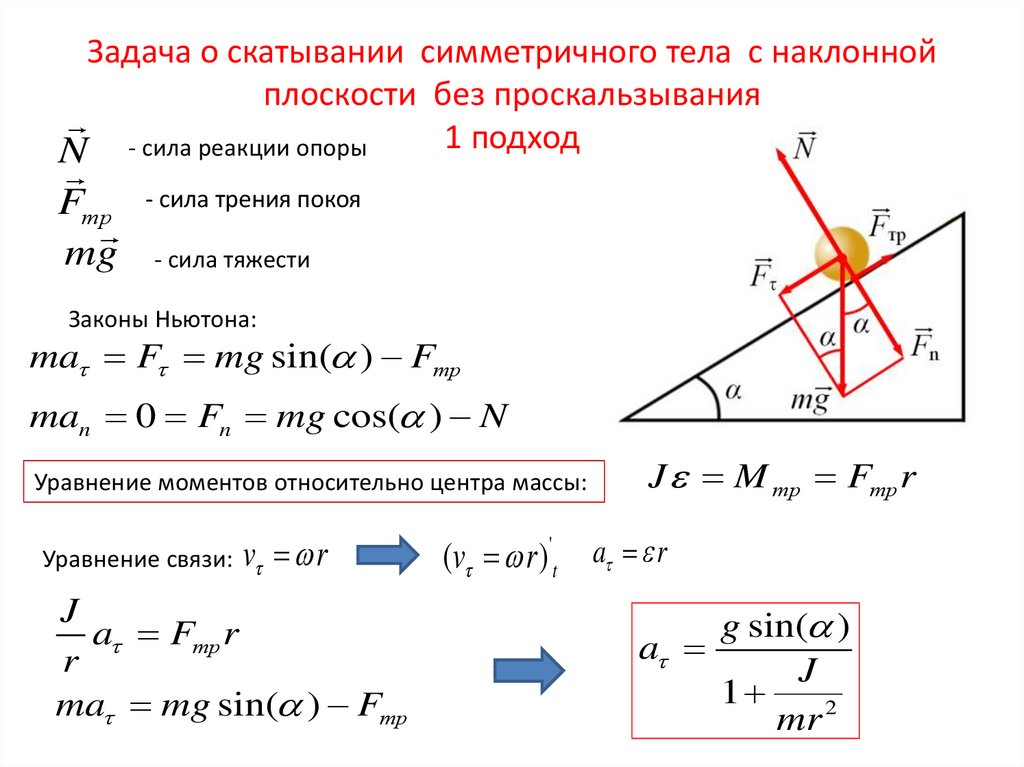 Следовательно,
Следовательно,