Сила тяжести | Физика

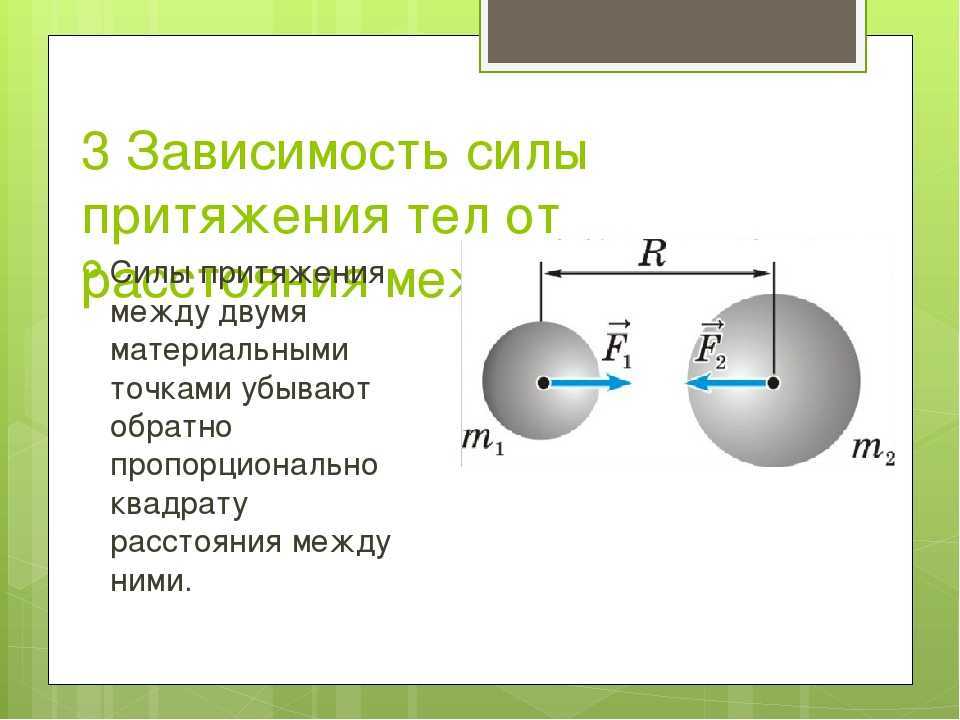
Почему мяч, брошенный в горизонтальном направлении (рис. 28), через некоторое время оказывается на земле? Почему камень, выпущенный из рук (рис. 29), падает вниз? Почему прыгнувший вверх человек вскоре снова оказывается внизу? У всех этих явлений одна и та же причина — притяжение Земли.Земля притягивает к себе все тела: людей, деревья, воду, дома, Луну и т. д.

Сила притяжения к Земле называется силой тяжести. Сила тяжести всегда направлена вертикально вниз. Обозначается она так:

F_T — сила тяжести.

Когда тело под действием притяжения к Земле падает вниз, на него действует не только Земля, но и сопротивление воздуха. В тех случаях, когда сила сопротивления воздуха пренебрежимо мала по сравнению с силой тяжести, падение тела называют свободным.

Для наблюдения свободного падения различных тел (например, дробинки, перышка и др.) их помещают в стеклянную трубку (трубку Ньютона), из которой откачивают воздух. Если вначале все эти предметы будут находиться на дне трубки, то после ее быстрого перевертывания они оказываются сверху, после чего начинают падать вниз (рис. 30). Наблюдая за их падением, можно заметить, что и свинцовая дробинка, и легкое перышко достигают дна трубки одновременно. Пройдя за одинаковое время один и тот же путь, эти тела с одной и той же скоростью ударяются о ее дно. Происходит это потому, что сила тяжести обладает следующим замечательным свойством: за каждую секунду она увеличивает скорость любого свободно падающего тела (независимо от его массы) всегда на одну и ту же величину.

Измерения показывают, что вблизи поверхности Земли скорость любого свободно падающего тела за каждую секунду падения возрастает на 9,8 м/с. Эту величину обозначают буквой g и называют ускорением свободного падения.

Зная ускорение свободного падения, можно найти силу, с которой Земля притягивает к себе любое, находящееся вблизи нее тело.

Чтобы определить силу тяжести, действующую на тело, надо массу этого тела умножить на ускорение свободного падения:

F_T = mg.

Из этой формулы следует, что g = F_T/m. Но F_T измеряется в ньютонах, a m — в килограммах. Поэтому величину g можно измерять в ньютонах на килограмм:

g = 9,8 Н/кг ≈10 Н/кг.

С увеличением высоты над Землей ускорение свободного падения постепенно уменьшается. Например, на высоте 297 км оно оказывается равным не 9,8 Н/кг, а 9 Н/кг. Уменьшение ускорения свободного падения означает, что и сила тяжести по мере увеличения высоты над Землей также уменьшается. Чем дальше тело находится от Земли, тем слабее она его притягивает.

1. Что является причиной падения всех тел на землю? 2. Какую силу называют силой тяжести? 3. В каком случае падение тела называют свободным? 4. Чему равно ускорение свободного падения вблизи поверхности Земли? 5. По какой формуле находится сила тяжести? 6. Что произойдет с силой тяжести, ускорением и временем падения при увеличении массы падающего тела в 2 раза? 7. Как изменяются сила тяжести и ускорение свободного падения при удалении от Земли?
Экспериментальные задания.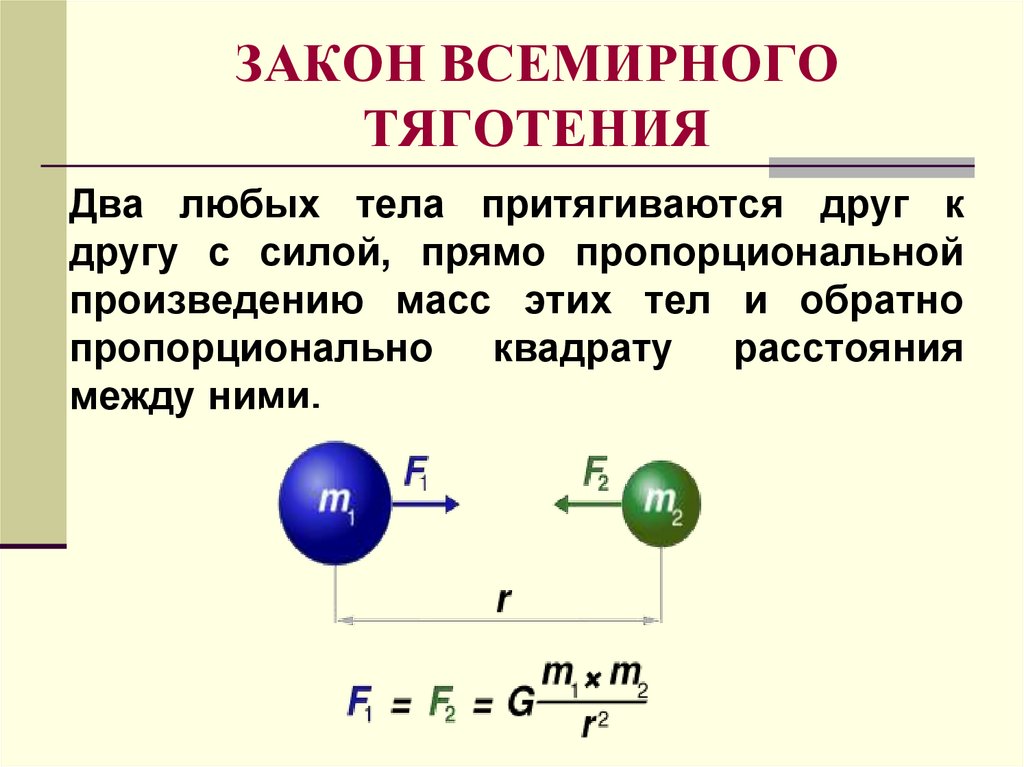 1. Возьмите в руки лист бумаги и отпустите его. Пронаблюдайте за его падением. Теперь скомкайте этот лист и снова отпустите. Как изменится характер его падения? Почему? 2. Возьмите в одну руку металлический кружок (например, монету), а в другую — бумажный кружок чуть меньшего размера. Одновременно отпустите их. Одинаковое ли время они будут падать? Теперь возьмите в руку металлический кружок и сверху на него положите бумажный (рис. 31). Отпустите кружки. Почему теперь они падают одновременно?

Тяжесть под землей. Движение. Теплота

Тяжесть под землей

Нам осталось осветить еще один интересный вопрос. Как будет меняться сила тяжести, если углубляться под землю?

Вес предмета – это результат натяжения незримых нитей, протянутых к этому предмету от каждого кусочка вещества Земли. Вес – это суммарная сила, результат сложения элементарных сил, действующих на предмет со стороны частиц Земли. Все эти силы, хотя и направлены под разными углами, тянут тело «вниз» – к центру Земли.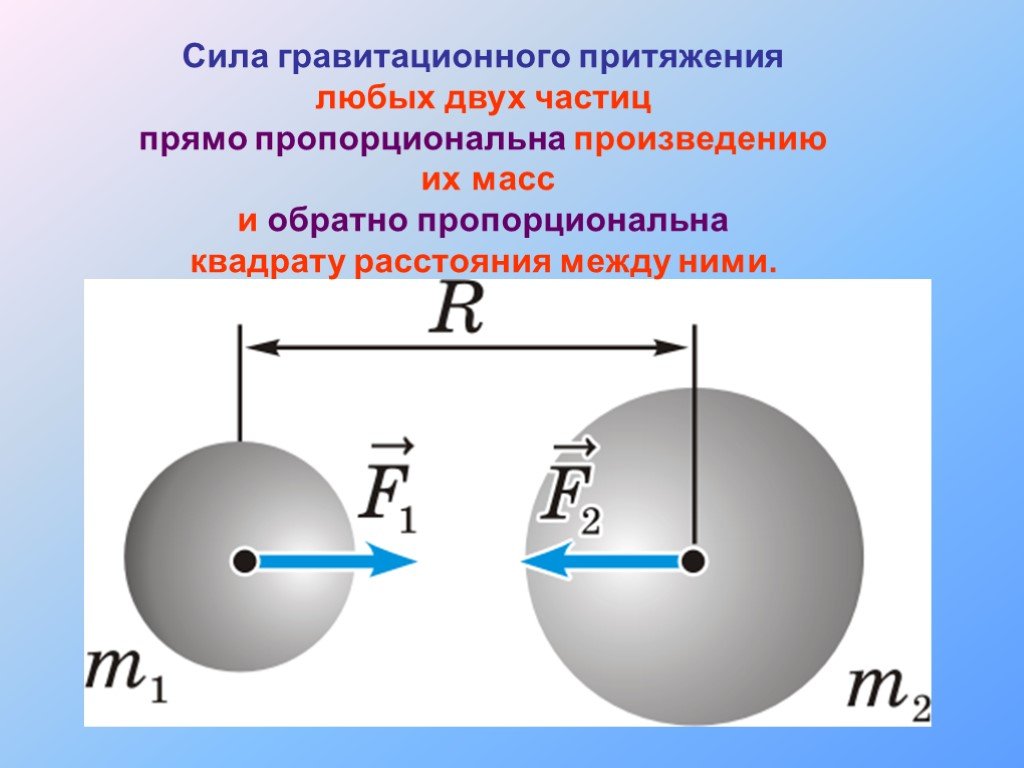

А какова будет тяжесть предмета, находящегося в подземной лаборатории? На него будут действовать силы притяжения и с внутренних, и с внешних слоев Земли.

Рассмотрим силы тяготения, действующие в точке, лежащей внутри земного шара, со стороны внешнего слоя. Если разбить этот слой на тонкие слои, вырезать в одном из них маленький квадратик со стороной a₁ и протянуть линии от периметра квадрата через точку

О, тяжесть в которой нас интересует, то в другом месте слоя получится квадратик другого размера со стороной а₂ (рис. 67). Силы притяжения, действующие в точке О со стороны двух квадратиков, направлены противоположно и пропорциональны по закону тяготения m₁/r₁² и m₂/r₂². Но массы квадратов m₁ и m₂ пропорциональны площадям квадратов. Поэтому силы тяготения пропорциональны выражениям a₁²r₁² и a₂²/r₂².

Однако эти отношения равны. Из рис. 67 видно, что а₁/r₁ и a₂/r₂ суть отношения соответственных сторон треугольников ОА₁В₁ и ОА₂В₂, которые будут подобными, если взять стороны квадратиков А₁В₁ и А₂В₂ очень малыми. А это мы всегда можем сделать.

Действительно, если квадраты малы, то направления отрезков А₁В₁ и А

2В₂ мало отличаются от направлений касательных к этим точкам. Тогда можно считать угол В₁А₁О и угол, дополнительный к A₂B₂O равными как углы, образованные касательной и хордой, опирающиеся на одну и ту же дугу.

Следовательно, . Кроме того, равны углы и при вершине.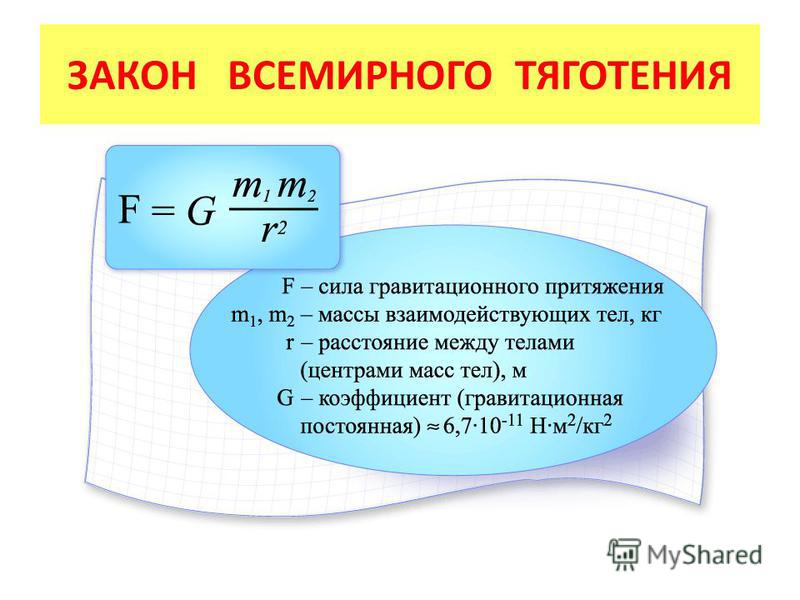 Значит, и треугольники подобны.

Из этого геометрического доказательства следует, что a₁/r₁ = a₂/r₂, а значит, силы притяжения, действующие в точке

О со стороны двух квадратиков, уравновешиваются.

Разбив тонкий слой на подобные пары «противоположных» квадратов, мы установили замечательный факт: тонкий однородный шаровой слой не действует на точку, расположенную внутри него. Но это верно для всех тонких слоев, на которые мы разбили шаровой пояс, лежащий над интересовавшей нас подземной точкой.

Значит, земной слой, находящийся над телом, все равно что отсутствует. Действие отдельных его частей на тело уравновешивается, и суммарная сила притяжения со стороны внешнего слоя равняется нулю.

Конечно, во всех этих рассуждениях мы считали плотность Земли постоянной внутри каждого слоя.

Результат наших рассуждений позволяет легко получить формулу для силы тяжести, действующей на любой глубине

H под землей. Точка, расположенная на глубине H, испытывает лишь притяжение со стороны внутренних слоев Земли. Формула для ускорения силы тяжести g = ?(M/R) применима и для этого случая, но M и R – это масса и радиус не всей Земли, а ее «внутренней» по отношению к этой точке части.

Если бы Земля имела одинаковую плотность во всех слоях, то формула для g приняла бы вид:

где ? – плотность, R_З – радиус Земли.

Это значит, что g менялось бы прямо пропорционально (

R_З – H): чем больше глубина H, тем меньше было бы g.

На самом же деле поведение g вблизи земной поверхности – мы можем проследить за ним вплоть до глубин 5 км (ниже уровня моря) – совсем не подчиняется этому закону. Опыт показывает, что в этих слоях g, наоборот, растет с глубиной. Расхождение опыта с формулой объясняется тем, что не было учтено различие плотности на разных глубинах.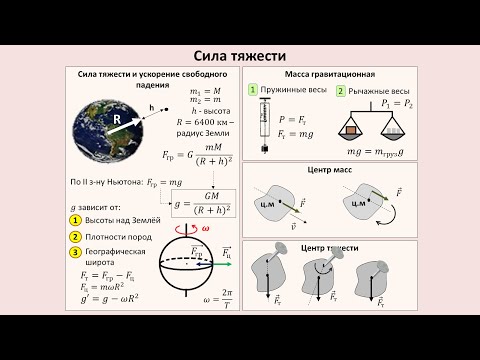

Средняя плотность Земли легко находится делением массы на объем земного шара. Это приводит нас к цифре 5,52. В то же время плотность поверхностных пород много меньше – она равна 2,75. Плотность земных слоев растет с глубиной. В поверхностных слоях Земли этот эффект берет верх над идеальным уменьшением, которое следует из выведенной формулы, и величина

g возрастает.

II Всемирное тяготение и земная тяжесть

II Всемирное тяготение и земная тяжесть Прежде чем приступить к этим поискам, уделим минуту внимания тем невидимым цепям, которые приковывают нас к земному шару, — познакомимся поближе с действием силы всемирного тяготения. Ведь с нею-то и предстоит, главным образом,

V Можно ли ослабить земную тяжесть?

V Можно ли ослабить земную тяжесть? Если несбыточны надежды укрыться от силы тяжести, то, быть-может, существуют способы хотя бы ослабить тяжесть на земной

3.

3. Астероиды, сближающиеся с Землей

3.3. Астероиды, сближающиеся с Землей Астероиды с перигелийными расстояниями, меньшими или равными 1,3 а.е., принято называть астероидами, сближающимися с Землей (АСЗ). Первый астероид с такой орбитой был открыт в 1898 г. Он получил номер и название (433) Eros (a = 1,458 а.е., q = 1,133 а.е.).

6.4. Проекты систем космического базирования для обнаружения объектов, сближающихся с Землей

6.4. Проекты систем космического базирования для обнаружения объектов, сближающихся с Землей Необходимость надежного обнаружения опасных небесных тел выдвигает перед космическим сегментом наблюдения множество далеко не простых требований: по обеспечению

7.2. Нелинейный характер распространения ошибок начальных данных. Поиск потенциально опасных сближений астероидов с Землей и оценка вероятности столкновений

7. 2. Нелинейный характер распространения ошибок начальных данных. Поиск потенциально опасных сближений астероидов с Землей и оценка вероятности столкновений После того как номинальная орбита астероида определена, появляется возможность предвычислить его движение в

7.4. Траектория сближения тела с Землей и другими массивными телами. Гравитационный маневр. Радиус захвата. Плоскость цели

7.4. Траектория сближения тела с Землей и другими массивными телами. Гравитационный маневр. Радиус захвата. Плоскость цели При оценке вероятности столкновения естественных космических тел друг с другом или искусственных космических аппаратов с естественными телами

Глава 9 Частота столкновений малых тел с Землей и оценки рисков

Глава 9 Частота столкновений малых тел с Землей и оценки рисков Можно считать курьезом, что научное сообщество ревностно изучает далекие галактики и в то же время игнорирует любую возможность серьезного столкновения Земли с космическими объектами.

Для меня это типичный

9.2. Оценки риска погибнуть в результате столкновения небесного тела с Землей

9.2. Оценки риска погибнуть в результате столкновения небесного тела с Землей Зная частоту ударов, мы можем рассчитать и средний промежуток времени между ударами тел данного диаметра. Для определенного тела можно оценить размер зоны разрушений и, используя данные о

Приложение 2 Зафиксированные сближения комет и астероидов с Землей

Приложение 2 Зафиксированные сближения комет и астероидов с Землей Таблица 2а. Состоявшиеся сближения комет с Землей. Приведены данные по сближениям комет с Землей после 1700 г. на расстояния, меньшие чем 0,1020 а.е. (по данным Центра малых планет,

Как рассчитать силу гравитации на поверхности Земли

Исследуйте книгу Купить на Amazon

Начав с физического уравнения для силы тяжести, вы можете подставить массу и радиус Земли, чтобы рассчитать силу гравитации вблизи поверхности Земли.

Уравнение силы тяжести равно

, и это справедливо независимо от того, насколько далеко друг от друга находятся две массы.

Гравитационная сила между массой и Землей составляет вес объекта . Масса считается мерой инерции объекта, а его вес — силой, действующей на объект в гравитационном поле. На поверхности Земли две силы связаны ускорением свободного падения:

F _г = мг . Килограммы и слаги — это единицы массы; ньютоны и фунты — единицы веса.

Вы можете использовать закон всемирного тяготения Ньютона, чтобы получить ускорение свободного падения, g , на поверхности Земли, просто зная гравитационную постоянную G , радиус Земли и массу Земли. Сила, действующая на объект массой м ₁ вблизи поверхности Земли, равна

F = м ₁ г

Эта сила обеспечивается гравитацией между объектом и Землей, согласно формуле гравитации Ньютона, поэтому вы можете написать

Радиус Земли, r _e , составляет около 6,38 × 10 ⁶ метров, а масса Земли составляет 5,98 × 10 ²⁴ кг. Если подсчитать, получится

.

Разделив обе стороны на м ₁ , вы получите ускорение свободного падения:

Закон всемирного тяготения Ньютона дает ускорение свободного падения вблизи поверхности Земли: 90,8 м/с ² .

Конечно, вы можете измерить г , бросив яблоко и засекая время, но что в этом интересного, когда вы можете вычислить его окольным путем, который требует, чтобы вы сначала измерили массу Земли?

Эта статья из книги:

• Физика I Для чайников,

Об авторе книги:

Доктор Стивен Хольцнер написал более 40 книг по физике и программированию. Он был пишущим редактором в 9 лет.0025 PC Magazine и преподавал в Массачусетском технологическом институте и Корнелле. Он является автором книг для чайников, в том числе «Физика для чайников», и «Основы физики для чайников». Доктор Хольцнер получил докторскую степень в Корнелле.

Эту статью можно найти в категории:

• Физика ,

Ускорение под действием силы тяжести Учебное пособие

Все тела на Земле сталкиваются с постоянной силой и ускорением под действием силы тяжести.

Что вы ожидаете, когда одновременно роняете перо и кирпич? Ответ заключается в том, что все они упадут одновременно; хотя некоторые объекты, например перья, кажутся медленнее из-за сопротивления воздуха. Для того, чтобы увидеть истинную природу гравитации, влияющей на перья, нужно удалить из помещения весь воздух. Причина этого в том, что в вакууме оба будут сталкиваться с одинаковым ускорением из-за гравитации!

Источник

УСКОРЕНИЕ И ТЯЖЕСТИ

• Под ускорением понимается любой процесс, в котором скорость (которая является мерой скорости и направления движения тела) изменяется со временем.

• Математически представленный как dv/dt (изменение скорости/периода времени), это векторная величина , которая может быть положительной, отрицательной или нулевой в зависимости от скорости и ее направления .

• Значение гравитации , с другой стороны, это сила, которая притягивает объект к центру Земли.

• F= мг — сила тяжести, действующая на тело,

, где f — сила, действующая на тело,

m — его масса,

и g — ускорение свободного падения.

УСКОРЕНИЕ СИЛЫ ТЯЖЕСТИ

• Чем дальше объект опускается вперед к низу, тем больше гравитация заставляет его падать все быстрее и быстрее.
• На практике скорость объекта увеличивается на 9,8 м/с2 (значение ускорения из-за силы тяжести на Земле).
• Следовательно, через 1 секунду после начала падения скорость тела составляет 9,8 м/с.
• Его скорость будет продолжать увеличиваться со временем из-за ускорения гравитации .
• Единица СИ для ускорения свободного падения такая же, как и для ускорения, м/с2 .

Источник

Универсальный закон всемирного тяготения гласит, что f = GmM/(r+h)2

Где f обозначает силу между двумя телами

G (6,6710-11 Нм2/кг2) универсальная гравитационная постоянная

м масса объекта0002 r — радиус Земли, а

h = расстояние между телом и поверхностью земли.

Поскольку высота будет намного меньше по сравнению с радиусом Земли

f = GmM/r2

Сравнивая оба уравнения, мы получаем

g = GM/r2 , формула для ускорение силы тяжести.

Это позволяет нам понять следующее:

• Гравитация ускоряет все тела с одинаковой скоростью, независимо от их массы.