Вопрос 16.Момент силы относительно точки

Одним из основных понятий механики наряду с моментом пары является понятие момента силы относительно данной точки. С этим понятием мы уже встречались при рассмотрении равновесия рычага.

Во всех задачах статики, относящихся к плоской системе сил, мы будем рассматривать момент силы как величину алгебраическую. Момент силы относительно данной точки положительный, если сила направлена относительно этой точки против движения часовой стрелки, и отрицательный, если сила направлена по движению часовой стрелки.

Абсолютное значение момента силы относительно данной точки равно произведению модуля силы на ее плечо (длину перпендикуляра, опущенного из этой точки на линию действия силы). Поэтому для силы F на рис.5.1 момент равен .

Рис.5.1. Рис.5.2.

В случае на рис.5.2 момент силы равен Из рисунков видно, что абсолютное значение момента силы

F относительно точки О численно равно двойной площади треугольника ОАВ, так как отрезок АВ=F является основанием этого треугольника, а плечо h – высотой. Точно также момент силы F₁ относительно точки Очисленно равен удвоенной площади треугольника ОА₁В₁.

Из данного определения момента силы следует:

1. Момент силы относительно данной точки на изменяется при переносе точки приложения силы по линии ее действия.

2. Момент силы относительно данной точки обращается в нуль в том случае, когда линия действия силы проходит через эту точку, так как в этом случае плечо силы равно нулю.

3. Сумма моментов двух равных по модулю сил, направленных по одной прямой в противоположные стороны, относительно любой точки равна нулю, так как моменты таких сил равны по абсолютной величине, но противоположны по знаку.

Задача сложения плоской системы сил.

Пусть на данное тело действует плоская система сил F₁, F₂, F₃, …, F_n.

Применяя способ последовательного сложения сил, такую систему можно привести или к одной равнодействующей силе, или к одной паре, если эта система сил не находится в равновесии.

Существует способ приведения плоской системы сил более эффективный, чем способ последовательного сложения сил, который называется приведением системы сил к данному центру. Он основан на следующей теореме:

Любая данная система сил эквивалентна по модулю и направлению силе, но приложенной в другой точке тела, и некоторой паре.

Доказательство. Пусть имеем силу

F, приложенную к телу в точке А (рис.5.3).

Рис.5.3.

В произвольно выбранной точке В тела приложим две равные по модулю и противоположные по направлению силы F’ и F», действующие по прямой параллельной силе F, причем F’=F»=F. Согласно аксиоме 2 (лекция1) система трех сил F, F’ и F» эквивалентна данной силе F.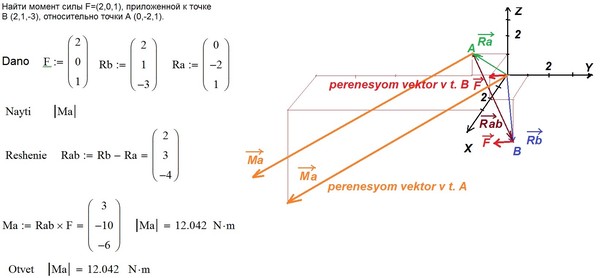 Таким образом, данную силу F можно заменить равной ей силой F’, приложенной в произвольно выбранной точке В, и парой (F,F»), что и требовалось доказать.

Эта теорема показывает, что данную силу можно переносить параллельно самой себе в любую точку тела с присоединением соответствующей пары. Поэтому пару (F,F»), получающуюся при переносе точки приложения силы F из точки А в точку В, называют присоединенной парой.

Момент присоединенной пары (F,F») равен: , где h – плечо этой пары. С другой стороны, произведение Fh представляет собой момент силы F относительно точки В, следовательно,

Мы получили это равенство для случая, представленного на рисунке 5.3, когда сила F стремится вращать тело вокруг точки В против движения часовой стрелки, т.е. когда и момент присоединенной пары и момент силы

F положительны. Очевидно, что это равенство будет иметь место в случае, когда момент силы F относительно точки В отрицателен.

Момент присоединенной пары (F,F») равен (по абсолютной величине и знаку) моменту силы F относительно новой точки приложения силы.

Пусть имеем плоскую систему сил F₁, F₂ и F₃, приложенных соответственно в точках А

1, А₂, А₃ (рис.5.4). Возьмем в плоскости этих сил какую-нибудь точку О, называемую центром приведения, и, пользуясь предыдущей теоремой, перенесем точки приложения данных сил в точку О. Получим силы F’₁, F’₂ и F’₃ и соответствующие присоединенные пары (F₁,F₁»), (F₂,F₂») и (F₃,F₃»). Силы F’ ₁, F’₂ и F’₃, как приложенные в одной точке О, мы можем сложить по правилу силового многоугольника. Получим равнодействующую R’, приложенную к той же точке О и равную их векторной сумме: или , так как силы F’₁, F’₂ и F’₃ равны соответственно силам F₁, F₂ и F₃.

Рис.5.4.

Сложив пары (F₁,F₁»), (F₂,F₂

») и (F₃,F₃») получим согласно теореме о сложении пар, лежащих в одной плоскости, одну равнодействующую пару, алгебраическую величину момента которой обозначим через М_О.

Так как при сложении пар, лежащих в одной плоскости, момент равнодействующей пары равен алгебраической сумме моментов слагаемых пар, то, обозначая алгебраическое значение момента присоединенной пары (F_i,F_i») через m_i, будем иметь:

Момент присоединенной пары, получаемой при изменении точки приложения силы, равен моменту силы относительно ее новой точки приложения.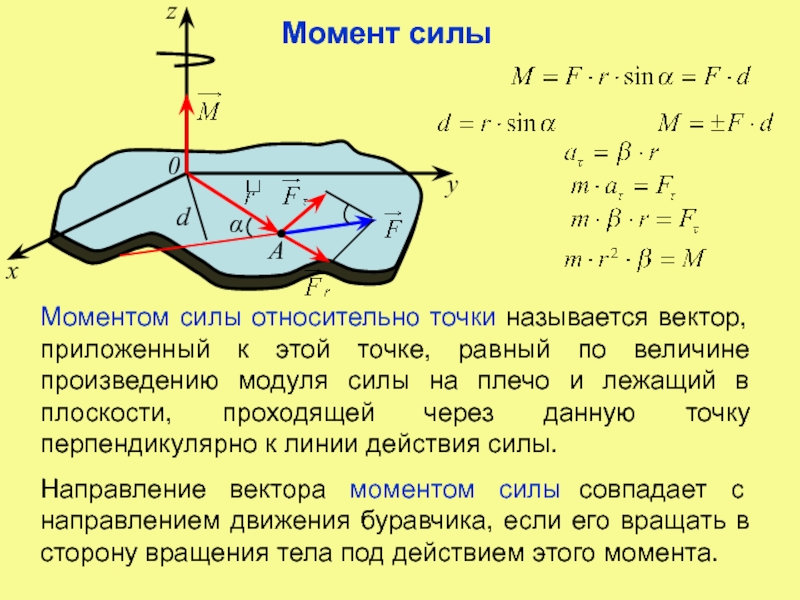

Следовательно: , поэтому

Векторная сумма всех сил системы называется главным вектором данной системы сил:

Сумма моментов всех сил системы относительно какого-нибудь центра называется главным моментом системы сил относительно данного центра.

Плоскую систему сил в общем случае можно привести к одной силе, приложенной в произвольно выбранной точке и равной главному вектору данной системы сил: , и к одной паре, момент которой равен главному моменту данной системы сил относительно той же точки:

Важно заметить, что сила R’, приложенная в точке О, не является равнодействующей данной системы сил F₁, F₂ и F₃, так как эта система не эквивалентна одной силе R’. Так как главный вектор равен геометрической сумме сил данной системы, ни модуль, ни его направление не зависят от выбора центра приведения. Если за центр приведения брать различные точки плоскости, то во всех этих точках главный вектор будет один и тот же по модулю и по направлению. Значение главного момента зависит от выбора центра приведения, так как с изменением центра приведения плечи данной системы, а, следовательно, их моменты изменяются. Каждой точке плоскости соответствует определенное значение главного момента. Поэтому, когда говорят о главном моменте данной системы сил, то всегда нужно указывать, к какому центру приведения относится этот момент.

Выведем формулы, определяющие модуль и направление главного вектора R’.

Проведем через центр О координатные оси Ох и Оу (рис.5.4). Проекции данных сил F_i на эти оси обозначим через Х_i и Y_i, а проекции силы R’ обозначим через R’

х и R’_у. Из векторного равенства на основании теоремы о проекции суммы данных векторов имеем: ;

Отсюда находим:

Эта формула позволяет вычислить модуль главного вектора R’. Направление главного вектора определяется углом α между этим вектором и положительным направлением оси х. Этот угол находится по формулам:

,

Момент силы относительно центра (или точки)

⇐ Предыдущая3456789101112Следующая ⇒

Момент силы относительно центра. Пара сил

 

Введем важное понятие о моменте силы относительно точки. Точку, относительно которой берется момент, называют центром момента, а момент силы относительно этой точки – моментом относительно центра.

Если под действием приложенной силы тело может вращаться вокруг некоторой закрепленной точки, то момент силы относительно этой точки будет характеризовать вращательный эффект силы. Вращательное действие силы на тело будет зависеть от модуля силы, расстояния линии действия силы до точки закрепления и от направления вращения в этой плоскости.

Рисунок 5.1

Так, например, если к телу, закрепленному неподвижно в точке О (рисунок 5. 1), приложена в точке A₁ сила , то тело будет вращаться вокруг оси OZ₁, перпендикулярно плоскости треугольника OA₁B₁, в направлении, указанном на рисунке. Если к этому же телу приложена сила в точке A₂, то тело будет вращаться вокруг оси OZ₂, перпендикулярно к плоскости треугольника OA₂B₂.

Мерой вращательного действия силы на тело с закрепленной точкой является момент силы относительно точки.

Алгебраическая величина момента силы относительно точки, определяется произведением модуля силы на ее плечо.

Рассмотрим силу F, приложенную в точке А (рисунок 5.3). Из некоторого центра О опустим перпендикуляр на линию действия силы ; длину h этого перпендикуляра называют плечом силы относительно центра О.

 

Рисунок 5.2

Момент силы относительно центра О определяется:

1) модулем момента, равным произведению F·h;

2) положением в пространстве плоскости ОАВ («плоскости поворота»), проходящей через центр О и силу ;

3) направлением поворота в этой плоскости.

Из геометрии известно, что положение плоскости в пространстве определяется направлением нормали «n» (перпендикуляра) к этой плоскости. Таким образом, момент силы относительно центра характеризуется не только его числовым значением, но и направлением в пространстве, т.е. является величиной векторной.

Моментом силы F относительно центра О называется приложенный в центре О вектор , модуль которого равен произведению модуля силы на ее плечо h и который направлен перпендикулярно плоскости, проходящей через центр О и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки (рисунок 5.3).

Согласно этому определению

(5.1)

Этот результат следует из того, что пл. Δ ОАВ= АВ·h/2=Fh/2. Измеряется момент силы в Ньютон-метрах (Нм). Выведем формулу, для вектора-момента силы относительно точки О. Для этого рассмотрим векторное произведение векторов и (рисунок 5.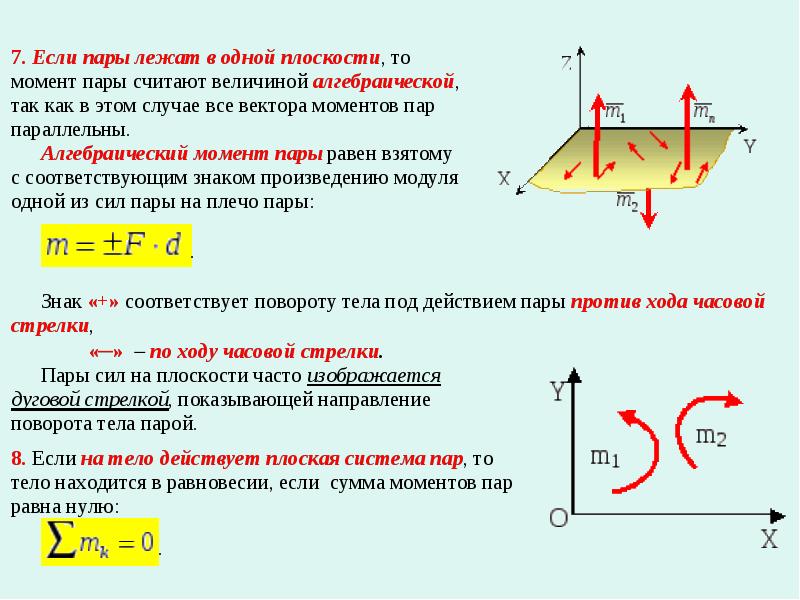 3). Как известно из векторной алгебры, это будет вектор, перпендикулярный к плоскости, в которой расположены векторы и , и направленный в такую сторону, чтобы с его конца видеть поворот от к кратчайшим путем против хода часовой стрелки. Модуль этого вектора или .

Поэтому

или , (5.2)

где – радиус-вектор точки А, проведенный из центра О.

Таким образом, вектор-момент силы относительно точки равен векторному произведению радиуса-вектора точки приложения силы на вектор силы.

Обозначая алгебраическое значение момента силы относительно точки О через , будет иметь

(5.3)

Из формулы (5.3) следует, момент силы относительно точки, лежащей на линии действия этой силы, равен нулю (т.к. h=0).

Пример.

Вычислить моменты сил , относительно точки O.

Решение

Вектор направлен перпендикулярно плоскости OAEN, т.е. по прямой OL. , т.к. линия действия силы проходит через точку O.

Векторы и перпендикулярны к плоскости ОВDN, но направлены в противоположные стороны. Вектор перпендикулярен к плоскости ОАВL и направлен по прямой ON.

 

 

5.2 Пара сил. Момент пары сил

Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело (рисунок 5.3, а).

а) б)

Рисунок 5.3

Система сил , , образующих пару, не находится в равновесии (эти силы не направлены вдоль одной прямой). В то же время пара сил не имеет равнодействующей, т.к. равнодействующая любой системы сил равна ее главному вектору , т.е. сумме этих сил, но для пары сил , поэтому свойства пары сил, как особой меры механического взаимодействия тел, рассмотрим отдельно.

Плоскость, проходящая через линии действия пары сил называется плоскостью действия пары. Расстояние d между линиями действия сил пары называется плечом пары. Действие пары сил на твердое тело сводится к вращательному эффекту, который характеризуется величиной, называемой моментом пары. Этот момент определяется:

1) Его модулем, равным произведению F·d;

2) положением в пространстве плоскости действия пары;

3) направлением поворота пары в этой плоскости.

Таким образом, как и момент силы относительно центра, это величина векторная. Поэтому моментом пары сил называется вектор (или ), модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки (рисунок 5.3, б).

Следует отметить, что так как плечо силы относительно точки А равно d (рисунок 5.3, а), а плоскость, проходящая через точку А и силу , совпадает с плоскостью действия пары, то одновременно .

В отличие от момента силы может быть приложен в любой точке (такой вектор называется свободным). Измеряется момент пары, как и момент силы, в Н·м.

Покажем, что моменту пары можно дать другое выражение: момент пары равен сумме моментов относительно любого центра О сил, образующих пару, т.е.

(5.4)

Для доказательства проведем из произвольной точки О (рисунок 5.4) радиусы-векторы и .

Рисунок 5.4

Тогда согласно формуле (5.2), учитывая, что , получим ;

и, следовательно,

Так как , то справедливость (5.4) доказана. Отсюда следует, что или (5.5)

т.е. момент пары равен моменту одной из ее сил относительно точки приложения другой силы. Отметим еще, что модуль момента пары

(5.5^/)

Так как действие пары сил на твердое тело определяется значением суммы моментов сил пары относительно любого центра О, то из формулы (5.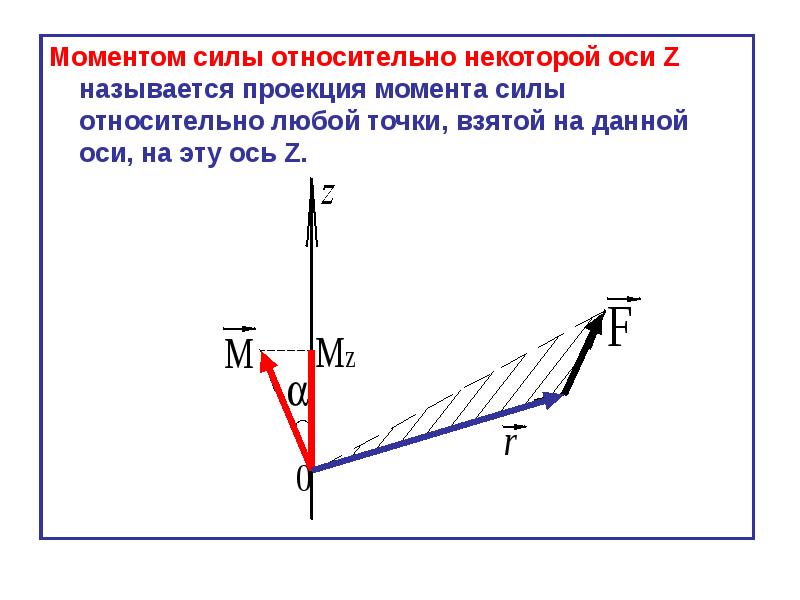 4) следует, что две пары сил, имеющие одинаковые моменты, эквивалентны, т.е. оказывают на тело одинаковое механическое действие. Это означает, что две пары сил, независимо от того, где каждая из них расположена в данной плоскости (или в параллельных плоскостях) и чему равны в отдельности модули их сил и их плечи, если моменты имеют одно и то же значение , будут эквивалентны. Так как выбор центра О произволен, то вектор можно считать приложенным в любой точке, т.е. это свободный вектор.

В дальнейшем будем на чертеже вместо пары изображать полностью ее характеризующий вектор . При этом модуль определяет модуль момента пары [формула (5.5)], а направление определяет плоскость действия пары и направление поворота в этой плоскости.

Из формулы (5.4) следует, еще, что если на тело действует несколько пар с моментами ; …. , то сумма моментов всех сил, образующих эти пары относительно любого центра будет равна + +…+ , а следовательно, вся совокупность этих пар эквивалентна одной паре с моментом

(5. 6)

Этот результат выражает теорему о сложении пар.

Из формулы (5.6) следует, при равновесии системы пар, действующих на твердое тело, должно быть

или (5.7)

Таким образом, отметим следующие свойства пар сил:

1) Пары сил, лежащие в одной плоскости, эквивалентны, если их моменты численно равны и одинаковы по знаку.

2) Пару сил, не изменяя ее действия на твердое тело, можно переносить в любое место в плоскости ее действия, поворачивать ее плечо на любой угол, а также изменять величины ее момента и направления вращения.

3) Пары сил в пространстве эквивалентны, если их моменты геометрически равны.

4) Не изменяя действия пары сил на твердое тело, пару сил можно переносить в любую плоскость, параллельную плоскости ее действия, а также изменять ее силы и плечо, сохраняя неизменным модуль и направление ее момента. Таким образом, вектор-момент пары можно переносить в любую точку, т.е. вектор-момент пары сил является свободным вектором.

5) Геометрическая сумма моментов составляющих пар равна моменту эквивалентной им пары сил:

или

(5.7)

6) Пары сил, произвольно расположенные в пространстве, взаимно уравновешиваются в том случае, если геометрическая сумма их моментов равна нулю, т.е. условие равновесия пар сил в пространстве имеет вид:

(5.8)

7) Момент пары сил эквивалентной системе пар сил на плоскости, равен алгебраической сумме моментов составляющих пар:

(5.9)

8) Пары сил, расположенные в одной плоскости, взаимно уравновешиваются, если алгебраическая сумма их моментов равна нулю.

(5.10)

Т.е. выражение 5.10 является условием равновесия пар сил на плоскости, а (5.8) – в пространстве.

 

Вопросы для самоконтроля

Момент силы относительно точки

1. Что называется моментом силы относительно точки?

2. Как направлен вектор момента силы относительно точки?

3. Запишите формулу, по которой определяется алгебраический момент силы относительно точки.

4. Какой площадью можно определить числовое значение момента силы относительно заданной точки?

5. Изменится ли момент силы относительно данной точки при переносе силы вдоль линии ее действия?

6. В каком случае момент силы относительно данной точки равен нулю?

7. Определите геометрическое место точек пространства, относительно которых моменты данной силы:

a. геометрически равны;

b. равны по модулю.

8. Определите момент силы относительно точки O, если F=200H; OA=0.5м (рисунок 6,а).

Рисунок 6

9. Определить моменты сил и относительно координатных осей, если КН, КН, ОА = 0,4 м; ОВ = 0,6 м; ОС = 0,3 м (рисунок 6,б).

Пара сил

1. Какая система сил называется парой?

2. Почему пара сил не имеет равнодействующей?

3. Чем характеризуется действие пары сил на тело?

4. Как направлен вектор момента пары сил?

5. Как определяются моменты пар сил, лежащих в одной плоскости.

6. Каковы условия эквивалентности пар сил на плоскости и в пространстве?

7. Какие преобразования пары не изменяют ее действие на твердое тело?

8. Почему момент пары сил является свободным вектором?

9. ему равен момент сил, эквивалентной двум парам сил, расположенным в перпендикулярных плоскостях, если M₁=10мм; М₂=20нм?

10. Чему равен момент пары сил, эквивалентной системе пар сил, расположенных в пространстве и в одной плоскости?

11. Каковы условия равновесия системы пар сил, расположенных в пространстве и в одной плоскости?

12. Чем можно уравновесить заданную пару сил?

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться с друзьями:

---

Дата добавления: 2015-06-04; Просмотров: 3972; Нарушение авторских прав?; Мы поможем в написании вашей работы!

---

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

---

---

Моменты и равновесие: принцип и примеры

Вы когда-нибудь видели двух детей на качелях и наблюдали за их движением? Качели вращаются вокруг фиксированной точки, известной как точка опоры, одна сторона поднимается, а другая опускается, но задумывались ли вы когда-нибудь, какова физика движения качелей? Качели воздействуют на важное понятие в физике, известное как момент.

Рис. 1: Качели — это балка, закрепленная на рычаге.

Теперь предположим, что по какой-то причине качели идеально балансируют в центре. Такое может случиться, конечно, с какой-то физикой, и это понятие в физике называется равновесием моментов, о котором и пойдет речь в этой статье. Чтобы понять принцип равновесия, нам нужно получить представление о том, что такое момент. Позже мы рассмотрим принцип момента, изображая моменты и равновесие.

Взаимосвязь момента и равновесия

Если вы возьмете мизинец и попытаетесь закрыть им открытую дверь, поднеся палец к дверной ручке, дверь легко закроется. Теперь попытайтесь снова закрыть дверь мизинцем, но на этот раз попробуйте толкнуть дверь, поместив палец рядом с петлей. Закрывается ли дверь так же легко, как если бы вы приложили мизинец к ручке?

Было бы гораздо труднее закрыть дверь, поместив палец рядом с петлей. Почему это? Расстояние или, в частности, перпендикулярное расстояние от петли до дверной ручки больше, поэтому сила, создаваемая для создания эффекта поворота, также больше.

Рис. 2: Расстояние \(d_2\) создает большую вращающую силу по сравнению с \(d_1\).

Мы часто используем силы, чтобы заставить объект вращаться, другими словами, нам нужны силы, чтобы создать момент. Момент также может объяснить, почему легче использовать более длинный гаечный ключ, чем более короткий.

Сила в точке A вызовет меньший вращательный эффект по сравнению с силой в точке B. Wikimedia

Момент силы

Вращательный или вращательный эффект силы называется момент силы.

Мы можем рассчитать момент силы, используя уравнение:

\[M=Fd\]

Где M — момент в Нм, F — сила в ньютонах, а d — расстояние вдоль нормаль к силе в м. Одна вещь, которую важно иметь в виду в приведенном выше уравнении, заключается в том, что расстояние d является перпендикулярным расстоянием от линии действия силы до оси вращения. Таким образом, большая сила должна быть приложена далеко от точки поворота для большего момента.

Перпендикулярное расстояние означает расстояние под прямым углом. На рисунке ниже расстояние по перпендикуляру от точки, в которой действует приложенная сила A, до оси B (центра гайки), поскольку сила и расстояние до оси составляют прямые углы друг к другу.

Приложенная сила образует прямой угол с расстоянием от оси вращения. Адаптировано из Викимедиа.

Если приложенная сила оказывается не под прямым углом, как показано на рисунке ниже, момент, возникающий при повороте, также будет меньше. Расстояние от точки поворота B до приложенной силы A не перпендикулярно на рисунке ниже; но вам не о чем беспокоиться, так как перпендикулярное расстояние будет указано в любой задаче, которую вам попросят решить.

Сила, приложенная под углом к ​​расстоянию от оси вращения, не считается перпендикулярным расстоянием. Адаптировано из Викимедиа.

Рассчитайте момент, создаваемый гаечным ключом, если приложенная сила равна 40 Н, а расстояние по перпендикуляру от точки приложения силы до центра гайки составляет 0,4 м.

Решение:

Перпендикулярное расстояние от оси вращения до приложенной силы составляет 0,4 м, а приложенная сила равна 40 Н. Используя формулу момента, получаем

M=Fd=40N×0,4m=16Nm.

M=F×dM=40×0,4M=16 Н·м

Обратите внимание, что момент может быть направлен против часовой стрелки (положительное направление) или по часовой стрелке (отрицательное направление), поскольку по сути это вращение, которое может быть в любом направлении в зависимости от расстояния и направления приложенной силы. Теперь, конечно, на объект может действовать и более одного момента, например, два человека на качелях. Но направления по часовой стрелке и против часовой стрелки и множественные моменты приводят к важной концепции в физике, известной как принцип равновесия момента или просто принцип момента.

Принцип момента и равновесия

Принцип момента и равновесия утверждает, что когда система находится в равновесии, сумма моментов по часовой стрелке равна сумме моментов против часовой стрелки.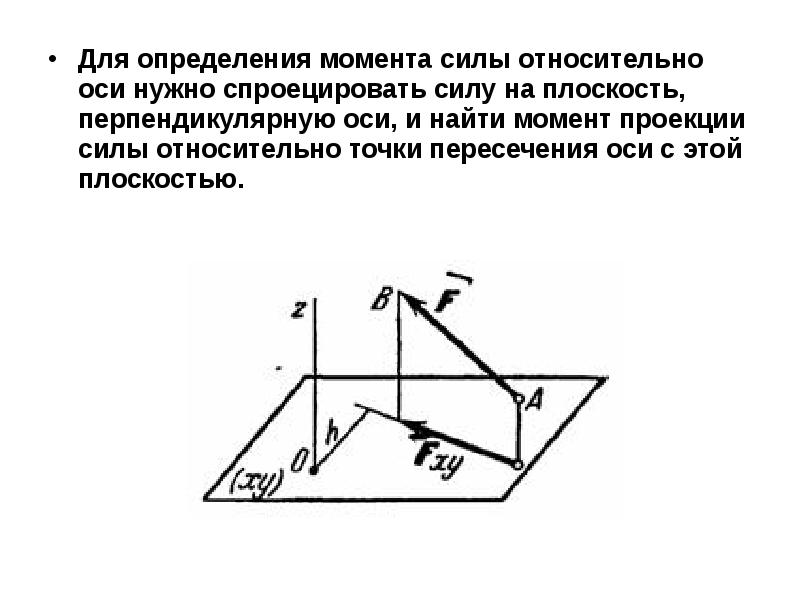

Механическая измерительная шкала, подобная показанной на рисунке ниже, демонстрирует принцип момента и равновесия. Мы используем весы, чтобы сравнить вес двух тел.

Весы используются для сравнения разницы в массе двух объектов. Викимедиа.

Когда гири разбалансированы, инструмент наклоняется так, что шкала с более тяжелым объектом опускается, а шкала с более легким объектом поднимается. Этот «наклон» представляет собой момент против часовой стрелки или по часовой стрелке, возникающий из-за дисбаланса направленных вниз сил с обеих сторон. Поскольку длина каждого рычага, к которому подвешены весы, одинакова, если мы хотим сбалансировать инструмент, вес объектов с обеих сторон должен быть одинаковым. Это приведет к тому, что момент по часовой стрелке и момент против часовой стрелки станут равными, и, следовательно, тело будет в равновесии.

Весы находятся в равновесии, если момент по часовой стрелке и момент против часовой стрелки становятся равными. Адаптировано из Викимедиа.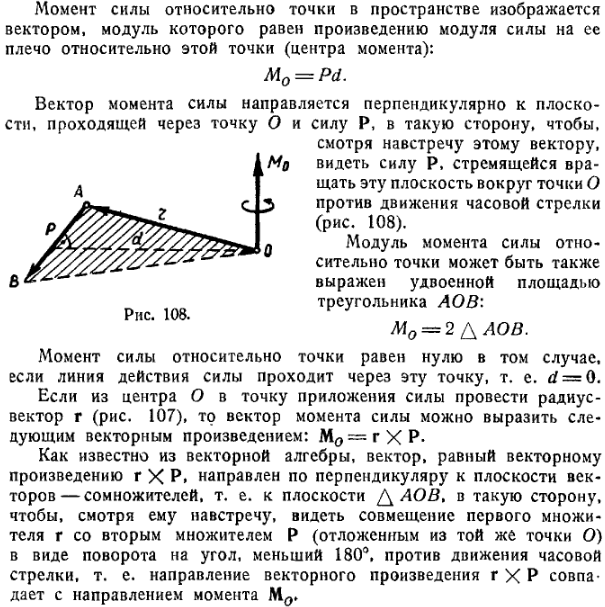

Моменты и примеры равновесия

Допустим, Джон сидит на правой стороне качелей относительно нас. Сила из-за его веса составляет 600 Н, и он сидит на расстоянии 2 м от оси вращения. Как упоминалось ранее, моменты могут быть по часовой стрелке или против часовой стрелки, и в случае Джона создаваемый момент будет по часовой стрелке. Момент по часовой стрелке для случая Джона будет:

M=FdM=600N×2mM=1200Nm

На этой диаграмме общий момент, действующий на качели, направлен по часовой стрелке (отрицательный), поскольку существует один момент, действующий по часовой стрелке из-за веса человека, сидящего на качелях.

Вскоре после этого Питер присоединяется к Джону на качелях, которые создают момент против часовой стрелки. Если мы хотим рассчитать общий момент качелей, нам нужно будет принять во внимание как момент по часовой стрелке, так и момент против часовой стрелки, а затем посмотреть, какой момент больше, чем другой.

Момент по часовой стрелке и против часовой стрелки создается качелями в результате действия двух сил, действующих в одном направлении на противоположных концах. Адаптировано из Викимедиа.

Если каким-то образом два момента станут равными, а это означает, что момент против часовой стрелки равен моменту по часовой стрелке, то качели не будут вращаться. Другими словами, если моменты станут равными, то качели будут в равновесии, что и утверждает принцип момента.

Моменты и уравнение равновесия

В сценарии Питера и Джона, на каком расстоянии от равновесия должен сидеть Питер, чтобы качели достигли равновесия? Мы рассчитали момент, создаваемый силой Джона, поэтому момент Питера должен быть таким же, как момент Джона. Мы знаем, что сила со стороны Питера равна 800 Н, поэтому мы можем написать:

Сумма моментов по часовой стрелке = Сумма моментов против часовой стрелки F1d1 = F2d2600 Н × 2 м = 800 Н × d2d2 = 600 Н × 2 м 800Nd2 = 1,5 м

Таким образом, Петр должен сидеть на расстоянии 1,5 м от оси вращения. чтобы качели были сбалансированы.

Применение моментов и равновесия

Существует ряд применений моментов и равновесий, которые мы используем в повседневной жизни. Здесь мы перечислим и обсудим несколько примеров, чтобы завершить эту статью.

Классический пример, который мы уже рассмотрели, — качели. Это простое, но забавное игровое оборудование не могло бы работать без принципов моментов. Момент на каждом конце качелей обеспечивается толчком людей, сидящих на любом из рычагов качелей, или их откидыванием назад, чтобы изменить свой центр масс так, чтобы он находился дальше от оси вращения.

Другое приложение, которое мы изучили, это весы. Весы работают по принципу, согласно которому уравновешивание моментов по часовой стрелке и против часовой стрелки приводит к тому, что рассматриваемая система находится в состоянии равновесия, т. е. чистого движения нет, поскольку чистый момент равен нулю. Мы можем сбалансировать объект на одной чаше весов и постепенно добавлять гири известной массы на другую чашу весов, пока весы не будут уравновешены. Суммируя массу гирь, необходимых для уравновешивания весов, получим общую массу взвешиваемого объекта.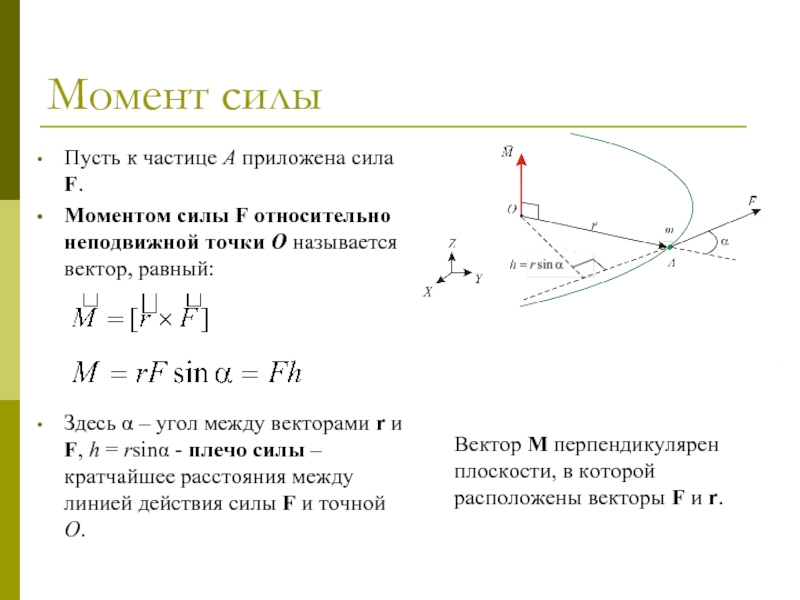

Моменты и равновесие – основные выводы

• Вращательное или вращательное действие силы называется моментом силы.
• Мы можем рассчитать момент силы, используя уравнение:

M=Fd

• Расстояние d в формуле момента представляет собой перпендикулярное расстояние от линии действия силы до оси вращения.
• Для более важного момента необходимо приложить большую силу вдали от точки поворота.
• Принцип момента гласит, что когда система находится в равновесии, момент по часовой стрелке становится равным моменту против часовой стрелки.

Вычисление крутящего момента, перпендикулярного приложенной силе

В физике величина крутящего момента, приложенного к объекту, зависит от двух вещей: прилагаемой силы, F ; и рычаг . Также называется моментом .0120 r , по

угол между силой и линией от оси до точки приложения силы.

Крутящий момент, прилагаемый к двери, зависит от того, куда вы ее толкаете.

Предположим, что вы пытаетесь открыть дверь, как в различных сценариях на рисунке. Вы знаете, что если вы нажмете на петлю, как на схеме А, дверь не откроется; если нажать на середину двери, как на схеме Б, дверь откроется; но если вы нажмете на край двери, как на диаграмме C, дверь откроется легче.

На рисунке плечо рычага, l, — это расстояние r от шарнира до точки приложения усилия. Крутящий момент является произведением величины перпендикулярной силы на плечо рычага. Он имеет специальный символ, греческую букву тау:

Единицы крутящего момента — это единицы силы, умноженные на единицы расстояния, которые представляют собой ньютон-метры в системе МКС (метр-килограмм-секунды) и фут-фунты в фут-фунтах. -вторая система.

Например, плечо рычага на рисунке равно расстоянию r (поскольку это плечо рычага перпендикулярно силе), поэтому

Если вы толкаете с силой 200 ньютонов, а r составляет 0,5 метра, какой крутящий момент вы видите на рисунке? На диаграмме A вы нажимаете на шарнир, так что ваше расстояние от точки вращения равно нулю, а значит, и плечо рычага равно нулю.