Равнодействующая сила – формула, модуль, законы Ньютона
4.7
Средняя оценка: 4.7
Всего получено оценок: 158.
Обновлено 31 Октября, 2021
4.7
Средняя оценка: 4.7
Всего получено оценок: 158.
Обновлено 31 Октября, 2021
Законы Ньютона – математическая абстракция. В реальности причиной движения или покоя тел, а также их деформации, выступают сразу несколько сил. Поэтому важным дополнениям к законам механики будет введение понятия равнодействующей силы и его применение.
О причинах изменений
Классическая механика разделена на два раздела – кинематику, при помощи уравнений описывающую траекторию движения тел, и динамику, которая разбирается с причинами изменения положения объектов или самих объектов.
Причиной изменений выступает некоторая сила, которая есть мера действия на тело других тел или силовых полей (например, электромагнитное поле или гравитация). К примеру, сила упругости вызывает деформацию тела, сила тяжести – падение тел на Землю.
Теперь дадим строгое определение: равнодействующая сила есть векторная сумма всех сил, оказывающих влияние на тело.
Разберем правила треугольника и параллелограмма. Графически это выглядит так:
Рис. 3. Правило треугольника и параллелограмма.Внешне они кажутся различными, но когда доходит до вычислений, сводятся к нахождению третьей стороны треугольника (или, что тоже самое, диагонали параллелограмма) по теореме косинусов.
Если сил больше двух, иногда удобней пользоваться правилом многоугольника. По своей сути – это всё тот же треугольник, только повторенный на одном рисунке некоторое количество раз. В случае, если по итогу контур получился замкнутым, общее действие сил равно нулю и тело покоится.
Задачи
- На ящик, размещенный в центре декартовой прямоугольной системы координат, действуют две силы: $F_1 = (5, 0)$ и $F_2 = (3, 3)$. Рассчитать равнодействующую двумя методами: по правилу треугольника и при помощи покомпонентного сложения векторов.
 2 + 2F_1F_2 sin45} = \sqrt{25 + 18 + 2 \cdot 5 \cdot 4,2 \cdot sin45} = 8,5 Н$
2 + 2F_1F_2 sin45} = \sqrt{25 + 18 + 2 \cdot 5 \cdot 4,2 \cdot sin45} = 8,5 Н$- На машину действуют три силы: $F_1 = (-5, 0)$, $F_2 = (-2, 0)$, $F_1 = (7,0)$. Какова их равнодействующая?
Решение
Достаточно сложить иксовые компоненты векторов:
$F = -5 – 2 + 7 = 0$
Что мы узнали?
В ходе урока было введено понятие равнодействующей сил и рассмотрены различные методы ее расчета, а также введена запись второго закона Ньютона для общего случая, когда количество сил неограниченно.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 158.
А какая ваша оценка?
формула, как найти, куда направлена
Содержание:
- Сила натяжения нити — формулировка
-
Как определить силу, формулы
- С неподвижно закрепленным верхним концом
- Если нить под углом
- Формула с учетом ускорения и массы
-
Сила натяжения во вращающейся системе
- Описание
- Формула расчета
- Обозначение, единица измерения
- Примеры решения задач
Содержание
- Сила натяжения нити — формулировка
-
Как определить силу, формулы
- С неподвижно закрепленным верхним концом
- Если нить под углом
- Формула с учетом ускорения и массы
-
Сила натяжения во вращающейся системе
- Описание
- Формула расчета
- Обозначение, единица измерения
- Примеры решения задач
Сила натяжения нити — формулировка
Определение
Силой натяжения называют силу, приложенную к концам объекта и создающую внутри него упругую деформацию.

Длина тела, к которому приложена сила, обычно многократно больше, чем его толщина. Примерами таких объектов являются веревка, канат, трос, леска, проволока. Сила натяжения визуально проявляется в следующих примерах:
- создание строительного отвеса;
- установка растяжек для фиксации радиоантенн;
- поведение арматуры внутри напряженного бетона;
- устройство корабельного такелажа.
Как определить силу, формулы
Натяжение проявляется по-разному. Поэтому сила натяжения может рассчитываться определенным образом, в зависимости от окружающих условий.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
С неподвижно закрепленным верхним концом
Простейшим примером проявления силы натяжения является нить с закрепленным на ней грузом. Верхний конец такого подвеса фиксируется неподвижно.
 В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:
В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:\(F=F_{тяж}=m*g\)
где m – это масса тела, а g представляет собой ускорение свободного падения.
Если нить под углом
В случае, когда груз расположен под определенным углом, характер силы натяжения несколько изменяется. Примером такой системы выступает маятник.
\(F_n=m*g*cos(a)\)
где а равен углу отклонения.
Формула с учетом ускорения и массы
В ситуации, при которой на груз оказывается сила натяжения, приводящая его в движение вверх, следует использовать такую формулу для ее расчета:
\(F=F_{тяж}+m*a\)
Сила натяжения во вращающейся системе
Описание
Такое явление можно наблюдать, когда система из нити и тела вращается во время раскручивания подвеса вокруг своей оси с закрепленным на одном его конце объектом: центрифуга, маятник, качели.

Задание 2
На иллюстрации изображен шар, который обладает массой m=0.1 кг. Будучи зафиксирован на нити, шарик совершает движение по окружности в горизонтальной плоскости. Длина подвеса составляет l=5 м, а радиус окружности – R=3 м. Требуется вычислить модуль силы натяжения нити.
Решение
Необходимо воспользоваться вторым законом Ньютона и записать его для сил, которые действуют на шар. Центростремительное ускорение при его вращении по окружности будет записано следующим образом:
\(\bar{T}+m\bar{g}=m\bar{a}\)
Источник: webmath.ruПроекции данной формулы по осям определяются следующим образом:
X: \(T sin α = ma = mω2R\)
Y: \(-mg + T cos α = 0\)
Таким образом, из уравнения Y получаем расчет модуля силы натяжения нити:
\(T=\frac{mg}{\cos \alpha }\)
Анализ рисунка позволяет вывести следующее уравнение:
\(\sin \alpha = \frac{R}{l}\rightarrow \cos \alpha = \sqrt{1-\left(\frac{R}{l} \right)^{2}}\)
Если cos α заменить уравнением для расчета модуля силы натяжения нити, то получим следующую формулу:
\(T=\frac{mg}{\sqrt{1-\left(\frac{R}{l} \right)^{2}}}= \frac{mgl}{\sqrt{l^{2}-R^{2}}}\)
Значения основных величин, выраженные в СИ, можно подставить в конечную формулу для расчета силы натяжения нити:
\(T=\frac{0,1*9,8*5}{\sqrt{5^{2}-3^{2}}}=1,225\left(H \right)\)
Ответ: Т=1,225 H
Насколько полезной была для вас статья?
Рейтинг: 3.
 57 (Голосов: 28)
57 (Голосов: 28)Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Калькулятор нормальной силы | Плоская и наклонная поверхность
Создано Юлией Жулавинской
Отзыв от Bogna Szyk и Jack Bowater
Последнее обновление: 21 декабря 2022 г.
Содержание:- Что такое нормальная сила?
- Формула нормальной силы с внешней силой
- Как использовать уравнение нормальной силы — пример
- Часто задаваемые вопросы
Калькулятор нормальной силы поможет вам найти силу, с которой поверхность препятствует падению предмета через нее. В следующем тексте мы предоставим вам некоторые формулы нормальной силы и ответ на простой вопрос: что такое нормальная сила? При этом мы также упомянем третий закон движения Ньютона. Прокрутите вниз, чтобы узнать, как рассчитать нормальную силу.
Раз уж вы здесь, возможно, вам понравится наш калькулятор второго закона Ньютона.

Что такое нормальная сила?
Нормальная сила — это перпендикулярная сила, с которой поверхность действует на объект . Например, если вы положите книгу на стол, сила гравитации притянет ее к земле. Чтобы противодействовать этой силе, стол воздействует на книгу, не давая ей упасть. Эта противодействующая сила называется нормальной силой и представлена как FN\footnotesize F_N FN, или N\footnotesize N N. Единицей для нормальной силы является ‘ N ‘ (Ньютон).
Нормальная сила является типичным примером третьего закона движения Ньютона.
Если один объект воздействует на второй объект, второй объект оказывает на первый объект силу равной величины и противоположного направления (действие равно противодействию).
Итак, нормальная сила равна силе, с которой объект действует на поверхность. Его формулы меняются в зависимости от наклона поверхности.
Для объекта, лежащего на плоской поверхности, формула:
FN=m⋅g\размер сноски F_N = m ⋅ g FN=m⋅g
где
- м\размер сноски мм — масса объекта.

- g\footnotesize gg — ускорение свободного падения.
Согласно третьему закону Ньютона нормальная сила (FN\footnotesize F_N FN) для объекта на плоской поверхности равна его гравитационной силе (W\footnotesize WW).
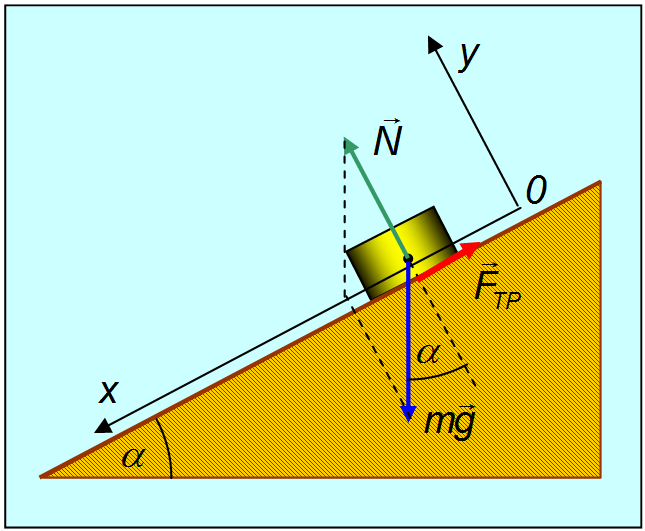
Для объекта, расположенного на наклонной поверхности, уравнение нормальной силы имеет вид:
FN=m⋅g⋅cos(α)\размер сноски F_N = m⋅g⋅cos(\alpha) FN=m⋅g⋅cos(α)
где
- α\размер сноски \альфа α угол наклона поверхности.
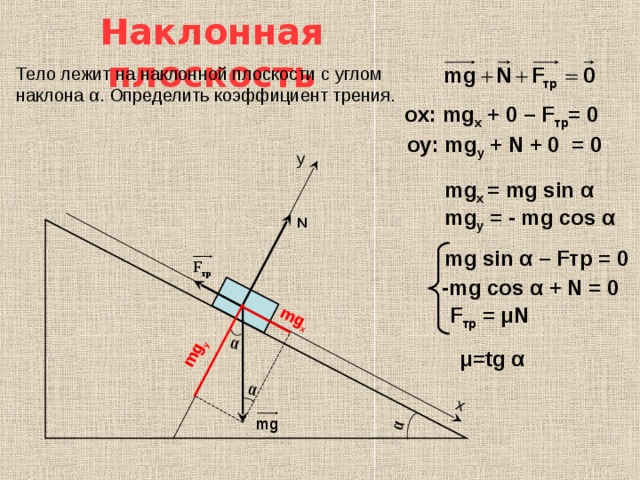
На наклонной поверхности (при условии, что объект не соскальзывает вниз) вес объекта поддерживается как нормальной силой, так и трением. Сила гравитации объекта не противоположна и не равна нормальной силе, а является одной из составляющих вектора силы тяжести.
Чтобы узнать, как рассчитать нормальную силу с учетом трения, воспользуйтесь калькулятором трения.
Для объектов на плоской поверхности нормальная сила противодействует весу объектов .
 (Не путайте с массой! Вес — это то же самое, что сила тяжести.) Это только в том случае, когда на объект не действует внешняя сила, или, если она есть, внешняя сила параллельна поверхности. Давайте посмотрим, что произойдет, если есть внешняя сила, которая не действует одновременно с поверхностью!
(Не путайте с массой! Вес — это то же самое, что сила тяжести.) Это только в том случае, когда на объект не действует внешняя сила, или, если она есть, внешняя сила параллельна поверхности. Давайте посмотрим, что произойдет, если есть внешняя сила, которая не действует одновременно с поверхностью!Формула нормальной силы с внешней силой
В расчетах, включающих внешнюю силу, следует учитывать только параллельную составляющую вектора. Вот почему в приведенные ниже уравнения нормальной силы включены углы.
- Внешняя направленная вниз сила
FN=m⋅g+F⋅sin(x)\footnotesize F_N = m ⋅ g + F ⋅ sin(x) FN=m⋅g+F⋅sin(x)
, где:
- F \footnotesize F F — значение внешней силы.
- x\footnotesize x x угол между поверхностью и внешней силой.
- Внешняя восходящая сила
FN=m⋅g−F⋅sin(x)\footnotesize F_N = m ⋅ g — F ⋅ sin(x) FN=m⋅g−F⋅sin(x)
Если существует внешняя сила, которая направлена вниз, необходимо добавить к весу объекта его векторную составляющую.
 Это увеличивает нормальную силу, внешняя сила толкает объект в землю. Противоположный случай для внешней силы, направленной вверх. Он оттягивает объект от земли, поэтому нормальная сила уменьшается.
Это увеличивает нормальную силу, внешняя сила толкает объект в землю. Противоположный случай для внешней силы, направленной вверх. Он оттягивает объект от земли, поэтому нормальная сила уменьшается.Если сила направлена прямо вверх и равна силе гравитации, то нормальная сила равна нулю. Почему? Потому что он полностью противодействует силе тяжести.
Как пользоваться уравнением нормальной силы — пример
Как найти нормальную силу самостоятельно? Представьте, что на земле лежит ящик, который вы хотите передвинуть. Весит 100 кг. Вы нажимаете на него под углом 45 градусов с силой 250 Н.
FN=100⋅9,807+250⋅sin(45°)=980,7+25022=1157,4N\размер сноски F_N = 100 ⋅ 90,807 + 250 ⋅ sin(45\градус) = 980,7 + 250 \frac{\sqrt2}{2} = 1157,4 Н FN=100⋅9,807+250⋅sin(45°)=980,7+25022=1157,4 Н
Земля воздействует на ящик с силой 1 157,4 Н . Если бы коробка стояла на мягкой поверхности, из-за вашей дополнительной силы она могла бы рухнуть. Таким образом, чтобы сохранить силы, лучше всего толкать вещи рядом с ними, прямо к месту назначения.

Вам понравился наш калькулятор нормальной силы? Проверьте также калькулятор работы и мощности!
Часто задаваемые вопросы
Как найти нормальную силу на склоне?
Чтобы найти нормальную силу тела на наклонной поверхности, вам необходимо:
- Найти массу тела. (Должно быть указано в кг.)
- Найдите угол наклона поверхности.
- Умножьте массу, ускорение свободного падения и косинус угла наклона.
Нормальная сила = m x g x cos(α) - Вы можете проверить свой результат в нашем калькуляторе нормальной силы.
Какая нормальная сила действует на книгу весом 0,6 кг?
Это 5.884 N . Чтобы найти нормальную силу книги, лежащей на горизонтальной поверхности, нужно умножить массу книги (0,6 кг) на ускорение свободного падения (9,807 м/с²).
Всегда ли нормальная сила и вес равны?
Нормальная сила и вес не всегда равны . Они равны, когда:
- Нет других сил, действующих в вертикальном направлении; и
- Объект находится на плоской поверхности.

Нормальная сила и вес не равны, когда:
- Существует дополнительная сила, которая хотя бы частично действует в вертикальном направлении; или
- Объект находится на наклонной поверхности.
Может ли нормальная сила быть отрицательной?
Да, нормальная сила может быть отрицательной . Силы — это векторы, поэтому нам решать, в каком направлении они будут положительными, а какие — отрицательными. Если предмет лежит на плоской поверхности и мы предполагаем, что вес положителен, то нормальная сила будет отрицательной.
Юлия Жулавиньская
Поверхность
Нормальная сила
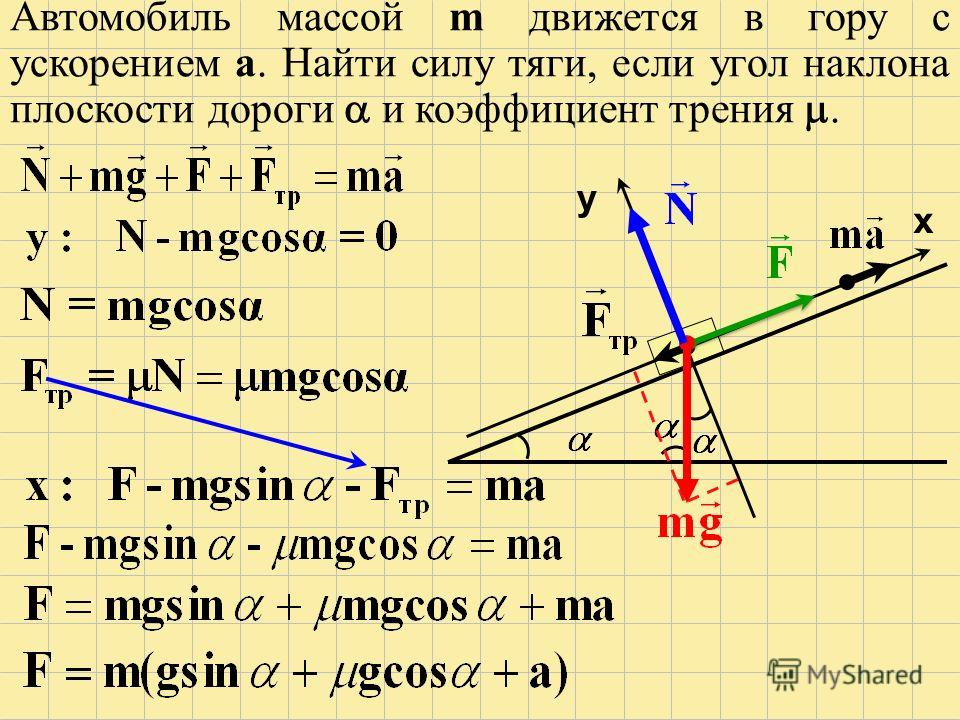
Посмотрите 10 похожих калькуляторов динамики — почему вещи движутся ➡️ прикладывать силу под углом, а не параллельно направлению движения, вам придется приложить больше силы, чтобы выполнить тот же объем работы. Вы можете использовать физику, чтобы рассчитать, сколько работы требуется, например, когда вы перетаскиваете объект с помощью буксирного троса, как показано на рисунке.

Для выполнения той же работы требуется больше усилий, если тянуть под большим углом.
Когда вы тянете под углом тета , , вы не прикладываете силу в том же направлении, что и направление движения. Чтобы найти работу в этом случае, все, что вам нужно сделать, это найти составляющую силы вдоль направления движения или перемещения. Правильно определенная работа — это сила в направлении смещения, умноженная на величину смещения, с :
Допустим, вы используете веревку, чтобы перетащить золотой слиток, и веревка находится под углом 10 градусов к земле, а не параллельно. В этом примере тета = 10 градусов. Если вы хотите приложить такое же количество силы, параллельной земле, как и раньше, вам потребуется, чтобы составляющая вашей силы, направленная в направлении смещения, была такой же, как если бы вы применяли параллельную силу — в этом случае , 2450 ньютонов. Это означает, что
Если вы вычислите величину вашей силы, у вас будет
Если тянуть под углом 10 градусов, вам придется приложить около 40 дополнительных ньютонов силы.
 Но будете ли вы в конечном итоге делать тот же объем работы? Вы бы сделали это, если бы тянули с этой силой. Но подумайте о ситуации немного подробнее — на самом деле вам не нужно делать так много работы.
Но будете ли вы в конечном итоге делать тот же объем работы? Вы бы сделали это, если бы тянули с этой силой. Но подумайте о ситуации немного подробнее — на самом деле вам не нужно делать так много работы.Если вы тянете под углом, часть прилагаемой силы, направленная вдоль пола — в направлении смещения — выполняет работу. Компонент силы, который вы прикладываете, направленный под прямым углом к этому — прямо вверх — не работает, но он каким-то образом способствует подъему слитка (или того, что вы буксируете). Сила недостаточно велика, чтобы оторвать слиток от земли, но она уменьшает его обычную силу с землей, и вы знаете, что это значит: меньше трения.
Определите, какая сила трения у вас будет, если вы перетащите слиток на веревке под углом 10 градусов. Коэффициент трения такой же, как если бы вы толкали слиток, но теперь нормальная сила с землей определяется весом слитка за вычетом направленной вверх составляющей силы, которую вы прикладываете. Следовательно, сила трения равна
.
Здесь вертикальная составляющая силы, приложенной к слитку, определяется как
.Сила трения должна быть меньше, чем если бы вы тянули слиток параллельно земле, потому что нормальная сила меньше — вы уже видите, что вам нужно совершить меньшую работу, чтобы сдвинуть слиток.
Поскольку вы хотите выполнить наименьший объем работы, вы хотите тащить слиток по земле с наименьшей силой, необходимой для преодоления трения. Поэтому установите горизонтальную составляющую вашей силы равной силе трения:
Теперь подключите силу трения, что даст вам следующее:
Если вы переформулируете это уравнение, чтобы решить для F тянуть , , вы можете найти величину силы, которую необходимо приложить:
Это немного меньше, чем сила, которую вам пришлось бы приложить, если бы вы тянули слиток прямо. Теперь скажите, что вы хотите перевезти слиток в свой дом, который находится в 3 километрах от вас. Если веревка находится под углом 10 градусов, работа, которую вы совершите, чтобы протащить слиток на горизонтальное расстояние в 3 километра (3000 метров), составит
.


 2 + 2F_1F_2 sin45} = \sqrt{25 + 18 + 2 \cdot 5 \cdot 4,2 \cdot sin45} = 8,5 Н$
2 + 2F_1F_2 sin45} = \sqrt{25 + 18 + 2 \cdot 5 \cdot 4,2 \cdot sin45} = 8,5 Н$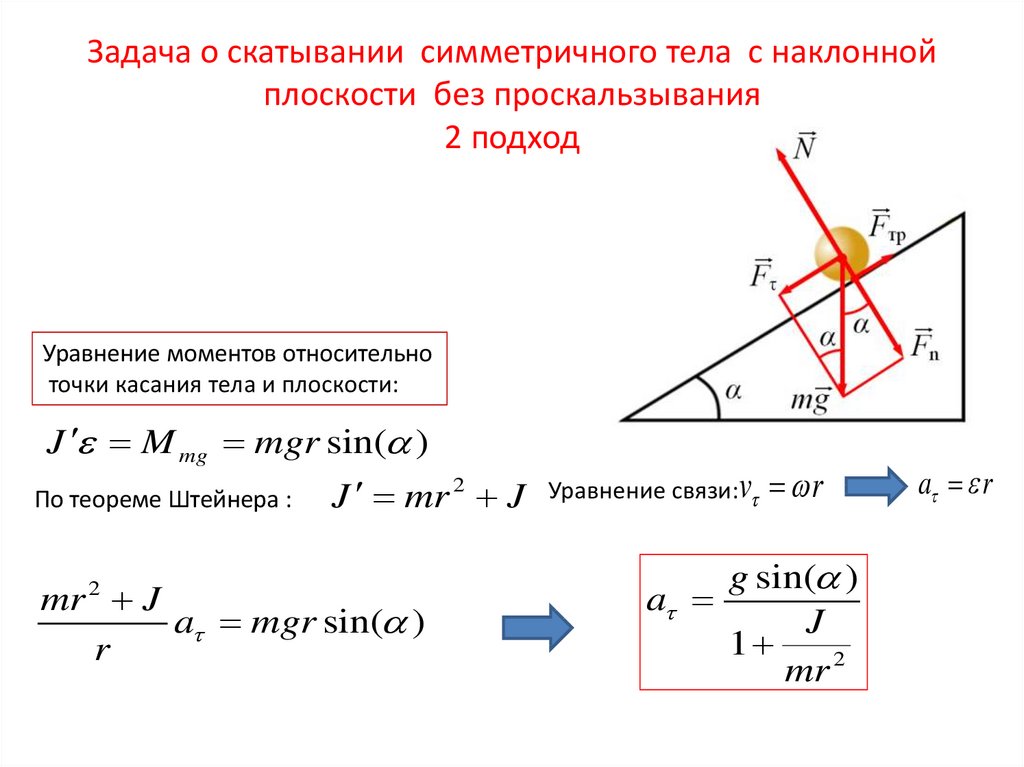
 В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:
В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета: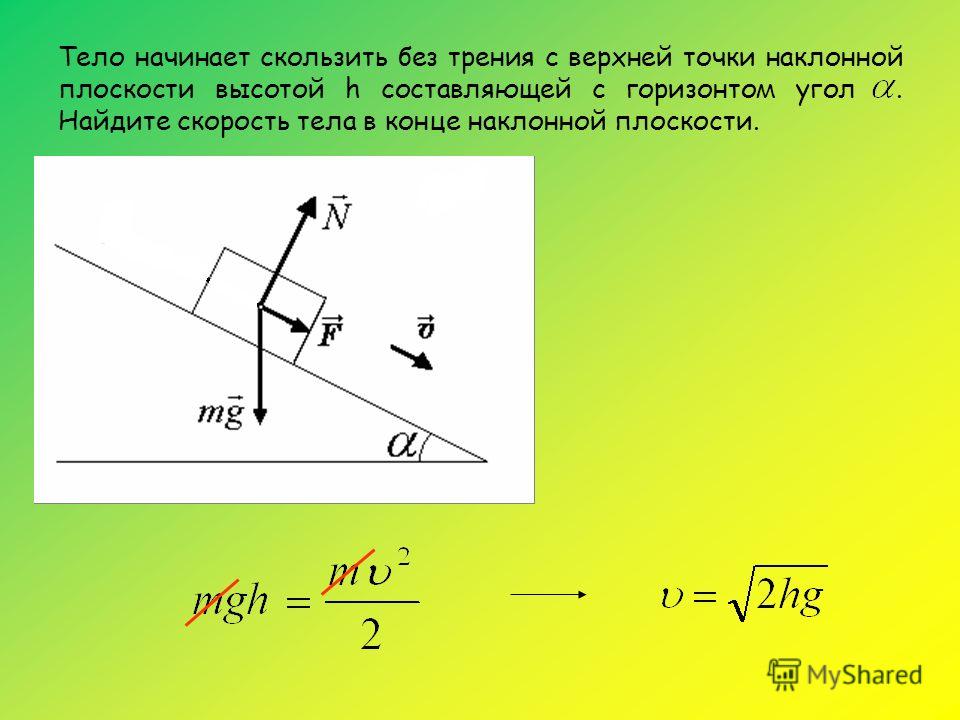
 57 (Голосов: 28)
57 (Голосов: 28)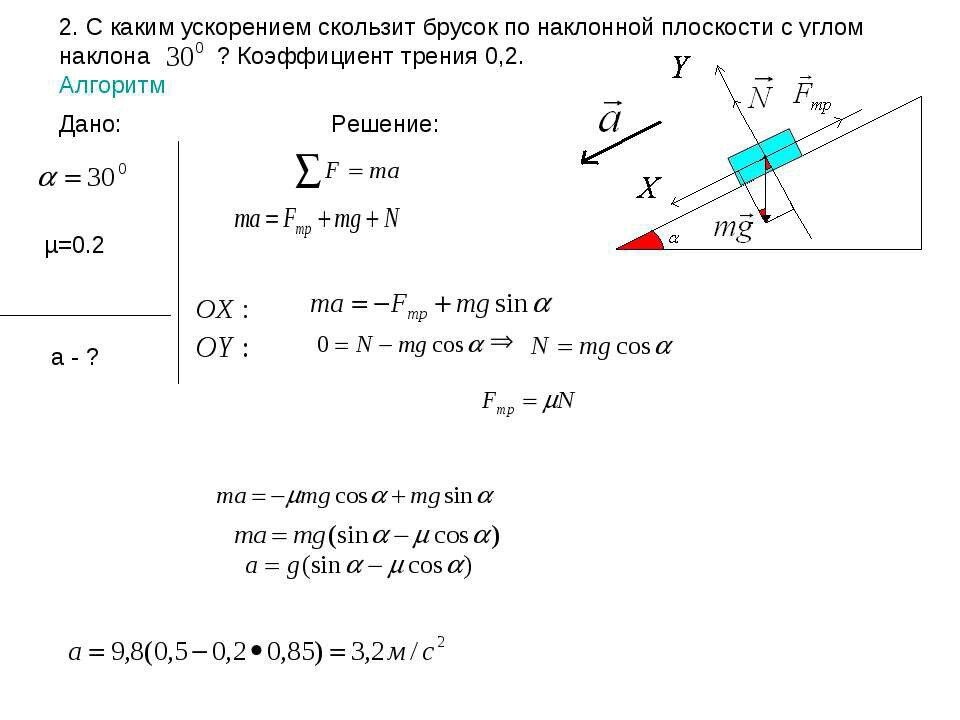

 (Не путайте с массой! Вес — это то же самое, что сила тяжести.) Это только в том случае, когда на объект не действует внешняя сила, или, если она есть, внешняя сила параллельна поверхности. Давайте посмотрим, что произойдет, если есть внешняя сила, которая не действует одновременно с поверхностью!
(Не путайте с массой! Вес — это то же самое, что сила тяжести.) Это только в том случае, когда на объект не действует внешняя сила, или, если она есть, внешняя сила параллельна поверхности. Давайте посмотрим, что произойдет, если есть внешняя сила, которая не действует одновременно с поверхностью! Это увеличивает нормальную силу, внешняя сила толкает объект в землю. Противоположный случай для внешней силы, направленной вверх. Он оттягивает объект от земли, поэтому нормальная сила уменьшается.
Это увеличивает нормальную силу, внешняя сила толкает объект в землю. Противоположный случай для внешней силы, направленной вверх. Он оттягивает объект от земли, поэтому нормальная сила уменьшается.

 Но будете ли вы в конечном итоге делать тот же объем работы? Вы бы сделали это, если бы тянули с этой силой. Но подумайте о ситуации немного подробнее — на самом деле вам не нужно делать так много работы.
Но будете ли вы в конечном итоге делать тот же объем работы? Вы бы сделали это, если бы тянули с этой силой. Но подумайте о ситуации немного подробнее — на самом деле вам не нужно делать так много работы.