Сила Лоренца | Магниты и магнитное поле
Может показаться странным, но силу того или иного магнитного поля мы можем определить исходя из того, как оно воздействует на движущийся внутри него электрический заряд, в роли которого обычно выступает какая-то заряженная элементарная частица.
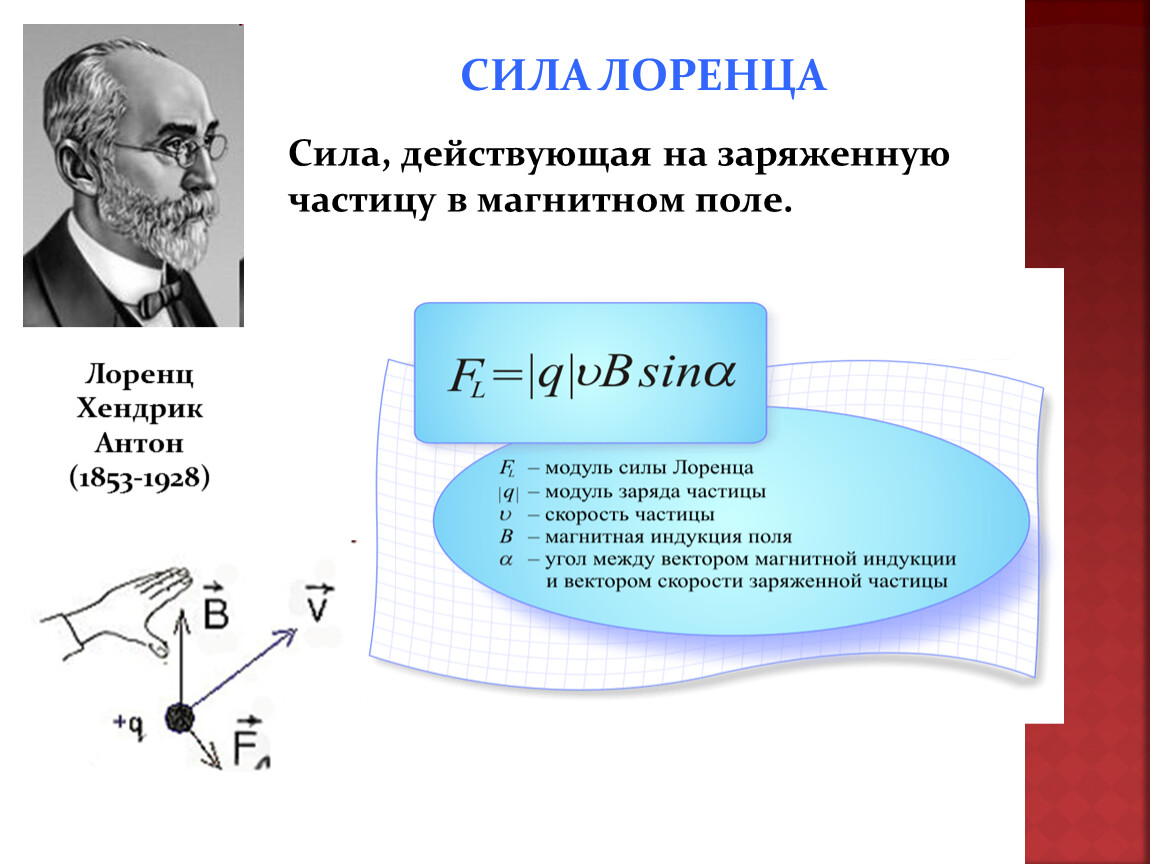
Силу, о которой идет речь, принято называть силой Лоренца. Обыкновенно она обозначается как \vec{F_л}, значение ее можно определить благодаря следующей формуле:
\boxed{F_л=qvB\sin\alpha}
Где q – это модуль движущегося электрического заряда. Впрочем, давайте прямо по косточкам разберем это выражение.
Во-первых, если, например, элементарная частица не будет обладать зарядом, значит q=0, и магнитное поле на нее действовать не будет. То есть нейтроны магнитное поле мало интересуют.
Во-вторых, как уже не раз было сказано, заряд должен двигаться, чтобы ощутить воздействие со стороны магнитного поля. Если подумать, это уже поинтереснее, чем ситуация с нейтроном: для магнитного поля существует какая-то разница между подвижным и неподвижным электрическим зарядом, что весьма таинственно.
В-третьих… Ну после этого мы видим вектор магнитной индукции, ничего занятного. Сложно заметить действие магнитного поля хоть на что-то, когда этого поля нет. А вот дальше идет синус какого-то угла.
Этот угол находится между вектором скорости заряженной частицы и вектором магнитной индукции. Обратите внимание, что если частица будет двигаться вдоль линий магнитного поля, то угол \alpha=0, а вместе с ним и его синус равен нулю. Сила Лоренца действовать не будет.
Вообще, все, что расположено с правой стороны в нашем уравнении, за исключение модуля заряда, математики называют векторным произведением. Мы уже что-то знаем о скалярном произведении векторов, его результатом является число, в частности механическую работу так находят. А вот результатом векторного произведения векторов является вектор, который перпендикулярен обоим исходным векторам.
Это, кстати, еще один вопрос. Сила Лоренца – это вектор, значит, у нее, помимо величины, должно быть и направление.
То, что она перпендикулярна вектору скорости некоторой элементарной частицы и вектору магнитной индукции, конечно, замечательно, но все-таки остается еще аж два варианта ее направления – вверх она смотрит относительно исходных векторов или вниз? Здесь нам придется различать две ситуации.
Если нам попалась положительно заряженная частица вроде протона, движущаяся в однородном магнитном поле (то есть в таком поле, у которого вектор магнитной индукции не меняется ни по величине, ни по направлению), тогда нам следует воспользоваться правилом левой руки: если сделайте так, чтобы в ладонь этой руки втыкались векторы магнитной индукции и чтобы все пальцы были сонаправлены с вектором скорости, тогда отогнутый на 90 градусов большой палец покажет направление силы Лоренца.
Вот вам маленький квест. Попробуйте самостоятельно разобраться, куда будет направлена сила Лоренца в данном случае.
Если внезапность задания не сбила вас с толку, скорее всего вы правильно определили, что сила Лоренца будет направлена от нас.
Надо бы придумать, как это можно показать на рисунке. Хотя нет, физики уже все за нас придумали и выбрали следующие записи для необычно направленных векторов.
Все очень просто, здесь используется аналогия со стрелой, выпущенной из лука. Когда такая стрела летит от нас, мы видим ее заднее оперение, а когда она летит на нас (что, на самом деле, не слишком хорошо), мы видим ее кончик в виде точки. При этом обратите внимание, что линии, составляющие крестик в первом случае, не нужно доводить до конца – получится обозначение лампы накаливания.
Для отрицательно заряженных частиц вроде электрона, применяется правило правой руки: все тоже самое, только теперь нужно опираться на показания большого пальца именно этой руки.
И снова небольшое задание. Пожалуйста, определите направление силы Лоренца:
В плоскости рисунка сила Лоренца будет направлена вертикально вверх.
Ускорители силы Лоренца (LFA) | Лаборатория электродвижения и динамики плазмы
Мотивация
Перспектива достижения высокой плотности тяги в сочетании с высоким удельным импульсом является мотивацией
за исследованиями литиевых и аргоновых ускорителей силы Лоренца (LiLFA и ALFA соответственно).
Комбинация этих характеристик подруливающего устройства обеспечивает экономию средств при использовании электрического двигателя.
двигательная установка для миссий, требующих короткого времени в пути, таких как пилотируемые миссии на Марс.
и не только. LFA обеспечивает более высокую плотность тяги, чем любой летающий в настоящее время электрический двигатель.
устройство и реально ограничивается по тяге только количеством доступной мощности.
Одним предложением: Мы хотим отправить людей на Марс, но не хотим тратить много денег.
Рисунок 1. Запуск LiLFA 7 мая 2015 г. Рисунок 2. Запуск ALFA 12 сентября 2017 г. Механизмы создания тяги топлазмодинамический двигатель (AF- MPDT) с использованием лития в качестве
пропеллент, так как литий имеет ряд преимуществ перед более традиционными пропеллентами, такими как ксенон, криптон или аргон.
Литий имеет более низкий первый потенциал ионизации (5,4 эВ), чем обычно используемые ракетные топлива (12,1 эВ для
ксенон), что означает, что больше энергии может пойти на создание тяги, а не на ионизацию.
Кроме того, это
имеет высокий второй потенциал ионизации по сравнению с другими порохами (75,6 эВ по сравнению с 21,0 для
ксенон), уменьшая потери потока при замерзании. Литий также обладает тем преимуществом, что снижает работу выхода
вольфрама (материал, из которого изготовлен катод) от 4,5 до 2,1 эВ при использовании бария в качестве
добавка, уменьшающая эрозию и увеличивающая срок службы нашего двигателя.В ALFA используется аргоновое топливо, которое уступает литию по всем вышеперечисленным причинам, но имеет то преимущество в лабораторных условиях, что оно значительно менее опасно и требует больше времени для проведения испытаний. Этот двигатель является новым для лаборатории по состоянию на 2017 год, и более подробная информация о нем приведена в разделе «Текущие исследования» ниже.
Существует три основных механизма создания тяги, каждый из которых описан ниже.
- Компонент собственного поля
В простейшей конфигурации MPDT работают в так называемом режиме собственного поля, который показан на рис.
3.
В этой конфигурации тяга создается перекрестным произведением тока, проходящего радиально от анода к центральному катоду, и магнитного поля, создаваемого этим током, проходящим через катод,
в результате возникает осевая сила.
Несмотря на то, что MPDT Self-Field имеют самую простую конструкцию, для них требуется мощность в мегаваттах, которая выходит за рамки возможностей любых современных источников питания космического базирования. Применение внешнего магнитного поля может снизить требования к мощности, позволяя работать от 10 до 100 кВт. В конфигурации с приложенным полем существует дополнительный механизм создания тяги, описанный в разделе 2.9.2 \), где \( J \) — ток через электроды, а \( b \) — геометрический коэффициент масштабирования.
- Applied-Field Component
Перекрестное произведение тока между электродами с расходящимся в осевом направлении магнитным полем приводит к возникновению силы, закручивающей плазму.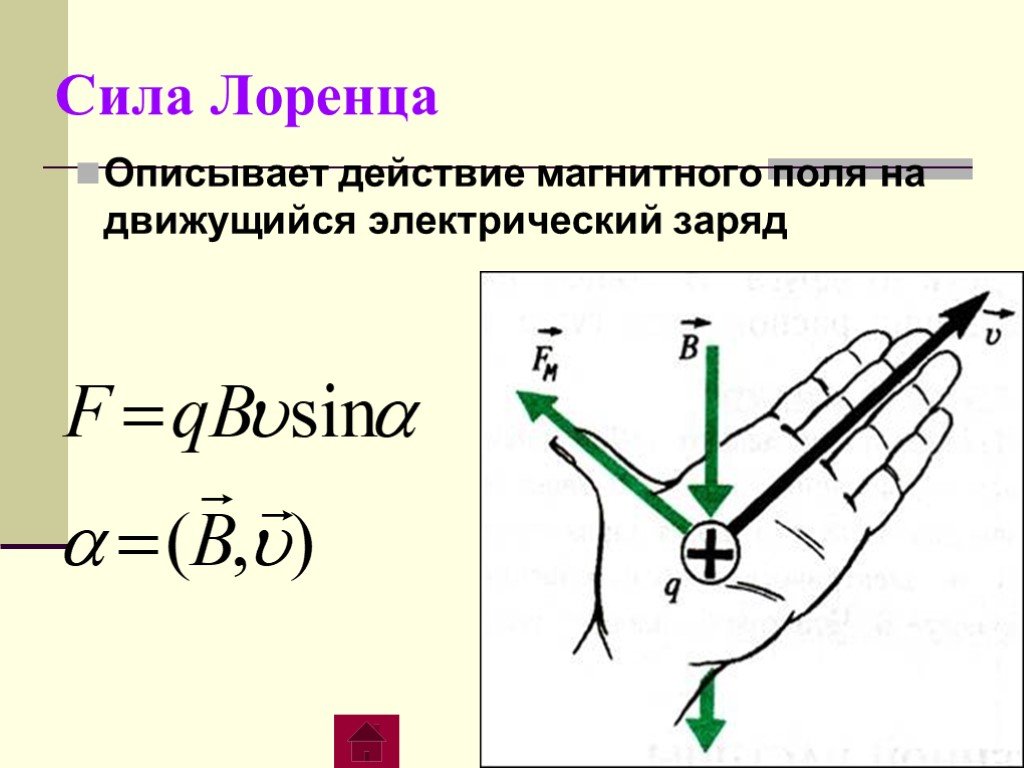
Экспериментально показано, что составляющая тяги приложенного поля равна \( T_{AF} =k J B_A r_a \), где \(k\) — константа, \(B_A\) — напряженность приложенного магнитного поля, а \(r_a\) — эффективный радиус анода.
- Компонент холодного газа
Поскольку мы расширяем газ через сопло, также создается тяга, которая зависит от
наш массовый расход (\(\dot{m}\)), газодинамическое давление (\(P\)) и площадь, на которой
давление давит (\(A\)).
Тогда холодная газовая составляющая тяги определяется выражением
\(T_{CG} = c_s \dot{m} + P A\), где \(c_s\) — скорость звука пороха.
Текущие исследования
Исследования LiLFA в настоящее время проводятся по следующим темам:
- Датчик динамического сопротивления.
Создан и успешно протестирован новый датчик, датчик динамического сопротивления (DRP). впервые (май 2015 г.) для измерения скорости осаждения лития. Дальнейшее тестирование покажет, если это зонд достаточно чувствителен, чтобы измерять скорость осаждения перед двигателем, где топливо привязанность к космическому кораблю вызывает беспокойство.
- Измерение тяги.
Добавлена новая диагностика для измерения тяги, изолирующая составляющую силы на соленоиде.
встраивается в существующую опорную стойку.
Это поможет выявить механизм, с помощью которого приложенное поле создает тягу, обеспечивая
целевое измерение эффективного радиуса анода \( r_a \), описанное в предыдущем разделе.
- АЛЬФА. Мы начали тестовую кампанию для ALFA, которая была построена весной 2017 года. На рис. 6 показан графитовый анод, контур которого повторяет топологию магнитного поля. На рис. 7 показан вид в разрезе двигателя в собранном виде. На рис. 8 показан двигатель в полностью собранном виде.
Учреждения
EPPDyL в настоящее время (2016 г.) является единственным учреждением с действующим LiLFA. В настоящее время у нас есть два
Экспериментальные модели LiLFA в нашей лаборатории. Открытая тепловая трубка LiLFA (OHP-LiLFA) разработана и
построенный Thermacore Inc.
Литий загружается в топливный резервуар с помощью нашего перчаточного ящика, изображенного на рис. 10, который заполнен аргоном, чтобы предотвратить любое загрязнение лития реакцией с воздухом.
Рис. 10. Перчаточный ящик для работы с литием.У нас также есть соответствующая огнестойкая и химически стойкая одежда, а также система дыхания, для очистки загрязненного патронника после обжига литием. Кое-что из этого оборудование показано в работе на рис. 11.
Публикации
- Масштабирование тяги в магнитоплазмодинамических двигателях с приложенным полем (2018 г.
) - Метод измерения составляющей тяги плазменных двигателей с приложенным полем (2018 г.)
- Видеодиагностика экстремальных условий окружающей среды для литиевого ускорителя силы Лоренца (2017 г.)
- Полый катод с графитовым отверстием для аргонового магнитоплазмодинамического двигателя (2017 г.)
- Влияние топологии прикладного поля на тягу MPDT (2017 г.)
- Критический обзор моделей тяги для магнитоплазмодинамических двигателей прикладного поля (2017 г.)
- Полый катод с графитовым отверстием для аргонового магнитоплазмодинамического двигателя (2017 г.)
- Видеодиагностика экстремальных условий окружающей среды для литиевого ускорителя силы Лоренца (201 7)
- Прямой Измерение составляющей приложенного поля тяги литиевого ускорителя силы Лоренца (2016 г.)
- Измерение массового расхода жидкого металла с помощью индуктивного бесконтактного детектора для использования в сочетании с насосом JxB (2016 г.)
- Контроль и анализ системы подачи топлива в насос JxB для литиевого ускорителя силы Лоренца (2016 г. )
- Датчик динамического сопротивления для измерения скорости осаждения массы из ракетного двигателя на конденсируемом топливе (2015 г.)
- Проектирование и испытание топлива Система питания для литиевого ускорителя силы Лоренца (2015 г.)
- Исследование эффективности магнитоплазменно-динамических двигателей с прикладным полем (2012 г.)
- Масштабирование падения напряжения на анодной оболочке с учетом рабочих параметров в двигателях MPD с прикладным полем (2011 г.)
- Масштабирование эффективности приложенного магнитного поля в магнитоплазмодинамических двигателях (2010 г.)
- Критический обзор современного состояния производительности магнитоплазмодинамических двигателей с приложенным полем (2006 г.)
- Литиевые дуговые многоканальные и одиночные -Channel Hollow Cathode: Experiment and Theory (2006)
- Стенд тяги с перевернутым маятником для мощных электрических двигателей (2006)
- Исследование основных процессов в литиевом ускорителе силы Лоренца с помощью моделирования потока плазмы (2005)
- Термические воздействия на перевернутые маятниковые стенды для стационарных мощных плазменных двигателей (2003 г.
)
)
