Сила Лоренца — frwiki.wiki
Круг, описываемый магнитным полем в трехфазном двигателе.
Сила Лоренца или электромагнитная сила — это сила, испытываемая заряженной частицей в электромагнитном поле .
Это главное проявление электромагнитного взаимодействия . Сила Лоренца, применяемая в различных ситуациях, индуцирует все наблюдаемые электрические и магнитные взаимодействия; поэтому его в основном изучают в области физики и химии .
Квантовые эффекты, влияющие на электромагнитную силу, изучаются в контексте квантовой электродинамики .
Одноименным сила Лоренца является голландский физик Хендрик Антон Лоренц ( —).
Резюме
- 1 Математическое описание
- 2 Демонстрация формулы силы Лоренца
- 3 По порядку величины
- 4 работа силы Лоренца
- 5 Примечания и ссылки
- 6 См. Также
- 6.1 Библиография
- 6.

Математическое описание
Магнитное поле, создаваемое катушками Гельмгольца.
Электромагнитное поле оказывает следующие силы на частицы с ненулевым электрическим зарядом д
- F→знак равноqE→+qv→∧B→{\ displaystyle {\ vec {F}} = q {\ vec {E}} + q {\ vec {v}} \ wedge {\ vec {B}}}.
Векторы и — соответственно электрическое поле и магнитное поле, взятые в точке, где находится частица, представляют скорость частицы в исследуемой системе отсчета. Мы можем выделить два вклада в эту силу: E→{\ displaystyle {\ vec {E}}}B→{\ displaystyle {\ vec {B}}}v→{\ displaystyle {\ vec {vb}}}
- Fэль→знак равноqE→{\ displaystyle {\ vec {F _ {\ text {el}}}} = q {\ vec {E}}}, которая представляет собой электрическую силу;
- Fmag→знак равноqv→∧B→{\ displaystyle {\ vec {F _ {\ text {mag}}}} = q {\ vec {v}} \ wedge {\ vec {B}}}, которая является магнитной силой.
В случае, когда электрический заряд неподвижен в определенном названном положении , его скорость, следовательно, равна нулю, и он не подвергается воздействию какой-либо магнитной силы: перекрестное произведение равно нулю, и тогда на заряд действует сила, которая зависит только от электрическое поле .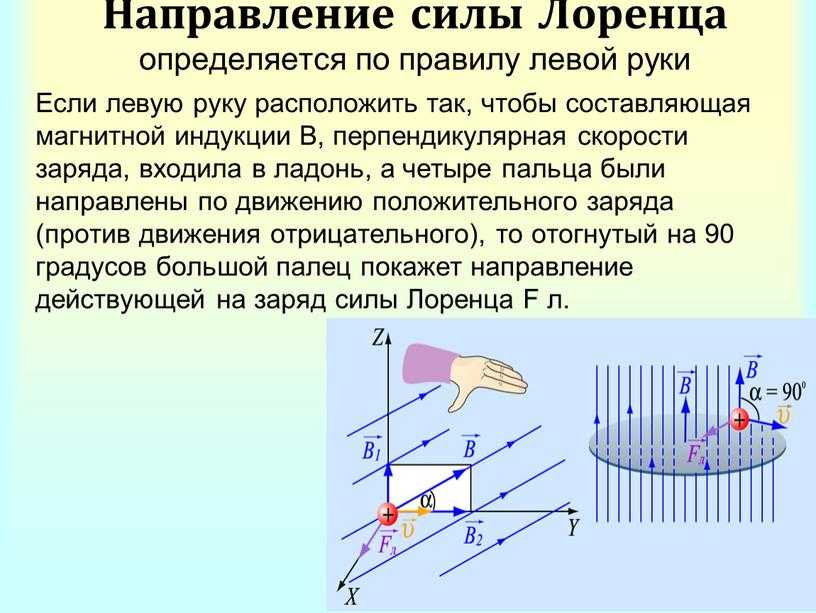 {3}}}},
{3}}}},
ε 0 является универсальной константой называется диэлектрической проницаемости в вакууме (должны быть заменены диэлектрической проницаемости среды, когда мы не в вакууме).
Сила рассчитывается только тогда, когда мы знаем значения полей и , которые в основном определяются распределением всех заряженных частиц, участвующих в исследуемой конфигурации. E→{\ displaystyle {\ vec {E}}}B→{\ displaystyle {\ vec {B}}}
Демонстрация формулы силы Лоренца
Исторически сила Лоренца не зависела от уравнения, описывающего электромагнитное поле. Мы можем найти силу Лоренца благодаря лагранжевому формализму . Лагранжиан, позволяющий найти уравнения Максвелла, также позволяет найти силу Лоренца. Уравнения Максвелла являются исходными уравнениями, а сила Лоренца — эволюционным уравнением (динамическим уравнением). Мы находим и то, и другое благодаря уравнению Эйлера-Лагранжа . Чтобы найти динамические уравнения, мы применяем уравнения Эйлера-Лагранжа к координатам пространств (положения, скорости), а для нахождения исходных уравнений (уравнение Максвелла) мы применяем уравнения Эйлера-Лагранжа к обобщенным координатам (полям и производным поля).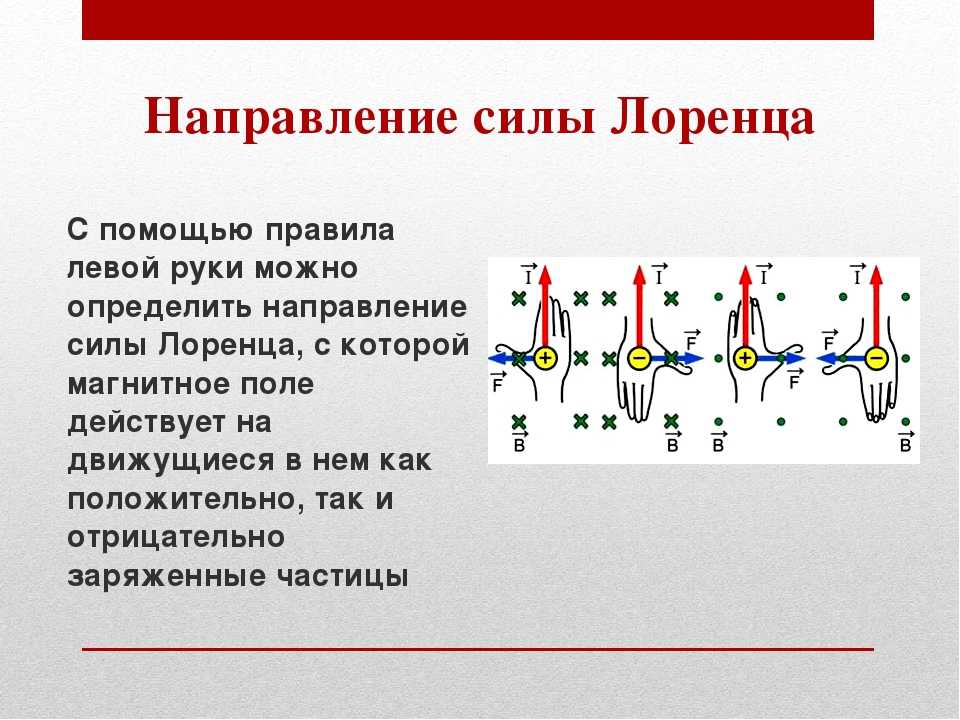
Рейтинг немного оскорбительный. Тогда уравнение Эйлера-Лагранжа говорит нам, что: ∂L∂V→{\ displaystyle {\ frac {\ partial L} {\ partial {\ vec {V}}}}}
- dΠdтзнак равноd(п→+qВ→)dтзнак равно∂L∂Икс→знак равно-q∇ϕ+q∇(В→.V→){\ displaystyle {\ frac {d \ Pi} {dt}} = {\ frac {d ({\ vec {P}} + q {\ vec {A}})} {dt}} = {\ frac {\ частичное L} {\ partial {\ vec {x}}}} = — q \ nabla \ phi + q \ nabla ({\ vec {A}}. {\ vec {V}})}.
а также
- dВ→dтзнак равно∂В→∂т+(V→.∇)В→{\ displaystyle {\ frac {d {\ vec {A}}} {dt}} = {\ frac {\ partial {\ vec {A}}} {\ partial t}} + ({\ vec {V}} . \ nabla) {\ vec {A}}}.
следовательно
- dп→dт+q∂В→∂т+q(V→.∇)В→знак равно-q∇ϕ+q∇(В→.V→){\ displaystyle {\ frac {d {\ vec {P}}} {dt}} + q {\ frac {\ partial {\ vec {A}}} {\ partial t}} + q ({\ vec {V }}. \ nabla) {\ vec {A}} = — q \ nabla \ phi + q \ nabla ({\ vec {A}}. {\ vec {V}})}.
И используя векторную идентичность
- V→∧(∇∧В→)знак равно∇(В→⋅V→)-(V→⋅∇)В→{\ displaystyle {\ vec {V}} \ wedge (\ nabla \ wedge {\ vec {A}}) = \ nabla ({\ vec {A}} \ cdot {\ vec {V}}) — ({\ vec {V}} \ cdot \ nabla) {\ vec {A}}}.

мы получаем
- dп→dтзнак равно-q∂В→∂т-q∇ϕ+q(V→∧(∇∧В→)){\ displaystyle {\ frac {d {\ vec {P}}} {dt}} = — q {\ frac {\ partial {\ vec {A}}} {\ partial t}} — q \ nabla \ phi + q \ left ({\ vec {V}} \ wedge (\ nabla \ wedge {\ vec {A}}) \ right)}.
или сила Лоренца, если
- ∇∧В→знак равноB→{\ Displaystyle \ набла \ клин {\ vec {A}} = {\ vec {B}}}.
а также
- E→знак равно-∇ϕ-∂В→∂т{\ displaystyle {\ vec {E}} = — \ nabla \ phi — {\ frac {\ partial {\ vec {A}}} {\ partial t}}}.
Мы также можем заставить проявиться силу Лоренца благодаря уравнениям Максвелла, она выступает в качестве источника в уравнении непрерывности плотности импульса электромагнитного поля. Является
- ∂(E→∧B→)μ0∂т+ρE→+j→∧B→-∇σзнак равно0{\ displaystyle {\ frac {\ partial ({\ vec {E}} \ wedge {\ vec {B}})} {\ mu _ {0} \ partial t}} + \ rho {\ vec {E}} + {\ vec {j}} \ wedge {\ vec {B}} — \ nabla \ sigma = 0}.
с тензором напряжений Максвелла.
Величина
Электромагнитное взаимодействие является вторым из четырех элементарных взаимодействий по порядку мощности. При низкой энергии, то есть при химических или ядерных реакциях, оно примерно в сто раз слабее сильного взаимодействия , но превосходит слабое и гравитационное взаимодействия в 10 11 и 10 42 раз соответственно. За исключением гравитационных явлений, электромагнитное взаимодействие в атомном масштабе отвечает за большинство явлений, наблюдаемых в макроскопическом масштабе. В самом деле, в макроскопическом масштабе электромагнитное взаимодействие не позволяет одному объекту пересекать другой, позволяет объекту применять силу к другому ( принцип действие-реакция ) или отвечает за силы трения.
Работа силы Лоренца
Работа силы Лоренца соответствует энергии, передаваемой электромагнитным полем заряженным частицам.
При элементарном смещении точки приложения силы элементарная работа силы Лоренца по определению равна:
dℓ→{\ displaystyle d {\ vec {\ ell}}}F→{\ displaystyle {\ vec {F}}}
- δWзнак равноF→⋅dℓ→{\ displaystyle \ delta W = {\ vec {F}} \ cdot d {\ vec {\ ell}}}
- δWзнак равно(qE→+qv→∧B→)⋅dℓ→{\ displaystyle \ delta W = (q {\ vec {E}} + q {\ vec {v}} \ wedge {\ vec {B}}) \ cdot d {\ vec {\ ell}}}
По определению , это происходит: dℓ→знак равноv→dт{\ displaystyle d {\ vec {\ ell}} = {\ vec {v}} dt}
- δWзнак равноqE→⋅v→dт+qv→∧B→⋅v→dт{\ displaystyle \ delta W = q {\ vec {E}} \ cdot {\ vec {v}} dt + q {\ vec {v}} \ wedge {\ vec {B}} \ cdot {\ vec {v }} dt}
Второй член обращается в нуль, полученный вектор ортогонален . Таким образом, мы наконец находим:
v→∧B→{\ Displaystyle {\ vec {vb}} \ клин {\ vec {B}}}v→{\ displaystyle {\ vec {vb}}}
Таким образом, мы наконец находим:
v→∧B→{\ Displaystyle {\ vec {vb}} \ клин {\ vec {B}}}v→{\ displaystyle {\ vec {vb}}}
- δWзнак равноqE→⋅v→dт{\ displaystyle \ delta W = q {\ vec {E}} \ cdot {\ vec {v}} dt}
Следовательно, работа силы Лоренца в общем случае не равна нулю. С другой стороны, мы видим, что магнитная сила не работает, работает только электрическая составляющая и, следовательно, может изменять кинетическую энергию заряженной частицы.
Примечания и ссылки
- ↑ Diu and Leclecrq 2005 , sv Lorentz (сила), стр. 391.
- ↑ Taillet, Villain and Febvre 2018 , sv force de Lorentz,
 315, цв. 1 .
315, цв. 1 .
Смотрите также
Библиография
- [Diu and Leclecrq 2005] Бернар Диу и Бенедикт Леклерк , La Physique word à mot , Париж, О. Якоб , колл. «Науки»,,
 и рис. 15,5 × 24 см ( ISBN 2-7381-1578-0 , EAN 9782738115782 , OCLC 300488981 , уведомление BnF п о FRBNF39927635 , SUDOC 08469470X , онлайн презентации , читать онлайн ) , св Лоренц (сила де), стр. 391–392.
и рис. 15,5 × 24 см ( ISBN 2-7381-1578-0 , EAN 9782738115782 , OCLC 300488981 , уведомление BnF п о FRBNF39927635 , SUDOC 08469470X , онлайн презентации , читать онлайн ) , св Лоренц (сила де), стр. 391–392. - [Taillet, Villain and Febvre 2018] Ричард Тейе , Лоик Злодей и Паскаль Февр , Словарь физики , Лувен-ля-Нев, De Boeck Supérieur , за пределами кол. / наука,, 4- е изд.
 ( 1- е изд. ), 1 т. , X -956 с. , плохо. и рис. 17 × 24 см ( ISBN 978-2-8073-0744-5 , EAN 9782807307445 , OCLC 1022951339 , уведомление BnF п О FRBNF45646901 , SUDOC 224228161 , онлайн презентации , читать онлайн ) , св сила Лоренца де, стр.
( 1- е изд. ), 1 т. , X -956 с. , плохо. и рис. 17 × 24 см ( ISBN 978-2-8073-0744-5 , EAN 9782807307445 , OCLC 1022951339 , уведомление BnF п О FRBNF45646901 , SUDOC 224228161 , онлайн презентации , читать онлайн ) , св сила Лоренца де, стр. 315, цв. 1.
315, цв. 1.
Статьи по Теме
- Электростатический
- Магнитостатический
- Электромагнетизм
- Сила Лапласа
- Приложения магнетизма
- Униполярный генератор
Электромагнетизм | |
|---|---|
| Электростатический |
|
| Магнитостатический |
|
| Электрокинетический |
|
| Магнетизм |
|
<img src=»https://fr. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Сила Лоренца
Си́ла Ло́ренца — сила, що діє на рухомий електричний заряд, який перебуває в електромагнітному полі.
- F=qE+q[v×B]{\displaystyle \mathbf {F} =q\mathbf {E} +{q}[\mathbf {v} \times \mathbf {B} ]}.
ТутF{\displaystyle \mathbf {F} }
— сила,q{\displaystyle q} — величина заряду,E{\displaystyle \mathbf {E} } — напруженість електричного поля,v{\displaystyle \mathbf {v} } — швидкість руху заряду,B{\displaystyle \mathbf {B} } — вектор магнітної індукції. Іноді силою Лоренца називають лише другу складову цього виразу — силу, яка діє на заряд, що рухається, з боку магнітного поля (F=q[v×B]{\displaystyle \mathbf {F} ={q}[\mathbf {v} \times \mathbf {B} ]}).Електричне поле діє на заряд із силою, направленою вздовж силових ліній поля. Магнітне поле діє лише на рухомі заряди. Сила дії магнітного поля перпендикулярна до силових ліній поля й до швидкості руху заряду. {3}}}\mathbf {r} }.
{3}}}\mathbf {r} }.
Для того, щоб визначити, як буде виглядати ця сила в інерціальній системі відліку, що рухається, можна розглянути наступний «віртуальний» експеримент.
Нехай у вакуумі знаходяться два заряди, скріплені пружинкою. Заряди розглядаються відносно інерціальної системи відліку, у якій вони перебувають у спокої протягом досить великого проміжку часу. Пружинка забезпечує статичність зарядів, а розтяг пружинки чисельно характеризує силу взаємодії зарядів. Якщо прибрати пружинку й розглянути деяке мале відхилення від статичного стану, наприклад, одного заряду, то можна проаналізувати час, за який другий заряд «відчує» зміну стану першого, тим самим експериментально визначивши швидкість розповсюдження взаємодії між зарядами. Проте в рамках експерименту (заряди скріплені пружинкою) про швидкість розповсюдження взаємодії нічого не можна сказати, оскільки система є статичною. Таким чином, закон Кулона, який описує взаємодію статичних зарядів, не несе, без додаткових припущень, жодної інформації про швидкість розповсюдження взаємодії між зарядами. А отже, релятивістський та класичний опис взаємодії зарядів у статичному випадку збігаються.
А отже, релятивістський та класичний опис взаємодії зарядів у статичному випадку збігаються.
Для подальшого аналізу взаємодії цих зарядів можна розглянути їх відносно інерційної системи відліку, що довільно рухається. У такому разі, система вже не буде статичною, а це означає, що можна оцінити швидкість розповсюдження взаємодії. Якщо припустити, що виконується аксіома абсолютності одночасності, то швидкість розповсюдження взаємодії нескінченна, а це, загалом, означає, що до закона Кулона застосовуються перетворення Галілея, що залишають його інваріантним відносно вибору інерціальної системи відліку. А якщо припустити, що аксіома абсолютності одночасності не виконується, то швидкість розповсюдження взаємодії скінченна, і це означає, що до закону Кулона застосовуються перетворення Лоренца, які не залишають вираз для сили Кулона інваріантним відносно вибору інерційної системи відліку.
Саме останньому випадку і присвячені наступні викладки.
Можна записати вираз для сили Кулона точкового зарядуQ{\displaystyle \ Q} відносно системи відліку K’, що рухається у вакуумі зі швидкістюu{\displaystyle \ \mathbf {u} } відносно системиS{\displaystyle \ S}, у якій зарядQ{\displaystyle \ Q} перебуває у спокої, а зарядq{\displaystyle \ q} рухається із швидкістюv{\displaystyle \ \mathbf {v} } відносно нього. {2}}{2m}}+q\varphi },
{2}}{2m}}+q\varphi },
деA{\displaystyle \mathbf {A} } — векторний, аφ{\displaystyle \varphi } — електричний потенціал, аp{\displaystyle \mathbf {p} } — імпульс частинки.
В однорідному магнітному полі заряджена частинка рухається по гвинтовій лінії, яку в фізиці дещо нестрого часто називають спіраллю. Радіус гвинтової лінії (циклотронний радіус) визначається перпендикулярною до поля складовою початкової швидкості частинки. Крок гвинтової лінії — паралельною до поля складовою початкової швидкості частинки. Гвинтова лінія закручена за чи проти годинникової стрілки, в залежності від знаку заряду частинки.
- Перетворення Лоренца
- Перетворення Лоренца для полів
- Вимірювання швидкості силою Лоренца
- Формули на цій сторінці записані в системі СГС (СГСГ). Для перетворення в Міжнародну систему величин (ISQ) дивись Правила переводу формул із системи СГС в систему ISQ.
Ця стаття не містить посилань на джерела. Ви можете допомогти поліпшити цю статтю, додавши посилання на надійні (авторитетні) джерела. Матеріал без джерел може бути підданий сумніву та вилучений. (листопад 2011) Ви можете допомогти поліпшити цю статтю, додавши посилання на надійні (авторитетні) джерела. Матеріал без джерел може бути підданий сумніву та вилучений. (листопад 2011) |
Векторная величина — Википедия
Ве́кторная величина́ — физическая величина, являющаяся вектором (тензором ранга 1). Противопоставляется с одной стороны скалярным (тензорам ранга 0), с другой — тензорным величинам (строго говоря — тензорам ранга 2 и более). Также может противопоставляться тем или иным объектам совершенно другой математической природы.
В большинстве случаев термин вектор употребляется в физике для обозначения вектора в так называемом «физическом пространстве», то есть в обычном трёхмерном пространстве классической физики или в четырёхмерном[1] пространстве-времени в современной физике (в последнем случае понятие вектора и векторной величины совпадают с понятием 4-вектора и 4-векторной величины).
Употребление словосочетания «векторная величина» практически исчерпывается этим. Что же касается употребления термина «вектор», то оно, несмотря на тяготение по умолчанию к этому же полю применимости, в большом количестве случаев всё же весьма далеко выходит за такие рамки. Об этом см. ниже.
Что же касается употребления термина «вектор», то оно, несмотря на тяготение по умолчанию к этому же полю применимости, в большом количестве случаев всё же весьма далеко выходит за такие рамки. Об этом см. ниже.
Содержание
- 1 Употребление терминов вектор и векторная величина в физике
- 2 Генезис векторных величин
- 2.1 Классический трёхмерный случай
- 2.2 Современный четырёхмерный случай
- 3 Виды векторов применительно к физике
- 4 Примечания
Употребление терминов вектор и
векторная величина в физикеПравитьНесмотря на то, что понимание вектора с физической и математической сторон практически едино, в силу разной степени абстракции появляется терминологическая специфика.
Относительно физики в математике понятие вектора избыточно: любой вектор может иметь любую природу, бесчисленно абстрактное пространство и размерность. Когда требуется конкретика, необходимо либо длинно уточнять, либо учитывать явно описанный контекст, что зачастую приводит к путанице.
В физике же речь практически всегда идёт не о математических объектах (обладающих теми или иными формальными свойствами) вообще, а об их определённой, конкретной, «физической» привязке. Учитывая эти соображения конкретности с соображениями краткости и удобства, можно понять, что терминологическая практика в физике заметно отличается от математической. Однако она не входит с последней в явное противоречие. Этого удаётся достичь несколькими несложными способами. Прежде всего, это соглашение, заключающееся в наличии некоторого употребления термина по умолчанию — в неявном контексте. Так в физике, в отличие от математики, под словом вектор обычно понимается не «какой-то вектор любого линейного пространства вообще», а прежде всего вектор, который связан с «обычным физическим пространством» (трёхмерным пространством классической физики или четырёхмерным пространством-временем[2] физики релятивистской). Для векторов же пространств, не связанных прямо и непосредственно с «физическим пространством» или «пространством-временем», как раз применяют специальные названия (иногда включающие слово «вектор», но с уточнением). Если вектор некоторого пространства, не связанного прямо и непосредственно с «физическим пространством» или «пространством-временем» (и которое трудно сразу как-то определённо охарактеризовать), вводится в теории, он часто специально описывается как «абстрактный вектор».
Если вектор некоторого пространства, не связанного прямо и непосредственно с «физическим пространством» или «пространством-временем» (и которое трудно сразу как-то определённо охарактеризовать), вводится в теории, он часто специально описывается как «абстрактный вектор».
Всё сказанное ещё в большей степени, чем к термину «вектор», относится к термину «векторная величина». Умолчание в этом случае ещё более явно подразумевает привязку к «обычному пространству» или пространству-времени, а употребление по отношению к элементам абстрактных векторных пространств скорее практически не встречается (по крайней мере, оно является очень редким исключением).
В физике векторами чаще всего (а векторными величинами — практически всегда) называют векторы двух сходных между собою классов:
- в классической физике (классической механике, электродинамике в классической трёхмерной формулировке и в других областях физики, преимущественно сформировавшихся до начала XX века) векторными величинами или просто векторами называют, как правило, векторы обычного трёхмерного пространства — то есть обычные «геометрические» векторы или, быть может, отличающиеся от таковых на скалярный множитель (в том числе и на множитель размерный).
 Хотя в этих областях физики фактически и применялись разнообразные объекты, идентифицируемые нынешней математикой как векторы, в физической терминологии это получило очень малый отклик (так например, преобразование Фурье в классической электродинамике и классической теории сплошных сред весьма интенсивно применяется, но традиционно почти не рассматривается в контексте классической с использованием слова «вектор» применительно к функциям, хотя с математической точки зрения это было бы вполне законно[3]). Пожалуй, единственным заметным исключением из правил является достаточно свободное оперирование векторами элементов фазового или конфигурационного пространств[4].
Хотя в этих областях физики фактически и применялись разнообразные объекты, идентифицируемые нынешней математикой как векторы, в физической терминологии это получило очень малый отклик (так например, преобразование Фурье в классической электродинамике и классической теории сплошных сред весьма интенсивно применяется, но традиционно почти не рассматривается в контексте классической с использованием слова «вектор» применительно к функциям, хотя с математической точки зрения это было бы вполне законно[3]). Пожалуй, единственным заметным исключением из правил является достаточно свободное оперирование векторами элементов фазового или конфигурационного пространств[4]. - в релятивистской физике[5] (начиная с Пуанкаре, Планка и Минковского) и, в значительной степени, в современной теоретической физике под векторами и векторными величинами понимаются прежде всего векторы четырёхмерного пространства-времени[6] и непосредственно с ним связанные (отличающиеся на скалярный множитель от векторов 4-перемещения) — 4-векторы.

- в квантовой механике, квантовой теории поля и др. слово «вектор» стандартно стало применяться и для обозначения такого объекта, как вектор состояния. Этот вектор может иметь, в принципе, любую размерность, и, как правило, он бесконечномерен. Однако путаницы практически не возникает, поскольку слово вектор тут используется исключительно в устойчивом сочетании вектор состояния, и никогда раздельно, за исключением разве что случаев, когда контекст уже настолько очевиден, что путаница просто невозможна (например, при повторном употреблении отдельного слова вектор в отношении объекта, который только что перед этим был назван, как вектор состояния или при использовании однозначных специфических обозначений — таких, например, как скобки Дирака — или соответствующих им терминов. Для ряда векторов специфических пространств используются специальные слова (такие, как, например, спиноры) или явные названия (вектор цветового пространства, изотопический спин). Более того, словосочетание «векторная величина» практически никогда не применяется к таким абстрактным векторам.
 Все это позволило сохранить термину «вектор», пожалуй, своё основное значение — значение 4-векторa. Именно этот смысл вкладывается в термины векторное поле, векторная частица (векторный бозон, векторный мезон). Сопряжённое значение в подобных терминах имеет и слово «скалярный».
Все это позволило сохранить термину «вектор», пожалуй, своё основное значение — значение 4-векторa. Именно этот смысл вкладывается в термины векторное поле, векторная частица (векторный бозон, векторный мезон). Сопряжённое значение в подобных терминах имеет и слово «скалярный».
Примеры векторных физических величин: скорость, сила, поток тепла.
Генезис векторных величинПравить
Каким образом физические «векторные величины» привязаны к пространству? Прежде всего, бросается в глаза то, что размерность векторных величин (в том обычном смысле употребления этого термина, который разъяснён выше) совпадает с размерностью одного и того же «физического» (и «геометрического») пространства, например, пространство трёхмерно и вектор электрического поля трехмерен. Интуитивно можно заметить также, что любая векторная физическая величина, какую бы туманную связь она не имела с обычной пространственной протяжённостью, тем не менее имеет вполне определённое направление именно в этом обычном пространстве.
Однако оказывается, что можно достичь и гораздо большего, прямо «сведя» весь набор векторных величин физики к простейшим «геометрическим» векторам, вернее даже — к одному вектору — вектору элементарного перемещения, а более правильно было бы сказать — произведя их всех от него.
Эта процедура имеет две различные (хотя по сути детально повторяющие друг друга) реализации для трёхмерного случая классической физики и для четырёхмерной пространственно-временной формулировки, обычной для современной физики.
Классический трёхмерный случайПравить
Будем исходить из обычного трёхмерного «геометрического» пространства, в котором мы живём и можем перемещаться.
В качестве исходного и образцового вектора возьмём вектор бесконечно малого перемещения. Довольно очевидно, что это обычный «геометрический» вектор (как и вектор конечного перемещения).
Заметим теперь сразу, что умножение вектора на скаляр всегда даёт новый вектор. То же можно сказать о сумме и разности векторов.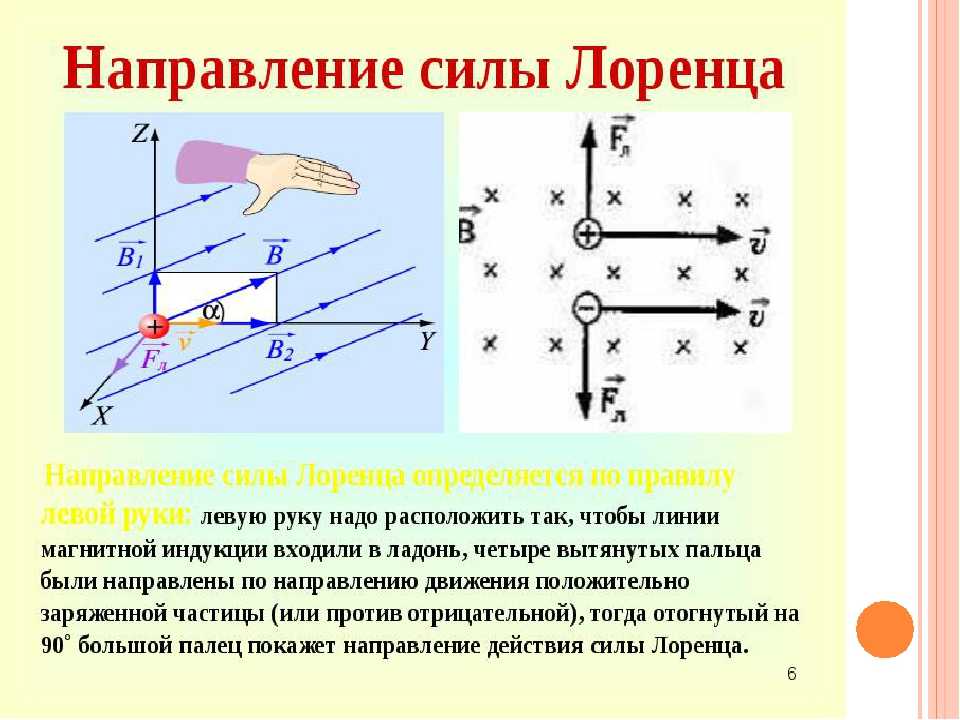 В этой главе мы не будем делать разницы между полярными и аксиальными векторами[7], поэтому заметим, что и векторное произведение двух векторов даёт новый вектор.
В этой главе мы не будем делать разницы между полярными и аксиальными векторами[7], поэтому заметим, что и векторное произведение двух векторов даёт новый вектор.
Также новый вектор даёт дифференцирование вектора по скаляру (поскольку такая производная есть предел отношения разности векторов к скаляру). Это можно сказать дальше и о производных всех высших порядков. То же верно по отношению к интегрированию по скалярам (времени, объёму).
Теперь заметим, что, исходя из радиус-вектора r или из элементарного перемещения dr, мы легко понимаем, что векторами являются (поскольку время — скаляр) такие кинематические величины, как
- скорость v=dr/dt,{\displaystyle \mathbf {v} =d\mathbf {r} /dt,}
- ускорение a=dv/dt.{\displaystyle \mathbf {a} =d\mathbf {v} /dt.}
Из скорости и ускорения, умножением на скаляр (массу), появляются
- импульс,
- сила.
Поскольку нас сейчас интересуют и псевдовекторы, заметим, что
- угловая скорость,
- момент импульса — появляются совершенно понятным образом.
 [8]
[8]
- с помощью формулы силы Лоренца напряжённость электрического поля и вектор магнитной индукции привязаны к векторам силы и скорости.
Продолжая эту процедуру, мы обнаруживаем, что все известные нам векторные величины оказываются теперь не только интуитивно, но и формально, привязаны к исходному пространству. А именно все они в некотором смысле являются его элементами, так как выражаются в сущности как линейные комбинации других векторов (со скалярными множителями, возможно, и размерными, но скалярными, а поэтому формально вполне законными).
Современный четырёхмерный случайПравить
Ту же процедуру можно проделать исходя из четырёхмерного перемещения. Оказывается, что все 4-векторные величины «происходят» от 4-перемещения, являясь поэтому в некотором смысле такими же векторами пространства-времени, как и само 4-перемещение.
Виды векторов применительно к физикеПравить
- Полярный или истинный вектор — обычный вектор.

- Аксиальный вектор (псевдовектор) — на самом деле не является настоящим вектором, однако формально почти не отличается от последнего, за исключением того, что меняет направление на противоположное при изменении ориентации системы координат (например, при зеркальном отражении системы координат). Примеры псевдовекторов: все величины, определяемые через векторное произведение двух полярных векторов.
- Для сил выделяется несколько различных классов эквивалентности.
- ↑ Во многих современных теориях размерность фундаментального пространства-времени больше, чем 4; впрочем, это в принципе довольно мало что меняет, к тому же ни одна из этих теорий пока не достигла статуса общепризнанной и достаточно подтвержденной.
- ↑ Во многих современных теориях, например, в теории струн, пространство-время не 4-мерно, а имеет большее количество измерений, однако является чаще всего достаточно прямым и простым обобщением своего 4-мерного прототипа, а возможность путаницы практически исключена контекстом самих этих теорий (не говоря уже о том, что размерность тогда часто указывается явно, а других, кроме размерности, отличий от обычного пространства-времени не предполагается).

- ↑ Для того, чтобы избежать противоречий между физической и математической терминологией, существует такой способ: вместо выражения «вектор такого-то пространства» можно употребить синонимичное — «элемент такого-то пространства». Математически оно полностью эквивалентно, но не создаёт путаницы при употреблении наряду с типичными для физики терминологическими традициями.
- ↑ трудно сказать, что послужило этому в большей степени: то, что эти пространства (особенно конфигурационное) выглядят слишком прямым обобщением обычного физического пространства, в частных случаях просто с последним совпадающим, или то, что теоретическая механика, в которой эти понятия возникли, считается разделом не физики, а математики.
- ↑ Под релятивистской физикой тут прежде всего понимается стандартная 4-мерная формулировка релятивистской механики, электродинамики и других теорий. В принципе, такая формулировка используется и для квантовых теорий, и для неквантовых.
- ↑ Наиболее явным выходом за эти рамки по умолчанию (то есть без специальных терминологических уточняющих маркеров) являются уже упоминавшиеся теории, основанные на предположении о большей, чем 4, размерности фундаментального физического пространства-времени, начиная с теории Калуцы, до теории струн и т.
 д.
д. - ↑ При нужде такое разделение легко произвести, но нас сейчас интересует в первую построение наиболее полного набора векторных физических величин, а не их классификация, на этом мы и сосредоточимся.
- ↑ Для угловой скорости, правда, проще всего применить обратное рассуждение: поскольку векторное произведение угловой скорости и радиус-вектора есть скорость, значит угловая скорость — вектор (точнее — псевдовектор).
Закон силы Лоренца (магнитные и смешанные поля)
июль Томас а также Шравант С. внес
Содержание
- Физические эффекты на движение частицы
- Частица, циркулирующая в однородном магнитном поле
- Масс-спектрометр
- Сила Лоренца из-за электрических и магнитных полей
- использованная литература
[1]
По определению векторного произведения магнитная сила должна быть перпендикулярна как скорости, так и магнитному полю. В результате перпендикулярности скорости магнитное поле не может изменить скорость, а только направление скорости. Следовательно, это всегда центростремительная сила. 92/rqvB=mv2/r
В результате перпендикулярности скорости магнитное поле не может изменить скорость, а только направление скорости. Следовательно, это всегда центростремительная сила. 92/rqvB=mv2/r
r=mvqBr=\frac{mv}{qB}r=qBmv
Найдите радиус орбиты частицы с зарядом q=5 Cq=5 \text{ C}q=5 C и массой m=20 кгm=20\text{ кг}m=20 кг, движущейся со скоростью v=16msv = 16 \frac{\text{m}}{\text{s}}v=16см через однородное магнитное поле B=2 T.B = 2\text{ T}.B=2 T.
r=mvqB=(20 кг)(16 мс)(5 C)(2 T)=32 mr=\frac{mv}{qB}=\frac{(20\text{ кг})(16 \frac{ \text{m}}{\text{s}})}{(5 \text{C})(2\text{T})}=32\text{m}r=qBmv=(5 C)( 2 Т)(20 кг)(16см)=32 м
Многие устройства используют круговое движение заряженной частицы, движущейся через однородное поле. Одним из таких устройств является масс-спектрометр , который сортирует ионы в образце в соответствии с отношением их массы к заряду.
Найдите отношение заряда к массе частицы, которая движется со скоростью v=4 м/сv=4\text{м/с}v=4 м/с через масс-спектрометр, настроенный на B=100 mTB=100\text{ mT}B =100 мТл по орбите радиусом r=20 см.
r = 20\text{ см}.r=20 см.
Из r=mvqB,r=\frac{mv}{qB},r=qBmv отношение заряда к массе равно qm=vrB=4(0,20)(0,1)=200Ckg.\frac{q}{m} = \frac{v}{rB} = \frac{4}{(0,20)(0,1)} = 200\frac{ \text{C}}{\text{кг}}.mq=rBv=(0,20)(0,1)4=200 кгC.
1 мм1\текст{ мм}1 мм 10 см10\текст{ см}10 см 10 м10\text{ м}10 м 1 км1 \text{ км}1 км
Простейший способ обогащения урана для использования в ядерной энергетике или оружии заключается в пропускании ионизированного пучка испаренного урана через модифицированный масс-спектрометр, известный как калютрон . Предположим, что электрон-магнит, создающий магнитное поле величиной B=1 TB = 1\text{ T}B=1 T, и печь с напряжением, рассчитанным на разность потенциалов V=2 kVV = 2\text{ kV}V=2 kV имеются, каков радиус пути, проходимого изолируемым ураном-235? Предположим, что пучок испаряемого урана ионизирован до заряда q = 1,6 × 10–19.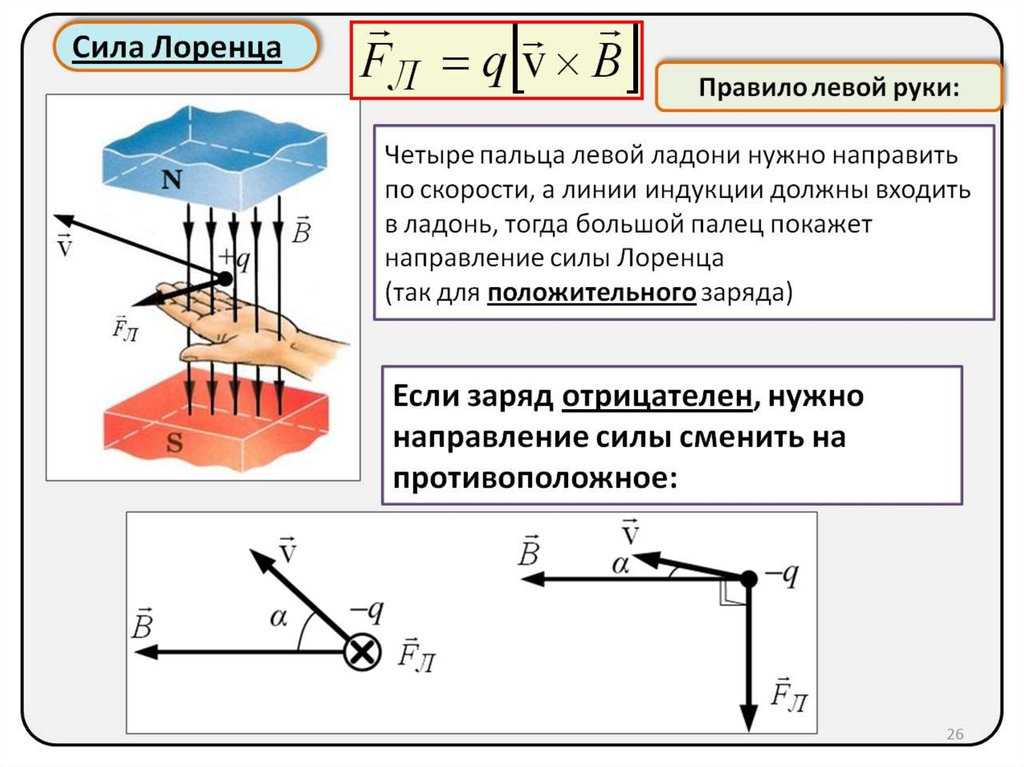 {-19}\text{C}.q=1,6×10−19C.
{-19}\text{C}.q=1,6×10−19C.
Сила Лоренца — это сила, ощущаемая частицей с зарядом qqq, движущейся со скоростью v⃗\vec{v}v через область с электрическим полем E⃗\vec{E}E и магнитным полем B⃗.\ vec{B}.B.
F⃗Лоренц=q(E⃗+v⃗×B⃗)\vec{F}_{Лоренц} = q(\vec{E} + \vec{v}\times\vec{B})FLorentz=q(E+ v×B)
Суммарная сила, действующая на частицу, движущуюся через область с электрическим и магнитным полями, представляет собой просто векторную сумму полей. F⃗Лоренц=F⃗E+F⃗B=qE⃗+qv⃗×B⃗=q(E⃗+v⃗×B⃗)\vec{F}_{Лоренц} = \vec{F}_E + \vec{F}_B=q\vec{E} + q\vec{v}\times\vec{B}=q(\vec{E} + \vec{v}\times\vec{B})FLorentz=FE+FB=qE+qv×B =q(E+v×B) 9Н.
Вдоль плоскости xzxzxz По плоскости изызыза Строго ххх Ни один из этих вариантов Строго ггг Вдоль плоскости xyxyxy Строго zzz
Позитрон движется через область, в которой электрические поля однородны в направлении xxx, а магнитное поле однородно в направлении yyy. Куда направлена конечная скорость позитрона?
Куда направлена конечная скорость позитрона?
- Индианфейс, ., & Примфак, . Действие силы Лоренца, искривляющей траекторию электрона в магнитном поле . Получено 4 мая 2016 г., из https://commons.wikimedia.org/wiki/File:Action_of_the_Lorentz_force_bending_the_path_of_an_electron_in_a_ Magnetic_field.gif
Процитировать как: Закон силы Лоренца (магнитные и смешанные поля). Brilliant.org . Извлекаются из https://brilliant.org/wiki/lorentz-force-law-magnetic-fields/
Сила Лоренца вики | TheReaderWiki
MinecraftStatus.net | CheckTheIP.com | TheDicts.com | TheReaderВеб | Википедия
Сила Лоренца, действующая на быстро движущиеся заряженные частицы в пузырьковой камере. Траектории положительных и отрицательных зарядов изгибаются в противоположных направлениях.
В физике (особенно в электромагнетизме) сила Лоренца (или электромагнитная сила ) представляет собой комбинацию электрической и магнитной сил на точечный заряд из-за электромагнитных полей. Частица с зарядом q движется со скоростью v в электрическом поле E и магнитном поле B испытывает силу
Частица с зарядом q движется со скоростью v в электрическом поле E и магнитном поле B испытывает силу
Историки предполагают, что закон подразумевается в статье Джеймса Клерка Максвелла, опубликованной в 1865 году. [3] Хендрик Лоренц прибыл при полном выводе в 1895 г., [4] , определяющем вклад электрической силы, через несколько лет после того, как Оливер Хевисайд правильно определил вклад магнитной силы. [5]
Закон силы Лоренца как определение E и B
Заряженные частицы, на которые действует сила Лоренца.
Во многих учебниках по классическому электромагнетизму закон силы Лоренца используется как определение электрических и магнитных полей E и B . [6] [7] [8] В частности, сила Лоренца понимается как следующее эмпирическое утверждение:
Электромагнитная сила F , действующая на пробный заряд в данный момент и время, является некоторой функцией его заряда q и скорости v , который может быть параметризован ровно двумя векторами E и B в функциональной форме :
Это верно даже для частиц, приближающихся к скорости света (то есть величина v , | v | ≈ c ). [9] Таким образом, два векторных поля E и B определены в пространстве и времени и называются «электрическим полем» и «магнитным полем». Поля определяются повсюду в пространстве и времени в зависимости от того, какую силу испытает пробный заряд, независимо от того, присутствует ли заряд, испытывающий эту силу.
[9] Таким образом, два векторных поля E и B определены в пространстве и времени и называются «электрическим полем» и «магнитным полем». Поля определяются повсюду в пространстве и времени в зависимости от того, какую силу испытает пробный заряд, независимо от того, присутствует ли заряд, испытывающий эту силу.
Как определение E и B , сила Лоренца является только определением в принципе, потому что реальная частица (в отличие от гипотетического «пробного заряда» с бесконечно малой массой и зарядом) будет генерировать свои собственные конечные E и B поля, которые могут изменить электромагнитную силу, с которой он сталкивается. [10] Кроме того, если заряд испытывает ускорение, как если бы он был вынужден двигаться по кривой траектории, он испускает излучение, которое приводит к потере кинетической энергии. См., например, тормозное излучение и синхротронный свет. Эти эффекты возникают как за счет прямого воздействия (называемого силой реакции излучения), так и косвенного (за счет воздействия на движение близлежащих зарядов и токов).
Уравнение
Заряженная частица
Сила Лоренца F на заряженную частицу (с зарядом q) в движении (мгновенная скорость v ). Поле E и поле B различаются в пространстве и времени.
Сила F , действующая на частицу электрического заряда q с мгновенной скоростью v , обусловленная внешним электрическим полем E и магнитным полем B , определяется выражением (в единицах СИ [1] ): [11]
где × векторное векторное произведение (все величины, выделенные жирным шрифтом, являются векторами). В декартовых компонентах имеем:
В общем случае электрические и магнитные поля являются функциями положения и времени. Следовательно, в явном виде сила Лоренца может быть записана как:
, где r — вектор положения заряженной частицы, t — время, а надточка — производная по времени.
Положительно заряженная частица будет ускорена в имеет ту же линейную ориентацию , что и поле E , но будет искривляться перпендикулярно как вектору мгновенной скорости v , так и полю B в соответствии с правилом правой руки (детально, если пальцы правой руки вытянуты в точку в направлении v и затем свернуты в точку в направлении B , тогда вытянутый большой палец будет указывать в направлении F ).
Термин q E называется электрической силой , а термин q ( v × B ) называется магнитной силой . [12] Согласно некоторым определениям, термин «сила Лоренца» относится конкретно к формуле для магнитной силы, [13] с общей электромагнитной силой (включая электрическую силу) с учетом некоторых других (нестандартных) имя. Эта статья будет , а не следовать этой номенклатуре: В дальнейшем термин «сила Лоренца» будет относиться к выражению полной силы.
Магнитная составляющая силы Лоренца проявляется как сила, действующая на проводник с током в магнитном поле. В этом контексте ее также называют силой Лапласа.
Сила Лоренца — это сила, действующая со стороны электромагнитного поля на заряженную частицу, то есть скорость, с которой линейный импульс передается от электромагнитного поля к частице. С ним связана мощность, которая представляет собой скорость, с которой энергия передается от электромагнитного поля к частице. Эта сила равна
Непрерывное распределение заряда
Сила Лоренца (на единицу 3-го объема) f при непрерывном распределении заряда (плотность заряда ρ ) в движении. 3-плотность тока Дж соответствует движению элемента заряда dq в элементе объема dV и изменяется по континууму.
Для непрерывного распределения заряда в движении уравнение силы Лоренца принимает вид:
где
г
Ф
{\ Displaystyle \ mathrm {d} \ mathbf {F}}
сила, действующая на небольшой участок распределения заряда с зарядом
г
д
{\ Displaystyle \ mathrm {д} д}
.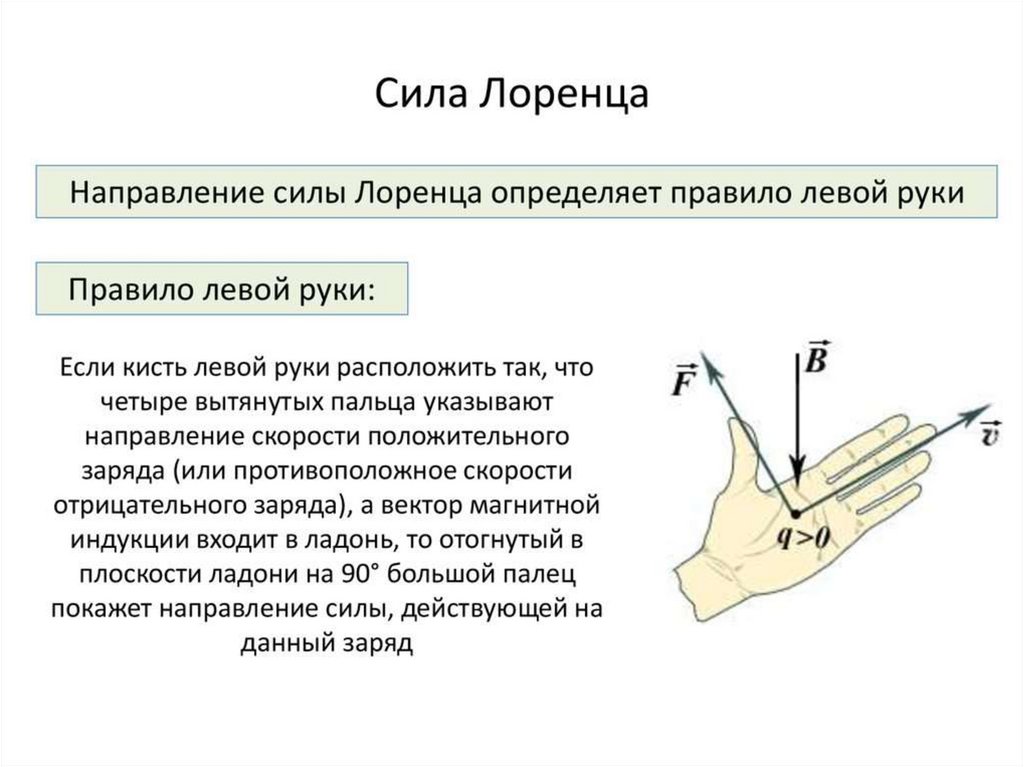 Если обе части этого уравнения разделить на объем этого маленького кусочка распределения заряда
г
В
{\ Displaystyle \ mathrm {д} В}
, результат:
Если обе части этого уравнения разделить на объем этого маленького кусочка распределения заряда
г
В
{\ Displaystyle \ mathrm {д} В}
, результат:
Суммарная сила представляет собой объемный интеграл по распределению заряда:
Путем исключения
р
{\ Displaystyle \ ро}
а также
Дж
{\ Displaystyle \ mathbf {J}}
, используя уравнения Максвелла и манипулируя с помощью теорем векторного исчисления, эту форму уравнения можно использовать для получения тензора напряжений Максвелла
о
{\ Displaystyle {\boldsymbol {\сигма}}}
, в свою очередь, это можно комбинировать с вектором Пойнтинга
С
{\ Displaystyle \ mathbf {S}}
для получения электромагнитного тензора энергии-импульса T используется в общей теории относительности.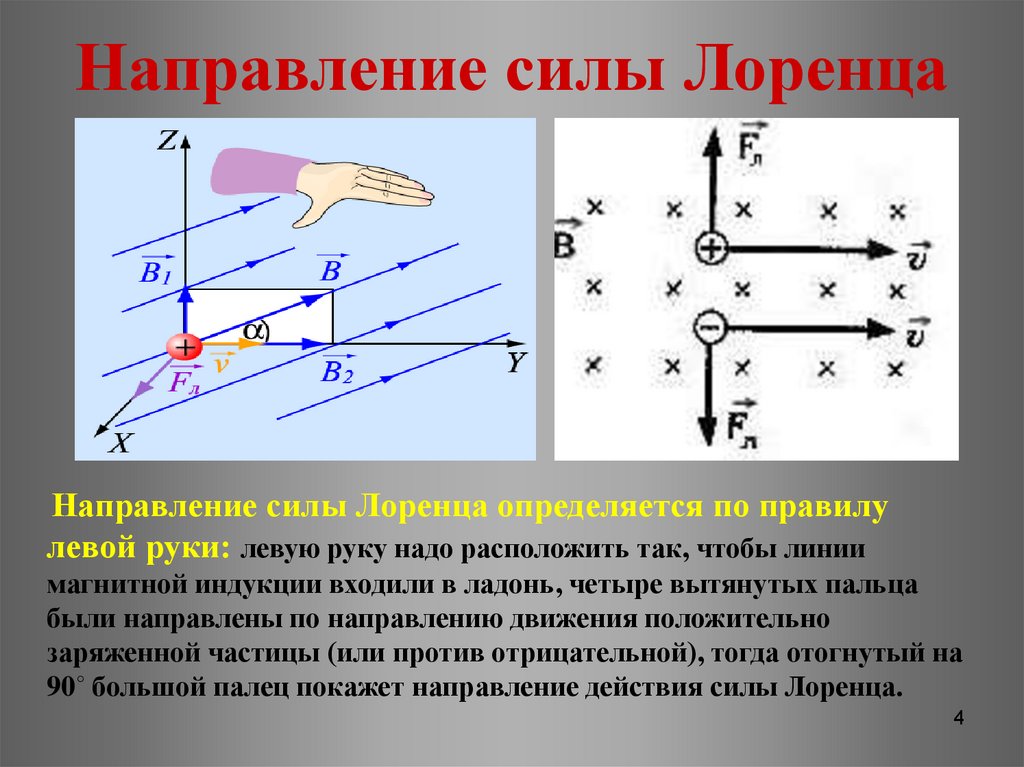 [14]
[14]
В пересчете на о {\ Displaystyle {\boldsymbol {\сигма}}} а также С {\ Displaystyle \ mathbf {S}} , другой способ записать силу Лоренца (на единицу объема): [14]
Плотность мощности, связанная с силой Лоренца в материальной среде, равна
. Если мы разделим общий заряд и полный ток на их свободные и связанных частей, получаем, что плотность силы Лоренца равна
где:
р
ф
{\ Displaystyle \ ро _ {е}}
– плотность свободного заряда;
п
{\ Displaystyle \ mathbf {Р}}
– плотность поляризации;
Дж
ф
{\ Displaystyle \ mathbf {J} _ {е}}
– плотность свободного тока; а также
М
{\ Displaystyle \ mathbf {М}}
плотность намагниченности. Таким образом, сила Лоренца может объяснить крутящий момент, приложенный к постоянному магниту магнитным полем. Плотность связанной мощности равна
Таким образом, сила Лоренца может объяснить крутящий момент, приложенный к постоянному магниту магнитным полем. Плотность связанной мощности равна
Уравнение в единицах СГС
Вышеупомянутые формулы используют единицы СИ, которые являются наиболее распространенными. В более старых единицах СГС-Гаусса, которые несколько более распространены среди некоторых физиков-теоретиков, а также среди экспериментаторов в области конденсированных сред, вместо этого используется теория электронов Лоренца. Формулы для силы Лоренца (I, пондеромоторная сила) и уравнения Максвелла для дивергенции электрического поля E (II) и магнитного поля B (III), Электромагнитная теория Максвелла и его сыновья, прилагаемые к корпусу, движущемуся , 1892, с. 451. V — скорость света.
Первые попытки количественного описания электромагнитной силы были предприняты в середине 18 века. Было высказано предположение, что сила на магнитных полюсах Иоганна Тобиаса Майера и других в 1760, [15] и электрически заряженных объектах Генри Кавендишем в 1762 году, [16] подчиняется закону обратных квадратов. Однако в обоих случаях экспериментальное доказательство не было ни полным, ни окончательным. Только в 1784 году Шарль-Огюстен де Кулон, используя крутильные весы, смог окончательно показать экспериментально, что это правда. [17] Вскоре после открытия Гансом Христианом Эрстедом в 1820 г. того, что на магнитную стрелку действует гальванический ток, Андре-Мари Ампер в том же году смог экспериментально вывести формулу угловой зависимости силы между два текущих элемента. [18] [19] Во всех этих описаниях сила всегда описывалась в терминах свойств материи и расстояний между двумя массами или зарядами, а не в терминах электрических и магнитных полей. [20]
Однако в обоих случаях экспериментальное доказательство не было ни полным, ни окончательным. Только в 1784 году Шарль-Огюстен де Кулон, используя крутильные весы, смог окончательно показать экспериментально, что это правда. [17] Вскоре после открытия Гансом Христианом Эрстедом в 1820 г. того, что на магнитную стрелку действует гальванический ток, Андре-Мари Ампер в том же году смог экспериментально вывести формулу угловой зависимости силы между два текущих элемента. [18] [19] Во всех этих описаниях сила всегда описывалась в терминах свойств материи и расстояний между двумя массами или зарядами, а не в терминах электрических и магнитных полей. [20]
Современная концепция электрических и магнитных полей впервые возникла в теориях Майкла Фарадея, в частности, в его идее силовых линий, которые позднее были полностью математически описаны лордом Кельвином и Джеймсом Клерком Максвеллом. [21] С современной точки зрения можно идентифицировать в формулировке уравнений поля Максвелла 1865 года форму уравнения силы Лоренца по отношению к электрическим токам, [3] , хотя во времена Максвелла это не было очевидным как его уравнения связаны с силами, действующими на движущиеся заряженные объекты.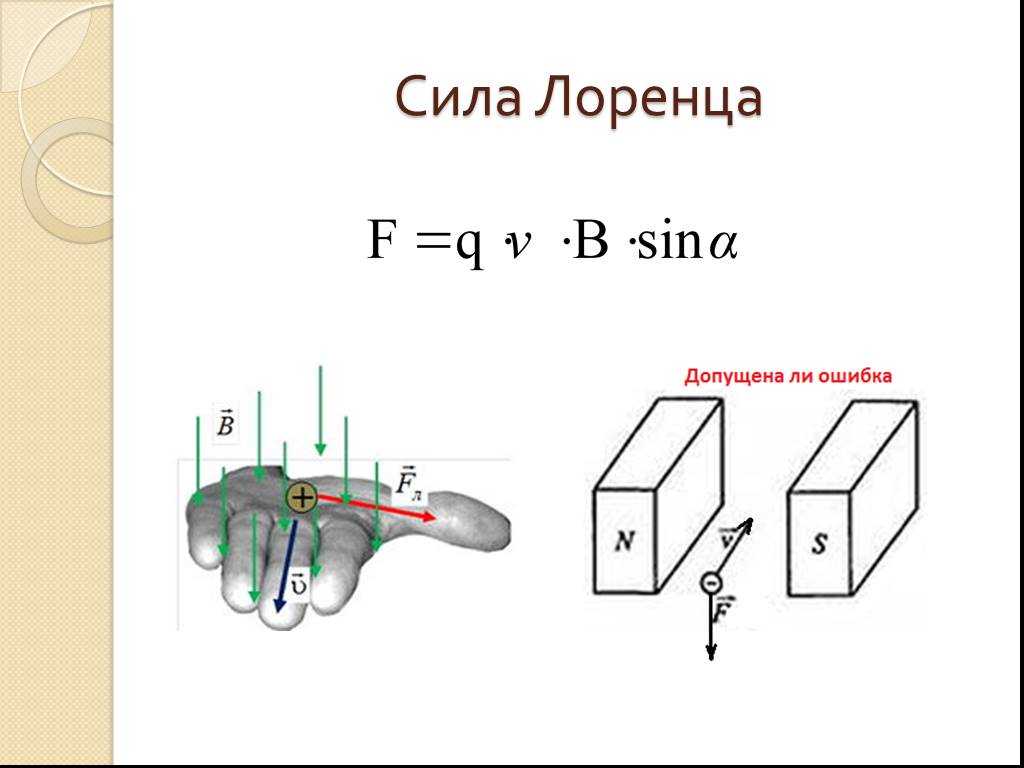 Дж. Дж. Томсон был первым, кто попытался вывести из уравнений поля Максвелла электромагнитные силы, действующие на движущийся заряженный объект, с точки зрения свойств объекта и внешних полей. Заинтересовавшись определением электромагнитного поведения заряженных частиц в катодных лучах, Томсон опубликовал статью в 1881 г., в которой он определил силу, действующую на частицы, вызванную внешним магнитным полем, как [5] [22]
Дж. Дж. Томсон был первым, кто попытался вывести из уравнений поля Максвелла электромагнитные силы, действующие на движущийся заряженный объект, с точки зрения свойств объекта и внешних полей. Заинтересовавшись определением электромагнитного поведения заряженных частиц в катодных лучах, Томсон опубликовал статью в 1881 г., в которой он определил силу, действующую на частицы, вызванную внешним магнитным полем, как [5] [22]
Траектории частиц под действием силы Лоренца
Основная статья: Направляющий центр
Заряженная частица дрейфует в однородном магнитном поле. (A) Без возмущающей силы (B) С электрическим полем, E (C) С независимой силой, F (например, силой тяжести) (D) В неоднородном магнитном поле, град H
Во многих случаях, представляющих практический интерес, движение в магнитном поле электрически заряженной частицы (например, электрона или иона в плазме) можно рассматривать как суперпозицию относительно быстрого кругового движения вокруг точки, называемой направляющий центр и относительно медленный дрейф этой точки. Скорость дрейфа может различаться для разных видов в зависимости от их состояния заряда, массы или температуры, что может привести к электрическим токам или химическому разделению.
Скорость дрейфа может различаться для разных видов в зависимости от их состояния заряда, массы или температуры, что может привести к электрическим токам или химическому разделению.
Значение силы Лоренца
В то время как современные уравнения Максвелла описывают, как электрически заряженные частицы и токи или движущиеся заряженные частицы порождают электрические и магнитные поля, закон силы Лоренца дополняет эту картину, описывая силу, действующую на движущийся точечный заряд q в присутствии электромагнитных полей. [11] [28] Закон силы Лоренца описывает действие E и B на точечный заряд, но такие электромагнитные силы не являются полной картиной. Заряженные частицы, возможно, связаны с другими силами, особенно гравитацией и ядерными силами. Таким образом, уравнения Максвелла не стоят отдельно от других физических законов, а связаны с ними через плотности заряда и тока. Реакция точечного заряда на закон Лоренца — это один аспект; поколение E и B по токам и зарядам — это другое.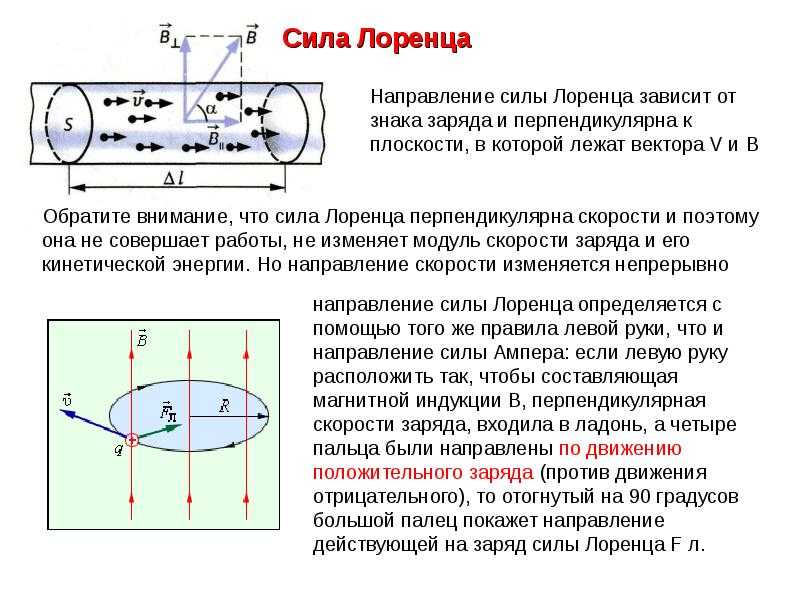
В реальных материалах сила Лоренца неадекватна для описания коллективного поведения заряженных частиц, как в принципе, так и с точки зрения вычислений. Заряженные частицы в материальной среде не только реагируют на поля E и B , но и генерируют эти поля. Для определения временной и пространственной реакции зарядов необходимо решать сложные уравнения переноса, например, уравнение Больцмана, уравнение Фоккера-Планка или уравнения Навье-Стокса. Например, см. магнитогидродинамику, гидродинамику, электрогидродинамику, сверхпроводимость, звездную эволюцию. Разработан целый физический аппарат для решения этих вопросов. См., например, отношения Грина-Кубо и функцию Грина (теория многих тел).
Сила, действующая на провод с током
Правило правой руки для провода с током в магнитном поле B
Когда провод, по которому течет электрический ток, помещается в магнитное поле, каждый из движущихся зарядов, которые составляют ток, испытывает силу Лоренца, и вместе они могут создать макроскопическую силу на проводе (иногда называемую силой Лапласа ). Комбинируя закон силы Лоренца, приведенный выше, с определением электрического тока, в случае прямого неподвижного провода получается следующее уравнение: [29]
Комбинируя закон силы Лоренца, приведенный выше, с определением электрического тока, в случае прямого неподвижного провода получается следующее уравнение: [29]
где ℓ — вектор, величина которого равна длине провода и направление которого совпадает с направлением обычного тока заряда I.
Если провод не прямой, но изогнутой, силу, действующую на нее, можно вычислить, применив эту формулу к каждому бесконечно малому отрезку проволоки. г ℓ {\ displaystyle \ mathrm {d} {\ boldsymbol {\ ell}}} , затем сложив все эти силы интегрированием. Формально результирующая сила, действующая на неподвижный жесткий провод, по которому течет постоянный ток I, равна
Это чистая сила. Кроме того, обычно возникает крутящий момент и другие эффекты, если проволока не является идеально жесткой.
Одним из приложений этого закона является закон силы Ампера, который описывает, как два проводника с током могут притягиваться или отталкиваться друг от друга, поскольку на каждый из них действует сила Лоренца от магнитного поля другого. Для получения дополнительной информации см. статью: Закон силы Ампера.
Для получения дополнительной информации см. статью: Закон силы Ампера.
ЭДС
Магнитная сила ( q v × B ) составляющая силы Лоренца отвечает за движущая электродвижущая сила (или движущая ЭДС ), явление, лежащее в основе многих электрических генераторов. Когда проводник движется через магнитное поле, магнитное поле оказывает противоположное воздействие на электроны и ядра в проводе, и это создает ЭДС. К этому явлению применяется термин «двигательная ЭДС», поскольку ЭДС возникает из-за движения провода.
В других электрических генераторах магниты двигаются, а проводники нет. В этом случае ЭДС обусловлена электрической силой ( q E ) член в уравнении силы Лоренца. Рассматриваемое электрическое поле создается изменяющимся магнитным полем, что приводит к индуцированной ЭДС , как описано уравнением Максвелла – Фарадея (одно из четырех современных уравнений Максвелла). [30]
[30]
Обе эти ЭДС, несмотря на их кажущееся разное происхождение, описываются одним и тем же уравнением, а именно, ЭДС есть скорость изменения магнитного потока через провод. (Это закон индукции Фарадея, см. ниже.) Специальная теория относительности Эйнштейна была частично мотивирована желанием лучше понять эту связь между двумя эффектами. [30] На самом деле электрическое и магнитное поля являются разными гранями одного и того же электромагнитного поля, и при переходе от одной инерциальной системы отсчета к другой соленоидальная часть векторного поля E -поля может изменяться полностью или частично. часть B -field или наоборот . [31]
Сила Лоренца и закон индукции Фарадея
Сила Лоренца — изображение на стене в Лейдене
Основная статья: Закон индукции Фарадея
Учитывая петлю провода в магнитном поле, закон индукции Фарадея утверждает, что индуцированная электродвижущая сила (ЭДС) в проводе равна:
Знак ЭДС определяется законом Ленца. Обратите внимание, что это справедливо не только для стационарного провода , но и для подвижного провода .
Обратите внимание, что это справедливо не только для стационарного провода , но и для подвижного провода .
Из закона индукции Фарадея (который справедлив для движущегося провода, например, в двигателе) и уравнений Максвелла можно вывести силу Лоренца. Верно и обратное: силу Лоренца и уравнения Максвелла можно использовать для вывода закона Фарадея.
Пусть Σ( t ) — движущаяся проволока, движущаяся вместе без вращения и с постоянной скоростью v , а Σ( t ) — внутренняя поверхность проволоки. ЭДС вокруг замкнутого пути ∂Σ( t ) определяется как: [32]
где
NB: Оба d ℓ и d A имеют неоднозначность знака; чтобы получить правильный знак, используется правило правой руки, как объясняется в статье Теорема Кельвина – Стокса.
Приведенный выше результат можно сравнить с версией закона индукции Фарадея, которая появляется в современных уравнениях Максвелла, называемых здесь Уравнение Максвелла-Фарадея :
Уравнение Максвелла-Фарадея также может быть записано в интегральной форме с использованием теоремы Кельвина-Стокса. [33]
Таким образом, мы имеем уравнение Максвелла Фарадея:
и закон Фарадея,
. Они эквивалентны, если провод не движется. Используя интегральное правило Лейбница и то, что div B = 0, приводит к
и используя уравнение Максвелла Фарадея,
, поскольку это справедливо для любого положения проволоки, это означает, что
Закон индукции Фарадея выполняется независимо от того, неподвижна ли проволочная петля, находится ли она в движении или в процессе деформации, а также независимо от того, постоянно ли магнитное поле во времени или изменяется. Однако бывают случаи, когда закон Фарадея либо неадекватен, либо сложен в использовании, и необходимо применение основного закона силы Лоренца. См. неприменимость закона Фарадея.
Однако бывают случаи, когда закон Фарадея либо неадекватен, либо сложен в использовании, и необходимо применение основного закона силы Лоренца. См. неприменимость закона Фарадея.
Если магнитное поле фиксировано во времени и проводящая петля движется через поле, магнитный поток Φ B Связывание петли можно изменить несколькими способами. Например, если поле B изменяется в зависимости от положения и цикл перемещается в место с другим полем B , Φ B изменится. В качестве альтернативы, если петля меняет ориентацию относительно поля B , дифференциальный элемент B ⋅ d A изменится из-за разного угла между B и d A , а также изменится Φ Б . В качестве третьего примера, если часть цепи проходит через однородное, не зависящее от времени B -поле, а другая часть цепи удерживается неподвижной, поток, связывающий всю замкнутую цепь, может измениться из-за сдвига в взаимное расположение составных частей схемы во времени (поверхность ∂Σ( t ) зависит от времени). Во всех трех случаях закон индукции Фарадея затем предсказывает ЭДС, создаваемую изменением Φ B .
Во всех трех случаях закон индукции Фарадея затем предсказывает ЭДС, создаваемую изменением Φ B .
Обратите внимание, что уравнение Максвелла Фарадея подразумевает, что электрическое поле E не является консервативным, когда магнитное поле B изменяется во времени, и не может быть выражено как градиент скалярного поля, и не подлежит градиентной теореме, поскольку его вращение не равно нулю. [32] [34]
Сила Лоренца в терминах потенциалов
См. также: Математические описания электромагнитного поля, уравнения Максвелла и разложение Гельмгольца
Поля E и B можно заменить магнитным векторным потенциалом A и (скалярным) электростатическим потенциалом ϕ на
Сила становится
Используя тождество для тройного произведения, это можно переписать as,
(Обратите внимание, что координаты и компоненты скорости должны рассматриваться как независимые переменные, поэтому оператор del действует только на
А
{\ Displaystyle \ mathbf {А}}
, не на
в
{\ Displaystyle \ mathbf {v}}
; таким образом, нет необходимости использовать индекс Фейнмана в уравнении выше). По цепному правилу полная производная
А
{\ Displaystyle \ mathbf {А}}
это:
По цепному правилу полная производная
А
{\ Displaystyle \ mathbf {А}}
это:
, так что приведенное выше выражение принимает вид:
С учетом v = ẋ мы можем представить уравнение в удобной форме Эйлера–Лагранжа
где
сила Лоренца и аналитическая механика Лагранжиан для заряженной частицы с массой
m и зарядом q в электромагнитном поле эквивалентно описывает динамику частицы в терминах ее энергии , а не силы, действующей на нее. Классическое выражение дается: [35], где A и ϕ — потенциальные поля, указанные выше. Количество
В
знак равно
д
(
ф
−
А
⋅
р
˙
)
{\ displaystyle V = q (\ phi — \ mathbf {A} \ cdot \ mathbf {\ dot {r}})}
можно рассматривать как потенциальную функцию, зависящую от скорости. [36] Используя уравнения Лагранжа, можно снова получить приведенное выше уравнение для силы Лоренца.
[36] Используя уравнения Лагранжа, можно снова получить приведенное выше уравнение для силы Лоренца.
Потенциальная энергия зависит от скорости частицы, поэтому сила зависит от скорости, поэтому она не является консервативной.
Релятивистский лагранжиан равен
Действие — это релятивистская длина дуги пути частицы в пространстве-времени за вычетом вклада потенциальной энергии плюс дополнительный вклад, который с точки зрения квантовой механики представляет собой дополнительную фазу, которую получает заряженная частица, когда она движется по векторный потенциал.
Релятивистская форма силы Лоренца
Ковариантная форма силы Лоренца
Основные статьи: Ковариантная формулировка классического электромагнетизма и математическое описание электромагнитного поля
Используя метрическую сигнатуру (1, −1, −1, −1), сила Лоренца для заряда q можно записать в ковариантной форме [37] :
, где p α — четырехимпульс, определяемый как
τ собственное время частицы, F 20αβ контравариантный электромагнитный тензор
и U есть ковариантная 4-скорость частицы, определяемая как:
Поля преобразуются в систему отсчета, движущуюся с постоянной относительной скоростью: — тензор преобразования Лоренца.
α = 1 компонент ( x -компонент) силы равен
Подстановка компонентов ковариантного электромагнитного тензора F дает
Использование компонентов ковариантных четырех скоростей дает
Расчет для α = 2, 3 (компоненты силы в направлениях y и z ) дает аналогичные результаты, поэтому объединение 3 уравнений в одно :
Это в точности закон силы Лоренца, однако важно отметить, что p является релятивистским выражением,
Сила Лоренца в алгебре пространства-времени (STA)
Электрические и магнитные поля зависят от скорости наблюдатель, поэтому релятивистская форма закона силы Лоренца может быть лучше всего представлена начиная с независимого от координат выражения для электромагнитного и магнитного полей
Ф
{\ Displaystyle {\ mathcal {F}}}
, и произвольное направление времени,
γ
0
{\ Displaystyle \ гамма _ {0}}
. Это можно решить с помощью алгебры пространства-времени (или геометрической алгебры пространства-времени), разновидности алгебры Клиффорда, определенной в псевдоевклидовом пространстве 9.0019 [38] как
Это можно решить с помощью алгебры пространства-времени (или геометрической алгебры пространства-времени), разновидности алгебры Клиффорда, определенной в псевдоевклидовом пространстве 9.0019 [38] как
Правильная форма (инвариант — неподходящий термин, поскольку преобразование не определено) форма закона силы Лоренца просто
Обратите внимание, что порядок важен, потому что между бивектором и вектором скалярное произведение антисимметричный. При подобном расщеплении пространства-времени можно получить скорость и поля, как указано выше, что дает обычное выражение.
Сила Лоренца в общей теории относительности
В общей теории относительности уравнение движения для частицы с массой м {\ Displaystyle м} и заряжать е {\ Displaystyle е} , движущийся в пространстве с метрическим тензором грамм а б {\ displaystyle g_ {ab}} и электромагнитное поле Ф а б {\ Displaystyle F_ {аб}} , определяется как
Уравнение также можно записать как
Применение
Сила Лоренца используется во многих устройствах, включая:
- Циклотроны и другие ускорители частиц с круговым движением
- Масс-спектрометры
- Скоростные фильтры
- Магнетроны
- Сила Лоренца для измерения скорости
В своем проявлении в виде силы Лапласа, действующей на электрический ток в проводнике, эта сила проявляется во многих устройствах, включая:
- Электродвигатели
- Рейлганы
- Линейные двигатели
- Громкоговорители
- Магнитоплазмодинамические двигатели
- Электрогенераторы
- Униполярные генераторы
- Линейные генераторы
См.
 также
также- Эффект Холла
- Электромагнетизм
- Гравитомагнетизм
- Закон силы Ампера
- Хендрик Лоренц
- уравнения Максвелла
- Формулировка уравнений Максвелла в специальной теории относительности
- Проблема с движущимся магнитом и проводником
- сила Абрахама-Лоренца
- Формула Лармора
- Циклотронное излучение
- Магнитосопротивление
- Скалярный потенциал
- Разложение Гельмгольца
- Направляющий центр
- Полевая линия
- Закон Кулона
- Электромагнитная плавучесть
Сноски 9
Хестенес, Дэвид. «Исчисление пространства-времени».Каталожные номера
Пронумерованные каталожные номера частично относятся к приведенному ниже списку.
- Фейнман, Ричард Филлипс; Лейтон, Роберт Б.
 ; Сэндс, Мэтью Л. (2006). Фейнмановские лекции по физике (3 тома) . Пирсон / Эддисон-Уэсли. ISBN 0-8053-9047-2 . : том 2.
; Сэндс, Мэтью Л. (2006). Фейнмановские лекции по физике (3 тома) . Пирсон / Эддисон-Уэсли. ISBN 0-8053-9047-2 . : том 2. - Гриффитс, Дэвид Дж. (1999). Введение в электродинамику (3-е изд.). Река Аппер-Сэдл, [Нью-Джерси]: Прентис-Холл. ISBN 0-13-805326-X .
- Джексон, Джон Дэвид (1999). Классическая электродинамика (3-е изд.). Нью-Йорк, [Нью-Йорк]: Wiley. ISBN 0-471-30932-X .
- Сервэй, Рэймонд А.; Джуэтт, Джон В. младший (2004). Физика для ученых и инженеров с современной физикой . Белмонт, [Калифорния]: Томсон Брукс/Коул. ISBN 0-534-40846-X .
- Средненицкий, Марк А. (2007). Квантовая теория поля . Кембридж, [Англия] ; Нью-Йорк [Нью-Йорк]: Издательство Кембриджского университета. ISBN 978-0-521-86449-7 .
Внешние ссылки
- Сила Лоренца (демонстрация)
- Закон Фарадея: Танкерсли и Моска
- Заметки по физике и астрономии HyperPhysics в Университете штата Джорджия; см.
 также домашнюю страницу
также домашнюю страницу - Интерактивный Java-апплет, посвященный магнитному отклонению пучка частиц в однородном магнитном поле. Архивировано 13 августа 2011 г. в Wayback Machine Вольфгангом Бауэром 9.0008
- Формула силы Лоренца на стене прямо напротив дома Лоренца в центре Лейдена. Архивировано 17 октября 2020 г. в Wayback Machine .
Электронный циклотронный резонанс — Химия твердого тела @Aalto
Перейти к концу метаданных
Электронный циклотронный резонанс — это движение электрона по винтовой траектории, возникающее из-за воздействия как магнитного поля, так и электромагнитного излучения. Он назван в честь циклотрона, ускорителя частиц, который использует колеблющееся электрическое поле, настроенное на резонансную частоту, для добавления кинетической энергии заряженным частицам, который был изобретен и запатентован Эрнестом О. Лоуренсом в 19 году.32 [1] . Резонансные явления в твердых телах широко изучались с 1940-х годов.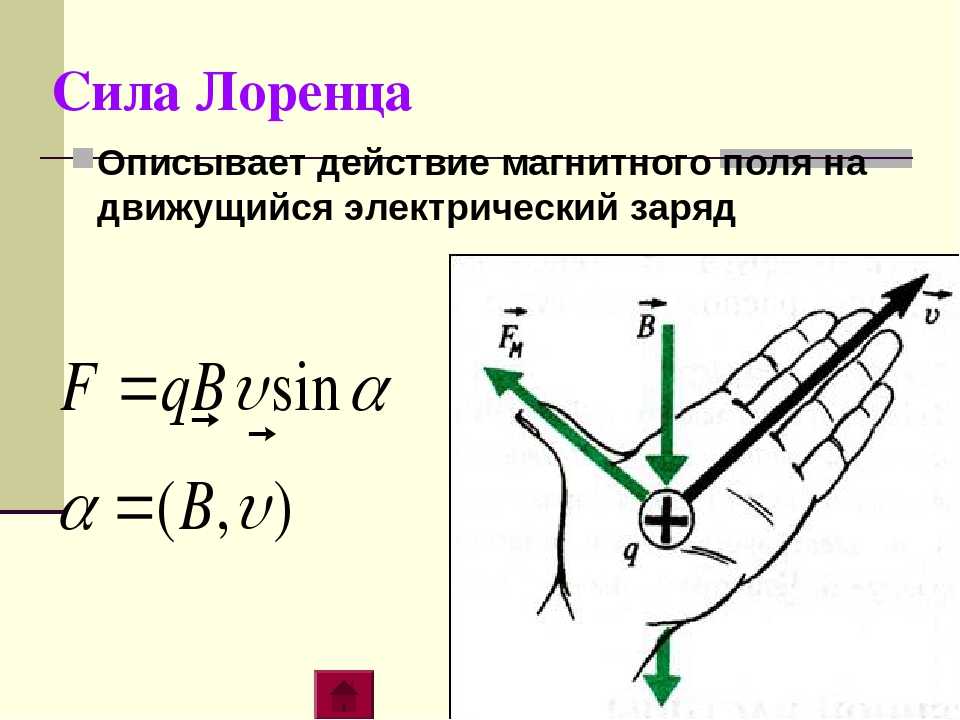 Циклотронный резонанс был впервые открыт физиками-ионосферниками и изучался в ионизированных газах, а также со свободными электронами [2] . Циклотронный резонанс показал свой огромный потенциал в качестве инструмента фундаментальных исследований. Многие исследователи рассматривали возможность проведения экспериментов по циклотронному резонансу на твердых телах. В 1951 году Дорфманн [3] опубликовал предложение о возможном применении циклотронного резонанса к твердым телам. Эксперименты с циклотронным резонансом в твердых телах дают очень разные типы информации. Эксперименты с циклотронным резонансом, проведенные в полупроводниках, продемонстрировали основные предсказания квантовой механики применительно к твердым телам. Результаты предоставили экспериментальные доказательства существования энергетических зон и эффективной массы электрона в твердом теле.
Циклотронный резонанс был впервые открыт физиками-ионосферниками и изучался в ионизированных газах, а также со свободными электронами [2] . Циклотронный резонанс показал свой огромный потенциал в качестве инструмента фундаментальных исследований. Многие исследователи рассматривали возможность проведения экспериментов по циклотронному резонансу на твердых телах. В 1951 году Дорфманн [3] опубликовал предложение о возможном применении циклотронного резонанса к твердым телам. Эксперименты с циклотронным резонансом в твердых телах дают очень разные типы информации. Эксперименты с циклотронным резонансом, проведенные в полупроводниках, продемонстрировали основные предсказания квантовой механики применительно к твердым телам. Результаты предоставили экспериментальные доказательства существования энергетических зон и эффективной массы электрона в твердом теле.
Циклотронный резонанс эффективно используется для определения эффективной массы носителей заряда и исследования зонных структур в полупроводниках. В 1953 г. были проведены первые исследования циклотронного резонанса в кристаллах германия и кремния G. Dresselhaus et al., 1953, 1955 [3] , Lax et al., 1953 [2] , которые в сочетании с Теория эффективной массы Латтингера и Кона, 1955. Они смогли успешно определить параметры края полосы для этих материалов с исключительной точностью. С тех пор это явление было исследовано в большом количестве элементарных и составных материалов, их сплавов и гетероструктур 9 .0019 [4] .
В 1953 г. были проведены первые исследования циклотронного резонанса в кристаллах германия и кремния G. Dresselhaus et al., 1953, 1955 [3] , Lax et al., 1953 [2] , которые в сочетании с Теория эффективной массы Латтингера и Кона, 1955. Они смогли успешно определить параметры края полосы для этих материалов с исключительной точностью. С тех пор это явление было исследовано в большом количестве элементарных и составных материалов, их сплавов и гетероструктур 9 .0019 [4] .
Если к материалу приложено однородное магнитное поле, электроны в материале будут двигаться по круговой траектории или по орбите под действием силы Лоренца. Это круговое движение, которое происходит за счет магнитного поля, известно как циклотрон. Когда электромагнитный сигнал подается на тот же материал, электроны, которые двигались по круговой траектории, будут ускоряться за счет поглощения энергии, и электроны будут двигаться по спиральной траектории [2] [4] .
На рис. 1 показана заряженная частица с эффективной массой m*, зарядом q, вращающаяся по винтовой траектории за счет магнитной силы- B и электромагнитного излучения [2] .
Рисунок 1. Заряженная частица движется по винтовой траектории (Рисунок: Wathsala Jayarathne).
Циклотронный резонанс — явление, когда частота электромагнитного излучения (осциллирующего электрического поля) совпадает с частотой вращения заряженной частицы.
Частота циклотронного резонанса может быть записана как 9{*} \ (1)
\end{уравнение} \)
В условиях циклотронного резонанса максимальная энергия будет поглощаться заряженной частицей.
Когда магнитное поле прикладывается к полупроводниковому материалу, и электроны, и дырки совершают циклотронное движение, противоположное по направлению из-за противоположных зарядов. Таким образом, различают две циклотронные частоты для электронов и дырок соответственно [3] 9{*} \ (3)
\end{уравнение} \)
Когда электромагнитное излучение воздействует на полупроводниковый материал извне, носители заряда в полупроводнике поглощают энергию.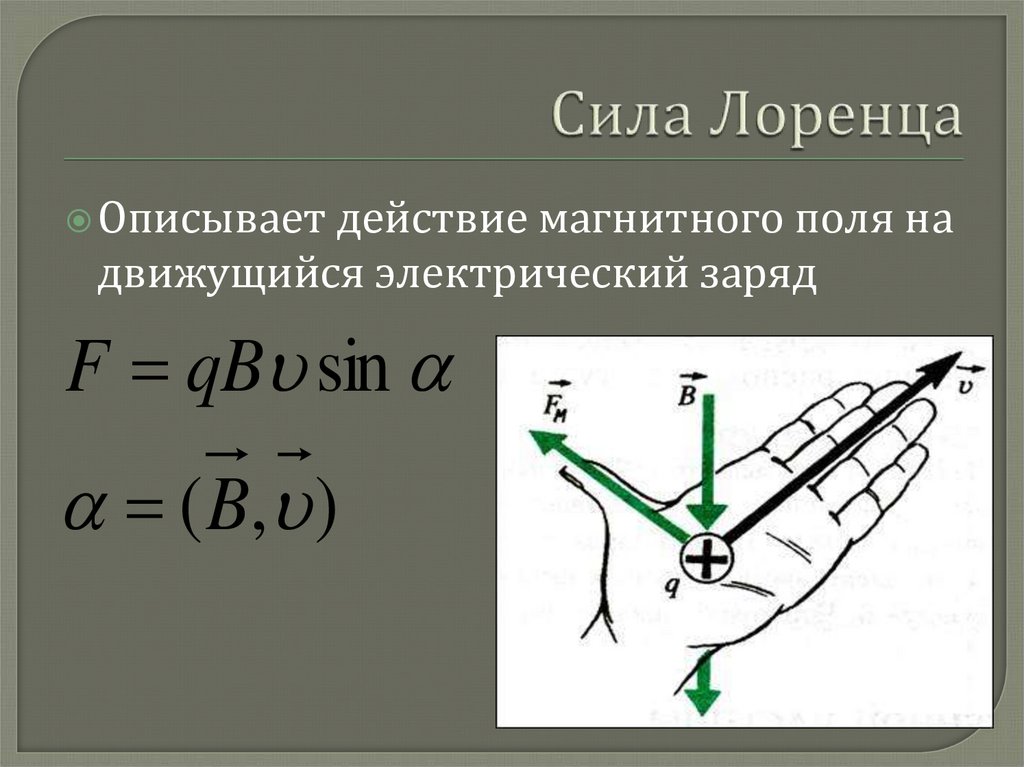 Максимальное поглощение или циклотронный резонанс будет иметь место, когда частота электромагнитного излучения будет равна либо ω ce , либо ω ch в зависимости от основных носителей заряда в полупроводнике. Эксперименты проводятся путем приложения магнитного поля и микроволнового излучения к определенному полупроводнику. Магнитное поле изменяется до тех пор, пока не будет достигнут резонанс. Спектр поглощенной энергии получен для характеристики полупроводника. Различные пики в спектрах поглощения указывают на наличие дырок и электронов. Эффективную массу носителей можно найти с помощью приведенных выше уравнений (2) и (3).
Максимальное поглощение или циклотронный резонанс будет иметь место, когда частота электромагнитного излучения будет равна либо ω ce , либо ω ch в зависимости от основных носителей заряда в полупроводнике. Эксперименты проводятся путем приложения магнитного поля и микроволнового излучения к определенному полупроводнику. Магнитное поле изменяется до тех пор, пока не будет достигнут резонанс. Спектр поглощенной энергии получен для характеристики полупроводника. Различные пики в спектрах поглощения указывают на наличие дырок и электронов. Эффективную массу носителей можно найти с помощью приведенных выше уравнений (2) и (3).
Экспериментальная процедура
Полупроводники, используемые для эксперимента, представляют собой чистые образцы. Типичный образец представляет собой диск диаметром около 3 мм и толщиной около 0,5 мм. Образцы обычно готовили путем грубой резки из монокристалла, шлифования абразивами и травления поверхности в течение нескольких минут в травителе, состоящем из 1 куб. см HF, 1 куб. ) и 4 см3 H 2 O [3] .
см HF, 1 куб. ) и 4 см3 H 2 O [3] .
Эксперименты проводятся в основном с использованием микроволнового излучения и сильных магнитных полей. В ходе эксперимента также используется низкая температура для уменьшения рассеяния и тепловых колебаний решетки. Низкие температуры обеспечиваются жидким гелием. Варьируется магнитное поле и получается спектр поглощения в зависимости от магнитного поля.
Спектр циклотронного поглощения
На рис. 2 показаны результаты циклотронного резонанса в кремнии при ω = 24 ГГц и T = 4K. Магнитное поле приложено в плоскости (110) на 30 0 от оси [100]. [3] .
Рис. 2. Спектр поглощения циклотронного резонанса в кремнии (рис.: Wathsala Jayarathne).
Согласно спектру поглощения для электронов имеются два резонансных пика, что соответствует продольной массе ( м 9049{-1/2} \ (4)
\end{уравнение} \)
m c * обозначает эффективную массу, когда магнитное поле составляет угол θ с продольной осью энергетической поверхности.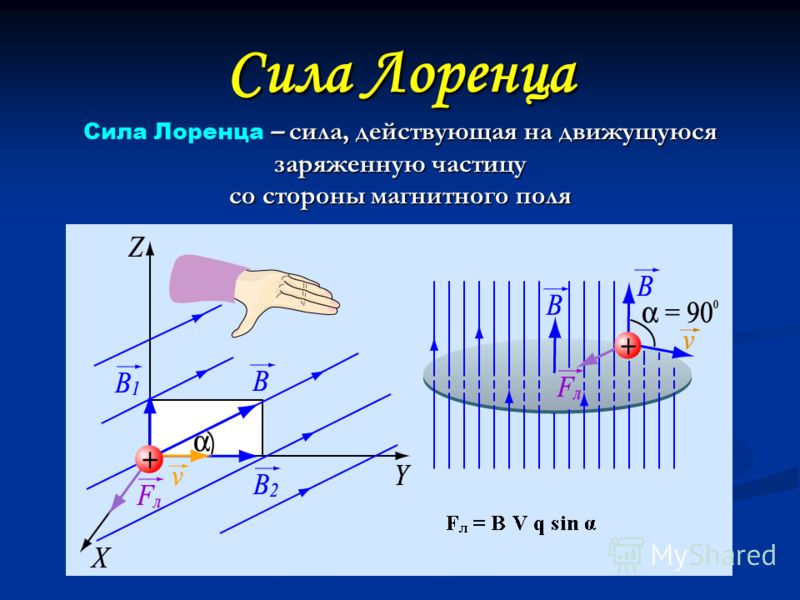
Магнитное поле образует разные углы с продольной осью энергетической поверхности при изменении направления от [001] к направлению [110], что приводит к различным резонансным пикам в спектре поглощения. Каждый резонансный пик приводит к различной эффективной массе. Путем подгонки данных поглощения к уравнению Шокли было получено, что M L = 0,97 M 0 и M T = 0,19 M 0 , где M 0 .
На рис. 3 показаны результаты циклотронного резонанса в германии при ω = 24 ГГц и T = 4K. Магнитное поле приложено в точке (110) на расстоянии 60 0 от оси [100]. [3] .
Рис. 3. Спектр поглощения циклотронного резонанса в германии (рис.: Wathsala Jayarathne).
Для германия было получено, что M L = 1,58 M 0 и M T = 0,082 M T = 0,082 M T = 0,082 M 9. 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9.9085 9085 9085 9.9085 9085 9. . события рассеяния из-за примесей и несовершенств. Заряженные частицы в полупроводниках должны совершить несколько круговых орбиталей, позволяющих сформировать циклотрон, прежде чем подвергнуться рассеянию. Если есть примеси, трудно определить, происходит ли поглощение от носителей заряда или от примесей [2] .
9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9085 9.9085 9085 9085 9.9085 9085 9. . события рассеяния из-за примесей и несовершенств. Заряженные частицы в полупроводниках должны совершить несколько круговых орбиталей, позволяющих сформировать циклотрон, прежде чем подвергнуться рассеянию. Если есть примеси, трудно определить, происходит ли поглощение от носителей заряда или от примесей [2] .
Важность анизотропии эффективных масс кремния и германия требует получения данных в зависимости от ориентации кристалла. Образец, вырезанный поверхностью в плоскости (110), ориентированный таким образом, чтобы приложенное поле можно было направить вдоль направлений [001], [110] и [111] путем вращения образца [3] .
Чтобы проверить знак носителей заряда, этот эксперимент можно провести с использованием микроволн с круговой поляризацией. Поглощение можно наблюдать только тогда, когда направление круговой поляризации соответствовало направлению вращения носителей заряда.
Помимо изучения зонных структур полупроводников, явление электронного циклотронного резонанса используется в ряде других областей.
Ионный циклотронный резонанс (ICR)
Концепция электронного циклотрона преобразована в ионный циклотронный резонанс для использования в различных исследовательских экспериментах. Ионный циклотронный резонанс возникает, когда ионы, вращающиеся в магнитном поле, резонируют с внешним электрическим полем. Масс-спектрометрия с ионным циклотронным резонансом с преобразованием Фурье (FTICR) является широко используемым методом характеризации, основанным на концепции ICR [6] .
Масс-спектрометрия ионного циклотронного резонанса с преобразованием Фурье представляет собой тип масс-анализатора, используемый для определения отношения массы к заряду ионов на основе явлений циклотронного резонанса ионов. Это используется для изучения систем с большим отношением массы к заряду или систем, которые имеют очень сложные изотопные структуры и химические характеристики природных сложных смесей.
Метод возбуждения в плазменной технике
Другим важным преимуществом является использование циклотронного резонанса в качестве передового метода возбуждения в плазменной технике [7] . Здесь ионы производятся в удерживаемой магнитом плазме, которая нагревается микроволнами с использованием эффекта резонанса. Производительность источника ионов играет решающую роль во многих областях техники. Несколько примеров упомянуты ниже.
- Усовершенствованное производство полупроводников
- Усовершенствованное лечение рака
- Электрические двигательные установки для космических кораблей
- Для ускорителей частиц, онлайн-разделения масс и воспроизводства заряда радиоактивных ионов
| 1. | 1 https://en.wikipedia.org/wiki/Циклотрон |
| 2. | 1 2 3 4 5 Б. |
| 3. | 1 2 3 4 5 6 7 Г. Дрессельхаус, А. Кип и К. Киттель, Циклотронный резонанс электронов и дырок в кристаллах кремния и германия, Physical Review , 1955 , 98 , 368-384, (DOI: 10.1103/physrev.98.368). |
| 4. | 1 2 3 Д. Хилтон, Т. Арикава и Дж. Коно, Циклотронный резонанс, Характеристика материалов , 2012 (DOI: 10.1002/0471266965.com068.pub2). |
| 5. | 1 Х. Эль-Саба Мухаммад, Электронные инженерные материалы и нанотехнологии, Hakim Press, 2014 |
6. |


 315, цв. 1 .
315, цв. 1 . и рис. 15,5 × 24 см ( ISBN 2-7381-1578-0 , EAN 9782738115782 , OCLC 300488981 , уведомление BnF п о FRBNF39927635 , SUDOC 08469470X , онлайн презентации , читать онлайн ) , св Лоренц (сила де), стр. 391–392.
и рис. 15,5 × 24 см ( ISBN 2-7381-1578-0 , EAN 9782738115782 , OCLC 300488981 , уведомление BnF п о FRBNF39927635 , SUDOC 08469470X , онлайн презентации , читать онлайн ) , св Лоренц (сила де), стр. 391–392. ( 1- е изд. ), 1 т. , X -956 с. , плохо. и рис. 17 × 24 см ( ISBN 978-2-8073-0744-5 , EAN 9782807307445 , OCLC 1022951339 , уведомление BnF п О FRBNF45646901 , SUDOC 224228161 , онлайн презентации , читать онлайн ) , св сила Лоренца де, стр.
( 1- е изд. ), 1 т. , X -956 с. , плохо. и рис. 17 × 24 см ( ISBN 978-2-8073-0744-5 , EAN 9782807307445 , OCLC 1022951339 , уведомление BnF п О FRBNF45646901 , SUDOC 224228161 , онлайн презентации , читать онлайн ) , св сила Лоренца де, стр. 315, цв. 1.
315, цв. 1. Хотя в этих областях физики фактически и применялись разнообразные объекты, идентифицируемые нынешней математикой как векторы, в физической терминологии это получило очень малый отклик (так например, преобразование Фурье в классической электродинамике и классической теории сплошных сред весьма интенсивно применяется, но традиционно почти не рассматривается в контексте классической с использованием слова «вектор» применительно к функциям, хотя с математической точки зрения это было бы вполне законно[3]). Пожалуй, единственным заметным исключением из правил является достаточно свободное оперирование векторами элементов фазового или конфигурационного пространств[4].
Хотя в этих областях физики фактически и применялись разнообразные объекты, идентифицируемые нынешней математикой как векторы, в физической терминологии это получило очень малый отклик (так например, преобразование Фурье в классической электродинамике и классической теории сплошных сред весьма интенсивно применяется, но традиционно почти не рассматривается в контексте классической с использованием слова «вектор» применительно к функциям, хотя с математической точки зрения это было бы вполне законно[3]). Пожалуй, единственным заметным исключением из правил является достаточно свободное оперирование векторами элементов фазового или конфигурационного пространств[4].
 Все это позволило сохранить термину «вектор», пожалуй, своё основное значение — значение 4-векторa. Именно этот смысл вкладывается в термины векторное поле, векторная частица (векторный бозон, векторный мезон). Сопряжённое значение в подобных терминах имеет и слово «скалярный».
Все это позволило сохранить термину «вектор», пожалуй, своё основное значение — значение 4-векторa. Именно этот смысл вкладывается в термины векторное поле, векторная частица (векторный бозон, векторный мезон). Сопряжённое значение в подобных терминах имеет и слово «скалярный». [8]
[8]

 д.
д.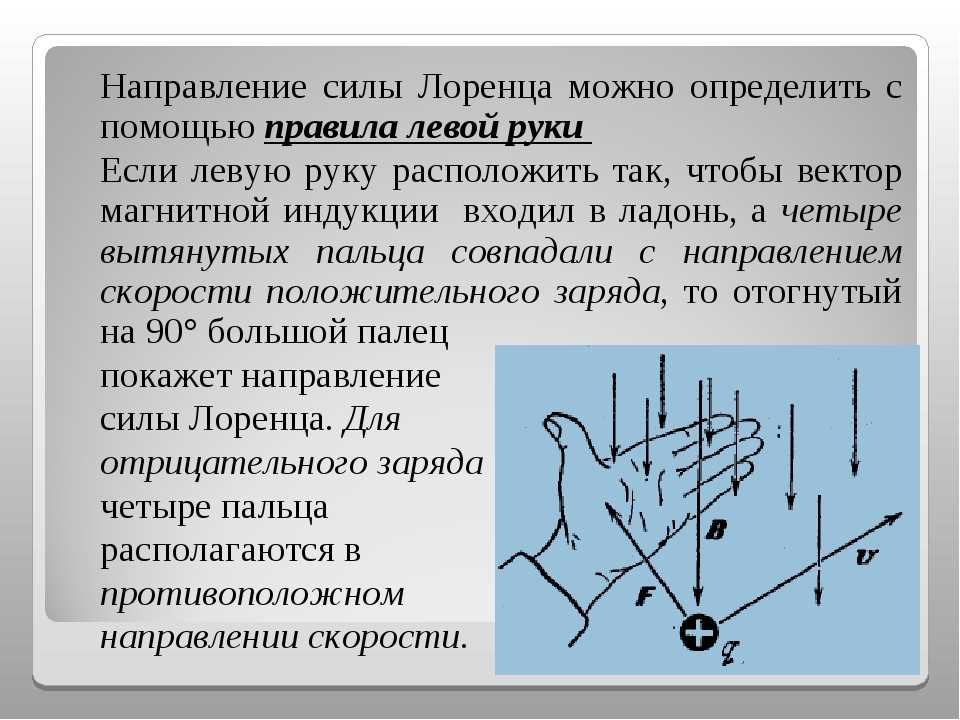 r = 20\text{ см}.r=20 см.
r = 20\text{ см}.r=20 см.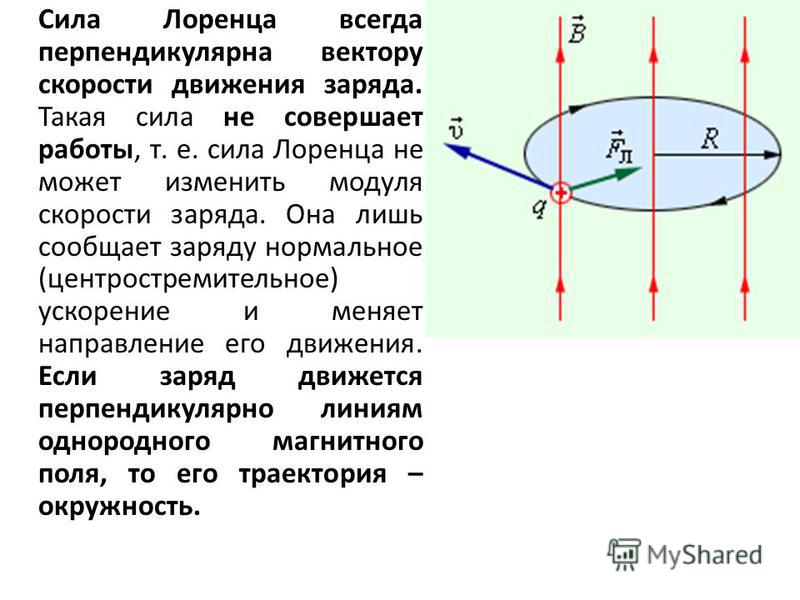 ; Сэндс, Мэтью Л. (2006). Фейнмановские лекции по физике (3 тома) . Пирсон / Эддисон-Уэсли. ISBN 0-8053-9047-2 . : том 2.
; Сэндс, Мэтью Л. (2006). Фейнмановские лекции по физике (3 тома) . Пирсон / Эддисон-Уэсли. ISBN 0-8053-9047-2 . : том 2. также домашнюю страницу
также домашнюю страницу Лакс, Cyclotron Resonance, Science, 1979 , 134, 1333-1340 (DOI: 10.1126/science.134.3487.1333).
Лакс, Cyclotron Resonance, Science, 1979 , 134, 1333-1340 (DOI: 10.1126/science.134.3487.1333).