Электричество и магнетизм

Если начальная скорость заряженной частицы v перпендикулярна магнитному полю В, то в этом случае частица под действием силы Лоренца будет двигаться по окружности постоянного радиуса R (рис. 5.13)

(5.6)

Рис. 5.13. Движение отрицательно заряженной частицы в однородном магнитном поле 

Сила Лоренца F_L, направленная по радиусу к центру окружности, вызывает радиальное ускорение. По второму закону Ньютона имеем

следовательно, можем записать уравнение

(5.7)

из которого легко получить выражение для угловой скорости частицы

(5. 8)

Если q, m и B — постоянные величины, то угловая скорость, а следовательно, и период

(5.9)

тоже являются постоянными величинами, не зависящими от энергии частицы. От скорости движения частицы зависит только радиус орбиты

(5.10)

Сила Лоренца создает только нормальное ускорение и, соответственно, направлена к центру окружности. Следовательно, направление вращения положительно заряженной частицы таково, что вращающийся в том же направлении винт будет двигаться против направления поля. Отрицательно заряженная частица вращается в противоположном направлении (см.  рис. 5.14, 5.15).

Рис. 5.14. Движение положительно и отрицательно заряженных частиц в однородном магнитном поле.
Направление магнитного поля указано точками 

Если начальная скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю. Частица будет продолжать двигаться в том же направлении прямолинейно и равномерно. 

Наконец, в общем случае можно представить себе, что частица влетает в область однородного магнитного поля со скоростью v, составляющей угол q с направлением магнитного поля. Эту скорость можно разложить на компоненту две составляющих, одна из которых

направлена вдоль поля, а вторая

перпендикулярна полю. Соответственно, движение частицы является суммой двух движений: равномерного вдоль поля со скоростью  и вращения по окружности с угловой скоростью  . Траектория частицы, таким образом, является спиралью с радиусом R и шагом h (рис.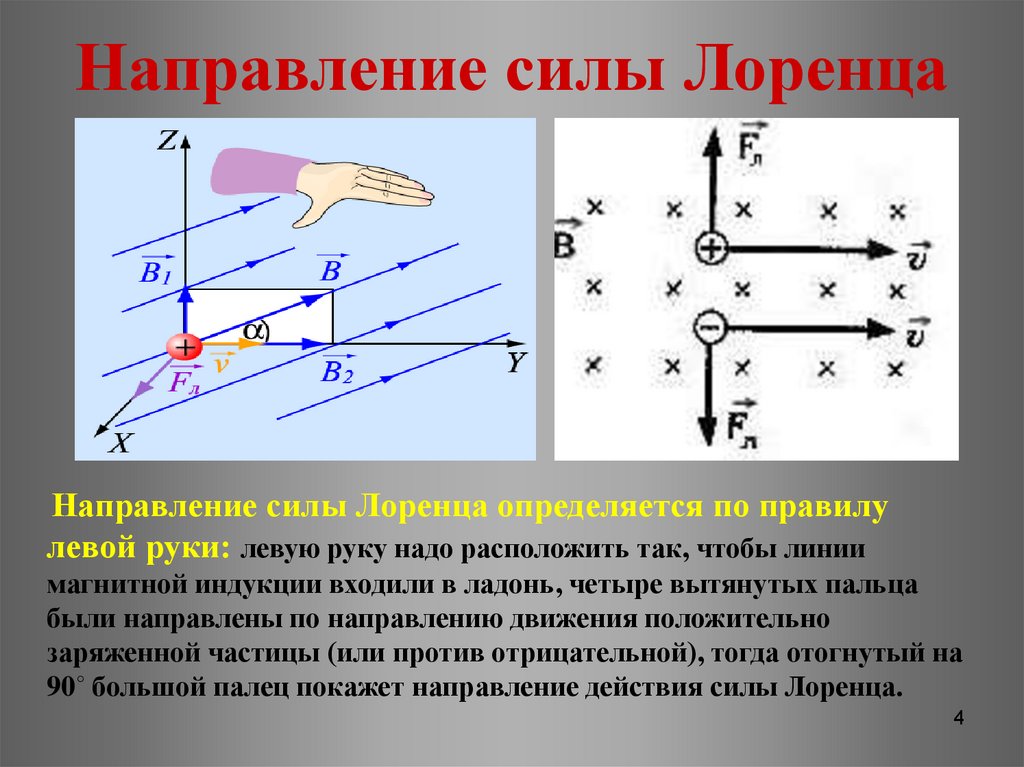 5.15):

(5.11)

 

Рис. 5.15. Движение заряженной частицы по спирали в однородном магнитном поле 

Пример. В однородном магнитном поле с индукцией 2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом 10 см и шагом 60 см. Определить скорость и кинетическую энергию протона. Какую ускоряющую разность потенциалов U  прошел протон перед тем, как влететь в магнитное поле?

Решение. Из уравнений (5.11) находим угол между скоростью протона и полем

(5.12)

откуда

(5. 13)

Кинетическая энергия протона будет

(5.14)

Мы могли использовать нерелятивистскую формулу для энергии, так как скорость протона много меньше скорости света.

Если протон ускорялся электрическим полем, то при прохождении разности потенциалов

U он приобрел энергию eU. Отсюда находим разность потенциалов

(5.15)

 

Джоуль — слишком большая энергия в мире элементарных частиц. Здесь используют внесистемную единицу — электронвольт (эВ).  

Электрон-вольт (эВ) — это внесистемная единица энергии, численно равная энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов 1 В

Она удобна тем, что любая другая частица с зарядом по модулю равным заряду электрона, ускоренная разностью потенциалов в 3,66 МэВ, как в нашем примере, имеет кинетическую энергию 3,66 МэВ (мегаэлектронвольт).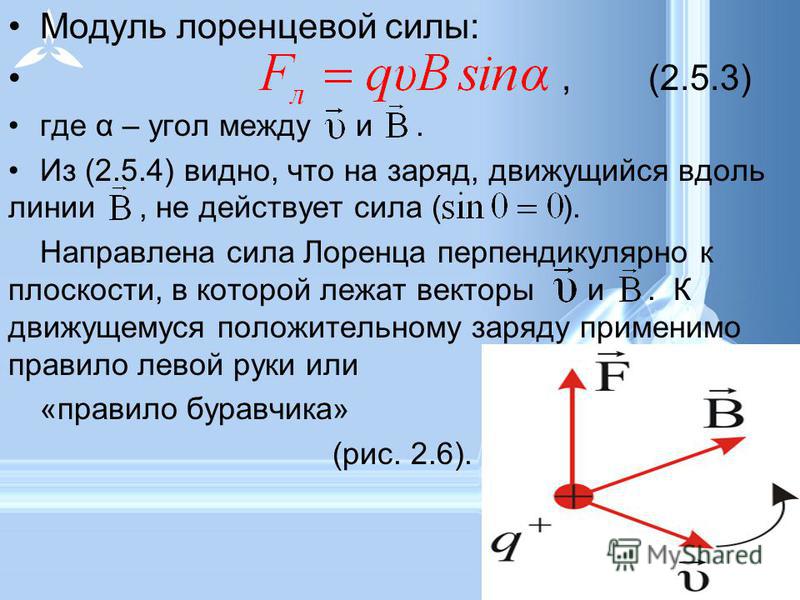

Сила Лоренца (эл. И магн. Часть). Закон Ампера. Действие магнитного поля на движущийся заряд. Сила Лоренца

Электрический ток – это совокупность упорядоченно движущихся заряженных частиц. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника.

Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют

силой Лоренца.

Модуль силы Лоренца равен отношению модуля силы Ампера, действующей на участок проводника, к числу заряженных частиц в этом участке проводника:

Сила Ампера равна , сила тока равна(см. стр. 12). Подставив эти выражения в формулу для силы Лоренца, получим:

где — угол между векторами скорости и магнитной индукции.

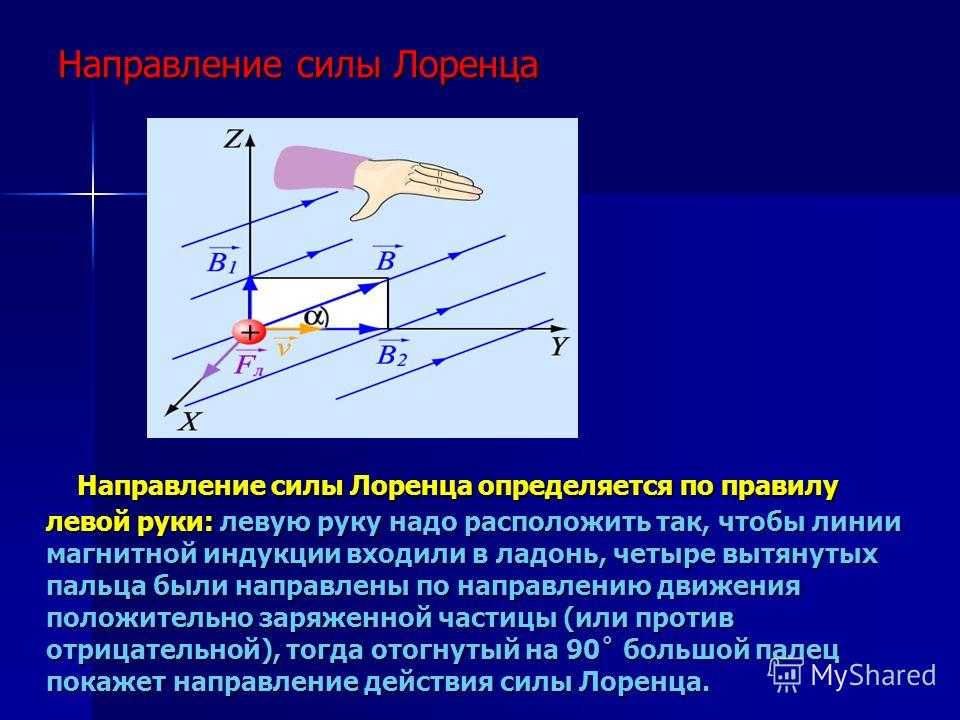
Направление силы Лоренца определяют для положительного заряда по правилу левой руки.

(Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону).

Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. А, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.

Закон Ампера

Поместим в магнитное поле проводник длинной l, по которому течет ток I. На проводник действует сила, прямо пропорциональная силе тока, текущего по проводнику, индукции магнитного поля, длине проводника, и зависящая от ориентации проводника в магнитном поле. |F|=IB

lsin, где  — угол между направлением тока в проводнике и направлением вектора магнитной индукции B, Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, что магнитные силовые линии входят в ладонь, четыре вытянутых пальца направить по току, то отогнутый большой палец укажет направление силы. Очевидно, что сила Ампера равна нулю, если проводник расположен вдоль силовых линий поля и максимальна, если проводник перпендикулярен силовым линиям. Движение заряженных частиц в магнитном поле. На проводник с током в магнитном поле действует сила Ампера F

А IBlsin.Ток, в свою очередь, это направленное движение заряженных частиц. Сила тока равна I=qnvS, где q – заряд частицы, n-концентрация движущихся заряженных частиц, v-средняя скорость их направленного движения, S-площадь поперечного сечения проводника. Подставив I в выражение для F_А, получим F_А= qnvSBlsin, где nsl=N – общее число частиц, создающих ток. Тогда сила, действующая на отдельный движущийся заряд – сила Лоренца, равна Fл=qvBsin. где  — угол между векторами скорости и магнитной индукции. Направление силы Лоренца определяется для положительно заряженной частицы по правилу левой руки.

Закон Ампера

Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.

Экспериментальное изучение магнитного взаимодействия показывает, что модуль силы Ампера пропорционален длине проводника с током, силе тока и зависит от ориентации проводника в магнитном поле.

Опыт показывает, что магнитное поле, вектор индукции которого направлен вдоль проводника с током, не оказывает влияния на ток. Поэтому модуль силы зависит лишь от модуля составляющей вектора магнитной индукции, перпендикулярной проводнику.

Закон Ампера заключается в следующем. Сила Ампера равна произведению магнитной индукции поля на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника:

Направление силы ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая магнитной индукции входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 большой палец покажет направление силы, действующей на отрезок проводника.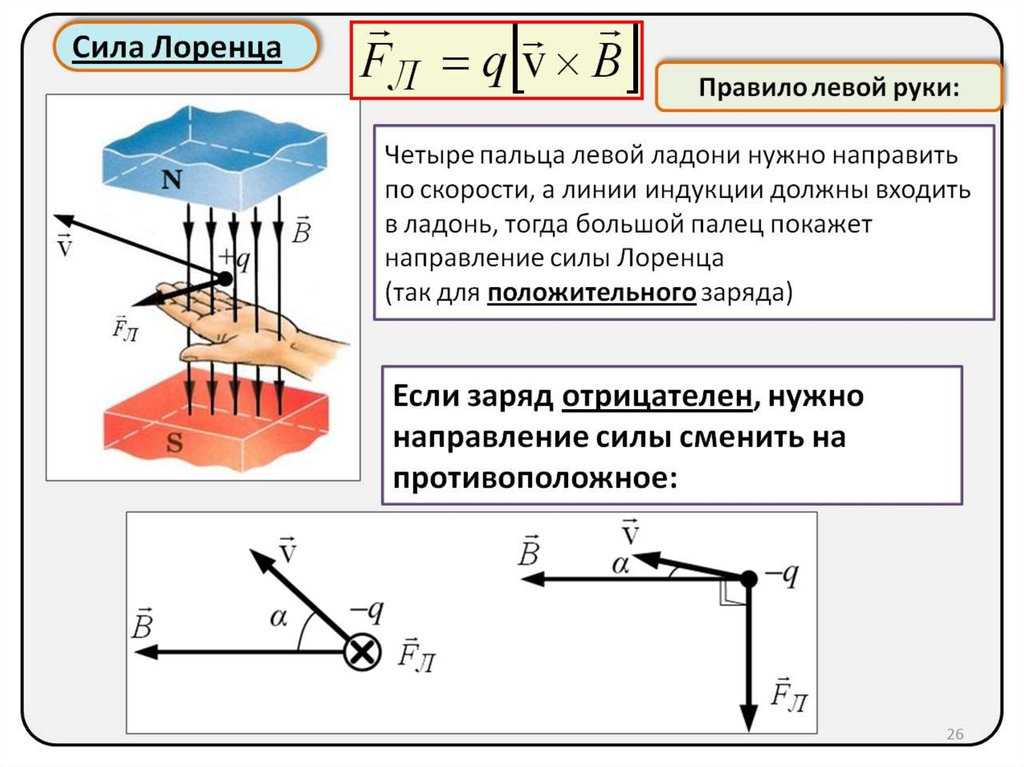

Магнитное взаимодействие проводников с током используется в Международной системе для определения единицы сила тока –ампера.

Ампер –сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывал бы между этими проводниками силу магнитного взаимодействия, равную Н на каждый метр длины.

электромагнетизм — Почему сила равна нулю, когда скорость параллельна магнитному полю

спросил 6 лет, 2 месяца назад

Изменено 6 лет, 2 месяца назад

Просмотрено 5к раз

$\begingroup$

Для меня не имеет смысла, что когда заряд движется параллельно магнитному полю, сила, действующая на заряд магнитным полем, равна нулю специальная теория относительности, так почему же заряд не испытывает силы 9?0005

• электромагнетизм
• специальная теория относительности
• лоренц-симметрия

$\endgroup$

1

$\begingroup$

B-поле действует на движущийся заряд в направлении, перпендикулярном B-полю.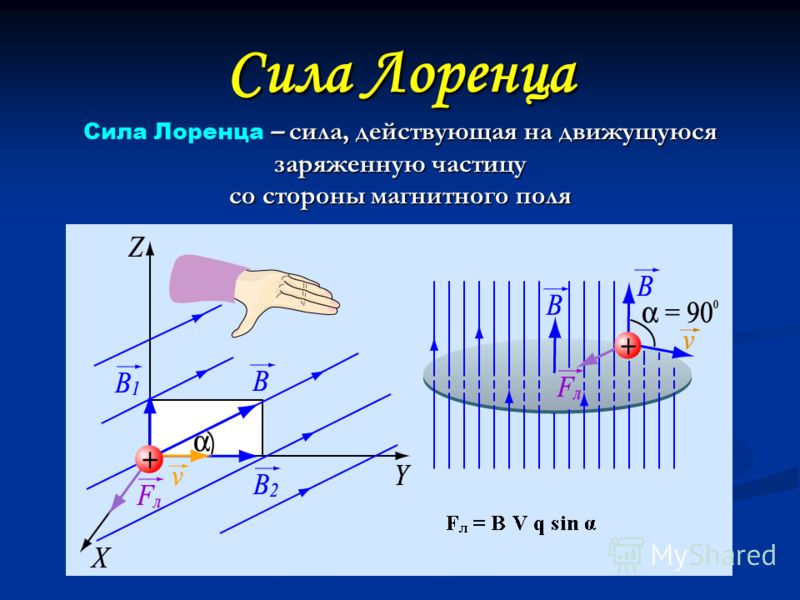 Если поле B и скорость заряда имеют одно и то же направление, то невозможно различить какое-либо одно направление результирующего сила (существует разброс перпендикулярных направлений на 360 градусов). Таким образом, единственный вектор силы, который не имеет направления, должен быть правильным ответом (то есть нулевой силой).

B-поле воздействует на движущийся заряд в направлении, перпендикулярном движению заряда. По аналогии с вышеизложенным, это также означает сила должна быть равна нулю, когда B и скорость заряда параллельны.

$\endgroup$

2

$\begingroup$

Вы спросите, почему это происходит, и я расскажу вам, как это происходит. Я полагаю, вы знаете, что электрон обладает неотъемлемыми свойствами магнитного дипольного момента и спина. Это вращение из-за Эйнштейна-де Хааза- эксперимент ведет себя как гироскоп, если ось вращения и внешняя сила не соосны, гироскоп движется перпендикулярно как оси, так и направлению силы.

Внешнее магнитное поле в любом случае (стационарном заряде, не параллельном или параллельном этому полю движущемся заряде) будет выравнивать магнитный дипольный момент электронов. В случае стационарного или параллельного однородному магнитному полю больше ничего не происходит.

В другом случае непараллельно движущихся зарядов в игру вступает гироскопический эффект, отклоняющий частицу, который равен ускорению частицы. Как известно, ускорение электронов сопровождается испусканием фотонов, и это действительно наблюдаемый факт. Поскольку излучение фотонов отклоняет магнитный диполь электронов от внешнего поля, мы получаем циклический процесс. В результате получается спиральная дорожка (из мандариновых долек).

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

электромагнетизм — Всегда ли работа, совершаемая магнитным полем, равна нулю?

спросил 1 год, 5 месяцев назад

Изменено 1 год, 5 месяцев назад

Просмотрено 1к раз

$\begingroup$

В этом случае ток течет в прямом направлении, из-за чего сила магнитного поля действует вправо и стержень движется вправо.

Здесь, в этом случае, я говорю, что сила, вызывающая движение, связана с магнитным полем, и движение также происходит в его направлении, но все время во всех местах я слышал и читал, что «Работа, совершаемая магнитным полем, всегда равна нулю». Если вы говорите, что утверждение верно, то не могли бы вы помочь мне найти решение.

• электромагнетизм
• магнитные поля
• электрический ток
• работа

$\endgroup$

$\begingroup$

читал, что «Работа, совершаемая магнитным полем, всегда равна нулю»

Это заблуждение/неправда в целом. В макроскопической физике (макроскопических) магнитных сил совершают работу , например, магнитная сила из-за внешнего поля, действующего на проводник с током $BIL$, работает, когда проводник движется (например, в вашем примере), а также эта сила может совершать работа с магнитными телами, такими как железные/стальные тела или магниты.

Однако в приведенном утверждении есть доля истины: работа магнитной силы, действующей на движущуюся точечную заряженную частицу (так называемая сила Лоренца), всегда равна нулю, поскольку сила всегда перпендикулярна скорости.

Это согласуется с макроскопической физикой, потому что работа макроскопической магнитной силы на движущийся проводник с током или магнитное тело представляет собой просто сумму работ сил Лоренца, вызванных внешним магнитным полем; здесь также участвуют индуцированные внутренние силы между заряженными частицами, образующими ток, и остальной частью проводника, и они выполняют работу.