|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного… Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж… Интересное: Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления. Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
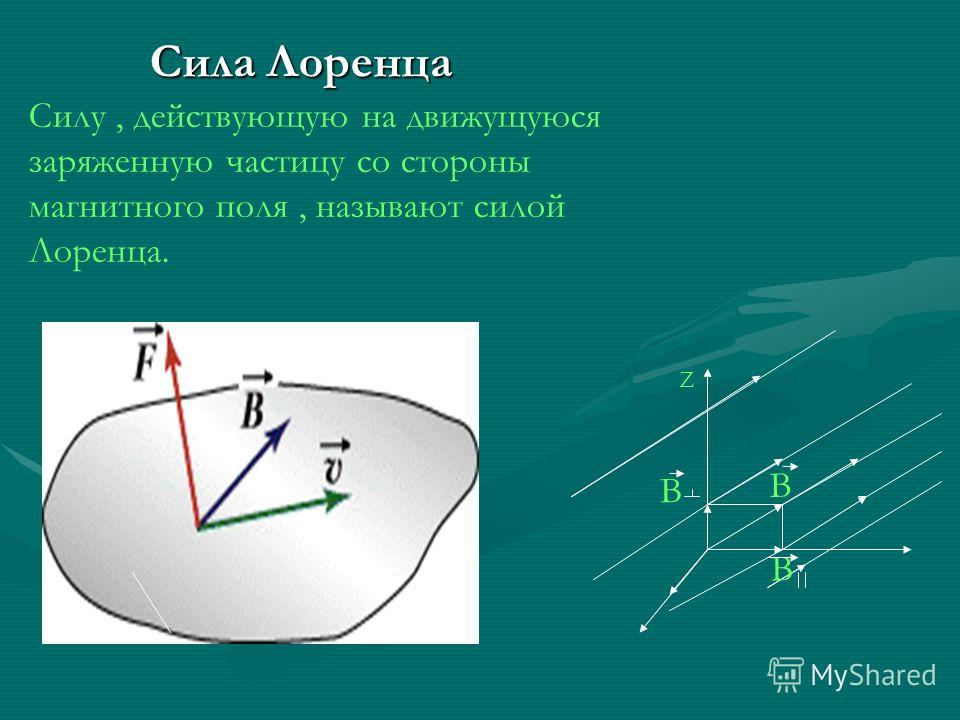
⇐ ПредыдущаяСтр 4 из 7Следующая ⇒ Своё название сила получила в честь выдающегося голландского физика Хендрика Антона Лоренца — основателя электронной теории строения вещества.
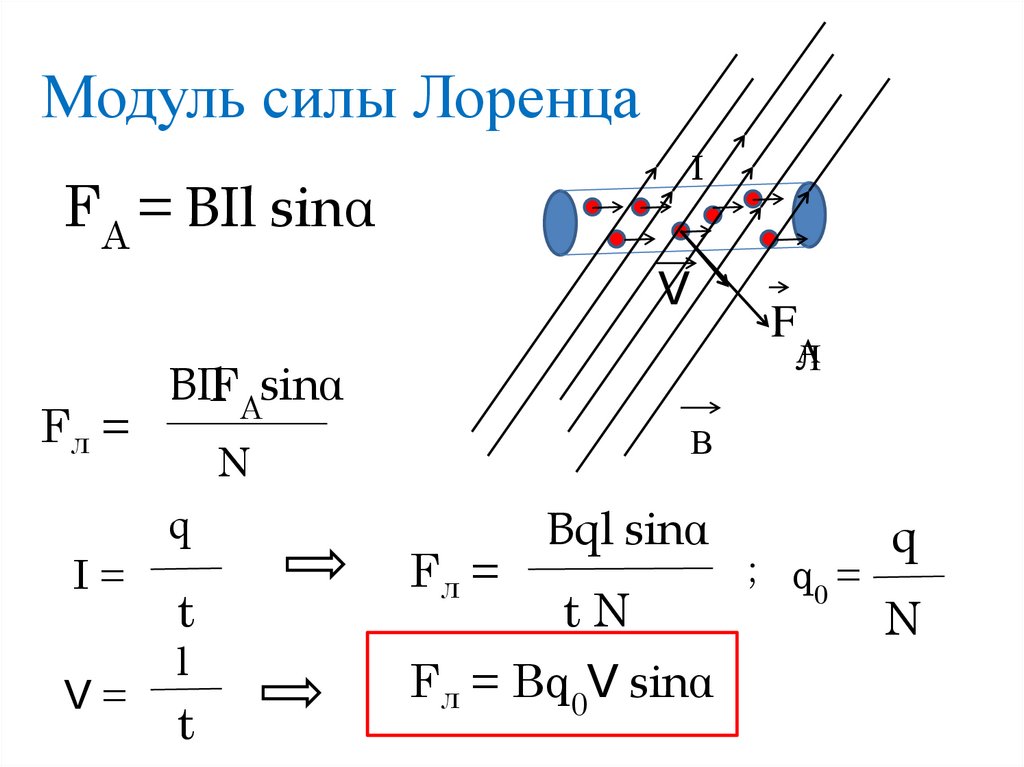
Модуль силы Лоренца определяется отношением силы Ампера, действующей на участок проводника, находящийся в магнитном поле, к числу заряженных частиц, упорядоченно движущихся в этом участке проводника: Давайте с вами рассмотрим прямолинейный участок проводника с током длиной Δl и площадью поперечного сечения S. При этом будем считать, что длина участка проводника и его площадь поперечного сечения настолько малы, что вектор магнитной индукции поля можно считать одинаковым в пределах этого участка проводника. Итак, на участок проводника с током, находящимся в магнитном поле, действует сила Ампера, модуль которой равен произведению силы тока, модуля вектора магнитной индукции, длины отрезка проводника и синуса угла между направлениями вектора магнитной индукции и элемента тока: Теперь давайте с вами вспомним, что сила тока в проводнике определяется зарядом, прошедшим через поперечное сечение проводника за единицу времени: Здесь ∆t — это промежуток времени, за который заряженная частица проходит участок проводника длиной ∆l. Пусть модуль заряда одной частицы равен q. Тогда суммарный заряд всех частиц равен произведению модуля заряда одной частицы на общее число частиц в выбранном участке проводника: Перепишем уравнение для силы тока с учётом последнего равенства. Полученное равенство подставим в закон Ампера: Обратите внимание на отношение ∆l/∆t — это есть не что иное, как модуль средней скорости заряженной частицы, упорядоченно движущейся в магнитном поле внутри проводника: Теперь подставим полученное выражение для силы Ампера в формулу для силы Лоренца: После упрощения получим, что модуль силы Лоренца равен произведению заряда частицы, модуля её средней скорости, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и вектором скоростью движения частицы: Направление силы Лоренца определяют по правилу левой руки: если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости упорядоченного движения заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (или против движения отрицательного заряда), то отогнутый на 90о большой палец укажет направление действующей на заряд силы Лоренца. Анализ данного правила позволяет нам утверждать, что сила Лоренца, действующая на движущуюся в магнитном поле частицу, перпендикулярна вектору скорости этой частицы. Следовательно, сила Лоренца Вид траектории заряженной частицы в магнитном поле зависит от угла между скоростью влетающей в поле частицы и магнитной индукцией. Рассмотрим такую ситуацию. Пусть протон, ускоренный разностью потенциалов U влетает в однородное магнитное поле сначала параллельно линиям индукции, затем — перпендикулярно, и, наконец, под некоторым углом к ним. Индукция магнитного поля равна 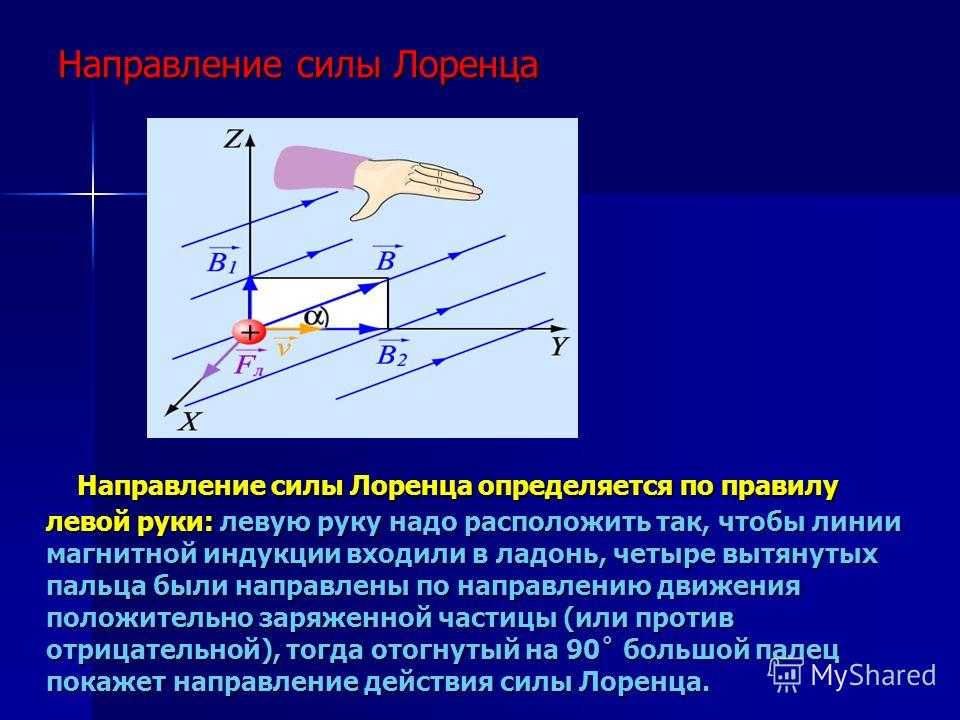 Для каждого случая определите радиус кривизны траектории протона и период его обращения. Для каждого случая определите радиус кривизны траектории протона и период его обращения.Итак, рассмотрим первый случай, когда протон, двигаясь по силовой линии в электрическом поле ускоренно, приобретает скорость, с которой влетает в однородное магнитное поле так, что его вектор скорости направлен вдоль поля (или противоположно направлению индукции магнитного поля). Очевидно, что в этом случае угол между направлением вектора скорости и индукции магнитного поля либо равен нулю, либо 180 Тогда, согласно формуле, сила Лоренца, действующая на протон, равна нулю и частица будет продолжать двигаться равномерно прямолинейно. Теперь рассмотрим второй случай, когда протон влетает в однородное магнитное поле перпендикулярно линиям его индукции. В этом случае на протон в магнитном поле действует сила Лоренца, направленная перпендикулярно вектору скорости (направление силы Лоренца определяем по правилу левой руки). Как мы уже выяснили, сила Лоренца не может изменить модуль скорости заряженной частицы — она лишь меняет её направление. С другой стороны, такое движение заряженной частицы в магнитном поле будет подчиняться второму закону Ньютона: И нам осталось рассмотреть последний случай, когда частица влетает в магнитное поле под заданным углом к силовым линиям. Подобное явление происходит в магнитном поле Земли. Движущиеся с огромными скоростями заряженные частицы из космоса «захватываются» магнитным полем Земли и образуют вокруг неё радиационные пояса. В них заряженные частицы перемещаются по винтообразным траекториям между северным и южным магнитными полюсами. И только в полярных областях небольшая часть частиц вторгается в верхние слои атмосферы, вызывая восхитительные полярные сияния. В заключении урока отметим, что действие магнитного поля на движущийся заряд широко используется в технике. Сила Лоренца используется и в циклотронах — особых ускорителях заряженных частиц. Обычный циклотрон состоит из двух полых полуцилиндров разного диаметра (дуантов), находящихся в однородном магнитном поле. Его принцип действия достаточно прост. В зазоре между цилиндрами находится заряженная частица. В этом зазоре создаётся переменное электрическое поле с постоянным периодом, равным периоду обращения частицы. Это поле каждые пол периода разгоняет частицу, увеличивая при этом радиус её обращения (период обращения частицы не увеличивается). На последнем витке частица вылетает из циклотрона. Действие силы Лоренца используют и в масс-спектрографах — устройствах, предназначенных для разделения частиц по их удельным зарядам, то есть по отношению заряда частицы к её массе, и по полученным результатам точно определять массы частиц. За диафрагмой создаётся постоянное магнитное поле, заставляющее заряженные частицы двигаться по окружности, радиус кривизны которой можно измерить, поставив на пути частиц фотопластинку. Так как скорость частиц одинакова и определяется постоянной прибора, то, зная заряд ионов, можно легко определить их массу. Ещё одно устройство, в котором применяется действие силы Лоренца — это ТОКАМАК (тороидальная камера с магнитными катушками).
В нём плазма (напомним, что это частично или полностью ионизированный газ) удерживается в специально создаваемом сильном магнитном поле. Домашнее задание сфотографировать или скан и прислать на почту helen . mails @ mail . ru Сила Лоренца Цель – Углубить и закрепить полученные знания по теме – сила Лоренца Задачи урока 1. Изучить силу Лоренца 2.Закрепить знания при решении задач (тестирование) ⇐ Предыдущая1234567Следующая ⇒ Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого. |
Сила Лоренца
Содержание статьи
1. Определение силы магнитной силы
2. Направление магнитной силы
3. Свойства силы магнитной силы
4. Сила Лоренца
Определение силы магнитной силы
Определение
Если заряд движется в магнитном поле, то на него действует сила ($\overrightarrow{F}$), которая зависит от величины заряда (q), скорости движения частицы ($\overrightarrow{v}$) относительно магнитного поля, и индукции магнитного поля ($\overrightarrow{B}$). Эта сила была установлена экспериментально, называется она магнитной силой.
И имеет в системе СИ вид:
\[\overrightarrow{F}=q\left[\overrightarrow{v}\overrightarrow{B}\right]\ \left(1\right).\]
Модуль силы в соответствии с (1) равен:
\[F=qvBsin\alpha \ \left(2\right),\]
где $\alpha $ — угол между векторами $\overrightarrow{v\ }и\ \overrightarrow{B}$.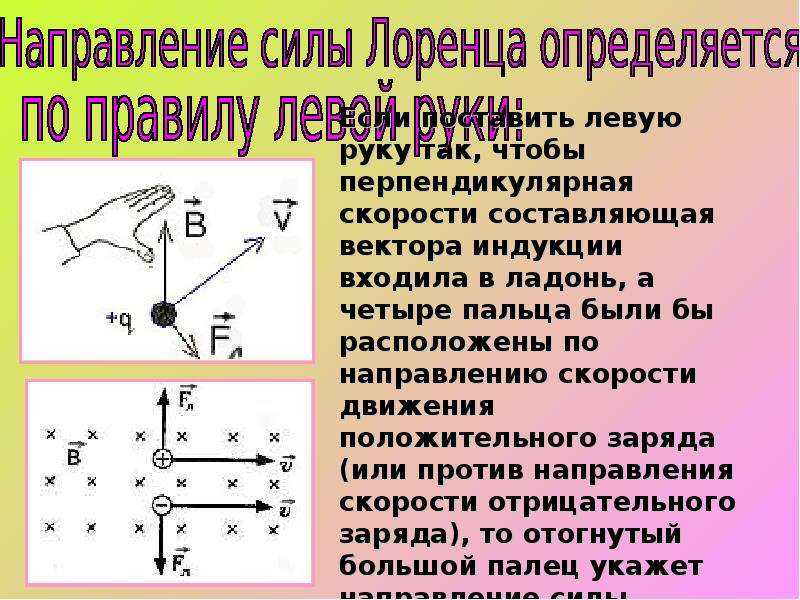 Из уравнения (2) следует, что если заряженная частица движется вдоль линии магнитного поля, то не испытывает действия магнитной силы.
Из уравнения (2) следует, что если заряженная частица движется вдоль линии магнитного поля, то не испытывает действия магнитной силы.
Направление магнитной силы
Магнитная сила, исходя из (1) направлена перпендикулярно плоскости, в которой лежат векторы $\overrightarrow{v\ }и\ \overrightarrow{B}$. Ее направление совпадает с направлением векторного произведения $\overrightarrow{v\ }и\ \overrightarrow{B}$ в том случае, если величина движущегося заряда больше нуля, и направлена в противоположную сторону, если $q
Рис. 1
Свойства силы магнитной силы
Магнитная сила работы над частицей не свершает, так как всегда направлена перпендикулярно скорости ее движения. Из этого утверждения следует, что с помощью воздействия на заряженную частицу с помощью постоянного магнитного поля ее энергию изменить нельзя.
Сила Лоренца
Если на частицу, обладающую зарядом, действуют одновременно электрическое и магнитное поля, то равнодействующая сила может быть записана как:
\[\overrightarrow{F}=q\overrightarrow{E}+q\left[\overrightarrow{v}\overrightarrow{B}\right]\ \left(3\right). \]
\]
Сила, указанная в выражении (3) называется силой Лоренца. Часть $q\overrightarrow{E}$ является силой, действующей со стороны электрического поля на заряд, $q\left[\overrightarrow{v}\overrightarrow{B}\right]$ характеризует силу действия магнитного поля на заряд. Сила Лоренца проявляется при движении электронов и ионов в магнитных полях.
Пример 1
Задание: Протон ($p$) и электрон ($e$), ускоренный одинаковой разностью потенциалов влетают в однородное магнитное поле. Во сколько раз радиус кривизны траектории движения протона $R_p$отличается от радиуса кривизны траектории электрона $R_e$. Углы, под которыми влетают частицы в поле, одинаковы.
Решение:
Если действием силы тяжести в сравнении с действием магнитной силы пренебречь, то второй закон Ньютона запишем как:
\[ma_n=qvBsin\alpha \ \left(1.1\right).\]
В формуле (1.1) мы учли, что вектор магнитной составляющей силы Лоренца перпендикулярен скорости и, следовательно, сообщает заряженной частице нормальное ускорение ($a_n$). {-31}}}\approx 42.\]
{-31}}}\approx 42.\]
Ответ: Радиус кривизны протона в 42 раза больше, чем радиус кривизны электрона.
Пример 2
Задание: Найдите напряженность электрического поля (E), если протон в скрещенном магнитном и электрическом полях движется прямолинейно. В эти поля он влетел, пройдя ускоряющую разность потенциалов равную U. Поля скрещены под прямым углом. Индукция магнитного поля равна B.
Решение:
На частицу, по условиям задачи действует сила Лоренца, имеющая две составные части: магнитную и электрическую. Первая составляющая магнитная она равна:
\[\overrightarrow{F_m}=q\left[\overrightarrow{v}\overrightarrow{B}\right]\ \left(2.1\right).\]
$\overrightarrow{F_m}$ — направлена перпендикулярно $\overrightarrow{v\ }и\ \overrightarrow{B}$. Электрическая составляющая силы Лоренца равна:
\[\overrightarrow{F_q}=q\overrightarrow{E}\left(2.2\right).\]
Сила $\overrightarrow{F_q}$- направлена по напряженности $\overrightarrow{E}$. 2}{2}=qU\to v=\sqrt{\frac{2qU}{m}}\left(2.5\right).\]
2}{2}=qU\to v=\sqrt{\frac{2qU}{m}}\left(2.5\right).\]
Подставим (2.5) в (2.4), получим:
\[E=B\sqrt{\frac{2qU}{m}}.\]
Ответ: $E=B\sqrt{\frac{2qU}{m}}.$
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 10.02.2022
Сила Лоренца. Движение заряженных частиц в магнитном поле.
Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на заряд q ,движущийся в магнитном поле со скоростью , называется силой Лоренца.
— установлено опытным путем
Направление
силы Лоренца определяется для положительных
зарядов правилом левой руки (т.к.
направление и для совпадают): если ладонь левой руки
расположить так, чтобы вектор входил в нее, а 4 вытянутых пальца
сонаправить с движением положительного
заряда, то отогнутый большой палец
покажет направление силы Лоренца.
Для отрицательных зарядов берется противоположное направление.
Сила Лоренца всегда направлена перпендикулярно скорости заряда и сообщает ему нормальное ускорение. Не изменяя модуля скорости, а лишь изменяя ее направление, сила Лоренца не совершает работы и кинетическая энергия заряженной частицы при движении в магнитном поле не изменяется.
Если на движущийся электрический заряд помимо магнитного поля действует и электрическое поле напряженностью , то результирующая сила
— формула Лоренца.
1. Движение заряженной частицы вдоль силовой линии, .
,
магнитное поле не действует на частицу.
Заряженная частица движется по инерции равномерно прямолинейно.
2. Движение заряженной частицы перпендикулярно силовым линиям, .
Пусть
в однородное магнитное поле с индукцией влетела заряженная частица массой m
с зарядом q перпендикулярно
магнитным силовым линиям со скоростью
.
В каждой точке поля на частицу действует . Т.к. , то . Ускорение изменяет только направление скорости, , значит, . В этих условиях тело (заряженная частица) движется равномерно по окружности.
Согласно II закону Ньютона:
(1)
Т.к. все величины, входящие в (1), постоянны, радиус кривизны R будет оставаться постоянным. Постоянный радиус кривизны имеет только окружность. Следовательно, движение заряда в плоскости, перпендикулярной магнитному полю, будет происходить по окружности. Чем больше , тем меньше R. При , т.е. заряд движется по прямой.
Важным результатом для приложения является тот факт, что период обращения заряда в однородном магнитном поле не зависит от его скорости.
если . (2)
Частицы, имеющие бóльшую скорость,
движутся по окружности бóльшего радиуса,
однако время одного полного оборота
будет таким же, что и для более медленных
частиц, движущихся по окружности меньшего
радиуса. Данный результат положен в
основу действия циклических ускорителей
элементарных частиц.
Данный результат положен в
основу действия циклических ускорителей
элементарных частиц.
3. Движение заряженной частицы произвольно по отношению к линиям магнитной индукции. Вектор скорости можно разложить на 2 составляющие:
В направлении сила Лоренца на заряд не действует, поэтому в этом направлении он движется равномерно, прямолинейно с . В направлении, перпендикулярном , он движется по окружности со скоростью Движение заряда представляет собой суперпозицию этих двух движений и происходит по винтовой линии, ось которой параллельна .
Радиус витка с учетом (1):
(3)
Шаг винтовой линии (расстояние между соседними витками)
с учетом (2):
.
Если движение происходит в неоднородном
магнитном поле, индукция которого
возрастает в направлении движения
частицы, то R уменьшается
с ростом В согласно (3).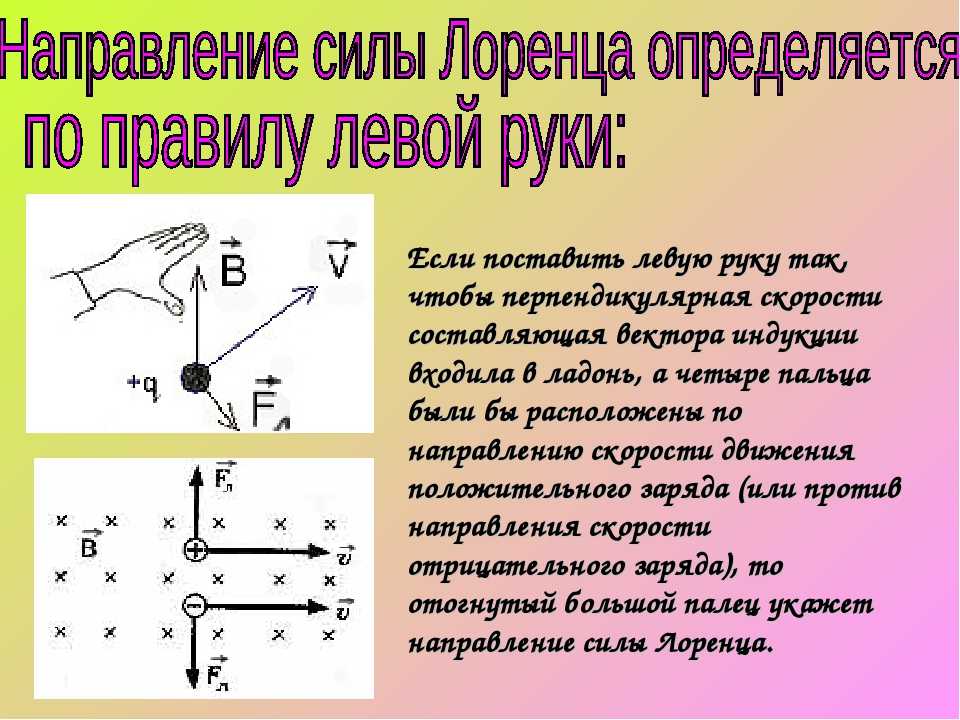 На этом основана
фокусировка пучка заряженных частиц в
магнитном поле. Таким образом, с помощью
неоднородного магнитного поля можно
управлять пучками заряженных частиц,
собирать их или рассеивать подобно
тому, как управляют поведением пучков
световых лучей с помощью оптических
линз.
На этом основана
фокусировка пучка заряженных частиц в
магнитном поле. Таким образом, с помощью
неоднородного магнитного поля можно
управлять пучками заряженных частиц,
собирать их или рассеивать подобно
тому, как управляют поведением пучков
световых лучей с помощью оптических
линз.
Рассмотренный принцип положен в основу действия электронных микроскопов.
Ускорители заряженных частиц.
Свойство независимости периода от скорости обращения используют для того, чтобы превратить траекторию ускоряемой частицы в спираль и уменьшить размеры ускорителя. Такой принцип положен в основу работы циклотрона — родоначальника целого семейства ускорителей с магнитным полем: синхротрона, синхрофазотрона и т.д.
Ускорительная камера
циклотрона представляет собой вакуумную
цилиндрическую коробку, помещенную
между полюсами сильного электромагнита.
Камера состоит из двух металлических
половинок — дуантов, между которыми
создается с помощью генератора переменное
электрическое напряжение с амплитудой
порядка (поле только в зазоре). Частицы вводятся
внутрь камера с помощью специального
впускного устройства (А).
Частицы вводятся
внутрь камера с помощью специального
впускного устройства (А).
При каждом пересечении зазора частица приобретает энергию E1 = qU. За N оборотов E = qUN, Emax~107эВ.
Большая энергия в циклотроне не может быть достигнута: как следует из теории относительности: m = f(V), а при росте массы уменьшается частота обращения.
В синхроциклотронах (фазотронах) медленно уменьшается частота подаваемого напряжения.
Фазотрон — изменяется .
В синхротронах меняется индукция магнитного поля .
Синхротрон — изменяется
В синхрофазотронах — изменяется и B.
E~109 — 1010 эВ.
Ускорители заряженных
частиц — устройства, в которых создаются
и управляются пучки высокоэнергетических
заряженных частиц под действием
электрических и магнитных полей.
Принцип автофазировки предложены советским физиком Векслером (1944 г.) и американским Мак-Милланом (1945 г.).
Магнитогидродинамический (МГД) генератор — установка для непосредственного преобразования тепловой энергии в электрическую (создан в 50-х годах).
Это источник тока, принцип действия которого основан на действии магнитного поля на заряженные частицы плазмы электролитов и жидких металлов. Плазма представляет собой поток раскаленного газа, все молекулы которого ионизированы высокой температурой (~2000K).
Поток плазмы, проходя через расширяющееся сопло, ускоряется до 2000-2500 м/с и попадает в сильное магнитное поле, разделяющее положительные и отрицательные заряды, отбрасывая их на электроды. При этом во внешней цепи возникает электрический ток.
т.к. Tпл >>Твн.среды, — велико.
Применение:
в ускорителях;
в НГД — генераторах;
датчиках Холла;
для осуществления управляемых термоядерных реакций;
при регистрации и исследовании заряженных частиц;
в магнетронах.

Сила Лоренца — Citizendium
Из Citizendium
Перейти к навигацииПерейти к поиску
| | Основной артикул | Обсуждение | Статьи по теме [?] | Библиография [?] | Внешние ссылки [?] | Версия для цитирования [?] |
| ||||||||||||
| Эта редактируемая Основная статья находится в разработке и подлежит отказу от ответственности . [изменить введение] | |||||||||||||||||||
В физике сила Лоренца — это сила, действующая на электрически заряженную частицу, которая движется через магнитное и электрическое поля.
Сила Лоренца имеет две векторные составляющие: одна пропорциональна магнитному полю, а другая пропорциональна электрическому полю. Эти компоненты должны быть добавлены векторно, чтобы получить общую силу.
1. Сила (абсолютная величина) магнитной составляющей пропорциональна четырем факторам: заряду q частицы, скорости v частицы, напряженности B магнитной индукции, и синус угла между векторами v и B . Направление магнитного компонента задается правилом правой руки: положите правую руку вдоль v пальцами, указывающими в направлении v и открытая ладонь в сторону вектора B . Вытяните большой палец правой руки, тогда вдоль него действует сила Лоренца, направленная от запястья к кончику большого пальца.
2. электрическая составляющая силы Лоренца равна q • E (заряд частицы, умноженный на электрическое поле). Он находится в том же направлении, что и E для положительно заряженных частиц, и в направлении, противоположном E для отрицательно заряженных частиц.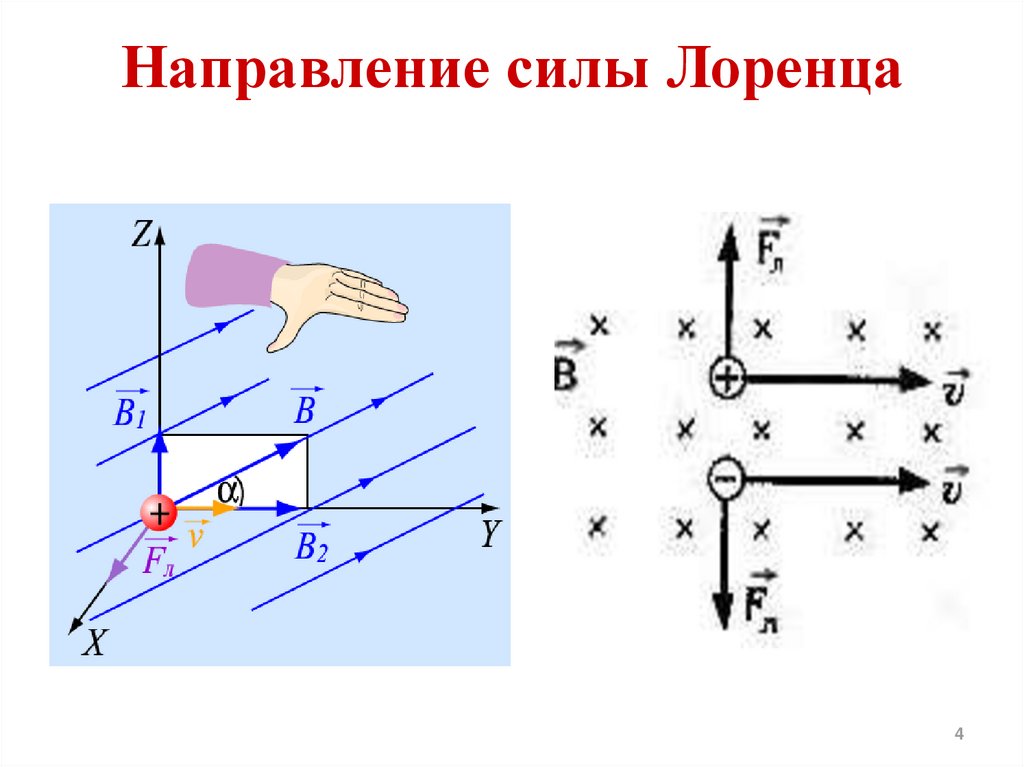
Сила названа в честь голландского физика Хендрика Антона Лоренца, который дал ее уравнение в 1892 году.
- F = q (E + kv × B), {\ displaystyle \ mathbf {F} = q (\ mathbf {E} + k \ mathbf {v} \ times \ mathbf {B}),}
где k — константа, зависящая от единиц измерения. В единицах СИ к = 1; в гауссовских единицах k = 1/ c , где c — скорость света в вакууме (точно 299 792 458 м с −1 ). Величина q — это электрический заряд частицы, а v — ее скорость. Вектор B представляет собой магнитную индукцию. Произведение v × B является векторным произведением, также называемым перекрестным произведением.
Как и любое векторное поле, электрическое поле E , возникающее в силе Лоренца F , представляет собой сумму продольной (свободной от завитков) и поперечной (бездивергентной) составляющих. Следующий вид имеет место, когда кулоновская калибровка ∇ • Выбирается = 0,
- E (r, t) = -∇V (r, t) -k∂A (r, t) ∂t, {\ displaystyle \ mathbf {E} (\ mathbf {r}, t) = — { \boldsymbol {\nabla}} V (\ mathbf {r}, t) -k {\ frac {\ partial \ mathbf {A} (\ mathbf {r}, t)} {\ partial t}},}
, где В — скалярный (электрический) потенциал, а (магнитный) векторный потенциал А соединен с В через
- В (г, т) = ∇ × А (г, т).
 A} (\mathbf {r},t).}
A} (\mathbf {r},t).}
Оператор ∇ , действующий на V , дает градиент V , а ∇ × A является завихрением A . Поскольку ∇ × ( ∇ V ) = 0 и ∇ • A = 0, компоненты E действительно не имеют завихрений и не расходятся соответственно.
Обратите внимание, что сила Лоренца не зависит от среды; электрическая сила не содержит диэлектрическую проницаемость ε, а магнитная сила не содержит магнитной проницаемости μ.
Если B статичен (не зависит от времени), то A также статичен и
- E = -∇VandF = -q∇V. {\ displaystyle \ mathbf {E} = — {\boldsymbol {\ nabla}} V \ quad {\ hbox {and}} \ quad \ mathbf {F} = -q{\boldsymbol {\nabla}}V.}
Нерелятивистски электрическое поле E может отсутствовать (ноль), тогда как B статично и не равно нулю; тогда сила Лоренца определяется выражением
- F = kqv × B, с F = kqvBsinα, {\ displaystyle \ mathbf {F} = k \, q \, \ mathbf {v} \ times \ mathbf {B}, \ quad {\ hbox {с }}\quad F=k\,q\,v\,B\sin \alpha ,}
, где k = 1 для единиц СИ и 1/ c для единиц Гаусса, а α угол между v и B . Величины, выделенные курсивом, не выделенные жирным шрифтом, представляют собой силы (длины) соответствующих векторов.
Величины, выделенные курсивом, не выделенные жирным шрифтом, представляют собой силы (длины) соответствующих векторов.
- F≡|F|,v≡|v|,B≡|B|.{\displaystyle F\equiv |\mathbf {F} |,\quad v\equiv |\mathbf {v} |,\quad B\equiv |\mathbf {B} |.}
Сила Лоренца как векторное (перекрестное) произведение было дано Оливером Хевисайдом в 1889 году, за три года до Лоренца. [2]
В специальной теории относительности сила Лоренца преобразуется как четырехвектор при преобразовании Лоренца. Поскольку с релятивистской точки зрения поля E и B являются компонентами одного и того же тензора второго ранга, преобразование Лоренца дает линейную комбинацию E и B , и, следовательно, в теории относительности эти два поля не существуют независимо друг от друга. . [3]
Примечания
- ↑ Х. А. Лоренц, La théorie électromagnétique de Maxwell et son application aux corps mouvants [Электромагнитная теория Максвелла и ее приложение к движущимся телам], Archives néerlandaises des Sciences calculatees et naturelles, vol.
 25 стр. 363 (1892 г.).
25 стр. 363 (1892 г.). - ↑ Э. Уиттакер, История теорий эфира и электричества , том. I, 2-е издание, Нельсон, Лондон (1951). Перепечатано Американским институтом физики (1987 г.). п. 310. Интересно отметить, что Джеймс Клерк Максвелл дал выражение для силы Лоренца еще в своих исторических мемуарах 1865 г. (J. Clerk Maxwell, 9).0049 Динамическая теория электромагнитного поля , Фил. Транс. Рой. Соц., том. 155 , стр. 459–512 (1865) онлайн)
- ↑ Дж. Д. Джексон, Классическая электродинамика , Джон Вили, Нью-Йорк, 2-е изд. (1975), с. 553
Знать определение, формулу, важность и применение.
0
Сохранить
Скачать публикацию в формате PDF Электромагнетизм можно определить как явление, при котором электрическое поле, создаваемое частицами, взаимодействует с магнитным полем. Это взаимодействие известно как электромагнитная сила, и электромагнетизм в основном изучает эту силу. Сила, создаваемая комбинацией магнитной силы и электрической силы, известна как сила Лоренца.
Читайте дальше, чтобы узнать больше о силе Лоренца, ее определении, формуле, важности и применении, а также о некоторых часто задаваемых вопросах.
Сила Лоренца
Сила Лоренца может быть определена как сила, создаваемая комбинацией магнитной силы и электрической силы. Наличие электромагнитного поля из-за магнитного поля и электрического поля заставляет его действовать на точечный заряд. Его также называют электромагнитной силой. Он был открыт Хендриком Лоренцем в 1895 году. На изображении ниже показано создание силы Лоренца из-за магнитной и электрической сил соответствующими полями.
Специалисты называют силу Лоренца комбинацией электрических и магнитных сил. Эта сила также действует на точечный заряд за счет электромагнитного поля. Сила Лоренца описывает уравнения математической природы и физическое значение сил, действующих на заряженные частицы. Эти частицы также могут путешествовать в пространстве, содержащем электрическое и магнитное поле. Одним из ее примеров является электронно-лучевая трубка, которая используется в нашем телевидении и компьютерных мониторах.
Одним из ее примеров является электронно-лучевая трубка, которая используется в нашем телевидении и компьютерных мониторах.
Формула силы Лоренца выглядит следующим образом:
\( {F} = {q} ({E} + {v} \times {B}) \)
Где F — сила, действующая на частица.
q — электрический заряд частицы.
v — скорость.
E — электрическое поле.
B — магнитное поле.
Сила Лоренца может быть выражена в следующей производной форме:
\( {F} = {q} {v} {B} {Sinθ} \)
частица.
q — заряд частицы.
Если частица движется в направлении магнитного поля, не пересекая силовые линии, то θ равно 0. Сила Лоренца не действует на частицу.
Если частица движется перпендикулярно магнитному полю, то Sinθ будет равно 1, и она будет совершать круговое движение с радиусом r. Это можно сделать, приравняв центростремительную силу и силу Лоренца. Следовательно, теперь уравнение будет таким: 92} {r} = {q} {v} {B} \).
Допустим, у вас есть электрическое поле Е в космосе. Тогда сила, действующая в пространстве со стороны электрического поля E независимо от скорости на заряд q, может быть выражена как
\( {F} = {q} {E} \)
у вас есть два варианта: нулевая скорость или ненулевая скорость. Магнитная сила не действует на частицу с зарядом Q, если ее скорость равна нулю. Если заряд имеет нулевую скорость, то на него не действует никакая магнитная сила. Частица движется по круговой орбите, потому что магнитное поле стремится не действовать на нее. Сила равна
\( {F} = {q({v} \times {B})} \)
Поскольку сила действует в направлении, параллельном скорости и магнитному полю B, она движется по круговой орбите. Здесь мы знаем, что движение частицы, когда E или B в настоящее время объединены, называется силой Лоренца.
\( {F} = {q} {E} + {q({v} x {B})} \)
Применение силы Лоренца определяется следующим образом:
- Используется в медицине промышленности в виде инструмента, известного как гидрофон.

- Он также используется в качестве ультразвукового преобразователя в медицине.
- Сила Лоренца также используется в электроимпедансной томографии, которая представляет собой метод визуализации.
- Сила Лоренца также создает поперечные волны в мягких тканях. Работа заключалась в подаче электрического тока на два электрода, встроенных в мягкое вещество, помещенное в магнитное поле.
Обучение теперь доступно и доступно с помощью приложения Testbook. В нем есть концепция очистки заметок по физике и пробные тесты для практики. Вы можете добиться успеха на конкурсных экзаменах с помощью приложения Testbook. Скачайте прямо сейчас!
Q.1 Что такое сила Лоренца?
Ans.1 Сила Лоренца может быть определена как сила, создаваемая комбинацией магнитной силы и электрической силы.
Q.2 Что такое магнитная сила Лоренца?
Ans.2 Магнитная сила Лоренца может быть определена как сила, действующая на заряженную частицу, движущуюся с некоторой скоростью через электрические и магнитные поля.
Q.3 Может ли сила Лоренца выполнять работу?
Ответ 3 Нет, сила Лоренца никогда не может выполнять работу.
Q.4 Как создается сила Лоренца?
Ответ 4 Сила Лоренца возникает, когда электрическое поле объединяется с магнитным полем.
В.5 Как преобразовать силу Лоренца в силу?
Ответ 5 Сила Лоренца может быть преобразована в силу по следующей формуле: \( {F} = {qE} + {qv} × {B} \).
Скачать публикацию в формате PDFДвижение заряженной частицы в магнитном поле | безграничная физика |
Электрические и магнитные силы
И электрические, и магнитные силы влияют на траекторию заряженных частиц, но качественно по-разному.
Цели обучения
Сравните влияние электрического и магнитного полей на заряженную частицу
Ключевые выводы
Ключевые моменты
- Сила, действующая на заряженную частицу из-за электрического поля, направлена параллельно вектору электрического поля в случае положительного заряд, и антипараллельно в случае отрицательного заряда.
 Она не зависит от скорости частицы.
Она не зависит от скорости частицы. - Напротив, магнитная сила, действующая на заряженную частицу, ортогональна вектору магнитного поля и зависит от скорости частицы. Для определения направления силы можно использовать правило правой руки.
- Электрическое поле может совершать работу над заряженной частицей, тогда как магнитное поле не совершает работы.
- Сила Лоренца представляет собой комбинацию электрической и магнитной сил, которые часто рассматриваются вместе для практических приложений.
- Линии электрического поля генерируются на положительных зарядах и заканчиваются на отрицательных. Силовые линии изолированного заряда направлены прямо радиально наружу. Электрическое поле касается этих линий.
- Линии магнитного поля в случае магнита генерируются на северном полюсе и заканчиваются на южном полюсе. Магнитные полюса не существуют изолированно. Как и в случае силовых линий электрического поля, магнитное поле касается силовых линий. Заряженные частицы будут вращаться вокруг этих силовых линий.

Ключевые термины
- ортогональный : Из двух объектов под прямым углом; перпендикулярны друг другу.
Электрические и магнитные силы
Сила, обусловленная как электрическими, так и магнитными силами, будет влиять на движение заряженных частиц. Однако результирующее изменение траектории частиц будет качественно различаться между двумя силами. Ниже мы кратко рассмотрим два типа сил, а также сравним и сопоставим их воздействие на заряженную частицу.
Сила электростатического и магнитного поля, действующая на заряженную частицу
Напомним, что в статическом неизменном электрическом поле E сила, действующая на частицу с зарядом q, будет:
F=qE\text{F}=\text{qE}F=qE
Где F — вектор силы, q — заряд, а E — вектор электрического поля. Обратите внимание, что направление F идентично E в случае позитивистского заряда q и противоположное направление в случае отрицательно заряженной частицы.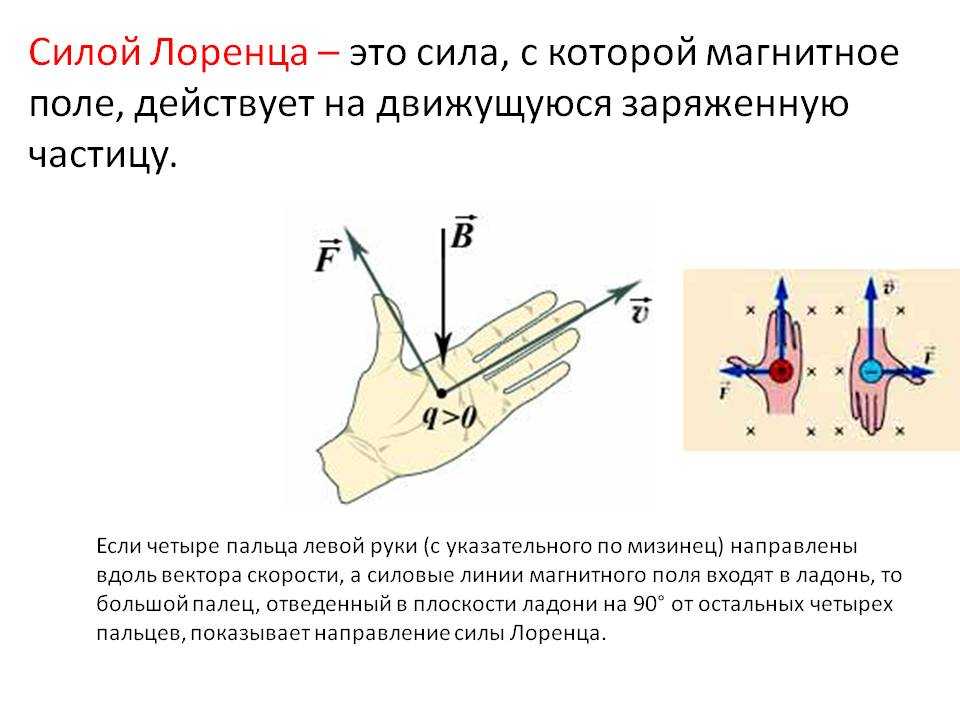 {2}}E=∣
{2}}E=∣
∣qF∣
∣=k∣
∣qr2qQ∣
∣=kr2∣Q∣
Следует подчеркнуть, что электрическая сила действует параллельно электрической силе F F Э . Завиток электрической силы равен нулю, т. е.: заряд в чистом электрическом поле будет следовать по касательной к линии электрического поля .
Напротив, вспомним, что магнитная сила, действующая на заряженную частицу, ортогональна магнитному полю, так что:
F=qv×B=qvBsinθ\text{F}=\text{qv} \times \text{B}= \text{qvBsin}\thetaF=qv×B=qvBsinθ
, где B — вектор магнитного поля, v — скорость частицы, а θ — угол между магнитным полем и скоростью частицы. Направление F можно легко определить с помощью правила правой руки.
Правило правой руки : Магнитные поля воздействуют на движущиеся заряды. Эта сила является одной из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B, и следует правилу правой руки-1 (RHR-1), как показано. Величина силы пропорциональна q, v, B и синусу угла между v и B.
Эта сила является одной из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B, и следует правилу правой руки-1 (RHR-1), как показано. Величина силы пропорциональна q, v, B и синусу угла между v и B.
Если скорость частицы параллельна магнитному полю или равна нулю, магнитная сила будет равна нулю. Это отличается от случая электрического поля, где скорость частицы в любой данный момент не имеет отношения к величине или направлению электрической силы.
Угловая зависимость магнитного поля также заставляет заряженные частицы двигаться перпендикулярно силовым линиям магнитного поля по окружности или спирали, в то время как частица в электрическом поле будет двигаться по прямой линии вдоль линии электрического поля.
Еще одно различие между магнитными и электрическими силами заключается в том, что магнитные поля не связаны между собой, поскольку движение частиц является круговым и, следовательно, заканчивается в одном и том же месте. Выразим это математически как:
Выразим это математически как:
W=∮B⋅dr=0\text{W}=\oint \text{B} \cdot \text{dr} = 0W=∮B⋅dr=0
Сила Лоренца
Сила Лоренца — это комбинированная сила, действующая на заряженную частицу из-за электрического и магнитного полей, которые часто рассматриваются вместе для практических приложений. Если частица с зарядом q движется со скоростью v в присутствии электрического поля E и магнитного поля B , то на нее будет действовать сила:
F=q[E+vBsinθ]\ text{F}=\text{q}[\text{E}+\text{vBsin}\theta]F=q[E+vBsinθ]
Линии электрического и магнитного поля
Выше мы вкратце упомянули, что движение заряженных частиц относительно силовых линий различается в зависимости от того, имеем ли мы дело с электрическими или магнитными полями. Есть некоторые заметные различия между тем, как концептуализируются силовые линии электрического и магнитного поля. Линии электрического поля от положительного изолированного заряда представляют собой просто последовательность равномерно расположенных радиально направленных линий, направленных наружу от заряда. В случае отрицательного заряда направление поля меняется на противоположное. Электрическое поле направлено по касательной к силовым линиям. Конечно, мы воображаем, что силовые линии тем плотнее упакованы, чем больше заряды. Можно ясно видеть, что ротор электрической силы равен нулю.
В случае отрицательного заряда направление поля меняется на противоположное. Электрическое поле направлено по касательной к силовым линиям. Конечно, мы воображаем, что силовые линии тем плотнее упакованы, чем больше заряды. Можно ясно видеть, что ротор электрической силы равен нулю.
Электрическое поле, создаваемое точечными зарядами : Электрическое поле, окружающее три различных точечных заряда: (a) положительный заряд; б) отрицательный заряд равной величины; в) больший отрицательный заряд.
Если задействовано несколько зарядов, линии поля генерируются на положительных зарядах и заканчиваются на отрицательных.
В случае магнитов силовые линии возникают на северном полюсе (+) и заканчиваются на южном полюсе (-) — см. рисунок ниже. Однако магнитные «заряды» всегда идут парами — нет магнитных монополей (изолированных северных или южных полюсов). Следовательно, ротор магнитного поля, создаваемого обычным магнитом, всегда отличен от нуля. Заряженные частицы будут вращаться вокруг этих силовых линий до тех пор, пока у частиц есть некоторая ненулевая составляющая скорости, направленная перпендикулярно силовым линиям.
Заряженные частицы будут вращаться вокруг этих силовых линий до тех пор, пока у частиц есть некоторая ненулевая составляющая скорости, направленная перпендикулярно силовым линиям.
Модель магнитного полюса : Модель магнитного полюса: два противоположных полюса, северный (+) и южный (-), разделенные расстоянием d, создают H-поле (линии).
Магнитное поле также может быть создано током с линиями поля, представленными в виде концентрических окружностей вокруг провода с током. Магнитная сила в любой точке в этом случае может быть определена с помощью правила правой руки и будет перпендикулярна обеим сторонам. тока и магнитного поля.
Постоянная скорость создает прямую линию
Если скорость заряженной частицы параллельна магнитному полю, результирующая сила отсутствует, и частица движется по прямой линии.
Цели обучения
Определите условия, необходимые для того, чтобы частица двигалась по прямой линии в магнитном поле
Ключевые выводы
Ключевые моменты
- Первый закон движения Ньютона гласит, что если на объект не действует результирующая сила, то его скорость постоянна.

- Частица с постоянной скоростью будет двигаться по прямой в пространстве.
- Если скорость заряженной частицы полностью параллельна магнитному полю, магнитное поле не будет воздействовать на частицу, и поэтому скорость останется постоянной.
- В случае, когда вектор скорости не параллелен и не перпендикулярен магнитному полю, составляющая скорости, параллельная полю, останется постоянной.
Ключевые термины
- прямолинейное движение : движение, происходящее в одном направлении
Постоянная скорость создает прямолинейное движение
Вспомним первый закон движения Ньютона. Если на объект не действует результирующая сила, то его скорость постоянна: объект либо покоится (если его скорость равна нулю), либо движется по прямой линии с постоянной скоростью (если его скорость отлична от нуля).
Во многих случаях на частицу может не действовать результирующая сила. Частица могла существовать в вакууме вдали от любых массивных тел (которые проявляют гравитационные силы) и электромагнитных полей. Или на частицу могут действовать две или более сил, которые уравновешены так, что результирующая сила равна нулю. Так обстоит дело, скажем, с частицей, подвешенной в электрическом поле, где электрическая сила точно уравновешивает гравитацию.
Частица могла существовать в вакууме вдали от любых массивных тел (которые проявляют гравитационные силы) и электромагнитных полей. Или на частицу могут действовать две или более сил, которые уравновешены так, что результирующая сила равна нулю. Так обстоит дело, скажем, с частицей, подвешенной в электрическом поле, где электрическая сила точно уравновешивает гравитацию.
Если результирующая сила, действующая на частицу, равна нулю, то ускорение обязательно равно нулю по второму закону Ньютона: F=ma. Если ускорение равно нулю, любая скорость, которую имеет частица, будет поддерживаться бесконечно (или до тех пор, пока результирующая сила больше не будет равна нулю). Поскольку скорость является вектором, направление остается неизменным вместе со скоростью, поэтому частица движется в одном направлении, например, по прямой линии.
Заряженные частицы, движущиеся параллельно магнитным полям
Сила, которую заряженная частица «чувствует» благодаря магнитному полю, зависит от угла между вектором скорости и вектором магнитного поля B . Напомним, что магнитная сила равна:
Напомним, что магнитная сила равна:
Нулевая сила, когда скорость параллельна магнитному полю : В приведенном выше случае магнитная сила равна нулю, потому что скорость параллельна линиям магнитного поля.
F=qvBsinθ\text{F}=\text{qvBsin} \thetaF=qvBsinθ
Если магнитное поле и скорость параллельны (или антипараллельны), то sinθ равен нулю и силы нет. В этом случае заряженная частица может продолжать прямолинейное движение даже в сильном магнитном поле. Если между 0 и 90 градусов, то составляющая v , параллельная B , остается неизменной.
Круговое движение
Поскольку магнитная сила всегда перпендикулярна скорости заряженной частицы, частица будет совершать круговое движение.
Цели обучения
Описать условия, которые приводят к круговому движению заряженной частицы в магнитном поле
Ключевые выводы
Ключевые моменты
- Магнитное поле не совершает работы, поэтому кинетическая энергия и скорость заряженной частицы в магнитном поле остаются постоянными .
 9{2}}{\text{r}}qvB=rmv2 .
9{2}}{\text{r}}qvB=rmv2 . - Решение для r выше дает гриорадиус, или радиус кривизны пути частицы с зарядом q и массой m, движущейся в магнитном поле напряженностью B. Тогда гриорадиус определяется как
r=mvqB\text{r} =\frac{\text{mv}}{\text{qB}}r=qBmv
. - Циклотронная частота (или, что то же самое, гирочастота) – это число циклов, совершаемых частицей по кругу за каждую секунду, и определяется как
f=qB2πm\text{f}=\frac{\text{qB}}{2 \pi \text{m}}f=2πmqB
.
Ключевые термины
- гирорадиус : Радиус кругового движения заряженной частицы в присутствии однородного магнитного поля.
- циклотронная частота : Частота заряженной частицы, движущейся перпендикулярно направлению однородного магнитного поля B (постоянной величины и направления). Дано равенством центростремительной силы и магнитной силы Лоренца.
Круговое движение заряженной частицы в магнитном поле
Магнитные силы могут заставить заряженные частицы двигаться по кругу или по спирали. Ускорители частиц удерживают протоны по круговым траекториям с магнитной силой. Космические лучи будут двигаться по спирали при столкновении с магнитным полем астрофизических объектов или планет (одним из примеров является магнитное поле Земли). Фотография пузырьковой камеры на рисунке ниже показывает заряженные частицы, движущиеся по таким изогнутым траекториям. Искривленные траектории заряженных частиц в магнитных полях лежат в основе ряда явлений и даже могут использоваться аналитически, например, в масс-спектрометре. показывает путь, пройденный частицами в пузырьковой камере.
Ускорители частиц удерживают протоны по круговым траекториям с магнитной силой. Космические лучи будут двигаться по спирали при столкновении с магнитным полем астрофизических объектов или планет (одним из примеров является магнитное поле Земли). Фотография пузырьковой камеры на рисунке ниже показывает заряженные частицы, движущиеся по таким изогнутым траекториям. Искривленные траектории заряженных частиц в магнитных полях лежат в основе ряда явлений и даже могут использоваться аналитически, например, в масс-спектрометре. показывает путь, пройденный частицами в пузырьковой камере.
Пузырьковая камера : Следы пузырьков образуются заряженными частицами высокой энергии, движущимися через перегретый жидкий водород в этом художественном исполнении пузырьковой камеры. Существует сильное магнитное поле, перпендикулярное странице, что приводит к искривлению траекторий частиц. Радиус пути можно использовать для определения массы, заряда и энергии частицы.
Итак, вызывает ли магнитная сила круговое движение? Магнитная сила всегда перпендикулярна скорости, поэтому на заряженную частицу она не действует. Таким образом, кинетическая энергия и скорость частицы остаются постоянными. Направление движения влияет, но не скорость. Это характерно для равномерного кругового движения. Простейший случай имеет место, когда заряженная частица движется перпендикулярно однородному В-полю, как показано на рис. (Если это происходит в вакууме, магнитное поле является доминирующим фактором, определяющим движение.) Здесь магнитная сила (Лоренц сила) создает центростремительную силу 9{2}}{\text{r}}qvB=rmv2
Таким образом, кинетическая энергия и скорость частицы остаются постоянными. Направление движения влияет, но не скорость. Это характерно для равномерного кругового движения. Простейший случай имеет место, когда заряженная частица движется перпендикулярно однородному В-полю, как показано на рис. (Если это происходит в вакууме, магнитное поле является доминирующим фактором, определяющим движение.) Здесь магнитная сила (Лоренц сила) создает центростремительную силу 9{2}}{\text{r}}qvB=rmv2
решение для r дает
r=mvqB\text{r}=\frac{\text{mv}}{\text{qB}}r= qBmv
Здесь r , называемый гирорадиусом или циклотронным радиусом, представляет собой радиус кривизны пути заряженной частицы с массой m и зарядом q , движущейся со скоростью v перпендикулярно магнитное поле напряженностью B . Другими словами, это радиус кругового движения заряженной частицы в присутствии однородного магнитного поля. Если скорость не перпендикулярна магнитному полю, то v — составляющая скорости, перпендикулярная полю. Составляющая скорости, параллельная полю, не изменяется, так как магнитная сила равна нулю при движении параллельно полю. Мы рассмотрим последствия этого случая в следующем разделе, посвященном спиральному движению.
Составляющая скорости, параллельная полю, не изменяется, так как магнитная сила равна нулю при движении параллельно полю. Мы рассмотрим последствия этого случая в следующем разделе, посвященном спиральному движению.
Частица, совершающая круговое движение из-за однородного магнитного поля, называется находящейся в циклотронном резонансе . Этот термин происходит от названия циклического ускорителя частиц, называемого циклотроном, показанного на рис.0437 v выше и заменив частоту циркуляции так, чтобы
Циклотрон : Французский циклотрон, произведенный в Цюрихе, Швейцария, в 1937 г.
f=v2πr\text{f}=\frac{\text{v}}{ 2 \pi \text{r}}f=2πrv
становится
f=qB2πm\text{f}=\frac{\text{qB}}{2 \pi \text{m}}f=2πmqB
Циклотронная частота тривиально выражается в радианах в секунду как
ω=qBm\omega=\frac{\text{qB}}{\text{m}}ω=mqB
.
Винтовое движение
Винтовое движение возникает, когда вектор скорости не перпендикулярен вектору магнитного поля.
Цели обучения
Опишите условия, которые приводят к винтовому движению заряженной частицы в магнитном поле
Ключевые выводы
Ключевые моменты
- Ранее мы видели, что круговое движение возникает, когда скорость заряженной частицы перпендикулярна магнитному полю. Скорость и кинетическая энергия частицы остаются постоянными, но направление изменяется в каждый момент перпендикулярной магнитной силой.
- Если скорость не перпендикулярна магнитному полю, при расчетах мы учитываем только ту составляющую v, которая перпендикулярна полю.
- Составляющая скорости, параллельная полю, не изменяется, так как магнитная сила равна нулю при движении параллельно полю. Это приводит к винтовому движению.
- Заряды могут двигаться по спирали вдоль силовых линий. Если сила магнитного поля увеличивается в направлении движения, поле будет оказывать силу, чтобы замедлить заряды и даже изменить их направление.
 Это известно как магнитное зеркало.
Это известно как магнитное зеркало.
Ключевые термины
- спиральное движение : Движение, которое возникает, когда одна составляющая скорости постоянна по величине и направлению (т. е. прямолинейное движение), а другая составляющая постоянна по скорости, но равномерно изменяется по направлению. (то есть круговое движение). Это суперпозиция прямолинейного и кругового движения.
- магнитное зеркало : Конфигурация магнитного поля, при которой напряженность поля изменяется при движении вдоль силовой линии. Зеркальный эффект приводит к стремлению заряженных частиц отскакивать от области сильного поля.
Винтовое движение
В разделе о круговом движении мы описали движение заряженной частицы с вектором магнитного поля, ориентированным перпендикулярно скорости частицы. В этом случае магнитная сила также перпендикулярна скорости (и, конечно, вектору магнитного поля) в любой момент времени, что приводит к круговому движению.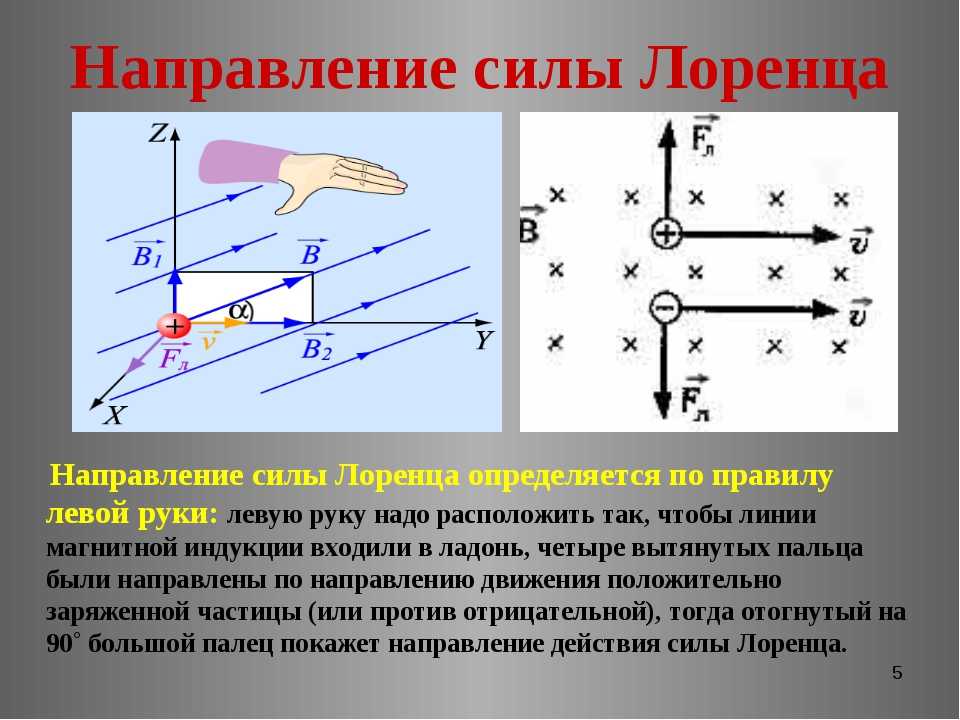 Скорость и кинетическая энергия частицы остаются постоянными, но направление изменяется в каждый момент перпендикулярной магнитной силой. быстро просматривается эта ситуация в случае отрицательно заряженной частицы в магнитном поле, направленном внутрь страницы.
Скорость и кинетическая энергия частицы остаются постоянными, но направление изменяется в каждый момент перпендикулярной магнитной силой. быстро просматривается эта ситуация в случае отрицательно заряженной частицы в магнитном поле, направленном внутрь страницы.
Круговое движение заряженной частицы в магнитном поле : Отрицательно заряженная частица движется в плоскости страницы в области, где магнитное поле перпендикулярно странице (представлено маленькими кружками с крестиком — как хвосты стрелок). ). Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине. Результат равномерного кругового движения.
Что, если скорость не перпендикулярна магнитному полю? Тогда мы рассматриваем только 92}{\text{r}}Fc=rmv⊥2
F=qvBsinθ=qv⊥B\text{F}=\text{qvBsin} \theta=\text{qv}_{\perp} \text{B}F=qvBsinθ=qv⊥B
Составляющая скорости, параллельная полю, не изменяется, поскольку магнитная сила равна нулю при движении параллельно полю. Это производит спиральное движение (то есть спиральное движение), а не круговое движение.
Это производит спиральное движение (то есть спиральное движение), а не круговое движение.
показывает, как электроны, движущиеся не перпендикулярно силовым линиям магнитного поля, следуют за силовыми линиями. Составляющая скорости, параллельная линиям, не изменяется, поэтому заряды закручиваются вдоль силовых линий. Если напряженность поля увеличивается в направлении движения, поле будет оказывать силу, чтобы замедлить заряды (и даже изменить их направление), образуя своего рода магнитное зеркало.
Винтовое движение и магнитные зеркала : Когда заряженная частица движется вдоль линии магнитного поля в область, где поле становится сильнее, на частицу действует сила, уменьшающая составляющую скорости, параллельную полю. Эта сила замедляет движение вдоль силовой линии, а здесь меняет его направление, образуя «магнитное зеркало».
Движение заряженных частиц в магнитных полях связано с такими разными вещами, как Aurora Borealis или Aurora Australis (северное и южное сияние) и ускорителями частиц. Заряженные частицы, приближающиеся к силовым линиям магнитного поля, могут попасть в ловушку на спиральных орбитах вокруг линий, а не пересекать их , как показано выше. Некоторые космические лучи, например, следуют линиям магнитного поля Земли, проникая в атмосферу вблизи магнитных полюсов и вызывая южное или северное сияние за счет ионизации молекул в атмосфере. Те частицы, которые приближаются к средним широтам, должны пересекать силовые линии магнитного поля, и многие из них не могут проникнуть в атмосферу. Космические лучи являются компонентом фонового излучения; следовательно, они дают более высокую дозу радиации на полюсах, чем на экваторе.
Заряженные частицы, приближающиеся к силовым линиям магнитного поля, могут попасть в ловушку на спиральных орбитах вокруг линий, а не пересекать их , как показано выше. Некоторые космические лучи, например, следуют линиям магнитного поля Земли, проникая в атмосферу вблизи магнитных полюсов и вызывая южное или северное сияние за счет ионизации молекул в атмосфере. Те частицы, которые приближаются к средним широтам, должны пересекать силовые линии магнитного поля, и многие из них не могут проникнуть в атмосферу. Космические лучи являются компонентом фонового излучения; следовательно, они дают более высокую дозу радиации на полюсах, чем на экваторе.
Спираль заряженных частиц вдоль силовых линий магнитного поля Земли : Энергичные электроны и протоны, составляющие космические лучи, исходящие от Солнца и глубокого космоса, часто следуют силовым линиям магнитного поля Земли, а не пересекают их. (Напомним, что северный магнитный полюс Земли на самом деле является южным полюсом с точки зрения стержневого магнита. )
)
Примеры и приложения
Циклотроны, магнетроны и масс-спектрометры представляют собой практическое технологическое применение электромагнитных полей.
Цели обучения
Обсудить применение масс-спектрометров, движение заряженных частиц в циклотроне и то, как микроволны генерируются в резонаторном магнетроне
Ключевые выводы
Ключевые моменты
- Циклотрон — это тип ускорителя частиц, в котором заряженные частицы ускоряются наружу от центр по спирали. Частицы удерживаются на спиральной траектории постоянным магнитным полем и ускоряются быстро меняющимся электрическим полем.
- Резонаторный магнетрон представляет собой мощную вакуумную лампу, генерирующую микроволны с помощью взаимодействия потока электронов с магнитным полем. Магнетрон применяется в радиолокации, отоплении и освещении.
- Масс-спектрометры измеряют отношение массы к заряду заряженных частиц с помощью электромагнитных полей для разделения частиц с разными массами и/или зарядами.
 Его можно использовать для определения элементного состава молекулы или образца.
Его можно использовать для определения элементного состава молекулы или образца.
Ключевые термины
- циклотрон : Ускоритель первых частиц, в котором заряженные частицы генерировались в центральном источнике и ускорялись по спирали наружу посредством постоянного магнитного и переменного электрического полей.
- масс-спектрометр : устройство, используемое в масс-спектрометрии для определения массового состава данного вещества.
- магнетрон : устройство, в котором электроны заставляют резонировать в камере особой формы и, таким образом, производить микроволновое излучение; используется в радарах и в микроволновых печах.
Примеры и приложения — движение заряженной частицы в магнитном поле
Обзор
Напомним, что заряженные частицы в магнитном поле будут следовать по круговой или спиральной траектории в зависимости от совмещения вектора их скорости с вектором магнитного поля. Последствия такого движения могут иметь глубокое практическое применение. Многие технологии основаны на движении заряженных частиц в электромагнитных полях. Мы рассмотрим некоторые из них, в том числе циклотрон и синхротрон, резонаторный магнетрон и масс-спектрометр.
Последствия такого движения могут иметь глубокое практическое применение. Многие технологии основаны на движении заряженных частиц в электромагнитных полях. Мы рассмотрим некоторые из них, в том числе циклотрон и синхротрон, резонаторный магнетрон и масс-спектрометр.
Циклотроны и синхротроны
Циклотрон — это тип ускорителя частиц, в котором заряженные частицы ускоряются наружу от центра по спиральной траектории. Частицы удерживаются на спиральной траектории постоянным магнитным полем и ускоряются быстро меняющимся (радиочастотным) электрическим полем.
Эскиз циклотрона : Эскиз частицы, ускоряемой в циклотроне и выбрасываемой через луч.
Циклотроны ускоряют пучки заряженных частиц с помощью высокочастотного переменного напряжения, которое прикладывается между двумя электродами в форме буквы «D» (также называемыми «ди»). Дополнительное статическое магнитное поле прикладывается в направлении, перпендикулярном плоскости электрода, что позволяет частицам повторно сталкиваться с ускоряющим напряжением много раз в одной и той же фазе.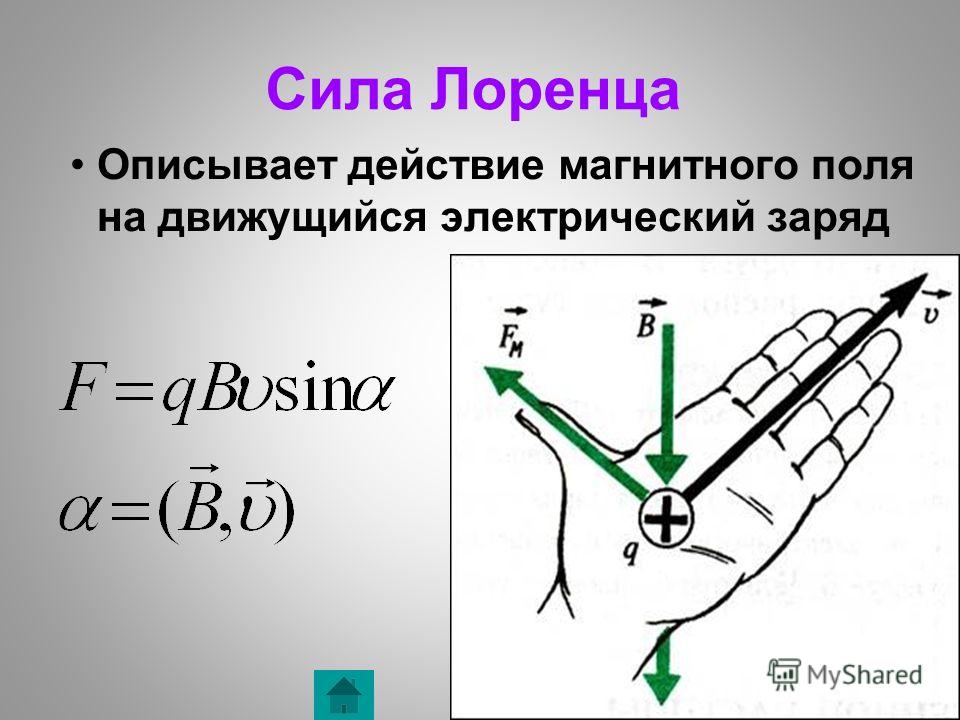 Для этого частота напряжения должна соответствовать частоте циклотронного резонанса частицы,
Для этого частота напряжения должна соответствовать частоте циклотронного резонанса частицы,
f=qB2πm\text{f}=\frac{\text{qB}}{2 \pi \text{m}}f=2πmqB
с релятивистской массой m и зарядом q . Эта частота определяется равенством центростремительной силы и магнитной силы Лоренца. Частицы, инжектированные вблизи центра магнитного поля, увеличивают свою кинетическую энергию только при рециркуляции через зазор между электродами; таким образом, они движутся наружу по спиральному пути. Их радиус будет увеличиваться до тех пор, пока частицы не попадут в цель по периметру вакуумной камеры или не покинут циклотрон с помощью лучевой трубки, что позволит их использовать. Частицы, ускоренные циклотроном, можно использовать в терапии частицами для лечения некоторых видов рака. Кроме того, циклотроны являются хорошим источником высокоэнергетических пучков для ядерно-физических экспериментов.
Синхротрон представляет собой усовершенствование циклотрона, в котором направляющее магнитное поле (изгибающее частицы по замкнутому пути) зависит от времени и синхронизируется с пучком частиц с возрастающей кинетической энергией. Синхротрон — одна из первых концепций ускорителя, которая позволяет создавать крупномасштабные установки, поскольку изгибание, фокусировку луча и ускорение можно разделить на разные компоненты.
Синхротрон — одна из первых концепций ускорителя, которая позволяет создавать крупномасштабные установки, поскольку изгибание, фокусировку луча и ускорение можно разделить на разные компоненты.
Резонаторный магнетрон
Резонаторный магнетрон представляет собой мощную вакуумную лампу, генерирующую микроволны за счет взаимодействия потока электронов с магнитным полем. Все резонаторные магнетроны состоят из горячего катода с высоким (постоянным или импульсным) отрицательным потенциалом, создаваемым высоковольтным источником питания постоянного тока. Катод встроен в центр вакуумированной лопастной круглой камеры. Магнитное поле, параллельное нити накала, создается постоянным магнитом. Магнитное поле заставляет электроны, притянутые к (относительно) положительной внешней части камеры, двигаться по спирали наружу по круговой траектории, что является следствием силы Лоренца. По краю камеры расположены цилиндрические полости. Полости открыты по своей длине и соединяют общее полостное пространство.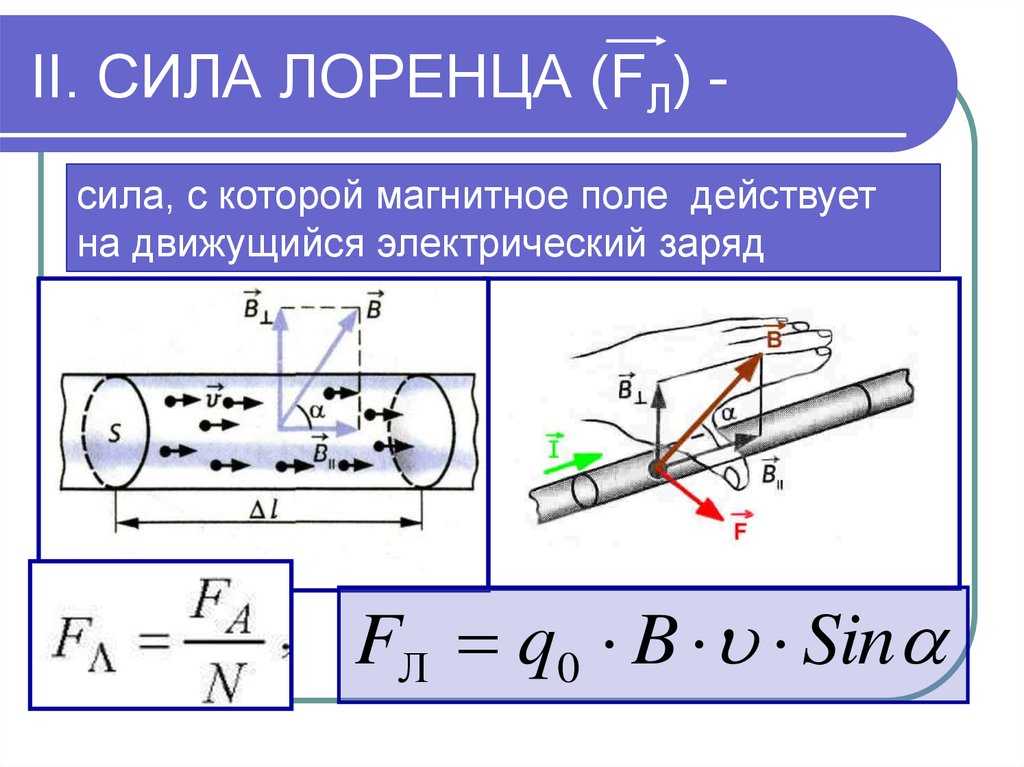 Когда электроны проносятся мимо этих отверстий, они индуцируют в полости резонансное высокочастотное радиополе, которое, в свою очередь, заставляет электроны группироваться в группы.
Когда электроны проносятся мимо этих отверстий, они индуцируют в полости резонансное высокочастотное радиополе, которое, в свою очередь, заставляет электроны группироваться в группы.
Схема резонаторного магнетрона : Схема поперечного сечения резонаторного магнетрона. Магнитные силовые линии параллельны геометрической оси этой структуры.
Размеры полостей определяют резонансную частоту и тем самым частоту излучаемых микроволн. Магнетрон представляет собой автоколебательное устройство, не требующее никаких внешних элементов, кроме источника питания. Магнетрон имеет практическое применение в радиолокации, нагреве (как основной компонент микроволновой печи) и освещении.
Масс-спектрометрия
Масс-спектрометрия — это аналитический метод, который измеряет отношение массы заряженных частиц к заряду. Он используется для определения массы частиц и определения элементного состава образца или молекулы.
Масс-анализаторы разделяют ионы в соответствии с отношением их массы к заряду. Следующие два закона управляют динамикой заряженных частиц в электрическом и магнитном полях в вакууме:
F=Q(E+v×B)\text{F}=\text{Q}(\text{E}+\ текст {v} \times \text{B})F=Q(E+v×B)
(сила Лоренца)
F=ma\text{F}=\text{ma}F=ma
Приравнивая приведенные выше выражения для силы, приложенной к иону, получаем:
(м/Q)a=E +v×B(\text{m}/\text{Q})\text{a}=\text{E}+\text{v} \times \text{B}(m/Q)a=E+ v×B
Это дифференциальное уравнение вместе с начальными условиями полностью определяет движение заряженной частицы в терминах m/Q. Существует много типов масс-анализаторов, использующих статические или динамические поля, магнитные или электрические поля, но все они работают в соответствии с приведенным выше дифференциальным уравнением.
На следующем рисунке показан один тип масс-спектрометра. Отклонения частиц зависят от отношения массы к заряду.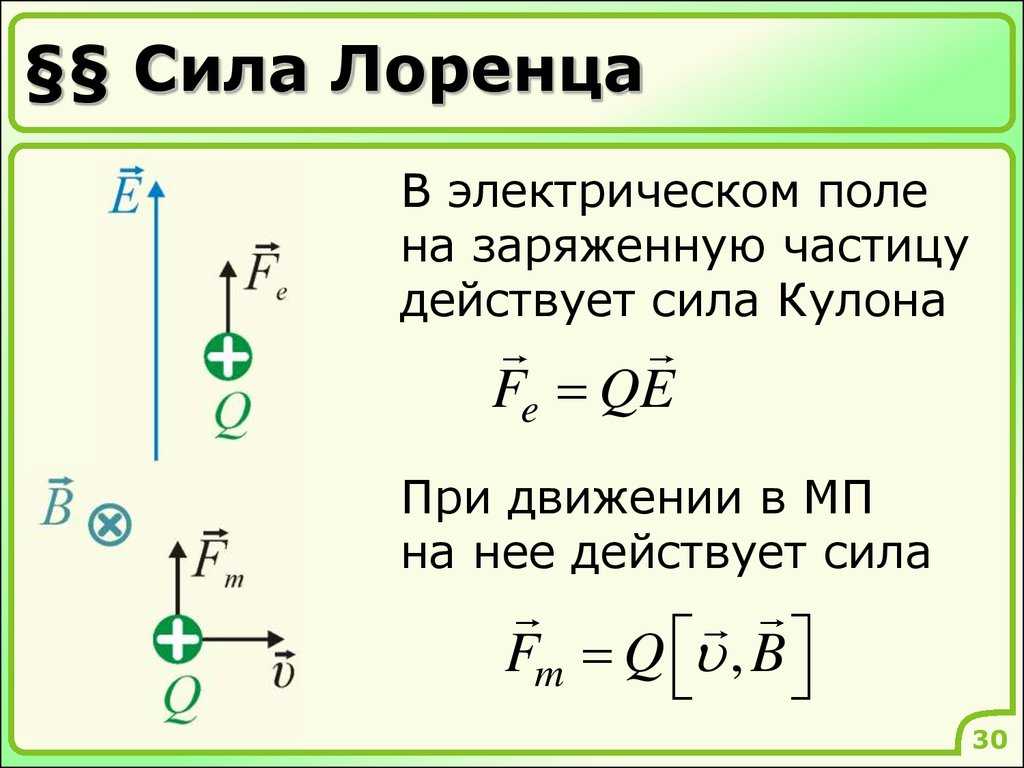 В случае изотопного диоксида углерода все молекулы имеют одинаковый заряд, но разные массы. Масс-спектрометр будет разделять частицы в пространстве, позволяя детектору измерять отношение массы к заряду каждой частицы. Поскольку заряд известен, абсолютную массу можно определить тривиально. Относительное содержание можно определить, подсчитав количество частиц каждой заданной массы.
В случае изотопного диоксида углерода все молекулы имеют одинаковый заряд, но разные массы. Масс-спектрометр будет разделять частицы в пространстве, позволяя детектору измерять отношение массы к заряду каждой частицы. Поскольку заряд известен, абсолютную массу можно определить тривиально. Относительное содержание можно определить, подсчитав количество частиц каждой заданной массы.
Масс-спектрометрия : Схема простого масс-спектрометра с масс-анализатором секторного типа. Это для измерения соотношения изотопов углекислого газа (IRMS), как в дыхательном тесте с мочевиной на углерод-13.
Лицензии и атрибуции
Контент под лицензией CC, совместно используемый ранее
- Курирование и доработка. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензионный контент CC, конкретное указание авторства
- Колледж OpenStax, Колледж физики.
 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция - Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Электрическая сила. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Электрическое поле. Предоставлено : Википедия.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Линии магнитного поля. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Магнитная сила. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- ортогональная. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики.
 10 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
10 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution - Линии магнитного поля. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторские права
- OpenStax College, College Physics. 14 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Законы Ньютона. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничная. Предоставлено : Безграничное обучение.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - Колледж OpenStax, Колледж физики. 10 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Линии магнитного поля. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторские права
- OpenStax College, College Physics. 14 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 28 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Циклотронный резонанс. Предоставлено : Википедия.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - Циклотрон. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Gyroradius. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Гирорадиус. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- циклотронная частота. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 декабря 2012 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution - Линии магнитного поля. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторские права
- OpenStax College, College Physics. 14 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 28 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики.
 26 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
26 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution - Циклотрон. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Cyclotron. Лицензия : Общественное достояние: неизвестно Авторские права
- Магнитное зеркало. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Безграничная. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- магнитное зеркало. Предоставлено : Википедия.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - OpenStax College, College Physics. 10 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Линии магнитного поля. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторские права
- OpenStax College, College Physics. 14 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 28 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 16 января 2015 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция - Колледж OpenStax, Колледж физики. 26 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Циклотрон. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Cyclotron. Лицензия : Общественное достояние: неизвестно Авторские права
- OpenStax College, College Physics. 27 ноября 2012 г. Предоставлено : OpenStaxCNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 26 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики.
 27 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
27 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution - Масс-спектрометры. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Магнетрон. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Синхротрон. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Циклотрон. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- циклотрон.
 Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike - магнетрон. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- масс-спектрометр. Предоставлено : Викисловарь. Расположен по адресу : https://en.wiktionary.org/wiki/mass_spectrometer. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 10 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Линии магнитного поля. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторские права
- OpenStax College, College Physics. 14 ноября 2012 г.
 Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция - Колледж OpenStax, Колледж физики. 28 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 16 января 2015 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Колледж OpenStax, Колледж физики. 26 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Циклотрон. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Cyclotron. Лицензия : Общественное достояние: неизвестно Авторские права
- OpenStax College, College Physics.







 Вспомните хотя бы электронно-лучевые трубки, применяемые в кинескопах телевизоров, где пучок летящих к экрану электронов отклоняется с помощью магнитных катушек.
Вспомните хотя бы электронно-лучевые трубки, применяемые в кинескопах телевизоров, где пучок летящих к экрану электронов отклоняется с помощью магнитных катушек.
 ТОКАМАК считается наиболее перспективным устройством для осуществления управляемого термоядерного синтеза.
ТОКАМАК считается наиболее перспективным устройством для осуществления управляемого термоядерного синтеза. ..
..
 A} (\mathbf {r},t).}
A} (\mathbf {r},t).} 25 стр. 363 (1892 г.).
25 стр. 363 (1892 г.).
 Она не зависит от скорости частицы.
Она не зависит от скорости частицы.

 9{2}}{\text{r}}qvB=rmv2 .
9{2}}{\text{r}}qvB=rmv2 . Это известно как магнитное зеркало.
Это известно как магнитное зеркало. Его можно использовать для определения элементного состава молекулы или образца.
Его можно использовать для определения элементного состава молекулы или образца. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  10 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
10 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution  26 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
26 ноября 2012 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция  27 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
27 ноября 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution  Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike 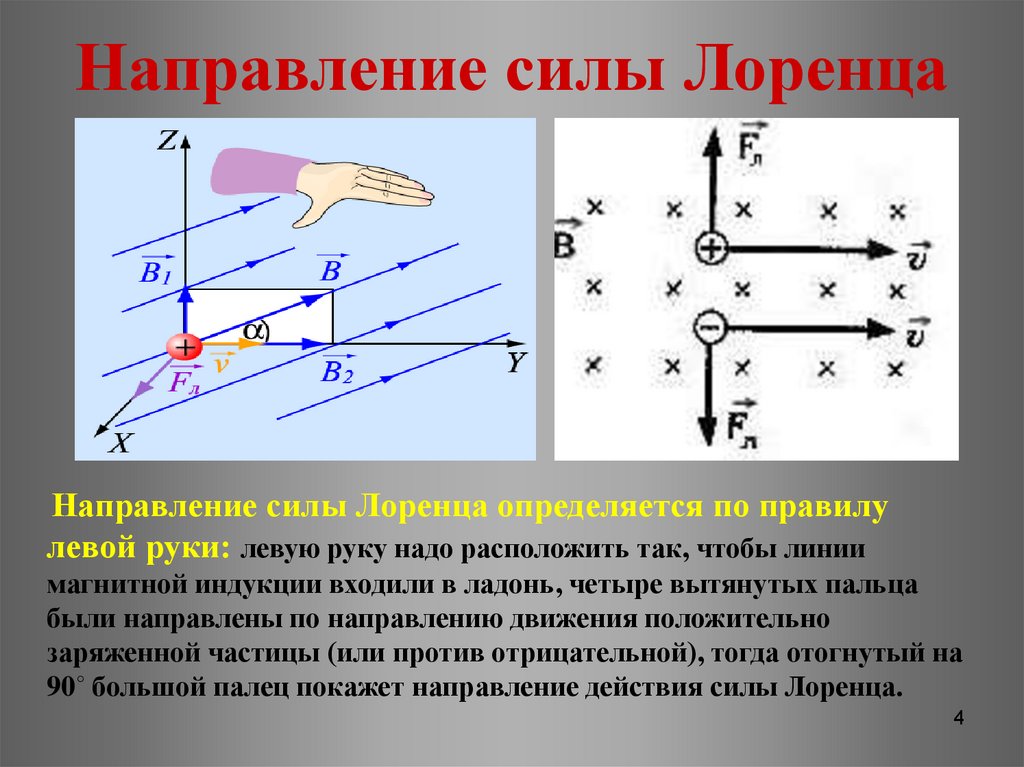 Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция