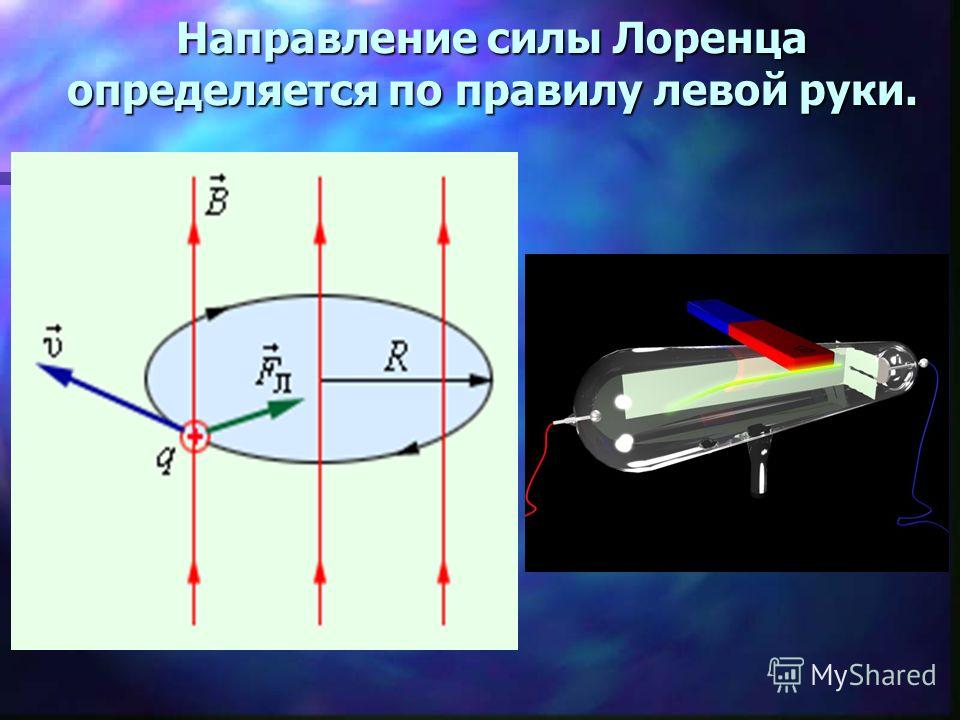
15. Преобразования Галилея и Лоренца
Преобразования Галилея — в классической механике (механике Ньютона)преобразования координат и времени при переходе от одной инерциальной системы отсчета (ИСО) к другой.
Вид преобразований при коллинеарных осях
Если ИСО S’ движется относительно ИСО S с постоянной скоростью вдоль оси , а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид: Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах: Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для малых скоростей .
Преобразования Лоренца — математические преобразования в специальной теории относительности, которым подвергаются координаты события при переходе от одной инерциальной системы отсчёта (ИСО) — к другой.
Вывод преобразований Лоренца из принципа относительности
Приведем вывод
этих преобразований, основанный только
на принципе относительности (т. е. на
равноправии всех инерциальных систем
отсчета).
е. на
равноправии всех инерциальных систем
отсчета).
В этом выводе постулат постоянства скорости света не используется ad hoc, а оказывается следствием принципа относительности.
Обозначим множество всех инерциальных систем отсчета K. Рассмотрим две инерциальные системы отсчета k, k’ из K, движущиеся друг относительно друга со скоростью u. Выберем декартовы координаты в этих системах отсчета так, чтобы в начальный момент времени начала коор инат совпадали, а оси были параллельны.
В системе отсчета k моменты времени и координаты вдоль направления u будем обозначать t и x соответственно, в системе отсчета k’ — t’ и x’ .
Оси X и X’ направим так, чтобы система k’ двигалась со скоростью u относительно системы k вдоль оси X, а система k двигалась со скоростью -u вдоль оси X’ системы k’ .
Равномерное
движение свободной материальной точки
со скоростью v в системе k описывается
уравнением
а
в системе k’ – уравнением.
Преобразование координат t, x, y, z системы k в координаты t’, x’, y’, z’ системы k’ должно быть таким, чтобы уравнение (L1) переходило в уравнение (L2). Это означает, что прямая в пространстве r, t должна переходить в прямую в пространстве r’, t’.
Таким свойством обладает линейное преобразование.
t’ = att(u)t+atx(u)x+aty(u)y+atz(u)z,
x’ = axt(u)t+axx(u)x+axy(u)y+axz(u)z,
y’ = ayt(u)t+ayx(u)x+ayy(u)y+ayz(u)z,
z’ = azt(u)t+azx(u)x+azy(u)y+azz(u)z,
где величины aij зависят только от скорости относительного движения систем отсчета.
При нашем выборе направления этой скорости вдоль параллельных осей X, X’ общий вид линейных преобразований можно упростить:
t’ = att(u)t+atx(u)x,
x’ = axt(u)t+axx(u)x,
y’ = y, z’ = y.
Действительно, в
силу однородности и изотропности нашего
пространства, преобразования вдоль оси
X не должны зависеть от значения координат
y и z. Сами координаты y и z тоже не должны
преобразовываться, иначе поперечные
размеры тел будут зависеть от скорости
их движения, что приведет к неравноправию
различных инерциальных систем отсчета
Сами координаты y и z тоже не должны
преобразовываться, иначе поперечные
размеры тел будут зависеть от скорости
их движения, что приведет к неравноправию
различных инерциальных систем отсчета
Найдем явный вид четырех неизвестных функций att(u), atx(u), axt(u), axx(u), опираясь только на принцип относительности и с войства однородности и изотропности нашего пространства-времени.
Повернем оси координат в двух системах отсчета вокруг некоторого направления, перпендикулярного скорости u, на 180?. Это приведет замене x на -x и x’ на -x ‘. Если теперь заменить направление скорости u на противоположное, т. е. на -u, то преобразования (L3), (L4) примут вид
t’ = att(-u)t-atx(-u)x,
x’ =-axt(-u)t+axx(-u)x. (L6)
(L7)
Заметим, что
произведенные преобразования привели
к тому, что система k’ движется, как и
прежде, вдоль оси X системы k со скоростью
u. В силу изотропности нашего пространства
(равноправия всех направлений) вид
равенств (L3), (L4) не зависит от направления
осей X, X’ следовательно формулы (L6), (L7)
должны совпадать с (L3), (L4).
а функции axt(u), atx(u) — нечетные.
Теперь учтем, что точка x=0 движется со скоростью -u вдоль оси X’ в системе k’: x’=-ut’. Из уравнений (L3), (L4) следует axt(u)= vuatt(u).
Аналогично точка x’=0 движется со скоростью u вдоль оси X в системе k: x=ut. Из тех же уравнений следует axt(u)= -uaxx(u) или a xx(u)= att(u)?a(u). Вводя для симметрии вместо нечетной функции atx(u) четную функцию g(u) по формуле atx(u)= -ua(u)g(u), получаем t’ = a(u)[t-u g(u)x], x’ = a(u)[x -ut]. (L8)
(L9)
Рассмотрим еще одну инерциальную систему отсчета k», движущуюся со скоростью u ‘ вдоль о си X’ системы k’. Закон преобразования из системы k’ в систему k» должен иметь вид, аналогичный (L8), (L9): t» = a(u’)[t’-u’ g(u’)x’], x» = a(u’)[x’ -u’t’]. (L10) (L11) Подставляя в (L10), (L11) выражения для x’, t’ из (L8), (L9), получаем
С другой стороны, равенства (L12), (L13) описывают переход из системы k в систему k’ , дв ижущуюся вдоль оси X с некоторой скоростью u»:
x»
= a(u»)[x -u»t]. (L14)
(L14)
(L15)
Из сравнения соотношений (L12), (L13) с (L14), (L15) следуют равенства
g(u)=g(u’)=g=const, (L16)
a(u»)=a(u)a(u’)(1+uu’g), (L17)
u»=(u+u’)/(1+uu’g). (L18)
Равенство (L16) вводит некоторую постоянную величину, размерность которой — обратный квадрат скорости. Эта величина одинакова в о всех системах отсчета, и ее численное значение не может быть выведено из каких-либо общих принципов. Экспериментальное значение этой величины g=c-2 , где c — скорость света в вакууме. В классической нерелятивистской механике g=0.
Равенство (L17) — функциональное уравнение, из которого (с учетом (L18)) можно определить вид неизвестной функции a(u)
Галилео Галилей (1564-1642) — презентация онлайн
Галилео Галилей (1564-1642)
Галилей
заложил
фундамент
экспериментальноматематического
естествознания,
соединив
физику
как
науку
о
движении
реальных
тел
с
математикой как наукой
об идеальных объектах.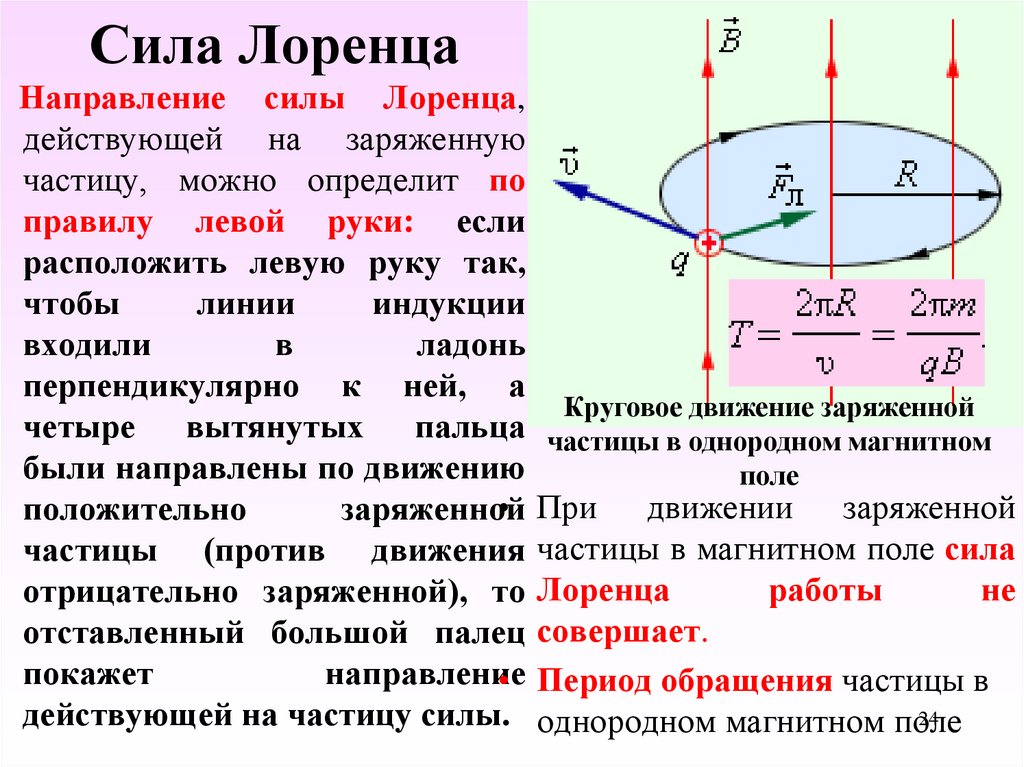
1
2. Метод Галилея
Научный экспериментРассуждения об идеализированных
объектах и событиях
Математизация.
«Книга
природы»
написана на языке математики, а потому
в математике единственно надежный
инструмент для построения научной
системы физики.
«Измеряй
все
доступное
измерению,
и
недоступное
измерению делай доступным»
3. Механистическая картина мира
Аристотельвсякое
движение
предполагает двигатель
2 — любое тело оказывает
сопротивление
движению,
это сопротивление должно
быть преодолено, чтобы
началось
движение,
и
постоянно преодолеваемо,
чтобы
движение
продолжалось
(сопротивление есть причина
последовательности
в
движении).
1
Галилей
1. Если на движущееся тело не
действует силы трения, то
его
движение
по
горизонтальной
плоскости
будет вечным. Движениесобственное и основное,
естественное
состояние
тел.
4. Вклад в становление классической физики
Принцип инерции – если надвижущееся тело не действуют
силы трения, то его движение по
горизонтальной плоскости будет
вечным, оно не может быть
уменьшено,
а
тем
более
уничтожено
5. Инерциальные системы
Подинерциальными
системами
отсчета понимают две (или более)
системы, которые находятся друг
относительно друга в состоянии
либо покоя, либо равномерного
движения.
Новое понимание движения
Движение
–
собственное
и
основное, естественное состояние
тел
Принцип
относительности
движения . (Всякое механическое
явление при одних и тех же
начальных
условиях
протекает
одинаково в любой инерциальной
системе отсчёта.)
Формулировка
закона свободного
падения тел.
1.Приведенное однажды
в
движение
тело
продолжает
двигаться,
пока это движение не
задержится какими-либо
встречными телами.
2.Каждая
частица
материи в отдельности
стремится
продолжить
движение не по кривой, а
исключительно
по
прямой линии.
3. Декартова система
координат
Р. Декарт (1596-1650)
7
Ньютон (1642-1727)
На фундаменте, заложенном
трудами Коперника,
Кеплера, Галилея, Декарта,
построил здание
классической физики.
Сформулировал
I
закон
механики , в котором
объединил идеи Галилея и
Декарта.
«Математические
начала
натуральной философии» –
книга, вошедшая в золотой
фонд науки.
8
9. Аксиомы или законы движения Закон I (закон инерции)
Всякое тело продолжает удерживаться всвоем состоянии покоя или равномерного и
прямолинейного движения, пока и поскольку
оно не понуждается приложенными силами
изменить это состояние.
(Существуют
такие
системы
отсчета,
называемые инерциальными, относительно
которых материальные точки, когда на них не
действуют никакие силы (или действуют силы
взаимно уравновешенные), находятся в
состоянии
покоя
или
равномерного
прямолинейного движения).
10. Закон II (закон ускорения)
Изменениеколичества
движения
пропорционально
приложенной
движущей силе и происходит по
направлению той прямой, по которой
эта
сила
действует.
(Ускорение
движущегося
тела
прямо
пропорционально действующей на него
силе, обратно пропорционально массе
тела и совпадает по направлению с
действующей силой.
11. Закон III
Действию всегда есть равное ипротивоположное
противодействие,
иначе взаимодействия двух тел друг на
друга между собой равны и направлены
в противоположные стороны.
12. Закон всемирного тяготения
Две любые материальные частицыс массами m1 и m2 притягиваются
по направлению к друг другу с
силой F, прямо пропорциональной
произведению масс и обратно
пропорциональной
квадрату
расстояния r между ними.
13. Научная картина мира
НКМ – множество теорий в совокупностиописывающих известный человеку природный
мир, целостная система представлений об
общих принципах и законах устройства
мироздания, особая форма теоретического
знания,
репрезентирующая
предмет
исследования
науки
соответственно
определенному этапу её исторического
развития, посредством которой интегрируются
и систематизируются конкретные знания,
полученные в различных областях научного
поиска
14.
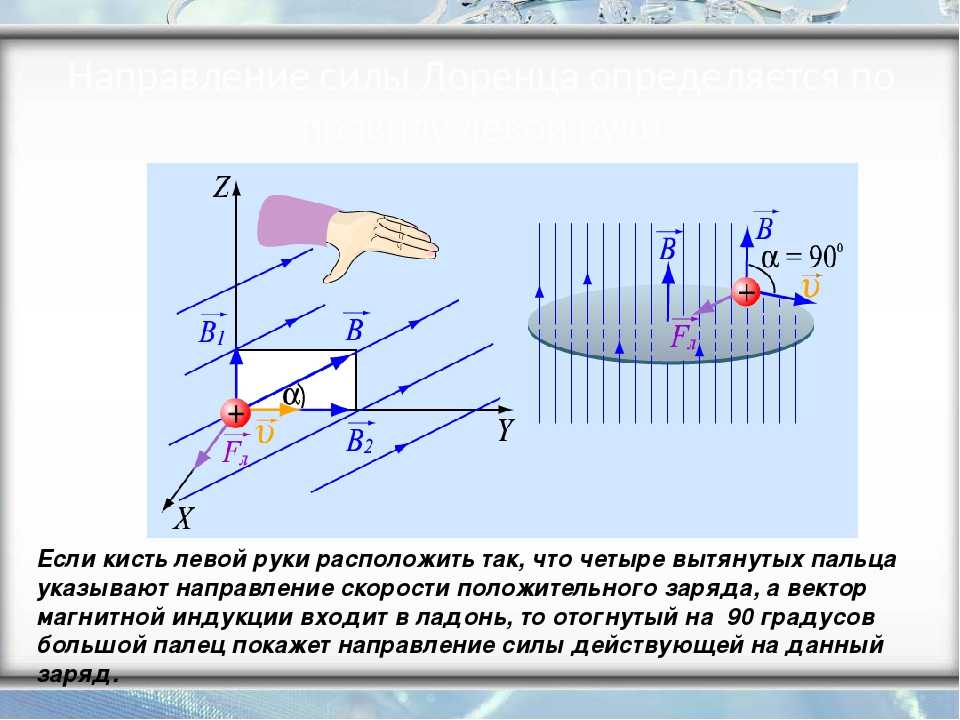 Научная картина мира— научная картина мира представляет систему
Научная картина мира— научная картина мира представляет системуважнейших понятий, законов, принципов,
лежащих в основе понимания окружающей
нас природы.
— научная картина мира функционирует как
особая
исследовательская
программа,
которая
направляет
постановку
задач
эмпирического и теоретического поиска и
осуществляет выбор средств их решения.
15. КМ в истории естествознания
НАТУРФИЛОСОФСКАЯМЕХАНИСТИЧЕСКАЯ
КВАНТОВО-РЕЛЯТИВИСТСКАЯ
ЭВОЛЮЦИОННАЯ
16. Физическая картина мира
Физическая картина мира – это физическая модельприроды, включающая в себя фундаментальные
физические и философские идеи, физические
теории, наиболее общие понятия, принципы и
методы познания, соответствующие определенному
этапу развития физики. Физическая картина мира
обобщает все ранее полученные знания о природе, а
также вводит в физику новые философские идеи и
обусловленные ими понятия, принципы и гипотезы,
которых до этого не было и которые коренным
образом меняют основы физического теоретического
знания.

17. В развитии физического знания выделяют
— Механистическую— Электромагнитную
— Квантово-релятивистскую
картины мира
Ньютоновская механика:
Движение – как вечное и естественное состояние
тел
Абсолютизация механического движения.
Вещественное понимание материи. Масса тела не
зависит от того, движется или покоится тело.
Пространство однородно, размеры тел во всех
системах отсчёта одинаковы, время во всех
инерциальных
системах
отсчёта
течёт
одинаково.
Полная энергия замкнутой системы величина
постоянная.
18
19. Выводы
Механистическаякартина
мира
базируется на корпускулярной теории
строения
материи,
принципе
дальнодействия, представлении об
абсолютном
пространстве
и
абсолютном
времени,
жестком
(лапласовском) детерминизме.
20. Выводы
В основе механической картины мира лежаттакие философские принципы, как принцип
материального единства мира, принцип
причинности
и
законосообразности
природных процессов.
Развитие
экспериментального
естествознания приводит к появлению
принципа экспериментального обоснования
знания,
отказу
от
созерцательности,
установке
на
соединение
экспериментального исследования природы с
описанием ее законов на языке математики.
21. Теория электромагнитного поля и кризис МКМ
Открытия, сделанные в XIX веке,подвергли сомнению возможности
законов
механики
Ньютона
в
качестве универсальных законов
природы.
Такими открытиями в физике стала
теория
электромагнитного
поля
М. Фарадея и Дж. Максвелла, успехи
электродинамики (законы Ампера, Ома).
Эксперименты
Ампера
демонстрировали
два
взаимодополняющих факта о природе
электричества и магнетизма: во-первых,
любой электрический ток порождает
магнитное поле; во-вторых, магнитные
поля оказывают силовое воздействие на
движущиеся электрические заряды.
22
Разрушение идеалов и норм
классической
науки
(механической картины мира)
началось
с
исследования
Фарадеем
явлений
электричества и магнетизма.
Майкл Фарадей (1791–1867)
показал в серии блестящих
экспериментов,
что
взаимодействие
между
движущимися
электрически
заряженными
телами
осуществляется
посредством
электромагнитного поля.
23
Джеймс
Максвелл
(1831–1879) осуществил в
области электродинамики
то же самое, что сделал
Ньютон в механике –
представил в изящной
математической
форме
результаты экспериментов
в
виде
знаменитой
системы
из
четырёх
уравнений
Максвелла
(1860-е гг.).
24
Уравнения
Максвелла
в
электродинамике – это как законы
Ньютона в классической механике
или как постулаты Эйнштейна в
теории относительности.
Уравнения Максвелла – это система
уравнений в дифференциальной
или
интегральной
форме,
описывающая
любые
электромагнитные
поля,
связь
между токами и электрическими
зарядами в любых средах.
Эти уравнения позволили сделать несколько
ключевых выводов:
— Изменяющееся во времени магнитное поле
порождает вихревое электрическое поле,
а переменное электрическое поле является
источником магнитного.

Таким образом, электрическое и магнитное поля
могут существовать без токов и зарядов, непрерывно
возбуждая друг друга.
В результате чего возникают электромагнитные
волны, которые как показал теоретически Максвелл
(1865) и подтвердил экспериментально Г. Герц (1888),
распространяются в вакууме со скоростью света.
26
В соответствии с электромагнитной теорией
мир
представляет
единую
электродинамическую
систему,
построенную из электрически заряженных
частиц, взаимодействующих посредством
электромагнитного
поля.
Важнейшими
понятиями этой теории являются: заряд,
который может быть как положительным, так
и отрицательным; напряженность поля –
сила, которая действует на тело, несущее
единичный заряд, если оно находится в
рассматриваемой точке.
Электромагнитная
картина
мира
базировалась
на
идеях
непрерывности материи, материального
электрического
поля,
неразрывности
материи и движения, связи пространства
и времени как между собой, так и с
движущейся материей.
 Однако дальнейшее
Однако дальнейшееее развитие показало, что она имеет
относительный характер. Поэтому на смену
ей пришла новая квантово-полевая картина
мира, объединившая в себе дискретность
механической картины мира и непрерывность
электромагнитной картины мира
Важным следствием всего этого стал
вывод об электромагнитной природе света.
Тем самым материя предстала не только
как вещество (как в механике Ньютона), но
и как электромагнитное поле.
Как писал А. Эйнштейн, «первый удар по
учению Ньютона о движении как программе
для всей теоретической физики нанесла
максвелловская
теория
электромагнетизма…;
наряду
с
материальной точкой и её движением
появилась
нового
рода
физическая
реальность – поле».
29
Меньше наглядности
Наука на этом этапе становится всё более
математизированной и менее наглядной.
Другими
словами,
тип
научного
объяснения и обоснования изучаемого
объекта
через
построение
наглядной
механической модели уступает место другому
типу объяснения, выраженному в требовании
непротиворечивого
математического
описания объекта, даже в ущерб наглядности.

30
Электромагнитная картина мира
Успехи электродинамики привели к созданию
электромагнитной картины мира, которая объясняла
очень широкий круг явлений на основе одних и тех же
законов (Ампера, Ома, Био–Савара–Лапласа) и более
глубоко выражала единство мира.
Так как электромагнитные явления не сводились
к механическим, то на роль универсальных законов
природы теперь могли претендовать законы
электромагнитных явлений.
31
В 1895-1897 гг. открыты:
— лучи Рентгена,
— радиоактивность (Беккерель), радий (Мария
Склодовская –Кюри и Пьер Кюри),
— Джозеф Томпсон англ. (1856-1940) в 1897 году
открыл электрон и предложил электромагнитную
модель атомов.
Немецкий физик Макс Планк в 1900 г. ввел квант
действия и, исходя из идеи квантов, вывел закон
излучения: «электромагнитная энергия излучается и
поглощается дискретно, порциями (квантами)».
Естественно это входило в противоречие с
понятием материи в теории Максвелла как
непрерывном электромагнитном поле.
Все вышеназванные открытия опровергли
представление об атоме, как о последнем
«неделимом кирпичике» мироздания («материя
32
исчезла»).
В 1911 г. англ. Эрнест Резерфорд в серии
экспериментов обнаружил у атома ядро, размер
которого мал по сравнению с размером атома, но в
котором сосредоточена основная масса атома.
Он предложил планетарную модель атома: ядро и
вращающиеся вокруг него электроны. Резерфорд
открыл – и – лучи, предсказал существование
нейтрона. Но его планетарная модель была
несовместима
с
электромагнитной
теорией
Максвелла.
33
Нильс Бор (1885-1962) в 1913 г. на основе идей
Резерфорда и Планка предложил свою модель атома,
в которой предположил, что электроны вращаются по
нескольким дискретным стационарным орбитам, при
этом вопреки электродинамике не излучают энергии.
Поглощая или испуская кванты энергии, электроны
могут переходить с одной стационарной орбиты на
другую. При переходе – на орбиты более удалённые от
ядра происходит увеличение энергии атома, и
наоборот.

34
Несмотря на обилие экспериментальных результатов,
физики испытывали трудности в согласовании
концептуальных основ механики Ньютона и
электродинамики Максвелла–Лоренца.
А. Эйнштейну в своей теории относительности заявил
о бессмысленности рассмотрения отдельно
электрического и магнитного полей.
35
ОТО и СТО
Две теории
относительности
(общая и специальная),
разработанные
Альбертом
Эйнштейном (18791955) в начале 20 века,
показали
ограниченность
ньютоновской
механики и выход из
противоречий в теории
электромагнетизма.
36
Теория относительности Эйнштейна основана на
двух постулатах:
1) Скорость света одинакова во всех системах
отсчета, движущихся прямолинейно и
равномерно друг относительно друга.
2) Все законы природы одинаковы во всех системах
координат, движущихся прямолинейно и
равномерно друг относительно друга.
СТО (1905 г.) можно представить уравнением
E=mc2, связывающим энергию релятивистских
частиц и их массу.
 Здесь c – скорость света.
Здесь c – скорость света.37
Общая теория относительности (1916 г.)
показала взаимосвязь пространства, времени,
массы и энергии.
Известный тезис этой теории касался того, что
сильное поле тяготения искривляет световые лучи
(пространство).
Это было дополнительно подтверждено
наблюдением отклонения местоположения звёзд во
время солнечного затмения. Пространство и время
испытывают воздействие сил гравитации: при
усилении тяготения пространство сжимается, а
время ускоряется. Гравитация прямо
пропорциональна массе, а согласно СТО масса
связана с энергией.
38
Таким образом, СТО утверждает, что пространство
и время не абсолютны. Они органически связаны с
материей, движением и между собой.
Эти идеи привели к отрицанию единственной и
непререкаемой системы отсчета.
Оказалось, что при наблюдении необходимо
учитывать также положение и движение самого
наблюдателя. Во времена Ньютона Землю
принимали за неподвижную систему отсчёта,
относительно которой можно наблюдать всё
остальное, но Эйнштейн убедительно показал, что
не существует неизменной точки отсчёта – всё
является относительным.

39
40. Общие выводы
Ньютоновская механика:Пространство однородно,
размеры
тел
во
всех
системах отсчёта одинаковы,
время во всех инерциальных
системах
отсчёта
течёт
одинаково.
Полная
энергия
замкнутой системы величина
постоянная.
Масса тела не зависит от
того, движется или покоится
тело.
СТО
(на
основе
математических следствий из
преобразований
Лоренца):
значения пространственных
и временных характеристик
зависят
от
значений
скоростей,
с
которыми
движутся тела.
Длина
тела,
двигающегося со скоростью
близкой к скорости света,
сокращается.
Часы
в
аналогичной ситуации идут
медленнее. В релятивистской
динамике полная энергия и
масса
тела
зависят
от
характера его движения.
41. Спасибо за внимание!
412.3.3 Эксперимент Галилео Галилея. Физика от Аристотеля до Ньютона
Физика от Аристотеля до Ньютона
курсовая работа
В XVII веке господствовала точка зрения Аристотеля, который учил, что скорость падения тела зависит от его массы. Чем тяжелее тело, тем быстрее оно падает. Наблюдения, которые каждый из нас может проделать в повседневной жизни, казалось бы, подтверждают это. Попробуйте одновременно выпустить из рук легкую зубочистку и тяжелый камень. Камень быстрее коснется земли. Подобные наблюдения привели Аристотеля к выводу о фундаментальном свойстве силы, с которой Земля притягивает другие тела. В действительности на скорость падения влияет не только сила притяжения, но и сила сопротивления воздуха. Соотношение этих сил для легких предметов и для тяжелых различно, что и приводит к наблюдаемому эффекту.
Чем тяжелее тело, тем быстрее оно падает. Наблюдения, которые каждый из нас может проделать в повседневной жизни, казалось бы, подтверждают это. Попробуйте одновременно выпустить из рук легкую зубочистку и тяжелый камень. Камень быстрее коснется земли. Подобные наблюдения привели Аристотеля к выводу о фундаментальном свойстве силы, с которой Земля притягивает другие тела. В действительности на скорость падения влияет не только сила притяжения, но и сила сопротивления воздуха. Соотношение этих сил для легких предметов и для тяжелых различно, что и приводит к наблюдаемому эффекту.
Итальянец Галилео Галилей усомнился в правильности выводов Аристотеля и нашел способ их проверить. Для этого он сбрасывал с Пизанской башни в один и тот же момент пушечное ядро и значительно более легкую мушкетную пулю. Оба тела имели примерно одинаковую обтекаемую форму, поэтому и для ядра, и для пули силы сопротивления воздуха были пренебрежимо малы по сравнению с силами притяжения. Галилей выяснил, что оба предмета достигают земли в один и тот же момент, то есть скорость их падения одинакова.
Результаты, полученные Галилеем. — следствие закона всемирного тяготения и закона, в соответствии с которым ускорение, испытываемое телом, прямо пропорционально силе, действующей на него, и обратно пропорционально массе.
Делись добром 😉
Графен и его свойства
5.2 Эксперимент
Подавляющее большинство экспериментальных работ посвящено графену, полученному отшелушиванием объёмного кристалла пиролитического графита…
Действие Комптон-эффекта
1. Эксперимент А.Комптона
Концепция фотонов, предложенная А. Эйнштейном в 1905 г. для объяснения фотоэффекта, в 1922 г. получила экспериментальное подтверждение в опытах американского физика А. Комптона…
Измерение состава сплава висмут-сурьма по длине слитка после направленной кристаллизации методом энергодисперсионного зондирования электронным пучком
2. Эксперимент
2.1 Подготовка образца
В качестве объекта исследования был выбран сплав: Bi-92% Gd-3% Sb-5%.
Для того чтобы провести рентгеноспектральный микроанализ в электронном микроскопе. ..
..
Измерение состава сплава висмут-сурьма по длине слитка после направленной кристаллизации методом энергодисперсионного зондирования электронным пучком
2.2 Эксперимент
Для проведения рентгеноструктурного микроанализа применяется электронный микроскоп растрового типа EVO-40 фирмы Zeiss. Однако для большей достоверности данных в EVO-40 встроены также датчики первичных, вторичных электронов…
История кинематики. Основные понятия кинематики
1.2 Учения Галилео Галилея. Опыт на Пизанской башне
Галилео Галилей (1564-1642) — итальянский физик, механик, астроном, философ и математик, оказавший значительное влияние на науку своего времени. Галилей — основатель экспериментальной физики…
Механика Галилея
2. Теория движения Галилея
Понятия бесконечного и неделимого выполняют важную методологическую функцию в механике Галилея; парадоксальный характер этих понятий кладет свою печать и на галилеевскую теорию движения. Переворот…
Механика Галилея
3.
 Причина и закон в механике Галилея
Причина и закон в механике ГалилеяЕсть у Галилея рассуждение, весьма существенное для понимания его подхода к изучению движения свободного падения тел. Сагредо, как видно из дальнейшего, излагает здесь собственные соображения Галилея…
Нейтринные осцилляции
3.2. Эксперимент Homestake.
За более чем два десятилетия, Дэвис и его помощники регистрировали солнечные нейтрино в глубокой шахте в Южной Дакоте, США. Их детектор содержит атомов C2Cl4. Из таблицы видно, что порог энергии равен 0.814 МэВ…
Основы аэронавтики
3. Демонстрационный эксперимент
Рассмотрим 2 шарика: FА = сг . g . Vm Vm(1) = Vm(2) mg = (mоб + mг)g mоб(1) = mоб(2) т.к. М(возд) = 29 . 10-3 кг/моль, а М(Не) = 4 . 10-3 кг/моль, то М(возд) › М(Не), из этого получаем: m(возд) › m(Не), т.е…
Развитие взглядов на природу света. Явление интерференции света
Эксперимент Майкельсона
В 1881 году американский физик Альберт Абрахам Майкельсон и провёл эксперимент по проверке гипотезы голландского физика-теоретика Хендрика Антона Лоренца, согласно которой должна существовать избранная система отсчёта. ..
..
Развитие оптики
3.1.1 Телескоп и микроскоп Галилея
Первая зрительная труба появилась на рубеже XVI и XVII веков в Голландии, о чем сообщил в 1608г. очковых дел мастер Липперсгейм…
Факторный анализ результатов испытаний генератора (подшипниковый узел) на надежность
1. Полнофакторный эксперимент (ПФЭ)
Факторное планирование эксперимента (ПФЭ). Факторный анализ результатов испытаний генератора (подшипниковый узел) на надежность…
Физика от Аристотеля до Ньютона
2.3.4 Другой эксперимент Галилео Галилея
Галилей замерял расстояние, которое шары, катящиеся по наклонной доске, преодолевали за равные промежутки времени, измеренный автором опыта по водяным часам. Ученый выяснил, что если время увеличить в два раза…
Физика от Аристотеля до Ньютона
3.4 Эксперимент Генри Кавендиша
Установление Ньютоном закона всемирного тяготения явилось важнейшим событием в истории физики. Его значение определяется, прежде всего, универсальностью гравитационного взаимодействия. ..
..
Экспериментальная установка ИРЕН
3.1 Эксперимент
В нашем эксперименте ставилась задача: определить элементный и изотопный состав образца, привезенного из Монголии. Эксперимент проводился на пролетной базе длиной 58,3 м. Площадь образца составлял 314 см2, а масса 547 г…
Уже в 1907 году, когда Эйнштейн и другие исследовали последствия своей специальной теории относительности, он уже думал о более общая теория.
Как он часто делал в своей работе, Эйнштейн использовал «мысленный эксперимент».
Предположим, что ученый заключен где-то в большом ящике, и
что он выпускает камень. Эйнштейн начал искать частные уравнения
— те, которые связывали бы измерения, сделанные двумя наблюдателями
которые движутся произвольным образом относительно друг друга.
Поиски были тяжелыми, целые годы прошли в тупиковых переулках.
Успех в его теоретической работе был закреплен в
1915. Новые уравнения гравитации имели существенное логическое
простота, несмотря на их незнакомую математическую форму. |
ЭЛЕКТРОДИНАМИКА ДВИЖУЩИХСЯ ТЕЛ | Принципы и теории относительности от Галилея до Эйнштейна
Фильтр поиска панели навигации Oxford AcademicПринципы и теории относительности от Галилея до ЭйнштейнаВычислительная физикаИстория физикиМатематическая и статистическая физикаКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicПринципы и теории относительности от Галилея до ЭйнштейнаВычислительная физикаИстория физикиМатематическая и статистическая физикаКнигиЖурналы Термин поиска на микросайте
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
Ссылка
Дарригол, Оливье,
‘Электродинамика движущихся тел
,
Принципы относительности и теории от Галилея до Эйнштейна
(
Oxford,
201111;
(Oxford,
. , 18 августа 2022 г.
, 18 августа 2022 г.
), https://doi.org/10.1093/oso/9780192849533.003.0005,
, по состоянию на 8 октября 2022 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford AcademicПринципы и теории относительности от Галилея до ЭйнштейнаВычислительная физикаИстория физикиМатематическая и статистическая физикаКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicПринципы и теории относительности от Галилея до ЭйнштейнаВычислительная физикаИстория физикиМатематическая и статистическая физикаКнигиЖурналы Термин поиска на микросайте
Advanced Search
Abstract
Электродинамика раньше предполагала относительное движение тел через явление индукции Фарадея. Правила Фарадея и немецкие теории электродинамики предполагали полную относительность электродинамических явлений в самой своей основе. Напротив, максвелловские теории поля подразумевали эффекты движения тел по отношению к эфиру. Максвелл, Герц и Хевисайд восстановили относительность индукции, допустив полное торможение эфира материей вопреки Френелю. Они все еще воображали эффекты движения в эфире, например, уменьшение отталкивания зарядов, путешествующих вместе в эфире. К концу века Лоренц согласовал теорию электромагнитного поля с оптической относительностью, заставив атомы, ионы и электроны свободно перемещаться в неподвижном эфире. Он опирался на преобразования, формально связывающие состояния электродинамической системы, переносимой Землей через эфир, с состоянием той же системы, покоящейся в эфире.
Правила Фарадея и немецкие теории электродинамики предполагали полную относительность электродинамических явлений в самой своей основе. Напротив, максвелловские теории поля подразумевали эффекты движения тел по отношению к эфиру. Максвелл, Герц и Хевисайд восстановили относительность индукции, допустив полное торможение эфира материей вопреки Френелю. Они все еще воображали эффекты движения в эфире, например, уменьшение отталкивания зарядов, путешествующих вместе в эфире. К концу века Лоренц согласовал теорию электромагнитного поля с оптической относительностью, заставив атомы, ионы и электроны свободно перемещаться в неподвижном эфире. Он опирался на преобразования, формально связывающие состояния электродинамической системы, переносимой Землей через эфир, с состоянием той же системы, покоящейся в эфире.
Ключевые слова: электромагнитная индукция, Фарадей, Вильгельм Вебер, Франц Нейман, Максвелл, Хевисайд, Герц, Лоренц, местное время, неподвижный эфир
Предмет
Математическая и статистическая физикаВычислительная физикаИстория физики
В настоящее время у вас нет доступа к этой главе.
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.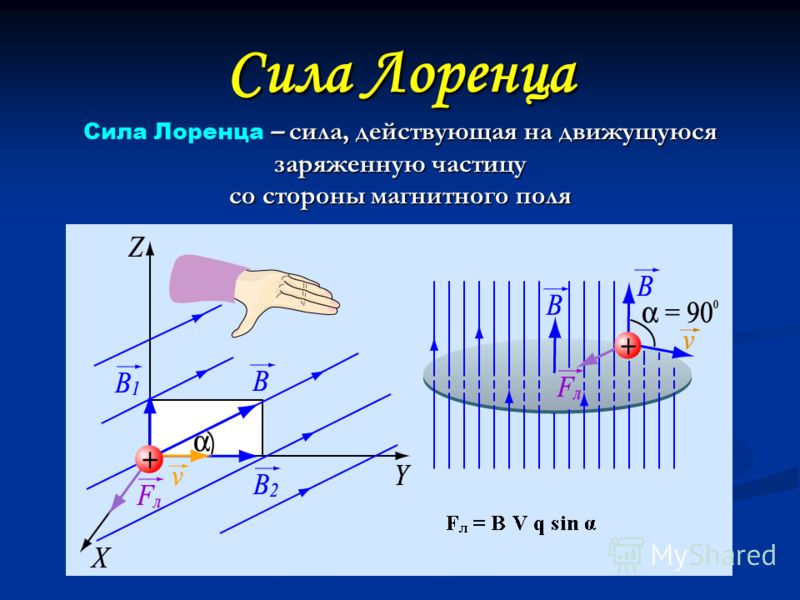
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
д.
Покупка
Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.
Информация о покупке
[PDF] Гравитомагнетизм и гравитационные волны в галилео-ньютоновской физике.
- Идентификатор корпуса: 198179440
@article{Behera2019GravitomagnetismAG,
title={Гравитомагнетизм и гравитационные волны в галилео-ньютоновской физике.},
автор={Харихар Бехера},
Journal={arXiv: Общая физика},
год = {2019}
} - Х. Бехера
- Опубликовано 17 июля 2019 г.
- Физика
- arXiv: General Physics
Принятие формализма Швингера для вывода уравнений Максвелла-Лоренца (MLE) и объединение трех составляющих: (i) законов гравитостатики, (ii) принципа относительности Галилея-Ньютона и (iii) существования гравитационных волн, распространяющихся в вакууме с конечная скорость $c_g$, мы получили два набора уравнений гравито-Максвелла-Лоренца (g-MLEs).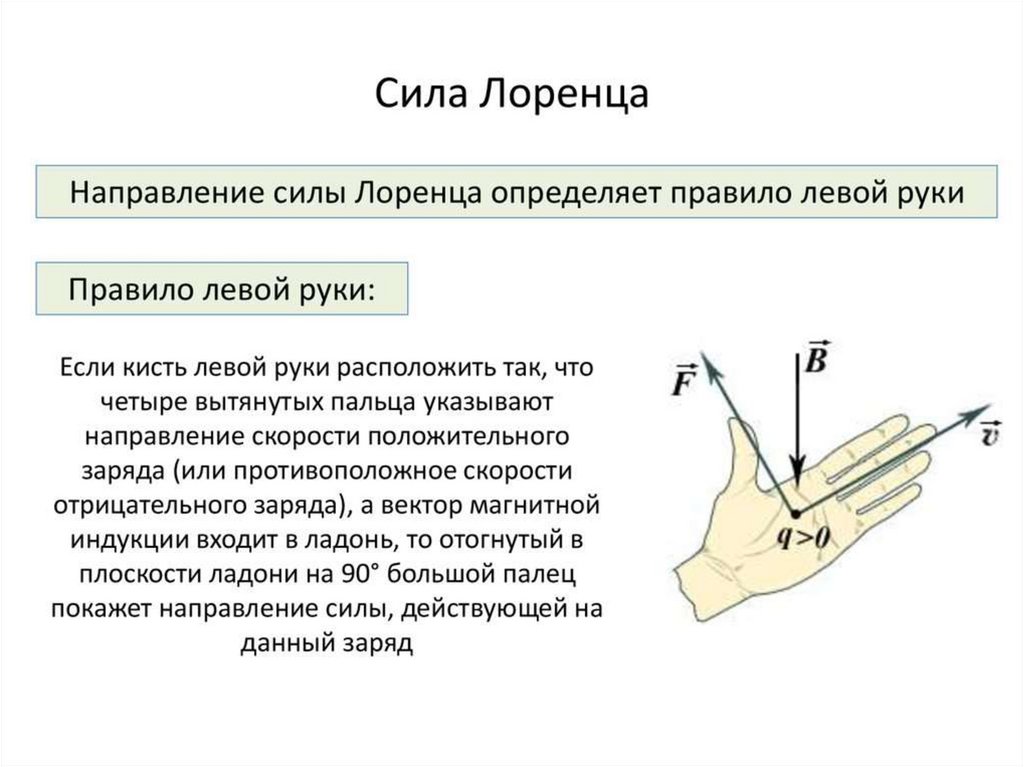 Один из этих наборов соответствует гравитации Хевисайда 1893 года, а другой набор соответствует тому, что мы называем максвелловской гравитацией (МГ). HG и MG…
Один из этих наборов соответствует гравитации Хевисайда 1893 года, а другой набор соответствует тому, что мы называем максвелловской гравитацией (МГ). HG и MG…
[PDF] Semantic Reader
A New Set of Maxwell-Lorentz Equations and Rediscovery of Heaviside-Maxwellian (Vector) Gravity from Quantum Field Theory
- H. Behera, N. Barik
Physics
- 2018
Мы показываем, что если мы начнем со свободного лагранжиана Дирака и потребуем локальной фазовой инвариантности, принимая во внимание полную фазу, происходящую от двух независимых вкладов, связанных с зарядом и массой… Калибровочная инвариантность лагранжиана для массивной нейтральной дираковской частицы
- Х. Бехера
Физика
- 2020
. Начиная с лагранжиана Дирака для свободных массивных электрически нейтральных дираковских частиц и требуя локальной фазовой инвариантности, мы вынуждены ввести безмассовое векторное поле ( ) и найти… в плоском пространстве-времени
- Х.
 Бехера, Н. Барик
Бехера, Н. Барик Физика
- 2020
Эксперимент НАСА с гравитационным зондом B (GP-B) был направлен на проверку теоретических предсказаний релятивистской тензорной теории гравитации Эйнштейна 1916 года в искривленном пространстве-времени (Общая теория относительности (ОТО))…
ПОКАЗАНО 1 -10 ИЗ 44 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантность Наиболее влиятельные статьи Недавность
Фундаментальные физические основы гравитомагнетизма Максвелла-Хевисайда
- Г. Г. Нямбуя
Физика, геология42
- 20094 2015
Гравитомагнетизм общепризнан в современной физике как линейное приближение первого порядка уравнений поля Эйнштейна, вытекающих из общей теории…
Гравитационная связь четырехвекторов распространения волновых функций материи сформулирована в пространстве-времени. Связь на уровне импульса, а не на уровне «силы-закона», значительно упрощает…
Ковариантная теория гравитации в рамках специальной теории относительности.
 относительность. Вводя ковариантность гравитационной силы по отношению к преобразованиям Лоренца, мы…
относительность. Вводя ковариантность гравитационной силы по отношению к преобразованиям Лоренца, мы…ГРАВИТОМАГНИТНЫЕ МОМЕНТЫ И ДИНАМИКА ДИРАКОВСКИХ (СПИН ½) ФЕРМИОНОВ В ПЛОСКОМ ПРОСТРАНСТВЕ-ВРЕМЕНИ МАКСВЕЛЛОВСКАЯ ТЯГОТЕНИЕ
- H. Behera, P.C. Naik
Physics
- 2004
Гравитационные эффекты в релятивистской квантовой механике исследуются в релятивистски выведенной версии пространственно-временной спекулятивной гравитации Хевисайда…
Причинность электромагнитной индукции и гравитации. Иной подход к теории электромагнитного и гравитационного полей.
- Ефименко О.
Физика
- 1992
Чтобы сформировать какое-либо представление о потоке гравитационной энергии, мы должны сначала локализовать энергию. В этом отношении он напоминает легендарного зайца из кулинарной книги. Получится ли идея…
Гравитационные волны от орбитальных двойных систем без общей теории относительности
- Р.
 Хилборн
Хилборн Физика
- 2018
Используя аналогии с гравитационным расчетом электромагнитного излучения, мы излучается при движении по орбите бинарных объектов. Расчет дает результаты, которые имеют…
Линейные уравнения для гравитационного поля
- Д. Каттани
Физика
- 1980
Резюме О введении нового поля (называемого хевисидианским полем зарядов), которое зависит от скорости гравитационного поля так же, как и его магнитная скорость. поле зависит от скоростей электрических…
Комментарии о гравитоэлектромагнетизме Уммарино и Галлерати в «Сверхпроводнике в слабом статическом гравитационном поле» по сравнению с другими версиями
- Х. Бехера
Физика
- 2017
Недавно сообщалось [Eur. физ. JC, 77, 549 (2017). https://doi.org/10.1140/epjc/s10052-017-5116-y] гравитоэлектромагнитные уравнения Уммарино и Галлерати (УГ) в их линеаризованной версии… Физика, образование
Природа
Происхождение инерции веками интересовало ученых и философов, и общая теория относительности Эйнштейна предсказывает, что вращающаяся масса будет «тащить» за собой инерциальную систему отсчета, обзор которой представлен здесь.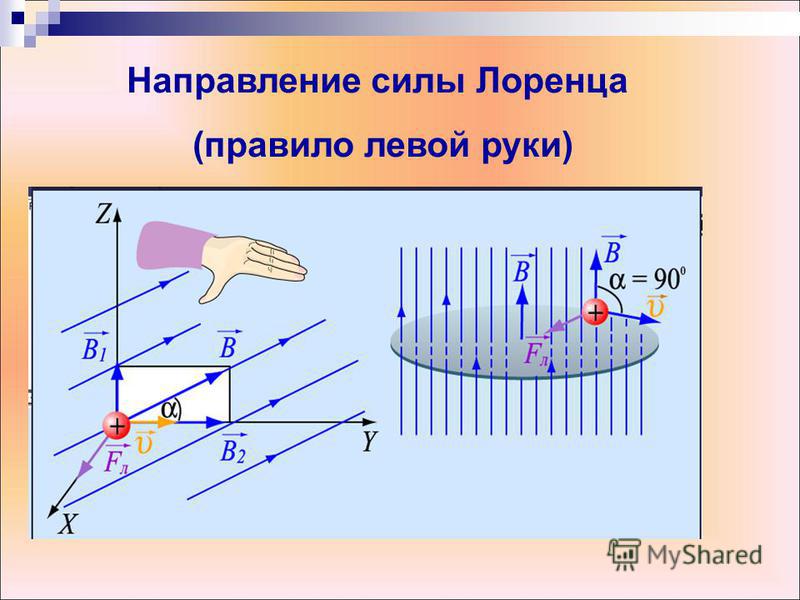


 Специальная теория показала, как соотносить измерения, сделанные в одной лаборатории, к измерениям, сделанным в другой лаборатории, движущейся равномерно относительно первая лаборатория. Мог ли он расширить теорию, чтобы иметь дело с лабораториями? двигаться произвольным образом, ускоряясь, замедляясь, меняя направление? Эйнштейн видел возможную связь между таким ускоренным движением и Знакомая сила тяжести. Он был впечатлен фактом, известным Галилею и Ньютону, но не был полностью оценен до Эйнштейна озадачился этим. Все тела, какими бы разными они ни были, если их освободить от одна и та же высота будет падать с точно таким же постоянным ускорением (при отсутствии сопротивления воздуха). Как инвариантная скорость света, на котором Эйнштейн основал свою специальную теорию относительности, здесь была инвариантность, которая могла бы стать отправной точкой для теории.
Специальная теория показала, как соотносить измерения, сделанные в одной лаборатории, к измерениям, сделанным в другой лаборатории, движущейся равномерно относительно первая лаборатория. Мог ли он расширить теорию, чтобы иметь дело с лабораториями? двигаться произвольным образом, ускоряясь, замедляясь, меняя направление? Эйнштейн видел возможную связь между таким ускоренным движением и Знакомая сила тяжести. Он был впечатлен фактом, известным Галилею и Ньютону, но не был полностью оценен до Эйнштейна озадачился этим. Все тела, какими бы разными они ни были, если их освободить от одна и та же высота будет падать с точно таким же постоянным ускорением (при отсутствии сопротивления воздуха). Как инвариантная скорость света, на котором Эйнштейн основал свою специальную теорию относительности, здесь была инвариантность, которая могла бы стать отправной точкой для теории.
 Ученый видит, как камень падает на
пол коробки с постоянным ускорением. Он мог бы заключить
что его коробка находится в месте, где есть сила тяжести, притягивающая
вниз. Но это может быть неправдой. Вся коробка может быть бесплатной
от силы тяжести, но с ускорением вверх в пустом пространстве на ракете:
камень мог стоять неподвижно, а пол поднимался ему навстречу.
Эйнштейн заметил, что физик в ящике не может отличить
между двумя случаями. Поэтому должна быть какая-то глубокая связь
между ускоренным движением и силой тяжести. Осталось
отработать эту связь.
Ученый видит, как камень падает на
пол коробки с постоянным ускорением. Он мог бы заключить
что его коробка находится в месте, где есть сила тяжести, притягивающая
вниз. Но это может быть неправдой. Вся коробка может быть бесплатной
от силы тяжести, но с ускорением вверх в пустом пространстве на ракете:
камень мог стоять неподвижно, а пол поднимался ему навстречу.
Эйнштейн заметил, что физик в ящике не может отличить
между двумя случаями. Поэтому должна быть какая-то глубокая связь
между ускоренным движением и силой тяжести. Осталось
отработать эту связь. Эйнштейну пришлось овладеть более сложными математическими методами, чем
он когда-либо ожидал, что понадобится, и работать на более высоком уровне абстракции
чем когда-либо прежде. Его друг Мишель
Здесь Бессо оказал решающую помощь. Между тем жизнь его была неустроена.
Он отделился от жены. И он стал участвовать в политике
после того, как разразилась Первая мировая война.
Эйнштейну пришлось овладеть более сложными математическими методами, чем
он когда-либо ожидал, что понадобится, и работать на более высоком уровне абстракции
чем когда-либо прежде. Его друг Мишель
Здесь Бессо оказал решающую помощь. Между тем жизнь его была неустроена.
Он отделился от жены. И он стал участвовать в политике
после того, как разразилась Первая мировая война. Описать
действие гравитации, уравнения показали, как присутствие
материи исказила саму структуру пространства и времени. Этот
деформация будет определять, как объект перемещается. Эйнштейн испытал
свою теорию, правильно рассчитав небольшое несоответствие в
движение планеты Меркурий, несоответствие, которое астрономы
долго не мог объяснить.
Описать
действие гравитации, уравнения показали, как присутствие
материи исказила саму структуру пространства и времени. Этот
деформация будет определять, как объект перемещается. Эйнштейн испытал
свою теорию, правильно рассчитав небольшое несоответствие в
движение планеты Меркурий, несоответствие, которое астрономы
долго не мог объяснить. Бехера, Н. Барик
Бехера, Н. Барик Хилборн
Хилборн