Курс общей физики, Т.2

Курс общей физики, Т.2

Савельев И. В. Курс общей физики: Учеб. пособие. В 3-х т. Т. 2. Электричество и магнетизм. Волны. Оптика. — 3-е изд., испр. — М.: Наука. Гл. ред. физ.-мат. лит., 1988. — 496 с. Второй том трехтомного курса общей физики, созданного профессором Московского инженерно-физического института, заслуженным деятелем науки и техники РСФСР, лауреатом Государственной премии СССР И. В. Савельевым. Главная цель книги — ознакомить студентов с основными идеями и методами физики. Особое внимание обращено на разъяснение смысла физических законов и на сознательное применение их. Для втузов с расширенной программой по физике, однако изложение построено так, что, опустив отдельные места, книгу можно использовать для втузов с обычной программой. Оглавление ПРЕДИСЛОВИЕ МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ЧАСТЬ 1. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ § 1. Электрический заряд § 2. Закон Кулона § 3. Системы единиц § 4. Рационализованная запись формул § 5. Электрическое поле. Напряженность поля § 6. Потенциал § 7. Энергия взаимодействия системы зарядов § 8. Связь между напряженностью электрического поля и потенциалом § 9. Диполь § 10. Поле системы зарядов на больших расстояниях § 11. Описание свойств векторных полей Дивергенция. Циркуляция. Теорема Стокса. § 12. Циркуляция и ротор электростатического поля § 13. Теорема Гаусса § 14. Вычисление полей с помощью теоремы Гаусса Поле двух разноименно заряженных плоскостей. Поле заряженной сферической поверхности. Поле объемно-заряженного шара. ГЛАВА II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ § 15. Полярные и неполярные молекулы § 16. Поляризация диэлектриков § 17. Поле внутри диэлектрика § 18. Объемные и поверхностные связанные заряды § 19. Вектор электрического смешения § 20. Примеры на вычисление поля в диэлектриках § 21. Условия на границе двух диэлектриков § 22. Силы, действующие на заряд в диэлектрике § 23. Сегнетоэлектрики ГЛАВА III. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ § 24. Равновесие зарядов на проводнике § 25. Проводник во внешнем электрическом поле § 26. Электроемкость § 27. Конденсаторы ГЛАВА IV. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ § 28. Энергия заряженного проводника § 29. Энергия заряженного конденсатора § 30. Энергия электрического поля ГЛАВА V. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 31. Электрический ток § 32. Уравнение непрерывности § 33. Электродвижущая сила § 34. Закон Ома. Сопротивление проводников § 35. Закон Ома для неоднородного участка цепи § 36. Разветвленные цепи. Правила Кирхгофа § 37. Мощность тока § 38. Закон Джоуля — Ленца ГЛАВА VI. МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ § 39. Взаимодействие токов § 40. Магнитное поле § 41. Поле движущегося заряда § 42. Закон Био — Савара § 43. Сила Лоренца § 44. Закон Ампера § 45. Магнитное взаимодействие как релятивистский эффект § 46. Контур с током в магнитном поле § 47. Магнитное поле контура с током § 48. Работа, совершаемая при перемещении тока в магнитном § 49. Дивергенция и ротор магнитного поля § 50. Поле соленоида и тороида ГЛАВА VII. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ § 51. Намагничение магнетика § 52. Напряженность магнитного поля § 53. Вычисление поля в магнетиках § 54. Условия на границе двух магнетиков § 55. Виды магнетиков § 56. Магнитомеханические явления § 57. Диамагнетизм § 58. Парамагнетизм § 59. Ферромагнетизм ГЛАВА VIII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 60. Явление электромагнитной индукции § 61. Электродвижущая сила индукции § 62. Методы измерения магнитной индукции § 63. Токи Фуко § 64. Явление самоиндукции § 65. Ток при замыкании и размыкании цепи § 66. Взаимная индукция § 67. Энергия магнитного поля § 68. Работа перемагничивания ферромагнетика ГЛАВА IX. УРАВНЕНИЯ МАКСВЕЛЛА § 69. Вихревое электрическое поле § 70. Ток смещения § 71. Уравнения Максвелла ГЛАВА X. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ПОЛЯХ § 72. Движение заряженной частицы в однородном магнитном поле § 73. Отклонение движущихся заряженных частиц электрическим и магнитным полями § 74. Определение заряда и массы электрона § 75. Определение удельного заряда ионов. Масс-спектрографы § 76. Ускорители заряженных частиц ГЛАВА XI. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ § 77. Природа носителей тока в металлах § 78. Элементарная классическая теория металлов § 79. Эффект Холла ГЛАВА XII. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ § 80. Несамостоятельная и самостоятельная проводимость § 81. Несамостоятельный газовый разряд § 82. Ионизационные камеры и счетчики § 83. Процессы, приводящие к появлению носителей тока при самостоятельном разряде § 84. Газоразрядная плазма § 85. Тлеющий разряд § 86. Дуговой разряд § 87. Искровой и коронный разряды ГЛАВА XIII. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ § 88. Квазистационарные токи § 89. Свободные колебания в контуре без активного сопротивления § 90. Свободные затухающие колебания § 91. Вынужденные электрические колебания § 92. Переменный ток ЧАСТЬ 2. ВОЛНЫ § 93. Распространение волн в упругой среде § 94. Уравнения плоской и сферической волн § 95. Уравнение плоской волны, распространяющейся в произвольном направлении § 96. Волновое уравнение § 97. Скорость упругих волн в твердой среде § 98. Энергия упругой волны § 99. Стоячие волны § 100. Колебания струны § 101. Звук § 102. Скорость звука в газах § 103. Эффект Доплера для звуковых волн ГЛАВА XV. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ § 104. Волновое уравнение для электромагнитного поля § 105. Плоская электромагнитная волна § 106. Экспериментальное исследование электромагнитных волн § 107. Энергия электромагнитных волн § 108. Импульс электромагнитного поля § 109. Излучение диполя ЧАСТЬ 3. ОПТИКА § 110. Световая волна § 111. Представление гармонических функций с помощью экспонент § 112. Отражение и преломление плоской волны на границе двух диэлектриков § 113. Световой поток § 114. Фотометрические величины и единицы § 115. Геометрическая оптика § 116. Центрированная оптическая система § 117. Тонкая линза § 118. Принцип Гюйгенса ГЛАВА XVII. ИНТЕРФЕРЕНЦИЯ СВЕТА § 119. Интерференция световых волн § 120. Когерентность § 121. Способы наблюдения интерференции света § 122. Интерференция света при отражении от тонких пластинок § 123. Интерферометр Майкельсона § 124. Многолучевая интерференция ГЛАВА XVIII. ДИФРАКЦИЯ СВЕТА § 126. Принцип Гюйгенса—Френеля § 127. Зоны Френеля § 128. Дифракция Френеля от простейших преград § 129. Дифракция Фраунгофера от щели § 130. Дифракционная решетка § 131. Дифракция рентгеновских лучей § 132. Разрешающая сила объектива § 133. Голография ГЛАВА XIX. ПОЛЯРИЗАЦИЯ СВЕТА § 134. Естественный и поляризованный свет § 135. Поляризация при отражении и преломлении § 136. Поляризация при двойном лучепреломлении § 137. Интерференция поляризованных лучей § 138. Прохождение плоскополяризованного света через кристаллическую пластинку § 139. Кристаллическая пластинка между двумя поляризаторами § 140. Искусственное двойное лучепреломление § 141. Вращение плоскости поляризации ГЛАВА XX. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН С ВЕЩЕСТВОМ § 142. Дисперсия света § 143. Групповая скорость § 144. Элементарная теория дисперсии § 145. Поглощение света § 146. Рассеяние света § 147. Эффект Вавилова — Черенкова ГЛАВА XXI. ОПТИКА ДВИЖУЩИХСЯ СРЕД § 148. Скорость света § 149. Опыт Физо § 150. Опыт Майкельсона § 151. Эффект Доплера ПРИЛОЖЕНИЯ I. Единицы электрических и магнитных величин в СИ и в гауссовой системе Приложение II. Основные формулы электромагнетизма в СИ и в гауссовой системе Приложение III. Векторный потенциал

. Сила Лоренца

Сила Лоренца – это сила, действующая на электрический заряд, движущийся в магнитном поле.

Модуль силы: . (10.2.1)

Здесь q − величина движущегося заряда,

υ – скорость, с которой заряд влетает в магнитное поле, В − модуль индукции магнитного поля, α − угол между векторами и .

Н аправление силы, действующей на положительный заряд, определяется по правилу левой руки: вектор входит в ладонь, четыре вытянутых пальца направлены по скорости, большой отогнутый на 90⁰ палец показывает направление силы Лоренца. На отрицательный

заряд сила Лоренца действует в противоположном Рис. 10.2.1

направлении.

Траектория движения частицы в магнитном поле зависит от взаимной ориентации векторов и :

1. Если скорость частицы перпендикулярна вектору (α=90⁰), то в магнитном поле частица движется по окружности.

На рис. 10.2.2, а и b вектор магнитного поля направлен к читателю из листа (точка в кружке), на рис. 10.2.2, c и d  от читателя (крестик в кружке). Пунктирная окружность – область магнитного поля. На рис. 10.2.2, а представлено движение положительно заряженной частицы. Воспользовавшись правилом левой руки, делаем вывод, что в момент попадания частицы в магнитное поле сила Лоренца направлена вертикально вниз (на рис. 10.2.2, а не указана). Эта сила приводит к постепенному изменению направления скорости, в результате чего частица движется по окружности «вниз». Аналогично правилом левой руки объясняется характер движения частиц на рис. 10.2.2, b,c,d.

Рис. 10.2.2

Частица движется по окружности, поскольку сила Лоренца является центростремительной:

(10.2.2)

или

. (10.2.3)

Выражение (10.2.3) позволяет получить формулы для расчета радиуса окружности R и периода обращения T соответственно:

, (10.2.4)

. (10.2.5)

Отметим, что сила Лоренца в данном случае не совершает работы, поэтому при движении частицы ее кинетическая энергия не изменяется.

2. Если скорость частицы параллельна вектору (α=0⁰), то при попадании в магнитное поле модуль и направление скорости не изменяются, т. е. частица движется равномерно и прямолинейно.

3. Если скорость частицы направлена под углом к вектору (0⁰<α<90⁰), то в магнитном поле частица движется по спирали, ось которой параллельна магнитному полю.

4. Если на движущуюся частицу одновременно действуют и магнитное, и электрическое поля, то результирующая сила: . Траектория движения зависит от взаимного направления полей и скорости частицы.

Сила Ампера – это сила, действующая на проводник с током, помещенный в магнитное поле.

Модуль силы: . (10.3.1)

Здесь I – сила тока, l – длина проводника, В − модуль индукции магнитного поля, α − угол между вектором и проводником с током.

Сила ампера, приложенная к малому элементу проводника с током I, равна геометрической сумме сил, которые действуют со стороны магнитного поля на движущиеся в проводнике носители тока.

Н аправление силы, действующей на проводник, определяется по правилу левой руки: перпендикулярная составляющая вектора входит в ладонь, четыре вытянутых пальца направлены по току, большой отогнутый на 90° палец показывает направление силы Ампера. Рис. 10.3.1

Взаимодействие параллельных токов: между двумя параллельно расположенными бесконечно длинными проводниками, по которым протекают постоянные токи I₁ и I₂, возникает сила взаимодействия, модуль которой равен

, (10.3.2)

где R — расстояние между проводниками.

Проводники с одинаково направленными токами притягиваются, с противоположно направленными токами — отталкиваются.

Работа по перемещению проводника и контура с током в магнитном поле:

(10.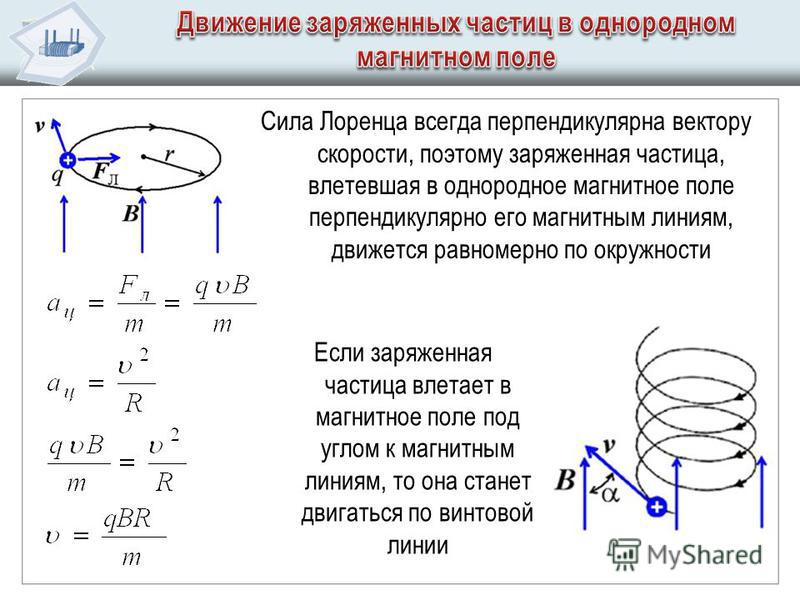 3.3)

или

. (10.3.4)

Здесь dS – площадь, пересекаемая проводником при перемещении в магнитном поле, dФ – магнитный поток.

электромагнетизм — Какова *причина* силы Лоренца

В чем причина силы Лоренца?

«Винтовая» природа электромагнетизма. Минковский упоминал об этом в «Пространстве и времени», как и Максвелл в «О физических силовых линиях: », «поступательное движение вдоль оси не может вызвать вращение вокруг этой оси, если оно не встречается с каким-то особым механизмом, например, с винтом» . . Вот почему правило правой руки применимо как к электромагнетизму, так и к резьбе. ИМХО, чтобы действительно «понять» это, вы должны принять к сведению классическую электродинамику Джексона: «правильно следует говорить об электромагнитном поле Fμν, а не отдельно о E или B». Затем нужно изобразить Fμν для электрона. Один упрощенный способ сделать это — скомбинировать радиальные линии электрического поля с концентрическими линиями магнитного поля, например:

Это упрощенно, но теперь вы начинаете понимать «спинорную» природу электрона.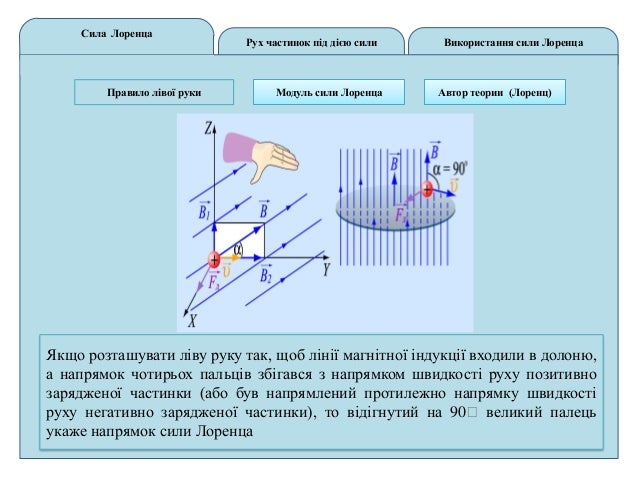 И если вы обратили внимание на заголовок страницы Максвелла, вы можете понять, что вихрей, вращающихся в противоположных направлениях, притягивают и 9 вихрей.0007 вихри, вращающиеся в одном направлении, отталкивают . Хотя электрон не связан с каким-либо движением жидкости, существует вектор Пойнтинга и «циркулирующий поток энергии», так что аналогия работает. В результате, если вы поместите электрон рядом с позитроном, они будут двигаться навстречу друг другу по прямой линии. Но если бросить электрон мимо позитрона, они тоже будут двигаться вокруг друг друга, примерно так:

Это то, что мы видим в позитронии, а теперь сила Лоренца $\mathbf{F} = q\left[\ mathbf{E} + (\mathbf{v} \times \mathbf{B})\right]$ выглядит очевидным. Это просто комбинация линейной и вращательной силы, возникающая в результате «спинорного» взаимодействия электромагнитного поля. И это соответствует КЭД в том смысле, что электрон и позитрон «обмениваются полем». Позитроний подобен водороду, но легче и недолговечен, а, как вы знаете, у водорода нет сильного поля $^*$.

Можно ли объяснить, что на самом деле вызывает силу, действующую на проводник с током в магнитном поле?

Да. Вы можете достаточно легко понять линейные и вращательные силы между заряженными частицами. Следующим шагом является понимание силы вращения заряженной частицы вблизи проводника с током. По сути, это неподвижный столб ионов металлов и движущийся столб электронов. Вы когда-нибудь читали, что Эйнштейн говорил о поле как о состоянии пространства? Хорошо, видите гравитомагнитное поле, которое автор НАСА Тони Филлипс описывает как «искривленное пространство»? Вы можете думать об электромагнитном поле как о чем-то подобном, но немного более интенсивном. Только если бы у вас было движение относительно него, вы могли бы подумать об этом как о «поворотном пространстве» и начать говорить о завитке, также известном как гниение, что является сокращением от ротора. ИМХО, это ключ к пониманию того, как работают магниты. Все электроны имеют отрицательное электромагнитное поле, а все ионы металлов имеют положительное электромагнитное поле с противоположной хиральностью. *$. Однако электроны движутся вверх по проводу:

Получается, что вы движетесь по одному набору поворотных полей, но не по другому. И когда у вас есть движение относительно поля кручения, вы думаете о нем как о поле вращений, , и это то, что представляет собой магнитное поле . Итак, то, что вы «видите», — это остаточное магнитное поле вокруг провода. Электрон, брошенный мимо провода, движется по кругу не из-за какой-то магической силы, действующей на расстоянии, а потому, что это «динамический спинор в пространстве, затянутом системой отсчета».

Последний шаг — понять, почему два провода движутся вместе. Для этого вы можете представить себе, что ваш электрон заключен в соседний провод. Он движется вверх, и он движется по кругу. Это вращение означает, что остаточное поле поворота выглядит как поле закручивания, а поскольку вращения представляют собой противоположные вращения влево и вправо, вы снова находитесь в ситуации, когда вихрей, вращающихся в противоположных направлениях, притягивают .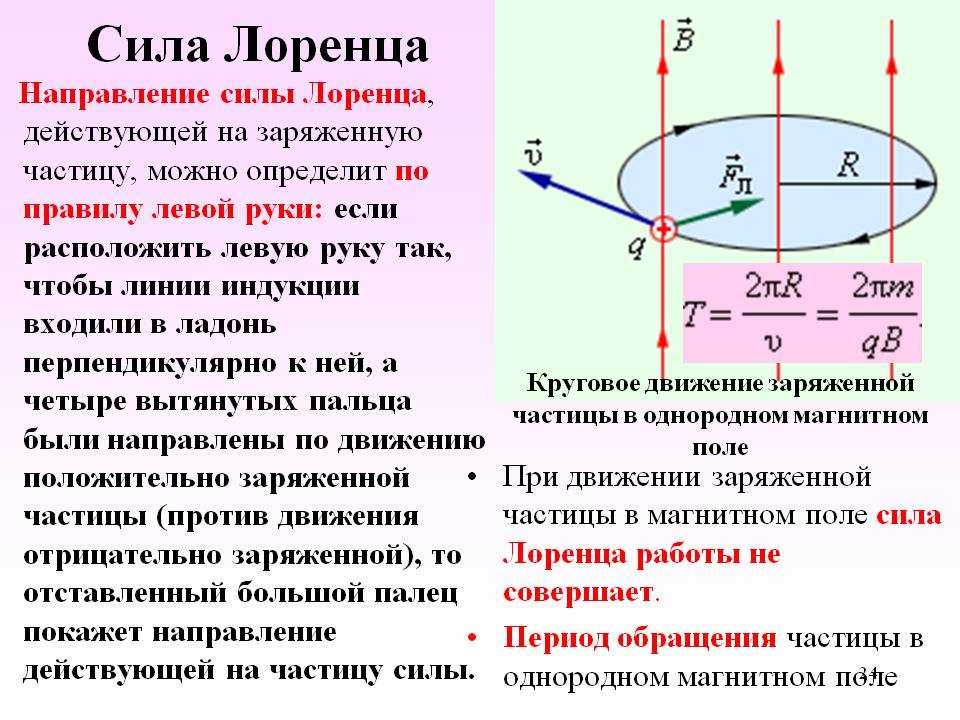 Между двумя проводами существует чистое линейное притяжение. Для катапульты согните один из проводов в петлю, чтобы сделать примитивный соленоид, а затем в несколько петель, чтобы получить лучший соленоид, который похож на стержневой магнит. Затем согните его в форме подковы и поместите другой провод между полюсами следующим образом:

_{Изображение предоставлено физикой SPM}

Опять же, он движется.

$*$ _{Остаточное поле существует, но мы не называем его электрическим полем или магнитным полем. Или электромагнитное поле. Или гравитомагнитное поле.}

Сила Лоренца Определение и значение

• Основные определения
• Викторина
• Примеры
• Научная

Показывает уровень сложности слова.

Сохрани это слово!

Показывает уровень оценки в зависимости от сложности слова.

---

сущ. Электричество.

сила, действующая на заряженную частицу, движущуюся через область, содержащую как электрические, так и магнитные поля.

ВИКТОРИНА

ВЫ ПРОЙДЕТЕ ЭТИ ГРАММАТИЧЕСКИЕ ВОПРОСЫ ИЛИ НАТЯНУТСЯ?

Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!

Вопрос 1 из 7

Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.

Происхождение силы Лоренца

Впервые зафиксировано в 1960–65; имени Г. А. Лоренца

Слова рядом сила Лоренца

Лорелей, Лорен, Лорена, Лоренц, Лоренц-Фицджеральд сокращение, сила Лоренца, преобразование Лоренца, Лоренц, Лоренцетти, Лоренцо, lo-res

Dictionary.com Unabridged Основано на словаре Random House Unabridged Dictionary, © Random House, Inc. 2023

Как использовать силу Лоренца в предложении

• Тем не менее в течение десятилетия или около того аморальность была, как ни парадоксально, силой для грамотности и расширения прав и возможностей.

  Как криминальное чтиво спасло литературу|Венди Смит|8 января 2015|DAILY BEAST

• Вскоре после рассвета произошла еще одна вспышка смертоносной силы.

  Франция скорбит и охотится|Нико Хайнс, Кристофер Дики|8 января 2015 г.|DAILY BEAST

• И оценщики ВВС первыми говорят, что такое изображение никогда не рассказывает всей истории.

  Пентагон не знает, сколько людей было убито в войне с ИГИЛ|Нэнси А. Юссеф|7 января 2015 г.|DAILY BEAST

• Детективы с оперативной группой по поиску беглецов настигли Поланко и его друга на улице Бронкса ранним днем.

  Сбит во время замедления работы полиции Нью-Йорка|Майкл Дейли|7 января 2015 г.|DAILY BEAST

• Пентагон сообщил, что Фаал служил в ВВС семь лет, за это время он стал гражданином США.

  Темный ветеран США, который пытался свергнуть страну|Джейкоб Сигел|6 января 2015 г.|DAILY BEAST

• Голиаф не отвечал; Дублин сказал, что силы уходят, и мы вообще не можем связаться с солдатами.

  Дневник Галлиполи, Том I|Иэн Гамильтон

• Для такого использования голоса в особой службе силы воли или движущей силы необходимо сначала проверить его свободу.

  Выразительный голос Культура|Джесси Элдридж Саутвик

• Но вы ошибаетесь, думая, что силы запада состоят из всей Меррилл Хорс.

  Курьер Озарков|Байрон А. Данн

• Она и ее младшая сестра Джанет много ссорились по злополучной привычке.

  Пробуждение и избранные рассказы|Кейт Шопен

• Во время разрушения они изольют свою силу и умилостивят гнев того, кто их сотворил.

  Библия, Версия Дуэ-Реймса|Разные

Научные определения силы Лоренца

Сила Лоренца

---

Суммарная сила, действующая на заряженную частицу электрическим и магнитным полями. На все заряженные частицы действует сила электрического поля, ориентированная в направлении поля (или в противоположном направлении, в зависимости от знака заряда), а движущиеся заряженные частицы также сталкиваются с силой, направленной под прямым углом к ​​обоим направлениям.