PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

Определение направления силы лоренца. Сила лоренца

Наряду с силой Ампера, кулоновского взаимодействия, электромагнитными полями в физике часто встречается понятие сила Лоренца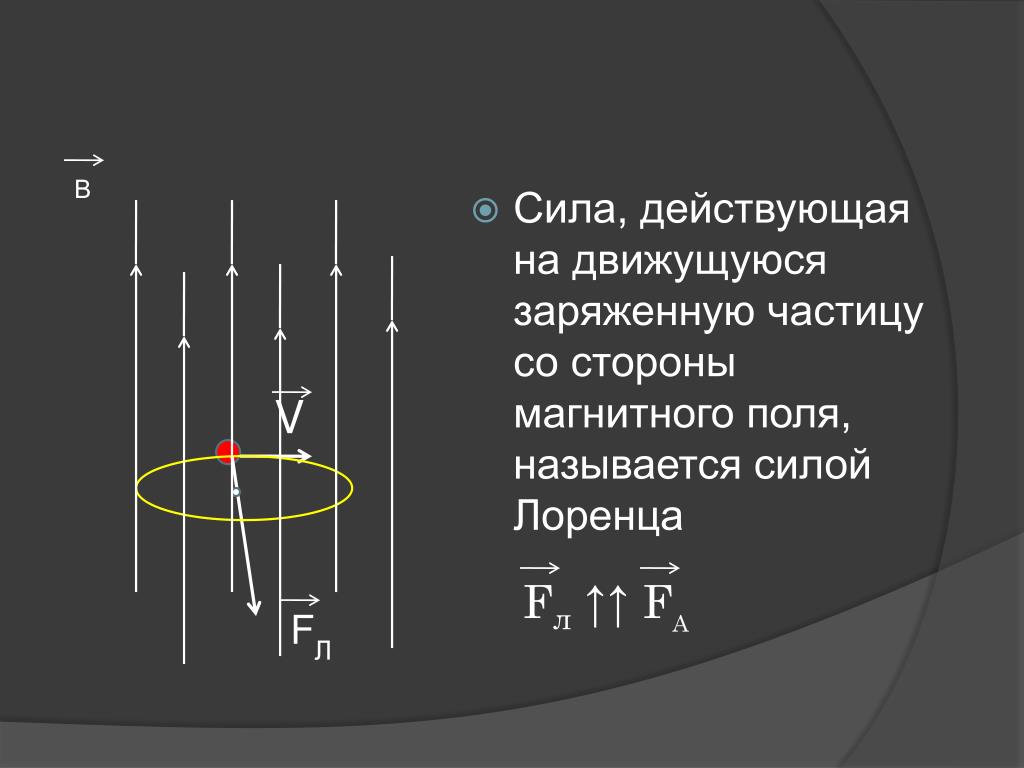. Это явление является одним из основополагающих в электротехнике и электронике, на ряду с , и прочими. Она воздействует на заряды, которые двигаются в магнитном поле. В этой статье мы кратко и понятно рассмотрим, что такое сила Лоренца и где она применяется.

Определение

Когда электроны движутся по проводнику – вокруг него возникает магнитное поле. В то же время, если поместить проводник в поперечное магнитное поле и двигать его – возникнет ЭДС электромагнитной индукции. Если через проводник, который находится в магнитном поле, протекает ток – на него действует сила Ампера.

Её величина зависит от протекающего тока, длины проводника, величины вектора магнитной индукции и синуса угла между линиями магнитного поля и проводником. Она вычисляются по формуле:

Рассматриваемая сила отчасти похожа на ту, что рассмотрена выше, но действует не на проводник, а на движущуюся заряженную частицу в магнитном поле. Формула имеет вид:

Важно! Сила Лоренца (Fл) действует на электрон, движущийся в магнитном поле, а на проводник – Ампера.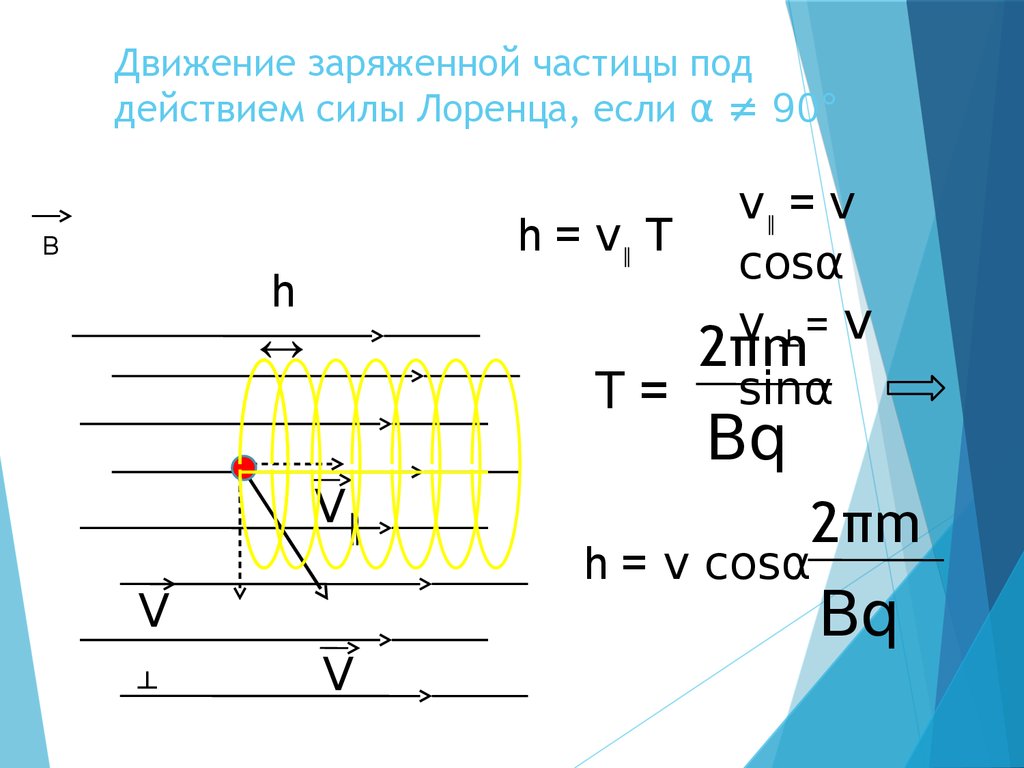

Из двух формул видно, что и в первом и во втором случае, чем ближе синус угла aльфа к 90 градусам, тем большее воздействие оказывает на проводник или заряд Fа или Fл соответственно.

Итак, сила Лоренца характеризует не изменение величины скорости, а то, какое происходит воздействие со стороны магнитного поля на заряженный электрон или положительный ион. При воздействии на них Fл не совершает работы. Соответственно изменяется именно направление скорости движения заряженной частицы, а не её величина.

Что касается единицы измерения силы Лоренца, как и в случае с другими силами в физике используется такая величина как Ньютон. Её составляющие:

Как направлена сила Лоренца

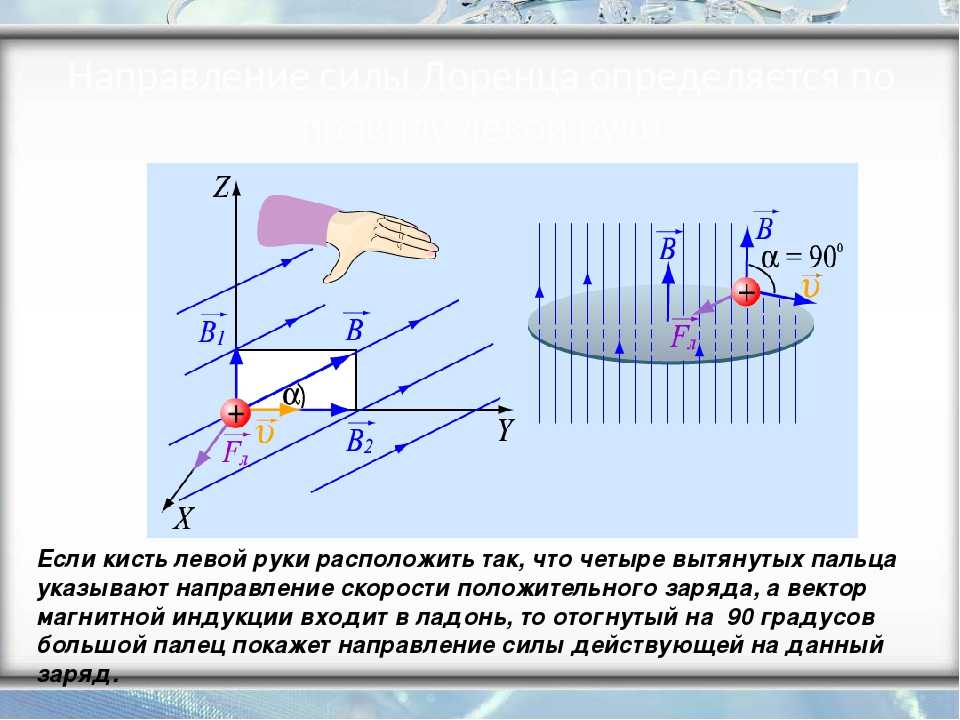
Чтобы определить направление силы Лоренца, как и с силой Ампера, работает правило левой руки. Это значит, чтобы понять, куда направлено значение Fл нужно раскрыть ладонь левой руки так, чтобы в руку входили линии магнитной индукции, а вытянутые четыре пальца указывали направление вектора скорости.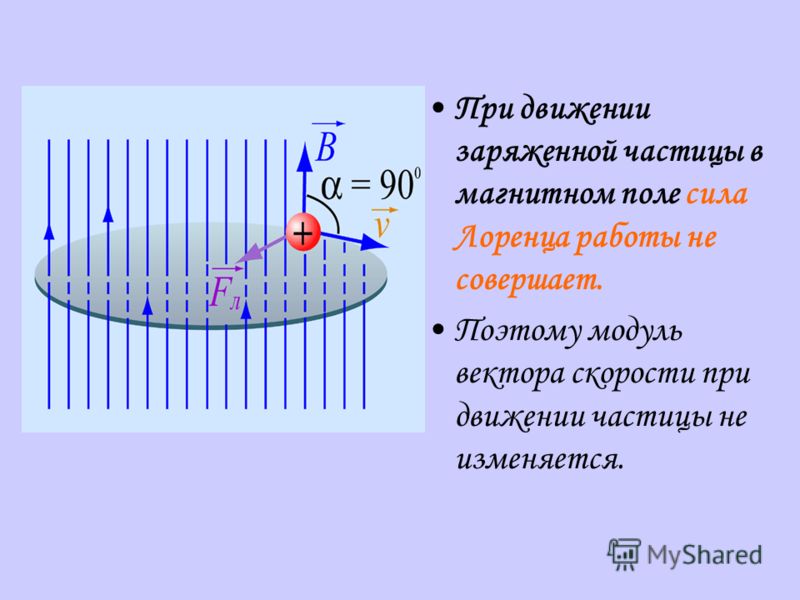

Тогда большой палец, отогнутый под прямым углом к ладони, указывает направление силы Лоренца. На картинке ниже вы видите, как определить направление.

Внимание! Направление Лоренцового действия перпендикулярно движению частицы и линиям магнитной индукции.

При этом, если быть точнее, для положительно и отрицательно заряженных частиц имеет значение направление четырёх развернутых пальцев. Выше описанное правило левой руки сформулировано для положительной частицы. Если она заряжена отрицательно, то линии магнитной индукции должны быть направлены не в раскрытую ладонь, а в её тыльную сторону, а направление вектора Fл будет противоположным.

Теперь мы расскажем простыми словами, что даёт нам это явление и какое реальное воздействие она оказывает на заряды. Допустим, что электрон движется в плоскости, перпендикулярной направлению линий магнитной индукции. Мы уже упомянули, что Fл не воздействует на скорость, а лишь меняет направление движения частиц.

Тогда сила Лоренца будет оказывать центростремительное воздействие. Это отражено на рисунке ниже.

Применение

Из всех сфер, где используется сила Лоренца, одной из масштабнейших является движение частиц в магнитном поле земли. Если рассмотреть нашу планету как большой магнит, то частицы, которые находятся около северного магнитного полюсов, совершают ускоренное движение по спирали. В результате этого происходит их столкновение с атомами из верхних слоев атмосферы, и мы видим северное сияние.

Тем не менее, есть и другие случаи, где применяется это явление. Например:

• Электронно-лучевые трубки. В их электромагнитных отклоняющих системах. ЭЛТ применялись больше чем 50 лет подряд в различных устройствах, начиная от простейшего осциллографа до телевизоров разных форм и размеров. Любопытно, что в вопросах цветопередачи и работы с графикой некоторые до сих пор используют ЭЛТ мониторы.
• Электрические машины – генераторы и двигатели. Хотя здесь скорее действует сила Ампера. Но эти величины можно рассматривать как смежные. Однако это сложные устройства при работе которых наблюдается воздействие многих физических явлений.
• В ускорителях заряженных частиц для того, чтобы задавать им орбиты и направления.

Заключение

Подведем итоги и обозначим четыре основных тезиса этой статьи простым языком:

1. Сила Лоренца действует на заряженные частицы, которые движутся в магнитном поле. Это вытекает из основной формулы.
2. Она прямо пропорциональна скорости заряженной частицы и магнитной индукции.
3. Не влияет на скорость частицы.
4. Влияет на направление частицы.

Её роль достаточно велика в «электрических» сферах. Специалист не должен упускать из вида основные теоретические сведения об основополагающих физических законах. Эти знания пригодятся, как и тем, кто занимается научной работой, проектированием и просто для общего развития.

Теперь вы знаете, что такое сила Лоренца, чему она равна и как действует на заряженные частицы.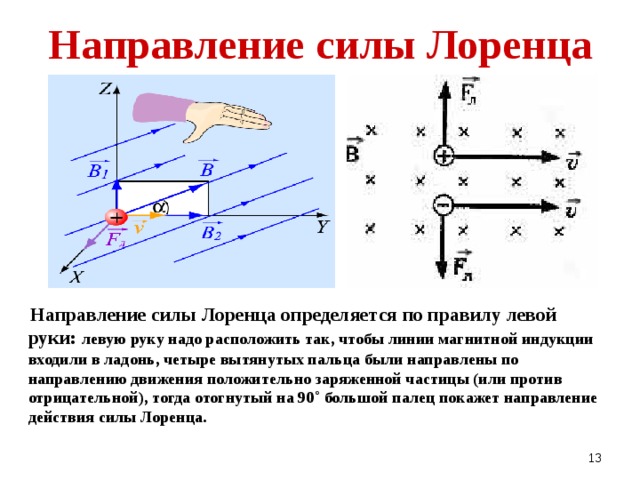

Если возникли вопросы, задавайте их в комментариях под статьей!

Материалы

ОПРЕДЕЛЕНИЕ

Сила Лоренца – сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле.

Она равна произведению заряда, модуля скорости частицы, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и скоростью движения частицы.

Здесь – сила Лоренца, – заряд частицы, – модуль вектора индукции магнитного поля, – скорость частицы, – угол между вектором индукции магнитного поля и направления движения.

Единица измерения силы – Н (ньютон) .

Сила Лоренца — векторная величина. Сила Лоренца принимает своё наибольшее значение когда векторы индукции и направления скорости частицы перпендикулярны ().

Направление силы Лоренца определяют по правилу левой руки:

Если вектор магнитной индукции входит в ладонь левой руки и четыре пальца вытянуты в сторону направления вектора движения тока, тогда отогнутый в сторону большой палец показывает направление силы Лоренца.

В однородном магнитном поле частица будет двигаться по окружности, при этом сила Лоренца будет центростремительной силой. Работа при этом не будет совершаться.

Примеры решения задач по теме «Сила Лоренца»

ПРИМЕР 1

ПРИМЕР 2

Задание	Под действием силы Лоренца частица массы m с зарядом q движется по окружности. Магнитное поле однородно, его напряжённость равна B. Найти центростремительное ускорение частицы.
Решение	Вспомним формулу силы Лоренца: Кроме того, по 2 закону Ньютона: В данном случае сила Лоренца направлена к центру окружности и ускорение, ею создаваемое, направлено туда же, то есть это и есть центростремительное ускорение. Значит:

но ток причем , тогда

Т.к. nS dl – число зарядов в объёме S dl , тогда для одного заряда

или

,

(2. 5.2)

Сила Лоренца – сила, действующая со стороны магнитного поля на движущийся со скоростью положительный заряд (здесь – скорость упорядоченного движения носителей положительного заряда ). Модуль лоренцевой силы:

,

(2.5.3)

где α – угол между и .

Из (2.5.4) видно, что на заряд, движущийся вдоль линии , не действует сила ().

Лоренц Хендрик Антон (1853–1928) – нидерландский физик-теоретик, создатель классической электронной теории, член Нидерландской АН. Вывел формулу, связывающую диэлектрическую проницаемость с плотностью диэлектрика, дал выражение для силы, действующей на движущийся заряд в электромагнитном поле (сила Лоренца), объяснил зависимость электропроводности вещества от теплопроводности, развил теорию дисперсии света. Разработал электродинамику движущихся тел. В 1904 г. вывел формулы, связывающие между собой координаты и время одного и того же события в двух различных инерциальных системах отсчета (преобразования Лоренца).

Направлена сила Лоренца перпендикулярно к плоскости, в которой лежат векторы и . К движущемуся положительному заряду применимо правило левой руки или «правило буравчика » (рис. 2.6).

Направление действия силы для отрицательного заряда – противоположно, следовательно, к электронам применимо правило правой руки .

Так как сила Лоренца направлена перпендикулярно движущемуся заряду, т.е. перпендикулярно , работа этой силы всегда равна нулю . Следовательно, действуя на заряженную частицу, сила Лоренца не может изменить кинетическую энергию частицы.

Часто лоренцевой силой называют сумму электрических и магнитных сил :

,

(2.5.4)

здесь электрическая сила ускоряет частицу, изменяет ее энергию.

Повседневно действие магнитной силы на движущийся заряд мы наблюдаем на телевизионном экране (рис. 2.7).

Движение пучка электронов по плоскости экрана стимулируется магнитным полем отклоняющей катушки. Если поднести постоянный магнит к плоскости экрана, то легко заметить его воздействие на электронный пучок по возникающим в изображении искажениям.

Действие лоренцевой силы в ускорителях заряженных частиц подробно описано в п. 4.3.

Определение силы магнитной силы

Определение

Если заряд движется в магнитном поле, то на него действует сила ($\overrightarrow{F}$), которая зависит от величины заряда (q), скорости движения частицы ($\overrightarrow{v}$) относительно магнитного поля, и индукции магнитного поля ($\overrightarrow{B}$). Эта сила была установлена экспериментально, называется она магнитной силой.

И имеет в системе СИ вид:

\[\overrightarrow{F}=q\left[\overrightarrow{v}\overrightarrow{B}\right]\ \left(1\right).\]

Модуль силы в соответствии с (1) равен:

где $\alpha $ — угол между векторами $\overrightarrow{v\ }и\ \overrightarrow{B}$. Из уравнения (2) следует, что если заряженная частица движется вдоль линии магнитного поля, то не испытывает действия магнитной силы.

Направление магнитной силы

Магнитная сила, исходя из (1) направлена перпендикулярно плоскости, в которой лежат векторы $\overrightarrow{v\ }и\ \overrightarrow{B}$. Ее направление совпадает с направлением векторного произведения $\overrightarrow{v\ }и\ \overrightarrow{B}$ в том случае, если величина движущегося заряда больше нуля, и направлена в противоположную сторону, если $q

Свойства силы магнитной силы

Магнитная сила работы над частицей не свершает, так как всегда направлена перпендикулярно скорости ее движения. Из этого утверждения следует, что с помощью воздействия на заряженную частицу с помощью постоянного магнитного поля ее энергию изменить нельзя.

Если на частицу, обладающую зарядом, действуют одновременно электрическое и магнитное поля, то равнодействующая сила может быть записана как:

\[\overrightarrow{F}=q\overrightarrow{E}+q\left[\overrightarrow{v}\overrightarrow{B}\right]\ \left(3\right). {-31}}}\approx 42.\]

Ответ: Радиус кривизны протона в 42 раза больше, чем радиус кривизны электрона.

Пример 2

Задание: Найдите напряженность электрического поля (E), если протон в скрещенном магнитном и электрическом полях движется прямолинейно. В эти поля он влетел, пройдя ускоряющую разность потенциалов равную U. Поля скрещены под прямым углом. Индукция магнитного поля равна B.

На частицу, по условиям задачи действует сила Лоренца, имеющая две составные части: магнитную и электрическую. Первая составляющая магнитная она равна:

\[\overrightarrow{F_m}=q\left[\overrightarrow{v}\overrightarrow{B}\right]\ \left(2.1\right).\]

$\overrightarrow{F_m}$ — направлена перпендикулярно $\overrightarrow{v\ }и\ \overrightarrow{B}$. Электрическая составляющая силы Лоренца равна:

\[\overrightarrow{F_q}=q\overrightarrow{E}\left(2.2\right).\]

Сила $\overrightarrow{F_q}$- направлена по напряженности $\overrightarrow{E}$. Мы помним, что протон имеет положительный заряд. 2}{2}=qU\to v=\sqrt{\frac{2qU}{m}}\left(2.5\right).\]

Подставим (2.5) в (2.4), получим:

Ответ: $E=B\sqrt{\frac{2qU}{m}}.$

Нидерландский физик X. А. Лоренц в конце XIX в. установил, что сила, действующая со стороны магнитного поля на движущуюся заряженную частицу, всегда перпендикулярна направле­нию движения частицы и силовым линиям магнитного поля, в котором эта частица движется. Направление силы Лоренца можно определить с помощью правила левой руки. Если расположить ладонь левой руки так, чтобы четыре вытянутых пальца указывали на­правление движения заряда, а вектор магнитной индукции поля входил в отставленный большой палец укажет направление силы Лоренца, действующей на положительный заряд.

Если заряд частицы отрицательный, то сила Лоренца будет направлена в противоположную сторону.

Модуль силы Лоренца легко определяется из закона Ампера и составляет:

F = | q | vB sin? ,

где q — заряд частицы, v — скорость ее движения , ? — угол между векторами скорости и индукции магнитного поли.

Если кроме магнитного поля есть еще и электрическое поле , которое действует на заряд с силой , то полная сила, действующая на заряд, равна:

.

Часто именно эту силу называют силой Лоренца, а силу, выраженную формулой (F = | q | vB sin? ) называют магнитной частью силы Лоренца .

Поскольку сила Лоренца перпендикулярна направлению движения частицы, она не может изменить ее скорость (она не совершает работы), а может изменить лишь направление ее движения, т. е. искривить траекторию .

Такое искривление траектории электронов в кинескопе телевизо­ра легко наблюдать, если поднести к его экрану постоянный магнит — изображение исказится.

Движение заряженной частицы в однородном магнитном поле. Пусть заряженная частица влетает со скоростью v в однородное магнитное поле перпендикулярно линиям напряженности.

Сила, действующая со стороны магнитного поля на частицу, заставит ее равномерно вращаться по окружности радиусом r , который легко найти, воспользовавшись вторым законом Ньютона , выражением целеустремленного ускорения и формулой (F = | q | vB sin? ):

.

Отсюда получим

.

где m — масса частицы.

Применение силы Лоренца.

Действие магнитного поля на дви­жущиеся заряды применяется, например, в масс-спектрографах , позволяющих разделять заряженные частицы по их удельным за­рядам, т. е. по отношению заряда частицы к ее массе, и по полу­ченным результатам точно определять массы частиц.

Вакуумная камера прибора помещена в поле (вектор индукции перпендикулярен рисунку). Ускоренные электрическим полем заряженные частицы (электроны или ионы), описав дугу, попада­ют на фотопластину, где оставляют след, позволяющий с большой точностью измерить радиус траектории r . По этому радиусу опре­деляется удельный заряд иона. Зная заряд иона, легко вычислите его массу.

Калькулятор силы Лоренца

Создано Krishna Nelaturu

Последнее обновление: 09 октября 2022 г.

Содержание:

• Закон силы Лоренца
• Формула величины силы Лоренца
• Как использовать силу Лоренца 9008 калькулятор

Наш калькулятор силы Лоренца поможет вам рассчитать силу, действующую на заряженных частиц , движущихся через магнитное поле . Если вам интересно понять влияние магнитного поля на заряженные частицы, вы обратились по адресу! Здесь мы рассмотрим закон силы Лоренца и уравнение для силы Лоренца. Мы также рассмотрим некоторые приложения силы Лоренца.

Если вас интересует электромагнитное взаимодействие между двумя заряженными частицами, посетите наш калькулятор закона Кулона.

Закон силы Лоренца

Закон Лоренца описывает взаимосвязь между электромагнитной силой , действующей на заряженную частицу , движущуюся через электрическое и магнитное поля . В данном случае электромагнитная сила также известна как сила Лоренца . Уравнение для силы Лоренца имеет вид:

F=q(E+v×B)\mathbf{F} = q(\mathbf{E} + \mathbf{v} \times \mathbf{B})F=q(E+v×B)

Где:

• F\mathbf{F}F — сила Лоренца ;
• qqq — Заряд заряженной частицы;
• E\mathbf{E}E — Электрическое поле вектор;
• v\mathbf{v}v — Скорость заряженной частицы; и
• B\mathbf{B}B — Магнитное поле вектор.

Обратите внимание, что все величины, за исключением заряда qqq, являются векторными величинами, т. е. имеют величину и направление. Термин qEq\mathbf{E}qE дает электрическая сила , а член q(v×B)q(\mathbf{v} \times \mathbf{B})q(v×B) дает магнитную силу , действующую на заряженную частицу.

🔎 Некоторые определения рассматривают магнитную силу только как силу Лоренца. Однако наш калькулятор силы Лоренца предполагает, что общая электромагнитная сила равна силе Лоренца. Но не волнуйтесь — если вы предпочитаете вычислять только магнитную половину этой силы, введите 000 в качестве напряженности электрического поля, и все готово! ✌️

Формула силы Лоренца 9 величины0025

Формула для величины силы Лоренца:

F=q(E+vBsin⁡θ)F = q(E + vB\sin\theta)F=q(E+vBsinθ)

Где:

• EEE — Напряженность электрического поля;
• vvv — Величина скорости заряженной частицы;
• ВВВ — Сила магнитного поля; и
• θ\thetaθ — Угол между движением частицы и магнитным полем.

Этот калькулятор использует эту формулу силы Лоренца для расчета силы Лоренца. По умолчанию угол θ\thetaθ установлен равным 90°90\градус90°.

Сила Лоренца максимальна, когда начальный путь частицы перпендикулярен магнитному полю, θ=90°\тета = 90\градус θ=90°. Магнитный член в силе Лоренца равен нулю, когда начальный путь параллелен магнитному полю.

Вместе с уравнениями Максвелла мы можем использовать закон силы Лоренца для вывода закона электромагнитной индукции Фарадея.

Применение силы Лоренца

Сила Лоренца проявляется во многих электрических устройствах. В физике элементарных частиц сила Лоренца ускоряет заряженные частицы за циклотроны . Он также используется в масс-спектрометрии заряженных частиц.

Как часть силы Лапласа, она встречается во многих повседневных устройствах, таких как электродвигатели и громкоговорители.

Как пользоваться калькулятором силы Лоренца

Использовать наш калькулятор силы Лоренца очень просто:

• Введите заряд заряженной частицы и начальную скорость .
• Обеспечьте сильные стороны из электрические и магнитные поля .
• Введите угол между начальным путем частицы и магнитным полем. По умолчанию установлено значение 90°90\градус90°, но при необходимости его можно изменить.
• С помощью этих данных наш инструмент рассчитает силу Лоренца, используя формулу силы Лоренца.

Кришна Нелатуру

Сила, действующая на движущийся заряд в магнитном поле: примеры и приложения

Цели обучения

К концу этого раздела вы сможете:

• Описывать воздействие магнитного поля на движущийся заряд.
• Рассчитайте радиус кривизны пути заряда, движущегося в магнитном поле.

Магнитная сила может заставить заряженную частицу двигаться по круговой или спиральной траектории. Космические лучи — это энергичные заряженные частицы в космическом пространстве, некоторые из которых приближаются к Земле. Магнитное поле Земли может заставить их двигаться по спирали. Протоны в гигантских ускорителях удерживаются на круговой траектории благодаря магнитной силе. На фотографии пузырьковой камеры на рисунке 1 показаны заряженные частицы, движущиеся по таким изогнутым траекториям. Искривленные траектории заряженных частиц в магнитных полях лежат в основе ряда явлений и даже могут использоваться аналитически, например, в масс-спектрометре.

Рис. 1. Следы пузырьков образуются заряженными частицами высокой энергии, движущимися через перегретый жидкий водород, в этой художественной интерпретации пузырьковой камеры. Существует сильное магнитное поле, перпендикулярное странице, что приводит к искривлению траекторий частиц. Радиус пути можно использовать для определения массы, заряда и энергии частицы.

Значит, магнитная сила вызывает круговое движение? Магнитная сила всегда перпендикулярна скорости, поэтому на заряженную частицу она не действует. Таким образом, кинетическая энергия и скорость частицы остаются постоянными. Направление движения влияет, но не скорость. Это характерно для равномерного кругового движения. Простейший случай имеет место, когда заряженная частица движется перпендикулярно однородной B -поле, такое как показано на рисунке 2. (Если это происходит в вакууме, магнитное поле является доминирующим фактором, определяющим движение.) Здесь магнитная сила обеспечивает центростремительную силу F _c  = мв ² / р . Заметив, что sin θ = 1, мы видим, что F = qvB .

Рис. 2. Отрицательно заряженная частица движется в плоскости страницы в области, где магнитное поле перпендикулярно странице (представлено маленькими кружками с крестиком — как хвосты стрелок). Магнитная сила перпендикулярна скорости, поэтому скорость изменяется по направлению, но не по величине. Результат равномерного кругового движения. 9{2}}{r}\\[/латекс].

Решение для r дает

[latex]r=\frac{mv}{qB}\\[/latex].

Здесь r – радиус кривизны пути заряженной частицы массой м и зарядом q , движущейся со скоростью v перпендикулярно магнитному полю напряженностью B . Если скорость не перпендикулярна магнитному полю, то v — составляющая скорости, перпендикулярная полю. Составляющая скорости, параллельная полю, не изменяется, так как магнитная сила равна нулю при движении параллельно полю. Это создает спиральное движение, а не круговое.

Пример 1. Расчет кривизны пути электрона, движущегося в магнитном поле: магнит на экране телевизора вместо ЖК-экранов) сильно искажает его изображение, изменяя путь электронов, которые заставляют его люминофоры светиться.

(Не пытайтесь повторить это дома, так как это приведет к необратимому намагничиванию и повреждению телевизора.) Чтобы проиллюстрировать это, рассчитайте радиус кривизны пути электрона со скоростью 6,00 × 10 ⁷ м/с (соответствует ускоряющему напряжению около 10,0 кВ, используемому в некоторых телевизорах) перпендикулярно магнитному полю с напряженностью В = 0,500 Тл (можно получить с помощью постоянных магнитов).

Рис. 1. Вид сбоку, показывающий, что происходит, когда магнит входит в контакт с монитором компьютера или экраном телевизора. Электроны движутся к экрану по спирали вокруг силовых линий магнитного поля, сохраняя составляющую своей скорости, параллельную силовым линиям. Это искажает изображение на экране. 9{-4}\text{ m}\end{массив}\\[/latex]

или

r  = 0,683 мм.

Обсуждение

Малый радиус указывает на большой эффект. Электроны в кинескопе телевизора вынуждены двигаться по очень узким кругам, сильно меняя свои траектории и искажая изображение.

На рисунке 2 показано, как электроны, движущиеся не перпендикулярно силовым линиям магнитного поля, следуют за силовыми линиями. Составляющая скорости, параллельная линиям, не изменяется, поэтому заряды закручиваются вдоль силовых линий. Если напряженность поля увеличивается в направлении движения, поле будет прикладывать силу для замедления зарядов, образуя своего рода магнитное зеркало, как показано ниже.

Рис. 2. Когда заряженная частица движется вдоль линии магнитного поля в область, где поле становится сильнее, на частицу действует сила, уменьшающая составляющую скорости, параллельную полю. Эта сила замедляет движение вдоль силовой линии, а здесь меняет его направление, образуя «магнитное зеркало».

Свойства заряженных частиц в магнитных полях связаны с такими разными вещами, как Aurora Australis или Aurora Borealis и ускорителями частиц. Заряженные частицы, приближающиеся к силовым линиям магнитного поля, могут захватываться спиральными орбитами вокруг линий, а не пересекать их , как показано выше. Некоторые космические лучи, например, следуют линиям магнитного поля Земли, проникая в атмосферу вблизи магнитных полюсов и вызывая южное или северное сияние за счет ионизации молекул в атмосфере. Это свечение возбужденных атомов и молекул видно на рисунке 1 на стр. Те частицы, которые приближаются к средним широтам, должны пересекать силовые линии магнитного поля, и многие из них не могут проникнуть в атмосферу. Космические лучи являются компонентом фонового излучения; следовательно, они дают более высокую дозу радиации на полюсах, чем на экваторе.

Рис. 3. Энергичные электроны и протоны, компоненты космических лучей, от Солнца и глубокого космоса часто следуют за силовыми линиями магнитного поля Земли, а не пересекают их. (Напомним, что северный магнитный полюс Земли на самом деле является южным полюсом с точки зрения стержневого магнита.)

Некоторые прилетающие заряженные частицы захватываются магнитным полем Земли, образуя два пояса над атмосферой, известные как радиационные пояса Ван Аллена после первооткрыватель Джеймс А. Ван Аллен, американский астрофизик. (См. рис. 4.) Частицы, попавшие в эти пояса, образуют радиационные поля (аналогичные ядерному излучению) настолько интенсивные, что пилотируемые космические полеты избегают их, а спутники с чувствительной электроникой не попадают в них. За несколько минут, которые потребовались лунным миссиям для пересечения радиационных поясов Ван Аллена, астронавты получили дозы радиации, более чем в два раза превышающие допустимую годовую дозу радиационных работников. Подобные пояса есть и у других планет, особенно у тех, у которых сильные магнитные поля, таких как Юпитер.

Рис. 4. Радиационные пояса Ван Аллена представляют собой две области, в которых энергичные заряженные частицы захватываются магнитным полем Земли. Один пояс лежит на высоте около 300 км над поверхностью Земли, другой — около 16 000 км. Заряженные частицы в этих поясах мигрируют вдоль силовых линий магнитного поля и частично отражаются от полюсов более сильными там полями. Заряженные частицы, попадающие в атмосферу, восполняются Солнцем и источниками в глубоком космосе.

На Земле у нас есть устройства, использующие магнитные поля для удержания заряженных частиц. Среди них гигантские ускорители частиц, которые использовались для изучения субструктуры материи. (См. рис. 5.) Магнитные поля не только контролируют направление заряженных частиц, они также используются для фокусировки частиц в пучки и преодоления отталкивания одноименных зарядов в этих пучках.

Рис. 5. Лаборатория Фермилаб в Иллинойсе имеет большой ускоритель частиц (самый мощный в мире до 2008 г.), который использует магнитные поля (магниты показаны здесь оранжевым цветом) для сдерживания и направления луча. Этот и другие ускорители используются уже несколько десятилетий и позволили нам открыть некоторые законы, лежащие в основе всей материи. (кредит: ammcrim, Flickr)

Термоядерный синтез (подобный происходящему на Солнце) — это надежда на источник чистой энергии в будущем. Одним из самых перспективных устройств является 9Токамак 0031 , который использует магнитные поля для удержания (или захвата) и направления реактивных заряженных частиц. (См. рис. 6.) Менее экзотические, но более практичные усилители в микроволновых печах используют магнитное поле для сдерживания колеблющихся электронов. Эти колеблющиеся электроны генерируют микроволны, направляемые в духовку.

Рисунок 6. Токамаки, подобные показанному на рисунке, изучаются с целью экономичного производства энергии путем ядерного синтеза. Магнитные поля в устройстве в форме пончика удерживают и направляют реактивные заряженные частицы. (кредит: Дэвид Меллис, Flickr)

Масс-спектрометры имеют различные конструкции, и многие из них используют магнитные поля для измерения массы. Кривизна пути заряженной частицы в поле связана с ее массой и измеряется для получения информации о массе. (См. Дополнительные применения магнетизма .) Исторически такие методы использовались при первых прямых наблюдениях за зарядом и массой электрона. Сегодня масс-спектрометры (иногда в сочетании с газовыми хроматографами) используются для определения состава и последовательности крупных биологических молекул.

• Магнитная сила может создавать центростремительную силу и заставлять заряженную частицу двигаться по круговой траектории радиуса

  [латекс]r=\frac{mv}{qB}\\[/латекс]

  где v  это составляющая скорости, перпендикулярная B  для заряженной частицы с массой m   и зарядом q .

Концептуальные вопросы

1. Как можно использовать движение заряженной частицы, чтобы отличить магнитное поле от электрического?

2. Высокоскоростные заряженные частицы могут повреждать биологические клетки и являются компонентом радиационного облучения в самых разных местах, от исследовательских учреждений до естественного фона. Опишите, как вы можете использовать магнитное поле, чтобы защитить себя.

3. Если протон космических лучей приблизится к Земле из космоса по линии к центру Земли, лежащей в плоскости экватора, в какую сторону он будет отклонен магнитным полем Земли? А электрон? Нейтрон?

4. Каковы знаки зарядов частиц на рис. 9?

Рисунок 9.

5. Какая из частиц на рисунке 10 имеет наибольшую скорость, если предположить, что они имеют одинаковые заряды и массы?

Рисунок 10.

6. Какая из частиц на рисунке 10 имеет наибольшую массу, если предположить, что все они имеют одинаковые заряды и скорости?

7. Во время работы высокоточный ТВ-монитор кладут на бок во время технического обслуживания. Изображение на мониторе меняет цвет и слегка расплывается. Обсудите возможную связь этих эффектов с магнитным полем Земли.

Задачи и упражнения

Если вам нужна дополнительная поддержка по этим задачам, см. Дополнительные приложения магнетизма.

1. Электрон космического луча движется со скоростью 7,50 × 10 ⁶ м/с перпендикулярно магнитному полю Земли на высоте, где напряженность поля составляет 1,00 × 10 ⁻⁵ Тл. Каков радиус кругового пути электрона? следует?

2. Протон движется со скоростью 7,50 × 10 ⁷ перпендикулярно магнитному полю. Поле заставляет протон двигаться по круговой траектории радиусом 0,800 м. Какова напряженность поля?

3. (a) Зрители Star Trek слышат о приводе антиматерии на звездолете Enterprise . Одна из возможностей такого футуристического источника энергии — хранить заряженные частицы антивещества в вакуумной камере, циркулирующей в магнитном поле, а затем извлекать их по мере необходимости. Антивещество аннигилирует с обычным веществом, производя чистую энергию. Магнитное поле какой силы необходимо для удержания антипротонов, движущихся со скоростью 5,00 × 10 ⁷ м/с по круговой траектории радиусом 2,00 м? Антипротоны имеют ту же массу, что и протоны, но противоположный (отрицательный) заряд. (б) Достижима ли эта напряженность поля с помощью сегодняшних технологий или это футуристическая возможность?

4. (a) Ион кислорода-16 с массой 2,66 × 10 ⁻²⁶ кг движется со скоростью 5,00 × 10 ⁶ м/с перпендикулярно магнитному полю напряженностью 1,20 Тл, что заставляет его двигаться в дуга окружности радиусом 0,231 м. Какой положительный заряд имеет ион? б) Каково отношение этого заряда к заряду электрона? (c) Обсудите, почему отношение, найденное в (b), должно быть целым числом.

5. Круговой путь какого радиуса проходит электрон, если он движется с той же скоростью и в том же магнитном поле, что и протон под номером 2?

6. Селектор скорости в масс-спектрометре использует магнитное поле 0,100 Тл. а) Какая напряженность электрического поля необходима, чтобы выбрать скорость 4,00 × 10 ⁶ м/с? б) Чему равно напряжение между пластинами, если расстояние между ними 1 см?

7. Электрон в ТВ ЭЛТ движется со скоростью 6,00 × 10 ⁷  м/с в направлении, перпендикулярном полю Земли, напряженность которого составляет 5,00 × 10 ⁻⁵ Тл. ) Электрическое поле какой напряженности необходимо приложить перпендикулярно полю Земли, чтобы заставить электрон двигаться прямолинейно? (b) Если это сделать между пластинами, расстояние между которыми составляет 1,00 см, какое напряжение будет приложено? (Обратите внимание, что телевизоры обычно окружены ферромагнитным материалом для защиты от внешних магнитных полей и устранения необходимости такой коррекции.)

8. (a) С какой скоростью протон будет двигаться по круговой траектории того же радиуса, что и электрон в вопросе 2? б) Каким был бы радиус пути, если бы скорость протона была такой же, как у электрона? в) Чему был бы равен радиус, если бы протон имел ту же кинетическую энергию, что и электрон? г) один и тот же импульс?

9. Масс-спектрометр используется для отделения обычного кислорода-16 от гораздо более редкого кислорода-18, взятого из образца старого ледникового льда. (Относительное содержание этих изотопов кислорода связано с климатической температурой во время отложения льда.) Отношение масс этих двух ионов составляет 16 к 18, масса кислорода-16 составляет 2,66 × 10 9 .0165 −26 кг, однозарядные и движутся со скоростью 5,00 × 10 ⁶ м/с в магнитном поле 1,20 Тл. Каково расстояние между их путями, когда они попадают в цель после прохождения полукруга?

10. (a) Трехзарядные ионы урана-235 и урана-238 разделяются в масс-спектрометре. (Намного реже уран-235 используется в качестве реакторного топлива.) Массы ионов составляют 3,90 × 10 ^-25 кг и 3,95 × 10 ^-25 кг соответственно, и они движутся со скоростью 3,00 × 10 ⁵  м/с в поле 0,250 Тл. Каково расстояние между их путями, когда они попадают в цель после прохождения полукруга? (b) Обсудите, кажется ли это расстояние между их путями достаточно большим, чтобы его можно было использовать при отделении урана-235 от урана-238.