Действие магнитного поля на движущийся электрический заряд 11 класс онлайн-подготовка на Ростелеком Лицей
«Модели эфиров»
Если бы Андре Мари Ампер (рис. 1) знал о действии электрического тока, то продвинулся бы гораздо дальше в своих открытиях.
Рис. 1. Андри Мари Ампер (Источник)
Как и многие ученые того периода, Ампер придерживался «модели эфира»: электрический ток – эфир, некая жидкость, которая протекает по проводникам. Именно отсюда и сам термин «электрический ток» – то, что течет. Только в самом конце XIX века – начале ХХ модели эфиров стали отходить, а на смену им стали появляться новые модели, адекватнее отражающие наблюдаемые явления. В частности, были открыты катодные лучи, была выявлена радиоактивность, проведены исследования Фарадея по электролизу – все это наводило на мысль о существовании заряженных частиц, которые как-то движутся.
Электронная модель Хендрика Лоренца
Ученый Хендрик Лоренц (рис. 2) предложил так называемую «электронную модель» металлов.
2) предложил так называемую «электронную модель» металлов.
Рис. 2. Хендрик Лоренц (Источник)
При образовании кристаллической решетки металлов от каждого атома металла отрывается по одному внешнему электрону, таким образом, в узлах кристаллической решетки находятся положительные ионы, а в объеме этой решетки почти свободно могут двигаться электроны (рис. 3).
Рис. 3. Кристаллическая решетка
Модель, предложенная Лоренцом, была хороша хотя бы тем, что достаточно легко объясняла возникновение электрического тока в металлах. При обычных условиях эти электроны находятся в беспорядочном движении вокруг кристаллической решетки. И только при подаче разности потенциалов на конце проводника, когда внутри проводника появляется электрическое поле, кроме этой хаотической составляющей появляется другая – упорядоченная составляющая, или направленное движение. Именно это движение, согласно модели Лоренца, представляет собой электрический ток.
Вы знаете, что стороны магнитного поля (B) на проводник с током (I) действует сила Ампера (F), перпендикулярная направлению тока и направлению линий магнитного поля (рис. 4).
4).
Рис. 4. Направление силы Ампера
«Если электрический ток представляет собой направленное движение зарядов, то не будет ли со стороны магнитного поля действовать такая же сила на сами заряды?» – примерно так рассуждал Лоренц. В выражение для силы Ампера вместо силы тока подставим определение силы тока – отношение перенесенного заряда в проводнике ко времени, за которое было осуществлено данное перенесение:
Также заметим, что отношение элемента длины проводника к интервалу времени – скорость движения заряда:
Тогда выражение принимает вид:
Модуль силы равен произведению величины магнитной индукции поля на количество переносимого через проводник заряда на скорость частиц, которые переносят заряд и на синус угла между направлением движения заряда и направлением вектора магнитной индукции.
Учтем, что носителями электрического тока в проводнике являются электроны, величина зарядов которых одинакова. Поэтому можно записать, что совокупный заряд, переносимый через поперечное сечение проводника, – произведение заряда электрона q на количество электронов N, переносимых через поперечное сечение проводника.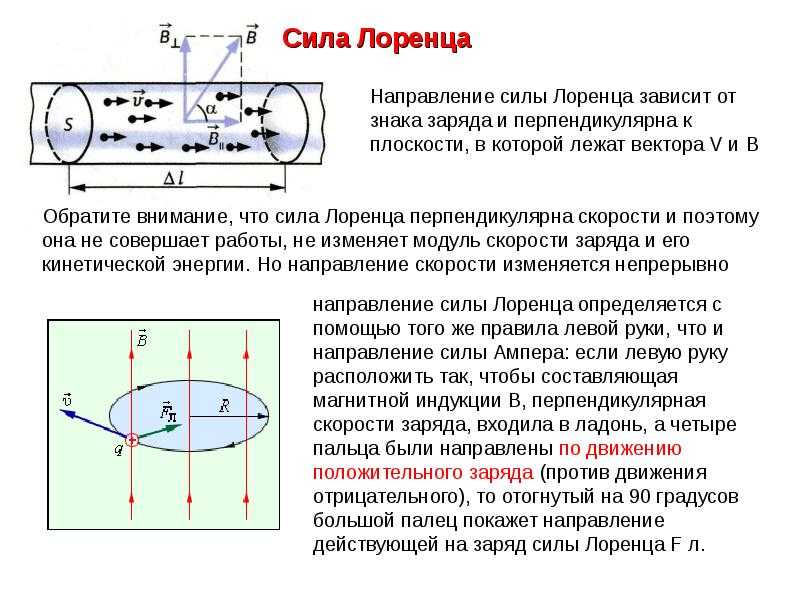
Тогда:
Вывод приведенной формулы был сугубо формальным, однако даже такой вывод позволял предположить, что не только на проводник с током, но и на отдельный заряд в магнитном поле будет действовать сила со стороны этого поля. Предположим, что число зарядов равно единице и этот заряд движется не внутри кристаллической решетки, а в свободном пространстве. Возникает вопрос: что произойдет с этим зарядом, если он войдет в область, где существует однородное магнитное поле? Согласно нашей гипотезе, на частицу, движущуюся в однородном магнитном поле, должна действовать сила, которая перпендикулярна скорости этой частицы (поскольку именно так будет направлен электрический ток, связанный с движением этих частиц) и перпендикулярна линиям магнитного поля (рис. 5).
Рис. 5. Направление действия силы на движущийся заряд
Величина этой силы будет определяться так:
Проверка гипотезы Лоренца. Принцип работы электронно-лучевой трубки
Открытие катодных лучей, а также радиоактивности позволили проверить экспериментально гипотезу Лоренца.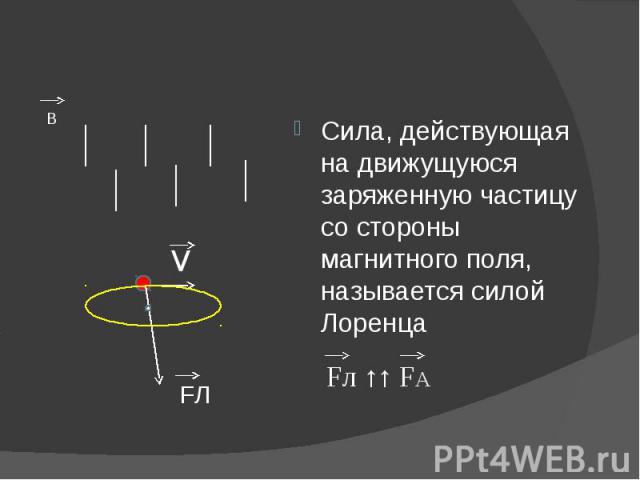 Воспользуемся электронно-лучевой трубкой.
Воспользуемся электронно-лучевой трубкой.
В вакуумной трубке размещены две пластины: анод и катод. На катод подается отрицательный потенциал, на анод – положительный. Для того чтобы в трубке возникли свободные электроны, катод нагревается нитью накала. Свободные электроны металлического катода вблизи его поверхности могут покидать эту поверхность, обладая высокой кинетической энергией за счет нагревания – явление термоэлектронной эмиссии. Свободные электроны, покинувшие поверхность катода, попадают в зону действия электрического поля между анодом и катодом. Линии напряженности этого поля направлены от анода к катоду (изображены белыми стрелками). Электроны, будучи отрицательно заряженными частицами, движутся от катода к аноду – против линии напряженности поля (направление движения изображено красными стрелками). Так, в трубке возникает электрический ток, направленный от анода к катоду (рис. 6).
Рис. 6. Электронно-лучевая трубка
Если использовать экран, покрытый специальным материалом, который светится при попадании на него заряженных частиц, можно пронаблюдать место попадания электронов по световому пятну. Именно так и работает электронно-лучевая трубка. При подаче напряжения на анод и катод мы видим небольшое зеленое пятно на экране – это место бомбардировки экрана электронами (рис. 7).
Именно так и работает электронно-лучевая трубка. При подаче напряжения на анод и катод мы видим небольшое зеленое пятно на экране – это место бомбардировки экрана электронами (рис. 7).
Рис. 7. Работа электронно-лучевой трубки
Опыты с осциллографом
Воспользуемся осциллографом. Для удобства будем следить не за световым пятном, а за светящейся линией (рис. 8).
Рис. 8. Светящаяся линия на экране осциллографа
Когда одним из полюсов подводят к горизонтальной линии, находящейся на осциллографе, она отклоняется от своего первоначального значения в направлении, перпендикулярном направлению скорости и направлению линий магнитного поля, поскольку магнитное поле направлено от северного полюса к южному. Это на качественном уровне подтверждает гипотезу (рис. 9).
Рис. 9. Отклонения электронов в электронно-лучевой трубке
Попытаемся получить не только качественные, но и количественные результаты. Для этого будем проверять зависимость силы, действующей со стороны магнитного поля, от различных факторов. В частности, от скорости движения электронов. Каким образом можно поменять скорость движения электронов в осциллографе? При помощи регулировки яркости линии на осциллографе можно изменить скорость движения электронов в осциллографе. Чем ярче линия, тем быстрее движутся электроны внутри трубки. Если поднести магнит к осциллографу северным полюсом и менять скорость движения электронов, то по мере уменьшения яркости искажение линии также будет уменьшаться (рис. 10). Это означает, что сила, действующая со стороны магнитного поля на электроны, при уменьшении скорости электронов тоже уменьшается. Более точные измерения дадут нам прямую пропорциональность между силой, действующей со стороны магнитного поля на движущиеся заряды, и скоростью этих зарядов.
Для этого будем проверять зависимость силы, действующей со стороны магнитного поля, от различных факторов. В частности, от скорости движения электронов. Каким образом можно поменять скорость движения электронов в осциллографе? При помощи регулировки яркости линии на осциллографе можно изменить скорость движения электронов в осциллографе. Чем ярче линия, тем быстрее движутся электроны внутри трубки. Если поднести магнит к осциллографу северным полюсом и менять скорость движения электронов, то по мере уменьшения яркости искажение линии также будет уменьшаться (рис. 10). Это означает, что сила, действующая со стороны магнитного поля на электроны, при уменьшении скорости электронов тоже уменьшается. Более точные измерения дадут нам прямую пропорциональность между силой, действующей со стороны магнитного поля на движущиеся заряды, и скоростью этих зарядов.
Рис. 10. При уменьшении яркости искажение линии уменьшается
Сила, действующая на заряды со стороны магнитного поля, пропорциональна индукции – если поднести несколько магнитов к осциллографу, то искажение будет гораздо сильнее.
Рис. 11. При усилении магнитного поля искажение линии увеличивается
Величина силы действующей со стороны магнитного поля на движущийся заряд зависит от взаимного направления вектора магнитной индукции и вектора скорости движения частиц. При поднесении магнитов к осциллографу южным полюсом линия будет искажаться в противоположном направлении.
Рис. 12. При поднесении магнитов южным полюсом линия искажается в противоположном направлении
Сила Лоренца
Обобщим выводы из проделанных экспериментов. На движущийся в магнитном поле заряд (q) со стороны магнитного поля действует сила (F), направление которой зависит от взаимного направления вектора скорости движения (v) заряда и вектора магнитной индукции поля (В). Величина силы пропорциональна скорости движения заряда и модулю магнитной индукции. Направление силы определяется по правилу «левой руки».
Таким образом, полученное ранее выражение для силы описывает взаимодействие магнитного поля с движущимся в этом поле электрическим зарядом. Открытие силы действия магнитного поля на движущийся в нем заряд стало возможным только благодаря улучшению представлений о строении вещества, электрическом токе в металлах, движении заряженных частиц. И огромную роль во всех этих задачах сыграл Лоренц, поэтому открытая сила и получила название сила Лоренца.
Открытие силы действия магнитного поля на движущийся в нем заряд стало возможным только благодаря улучшению представлений о строении вещества, электрическом токе в металлах, движении заряженных частиц. И огромную роль во всех этих задачах сыграл Лоренц, поэтому открытая сила и получила название сила Лоренца.
Формулы, описывающие движение заряженной частицы в магнитном поле
Сделаем еще несколько замечаний.
1. Вектор силы Лоренца перпендикулярен вектору скорости:
2. Если сила перпендикулярна вектору скорости, то она называется центростремительной. Под ее действием тело движется по окружности. Следовательно, сила Лоренца – центростремительная сила.
3. Под действием силы Лоренца заряд движется по дуге окружности, следовательно, он обладает центростремительным ускорением. Центростремительное ускорение может быть рассчитано как квадрат скорости движения, деленный на радиус окружности, который описывает тело:
4. Согласно второму закону Ньютона, сила может быть определена как произведение массы тела на приобретаемое им ускорение:
Согласно второму закону Ньютона, сила может быть определена как произведение массы тела на приобретаемое им ускорение:
Подставив выражения для силы Лоренца, получим:
Подставим выражение для центростремительного ускорения:
(1.14)
После сокращения скорости получим следующие соотношения:
Список литературы
- Касьянов В. А. Физика 11 кл.: Учебн. для общеобразоват. учреждений. 4-е изд., стереотип. – М.: Дрофа, 2004. – 416 с.: ил., 8 л. цв. вкл.
- Степанова Г. Н. Физика 11. – М.: Русское слово.
- Пурышева Н. С., Важеевская Н. Е., Исаев Д. А., Чаругин В. М. Физика 11. – М.: Дрофа.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «fizika.in» (Источник)
- Интернет-портал «Классная физика» (Источник)
- Интернет-портал «balancer.ru» (Источник)
Домашнее задание
- Касьянов В.
 А. Физика 11 кл.: Учебн. для общеобразоват. учреждений. 4-е изд., стереотип. – М.: Дрофа, 2004. – 416с.: ил., 8 л. цв. вкл., ст. 85, в. 5, з. 2–4.
А. Физика 11 кл.: Учебн. для общеобразоват. учреждений. 4-е изд., стереотип. – М.: Дрофа, 2004. – 416с.: ил., 8 л. цв. вкл., ст. 85, в. 5, з. 2–4. - Какая сила действует на протон, который движется со скоростью 2 ∙ 106 м/с в однородном магнитном поле с индукцией 0,1 Тл? Протон движется под углом 60° по отношению к линиям магнитной индукции поля.
- На рис. 13 и 14 схематически показаны разные случаи взаимодействия заряженной частицы, которая движется, и магнитного поля. Сформулируйте задачу в каждом случае и решите ее.
| Рис. 13 | Рис. 14 |
4. * Электрон, который влетел в однородное магнитное поле под углом 60° по отношению к линиям магнитной индукции, двигается по винтовой линии радиусом 2 см, делая один оборот за 30 нс. Определите магнитную индукцию поля и шаг винтовой линии.
Действие магнитного поля на движущийся заряд кратко – определение силы Лоренца (11 класс)
4.7
Средняя оценка: 4.7
Всего получено оценок: 61.
4.7
Средняя оценка: 4.7
Всего получено оценок: 61.
Электричество и магнетизм долгое время считались мало связанными явлениями. Однако в середине XIX в. было обнаружено, что, хотя статичные электрические заряды никак не реагируют на магнитное поле, движущиеся заряды с ним взаимодействуют. Расскажем кратко о действии магнитного поля на движущийся электрический заряд.
Сила Ампера
Связь между электричеством и магнетизмом обнаружили после того, как в начале XIX в. были сконструированы гальванические элементы и физики научились создавать в проводниках электрический ток, текущий долгое время. В середине XIX в. Х. Эрстед показал, что ток, протекающий по проводнику, порождает магнитное поле, которое отклоняет стрелку компаса. Обратное явление — отклонение проводника с током в магнитном поле — открыл А.
Несмотря на правильное математическое описание, закон Ампера не раскрывает механизма возникновения силы, действующей на проводник в магнитном поле. Механизм возникновения силы Ампера был установлен только к концу XIX в., когда было доказано, что электрический ток представляет собой движение носителей заряда в проводнике, а на любой движущийся заряд со стороны магнитного поля действует сила, названная впоследствии силой Лоренца. Кратко говоря, сложение всех сил Лоренца, действующих на все заряды в проводнике, дает в итоге силу Ампера.
Сила Лоренца
Для определения действия магнитного поля на движущийся заряд можно использовать закон Ампера. Очевидно, что сила Лоренца, действующая на отдельный заряд, равна отношению силы Ампера, действующей на проводник, к количеству зарядов в этом проводнике. Из курса физики за 11 класс известно, что сила, действующая на проводник со стороны магнитного поля с индукцией $\overrightarrow B$, равна:
Из курса физики за 11 класс известно, что сила, действующая на проводник со стороны магнитного поля с индукцией $\overrightarrow B$, равна:
$$F= I |\overrightarrow B| Δl sin \alpha$$
А ток в проводнике связан с зарядом $q$ и концентрацией носителей $n$ соотношением:
$$I = qnvS$$
В этой формуле $v$ — это линейная скорость движения носителей, а $S$ — площадь поперечного сечения проводника. Подставив значение тока в предыдущую формулу, получим выражение для силы Ампера:
$$F_A= |q| nvS |\overrightarrow B| Δl sin \alpha$$
Число носителей заряда в проводнике равно:
$$N = nSΔl$$
Чтобы найти силу, действующую на каждый носитель (силу Лоренца), необходимо силу Ампера поделить на число носителей. В результате имеем:
$$F_Л={F_A\over N}= |q| v B sin \alpha$$
Поскольку носители заряда движутся в направлении электрического тока, то угол $\alpha$ равен углу между вектором скорости движения заряда и вектором магнитной индукции.
Направление силы Лоренца определяется так же, как и направление силы Ампера, по правилу левой руки. Только направление тока заменяется на направление движения положительного заряда: если четыре вытянутых пальца левой руки указывают направление движения положительного заряда, а вектор магнитной индукции прокалывает ладонь (входит в ладонь), то отставленный большой палец укажет направление силы Лоренца.
Только направление тока заменяется на направление движения положительного заряда: если четыре вытянутых пальца левой руки указывают направление движения положительного заряда, а вектор магнитной индукции прокалывает ладонь (входит в ладонь), то отставленный большой палец укажет направление силы Лоренца.
Направление силы Лоренца всегда перпендикулярно скорости, а значит, траекторией движения заряда в магнитном поле является окружность (или спираль) некоторого радиуса. Отметим также, что сила Лоренца не совершает работы и не меняет кинетическую энергию частицы. Она лишь меняет направление ее движения.
Что мы узнали?
На заряд, движущийся в магнитном поле, действует сила Лоренца. Ее направление перпендикулярно векторам скорости и магнитной индукции. Определяется оно так же, как сила Ампера: мнемоническим правилом левой руки.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 61.
А какая ваша оценка?
Движущиеся заряды в магнитном поле
Когда мы строим цепи, никогда не стоит использовать рядом с ними магниты. Причина этого в том, что основными единицами электрического поля являются электрические заряды, на которые воздействуют магнитные поля. Давайте посмотрим на электромагнитное влияние на электрический заряд, чтобы увидеть, что происходит, когда мы устанавливаем электрическое поле равным нулю.
Магнитные поля и электрические заряды
Современная физика основана на использовании полей, которые являются зависящими от времени физическими объектами, распространяющимися в пространстве. Для электрических явлений мы используем электрические поля и законы, управляющие их поведением, а для магнитных явлений мы используем магнитные поля и законы, управляющие их поведением.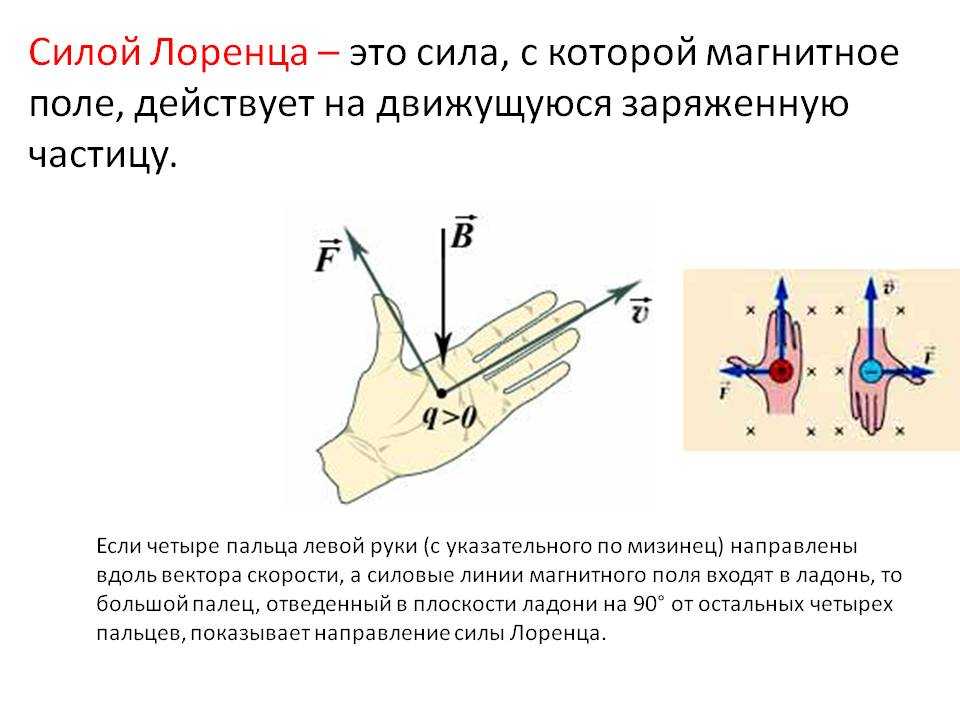
Важно отметить, что электрические и магнитные поля не являются независимыми друг от друга. Исторически было трудно понять, что оба физических поля являются частью одного общего описания, основанного на зарядах, которые, если они статичны, генерируют только электрическое поле, но при движении также генерируют магнитное поле.
Здесь нам нужно только рассматривать магнитное поле B как зависящее от времени и пространства векторное поле. Магнитные поля измеряются в Теслах (Тл). Мы также будем рассматривать только точечные частицы с определенным значением заряда q, измеряемым в кулонах (Кл).
Произведение векторовПроизведение векторов — это операция между двумя векторами, которая дает другой вектор. Результирующий вектор перпендикулярен двум перемноженным векторам и имеет модуль, который можно вычислить как:
Здесь, | | указывает модуль вектора, а угол — это угол, образованный между векторами. Векторное произведение обладает следующим свойством: изменение порядка векторов в векторном произведении равно глобальному знаку минус, т.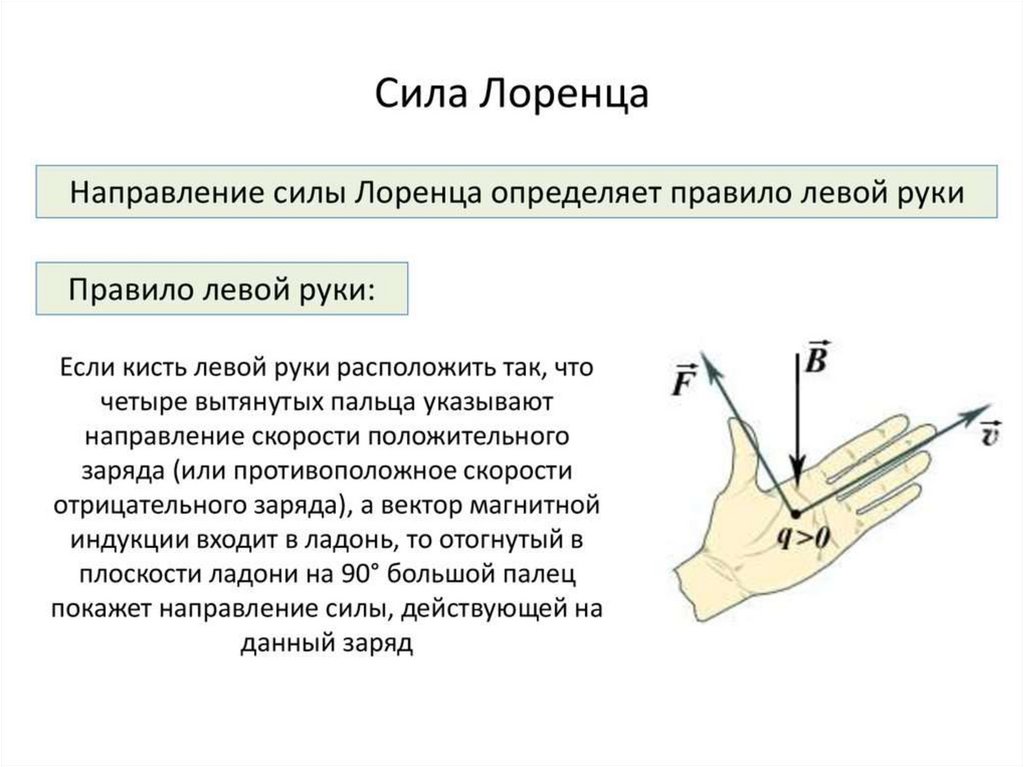 е.:
е.:
Основным следствием рассмотрения векторных произведений является то, что результирующий вектор перпендикулярен плоскости, определяемой двумя другими векторами, и что если их угол равен нулю или 180º, векторное произведение является нулевым вектором.
Полезным способом определения направления результирующего вектора является использование правила правой руки, показанного на рисунке ниже.
Рис. 1. Правило правой руки. Acdx, Wikimedia Commons (CC BY-SA 3.0).
Движущиеся заряды в магнитном полеОбщий закон поведения электрического заряда в присутствии электромагнитного поля известен как сила Лоренца. В общее выражение входит и влияние внешнего электрического поля, но здесь мы ограничимся ситуациями, когда присутствует только магнитное поле.
Выражение для силы, действующей со стороны магнитного поля на движущийся электрический заряд:
Здесь v — векторная скорость, а произведение скорости на магнитное поле — векторное произведение.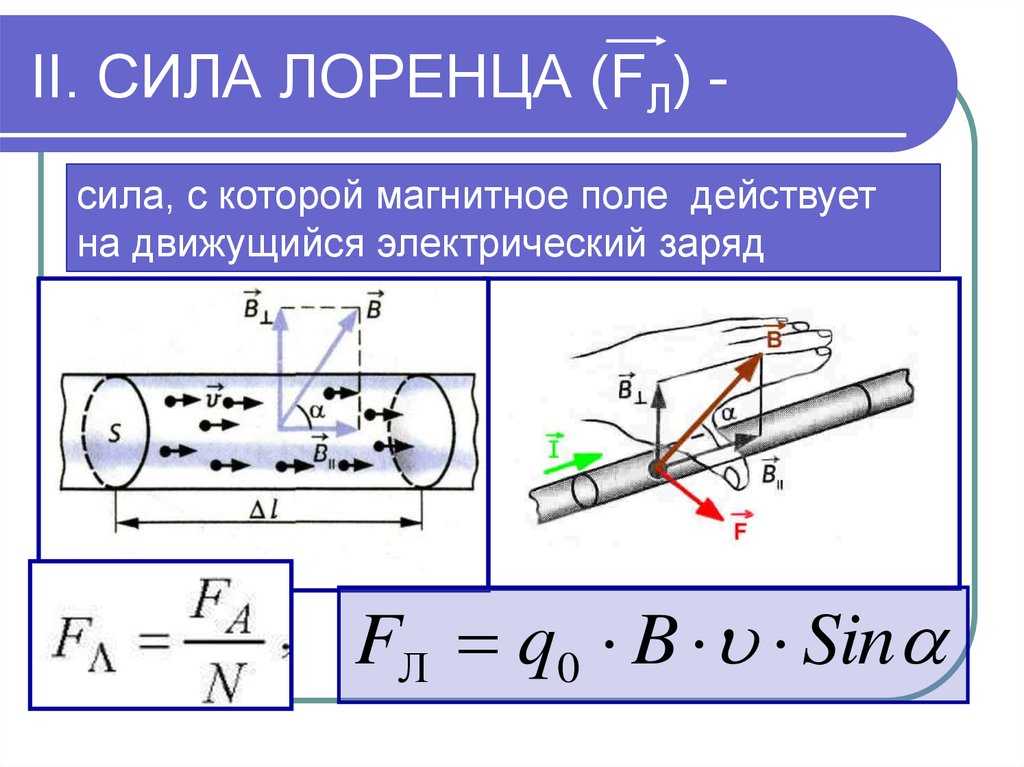
Векторное произведение означает, что сила, действующая со стороны магнитного поля на движущийся заряд, перпендикулярна направлению поля и скорости заряда. Это также означает, что заряды, которые не движутся, не «видят» магнитное поле, поскольку оно на них не действует. Кроме того, если заряд движется в том же направлении, что и магнитное поле, он не почувствует его влияния.
Заряды, движущиеся в однородном магнитном поле
Используя математический аппарат предыдущего раздела, мы можем дать феноменологическое описание того, что происходит, когда электрический заряд движется в области, где есть магнитное поле. По формуле силы Лоренца мы можем изучать динамические траектории, а также энергию частиц.
Математическое описаниеОграничимся теперь случаем, когда магнитное поле имеет постоянное фиксированное значение B, не зависящее ни от пространства, ни от времени. Ограничимся также случаем постоянной начальной скорости v.
Наша постановка следующая: точечная частица с зарядом q движется в фиксированном направлении с постоянной скоростью. Без ограничения общности мы можем считать это направление осью x. Частица движется в области, где нет магнитного поля, пока внезапно не включается. Мы будем считать, что магнитное поле перпендикулярно скорости, поэтому у нас есть максимальный вектор от векторного произведения (с синусоидальной функцией, равной единице).
Без ограничения общности мы можем считать это направление осью x. Частица движется в области, где нет магнитного поля, пока внезапно не включается. Мы будем считать, что магнитное поле перпендикулярно скорости, поэтому у нас есть максимальный вектор от векторного произведения (с синусоидальной функцией, равной единице).
Рис. 2. Заряды противоположных знаков, приближающиеся к области с магнитным полем, входящим в страницу., Wikimedia Commons
Как только магнитное поле включается, магнитная сила заставляет частицу повернуться в направлении, определяемом лоренцевской сила. При этом, согласно формуле, указательный палец указывает в направлении движения заряда, а средний — в направлении магнитного поля. Поскольку скорость изменяется из-за действия этой силы, сила теперь действует в другом направлении. Если вы медленно поворачиваете пальцы по правилу правой руки, то понимаете, что частица обязана описывать окружность, так как направление силы постоянно меняется.
Для такого рода установки существует соглашение о направлении магнитного поля, в соответствии с которым мы используем крестики для обозначения магнитного поля, входящего в страницу, и кружки для обозначения магнитного поля, которое выходит из нее, будучи направленным к наблюдателю.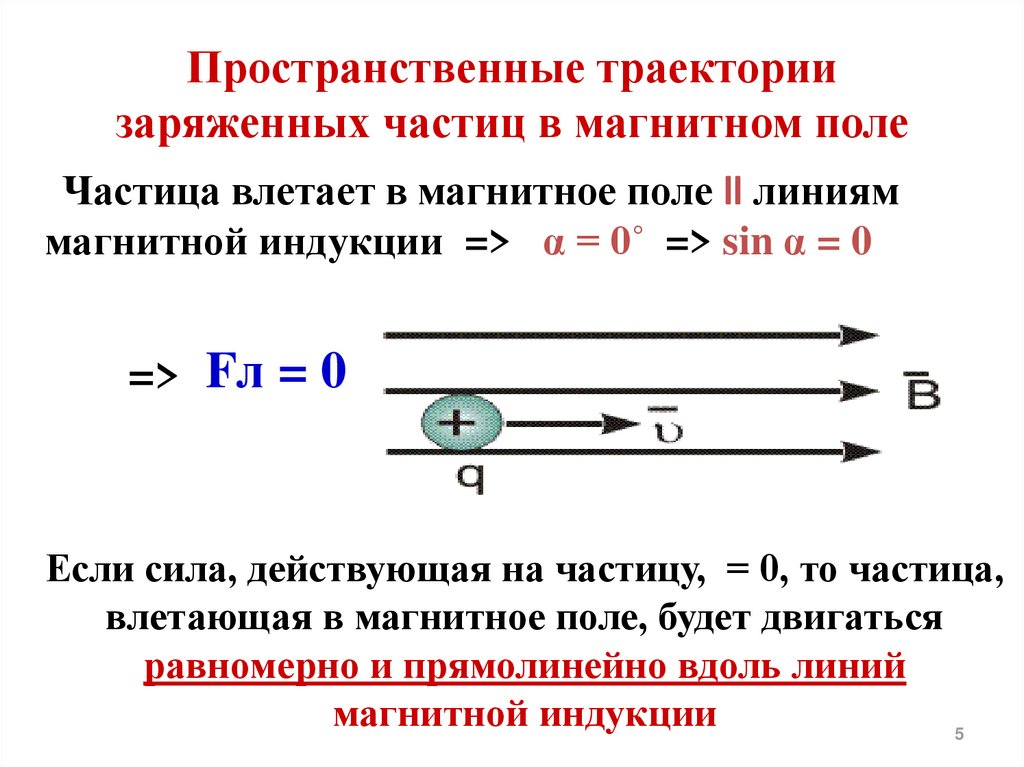
Рисунок 3. Траектория заряда в магнитном поле, входящего на страницу Wikimedia Commons
Мы видели, что движущиеся заряды в однородном магнитном поле описывают круговые траектории. Общая теория кругового движения утверждает, что скорость объекта, описывающего его, не изменяется, в то время как изменяется его скорость (направление), что и происходит с силой Лоренца. Это влияет на энергию частицы, поскольку кинетическая энергия пропорциональна к квадрату скорости. При постоянной скорости магнитное поле не изменяет энергию. Это требует тщательного рассмотрения при изучении того, как магниты притягивают металлы, поскольку при этом меняется энергия.
Что такое циклотроны?
Наконец, мы рассмотрим применение только что изученного эффекта: циклотроны, ускорители частиц, основанные на силе Лоренца.
По сути, частицы сначала ускоряются благодаря электрическому полю (по прямой линии), а затем попадают в область, где есть магнитное поле, которое заставляет их описывать круговое движение.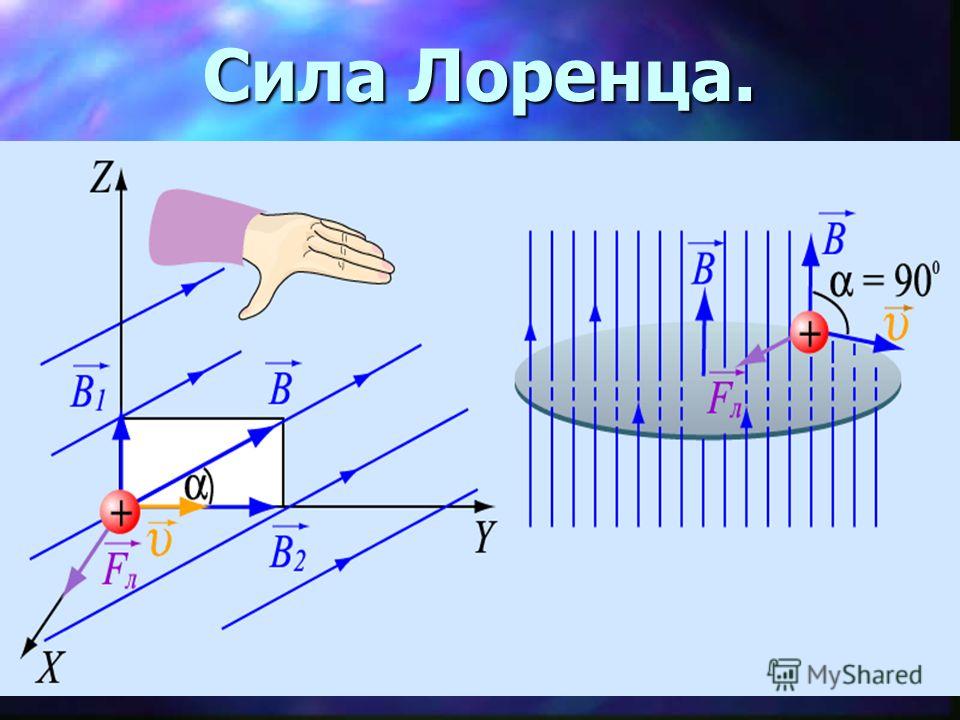 Интенсивность магнитного поля можно изменить, чтобы воздействовать на частицу с большей силой и изменить ее скорость и скорость. Это позволяет ускорять частицы в круговом контуре.
Интенсивность магнитного поля можно изменить, чтобы воздействовать на частицу с большей силой и изменить ее скорость и скорость. Это позволяет ускорять частицы в круговом контуре.
Рис. 4. Схема циклотрона, Wikimedia Commons
Циклотроны были достижением 20-го века, поскольку до этого использовались только линейные ускорители, которые не позволяли поддерживать ускорение. С другой стороны, когда они достигают скорости, близкой к скорости света, эксперименты предполагают, что мы должны искать более совершенные устройства, которые учитывают как радиационные, так и релятивистские эффекты. Эти усовершенствованные устройства известны как синхротроны, которые используются, например, для производства короткоживущих радиоактивных изотопов.
Ключевые выводыНа заряженную движущуюся частицу воздействует магнитное поле. И заряд, и движение необходимы для того, чтобы поле оказывало силу. Сила, действующая со стороны магнитного поля на заряженную движущуюся частицу, известна как сила Лоренца. Это перпендикулярно направлению движения частицы и магнитному полю. Движущаяся заряженная частица в области с однородным магнитным полем описывает круговую траекторию. Однако его скорость и энергия остаются неизменными. Циклотроны и синхротроны — это ускорители частиц, основанные на силе Лоренца.
Это перпендикулярно направлению движения частицы и магнитному полю. Движущаяся заряженная частица в области с однородным магнитным полем описывает круговую траекторию. Однако его скорость и энергия остаются неизменными. Циклотроны и синхротроны — это ускорители частиц, основанные на силе Лоренца.
Движение зарядов в магнитном поле
Как движется заряженная частица в магнитном поле?
Движется согласно выражению силы Лоренца, которая перпендикулярна магнитному полю и его скорости.
Работают ли магниты в вакууме?
Да, электромагнитное поле и, в частности, магнитное поле не нуждаются в среде для распространения.
Почему движущийся заряд создает магнитное поле?
Потому что движущийся заряд можно интерпретировать как электрический ток, основными объектами которого являются создания магнитных полей и на которые они воздействуют.
Что происходит, когда электроны погружаются в магнитное поле?
Они будут отклоняться магнитным полем в соответствии с силой Лоренца, если направление их движения не параллельно магнитному полю.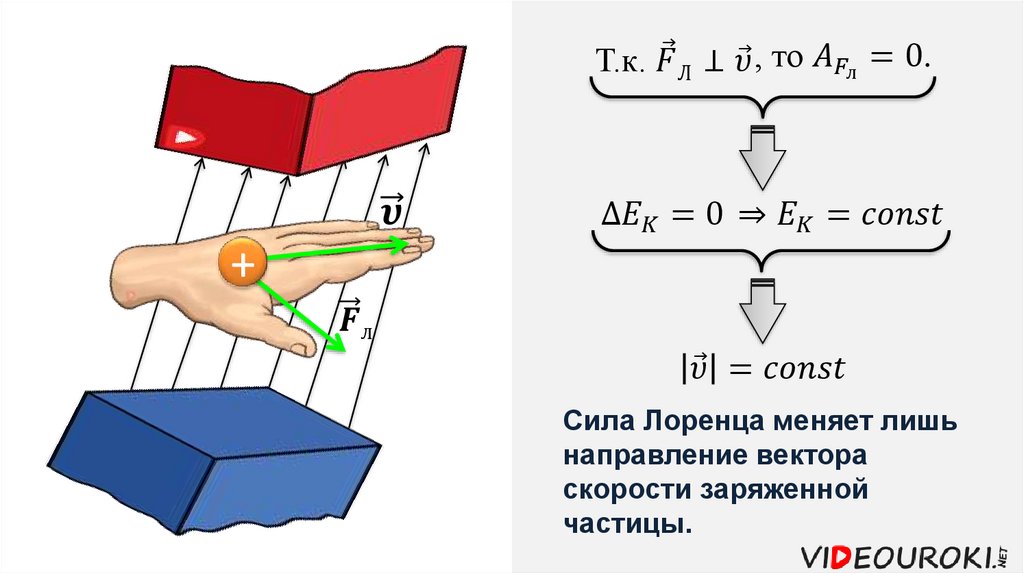
Изменяется ли энергия движущегося заряда в магнитном поле?
Его кинетическая энергия остается неизменной, потому что он описывает круговые траектории, которые не изменяют скорость заряда, а только направление его скорости.
электромагнетизм — Сила, ощущаемая движущимся зарядом из-за собственного магнитного поля?
$\begingroup$
Предположим, что движущийся протон пересекает однородное магнитное поле с постоянной скоростью. Обратите внимание, что поскольку протон движется, он создает собственное магнитное поле.
Объясняется ли магнитная сила, испытываемая протоном , полностью законом силы Лоренца, т. е. F = q (v x B)?
Или протон тоже испытывает дополнительную магнитную силу, возникающую из-за взаимодействия собственного магнитного поля с внешним полем? Если это неверно, то является ли закон силы Лоренца на самом деле просто описанием результата взаимодействий протонного поля с внешним полем, так что
- электромагнетизм
- магнитные поля
$\endgroup$
2
$\begingroup$
Магнитные поля не взаимодействуют с магнитными полями; они просто накладываются друг на друга.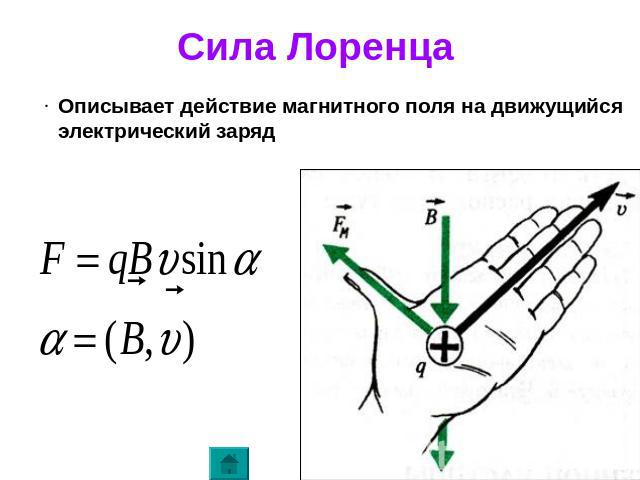
Разумно спросить, чувствует ли движущаяся заряженная частица собственное магнитное поле, так же как разумно спросить, чувствует ли неподвижная (или движущаяся) заряженная частица собственное электрическое поле.
Ответ в случае стационарной или равномерно движущейся заряженной частицы состоит в том, что эти электрические и магнитные самосилы наблюдаются равными нулю. Для точечной частицы ее электрические и магнитные поля становятся бесконечно большими вблизи частицы, но их можно понимать как действующие на частицу симметричным образом, так что результирующая сила отсутствует в каком-либо направлении.
В случае ускоряющейся заряженной частицы дело обстоит сложнее. Тогда сила Лоренца, вызванная внешними полями, — это еще не все. Ускоряющий заряд излучает электромагнитные волны, уносящие энергию, импульс и угловой момент в бесконечность. Энергия в этих волнах должна исходить от кинетической энергии частицы, поэтому должно быть обратная реакция сила, действующая на частицу, замедляющая ее с целью сохранения энергии.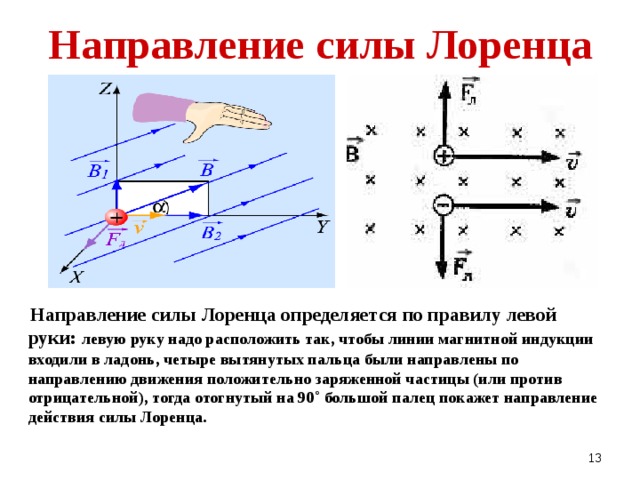


 А. Физика 11 кл.: Учебн. для общеобразоват. учреждений. 4-е изд., стереотип. – М.: Дрофа, 2004. – 416с.: ил., 8 л. цв. вкл., ст. 85, в. 5, з. 2–4.
А. Физика 11 кл.: Учебн. для общеобразоват. учреждений. 4-е изд., стереотип. – М.: Дрофа, 2004. – 416с.: ил., 8 л. цв. вкл., ст. 85, в. 5, з. 2–4.