Сила Лоренца

Рассмотрим подробнее вторую составляющую силы Лоренца.

Именно эту компоненту, зависящую от скорости, чаще всего и называют силой Лоренца. Получим её из силы Ампера. Ток это совокупность большого числа движущихся зарядов. Найдём силу, действующую на один заряд со стороны магнитного поля.

Причём , тогда запишем.

Мы учли что

– число зарядов в объёме Sdl.

В итоге получаем силу Лоренца, силу, действующую со стороны магнитного поля на движущийся со скоростью заряд.

Здесь под скоростью нужно понимать любую скорость. Но тепловая скорость хаотична по направлениям и равнодействующая этой силы будет равна нулю. Вклад даёт только скорость упорядоченного движения.

Исходя из векторного произведения, модуль силы Лоренца можно записать в следующем виде.

 – угол между векторами v и B. Следовательно, заряд, движущийся вдоль линии магнитной индукции не испытывает силы (так как

sin0^o = 0).

Направление силы Лоренца перпендикулярно к плоскости, в которой лежат вектора v и B. К движущемуся положительному заряду применимо правило левой руки. Или правило правого буравчика: вращать вектор v к B – поступательное движение укажет направление сила F_Л. Направление действия силы для отрицательного заряда – противоположное. Следовательно, к электронам следует применять правило правой руки.

Поскольку сила Лоренца всегда направлена перпендикулярно к движению заряда (т.е. ),

она работы над частицей не совершает. Следовательно, действуя на заряженные частицы постоянным магнитным полем, изменить энергию частицы нельзя. Это справедливо только для постоянного магнитного поля.

П усть заряд q влетает в однородное магнитное поле, индукция которого равна B, со скоростью v, направленной под углом  к направлению вектора магнитной индукции.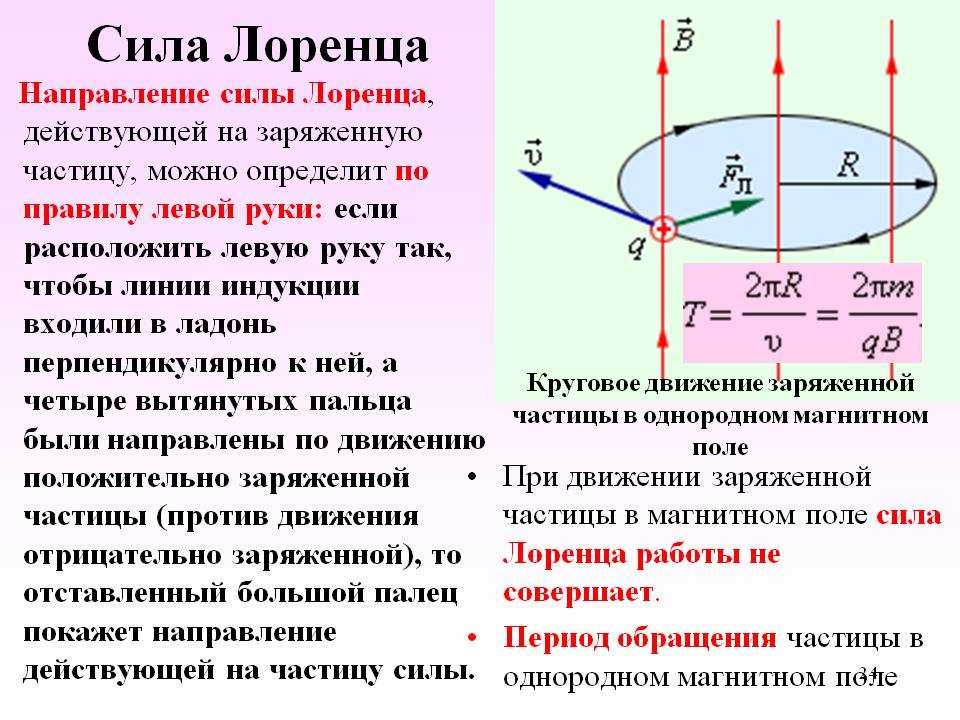 Под действием силы Лоренца заряд приобретает постоянное по величине нормальное ускорение.

 — угол между векторами скорости и магнитной индукции.

Если скорость изменяется только по направлению, т.е. движение с постоянным по величине нормальным ускорением, есть движение по окружности, радиус которой определяется следующим выражением.

Отсюда радиус будет равен.

(1)

Отношение заряда к массе (q/m) называется удельным зарядом.

Найдём время одного оборота (период) T. Для этого нужно разделить длину окружности 2R на v_ (скорость вращения заряда).

Период вращения заряженной частицы оказывается не зависящим от скорости. Собственная круговая частота (число оборотов за 2 секунд) равна.

Составляющая силы Лоренца в направлении вектора магнитной индукции (или в направлении v_) равна нулю. Поэтому повлиять на величину скорости v_ сила Лоренца не может.

Движение заряженной частицы в магнитном поле можно представить как наложение двух движений: 1) перемещение вдоль вектора

B со скоростью v_ = vcos; и 2) равномерное вращение в плоскости перпендикулярной вектору B. Радиус окружности, по которой происходит вращение, определяется формулой (1). Траектория движения – спираль, ось которой совпадает по направлению с направлением вектора B. Шаг спирали будет определяться выражением.

Курс общей физики, Т.2

Курс общей физики, Т.2

Савельев И. В. Курс общей физики: Учеб. пособие. В 3-х т. Т. 2. Электричество и магнетизм. Волны. Оптика. — 3-е изд., испр. — М.: Наука. Гл. ред. физ.-мат. лит., 1988. — 496 с. Второй том трехтомного курса общей физики, созданного профессором Московского инженерно-физического института, заслуженным деятелем науки и техники РСФСР, лауреатом Государственной премии СССР И. В. Савельевым. Главная цель книги — ознакомить студентов с основными идеями и методами физики. Особое внимание обращено на разъяснение смысла физических законов и на сознательное применение их. Для втузов с расширенной программой по физике, однако изложение построено так, что, опустив отдельные места, книгу можно использовать для втузов с обычной программой. Оглавление ПРЕДИСЛОВИЕ МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ЧАСТЬ 1. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ § 1. Электрический заряд § 2. Закон Кулона § 3. Системы единиц § 4. Рационализованная запись формул § 5. Электрическое поле. Напряженность поля § 6. Потенциал § 7. Энергия взаимодействия системы зарядов § 8. Связь между напряженностью электрического поля и потенциалом § 9. Диполь § 10. Поле системы зарядов на больших расстояниях § 11. Описание свойств векторных полей Дивергенция. Циркуляция. Теорема Стокса. § 12. Циркуляция и ротор электростатического поля § 13. Теорема Гаусса § 14. Вычисление полей с помощью теоремы Гаусса Поле двух разноименно заряженных плоскостей. Поле заряженной сферической поверхности. Поле объемно-заряженного шара. ГЛАВА II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ § 15. Полярные и неполярные молекулы § 16. Поляризация диэлектриков § 17. Поле внутри диэлектрика § 18. Объемные и поверхностные связанные заряды § 19. Вектор электрического смешения § 20. Примеры на вычисление поля в диэлектриках § 21. Условия на границе двух диэлектриков § 22. Силы, действующие на заряд в диэлектрике § 23. Сегнетоэлектрики ГЛАВА III. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ § 24. Равновесие зарядов на проводнике § 25. Проводник во внешнем электрическом поле § 26. Электроемкость § 27. Конденсаторы ГЛАВА IV. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ § 28. Энергия заряженного проводника § 29. Энергия заряженного конденсатора § 30. Энергия электрического поля ГЛАВА V. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 31. Электрический ток § 32. Уравнение непрерывности § 33. Электродвижущая сила § 34. Закон Ома. Сопротивление проводников § 35. Закон Ома для неоднородного участка цепи § 36. Разветвленные цепи. Правила Кирхгофа § 37. Мощность тока § 38. Закон Джоуля — Ленца ГЛАВА VI. МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ § 39. Взаимодействие токов § 40. Магнитное поле § 41. Поле движущегося заряда § 42. Закон Био — Савара § 43. Сила Лоренца § 44. Закон Ампера § 45. Магнитное взаимодействие как релятивистский эффект § 46. Контур с током в магнитном поле § 47. Магнитное поле контура с током § 48. Работа, совершаемая при перемещении тока в магнитном § 49. Дивергенция и ротор магнитного поля § 50. Поле соленоида и тороида ГЛАВА VII. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ § 51. Намагничение магнетика § 52. Напряженность магнитного поля § 53. Вычисление поля в магнетиках § 54. Условия на границе двух магнетиков § 55. Виды магнетиков § 56. Магнитомеханические явления § 57. Диамагнетизм § 58. Парамагнетизм § 59. Ферромагнетизм ГЛАВА VIII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 60. Явление электромагнитной индукции § 61. Электродвижущая сила индукции § 62. Методы измерения магнитной индукции § 63. Токи Фуко § 64. Явление самоиндукции § 65. Ток при замыкании и размыкании цепи § 66. Взаимная индукция § 67. Энергия магнитного поля § 68. Работа перемагничивания ферромагнетика ГЛАВА IX. УРАВНЕНИЯ МАКСВЕЛЛА § 69. Вихревое электрическое поле § 70. Ток смещения § 71. Уравнения Максвелла ГЛАВА X. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ПОЛЯХ § 72. Движение заряженной частицы в однородном магнитном поле § 73. Отклонение движущихся заряженных частиц электрическим и магнитным полями § 74. Определение заряда и массы электрона § 75. Определение удельного заряда ионов. Масс-спектрографы § 76. Ускорители заряженных частиц ГЛАВА XI. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ § 77. Природа носителей тока в металлах § 78. Элементарная классическая теория металлов § 79. Эффект Холла ГЛАВА XII. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ § 80. Несамостоятельная и самостоятельная проводимость § 81. Несамостоятельный газовый разряд § 82. Ионизационные камеры и счетчики § 83. Процессы, приводящие к появлению носителей тока при самостоятельном разряде § 84. Газоразрядная плазма § 85. Тлеющий разряд § 86. Дуговой разряд § 87. Искровой и коронный разряды ГЛАВА XIII. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ § 88. Квазистационарные токи § 89. Свободные колебания в контуре без активного сопротивления § 90. Свободные затухающие колебания § 91. Вынужденные электрические колебания § 92. Переменный ток ЧАСТЬ 2. ВОЛНЫ § 93. Распространение волн в упругой среде § 94. Уравнения плоской и сферической волн § 95. Уравнение плоской волны, распространяющейся в произвольном направлении § 96. Волновое уравнение § 97. Скорость упругих волн в твердой среде § 98. Энергия упругой волны § 99. Стоячие волны § 100. Колебания струны § 101. Звук § 102. Скорость звука в газах § 103. Эффект Доплера для звуковых волн ГЛАВА XV. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ § 104. Волновое уравнение для электромагнитного поля § 105. Плоская электромагнитная волна § 106. Экспериментальное исследование электромагнитных волн § 107. Энергия электромагнитных волн § 108. Импульс электромагнитного поля § 109. Излучение диполя ЧАСТЬ 3. ОПТИКА § 110. Световая волна § 111. Представление гармонических функций с помощью экспонент § 112. Отражение и преломление плоской волны на границе двух диэлектриков § 113. Световой поток § 114. Фотометрические величины и единицы § 115. Геометрическая оптика § 116. Центрированная оптическая система § 117. Тонкая линза § 118. Принцип Гюйгенса ГЛАВА XVII. ИНТЕРФЕРЕНЦИЯ СВЕТА § 119. Интерференция световых волн § 120. Когерентность § 121. Способы наблюдения интерференции света § 122. Интерференция света при отражении от тонких пластинок § 123. Интерферометр Майкельсона § 124. Многолучевая интерференция ГЛАВА XVIII. ДИФРАКЦИЯ СВЕТА § 126. Принцип Гюйгенса—Френеля § 127. Зоны Френеля § 128. Дифракция Френеля от простейших преград § 129. Дифракция Фраунгофера от щели § 130. Дифракционная решетка § 131. Дифракция рентгеновских лучей § 132. Разрешающая сила объектива § 133. Голография ГЛАВА XIX. ПОЛЯРИЗАЦИЯ СВЕТА § 134. Естественный и поляризованный свет § 135. Поляризация при отражении и преломлении § 136. Поляризация при двойном лучепреломлении § 137. Интерференция поляризованных лучей § 138. Прохождение плоскополяризованного света через кристаллическую пластинку § 139. Кристаллическая пластинка между двумя поляризаторами § 140. Искусственное двойное лучепреломление § 141. Вращение плоскости поляризации ГЛАВА XX. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН С ВЕЩЕСТВОМ § 142. Дисперсия света § 143. Групповая скорость § 144. Элементарная теория дисперсии § 145. Поглощение света § 146. Рассеяние света § 147. Эффект Вавилова — Черенкова ГЛАВА XXI. ОПТИКА ДВИЖУЩИХСЯ СРЕД § 148. Скорость света § 149. Опыт Физо § 150. Опыт Майкельсона § 151. Эффект Доплера ПРИЛОЖЕНИЯ I. Единицы электрических и магнитных величин в СИ и в гауссовой системе Приложение II. Основные формулы электромагнетизма в СИ и в гауссовой системе Приложение III. Векторный потенциал

электромагнетизм — выражение силы Лоренца

спросил 4 года 9 месяцев назад

Изменено 3 года, 3 месяца назад

Просмотрено 894 раза

$\begingroup$

Поскольку выражение силы Лоренца дается формулой $F=qBv\sin\theta$. Теперь я сомневаюсь, почему мы не можем взять $v \cos\theta$ в выражении и как насчет направления магнитного поля?

• электромагнетизм
• магнитные поля

$\endgroup$

3

$\begingroup$

Определение силы Лоренца, которое вы дали, не самое общее. Для магнитного поля $B$ и частицы с зарядом $q$, движущейся со скоростью $v$, сила Лоренца определяется выражением $$F_L=q v\times B\; , $$, где $\times$ обозначает векторное произведение. Итак, если угол между векторами $B$ и $v$ равен $\theta$, сила Лоренца принимает вид $$ |F_L|= q|v| |B|\sin\тета\; ,$$ как вы написали. Кроме того, если приложить электрическое поле $E$, сила Лоренца превращается в $$ F_L=q(E+v\times B)\; .$$

$\endgroup$

2

$\begingroup$

Сила Лоренца (в отсутствие электрического поля) определяется как $\vec{F}=q(\vec{v}\times \vec{B})=qvB\sin\theta\hat{l} $. Где $\hat{l}$ — единичный вектор, определяемый правилом правой руки в векторном произведении скорости и магнитного поля. Как видите, сила Лоренца — правильное векторное уравнение, которое действительно учитывает направление магнитного поля (а также скорость). Сила направлена ​​на 90 градусов как к скорости, так и к магнитному полю. Фактор $\sin\theta$ возникает из-за того, что это векторное произведение.

$\endgroup$

$\begingroup$

Что ж, кажется, вы впервые столкнулись с Законом Лоренца . Надо сказать, что Закон Лоренца — чисто экспериментальный результат. Дело было в том, что когда они включали магнитное поле, заряженная частица, двигавшаяся с некоторой скоростью $v$, случайно ощущала ускорение в направлении, перпендикулярном как направлению ее скорости, так и направлению магнитного поля. Теперь, когда они измерили величину ускорения и умножили эту величину на массу заряженной частицы (что и есть сила, закон Ньютона), результат всегда был $$ q~v~B~sin\theta$$, где $ q$ — величина заряда, $v$ — величина скорости, B — величина магнитного поля (я рассматриваю однородное и не зависящее от времени поле), а $\theta$ — угол между магнитным полем и направление скорости. Вы можете увидеть демонстрацию здесь.

В 1773 г. Дж. Л. Лагранж определил векторное произведение на покомпонентно, и из него можно было вывести $sin\theta$-форму векторного произведения на . Итак, эта штука перекрестное произведение стало в то время обычным явлением в динамике и очень привычным.

Таким образом, объединив экспериментальные результаты движения заряженной частицы в магнитном поле с математическими выводами, с предельной уверенностью были получены следующие выводы: и $\mathbf{B}$.

Его величина $F= q~v~B~sin\theta$

Следовательно, $\mathbf{F} = q(\mathbf{v} \times \mathbf{B})$ .

Надеюсь, это поможет.

P.S.: Все, что я сказал, было просто для иллюстрации, я не могу утверждать, что они на самом деле сделали. Утверждение о Ж. Л. Лагранже взято из википедии, а видео с ютуба.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Сила Лоренца: формула, определение и направление

Наряду с силой Ампера, кулоновским взаимодействием, электромагнитными полями в физике часто встречается понятие силы Лоренца. Это явление является одним из фундаментальных в электротехнике и электронике, наряду с законом подвеса, электромагнитной индукцией Фарадея и другими. Он действует на заряды, движущиеся в магнитном поле. В этой статье мы кратко и наглядно рассмотрим, что такое сила Лоренца и где она применяется.

• Определение
• Как направлена ​​сила Лоренца
• Применение
• Заключение

Определение

Когда электроны движутся вдоль проводника, вокруг него возникает магнитное поле. В то же время, если поместить проводник в поперечное магнитное поле и перемещать его, возникнет ЭДС электромагнитной индукции. Если по проводнику, находящемуся в магнитном поле, течет ток, на него действует сила Ампера.

Его значение зависит от протекающего тока, длины проводника, величины вектора магнитной индукции и синуса угла между линиями магнитного поля и проводником. Она рассчитывается по формуле:

Рассматриваемая сила несколько аналогична рассмотренной выше, но действует не на проводник, а на движущуюся заряженную частицу в магнитном поле. Формула:

Важно! На электрон, движущийся в магнитном поле, действует сила Лоренца (ФЛ), а на проводник — Ампер.

Из двух формул видно, что в первом и втором случаях чем ближе синус угла альфа к 90 градусам, тем больше влияние на проводник или заряд Fa или Fl соответственно.

Итак, сила Лоренца характеризуется не изменением величины скорости, а действием магнитного поля на заряженный электрон или положительный ион. При воздействии на них ФЛ не совершает работы. Соответственно, меняется именно направление скорости движения заряженной частицы, а не ее величина.

Что касается единицы измерения силы Лоренца, то, как и в случае с другими силами в физике, используется такая величина, как Ньютон. Его составляющие:

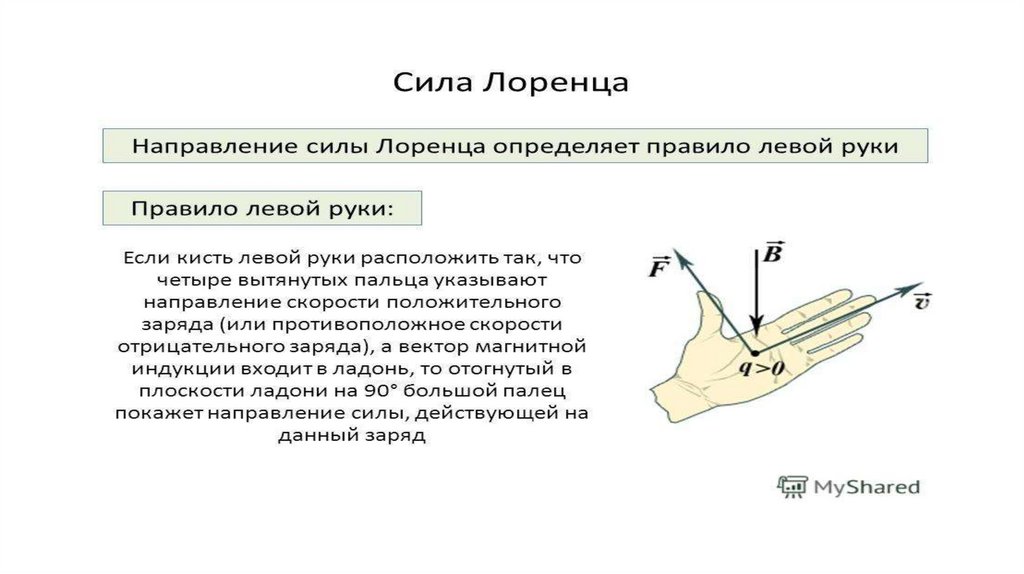
Как направлена ​​сила Лоренца

Для определения направления силы Лоренца, как и с силой Ампера, работает правило левой руки. Это означает, что для того, чтобы понять, куда направлена ​​величина Fl, нужно раскрыть ладонь левой руки так, чтобы линии магнитной индукции вошли в руку, а вытянутые четыре пальца указывали направление вектора скорости. Затем большой палец, согнутый под прямым углом к ​​ладони, указывает направление силы Лоренца. На картинке ниже вы видите, как определить направление.

Внимание! Направление действия Лоренца перпендикулярно движению частицы и линиям магнитной индукции.

В то же время, если быть точнее, для положительно и отрицательно заряженных частиц имеет значение направление четырех вытянутых пальцев. Описанное выше правило левой руки сформулировано для положительной частицы. Если она заряжена отрицательно, то линии магнитной индукции должны быть направлены не на раскрытую ладонь, а на ее тыльную сторону, и направление вектора Fl будет быть противоположным.

Теперь расскажем простыми словами, что дает нам это явление и какое реальное влияние оно оказывает на заряды. Предположим, что электрон движется в плоскости, перпендикулярной направлению линий магнитной индукции. Мы уже упоминали, что Fl не влияет на скорость, а только меняет направление движения частиц. Тогда сила Лоренца будет иметь центростремительное действие. Это отражено на рисунке ниже.

Заявка

Из всех областей, где используется сила Лоренца, одной из крупнейших является движение частиц в магнитном поле Земли. Если рассматривать нашу планету как большой магнит, то частицы, находящиеся вблизи северных магнитных полюсов, совершают ускоренное движение по спирали. В результате этого они сталкиваются с атомами из верхних слоев атмосферы, и мы видим северное сияние.

Однако есть и другие случаи, когда это явление применимо. Например:

• Электронно-лучевые трубки. В их электромагнитных системах отклонения. ЭЛТ используются уже более 50 лет подряд в различных устройствах, от простейшего осциллографа до телевизоров самых разных форм и размеров. Любопытно, что в вопросах цветопередачи и графики некоторые до сих пор используют ЭЛТ-мониторы.
• Электромобили — генераторы и двигатели. Хотя здесь скорее действует сила Ампера. Но эти значения можно считать соседними. Однако это сложные устройства, при работе которых наблюдается влияние многих физических явлений.
• В ускорителях заряженных частиц для придания им орбит и направлений.

Заключение

Подытожим и изложим четыре основных пункта этой статьи простым языком:

1. Сила Лоренца действует на заряженные частицы, которые движутся в магнитном поле. Это следует из основной формулы.
2. Прямо пропорциональна скорости заряженной частицы и магнитной индукции.
3. Не влияет на скорость частиц.
4. Влияет на направление частицы.

Его роль довольно велика в «электрических» областях. Специалист не должен упускать из виду основные теоретические сведения об основных физических законах. Эти знания пригодятся, а также тем, кто занимается научной работой, дизайном и просто для общего развития.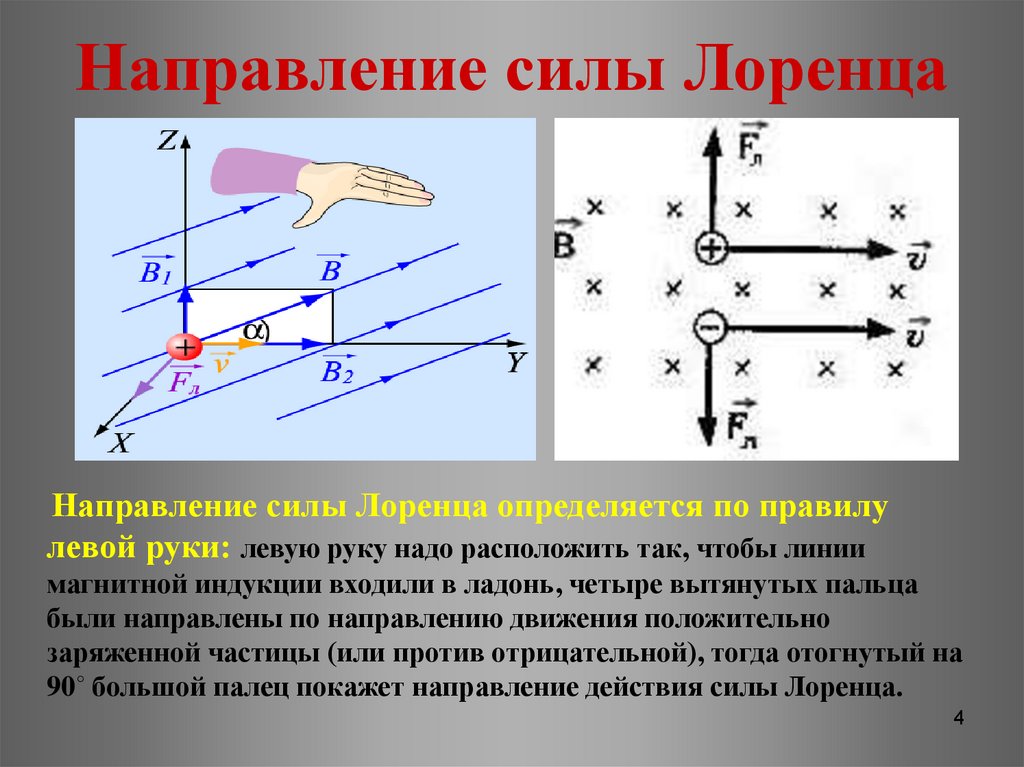

Напоследок рекомендуем посмотреть полезные видео для закрепления изученного материала:

Теперь вы знаете, что такое сила Лоренца, чему она равна и как действует на заряженные частицы. Если у вас есть вопросы, задавайте их в комментариях под статьей!

Материалы по теме:

• Правило буравчика простыми словами
• Что такое электрический заряд
• Как перевести ампер в киловатт
• Контактное сопротивление