Сила Лоренца

      Электрический ток это совокупность большого числа n движущихся со скоростью υ зарядов. Найдем силу, действующую на один заряд со стороны магнитного поля. По закону Ампера сила, действующая на проводник с током в магнитном поле,

,

(2.5.1)

но ток  причем , тогда

.

Т.к.   nSdl –число зарядов в объёме Sdl,  тогда для одного заряда

 или

,

(2.5.2)

      Сила Лоренца – сила, действующая со стороны магнитного поля на движущийся со скоростью  положительный заряд (здесь  – скорость упорядоченного движения носителей положительного заряда

). Модуль лоренцевой силы:

,

(2.5.3)

где α – угол между  и .

      Из (2.5.4) видно, что на заряд, движущийся вдоль линии , не действует сила ( ).

Лоренц Хендрик Антон (1853–1928) – нидерландский физик-теоретик, создатель классической электронной теории, член Нидерландской АН. Вывел формулу, связывающую диэлектрическую проницаемость с плотностью диэлектрика, дал выражение для силы, действующей на движущийся заряд в электромагнитном поле (сила Лоренца), объяснил зависимость электропроводности вещества от теплопроводности, развил теорию дисперсии света. Разработал электродинамику движущихся тел. В 1904 г. вывел формулы, связывающие между собой координаты и время одного и того же события в двух различных инерциальных системах отсчета (преобразования Лоренца).

      Направлена сила Лоренца перпендикулярно к плоскости, в которой лежат векторы  и .  К движущемуся положительному заряду применимо правило левой руки или «правило буравчика» (рис. 2.6).

             

Рис. 2.6

      Направление действия силы для отрицательного заряда – противоположно, следовательно, к электронам применимо правило правой руки

.

      Так как сила Лоренца направлена перпендикулярно движущемуся заряду, т.е. перпендикулярно , работа этой силы всегда равна нулю. Следовательно, действуя на заряженную частицу, сила Лоренца не может изменить кинетическую энергию частицы.

      Часто лоренцевой силой называют сумму электрических и магнитных сил:

,

(2.5.4)

здесь электрическая сила  ускоряет частицу, изменяет ее энергию.

      Повседневно действие магнитной силы на движущийся заряд мы наблюдаем на телевизионном экране (рис. 2.7).

Рис. 2.7

      Движение пучка электронов по плоскости экрана стимулируется магнитным полем отклоняющей катушки. Если поднести постоянный магнит к плоскости экрана, то легко заметить его воздействие на электронный пучок по возникающим в изображении искажениям.

      Действие лоренцевой силы в ускорителях заряженных частиц подробно описано в п. 4.3.

---

Сила Лоренца — Википедия

Материал из Википедии — свободной энциклопедии

Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью v{\displaystyle \mathbf {v} } заряд q {\displaystyle q\ } лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще

[1], иначе говоря, со стороны электрического E{\displaystyle \mathbf {E} } и магнитного B{\displaystyle \mathbf {B} } полей. В Международной системе единиц (СИ) выражается как:

F=q(E+[v×B]).{\displaystyle \mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).}

Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом

[2].

Макроскопическим проявлением силы Лоренца является сила Ампера.

Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца^[3].

Уравнение (единицы СИ)

Заряженная частица

Сила F{\displaystyle \mathbf {F} }, действующая на частицу с электрическим зарядом q{\displaystyle q}, движущуюся со скоростью v{\displaystyle \mathbf {v} }, во внешнем электрическом E{\displaystyle \mathbf {E} } и магнитном B{\displaystyle \mathbf {B} } полях, такова:

F=q(E+v×B),{\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}

где ×{\displaystyle \times } — векторное произведение. Все величины, выделенные жирным, являются векторами. Более явно:

F(r,t,q)=qE(r,t)+qr˙×B(r,t),{\displaystyle \mathbf {F} (\mathbf {r} ,t,q)=q\mathbf {E} (\mathbf {r} ,t)+q\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t),}

где r{\displaystyle \mathbf {r} } — радиус-вектор заряженной частицы, t{\displaystyle t} — время, точкой обозначена производная по времени.

Непрерывное распределение заряда

Для непрерывного распределения заряда, сила Лоренца принимает вид:

dF=dq(E+v×B),{\displaystyle d\mathbf {F} =dq\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),}

где dF{\displaystyle d\mathbf {F} } — сила, действующая на маленький элемент dq{\displaystyle dq}.

Ковариантная запись

4-сила выражается через вектор 4-скорости частицы по формуле

Fμ=qFνμuν,{\displaystyle {\mathcal {F}}^{\mu }=qF^{\nu \mu }u_{\nu },}

где Fμ{\displaystyle {\mathcal {F}}^{\mu }} — 4-сила, q{\displaystyle q} — заряд частицы, Fνμ{\displaystyle F^{\nu \mu }} — тензор электромагнитного поля, uν{\displaystyle u_{\nu }} — 4-скорость.

Частные случаи

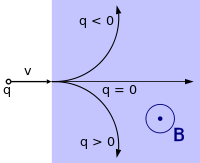Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)

В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r{\displaystyle r} (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:

СГС	СИ
mv2r=|q|cvB⇒r=cm|q|⋅vB{\displaystyle {mv^{2} \over r}={|q| \over c}vB\Rightarrow r={cm \over |q|}\cdot {v \over B}}	mv2r=|q|vB⇒r=m|q|⋅vB{\displaystyle {mv^{2} \over r}=|q|vB\Rightarrow r={m \over |q|}\cdot {v \over B}}

Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости v {\displaystyle v\ }, намного меньшей скорости света, круговая частота ω {\displaystyle \omega \ } не зависит от v {\displaystyle v\ }:

СГС	СИ
ω=|q|Bmc{\displaystyle \omega ={|q|B \over mc}}	ω=|q|Bm{\displaystyle \omega ={|q|B \over m}}

Если заряженная частица движется в магнитном поле так, что вектор скорости v {\displaystyle v\ } составляет с вектором магнитной индукции B{\displaystyle \mathbf {B} } угол α {\displaystyle \alpha \ }, то траекторией движения частицы является винтовая линия с радиусом r {\displaystyle r\ } и шагом винта h {\displaystyle h\ }:

СГС	СИ
r=mc|q|⋅vsin⁡αB{\displaystyle r={mc \over |q|}\cdot {v\sin \alpha \over B}}, h=2πB⋅mc|q|⋅vcos⁡α{\displaystyle h={2\pi \over B}\cdot {mc \over |q|}\cdot v\cos \alpha }	r=m|q|⋅vsin⁡αB{\displaystyle r={m \over |q|}\cdot {v\sin \alpha \over B}}, h=2πB⋅m|q|⋅vcos⁡α{\displaystyle h={2\pi \over B}\cdot {m \over |q|}\cdot v\cos \alpha }

Использование

Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне

См. также

Примечания

1. ↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
2. ↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
3. ↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.

Сила Лоренца

Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика Х. Лоренца (1853 — 1928) — основателя электронной теории строения вещества. Силу Лоренца можно найти с помощью закона Ампера.

Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:

Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка Δl и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля можно считать одинаковым в пределах этого отрезка проводника. Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:

I = qnvS ( 2 )

Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен:

F = | I |B Δl sin α

Подставляя в эту формулу выражение ( 2 ) для силы тока, получаем:

F = | q | nvS Δl B sin α = v | q | NB sin α, где N = nSΔl — число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная: где α — угол между вектором скорости и вектором магнитной индукции. Сила Лоренца перпендикулярна векторам магнитной индукции и скорости упорядоченного движения заряженных частиц. Ее направление определяется с помощью того же правила левой руки, что и направление силы Ампера.

Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работы. Согласно теореме о кинетической энергии это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.

---

Другие заметки по физике

Лоренца сила — это… Что такое Лоренца сила?

ЛОРЕНЦА СИЛА — сила, действующая на заряж. ч цу, движущуюся в эл. магн. поле. Ф ла для Л. с. F впервые получена X. А. Лоренцем, обобщившим эксперим. данные, имеет вид: F = eE+e/c(vB), (*) где е заряд ч цы, Е напряжённость электрич. поля, В магнитная индукция, v …   Физическая энциклопедия

ЛОРЕНЦА СИЛА — ЛОРЕНЦА СИЛА, сила (f), действующая на заряженную частицу, движущуюся в электромагнитном поле; выражается установленной Х.А. Лоренцем в конце 19 в. формулой f= qE+q(vxB) (в СИ), где q, v заряд и скорость частицы соответственно; E напряженность… …   Современная энциклопедия

ЛОРЕНЦА СИЛА — сила (f), действующая на заряженную частицу, движущуюся в электромагнитном поле; выражается установленной Х. А. Лоренцем в кон. 19 в. формулой: (в СГС системе единиц), где ?, ? заряд и скорость частицы, Е напряженность электрического поля, В… …   Большой Энциклопедический словарь

Лоренца сила — ЛОРЕНЦА СИЛА, сила (f), действующая на заряженную частицу, движущуюся в электромагнитном поле; выражается установленной Х.А. Лоренцем в конце 19 в. формулой f= qE+q(vxB) (в СИ), где q, v заряд и скорость частицы соответственно; E напряженность… …   Иллюстрированный энциклопедический словарь

Лоренца сила — сила (f), действующая на заряженную частицу, движущуюся в электромагнитном поле; выражается установленной Х. А. Лоренцем в конце XIX в. формулой: (в СГС системе единиц), где e, v  заряд и скорость частицы, E  напряжённость электрического поля, B  …   Энциклопедический словарь

Лоренца сила —         сила, действующая на заряженную частицу, движущуюся в электромагнитном поле. Формула для Л. с. F была впервые получена Х. А. Лоренцом как результат обобщения опыта и имеет вид:          F = eE + υB].          Здесь е заряд частицы, Е… …   Большая советская энциклопедия

ЛОРЕНЦА СИЛА — сила, действующая со стороны заданного электромагнитного поля на движущуюся заряженную частицу. Выражение для Л. с. Fбыло впервые дано Г. Лоренцем (см. [1]): где Е напряженность электрич. поля, В магнитная индукция, V скорость заряженной частицы… …   Математическая энциклопедия

ЛОРЕНЦА СИЛА — сила, действующая со стороны электромагнитного поля на движущуюся заряж. частицу. Л. с. F равна F = QE + О [v, В], где О заряд частицы, Е напряжённость электрич. поля, В магнитная индукция, a v скорость частицы относительно той инерциальной… …   Большой энциклопедический политехнический словарь

ЛОРЕНЦА СИЛА — сила (f), действующая на заряженную частицу, движущуюся в эл. магн. поле; выражается установленной X. А. Лоренцем и кон. 19 в. ф лой: f= е(Е+1/C[vB]) (в СГС системе единиц), где е, v заряд и скорость частицы, Е напряжённость электрич. поля, В… …   Естествознание. Энциклопедический словарь

СИЛА — векторная величина мера механического воздействия на тело со стороны др. тел, а также интенсивности др. физ. процессов и полей. Силы бывают различными: (1) С. Ампёра сила, с которой (см.) действует на проводник с током; направление вектора силы… …   Большая политехническая энциклопедия

ЛОРЕНЦА СИЛА — это… Что такое ЛОРЕНЦА СИЛА?

ЛОРЕНЦА СИЛА — сила, действующая на заряж. ч цу, движущуюся в эл. магн. поле. Ф ла для Л. с. F впервые получена X. А. Лоренцем, обобщившим эксперим. данные, имеет вид: F = eE+e/c(vB), (*) где е заряд ч цы, Е напряжённость электрич. поля, В магнитная индукция, v …   Физическая энциклопедия

ЛОРЕНЦА СИЛА — сила (f), действующая на заряженную частицу, движущуюся в электромагнитном поле; выражается установленной Х. А. Лоренцем в кон. 19 в. формулой: (в СГС системе единиц), где ?, ? заряд и скорость частицы, Е напряженность электрического поля, В… …   Большой Энциклопедический словарь

Лоренца сила — ЛОРЕНЦА СИЛА, сила (f), действующая на заряженную частицу, движущуюся в электромагнитном поле; выражается установленной Х.А. Лоренцем в конце 19 в. формулой f= qE+q(vxB) (в СИ), где q, v заряд и скорость частицы соответственно; E напряженность… …   Иллюстрированный энциклопедический словарь

Лоренца сила — сила (f), действующая на заряженную частицу, движущуюся в электромагнитном поле; выражается установленной Х. А. Лоренцем в конце XIX в. формулой: (в СГС системе единиц), где e, v  заряд и скорость частицы, E  напряжённость электрического поля, B  …   Энциклопедический словарь

Лоренца сила —         сила, действующая на заряженную частицу, движущуюся в электромагнитном поле. Формула для Л. с. F была впервые получена Х. А. Лоренцом как результат обобщения опыта и имеет вид:          F = eE + υB].          Здесь е заряд частицы, Е… …   Большая советская энциклопедия

ЛОРЕНЦА СИЛА — сила, действующая со стороны заданного электромагнитного поля на движущуюся заряженную частицу. Выражение для Л. с. Fбыло впервые дано Г. Лоренцем (см. [1]): где Е напряженность электрич. поля, В магнитная индукция, V скорость заряженной частицы… …   Математическая энциклопедия

ЛОРЕНЦА СИЛА — сила, действующая со стороны электромагнитного поля на движущуюся заряж. частицу. Л. с. F равна F = QE + О [v, В], где О заряд частицы, Е напряжённость электрич. поля, В магнитная индукция, a v скорость частицы относительно той инерциальной… …   Большой энциклопедический политехнический словарь

ЛОРЕНЦА СИЛА — сила (f), действующая на заряженную частицу, движущуюся в эл. магн. поле; выражается установленной X. А. Лоренцем и кон. 19 в. ф лой: f= е(Е+1/C[vB]) (в СГС системе единиц), где е, v заряд и скорость частицы, Е напряжённость электрич. поля, В… …   Естествознание. Энциклопедический словарь

Лоренца сила — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм Электростатика Закон Кулона …   Википедия

СИЛА — векторная величина мера механического воздействия на тело со стороны др. тел, а также интенсивности др. физ. процессов и полей. Силы бывают различными: (1) С. Ампёра сила, с которой (см.) действует на проводник с током; направление вектора силы… …   Большая политехническая энциклопедия

Велосиметрия силой Лоренца — Википедия

Велосиметрия силой Лоренца (ВСЛ)

^[1] — это бесконтактный электромагнитный способ измерения скорости и расхода электропроводной жидкости. ВСЛ применяется, в частности, для исследования жидких металлов, таких как сталь или алюминий, и в данное время метод находится на стадии разработки для применения в металлургии. Измерение скорости и расхода таких высокотемпературных и агрессивных жидкостей, как расплав стекла — серьёзный вызов для технической гидромеханики. Именно для решения этой проблемы может быть применён метод ВСЛ. Кроме исследования жидкостей, ВСЛ может также использован как для измерения скорости твёрдых электропроводных материалов, так и для обнаружения в них структурных микро-дефектов.

Измерительные системы, использующие для работы принцип ВСЛ, называются расходомеры силой Лоренца (РСЛ). РСЛ измеряют интегрированную или объёмную силу Лоренца, возникающую в результате взаимодействия движущегося жидкого проводника и приложенного магнитного поля. В этом случае характерный размер зоны влияния магнитного поля имеет тот же порядок, что и размер канала с жидкостью. Стоит подчеркнуть, что в случае использования ограниченного по размеру магнитного поля возможно измерение локальной скорости потока, поэтому и в этом случае может быть использован термин РСЛ.

Самое раннее использование магнитного поля для измерения потока жидкости датируется XIX веком, когда в 1832 году Майкл Фарадей пытался определить скорость течения реки Темза. Фарадей применил метод, в котором поток (течение реки) подвергался воздействию магнитного поля (магнитное поле Земли) и возникающая разница потенциалов измерялась при помощи двух электродов, расположенных поперёк реки. По этому же принципу работает один из самых коммерчески успешных электромагнитных приборов для изучения потока жидкости — кондукционный расходомер. Теоретическая основа для создания подобных приборов была разработана английским физиком Артуром Шерклифом^[2] (Arthur Shercliff) в 50-х годах двадцатого века. Хотя кондукционные расходомеры широко применяются для определения расхода различных жидкостей при комнатной температуре в химической, фармацевтической и пищевой промышленности, они практически не применимы для исследования высокотемпературных и агрессивных сред или для измерения локальной скорости в случае ограниченного доступа к каналу или трубе. Так как использование метода предполагает применение электродов, погруженных в жидкость, кондукционная расходометрия ограничена областью относительно невысоких температур, лежащих значительно ниже точки плавления большинства металлов.

Термин Велосиметрия силой Лоренца был предложен Артуром Шерклифом ещё в середине прошлого века. Но, несмотря на это, практическое применение метода стало возможным лишь с относительно недавнего времени; отправной точкой здесь послужило создание сильных постоянных магнитов на основе редкоземельных материалов, разработка прецизионных методик силовых измерений, появление высокотехнологичного программного обеспечения для моделирования процессов магнитной гидродинамики (МГД). Всё это позволило ВСЛ стать конкурентоспособной методикой измерения расхода жидкостей. В данное время метод ВСЛ продолжает своё развитие, как техника измерения расхода в прикладной металлургии^[3] и других областях^[4].

Основываясь на предложенной Шерклифом теории были разработаны несколько методов измерения расхода, не требующих какого-либо механического контакта с исследуемой жидкостью^[5][6]. Среди них расходомер на основе действия вихревых токов, который измеряет возбуждённые потоком жидкости изменения электрического сопротивления стержней, взаимодействующих с потоком. Существует также бесконтактный расходомер, действие которого основано на измерении деформации приложенного магнитного поля под действием потока жидкости^[7][8].

Принцип действия ВСЛ основывается на измерении силы Лоренца, которая возникает под влиянием изменения магнитного поля. Согласно закону Фарадея, при движении металла или проводящей жидкости через приложенное магнитное поле в зонах наибольшего градиента поля (в данном случае на «входе» и «выходе» из поля) внутри жидкости возникает э.д.с., приводящая к появлению вихревых токов. В свою очередь, вихревые токи создают индуцированное магнитное поле в соответствии с законом Ампера-Максвелла. Взаимодействие между вихревыми токами и результирующим полем приводит к появлению силы Лоренца. Возникающая таким образом сила оказывает тормозящее действие на поток и, согласно третьему закону Ньютона (сила действия равна силе противодействия), она равна по модулю силе, действующей на постоянный магнит. Прямое измерение силы реакции магнита позволяет определить скорость движения жидкости, поскольку амплитуда силы Лоренца пропорциональна скорости потока. Возникновение силы Лоренца при ВСЛ не имеет ничего общего с классическими силами притяжения и отталкивания магнитных тел. Её воздействие обусловлено исключительно вихревыми токами, которые, в свою очередь, зависят от электропроводности и скорости движения жидкости, а также от силы влияния и формы магнитного поля.

Исходя из вышеизложенного, при пересечении потока жидкого металла и линий магнитного поля (которое, в свою очередь, генерируется катушкой с током либо постоянным магнитом), возникающие вихревые токи индуцируют возникновение силы Лоренца (плотностью f→=j→×B→{\displaystyle {\vec {f}}={\vec {j}}\times {\vec {B}}}) . Согласно определению:

f∼σvB2{\displaystyle f\sim \sigma vB^{2}}

где σ{\displaystyle \sigma } — электропроводность жидкости, v{\displaystyle v} — скорость, и B{\displaystyle B} — индукция магнитного поля. Этот факт известен и широко применяется на практике. Эта сила пропорциональна скорости и электрической проводимости жидкости, и её измерение — ключевая идея ВСЛ. В результате последних достижений в области производства постоянных магнитов из редкоземельных материалов (изготовление таких магнитов как, например, неодимовые магниты (NdFeB), самарино-кобальтовые магниты (SmCo)) и в области конструирования измерительных приборов для системы постоянных магнитов позволили расширить область практического применения ВСЛ.

Первичное магнитное поле B→(r→){\displaystyle {\vec {B}}\left({\vec {r}}\right)} может быть индуцировано под воздействием постоянного магнита или первичного тока J→(r→){\displaystyle {\vec {J}}\left({\vec {r}}\right)} (see Fig. 1). В движущейся сквозь первичное магнитное поле жидкости возникают вихревые токи, как изображено на рис. 3. Они обозначены как j→(r→){\displaystyle {\vec {j}}\left({\vec {r}}\right)} и называются вторичными токами. Взаимодействие вторичных токов и первичного магнитного поля индуцирует силу Лоренца, которая тормозит течение жидкости

F→f=∫fj→×B→d3r→{\displaystyle {\vec {F}}_{f}=\int _{f}{\vec {j}}\times {\vec {B}}d^{3}{\vec {r}}}

.

Вторичные токи, в свою очередь, создают магнитное поле b→(r→){\displaystyle {\vec {b}}\left({\vec {r}}\right)} — вторичное магнитное поле. Взаимодействие первичных вихревых токов и вторичного магнитного поля приводит к появлению силы Лоренца, действующей на магнитную систему

F→m=∫mJ→×b→d3r→{\displaystyle {\vec {F}}_{m}=\int _{m}{\vec {J}}\times {\vec {b}}d^{3}{\vec {r}}}

.

Принцип взаимности в ВСЛ выражается в том, что электромагнитные силы одинаково влияют как на жидкость, так и на систему магнитов, но действуют в противоположных направлениях, как можно увидеть из:

F→m=−F→f{\displaystyle {\vec {F}}_{m}=-{\vec {F}}_{f}}

Основная градуировочная функция отношения измеряемой силы к скорости потока может быть получена, как это проиллюстрировано на упрощённой схеме (рис. 2). Здесь небольшой постоянный магнит с дипольным моментом m{\displaystyle m} расположен на расстоянии L{\displaystyle L} над полубесконечным потоком жидкости, движущейся с постоянной скоростью v{\displaystyle v} параллельно своей открытой поверхности.

Для количественного анализа градуировочной функции примем, что магнит является точечным диполем с дипольным моментом m→=me^z{\displaystyle {\vec {m}}=m{\hat {e}}_{z}}, магнитное поле которого может быть определено как:

B→(R→)=μ04π{3(m→⋅R→)R→R5−m→R3}{\displaystyle {\vec {B}}\left({\vec {R}}\right)={\frac {\mu _{0}}{4\pi }}\left\lbrace 3{\frac {\left({\vec {m}}\cdot {\vec {R}}\right){\vec {R}}}{R^{5}}}-{\frac {\vec {m}}{R^{3}}}\right\rbrace }

где R→=r→−Le^z{\displaystyle {\vec {R}}={\vec {r}}-L{\hat {e}}_{z}} и R=∣R→∣{\displaystyle R=\mid {\vec {R}}\mid }. Принимая поле скорости v→=ve^x{\displaystyle {\vec {v}}=v{\hat {e}}_{x}} для z<0{\displaystyle z<0}, вихревые токи могут быть рассчитаны при помощи закона Ома для движущейся электропроводной жидкости

J→=σ(−∇ϕ+v→×B→){\displaystyle {\vec {J}}=\sigma \left(-\nabla \phi +{\vec {v}}\times {\vec {B}}\right)}

по отношению к граничным условиям Jz=0{\displaystyle J_{z}=0} в z=0{\displaystyle z=0} и Jz→0{\displaystyle J_{z}\to 0} как z→1{\displaystyle z\to 1}. Во первых, скалярное значение электрического потенциала может быть получено как

ϕ(r→)=−μ0vm4πxR3{\displaystyle \phi \left({\vec {r}}\right)=-{\frac {\mu _{0}vm}{4\pi }}{\frac {x}{R^{3}}}}

откуда несложно рассчитать плотность тока. И, с помощью полученных выше данных и закона Био-Саварра, можно вычислить значение индуцированного (вторичного) магнитного поля b→(r→){\displaystyle {\vec {b}}\left({\vec {r}}\right)}. Наконец, сила может быть получена как

F→=(m→⋅∇)b→{\displaystyle {\vec {F}}=\left({\vec {m}}\cdot \nabla \right){\vec {b}}}

где градиент b→{\displaystyle {\vec {b}}} может быть определён для положения диполя. Все эти шаги могут быть произведены аналитически и решение проблемы без использования каких-либо приближений будет выглядеть как

F=μ02σvm2128πL3e^z{\displaystyle F={\frac {\mu _{0}^{2}\sigma vm^{2}}{128\pi L^{3}}}{\hat {e}}_{z}}

Что приводит нас к величине

F∼μ02σvm2L−3{\displaystyle F\sim \mu _{0}^{2}\sigma vm^{2}L^{-3}}

Расходомеры силы Лоренца могут быть поделены на следующие типы согласно способу измерения. Это статические расходомеры, магнитная система которых неподвижна и измеряет силу, действующую на неё. И расходомеры вращения, в которых магниты расположены на вращающемся диске и для определения расхода измеряется крутящий момент или угловая скорость. Согласно расположению постоянных магнитов относительно канала расходомеры силы Лоренца можно также классифицировать как продольные и поперечные (рис. 3).

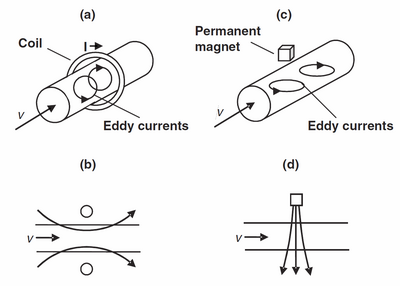Рис. 3 : Принципиальная схема ВСЛ: расположение катушки (a) и структура приложенного (первичного) магнитного поля (b) для продольного расходомера. (c, d) То же для поперечного расходомера. Взято из источника [1].

Принцип измерения с помощью расходомеров вращения основывается на использовании вращающихся постоянных магнитов^[9] (либо массива магнитов, закреплённых на диске, как это показано на рис. 4). Линии магнитного поля постоянных магнитов перпендикулярны поверхности, в которую они встроены. Когда подобная система расположена рядом с каналом с движущейся электропроводной жидкостью, диск вращается так, что движущий момент, возникший в результате действия вихревых токов, уравновешивается за счёт тормозящего момента, возникающего в результате самого вращения диска. Скорость вращения при этом прямо пропорциональна скорости потока и обратно пропорциональна расстоянию между магнитом и каналом. В этом случае возможно измерение как момента вращения, так и угловой скорости магнитной системы.

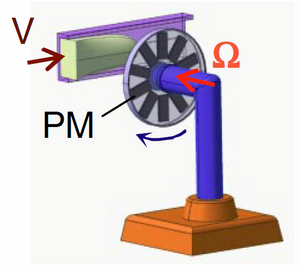Рис. 4 : Упрощённая схема ВСЛ вращения. Взято из источника [1].

Примеры практического применения ВСЛ[править | править код]

Метод ВСЛ может быть использован практически для всех жидкостей и твёрдых тел при условии, что они являются проводниками. Как было доказано ранее, сила Лоренца прямо пропорциональна проводимости материала. В обычных случаях электрическая проводимость жидких металлов составляет порядка 106{\displaystyle 10^{6}} См/м поэтому возникающая в них сила Лоренца не превышает нескольких мН. В то же время такие жидкости как расплавы стекла и растворы электролитов имеют электропроводность около ∼ 1{\displaystyle \sim ~1} См/м, и возникающая в результате сила Лоренца имеет порядок мкН.

Высокопроводящая среда: жидкие или твёрдые металлы[править | править код]

Среди разнообразных возможностей измерения эффекта на магнитную систему, успешно применяются методы, действие которых основано на измерении отклонения параллельных упругих элементов под влиянием приложенной силы.^[10] Например с помощью тензодатчиков на кварцевых упругих элементах совместно с интерферометром возможно зафиксировать деформацию до 0,1 нм.

Низкопроводящие среды: растворы электролитов и расплавы стекла[править | править код]

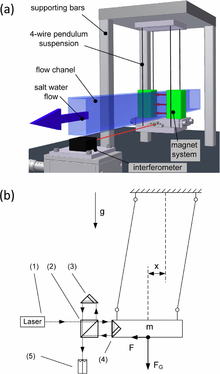Рис. 5 : Схема бесконтактного ВСЛ расходомера, используемого при эксперименте: (a) Турбулентное течение солёной воды (с значением числа Рейнольдса между 3.2⋅104{\displaystyle 3.2\cdot 10^{4}} и 1.3⋅105{\displaystyle 1.3\cdot 10^{5}}) подвергается воздействию магнитного поля, генерируемого легковесной системой постоянных магнитов четырёх-проводного маятника. Смещение маятника измеряется с помощью интерферометра как показано на (b): 1 — He-Ne лазер, 2 — излучатель, 3 — эталонный кубический угловой отражатель, 4 — фотодетектор, и 5 — измеритель кубического углового отражателя. Источник^[11]

Последние достижения в ВСЛ сделали возможными измерения расхода жидкости даже для низкопроводящих сред, в частности за счёт использования современных датчиков силы. Это позволяет определять скорость потока сред с электропроводностью, которая в 10⁶ раз ниже, чем у жидких металлов. Существует множество направлений в научной и производственной сферах, где применяются подобные растворы, и в некоторых случаях необходимо определять расход бесконтактно либо сквозь непрозрачные стенки. В качестве примера здесь можно привести измерение потока химических и пищевых продуктов, крови, водных растворов в фармацевтической промышленности, соляных расплавов в реакторах электростанций,^[12][13] а также расплавленного стекла при производстве высокоточных оптических приборов.^[14]

Бесконтактные расходомеры могут быть использованы в отсутствии механического контакта как с самой жидкостью, так и со стенками сосуда с протекающей жидкостью, поэтому они могут применяться в случае загрязнённых стенок, как, например, при работе с радиоактивными материалами либо при сильной вибрации каналов, для чего предусмотрены портативные расходомеры. Если стенки и жидкость прозрачны, а также есть возможность использовать сигнальные частицы, для бесконтактного измерения расхода обычно отдают предпочтение оптическим методам.^[15][16]

В настоящее время существует два прототипа расходомера ВСЛ для низкопроводящих сред, которые успешно прошли испытания и используются в лабораторных условиях. Действие обоих приборов основывается на измерении смещения маятнико-подобного механизма. Один из расходомеров содержит два высокомощных (410 мТл) постоянных магнита из NdFeB, находящиеся с двух сторон канала с жидкостью и создающие магнитное поле перпендикулярно потоку. Смещение магнитов в результате действия возникающей силы Лоренца измеряется при помощи интерферометрической системы,^[17] (Рис. 5 а). Вторая система состоит из современной системы измерения веса, к которой подвешена оптимизированная магнитная сборка Халбаха.

И в первом, и во втором случае общая масса магнитной системы равна (1 kg), но сигнал, измеряемый с помощью магнитной сборки Халбаха, в три раза превышает сигнал от обычной магнитной системы при заданном профиле скорости. Для измерения отклика системы желательно использовать очень чувствительные датчики силы, так как скорость потока конвертируется из крайне низких значений фиксируемой силы Лоренца. Эта сила в комбинации с неизбежным влиянием веса конструкции FG=m⋅g{\displaystyle F_{G}=m\cdot g} составляет около F/FG=10−7{\displaystyle F/F_{G}=10^{-7}}.

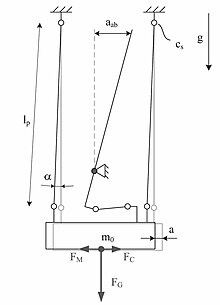Рис. 6 : Измерительный принцип, элементы отклонения: FM{\displaystyle F_{M}}-измеряемая сила, FG{\displaystyle F_{G}}-сила гравитации, FC{\displaystyle F_{C}}-сила в результате действия упругого элемента, cs{\displaystyle c_{s}}-коэффициент жёсткости, lp{\displaystyle l_{p}}-плечо, a -величина смещения, aab{\displaystyle a_{ab}}-смещение плеча, α{\displaystyle \alpha } -угол смещения, m0{\displaystyle m_{0}}-вес конструкции, g{\displaystyle g} -ускорение свободного падения. Источник^[18]

Сигмометрия силой Лоренца[править | править код]

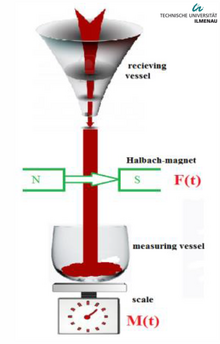Рис. 7 : LOFOS, принцип работы.

Сигмометрия силой Лоренца^[19] (LOFOS — от анг. LOrentz FOrce Sigmometry) — это бесконтактный метод измерения теплофизических свойств материалов, находящихся как в жидком так и в твёрдом состоянии. Точное определение электрических значений, плотности, вязкости, теплопроводности и поверхностного натяжения расплавленных металлов очень важно для промышленного применения. Одна из наибольших проблем, возникающих при экспериментальном определении теплофизических свойств жидкостей в условиях высокой температуры (>1000 K) — проблема химической реакции между исследуемой средой и электрическим зондом. Основное уравнение расчёта электропроводности может быть выведено из уравнения, связывающего массовый расход m˙{\displaystyle {\dot {m}}} и силу Лоренца F{\displaystyle F}, индуцированную магнитным полем:

m˙(t)=KΣF(t){\displaystyle {\dot {m}}\left(t\right)={\frac {K}{\Sigma }}F\left(t\right)\quad }

где Σ=σρ{\displaystyle \Sigma ={\frac {\sigma }{\rho }}} — удельная электропроводность, равная отношению электропроводности σ{\displaystyle \sigma } и плотности массы жидкости ρ{\displaystyle \rho }. K{\displaystyle K} — это эмпирическая константа, зависящая от геометрии системы LOFOS.

Из уравнения выше суммарная масса может быть найдена как:

M=∫t1t2m˙(t)dt=KΣ∫t1t2F(t)dt=KΣF~,{\displaystyle M=\int _{t1}^{t2}{\dot {m}}\left(t\right)dt={\frac {K}{\Sigma }}\int _{t1}^{t2}F\left(t\right)dt={\frac {K}{\Sigma }}{\tilde {F}}\quad ,}

где F~{\displaystyle {\tilde {F}}} — интегральная сила Лоренца за время процесса. Из этого уравнения и принимая во внимание формулу удельной электропроводности, можно вывести финальное уравнение для вычисления электропроводности жидкости в форме:

σ=ρKF~M.{\displaystyle \sigma =\rho K{\frac {\tilde {F}}{M}}\quad .}

Времяпролётная велосиметрия силой Лоренца[править | править код]

Времяпролётная велосиметрия силой Лоренца,^[20][21] предназначена для бесконтактного определения расхода проводящих жидкостей.

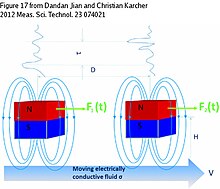Рис. 8 : Времяпролётная ВСЛ: принцип работы. Источник^[20]

Метод может быть успешно применён даже при отсутствии такой информации о свойствах исследуемого материала, как электропроводность или плотность. Это преимущество времяпролётной ВСЛ делает её особенно привлекательной для применения в промышленных условиях, например при работе со сплавами или в изменяемых внешних условиях.

При использовании метода (Рис. 8) две идентичных измерительных системы располагаются вдоль канала с электропроводящей жидкостью. Каждая система состоит из двух постоянных магнитов и жёстко прикреплённого к ним датчика силы, так что происходит одновременное возбуждение силы Лоренца и её измерение с помощью одного и того же приспособления. Принцип измерения основывается на получении перекрёстной функции сигналов, зарегистрированных с помощью измерительных систем. Каждая перекрёстная функция полезна только при наличии качественной разницы между сравниваемыми сигналами и для создания подобного различия используются искусственно созданные турбулентные возмущения.

Исследуемая жидкость, текущая по каналу, до прохождения участка с измерительными системами минует специальное приспособление для создания сильных возмущений — генератор вихрей. Когда созданный таким образом вихрь достигает магнитного поля измерительной системы, она фиксирует возмущение измеряемой силы и на перекрёстной функции возникает пик, так как через вторую измерительную систему всё ещё протекает стабильный поток. Затем вихрь достигает второй системы и пик возникает снова. Так как расстояние между измерительными системами точно известно, а время между пиками можно вычислить из перекрёстной функции, скорость потока может быть определена как отношение расстояния ко времени. Если учесть, что объёмный расход жидкости в канале неизменного сечения равен произведению скорости и площади сечения, расход жидкости может быть получен с помощью выражения:

Qflow=kDτ{\displaystyle Q_{flow}=k{\frac {D}{\tau }}}

где D{\displaystyle D} — расстояние между магнитными системами, τ{\displaystyle \tau } — время между пиками, а k{\displaystyle k} — экспериментально полученный коэффициент, зависящий от геометрии канала.

Токовихревая дефектоскопия силой Лоренца (ТДЛ)[править | править код]

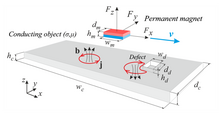Рис. 9 : Принцип работы ТДЛ. Источник^[22]

Другая, но физически сходная задача — определение глубокозалегающих каверн и неоднородностей в электропроводящих твёрдых материалах.

В более традиционной версии токовихревой дефектоскопии для генерирования вихревых токов в исследуемом материале используется переменное магнитное поле. Если материал содержит трещины или каверны, пространственное распределение электропроводности становится неоднородным и траектория вихревых токов подвергается возмущениям, в результате чего изменяется индуктивность катушки, которая создаёт переменное магнитное поле. С помощью измерения индуктивности этой катушки и могут быть обнаружены дефекты. Но исходя из того, что вихревые токи создаются переменным магнитным полем, их проникновение в область материала ограничивается скин-эффектом. В результате этого применимость традиционной версии токовихревой дефектоскопии ограничена анализом области поверхности материала, обычно глубиной порядка одного миллиметра. Попытки обойти эти ограничения с помощью использования низкочастотных катушек и сверхпроводящих датчиков магнитного поля пока не привели к желаемым результатам.

Современная методика, названная вихревой дефектоскопией силой Лоренца,^[22][23] имеет существенное преимущество перед предыдущей за счёт применения постоянного магнитного поля и взаимного перемещения материала и источника магнитного поля, что позволяет глубоко и относительно быстро исследовать электропроводящий материал. В принципе, ТДЛ представляет собой модификацию традиционной токовихревой дефектоскопии, из которой можно выделить два аспекта: (1) как генерируются вихревые токи и (2) как регистрируются их возмущения. В ТДЛ вихревые токи генерируются за счёт взаимного перемещения исследуемого проводника и постоянного магнита (Рис. 9). Когда магнит проходит над дефектом, сила Лоренца, действующая на него, искажается и обнаружение этого искажения и есть основной принцип измерения ТДЛ. Если исследуемый объект не содержит дефектов, результирующая сила Лоренца остаётся постоянной.

Этот метод относится к бесконтактным техникам измерения скорости потока жидкости. Он не требует присутствия сигнальных частиц или погружаемого зонда, поэтому может быть использован при изучении как скорости, так и расхода таких агрессивных и высокотемпературных материалов, как жидкие металлы.

Ещё одним преимуществом метода является возможность определения средней скорости потока независимо от влияния неоднородностей и присутствия зон турбулентности.

К недостаткам метода ВСЛ можно отнести следующие ограничения:

1. Необходимость предварительной калибровки измерительной системы с целью определения коэффициента зависимости силы Лоренца от скорости потока.
2. Небольшие значения силы магнитного поля постоянных магнитов, применяемых для генерирования силы Лоренца, что приводит к низким значениям силы, для регистрации которых необходимы высокоточные приборы.
3. Ограничение зоны измерения скорости размером магнита.
4. Необходимость контроля температуры постоянных магнитов, которая не должна превышать точку Кюри.

1. ↑ Thess, A., Votyakov, E. and Kolesnikov, Y. Lorentz Force Velocimetry. Phys. Rev. Lett. 96, 2006 (англ.)
2. ↑ Arthur J. Shercliff: Theory of Electromagnetic Flow Measurement. Cambridge University Press, ISBN 978-0-521-33554-6(англ.)
3. ↑ Y. Kolesnikov, C. Karcher, A. Thess, Lorentz Force Flowmeter for Liquid Aluminum: Laboratory Experiments and Plant Tests (in German), Metall. Mat. Trans. B 42B (2011) pp. 241—250., doi:10.1007/s11663-011-9477-6(англ.)
4. ↑ Research Training Group LORENTZ FORCE
5. ↑ J. Priede, D. Buchenau., G. Gerbeth, Contactless Electromagnetic Phase-Shift Flowmeter for Liquid Metals, Measur. Sci. Tech. 22 (2011) 055402, 2011(англ.)
6. ↑ A. Thess et al., Theory of the Lorentz force flowmeter, 2007 New J. Phys. 9 299(англ.)
7. ↑ J. Baumgartl, A. Hubert, and G. M¨uller , The use of magnetohydrodynamic effects to investigate fluid flow in electrically conducting melts, Phys. Fluids A 5, 3280 (1993)
8. ↑ Stefani F., Gundrum T., Gerbeth G., Contactless inductive flow tomography,Phys Rev E 70,056306 (2004)
9. ↑ J. Priede, D. Buchen