3.5.Сила Лоренца
§ 3.5. Действие магнитного поля на заряды. Сила Лоренца
Магнитное поле – порождается любыми движущимися зарядами и действует магнитное поле только на движущиеся электрические заряды. Таким образом, между движущимися друг относительно друга электрическими зарядами, кроме электрических сил, действуют еще и магнитные силы.
Опыт
показывает, что на движущийся в магнитном
поле заряд  действует сила
действует сила 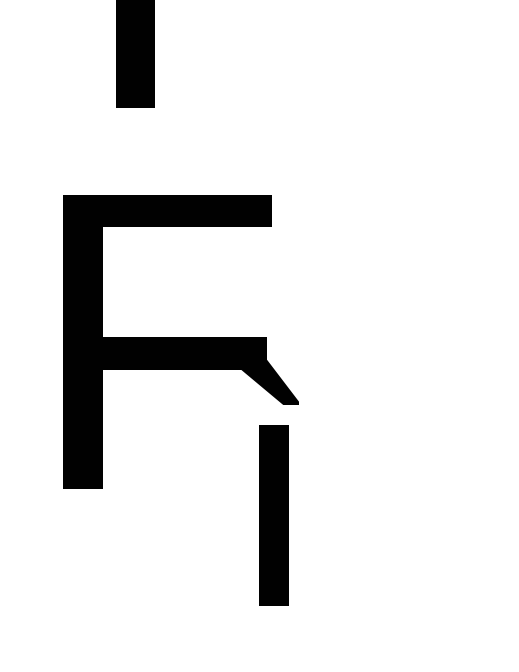 ,
величина которой зависит от величины
заряда, а также от величины и направления
скорости. Направление силы зависит от
направления вектора скорости. Если
двигать пробный заряд через какую-либо
фиксированную точку поля с одной и той
же по величине скоростью, но в разных
направлениях, то магнитная сила каждый
раз будет разной. Однако всегда
,
величина которой зависит от величины
заряда, а также от величины и направления
скорости. Направление силы зависит от
направления вектора скорости. Если
двигать пробный заряд через какую-либо
фиксированную точку поля с одной и той
же по величине скоростью, но в разных
направлениях, то магнитная сила каждый
раз будет разной. Однако всегда 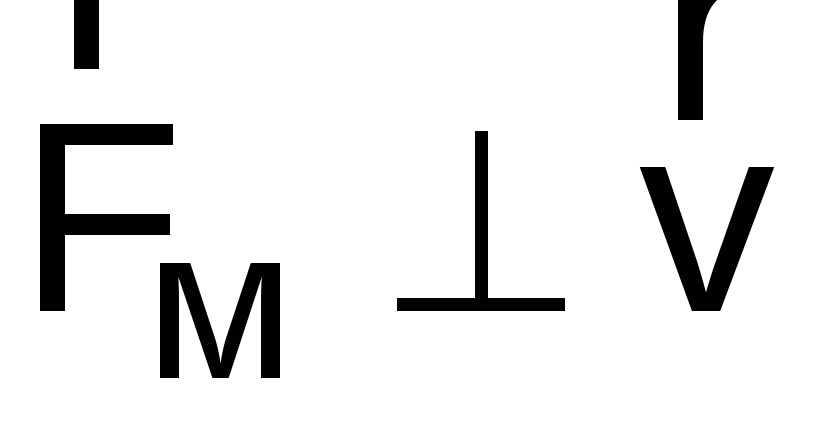
Если двигать заряд по этому направлению с любой скоростью, то
 .
.Если скорость заряда составляет некоторый угол с этим направлением, то величина магнитной силы пропорциональна синусу этого угла

П
 ри
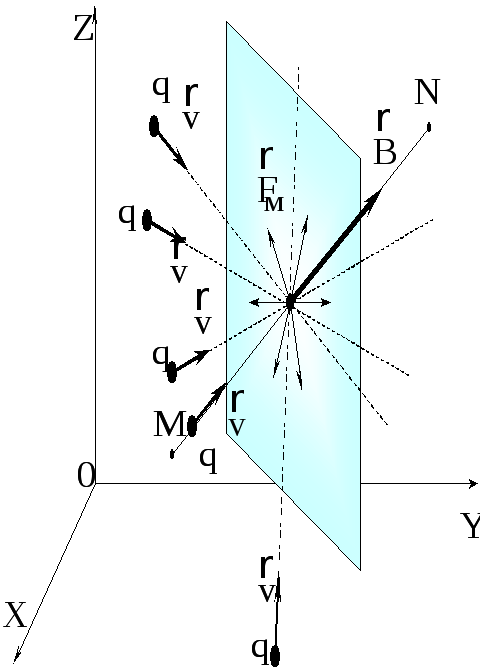
всевозможных движениях заряда
ри
всевозможных движениях заряда  всегда перпендикулярна этому выделенному
направлению, то есть все
всегда перпендикулярна этому выделенному
направлению, то есть все  лежат в одной плоскости перпендикулярной
MN.
лежат в одной плоскости перпендикулярной
MN.
Если
вдоль направления MN
направить некоторый вектор 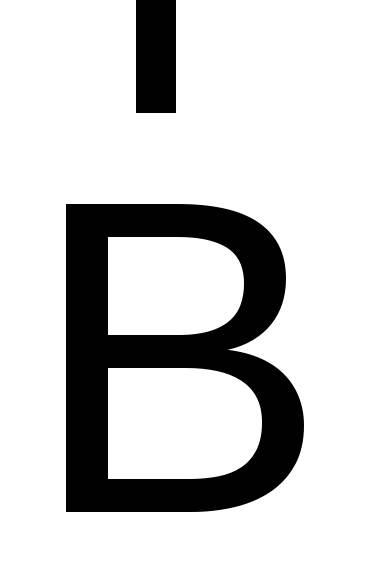
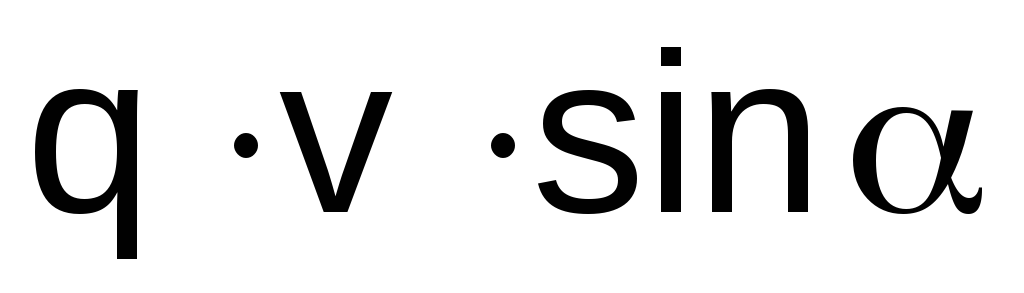 ,
то задание
,
то задание  ,
,  и
и 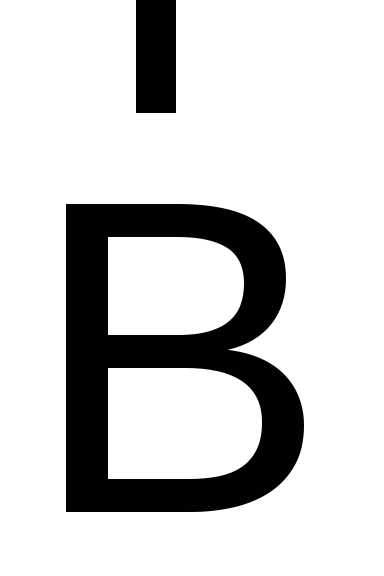 однозначно характеризует то состояние
поля, которое обусловливает появление
магнитной силы
однозначно характеризует то состояние
поля, которое обусловливает появление
магнитной силы 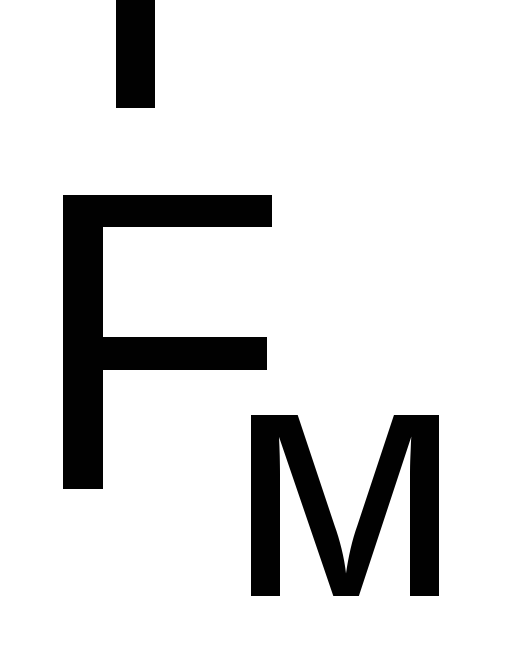
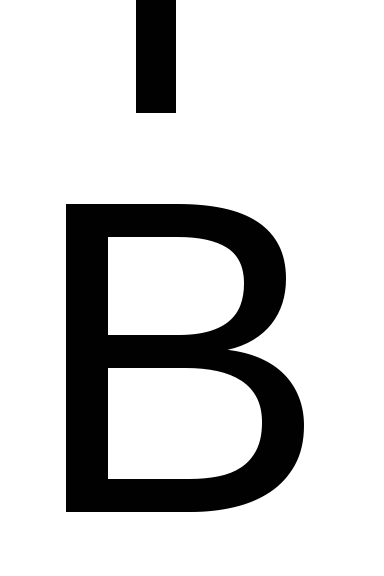 и есть вектор магнитной индукции. Так
как
и есть вектор магнитной индукции. Так
как  и
и  ,
, 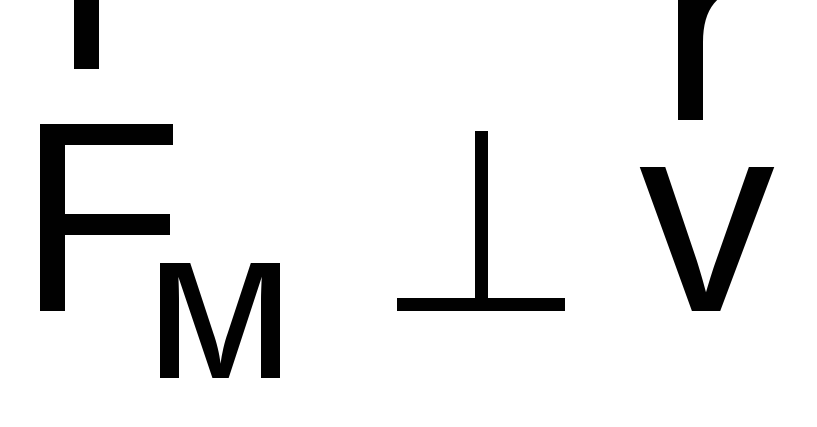 и
и 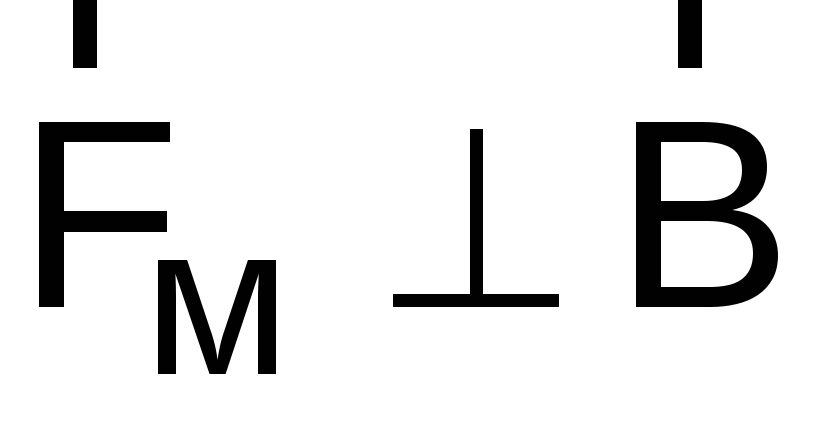 ,
то
,
то 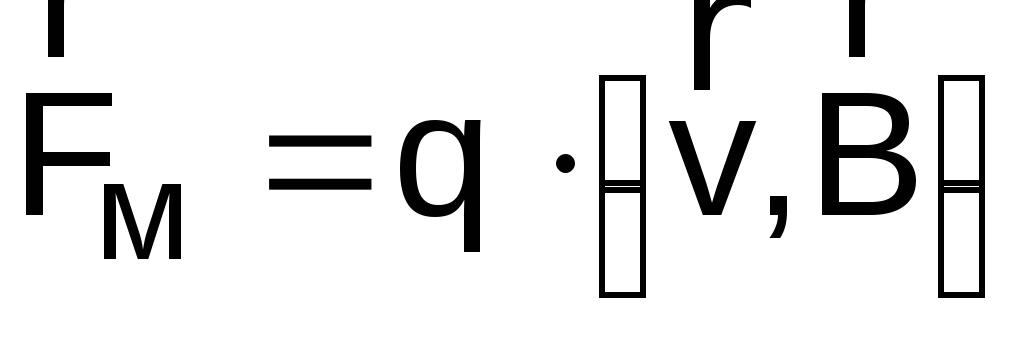 .
. Магнитную
силу называют силой Лоренца 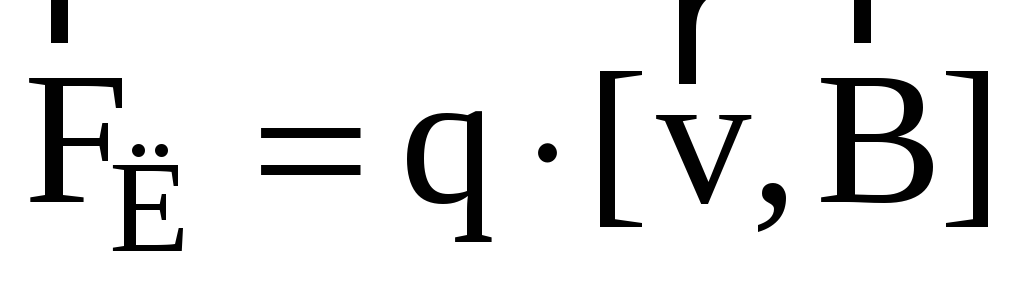
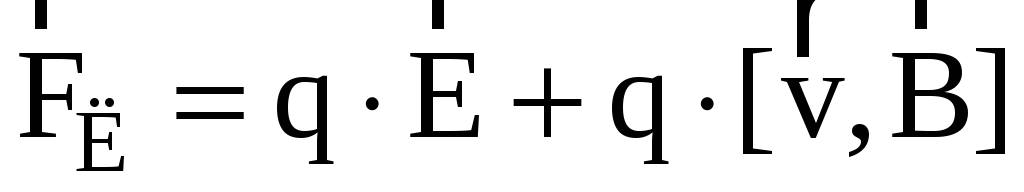 .
.Движение частиц в магнитном поле.
Пусть
частица массой m
с зарядом q,
имеющая скорость  ,
попадает в однородное магнитное поле
(). Траектория и скорость движения частицы
в магнитном поле зависят от величины
угла между вектором скорости частицы
и индукции магнитного поля.
,
попадает в однородное магнитное поле
(). Траектория и скорость движения частицы
в магнитном поле зависят от величины
угла между вектором скорости частицы
и индукции магнитного поля.
А.
Если скорость частицы  параллельна вектору , то в этом случае
параллельна вектору , то в этом случае 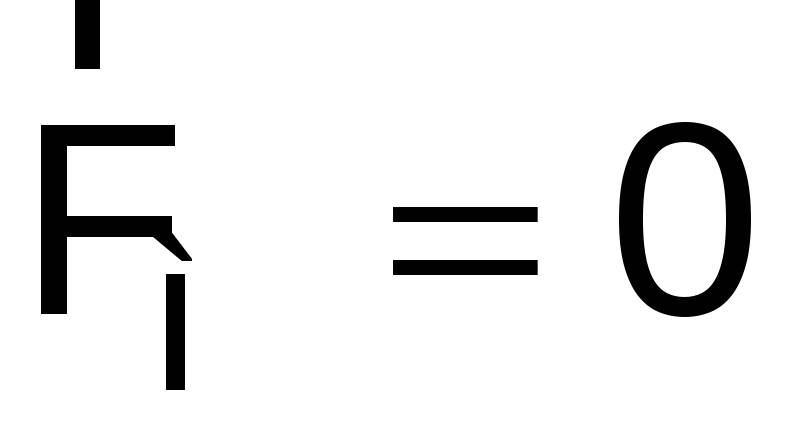 и
частица будет продолжать двигаться с
постоянной по величине и направлению
скоростью (прямолинейно и равномерно).
и
частица будет продолжать двигаться с
постоянной по величине и направлению
скоростью (прямолинейно и равномерно).
Б.  Пусть
скорость частицы
Пусть
скорость частицы  перпендикулярна вектору . В этом случае
магнитное поле обычно изображается
системой равноотстоящих друг от друга
точек (если вектор направлен перпендикулярно
чертежу к нам, как на рисунке) или крестов
(если вектор направлен перпендикулярно
чертежу от нас). Для микрочастиц сила
тяжести много меньше магнитной силы
(mg<<F
перпендикулярна вектору . В этом случае
магнитное поле обычно изображается
системой равноотстоящих друг от друга
точек (если вектор направлен перпендикулярно
чертежу к нам, как на рисунке) или крестов
(если вектор направлен перпендикулярно
чертежу от нас). Для микрочастиц сила
тяжести много меньше магнитной силы
(mg<<F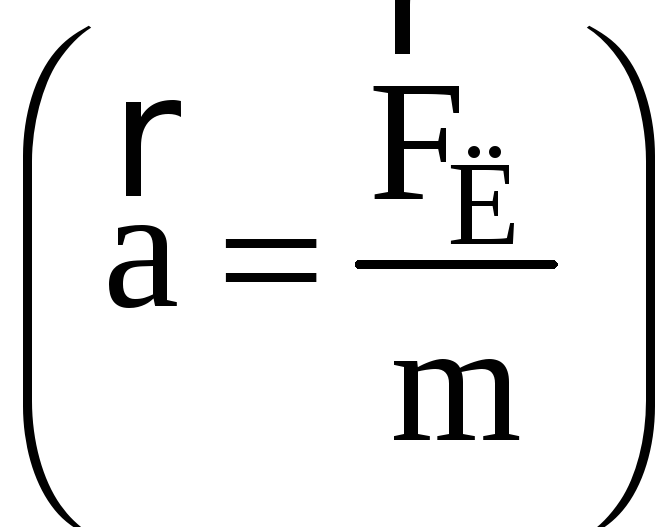 для частицы будет иметь вид:
для частицы будет иметь вид: 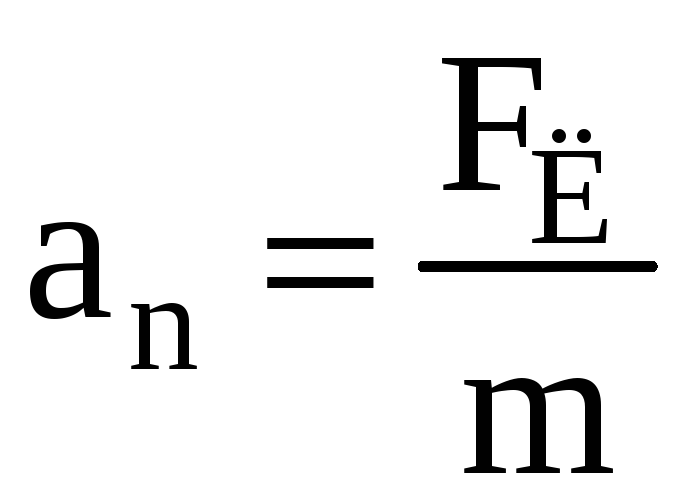 или
или 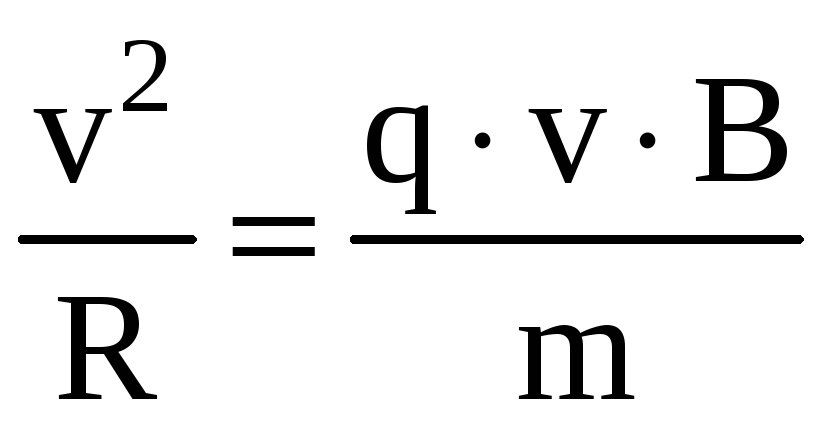
В. 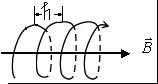
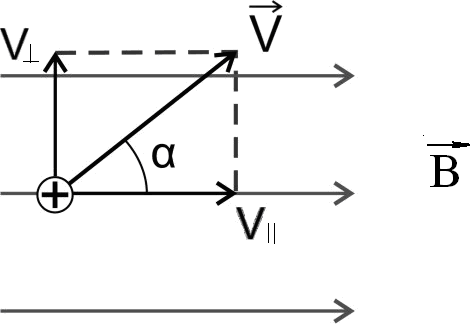 Если
начальная скорость частицы составляет
угол α с направлением вектора , то для
удобства рассмотрения разложим вектор
Если
начальная скорость частицы составляет
угол α с направлением вектора , то для
удобства рассмотрения разложим вектор  на составляющие, параллельную —
на составляющие, параллельную — 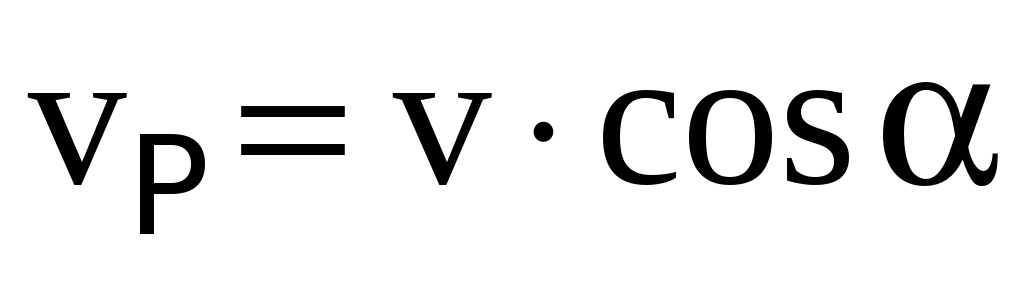
 .
Уравнение 2-го закона Ньютона в этом
случае:
.
Уравнение 2-го закона Ньютона в этом
случае: 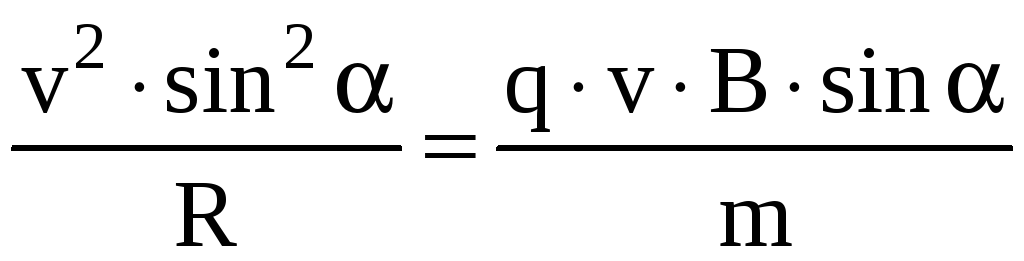 .
Отсюда
радиус окружности . В направлении вектора
частица движется с постоянной скоростью
.
Отсюда
радиус окружности . В направлении вектора
частица движется с постоянной скоростью 
3
Сила Лоренца: формула, определение и направление
Наряду с силой Ампера, кулоновского взаимодействия, электромагнитными полями в физике часто встречается понятие сила Лоренца. Это явление является одним из основополагающих в электротехнике и электронике, на ряду с законом Кулона, электромагнитной индукцией Фарадея и прочими. Она воздействует на заряды, которые двигаются в магнитном поле. В этой статье мы кратко и понятно рассмотрим, что такое сила Лоренца и где она применяется.Определение
Когда электроны движутся по проводнику – вокруг него возникает магнитное поле. В то же время, если поместить проводник в поперечное магнитное поле и двигать его – возникнет ЭДС электромагнитной индукции. Если через проводник, который находится в магнитном поле, протекает ток – на него действует сила Ампера.

Её величина зависит от протекающего тока, длины проводника, величины вектора магнитной индукции и синуса угла между линиями магнитного поля и проводником. Она вычисляются по формуле:

Рассматриваемая сила отчасти похожа на ту, что рассмотрена выше, но действует не на проводник, а на движущуюся заряженную частицу в магнитном поле. Формула имеет вид:

Важно! Сила Лоренца (Fл) действует на электрон, движущийся в магнитном поле, а на проводник – Ампера.
Из двух формул видно, что и в первом и во втором случае, чем ближе синус угла aльфа к 90 градусам, тем большее воздействие оказывает на проводник или заряд Fа или Fл соответственно.
Итак, сила Лоренца характеризует не изменение величины скорости, а то, какое происходит воздействие со стороны магнитного поля на заряженный электрон или положительный ион. При воздействии на них Fл не совершает работы. Соответственно изменяется именно направление скорости движения заряженной частицы, а не её величина.
Что касается единицы измерения силы Лоренца, как и в случае с другими силами в физике используется такая величина как Ньютон. Её составляющие:

Как направлена сила Лоренца
Чтобы определить направление силы Лоренца, как и с силой Ампера, работает правило левой руки. Это значит, чтобы понять, куда направлено значение Fл нужно раскрыть ладонь левой руки так, чтобы в руку входили линии магнитной индукции, а вытянутые четыре пальца указывали направление вектора скорости. Тогда большой палец, отогнутый под прямым углом к ладони, указывает направление силы Лоренца. На картинке ниже вы видите, как определить направление.

Внимание! Направление Лоренцового действия перпендикулярно движению частицы и линиям магнитной индукции.

При этом, если быть точнее, для положительно и отрицательно заряженных частиц имеет значение направление четырёх развернутых пальцев. Выше описанное правило левой руки сформулировано для положительной частицы. Если она заряжена отрицательно, то линии магнитной индукции должны быть направлены не в раскрытую ладонь, а в её тыльную сторону, а направление вектора Fл будет противоположным.

Теперь мы расскажем простыми словами, что даёт нам это явление и какое реальное воздействие она оказывает на заряды. Допустим, что электрон движется в плоскости, перпендикулярной направлению линий магнитной индукции. Мы уже упомянули, что Fл не воздействует на скорость, а лишь меняет направление движения частиц. Тогда сила Лоренца будет оказывать центростремительное воздействие. Это отражено на рисунке ниже.

Применение
Из всех сфер, где используется сила Лоренца, одной из масштабнейших является движение частиц в магнитном поле земли. Если рассмотреть нашу планету как большой магнит, то частицы, которые находятся около северного магнитного полюсов, совершают ускоренное движение по спирали. В результате этого происходит их столкновение с атомами из верхних слоев атмосферы, и мы видим северное сияние.
Тем не менее, есть и другие случаи, где применяется это явление. Например:
- Электронно-лучевые трубки. В их электромагнитных отклоняющих системах. ЭЛТ применялись больше чем 50 лет подряд в различных устройствах, начиная от простейшего осциллографа до телевизоров разных форм и размеров. Любопытно, что в вопросах цветопередачи и работы с графикой некоторые до сих пор используют ЭЛТ мониторы.
- Электрические машины – генераторы и двигатели. Хотя здесь скорее действует сила Ампера. Но эти величины можно рассматривать как смежные. Однако это сложные устройства при работе которых наблюдается воздействие многих физических явлений.
- В ускорителях заряженных частиц для того, чтобы задавать им орбиты и направления.
Заключение
Подведем итоги и обозначим четыре основных тезиса этой статьи простым языком:
- Сила Лоренца действует на заряженные частицы, которые движутся в магнитном поле. Это вытекает из основной формулы.
- Она прямо пропорциональна скорости заряженной частицы и магнитной индукции.
- Не влияет на скорость частицы.
- Влияет на направление частицы.
Её роль достаточно велика в «электрических» сферах. Специалист не должен упускать из вида основные теоретические сведения об основополагающих физических законах. Эти знания пригодятся, как и тем, кто занимается научной работой, проектированием и просто для общего развития.
Напоследок рекомендуем просмотреть полезные видео для закрепления изученного материала:
Теперь вы знаете, что такое сила Лоренца, чему она равна и как действует на заряженные частицы. Если возникли вопросы, задавайте их в комментариях под статьей!
Материалы по теме:
определение, формула, физический смысл, применение
 Силой Лоренца называют силу, которая действует со стороны электромагнитного поля на движущийся электрический заряд. Весьма нередко силой Лоренца называют лишь магнитную составляющую этого поля. Формула для определения:
Силой Лоренца называют силу, которая действует со стороны электромагнитного поля на движущийся электрический заряд. Весьма нередко силой Лоренца называют лишь магнитную составляющую этого поля. Формула для определения:
F = q(E+vB),
где q — заряд частицы; Е — напряжённость электрического поля; B — магнитная индукция поля; v — скорость частицы.
Сила Лоренца очень похожа по своему принципу на силу Ампера, разница заключается в том, что последняя действует на весь проводник, который в целом электрически нейтральный, а сила Лоренца описывает влияние электромагнитного поля лишь на единичный движущийся заряд.
 Она характеризуется тем, что не изменяет скорость перемещения зарядов, а лишь воздействует на вектор скорости, то есть способна изменять направление движения заряженных частиц.
Она характеризуется тем, что не изменяет скорость перемещения зарядов, а лишь воздействует на вектор скорости, то есть способна изменять направление движения заряженных частиц.
В природе сила Лоренца позволяет защищать Землю от воздействия космической радиации. Под её воздействием падающие на планету заряженные частицы отклоняются от прямой траектории благодаря присутствию магнитного поля Земли, вызывая полярные сияния.
В технике сила Лоренца используется очень часто: во всех двигателях и генераторах именно она приводит во вращение ротор под действием электромагнитного поля статора.
Таким образом, в любых электромоторах и электроприводах основным видом силы является Лоренцева. Кроме того, она применяется в ускорителях заряженных частиц, а также в электронных пушках, которые раньше устанавливались в ламповых телевизорах. В кинескопе испускаемые пушкой электроны отклоняются под влиянием электромагнитного поля, что происходит при участии Лоренцевой силы.
Кроме того, эта сила используется в масс-спектрометрии и масс-электрографии для приборов, способных сортировать заряженные частицы в зависимости от их удельного заряда (отношение заряда к массе частицы). Это позволяет с высокой точностью определять массу частиц. Также находит применение в других КИП, например, в бесконтактном способе измерения расхода электропроводящих жидких сред (расходомеры). Это очень актуально, если жидкая среда обладает очень высокой температурой (расплав металлов, стекла и др.).
Сила Лоренца и ее воздействие на электрический заряд
Электрические заряды, движущиеся в определенном направлении, создают вокруг себя магнитное поле, скорость распространения которого в вакууме равно скорости света, а в других средах чуть меньше. Если движение заряда происходит во внешнем магнитном поле, то между внешним магнитным полем и магнитным полем заряда возникает взаимодействие. Так как электрический ток – это направленное движение заряженных частиц, то сила, которая будет действовать в магнитном поле на проводник с током, будет являться результатом отдельных (элементарных) сил, каждая из которых прикладывается к элементарному носителю заряда.
Процессы взаимодействия внешнего магнитного поля и движущихся зарядов исследовались Г. Лоренцом, который в результате многих своих опытов вывел формулу для расчета силы, действующей на движущуюся заряженную частицу со стороны магнитного поля. Именно поэтому силу, которая действует на движущийся в магнитном поле заряд, называют силой Лоренца.
Сила, действующая на проводник стоком (из закона Ампера), будет равна:

По определению сила тока равна I = qn (q – заряд, n – количество зарядов, проходящее через поперечное сечение проводника за 1 с). Отсюда следует:

Где: n0 – содержащееся в единице объема количество зарядов, V – их скорость движения, S – площадь поперечного сечения проводника. Тогда:

Подставив данное выражение в формулу Ампера, мы получим:

Данная сила будет действовать на все заряды, находящиеся в объеме проводника: V = Sl. Количество зарядов, присутствующих в данном объеме будет равно:

Тогда выражение для силы Лоренца будет иметь вид:

Отсюда можно сделать вывод, что сила Лоренца, действующая на заряд q, который двигается в магнитном поле, пропорциональна заряду, магнитной индукции внешнего поля, скорости его движения и синусу угла между V и В, то есть:

За направление движения заряженных частиц принимают направление движения положительных зарядов. Поэтому направление данной силы может быть определено с помощью правила левой руки.
Сила, действующая на отрицательные заряды, будет направлена в противоположную сторону.
Сила Лоренца всегда направлена перпендикулярно скорости V движения заряда и поэтому работу она не совершает. Она изменяет только направление V, а кинетическая энергия и величина скорости заряда при его движении в магнитном поле остаются неизменными.
Когда заряженная частица движется одновременно в магнитном и электрическом полях, на него будет действовать сила:

Где Е – напряженность электрического поля.
Рассмотрим небольшой пример:
Электрон, прошедший ускоряющую разность потенциалов 3,52∙103 В, попадает в однородное магнитное поле перпендикулярно линиям индукции. Радиус траектории r = 2 см, индукция поля 0,01 Т. Определить удельный заряд электрона.
Решение:
Удельный заряд – это величина, равная отношению заряда к массе, то есть e/m.
В магнитном поле с индукцией В на заряд, движущийся со скоростью V перпендикулярно линиям индукции, действует сила Лоренца FЛ = BeV. Под ее действием заряженная частица будет перемещаться по дуге окружности. Так как при этом сила Лоренца вызовет центростремительное ускорение, то согласно 2-му закону Ньютона можно записать:

Кинетическую энергию, которая будет равна mV2/2, электрон приобретает за счет работы А сил электрического поля (А = eU), подставив в уравнение получим:

Преобразовав эти соотношения и исключив из них скорость, получим формулу для определения удельного заряда электрона:

Подставив исходные данные, выраженные в СИ, получим:

Проверяем размерность:

И кому интересно — видео о движении заряженных частиц:
Сила Лоренца
Известно, что на
каждый элемент тока  в магнитном поле действует сила Ампера:
в магнитном поле действует сила Ампера:
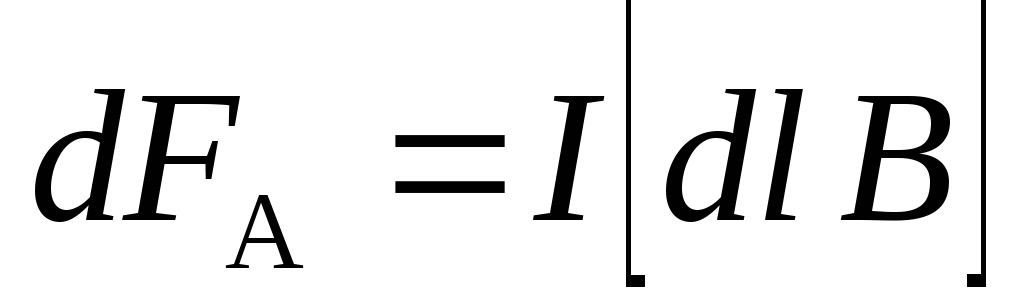 . (9.9)
. (9.9)
Если поместить в магнитное поле проводник
без тока, то никакой силы мы не обнаружим.
Это означает, что магнитное поле «не
чувствует» неподвижные заряды. Но стоит
им придти в направленное движение, в
проводнике появляется ток и на проводник
начинает действовать сила (9.9). Можно
предположить, что магнитное поле
действует на каждый отдельный носитель
заряда, направленно движущийся в
проводнике, а сила Ампера — интегральный
результат сложения всех этих сил. Тогда
силу, действующую в магнитном поле на
движущийся заряд, можно вычислить,
разделив силу Ампера на число носителей
заряда dN, движущихся
со скоростью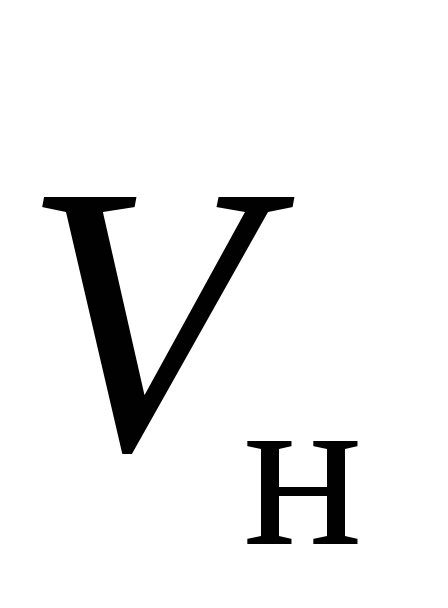 на элементе проводникаdl:
на элементе проводникаdl:
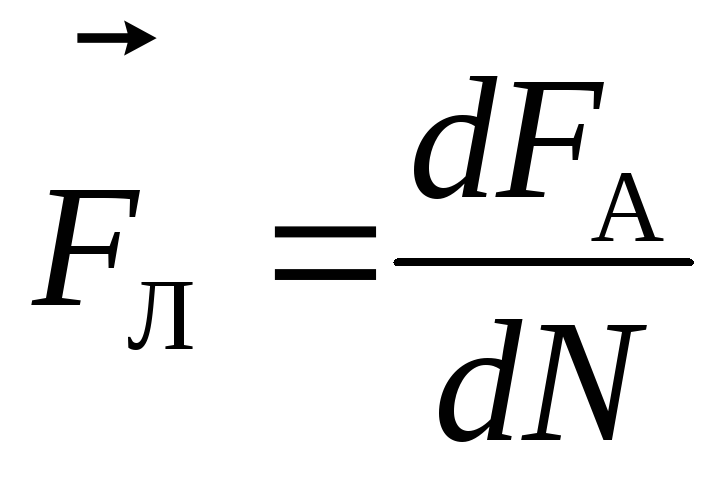 .
.
Здесь dN=nSdl— число носителей заряда. Вспомнив, чтоI=iS, а плотность токаi=nqVн, представим (9.8) в таком виде:
 . (9.10)
. (9.10)
По определению, вектор  совпадает по направлению с векторами
плотности тока
совпадает по направлению с векторами
плотности тока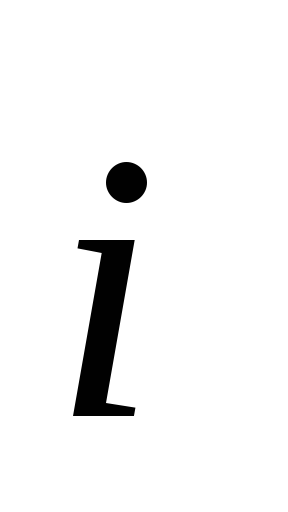 и скорости направленного движения
и скорости направленного движения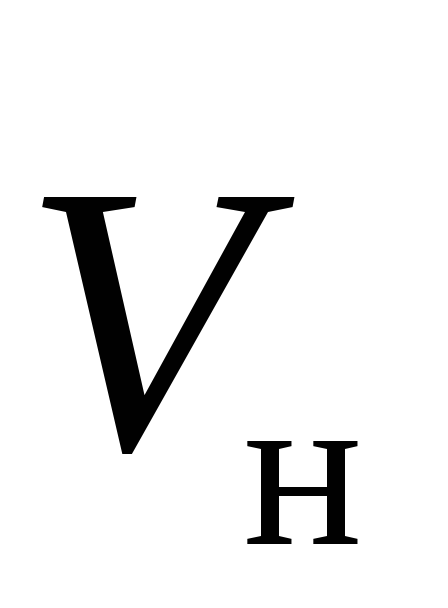 .
Поэтому (9.10) можно переписать ещё и так:
.
Поэтому (9.10) можно переписать ещё и так:
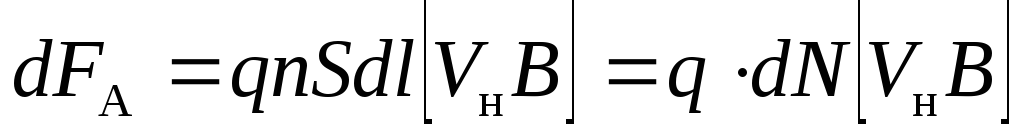 .
.
Теперь, разделив эту силу на число
носителей заряда dN,
получим силу Лоренца — силу, действующую
на зарядq, движущийся
со скоростью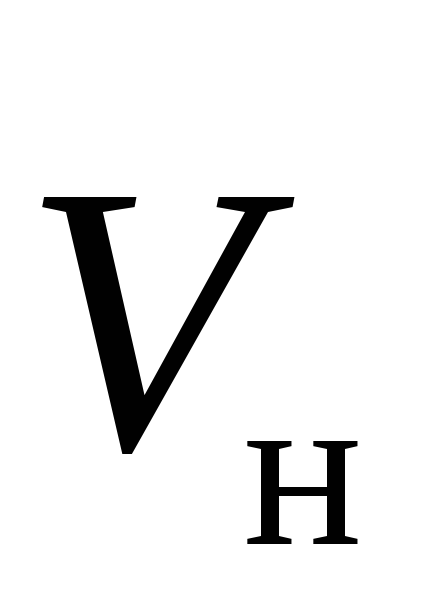 в магнитном поле
в магнитном поле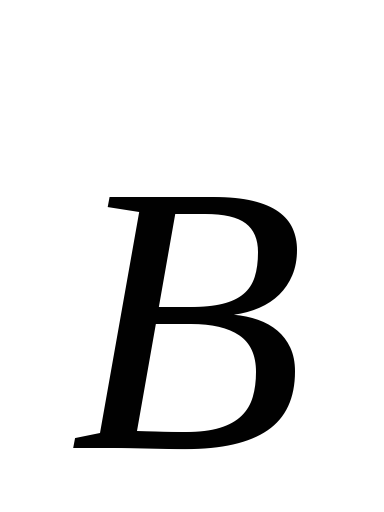 :
:
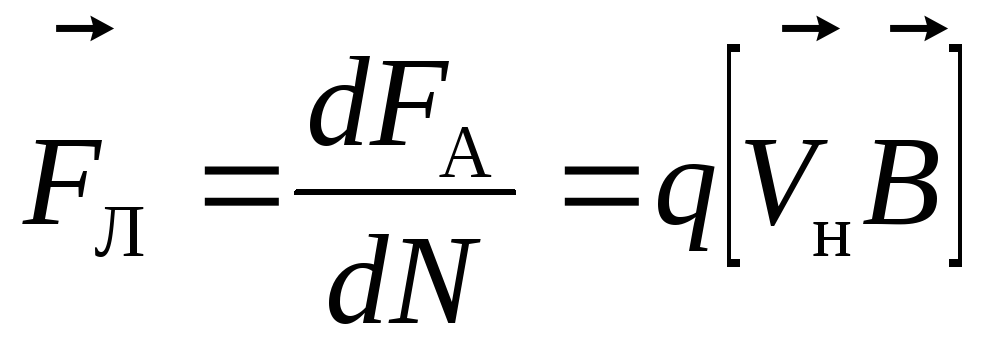 . (9.11)
. (9.11)
Сила Лоренца пропорциональна заряду
движущейся частицы q,
её скоростиVни величине индукции магнитного поляB.
Кроме того, эта сила зависит от угламежду векторами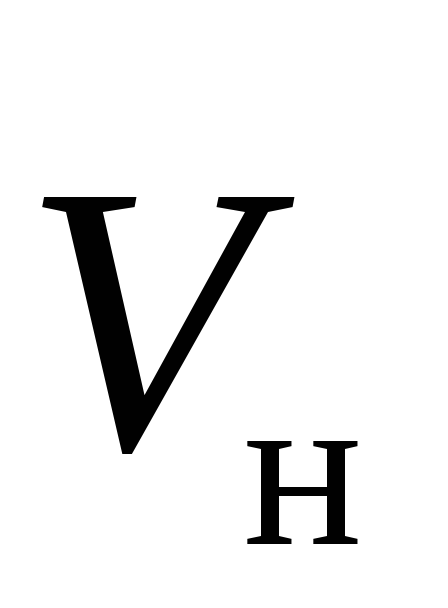 и
и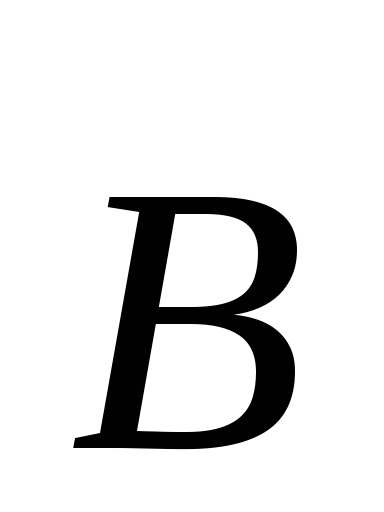 (рис. 9.2.):
(рис. 9.2.):
FЛ=qVнBsin.

Рис. 9.2.
В любом случае сила Лоренца перпендикулярна
и вектору 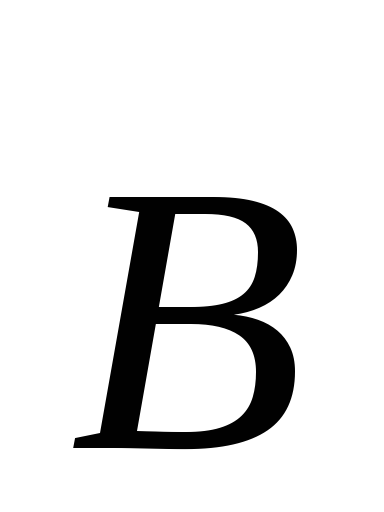 и скорости движения частицы
и скорости движения частицы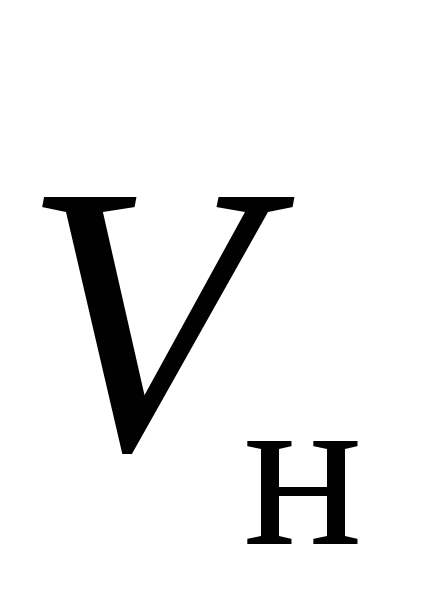 .
Последний результат представляет особый
интерес. Если
.
Последний результат представляет особый
интерес. Если
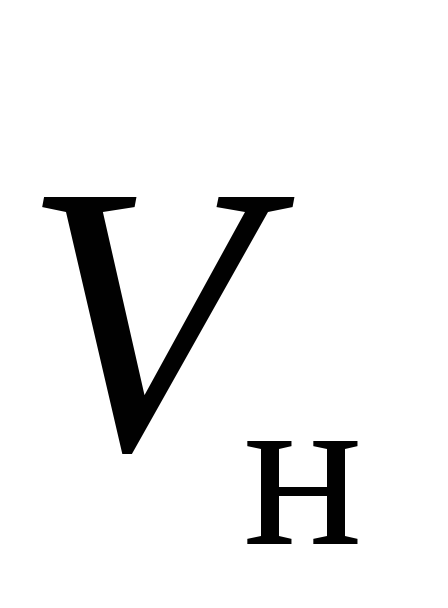 ,
то работа такой силы всегда равна нулю:
,
то работа такой силы всегда равна нулю:
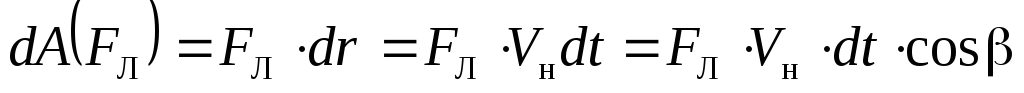 =0.
=0.
Здесь =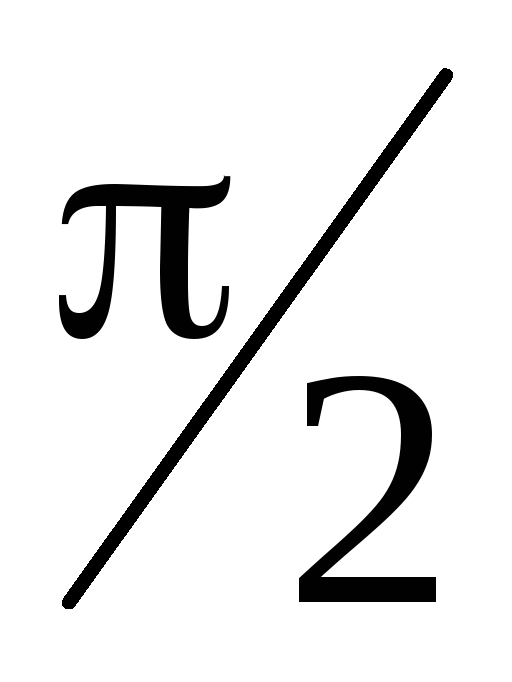 — угол между векторами
— угол между векторами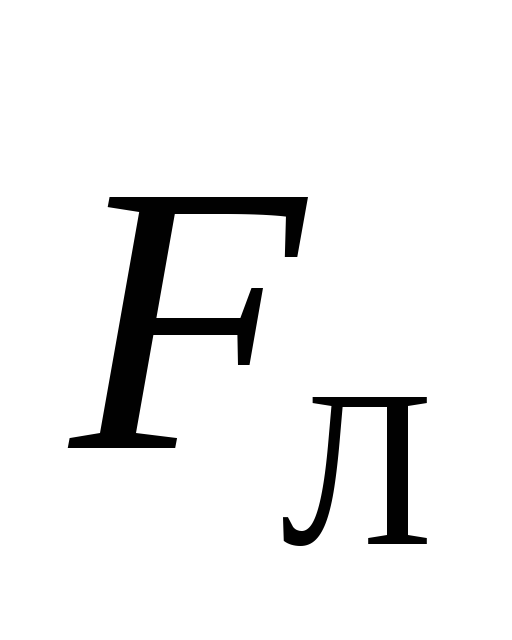 и
и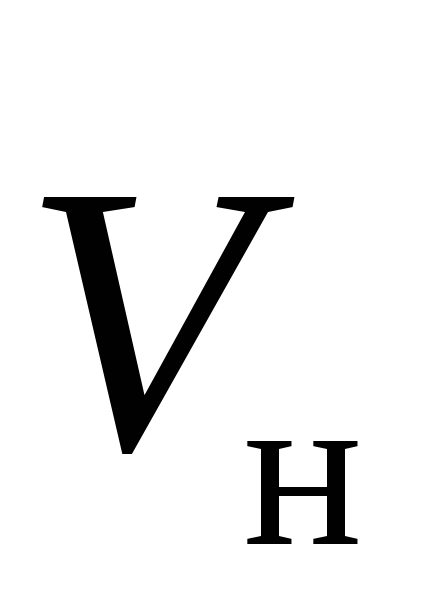 ;
следовательно,cos= 0 и работа
;
следовательно,cos= 0 и работа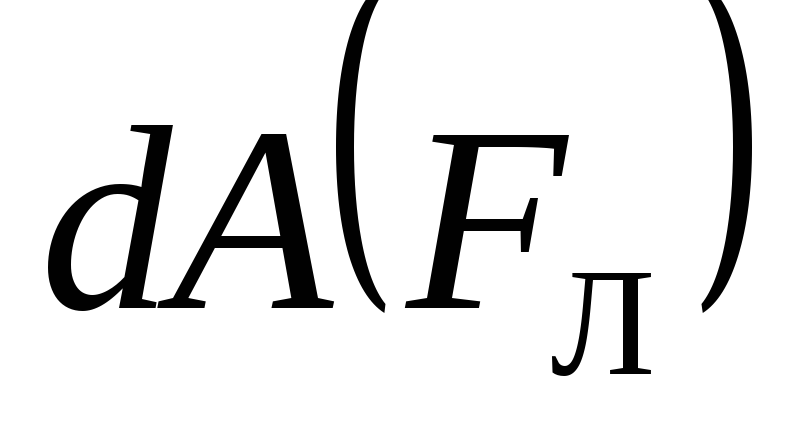 =
0. Это тот случай, когда есть сила, есть
перемещение точки её приложения, но
работа отсутствует, благодаря особой
взаимной ориентации этих двух векторов.
Действие такой силы не может привести
к изменению величины скорости частицы
и её кинетической энергии. Действительно,
согласно теореме о кинетической энергии,
её изменение равно работе силы:
=
0. Это тот случай, когда есть сила, есть
перемещение точки её приложения, но
работа отсутствует, благодаря особой
взаимной ориентации этих двух векторов.
Действие такой силы не может привести
к изменению величины скорости частицы
и её кинетической энергии. Действительно,
согласно теореме о кинетической энергии,
её изменение равно работе силы:
dкин=dA.
Но если работа не производится, то и кинетическая энергия не меняется. Неизменность кинетической энергии означает постоянство скорости частицы.
Если заряженная частица движется со
скоростью  одновременно в двух полях: и в магнитном
и в электростатическом, то сила,
действующая на неё — сила Лоренца —
будет в этом случае складываться из
двух сил (опять принцип суперпозиции —
теперь сил!):
одновременно в двух полях: и в магнитном
и в электростатическом, то сила,
действующая на неё — сила Лоренца —
будет в этом случае складываться из
двух сил (опять принцип суперпозиции —
теперь сил!):
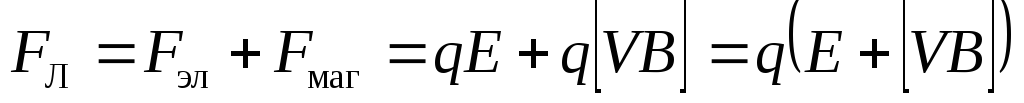 . (9.12)
. (9.12)
Теорема Гаусса и теорема о циркуляции магнитного поля. Система уравнений Максвелла электро- и магнитостатики.
Вычислив магнитное поле прямолинейного тока (8.7), мы обнаружили, что силовые линии этого поля — замкнутые окружности, охватывающие проводник с током (рис. 9.3.). Это поле можно «увидеть», разместив вокруг проводника небольшие магнитные стрелки (рис. 9.4.). Они укажут направление магнитных силовых линий в различных точках пространства.
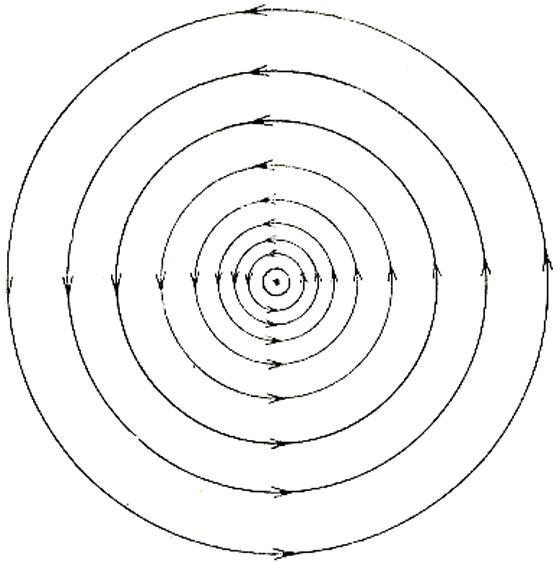
Рис. 9.3.
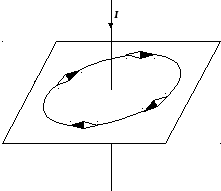
Рис. 9.4.
Ограниченное число магнитных стрелок можно заменить железными опилками. Каждый такой кусочек металла будет представлять собой магнитную микрострелку, которая будет ориентироваться вдоль магнитных силовых линий поля. На рис. 9.5. представлены магнитные поля кругового тока и катушки с током (соленоида), полученные с помощью таких опилок. Опилки насыпают на лист картона, пронизанный проводником с током. При постукивании по картону опилки распределяются вдоль магнитных силовых линий.

Рис. 9.5.
Присмотревшись к рисункам 9.4. и 9.5., легко обнаружить, что замкнуты не только силовые линии магнитного поля прямолинейного тока, но и силовые линии магнитных полей кругового тока и соленоида.
Можно показать, что замкнутость силовых линий магнитного поля — особенность любых магнитных полей. Здесь уместно напомнить, что силовые линии электростатического поля разомкнуты: они начинаются на положительных зарядах и заканчиваются на отрицательных. Замкнутость магнитных силовых линий приобретает принципиальное значение: из этого свойства следует вывод, что в природе нет магнитных зарядов. Электрические заряды существуют в природе. Они и являются источниками потенциальных электростатических полей. Магнитных зарядов в природе нет. Как же создаются тогда магнитные поля? Их источниками являются электрические токи. В отличие от электростатических полей, магнитные поля не потенциальные.Они называются вихревыми или соленоидальными.
Теперь обратимся к теореме Гаусса для магнитного поля. В этой теореме рассматривается поток вектора магнитной индукции через произвольную замкнутую поверхность:
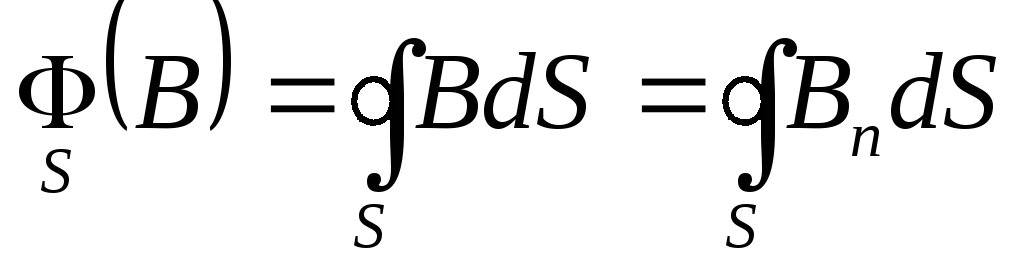 . (9.13)
. (9.13)
На рис. 9.6. замкнутая гауссова поверхность выбрана в магнитном поле прямолинейного тока.
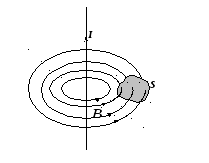
Рис. 9.6.
Если густота магнитных силовых линий соответствует величине вектора магнитной индукции в выбранной точке пространства, то интеграл (9.12) — есть алгебраическая сумма числа силовых линий входящих (–) и покидающих (+) замкнутую поверхность. Учитывая соленоидальность магнитного поля, то есть замкнутость его силовых линий, придём к выводу: число входящих и выходящих силовых линий одинаково и их сумма всегда равна нулю:
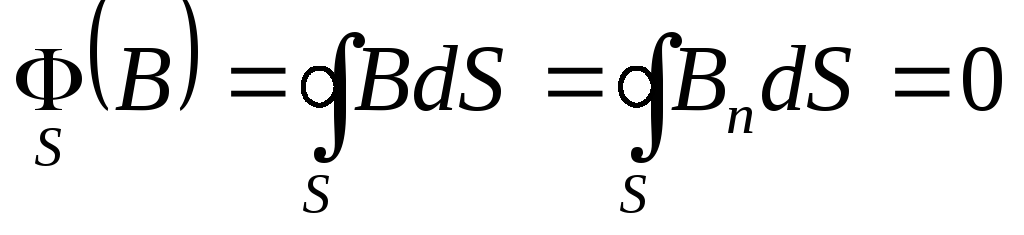 . (9.14)
. (9.14)
Полученное выражение (9.13) — математическая запись теоремы Гаусса для магнитного поля: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
Иными словами, эта теорема утверждает: в природе нет магнитных зарядов.
Напомним, что совсем по-другому заканчивается теорема Гаусса для электростатического поля:
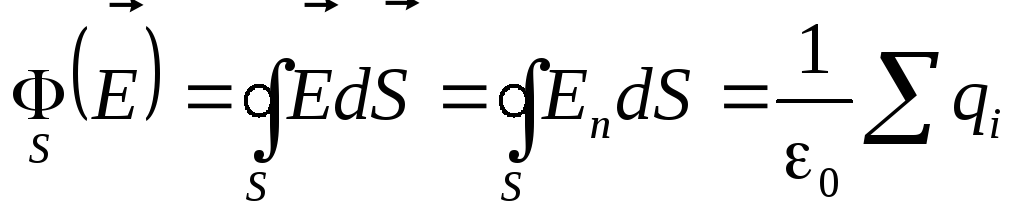 .
.
Поток вектора напряжённости электростатического поля через любую замкнутую поверхность пропорционален величине заряда,заключённого внутри этой поверхности.
Это означает, что электрические заряды — реальность природы, а вот магнитных зарядов в природе нет.
Теорема о циркуляции магнитного поля
Теперь займёмся вычислением циркуляции
вектора магнитной индукции 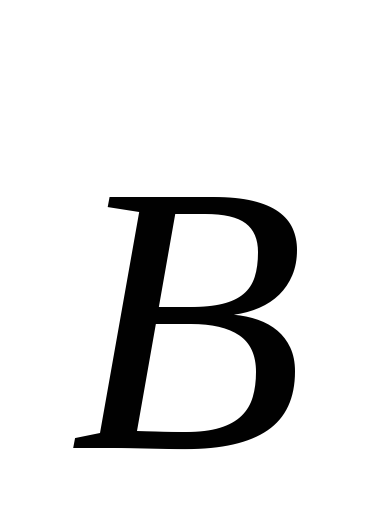 по замкнутому контуру. Начнём с простого
контура. Пусть для начала контур совпадает
с силовой линией магнитного поля
прямолинейного тока (рис. 9.7.). По
определению, циркуляция вектора по
замкнутому контуру равна следующему
интегралу:
по замкнутому контуру. Начнём с простого
контура. Пусть для начала контур совпадает
с силовой линией магнитного поля
прямолинейного тока (рис. 9.7.). По
определению, циркуляция вектора по
замкнутому контуру равна следующему
интегралу:
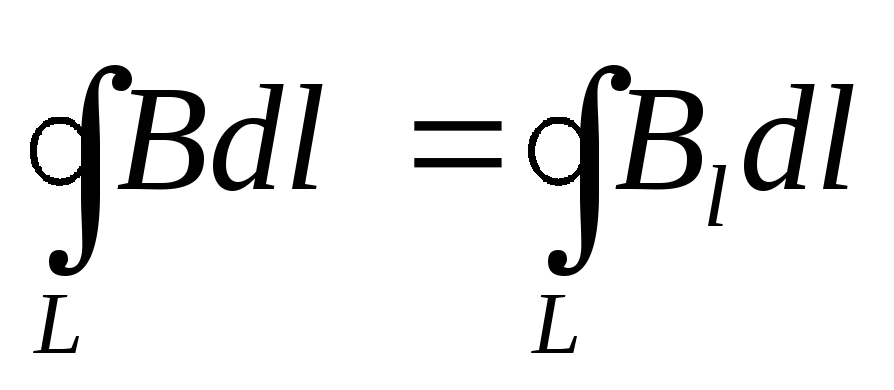 .
.

Рис. 9.7.
Обратим внимание на то, что модуль вектора магнитной индукции в нашем случае одинаков во всех точках силовой линии и, следовательно, контура L:
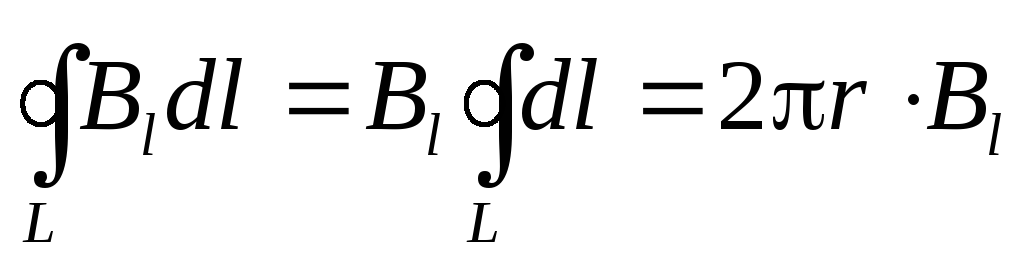 . (9.15)
. (9.15)
Согласно (9.8), 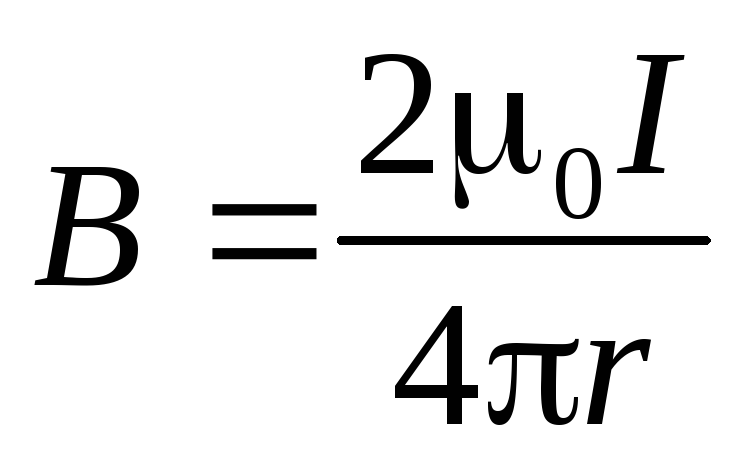 .
Поэтому циркуляцию вектора
.
Поэтому циркуляцию вектора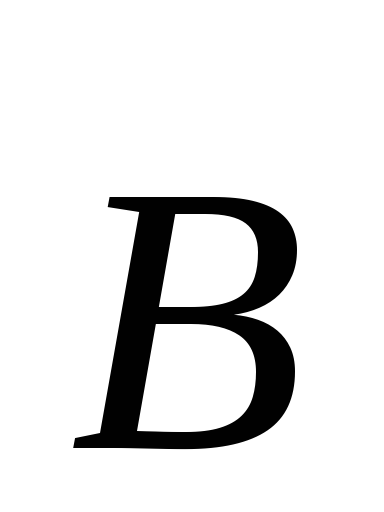 (9.15) можно записать так:
(9.15) можно записать так:
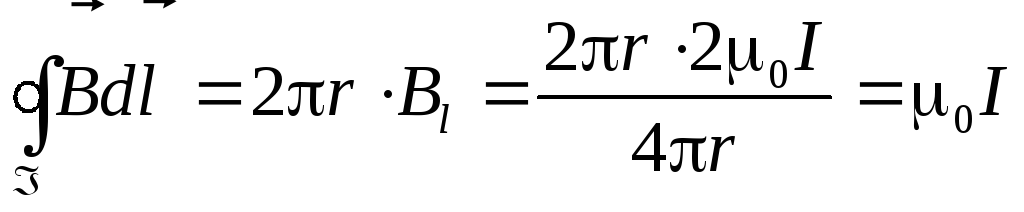 .
.
Вывод. В рассмотренном частном случае циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна току, охватываемому этим контуром.
Усложним задачу.
Выберем теперь почти произвольный
контур L в магнитном поле прямолинейного тока I.
Контур по-прежнему охватывает ток и
лежит в плоскости, перпендикулярной
проводнику с током (рис. 9.8.). Циркуляция  на участке контура
на участке контура равна:
равна:
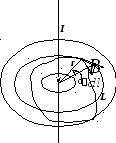
Рис. 9.8.
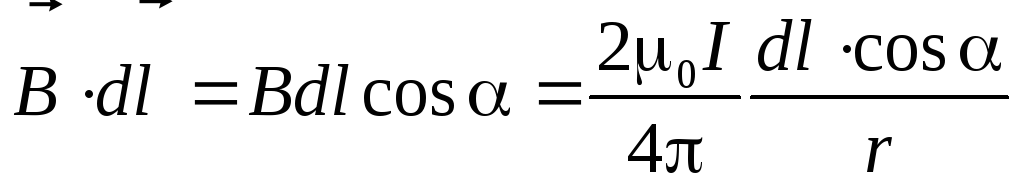
Здесь 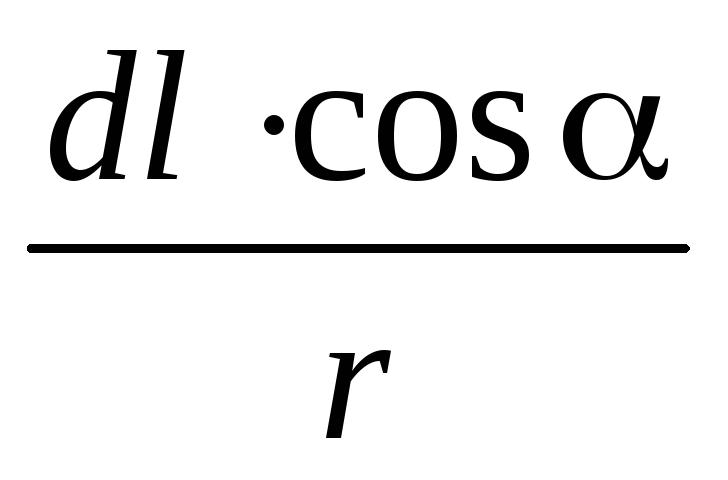 =d,
поэтому циркуляцию по всему замкнутому
контуруLможно записать
так:
=d,
поэтому циркуляцию по всему замкнутому
контуруLможно записать
так:
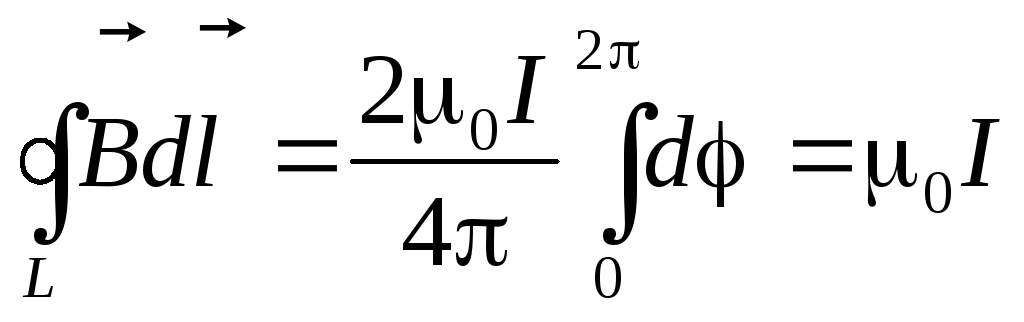 .
.
Мы вновь пришли к прежнему результату: циркуляция магнитного поля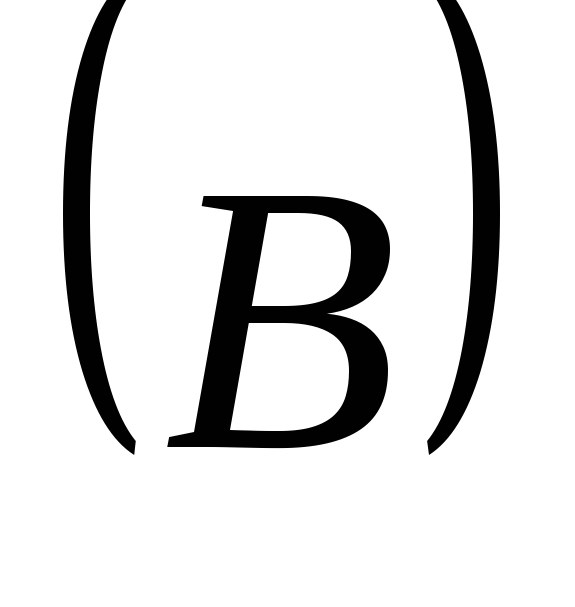 по замкнутому контуру пропорциональна
току, охватываемому этим контуром.
по замкнутому контуру пропорциональна
току, охватываемому этим контуром.
Что произойдёт, если контур не охватывает ток (рис. 9.9.)?
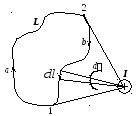
Рис. 9.9.
Циркуляция на участке  по-прежнему будет равна:
по-прежнему будет равна:
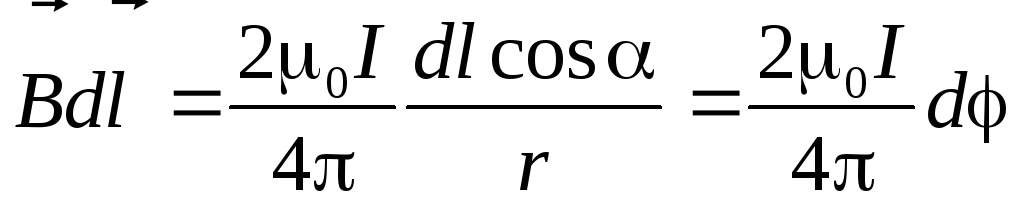 .
.
При обходе такого контура на участке 1-а-2 угол будет расти от нуля, а на участке 2-b-1 — уменьшаться до нуля. Поэтому циркуляция в этом случае окажется равно нулю:
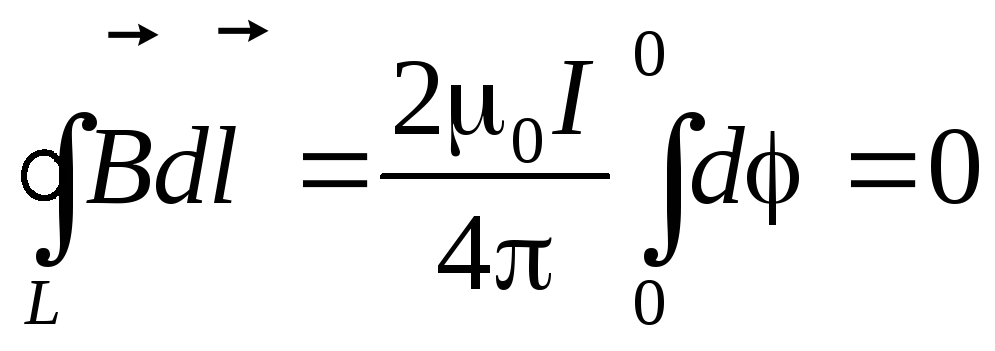 .
.
Сделаем ещё одно важное замечание.
Циркуляция вектора 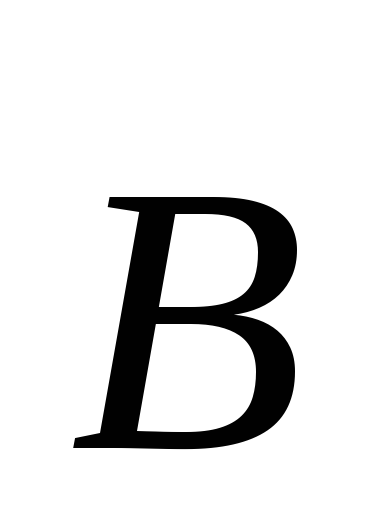 — скалярная величина. Она может быть
положительной и отрицательной.
— скалярная величина. Она может быть
положительной и отрицательной.
Циркуляция положительна, когда направление обхода контура связано с направлением тока правилом буравчика (рис. 9.10.a). В противном случае циркуляция отрицательна (рис. 9.10.b).

Рис. 9.10.
Если магнитное поле создаётся не одним, а несколькими токами, то циркуляция такого поля по замкнутому контуру будет пропорциональна алгебраической сумме токов, охватываемыхэтим контуром:
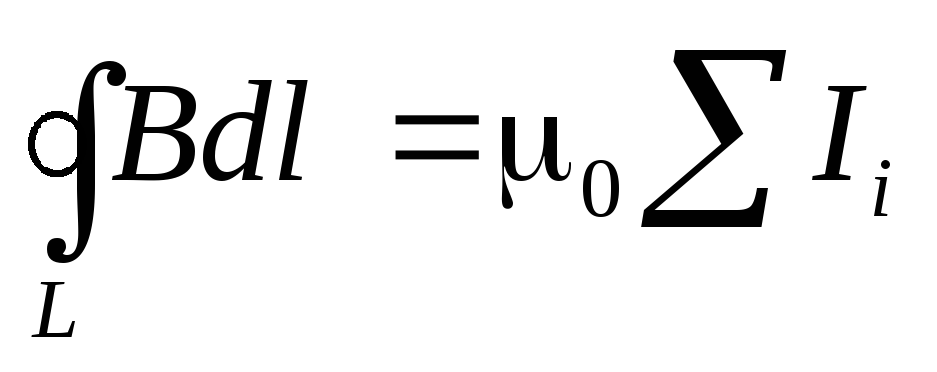 . (9.16)
. (9.16)
Для случая, представленного на рис. 9.11.:
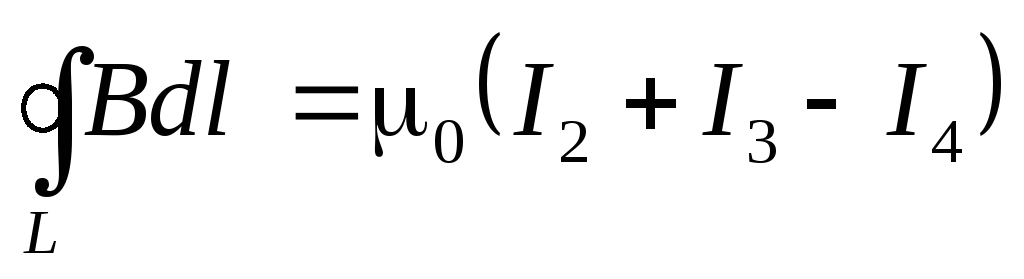 .
.
При выбранном направлении обхода контура (по часовой стрелке — на рис. 9.11.) знак тока определяется правилом буравчика. Токи I1иI5не вошли в сумму токов, так как они оказались вне замкнутого контура.
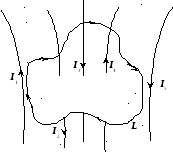
Рис. 9.11.
Подводя итог, сформулируем теорему о циркуляции магнитного поля: циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна алгебраической сумме токов, охватываемых этим контуром.
Здесь заканчивается важный этап нашей работы: мы записали последнее уравнение системы уравнений Максвелла для электро- и магнитостатики. Вот эти уравнения:
| (I) |
| (III) |
| (II) |
| (IV) |
Система включает два уравнения потока (IиIII) и два уравнения циркуляции (IIиIV) для электростатических и магнитных полей.
Повторим физическое содержание этих уравнений:
I — | источником электростатического поля являются электрические заряды; |
II — | электростатическое поле потенциально; |
III — | в природе отсутствуют магнитные заряды; |
IV — | источником магнитного поля является электрический ток. |
Действие магнитного поля на движущийся заряд. Сила Лоренца
Действие магнитного поля на движущийся заряд. Сила Лоренца
«Физика — 11 класс»
Магнитное поле действует с силой на движущиеся заряженные частицы, в то числе и на проводники с током.
Какова же сила, действующая на одну частицу?
1.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика X. Лоренца, создавшего электронную теорию строения вещества.
Силу Лоренца можно найти с помощью закона Ампера.
Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:
Так как сила (сила Ампера), действующая на участок проводника со стороны магнитного поля
равна F = | I | BΔl sin α,
а сила тока в проводнике равна I = qnvS
где
q — заряд частиц
n — концентрация частиц (т.е. число зарядов в единице объема)
v — скорость движения частиц
S — поперечное сечение проводника.
тогда получаем:
На каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:
где α — угол между вектором скорости и вектором магнитной индукции.
Сила Лоренца перпендикулярна векторам и .
2.
Направление силы Лоренца
Направление силы Лоренца определяется с помощью того же правила левой руки, что и направление силы Ампера:
Если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° большой палец укажет направление действующей на заряд силы Лоренца Fл.
3.
Если в пространстве, где движется заряженная частица, существует одновременно и электрическое поле, и магнитное поле, то суммарная сила, действующая на заряд, равна:
= эл + л
где сила, с которой электрическое поле действует на заряд q, равна Fэл = q.
4.
Cила Лоренца не совершает работы, т.к. она перпендикулярна вектору скорости частицы.
Значит сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости.
Под действием силы Лоренца меняется лишь направление скорости частицы.
5.
Движение заряженной частицы в однородном магнитном поле
Сила Лоренца зависит от модулей векторов скорости частицы и индукции магнитного поля.
Магнитное поле не меняет модуль скорости движущейся частицы, значит остается неизменным и модуль силы Лоренца.
Сила Лоренца перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы.
Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что
В однородном магнитном поле заряженная частица равномерно движется по окружности радиусом r.
Согласно второму закону Ньютона
Тогда радиус окружности, по которой движется частица, равен:
Время, за которое частица делает полный оборот (период обращения), равно:
6.
Использование действия магнитного поля на движущийся заряд.
Действие магнитного поля на движущийся заряд используют в телевизионных трубках-кинескопах, в которых летящие к экрану электроны отклоняются с помощью магнитного поля, создаваемого особыми катушками.
Сила Лоренца используется в циклотроне — ускорителе заряженных частиц для получения частиц с большими энергиями.
На действии магнитного поля основано также и устройство масс-спектрографов, позволяющих точно определять массы частиц..
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Магнитное поле. Физика, учебник для 11 класса — Класс!ная физика
Магнитное поле и взаимодействие токов — Магнитная индукция. Линии магнитной индукции — Модуль вектора магнитной индукции. Сила Ампера — Электроизмерительные приборы. Громкоговоритель — Действие магнитного поля на движущийся заряд. Сила Лоренца — Магнитные свойства вещества — Примеры решения задач — Краткие итоги главы
Сила Лоренца — FizikatTYT
Сила Лоренца — сочетание электрического и магнитного взаимодействия, которое возникает, когда положительно или отрицательно заряженная частица движется в электромагнитном поле. Она перпендикулярна направлениям векторов магнитной индукции и скорости заряда. Под её действием частица изменяет траекторию своего движения и скорость.
Этот вид сил впервые описал Джеймс Максвелл в 1865 году, а в 1892 году голландский физик Хендрик Лоренц записал для неё математическое выражение. Хотя первый вывод формулы исследователи приписывают Оливеру Хевисайду.
Вариация этой базовой силы действует на проводник с током, когда его помещают между полюсами магнита. Если в проводнике существует ток, то он будет отклоняться во внешнем магнитном поле, так как сила Лоренца будет действовать на все движущиеся в нём электроны. В какую сторону отклонится провод с током наглядно продемонстрирует правило левой руки.
Это явление и возникающую силу используют в экспериментальной физике для:
- увеличения скорости элементарных частиц и ионов в различных циклотронах и других ускорителях;
- определения удельного заряда и массы положительных ионов, относительной атомной массы изотопов химических элементов в масс-спектрографии;
- в магнетронах и скоростных фильтрах.
В быту такое воздействие на заряженную частицу нашло применение в телевизорах с электронно-лучевой трубкой, электродвигателях, колонках, генераторах.
Какова природа силы?
Эта сила принадлежит спектру сил электромагнитного взаимодействия. Магнитное поле создают заряженные частицы, такие как протон или электрон, во время своего движения. Движущийся заряд поместим во внешнее поле, например, между полюсами магнита. Поле точечного заряда и внешнее поле будут взаимодействовать определённым образом: притягиваться или отталкиваться. Это зависит от знака заряда и от взаимного расположения линий магнитной индукции полей.
Формула для вычисления модуля силы Лоренца демонстрирует её зависимость от скорости частицы v, абсолютного значения её заряда q, от модуля индукции внешнего магнитного поля B и угла α, показывающего взаимное расположение векторов скорости и магнитной индукции.
На рисунке представлены все величины, фигурирующие в формуле:
Из уравнения видно, что если v (скорость) стремится к нулю, то на точечный заряд не будет действовать и сила Лоренца. Кроме того, если заряд перемещается в направлении, параллельном направлению вектора магнитной индукции, то есть sin (0) = 0, снова будем наблюдать отсутствие внешней силы (Fл=0). А при движении, перпендикулярном линиям внешнего магнитного поля, сила Лоренца становится центростремительной и искривляет траекторию объекта (наблюдается движение по окружности). Протон представлен на рисунке а), рисунок б) описывает электрон.
Правило левой руки
Для положительно заряженной частицы необходимо расположить ладонь левой руки, чтобы четыре вытянутых пальца направить параллельно её движению, а линии магнитной индукции входили в ладонь перпендикулярно, то отогнутый на 90° большой палец покажет направление силы Лоренца. А для отрицательного заряда силу Лоренца направляем в противоположную сторону.


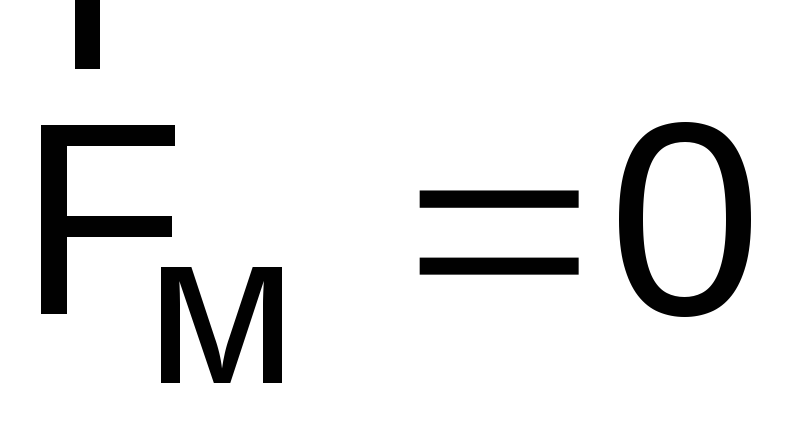 .
.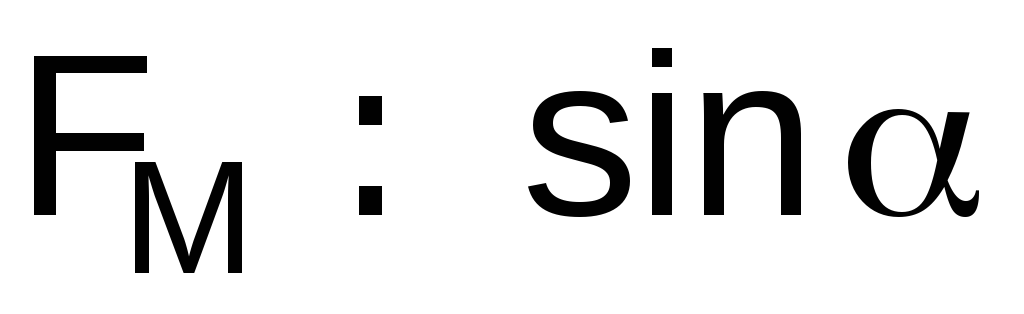
 ри
всевозможных движениях заряда
ри
всевозможных движениях заряда 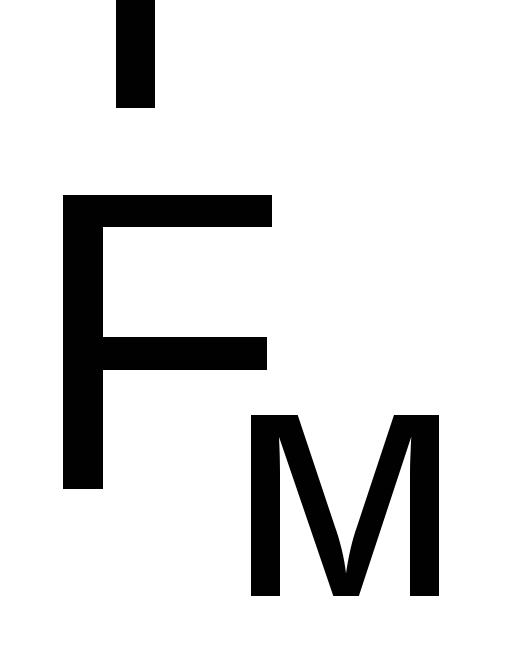 всегда перпендикулярна этому выделенному
направлению, то есть все
всегда перпендикулярна этому выделенному
направлению, то есть все  лежат в одной плоскости перпендикулярной
MN.
лежат в одной плоскости перпендикулярной
MN. ,
,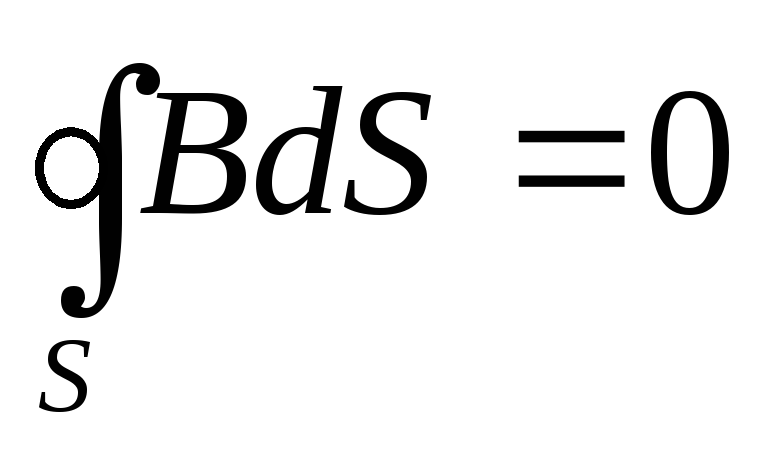 ,
,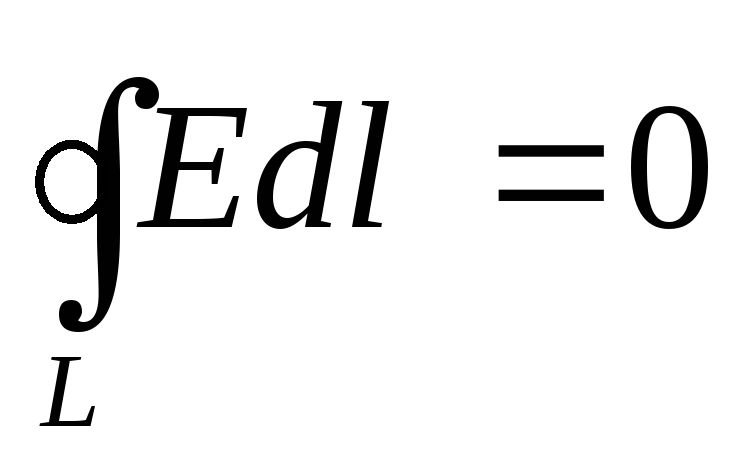 ,
,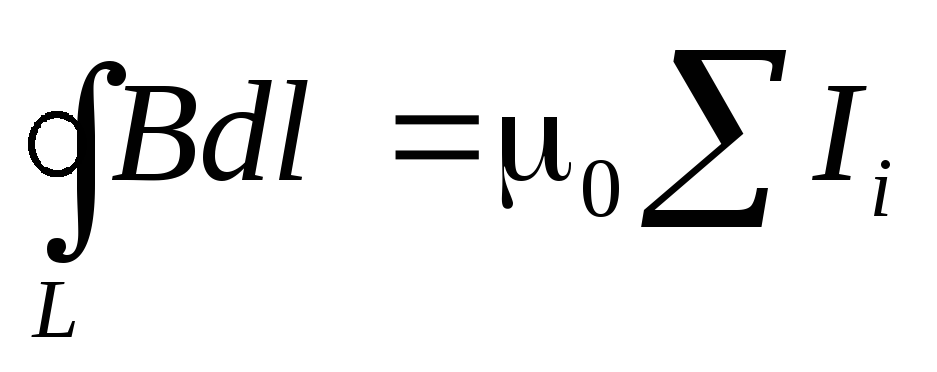 .
.