Закон Кулона. Силы и ускорения.

В статье рассмотрены задачи, сочетающие законы динамики и взаимодействие зарядов. Здесь встретится и сила упругости, и сила натяжения нити, и нормальное ускорение при движении по окружности. Задачи среднего уровня сложности.

 

Задача 1. Два одинаковых заряда , соединенных резиновыми шнурами со стенками так, как показано на рисунке, находятся на расстоянии друг от друга. Расстояние между стенками , длина каждого недеформированного шнура . Определить жесткость шнура, массой зарядов пренебречь.

Жесткость шнура равна  , где – сила натяжения шнура, – удлинение шнура.

Определим, насколько шнур стал длиннее.

   

К задаче 1.

Определим силу кулоновского взаимодействия зарядов:

   

Определим силу натяжения шнура, для этого приравняем проекции сил кулоновского взаимодействия и натяжения шнуров:

   

   

Найдем косинус угла из геометрических соображений:

   

Тогда можем подставить все в формулу для жесткости:

   

Ответ: .

 

Задача 2. Внутри гладкой сферы диаметром находится маленький заряженный шарик. Какой минимальной величины заряд нужно поместить в нижней точке сферы, для того чтобы шарик находился в ее верхней точке в устойчивом равновесии? Заряд шарика , его масса .

К задаче 2

Минимальная сила, которая может нам понадобиться, это кулонова сила, равная силе тяжести. Тогда

   

   

Посмотрим, достаточно ли этого, чтобы равновесие было устойчивым: если шарик отклонится на небольшой угол от вертикали, то кулонова сила может быть разложена на две составляющие, причем раскладывать силу будем, направив ось по касательной к сфере, а ось – перпендикулярно касательной. Тогда проекция кулоновой силы на данное направление равна , а проекция силы тяжести на это же направление равна . Чтобы шарик возвращался назад в точку равновесия нужно, чтобы проекция кулоновой слы была бы больше проекции силы тяжести. Осталось установить, как соотносятся углы и . Посмотрим на рисунок: угол – центральный, а угол – вписанный. Поэтому .

Тогда:

   

В силу малости углов можно принять , . Тогда

   

   

   

Иными словами, устойчивым равновесие будет, если

   

Ответ:

 

Задача 3. Два заряженных шарика соединены нитью см. Отношение масс шариков , заряды по модулю одинаковы Кл, но противоположны по знаку. Какую минимальную внешнюю силу надо приложить к шарику массой , чтобы в процессе движения нить не провисала?

Шарики заряжены одноименно, то есть будут притягиваться. Нужно, чтобы левый шарик «убегал» от правого с определенным ускорением. Нарисуем чертеж:

К задаче 3

Запишем второй закон Ньютона для левого шарика:

   

Здесь – внешняя сила, – кулонова сила, – сила натяжения нити.

Для правого шарика

   

Чтобы нить не провисала, достаточно чтобы натяжение нити было нулевым, :

   

   

Подставим второе в первое:

   

   

Подставим ускорение из записанного ранее равенства:

   

   

   

Ответ: 27 мН

 

Задача 4. Вокруг неподвижного положительного заряда Кл движется по окружности отрицательный заряд. Радиус окружности 1 см. Один оборот заряд совершает за время с.  Найти отношение заряда к массе для движущегося заряда.

При движении по окружности всегда присутствует нормальное ускорение, поворачивающее вектор скорости. Чтобы его найти, надо бы узнать скорость движения заряда. Мы знаем время прохождения одного оборота, длина же окружности радиуса равна , поэтому линейная скорость движения заряда равна .

Нормальное ускорение:

   

Кулонова сила равна центростремительной:

   

   

Запишем иначе:

   

   

Ответ: Кл/кг

 

Задача 5. Шарик массой и зарядом , подвешенный на непроводящей нити длиной  ,  вращается вокруг вертикальной оси так, что нить образует с вертикалью угол . Определить период  обращения шарика  и  силу натяжения нити, если неподвижный точечный заряд находится: а) в точке подвеса; б) в центре окружности, описываемой шариком; в) на оси вращения, на расстоянии от шарика  внизу.

Первый случай. Заряд – в месте прикрепления нити к потолку, сила кулоновского взаимодействия направлена вдоль нити вниз. Нарисуем картинку и запишем второй закон Ньютона.

К задаче 5 а)

В векторной форме:

   

Здесь – сила натяжения нити, – кулонова сила, – сила, обусловленная наличием нормального ускорения.

Разложим теперь вектора на проекции вдоль координатных осей. Ось абсцисс направим горизонтально вправо, ось ординат – вверх. Тогда:

   

   

Определим отсюда силу натяжения нити:

   

Теперь займемся периодом. Для его определения нужно знать скорость шарика. Распишем второе уравнение, подставив силу натяжения нити и нормальное ускорение:

   

   

Так как , то

   

   

   

Второй случай – заряд в центре окружности.

Сила кулоновского взаимодействия направлена вдоль радиуса, наружу. Нарисуем картинку и запишем второй закон Ньютона.

К задаче 5 б)

В векторной форме:

   

Разложим теперь вектора на проекции вдоль координатных осей. Ось абсцисс направим горизонтально вправо, ось ординат – вверх. Тогда:

   

   

Определим отсюда силу натяжения нити:

   

Тогда первое уравнение:

   

   

   

   

Определим период. Скорость знаем, длину окружности – тоже. Тогда:

   

Упростим немного выражение:

   

   

   

   

   

Наконец, рассмотрим третий случай, когда заряд находится на оси вращения внизу. Сила кулоновского взаимодействия направлена вдоль линии, проведенной через заряды, вверх и влево.

Нарисуем картинку и запишем второй закон Ньютона.

К задаче 5 в)

В векторной форме:

   

Разложим теперь вектора на проекции вдоль координатных осей. Ось абсцисс направим горизонтально вправо, ось ординат – вверх. Тогда:

   

   

Определим отсюда силу натяжения нити:

   

   

   

   

   

Зная скорость, определим период:

   

   

 

 

 

1 Закон Кулона

При определенных условиях тела электризуются, т.е. приобретают некоторый заряд. Существуют заряды отрицательные и положительные. Одноименные заряды отталкиваются, а разноименные притягиваются. Ед заряда в СИ – кулон. По определению, 1 кулон равен заряду, протекающему через поперечное сечение проводника за 1 с при силе тока 1 А. Носителем элементарного отрицательного заряда является электрон, q_e= -1,6*10^-19Кл, m_е=9,1*10^-31кг. Носителем элементарного положительного заряда является протон q _р=+1,6*10^-19Кл, масса m_р=1,67*10^-27кг. Электрический заряд имеет дискретную природу -заряд любого тела кратен заряду электрона q=Nq_e. В изолированной системе, т.е. в системе, тела которой не обмениваются зарядами с внешними по отношению к ней телами, алгебраическая сумма зарядов сохраняется (закон сохранения заряда). Закон Кулона — сила взаимодействия двух точечных электрических зарядов, находящихся в вакууме, прямо пропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояний между ними и направлена вдоль прямой, соединяющей заряды. Заряженное тело, размером и формой которого можно пренебречь по сравнению с расстоянием до других заряженных тел, называется точечным зарядом. Закон Кулона справедлив только для точечных зарядов и выражается следующей формулой: F=k|q₁||q₂|/r², где q₁ и q₂ – величины взаимодействующих зарядов, r – расстояние между ними, k – коэффициент, зависящий от выбора системы единиц. В СИ имеем k=1/4₀ = 9*10⁹Н*м²/Кл², где ₀ –электрическая постоянная, равная ₀ =8,85*10^-12Ф/м [Ф/м=Кл²/Н*м²]. Если заряды находятся в идеально однородной среде, то сила взаимодействия между ними уменьшается в  раз,  — относительная диэлектрическая проницаемость среды. Если имеется система точ зарядов, то сила, действ на каждый из них, опред как вект сумма сил, действующих на данный заряд со стороны всех др зарядов системы

принцип суперпрозиц. Напряженность электрического поля. Заряды, находясь на некот расстоянии один от другого, взаимодействуют. Это взаимод осущ посредством электрического поля. Наличие электрического поля можно обнаружить, помещая в различные точки пространства электрические заряды. Силовой хар-кой электрического поля служит напряженность E. Если на находящийся в некоторой точке заряд q₀ действует сила F, то напряженность электрического поля Е равна: Е=F/q₀. Графически силовые поля изображают силовыми линиями. Силовая линия – это линия, касательная в каждой точке которой совпадает с вектором напряженности электрического поля в этой точке.

2 Сила Лоренца

На проводник с током в магнитном поле действует сила Ампера F_А=IBlsin.Ток, в свою очередь, это направленное движение заряженных частиц. Сила тока равна I=qnvS, где q – заряд частицы, n-концентрация движущихся заряженных частиц, v-средняя скорость их направленного движения, S-площадь поперечного сечения проводника. Подставив I в выражение для F_А, получим F_А= qnvSBlsin, где nsl=N – общее число частиц, создающих ток. Тогда сила, действующая на отдельный движущийся заряд – сила Лоренца, равна Fл=qvBsin. где  — угол между векторами скорости и магнитной индукции. Направление силы Лоренца определяется для положительно заряженной частицы по правилу левой руки.

Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца. Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. Сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.

3

Закон Кулона: равнодействующие и моменты сил

В этой статье собраны задачи, где потребуется найти равнодействующую сил, а для этого нужно обладать и минимумом геометрических знаний. Также понадобится вспомнить, как определить силу упругости, и как определить момент силы.

Задача 1. Два электрона находятся в точках, определяемых радиус-векторами и соответственно.  Вычислить ускорение, сообщаемое одним электроном другому.

Ускорение будет определяться силой кулоновского отталкивания между электронами:

   

Сила зависит от расстояния, а расстояние можно определить как длину вектора, являющегося разностью радиус-векторов электронов:

   

   

Тогда ускорение:

   

Ответ: 14,9 м/с.

 

Задача 2.  Три точечных заряда Кл, Кл и Кл расположены последовательно вдоль одной прямой и связаны двумя нитями длиной м каждая. Найти натяжение нитей, если заряд находится посередине.

К задаче 2

Все заряды являются одноименными и, следовательно, отталкиваются. На первый из них действует две силы: одна – сила взаимодействия со вторым зарядом, вторая – с третьим:

   

   

Аналогично, на третий заряд будут действовать силы:

   

   

Из рисунка видно, что

   

   

Тогда:

   

   

Ответ: Н, или 0,1 Н, Н, или 0,074 Н

 

Задача 3.  Три одинаковых шарика, расположенных вдоль одной прямой, соединили вместе двумя одинаковыми пружинами жесткостью каждая. Расстояние между крайними шариками равно . Затем всем шарикам сообщили одинаковый заряд, при этом расстояние между крайними шариками стало .  Найти величину заряда , сообщенного каждому шарику.

Определим, насколько увеличилось расстояние.

   

Сила упругости пружин равна:

   

Жесткость обозначили , чтобы отличать от коэффициента в формуле кулоновой силы.

Сила кулоновского отталкивания, аналогично предыдущей задаче, будет складываться для крайнего левого шарика из силы взаимодействия с крайним правым и силы взаимодействия с тем шариком, что посередине:

   

Приравняем силу упругости и кулонову силу:

   

   

Теперь можно «вытащить» из этого равенства заряд:

   

 

   

Ответ:

Задача 4. Электрическое поле образовано двумя зарядами   Кл и Кл, расположенными на расстоянии см  друг от друга  в  точках A и В. Какая сила будет действовать на капельку  С, находящуюся на расстоянии 5 см от середины отрезка АВ, если заряд капельки равен заряду 10 электронов?

К задаче 4

Капелька будет взаимодействовать с обоими зарядами: к одному (первому) притягиваться, а от второго – отталкиваться, и по модулю, в силу равенства зарядов по модулю, силы будут равны. Поэтому, чтобы найти суммарную силу (равнодействующую), нужно сложить обе силы векторно. Заметим, что вектора сил будут образовывать прямоугольный треугольник, поэтому равнодействующую можно определить по теореме Пифагора.

   

   

   

Теперь можем определить равнодействующую:

   

Ответ: Н, или 2 нН.

 

Задача 5. На концах невесомого непроводящего стержня длиной находятся два невесомых шарика с зарядами и . На перпендикуляре, проведенном через середину стержня, на расстоянии от основания перпендикуляра расположен точечный заряд .  Определить вращающий момент, действующий на стержень.

К задаче 5

Так как заряды разноименные, то заряд один из них будет притягивать, а другой – отталкивать, отсюда вращающий момент. Момент – это пара сил, это, кроме того, произведение силы на плечо.

Модули сил взаимодействия зарядов одинаковы:

   

Определим расстояние между зарядами:

   

Вращать стержень будут только изображенные на рисунке красным составляющие кулоновых сил,  а они равны . Определим из рисунка синус соответствующего угла:

   

Тогда момент сил равен удвоенному произведению силы на плечо (так как сил – две):

   

   

 

Задача 6. Одноименные заряды мкКл, мкКл и мкКл расположены в вершинах треугольника со сторонами см, см и см. Определить модуль силы, действующей на заряд .

К задаче 6

Снова предстоит найти векторную сумму сил и , которые являются силами взаимодействия зарядов 1 – 3 и 2 – 3.

Модуль силы равен:

   

Модуль силы равен:

   

Модуль равнодействующей может быть определен по теореме косинусов:

   

   

Нам неизвестен , однако он равен , а косинус этого угла мы тоже можем найти из теоремы косинусов:

   

   

Тогда косинус нужного нам угла равен:

   

Определим результирующую силу:

   

   

Подставим числа:

   

Ответ: 0,77 Н

Самостоятельная работа по теме «Закон Кулона»

Вариант-1

1.С какой силой взаимодействуют два точечных заряда 10нКл и 15нКл, находящиеся на расстоянии 5см друг от друга?

2.Два неподвижных точечных заряда действуют друг на друга с силами, модуль которых равен F.Во сколько раз увеличится модуль этих сил, если один заряд увеличить в 4 раза, другой заряд уменьшить в 2 раза, а расстояние между ними оставить прежним?

3.Как направлена (вправо, влево, вверх, вниз) кулоновская сила, действующая на положительный точечный электрический заряд

+ 2q, помещенный в центр квадрата, в вершинах которого находятся заряды +q, +q, — q, — q?

Вариант-2

1.На каком расстоянии друг от друга находятся два заряда 10нКл и 15нКл, если они взаимодействуют с силой 5,4·10^-4Н?

2.Два неподвижных точечных заряда действуют друг на друга с силами, модуль которых равен F.Во сколько раз увеличится модуль этих сил, если один заряд увеличить в 3 раза, другой заряд уменьшить в 2 раза, а расстояние между ними оставить прежним?

3.Точечный отрицательный зарядq помещен между разноименно заряженными шариками.Куда направлена (вправо, влево, вверх, вниз) равнодействующая кулоновских сил, действующих на зарядq?

Вариант-3

1.Два точечных заряда , находящиеся на расстоянии 5см друг от друга, взаимодействуют с силой5,4·10^-4Н. Какова величина второго заряда, если первый заряд равен 10 нКл?

2.Два неподвижных точечных заряда действуют друг на друга с силами, модуль которых равен F.Во сколько раз уменьшится модуль этих сил, если один заряд уменьшить в 5 раз, другой заряд увеличить в 2 раза, а расстояние между ними оставить прежним?

3.Как направлена (вправо, влево, вверх, вниз) кулоновская сила,

действующая на положительный точечный электрический заряд + q, помещенный в центр квадрата, в вершинах

которого находятся заряды +q, +q, — q, — q?

Вариант-4

1.Два точечных заряда , находящиеся на расстоянии 5см друг от друга, взаимодействуют с силой 5,4·10^-4Н. Какова величина первого заряда, если второй заряд равен 15 нКл?

2.Два маленьких шарика, обладающих зарядами q каждый, находятся на расстоянии r друг от друга и притягиваются с силой 3F.Какова сила электростатического притяжения двух других шариков, если заряд одного 3q,заряд другого q/3, а расстояние между их центрами 3r?

3.Точечный отрицательный заряд помещен вблизи одинаковых одноименно заряженных шариков .Как направлена (вверх, вниз, влево, вправо, к наблюдателю, от наблюдателя) равнодействующая кулоновских сил, действующих на заряд?

Ответы

Вариант-1

1.5,4·10^-4Н 2.В 2 раза 3.Влево

Вариант-2

1.5см 2.В 1,5 раза 3.Вправо

Вариант-3

1.15нКл 2.В 2,5 раза 3.Вниз

Вариант-4

1.10нКл 2.F/3 3.Влево

Источники информации

1.Громцева О.И. ЕГЭ. Физика. Высший балл. Самостоятельная подготовка к ЕГЭ/

О. И. Громцева. – М.: Издательство «Экзамен», 2017.

2.Демидова М.Ю. ЕГЭ 2015. – Физика. Типовые тестовые задания/ М.Ю.Демидова, В.А. Грибов, — М.: Издательство «Экзамен», 2015.

Как определить направление силы, действующей на НЕПОДВИЖНЫЙ положительный заряд?

Вниз. Поскольку о движении зарядов +q и -q в условии ничего не сказано, будем считать их тоже неподвижнымии. Поскольку расстояния между зарядами не указаны, берём их с рисунка, на котором заряды расположены в углах квадрата, в центре которого находится точка А. Разбиваем систему из 4 зарядов на 2 подсистемы: из двух верхних и из двух нижних зарядов. 2 верхних одинаковы и одного знака с зарядом в точке А, значит, отталкивают заряд А с равной силой, значит, вектор их равнодействующей направлен вниз. Два нижних тоже одинаковы между собой, они разного знака с зарядом А, значит, притягивают его к себе с одинаковой силы, вектор равнодействующей направлен вниз. Два вектора равнодействующих от двух подсистем, эти два вектора оба направлены вниз, так что в сумме они по-любому дадут вектор, направленный тоже вниз.

магнит приподнести. куда стрелка мотанётся, туда и сила электрического поля направлена.

Вопрос не нелепый — а неполный. Что за сила, откуда? Если заряд покоится в постоянном магнитном поле — то магнитное поле на него НИКАК НЕ ДЕЙСТВУЕТ — только электростатическое, кулоновская сила….

Ну пипец! Направление электростатической силы совпадает с направлением вектора напряжённости электрического поля (по определению напряжённости). Кулоновская сила действует между двумя зарядами и направлена по линии, соединяющей заряды. Если зарядов несколько, то на пробный заряд они воздействуют независимо, как бкдто остальных зарядов и нет, а силы просто складываются по векторному закону. Этот принцип носит название принципа суперпозиции (т. е. независимого наложения) . В случае Вашей задачи просто рисуете вектора сил, действующих на пробный заряд со стороны трёх других (для каждого независимо и не забыв учесть отталкивание это или притяжение) , и ищете равнодействующую силу, как векторную сумму трёх сил.

Одноименные заряды отталкиваются, а разноименные притягиваются. Ответ вниз

Сила Кулона, закон Кулона, границы применимости, напряженность электростатического поля, принцип суперпозиции.

⇐ ПредыдущаяСтр 3 из 9Следующая ⇒

 

Опыты по притяжению и отталкиванию наэлектризованных тел позволяют предположить, что эл.заряды взаимодействуют. Причем взаимодействие зависит от расстояния (чем ближе – тем сильнее). Предположение – заряд передается через воздух. Опыт – заряженный электроскоп поместили под колокол, воздух откачали, а листочки электроскопа по-прежнему отталкивались. В результате исследований было установлено, что эл.заряды окружены эл.полем.

Электрическое поле (часть эл.магнитного) – особый вид материи, который создается эл.зарядами, неразрывно с ними связан и воздействует на заряды одинаково, независимо от того, двигаются они или покоятся в данной инерциальной системе отсчета.

Электрическое поле, создаваемое неподвижными зарядами – электростатическое. Его характеристиками являются напряженность и потенциал.

Электрическое поле взаимодействует с зарядом. Энергия этого взаимодействия — потенциальная.

Потенциал электрического поля – скалярная величина, энергетическая характеристика, равная отношению потенциальной энергии пробного заряда к величине этого заряда.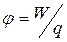

Пробным называют тот заряд, который существенно не меняет поле, с которым взаимодействует (элементарный заряд –равный 1,6*10^-19 Кл ).

Напряженность (силовая характеристика)в данной точке электростатического поля — векторная физическая величина, равная отношению силы, действующей в данной точке поля, на точечный пробный заряд, к этому заряду. E = F/q. (E = F при q = 1). Ед. измерения 1 В/м = 1 Дж/(м*Кл) = 1Н/м или Н/кл

В каждой точке поля напряженность имеет определенное значение и зависит от координат. В случае переменных полей она зависит и от времени.

Направление вектора Е совпадает с на­правлением силы, действующей на «+» заряд. Если поле создается «-» зарядом, то вектор Е направлен к заряду и противонаправлен силе. Линии напряженности начинаются у «+» зарядов (или в бесконечности) и оканчиваются у «-» зарядов. По густоте линий можно судить о величине Е

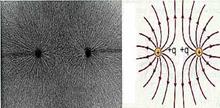
Разные заряды одноименные заряды пластина

Картина будет более наглядной, если рисовать не векторы в отдельных точках, а непрерывные линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности. Эти линии называются линиями напряженности или силовыми линиями электрического поля. За направление силовых линий принимается направление вектора Е.

Напряженность поля увеличивается по мере приближения к заряду, а силовые линии при этом сгущаются.

Линии напряженности электростатических полей не замкнуты. Отметим, что напряженность поля в диэлектрике меньше, чем в вакууме из-за явления поляризации и, следовательно, густота силовых линий в диэлектрике меньше. Отношение напряженности поля в вакууме к напряженности в данной среде называют диэлектрической проницаемостью вещества. E_вак./E.

Напряженность электростатического поля в металле равняется нулю, так как поле свободных зарядов, существующих в нем, через достаточно короткий промежуток времени уравновесит внешнее поле и ток в металле будет равен нулю. Поэтому силовые линии в металл не проникают.

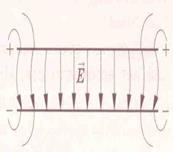
Однородным называется электростатическое поле, во всех точках которого напряженность одинакова по величине и направлению

Электрическая сила (Кулоновская) – сила, с которой электрическое поле действует на внесенный в него электрический заряд независимо от того, двигается он или покоится в данной инерциальной системе отсчета.

Подносим заряженную «+» палочку к заряженной «-» гильзе. По мере приближения палочки угол отклонения гильзы будет увеличиваться. Следовательно, чем ближе расположены тела, тем сильнее действие поля.

Закон взаимодействия электрических зарядов (закон Кулона) – два точечных неподвижных заряда взаимодействуют в вакууме с силой, прямопропорциональной произведению их зарядов и обратнопропорциональной квадрату расстояния между ними, 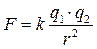где 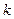—коэффициент пропорциональности, 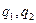— заряды, 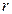— расстояние между ними.

 

Границы применимости закона Кулона –

1. Заряженные тела должны быть точечными. Если же размеры и расстояния соизмеримы, то необходимо мысленно «разбить» тело на такие малые объемы, чтобы каждый из них отвечал условию точечности. Суммирование сил, действующих между элементарными объемами заряженных тел, дает возможность определить электрическую силу.

2. Заряженные тела должны быть неподвижными, т.к. при движении заряженных тел проявляется действие магнитного поля, возникающего в результате этого движения.

Принцип суперпозиции

Если на тело действует несколько сил, то по законам механики Ньютона результирующая сила равна их геометрической сумме. В нашем случае – телом является электрический заряд. На электрические заряды действуют силы со стороны поля. Если при наложении в пространстве полей от нескольких зарядов эти поля не влияют друг на друга, то результирующая сила со стороны всех полей на заряд должна быть равна геометрической сумме сил со стороны каждого поля. Это означает, что напряженности полей складываются геометрически, так как напряженности прямо пропорциональны силам.

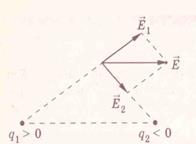Т.о. принцип суперпозиции или принцип независимого наложения полей – если в данной точке пространства различные заряды создают электрические поля, напряженность которых 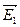, , 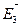и т.д., то результирующая напряженность поля в этой точке равна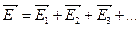

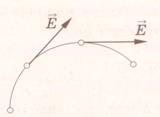
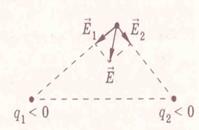На рисунке показано, как геометрически определять напряженность поля, созданного двумя зарядами.

Для определения напряженности поля надо мысленно разделить на маленькие элементы, каждый из которых можно считать точечным. Определить заряды всех этих элементов и найти напряженности полей, созданных всеми ими в заданной точке. После этого геометрически сложить напряженности от всех элементов и найти результирующую.

Поля, удовлетворяющие этому принципу, называют линейными. Т.е. у них нет взаимодействия между отдельными участками, поле не действует само на себя. Гравитационное поле – нелинейно, как и поля взаимодействия кварков.