Задание 22 ЕГЭ по физике

Механика — квантовая физика, методы научного познания

В. З. Шапиро

     В задании 22 ЕГЭ по физике проверяется, как вы применяете знание физики в практической деятельности и повседневной жизни. В задании дается изображение какого-либо школьного физического прибора, по которому надо определить показания с учетом погрешности измерения.

Что необходимо знать и уметь?

1. Вычислять цену деления измерительного прибора. Для этого надо найти два ближайших штриха, обозначенных числами, из большего вычесть меньшее и поделить на число делений.
2. Определить границы измерения для приборов, имеющих две шкалы измерения, например, вольтметра, амперметра, барометра. Соответственно, надо выбрать необходимую шкалу для определения показаний прибора.
3. Определить погрешность измерения в соответствии с ее описанием в условии. Погрешность измерения может быть равна цене деления или половине цены деления измерительного прибора. Расчет в соответствии с условием задачи.
4. В некоторых задачах погрешности измерений могут быть приведены в условии для разных шкал. При выборе определенной шкалы измерений выбирается соответствующая ей погрешность.
5. Запись ответа в бланк с учетом требований: каждая цифра и запятая в отдельной клеточке. Если погрешность указана до десятых (или сотых), то показания прибора точно также должны быть указаны до десятых (или сотых).

 

1. Чему равна сила тока в лампочке (см. рисунок), если погрешность прямого измерения силы тока амперметром на пределе измерения 3 А равна 0,15 А, а на пределе измерения 0,6 А равна 0,03 А?

Ответ: (                 ±                  ) А.

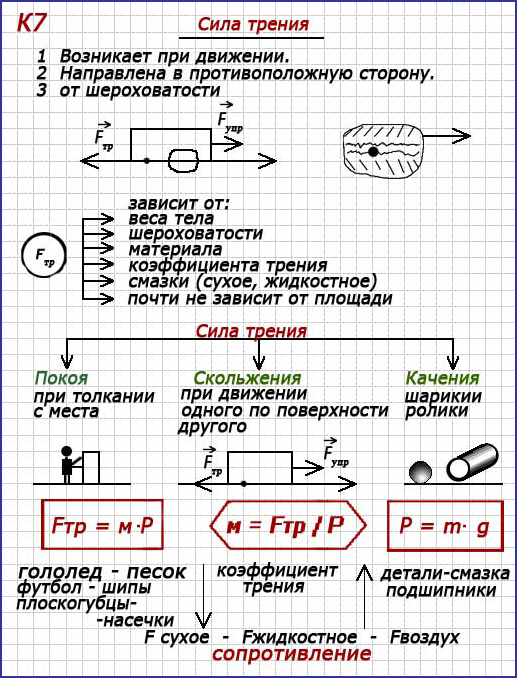Согласно рисунку, амперметр подключен к зажимам 0 и 0,6 А. Поэтому определять показания необходимо по нижней шкале. Цена деления этой шкалы равна (0,4 — 0,2):5 =  0,02 (А). Показания амперметра равны 0,28 А.      Для выбранной шкалы погрешность измерений указана в условии задачи. Она равна 0,03 А.

Ответ: (0,28 ±  0,03) А.

В бланк надо записать ответ в следующем виде:

0

,

2

8

0

,

0

3

Секрет решения. Задание является достаточно простым, но требует внимательного чтения условия. Если в задаче приводится в качестве измерительного прибора термометр со шкалой, проградуированной в градусах Цельсия, а ответ требуется дать по шкале Кельвина, то надо учесть, что погрешности по этим двум шкалам одинаковые. Добавление к погрешности +273 является грубой ошибкой.

+273 требуется только для перевода температуры из шкалы Цельсия в шкалу Кельвина.

 2. Погрешность прямого измерения силы динамометром, на котором висит груз, равна цене деления. Каков вес груза?

Ответ: (                  ±                  ) Н.

Цена деления динамометра определяется следующим расчетом:

(1,5 – 1) : 5 = 0,1 (Н).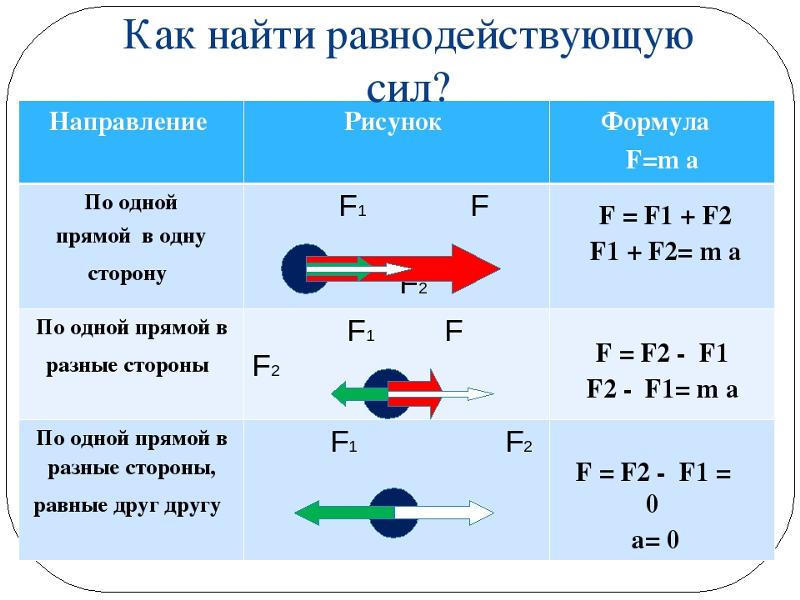

Показания динамометра равны 1,1 Н.

Погрешность измерения, согласно условию задачи, равна цене деления, т.е. 0,1 Н.

Ответ: (1,1 ± 0,1) Н.

В бланк надо записать ответ в следующем виде:

1

,

1

0

,

1

 

Секрет решения. Задание достаточно простое, но требует внимательного проведения простых расчетов. Главное – правильная запись в бланк ответов №1 показаний динамометра с учетом погрешности измерений.

3. Определите показания вольтметра (см. рисунок), если погрешность прямого измерения напряжения составляет половину цены деления вольтметра.

Ответ: ( ___________ ±    ___________) В.

Цена деления вольтметра определяется следующим расчетом:

(2 – 1) : 5 = 0,2 (Н).

Показания вольтметра равны 2 В.

Погрешность измерения, согласно условию задачи, составляет половину цены деления, т. е. 0,1 В.

Ответ: (2,0 ± 0,1) В.

2

,

0

0

,

1

Секрет решения. В этой задаче надо обратить внимание на то, что погрешность измерений равна половине цены деления. При заполнении бланка ответов №1 показания вольтметра необходимо указать с учетом десятичной записи числа (2,0).

Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Задание 22 ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена: 06.01.2023

Архимедова сила – формула закона Архимеда, как найти (физика, 7 класс)

4. 4

Средняя оценка: 4.4

Всего получено оценок: 358.

4.4

Средняя оценка: 4.4

Всего получено оценок: 358.

Наблюдения и опыты показывают, что на тела, помещенные в жидкость и газ оказывается давление. Давление жидкости и газа на одной высоте одинаково во всех направлениях. С изменением высоты происходит изменение давления. По этой причине возникает выталкивающая сила, которую называют архимедовой силой. Узнаем чему равна архимедова сила в жидкости и газе.

Чему равно давление в газах и жидкостях

Напомним определение давления. Давлением p называют физическую величину, равную отношению силы F, направленной перпендикулярно поверхности с площадью S:

$p={F\over S}$ (1)

Французский исследователь Блез Паскаль открыл закон, названный в последствии его именем, который звучит так: жидкости и газы передают производимое на них давление во все стороны одинаково.

На основании закона Паскаля и формулы (1) можно вычислить давление столба жидкости:

$p={F\over S}={m*g\over S}$ (2)

где: m — масса жидкости, g = 9,8 Н/кг — ускорение свободного падения.

2]}$$

Часто используются кратные единицы давления: килопаскаль (кПа) и мегапаскаль (МПа).

Закон Архимеда

Тяжелый предмет, который мы с огромным трудом отрываем от земли, удается довольно легко поднять, когда он находится в воде. Если взять пустую пластиковую бутылку с закрытой пробкой, погрузить ее полностью в воду и отпустить, то бутылка всплывет. Почему это происходит?

Для объяснения этих явлений достаточно взглянуть на последнюю формулу (4). Зависимость давления p в жидкости или газе от глубины h (высоты), приводит к появлению выталкивающей силы, действующей на любое тело, погруженное в жидкость или газ. Эта сила называется архимедовой силой.

Рис. 1. Портрет, изображение Архимеда

Древнегреческий математик, инженер и физик Архимед (287-212 г.г. до н.э.) не только обнаружил это явление, но смог найти ему объяснение и вывел формулу для расчета выталкивающей силы. Кроме закона Архимеда он открыл знаменитое правило рычага, первым вывел математические формулы для вычисления площадей и объемов сложных геометрических поверхностей, открыл первый планетарий, изобрел много полезных приспособлений.

Рис. 2. Действие выталкивающей силы на тело, погруженное в воду

Рисунок, на котором изображен прямоугольный параллелепипед (высотой

h и площадью основания S), помещенный в жидкость, поможет ответить на вопрос: как найти архимедову силу. Силы давления на боковые грани уравновешивают друг друга, а силы F₂ и F₁ отличаются, поскольку согласно формулы (4) давление на верхнюю и нижнюю грани будут разными из-за того, что h₂ > h₁:

Получим формулу для результирующей силы F_A , равную разности F₂ и F₁:

$F_А=F_2−F_1=p_2*S−p_1*S=ρ*g*h_2*S−ρ*g*h_1*S=$
$ρ*g*S*{(h_2− h_1)}=ρ*g*S*h$ (5)

где: $S*h=V$ — объем, а $ρ*V=m$ — масса жидкости, которую вытеснило тело. Тогда, поскольку

m*g — это вес вытесненной жидкости, то получаем окончательную формулу архимедовой силы F_A:

$F_A =m*g=ρ*V*g$ (6)

Полученная формула позволяет сформулировать закон Архимеда:

Сила, выталкивающая погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом.

Погружение, равновесие, всплытие

Теперь становится понятно почему в воде мы запросто поднимаем тяжелые камни: нам “помогает” архимедова сила, т.к. она направлена противоположно силе тяжести. По этой же причине вес тела при взвешивании в жидкости будет всегда меньше веса, измеренного в воздухе.

Из формулы (6) следует, что величина архимедовой силы зависит прямо пропорционально от плотности жидкости ρ и от объема погруженного тела V. Плотность вещества, из которого изготовлено тело, может быть любой — на величину выталкивающей силы она не влияет. В зависимости от соотношения архимедовой силы F_A и силы тяжести F_g возможно три положения тела в жидкости:

• Если FA > Fg, то тело будет выталкиваться наверх — “всплывать”;
• Если FA
• Если FA = Fg, то тело может находиться в жидкости на любой глубине в состоянии равновесия.

Закон Архимеда положен в основу ареометра — прибора для измерения плотности жидкости. Ареометр представляет собой стеклянную, герметичную колбу, утяжеленную с нижнего конца грузиком. Верхняя часть выполнена в виде длинного отростка, на котором нанесена измерительная шкала. При помещении в жидкость ареометр погружается на большую или меньшую глубину в зависимости от плотности жидкости. Чем больше плотность жидкости, тем меньше погружается ареометр. Показания на шкале указывают на плотность данной жидкости, когда ареометр занимает равновесное положение.

Рис. 3. Ареометр

Что мы узнали?

Итак, мы узнали, почему возникает архимедова сила в газах и жидкостях, и от каких величин зависит ее значение. На тело, погруженное в жидкость (или газ) действует выталкивающая сила. Сила, выталкивающая погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Для более подробного доклада об архимедовой силе можно подготовить интересные примеры с разными жидкостями, отличными от воды, например с керосином или ртутью. Тема этой статьи тесно связана с особенностями плавания и воздухоплавания тел, которые мы рассмотрим в следующих главах курса физики за 7 класс.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Ирина Кудинова

  8/10

• Кирилл Тугаринов

  10/10

• Елена Ратных

  10/10

Оценка доклада

4.4

Средняя оценка: 4.4

Всего получено оценок: 358.

---

А какая ваша оценка?

6.2: Модель Силы — Physics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

56285

• Дина Жабинская
• UC Davis

Определение силы

Сила — это еще один тип вектора, который мы подробно изучим в этом курсе. Силы дадут нам информацию о динамике объектов: они объяснят, почему одни объекты остаются неподвижными и почему другие объекты будут двигаться именно так, как они. Сила — это толчок или притяжение , описывающее взаимодействие между двумя объектами. Слово объект  используется здесь в общем смысле для обозначения любой идентифицируемой массы, которая может быть определенным объемом жидкости или отдельным электроном, а также обычными объектами, такими как стол, книга или автомобиль. Основная идея здесь заключается в том, что силы не существуют в отсутствие взаимодействующих объектов. Когда вы «толкаете» рукой, участвуют два объекта: ваша рука — это объект, который вы толкаете. Сила — это векторная величина, которая описывает как силу толчка или тяги (величину вектора силы), так и направление толчка и тяги. Как мы увидим в следующих нескольких главах, и сила, и направление силы важны для описания динамики объектов. Наше понимание того, что такое сила, как ее использовать для предсказания или объяснения движения , станет более четким и точным по мере того, как мы будем продвигаться по следующей паре глав.

Виды сил

Взаимодействие может происходить между объектами, находящимися в непосредственном физическом контакте, а также между объектами, далеко разнесенными в пространстве. Примером первого является сила, которую вы прикладываете к объекту, когда толкаете его, или сила, с которой ваша бита действует на мяч, когда вы отбиваете его в левое поле. Примером последнего является сила тяжести, которую Земля оказывает на орбитальный спутник на высоте 200 миль над поверхностью Земли. Гравитационное взаимодействие между Землей и другими объектами, которые могут касаться или не касаться Земли, называется дальний радиус . Электрическая сила между заряженными частицами — еще один пример дальнодействующей силы. Сила, возникающая в результате взаимодействия, продолжает существовать, даже когда нет прямого контакта. Это заметно отличается от примера с битой и мячом: когда мяч находится в воздухе после того, как бита ударила его, бита больше не оказывает силы на мяч. Тип сил, таких как сила удара битой по мячу, часто называют контактными силами , поскольку взаимодействия или силы нет, если бита и мяч не находятся в физическом контакте (в макроскопическом смысле).

Электрические и гравитационные силы называются дальнодействующими силами , также известными как фундаментальные силы. Они называются фундаментальными , поскольку все другие силы между макроскопическими объектами, которые будут описаны в ближайшее время, могут быть описаны в терминах фундаментальных сил (кроме гравитации) в микроскопическом масштабе. Хотя сила дальнодействующих сил уменьшается с расстоянием, взаимодействия все еще существуют и оказывают сильное влияние даже на больших расстояниях. Величина электрического и гравитационного взаимодействия между двумя частицами уменьшается как 1/r ² , поэтому эти две силы часто называют силами закона обратных квадратов . В обоих случаях, электрическом и гравитационном, сила действует по направлению вектора от одной частицы к другой. Кроме того, каждая сила зависит от фундаментального свойства материи: электрического заряда и гравитационной массы соответственно. Эти две силы являются проявлениями двух из четырех фундаментальных взаимодействий: гравитационного, электромагнитного, слабоядерного и сильноядерного. Мы рассмотрим электромагнитную силу более подробно в Физике 7С.

Мы все время непосредственно ощущаем одну из фундаментальных сил, гравитационную силу . Мы знаем эту силу как вес объекта. Вес объекта на поверхности Земли пропорционален массе объекта, умноженной на ускорение под действием силы тяжести, г , что имеет значение 9,80 м/с ² , которое мы часто округляем до 10 м/с ^{. 2} . В основном мы будем использовать символ \(F_g\) для гравитационной силы, которая на поверхности Земли равна:

\[F_g=mg\]

Вспомните из раздела Физика 7А, что происходит, когда молекулы сближаются очень близко друг к другу. Тогда электроны оказывают друг на друга очень большие силы отталкивания. Вот почему вещества сопротивляются сжатию. Когда мы толкаем объект, это электрические силы между электронами в молекулах нашей кожи и электронами на атомах на поверхности того, что мы толкаем, действительно толкают. И именно электрические силы, удерживающие молекулы вместе, позволяют нам установить натяжение в натянутой проволоке или шнуре.

Итак, на самом деле мы постоянно сталкиваемся с электрическими силами. Но поскольку они по большей части возникают из-за взаимодействия электрически нейтральных молекул друг с другом, результирующие силы являются «короткодействующими» и не описываются нашей простой формулой. Мы часто описываем эти электрические силы как контактных сил . Другими словами, силы, которые электрически нейтральные объекты действуют друг на друга, когда они находятся в непосредственной близости друг от друга, действительно являются электрическими силами, но они очень короткодействующие и не описываются законом обратных квадратов. Мы часто классифицируем эти законы на основе типа взаимодействия, происходящего на макроскопическом уровне.

Вот основные описания некоторых из этих сил:

— нормальная сила:  сила отталкивания, «толкающая» из-за физического контакта объекта с поверхностью, которая всегда действует перпендикулярно (в этом смысл слова «нормальный»). «) на эту поверхность. Мы часто используем символ \(F_N\) для этой силы.

— сила натяжения: сила притяжения, которая передается через веревку или веревку. Мы часто используем символ \(T\) или \(F_t\) для этой силы.

— трение: сила, которая действует между двумя объектами параллельно их поверхностям и действует в направлении, противоположном их движению (известное как кинетическое трение ) или в направлении, противоположном их предполагаемому движению (известное как статическое трение ). Кинетическое трение объясняет, почему игрушечная машинка, которую толкают по неровной поверхности, в конце концов останавливается. Выражение для кинетического трения, которое определяется экспериментально, имеет вид:

\[F_k= \mu_k F_N\]

, где \(\mu_k\) – коэффициент кинетического трения  , а \(F_N\) – нормальная сила. Коэффициент кинетического трения зависит от природы трущихся друг о друга материалов. Чем более скользкие материалы, тем меньше эффект трения, что приводит к меньшему коэффициенту кинетического трения. Нормальная сила также влияет на то, насколько сильно два материала трутся друг о друга. Чем сильнее вы нажимаете перпендикулярно двум поверхностям, тем труднее им будет скользить относительно друг друга. Более тяжелый объект, приводящий к большей нормальной силе, остановится быстрее при движении по поверхности, чем более легкий объект.

Статическое трение объясняет, почему автомобиль, припаркованный на наклонном холме, просто не скатывается вниз или почему тяжелый предмет не сдвигается с места, когда его толкают. Для статического трения приложенная сила должна достичь критической величины, прежде чем трение будет преодолено, и объект начнет двигаться. Выражение для статического трения:

\[F_s\leq \mu_s F_N\]

где \(mu_s\) — коэффициент статического трения и \(F_N\) — нормальная сила. Когда объект неподвижен, все силы должны быть уравновешены. Если вы слегка надавите на тяжелый предмет, и он не сдвинется с места, то сила трения покоя будет равна вашему толчку. Если теперь вы нажмете немного сильнее, но объект по-прежнему не двигается, то сила статического трения теперь больше, чем раньше, чтобы уравновесить более сильный толчок. Максимальное значение, которое может иметь трение покоя, равно \(F_s =\mu_s F_N\). Коэффициент статического трения обычно больше, чем коэффициент кинетического трения. Начать движение труднее, чем поддерживать движение.

— трение воздуха или сила сопротивления : когда объект движется через газ или жидкость, возникают силы сопротивления или силы вязкости , замедляющие движение объекта. Эти силы действуют в направлении, противоположном скорости объекта, и равны нулю, если объект неподвижен. Когда парашют падает или автомобиль движется по шоссе на высокой скорости, воздух создает силу сопротивления, которую иногда называют трением воздуха 90 034.

 

—  усилие пружины:  Роберт Гук (современник Исаака Ньютона) в 1676 году обнаружил, что сила, создаваемая многими растянутыми пружинами, пропорциональна удлинению или сжатию пружины и направлена ​​в противоположную сторону относительно удлинения или сжатия. Константа пропорциональности зависит от способа изготовления конкретной пружины (ее материала, размера, количества витков и т. д.). Мы широко использовали эту модель для пружин в Физике 7А. В форме уравнения мы выражаем силу, действующую на пружину, известную как Закон Гука , as

\[\vec F_s=-k\Delta \vec x\]

где \(k\) — жесткость пружины, а \(\Delta \vec x\) — смещение от равновесие. Мы записываем закон Гука в векторной форме , чтобы подчеркнуть взаимосвязь между направлением силы и перемещением. Независимо от того, растянута или сжата пружина, вектор \(\Delta \vec x\) направлен в сторону от равновесия, в то время как сила пружины всегда направлена ​​в противоположном направлении, к равновесию, из-за знака минус в уравнении. Обратите внимание, что «\(\Delta\)» в выражении смещения не соответствует более распространенному применению символа «до и после». Это «\(\Delta\)» подчеркивает, что измеряется расстояние от равновесия. Если положение равновесия находится на некотором расстоянии \(x_o\), то \(\Delta \vec x=\vec x-\vec x_o\), где \(\vec x\) — положение пружины после того, как она была растянуты или сжаты.

Первый закон Ньютона 

До появления Исаака Ньютона, возможно, величайшего ученого всех времен, и навсегда изменившего представление о природе, такие мыслители, как Аристотель, утверждали, что для движения нужны силы. Другими словами, древнее (доньютоновское) понимание движения заключалось в том, что для того, чтобы объект двигался, на него должна действовать сила, и что в конце концов все останавливается. Ньютон утверждал обратное, что для того, чтобы объект оставался в покое или продолжал двигаться с постоянной скоростью (с постоянной скоростью, движущейся по прямой линии), на него не может действовать никакая полная сила. Это утверждение известно как Первый закон Ньютона .

Первый закон движения Ньютона

Объекты в состоянии покоя остаются в состоянии покоя, а объекты, движущиеся по прямой линии с постоянной скоростью, продолжают двигаться таким образом, если на них не действует внешняя суммарная сила.

Давайте хорошенько подумаем о последствиях Первого закона Ньютона, представив конкретный сценарий. Когда вы стоите на полу в терминале аэропорта, а час спустя, когда вы стоите в проходе реактивного самолета, летящего со скоростью 500 миль в час без турбулентности, вы испытываете те же ощущения на своем теле. Это иллюстрирует фундаментальный аспект 1-го Закона. Если общая результирующая сила равна нулю, когда вы стоите на полу терминала аэропорта, и результирующая сила, действующая на вас, также равна нулю, когда самолет движется с постоянной скоростью относительно земли, эффект тот же: нет изменение в движении. С вашей точки зрения, вы стоите неподвижно на земле и неподвижно стоите в самолете. Но с точки зрения другого человека в аэропорту, когда вы находитесь в самолете, вы двигаетесь с постоянной скоростью 500 миль в час. Очевидно, что быть неподвижным и двигаться с постоянной скоростью — это одно и то же с точки зрения того, как действуют силы. Поскольку силы работают таким образом, мы можем превратить движение с постоянной скоростью в неподвижное, переключившись на систему отсчета, которая движется с той же скоростью относительно исходной системы отсчета.

Слово общая сила (также называемая чистая сила ) в приведенном выше утверждении имеет очень важное значение. Первый закон Ньютона не утверждает, что никакие силы не могут воздействовать на объект, чтобы он оставался в покое или двигался с постоянной скоростью, а скорее общая сила, действующая на объект, должна быть равна нулю. На книгу, лежащую на столе, действует сила тяжести. Таким образом, первый закон Ньютона подразумевает, что на книгу должна действовать другая сила, которая должна баланс сила тяжести. Эта сила представляет собой нормальную силу, при которой стол давит на книгу. Другими словами, фундаментальный аспект Первого закона Ньютона заключается в том, что если все силы, действующие на объект, как контактные, так и дальнодействующие, уравновешены, а общая сила равна нулю, то все эти силы, действующие вместе, не влияют на объект. предмет. Как будто на объект не действуют никакие силы. Воздействие всех сил, действующих на конкретный объект, может быть представлено одним вектором, называемым полная сила или результирующая сила , которая определяется как сумма всех сил, действующих на этот объект:

\[\vec F_{net}=\Sigma\vec F\]

Математически первый закон Ньютона может быть указано как:

\[\textrm{if}~~\vec F_{net}=0, \textrm{then}~~\Delta\vec v=0\label{1stLaw}\]

Количество  \ (\Sigma\vec F\) является векторной суммой, поскольку отдельные силы, действующие на систему, являются векторными величинами. Чистая сила — это не физическая сила из-за конкретного взаимодействия с другим объектом, действующим на систему, а скорее эффект всех сил действующих на нашу систему. Из-за отсутствия связи с конкретным взаимодействием чистая сила является довольно абстрактным понятием, но оказывается очень полезным.

Первый закон Ньютона описывает ситуации, когда все силы, действующие на объект, уравновешены. Есть два взаимодополняющих способа применения 1-го закона. Если мы знаем, что без изменений движутся, то мы знаем, что силы, действующие на объект, должны быть уравновешены. Если мы знаем все силы, кроме одной, мы можем определить величину и направление неизвестной силы. Второй способ использования 1 закона — сложить известные силы и посмотреть, уравновешиваются ли они. Если да, то не может быть изменения в движении объекта.

Сумма всех сил \(\Sigma\vec F=0\) – это векторная величина, которую можно переписать в терминах своих компонентов, предполагая, что силы действуют только в двух измерениях, как:

\[\Sigma \vec F=(\Sigma F_x,\Sigma F_y)=(0,0)\]

Из приведенного выше уравнения следует, что для того, чтобы результирующая сила равнялась нулю, компоненты суммы всех сил в направлении x должны быть нуля, а также в направлении y. Другими словами, при уравновешивании сил вы действительно пытаетесь решить два независимых уравнения (если вы работаете в 2D), в направлении x и еще одно в направлении y. Технически приведенное выше уравнение может быть записано как набор из двух независимых уравнений:

\[\Sigma F_x=0\]

\[\Sigma F_y=0\]

Давайте посмотрим на пример, показанный ниже на рисунке 6.2.1, где мы хотели бы проанализировать коробку, которую толкают и удерживается неподвижно  прислоненным к стене человеком в соответствии с Первым законом Ньютона. Все силы, действующие на коробку, обозначены.

Обозначение силы

Чтобы подчеркнуть, что два объекта взаимодействуют, когда присутствует сила, при обозначении сил часто используется обозначение «на-по». Таким образом, если сила действует на объект А и действует на объект В, мы записываем это как:  \(F_\textrm{на объекте A по объекту B}\). Рисунок 6.2.1: Сбалансированные силы система находится в прямом физическом контакте с любыми силами дальнего действия. Если система находится в гравитационном поле (например, на Земле) и массой системы нельзя пренебречь, то мы всегда должны учитывать дальнодействующую гравитационную силу, действующую прямо вниз к поверхности Земли. На рисунке 6.2.1 гравитационная сила обозначена как \(F_{\textrm{на ящике от Земли}}\), чтобы подчеркнуть тот факт, что она представляет собой взаимодействие между двумя объектами, ящиком и Землей. «На коробке» связано с тем, что наша система является коробкой, а «на Земле» — это объект, который воздействует на нашу систему. Когда вы освоитесь в работе с силами, вы сможете сократить гравитационные силы, действующие на систему, просто \(F_g\). Поскольку коробка неподвижна (не скользит вниз), первый закон Ньютона говорит нам, что должна быть равная и противоположная сила, направленная вверх. Коробка находится в физическом контакте со стеной, что и обеспечивает силу, удерживающую коробку. Это горизонтальная сила между двумя поверхностями (коробкой и стеной), которую мы определили как силу трения. Обозначение \(F_{\textrm{на коробке у стены}}\) снова подчеркивает, что это контактная сила из-за взаимодействия между коробкой и стеной, но ее можно сократить как силу трения \(F_f \). Используя это обозначение, мы уравновешиваем две силы, суммируя их до нуля. Если мы определяем вверх как положительное направление, то результирующая сила в направлении y равна:

\[F_f-F_g=0,\]

в результате получается \(F_f=F_g\). Сила трения, создаваемая стеной на ящике при контакте, должна быть направлена ​​вверх и иметь ту же величину, что и сила гравитации на ящике со стороны Земли.

В направлении x человек толкает коробку рукой, поэтому на коробку действует сила, направленная вправо. Чтобы уравновесить эту силу, должна быть сила, направленная в противоположном направлении. Поскольку коробка касается стены, эта сила находится у стены и перпендикулярна поверхности, которую мы определили как нормальную силу. Обозначение этой нормальной силы может быть сокращено как \(F_N\), но снова обозначение \(F_{\textrm{на ящике у стены}}\) должно подчеркнуть, что эта сила возникает из-за взаимодействия нашей системы с стена. Определив положительное направление x как направленное вправо и уравновешивая силы в направлении x, мы получим:

\[F_{\textrm{на коробке рукой}}-F_N=0,\]

в результате получается \(F_{\textrm{на коробке рукой}}=F_N\), поэтому нормальная сила должна быть равным и противоположным силе толчка со стороны человека.

Как видно из этого примера, как перпендикулярная (нормальная сила), так и параллельная (трение) силы возникают в результате одного и того же взаимодействия коробки со стенкой. Таким образом, эти, казалось бы, две отдельные силы являются просто параллельными и перпендикулярными дополнениями одной силы, силы, действующей со стороны стены на коробку. Часто использование слов «нормальный» и «трение» носит абстрактный характер, поскольку прямо не говорит вам о конкретном взаимодействии. Вы всегда должны начинать свой анализ силы с рассмотрения физических объектов, которые взаимодействуют с вашей системой либо путем прямого контакта (например, со стеной), либо на расстоянии (например, с Землей).

Пример \(\PageIndex{1}\)

Объект движется со скоростью 5 м/с в положительном направлении оси y, и на него действуют три силы. Две силы показаны на рисунке ниже. Величина \(\vec F_1\) равна 16 Н, а величина \(\vec F_2\) равна 10 Н. Найдите величину и направление \(\vec F_3\).

Решение

Поскольку объект движется с постоянной скоростью, сумма трех сил должна равняться нулю: 9{\circ}\]

в юго-восточном направлении.

Второй закон Ньютона 

Первый закон Ньютона – это частный случай второго закона Ньютона , который описывает, что происходит, когда результирующая сила, действующая на систему, отлична от нуля. В нем говорится, что если чистая сила, действующая на объект, отлична от нуля, то он будет испытывать ускорение в направлении чистой силы.

Второй закон движения Ньютона

Суммарная сила, действующая на объект, равна произведению его массы на ускорение.

Математически второй закон Ньютона записывается так:

\[\vec F_{net}=m\vec a\label{2ndLaw}\]

изменения скорости или изменения движения. Некоторыми примерами влияния этой ненулевой результирующей силы могут быть неподвижный объект, начинающий двигаться, движущийся объект, ускоряющийся, замедляющийся или останавливающийся, движущийся объект, изменяющий свое направление, даже если его скорость остается постоянной. . Если на систему не действует результирующая сила, уравнение \ref{2ndLaw} утверждает, что ускорение равно нулю, что прямо подразумевает, что \(\Delta\vec v=0\), и мы восстанавливаем Первый закон Ньютона, как указано в уравнении \ref {1-й закон}.

Хотя уравнение \ref{2ndLaw} довольно просто с математической точки зрения, его физический смысл часто неверно истолковывается. Уравнение часто читается как: «объект, который ускоряется, несет силу, равную массе объекта, умноженной на его ускорение, и затем будет оказывать эту силу, если он взаимодействует с другим объектом». Такой способ интерпретации 2-го закона Ньютона совершенно неверен. Чтобы помочь решить эту интерпретацию, более физически можно подумать об уравнении \ref{2ndLaw} в обратном порядке: «объект, на который действует чистая внешняя сила, будет испытывать ускорение, равное этой чистой силе, деленной на его массу». Другими словами, распространенное неверное толкование связано с тем, что причина и следствие меняются местами: дело не в том, что ускоряющийся объект создает чистую силу, а в том, что результирующие силы приводят к ускорению. Таким образом, второй закон Ньютона лучше переписать так: 

\[\textrm{if}~~\vec F_{net}\neq 0, \textrm{then}~~\vec a=\frac{\vec F_{net}}{m}\label{2ndLaw- exp}\]

Запись 2-го закона, как указано выше, также делает более очевидным тот факт, что 1-й закон, указанный в уравнении \ref{1stLaw}, является частным случаем 2-го закона, когда результирующая сила равна нулю. . Мы более подробно рассмотрим применение 2-го закона Ньютона в последующих главах.

Третий закон Ньютона 

По мере того, как мы начинаем понимать силы более подробно, важно напомнить себе, что отправной точкой является очень важный аспект, что силы действуют парами, что является прямым следствием того факта, что силы описывают взаимодействия между двумя объектами. Чтобы иметь взаимодействие, мы должны иметь два взаимодействующих объекта . Предположим, что объект A взаимодействует с объектом B . Сосредоточившись на объекте B , мы бы сказали, что объект A воздействует на объект B . В качестве альтернативы, фокусируясь на объекте A , мы бы сказали, что объект B воздействует на объект A . Эти две силы, связанные с одним и тем же взаимодействием между одними и теми же двумя объектами, должны быть связаны друг с другом. Но как они связаны? Оказывается, эти силы равны и противоположны. Это известно как Третий закон Ньютона движения. Математически две силы между двумя взаимодействующими объектами, объект A и объект B , указывают в противоположных направлениях, и величина силы, которую объект A оказывает на объект B , имеет ту же величину, что и сила, которая объект B воздействует на объект A .

\[\vec F_{\textrm{on B by A}} = -\vec F_{\textrm{on A by B}}\label{3rdLaw}\]

На словах это отношение можно выразить как «Если объект А действует на объект В с силой, то объект В действует на объект А с силой, равной по величине и противоположной по направлению».

Эффект от взаимодействия с каждым из объектов, однако, не обязательно должен быть одинаковым, и обычно он не одинаков. эффект взаимодействия зависит от других свойств конкретного объекта, таких как его масса и его движение до взаимодействия. Например, когда жук сталкивается с ветровым стеклом движущегося автомобиля, третий закон Ньютона говорит нам, что автомобиль и жук испытывают силу одинаковой величины в противоположном направлении, но влияние на движение двух объектов, очевидно, сильно различается. . Это важное различие: взаимодействие всегда одинаково по отношению к двум объектам, но эффект, который взаимодействие оказывает на каждый из двух объектов, не обязательно должен быть одинаковым и обычно таковым не является. Очень важно помнить об этом различии, думая о силах. Второй закон Ньютона — это то, что дает нам ответ на вопрос, почему эффект различен, хотя силы одинаковы. Автомобиль, который имеет гораздо большую массу по сравнению с жуком, будет испытывать гораздо меньшее ускорение при той же величине силы. Таким образом, изменение движения автомобиля будет незначительным, а жук будет испытывать гораздо большее ускорение из-за своей мизерной массы.

На рисунке 6.2.2 ниже показан пример пары третьего закона , которая описывает две силы, участвующие в одном взаимодействии. В этом примере человек прикладывает силу к стене, нажимая на нее рукой, помеченной как \(F_{\textrm{на стене рукой}}\) и нарисованной стрелкой, указывающей вправо, к стене. . Третий закон Ньютона говорит нам, что стена должна воздействовать на руку с той же силой, что и толчок руки в противоположном направлении. Эта сила обозначена на рисунке как \(F_{\textrm{на руке у стены}}\) и показана стрелкой той же длины, что и \(F_{\textrm{на стене рукой}}\), но в обратном направлении, к руке.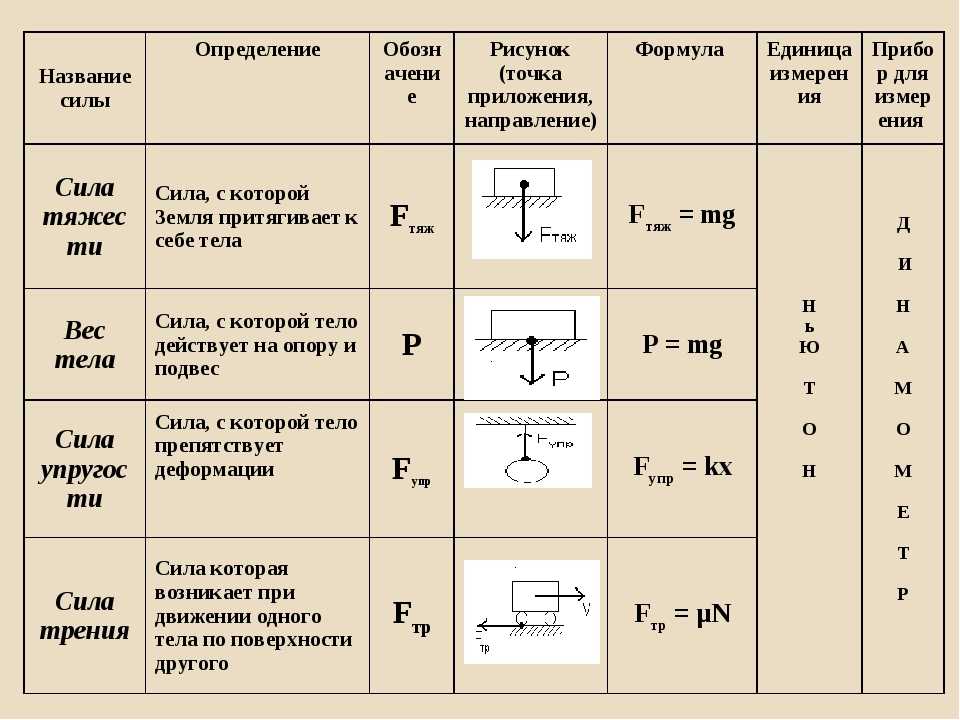

Рисунок 6.2.2: Пара из третьего закона

Пара из третьего закона всегда может быть распознана, если посмотреть на нотацию «on by», когда объекты в этом обозначении перевернуты, распознается пара из 3-го закона. Это еще одна причина придерживаться обозначения «включено» при анализе сил, поскольку это четкий способ отследить, какой объект испытывает силу, а какой объект ее оказывает.

Вот еще одно распространенное неверное толкование, которое часто возникает, когда мы думаем о Третьем законе Ньютона на этот раз: «поскольку для каждой силы существует равная и противоположная сила, как может что-либо двигаться, если все силы всегда уравновешиваются?». Важно различать силы, воздействующие на другие объекты со стороны конкретного объекта, и силы, воздействующие на исходный объект со стороны этих других объектов. Действуют только силы на объект влияет на этот объект. Силы, которые сам объект воздействует на другие объекты, не действуют на него самого. Поэтому при применении 1-го и 2-го законов Ньютона мы учитываем только силы, действующие на объект, движение которого мы анализируем, и игнорируем все силы, которые объект оказывает на другие объекты. Иногда легко спутать 1-й и 3-й законы, особенно когда на объект действуют две силы. Пары сил, которые уравновешивают друг друга в Первом законе, действуют на один и тот же объект, поэтому они не могут быть парами сил Третьего закона, даже если они равны и направлены в противоположные стороны.

Стена на Рисунке 6.2.2 не движется не потому, что две силы, показанные на рисунке, которые описывают 3-й закон, уравновешиваются, а потому, что стена прикреплена к полу, а пол оказывает на стену силу (статическая трение) в направлении, противоположном давлению на стену. Эти две силы (на стену рукой и на стену полом) уравновешивают и препятствуют движению стены в соответствии с Первым законом Ньютона.

---

Эта страница под названием 6.2: Модель Force распространяется под лицензией CC BY 4. 0, ее автор, ремикс и/или куратор — Дина Жабинская.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Дина Жабинская

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   На этой странице нет тегов.

Как рассчитать силу на основе давления

Автор: Стивен Хольцнер и

Обновлено: 07.10.2021

Из книги: Физика I Для чайников

Физика I Для чайников

Исследуйте книгу Купить на Amazon

Давление и сила взаимосвязаны, поэтому вы можете рассчитать одно, если знаете другое, используя уравнение физики P = F/A . Поскольку давление представляет собой силу, деленную на площадь, его единицами измерения метр-килограмм-секунда (МКС) являются ньютоны на квадратный метр, или Н/м ² . В системе фут-фунт-секунда (FPS) единицами измерения являются фунты на квадратный дюйм или фунты на квадратный дюйм.

Блок ньютона на квадратный метр настолько распространены в физике, что имеют специальное название: паскаля, , что равно 1 ньютону на квадратный метр. Паскаль обозначается аббревиатурой Па.

. Вам не обязательно находиться под водой, чтобы испытать давление жидкости. Воздух тоже оказывает давление из-за веса воздуха над вами. Вот какое давление оказывает на вас воздух на уровне моря:

Атмосферное давление на уровне моря — это стандартное давление, которое люди называют 1 атмосферы (сокращенно атм):

Если перевести атмосферу в фунты на квадратный дюйм, получится около 14,7 фунтов на квадратный дюйм. Это означает, что 14,7 фунтов силы давят на каждый квадратный дюйм вашего тела на уровне моря.

Ваше тело отталкивается с давлением 14,7 фунтов на квадратный дюйм, поэтому вы вообще не чувствуете никакого давления на себя. Но если бы вас внезапно перенесло в открытый космос, внутреннее давление воздуха, давящего на вас, исчезло бы, и все, что осталось бы, — это 14,7 фунтов на квадратный дюйм, которые ваше тело оказывает наружу. Вы не взорветесь, но ваши легкие могут взорваться, если вы попытаетесь задержать дыхание. Изменение давления также может привести к тому, что азот в вашей крови начнет образовывать пузырьки и вызывать изгибы тела!

Вот пример задачи давления с использованием давления воды. Скажем, вы находитесь в бассейне своего соседа и ждете у дна, пока ваши соседи не перестанут пытаться прогнать вас и не вернутся в дом. Вы находитесь рядом с глубоким концом бассейна и с помощью удобного манометра, который всегда носите с собой, измеряете давление на тыльную сторону ладони как

С какой силой вода действует на тыльную сторону ладони? Тыльная сторона ладони имеет площадь примерно

Вы полагаете, что если P = F/A, , тогда верно следующее:

F = PA

Подставив числа и решив, вы получите ответ:

Упс. Тысяча ньютонов! Вы достаете свой подводный калькулятор и обнаруживаете, что это около 230 фунтов. Силы быстро складываются, когда вы находитесь под водой, потому что вода — тяжелая жидкость. Сила, которую вы чувствуете, — это вес воды над вами.