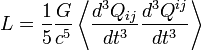| Адроны | msimagelist>|
| Альфа-распад | msimagelist>|
| Альфа-частица | msimagelist>|
| Аннигиляция | msimagelist>|
| Антивещество | msimagelist>|
| Антинейтрон | msimagelist>|
| Антипротон | msimagelist>|
| Античастицы | msimagelist>|
| Атом | msimagelist>|
| Атомная единица массы | msimagelist>|
| Атомная электростанция | msimagelist>|
| Барионное число | msimagelist>|
| Барионы | msimagelist>|
| Бета-распад | msimagelist>|
| Бетатрон | msimagelist>|
| Бета-частицы | msimagelist>|
| Бозе – Эйнштейна статистика | msimagelist>|
| Бозоны | msimagelist>|
| Большой адронный коллайдер | msimagelist>|
| Боттом. Боттомоний | msimagelist>|
| Брейта-Вигнера формула | msimagelist>|
| Быстрота | msimagelist>|
| Векторная доминантность | msimagelist>|
| Великое объединение | msimagelist>|
| Взаимодействие частиц | msimagelist>|
| Вильсона камера | msimagelist>|
| Виртуальные частицы | msimagelist>|
| Водорода атом | msimagelist>|
| Возбуждённые состояния ядер | msimagelist>|
| Волновая функция | msimagelist>|
| Волновое уравнение | msimagelist>|
| Волны де Бройля | msimagelist>|
| Встречные пучки | msimagelist>|
| Гамильтониан | msimagelist>|
| Гамма-излучение | msimagelist>|
| Гамма-квант | msimagelist>|
| Гамма-спектрометр | msimagelist>|
| Гамма-спектроскопия | msimagelist>|
| Гаусса распределение | msimagelist>|
| Гейгера счётчик | msimagelist>|
| Гигантский дипольный резонанс | |
| Гиперядра | msimagelist>|
| Глюоны | msimagelist>|
| Годоскоп | msimagelist>|
| Гравитационное взаимодействие | msimagelist>|
| Дейтрон | msimagelist>|
| Детекторы частиц | msimagelist>|
| Дирака уравнение | msimagelist>|
| Дифракция частиц | msimagelist>|
| Доза излучения | msimagelist>|
| Дозиметр | msimagelist>|
| Доплера эффект | msimagelist>|
| Единая теория поля | msimagelist>|
| Зарядовое сопряжение | msimagelist>|
| Зеркальные ядра | msimagelist>|
| Избыток массы (дефект массы) | msimagelist>|
| Изобары | msimagelist>|
| Изомерия ядерная | msimagelist>|
| Изоспин | msimagelist>|
| Изоспиновый мультиплет | msimagelist>|
| Изотопов разделение | msimagelist>|
| Изотопы | msimagelist>|
| Ионизирующее излучение | msimagelist>|
| Квантовая механика | msimagelist>|
| Квантовая теория поля | msimagelist>|
| Квантовые операторы | msimagelist>|
| Квантовые числа | msimagelist>|
| Квантовый переход | msimagelist>|
| Квант света | msimagelist>|
| Кварк-глюонная плазма | msimagelist>|
| Кварки | msimagelist>|
| Коллайдер | msimagelist>|
| Комбинированная инверсия | msimagelist>|
| Комптона эффект | msimagelist>|
| Комптоновская длина волны | msimagelist>|
| Конверсия внутренняя | msimagelist>|
| Константы связи | msimagelist>|
| Конфайнмент | msimagelist>|
| Корпускулярно волновой дуализм | msimagelist>|
| Космические лучи | msimagelist>|
| Критическая масса | msimagelist>|
| Лептоны | msimagelist>|
| Линейные ускорители | msimagelist>|
| Лоренца преобразования | msimagelist>|
| Лоренца сила | msimagelist>|
| Магические ядра | msimagelist>|
| Магнитный дипольный момент ядра | msimagelist>|
| Магнитный спектрометр | msimagelist>|
| Максвелла уравнения | msimagelist>|
| Масса частицы | msimagelist>|
| Масс-спектрометр | msimagelist>|
| Массовое число | msimagelist>|
| Масштабная инвариантность | msimagelist>|
| Мезоны | msimagelist>|
| Мессбауэра эффект | msimagelist>|
| Меченые атомы | msimagelist>|
| Микротрон | msimagelist>|
| Нейтрино | msimagelist>|
| Нейтрон | msimagelist>|
| Нейтронная звезда | msimagelist>|
| Нейтронная физика | msimagelist>|
| Неопределённостей соотношения | msimagelist>|
| Нормы радиационной безопасности | msimagelist>|
| Нуклеосинтез | msimagelist>|
| Нуклид | msimagelist>|
| Нуклон | msimagelist>|
| Обращение времени | msimagelist>|
| Орбитальный момент | msimagelist>|
| Осциллятор | msimagelist>|
| Отбора правила | msimagelist>|
| Пар образование | msimagelist>|
| Период полураспада | msimagelist>|
| Планка постоянная | msimagelist>|
| Планка формула | msimagelist>|
| Позитрон | msimagelist>|
| Поляризация | msimagelist>|
| Поляризация вакуума | msimagelist>|
| Потенциальная яма | msimagelist>|
| Потенциальный барьер | msimagelist>|
| Принцип Паули | msimagelist>|
| Принцип суперпозиции | msimagelist>|
| Промежуточные W-, Z-бозоны | msimagelist>|
| Пропагатор | msimagelist>|
| Пропорциональный счётчик | msimagelist>|
| Пространственная инверсия | msimagelist>|
| Пространственная четность | msimagelist>|
| Протон | msimagelist>|
| Пуассона распределение | msimagelist>|
| Пузырьковая камера | msimagelist>|
| Радиационный фон | msimagelist>|
| Радиоактивность | msimagelist>|
| Радиоактивные семейства | msimagelist>|
| Радиометрия | msimagelist>|
| Расходимости | msimagelist>|
| Резерфорда опыт | msimagelist>|
| Резонансы (резонансные частицы) | msimagelist>|
| Реликтовое микроволновое излучение | msimagelist>|
| Светимость ускорителя | msimagelist>|
| Сечение эффективное | msimagelist>|
| Сильное взаимодействие | msimagelist>|
| Синтеза реакции | msimagelist>|
| Синхротрон | msimagelist>|
| Синхрофазотрон | msimagelist>|
| Синхроциклотрон | msimagelist>|
| Система единиц измерений | msimagelist>|
| Слабое взаимодействие | msimagelist>|
| Солнечные нейтрино | msimagelist>|
| Сохранения законы | msimagelist>|
| Спаривания эффект | msimagelist>|
| Спин | msimagelist>|
| Спин-орбитальное взаимодействие | msimagelist>|
| Спиральность | msimagelist>|
| Стандартная модель | msimagelist>|
| Статистика | msimagelist>|
| Странные частицы | msimagelist>|
| Струи адронные | msimagelist>|
| Субатомные частицы | msimagelist>|
| Суперсимметрия | msimagelist>|
| Сферическая система координат | msimagelist>|
| Тёмная материя | msimagelist>|
| Термоядерные реакции | msimagelist>|
| Термоядерный реактор | msimagelist>|
| Тормозное излучение | msimagelist>|
| Трансурановые элементы | msimagelist>|
| Трек | msimagelist>|
| Туннельный эффект | msimagelist>|
| Ускорители заряженных частиц | msimagelist>|
| Фазотрон | msimagelist>|
| Фейнмана диаграммы | msimagelist>|
| Фермионы | msimagelist>|
| Формфактор | msimagelist>|
| Фотон | msimagelist>|
| Фотоэффект | msimagelist>|
| Фундаментальная длина | msimagelist>|
| Хиггса бозон | msimagelist>|
| Цвет | msimagelist>|
| Цепные ядерные реакции | msimagelist>|
| Цикл CNO | msimagelist>|
| Циклические ускорители | msimagelist>|
| Циклотрон | msimagelist>|
| Чарм. Чармоний | msimagelist>|
| Черенковский счётчик | msimagelist>|
| Черенковсое излучение | msimagelist>|
| Черные дыры | msimagelist>|
| Шредингера уравнение | msimagelist>|
| Электрический квадрупольный момент ядра | msimagelist>|
| Электромагнитное взаимодействие | msimagelist>|
| Электрон | msimagelist>|
| Электрослабое взаимодействие | msimagelist>|
| Элементарные частицы | msimagelist>|
| Ядерная физика | msimagelist>|
| Ядерная энергия | msimagelist>|
| Ядерные модели | msimagelist>|
| Ядерные реакции | msimagelist>|
| Ядерный взрыв | msimagelist>|
| Ядерный реактор | msimagelist>|
| Ядра энергия связи | msimagelist>|
| Ядро атомное | msimagelist>|
| Ядерный магнитный резонанс (ЯМР) | msimagelist>
2.6.2. Силы гравитационного взаимодействия
Гравитационное взаимодействие проявляется в притяжении друг к другу тел. Объясняется это взаимодействие наличием гравитационного поля вокруг каждого тела.
Модуль силы гравитационного взаимодействия 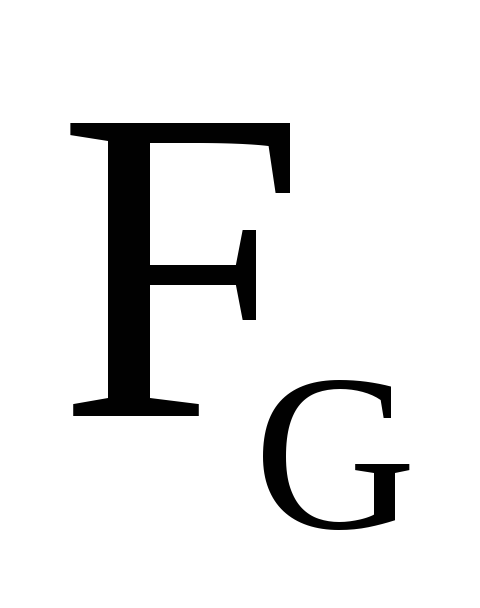 между двумя материальными точками
массойm1иm2расположенными на расстоянииrдруг от друга
между двумя материальными точками
массойm1иm2расположенными на расстоянииrдруг от друга
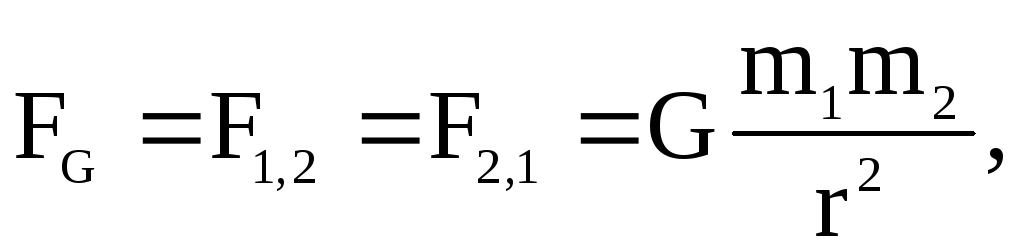 (2.49)
(2.49)
где
F1,2,F2,1–
силы взаимодействия направленные вдоль
прямой соединяющей материальные точки,G= 6,67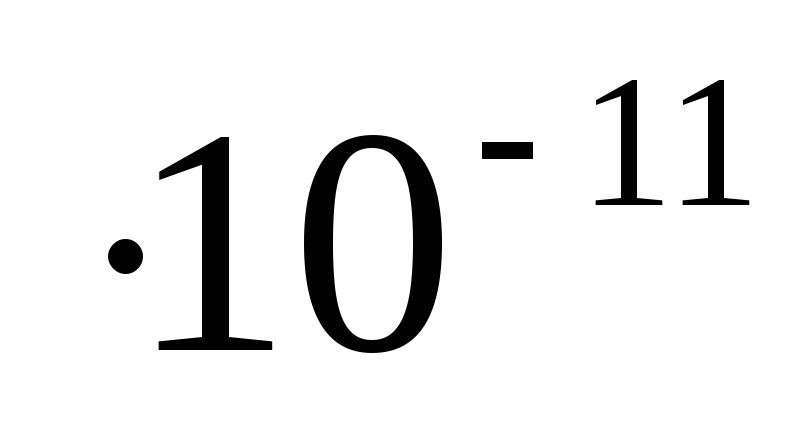
 – гравитационная постоянная.
– гравитационная постоянная.
Соотношение (2.3) носит название закона всемирного тяготенияоткрытого Ньютоном.
Гравитационное взаимодействие справедливо для материальных точек и тел со сферически-симметричным распределением масс, расстояние между которыми отсчитывается от их центров.
Если принять одно из взаимодействующих тел Землю, а второе – тело с массой m, находящееся вблизи или на её поверхности, то между ними действует сила притяжения
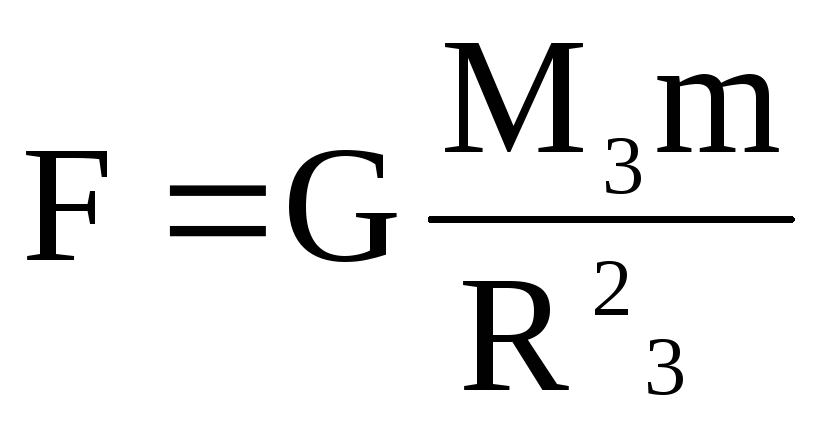 ,
(2.50)
,
(2.50)
где M3,R3– масса и радиус Земли.
Соотношение 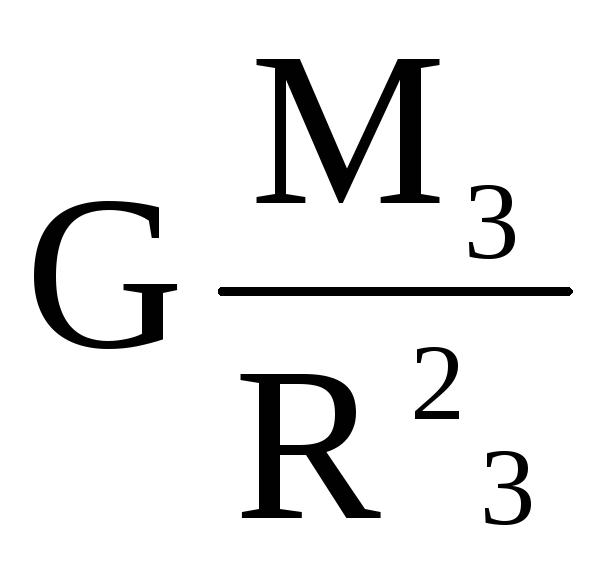 — постоянная величина равная 9,8 м/с2,
обозначаетсяg, имеет
размерность ускорения и называетсяускорением свободного падения.
— постоянная величина равная 9,8 м/с2,
обозначаетсяg, имеет
размерность ускорения и называетсяускорением свободного падения.
Произведение
массы тела mи ускорения
свободного падения ,
называетсясилой тяжести
,
называетсясилой тяжести
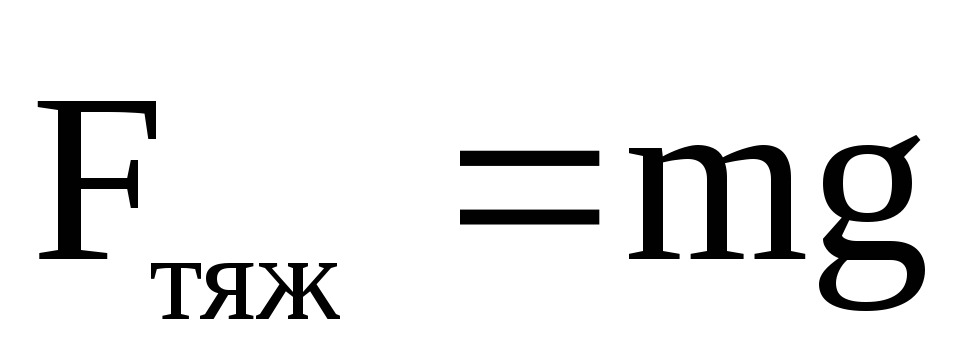 .
(2.51)
.
(2.51)
В отличие от силы гравитационного
взаимодействия  модуль силы тяжести
модуль силы тяжести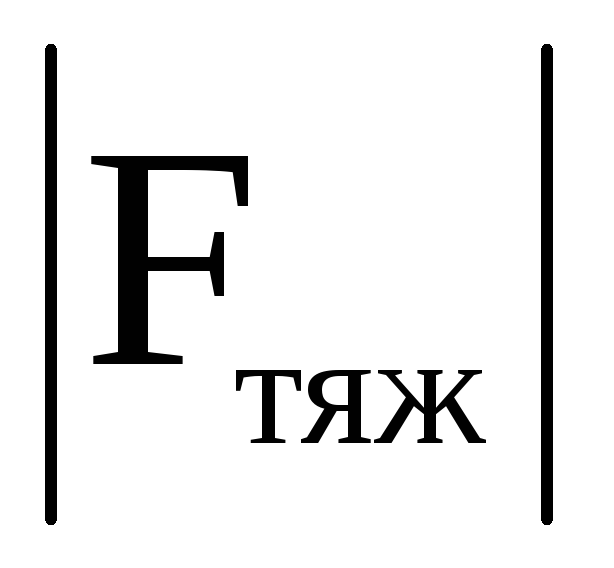 зависит от географической широты места
расположения тела на Земле. На полюсах
зависит от географической широты места
расположения тела на Земле. На полюсах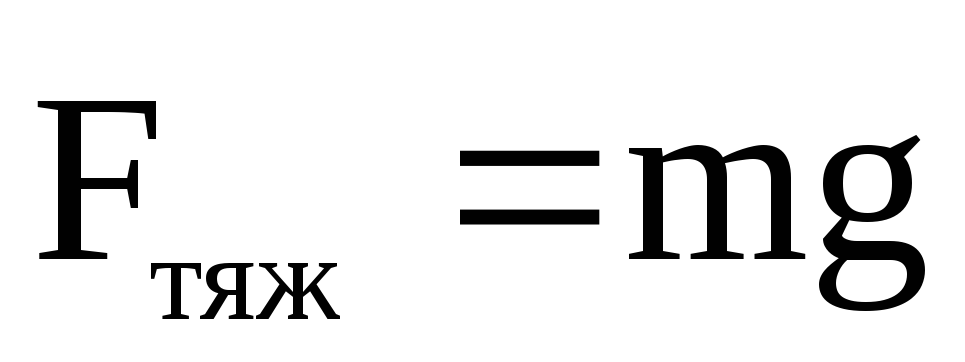 ,
а на экваторе уменьшается на 0,36%. Это
различие обусловлено тем, что Земля
вращается вокруг своей оси.
,
а на экваторе уменьшается на 0,36%. Это
различие обусловлено тем, что Земля
вращается вокруг своей оси.
С удалением тела относительно поверхности
Земли на высоту 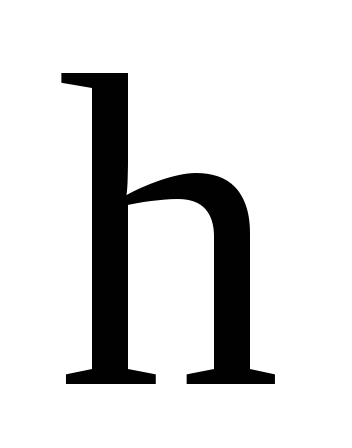 уменьшается сила тяжести
уменьшается сила тяжести
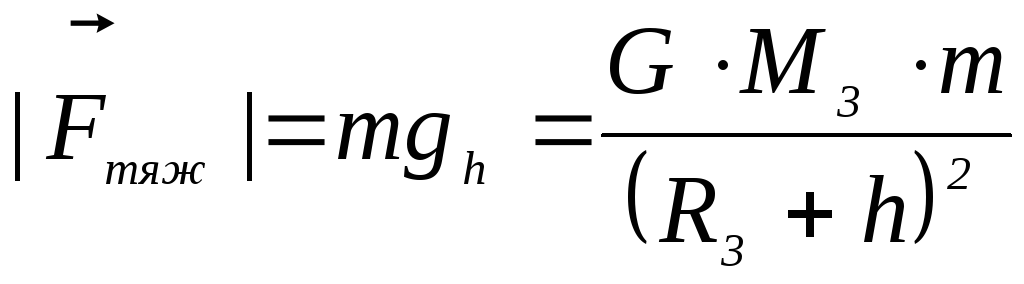 ,
(2.52)
,
(2.52)
где 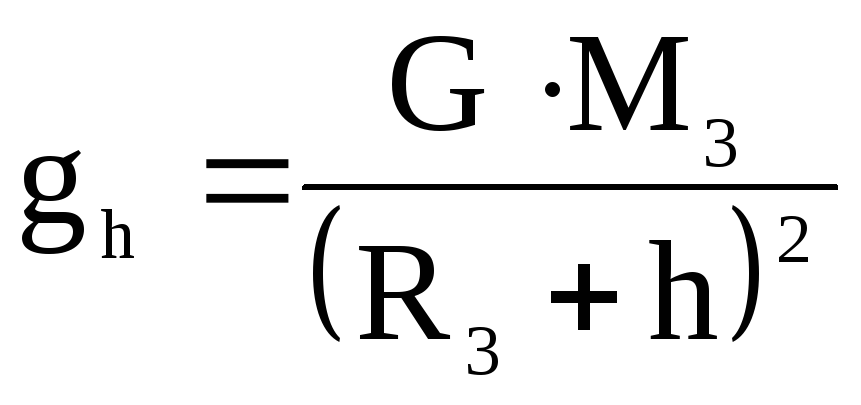 – ускорение свободного падения на
высотеhот Земли.
– ускорение свободного падения на
высотеhот Земли.
Масса в формулах (2.3-2.6) является мерой гравитационного взаимодействия.
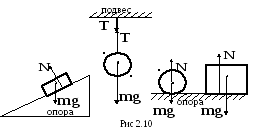
Если подвесить тело или положить его на неподвижную опору, оно будет покоиться относительно Земли, т.к. сила тяжести уравновешивается силой реакции, действующей на тело со стороны опоры или подвеса.
Сила реакции– сила, с которой действуют на данное тело другие тела, ограничивающие его движение.
Сила нормальной реакции опоры приложена к телу и направлена
перпендикулярно плоскости опоры.
приложена к телу и направлена
перпендикулярно плоскости опоры.
Сила реакции нити(подвеса) направлена вдоль нити (подвеса)
направлена вдоль нити (подвеса)
(рис. 2.10).
Вес тела  – сила, с которой тело давит на опору
или растягивает нить подвеса и приложена
к опоре или подвесу.
– сила, с которой тело давит на опору
или растягивает нить подвеса и приложена
к опоре или подвесу.
Вес численно равен силе тяжести если тело находится на горизонтальной поверхности опоры в состоянии покоя или равномерного прямолинейного движения. В других случаях вес тела и сила тяжести не равны по модулю.
2.6.3.Силы трения
Силы трения  возникают в результате взаимодействия
движущихся и покоящихся тел, соприкасающихся
друг с другом.
возникают в результате взаимодействия
движущихся и покоящихся тел, соприкасающихся
друг с другом.
Различают внешнее (сухое) и внутреннее (вязкое) трение.
Внешнее сухое трение делится на:
Перечисленным видам внешнего трения
соответствуют силы трения, покоя,
скольжения, качения.
С

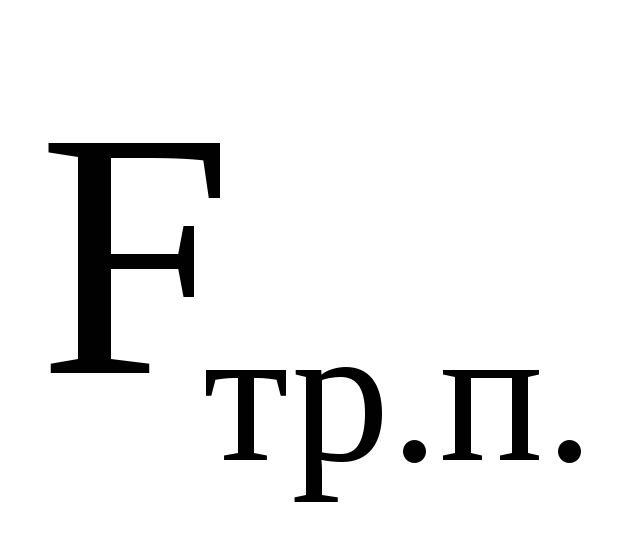 действует между поверхностями
взаимодействующих тел, когда
величина внешних сил недостаточна,
чтобы вызвать их относительное
перемещение.
действует между поверхностями
взаимодействующих тел, когда
величина внешних сил недостаточна,
чтобы вызвать их относительное
перемещение. Если к телу, находящемуся в соприкосновении
с другим телом, приложить возрастающую
внешнюю силу  ,
параллельную плоскости соприкосновения
(рис. 2.2.а), то при изменении
,
параллельную плоскости соприкосновения
(рис. 2.2.а), то при изменении от нуля до некоторого значения
от нуля до некоторого значения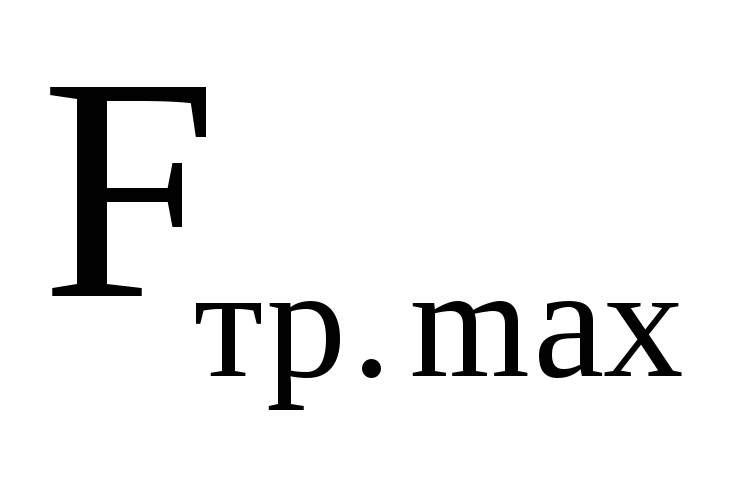 движение тела не возникает. Тело начинает
движение приF
движение тела не возникает. Тело начинает
движение приF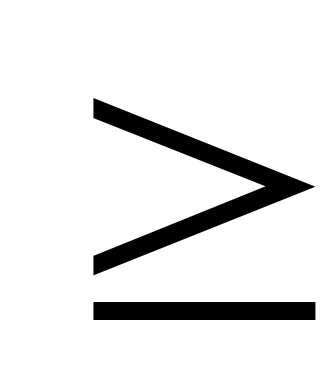 Fтр.max.
Fтр.max.
Максимальная сила трения покоя
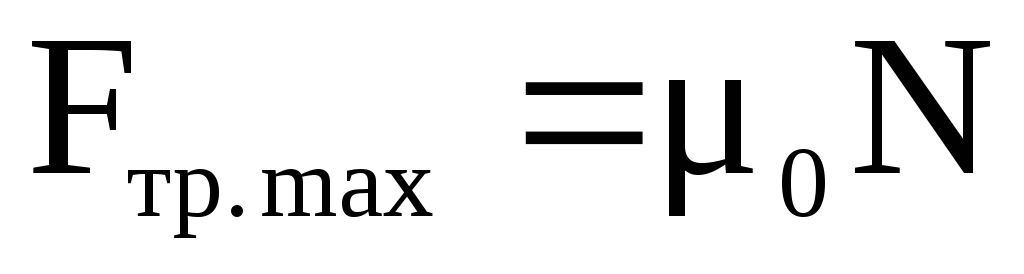 ,
(2.53)
,
(2.53)
где 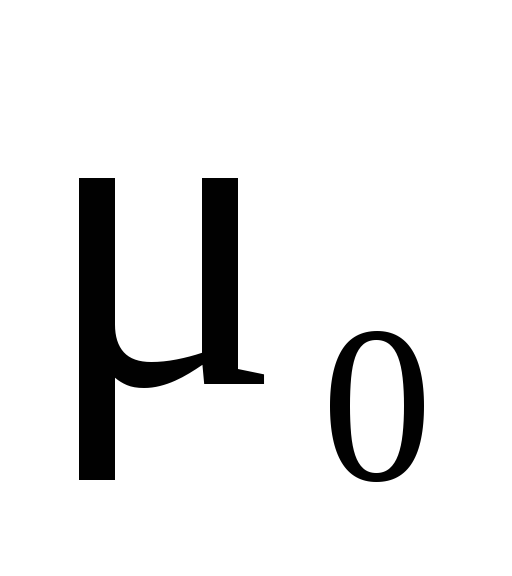 –
коэффициент трения покоя,N– модуль силы нормальной реакции опоры.
–
коэффициент трения покоя,N– модуль силы нормальной реакции опоры.
Коэффициент трения покоя 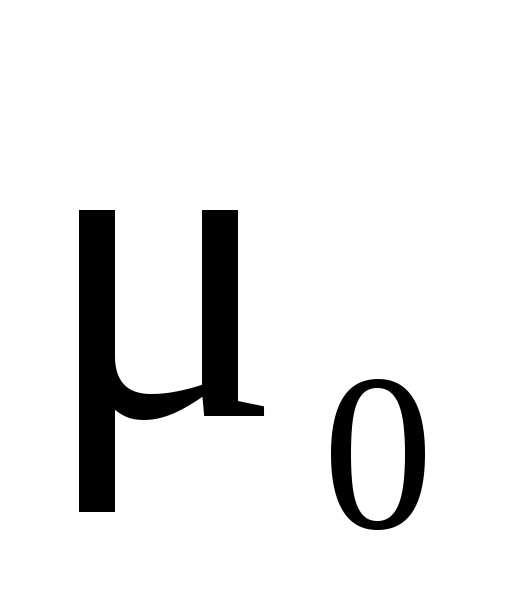 можно определить экспериментально,
нахождением тангенса угла наклона к
горизонту поверхности, с которой начинает
скатываться тело под действием его силы
тяжести.
можно определить экспериментально,
нахождением тангенса угла наклона к
горизонту поверхности, с которой начинает
скатываться тело под действием его силы
тяжести.
При F>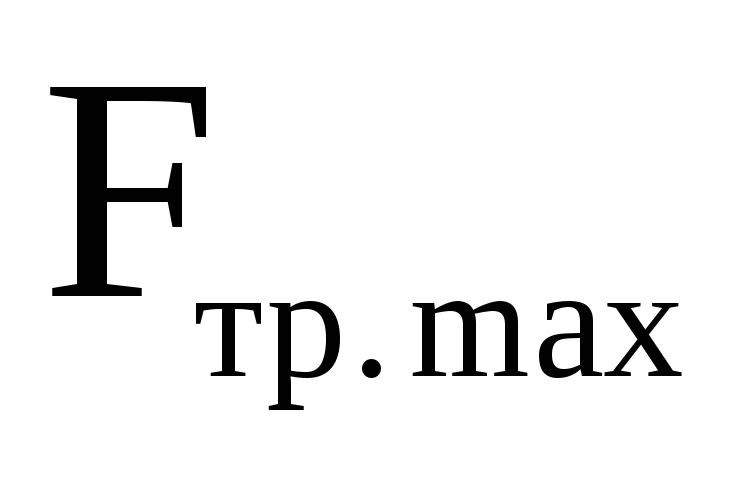 происходит
скольжение тел относительно друг друга
с некоторой скоростью
происходит
скольжение тел относительно друг друга
с некоторой скоростью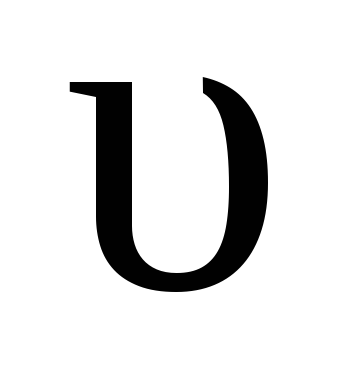 (рис. 2.11 б).
(рис. 2.11 б).
Сила трения скольжения направлена
против скорости  .
Модуль силы трения скольжения при малых
скоростях движения вычисляется в
соответствии с законом Амонтона
.
Модуль силы трения скольжения при малых
скоростях движения вычисляется в
соответствии с законом Амонтона
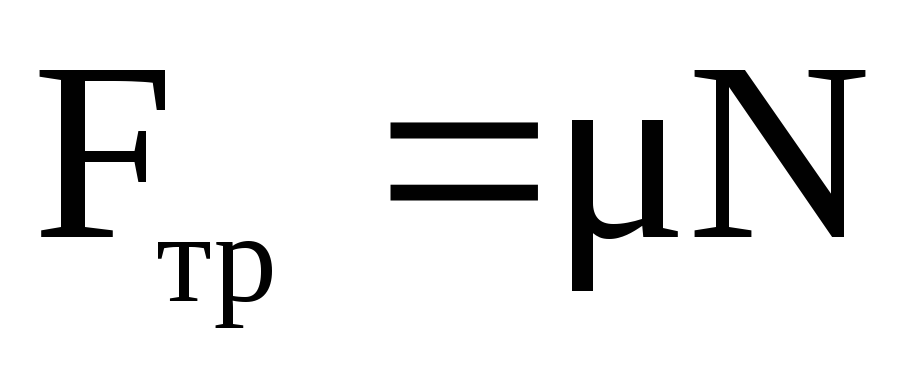 ,
(2.54)
,
(2.54)
где  – безразмерный коэффициент трения
скольжения, зависящий от материала и
состояния поверхности соприкасающихся
тел, и всегда меньше
– безразмерный коэффициент трения
скольжения, зависящий от материала и
состояния поверхности соприкасающихся
тел, и всегда меньше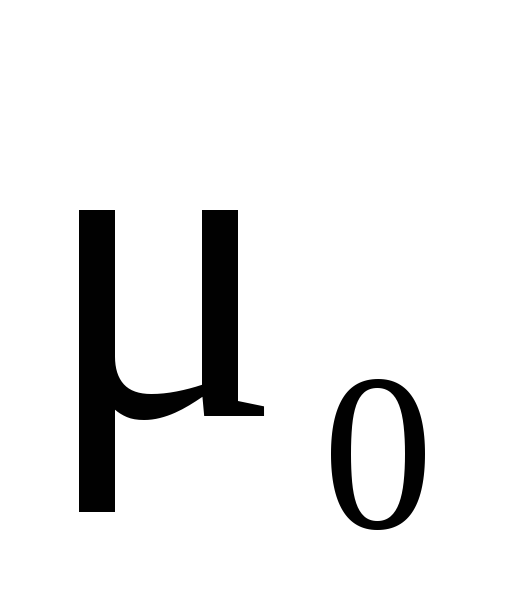 .
.
Сила трения качения возникает тогда, когда тело, имеющее форму цилиндра или шара радиусом R, катится по поверхности опоры. Численное значение силы трения качения определяется в соответствии с законом Кулона
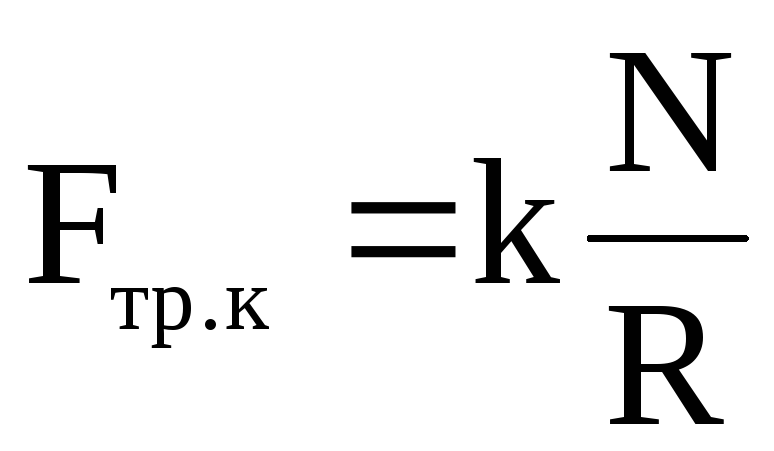 ,
(2.55)
,
(2.55)
где k[м] – коэффициент трения качения.
ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ • Большая российская энциклопедия
ГРАВИТАЦИО́ННОЕ ВЗАИМОДЕ́ЙСТВИЕ элементарных частиц, наиболее слабое из всех известных фундаментальных взаимодействий, характеризуемое участием гравитационного поля (поля тяготения). По совр. представлениям, любое взаимодействие частиц осуществляется путём обмена между ними виртуальными (или реальными) частицами – переносчиками взаимодействия. В электромагнитном, слабом и сильном взаимодействиях переносчиками являются фотон, промежуточные векторные бозоны и глюоны соответственно. Для Г. в. вопрос о переносчиках не прост, и сама теория Г. в. занимает особое место в физич. картине мира.
Согласно закону всемирного тяготения Ньютона, сила взаимодействия двух точечных масс (размеры которых малы по сравнению с расстоянием $r$ между ними) $$F_g=Gm_1m_2/r^2,\tag1$$где $m_1$, $m_2$ – массы частиц, $G$=6,67×10–11 м3/кг·с2 – гравитац. постоянная. Сила Г. в. двух протонов в 1036 раз меньше кулоновской силы электростатич. взаимодействия между ними. Это соотношение не изменяетcя и при учёте релятивистских эффектов вплоть до расстояний, равных комптоновской длине волны протона. Величину $m$ можно назвать «гравитационным зарядом». При таком определении «заряда» формула (1) совпадает с законом Кулона для взаимодействия электрич. зарядов. Гравитац. заряд пропорционален массе тела, поэтому, согласно второму закону Ньютона ($F=ma$), ускорение $a$, вызываемое силой (1), не зависит от массы ускоряемого тела. Этот факт, проверенный с большой точностью, называется эквивалентности принципом. В релятивистской теории Г. в. вследствие соотношения между массой и энергией ($E=mc^2$) гравитац. заряд пропорционален энергии, т. е. полной массе $m$, а не массе покоя, как в формуле (1). Это обусловливает универсальность Г. в. Нет такого вида материи, который имел бы нулевой гравитац. заряд. Именно это свойство Г. в. отличает его от др. фундам. взаимодействий элементарных частиц. Кроме того, при больших энергиях частиц Г. в. уже нельзя считать слабым. При энергии >1018 ГэВ гравитац. заряд частицы $E/c^2$ становится равным её электрич. заряду $e$, и при очень высоких энергиях Г. в. может стать основным.
Важнейшее свойство гравитац. поля состоит в том, что оно определяет геометрию пространства-времени, в котором движется материя. Геометрия мира не может быть задана изначально и изменяется при движении материи, создающей гравитац. поле (см. Тяготение). А. Эйнштейн сделал такой вывод из свойства универсальности Г. в. и построил релятивистскую теорию гравитации – общую теорию относительности (ОТО). Эксперименты подтверждают справедливость ОТО в случае слабых гравитац. полей (когда гравитац. потенциал по абсолютной величине много меньше $c^2$). Для сильных полей ОТО ещё не проверена, поэтому возможны и др. теории Г. в.
ОТО возникла как обобщение спец. теории относительности. Др. теории гравитации возникают как отражение успехов физики элементарных частиц – теоретической и экспериментальной. Напр., теория гравитации Эйнштейна – Картана – Траутмана (т. н. гравитация с кручением, Эйнштейн, А. Картан, А. Траутман, 1922–72) расширяет принцип эквивалентности в том смысле, что гравитац. поле в ней взаимодействует не только с энергией (тензором энергии-импульса) частиц, но и с их спином.
В т. н. $f–g$ теории гравитации К. Дж. Айшема, А. Салама и Дж. Стразди (1973) предполагается существование двух гравитац. полей: носителями одного из них являются безмассовые частицы со спином 2 (обычная, «слабая» гравитация ОТО), это поле взаимодействует с лептонами; др. поле переносится массивными частицами ($f$-мезонами) со спином 2 («сильная» гравитация) и взаимодействует с адронами.
Cкалярно-тензорная теория гравитации Бранса – Дикке – Йордана (К. Бранс, Р. Дикке, П. Йордан, 1959–61) явилась развитием идеи П. Дирака об изменении со временем фундам. физич. констант и констант взаимодействия.
А. Д. Сахаров выдвинул (1967) идею о гравитации как индуцированном взаимодействии, по аналогии с силами Ван дер Ваальса, которые имеют электромагнитную природу. В этой теории Г. в. – не фундам. взаимодействие, а результат квантовых флуктуаций всех др. полей. Успехи квантовой теории поля (КТП) сделали возможным вычисление индуцированной гравитац. постоянной $G$, которая в этом случае выражается через параметры этих квантовых полей.
Теория тяготения – классич. теория, квантовая теория гравитации ещё не создана. Необходимость квантования вызвана тем, что элементарные частицы – объекты квантовой природы, и поэтому соединение классич. взаимодействия и квантованных источников этого взаимодействия представляется непоследовательным.
Создание квантовой теории гравитации наталкивается на большие математич. трудности, возникающие вследствие нелинейности уравнений поля. Существует неск. методов квантования таких сложных математич. объектов; эти методы развиваются и совершенствуются (см. Квантовая теория тяготения). Как и в квантовой электродинамике (КЭД), при вычислениях появляются расходимости, однако, в отличие от КЭД, квантовая теория гравитации оказывается неперенормируемой. Здесь имеется аналогия с теорией слабого взаимодействия, которая тоже, взятая отдельно, вне связи с др. взаимодействиями, неперенормируема. Но объединение слабого и электромагнитного взаимодействий (на основе идеи о т. н. спонтанном нарушении симметрии) позволило построить единую перенормируемую теорию электрослабого взаимодействия. В этой связи большие надежды возлагаются на супергравитацию – теорию, в которой объединены все взаимодействия на основе суперсимметрии и в которой, кроме гравитонов (безмассовых частиц со спином 2, бозонов), имеются и др. переносчики Г. в. – фермионы, получившие назв. гравитино.
Интерес к созданию квантовой теории гравитации не является чисто академическим. Связь Г. в. со всеми видами материи и с пространственно-временны́м многообразием неизбежно приведёт в будущей квантовой теории к квантованию пространства-времени и к изменению наших взглядов не только на пространство и время на сверхмалых расстояниях и промежутках времени, но и на понятие «частицы», на процедуру измерений в микромире, а также к изменению структуры совр. теории элементарных частиц.
Некоторые контуры этих изменений уже просматриваются. Это прежде всего проблема расходимостей в КТП. Расходимость, напр., собств. энергии электрически заряженной частицы появляется уже в классич. электродинамике. Полная масса $M$ классич. заряженной тонкой сферы, имеющей заряд $e$ и размер $r_0$, равна $$M=M_0+e^2/2r_0c^2,\tag2$$где $M_0$ – затравочная масса. При $r_0→0$ масса $M$ становится бесконечной. Эта расходимость не устраняется и в квантовой теории, она становится только более слабой – логарифмической. Если учесть Г. в. и то, что оно зависит от полной массы $M$, расходимость собственной энергии исчезает уже в классич. теории.
К вопросу о расходимостях можно подойти с др. стороны. Взаимодействие в КТП представляет собой обмен виртуальными частицами сколь угодно больших энергий. Поэтому при интегрировании по этим энергиям получаются расходящиеся выражения. В ОТО частицы не могут быть точечными. Их минимальный размер определяется гравитационным радиусом $r_g$. Чем больше масса (энергия), тем больше гравитационный радиус: $$r_g=2GM/c^2.$$Если тело массы $M$ сжато до размеров, меньших $r_g$, то оно превращается в чёрную дыру размером $r_g$. В квантовой теории также есть предел локализации частицы – её комптоновская длина волны $l_C=\hbar /Mc$, которая, очевидно, не может быть меньше гравитац. радиуса. Поэтому появляется надежда, что в теории, учитывающей Г. в., промежуточные состояния со сколь угодно большими энергиями не возникнут и, следовательно, расходимости исчезнут. Макс. масса (энергия) частиц соответствует равенству $l_С=r_g$ и равна $M_{Pl}=\sqrt{\hbar c/G}≈10^{–5}$ г. Эта величина называется планковской массой, и ей соответствует планковская длина $l_{Pl}=\sqrt{\hbar G/c^3}≈10^{–33}$ см.
M. А. Марков предположил (1965), что могут существовать элементарные частицы массы $M_{Pl}$ и что эти частицы имеют максимально возможную для элементарной частицы массу. Он назвал эти частицы максимонами. Заряженные максимоны с массой $M=e/\sqrt{G}≈10^{–6}$ г Марков назвал фридмонами. Фридмоны и максимоны обладают рядом необычных свойств. Так, геометрия внутри этих частиц может существенно отличаться от геометрии снаружи, и можно представить такие фридмоны и максимоны, внутри которых находятся целые вселенные. Вполне возможно, что квантовые образования, подобные максимонам и фридмонам, определяли ранние этапы эволюции Вселенной и задавали начальный вакуум единого взаимодействия, которое при расширении Вселенной расчленилось, напр. посредством механизма спонтанного нарушения симметрии, на четыре взаимодействия, известные в настоящее время. Направление развития физики элементарных частиц не исключает, а, скорее, предполагает такую возможность.
Не только квантовая гравитация может оказать существенное влияние на теорию др. взаимодействий, несомненно и обратное влияние. Исследования КТП в искривлённом пространстве-времени, исследования испарения чёрных дыр и рождения частиц в космологии показывают, что КТП приводит к видоизменению уравнений Эйнштейна. В совр. объединённых теориях взаимодействия элементарных частиц плотность энергии вакуума может быть отлична от нуля и, следовательно, обладать собств. гравитац. полем. Доминантность этой плотности энергии ведёт к ускорению расширения совр. Вселенной. Наконец, в моделях многомерной гравитации процессы негравитационных взаимодействий происходят на 4-мерной бране (подпространстве) в многомерном пространстве-времени. При энергиях, подводящих частицу к границе браны, может наблюдаться нарушение лоренц-инвариантности, а Г. в. перестаёт быть слабым.
Всё это свидетельствует о том, что создание квантовой теории Г. в. невозможно без учёта других фундам. взаимодействий и, наоборот, теория др. взаимодействий не будет полна и свободна от внутр. противоречий без учёта Г. в. Достигнуть подобного объединения Г. в. с др. взаимодействиями, возможно, удастся в рамках интенсивно развивающейся теории струн. Исследованию такого объединения способствуют методы космомикрофизики, изучающей фундам. взаимосвязь микро- и макромира в сочетании её физич., космологич. и астрофизич. проявлений.
Гравитационное взаимодействие — это… Что такое Гравитационное взаимодействие?
Гравита́ция (всеми́рное тяготе́ние, тяготе́ние) (от лат. gravitas — «тяжесть») — дальнодействующее фундаментальное взаимодействие в природе, которому подвержены все материальные тела. По современным данным, является универсальным взаимодействием в том смысле, что, в отличие от любых других сил, всем без исключения телам независимо от их массы придаёт одинаковое ускорение. Главным образом гравитация играет определяющую роль в космических масштабах. Термин гравитация используется также как название раздела физики, изучающего гравитационное взаимодействие. Наиболее успешной современной физической теорией в классической физике, описывающей гравитацию, является общая теория относительности, квантовая теория гравитационного взаимодействия пока не построена.
Гравитационное взаимодействие
Гравитационное взаимодействие — одно из четырёх фундаментальных взаимодействий в нашем мире. В рамках классической механики, гравитационное взаимодействие описывается законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения между двумя материальными точками массы m1 и m2, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния — то есть
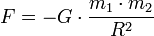 .
.Здесь G — гравитационная постоянная, равная примерно 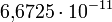 м³/(кг•с²). Знак минус означает, что сила, действующая на тело, всегда равна по направлению радиус-вектору, направленному на тело, то есть гравитационное взаимодействие приводит всегда к притяжению любых тел.
м³/(кг•с²). Знак минус означает, что сила, действующая на тело, всегда равна по направлению радиус-вектору, направленному на тело, то есть гравитационное взаимодействие приводит всегда к притяжению любых тел.
Закон всемирного тяготения — одно из приложений закона обратных квадратов, встречающегося так же и при изучении излучений (см. например, Давление света), и являющимся прямым следствием квадратичного увеличения площади сферы при увеличении радиуса, что приводит к квадратичному же уменьшению вклада любой единичной площади в площадь всей сферы.
Поле тяжести потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность поля тяжести влечёт за собой закон сохранения суммы кинетической и потенциальной энергии и при изучении движения тел в поле тяжести часто существенно упрощает решение. В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал зависит только от положения тела в данный момент времени.
Большие космические объекты — планеты, звезды и галактики имеют огромную массу и, следовательно, создают значительные гравитационные поля.
Гравитация — слабейшее взаимодействие. Однако, поскольку оно действует на любых расстояниях и все массы положительны, это тем не менее очень важная сила во Вселенной. Для сравнения: полный электрический заряд этих тел ноль, так как вещество в целом электрически нейтрально.
Также гравитация, в отличие от других взаимодействий, универсальна в действии на всю материю и энергию. Не обнаружены объекты, у которых вообще отсутствовало бы гравитационное взаимодействие.
Из-за глобального характера гравитация ответственна и за такие крупномасштабные эффекты, как структура галактик, черные дыры и расширение Вселенной, и за элементарные астрономические явления — орбиты планет, и за простое притяжение к поверхности Земли и падения тел.
Гравитация была первым взаимодействием, описанным математической теорией. В античные времена Аристотель считал, что объекты с разной массой падают с разной скоростью. Только много позже Галилео Галилей экспериментально определил, что это не так — если сопротивление воздуха устраняется, все тела ускоряются одинаково. Закон всеобщего тяготения Исаака Ньютона (1687) хорошо описывал общее поведение гравитации. В 1915 году Альберт Эйнштейн создал Общую теорию относительности, более точно описывающую гравитацию в терминах геометрии пространства-времени.
Небесная механика и некоторые её задачи
Раздел механики, изучающий движение тел в пустом пространстве только под действием гравитации называется небесной механикой.
Наиболее простой задачей небесной механики является гравитационное взаимодействие двух тел в пустом пространстве. Эта задача решается аналитически до конца; результат её решения часто формулируют в виде трёх законов Кеплера.
При увеличении количества взаимодействующих тел задача резко усложняется. Так, уже знаменитая задача трёх тел (то есть движение трёх тел с ненулевыми массами) не может быть решена аналитически в общем виде. При численном же решении, достаточно быстро наступает неустойчивость решений относительно начальных условий. В применении к Солнечной системе, эта неустойчивость не позволяет предсказать движение планет на масштабах, превышающих сотню миллионов лет.
В некоторых частных случаях удаётся найти приближённое решение. Наиболее важным является случай, когда масса одного тела существенно больше массы других тел (примеры: солнечная система и динамика колец Сатурна). В этом случае в первом приближении можно считать, что лёгкие тела не взаимодействуют друг с другом и движутся по кеплеровым траекториям вокруг массивного тела. Взаимодействия же между ними можно учитывать в рамках теории возмущений, и усреднять по времени. При этом могут возникать нетривиальные явления, такие как резонансы, аттракторы, хаотичность и т. д. Наглядный пример таких явлений — нетривиальная структура колец Сатурна.
Несмотря на попытки описать поведение системы из большого числа притягивающихся тел примерно одинаковой массы, сделать этого не удаётся из-за явления динамического хаоса.
Сильные гравитационные поля
В сильных гравитационных полях, при движении с релятивистскими скоростями, начинают проявляться эффекты общей теории относительности:
Гравитационное излучение
Одним из важных предсказаний ОТО является гравитационное излучение, наличие которого до сих пор не подтверждено прямыми наблюдениями. Однако, имеются косвенные наблюдательные свидетельства в пользу его существования, а именно: потери энергии в двойной системе с пульсаром PSR B1913+16 — пульсаром Халса-Тейлора — хорошо согласуются с моделью, в которой эта энергия уносится гравитационным излучением.
Гравитационное излучение могут генерировать только системы с переменным квадрупольным или более высокими мультипольными моментами, этот факт говорит о том, что гравитационное излучение большинства природных источников направленное, что существенно усложняет его обнаружение. Мощность гравитационного l-польного источника пропорциональна (v / c)2l + 2, если мультиполь имеет электрический тип, и (v / c)2l + 4 — если мультиполь магнитного типа [1], где v — характерная скорость движения источников в излучающей системе, а c — скорость света. Таким образом, доминирующим моментом будет квадрупольный момент электрического типа, а мощность соответствующего излучения равна:
где Qij — тензор квадрупольного момента распределения масс излучающей системы. Константа 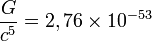 (1/Вт) позволяет оценить порядок величины мощности излучения.
(1/Вт) позволяет оценить порядок величины мощности излучения.
Начиная с 1969 года (эксперименты Вебера (англ.)) и до настоящего времени (февраль 2007) предпринимаются попытки прямого обнаружения гравитационного излучения. В США, Европе и Японии в настоящий момент существует несколько действующих наземных детекторов (GEO 600), а также проект космического гравитационного детектора [2] республики Татарстан.
Тонкие эффекты гравитации
Помимо классических эффектов гравитационного притяжения и замедления времени, общая теория относительности предсказывает существование других проявлений гравитации, которые в земных условиях весьма слабы и их обнаружение и экспериментальная проверка поэтому весьма затруднительны. До последнего времени преодоление этих трудностей представлялось за пределами возможностей экспериментаторов.
Среди них, в частности, можно назвать увлечение инерциальных систем отсчета (или эффект Лензе-Тирринга) и гравитомагнитное поле. В 2005 году автоматический аппарат НАСА Gravity Probe B провёл беспрецедентный по точности эксперимент по измерению этих эффектов вблизи Земли, но его полные результаты пока не опубликованы.
Квантовая теория гравитации
Несмотря на более чем полувековую историю попыток, гравитация — единственное из фундаментальных взаимодействий, для которого пока ещё не построена непротиворечивая перенормируемая квантовая теория. Впрочем, при низких энергиях, в духе квантовой теории поля, гравитационное взаимодействие можно представить как обмен гравитонами — калибровочными бозонами со спином 2.
Стандартные теории гравитации
Подробней см. статью Теории гравитации
В связи с тем, что квантовые эффекты гравитации чрезвычайно малы даже в самых экстремальных экспериментальных и наблюдательных условиях, до сих пор не существует их надёжных наблюдений. Теоретические оценки показывают, что в подавляющем большинстве случаев можно ограничиться классическим описанием гравитационного взаимодействия.
Существует современная каноническая[3] классическая теория гравитации — общая теория относительности, и множество уточняющих её гипотез и теорий различной степени разработанности, конкурирующих между собой (см. статью Альтернативные теории гравитации). Все эти теории дают очень похожие предсказания в рамках того приближения, в котором в настоящее время осуществляются экспериментальные тесты. Далее описаны несколько основных, наиболее хорошо разработанных или известных теорий гравитации.
Общая теория относительности
В стандартном подходе общей теории относительности (ОТО) гравитация рассматривается изначально не как силовое взаимодействие, а как проявление искривления пространства-времени. Таким образом, в ОТО гравитация интерпретируется как геометрический эффект, причём пространство-время рассматривается в рамках неевклидовой римановой (точнее псевдо-римановой) геометрии. Гравитационное поле (обобщение ньютоновского гравитационного потенциала) иногда называемое также полем тяготения, в ОТО отождествляется с тензорным метрическим полем или метрикой четырехмерного пространства-времени, а напряженность гравитационного поля — с аффинной связностью пространства-времени, определяемой метрикой. Стандартной задачей ОТО является определение компонент метрического тензора, в совокупности задающих метрику пространства-времени, по известному распределению источников энергии-импульса в рассматриваемой системе четырехмерных координат. В свою очередь знание метрики позволяет рассчитывать движение пробных частиц, что эквивалентно знанию свойств поля тяготения в данной системе. В связи с тензорным характером уравнений ОТО, а также со стандартным фундаментальным обоснованием ее формулировки, считается, что гравитация также носит тензорный характер. Одним из следствий является то, что гравитационное излучение должно быть не ниже квадрупольного порядка. Известно, что в ОТО имеются затруднения с объяснением факта неинвариантности энергии гравитационного поля, поскольку данная энергия не описывается тензором. В классической ОТО также возникает проблема описания спин-орбитального взаимодействия. Считается, что существуют определенные проблемы с однозначностью результатов и обоснованием непротиворечивости. Однако экспериментально ОТО считается подтверждающейся до самого последнего времени. Кроме того, многие альтернативные эйнштейновскому, но стандартные для современной физики, подходы к формулировке теории гравитации приводят к результату, совпадающему с ОТО в низкоэнергетическом приближении, которое в основном и доступно экспериментальной проверке.
Теория Эйнштейна-Картана
Теория Эйнштейна-Картана (ЭК) была разработана как расширение ОТО, внутренне включающее в себя описание воздействия на пространство-время кроме энергии-импульса также и спина объектов.[4] В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана-Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса. Один из них аналогичен ОТО, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением. Второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения. Получаемые поправки к ОТО настолько малы, что пока не видно даже гипотетических путей для их измерения.
Релятивистская теория гравитации
Релятивистская теория гравитации (РТГ) разрабатывается академиком Логуновым А. А. с группой сотрудников. [5] В ряде работ они утверждают, что РТГ имеет следующие отличия от ОТО[6] :
- Гравитация есть не геометрическое поле, а реальное физическое силовое поле, описываемое тензором.
- Гравитационные явления следует рассматривать в рамках плоского пространства Минковского, в котором однозначно выполняются законы сохранения энергии-импульса и момента количества движения. Тогда движение тел в пространстве Минковского эквивалентно движению этих тел в эффективном римановом пространстве.
- В тензорных уравнениях для определения метрики следует учитывать массу гравитона, а также использовать калибровочные условия, связанные с метрикой пространства Минковского. Это не позволяет уничтожить гравитационное поле даже локально выбором какой-то подходящей системы отсчёта.
Как и в ОТО, в РТГ под веществом понимаются все формы материи (включая и электромагнитное поле), за исключением самого гравитационного поля. Следствия из теории РТГ таковы: чёрных дыр как физических объектов, предсказываемых в ОТО, не существует; Вселенная плоская, однородная, изотропная, неподвижная и евклидовая.
C другой стороны, существуют не менее убедительные аргументы противников РТГ, сводящиеся к следующим положениям:
- РТГ есть биметрическая теория, в случае безмассового гравитона эквивалентная так называемой полевой трактовке ОТО как надстройке над ненаблюдаемым пространством Минковского: «В релятивистской теории гравитации… фигурируют в точности те же лагранжианы…, которые приводят к уравнениям гравитационного поля»[7], «математическое содержание РТГ сводится к математическому содержанию ОТО (в полевой формулировке)» [8]. Этот аргумент в таком изложении, правда, по-видимому не учитывает возможных топологических различий между обычной моделью ОТО и такой моделью, или же, по крайней мере, маскирует их.
- Случай массивного гравитона в РТГ не даёт правильного ньютоновского предела при переходе к массе равной 0, и, следовательно, бессмыслен.
- Дополнительные уравнения РТГ представляют собой всего лишь координатные условия: «Весь набор уравнений РТГ в терминах метрики искривленного пространства-времени можно свести к уравнениям Эйнштейна плюс гармоническое координатное условие, столь успешно использовавшееся Фоком» [8].
- Вышеприведённые следствия из РТГ являются лишь следствием неточностей: несуществование чёрных дыр — следствием невозможности покрыть одной координатной картой, эквивалентной пространству-времени Минковского, пространство-время сколлапсировавшего в чёрную дыру объекта; космологических предсказаний — следствием принятых координатных условий в сочетании с совершенно произвольным дополнительным допущением о вложенности световых конусов реального пространства в конусы пространства Минковского. (Как видим, этот аргумент явно противоречит первому, показывая расхождение РТГ и ОТО, которые вполне ощутимы; и, если оставить соображения, очевидно исходящие просто изнутри обычной логики ОТО, или суждения о произвольности постулатов, то решение о верности одного из этих подходов остается за экспериментом, если конечно не будет всё же доказана достаточно неочевидная их полная эквивалентность в области наблюдаемого).
Теория Бранса — Дикке
В скалярно-тензорных теориях, самой известной из которых является теория Бранса — Дикке (или Йордана — Бранса — Дикке), гравитационное поле как эффективная метрика пространства-времени определяется воздействием не только тензора энергии-импульса материи, как в ОТО, но и дополнительного гравитационного скалярного поля. Источником скалярного поля считается свёрнутый тензор энергии-импульса материи. Следовательно, скалярно-тензорные теории, как ОТО и РТГ, относятся к метрическим теориям, дающим объяснение гравитации, используя только геометрию пространства-времени и его метрические свойства. Наличие скалярного поля приводит к двум тензорным уравнениям для метрики. Теория Бранса — Дикке вследствие наличия скалярного поля может рассматриваться также как действующая в пятимерном многообразии, состоящем из пространства-времени и скалярного поля.[9]
Подобное имеет место и в РТГ, где второе тензорное уравнение вводится для учёта связи между неевклидовым пространством и пространством Минковского[10]. Благодаря наличию безразмерного подгоночного параметра в теории Йордана — Бранса — Дикке, появляется возможность выбрать его так, чтобы результаты теории совпадали с результатами гравитационных экспериментов.
| Теории гравитации |
Источники и примечания
- ↑ См. аналогии между слабым гравитационным полем и электромагнитным полем в статье гравитомагнетизм
- ↑ http://dulkyn.org.ru/ru/about.html
- ↑ Канонической эта теория является в том смысле, что она наиболее хорошо разработана и широко используется в современной небесной механике, астрофизике и космологии, причём количество надёжно установленных противоречащих ей экспериментальных результатов практически равно нулю.
- ↑ Иваненко Д. Д., Пронин П. И., Сарданашвили Г. А., Калибровочная теория гравитации. — М., Изд. МГУ, 1985.
- ↑ Логунов А. А., Мествиришвили М. А. Релятивистская теория гравитации. — М: Наука, 1989.
- ↑ Логунов А. А., Мествиришвили М. А. Тензор энергии-импульса материи как источник гравитационного поля. — Теоретическая и математическая физика, 1997, Т. 110, Вып. 1, Стр. 5 — 24.
- ↑ Зельдович Я. Б., Грищук Л. П. ТЯГОТЕНИЕ, ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ И АЛЬТЕРНАТИВНЫЕ ТЕОРИИ. УФН, 1986, Т. 149, № 4, с. 695—707. С. 704.
- ↑ 1 2 Зельдович Я. Б., Грищук Л. П. Общая теория относительности верна! УФН, 1988, Т. 155, № 3, с. 517—527. С. 521, 524.
- ↑ Brans, C. H.; Dicke, R. H. (November 1 1961). «Mach’s Principle and a Relativistic Theory of Gravitation». Physical Review 124 (3): 925—935. DOI:10.1103/PhysRev.124.925. Retrieved on 2006-09-23.
- ↑ С ортодоксальной точки зрения это уравение представляет собой координатное условие, см. выше.
Литература
- Визгин В. П. Релятивистская теория тяготения (истоки и формирование, 1900—1915). М.: Наука, 1981. — 352c.
- Визгин В. П. Единые теории в 1-й трети ХХ в. М.: Наука, 1985. — 304c.
- Иваненко Д. Д., Сарданашвили Г. А. Гравитация, 3-е изд. М.:УРСС, 2008. — 200с.
См. также
Ссылки
Wikimedia Foundation. 2010.
Гравитационное взаимодействие
Притяжение земли вызвано гравитацией. Гравитация это сила природы, которая притягивает всю существующую материю друг к другу. Притяжение всегда будет относительным. Измерение ведут как взаимодействие одного тела относительно другого. Величина силы гравитационного взаимодействия тел зависит от массы и расстояния между ними. На притяжение нашей планеты влияет гравитация других небесных объектов.
Ученые используют строгие понятия. Сила тяжести определяется как масса тела умноженная на ускорение свободного падения.
Сила тяжести — это частный, упрощённый случай применения формулы гравитационного взаимодействия. Формула применима только для объектов расположенных строго на поверхности земли, к тому же из-за разницы расстояний от центра до поверхности, т.е. радиуса нашего «шара» на экваторе и на полюсах, ускорение свободного падения (g) будет меняться. Величину гравитационного притяжения находят произведением их масс на гравитационную постоянную, которые делят на квадрат расстояния между ними. Дистанцию между объектами берут от центра масс вероятно расположенных в центре этих объектов. Гравитационная постоянная — крайне малое значение с десятком нулей после запятой, является константой.
Вес представляет собой силу, воздействующую на опору, соответственно измеряется в ньютонах, не допуская привычных для нас килограммов. Вес совпадает с силой тяжести.
На планете все стремится вниз к центру. Плотность — это отношение массы объекта к его объему. Чем она выше, тем ниже оказывается вещество, формируя облик нашего мира.
Физики пока не могут в полной мере объяснить природу этого явления, существует много теорий. Гравитационное взаимодействие тел сложный вопрос, включающий огромное количество факторов.
Силы гравитационного взаимодействия
Гравитационное взаимодействие проявляется в притяжении друг к другу тел. Объясняется это взаимодействие наличием гравитацион- ного поля вокруг каждого тела.
Модуль силы гравитационного взаимодействия FG между дву- мя материальными точками определяется законом всемирного тя- готения
F = F = F = G m1m2, (2.17)

G 1,2 2,1 r 2
где F1,2, F2,1 — силы взаимодействия, направленные вдоль прямой, со- единяющей материальные точки (см. п.2.5), G = 6,67 · 10–11 Нм2/кг2 — гравитационная постоянная, m1, m2, r — массы точек и расстояние между ними.
Закон всемирного тяготения справедлив не только для матери- альных точек, но и для тел со сферически-симметричным распреде- лением масс, а также тел произвольной формы, размеры которых во много раз меньше расстояний между ними.
Сила тяжести
Если принять одно из взаимодействующих тел Землю, а второе — тело с массой m, находящееся вблизи или на её поверхности, то тело притягивается с силой

(2.18)
где M3, R3 — масса и радиус Земли.
 Соотношение G M 3
Соотношение G M 3
R2
в формуле (2.18) есть постоянная величина

имеет размерность ускорения и называется ускорением свободного па- дения.
Сила тяжести — сила гравитационного притяжения Землей тела массой m
Fтяж
=mg. (2.19)
 �
�
В отличие от силы FG
модуль
зависит от географической ши-

роты места расположения тела на Земле. На полюсах Fтяж = mg , а на экваторе уменьшается на 0,36 %. Это различие обусловлено тем, что Земля вращается вокруг своей оси и образует неинерциальную сис-
тему отсчета.
С удалением тела относительно поверхности Земли на высоту h
уменьшается сила тяжести


 |
Fтяж
= mgn = (R
+h)2 ,
где, g =
G × M 3
— ускорение свободного падения на высоте h от
h
Земли.

(R3+h)
Масса в формулах (2.17–2.19) характеризует гравитационное взаимодействие тел, является его мерой и называется гравитацион- ной. В настоящее время с высокой точностью установлено равенст- во инертной (см. 2.2) и гравитационной масс тела, поэтому их не раз- личают и обозначают одной буквой m.
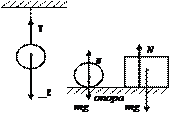
Если подвесить тело или положить его на не- подвижную опору, оно будет покоиться отно- сительно Земли, так как сила тяжести уравнове- шивается силой реак- ции, действующей на тело со стороны опоры или подвеса.
Силы реакции

подвес
Рис. 2.4
Сила реакции — сила, с которой действуют на данное тело другие
тела, ограничивающие его движени�е.
Сила нормальной реакции опоры N приложена к телу и направле-
на перпендикулярно плоскости опоры.
�
Сила реакции нити (подвеса) T приложена к телу и направлена
вдоль нити (подвеса) (рис. 2.4).
Вес тела
�
Вес тела Q — сила, с которой тело давит на опору или растягива-
ет нить подвеса и приложена к опоре или подвесу.
В соответствии с третьим законом Ньютона
� � � �



 Q = — N , Q = N ,
Q = — N , Q = N ,
 � �
� �
Q = —T ,
� �


 Q = T
Q = T
. Вес тела численно равен силе тяжести в том слу-
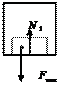

 чае, когда тело находится на гори- зонтальной поверхности опоры в состоянии покоя или равномерно-
чае, когда тело находится на гори- зонтальной поверхности опоры в состоянии покоя или равномерно-



 X го прямолинейного движения. �
X го прямолинейного движения. �
a a Возможны случаи, когда Q
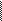
 больше или меньше и даже
больше или меньше и даже

 � Fтяж
� Fтяж
когда Q = 0. Рассмотрим тело,
Движение вниз
Движение вверх
находящееся в лифте, движущем- ся с ускорением (рис. 2.5).
Рис. 2.5
На тело дей�ствуют две силы: ре-
акции опоры N и сила тяжести F .
Запишем второй закон Ньютона
ma =
N Fтяж
тяж
. (2.20)
При движении с ускорением �
вверх равенство (2.20) с учетом
знака векторов сил и ускорения на ось X имеет вид
ma = N1 – Fтяж = N1 – mg, а при движении вниз
–ma = N2 – Fтяж = N2 – mg,
где N1 и N2 — силы реакции опоры. Из последних равенств следу- ет, что
N1 = m (g + a), N2 = m (g – a).
Согласно определению веса тела Q1 = N1 и Q2 = N2 имеем при уско- ренном подъеме тела Q1 > Fтяж, а при ускоренном спуске Q2 < Fтяж.
При спуске с ускорением a = g, Q = 0, тело находится в состоя- нии невесомости.
Силы трения
Сила трения — результат взаимодействия поверхностей соприка- сающихся тел.
Сила трения направлена по касательной к трущимся поверхностям в сторону, противоположную направлению относительного движения взаимодействующих тел.
Различают внешнее (сухое) и внутреннее (вязкое) трение.
Внешнее сухое трение возникает при относительном перемещении двух соприкасающихся тел и делится на:
— трение покоя;
— трение скольжения;
— трение качения. Перечисленным видам внеш-
него трения соответствуют силы: покоя, скольжения, качения.
Сила трения покоя 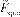 действу- ет между соприкасающимися по- верхностями взаимодействующих
действу- ет между соприкасающимися по- верхностями взаимодействующих
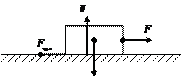 а
а
mg
 N υ б
N υ б
F > F
тел, когда величина внешних сил недостаточна, чтобы вызвать их относительное перемещение.
Если к телу, находящемуся в соприкосновении с другим телом,
Fтр
g
Рис. 2.6
тр. max
приложить возрастающую внешнюю силу F, параллельную плоско- сти соприкосновения (рис. 2.6а), то при изменении F от нуля до не- которого значения Fтр. max движения тела не возникает, что свидетель- ствует о неоднозначности силы трения покоя.
Максимальная сила трения покоя
Fтр. max = m0N,
где m0 – коэффициент трения покоя, N — модуль силы нормальной реакции опоры.
Коэффициент трения покоя m0 можно определить эксперимен- тально. Например, m0 = tga, где a – угол наклона к горизонту по- верхности опоры, с которой начинает скатываться тело под дейст- вием его силы тяжести.
При F > Fтр. max происходит скольжение тел относительно друг дру-
га с некоторой скоростью u (рис. 2.6б). �
Сила трения скольжения направлена против скорости u . Модуль силы трения скольжения при малых скоростях движения вычисляет- ся в соответствии с законом Амонтона по формуле
Fтр = mN, (2.21)
где m — безразмерный коэффициент трения движения, зависящий от материала и состояния поверхности соприкасающихся тел, и все- гда меньше m0.
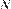 Сила трения качения возникает тогда, когда тело, имеющее фор- му цилиндра или шара, катится по поверхности опоры. Численное значение силы трения качения определяется в соответствии с зако- ном Кулона по формуле
Сила трения качения возникает тогда, когда тело, имеющее фор- му цилиндра или шара, катится по поверхности опоры. Численное значение силы трения качения определяется в соответствии с зако- ном Кулона по формуле
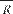 Fтр.к = k ,
Fтр.к = k ,
 где k — коэффициент трения качения имеет размерность длины и за- висит от материала соприкасающихся тел и состояния их поверхно- стей, R — радиус катящегося тела.
где k — коэффициент трения качения имеет размерность длины и за- висит от материала соприкасающихся тел и состояния их поверхно- стей, R — радиус катящегося тела.
 Рис. 2.7
Рис. 2.7
Сила внутреннего трения воз- никает между слоями одного и того же сплошного тела (жид- кости или газа). Силы внут- реннего (вязкого) трения зави- сят от относительной скорости смещения отдельных слоев газа или жидкости друг относитель- но друга. Например, вязкое тре-
ние возникает при течении жидкости или газа по трубам со скоро- стью u (рис. 2.7).
Скорость слоев жидкости уменьшается при приближении их к стенкам трубы. Отношение разности скоростей Äu в двух близких слоях, расположенных на расстоянии Äx, называется средним гра- диентом скорости.
В одномерной задаче, когда u = u(х), средняя сила внутренне- го трения
Fвн.тр = h× s × Äu, (2.22)
Äx
где h — коэффициент внутреннего трения, s — площадь взаимодей- ствующих слоев жидкости, Äu/Äх — средний градиент скорости.
Коэффициент внутреннего трения зависит от агрегатного состоя- ния и температуры вещества.
Сила гравитационного взаимодействия.
 |
 |
Любые материальные точки притягивают друг
друга с силой
Силы упругости.
Эти силы возникают в твердом теле при его
деформировании (изменении его формы).
Простейшим видом деформации тела является его
растяжение или сжатие. Например, оно возникает
в тонком стержне, один конец которого
закреплен, а к другому приложена сила f
перпендикулярно основанию стержня. Упругое
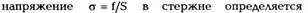
величиной силы f, отнесенной к площади
поперечного сечения стержня S. Это напряжение
одинаково вдоль всей длины стержня. Если
приложенная сила i не очень велика и можно
пренебречь изменением толщины стержня, то
справедлив закон Гука:

где 6L — удлинение стержня, Lo — длина стержня
до деформации. Коэффициент Е,
характеризующий упругие свойства материала
стержня, называется модулем Юнга.
 |
Применительно к пружине закон Гука
записывается в виде:
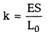 |
где
и х = 5L — абсолютное удлинение
пружины. Силами упругости являются и так
называемые силы натяжения нити Т и реакции
опоры N .
5. Закон сохранения импульса
Импульсомматериальной точки называется
векторная величина, равная произведению ее
массы m на вектор скорости частицы v :
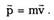
Из первого закона Ньютона следует, что
импульс свободной частицы не изменяется ни по
величине, ни по направлению, т.е. р = const. Если
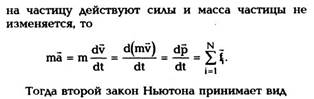 |
 |
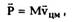 |
 |
 |
 |
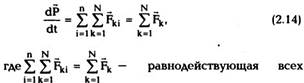 |
| Переписав (2.11) в виде |
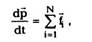 |
(2.8)
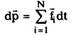 |
т.е. скорость изменения импульса частицы dp/dt
равна векторной сумме сил, действующих на нее.
Из (2.8) следует, что изменение импульса частицы
за время dt
систему взаимодействуют только между собой и
не взаимодействуют с телами, не входящими в
систему, то такая система называется замкнутой.
В противном случае система не является
замкнутой.
Импульсом системыР называется векторная
сумма импульсов всех частиц, входящих в
систему:
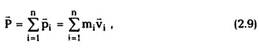
где т, — масса i-ой частицы и Vj — ее скорость в
выбранной ИСО. С течением времени импульсы
частиц изменяются, а сами частицы движутся по
каким-то своим траекториям Fj = Г|(1).
 |
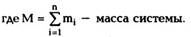 |
Центром масс(центром инерции) системы
частиц называется точка в пространстве, радиус-
вектор которой определяется из выражения:
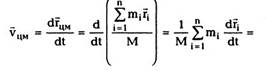 |
 |
Найдем теперь скорость, с которой движется
центр масс системы. По определению вектора
скорости
внешних сил, действующих на систему.
Соотношение (2.14) называется вторым законом
Ньютона для системы материальных точек:
скорость изменения импульса системы равна
векторной сумме внешних сил, действующих на
систему.
Используя (2.12), уравнение (2.14) можно,
переписать в виде
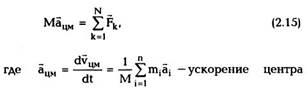
масс системы и а4 — ускорение i-ой частицы. Из
(2.15) видно, что второй закон Ньютона для
системы частиц по форме совпадает со вторым
законом Ньютона для материальной точки, только
вместо массы частицы стоит масса системы,
вместо ускорения частицы — ускорение центра
масс, а в правой части — не все, а только
внешние по отношению к системе силы.
Уравнение (2.14) можно записать в виде
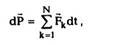
где dP — бесконечно малое изменение импульса
системы за время dt под действием импульсов
внешних сил Fkdt, то есть импульс системы могут
изменить только импульсы внешних сил.
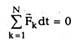 |
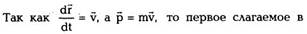 |
 |
 |
 |
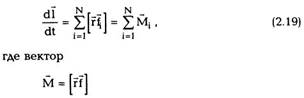 |
 |
 |
 |
| Если система замкнутая, то |
| и dP = 0 , то есть импульс замкнутой системы: |
Это утверждение носит название закона
сохранения импульса.Этот закон является одним
из фундаментальных законов природы и вытекает,
вообще говоря, из свойств нашего пространства, а
именно, из свойства однородности пространства:
физические процессы, протекающие в замкнутой
системе, не зависят от положения системы в
пространстве.
 |
Из соотношения (2.15) следует, что центр масс
замкнутой системы движется равномерно и
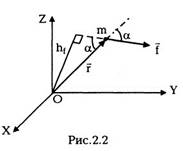
6. Закон сохранения момента
импульса
Помимо импульса р = mv , материальная точка
характеризуется еще одной динамической
переменной, которая называется моментом
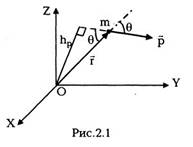
импульса. Моментом импульсачастицы I
относительно начала координат называется
векторная величина

где квадратные скобки обозначают векторное
произведение. По модулю
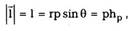 |
 |
 |
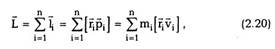 |
 |
 |
 |
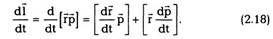 |
 |
Из (2.21) видно, что для замкнутой системы
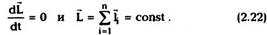
Это утверждение называется законом
сохранения момента импульса.Как и закон
сохранения импульса, этот закон вытекает из
свойства нашего пространства, которое
называется изотропностью пространства:
явления, протекающие в замкнутой системе, не
изменяются при повороте всей системы в
пространстве.
Рекомендуемые страницы: