| 2.1. Система параллельных сил. Сложение двух параллельных сил Сложение параллельных сил геометрическим способом по правилу параллелограмма сил не представляется возможным. Для решения поставленной задачи используем метод приведения параллельных сил к сходящимся силам. Рис.2.1 Приложим к телу в точках А и В две равные по величине, но противоположные по направлению силы и и сложим их с заданными силами и , получим равнодействующие этих сил и . Эти силы непараллельны и лежат в одной плоскости. Следовательно, они пересекаются в одной точке. Переносим эти силы и вдоль линии их действия и приложим их к точке К. Далее, разложим эти силы на составляющие , и , . Силы и можно отбросить как уравновешенные силы. Следовательно на тело к точке К будут действовать только две силы и , которые по величине равны силам и . Сумма сил и (равнодействующая ) направлена вдоль одной прямой: . Из подобия треугольников КСА и КМL и треугольников KCB и KON находим: , , , , отсюда , окончательно: Таким образом, две параллельные силы, направленные в одну сторону, имеют равнодействующую, параллельную им, равную по величине их сумме и направленную в ту же сторону. Линия действия равнодействующей силы расположена между линиями действия заданных сил и делит отрезок прямой между линиями действия этих сил на части, обратно пропорциональные силам. 2.2. Сложение двух параллельных сил, направленных в противоположные стороны Пусть к телу в точках А и В приложены две параллельные неравные по величине и противоположно направленные силы и , причем F1>F2 (рис. Рис. 2.2 Точку приложения силы определим, решая задачу о сложении двух параллельных сил и , где их равнодейтсвующая – сила . Поскольку , имеем: Две неравные параллельные силы, направленные в противоположные стороны, приводятся к равнодействующей силе, параллельной им, равной по величине их разности и направленной в сторону большей силы. Линия действия равнодействующей расположена за линией действия большей силы и делит отрезок прямой между линиями действия заданных сил на части, обратно пропорциональные силам. 2.3. Момент силы Моментом силы называется физическая величина, характеризующая вращательный эффект действия силы. 2.3.1. Момент силы относительно центра Момент силы относительно центра О есть вектор , приложенный в этом центре, который направлен перпендикулярно плоскости, проходящей через центр Момент силы относительно центра О характеризуется: Модуль момента силы определяется по правилу умножения векторов: модуль векторного произведения двух векторов равен произведению модулей этих векторов на синус угла между ними: т.к. , где h – кратчайшее расстояние от точки О до линии действия силы — называется плечом силы. Если сила стремится повернуть тело против хода часовой стрелки, то величина момента силы берётся со знаком «плюс», если по ходу часовой стрелки – знак «минус». Свойства момента силы: а) момент силы равен нулю, если сила равна нулю или когда плечо равно нулю, т.е. линия действия силы проходит через моментную точку, б) величина момента силы относительно точки не изменяется при переносе силы вдоль линии её действия, в) момент силы численно равен удвоенной площади треугольника, построенного на силе F и полюсе О (рис.2.3б). Рис.2.3 Таким образом, алгебраический моменты силы относительно точки Рис. 2.4 Пример. Веревка ВС длиной а, привязанная к столбу под углом α, натягивается с силой, величина которой равна Т (рис. 2.4). Определить момент этой силы относительно точки А. Система двух равных по величине, параллельных и противоположно направленных сил и , приложенных к твердому телу, называется парой сил (рис. 2.5). Так как , то . Следовательно, пара сил не имеет равнодействующей. В то же время, эта система сил не является уравновешенной, поскольку силы и не направлены вдоль одной прямой. Расстояние между линиями действия сил называется плечом пары d. Момент пары сил равен произведению одной из сил пары на плечо. Знак момента пары определяется так же, как и момент силы относительно центра. Рис. 2.5 Пару сил обычно прикладывают к твердому телу, чтобы сообщить ему вращение вокруг оси (рис. 2.6). Рис. 2.6 Силы, входящие в состав пары сил, обладают всеми свойствами любых других сил, приложенных к твердому телу. 2.3.3. Теорема об алгебраической сумме момента сил пары относительно любой точки, лежащей в плоскости действия пары Пусть на тело действует пара сил и . Выберем произвольную точку О и определим момент сил пары относительно этой точки (рис.2.7). Рис. 2.7 Алгебраическая сумма моментов сил пары, взятых относительно некоторой неподвижной точки, лежащей в плоскости действия пары, не зависит от выбора этой точки и равна моменту пары. 2.3.4. Теорема об эквивалентности пар Рассмотрим пару сил и , действующую на твёрдое тело (рис.2.8). Покажем, что пары и имеют одинаковые моменты:
Площади треугольников АВВ´´ и АВВ´ равны, так как у них общее основание АВ и одинаковая высота, т.к. АВ||В´В´´.
На чертежах пару сил принято изображать изогнутым вектором с указанием величины момента. 2.3.5. Сложение пар, расположенных в одной плоскости Система пар, расположенных в одной плоскости может быть заменена одной парой, расположенной в той же плоскости с моментом, равным алгебраической сумме моментов слагаемых пар. Рис. 2.10 Согласно теореме об эквивалентности пар, у любой пары можно произвольно менять силу и плечо пары, сохраняя неизменным его момент. Примем для всех пар одно и то же плечо d = AB (рис. 2.10). Следовательно, силы пар должны быть соответственно равны: Приложим силы к точкам А и В. Сложив силы, получим их равнодействующие: Силы и образуют новую пару, поскольку и , с общим плечом d: Если на тело действует n пар, лежащих в одной плоскости, то результирующая пара равна их алгебраической сумме: Из полученного результата вытекает условие равновесия пар: для равновесия пар, расположенных в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма моментов пар была равна нулю:
Момент равнодействующей плоской системы сходящихся сил относительно любой точки, лежащей в плоскости действия сил, равен алгебраической сумме моментов слагаемых сил относительно этой точки (рис. 2.11).
Рассмотрим систему сил, сходящихся в точке А.
Согласно теореме Вариньона: 2.4. Теорема о параллельном переносе силы (метод Пуансо) Пусть на тело действует сила , приложенная в точке А (рис.2.13).
Действие этой силы не изменится (согласно второй аксиомы статики), если в произвольной точке В тела приложить две уравновешенные силы и , такие, что , . Полученная система трех сил и представляет собой силу равную , но приложенную в точке В, и пару , момент которой равен .
Согласно доказанной теореме силу можно заменить силой , приложенной к концу А бруса и парой с моментом, модуль которого . Если плечо этой пары уменьшить до величины h, то образующие ее силы и надо увеличить так, чтобы . Следовательно, чтобы удержать брус за конец А, надо, кроме силы , приложить еще пару , . Этот результат, вытекающий из теоремы «ощущает» рука человека, удерживающего брус за середину или за конец. 2.5. Приведение произвольной плоской системы сил к данному центру Если на тело действует система сил, то, пользуясь методом Пуансо, все силы можно параллельно перевести в некоторый центр О и сложить их (рис. 2.15). Геометрическая сумма действующих на тело сил называется главным вектором .
Алгебраическая сумма сил пары называется главным моментом системы относительно центра приведения . 2.6. Приведение плоской системы сил к простейшему виду Частные случаи приведения плоской системы сил приведены в табл. 2.1. Таблица 2.1 Частные случаи приведения плоской системы сил к простейшему виду
2.7. Формы уравнений равновесия произвольной плоской системы сил Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы выполнялось одно из следующих условий равновесия (табл. 2.2). Таблица 2.2 Формы уравнений равновесия произвольной системы сил
Равновесие плоской системы параллельных сил. Таблица 2.3 Условия равновесия плоской системы параллельных сил
2.8. Методические указания к решению задач по исследованию условий равновесия произвольной плоской системы сил, приложенной к твердому телу При практическом решении задач можно пользоваться любой формой уравнений равновесия, так как все они совершенно равноправны. Изложим некоторые общие правила составления уравнения равновесия. Пример решения задачи с использованием первой (основной) формы уравнений равновесия Пример. Горизонтальная балка длиной 5 м заделана в стену (рис.2.16). На балку действует равномерно распределенная нагрузка интенсивностью q=1,5 Н/м на участке длиной 3 м, а также пара сил с моментом 2 Н•м и сила F = 4Н.
Определить реакции заделки (XA, YA, MA). Из трех уравнений можно определить три неизвестные величины. Проверка. Сумма моментов относительно точки В: Проверка сошлась. Пример решения задачи с использованием второй формы уравнений равновесия Пример. Однородная балка АВ весом 20 кг опирается на гладкий горизонтальный пол в точке В под углом 60° и, кроме того, поддерживается двумя опорами С и D (рис. 2.17). Решение: Задача сводится к определению реакций опор в точках В, С, D при действии на балку силы тяжести Р = 200Н.
Проверка. Сумма моментов относительно точки В: Проверка сошлась. Пример решения задачи с использованием третьей формы уравнений равновесия Пример. Тяжелая балка силой тяжести G удерживается в горизонтальном положении на трех тросах (рис. 2.18). Определить натяжения тросов. Рис. 2.18 Решение. Рассмотрим равновесие балки. К ней приложена активная сила . Отбросим связи, заменив их реакциями тросов: , и , численно равными искомым натяжениям.
Находим величины АС, ВС и СD: Тогда, решая полученную систему уравнений, получим, что: Проверка. Сумма проекций всех сил на ось Ox: Проверка сошлась. |
Момент силы. Формула момента силы — OneKu
Содержание статьи:- Момент силы в физике
- Скалярная форма записи M¯
- Физический смысл величины M
- Несколько действующих сил в системе
- Совершает ли работу момент силы
- Момент силы и момент импульса
- Равновесие нескольких тел
- Задача с движущимся диском
В физике рассмотрение задач с вращающимися телами или системами, которые находятся в равновесии, осуществляется с использованием концепции «момент силы». В этой статье будет рассмотрена формула момента силы, а также ее использование для решения указанного типа задач.
В этой статье будет рассмотрена формула момента силы, а также ее использование для решения указанного типа задач.
Момент силы в физике
Как было отмечено во введении, в данной статье пойдет речь о системах, которые могут вращаться либо вокруг оси, либо вокруг точки. Рассмотрим пример такой модели, изображенной на рисунке ниже.
Вам будет интересно:Что такое колыбельные песни: фольклор и классика
Мы видим, что рычаг серого цвета закреплен на оси вращения. На конце рычага имеется черный кубик некоторой массы, на который действует сила (красная стрелка). Интуитивно понятно, что результатом воздействия этой силы будет вращение рычага вокруг оси против часовой стрелки.
Моментом силы называется величина в физике, которая равна векторному произведению радиуса, соединяющего ось вращения и точку приложения силы (зеленый вектор на рисунке), и самой внешней силе. То есть формула момента силы относительно оси записывается следующим образом:
Вам будет интересно:Великий князь Алексей Александрович Романов: биография, семья, награды, военная служба
M¯ = r¯ * F¯
Результатом этого произведения будет вектор M¯. Направление его определяют, исходя из знания векторов-множителей, то есть r¯ и F¯. Согласно определению векторного произведения, M¯ должен быть перпендикулярен плоскости, образованной векторами r¯ и F¯, и направлен в соответствии с правилом правой руки (если четыре пальца правой руки расположить вдоль первого умножаемого вектора в направлении к концу второго, то отставленный вверх большой палец укажет, куда направлен искомый вектор). На рисунке можно видеть, куда направлен вектор M¯ (синяя стрелка).
Направление его определяют, исходя из знания векторов-множителей, то есть r¯ и F¯. Согласно определению векторного произведения, M¯ должен быть перпендикулярен плоскости, образованной векторами r¯ и F¯, и направлен в соответствии с правилом правой руки (если четыре пальца правой руки расположить вдоль первого умножаемого вектора в направлении к концу второго, то отставленный вверх большой палец укажет, куда направлен искомый вектор). На рисунке можно видеть, куда направлен вектор M¯ (синяя стрелка).
Скалярная форма записи M¯
На рисунке в предыдущем пункте сила (красная стрелка) действует на рычаг под углом 90o. В общем же случае она может быть приложена под совершенно любым углом. Рассмотрим изображение ниже.
Здесь мы видим, что на рычаг L сила F уже действует под некоторым углом Φ. Для этой системы формула момента силы относительно точки (показана стрелкой) в скалярном виде примет форму:
Вам будет интересно:Уголовное преследование за отрицание Холокоста
M = L * F * sin(Φ)
Из выражения следует, что момент силы M будет тем больше, чем ближе направление действия силы F к углу 90o по отношению к L. Наоборот, если F действует вдоль L, то sin(0) = 0, и сила не создает никакого момента (M = 0).
Наоборот, если F действует вдоль L, то sin(0) = 0, и сила не создает никакого момента (M = 0).
При рассмотрении момента силы в скалярной форме часто пользуются понятием «рычага силы». Эта величина представляет собой расстояние между осью (точкой вращения) и вектором F. Применяя это определение к рисунку выше, можно сказать, что d = L * sin(Φ) — это рычаг силы (равенство следует из определения тригонометрической функции «синус»). Через рычаг силы формулу для момента M можно переписать так:
M = d * F
Физический смысл величины M
Рассматриваемая физическая величина определяет способность внешней силы F оказывать вращательное воздействие на систему. Чтобы привести тело во вращательное движение, ему необходимо сообщить некоторый момент M.
Ярким примером этого процесса является открывание или закрывание двери в комнату. Взявшись за ручку, человек прикладывает усилие и поворачивает дверь на петлях. Каждый сможет это сделать. Если же попытаться открыть дверь, воздействуя на нее вблизи петель, то потребуется приложить большие усилия, чтобы сдвинуть ее с места.
Другим примером является откручивание гайки ключом. Чем короче будет этот ключ, тем труднее выполнить поставленную задачу.
Указанные особенности демонстрирует формула момента силы через плечо, которая была приведена в предыдущем пункте. Если M считать постоянной величиной, то чем меньше d, тем большую F следует приложить для создания заданного момента силы.
Несколько действующих сил в системе
Выше были рассмотрены случаи, когда на систему, способную к вращению, действует всего одна сила F, но как быть, когда таких сил несколько? Действительно, эта ситуация является более частой, поскольку на систему могут действовать силы различной природы (гравитационная, электрическая, трение, механическая и другие). Во всех этих случаях результирующий момент силы M¯ может быть получен с помощью векторной суммы всех моментов Mi¯, то есть:
M¯ = ∑i(Mi¯), где i — номер силы Fi
Из свойства аддитивности моментов следует важный вывод, который получил название теоремы Вариньона, названной так по фамилии математика конца XVII — начала XVIII века — француза Пьера Вариньона. Она гласит: «Сумма моментов всех сил, оказывающих воздействие на рассматриваемую систему, может быть представлена в виде момента одной силы, которая равна сумме всех остальных и приложена к некоторой точке». Математически теорему можно записать так:
Она гласит: «Сумма моментов всех сил, оказывающих воздействие на рассматриваемую систему, может быть представлена в виде момента одной силы, которая равна сумме всех остальных и приложена к некоторой точке». Математически теорему можно записать так:
∑i(Mi¯) = M¯ = d * ∑i(Fi¯)
Эта важная теорема часто используется на практике для решения задач на вращение и равновесие тел.
Совершает ли работу момент силы?
Анализируя приведенные формулы в скалярном или векторном виде, можно прийти к выводу, что величина M — это некоторая работа. Действительно, ее размерность равна Н*м, что в СИ соответствует джоулю (Дж). На самом деле момент силы — это не работа, а лишь величина, которая способна ее совершить. Чтобы это произошло, необходимо наличие кругового движения в системе и продолжительного во времени действия M. Поэтому формула работы момента силы записывается в следующем виде:
A = M * θ
В этом выражении θ — это угол, на который было произведено вращение моментом силы M.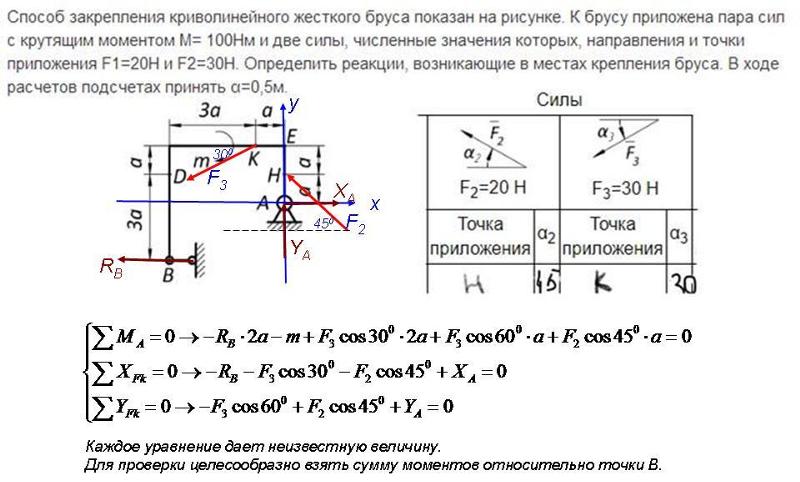 В итоге единицу работы можно записать как Н*м*рад или же Дж*рад. Например, значение 60 Дж*рад говорит о том, что при повороте на 1 радиан (приблизительно 1/3 окружности) создающая момент M сила F совершила работу в 60 джоулей. Эту формулу часто используют при решении задач в системах, где действуют силы трения, что будет показано ниже.
В итоге единицу работы можно записать как Н*м*рад или же Дж*рад. Например, значение 60 Дж*рад говорит о том, что при повороте на 1 радиан (приблизительно 1/3 окружности) создающая момент M сила F совершила работу в 60 джоулей. Эту формулу часто используют при решении задач в системах, где действуют силы трения, что будет показано ниже.
Момент силы и момент импульса
Как было показано, воздействие на систему момента M приводит к появлению в ней вращательного движения. Последнее характеризуется величиной, которая получила название «момент импульса». Его можно вычислить, применяя формулу:
L = I * ω
Здесь I — это момент инерции (величина, которая играет такую же роль при вращении, что и масса при линейном движении тела), ω — угловая скорость, она связана с линейной скоростью формулой ω = v/r.
Оба момента (импульса и силы) связаны друг с другом следующим выражением:
M = I * α, где α = dω / dt — угловое ускорение.
Приведем еще одну формулу, которая важна для решения задач на работу моментов сил. С помощью этой формулы можно вычислить кинетическую энергию вращающегося тела. Она выглядит так:
С помощью этой формулы можно вычислить кинетическую энергию вращающегося тела. Она выглядит так:
Ek = 1/2 * I * ω2
Далее приведем две задачи с решениями, где покажем, как пользоваться рассмотренными физическими формулами.
Равновесие нескольких тел
Первая задача связана с равновесием системы, в которой действуют несколько сил. На рисунке ниже приведена система, на которую действуют три силы. Необходимо рассчитать, какой массы предмет необходимо подвесить к этому рычагу и в какой точке это следует сделать, чтобы данная система находилась в равновесии.
Из условия задачи можно понять, что для ее решения следует воспользоваться теоремой Вариньона. На первую часть задачи можно ответить сразу, поскольку вес предмета, которые следует подвесить к рычагу, будет равен:
P = F1 — F2 + F3 = 20 — 10 + 25 = 35 Н
Знаки здесь выбраны с учетом того, что сила, вращающая рычаг против часовой стрелки, создает отрицательный момент.
Положение точки d, куда следует подвесить этот вес, вычисляется по формуле:
M1 — M2 + M3 = d * P = 7 * 20 — 5 * 10 + 3 * 25 = d * 35 => d = 165/35 = 4,714 м
Отметим, что с помощью формулы момента силы тяжести мы вычислили эквивалентную величину M той, которую создают три силы. Чтобы система находилась в равновесии, необходимо подвесить тело весом 35 Н в точке 4,714 м от оси с другой стороны рычага.
Чтобы система находилась в равновесии, необходимо подвесить тело весом 35 Н в точке 4,714 м от оси с другой стороны рычага.
Задача с движущимся диском
Решение следующей задачи основано на использовании формулы момента силы трения и кинетической энергии тела вращения. Задача: дан диск радиуса r = 0,3 метра, который вращается со скоростью ω = 1 рад/с. Необходимо рассчитать, какое расстояние способен он пройти по поверхности, если коэффициент трения качения равен μ = 0,001.
Эту задачу легче всего решить, если воспользоваться законом сохранения энергии. Мы располагаем начальной кинетической энергией диска. Когда он начнет катиться, то вся эта энергия расходуется на нагрев поверхности за счет действия силы трения. Приравнивая обе величины, получим выражение:
I * ω2/2 = μ * N/r * r * θ
Первая часть формулы — это кинетическая энергия диска. Вторая часть — это работа момента силы трения F = μ * N/r, приложенной к краю диска (M=F * r).
Учитывая, что N = m * g и I = 1/2m * r2, вычисляем θ:
θ = m * r2 * ω2/(4 * μ * m * g) = r2 * ω2/(4 * μ *g) = 0,32 * 12/(4 * 0,001 * 9,81) = 2,29358 рад
Поскольку 2pi радиан соответствуют длине 2pi * r, тогда получаем, что искомое расстояние, которое пройдет диск, равно:
s = θ * r = 2,29358 * 0,3 = 0,688 м или около 69 см
Отметим, что на данный результат масса диска никак не влияет.
Ответил: Определить момент приложенной силы…
Перейти к основному содержанию Химическая инженерияГражданское строительствоКомпьютерная инженерияИнформатикаКибербезопасностьСтруктуры данных и алгоритмыЭлектротехникаМашиностроениеЯзыкИспанскийМатематикаВысшая математикаАлгебраИсчислениеГеометрияВероятностьСтатистикаТригонометрияНаукаПродвинутая физикаАнатомия и физиологияБиохимияБиологияХимияНауки о ЗемлеНауки о здоровьеЗдоровье и питаниеСестринское делоФизикаСоциальные НаукаАнтропологияГеографияИсторияПолитологияПсихологияСоциологиявыучить
написать
плюс
Войти Международное издание — инженерная механика: статика, 4-е издание 4-е изданиеISBN: 978130 5501607
Автор: Эндрю Пытель и Яан Киусалас
Издатель: CENGAGE L
1 Введение в статику2 Основные операции с системами сил3 Результаты систем сил4 Компланарный анализ равновесия5 Трехмерное равновесие6 Балки и канаты7 Сухое трение8 Центроиды и распределенные нагрузки9Моменты и произведения инерции площадей10 Виртуальная работа и потенциальная энергия expand_more
Вопросы главы expand_more
Задача 1. 1P: Человек на Луне весит 30 фунтов, где g=5,32 фута/с2. Определите: а) массу человека; и (b)… Задача 1.2P: Радиус и длина стального цилиндра равны 40 мм и 110 мм соответственно. Если массовая плотность… Задача 1.3P: Преобразуйте следующее: (a) 400lbft в knm; б) от 6 м/с до миль/ч; (c) от 20 фунтов/дюйм2 до Па; и (d)… Задача 1.4P: Компактный автомобиль проезжает 30 миль на одном галлоне бензина. Определить расход бензина автомобиля в км/л. Примечание… Задача 1.5P: Кинетическая энергия автомобиля массы m, движущегося со скоростью v, равна E=mv2/2. Если m=1000 кг и v=6 м/с,… Задача 1.6P: В определенном приложении координата a и координата x положения частицы связаны… Задача 1.7P: Когда сила F действует на линейная пружина, удлинение x пружины определяется как F = kx, где k… Задача 1.8P: В некоторых приложениях, имеющих дело с очень высокими скоростями, скорость измеряется в мм/с. Преобразование 8 мм/с… Задача 1.9P: Учебник геометрии дает уравнение параболы как y=x2, где x и y измеряются в дюймах.
1P: Человек на Луне весит 30 фунтов, где g=5,32 фута/с2. Определите: а) массу человека; и (b)… Задача 1.2P: Радиус и длина стального цилиндра равны 40 мм и 110 мм соответственно. Если массовая плотность… Задача 1.3P: Преобразуйте следующее: (a) 400lbft в knm; б) от 6 м/с до миль/ч; (c) от 20 фунтов/дюйм2 до Па; и (d)… Задача 1.4P: Компактный автомобиль проезжает 30 миль на одном галлоне бензина. Определить расход бензина автомобиля в км/л. Примечание… Задача 1.5P: Кинетическая энергия автомобиля массы m, движущегося со скоростью v, равна E=mv2/2. Если m=1000 кг и v=6 м/с,… Задача 1.6P: В определенном приложении координата a и координата x положения частицы связаны… Задача 1.7P: Когда сила F действует на линейная пружина, удлинение x пружины определяется как F = kx, где k… Задача 1.8P: В некоторых приложениях, имеющих дело с очень высокими скоростями, скорость измеряется в мм/с. Преобразование 8 мм/с… Задача 1.9P: Учебник геометрии дает уравнение параболы как y=x2, где x и y измеряются в дюймах. … Задача 1.10P: Дифференциальное уравнение имеет вид d2ydt2=Ay2+Byt, где y представляет расстояние, а t – время. . Определите… Задача 1.11P: Координата положения x частицы определяется ее скоростью v и прошедшим временем t как… Задача 1.12P: Дифференциальное уравнение, встречающееся при колебании балок, имеет вид d4ydx4=2D, где x = расстояние… Задача 1.13P: Определите размерности констант A и B, относительно которых размерность следующего уравнения… Задача 1.14P: Типичная выходная мощность двигателя компактного автомобиля составляет 110 л.с. Какова эквивалентная мощность в (а)… Задача 1.15P: Два 12-килограммовых шара расположены на расстоянии 400 мм друг от друга. Выразите гравитационное притяжение, действующее между… Задача 1.16P: Два одинаковых шара радиусом 8 дюймов и весом 2 фунта на поверхности земли помещены в… Задача 1.17P: Человек весит 170 фунтов на поверхности земли. Вычислите его вес в самолете, летящем со скоростью… Задача 1.18P: Используйте уравнение. (1.4) чтобы показать, что вес объекта на Луне примерно равен 1/6 его веса на.
… Задача 1.10P: Дифференциальное уравнение имеет вид d2ydt2=Ay2+Byt, где y представляет расстояние, а t – время. . Определите… Задача 1.11P: Координата положения x частицы определяется ее скоростью v и прошедшим временем t как… Задача 1.12P: Дифференциальное уравнение, встречающееся при колебании балок, имеет вид d4ydx4=2D, где x = расстояние… Задача 1.13P: Определите размерности констант A и B, относительно которых размерность следующего уравнения… Задача 1.14P: Типичная выходная мощность двигателя компактного автомобиля составляет 110 л.с. Какова эквивалентная мощность в (а)… Задача 1.15P: Два 12-килограммовых шара расположены на расстоянии 400 мм друг от друга. Выразите гравитационное притяжение, действующее между… Задача 1.16P: Два одинаковых шара радиусом 8 дюймов и весом 2 фунта на поверхности земли помещены в… Задача 1.17P: Человек весит 170 фунтов на поверхности земли. Вычислите его вес в самолете, летящем со скоростью… Задача 1.18P: Используйте уравнение. (1.4) чтобы показать, что вес объекта на Луне примерно равен 1/6 его веса на. .. Задача 1.19P: Постройте график гравитационного ускорения Земли g(м/с2) в зависимости от высоты h (км) над поверхностью… Задача 1.20P: Найдите высоту h (км), на которой вес объекта составляет одну десятую его веса на поверхности… Задача 1.21P: Рассчитайте силу притяжения между Землей и Луной в ньютонах. Расстояние между… Задача 1.22P: Величины двух векторов скорости равны v1=5 м/с и v2=3 м/с. Определить их равнодействующую… Задача 1.23P: Определить величины векторов v1 и v2 так, чтобы их равнодействующая была горизонтальным вектором… Задача 1.24P: Столб AB удерживается веревкой, прикрепленной к B. Величина сила в веревке T = 240 фунтов …. Задача 1.25P: Разложите силу 20 кН на составляющие по осям u и v. Задача 1.26P: Вектор скорости лодки имеет две компоненты: v1 равен скорость воды, а v2 — это… Задача 1.27P: Два элемента фермы прикладывают силы, показанные к косынке. Если равнодействующая этих сил… Задача 1.28P: Два стержня фермы прикладывают указанные силы к косынке.
.. Задача 1.19P: Постройте график гравитационного ускорения Земли g(м/с2) в зависимости от высоты h (км) над поверхностью… Задача 1.20P: Найдите высоту h (км), на которой вес объекта составляет одну десятую его веса на поверхности… Задача 1.21P: Рассчитайте силу притяжения между Землей и Луной в ньютонах. Расстояние между… Задача 1.22P: Величины двух векторов скорости равны v1=5 м/с и v2=3 м/с. Определить их равнодействующую… Задача 1.23P: Определить величины векторов v1 и v2 так, чтобы их равнодействующая была горизонтальным вектором… Задача 1.24P: Столб AB удерживается веревкой, прикрепленной к B. Величина сила в веревке T = 240 фунтов …. Задача 1.25P: Разложите силу 20 кН на составляющие по осям u и v. Задача 1.26P: Вектор скорости лодки имеет две компоненты: v1 равен скорость воды, а v2 — это… Задача 1.27P: Два элемента фермы прикладывают силы, показанные к косынке. Если равнодействующая этих сил… Задача 1.28P: Два стержня фермы прикладывают указанные силы к косынке.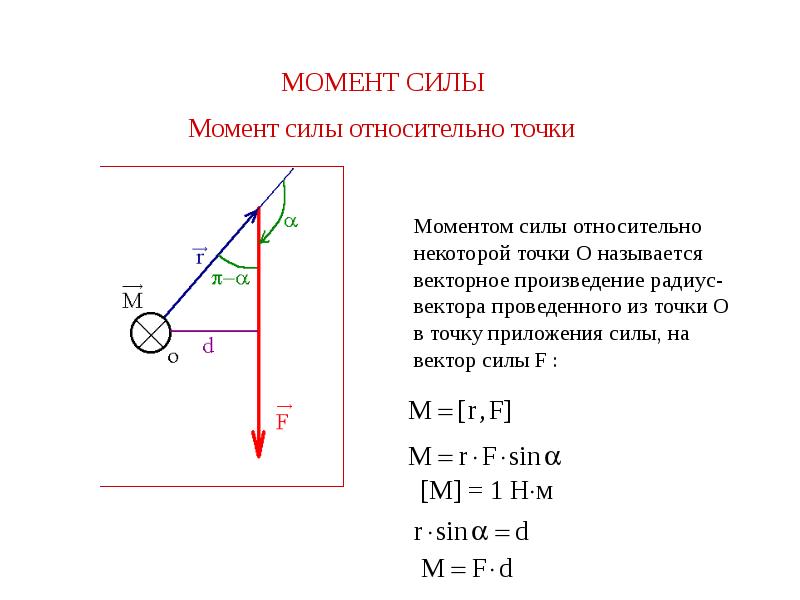 Зная, что P = 10000 фунтов,… Задача 1.29P: Определите равнодействующую векторов положения A и B. Задача 1.30P: Разложите вектор положения автомобиля A (отсчитываемый от фиксированной точки O) на компоненты, параллельные… Задача 1.31P: Разложите силу в 360 фунтов на компоненты вдоль кабелей AB и AC. Используйте =60 и =40. Задача 1.32P: Несущие тросы AB и AC ориентированы так, что компоненты 3604b действуют вдоль AB и… Задача 1.33P: Две показанные силы действуют на элемент конструкции AB. Определите величину P так, чтобы… Задача 1.34P: равнодействующая двух сил имеет величину 800 фунтов. Определите направление равнодействующей… Задача 1.35P: силы, действующие на груз маятника — его вес W (w = 2 фунта) и натяжение T шнура …. Задача 1.36P: Геодезист наводит цель в точке C из точек A и B. регистрируя показанные углы. Определите… Задача 1.37P: Зная, что равнодействующая двух сил вертикальна, определите угол Задача 1.38P: Чтобы сдвинуть бочку с маслом, равнодействующая трех показанных сил должна иметь величину 500 Н.
Зная, что P = 10000 фунтов,… Задача 1.29P: Определите равнодействующую векторов положения A и B. Задача 1.30P: Разложите вектор положения автомобиля A (отсчитываемый от фиксированной точки O) на компоненты, параллельные… Задача 1.31P: Разложите силу в 360 фунтов на компоненты вдоль кабелей AB и AC. Используйте =60 и =40. Задача 1.32P: Несущие тросы AB и AC ориентированы так, что компоненты 3604b действуют вдоль AB и… Задача 1.33P: Две показанные силы действуют на элемент конструкции AB. Определите величину P так, чтобы… Задача 1.34P: равнодействующая двух сил имеет величину 800 фунтов. Определите направление равнодействующей… Задача 1.35P: силы, действующие на груз маятника — его вес W (w = 2 фунта) и натяжение T шнура …. Задача 1.36P: Геодезист наводит цель в точке C из точек A и B. регистрируя показанные углы. Определите… Задача 1.37P: Зная, что равнодействующая двух сил вертикальна, определите угол Задача 1.38P: Чтобы сдвинуть бочку с маслом, равнодействующая трех показанных сил должна иметь величину 500 Н.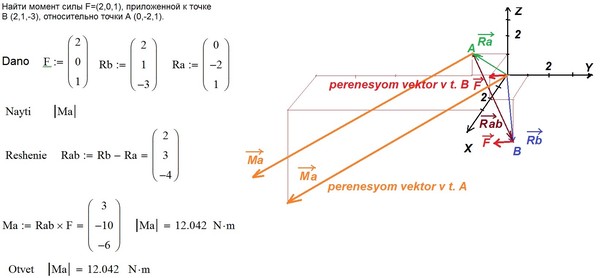 … Задача 1.39P: Равнодействующая сил 50 фунтов и 30 фунтов равна R. Если R = 65 фунтов, определите углы и . 1.41P: Длина вектора положения r составляет 240 мм. Определите прямоугольные компоненты (a) r; и… Задача 1.42P: Определите прямоугольные компоненты силы в 560 фунтов. Покажите компоненты на эскизе. Задача 1.43P: Координаты точек A и B равны (-3, 0, 2) фута и (4, 1, 7) фута соответственно. Определить (a)… Задача 1.44P: Ползун движется по направляющей AB со скоростью v = 8 м/г. Определите прямоугольную… Задача 1.45P: Найдите прямоугольное представление силы F, учитывая, что ее модуль равен 320 Н. Задача 1.46P: Модуль силы F равен 160 фунтам. Найдите ее прямоугольное представление. Задача 1.47P: Винтовка в точке А стреляет по цели в точке В. Если скорость пули составляет 1400 футов/с, определите… Задача 1.48P: На шест OB действует сила 6004b в точке В. Определите (а) прямоугольные компоненты… Задача 1.49P: Тросы AB и AC прикреплены к раме OBCD и предварительно натянуты до 35 кН.
… Задача 1.39P: Равнодействующая сил 50 фунтов и 30 фунтов равна R. Если R = 65 фунтов, определите углы и . 1.41P: Длина вектора положения r составляет 240 мм. Определите прямоугольные компоненты (a) r; и… Задача 1.42P: Определите прямоугольные компоненты силы в 560 фунтов. Покажите компоненты на эскизе. Задача 1.43P: Координаты точек A и B равны (-3, 0, 2) фута и (4, 1, 7) фута соответственно. Определить (a)… Задача 1.44P: Ползун движется по направляющей AB со скоростью v = 8 м/г. Определите прямоугольную… Задача 1.45P: Найдите прямоугольное представление силы F, учитывая, что ее модуль равен 320 Н. Задача 1.46P: Модуль силы F равен 160 фунтам. Найдите ее прямоугольное представление. Задача 1.47P: Винтовка в точке А стреляет по цели в точке В. Если скорость пули составляет 1400 футов/с, определите… Задача 1.48P: На шест OB действует сила 6004b в точке В. Определите (а) прямоугольные компоненты… Задача 1.49P: Тросы AB и AC прикреплены к раме OBCD и предварительно натянуты до 35 кН. Определите… Задача 1.50P: Две силы приложены к концу стрелы OA. Определите силу F так, чтобы равнодействующая… Задача 1.51P: Величины трех сил равны F1=1,6 кН, F2=1,2 кН и F3=1,0 кН. Вычислите их результирующую в… Задача 1.52P: Учитывая, что P=120lb и Q=130lb, найдите прямоугольное представление P+Q. Задача 1.53P: Зная, что P=90lb и что результирующая P и Q лежит в Положительное направление x, определите Q… Задача 1.54P: Если R является равнодействующей сил P и Q, найдите P и Q. Задача 1.55P: Сила R является равнодействующей P и 0. Определите Q и угол. Задача 1.56P: Вертикальная стойка закреплена тремя тросами. Кабели предварительно натянуты так, что результирующая… Задача 1.57P: Вычислите скалярное произведение A — B для каждого из следующих случаев. Определите единицы каждого продукта…. Задача 1.58P: Вычислите векторное произведение C=AB для каждого из случаев, указанных в Prob. 1.51 Определите единицы измерения каждого… Задача 1.59P: задано r=4i6j+2km (вектор положения) F=20i+40j30kN (вектор силы) =0,8j+0,6k (безразмерная единица.
Определите… Задача 1.50P: Две силы приложены к концу стрелы OA. Определите силу F так, чтобы равнодействующая… Задача 1.51P: Величины трех сил равны F1=1,6 кН, F2=1,2 кН и F3=1,0 кН. Вычислите их результирующую в… Задача 1.52P: Учитывая, что P=120lb и Q=130lb, найдите прямоугольное представление P+Q. Задача 1.53P: Зная, что P=90lb и что результирующая P и Q лежит в Положительное направление x, определите Q… Задача 1.54P: Если R является равнодействующей сил P и Q, найдите P и Q. Задача 1.55P: Сила R является равнодействующей P и 0. Определите Q и угол. Задача 1.56P: Вертикальная стойка закреплена тремя тросами. Кабели предварительно натянуты так, что результирующая… Задача 1.57P: Вычислите скалярное произведение A — B для каждого из следующих случаев. Определите единицы каждого продукта…. Задача 1.58P: Вычислите векторное произведение C=AB для каждого из случаев, указанных в Prob. 1.51 Определите единицы измерения каждого… Задача 1.59P: задано r=4i6j+2km (вектор положения) F=20i+40j30kN (вектор силы) =0,8j+0,6k (безразмерная единица.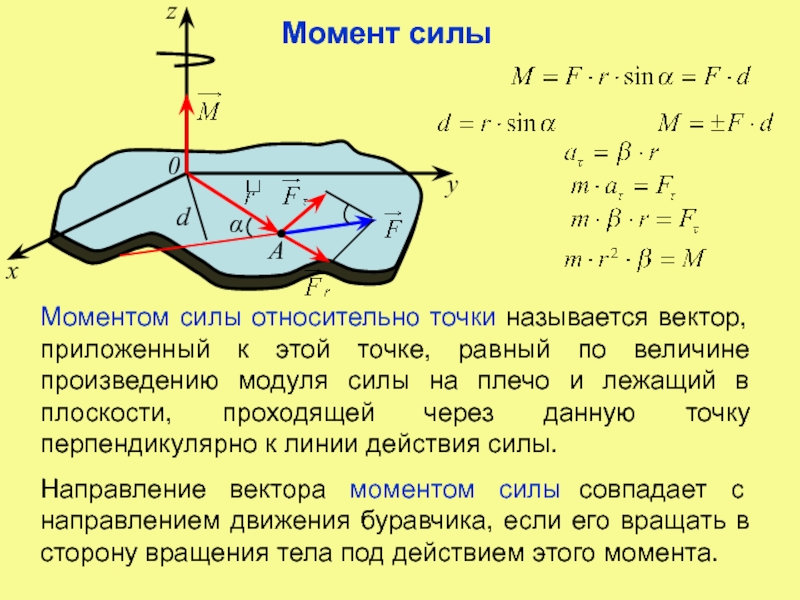 .. Задача 1.60P: вычислить AB и CB для показанных векторов положения. Задача 1.61P : Используйте скалярное произведение, чтобы найти угол между векторами положения A и B. Проверьте свои результаты с помощью… Задача 1.62P: Используйте скалярное произведение, чтобы найти угол между векторами положения A и B. Задача 1.63P: Пусть A и B — два непараллельных вектора, лежащих в общей плоскости S. Если C=A(AB), то какой из… Задача 1.64P: Определить (a) угол между векторами положения P и Q и (b) единичный вектор, перпендикулярный… Задача 1.65P: найти единичный вектор, который перпендикулярен как A=4i-3j-2km, так и B=2i4j+3km. Задача 1.66P: три точки A(0,2,2) ,B(1,4,1) и C(3,0,0) определяют плоскость. Координаты указаны в дюймах. Найти… Задача 1.67P: Для показанных векторов положения P и Q определить ортогональную составляющую P Ă— Q в… Задача 1.68P: Вычислить ортогональную составляющую F=6i+20j12klb в направлении вектора A=2i3j+5kft. Задача 1.69P: Вычислите значение скаляра a, для которого векторы A=3i+aj+2k и B=4ijk будут перпендикулярны.
.. Задача 1.60P: вычислить AB и CB для показанных векторов положения. Задача 1.61P : Используйте скалярное произведение, чтобы найти угол между векторами положения A и B. Проверьте свои результаты с помощью… Задача 1.62P: Используйте скалярное произведение, чтобы найти угол между векторами положения A и B. Задача 1.63P: Пусть A и B — два непараллельных вектора, лежащих в общей плоскости S. Если C=A(AB), то какой из… Задача 1.64P: Определить (a) угол между векторами положения P и Q и (b) единичный вектор, перпендикулярный… Задача 1.65P: найти единичный вектор, который перпендикулярен как A=4i-3j-2km, так и B=2i4j+3km. Задача 1.66P: три точки A(0,2,2) ,B(1,4,1) и C(3,0,0) определяют плоскость. Координаты указаны в дюймах. Найти… Задача 1.67P: Для показанных векторов положения P и Q определить ортогональную составляющую P Ă— Q в… Задача 1.68P: Вычислить ортогональную составляющую F=6i+20j12klb в направлении вектора A=2i3j+5kft. Задача 1.69P: Вычислите значение скаляра a, для которого векторы A=3i+aj+2k и B=4ijk будут перпендикулярны. Задача 1.70P: Разложите A=3i+5j4k на две компоненты вектора: другая перпендикулярна… Задача 1.71P: К ручке двери приложена сила F=5i+12j+4k фунт. Определите ортогональную составляющую… Задача 1.72P: Определите значение скаляра a, если следующие три вектора лежат в одной плоскости:… Задача 1.73P: Разложите силу F=20i+30j+50klb в виде две компоненты — одна перпендикулярна плоскости ABC, а другая… Задача 1.74P: Можно показать, что плоская площадь может быть представлена вектором A=A, где A — площадь, а… Задача 1.75P: координаты углов треугольника ABC равны A(3,1,0),B(2,2,3) и C(0,0,4). Единицы… Задача 1.76P: Покажите, что |abc| равен объему параллелепипеда, ребра которого равны а, b и с. (Подсказка: см…. format_list_bulleted
Задача 1.70P: Разложите A=3i+5j4k на две компоненты вектора: другая перпендикулярна… Задача 1.71P: К ручке двери приложена сила F=5i+12j+4k фунт. Определите ортогональную составляющую… Задача 1.72P: Определите значение скаляра a, если следующие три вектора лежат в одной плоскости:… Задача 1.73P: Разложите силу F=20i+30j+50klb в виде две компоненты — одна перпендикулярна плоскости ABC, а другая… Задача 1.74P: Можно показать, что плоская площадь может быть представлена вектором A=A, где A — площадь, а… Задача 1.75P: координаты углов треугольника ABC равны A(3,1,0),B(2,2,3) и C(0,0,4). Единицы… Задача 1.76P: Покажите, что |abc| равен объему параллелепипеда, ребра которого равны а, b и с. (Подсказка: см…. format_list_bulleted
См. похожие учебники
1. Пожалуйста, решите эту задачу и покажите свое решение.
Транскрибированный текст изображения:1.
Определить момент данной силы F относительно точки 0, показанной на рисунке.
Фигура:
Ф = 180
+ у
5м
2 м
+ Х
а. Путем вычисления перпендикулярного расстояния между заданной силой F и центром момента 0.
Формула: (Mo = Fdo)
б. По теореме Вариньона. Формула: (М, = Fxy + Fyx)
%3D
Путем вычисления перпендикулярного расстояния между заданной силой F и центром момента 0.
Формула: (Mo = Fdo)
б. По теореме Вариньона. Формула: (М, = Fxy + Fyx)
%3D
Калькулятор крутящего момента
Создано Bogna Szyk
Отзыв Стивена Вудинга
Последнее обновление: 05 июня 2023 г.
Содержание:- Уравнение крутящего момента
- Как рассчитать крутящий момент
- Часто задаваемые вопросы
Этот калькулятор крутящего момента поможет вам найти крутящий момент, возникающий во вращающемся объекте. Что именно представляет собой этот крутящий момент? Представьте себе объект, который может вращаться вокруг некоторой точки, называемой точкой вращения. Если приложить силу на некотором расстоянии от точки опоры, то хоть сила и будет действовать по прямой линии, объект начнет вращаться. Продолжайте читать, если вы хотите узнать, как рассчитать крутящий момент, и получить подробное объяснение формулы крутящего момента.
Если вам нужен крутящий момент в контексте автомобильной промышленности, то калькулятор крутящего момента в л. с. может быть для вас!
с. может быть для вас!
Уравнение крутящего момента
Крутящий момент (склонность объекта к вращению) зависит от трех разных факторов:
τ = rFsin(θ)
где:
-
r— плечо рычага — расстояние между точка поворота и точка приложения силы; -
F— сила, действующая на объект; -
θ— угол между вектором силы и плечом рычага. Обычно он равен 90°; и -
τ— крутящий момент. Единицами крутящего момента являются ньютон-метры (обозначение: Н·м).
Представьте, что вы пытаетесь открыть дверь. Точка поворота — это просто место, где расположены петли. Чем ближе вы к петлям, тем большее усилие вы должны приложить. Однако, если вы используете ручку, плечо рычага увеличится, и дверь откроется с меньшим усилием.
💡 Не путайте это понятие с центробежной силой — центробежная сила направлена к точке поворота, параллельно плечу рычага. Такая сила не вызывает крутящего момента (это можно проверить, подставив угол 0° в формулу крутящего момента).
Такая сила не вызывает крутящего момента (это можно проверить, подставив угол 0° в формулу крутящего момента).
Как рассчитать крутящий момент
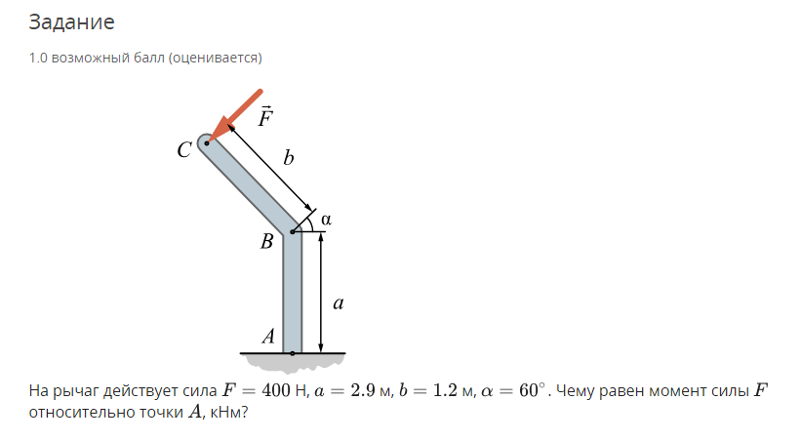
- Начните с определения силы, действующей на объект. Предположим, что
F = 120 N. - Выберите длину плеча рычага. В нашем примере
r = 0,5 м. - Выберите угол между вектором силы и плечом рычага. Если он не равен 90° по умолчанию, откройте расширенный режим калькулятора, чтобы изменить его. Предположим, что
θ = 90°. Используйте расширенный режим для изменения значения θ. - Введите эти значения в наш калькулятор крутящего момента. В нем используется уравнение крутящего момента:
τ = rFsin(θ) = 0,5 * 120 * sin(90°) = 60 Н·м. - Калькулятор крутящего момента также может работать в обратном направлении, определяя силу или плечо рычага, если задан крутящий момент.
Если вы хотите узнать больше о концепции силы и втором законе Ньютона, попробуйте калькулятор ускорения и калькулятор второго закона Ньютона.
Часто задаваемые вопросы
Как рассчитать крутящий момент?
Для расчета крутящего момента следуйте приведенным инструкциям:
Узнать величину приложенной силы,
F.Измерьте расстояние ,
r, между точкой вращения и точкой приложения силы.Определите угол
θмежду направлением приложенной силы и вектором между точкой приложения силы и точкой поворота.Умножьте
rнаFиsin θи вы получите крутящий момент.
Что такое единица крутящего момента в системе СИ?
Единицей крутящего момента в системе СИ является ньютон-метр или Н⋅м . Чтобы выразить крутящий момент в имперские единицы мы используем фунт-сила-фут или lbf·ft .



 2.2). Разложим силу на две составляющие силы, одна из которых равна , а вторая .
2.2). Разложим силу на две составляющие силы, одна из которых равна , а вторая . 2.3а).
2.3а).
 Из треугольника АВD имеем: .
Из треугольника АВD имеем: .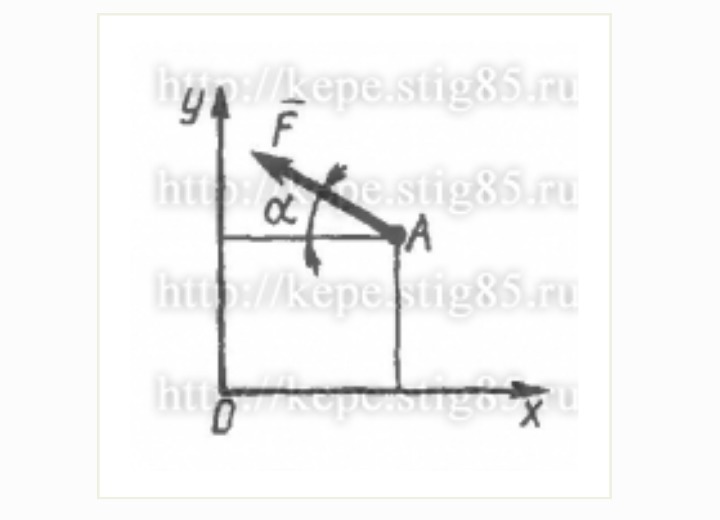 Они являются скользящими векторами, их можно складывать с другими силами системы сил, добавлять к паре сил и отбрасывать системы сил, эквивалентные нулю. Действие пары сил на твердое тело зависит от плоскости действия пары сил, ее момента, определяющего вращательную способность и направление вращения, в котором пара сил стремиться вращать тело.
Они являются скользящими векторами, их можно складывать с другими силами системы сил, добавлять к паре сил и отбрасывать системы сил, эквивалентные нулю. Действие пары сил на твердое тело зависит от плоскости действия пары сил, ее момента, определяющего вращательную способность и направление вращения, в котором пара сил стремиться вращать тело.
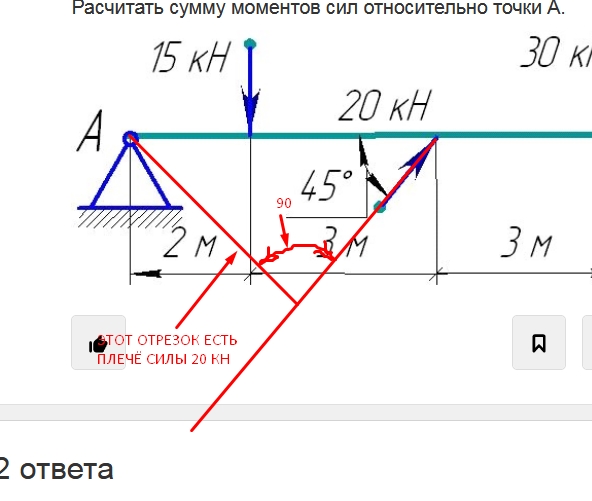
 3.6. Теорема о моменте равнодействующей плоской системы сходящихся сил (теорема Вариньона)
3.6. Теорема о моменте равнодействующей плоской системы сходящихся сил (теорема Вариньона)
 Тогда , где , .
Тогда , где , . Присоединённые пары сил также можно сложить.
Присоединённые пары сил также можно сложить.


 В том случае, когда все силы параллельны друг другу, одну из координатных осей следует направить параллельно силам.
В том случае, когда все силы параллельны друг другу, одну из координатных осей следует направить параллельно силам.
 Тогда при составлении уравнений проекций неизвестные, перпендикулярные к осям, в эти уравнения не войдут. За моментные целесообразно брать такие точки, в которых пересекаются линии действия двух неизвестных сил. Тогда в уравнение моментов войдет только одна искомая сила.
Тогда при составлении уравнений проекций неизвестные, перпендикулярные к осям, в эти уравнения не войдут. За моментные целесообразно брать такие точки, в которых пересекаются линии действия двух неизвестных сил. Тогда в уравнение моментов войдет только одна искомая сила.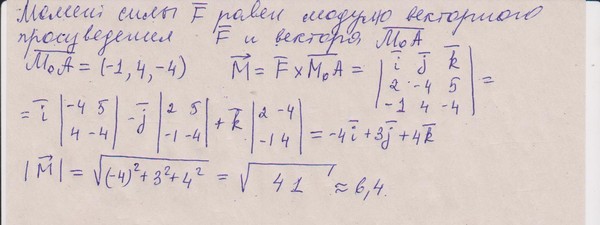
 Для этого следует составить не применявшуюся при решении сумму моментов или проекций, при этом необходимо учитывать уже исправленные направления реакций. Равенство нулю алгебраической суммы проекций или моментов подтвердит правильность решения задачи.
Для этого следует составить не применявшуюся при решении сумму моментов или проекций, при этом необходимо учитывать уже исправленные направления реакций. Равенство нулю алгебраической суммы проекций или моментов подтвердит правильность решения задачи.
 Задача статически определима, так как имеется три неизвестных. Выберем три моментные точки А, В и С (рис. 2.19), в каждой из которых пересекаются по две неизвестные силы, и составим три уравнения:
Задача статически определима, так как имеется три неизвестных. Выберем три моментные точки А, В и С (рис. 2.19), в каждой из которых пересекаются по две неизвестные силы, и составим три уравнения: