Виды сил. Видеоурок. Физика 7 Класс

В ходе данного урока «Виды сил» мы ознакомимся с различными силами, которые действуют вокруг нас, научимся описывать их и решать задачи. Узнаем о равнодействующей силе сразу нескольких сил и о взаимодействии тел.

Тела взаимодействуют, и эти взаимодействия влияют на то, будет ли двигаться тело и как именно. Силы взаимодействия определяют ускорение. Какова природа этих сил? Можно толкнуть тело рукой, и оно сдвинется – с таким действием всё понятно. Но есть множество других взаимодействий. Например, если мы разожмём пальцы, то тело упадёт вниз. В воздухе тело упадет быстрее, чем тонуло бы в воде. Это означает, что на тело действуют какие-то силы. Тело лежит на столе и давит на него – тоже взаимодействие. Вещества состоят из структурных частиц – эти частицы как-то взаимодействуют друг с другом. Возникает вопрос, как это всё учесть и рассчитать, ведь нам приходится отвечать на вопрос: «Что, если…?», предсказывать явления.

Любые два тела притягиваются. Явление притяжения по-другому называют гравитацией. Мы её ощущаем по тому, что Земля притягивает тела: преодолеваем гравитацию, когда поднимаем что-то тяжелое, и наблюдаем её действие, когда тело падает. Сила притяжения зависит от масс тел и от расстояния между ними. Масса Земли огромна, поэтому к ней тела притягиваются заметно. Две книги на полке тоже притягиваются друг к другу, но так слабо из-за малых масс, что мы этого не замечаем.

Притягивает ли нас Луна? А Солнце? Да, но намного меньше, чем Земля, из-за большого расстояния. Мы на себе притяжение Луны не ощущаем, а вот приливы и отливы происходят из-за притяжения Луны и Солнца. А черные дыры обладают настолько большой массой, что притягивают даже свет: проходящие мимо лучи искривляются.

Все тела притягиваются. Возьмем тело, которое лежит на столе. Оно притягивается к Земле, но остается на месте. Чтобы сохранялось состояние покоя, силы, действующие на тело, должны быть уравновешены. Значит должна быть сила, которая уравновешивает силу тяжести. В данном случае это сила, с которой на тело действует стол. Такую силу назвали силой реакции опоры (см. рис. 1).

При этом тело давит на стол. Если мы рассматриваем, как движется тело, нам не важно, что происходит со столом. Но если мы рассматриваем, что произойдет со столом, то нужно будет учесть это воздействие. Силу, с которой тело действует на опору или подвес, назвали весом:

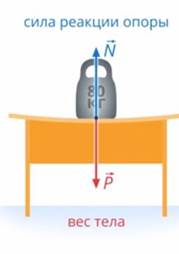
Рис. 1. Взаимодействие гири и стола

Чтобы сдвинуть любое тело, надо приложить силу. В этом и заключается инертность. Если мы попробуем сдвинуть гирю на столе, она до некоторого предела вообще не сдвинется. Значит и здесь возникает некоторая сила, которая уравновешивает наше воздействие. Эта сила – сила трения:

Рис. 2. Сила трения

 Что-то похожее происходит, когда мы поднимаем гирю. Она тоже сначала не поднимается, пока наша сила не превзойдет порог: здесь этот порог – сила притяжения Земли.

Если вместо стола будет пружина, она сожмется, и будет также действовать на это тело. Тело действует на стол или пружину, они прогибаются, их молекулы смещаются (см. рис. 3), а при смещении молекул между ними возникают силы отталкивания, препятствующие дальнейшей деформации:

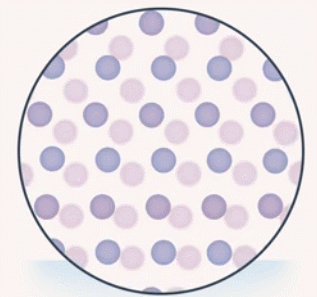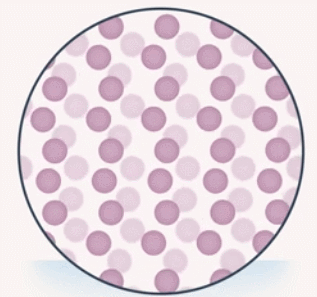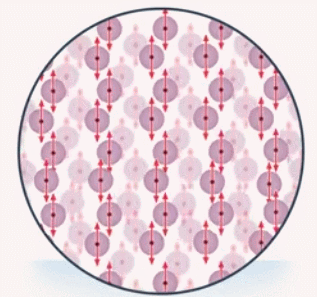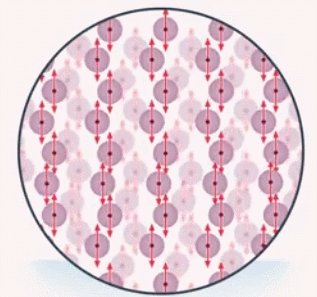
Рис. 3. Сила отталкивания

Отличие в том, что деформация стола чаще всего настолько мала, что ее трудно заме

Сила тяжести — Википедия

Cила тяжести mg складывается из гравитационного притяжения планеты GMm/r² и центробежной силы инерции mω²a.

Си́ла тя́жести — сила, действующая на любое физическое тело, находящееся вблизи поверхности Земли или другого астрономического тела.

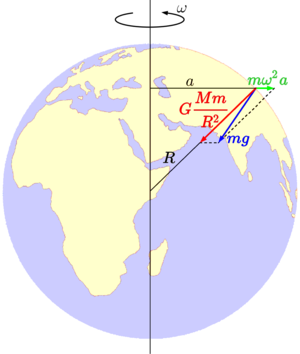
По определению, сила тяжести на поверхности планеты складывается из гравитационного притяжения планеты и центробежной силы инерции, вызванной суточным вращением планеты^[1][2].

Остальные силы (например, притяжение Луны и Солнца) ввиду их малости не учитывают или изучают отдельно как временные изменения гравитационного поля Земли

[3]^[4][5].

Сила тяжести сообщает всем телам, независимо от их массы, одно и то же ускорение^[6] и является консервативной силой^[7].

Сила тяжести P→{\displaystyle {\vec {P}}}, действующая на материальную точку массой m{\displaystyle m}, вычисляется по формуле^[6]:

P→=mg→{\displaystyle {\vec {P}}=m{\vec {g}}}

где:

Если в пределах протяжённого тела поле сил тяжести однородно, то равнодействующая сил тяжести, действующих на элементы этого тела, приложена к центру масс тела^[9].

На тела, движущиеся относительно поверхности Земли, кроме силы тяжести, также действует сила Кориолиса^[10][11]

^[12].

Аристотель объяснял силу тяжести движением тяжёлых физических стихий (земля, вода) к своему естественному месту (центру Вселенной внутри Земли), причём скорость тем больше, чем ближе тяжёлое тело к нему^[13].

Архимед рассмотрел вопрос о центре тяжести параллелограмма, треугольника, трапеции и параболического сегмента. В сочинении «О плавающих телах» Архимед доказал закон гидростатики, носящий его имя^[13].

Иордан Неморарий в сочинении «О тяжестях» при рассмотрении грузов на наклонной плоскости разлагал их силы тяжести на нормальную и параллельную наклонной плоскости составляющие, был близок к определению статического момента^[14]

.

Стевин экспериментально определил, что тела разных масс падают с одинаковым ускорением, установил теоремы о давлении жидкости в сосудах (давление зависит только от глубины и не зависит от величины, формы и объёма сосуда) и о равновесии грузов на наклонной плоскости (на наклонных плоскостях равной высоты силы, действующие со стороны уравновешивающихся грузов вдоль наклонных плоскостей, обратно пропорциональны длинам этих плоскостей). Доказал теорему, согласно которой в случае равновесия центр тяжести однородного плавающего тела должен находиться выше центра тяжести вытесненной жидкости^[15].

Галилей экспериментально исследовал законы падения тел (ускорение не зависит от веса тела), колебаний маятников (период колебаний не зависит от веса маятника) и движения по наклонной плоскости

[16].

Гюйгенс создал классическую теорию движения маятника, оказавшую значительное влияние на теорию тяготения^[16].

Декарт разработал кинетическую теорию тяготения, объяснявшую силу тяжести взаимодействием тел с небесным флюидом, выдвинул гипотезу о зависимости силы тяжести от расстояния между тяжёлым телом и центром Земли^[16].

Ньютон из равенства ускорений падающих тел и второго закона Ньютона сделал вывод о пропорциональности силы тяжести массам тел и установил, что сила тяжести является одним из проявлений силы всемирного тяготения

[17]^[18]. Для проверки этой идеи он сравнил ускорение свободного падения тел у поверхности Земли с ускорением Луны на орбите, по которой она движется относительно Земли.^[19]

Эйнштейн объяснил факт равенства ускорений падающих тел независимо от их массы (эквивалентность инертной и тяжёлой массы) как следствие принципа эквивалентности равномерно ускоренной системы отсчёта и системы отсчёта, находящейся в гравитационном поле^[20].

В соответствии с законом всемирного тяготения, сила гравитационного притяжения, действующая на материальную точку массой m{\displaystyle m} на поверхности сферически симметричного астрономического тела, имеющего массу M{\displaystyle M}, определяется соотношением:

F=G⋅M⋅mR2,{\displaystyle F=G\cdot {M\cdot m \over R^{2}},}

где:

Данное соотношение справедливо в предположении, что распределение массы по объёму тела сферически симметрично. В этом случае сила гравитационного притяжения направлена к центру тела.

Модуль центробежной силы инерции Q{\displaystyle Q}, действующей на материальную частицу, выражается формулой:

Q=maω2,{\displaystyle Q=ma\omega ^{2},}

где:

• a{\displaystyle a} — расстояние между частицей и осью вращения рассматриваемого астрономического тела,
• ω{\displaystyle \omega } — угловая скорость его вращения.

Центробежная сила инерции перпендикулярна оси вращения и направлена в сторону от неё.

Поправки, вносимые общей теорией относительности в закон всемирного тяготения Ньютона, в условиях Земли и других планет крайне малы (модуль гравитационного потенциала на поверхности Земли, равный половине квадрата второй космической скорости vII{\displaystyle v_{II}}, крайне мал по сравнению с квадратом скорости света c{\displaystyle c}: vII22c2∼10−10{\displaystyle {\frac {v_{II}^{2}}{2c^{2}}}\sim 10^{-10}})^[21].

Форма Земли (геоид) отличается от шарообразной и близка к сплюснутому эллипсоиду. В этом случае сила гравитационного притяжения, действующая на материальную точку массой m{\displaystyle m}, определяется более сложным выражением, чем ранее:

F→=Gm∫MdMR2R→R.{\displaystyle {\vec {F}}=Gm\int \limits _{M}{{dM} \over {R^{2}}}{{\vec {R}} \over R}.}

где:

• dM{\displaystyle dM} — элемент массы Земли,
• R→=r→−r→′,{\displaystyle {\vec {R}}={\vec {r}}-{\vec {r}}’,}
• r→{\displaystyle {\vec {r}}} и r→′{\displaystyle {{\vec {r}}’}} — радиус-векторы точки измерения и элемента Земли соответственно.

Интегрирование при этом выполняется по всей массе Земли.

В векторной форме выражение для центробежной силы инерции можно записать в виде

Q→=mω2R→0,{\displaystyle {\vec {Q}}=m\omega ^{2}{{\vec {R}}_{0}},}

где:

• R→0{\displaystyle {{\vec {R}}_{0}}} — вектор, перпендикулярный оси вращения и проведённый от неё к данной материальной точке, находящейся вблизи поверхности Земли.

При этом сила тяжести P→{\displaystyle {\vec {P}}}, как и раньше, равна сумме F→{\displaystyle {\vec {F}}} и Q→{\displaystyle {\vec {Q}}}:

P→=F→+Q→.{\displaystyle {\vec {P}}={\vec {F}}+{\vec {Q}}.}

Сила тяжести, действующая вблизи поверхности Земли, зависит от широты места φ{\displaystyle \varphi } и высоты его H{\displaystyle H} над уровнем моря. Приблизительное выражение для абсолютной величины силы тяжести в системе СИ имеет вид^[8]:

P=9,780318(1+0,005302sin⁡φ−0,000006sin2⁡2φ)m−0,000003086Hm.{\displaystyle P=9{,}780318(1+0{,}005302\sin \varphi -0{,}000006\sin ^{2}2\varphi )m-0{,}000003086Hm.}

Угол α{\displaystyle \alpha } между силой тяжести P→{\displaystyle {\vec {P}}} и силой гравитационного притяжения к Земле F→{\displaystyle {\vec {F}}} равен^[22]:

α≈0,0018sin⁡2φ{\displaystyle \alpha \approx 0{,}0018\sin {2\varphi }}.

Он изменяется в пределах от нуля (на экваторе, где φ=0∘{\displaystyle \varphi =0^{\circ }} и на полюсах, где φ=90∘{\displaystyle \varphi =90^{\circ }}) до 0,0018{\displaystyle 0{,}0018} рад или 6′{\displaystyle 6′} (на широте 45∘{\displaystyle 45^{\circ }}).

Движение тел под действием силы тяжести[править | править код]

В том случае, когда модуль перемещения тела много меньше расстояния до центра Земли, то можно считать силу тяжести постоянной, а движение тела равноускоренным. Если начальная скорость тела отлична от нуля и её вектор направлен не по вертикали, то под действием силы тяжести тело движется по параболической траектории.

При бросании тела с некоторой высоты параллельно поверхности Земли дальность полёта увеличивается с ростом начальной скорости. При больших значениях начальной скорости для вычисления траектории тела необходимо учитывать шарообразную форму Земли и изменение направления силы тяжести в разных точках траектории.

При некотором значении скорости, называемом первой космической скоростью, тело, брошенное по касательной к поверхности Земли, под действием силы тяжести при отсутствии сопротивления со стороны атмосферы может двигаться вокруг Земли по окружности, не падая на Землю. При скорости, превышающую вторую космическую скорость, тело уходит от поверхности Земли в бесконечность по гиперболической траектории. При скоростях, промежуточных между первой и второй космическими, тело движется вокруг Земли по эллиптической траектории^[23].

Потенциальная энергия поднятого над Землей тела[править | править код]

Потенциальной энергией поднятого над Землей тела называется взятая с обратным знаком работа силы тяжести, совершаемая при перемещении тела с поверхности Земли в это положение. Она равна:

Ep=GMm(1Rz−1R){\displaystyle E_{p}=GMm({\frac {1}{R_{z}}}-{\frac {1}{R}})},

где:

При удалении тела не небольшие по сравнению с радиусом Земли расстояния от поверхности Земли поле тяготения можно считать однородным, то есть ускорение свободного падения постоянно. В этом случае при подъеме тела массой m{\displaystyle m} на высоту h{\displaystyle h} от поверхности Земли сила тяжести совершает работу A=−mgh{\displaystyle A=-mgh}. Поэтому потенциальная энергия тела: Ep=mgh{\displaystyle E_{p}=mgh}. Потенциальная энергия тела может иметь как положительные, так и отрицательные значения. Тело, находящееся на глубине h{\displaystyle h} от поверхности Земли обладает отрицательным значением потенциальной энергии Ep=−mgh{\displaystyle E_{p}=-mgh}^[24].

При испарении воды с поверхности Земли солнечная радиация трансформируется в потенциальную энергию водяного пара в атмосфере. Затем при выпадении атмосферных осадков на сушу она переходит при стоке в кинетическую энергию и совершает эрозионную работу в процессе переноса денудационного материала всей суши и делает возможным жизнь органического мира на Земле^[25].

Потенциальная энергия перемещаемых тектоническими процессами масс горных пород в основном тратится на перемещение продуктов разрушения горных пород с повышенных участков поверхности на нижерасположенные^[26].

Сила тяжести играет важную роль в процессах эволюции звёзд. Для звёзд, находящихся на этапе главной последовательности своей эволюции, сила тяжести является одним из важных факторов, обеспечивающих условия, необходимые для термоядерного синтеза. На заключительных этапах эволюции звёзд, в процессе их коллапса, благодаря силе тяжести, не скомпенсированной силами внутреннего давления, звёзды превращаются в нейтронные звёзды или чёрные дыры.

Сила тяжести очень важна для формирования структуры внутреннего строения Земли и других планет и тектонической эволюции её поверхности^[27]. Чем больше сила тяжести, тем большая масса метеоритного материала выпадает на единицу её поверхности^[28]. За время существования Земли её масса существенно увеличилась благодаря силе тяжести: ежегодно на Землю оседает 30-40 млн. тонн метеоритного вещества, в основном в виде пыли, что значительно превышает рассеяние лёгких компонентов верхней атмосферы Земли в космосе^[29].

Без потенциальной энергии силы тяжести, непрерывно переходящей в кинетическую, круговорот вещества и энергии на Земле был бы невозможен^[30].

Сила тяжести играет очень важную роль для жизни на Земле^[31]. Только благодаря ей у Земли есть атмосфера. Вследствие силы тяжести, действующей на воздух, существует атмосферное давление^[32].

У всех живых организмов с нервной системой есть рецепторы, определяющие величину и направление силы тяжести и служащие для ориентировки в пространстве. У позвоночных организмов, в том числе человека, величину и направление силы тяжести определяет вестибулярный аппарат^[33].

Наличие силы тяжести привело к возникновению у всех многоклеточных наземных организмов прочных скелетов, необходимых для её преодоления. У водных живых организмов силу тяжести уравновешивает гидростатическая сила^[34].

Роль силы тяжести в процессах жизнедеятельности организмов изучает гравитационная биология^[35].

Сила тяжести и принцип эквивалентности инертной и гравитационной массы используются для определения масс предметов путём их взвешивания на весах. Сила тяжести используется при отстойной сепарации газовых и жидких смесей, в некоторых типах часов, в отвесах и противовесах, машине Атвуда, машине Обербека и жидкостных барометрах. Сила тяжести используется на железнодорожном транспорте для скатывания вагонов с уклона на сортировочных горках, на заводах строительных изделий для транспортировки материалов в спускных лотках и спускных трубах.^[36]

Точные измерения силы тяжести и её градиента (гравиметрия) используются при исследовании внутреннего строения Земли и при гравиразведке различных полезных ископаемых^[37].

Устойчивость тела в поле силы тяжести[править | править код]

Для тела в поле силы тяжести, опирающегося на одну точку (например при подвешивании тела за одну точку или помещении шара на плоскость) для устойчивого равновесия необходимо, что бы центр тяжести тела занимал наинизшее положение по сравнению со всеми возможными соседними положениями^[38].

Для тела в поле силы тяжести, опирающегося на несколько точек (например, стол) или на целую площадку (например, ящик на горизонтальной плоскости) для устойчивого равновесия необходимо, чтобы вертикаль, проведённая через центр тяжести, проходила внутри площади опоры тела. Площадью опоры тела называется контур, соединяющий точки опоры или внутри площадки, на которое опирается тело^[38].

Основной источник: ^[39]

Силу тяжести измеряют динамическими и статическими методами. Динамические методы используют наблюдение за движением тела под действием силы тяжести и измеряют время перехода тела из одного заранее определённого положения в другое. Они используют: колебания маятника, свободное падение тела, колебания струны с грузом. Статические методы используют наблюдение за изменением положения равновесия тела под действием силы тяжести и некоторой уравновешивающей её силы и измеряют линейное или угловое смещение тела.

Измерения силы тяжести бывают абсолютными и относительными. Абсолютные измерения определяют полное значение силы тяжести в заданной точке. Относительные измерения определяют разность силы тяжести в заданной точке и некоторого другого, заранее известного значения. Приборы, предназначенные для относительных измерений силы тяжести, называются гравиметрами.

Динамические методы определения силы тяжести могут быть как относительными, так и абсолютными, статические — только относительными.

Сила тяжести на поверхности^[40] некоторых небесных тел, за 1 принята сила тяжести на Земле^[41]

Земля	1,00	Солнце	27,85
Луна	0,165	Меркурий	0,375—0,381
Венера	0,906	Марс	0,394
Юпитер	2,442	Сатурн	1,065
Уран	0,903	Нептун	1,131

1. ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 372. — 560 с. — ISBN 5-9221-0225-7.
2. ↑ Тарг С. М. Сила тяжести // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 496. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
3. ↑ Миронов, 1980, с. 49.
4. ↑ Максимальное изменение силы тяжести, обусловленное притяжением Луны, составляет примерно 0,25⋅10−5{\displaystyle 0{,}25\cdot 10^{-5}} м/с², Солнца 0,1⋅10−5{\displaystyle 0{,}1\cdot 10^{-5}} м/с²
5. ↑ Миронов, 1980, с. 71.
6. ↑ ^{1 2} Савельев, 1987, с. 70.
7. ↑ Савельев, 1987, с. 82-83.
8. ↑ ^{1 2} Ускорение свободного падения // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5. — С. 245—246. — 760 с. — ISBN 5-85270-101-7.
9. ↑ Савельев, 1987, с. 156.
10. ↑ Тарасов, 2012, с. 200, 270.
11. ↑ Савельев, 1987, с. 128.
12. ↑ Бутенин, 1971, с. 253-259.
13. ↑ ^{1 2} Зубов В. П. Физические идеи древности // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 38, 54-55;
14. ↑ Зубов В. П. Физические идеи средневековья // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 114;
15. ↑ Зубов В. П. Физические идеи ренессанса // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 151;
16. ↑ ^{1 2 3} Кузнецов Б. Г. Генезис механического объяснения физических явлений и идеи картезианской физики // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 160-161, 169-170, 177;
17. ↑ Ньютон, 1989, с. 7.
18. ↑ Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 189-191;
19. ↑ Сивухин Д. В. Общий курс физики. Механика. — М., Наука, 1979. — Тираж 50 000 экз. — с. 323
20. ↑ Иваненко Д. Д. Основные идеи общей теории относительности // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 300;
21. ↑ Грищук Л. П., Зельдович Я. Б. Тяготение // Физика космоса. Маленькая энциклопедия. — М., Советская энциклопедия, 1986. — С. 676
22. ↑ Савельев, 1987, с. 122.
23. ↑ Жирнов Н. И. Классическая механика. — М., Просвещение, 1980. — Тираж 28000 экз. — с. 121
24. ↑ Кабардин О.Ф., Орлов В.А., Пономарева А.В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — Тираж 143 500 экз. — С. 151 — 152
25. ↑ Криволуцкий, 1985, с. 307.
26. ↑ Криволуцкий, 1985, с. 70, 234.
27. ↑ Криволуцкий, 1985, с. 208.
28. ↑ Криволуцкий, 1985, с. 77.
29. ↑ Криволуцкий, 1985, с. 48, 237-238.
30. ↑ Криволуцкий, 1985, с. 289.
31. ↑ Зельманов А. Л. Многообразие материального мира и проблема бесконечности Вселенной // Бесконечность и Вселенная. — М., Мысль, 1969. — Тираж 12000 экз. — С. 283
32. ↑ Хромов С. П., Петросянц М. А. Метеорология и климатология. — М., МГУ, 2006. — ISBN 5-211-05207-2. — C. 67
33. ↑ Юрий Фролов. https://www.nkj.ru/archive/articles/21172/ Наш гравитационный компас] // Наука и жизнь. — 2012. — № 10.
34. ↑ П. Кемп, К. Армс Введение в биологию. — М.: Мир, 1988. — ISBN 5-03-001286-9. — Тираж 125000 экз. — С. 75
35. ↑ Лозовская Е. Жизнь с гравитацией и без нее // Наука и жизнь. — 2004. — № 9.
36. ↑ Фиделев А. С. Подъемно-транспортные машины и механизмы. — Киев, Будивельник, 1967. — 187-188
37. ↑ Миронов, 1980, с. 1-543.
38. ↑ ^{1 2} Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика, теплота, молекулярная физика. — М., Наука, 1975. — Тираж 350 000 экз. — С. 189-190
39. ↑ Миронов, 1980, с. 94-262.
40. ↑ У газовых гигантов «поверхность» понимается как область высот в атмосфере, где давление равно атмосферному давлению на Земле на уровне моря (1,013×10⁵Па).
41. ↑ Данные взяты из статьи Википедии Ускорение свободного падения

• Ньютон И. Математические начала натуральной философии. — М.: Наука, 1989. — 688 с. — ISBN 5-02-000747-1.
• Савельев И. В. Курс общей физики. Т. 1. Механика. Молекулярная физика. — М.: Наука, 1987. — 688 с.
• Криволуцкий А. Е. Голубая планета. Земля среди планет. Географический аспект.. — М.: Мысль, 1985. — 335 с.
• Миронов В. С. Курс гравиразведки. — Л.: Недра, 1980. — 543 с.
• Тарасов В. Н., Бояркина И. В., Коваленко М. В., Федорченко Н. П., Фисенко Н. И. Теоретическая механика. — М.: ТрансЛит, 2012. — 560 с.
• Бутенин Н. В. Введение в аналитическую механику. — М.: Наука, 1971. — 264 с. — 25 000 экз.

Сила тяжести, трения, реакции опоры, упругости, Архимеда, сопротивления, вес. Направление, точка приложения, природа возникновения

Тестирование онлайн

Что надо знать о силе

Сила — векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом

Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!

Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.

Сила тяжести

На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле

Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.

Сила трения

Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:

Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.

Так как тело представляем в виде материальной точки, силу можно изображать с центра

Сила реакции опоры

Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».

Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.

Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как

Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.

Так как тело представляем в виде материальной точки, силу можно изображать с центра

Сила упругости

Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.

Закон Гука

Сила упругости направлена противоположно деформации.

Так как тело представляем в виде материальной точки, силу можно изображать с центра

При последовательном соединении, например, пружин жесткость рассчитывается по формуле

При параллельном соединении жесткость

Жесткость образца. Модуль Юнга.

Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.

Подробнее о свойствах твердых тел здесь.

Вес тела

Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!

Формулы определения веса нет. Обозначается эта силы буквой .

Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.

Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.

Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!

Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила

Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!

Перегрузка — отношение веса к силе тяжести

Сила Архимеда

Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:

В воздухе силой Архимеда пренебрегаем.

Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше — тонет.

Электрические силы

Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.

Схематичное обозначение действующих на тело сил

Часто тело моделируют материальной точкой. Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником.

Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.

Главное запомнить

1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы

Рассмотрим взаимное притяжение предмета и Земли. Между ними, согласно закону гравитации возникает сила

А сейчас сравним закон гравитации и силу тяжести

Величина ускорения свободного падения зависит от массы Земли и ее радиуса! Таким образом, можно высчитать, с каким ускорением будут падать предметы на Луне или на любой другой планете, используя массу и радиус той планеты.

Расстояние от центра Земли до полюсов меньше, чем до экватора. Поэтому и ускорение свободного падения на экваторе немного меньше, чем на полюсах. Вместе с тем, следует отметить, что основной причиной зависимости ускорения свободного падения от широты местности, является факт вращения Земли вокруг своей оси.

При удалении от поверхности Земли сила земного тяготения и ускорения свободного падения изменяются обратно пропорционально квадрату расстояния до центра Земли.

определение, формулы, правило левой руки

В статье расскажем про магнитную силу Лоренца, как она действует на проводник, рассмотрим правило левой руки для силы Лоренца и момент силы действующий на контур с током.

Сила Лоренца — это сила, которая действует на заряженную частицу, падающую с определенной скоростью в магнитное поле. Величина этой силы зависит от величины магнитной индукции магнитного поля B, электрического заряда частицы q и скорости v, с которой частица падает в поле.

То, как магнитное поле B ведет себя по отношению к нагрузке полностью отличается от того, как это наблюдается для электрического поля Е. Прежде всего, поле B не реагирует на нагрузку. Однако когда нагрузка перемещается в поле B, появляется сила, которая выражается формулой, которую можно рассматривать как определение поля B:

Таким образом, видно, что поле B выступает в качестве силы, перпендикулярной к направлению вектора скорости V нагрузок и направление вектора B. Это можно проиллюстрировать на диаграмме:

На диаграмме q положительный заряд!

Единицы поля B могут быть получены из уравнения Лоренца. Таким образом, в системе СИ единица B равна 1 тесла (1T). В системе CGS полевой единицей является Гаусс (1G). 1T = 10⁴G

Движение заряда в поле B показано на анимации

Для сравнения показана анимация движения как положительного, так и отрицательного заряда.

Когда поле B охватывает большую площадь, заряд q, движущийся перпендикулярно направлению вектора B, стабилизирует свое движение по круговой траектории. Однако, когда вектор v имеет компонент, параллельный вектору B, тогда путь заряда будет спиралью, как показано на анимации

Сила Лоренца на проводник с током

Сила, действующая на проводник с током, является результатом силы Лоренца, действующей на движущиеся носители заряда, электроны или ионы. Если в разделе направляющей длиной l, как на чертеже

полный заряд Q движется, тогда сила F, действующая на этот сегмент, равна

Частное Q / t является значением протекающего тока I и, следовательно, сила, действующая на участок с током, выражается формулой

Чтобы учесть зависимость силы F от угла между вектором B и осью отрезка, длина отрезка l была задана характеристиками вектора.

Только электроны движутся в металле под действием разности потенциалов; ионы металлов остаются неподвижными в кристаллической решетке. В растворах электролитов анионы и катионы подвижны.

Правило левой руки сила Лоренца

Правило левой руки сила Лоренца — определяющее направление и возврат вектора магнитной (электродинамической) энергии.

Если левая рука расположена так, что линии магнитного поля направлены перпендикулярно внутренней поверхности руки (чтобы они проникали внутрь руки), а все пальцы — кроме большого пальца — указывают направление протекания положительного тока (движущаяся молекула), отклоненный большой палец указывает направление электродинамической силы, действующей на положительный электрический заряд, помещенный в это поле (для отрицательного заряда, сила будет противоположная).

Второй способ определения направления электромагнитной силы заключается в расположении большого, указательного и среднего пальцев под прямым углом. При таком расположении указательный палец показывает направление линий магнитного поля, направление среднего пальца — направление движения тока, а также направление большого пальца силы. 

Момент силы, действующий на контур с током в магнитном поле

Момент силы, действующей на контур с током в магнитном поле (например, на проволочную катушку в обмотке электродвигателя), также определяется силой Лоренца. Если петля (отмеченная на схеме красным цветом) может вращаться вокруг оси, перпендикулярной полю B, и проводит ток I, то появляются две неуравновешенные силы F, действующие в стороны от рамы, параллельной оси вращения.

Момент этих сил М

Определим вектор магнитного момента контура

Теперь мы можем сохранить крутящий момент в виде

Эти силы, действующие на элементы петли перпендикулярно оси вращения, направлены и взаимно компенсируются.

Единицы силы. Динамометр. Видеоурок. Физика 7 Класс

Нам уже известно, что для описания взаимодействия тел используется физическая величина, называемая силой. На этом уроке мы подробнее познакомимся со свойствами этой величины, единицами силы и прибором, который используется для ее измерения – с динамометром.

Тема: Взаимодействие тел

Урок: Единицы силы. Динамометр

Прежде всего, вспомним, что такое сила. Когда на тело действует другое тело, физики говорят, что со стороны другого тела на данное тело действует сила.

Сила – это физическая величина, характеризующая действие одного тела на другое.

Сила обозначается латинской буквой F, а единица силы в честь английского физика Исаака Ньютона называется ньютоном (пишем с маленькой буквы!) и обозначается Н (пишем заглавную букву, так как единица названа в честь ученого). Итак,

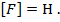
Наравне с ньютоном, используются кратные и дольные единицы силы:

килоньютон 1 кН = 1000 Н;

меганьютон 1 МН = 1000000 Н;

миллиньютон 1 мН = 0,001 Н;

микроньютон 1 мкН = 0,000001 Н и т. д.

Под действием силы скорость тела изменяется. Другими словами, тело начинает двигаться не равномерно, а ускоренно. Точнее, равноускоренно: за равные промежутки времени скорость тела меняется одинаково. Именно изменение скорости тела под действием силы физики используют для определения единицы силы в 1 Н.

Единицы измерения новых физических величин выражают через так называемые основные единицы – единицы массы, длины, времени. В системе СИ – это килограмм, метр и секунда.

Пусть под действием некоторой силы скорость тела массой 1 кг изменяет свою скорость на 1 м/с за каждую секунду. Именно такая сила и принимается за 1 ньютон.

Один ньютон (1 Н) – это сила, под действием которой тело массой 1 кг изменяет свою скорость на 1 м/с каждую секунду.

Экспериментально установлено, что сила тяжести, действующая вблизи поверхности Земли на тело массой 102 г, равна 1 Н. Масса 102 г составляет приблизительно 1/10 кг, или, если быть более точным,

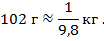
Но это означает, что на тело массой 1 кг, то есть на тело в 9,8 раз большей массы, у поверхности Земли будет действовать сила тяжести 9,8 Н. Таким образом, чтобы найти силу тяжести, действующую на тело любой массы, нужно значение массы (в кг) умножить на коэффициент, который принято обозначать буквой g:

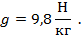
Мы видим, что этот коэффициент численно равен силе тяжести, которая действует на тело массой 1 кг. Он носит название ускорение свободного падения. Происхождение названия тесно связано с определением силы в 1 ньютон. Ведь если на тело массой 1 кг действует сила не 1 Н, а 9,8 Н, то под действием этой силы тело будет изменять свою скорость (ускоряться) не на 1 м/с, а на 9,8 м/с каждую секунду. В старшей школе этот вопрос будет рассмотрен более подробно.

Теперь можно записать формулу, позволяющую рассчитать силу тяжести, действующую на тело произвольной массы m(Рис. 1).

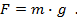
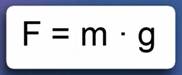
Рис. 1. Формула для расчета силы тяжести

Следует знать, что ускорение свободного падения равно 9,8 Н/кг только у поверхности Земли и с высотой уменьшается. Например, на высоте 6400 км над Землей оно меньше в

действующая сила — это… Что такое действующая сила?



действующая сила

сущ. agent

Большой англо-русский и русско-английский словарь. 2001.

• действующая производственная мощность
• действующая система

Смотреть что такое «действующая сила» в других словарях:

• действующая сила — veikiančioji jėga statusas T sritis fizika atitikmenys: angl. applied force; imposed force vok. Angriffskraft, f rus. действующая сила, f; приложенная сила, f pranc. force appliquée, f …   Fizikos terminų žodynas

• действующая сила — veikiančioji jėga statusas T sritis automatika atitikmenys: angl. applied force; imposed force vok. Angriffskraft, f rus. действующая сила, f pranc. force agissante, f …   Automatikos terminų žodynas

• действующая сила — veikiančioji jėga statusas T sritis Standartizacija ir metrologija apibrėžtis Jėga, veikianti tam tikrą kūną (dalelę) ar reiškinį. atitikmenys: angl. acting force vok. eingeprägte Kraft, f rus. действующая сила, f pranc. force d’action, f …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• ДЕЙСТВУЮЩАЯ СИЛА ПЕРЕМЕННОГО ТОКА — условный постоянный ток, к рый производит то же действие (тепловое, магнитное и т. д.), что и данный переменный ток. Амперметры, в цепи переменного тока показывают Д. с. п. т.; она составляет 0,71 наибольшего значения силы переменного тока,… …   Технический железнодорожный словарь

• кратковременная действующая сила — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN instantaneous force …   Справочник технического переводчика

• СИЛА — в физическом смысле способность изменять форму материальных масс, вызывать их движение, менять направление и скорость движения или приводить тело в состояние покоя. «Живая» сила (редко употребляемое теперь выражение), или действующая сила, – сила …   Философская энциклопедия

• СИЛА — векторная величина мера механического воздействия на тело со стороны др. тел, а также интенсивности др. физ. процессов и полей. Силы бывают различными: (1) С. Ампёра сила, с которой (см.) действует на проводник с током; направление вектора силы… …   Большая политехническая энциклопедия

• Сила инерции — (также инерционная сила)  термин, широко применяемый в различных значениях в точных науках, а также, как метафора, в философии, истории, публицистике и художественной литературе. В точных науках сила инерции обычно представляет собой понятие …   Википедия

• СИЛА ТЯЖЕСТИ — сила Р, действующая на любую материальную частицу, находящуюся вблизи земной поверхности, и определяемая как геом. сумма силы притяжения Земли F (рис.) и переносной силы инерции Jпер, учитывающей эффект суточного вращения Земли (аналогично… …   Физическая энциклопедия

• ДЕЙСТВУЮЩАЯ ЭЛЕКТРОДВИЖУЩАЯ СИЛА — условно постоянная по величине и направлению электродвижущая сила, к рая по вызываемому ею действию соответствует данной переменной электродвижущей силе. Д. э. с. равна 0,71 наибольшего значения переменной электродвижущей силы, изменяющейся по… …   Технический железнодорожный словарь

• СИЛА ТЯЖЕСТИ — СИЛА ТЯЖЕСТИ, сила P, действующая на любое тело, находящееся вблизи земной поверхности, и определяемая как геометрическая сумма силы притяжения Земли F и центробежной силы инерции Q, учитывающей эффект суточного вращения Земли. Направление силы… …   Современная энциклопедия

Книги

• Исцеляющие настрои. Мысли, творящие здоровую нервную систему. Мысли, творящие сильную волю (количество томов: 3), Сытин Г.. «Исцеляющие настрои» .»Исцеляющие настрои»— уникальный сборник наиболее востребованных и эффективных творящих мыслей, созданных Георгием Николаевичем Сытиным — признанным ученым,… Подробнее  Купить за 662 руб
• Рысь, Маннхарт Урс. Урс Маннхарт родился в 1975 году в Рорбахе (кантон Берн). Изучал германистику, англистику и философию. Совместно с Кристофом Симоном и драматургом Лоренцем Лангенэггером организовал… Подробнее  Купить за 431 руб
• Доктор Живаго, Б. Пастернак. В произведении, главная действующая сила которого — стихия революции, — образ представителя русской интеллигенции, не без колебаний и не без духовных потерь принявшей события Великого… Подробнее  Купить за 430 руб

Другие книги по запросу «действующая сила» >>

действующая сила — это… Что такое действующая сила?



действующая сила

effective force

Англо-русский словарь технических терминов. 2005.

• действующая проводимость
• действующая система

Смотреть что такое «действующая сила» в других словарях:

• действующая сила — veikiančioji jėga statusas T sritis fizika atitikmenys: angl. applied force; imposed force vok. Angriffskraft, f rus. действующая сила, f; приложенная сила, f pranc. force appliquée, f …   Fizikos terminų žodynas

• действующая сила — veikiančioji jėga statusas T sritis automatika atitikmenys: angl. applied force; imposed force vok. Angriffskraft, f rus. действующая сила, f pranc. force agissante, f …   Automatikos terminų žodynas

• действующая сила — veikiančioji jėga statusas T sritis Standartizacija ir metrologija apibrėžtis Jėga, veikianti tam tikrą kūną (dalelę) ar reiškinį. atitikmenys: angl. acting force vok. eingeprägte Kraft, f rus. действующая сила, f pranc. force d’action, f …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• ДЕЙСТВУЮЩАЯ СИЛА ПЕРЕМЕННОГО ТОКА — условный постоянный ток, к рый производит то же действие (тепловое, магнитное и т. д.), что и данный переменный ток. Амперметры, в цепи переменного тока показывают Д. с. п. т.; она составляет 0,71 наибольшего значения силы переменного тока,… …   Технический железнодорожный словарь

• кратковременная действующая сила — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN instantaneous force …   Справочник технического переводчика

• СИЛА — в физическом смысле способность изменять форму материальных масс, вызывать их движение, менять направление и скорость движения или приводить тело в состояние покоя. «Живая» сила (редко употребляемое теперь выражение), или действующая сила, – сила …   Философская энциклопедия

• СИЛА — векторная величина мера механического воздействия на тело со стороны др. тел, а также интенсивности др. физ. процессов и полей. Силы бывают различными: (1) С. Ампёра сила, с которой (см.) действует на проводник с током; направление вектора силы… …   Большая политехническая энциклопедия

• Сила инерции — (также инерционная сила)  термин, широко применяемый в различных значениях в точных науках, а также, как метафора, в философии, истории, публицистике и художественной литературе. В точных науках сила инерции обычно представляет собой понятие …   Википедия

• СИЛА ТЯЖЕСТИ — сила Р, действующая на любую материальную частицу, находящуюся вблизи земной поверхности, и определяемая как геом. сумма силы притяжения Земли F (рис.) и переносной силы инерции Jпер, учитывающей эффект суточного вращения Земли (аналогично… …   Физическая энциклопедия

• ДЕЙСТВУЮЩАЯ ЭЛЕКТРОДВИЖУЩАЯ СИЛА — условно постоянная по величине и направлению электродвижущая сила, к рая по вызываемому ею действию соответствует данной переменной электродвижущей силе. Д. э. с. равна 0,71 наибольшего значения переменной электродвижущей силы, изменяющейся по… …   Технический железнодорожный словарь

• СИЛА ТЯЖЕСТИ — СИЛА ТЯЖЕСТИ, сила P, действующая на любое тело, находящееся вблизи земной поверхности, и определяемая как геометрическая сумма силы притяжения Земли F и центробежной силы инерции Q, учитывающей эффект суточного вращения Земли. Направление силы… …   Современная энциклопедия

Книги

• Исцеляющие настрои. Мысли, творящие здоровую нервную систему. Мысли, творящие сильную волю (количество томов: 3), Сытин Г.. «Исцеляющие настрои» .»Исцеляющие настрои»— уникальный сборник наиболее востребованных и эффективных творящих мыслей, созданных Георгием Николаевичем Сытиным — признанным ученым,… Подробнее  Купить за 662 руб
• Рысь, Маннхарт Урс. Урс Маннхарт родился в 1975 году в Рорбахе (кантон Берн). Изучал германистику, англистику и философию. Совместно с Кристофом Симоном и драматургом Лоренцем Лангенэггером организовал… Подробнее  Купить за 431 руб
• Доктор Живаго, Б. Пастернак. В произведении, главная действующая сила которого — стихия революции, — образ представителя русской интеллигенции, не без колебаний и не без духовных потерь принявшей события Великого… Подробнее  Купить за 430 руб

Другие книги по запросу «действующая сила» >>