Физика для углубленного изучения. 2. Электродинамика. Оптика
Физика для углубленного изучения. 2. Электродинамика. Оптика
ОглавлениеВведениеI. ЭЛЕКТРОСТАТИКА § 1. Электрический заряд. Закон Кулона § 2. Электрическое поле. Напряженность поля § 3. Теорема Гаусса § 4. Потенциал электростатического поля. Энергия системы зарядов § 5. Расчет электрических полей § 6. Проводники в электрическом поле § 7. Силы в электростатическом поле § 8. Конденсаторы. Электроемкость § 9. Энергия электрического поля II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 10. Характеристики электрического тока. Закон Ома § 11. Соединение проводников в электрические цепи § 12. Закон Ома для неоднородной цепи § 14. Работа и мощность постоянного тока § 15. Магнитное поле постоянного тока § 16. Действие магнитного поля на движущиеся заряды III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ § 17. Явление электромагнитной индукции § 18. Электрические машины постоянного тока § 19. Энергия магнитного поля § 20.  Основы теории электромагнитного поля§ 21. Квазистационарные явления в электрических цепях IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 22. Цепи переменного тока. Закон Ома § 23. Работа и мощность переменного тока. Передача электроэнергии V. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ § 25. Колебательный контур § 26. Вынужденные колебания в контуре. Резонанс § 27. Незатухающие электромагнитные колебания § 28. Электромагнитные волны § 29. Свойства и применения электромагнитных волн VI. ОПТИКА § 30. Свет как электромагнитные волны. Интерференция § 31. Дифракция света § 32. Спектральные приборы. Дифракционная решетка § 33. Протяженные источники света § 34. Интерференция немонохроматического света § 35. Физические принципы голографии § 36. Геометрическая оптика § 37. Оптические приборы, формирующие изображение |
§13.
Силы в электрическом поле | Политех в СетиВсе силы, возникающие в электростатическом поле, являются в конечном итоге силами, действующими на заряд.
Сила, действующая на точечные заряды:
(13.1)
Если заряд распределен непрерывно с объемной плотностью
, то сила, действующая на непрерывно распределенный заряд
(13.2)
Объемная плотность этой силы равна
(13.3)
Сила, действующая на диполь:
На каждый из зарядов действует
и и результирующая сила равна их векторной сумме:
, тогда
(13.4)
Если поле однородное, то сила равна нулю, поскольку к зарядам диполя приложены противоположно направленные и равные по модулю силы.
Момент сил, действующих на диполь.
Силы, приложенные к зарядам диполя, составляют пару сил с моментом
.
(13.5)
Объемная сила, действующая на диэлектрик.
Это сила, приложенная к объему
диэлектрика. Она равна сумме сил, действующих на элементарные диполи внутри этого объема, т. е.
, где Означает суммирование по всем элементарным диполям в объеме .
В макроскопическом случае можно считать, что каждый диполь находится в одном и том же поле и
.
Можно записать
, тогда .
Объемная плотность этих сил
(13.6)
Если учесть, что вектор
æ, а , и , тогда объемная плотность сил, действующих на диэлектрик
(13.7)
Эта формула показывает, что в диэлектрике на элементарный объем действуют силы, стремящиеся сдвинуть объем в направлении максимальной скорости возрастания квадрата напряженности поля.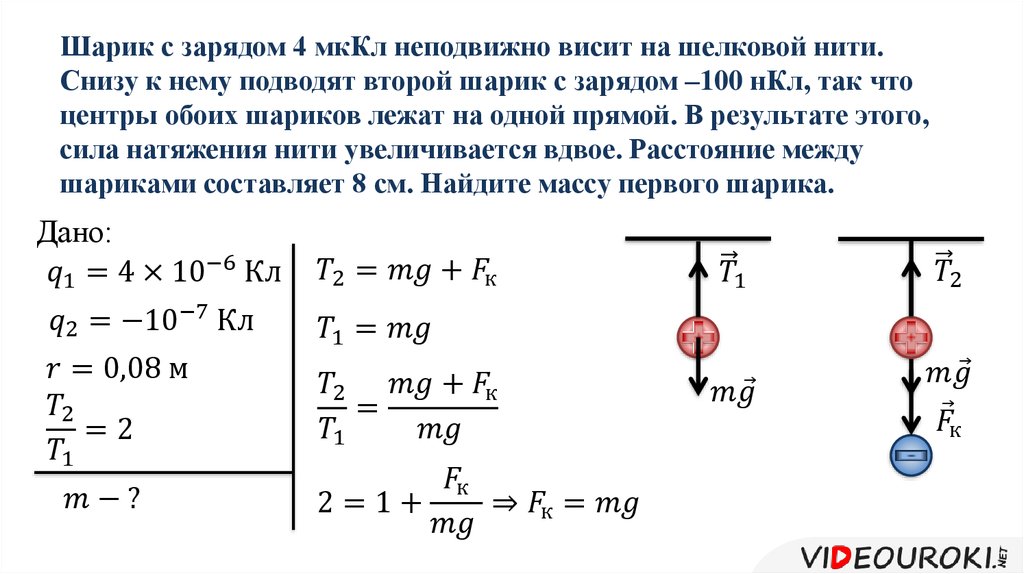
Иногда это выражают в виде утверждения, что элемент объема диэлектрика увлекается в направлении роста модуля напряженности.
Наряду с объемными у диэлектриков имеются также и поверхностные силы, которые возникают в поверхностном слое диэлектрика. Они действуют наряду с объемными.
Силы, действующие на проводник.
На заряд
, находящийся на элементе поверхности Проводника, действуют лишь половина напряженности поля, имеющегося у поверхности проводника, т. е. напряженность со стороны всех остальных зарядов, поскольку вторая половина S, создается самим зарядом элемента поверхности и не может на него действовать (см. §8).
Напряженность поля у поверхности проводника граничащего с диэлектриком определяется формулой
. (13.9)
Половину
дают все остальные заряды, находящиеся на проводнике вне . Тогда
.
(13.10)
Из последней формулы следует, что на поверхности проводника сила всегда действует в направлении внешней нормали и как бы стремится увеличить этот объем. Результирующая сила, действующая на проводник в целом, будет равна
, (13.11)
Где S – поверхность проводника.
Выражение (13.11) позволяет сразу же вычислить силу, приходящуюся на участок площадью S обкладки плоского конденсатора, заполненного диэлектрика:
, (13.12)
Поскольку поле при этом однородно, т. е.
и в подынтегральном выражении (13.11) являются постоянными.
Заряды в электрических полях – Узнайте – ScienceFlip
Заряды в электрических полях – Узнайте
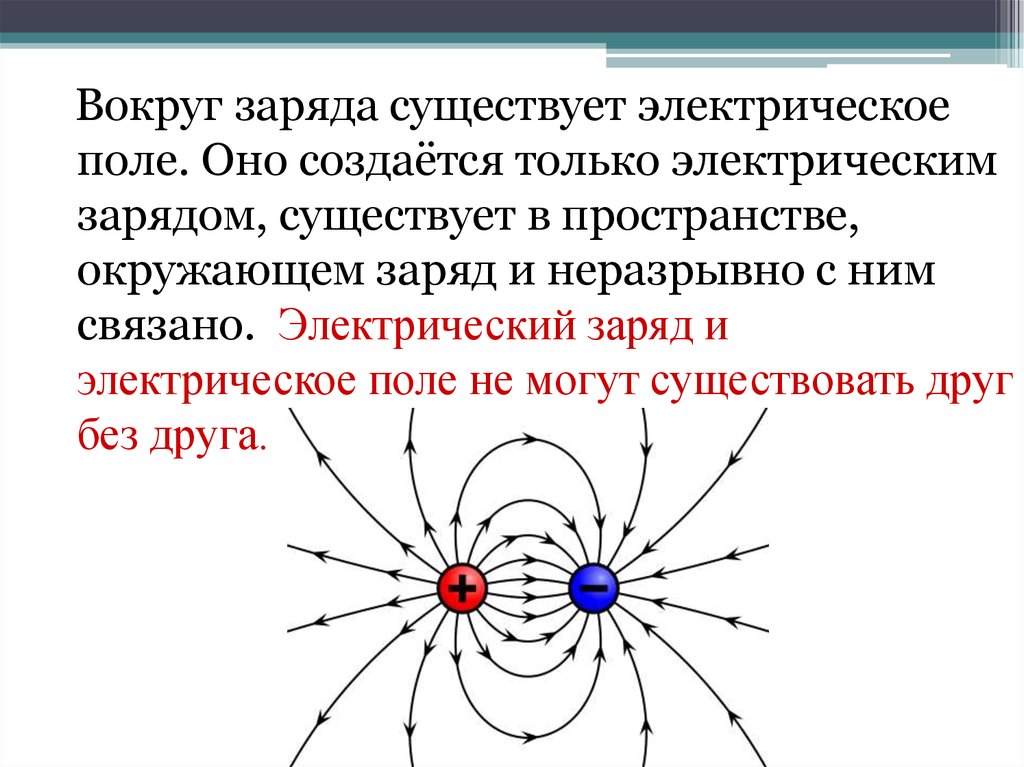
Электрическое поле существует вокруг заряженных частиц и объектов. Электрическое поле будет действовать на другие заряженные объекты. Испытываемая сила может быть силой притяжения или отталкивания в зависимости от типов взаимодействующих зарядов.
Направление электрического поля — это направление, в котором положительный пробный заряд будет испытывать силу, помещенную в это поле.
Однородные электрические поля
Однородные электрические поля существуют между заряженными пластинами. Если положительно и отрицательно заряженные пластины расположить лицом друг к другу, линии электрического поля в пространстве между пластинами будут равномерно распределены. Величина напряженности поля была бы постоянной. Это называется однородным электрическим полем .
На заряд, помещенный в однородное электрическое поле, действует постоянная электрическая сила:
Где:
– сила, действующая на заряженную частицу (Н)
– заряд объекта, на который действует сила (Кл)
– напряженность электрического поля в НЗ
Направление силы на положительный заряд будет в направлении поля, а сила на отрицательном заряде будет противоположно направлению поля.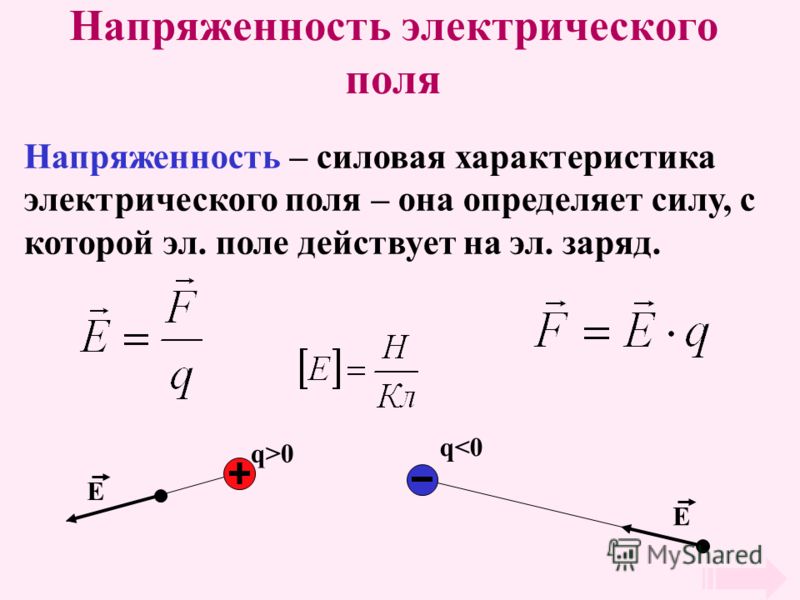
Поскольку сила, действующая на заряд, постоянна, ускорение этой заряженной частицы будет постоянным в пределах однородного электрического поля, что определяется уравнением .
Напряженность электрического поля в однородном электрическом поле
На приведенной ниже диаграмме показано электрическое поле между двумя заряженными пластинами, разделенными расстоянием d.
Существует разность потенциалов между пластинами V, вызванная тем, что одна пластина имеет более высокий потенциал, а другая пластина имеет более низкий потенциал. Напряженность электрического поля определяется как:
Где:
— напряженность электрического поля (Вм −1 )
– разность потенциалов (В)
– расстояние между пластинами (м)
Работа в однородных электрических полях
Работа равна изменению кинетической энергии частицы или объект. В электрическом поле необходимо совершить работу, чтобы переместить точечный заряд через электрическое поле.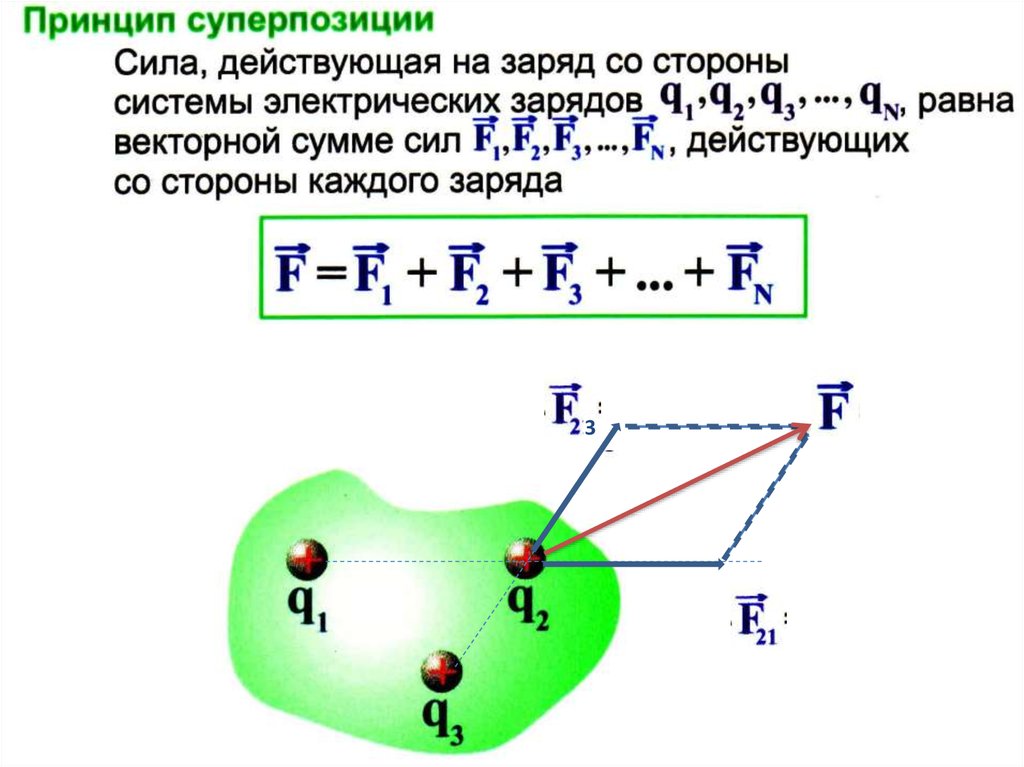
Источником этой работы может быть либо:
- электрическое поле на заряженном объекте, либо
- на электрическое поле, заставляя объект двигаться
Если заряд движется в том направлении, в котором его естественным образом двигало бы поле, то поле совершает работу. Если он движется против естественного направления, то на поле выполняется работа.
Для расчета работы, совершаемой точечным зарядом для его перемещения на расстояние d через разность потенциалов: Дж)
= заряд точечного заряда (в Кл)
= напряженность электрического поля (в В·м −1 или NC −1 )
= расстояние между точками, параллельными полю (в м)
Объединив два приведенных выше уравнения, мы можем вывести другое уравнение для проделанной работы:
Где:
= работа, выполненная над точечным зарядом или над полем (в Дж)
= заряд точечный заряд (в Кл)
– разность потенциалов (В)
Работа и кинетическая энергия
Поскольку работа равна изменению кинетической энергии, скорость частицы также может быть определена после расчета работы, совершаемой электрическим полем.
и
Сравнение электрического и гравитационного полей
Массы в гравитационных полях
- Масса, помещенная в точку гравитационного поля, будет испытывать силу: F = мг.
- Масса будет равномерно ускоряться вдоль поля (параллельно линиям поля и в том направлении, куда указывают линии поля) в соответствии со вторым законом Ньютона. Следовательно,
- Масса, движущаяся перпендикулярно гравитационному полю, движется по параболической траектории. Это связано с тем, что единственная действующая сила направлена вдоль силовых линий.
- Его движение состоит из двух компонентов: 1. Равномерная скорость по полю и 2. Равномерное ускорение по полю.
- Комбинация этих двух компонентов создает параболическую траекторию снаряда.
Заряды в электрических полях
- На заряд с массой, помещенный в точку электрического поля, действует сила: F = qE.
- В результате заряд будет ускоряться равномерно по полю, также в соответствии со вторым законом Ньютона, следовательно,
- Положительный заряд, движущийся со скоростью через электрическое поле, движется по параболической траектории. Это связано с тем, что единственная действующая сила направлена вдоль силовых линий.
- Его движение имеет две составляющие: 1. Равномерная скорость по полю 2. Равномерное ускорение по полю.
- Комбинация этих двух компонентов создает параболическую траекторию, очень похожую на движение снаряда.
Поскольку траектория заряженной частицы в электрическом поле напоминает траекторию снаряда и его свойства, уравнения движения также могут быть применены к этим задачам.
Пример 1:
Какое ускорение испытал бы электрон, если бы он двигался в электрическом поле напряженностью 1,5 × 10 −5 NC −1 ? (q e = -1.602 × 10 −19 C and m e = 9.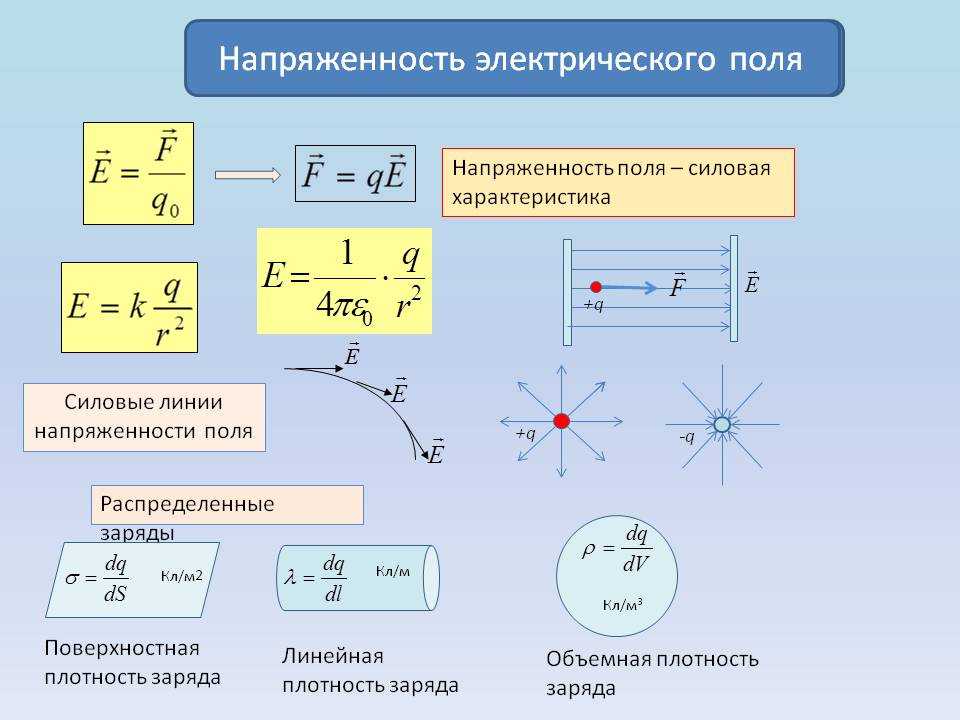
Answer:
Using:
(against the electric поле)
Расширение до 2-го закона Ньютона:
и
(в направлении, противоположном электрическому полю)
Пример 2: Какова напряженность электрического поля между заряженными пластинами на расстоянии 2 см и потенциале 6 В на пластинах?
Ответ:
Использование:
Пример 3:
A) Рассчитайте работу, выполненную на электронах, который перемещает 4 см между заряженными пластинами с электрическим полем 20 Вм 1 :
b) Если электрон изначально находился в покое, рассчитайте его конечную скорость (масса электрона = 9,109 × 10 −31 кг)
Ответ:
a) , используя: 90003
b) с использованием: и
Это говорит нам о том, что скорость направлена против поля.
Какова результирующая электрическая сила, действующая на заряд массой 5 у.е., расположенный в точке (3м,4м)?
Физика Электромагнетизм
Алара Э.
спросил 16.02.22 9-3 Н а я не уверен, как они его получили?Подписаться І 1
Подробнее
Отчет
1 ответ эксперта
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Энтони Т. ответил 16.02.22
Репетитор
5 (52)
Репетитор по математике и естественным наукам для пациентов
См. таких репетиторов
Смотрите таких репетиторов
Нарисуйте систему координат и найдите +2 мкС в начале координат и +5 мкС на (3, 4) метрах.
Данное однородное электрическое поле указывает в направлении положительной оси X. Сила, вызванная однородным полем на заряде 5 мкКл, направлена к оси X и определяется как 500i x 5 x 10 -6 = 2,5 x 10 -3 i Н (единицы измерения я опустил для упрощения уравнения) .
Заряд 2 мкКл действует на заряд 5 мкКл с силой, определяемой как 8,99 x 10 9 x 2×10 -6 x 5 x 10 -6 / 5 2 = 3,60 x 10-2 в направлении a 903 от линии, соединяющей два заряда. Эта сила имеет компонент X =
3,60 х 10 -3 х 3/5 i = 2,16 i Н (где 3/5 — косинус угла, образованного результирующим вектором). Компонент Y = 3,60 x 10 -3 x 4/5 = 2,88 x 10 -3 j N.
Складывая компоненты X, получаем F x = (2,5 x 10 -3 i + 2,16 x 10 3 i = 4,66 x 10 -3 i N. Имеется только один компонент Y = 2,88 x 10 -3 j N.
Я использовал уравнения F = E x Q и F = kQ1 x Q2 / d 2 ,
Голосовать за 1 Понизить
Подробнее
Отчет
Все еще ищете помощь? Получите правильный ответ, быстро.
