Введение в динамику жидкости

Бэтчелор Дж. Введение в динамику жидкости. М.: Мир, 1973. — 760 с. Книга содержит систематическое и оригинальное изложение основ динамики жидкости. Автор, как правило, указывает способ упрощения основных уравнений и обсуждает результаты, привлекая эксперимент. Это позволяет шире охватить предмет и его приложения к геофизике, физической гидродинамике, метеорологии и океанологии. Энциклопедичность содержания и методические достоинства книги Бэтчелора позволяют поставить ее в один ряд с такими известными трудами, как, например: Л. Прандтль Гидроаэромеханика (ИЛ, 1949, 1951) и Л. Милн-Томсон Теоретическая гидродинамика (Мир, 1964) Оглавление ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА ПРЕДИСЛОВИЕ 1. ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ 1. 1. Твердые тела, жидкости и газы 1.2. Гипотеза сплошной среды 1.3. Объемные и поверхностные силы, действующие на жидкость 1.4. Механическое равновесие жидкости 1.5. Классическая термодинамика 1.6. Явления переноса Линейное соотношение между потоком и градиентом скалярной интенсивности Уравнения диффузии и теплопроводности в покоящейся изотропной среде Молекулярный перенос количества движения в жидкости 1.7. Отличительные свойства газов Отклонения от законов совершенного газа Коэффициенты переноса в совершенном газе Другие проявления отклонений совершенного газа от равновесного состояния 1.8. Отличительные свойства жидкостей Свойства жидкости в состоянии равновесия Коэффициенты переноса 1.9. Условия на границе между двумя средами Равновесная форма границы между двумя неподвижными, жидкостями Соотношения перехода на жидкой границе 2. КИНЕМАТИКА ПОЛЯ ТЕЧЕНИЯ Дифференцирование по направлению движения жидкости 2. 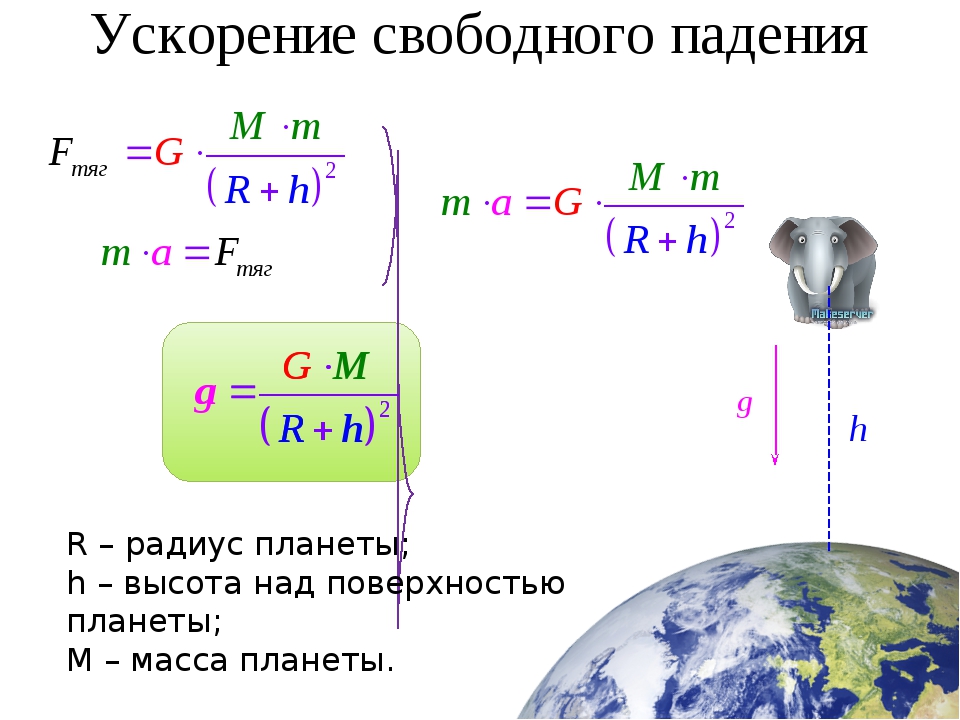2. Сохранение массы Использование функции тока для удовлетворения уравнения сохранения массы 2.3. Анализ относительного движения в окрестности точки Простое движение сдвига 2.4. Распределение скоростей при заданных скорости расширения и завихренности 2.5. Особенности скорости расширения. Источники и стоки 2.6. Распределение завихренности Вихревые нити Вихревая пелена 2.7. Распределения скорости при нулевой завихренности и нулевой скорости расширения Безвихревое соленоидалъное течение вблизи критической точки Комплексный потенциал двумерного безвихревого соленоидалъного течения 2.8. Безвихревое соленоидальное течение в двусвязных областях пространства Условия единственности для определения … 2.9. Трехмерные поля течения, простирающиеся в бесконечность Поведение потенциала на больших расстояниях Представление потенциала степенным рядом Безвихревое соленоидальное течение, вызываемое поступательным движением твердого тела 2. 10. Двумерные поля течения, простирающиеся в бесконечность Безвихревое соленоидалъное течение, вызываемое поступательным движением твердого тела 3. УРАВНЕНИЯ ДВИЖЕНИЯ ЖИДКОСТИ Скорости изменения субстанциональных интегралов Законы сохранения для движущейся жидкости 3.2. Уравнение движения для жидкости Применение уравнения количества движения в интегральной форме Уравнения движения в подвижных осях 3.3. Выражение для тензора напряжений Механическое определение давления в движущейся жидкости Связь между девиатором напряжений и скоростью деформации для ньютоновой жидкости Условия для скорости и напряжений на жидкой границе двух сред 3.4. Изменение внутренней энергии движущейся жидкости 3.5. Теорема Бернулли для установившегося течения невязкой и нетеплопроводной жидкости Специальные формы теоремы Бернулли Сохранение величины Н при пересечении области перехода в одномерном установившемся течении 3.6. Полная система уравнений движения жидкости Изэнтпропическое течение Условия, при которых поле скоростей можно приближенно считать соленоидальным 3. 7. Заключительные замечания к первым трем главам 4. РАВНОМЕРНЫЙ ПОТОК ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ Модификация давления с учетом влияния массовой силы 4.2. Установившееся течение одного направления Течение Пуазейля Течение в трубах некругового поперечного сечения Двумерное течение Модель малярной кисти 4.3. Неустановившееся течение одного направления Плоская граница, внезапно приводимая в движение в покоящейся жидкости Твердая граница, внезапно приводимая в движение относительно другой неподвижной границы Течение, вызываемое колебанием плоской границы Начало течения в трубе 4.4. Слой Экмана на границе вращающейся жидкости Слой на свободной поверхности Слой на твердой плоской границе 4.5. Течение с круговыми линиями тока 4.6. Установившаяся струя из точечного источника количества движения 4.7. Динамическое подобие и число Рейнольдса Другие безразмерные параметры, имеющие динамическое значение 4.8. Поля течений, в которых силы инерции пренебрежимо малы Теория смазки Течение в приборе Хеле-Шоу Фильтрация через пористую среду Двумерное течение в угловой области Теоремы единственности и минимума диссипации энергии 4. 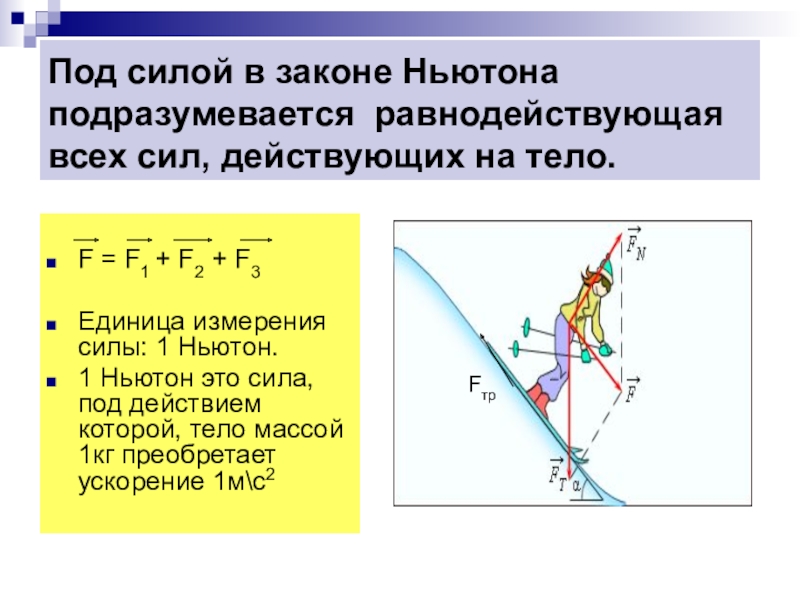9. Течение, вызываемое движением тела при малых числах Рейнольдса Сферическая капля в другой жидкости Тело произвольной формы 4.10. Уточненное уравнение Озеена для течения при малом числе Рейнольдса Твердая сфера Твердый круговой цилиндр 4.11. Вязкость разбавленной суспензии из малых частиц Сфера в чисто деформационном течении Повышенная скорость диссипации в несжимаемой суспензии Эффективная объемная вязкость жидкости, содержащей газовые пузырьки 4.12. Изменения в обтекании тел при возрастании числа Рейнольдса от 1 до 100 5. ТЕЧЕНИЕ ПРИ БОЛЬШОМ ЧИСЛЕ РЕЙНОЛЬДСА: ЭФФЕКТЫ ВЯЗКОСТИ Интенсификация завихренности при растяжении вихревых линий 5.3. Теорема Кельвина о циркуляции и законы распространения завихренности для невязкой жидкости Сохраняемость безвихревого движения 5.4. Возникновение завихренности при движениях жидкости из состояния покоя 5.5. Установившиеся течения, в которых диффузия завихренности, возникающей на твердой границе, ограничивается за счет конвекции (б) Течение в окрестности критической точки на твердой границе (в) Центробежное течение жидкости, вызванное вращающимся диском 5. m О расчетах установившегося пограничного слоя на движущемся в жидкости теле 5.10. Отрыв пограничного слоя 5.11. Течение при установившемся движении тел в жидкости Течение без отрыва пограничного слоя Течение с отрывом 5.12. Струи, свободные слои смешения и следы Свободные слои смешения Следы 5.13. Колеблющиеся пограничные слои Демпфирующая сила, действующая на колеблющееся тело Установившееся вторичное течение, обусловленное колеблющимся пограничным слоем Приложения теории установившегося вторичного течения 5.14. Течения со свободными поверхностями Сопротивление сферического газового пузырька при его установившемся всплывании в жидкости Затухание волн на поверхности тяжелой жидкости 5.15. Примеры применения теоремы о количестве движения Внезапное расширение трубы 6. ТЕОРИЯ БЕЗВИХРЕВОГО ТЕЧЕНИЯ И ЕЕ ПРИЛОЖЕНИЯ 6.2. Общие свойства безвихревого течения Интегрирование уравнения движения Выражения для кинетической энергии через интегралы по поверхности Теорема Кельвина о минимуме энергии Точки максимума скорости q и минимума давления р Локальное изменение величины скорости 6. 3. Установившееся течение; некоторые приложения теоремы Бернулли и теоремы о количестве движения Истечение из круглого отверстия в открытом сосуде Водослив через плотину Удар струи жидкости о плоскую стенку 6.4. Общие свойства безвихревого течения, обусловленного движущимся твердым телом Кинетическая энергия жидкости Сила, действующая на тело при его поступательном движении Реакция на ускорение 6.5. Использование комплексного потенциала в случае двумерного безвихревого течения Конформное преобразование плоскости течения Преобразование границы в бесконечную прямую Теорема об окружности 6.6. Двумерное безвихревое течение, вызванное движущимся цилиндром с циркуляцией Поступательное движение эллиптического цилиндра Сила и момент, действующие на цилиндр в установившемся поступательном движении 6.7. Двумерные профили Возникновение циркуляции вокруг профиля и обоснование гипотезы Жуковского Профили, получаемые преобразованием окружности Профили Жуковского Движение системы точечных вихрей 6. 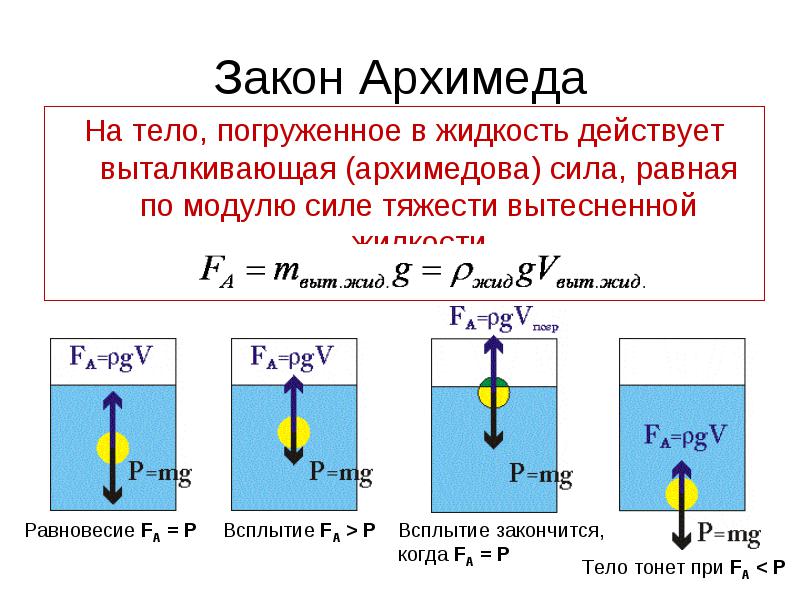8. Осесимметричное безвихревое течение, вызванное движением тела Движущаяся сфера Эллипсоиды вращения Тела, образуемые источниками на оси симметрии Полубесконечные тела 6.9. Приближенные результаты для тонких тел Тонкие тела в двух измерениях Тонкие профили в двух измерениях 6.10. Импульсивное движение жидкости Удар тела о свободную поверхность жидкости 6.11. Большие пузыри газа в жидкости Пузырь, поднимающийся в вертикальной трубе Расширяющийся сферический пузырь 6.12. Кавитация в жидкости Примеры образования каверн в неустановившемся течении Схлопывание нестационарной каверны Стационарные каверны 6.13. Теория течений со свободными линиями тока, установившиеся струи и каверны Двумерная струя, вытекающая на отверстия Двумерное обтекание пластины с каверной под давлением окружающей среды Стационарные каверны, присоединенные к телам в потоке жидкости 7. ВИХРЕВОЕ ТЕЧЕНИЕ ЭФФЕКТИВНО НЕВЯЗКОЙ ЖИДКОСТИ Самоиндуцированное движение вихревой нити 7. 2. Течение неограниченной жидкости, покоящейся на бесконечности Полная кинетическая энергия жидкости Течение с круговыми вихревыми линиями Вихревые кольца 7.3. Двумерное течение неограниченной жидкости, покоящейся на бесконечности Интегральные инварианты распределения завихренности 7.4. Установившееся двумерное вихревое движение жидкости Постоянная завихренность в области, ограниченной снаружи Жидкость, вращающаяся на бесконечности как твердое тело Жидкость, совершающая в бесконечности простой сдвиг 7.5. Установившееся осесимметричное течение с закруткой Влияние изменения поперечного сечения трубы на течение закрученной жидкости Влияние изменения внешней скорости на изолированный вихрь 7.6. Жидкие системы, вращающиеся как целое Установившееся течение при малом числе Россби Распространение волн во вращающейся жидкости Течение, обусловленное движением тела вдоль оси вращения Геострофическое течение Течение над неровной поверхностью Земли Планетарные волны 7. 8. Вихревая система крыла самолета Крылья большого относительного размаха и теория «несущей линии» Спутная вихревая система далеко за крылом Крылья с большой стреловидностью ПРИЛОЖЕНИЕ 1. Измеренные значения некоторых физических параметров различных жидкостей ПРИЛОЖЕНИЕ 2. Выражения для некоторых векторных дифференциальных величин в ортогональных криволинейных координатах СПИСОК ЛИТЕРАТУРЫ

Формула силы тяжести — справочник для студентов и школьников

ОПРЕДЕЛЕНИЕ

Сила тяжести, действующая на тело, расположенную на поверхности Земли, равна массе тела, умноженной на константу

Здесь F — сила тяжести, m — масса, g — ускорение силы тяжести.

Единицей измерения силы является Н (Ньютон).

Для тела, которое находится на определенной высоте над Землей, силу тяжести можно найти по формуле:

Здесь G – сила тяжести постоянная, m — масса тела, M — масса Земли , r — высота тела над Землей, R — радиус Земли

Из-за того, что Земля имеет сплюснутую форму, т. Е. Ее радиус не везде одинаковый, ускорение силы тяжести изменяется в зависимости от географической широты, от 9,832 на экваторе до 9,78 у полюсов. 9.8 — его среднее значение.

Сила тяжести действует на тело, имеющее опору или подвеску. Если тело их не имеет, то есть оно находится в состоянии свободного падения, тогда они говорят, что тело находится в невесомости. Сила тяжести всегда направлена к центру Земли.

Примеры решения проблем на тему «Гравитация»

ПРИМЕР 1

Задача

Найти силу тяжести тел весом 1 кг и 10 кг, расположенных на поверхности Земли.

Решение.

Подставим массы в формулу

Ответ

Силы тяжести — 9,8 и 98 ньютонов.

ПРИМЕР 2

Задача

Тело массы m расположено на высоте r над Землей. Сколько раз сила притяжения изменяется, когда она поднимается до высоты

Решение

На высоте сила тяжести была:

На высоте сила тяжестистала:

Найти соотношение сил:

Ответ.

Сила тяжести изменится раз.

Физика

166

Реклама и PR

31

Педагогика

80

Психология

72

Социология

7

Астрономия

9

Биология

30

Культурология

86

Экология

8

Право и юриспруденция

36

Политология

13

Экономика

49

Финансы

9

История

16

Философия

8

Информатика

20

Право

35

Информационные технологии

6

Экономическая теория

7

Менеджент

719

Математика

338

Химия

20

Микро- и макроэкономика

1

Медицина

5

Государственное и муниципальное управление

2

География

542

Информационная безопасность

2

Аудит

11

Безопасность жизнедеятельности

3

Архитектура и строительство

1

Банковское дело

1

Рынок ценных бумаг

6

Менеджмент организации

2

Маркетинг

238

Кредит

3

Инвестиции

2

Журналистика

1

Конфликтология

15

Этика

9

Длина волны Формула потенциальной энергии Формула кинетической энергии Формула силы трения Гравитация и инерция. Принципы эквивалентности

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю  Политику  конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Определение равнодействующей силы

Если вы читали уроки 1 и 2, то должны хорошо понимать первый закон движения Ньютона.

Объект в состоянии покоя имеет тенденцию оставаться в состоянии покоя, а объект в движении имеет тенденцию оставаться в движении с той же скоростью и в том же направлении, если на него не действует неуравновешенная сила.

В формулировке первого закона Ньютона неуравновешенная сила относится к той силе, которая не становится полностью уравновешенной (или нейтрализуется) другими отдельными силами. Если либо все вертикальные силы (вверх и вниз) не компенсируют друг друга, и/или все горизонтальные силы не компенсируют друг друга, то существует неуравновешенная сила. Существование неуравновешенной силы для данной ситуации можно быстро понять, посмотрев на диаграмму свободного тела для этой ситуации. Диаграммы свободного тела для трех ситуаций показаны ниже. Обратите внимание, что фактические величины отдельных сил указаны на диаграмме.

 

В каждой из вышеперечисленных ситуаций присутствует неуравновешенная сила. Обычно говорят, что в каждой ситуации на объект действует результирующая сила . Чистая сила представляет собой векторную сумму всех сил, действующих на объект. Другими словами, результирующая сила представляет собой сумму всех сил, принимая во внимание тот факт, что сила является вектором, и две силы равной величины и противоположного направления нейтрализуют друг друга.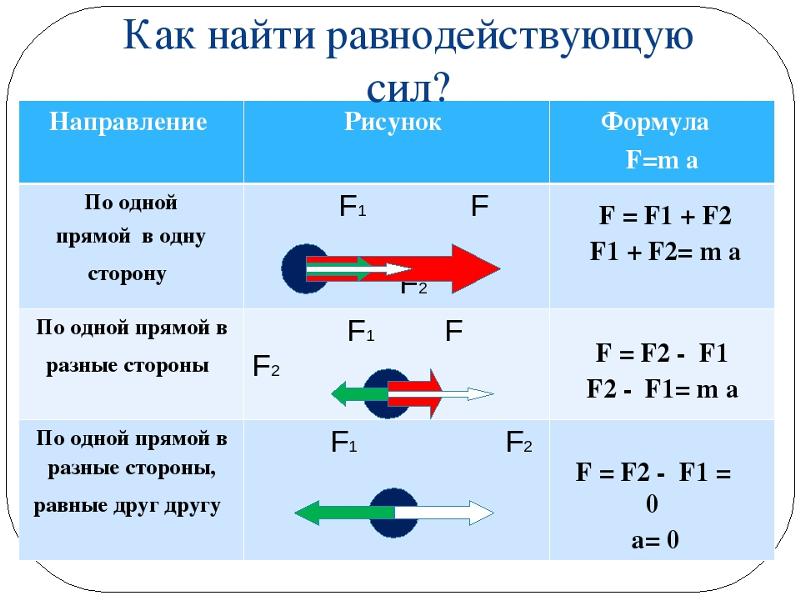 На этом этапе правила суммирования векторов (например, векторов силы) будут оставаться относительно простыми. Обратите внимание на следующие примеры суммирования двух сил:

 

Обратите внимание на приведенную выше диаграмму, что нисходящий вектор обеспечивает частичную или полную компенсацию восходящего вектора. А левый вектор обеспечит частичную или полную компенсацию правого вектора. Сложение векторов силы может быть выполнено таким же образом, чтобы определить результирующую силу (то есть векторную сумму всех отдельных сил). Рассмотрим три приведенные ниже ситуации, в которых результирующая сила определяется путем суммирования векторов отдельных сил, действующих на объекты.

 

Суммарная сила вызывает ускорение

Как упоминалось ранее, результирующая сила (т. е. неуравновешенная сила) вызывает ускорение. В предыдущем разделе обсуждались несколько способов представления ускоренного движения (графики положение-время и скорость-время, диаграммы бегущей строки, данные скорости-времени и т. д.). Объедините свое понимание ускорения и недавно полученные знания о том, что результирующая сила вызывает ускорение, чтобы определить, существует ли результирующая сила в следующих ситуациях. Нажмите на кнопку, чтобы просмотреть ответы.

 

Описание движения	Net Force: да или нет?

 

Проверьте свое понимание

1. Диаграммы свободного тела для четырех ситуаций показаны ниже. Для каждой ситуации определите результирующую силу, действующую на объект. Нажмите на кнопки, чтобы просмотреть ответы.

2. Диаграммы свободного тела для четырех ситуаций показаны ниже. Чистая сила известна для каждой ситуации. Однако величины некоторых отдельных сил неизвестны. Проанализируйте каждую ситуацию в отдельности и определите величину неизвестных сил. Затем нажмите кнопку, чтобы просмотреть ответы.

 

Перейти к следующему уроку:

Уравнение движения | Определение, формула и факты

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• В этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Обзор недели
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.