Сила, действующая на проводник с током в магнитном поле. Закон Ампера
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Экспериментальное изучение магнитного взаимодействия показывает, что модуль силы Ампера пропорционален длине проводника с током, силе тока и зависит от ориентации проводника в магнитном поле.
Опыт показывает, что магнитное поле, вектор индукции которого направлен вдоль проводника с током, не оказывает влияния на ток. Поэтому модуль силы зависит лишь от модуля составляющей вектора магнитной индукции, перпендикулярной проводнику.
Закон Ампера заключается в следующем. Сила Ампера равна произведению магнитной индукции поля на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника:
Направление
силы ампера определяется по правилу
левой руки: если левую руку расположить
так, чтобы перпендикулярная составляющая
магнитной индукции входила в ладонь, а
четыре вытянутых пальца были направлены
по направлению тока, то отогнутый на 90
большой палец покажет направление силы,
действующей на отрезок проводника.
Магнитное взаимодействие проводников с током используется в Международной системе для определения единицы сила тока –ампера.
Ампер –сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывал бы между этими проводниками силу магнитного взаимодействия, равную Н на каждый метр длины.
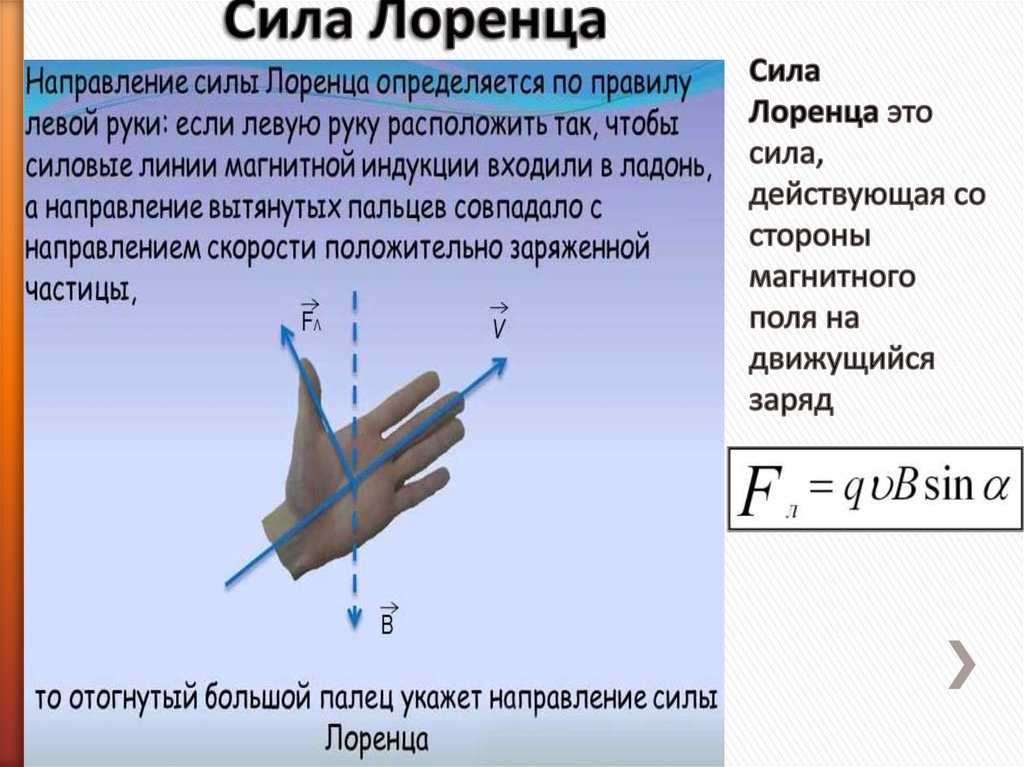
Действие магнитного поля на движущийся заряд. Сила Лоренца
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца.
Модуль силы Лоренца равен отношению модуля силы Ампера, действующей на участок проводника, к числу заряженных частиц в этом участке проводника:
Сила
Ампера равна ,
сила тока равна (см.
где — угол между векторами скорости и магнитной индукции.
Направление силы Лоренца определяют для положительного заряда по правилу левой руки. (Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону).
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. А, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.
Магнитные свойства вещества
Все вещества, помещенные в магнитное поле, намагничиваются, т. е. сами создают магнитное поле. Поэтому индукция магнитного поля в однородной среде отличается от индукции поля в вакууме.
Физическая величина, показывающая, во сколько раз индукция магнитного поля в однородной среде отличается по модулю от индукции магнитного поля в вакууме, называется магнитной проницаемостью:
Все
вещества в зависимости от их магнитной
проницаемости разделяют на ферромагнетики,
парамагнетики и диамагнетики.
К ферромагнетикам относятся железо, никель, кобальт и некоторые соединения этих металлов с другими элементами. У них значения магнитной проницаемости достигают тысяч единиц. Поэтому при внесении железного сердечника в катушку с током, индукция магнитного поля увеличивается во много раз.
К парамагнетикам относятся вещества, магнитная проницаемость которых немного больше единицы. (Платина, жидкий кислород)
К диамагнетикам можно отнести вещества с малой магнитной проницаемостью. Они ослабляют магнитное поле. (Серебро, свинец, кварц, висмут).
Ферромагнетизм
объясняется магнитными свойствами
электронов. Электрон эквивалентен
круговому току или вращающемуся
заряженному телу и поэтому обладает
собственным магнитным полем. В большинстве
кристаллов магнитные поля электронов
взаимно компенсируются благодаря
попарной антипараллельной ориентации
магнитных полей электронов. Лишь в
некоторых кристаллах, например в
кристалле железа, возникают условия
для параллельной ориентации собственных
магнитных полей электронов.
В результате
этого внутри кристалла ферромагнетика
возникают намагниченные области, которые
называются доменами. В отдельных
доменах магнитные поля имеют различные
направления и в большом кристалле
взаимно компенсируют друг друга. При
внесении ферромагнитного образца в
магнитное поле происходит упорядочение
ориентации магнитных полей отдельных
доменов.
С увеличением магнитной индукции внешнего поля возрастает степень упорядоченности ориентации отдельных доменов – магнитная индукция возрастает. При некотором значении индукции внешнего поля наступает полное упорядочение ориентации доменов, возрастание магнитной индукции прекращается. Это явление называется магнитным насыщением.
При вынесении ферромагнитного образца из внешнего магнитного поля значительная часть доменов сохраняет упорядоченную ориентацию – образец становится постоянным магнитом.
Упорядоченность
ориентации доменов в ферромагнетике
нарушается тепловыми колебаниями атомов
в кристалле.
Чем выше температура
кристалла, тем быстрее разрушается
порядок в ориентации доменов, вследствие
чего образец размагничивается.
Температура, выше которой вещество
перестает быть ферромагнетиком,
называется температурой Кюри.
Действие магнитного поля на проводник с током кратко
4.2
Средняя оценка: 4.2
Всего получено оценок: 272.
4.2
Средняя оценка: 4.2
Всего получено оценок: 272.
Магнитное взаимодействие
Французский физик Андре-Мари Ампер в 1820 г. обнаружил, что два проводника, по которым пропущен электрический ток, расположенные параллельно друг другу, притягиваются, если направления токов совпадают, и отталкиваются, если токи направлены в разные стороны.
Для объяснения этого явления Ампер ввел понятие магнитного поля, которое возникает вокруг любого движущегося электрического заряда. Магнитное поле непрерывно в пространстве и проявляет себя, оказывая силовое воздействие на другие движущиеся электрические заряды.
Предшественники Ампера пытались построить теорию магнитного поля по аналогии с электрическим полем с помощью магнитных зарядов с разными знаками (северным N и южным S). Однако, эксперименты показали, что отдельных магнитных зарядов в природе не существует. Магнитное поле возникает только в результате движения электрических зарядов.
Сила магнитного взаимодействия
Сила, действующая на проводник с током со стороны магнитного поля, была названа в честь первооткрывателя — силой Ампера. Эксперименты показали, что модуль силы Ампера F пропорционален длине проводника L и зависит от пространственного положения проводника в магнитном поле.
Для количественного описания действия магнитного поля на проводник с током была введена величина, названная магнитной индукцией B. Тогда сила Ампера будет равна:
$F = B*I*L$ (1),
где I — сила тока. Эта формула справедлива при вычислении модуля максимального значения силы Ампера, действующей на прямолинейный проводник в магнитном поле, вектор магнитного поля
$F = B*I*L*sinα$ (2).
Правило левой руки
Для определения направления вектора силы Ампера применяется “правило левой руки”.
Рис. 2. Правило левой руки для определения направления силы Ампера.Левая рука располагается так, чтобы пальцы ладони (все кроме большого) указывали направление тока в проводнике. Затем плоскость ладони устанавливается перпендикулярно плоскости, в которой находятся проводник с током и вектор магнитной индукции 
Вектор B должен входить в ладонь. Тогда большой палец левой руки, развернутый под прямым углом, укажет направление силы Ампера.
Единица измерения индукции
Единица индукции в системе СИ определяется как индукция такого магнитного поля, в котором на 1 м проводника при силе тока действует сила Ампера величиной 1 Н. Единица называется тесла (Тл).
$1 Тл = {1 Н\over {1 A*1 м}}$ (3).
Единица индукции названа в честь выдающегося сербского инженера, физика Николы Тесла (1856-1943 г.г.). Тесла изобрел электромеханические генераторы, высокочастотный трансформатор. Исследовал свойства токов высокой частоты, изобрел многофазный электродвигатель и системы передачи электроэнергии с помощью переменного тока. Тесла сформулировал основные принципы радиосвязи, изобрел мачтовую антенну для приемки и передачи радиосигналов.
Рис. 3. Портрет Никола Тесла.
Что мы узнали?
Итак, мы узнали что на проводник с током, помещенный в магнитное поле, действует сила Ампера.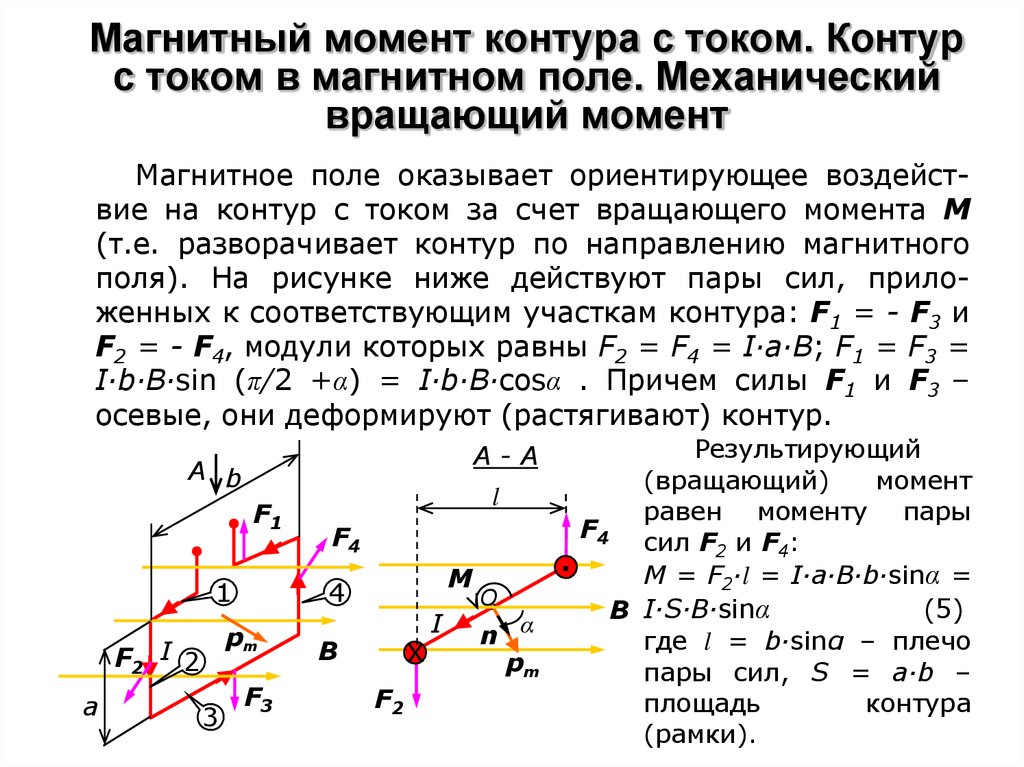
В статье рассказано кратко о действии магнитного поля на проводник с током. Дано определение понятия магнитной индукции. Приведены формулы для вычисления силы Ампера. Для определения направления силы Ампера дано описание “правила левой руки”.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Давид Мартиросов
9/10
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 272.
А какая ваша оценка?
22.7 Магнитное воздействие на проводник с током – Колледж физики, главы 1-17
22 Магнетизм
Магнитное воздействие на проводник с током
- Описать действие магнитной силы на проводник с током.
- Рассчитайте магнитную силу, действующую на проводник с током.
Поскольку обычно заряды не могут выйти из проводника, магнитная сила зарядов, движущихся в проводнике, передается самому проводнику.
Мы можем получить выражение для магнитной силы, действующей на ток, взяв сумму магнитных сил, действующих на отдельные заряды. (Силы складываются, поскольку они действуют в одном направлении.) Сила, действующая на отдельный заряд, движущийся со скоростью дрейфа vdvd, определяется выражением F=qvdBsinθF=qvdBsinθ. Принимая размер BB 12{B} {} за одинаковый по длине провода ll и равный нулю в других местах, общая магнитная сила, действующая на провод, равна F=(qvdBsinθ)(N)F=(qvdBsinθ)(N) размера 12{ F= ( ital «qv» rSub { size 8{d} } B»sin»θ ) ( N ) } {}, где NN size 12{N} {} — количество носителей заряда на отрезке провода длиной ll размера 12{l} {} . Теперь N=nVN=nV size 12{N= ital «nV»} {}, где nn size 12{n} {} — число носителей заряда в единице объема, а VV size 12{V} {} — объем провода в поле.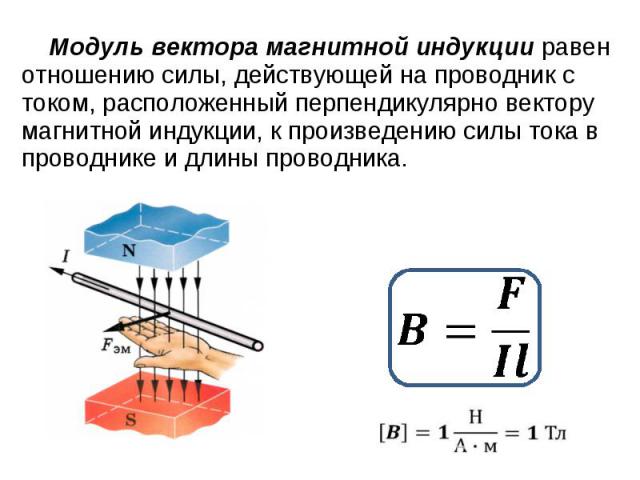
Учитывая, что V=AlV=Al размер 12{V= ital «Al»} {}, где AA размер 12{A} {} — площадь поперечного сечения провода, тогда сила на проводе равна F=(qvdBsinθ )(nAl)F=(qvdBsinθ)(nAl). Условия сбора,
F=(nqAvd)lBsinθ.F=(nqAvd)lBsinθ. size 12{F= ( ital «nqAv» rSub { size 8{d} } ) ital «lB»»sin»θ} {}
Поскольку nqAvd=InqAvd=I size 12{ ital «nqAv» rSub { size 8{d} } =I} {} (см. Current),
F=IlBsinθF=IlBsinθ размер 12{F= итал. “IlB””sin”θ} {}
— это уравнение для магнитной силы, действующей на длину ll провода с током II в однородном магнитном поле BB , как показано в [ссылка]. Если мы разделим обе части этого выражения на ll, то найдем, что магнитная сила на единицу длины провода в однородном поле равна Fl=IBsinθFl=IBsinθ size 12{ { {F} over {l} } = ital «IB» грех”θ} {}. Направление этой силы задается RHR-1, большим пальцем в направлении тока II размера 12{I}{}. Затем, с пальцами в направлении BB размера 12 {B} {}, перпендикуляр к ладони указывает в направлении FF размера 12 {F} {}, как в [ссылка].
Расчет силы магнитного поля на проводе с током: сильное магнитное поле
Рассчитайте силу на проводе, показанном в [ссылка], учитывая B=1,50 TB=1,50 T, размер 12{B=1 «.» «50» «T»} {}, l=5,00 смl=5,00 см размер 12{l=5 «.» «00»» см»} {} и I=20.0AI=20.0A размер 12{I=»20″ «.» 0 А} {}.
Стратегия
Силу можно найти с данной информацией, используя F=IlBsinθF=IlBsinθ размер 12{F= ital «IlB»”sin”θ} {} и отметив, что угол θθ размер 12{θ} {} между размером II 12{I} {} и размером BB 12{B} {} равно 90º90º, так что sinθ=1sinθ=1.
Решение
Ввод данных значений в F=IlBsinθF=IlBsinθ size 12{F= ital “IlB””sin”θ} {} дает
F=IlBsinθ=20,0 A0,0500 м1,50 T1. =IlBsinθ=20,0 A0,0500 м1,50 T1 . размер 12{F= ital «IlB»»sin»θ= левый («20» «. 0″ A» правый) левый (0 «.» «0500» «м» правый) левый (1 «.
» «50 ””T” справа ) слева (1 справа )} {}
Единицы для тесла: 1 T=NA⋅m1 T=NA⋅m size 12{“1 T”= {{N} over {A cdot m} } } {}; таким образом,
F=1,50 N.F=1,50 N. размер 12{F=1 «.» «50» «Н»} {}
Обсуждение
Это большое магнитное поле создает значительную силу на проводе небольшой длины.
Магнитная сила на проводниках с током используется для преобразования электрической энергии в работу. (Ярким примером являются двигатели — в них используются петли из проволоки, и они рассматриваются в следующем разделе.) Магнитогидродинамика (МГД) — это техническое название, данное умному приложению, в котором магнитная сила перекачивает жидкости без движущихся механических частей. (См. [ссылка].)
Магнитогидродинамика. Магнитная сила тока, проходящего через эту жидкость, может быть использована в качестве немеханического насоса. Сильное магнитное поле прикладывается к трубке, и ток проходит через жидкость под прямым углом к полю, в результате чего на жидкость действует сила, параллельная оси трубки, как показано на рисунке.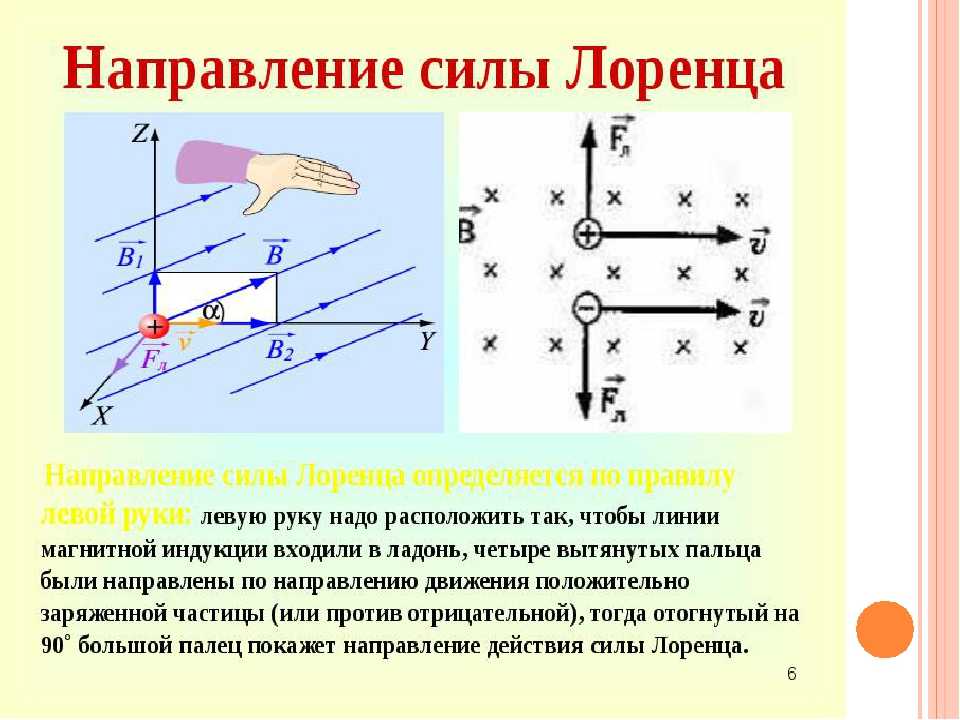
Отсутствие движущихся частей делает его привлекательным для перемещения горячего химически активного вещества, такого как жидкий натрий, используемый в некоторых ядерных реакторах. Экспериментальные искусственные сердца тестируются с использованием этой техники для перекачивания крови, возможно, для обхода неблагоприятных последствий механических насосов. (Однако на клеточные мембраны влияют большие поля, необходимые для МГД, что задерживает его практическое применение у людей.) Был предложен двигатель МГД для атомных подводных лодок, потому что он может быть значительно тише, чем обычные гребные двигатели. Сдерживающая ценность атомных подводных лодок основана на их способности скрыться и пережить первый или второй ядерный удар. По мере того, как мы медленно разбираем наши арсеналы ядерного оружия, подводные лодки будут выведены из эксплуатации последними из-за этой способности (см. [ссылка]). Существующие МГД-приводы тяжелые и неэффективные — требуется много доработок.
Разработка бесшумной подводной лодки была драматизирована в книге и фильме «Охота на Красный Октябрь ». - Магнитная сила, действующая на проводники с током, определяется выражением
F=IlBsinθ,F=IlBsinθ, размер 12{F= ital «IlB»”sin”θ} {}
где II размер 12{I} {} — ток, ll размер 12{l} {} — длина прямого проводника в однородном магнитном поле BB размера 12{B} {} и θθ размера 12{θ} {} — это угол между II размером 12{I} {} и BB размера 12{B} {} . Сила следует за RHR-1 большим пальцем в направлении II размера 12{I} {} .
Нарисуйте схему ситуации в [ссылка], показывающую направление электронов, несущих ток, и используйте RHR-1, чтобы проверить направление силы, действующей на провод.
Убедитесь, что направление силы в МГД-приводе, таком как в [ссылка], не зависит от знака зарядов, переносящих ток через жидкость.
Почему магнитогидродинамический привод лучше работает в морской воде, чем в пресной? Кроме того, зачем нужны сверхпроводящие магниты?
Что больше мешает показаниям компаса, переменный ток в вашем холодильнике или постоянный ток, когда вы заводите машину? Объяснять.
Каково направление магнитной силы на ток в каждом из шести случаев в [ссылка]?
(а) запад (слева)
(б) на страницу
(в) север (вверх)
(г) без сил
(д) восток (справа)
(е) юг (вниз)
Каково направление тока, на который действует магнитная сила, показанная в каждом из трех случаев в [ссылка], если предположить, что ток течет перпендикулярно BB размера 12{B} {}?
Каково направление магнитного поля, которое создает магнитную силу, показанную на токах в каждом из трех случаев в [ссылка], при условии, что размер BB 12{B} {} перпендикулярен размеру II 12{I} {}?
(a) на стр.
(b) запад (слева)
(c) вне стр.
(a) Какова сила на метр на молнию на экваторе, которая несет 20 000 А перпендикулярно Земле 3,00×10-5-T3,00×10-5-T размером 12{3 «.» «00» умножить на «10» rSup {размер 8{ – 5} } «-T»} {} поле? б) Каково направление силы, если течение направлено прямо вверх, а направление поля Земли строго на север, параллельно земле?
(a) Линия электропередачи постоянного тока для системы легкорельсового транспорта передает 1000 А под углом 30,0º30,0º к Земле размером 5,00×10−5-T5,00×10−5-T 12{5″.
«00» умножить на «10» rSup {размер 8{ – 5} } «-T»} {} поле. Какая сила действует на отрезке этой линии длиной 100 м? (b) Обсудите практические проблемы, которые это вызывает, если таковые имеются.
(а) 2,50 Н
(б) Это примерно полфунта силы на 100 м проволоки, что намного меньше веса самой проволоки. Поэтому особых опасений не вызывает.
Какая сила действует на воду в МГД-приводе с трубкой диаметром 25,0 см, если через трубку, перпендикулярную магнитному полю напряженностью 2,00 Тл, пропускают ток силой 100 А? (Относительно небольшой размер этой силы указывает на необходимость очень больших токов и магнитных полей для создания практических МГД-приводов.)
Проводник с током 30,0 А проходит между полюсами сильного магнита, перпендикулярного его полю, и испытывает силу 2,16 Н на 4,00 см провода в поле. Какова средняя напряженность поля?
1,80 т
(a) Участок кабеля длиной 0,750 м, по которому подается ток к стартеру автомобиля, образует угол 60º60º с полем Земли 5,50×10-5 Тл5,50×10-5 Тл.
Какова сила тока, когда на провод действует сила 7,00×10-3Н7,00×10-3Н? б) Если пропустить провод между полюсами сильного подковообразного магнита и подвергнуть его 5,00 см воздействию поля силой 1,75 Тл, какая сила будет действовать на этот отрезок провода?
а) Чему равен угол между проводом, по которому течет ток 8,00 А, и полем 1,20 Тл, в котором он находится, если на 50 см провода действует магнитная сила 2,40 Н? (b) Какова сила, действующая на проволоку, если ее повернуть на угол 90º90º размером 12{«90″°} {} с полем?
(a) 30º30º размер 12{“30″°} {}
(b) 4,80 Н
Сила, действующая на прямоугольную проволочную петлю в магнитном поле в [ссылка], может использоваться для измерения напряженности поля. Поле однородно, и плоскость петли перпендикулярна полю. а) Как направлена магнитная сила, действующая на петлю? Обоснуйте утверждение, что силы на сторонах петли равны и противоположны, независимо от того, какая часть петли находится в поле, и не влияют на результирующую силу, действующую на петлю.
(b) Если используется ток 5,00 А, какова сила на тесла на петле шириной 20,0 см?
5.6 Магнитное воздействие на проводник с током
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описать действие магнитной силы на проводник с током
- Расчет силы магнитного поля на проводнике с током
Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:
- 3.C.3.1 Учащийся может использовать правила правой руки для анализа ситуации, включающей проводник с током и движущийся электрически заряженный объект, чтобы определить направление магнитной силы, действующей на заряженный объект из-за магнитное поле, создаваемое проводником с током. (СП 1.
4)
4) Поскольку обычно заряды не могут покинуть проводник, магнитная сила, действующая на заряды, движущиеся в проводнике, передается самому проводнику.
Рис. 5.22 Магнитное поле воздействует на провод с током в направлении, заданном RHR-1 (то же направление, что и на отдельные движущиеся заряды). Эта сила легко может быть достаточно большой, чтобы сдвинуть провод, потому что типичные токи состоят из очень большого количества движущихся зарядов.
Мы можем получить выражение для магнитной силы, действующей на ток, взяв сумму магнитных сил, действующих на отдельные заряды. (Силы складываются, поскольку они действуют в одном направлении.) Сила, действующая на отдельный заряд, движущийся со скоростью дрейфа vdvd, определяется как F=qvdBsinθ.F=qvdBsinθ. Принимая размер BB 12{B} {} равным по длине провода ll и равным нулю в других местах, тогда общая магнитная сила на проводе равна F=(qvdBsinθ)(N),F=(qvdBsinθ)(N),size 12{F= \( ital «qv» rSub { size 8{d} } B»sin»θ \) \( N \) } {} где NN size 12{N} {} — число носителей заряда в отрезок провода длиной ll размер 12{l} {} .
Теперь N=nV,N=nV,size 12{N= ital «nV»} {}, где nn size 12{n} {} — число носителей заряда в единице объема, а VV size 12{V} {} – объем проволоки в поле. Отметив, что V=Al,V=Al,размер 12{V= ital «Al»} {}, где размер AA 12{A} {} – площадь поперечного сечения провода, тогда сила, действующая на провод, равна F= (qvdBsinθ)(nAl).F=(qvdBsinθ)(nAl). Условия сбора,
5,15 F=(nqAvd)lBsinθ.F=(nqAvd)lBsinθ. size 12{F= \( ital «nqAv» rSub { size 8{d} } \) ital «lB»»sin»θ} {}
Поскольку nqAvd=InqAvd=I size 12{ ital «nqAv» rSub { size 8{d} } =I} {} (см. Current),
5.16 F=IlBsinθF=IlBsinθ size 12{F= ital «IlB» «sin»θ} {}
— это уравнение для магнитной силы, действующей на длину ll провода, по которому течет ток II в однородном магнитном поле BB , как показано на рис. 5.23. Если мы разделим обе части этого выражения на l,l, то получим, что магнитная сила, приходящаяся на единицу длины провода в однородном поле, равна Fl=IBsinθ.Fl=IBsinθ.size 12{ { {F} over {l} } = ital «IB»»sin»θ} {} Направление этой силы задается RHR-1, большим пальцем в направлении текущего размера I.
I. 12{I} {} Затем пальцами в направлении B ,B,размер 12{B} {} перпендикуляр к ладони указывает в направлении F,F,размер 12{F} {}, как показано на рисунке 5.23.
Рис. 5.23 Сила, действующая на проводник с током в магнитном поле, равна F=IlBsinθ.F=IlBsinθ.size 12{F= ital «IlB»»sin»θ} {} Ее направление задается RHR-1.
Пример 5.4 Расчет силы магнитного поля на проводе с током: сильное магнитное поле
Рассчитайте силу на проводе, показанном на рисунке 5.22, при B=1,50 Тл, B=1,50 Тл, размере 12{B=1″. » «50» «T»} {}l=5,00 см,l=5,00 см,размер 12{l=5 «.» «00»» см»} {} и I=20.0A.I=20.0A.size 12{I=»20″ «.» 0 А} {}
Стратегия
Силу можно найти с данной информацией, используя F=IlBsinθF=IlBsinθ размер 12{F= ital «IlB»»sin»θ} {} и отметив, что угол θθ размер 12{θ} {} между II размером 12{I} {} и BB размером 12{B} {} составляет 90º, 90º, так что sinθ=1.sinθ=1.
Решение
Ввод заданных значений в F=IlBsinθF=IlBsinθ size 12{F= ital «IlB»»sin»θ} {} дает
5,17 F=IlBsinθ=20,0 T A0,0500 м1.
F=IlBsinθ=20,0 A0,0500 m1,50 T1 . размер 12{F= ital «IlB»»sin»θ= левый («20» «.» 0″ A» правый) левый (0 «.» «0500» «м» правый) левый (1 «.» «50 «» Т» правый ) левый (1 правый )} {}
Тесла: 1 T=NA⋅м; 1 T=NA⋅м; размер 12{«1 T»= {{N} над {A cdot m} } } {} таким образом,
5,18 F=1,50 N.F=1,50 N. размер 12{F=1 «.» «50» «N»} {}
Обсуждение
Это большое магнитное поле создает значительную силу на проводе небольшой длины.
Сила магнитного поля, действующая на проводники с током, используется для преобразования электрической энергии в работу. Ярким примером являются двигатели — в них используются петли из проволоки, и они рассматриваются в следующем разделе. Магнитогидродинамика (МГД) — это техническое название умного приложения, в котором магнитная сила перекачивает жидкости без движущихся механических частей. (См. рис. 5.24.)
Рис. 5.24 Магнитогидродинамика. Магнитная сила тока, проходящего через эту жидкость, может быть использована в качестве немеханического насоса.
К трубке приложено сильное магнитное поле, и ток проходит через жидкость под прямым углом к полю, в результате чего на жидкость действует сила, параллельная оси трубки, как показано на рисунке. Отсутствие движущихся частей делает его привлекательным для перемещения горячего химически активного вещества, такого как жидкий натрий, используемый в некоторых ядерных реакторах. Экспериментальные искусственные сердца тестируются с использованием этой техники для перекачивания крови, возможно, для обхода неблагоприятных последствий механических насосов. (Однако на клеточные мембраны влияют большие поля, необходимые для МГД, что задерживает его практическое применение у людей.) Был предложен двигатель МГД для атомных подводных лодок, потому что он может быть значительно тише, чем обычные гребные двигатели. Сдерживающая ценность атомных подводных лодок основана на их способности скрыться и пережить первый или второй ядерный удар. По мере того, как мы постепенно разбираем наши арсеналы ядерного оружия, подводные лодки будут выведены из эксплуатации последними из-за этой способности (см.
